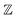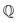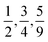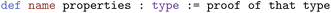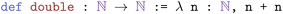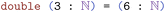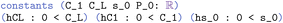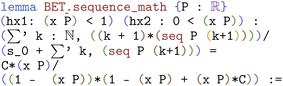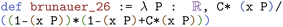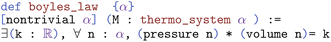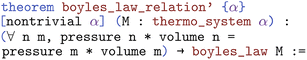Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formalizing chemical physics using the Lean theorem prover†
Maxwell P.
Bobbin
a,
Samiha
Sharlin
a,
Parivash
Feyzishendi
a,
An Hong
Dang
a,
Catherine M.
Wraback
a and
Tyler R.
Josephson
 *ab
*ab
aDepartment of Chemical, Biochemical, and Environmental Engineering, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA. E-mail: tjo@umbc.edu
bDepartment of Computer Science and Electrical Engineering, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA
First published on 16th November 2023
Abstract
Interactive theorem provers are computer programs that check whether mathematical statements are correct. We show how the mathematics of theories in chemical physics can be written in the language of the Lean theorem prover, allowing chemical theory to be made even more rigorous and providing insight into the mathematics behind a theory. We use Lean to precisely define the assumptions and derivations of the Langmuir and BET theories of adsorption. We can also go further and create a network of definitions that build off of each other. This allows us to define a common basis for equations of motion or thermodynamics and derive many statements about them, like the kinematic equations of motion or gas laws such as Boyle's law. This approach could be extended beyond chemistry, and we propose the creation of a library of formally-proven theories in all fields of science. Furthermore, the rigorous logic of theorem provers complements the generative capabilities of AI models that generate code; we anticipate their integration to be valuable for automating the discovery of new scientific theories.
1 Introduction
Theoretical derivations in the scientific literature are typically written in a semi-formal fashion, and rely on human peer reviewers to catch mistakes. When these theories are implemented in software, the translation from mathematical model to executable code also requires humans to catch errors. This reflects the gap between mathematical equations describing models in science and the software written to encode these.1 This occurs because the computer doesn't understand relationships among the scientific concepts and mathematical objects under study, it simply executes the code given it. Here, we recommend an alternative: interactive theorem provers that enable the mathematics and programming of science to be expressed in a rigorous way, with the logic checked by the computer.1.1 Theorem provers for chemical theory
Interactive theorem provers are a type of computer program used for the creation of formal proofs or derivations, which are a sequence of logical deductions used to prove a theorem‡ is correct.2 They provide a way to write a proof step by step, while the computer verifies each step is logically correct.3–8 Formal proofs are used extensively in mathematics to prove various theories. On the other hand, scientific theory tends to use informal proofs when deriving its theories, since they are easier to write and understand (see Table 1).| Hand-written proofs | Formal proofs |
|---|---|
| Informal syntax | Strict, computer language syntax |
| Only for human readers | Machine-readable and executable |
| Might exclude information | Cannot miss assumptions or steps |
| Might contain mistakes | Rigorously verified by computer |
| Requires human to proofread | Automated proof checking |
| Easy to write | Challenging to write |
Scientists are generally familiar with computer algebra systems (CAS) that can symbolically manipulate mathematical expressions (see Table 3). These systems include SymPy9 and Mathematica.12 These systems are used frequently for scientific applications but come at the cost of being unsound, meaning they can have false conclusions.
Theorem provers are more rigorous than computer algebra systems, because they require computer-checked proofs before permitting operations, thereby preventing false statements from being proven. For example, a × b = b × a is true when a and b are scalars, but A × B ≠ B × A when A and B are matrices. CAS impose special conditions to disallow A × B = B × A,9 whereas theorem provers only allow changes that are proven to be valid. Theorem provers construct all of their math from a small, base kernel of mathematical axioms, requiring computer-checked proofs for objects constructed from the axioms. Even the most complicated math can be reduced back to that kernel. Since this kernel is small, verifying it by human experts or with other tools is manageable. Then, all higher-level math built and proved from the kernel is just as trustworthy. This contrasts with how CAS represent and introduce mathematics; because proofs are not required when high-level math is introduced, mistakes could enter at any level, and would require humans to catch and debug them10 (see Table 2).
Historically, interactive theorem provers have been used to logically connect advanced math theorems to the foundational axioms of mathematics.14–19 Before computers, this “axiomatization” of mathematics was developed by hand, in works like Principia Mathematica by Alfred North Whitehead and Bertrand Russell20 – the aim is to write down a minimal list of fundamental assumptions (axioms), and then systematically derive all of mathematics from those axioms. Computers play a key role in modern formalization efforts because they can store and verify massive libraries of interconnected theorems collaboratively written by hundreds of mathematicians.21
An analogous program to “axiomatize” physics was famously articulated as Hilbert's sixth problem.22 Recent reviews have discussed progress and unsolved questions on this “endless road” to describe how all of physics can be derived from a minimal set of axioms.23,24 Our vision is somewhat distinct from this – we are inspired by Paleo's ideas for formalizing physics theories25as a collection of proofs, instead of aiming to represent science as a single edifice emerging from one set of axioms (though this structure may emerge in the future). In particular, we ask “How can we formally represent a collection of proofs/derivations using an interactive theorem prover?”
Theorem provers have previously been used to formalize derivations in physics: theorems from Newton's Principia,26,27 versions of relativity theory,28,29 electromagnetic optics,30 and geometrical optics31 have been described and proved using proof assistants. Artificial intelligence tools for scientific discovery have also used theorem provers in designing optical quantum experiments,32 as well as for rediscovering and deriving scientific equations from data and background theory.33
Here we focus on formalizing fundamental theories in the chemical sciences. Progress toward axiomatizing thermodynamics began with Carathéodory in 1909,34 with recent developments by Lieb and Yngvason.35 But broadly, these questions have not been addressed using theorem provers to check the mathematics, which have seen limited use in the chemical sciences. One notable application by Bohrer36 uses a proof assistant that reasons about differential equations and control algorithms37 to describe and prove properties of chemical reactors.
1.2 The Lean theorem prover
We have selected the Lean theorem prover38 for its power as an interactive theorem prover, the coverage of its mathematics library, mathlib,39 and the supportive online community of Lean enthusiasts40 with an aim to formalize the entire undergraduate math curriculum.21,41 Interesting projects in modern mathematics have emerged from its foundations, including Perfectoid Spaces,42 Cap Set Problem43 and Liquid Tensor44 have garnered attention in the media.45 A web-based game, the Natural Number Game,46 has been widely successful in introducing newcomers to Lean. As executable code, Lean proofs can be read by language modeling algorithms that find patterns in math proof databases, enabling automated proofs of formal proof statements, including International Math Olympiad problems.47,48We anticipate that Lean is expressive enough to formalize diverse and complex theories across quantum mechanics, fluid mechanics, reaction rate theory, statistical thermodynamics, and more. Lean gets its power from its ability to define mathematical objects and prove their properties, rather than just assuming premises for the sake of individual proofs. Lean is based on Type theory49,50 where both mathematical objects and the relation between them are modeled with types (see Fig. S1 in the ESI†). Everything in Lean is a term of a Type, and Lean checks to make sure that the Types match. Natural numbers, real numbers, functions, Booleans, and even proofs are types; examples of terms with these types include the number 1, Euler's number, f(x) = x2, TRUE, and the proof of BET theory, respectively. Lean is also expressive enough to allow us to define new types, just like mathematicians do,38 which allows us to define specific scientific theories and prove statements about them.
In this paper, we show how formalizing chemical theories may look, by demonstrating the tools of Lean through illustrative proofs in the chemical sciences. First, we introduce variables, types, premises, conjectures, and proof steps through a simple derivation of the Langmuir adsorption model. Next, we show how functions and definitions can be used to prove properties of mathematical objects by revising the Langmuir adsorption model through definitions and showing it has zero loading at zero pressure. Finally, we turn to more advanced topics, such as using geometric series to formalize the derivation of the BET equation and using structures to define and prove relationships in thermodynamics and motion.
2 Methods
Lean has a small kernel, based on dependent type theory,49,50 with just over 6000 lines of code that allows it to instantialize a version of the Calculus of Inductive Constructions (CoIC).51,52 The strong normalizing characteristic of the CoIC53 creates a robust programming language that is consistent. The CoIC creates a constructive foundation for mathematics allowing the entire field of mathematics to be built off of just 6000 lines of code.In Section 3 we outline the proofs formalized using Lean version 3.51.1. We host proofs on a website that provides a semi-interactive platform connecting to the Lean codes in our GitHub repository  (https://atomslab.github.io/LeanChemicalTheories/). An extended methods section introducing Lean is in the ESI† Section 5.1.
(https://atomslab.github.io/LeanChemicalTheories/). An extended methods section introducing Lean is in the ESI† Section 5.1.
3 Formalized proofs
3.1 Langmuir adsorption: introducing Lean syntax and proofs
We begin with an easy proof to introduce Lean and the concept of formalization. The Langmuir adsorption model describes the loading of adsorbates onto a surface under isothermal conditions.54 Several derivations have been developed;54–57 here we consider the original kinetic derivation.54 First, we present a derivation of the Langmuir model given by the eqn (6), as LaTeX equations, then transfer this into Lean and rigorously prove it. We also discuss how these proofs can be improved to be more robust.The Langmuir model assumes that all sites are thermodynamically equivalent, the system is at equilibrium, and that adsorption and desorption rates are first order. The adsorption and desorption rates are given by eqn (1) and eqn (2), respectively.
| rad = kadpA[S] | (1) |
| rd = kd[Aad] | (2) |
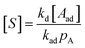 | (3) |
Using the site balance [S0] = [S] + [Aad], where [S0] represents the total concentration of available sites, we arrive at eqn (4).
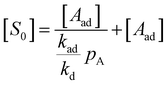 | (4) |
We can rearrange eqn (4) into, eqn (5).§
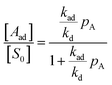 | (5) |
Using the definition of the fraction of adsorption, 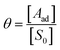 , and the definition of the equilibrium constant,
, and the definition of the equilibrium constant, 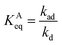 , we arrive at the familiar Langmuir absorption equation, eqn (6).
, we arrive at the familiar Langmuir absorption equation, eqn (6).
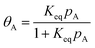 | (6) |
This informal proof is done in natural language, and it doesn't explicitly make clear which equations are premises to the proof and which are intermediate steps. While the key steps from the premises to the conclusion are shown, the fine details of the algebra are excluded. In contrast, Lean requires premises and conjecture to be precisely defined and requires that each rearrangement and cancellation is shown or performed computationally using a tactic. The next part shows how this proof is translated into Lean.
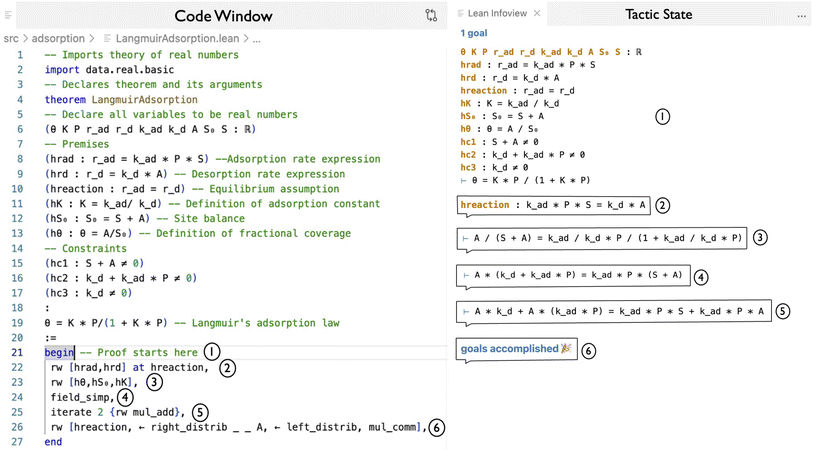
As shown in Fig. 1, every premise must be explicitly stated in Lean, along with the final conjecture and proof tactics used to show that the conjecture follows from the premises. Lean is an interactive theorem prover, meaning that the user is primarily responsible for setting up the theorem and writing the proof steps, while Lean continuously checks the work and provides feedback to the user. The central premises of the proof are expressions of adsorption rate (hrad), desorption rate (hrd), the equilibrium relation (hreaction), and the adsorption site balance (hS0). Additional premises include the definition of adsorption constant (hK) and surface coverage (hθ) from the first four premises, as well as mathematical constraints (hc1, hc2, and hc3) that appear during the formalization. The model assumes the system is in equilibrium, so the adsorption rate, rad = k_ad × P × S and desorption rate, rd = k_d × A are equal to each other, where kad and kd are the adsorption and desorption rate constant respectively, S is concentration of empty sites, and A is the concentration of sites occupied by A. After begin, a sequence of tactics rearranges the goal state until the conjecture is proved. Note when performing division, Lean is particular to require that the denominator terms are nonzero.
An interesting part of the proof is that only certain variables or their combinations are required to be not zero. When building this proof, Lean imports the real numbers and the formalized theorems and tactics for them in mathlib. Lean does not permit division by zero, and it will flag issues when a number is divided by another number that could be zero. Consequently, we must include additional hypotheses hc1–hc3 in order to complete the proof. These provide the minimum mathematical requirements for the proof; more strict constraints requiring rate constants and concentrations to be positive would also suffice. These ambiguities are better addressed by using definitions and structures, which enable us to prove properties about the object. Nonetheless, this version of the Langmuir proof is still a machine-readable, executable, formalized proof.
Though this is a natural way to write the proof, we can condense the premises by using local definitions. For instance, the first two premises hrad and hrd can be written into hreaction to yield k_ad × P × S = k_d × A and we can also write expressions of hθ and hK in the goal statement. While hrad, hrd, hθ, and hK each have scientific significance, in this proof, they are just combinations of real numbers. Alternative versions of this proof are described in ESI Section 5.2.1.†
3.2 Langmuir revisited: introducing functions and definitions in Lean
Functions in Lean are similar to functions in imperative programming languages like Python and C, in that they take in arguments and map them to outputs. However, functions in Lean (like everything in Lean) are also objects with properties that can be formally proved.Formally, a function is defined as a mapping of one set (the domain) to another set (the co-domain). The notation for a function is given by the arrow “→”. For instance, the function, conventionally written as Y = f(X) or Y(X), maps from set X to set Y is written as X → Y in arrow notion.¶
Importantly, the arrow “→” is also used to represent the conditional statement (if-then) in logic, but this is not a duplication of syntax. Because everything is a term of Type in Lean, functions map type X to type Y; when each type is a proposition, the resulting function is an if-then statement.
As stated in the introduction, Lean's power comes from the ability to define objects globally, not just postulate them for the purpose of local proof. When a mathematical object is formally defined in Lean, multiple theorems can be written about it with certainty that all proofs pertain to the same object. In Lean, we use def to define new objects and then prove statements about these objects. The def command has three parts: the arguments it takes in (the properties of the object), the type of the output, and the proof that the object has such a type. In Lean:
For instance, we can define a function that doubles a natural number:
The λ symbol comes from lambda calculus and is how an explicit function is defined. After the lambda symbol is the variable of the function, n with type 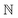 . After the comma is the actual function. By hand, we would write this as f(n) = n + n. This function doubles any natural number, as the name suggests. We could use it, for example, to show:
. After the comma is the actual function. By hand, we would write this as f(n) = n + n. This function doubles any natural number, as the name suggests. We could use it, for example, to show:
In the previous section, we showed an easy-to-read derivation of Langmuir adsorption, and in ESI Section 5.2.1,† we improved the proof using local definitions. Here, we improve it further by defining the Langmuir model as an object in Lean and then showing the kinetic derivation of that object. This way, the object defining the single-site Langmuir model can be reused in subsequent proofs, and all are certain to refer to the same object.
We define the model as a function that takes in pressure as a variable. Given a pressure value, the function will compute the fractional occupancy of the adsorption sites. In Lean, this looks like  (https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_single_site_model):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_single_site_model):
The λ symbol comes from λ-calculus58 and is one way to construct functions. It declares that P is a real number that can be specified. When the real number is specified, it will take the place of P in the equation. The definition also requires the equilibrium constant to be specified.||
With this, the kinetic derivation of Langmuir can be set up in Lean like this  (https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_single_site_kinetic_derivation):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_single_site_kinetic_derivation):
This derivation is almost exactly like the proof in ESI Section 5.2.1; the only difference is the use of the Langmuir model as an object. After the langmuir_single_site_model simplifies to the Langmuir equation, the proof steps are the same.
Using the definition makes it possible to write multiple theorems about the same Langmuir object. We can also prove that the Langmuir expression has zero loading at zero pressure, and in the future we can show that it has a finite loading in the limit of infinite pressure, and converges to Henry's Law in the limit of zero pressure  (https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_zero_loading_at_zero_pressure). Definitions and structures, as we will see in later sections, are crucial to building a web of interconnected scientific objects and theorems.
(https://atomslab.github.io/LeanChemicalTheories/adsorption/langmuir_kinetics.html#langmuir_zero_loading_at_zero_pressure). Definitions and structures, as we will see in later sections, are crucial to building a web of interconnected scientific objects and theorems.
3.3 BET adsorption: formalizing a complex proof
Brunauer, Emmett, and Teller introduced the BET theory of multilayer adsorption (see Fig. 2) in 1938.59 We formalize this derivation, beginning with eqn (26) from the paper, which is shown here in eqn (7):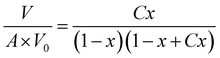 | (7) |
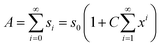 | (8) |
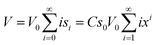 | (9) |
The variables y, x and C are expressed in the original paper as shown through eqn (10)–(12):
| y = PC1, where C1 = (a1/b1)eE1/RT | (10) |
| x = PCL, where CL = eEL/RT/g | (11) |
| C = y/x = C1/CL | (12) |
These constants, along with the surface area of the zeroth layer, given by s0, saturation pressure, and the three constraints are defined using the constant declaration in Lean. Mathematical objects can also be defined in other ways such as def, class or structure38 but for this proof we will use constant which is convenient for such simple objects. We will illustrate later in our thermodynamics proof how constants can be merged into a Lean structure for reusability.
In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#C_L):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#C_L):
With these constant declarations, we can now define y, x, and C in Lean as  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#BET_first_layer_adsoprtion_rate):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#BET_first_layer_adsoprtion_rate):
Since y and x are both functions of pressure, their definitions require pressure as an input. Alternatively, the input can be omitted if we want to deal with x as a function rather than as a number. Notice that the symbols we declared using constant do not need to be supplied in the inputs as they already exist in the global workspace.
We formalize eqn (7) by recognizing that the main math behind the BET expression is an infinite sequence that describes the surface area of adsorbed particles for each layer. The series is defined as a function that maps the natural numbers to the real numbers; the natural numbers represent the indexing. It is defined in two cases: if the index is zero, it outputs the surface area of the zeroth layer, and if the index is the n + 1, it outputs xn+1s0C.
| si = Cxis0 for i: [1,∞) | (13) |
In Lean, we define this sequence as  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#seq):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#seq):
Where si is the surface area of the ith layer, C and x are given by eqn (12) and eqn (11), respectively, and s0 is the surface area of the zeroth layer. The zeroth layer is the base surface and is constant.
We now have the area and volume equations both in terms of geometric series with well-defined solutions. The BET equation is defined as the ratio of volume absorbed to the volume of a complete unimolecular layer, given by eqn (14).
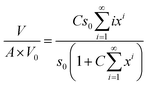 | (14) |
The main transformation in BET is simplifying this sequence into a simple fraction which involves solving the geometric series. The main math goal is given by eqn (15).
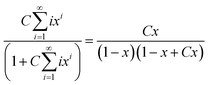 | (15) |
Before doing the full derivation, we prove eqn (15), which we call sequence_math. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#sequence_math):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#sequence_math):
In Lean, the apostrophe after the sum symbol denotes an infinite sum, which is defined to start at zero since it is indexed by the natural numbers, which start at zero. Since the infinite sum of eqn (15) starts at one, we add one to all the indexes, k, so that when k is zero, we get one, etc. We also define two new theorems that derive the solution to these geometric series with an index starting at one. After expanding seq, we use those two theorems, and then rearrange the goal to get two sides that are equal. We also use the tag lemma instead of theorem, just to communicate that it is a lower-priority theorem, intended to prove other theorems. The tag lemma has no functional difference from theorem in Lean, it's purpose is for mathematicians to label proofs.
With this we can formalize the derivation of eqn (7). First we define eqn (7) as a new object and then prove a theorem showing we can derive this object from the sequence. In Lean, the definition looks like this  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#brunauer_26):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#brunauer_26):
Here, we explicitly define this as a function, because we want to deal with eqn (7) normally as a function of pressure, rather then just a number. Now we can prove a theorem that formalizes the derivation of this equation  (https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#brunauer_26_from_seq):
(https://atomslab.github.io/LeanChemicalTheories/adsorption/BETInfinite.html#brunauer_26_from_seq):
Unlike the Langmuir proof introduced earlier in Fig. 1, the BET uses definitions that allow reusability of those definitions across the proof structure. The proof starts by showing that seq is summable. This means the sequence has some infinite sum and the ∑′ symbol is used to get the value of that infinite series. We show in the proof that both seq and k*seq is summable, where the first is needed for the area sum and the second is needed for the volume sum. After that, we simplify our definitions, move the index of the sum from zero to one so we can simplify the sequence, and apply the BET.sequence_math lemma we proved above. Finally, we use the field_simp tactic to rearrange and close the goal. With that, we formalized the derivation of eqn (7), just as Brunauer, et al. did in 1938.
In the ESI,† we continue formalizing BET theory by deriving eqn (28) from Brunauer et al.'s paper, given by eqn (16)
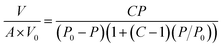 | (16) |
This follows from recognizing that 1/CL = P0. While Brunauer, et al. attempt to show this in the paper, we discuss the trouble with implementing the logic they present. Instead, we show a similar proof that eqn (7) approaches infinity as pressure approaches 1/CL, and assume as a premise in the derivation of eqn (16) that 1/CL ≡ P0.
3.4 Classical thermodynamics and gas laws: introducing Lean structures
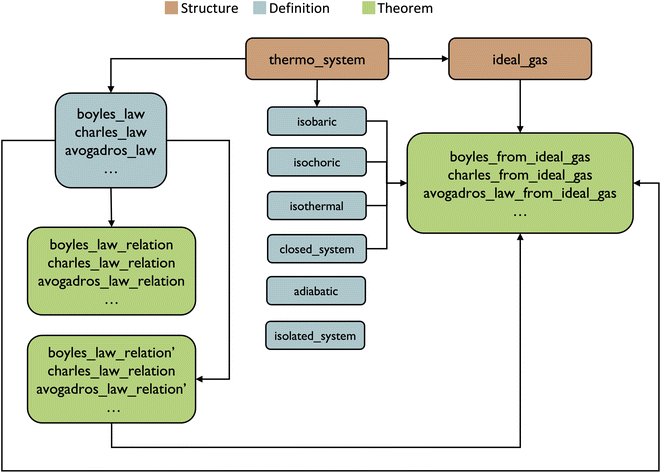
Lean is so expressive because it enables relationships between mathematical objects. We can use this functionality to precisely define and relate scientific concepts with mathematical certainty. We illustrate this by formalizing proofs of gas laws in classical thermodynamics.We can prove that the ideal gas law, PV = nRT follows Boyle's Law, P1V1 = P2V2, following the style of our derivation of Langmuir's theory: demonstrating that a conjecture follows from the premises  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/boyles_law.html). However, this proof style doesn't facilitate interoperability among proofs and limits the mathematics that can be expressed. z in contrast, we can prove the same, more systematically, by first formalizing the concepts of thermodynamic systems and states, extending that system to a specific ideal gas system, defining Boyle's Law in light of these thermodynamic states, and then proving that the ideal gas obeys Boyle's Law (see Fig. 3).
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/boyles_law.html). However, this proof style doesn't facilitate interoperability among proofs and limits the mathematics that can be expressed. z in contrast, we can prove the same, more systematically, by first formalizing the concepts of thermodynamic systems and states, extending that system to a specific ideal gas system, defining Boyle's Law in light of these thermodynamic states, and then proving that the ideal gas obeys Boyle's Law (see Fig. 3).
Classical thermodynamics describes the macroscopic properties of thermodynamic states and relationships between them.60,61 We formalize the concept of “thermodynamic system” by defining a Lean structure called thermo_system over the real numbers, with thermodynamic properties (e.g., pressure, volume, etc.) defined as functions from a type to the real numbers 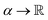 . Here, α is meant to represent a general indexing type. It could be the natural numbers if we wanted to use those to represent states of the system, real numbers to represent time, or anything else. The only requirement is that α is nontrivial, meaning it has at least two different elements. In Lean, this is
. Here, α is meant to represent a general indexing type. It could be the natural numbers if we wanted to use those to represent states of the system, real numbers to represent time, or anything else. The only requirement is that α is nontrivial, meaning it has at least two different elements. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#thermo_system):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#thermo_system):
We define six descriptions of the system: isobaric (constant pressure); isochoric (constant volume); isothermal (constant temperature); adiabatic (constant energy); closed (constant mass); and isolated (constant mass and energy). Each of these conditions has the type Prop, or proposition, considering them to be assertions about the system. We formally define these by stating that, for all (∀) pairs of states n and m, the property at those states is equal. We define these six descriptions to take in a thermo_system since we need to specify what system we are ascribing this property to. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#isobaric):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#isobaric):
We define an isolated system as just a closed system and (∧) adiabatic, rather than using the universal quantifier (∀), since it would be redundant.
Now that the basics of a thermodynamic system have been defined, we can define models that attempt to describe the system mathematically. These models can be defined as another structure, which extends the thermo_system structure. When a structure extends another structure, it inherits the properties of the structure it extended. This allows us to create a hierarchy of structures so we don't have to redefine properties repeatedly. The most well-known model is the ideal gas model, which comes with the ideal gas law equation of state. We define the ideal gas model to have two properties, the universal gas constant, R, and the ideal gas law. In the future, we plan to add more properties to the definition, especially as we expand on the idea of energy. We define the ideal gas law as an equation relating the products of pressure and volume to the product of temperature, amount of substance, and the gas constant. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#ideal_gas):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#ideal_gas):
To define a system modeled as an ideal gas, we write in Lean: (M: ideal_gas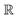 ). Now we have a system, M, modeled as an ideal gas.
). Now we have a system, M, modeled as an ideal gas.
Boyle's law states that the pressure of an ideal gas is inversely proportional to the system's volume in an isothermal and closed system.62 This is mathematically given by eqn (17), where P is pressure, V is volume, and k is a constant whose value is dependent on the system.
| PV = k | (17) |
In Lean, we define Boyle's law as  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law):
We use the existential operator (∃) on k, which can be read as there exists a k, because each system has a specific constant. We also define the existential before the universal, so it is logically correct. Right now, it reads, there exists a k, such that for all states, this relation holds. If we write it the other way, it would say for all states, there exists a k, such that this relation holds. The second way means that k is dependent on the state of the system, which isn't true. The constant is the same for any state of a system. Also, even though Boyle's law is a statement about an ideal gas, we define it as a general system so, in the future, we can look at what assumptions are needed for other models to obey Boyle's law.
Next, we prove a couple of theorems relating to the relations that can be derived from Boyle's law. From eqn (17), we can derive a relation between any two states, given by eqn (18), where n and m are two states of the system.
| PnVn = PmVm | (18) |
The first theorem we prove shows how eqn (18) follows from eqn (17). In Lean this looks like  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law_relation):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law_relation):
The right arrow can be read as implies, so the statement says that Boyle's law implies Boyle's relation. This is achieved using modus ponens, introducing two new names for the universal quantifier, then rewriting Boyle's law into the goal by specializing Boyle's law with n and m. We also want to show that the inverse relation holds, such that eqn (18) implies eqn (17). In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law_relation'):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_law_relation'):
We begin in the same way by using modus ponens and simplifying Boyle's law in the form of eqn (17). Next, we satisfy the existential by providing an old name. In our proof, we use P1V1 as an old name for k, then we specialize the relation with n and 1 and close the goal.
Finally, with these two theorems, we show that Boyle's law can be derived from the ideal gas law under the assumption of an isothermal and closed system. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_from_ideal_gas):
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html#boyles_from_ideal_gas):
This proof is completed by using the second theorem for Boyle's relation and simplifying the ideal gas relation using the two iso constraints.
We have implemented this framework to prove both Charles' and Avogadro's law  (https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html) illustrating the interoperability of these proofs. In the future, we plan to define energy and prove theorems relating to it, including the laws of thermodynamics.63
(https://atomslab.github.io/LeanChemicalTheories/thermodynamics/basic.html) illustrating the interoperability of these proofs. In the future, we plan to define energy and prove theorems relating to it, including the laws of thermodynamics.63
3.5 Kinematic equations: calculus in Lean
Calculus and differential equations are ubiquitous in chemical theory, and much has been formalized in mathlib. To illustrate Lean's calculus capabilities and motivate future formalization efforts, we formally prove that the kinematic equations follow from calculus-based definitions of motion, assuming constant acceleration. The analysis of physical equations of motion, particularly those based on Newtonian mechanics, is strongly related to the formulation of many theories in chemical physics, including reaction kinetics,64 diffusion and transport phenomena65 and molecular dynamics.66 These concepts are essential for understanding chemical reactions and how molecules move and interact.The equations of motion are a set of two coupled differential equations that relate the position, velocity, and acceleration of an object in an n-dimensional vector space.67 The differential equations are given by eqn (19) and (20), where x, v, and a represent position, velocity, and acceleration, respectively (bold type face signifies a vector quantity). All three variables are parametric equations, where each dimension of the vector is a function of time.**
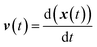 | (19) |
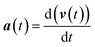 | (20) |
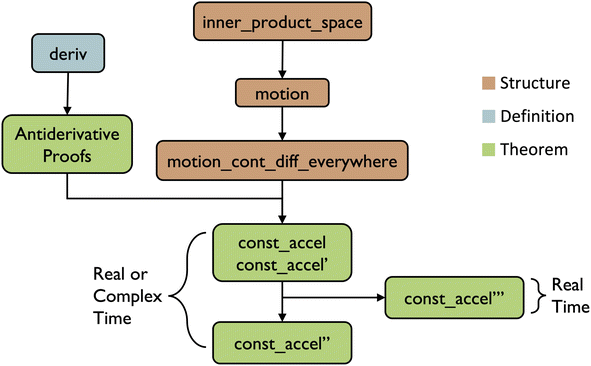
As in the thermodynamics section, we can define a structure, motion, to encompass these concepts (Fig. 4). This structure defines three new elements: position, velocity, and acceleration, which are functions, and two differential equations relating these three functions. This structure also requires the vector space to form an inner product space, which is a real or complex vector space with an operator (the inner product) over the field. The inner product is a generalization of the dot product for any vector space. By requiring inner_product_space, the motion structure inherits all of inner_product_space’s properties and allows us to access the calculus theorems in mathlib. In Lean, this is  (https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#motion):
(https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#motion):
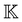 represents a field that we require to be either a real
represents a field that we require to be either a real 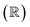 or complex
or complex 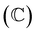 number, and E symbolizes a general vector field. In mathematics, a field is an algebraic structure with addition, subtraction, multiplication, and division operations. Our vector space could be an n-dimensional Euclidean vector space, but we instead use a general vector field to be as general as possible. This allows us to describe motion in a Euclidean vector space, as well as a hyperbolic vector space or a vector space with special properties.
number, and E symbolizes a general vector field. In mathematics, a field is an algebraic structure with addition, subtraction, multiplication, and division operations. Our vector space could be an n-dimensional Euclidean vector space, but we instead use a general vector field to be as general as possible. This allows us to describe motion in a Euclidean vector space, as well as a hyperbolic vector space or a vector space with special properties.
In Lean, if a function is not differentiable at a point, the derivative at that point returns zero.†† During our first formalization attempt, we tried to define a function to be constant by setting its derivative to zero. However, df/dx = 0 may also arise if a function is not differentiable at that point. To avoid this edge case, we define another structure to require the equations of motion to be n-times continuously differentiable everywhere. We only require the equations to be n-times differentiable instead of infinitely differentiable for generality reasons, however, a theorem can instantiate this structure and assume infinite differentiability. We also declare this as a separate structure, instead of in the motion structure, to allow future proofs that require the equations to be n-times continuously differentiable on a set or an interval rather than everywhere (e.g., a molecular mechanics force field with a non-smoothed cutoff is not differentiable at that point). That way, depending on the theorem, the user can choose the appropriate extension. In Lean, this structure looks like  (https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#motion_cont_diff_everywhere):
(https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#motion_cont_diff_everywhere):
The field contdiff states that for all n, defined as a natural number including positive infinity, and for all m, defined as a natural number, if m is less than n, then the mth derivative of position is continuously differentiable n-times.
When acceleration is constant, this set of differential equations has four useful analytical solutions, the kinematic equations, eqn (21)–(24), where the subscript naught denotes variables evaluated at t = 0.
| v(t) = at + v0 | (21) |
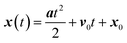 | (22) |
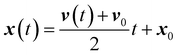 | (23) |
| v2(t) = v02 + 2a·d | (24) |
Under the assumption of one-dimensional motion, these equations simplify to the familiar introductory kinematic equations. Eqn (24), also known as the Torricelli equation, uses the shorthand square to represent the dot product, v2(t) ≡ v(t) × v(t).
With this, we can now begin deriving the four kinematic equations. The first three derivations for eqn (21)–(23), all use the same premises, given below:
The first line contains four premises to declare the field and vector space the motion space is defined on. The next line defines a motion space, M. The third line contains two premises, a variable, A, which represents the value of constant acceleration, and n, the number of times position can be differentiated. When applying these theorems, the top function, which means positive infinity in Lean, can be used to specify n. The final line is a premise that assumes acceleration is constant. The lambda function is constant because A is not a function of t, so for any value of t, the function outputs the same value, A. The three kinematic equations in Lean  (https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#const_accel) are given below (note, the premises are omitted since they have already been given above).
(https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#const_accel) are given below (note, the premises are omitted since they have already been given above).
The · symbol indicates scalar multiplication, such as when a vector is multiplied by a scalar. We normally use the · symbol for the dot product, but Lean uses the inner function for the dot product. Also, “velocity 0” means the velocity function evaluated at 0. Lean uses parentheses for orders of operations, not for function inputs, so f(x) in normal notation converts to f x in Lean. The proofs of the first two theorems use the two differential equations from the motion structure and the antiderivative, whose formalization we explain in the ESI† (these theorems weren't available in mathlib at the time of writing, so we proved them ourselves). The third theorem is proved by rearranging the previous two theorems.
Because we declared the field is_R_or_C, the above proofs hold for both real and complex time. However, we were unable to prove eqn (24), due to the complex conjugate that arises when simplifying the proof. Eqn (24) uses the inner product, a function that takes in two vectors from a vector space and outputs a scalar. If the vector space is a Euclidean vector space, this is just the dot product. The inner product is semi-linear, linear in its first argument, eqn (25), but sesquilinear in its second argument, eqn (26).
| 〈ax + by,z〉 = a〈x,z〉 + b〈y,z〉 | (25) |
〈x,ay + bz〉 = ā〈x,y〉 + ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) 〈x,z〉 〈x,z〉 | (26) |
The bar denotes the complex conjugate: for a complex number, g = a + bi, the complex conjugate is: ḡ = a − bi. If g is a real number, then g = ḡ. For the proof of eqn (24), we get to a form where one of the inner products has an addition in the second term that we have to break up, and no matter which way we rewrite the proof line, one of the inner products ends up with addition in the second term. To proceed, we instead defined the final kinematic equation to hold only for real time. In Lean, this looks like  (https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#real_const_accel'''):
(https://atomslab.github.io/LeanChemicalTheories/physics/kinematic_equations.html#real_const_accel'''):
While we haven't proved that eqn (24) doesn't hold for complex time, we encountered difficulties and contradictions when attempting to prove the complex case. Thus, eqn (24) currently only holds for real time.
An imaginary-time framework can be used to derive equations of motion from non-standard Lagrangians69,70 to examine hidden properties in classical and quantum dynamical systems in the future. By exploring these proofs in both real and complex time, we illustrate how a proof in one case can be adapted for related cases. Here, four proofs for real numbers can be easily extended to complex numbers by changing the type declared up front, and the validity of the proofs in the more general context is immediately apparent.
4 Conclusions and outlook
In this paper, we demonstrate how interactive theorem proving can be used to formally verify the mathematics in science and engineering. We found that, although formalization is slower and more challenging than writing hand-written derivations, our resulting proofs are more rigorous and complete. We observed that in some cases, translating scientific statements into formal language revealed hidden assumptions behind the mathematical derivations. For example, we make explicit common implicit assumptions, such as the denominator must not be zero when we deal with division. Furthermore, we reveal, in a more abstract way, we have attempted to reveal the formal definitions of equations, such as exactly how pressure is defined as a function or the assumptions of differentiability needed for kinematics. All of these are a result of formalizing these theorems. We concur with others who have discussed the limitations of hand-written proofs and their reliability;2,71,72 formalized proofs can provide greater assurance and robustness.Importantly, we emphasize that while our proofs are verified to be mathematically correct, this verification does not extend to the external world. This distinction between syntax (logical relationships among words and arguments in a language) and semantics (whether words are meaningful or arguments are true, according to external reality) in scientific reasoning has been emphasized by logicians such as Alfred Tarski73 and Rudolf Carnap.74,75 For scientists and engineers, whether a theory is true or meaningful is first and foremost about whether observational data support it – logical correctness of the derivation is required, of course, but this is typically assumed. Indeed, when one of us described our BET proof to an experimentalist in adsorption, their reply was, “but BET isn't accurate.” They knew that BET theory does not semantically match experiments in many contexts (in fact, much literature has discussed when BET analysis should not be applied, for instance76). BET theory has been a useful conceptual model for the field, but nonetheless relies on approximations that often drift far from reality. In this work, we only claim to rigorously establish the syntax of the theories we describe. Nonetheless, Lean operating with input/output functions can receive data from the external world, which may open possibilities for semantically grounding its logical conclusions in certain contexts, as well.
The Lean theorem prover is especially powerful, as it facilitates the re-use of theorems and the construction of higher-level mathematical objects from lower-level ones. We showed how this feature can be leveraged in science proofs; after a fundamental theory is formally verified, it can then be used in the development of other theories. This can be approached in two ways: definitions can be directly reused in subsequent proofs, and structures can enable hierarchies of related concepts, from general to more specific. Thus we have not just proved a few theorems about scientific objects but have begun to create an interconnected structure of formally verified proofs relating fields of science.
While learning Lean and writing the proofs appearing here, we routinely asked ourselves, “How do I close this goal? I wish there was a way to automate this.” In fact, the first vision for computer-assisted proofs in the 1950s and 60s was to automate the process fully;77interactive theorem provers that “merely” check human-written proofs didn't appear until later. But historically, automated theorem provers (ATPs) made progress on narrow classes of problems (e.g., problems in first-order logic78) but couldn't address proofs in advanced math (except when problems are described in such simple terms, like the Robbins Conjecture79). In short, theorem proving is like searching for a path from premises to conjecture, but in a realm with an “infinite action space48 – traditional algorithms have been inadequate. For complex proofs, interactive theorem provers (ITPs) have been more successful, because they facilitate human creativity in writing proofs, while leveraging the rigor of the computer for checking them and providing feedback to the user. Modern ITPs also use the computer for small-scale automation via tactics; the human provides strategy while the computer executes tactics. Complex tactics sometimes blur the line between automated and interactive theorem proving. For example, Isabelle (an ITP) has the Sledgehammer tactic,80 which takes the current proof state and attempts to transform it into an equivalent problem in first-order logic, which can then be efficiently solved using an ATP.
Recent approaches have leveraged machine learning to expand the capabilities of automated theorem proving. Theorem proving can be framed as a reinforcement learning problem,81,82 in which an agent is to learn an effective theorem proving policy via rewards from successfully proving theorems. “Autoformalization” refers to the translation of informal proofs into formal proofs, akin to translating text from one language to another (but with extremely strict requirements on the formal side).83 Theorem proving can also be framed as a next-word-prediction problem (“auto-complete” for math proofs) in which a database of formal math proofs is used to train a language model to predict the next word in the proof. Large language models (LLMs) like ChatGPT84,85 have some emergent reasoning abilities86 but often make mistakes and cannot be trusted. By connecting language models with ITPs to provide feedback, training them on proof databases like mathlib, and deploying them as part of traditional search algorithms, progress has been made toward automating proofs in Lean,47,87,88 even to the point of generating correct solutions to International Math Olympiad problems.89
This interplay between creative but unreliable generative algorithms and the strict logic of a proof-checking system may be a model for future AI-driven discovery in science, especially for discovering new theories. An early example of this is AI-Descartes, in which a symbolic regression algorithm generates equations to match experimental data, which is then combined with an automated theorem prover to establish the equations' “derivability” with respect to a scientific theory.33 However, in this work, each theory required human expertise to be expressed in formal language, and reliance on an automated theorem prover limited the scope of theories to those expressible in first-order logic. AI tools that can autoformalize the informal scientific literature, generate novel theories, and auto-complete complex proofs could open new avenues for automating theory discovery. LLMs have demonstrated capabilities in solving chemistry problems,90,91 as well as answering scientific question-and-answer problems invoking quantitative reasoning.92 However, LLMs are unreliable – they famously “hallucinate” (generate falsehoods) and are biased or unreliable evaluators of their own outputs.93,94 Pairing them with external tools95–97 improves their capabilities; theorem provers could play a role like that. How will these models be trained? We suggest two avenues: training on human-written databases of formal proofs in science and engineering (which are yet to be written) and leveraging interactive feedback from Lean through tools like LeanDojo.88 Beyond being formally grounded in axiomatic mathematics, formal proofs in science and engineering are machine-readable instances of correct mathematical logic that could serve as a foundation for artificial intelligences aiming to learn, reason, and discover in science.98–100
Our next goals are to continue building out classical thermodynamics, formalize statistical mechanics, and eventually construct proofs relating the two fields. We are also interested in laying the foundations for classical mechanics in Lean and formalizing more difficult proofs like Noether's theorem101 (a basis for deriving conservation laws) or establishing the 2nd law of thermodynamics axiomatically.35
The proofs in this paper were written in Lean 3,72 because the extensive mathlib library was only available in Lean 3 when we began. While Lean 3 was designed for theorem proving and management of large-scale proof libraries, the new version, Lean 4,102 is a functional programming language for writing proofs and programs, as well as proofs about programs.102,103 The Lean community finished porting mathlib to Lean 4 and Lean 3 is now deprecated; we recommend future proofs should be written in Lean 4, which is more capable, versatile, and easy to use compared to Lean 3. With Lean 4, we are bridging formally-correct proofs with executable functions for bug-free scientific computing; we will be elaborating on that in future work.
We hope these expository proofs in adsorption, thermodynamics, and kinematics will inspire others to consider what proofs and derivations could be formalized in their fields of expertise. Virtually all mathematical concepts can be established using dependent type theory; the density functionals, partial derivatives, N-dimensional integrals, and random variables appearing in our favorite theories should be expressible in Lean. Just as an ever-growing online community of mathematicians and computer scientists is building mathlib,40 we anticipate a similar group of scientists building a library of formally-verified scientific theories and engineering mathematics. To join, start learning Lean, join the online community, and see what we can prove!
Data availability
The Lean software used for this work is open source. All proofs are publicly available, and hosted on our GitHub repository: https://atomslab.github.io/LeanChemicalTheories/Author contributions
We summarize author contributions using the CRediT system. Conceptualization: TRJ; data curation: MPB, PF, SS; formal analysis: MPB, SS, PF, AHD, CMW, TRJ; funding acquisition: TRJ; methodology: MPB, TRJ; project administration: MPB, SS, TRJ; software: MPB, SS, TRJ; supervision: TRJ; validation: Lean; visualization: MPB, SS, PF, TRJ; writing, original draft: MPB, SS, PF, TRJ; writing, review and editing: MPB, SS, PF, TRJ.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We are grateful to the Lean prover community and contributors of mathlib on whose work this project is built. We especially thank Kevin Buzzard, Patrick Massot, Tomas Skrivan, Eric Wieser, and Andrew Yang for helpful comments and discussions around our proof structure and suggestions for improvement. We thank Charles Fox, Mauricio Collares, and Ruben Van de Velde for helping with the website. We thank two anonymous peer reviewers, as well as Rose Bohrer, John Keith, and Ben Payne for reading the manuscript and providing helpful feedback. This material is based upon work supported by the National Science Foundation under Grant No. (NSF #2138938), as well as startup funds from the University of Maryland, Baltimore County.References
- K. Hinsen, Computational science: shifting the focus from tools to models [version 2; peer review: 2 approved], F1000Research, 2014, 3(101), 1–10 Search PubMed.
- T. C. Hales, Formal proof, Not. Am. Math. Soc., 2008, 55(11), 1370–1380 Search PubMed.
- P. Rudnicki, An overview of the Mizar project, in Proceedings of the 1992 Workshop on Types for Proofs and Programs, 1992, pp. 311–330 Search PubMed.
- M. M. Wenzel, Isabelle/Isar - A versatile environment for human-readable formal proof documents, Technische Universität München, 2002 Search PubMed.
- B. Barras, S. Boutin, C. Cornes, J. Courant, J. C. Filliatre, E. Gimenez, et al., The Coq proof assistant reference manual: Version 6.1, Inria, 1997 Search PubMed.
- M. J. Gordon and T. F. Melham, Introduction to HOL: A theorem proving environment for higher order logic, Cambridge University Press, 1993 Search PubMed.
- T. Nipkow, M. Wenzel and L. C. Paulson, Isabelle/HOL: A proof assistant for higher-order logic, Springer, 2002 Search PubMed.
- S. Owre, J. M. Rushby and N. Shankar, PVS: A prototype verification system, in International Conference on Automated Deduction, Springer, 1992. pp. 748–752 Search PubMed.
- A. Meurer, C. P. Smith, M. Paprocki, O. Čertík, S. B. Kirpichev and M. Rocklin, et al., SymPy: Symbolic Computing in Python, PeerJ Comput. Sci., 2017, 3, e103 CrossRef.
- A. J. Durán, M. Pérez and J. L. Varona, The Misfortunes of a Trio of Mathematicians Using Computer Algebra Systems. Can We Trust in Them?, Not. Am. Math. Soc., 2014, 61(10), 1249 CrossRef . Available from: http://www.ams.org/notices/201410/rnoti-p1249.pdf.
- L. de Moura, S. Kong, J. Avigad, F. van Doorn and J. von Raumer. The Lean theorem prover (system description), Automated Deduction - CADE-25, 2015, pp. 378–388 Search PubMed.
- S. Wolfram, Mathematica: A system for doing mathematics by computer, Addison Wesley Longman Publishing Co., Inc., 1991 Search PubMed.
- T. M. Inc, Symbolic Math Toolbox - MATLAB: 9.14.0 (R2023b), The MathWorks Inc., Natick, Massachusetts, United States, 2023, available from: https://www.mathworks.com Search PubMed.
- K. Appel, W. Haken and J. Koch, Every planar map is four colorable. Part II: Reducibility, Illinois J. Math., 1977, 21(3), 491–567 Search PubMed.
- G. Gonthier, et al., Formal proof–the four-color theorem, Not. Am. Math. Soc., 2008, 55(11), 1382–1393 Search PubMed.
- S. Boldo, C. Lelay and G. Melquiond, Coquelicot: A user-friendly library of real analysis for Coq, Math. Comput. Sci., 2015, 9(1), 41–62 CrossRef.
- T. Hales, M. Adams, G. Bauer, T. D. Dang, J. Harrison, H. Le Truong, et al., A formal proof of the Kepler conjecture, in Forum of Mathematics, Pi, Cambridge University Press, vol. 5, 2017 Search PubMed.
- K. Buzzard, J. Commelin and P. Massot, Formalising perfectoid spaces, in Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, 2020, pp. 299–312 Search PubMed.
- K. Hartnett, Proof Assistant Makes Jump to Big-League Math 2021, accessed: 2022, https://www.quantamagazine.org/lean-computer-program-confirms-peter-scholze-proof-20210728/ Search PubMed.
- A. N. Whitehead and B. Russell, Principia Mathematica, Cambridge University Press, 1997 Search PubMed.
- K. Hartnett, Building the Mathematical Library of the Future, Quanta Magazine, 2020 Search PubMed.
- D. Hilbert, Mathematical problems, Bull. New Ser. Am. Math. Soc., 1902, 8(10), 437–479 CrossRef.
- L. Corry, David Hilbert and the axiomatization of physics (1894–1905), Arch. Hist. Exact Sci., 1997, 51, 83–198 CrossRef.
- A. N. Gorban, Hilbert's sixth problem: the endless road to rigour, The Royal Society Publishing, 2018 Search PubMed.
- B. W. Paleo, Physics and proof theory, Appl. Math. Comput., 2012, 219(1), 45–53 CrossRef PubMed.
- J. D. Fleuriot and L. C. Paulson, A combination of nonstandard analysis and geometry theorem proving, with application to Newton's Principia, ed. Carbonell J. G., Siekmann J., Goos G., Hartmanis J., Van Leeuwen J., Kirchner C., et al., Automated Deduction — CADE-15, Series Title: Lecture Notes in Computer Science, Springer Berlin Heidelberg, 1998, vol. 1421, pp. 3–16, available from: https://link.springer.com/10.1007/BFb0054241 Search PubMed.
- J. D. Fleuriot and L. C. Paulson. Proving Newton's Propositio Kepleriana Using Geometry and Nonstandard Analysis in Isabelle, ed. Goos G., Hartmanis J. and Van Leeuwen J., Automated Deduction in Geometry, Series Title: Lecture Notes in Computer Science, Springer Berlin Heidelberg, 1999, vol. 1669, pp. 47–66, available from: http://link.springer.com/10.1007/3-540-47997-X_4 Search PubMed.
- M. Stannett and I. Németi, Using Isabelle/HOL to verify first-order relativity theory, J. Autom. Reason., 2014, 52(4), 361–378 CrossRef.
- E. H. Lu. A formalization of elements of special relativity in Coq. Harvard University; 2017 Search PubMed.
- S. Khan-Afshar, U. Siddique, M. Y. Mahmoud, V. Aravantinos, O. Seddiki and O. Hasan, et al., Formal analysis of optical systems, Math. Comput. Sci., 2014, 8(1), 39–70 CrossRef.
- M. U. Siddique, Formal analysis of geometrical optics using theorem proving, Concordia University, 2015 Search PubMed.
- A. Cervera-Lierta, M. Krenn and A. Aspuru-Guzik, Design of quantum optical experiments with logic artificial intelligence, Quantum, 2022, 6, 836 CrossRef.
- C. Cornelio, S. Dash, V. Austel, T. R. Josephson, J. Goncalves and K. L. Clarkson, et al., Combining data and theory for derivable scientific discovery with AI-Descartes, Nat. Commun., 2023, 14(1), 1777 CrossRef CAS PubMed . Available from: https://www.nature.com/articles/s41467-023-37236-y.
- C. Carathéodory, Untersuchungen über die Grundlagen der Thermodynamik, Math. Ann., 1909, 67, 355–386 CrossRef.
- E. H. Lieb and J. Yngvason, The physics and mathematics of the second law of thermodynamics, Phys. Rep., 1999, 310(1), 1–96 CrossRef.
- R. Bohrer. Chemical Case Studies in KeYmaera X, Formal Methods for Industrial Critical Systems - 27th International Conference, FMICS 2022, Warsaw, Poland, September 14-15, 2022, Proceedings, vol. 13487 of Lecture Notes in Computer Science, ed. Groote J. F. and Huisman M., Springer, 2022, pp. 103–120, DOI:10.1007/978-3-031-15008-1_8.
- R. Alur. Formal verification of hybrid systems, in Proceedings of the ninth ACM international conference on Embedded software, 2011, pp. 273–278 Search PubMed.
- J. Avigad, L. de Moura and S. Kong, Theorem proving in Lean, Release, 2015, 3, 1–4 Search PubMed.
- The mathlib Community, The Lean mathematical library, in Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, ACM, 2020, DOI:10.1145/2F3372885.3373824.
- Lean Prover Community on Zulip, https://leanprover.zulipchat.com/.
- Undergraduate Mathematics in mathlib, https://leanprover-community.github.io/undergrad.html.
- K. Buzzard, J. Commelin and P. Massot, Formalising Perfectoid Spaces, in Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs. CPP 2020, Association for Computing Machinery, New York, NY, USA, 2020, pp. 299–312, DOI:10.1145/3372885.3373830.
- S. R. Dahmen, J. Hölzl and R. Y. Lewis, Formalizing the solution to the Cap Set problem, in 10th International Conference on Interactive Theorem Proving (ITP 2019). vol. 141 of Leibniz International Proceedings in Informatics (LIPIcs), Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, 2019, pp. 15:1–15:19, available from: http://drops.dagstuhl.de/opus/volltexte/2019/11070 Search PubMed.
- P. Scholze, Lean liquid, GitHub, 2020, https://github.com/leanprover-community/lean-liquid Search PubMed.
- K. Hartnett, Proof Assistant Makes Jump to Big-League Math, Quanta Magazine, 2021 Search PubMed.
- K. Buzzard and M. Pedramfar, Natural Number Game, GitHub, 2020, https://github.com/ImperialCollegeLondon/natural_number_game Search PubMed.
- J. M. Han, J. Rute, Y. Wu, E. W. Ayers and S. Polu, Proof artifact co-training for theorem proving with language models, arXiv, 2021, preprint, arXiv:2102.06203, DOI:10.48550/arXiv.2102.06203.
- S. Polu, J. M. Han, K. Zheng, M. Baksys, I. Babuschkin and I. Sutskever. Formal Mathematics Statement Curriculum Learning, in International Conference on Learning Representations, 2023 Search PubMed.
- G. W. Whitehead, Elements of Homotopy Theory, Springer Science & Business Media, vol. 61, 2012 Search PubMed.
- P. G. Goerss and J. F. Jardine, Simplicial Homotopy Theory, Springer Science & Business Media, 2009 Search PubMed.
- T. Coquand and G. Huet, The Calculus of Constructions, INRIA, 1986 Search PubMed.
- T. Coquand and C. Paulin, Inductively defined types, in International Conference on Computer Logic, Springer, 1988, pp. 50–66 Search PubMed.
- T. Coquand and J. H. Gallier. A proof of strong normalization for the theory of constructions using a Kripke-like interpretation, 1990 Search PubMed.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40(9), 1361–1403 CrossRef CAS.
- M. Volmer, Thermodynamische Folgerungen ans der Zustandsgleichung für adsorbierte Stoffe, Z. Phys. Chem., 1925, 115(1), 253–260 CrossRef CAS.
- R. I. Masel, Principles of adsorption and reaction on solid surfaces, John Wiley & Sons, vol. 3, 1996 Search PubMed.
- M. Kleman and O. D. Lavrentovich. Soft Matter Physics: An introduction. Springer; 2003 Search PubMed.
- H. Barendregt, W. Dekkers and R. Statman. Lambda calculus with types. Cambridge University Press; 2013 Search PubMed.
- S. Brunauer, P. H. Emmett and E. Teller, Adsorption of gases in multimolecular layers, J. Am. Chem. Soc., 1938, 60(2), 309–319 CrossRef CAS.
- K. D. Dahm and D. P. Visco. Fundamentals of Chemical Engineering Thermodynamics. Cengage Learning; 2015 Search PubMed.
- S. I. Sandler. Chemical, Biochemical, and Engineering Thermodynamics. John Wiley & Sons; 2017 Search PubMed.
- I. N. Levine. Physical Chemistry. McGraw-Hill; 1978 Search PubMed.
- P. Atkins. The Laws of Thermodynamics: A Very Short Introduction. OUP Oxford; 2010 Search PubMed.
- A. Frost and R. Pearson, Kinetics and Mechanism, J. Phys. Chem., 1961, 65(2), 384 CrossRef.
- R. B. Bird, Transport phenomena, Appl. Mech. Rev., 2002, 55(1), R1–R4 CrossRef.
- J. M. Haile, I. Johnston, A. J. Mallinckrodt and S. McKay, Molecular Dynamics Simulation: Elementary Methods, American Institute of Physics, vol. 7, 1993 Search PubMed.
- J. S. Beggs. Kinematics. CRC Press; 1983 Search PubMed.
- Division by zero in type theory: a FAQ — web.archive.org;. [Accessed 21-Jul-2023], https://web.archive.org/web/20230719150030/https://xenaproject.wordpress.com/2020/07/05/division-by-zero-in-type-theory-a-faq/.
- V. Popov, Imaginary-time method in quantum mechanics and field theory, Phys. At. Nucl., 2005, 68(4), 686–708 CrossRef CAS.
- E. N. A. Rami, T. Soulati and H. Rezazadeh, Non-standard complex Lagrangian dynamics, J. Adv. Res. Dyn. Control Syst., 2013, 5, 50–62 Search PubMed.
- A. Bundy, M. Jamnik and A. Fugard, What is a proof?, Philos. Trans. R. Soc., A, 2005, 363(1835), 2377–2391 CrossRef.
- J. Avigad and J. Harrison, Formally Verified Mathematics, Commun. ACM, 2014, 57(4), 66–75 CrossRef.
- A. Tarski, The semantic conception of truth: and the foundations of semantics, Philos. Phenomenol. Res., 1944, 4(3), 341–376 CrossRef.
- L. S. Stebbing. The logical syntax of language. by Rudolf Carnap. translated from the German by Amethe Smeaton (countess von zeppelin), Kegan Paul, Trench, Trubner amp; Co., Ltd, London, 1937, Philosophy, 1938, vol. 13, 52, pp. 485–486 Search PubMed.
- R. Carnap. Introduction to Semantics. 1942 Search PubMed.
- F. Ambroz, T. J. Macdonald, V. Martis and I. P. Parkin, Evaluation of the BET Theory for the Characterization of Meso and Microporous MOFs, Small Methods, 2018, 2(11), 1800173 CrossRef.
- J. Harrison, J. Urban and F. Wiedijk, History of Interactive Theorem Proving, Comput. Log., 2014, 9, 135–214 Search PubMed.
- L. Kovács and A. Voronkov. First-order theorem proving and Vampire, in International Conference on Computer Aided Verification, Springer, 2013, pp. 1–35 Search PubMed.
- W. McCune, Solution of the Robbins Problem, J. Autom. Reason., 1997, 19(3), 263–276 CrossRef.
- J. C. Blanchette, L. Bulwahn and T. Nipkow, Automatic proof and disproof in Isabelle/HOL, in Frontiers of Combining Systems: 8th International Symposium, FroCoS 2011, Saarbrücken, Germany, Proceedings 8, Springer, 2011, pp. 12–27 Search PubMed.
- C. Kaliszyk, J. Urban, H. Michalewski and M. Olšák, Reinforcement learning of theorem proving, Adv. Neural Inf. Process., 2018, 31, 1–11 Search PubMed.
- M. Crouse, I. Abdelaziz, B. Makni, S. Whitehead, C. Cornelio, P. Kapanipathi, et al., A deep reinforcement learning approach to first-order logic theorem proving, in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, 2021, pp. 6279–6287 Search PubMed.
- C. Szegedy, A promising path towards autoformalization and general artificial intelligence, in Intelligent Computer Mathematics: 13th International Conference, CICM 2020, Bertinoro, Italy, July 26–31, 2020, Proceedings, Springer, vol. 13, 2020, pp. 3–20 Search PubMed.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan and P. Dhariwal, et al., Language models are few-shot learners, Adv. Neural Inf. Process., 2020, 33, 1877–1901 Search PubMed.
- M. Chen, J. Tworek, H. Jun, Q. Yuan, H. PdO. Pinto, J. Kaplan, et al., Evaluating large language models trained on code, arXiv, 2021, preprint, arXiv:210703374, DOI:10.48550/arXiv.1805.07563.
- J. Wei, X. Wang, D. Schuurmans, M. Bosma, F. Xia and E. Chi, et al., Chain-of-thought prompting elicits reasoning in large language models, Adv. Neural Inf. Process., 2022, 35, 24824–24837 Search PubMed.
- J. M. Han. GPT-f in Lean. GitHub; 2020. https://github.com/jesse-michael-han/lean-gptf Search PubMed.
- K. Yang, A. M. Swope, A. Gu, R. Chalamala, P. Song, S. Yu, et al., LeanDojo: Theorem Proving with Retrieval-Augmented Language Models, arXiv, 2023, preprint, arXiv:230615626, DOI:10.48550/arXiv.2306.15626.
- K. Zheng, J. M. Han and S. Polu, MiniF2F: a cross-system benchmark for formal Olympiad-level mathematics; 2022 Search PubMed.
- G. M. Hocky and A. D. White, Natural language processing models that automate programming will transform chemistry research and teaching, Digital Discovery, 2022, 1(2), 79–83 RSC.
- A. D. White, G. M. Hocky, H. A. Gandhi, M. Ansari, S. Cox, G. P. Wellawatte, et al., Do large language models know chemistry?, Cambridge Open Engage, 2022 Search PubMed.
- A. Lewkowycz, A. Andreassen, D. Dohan, E. Dyer, H. Michalewski, V. Ramasesh, et al., Solving quantitative reasoning problems with language models. NeurIPS, 2022 Search PubMed.
- A. M. Bran, S. Cox, A. D. White and P. Schwaller. ChemCrow: Augmenting large-language models with chemistry tools, arXiv, 2023, preprint, arXiv:230405376, DOI:10.48550/arXiv.2304.05376.
- Y. Liu, D. Iter, Y. Xu, S. Wang, R. Xu and C. Zhu, NLG Evaluation using GPT-4 with Better Human Alignment, arXiv, 2023, preprint, arXiv:230316634, DOI:10.48550/arXiv.2303.16634.
- T. B. Richards, Auto-GPT: An Autonomous GPT-4 Experiment, GitHub, 2023, https://github.com/Significant-Gravitas/Auto-GPT Search PubMed.
- H. Chase, LangChain: Building applications with LLMs through composability. GitHub; 2022, https://github.com/langchain-ai/langchain Search PubMed.
- Function calling in GPT-4 and GPT-3.5, https://openai.com/blog/function-calling-and-other-api-updates.
- G. F. Bradshaw, P. W. Langley and H. A. Simon, Studying scientific discovery by computer simulation, Science, 1983, 222(4627), 971–975 CrossRef CAS PubMed.
- H. Kitano, Nobel Turing Challenge: creating the engine for scientific discovery, npj Syst. Biol. Appl., 2021, 7(1), 1–12 CrossRef PubMed.
- M. Krenn, R. Pollice, S. Y. Guo, M. Aldeghi, A. Cervera-Lierta and P. Friederich, et al., On scientific understanding with artificial intelligence, Nat. Rev. Phys., 2022, 1–9 Search PubMed.
- Y. Kosmann-Schwarzbach, The Noether theorems. Springer; 2011 Search PubMed.
- L. Moura and S. Ullrich, The Lean 4 theorem prover and programming language, in International Conference on Automated Deduction, Springer, 2021, pp. 625–635 Search PubMed.
- D. T. Christiansen, Functional Programming in Lean, 2023, https://leanprover.github.io/functional_programming_in_lean/ Search PubMed.
Footnotes |
† Electronic supplementary information (ESI) available: Additional background on how Lean works (Section 5.1) and all the additional proofs (Section 5.2), including an improved version of Langmuir adsorption model (5.2.1), the final derived form of BET adsorption model (5.2.2), and the antiderivative proofs (5.2.3) that was used for kinematic equations. All code and proofs for this project are available in our GitHub repository  (https://atomslab.github.io/LeanChemicalTheories/). See DOI: https://doi.org/10.1039/d3dd00077j (https://atomslab.github.io/LeanChemicalTheories/). See DOI: https://doi.org/10.1039/d3dd00077j |
| ‡ Mathematical terms that may be unfamiliar to the reader, like theorem, are defined in the glossary, cross-reference to Table 3. |
| § The manuscript we first submitted for peer review included a typo in eqn (5), with [S0] appearing as [S]. Neither the authors nor the peer reviewers detected this; it was identified by a community member who accessed the paper on arXiv. Of course, Lean catches such typos immediately. |
¶ These types are easily extended to functionals, which are central to density functional theory. A function that takes a function as an input can be defined by 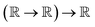 . . |
| || This definition can be specified in multiple ways. The pressure could be required as an input like the equilibrium constant, or the equilibrium constant can be specified as a variable in the function like pressure. Any of these definitions work, and it is possible to prove congruence between them. We chose this way to purposefully show both definitions and functions in Lean. |
| ** These proofs could also be constructed using partial differential equations, but mathlib doesn't currently have enough theorems for partial derivatives. |
†† Likewise, division by zero is defined to return zero instead of something like “undefined” or “NaN”. In Lean and other theorem provers, the symbol/is not used for mathematical division but instead points to a function called real.div. This function returns x/y if y is not zero, and 0 if y equals 0. Another case is the real square root function (real.sqrt), which outputs a real number for any input, even negatives since it is defined as 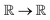 . These conventions may be unfamiliar to scientists and engineers, but they are used for convenience and won't lead to contradictions in a proof. Any invalid step in a proof involving these conventions will be caught when invoking a theorem not true for its definition. We wrestled with this convention for some time before finding clarity in this blog post archived for ref. 68. . These conventions may be unfamiliar to scientists and engineers, but they are used for convenience and won't lead to contradictions in a proof. Any invalid step in a proof involving these conventions will be caught when invoking a theorem not true for its definition. We wrestled with this convention for some time before finding clarity in this blog post archived for ref. 68. |
| This journal is © The Royal Society of Chemistry 2024 |