Open Access Article
Open Access ArticleMachine learning based feature engineering for thermoelectric materials by design†
U. S.
Vaitesswar‡
 a,
Daniil
Bash‡
a,
Daniil
Bash‡
 bc,
Tan
Huang‡
a,
Jose
Recatala-Gomez‡
d,
Tianqi
Deng
bc,
Tan
Huang‡
a,
Jose
Recatala-Gomez‡
d,
Tianqi
Deng
 efg,
Shuo-Wang
Yang
efg,
Shuo-Wang
Yang
 g,
Xiaonan
Wang
*ah and
Kedar
Hippalgaonkar
g,
Xiaonan
Wang
*ah and
Kedar
Hippalgaonkar
 *cd
*cd
aDepartment of Chemical and Biomolecular Engineering, National University of Singapore, Singapore 117585, Singapore. E-mail: chewxia@nus.edu.sg
bDepartment of Chemistry, National University of Singapore, 3 Science Drive 3, Singapore 117543, Singapore
cInstitute of Materials Research and Engineering, Agency for Science Technology and Research, 2 Fusionopolis Way, #08-03 Innovis, 138634, Singapore
dSchool of Materials Science and Engineering, Nanyang Technological University, 50 Nanyang Avenue, Block N4.1, 639798, Singapore. E-mail: kedar@ntu.edu.sg
eState Key Laboratory of Silicon Materials, School of Materials Science and Engineering, Zhejiang University, Hangzhou, Zhejiang 310027, China
fInstitute of Advanced Semiconductors, Zhejiang Provincial Key Laboratory of Power Semiconductor Materials and Devices, Hangzhou Innovation Center, Zhejiang University, Hangzhou, Zhejiang 311200, China
gInstitute of High Performance Computing, Agency for Science Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, 138632, Singapore
hDepartment of Chemical Engineering, Tsinghua University, Beijing, 100084, China
First published on 3rd January 2024
Abstract
Availability of material datasets through high performance computing has enabled the use of machine learning to not only discover correlations and employ materials informatics to perform screening, but also to take the first steps towards materials by design. Computational materials databases are well-labelled and provide a fertile ground for predicting both ground-state and functional properties of materials. However, a clear design approach that allows prediction of materials with the desired functional performance does not yet exist. In this work, we train various machine learning models on a dataset curated from a combination of Materials Project as well as computationally calculated thermoelectric electronic power factor using a constant relaxation time Boltzmann transport equation (BoltzTrap). We show that simple random forest-based machine learning models outperform more complex neural network-based approaches on the moderately sized dataset and also allow for interpretability. In addition, when trained on only cubic material systems, the best performing machine learning model employs a perturbative scanning approach to find new candidates in Materials Project that it has never seen before, and automatically converges upon half-Heusler alloys as promising thermoelectric materials. We validate this prediction by performing density functional theory and BoltzTrap calculations to reveal accurate matching. One of those predicted to be a good material, NbFeSb, has been studied recently by the thermoelectric community; from this study, we propose four new half-Heusler compounds as promising thermoelectric materials – TiGePt, ZrInAu, ZrSiPd and ZrSiPt. Our approach is generalizable to extrapolate into previously unexplored material spaces and establishes an automated pipeline for the development of high-throughput functional materials.
Introduction
Discovering novel materials and novel properties of existing materials is a complex process, and success can mostly be credited to luck or unconventional thinking.1 A general approach towards rational, automated and data-driven design of new materials is desired.2,3 The development of Density Functional Theory (DFT) was a big step towards the discovery of high-throughput (HT) materials.4 However, despite their wide usage, DFT calculations require significant computational resources, and rely on various assumptions by domain experts to obtain successful results. Therefore, laborious work is required before consistent mapping to experimental results.5 Nowadays, novel machine learning (ML) methods are being considered as an alternative to DFT calculations and can achieve similarly accurate results in a fraction of computational time and cost. Furthermore, they also help unravel previously unknown correlations between a priori unrelated material descriptors.6,7 Therefore, deployment of ML algorithms has accelerated the discovery and development of novel materials.8 For example, some of them target the prediction of the stability of crystal structures9,10 as well as crystal properties, e.g., melting points of binary mixtures,11 vibrational entropies and free energies of crystalline compounds,12 and band gaps of a specific type of materials such as perovskites.13 There is also a body of literature that focuses on the discovery of functional materials, like metallic glasses,14 lead-free hybrid organic–inorganic perovskites15 or new molecules for organic flow battery electrolytes.16 Efforts in applying ML to thermoelectrics have also been reported. Gorai et al. reported the very first database dedicated exclusively to thermoelectric materials, the TE Design Lab.17 It contains calculated thermoelectric properties, obtained combining ab initio calculations and modelled electron and phonon transport, offering insights into the intrinsic material properties underlying the thermoelectric figure of merit zT. Following this, Katsura et al. developed Starrydata2, an open web system, to accelerate a comprehensive digitization of data of materials from as-reported plot images in published papers.18 This database was used by Borg et al. to quantify the performance of machine learning models towards the discovery of novel TE materials.19 Along the lines of StarryData2, Na and Chang constructed a dataset containing 5205 chemical compositions of the experimentally synthesized thermoelectric materials and their experimental thermoelectric properties.20 All these approaches rely on manual or semi-manual extraction from the literature. Sierepeklis and Cole used a combination of web-scrapping and natural language processing to develop the first automatically generated database of thermoelectric materials and their properties from the existing literature, containing 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 805 data records, automatically generated from the scientific literature, spanning 10
805 data records, automatically generated from the scientific literature, spanning 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 641 unique extracted chemical names.21
641 unique extracted chemical names.21
In this work, we use suitable ML algorithms to directly predict functional properties using material descriptors. Specifically, we use Random Forest (RF), eXtreme Gradient (XG) Boost, Deep Neural Networks (DNNs), and Crystal Graph Convolutional Neural Networks (CGCNNs) to directly infer functional thermoelectric properties of materials. The efficiency of a thermoelectric material is determined by its figure of merit, zT = S2σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, temperature, and thermal conductivity, respectively.22,23 The thermal conductivity, in turn, can be expressed as the additive contribution of the heat carried by charge carriers (κel) and the heat carried by the vibrations of the crystal structure, or lattice thermal conductivity (κlat). Traditionally, full Boltzmann transport equations (BTEs)24 can be used to calculate the Seebeck coefficient and electrical conductivity. However, the fully accurate solution of BTEs, which requires detailed knowledge of scattering mechanisms and their strengths, is computationally expensive. The main computational difficulty resides in the electron–phonon interaction simulation, and numerical integration over the whole Brillouin zone. Therefore, such direct computation cannot serve as an efficient discovery tool. Alternatively, a constant relaxation time approximation (CRTA), taking DFT-computed band-structure as the input as implemented in BoltzTraP,25 is used for linearized BTE calculations to calculate S2σ/τ0 (henceforth called the power factor) where τ0 is the relaxation time. Although the scattering rates of charges are missing (and thus accuracy in power factor prediction is lowered), this can serve as a screening parameter that links the material's electronic structure to its thermoelectric performance26 and therefore is immensely useful. Leveraging upon detailed calculations performed by Ricci et al. and their open-source dataset,26 with additional descriptors, obtained from Materials Project Database,27 we adopt these computed power factors as outputs for training our ML algorithms and generate supervised models to enable automated, accelerated and high-throughput design without DFT calculations as shown in ESI 1.†
The models for materials by design are built upon the supervised models. First, we use CGCNN as a pre-trained model to extract the ground state features from crystal information. The extracted features along with other descriptor inputs are then fed into a random forest model to systematically search for high-performance thermoelectric materials in a candidate pool that the model has not seen before. The integrative method is based on the following rationale: random forest models overcome the drawback of overfitting and have better interpretability, which is critical for practical materials design, while the CNN is well known for capturing spatial features. Therefore, the as-designed framework not only obtains robust predictive capability, but also exhaustively exploits the structural information of materials via CGCNN. We test this method on cubic compounds, as many high-performance thermoelectric materials exhibit cubic crystal symmetry. The combination of domain-knowledge and ML algorithms resulted in the discovery of new half-Heusler materials, that have not been studied before as promising thermoelectric candidates. We then validate our prediction of high electronic power factor with DFT and BoltzTraP calculations. The results reveal that the predictive accuracy of our algorithmic framework towards such materials by design is high and could provide a general framework for the development of thermoelectric and other functional materials.
Experimental
Data retrieval and pre-processing
In this project, the dataset was obtained from the work of Ricci et al.26 This dataset was developed by retrieving the electronic band structures from Materials Project and utilizing them to compute the thermoelectric properties of materials using a BTE package called BoltzTrap.25 This dataset contains more than 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 entries of multi-level data for 8059 materials and is stored in separate json files. Particularly, there would be multiple entries for each material, each with a different temperature, doping level and carrier type. These 23
000 entries of multi-level data for 8059 materials and is stored in separate json files. Particularly, there would be multiple entries for each material, each with a different temperature, doping level and carrier type. These 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 json files were flattened and compiled into a single file for ease of use for ML application. The flattened dataset was augmented with elemental properties data, retrieved from the Materials Project Database (MPD)27 using the Matminer Python package.28 In short, CGCNN has 15 input features while DNN, XG Boost and RF models have a total of 26 input features. Table 1 shows the input parameters used in the different machine learning models.
000 json files were flattened and compiled into a single file for ease of use for ML application. The flattened dataset was augmented with elemental properties data, retrieved from the Materials Project Database (MPD)27 using the Matminer Python package.28 In short, CGCNN has 15 input features while DNN, XG Boost and RF models have a total of 26 input features. Table 1 shows the input parameters used in the different machine learning models.
| Feature type | Feature | Models |
|---|---|---|
| Index | All models | |
| Atomic descriptors | Range of atomic weight | |
| Mean atomic weight | ||
| Standard deviation of atomic weight | ||
| Range of covalent radius | ||
| Mean covalent radius | ||
| Standard deviation of covalent radius | ||
| Range of electronegativity | ||
| Mean electronegativity | ||
| Standard deviation of electronegativity | ||
| Number of elements | ||
| Molecular weight | ||
| Discriminative physical inputs | n/p type (one-hot encoded) | |
| Temperature | ||
| Doping | ||
| Crystallographic information file (cif) | Crystal structure | CGCNN |
| Number of sites in the unit cell (nsites) | DNN, XGB & RF | |
| DFT dependent descriptors | s fraction | |
| d fraction | ||
| p fraction | ||
| Formation energy per atom | ||
| Energy above hull | ||
| Final energy per atom | ||
| Volume | ||
| Density | ||
| Band gap | ||
| Fermi energy | ||
| Direct/indirect (one-hot encoded) | ||
| Output | Power factor | All models |
Values of S and σ in the dataset were obtained in the tensor format, separately for X, Y and Z directions of each inorganic crystal. These values were averaged using the following formulae:
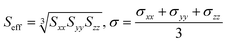 | (1) |
The following filters were applied to the data based on domain expertise before training the machine learning models.
(1) The band gap was set to be greater than 0.16 eV as this should cover most semiconducting thermoelectric materials even for high temperature performance. This criterion is based on the Goldsmid–Sharp criteria, which relates the maximum Seebeck coefficient that can be attained (along the temperature at which it is attained) by a material with its band gap: Smax ∼ Eg/2kBT.29,30 This range includes a correction factor of 1.6, considering the errors from DFT calculations.31 It is to be noted that such a linear transformation does not affect the prediction accuracy of the supervised models.
(2) The energy above the convex hull was restricted to less than 0.05 eV per atom, so that only stable compounds were considered.27 However, other authors have argued that a more accurate cut-off for the energy above the convex hull is 0.08 eV per atom.32 This could be one of the reasons for the low number of discovered compounds.
(3) Compounds with no data for Fermi energy (as estimated from DFT in Materials Project) were excluded.
(4) Data points with 0 value for the power factor were excluded.
(5) Compounds with a non-zero fraction of f-orbital contribution were excluded, as DFT calculations for f-orbitals are known to be challenging to obtain, as well as computationally time-consuming.33
(6) Data points with the following temperature and doping conditions were excluded:
(a) Doping level ≤ 1017 cm−3 for all temperature levels, as traditional thermoelectric materials (for instance PbTe and Bi2Te3) are typically degenerate semiconductors with doping levels ∼ 1019–21 cm−3.
(b) Doping level = 1018 cm−3 and temperatures greater than or equal to 1000 K, because of sparsity of data and our interest in lower to intermediate operating temperatures.
(7) Data points with log10(power factor) < 21 were excluded, as the skew in the dataset would render the training data inaccurate (refer to ESI 8†).
Finally, Box–Cox transformation was employed to normalize the distribution of the input and output features.34 Box–Cox transformation was especially necessary for neural network models as their predictions depend on the distribution of the input feature values unlike tree-based ensemble machine learning methods. Thus, an initial dataset was reduced employing these filters to 8059 unique materials.
Machine learning
The Crystal Graph Convolutional Neural Network (CGCNN) architecture was adapted in this project to predict power factor directly from a material's crystal structure together with some additional atomic descriptors.35 The original CGCNN model was demonstrated to be able to bypass DFT calculations and predict DFT-derived properties such as Fermi energy and band gap directly from the crystal structure of a material. In this work, this CGCNN model has been extended to predict the power factor of a thermoelectric material aiming to circumvent BTE calculations too. The second model trained in this study is a deep neural network (DNN) which has a standard neural network architecture. DNN requires DFT-dependent parameters unlike CGCNN. The other two models developed are random forest and XG boost which take in the same inputs as DNN. By comparing the performance of tree-based ensemble models (i.e., RF and XG boost) with DNN, we investigated if the architecture of machine learning algorithms plays a role in their prediction accuracy.Supervised model training results
The total number of points obtained after applying the filters mentioned in the data pre-processing section, was 529![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314. Of these 529
314. Of these 529![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314 points, 476
314 points, 476![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 points (90% of full dataset) were used for training the models while 52
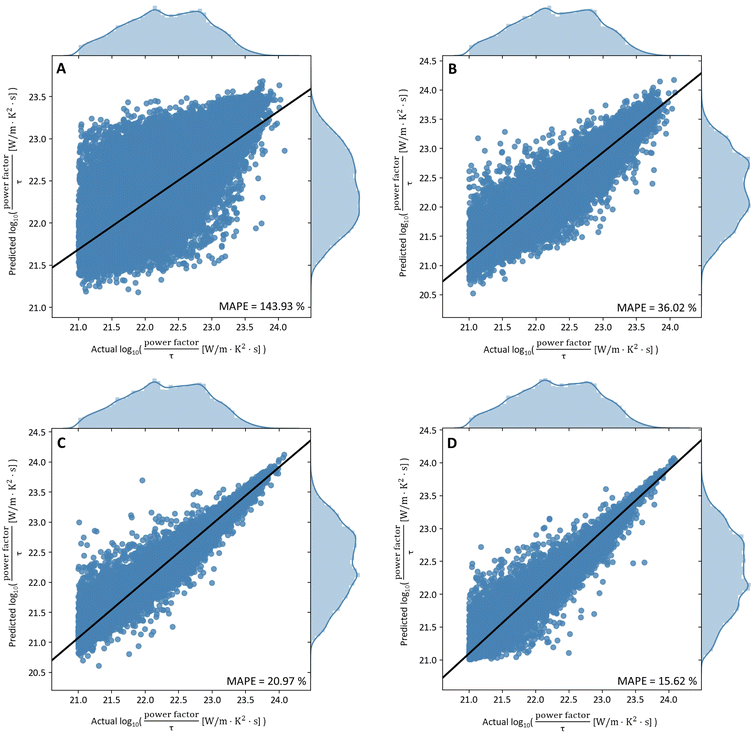
382 points (90% of full dataset) were used for training the models while 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932 points (10% of full dataset) were used for testing the accuracy of the trained models. The best hyperparameters for each machine learning model were determined after searching through the parameter space of possible values on the training data (ESI 6†). Fig. 1 summarises the performance of each model on the test set when trained with these hyperparameters.
932 points (10% of full dataset) were used for testing the accuracy of the trained models. The best hyperparameters for each machine learning model were determined after searching through the parameter space of possible values on the training data (ESI 6†). Fig. 1 summarises the performance of each model on the test set when trained with these hyperparameters.
The graphs shown in Fig. 1 were plotted for log10(power factor) values instead of power factor values as this transformed scale allows for better visualization of the models' performance. However, the errors shown in the plots were still computed using actual power factor values, as per eqn (2).
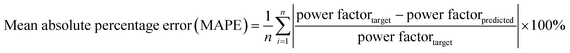 | (2) |
As shown in Fig. 1, random forest performs best on this dataset, followed by XG boost, DNN and finally CGCNN. Based on these results, we can conclude that:
(1) The thermoelectric property of a material cannot be predicted without some first-principles calculations – at least some ground state properties (e.g., Fermi energy), but some first-principles calculations have been replaced by machine learning models with relatively good accuracy (CGCNN for example). In contrast, the other three models, which had inputs comprising DFT-dependent variables, gave significantly better results.
(2) The performance of tree-based ensemble methods (i.e., RF and XG boost) was significantly better than that of neural network models (i.e., DNN) even though the inputs to RF, XG boost, and DNN were the same. A similar result was observed when a database of inorganic materials was trained for only the Seebeck coefficient of materials, which depends on the doping level and conductivity and not on the power factor.36 The difference in the performance of these models might be related to their algorithmic intricacies. For instance, the distribution of the input features does not matter for RF and XG boost as these models learn by separating data based on the reduction in variance of the output value at each split of the decision trees. Moreover, RF and XGboost are composed by a group of estimators, which are also called “trees”. Each tree takes in a portion of the whole dataset randomly, and the decision of the final prediction is by averaging the result of all the sub-trees, which endows them with the advantage of ensemble learning enabling lower variance and bias. In contrast, the actual distribution of the input variables does matter for neural network models: in particular, the under sampled classes could not be effectively trained. This was also the primary reason for applying Box–Cox transformations on the input data before passing to neural network models unlike tree-based ensemble models. More importantly, the tree-based ensemble methods are less computationally expensive and can effectively handle missing input values in model training and testing, with good interpretability.
(3) Among the two tree-based ensemble methods, RF is the clear winner having a relative absolute percentage error of 15.62%. This difference in performance might also be related to the way these models learn from the training data. XG boost focuses on training weak learners (i.e., decision trees with high bias and low variance) through boosting while random forest focuses on reducing the variance of fully grown decision trees through bootstrap aggregation. The depth of a decision tree in XG boost is 10-fold smaller than that in RF (ESI 6†). This means that the number of opportunities available for the XG boost model to make decisions is significantly limited. Hence, this might have prevented the decision trees in the XG boost model from learning the finer details of the underlying physics involved thus accounting for their poorer performance.
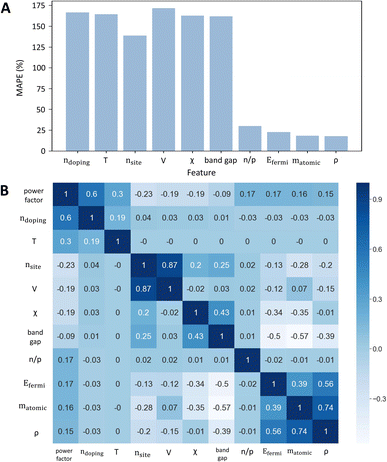
Then, random forest being the most accurate model, was used to determine the most important features in the input for predicting the power factor. Total gain was used as the metric for quantifying the importance of the features in the RF model. After obtaining the feature importance ranking from the random forest model, features were added in descending order of importance and the model's accuracy was computed progressively as seen in Fig. 2A. This means that doping, being the most important feature, was initially used alone to train a random forest model for the full dataset and its accuracy was computed (denoted by the first point of the graph). This result is consistent with the traditional picture of thermoelectric design: one of the first requirements of a thermoelectric material is the ability to position the Fermi level at the optimal point (usually through doping) crucial to achieve a maximum power factor.37 Then, features were progressively added until the model accuracy became almost the same as when all features were used to predict the power factor. As shown in Fig. 2A, by the addition of the 10th feature, MAPE dropped to 17.7% which is approximately the same as that of the RF model trained with all features.
In this way, it can be shown that the 10 most important features are alone sufficient to predict the power factor of a thermoelectric material. Fig. 2A suggests that volume, electronegativity, and band gap are relatively less important features for accurately predicting power factor, as the MAPE value increased after these features were added to the model. This hypothesis was investigated by training a random forest model which did not take in these 3 features as inputs. The MAPE value of this new random forest model was 33%, which is almost 2-fold higher than the original MAPE value (ESI 7†). Hence, the interplay of all 10 features was responsible for the model to predict accurately instead of being associated with some of the features only, as the inter-relationship of these features could be relevant. Fig. 2B shows the Spearman correlation matrix, which quantifies the strength of the monotonic correlation between the power factor and each of the 10 important features of random forest. The magnitude of the correlation coefficients shown in the first row of the matrix was used to generate a feature importance ranking. This ranking was then compared with the earlier ranking of features by total gain importance (see Table 2).
| Ranking | Random forest (total gain importance) | Spearman correlation (correlation coefficient) | Magnitude of correlation coefficient |
|---|---|---|---|
| 1 | Doping | Doping | 0.6 |
| 2 | Temperature | Temperature | 0.3 |
| 3 | n sites | n sites | 0.23 |
| 4 | Volume | Volume & mean electronegativity | 0.19 |
| 5 | Mean electronegativity | n/p type & Fermi energy | 0.17 |
| 6 | Bandgap | Mean atomic weight | 0.16 |
| 7 | n/p type | Density | 0.15 |
| 8 | Fermi energy | Bandgap | 0.092 |
| 9 | Mean atomic weight | — | — |
| 10 | Density | — | — |
Though Spearman correlation and total gain importance use different methods to rank the importance of the variables, Table 2 shows that the ranking is generally in agreement with each other. This serves as concrete evidence that the ranking of the 10 features given by random forest is reliable, with doping and temperature being the most important features. The results are in good agreement with conventional understanding of thermoelectric design and follows directly from the physical model provided by the Boltzmann transport equations, as the temperature and doping levels are known to strongly affect the non-equilibrium transport of charges, responsible for the magnitude of the electrical conductivity and Seebeck coefficient and therefore on the power factor. Number of sites and volume indirectly represent the crystal structure, mostly by referring to the size of the unit cell. On the other hand, mean atomic weight, density and mean electronegativity represent the composition of the material. Composition and structure, through the bonding network, determine the material's band structure, and therefore heavily influence the electrical properties. Fermi energy and bandgap are also indirect representatives of the band structure. Generally, a high power factor is expected for systems with high band degeneracy (Nv) and low inertial effective mass (mI).38–40 The results also seem to indicate that a larger number of sites per unit cell is detrimental for a high power factor. Whilst generally high symmetry crystal structures tend to have a larger valley degeneracy, and this may be associated with a low number of sites per unit cell, this should be taken carefully, as there are several examples where lower-symmetry structures have higher band degeneracies, for instance, in rhombohedral GeTe.41 This leads to the negative correlation between the power factor, and nsites and V. Increased electronegativity difference between elements strongly increases the band mass, due to their impact on bonding,42 so a negative correlation with PF is expected. This is explained considering that an increased electronegativity difference increases the polarity of the bonds, which effectively increases the ionic character of the bonding. Typically, ionic compounds have high effective masses and low mobilities. This will reduce the electrical conductivity and therefore decrease the power factor. A low inertial effective mass may come from a small band gap, which benefits the thermoelectric performance, as previously reported in other studies.40 Therefore, band gap has a negative impact on power factor. However, when the band gap is smaller than a factor of the thermal energy at which the material is operating,3 the bipolar effect is observed. This effect, in which minority charge carriers (holes in n-type materials and vice versa) contribute to the electrical transport is known to be detrimental to the overall power factor. Therefore, the dependence between band gap and power factor is rather complex, which explains the relatively weak correlation.
Feature engineering design
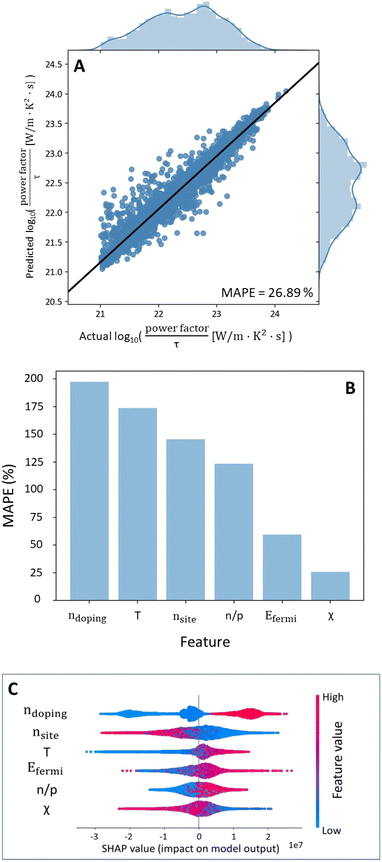
In order to carry out materials by design, it is essential that the model predicts the power factor only based on input features that can be directly obtained from the properties of the atoms in the crystal structure of the material. As seen from Table 2, features such as band gap and Fermi energy are DFT-dependent variables. Hence, material-by-design cannot be performed for a random forest model trained on a full dataset as we still cannot circumvent important DFT-obtained variables.In view of this, a new random forest model was trained for data comprising of cubic materials only with all features as shown in ESI 10.† For this model, after carrying out total gain feature importance analysis, 6 features namely doping, temperature, nsites, n/p type, Fermi energy and mean electronegativity were sufficient to predict the power factor of a cubic material as seen in Fig. 3B. The trained random forest model with the 6 important features is shown in Fig. 3A.
Shapley Additive explanations (SHAP) feature importance was also carried out to validate the feature importance ranking obtained from total gain importance (Fig. 3C).43 The general order of ranking follows total gain importance except that the rankings of nsites & temperature and n/p type & Fermi energy are swapped. However, we note that total gain importance is more reliable than SHAP importance as it is based on how the tree is constructed.
SHAP feature importance is also useful in obtaining the correlations between the input features and the target variable like Spearman correlation. A high level of doping, higher temperatures and large Fermi energy are seen to have a positive impact on the power factor, while n-type is seen to be preferable. On the other hand, a large electronegativity and nsites negatively impact the power factor. A comparison of correlations between SHAP and Spearman correlation was carried out as shown in Table 3. As seen in Table 3, the correlations between the 6 input features and power factor match exactly between SHAP and Spearman correlation.
| SHAP importance (type of correlation) | Spearman correlation (coefficient) |
|---|---|
| Doping (positive) | Doping (0.62) |
| n sites (negative) | n sites (−0.25) |
| Temperature (positive) | Temperature (0.32) |
| Fermi energy (positive) | Fermi energy (0.14) |
| n/p type (positive) | n/p type (0.11) |
| Mean electronegativity (negative) | Mean electronegativity (−0.19) |
In order to estimate the Fermi energy from the crystal structure of the material, the pre-trained CGCNN model was utilized (ESI 9†).35,36 Combining these two models, a general materials design method was developed in order to identify new cubic materials with good thermoelectric properties that are not part of the training set (methodology described in Fig. 4).
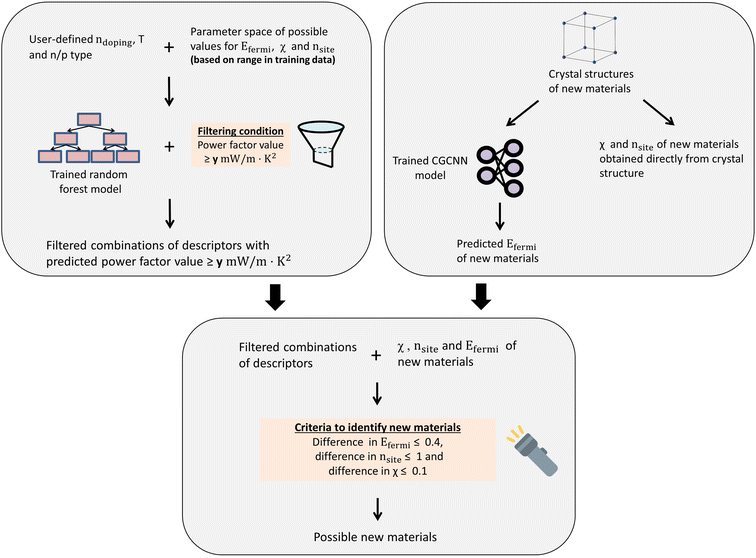 | ||
| Fig. 4 Graphical illustration of methodology to combine random forest model and CGCNN to identify new materials in Materials Project. | ||
This procedure was carried out on different user-defined combinations of ndoping, T and n/p type to identify materials which exhibit good thermoelectric properties over a wide range of conditions. Particularly, high doping levels (1018, 1019 and 1020 cm−3) were used to filter such materials, since generally the optimal carrier concentration falls in this range, and we only considered low and intermediate temperatures (300 K and 500 K) for validation purposes, though our method is generally applicable for higher temperatures too. We did not consider even higher doping (1021 cm−3) as it is possible that the electronic thermal conductivity will be higher, increases the total thermal conductivity and hence decreasing the figure of merit zT.
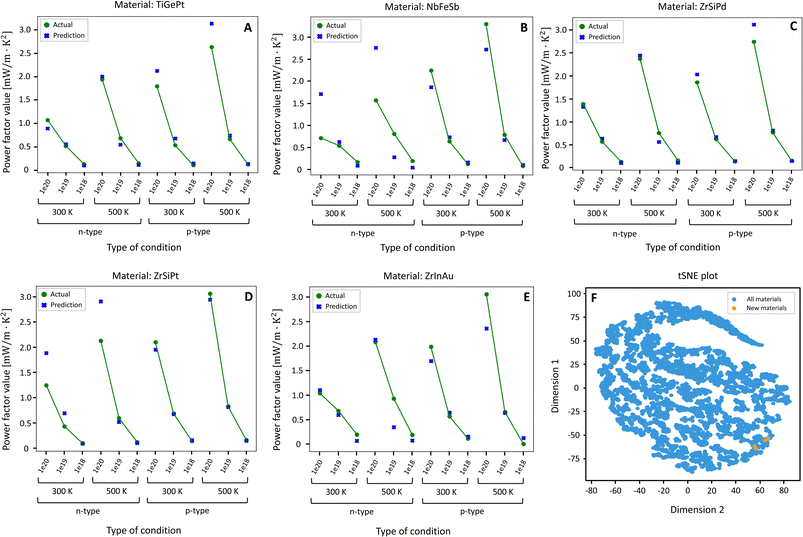
The approach shown in Fig. 4 was applied on 12 unique combinations of physical conditions as seen in Fig. 5. Then, cubic materials which appeared in 10 or more categories were identified as potentially good thermoelectric materials (ESI 12†). Following this approach, 809 compounds were identified as potentially good thermoelectric materials in a list of 6917 cubic structure compounds (ESI 12†). Of these, 4 materials were chosen at random to validate the performance of the filtering algorithm as shown in Fig. 5. As mentioned in ESI 12,† the target power factor values were benchmarked using NbFeSb as it has already been reported in the literature to have a good thermoelectric power factor.44 By comparing the power factor values of the 4 new materials with NbFeSb, it can be shown that they are also equally good thermoelectric materials. These power factor values are comparable to conventional cubic materials. The classic material for TE applications at the intermediate temperature range is cubic lead telluride (PbTe). PbTe is a direct band gap semiconductor, whose valence band maximum is located at the L-point. This band exhibits significant valley degeneracy (Nv = 4). This band has a nearby (∼100 meV of separation) secondary valence band along the Σ line, with its own Nv = 12. The energy separation between bands changes with temperature, and they are known to converge around 600 K. This phenomenon is referred to as band convergence and its effect is a net enhancement in the power factor, and it is responsible for the large power factor values of PbTe. At 600 K, PbTe (n = 5 × 1019 cm−3) has values of power factor between 10 and 13 μW cm−1 K−2 but it can be pushed further with increasing carrier concentration,45,46 reaching a maximum reported power factor of ∼34 μW cm−1 K−2 for n ∼ 1.7 × 1020 cm−3.47 More recently, an analogous telluride to PbTe, germanium telluride (GeTe) has gained momentum for intermediate and high temperature TE applications. Like PbTe, cubic GeTe also shows band convergence but at much lower energy than PbTe (∼64 meV), meaning that the L and Σ valence bands are more likely to converge, explaining the large values of power factor observed in GeTe, ranging from 30 to ∼50 μW cm−1 K−2.48–50 On the other hand, half-Heusler materials exhibit very large power factor values, normally above 30 μW cm−1 K−2, as it is the case for n-type doped ZrNiPb.51 This value can be much higher, as optimal power factor values for both n- and p-type TiNiSn, TaCoSn, YNiSb, NbFeSb, ScNiBi all exceed 50 μW cm−1 K−2.44 Specifically, Zhou et al. achieved a room temperature power factor value of 120 μW cm−1 K−2 for p-type NbFeSb, which decreased to ∼80 μW cm−1 K−2 at 600 K. Other top performing predicted materials with diverse chemistries were also studied, and the results can be found in ESI Section 12.†
A non-linear dimensionality reduction technique called t-distributed Stochastic Neighbour Embedding (t-SNE)52 was employed to investigate the similarity in the properties of the five materials in comparison with the 8059 materials (all crystal structures) from the training set (Fig. 5F). From Fig. 5F, it is observed that the 5 new compounds reside near each other and within the boundaries defined by the training set, which shows that these materials have a strong commonality with one another. The newly identified compounds are from a new dataset, taken from the MP and compared against the training and testing datasets of the supervised models. Therefore, the t-SNE result shows that the input features of the newly found materials have similar traits in the structural domain, as they are half-Heusler compounds that are of cubic symmetry.
Many other half-Heusler cubic structure compounds such as LiZnP, LiZnAs, VFeSb, TiCoSb, ZrNiSn and HfNiSn were also identified even though these materials were never seen by our machine learning algorithm.44,53–55
For validation, we performed DFT band structure calculation followed by BTE computation to obtain CRTA power factor from first principles. DFT calculation was performed using QUANTUM ESPRESSO56,57 with ultrasoft pseudopotentials.58 The charge density was obtained using 83k-points and the band structure was calculated on 483k-points. The band structure was then fed into BoltzTraP to compute the power factors for different temperatures and doping levels. The theoretical calculations validated that the five predicted candidates displayed high power factor. Moreover, the predicted values from machine learning algorithms closely matched the actual values from DFT, the MAE was as low as 0.189 mW m−1 K−2 (ESI Table 9†), which confirms the overall generalization ability of our algorithmic framework in the foreign dataset.
Driven by the results of this work, there are still certain areas of interest worth noting for future work. Firstly, although the validation of our approach on cubic systems is sufficient proof to demonstrate the viability of our design approach, the materials-by-design algorithm can be enhanced to include all materials since there already exist accurate pre-trained CGCNN models for band gap, final energy per atom and formation energy per atom.35 Secondly, excellent electronic transport is just half of the work in designing a good thermoelectric material. Particularly in half-Heusler alloys, it is well-known that the bottleneck limiting their widespread use is their high lattice thermal conductivity. Guo et al. performed phonon calculations to investigate the effect that vibrational entropy has on half-Heusler alloys.59 They concluded that, at high temperature, weakly bonded half-Heusler alloys such as Ti0.5Hf0.5NiGe are stabilized through the introduction of vibrational entropy. This weak bonding is associated with larger atom motion, which translates to a large phonon density of states at low frequency, indicating a low group velocity, effectively reducing the lattice thermal conductivity. Accordingly, we suggest introducing the following criteria in the design of half-Heusler materials: finding an element that will cause an increase in the bond length when doped, since vibrational entropy is rather sensitive to changes in the local bonding environment. Hence, alloying will serve a double purpose: optimizing the carrier concentration and introduction of vibrational entropy. Finding a compromise between these two effects could be the key advancing step in designing high performing half-Heusler thermoelectric materials. Finally, the architecture of the CGCNN model can be modified by changing the design of convolution layers (e.g., number of layers, type of activation functions or type of pooling) to predict the power factor from the crystal structure directly. In our work, the filtering algorithm used in the design approach was only able to identify existing materials in the literature that were previously not known to have good thermoelectric properties. However, an effective inverse design algorithm should be able to construct a new material (crystal structure) for a given set of attributes. This type of inverse design would prove to be more valuable as it will be able to suggest new combinations of materials that have not been explored yet.
Conclusions
Four machine learning models were considered in our work. We identify that random forest is the best supervised model for predicting the power factor of a thermoelectric material with a mean absolute percentage error (MAPE) as low as 15.62%. XG boost was the second-best model for predicting power factor. This can be generalized as tree-based ensemble machine learning algorithms are superior to neural networks for predicting the power factor of a thermoelectric material, most likely due to the nature of good labeling, strongly correlated material features and advantages of ensemble learning. Since random forest is the best supervised model for prediction of power factor, an RF based on pre-training on crystal information of cubic materials was developed. Pre-trained CGCNN was used to extract the Fermi energy values from crystal spatial information. The extracted Fermi energy along with other 5 features were adopted, which were confirmed as being sufficient to accurately predict power factor for cubic materials and adequate to determine the structure for practical design purposes. Therefore, a scanning method using the integrated framework aided by domain knowledge, was carried out to probe potentially high-performance thermoelectric materials in the parameter space. The results obtained five predicted candidates with high power factors and theoretical calculations successfully validated that the predicted values closely matched the actual values, with MAE as low as 0.189 mW m−1 K−2 (ESI Table 9†). More importantly, the high interpretability of our algorithmic framework should indeed be instructive for the oriented design of thermoelectric materials. The as-designed algorithmic framework can accelerate materials development and is applicable to precisely fine tune the structure–property relationship.Data availability
The dataset and processing scripts for this paper are available at the Machine_Learning_for_Thermoelectric_Materials repository at https://github.com/Vaitesswar/Machine_Learning_for_Thermoelectric_Materials.Conflicts of interest
KH owns equity in a company focused on accelerating materials development through machine learning and robotics.Acknowledgements
The authors acknowledge funding from the Accelerated Materials Development for Manufacturing Program at A*STAR via the AME Programmatic Fund by the Agency for Science, Technology and Research under grant no. A1898b0043. KH also acknowledges support from the NRF Fellowship NRF-NRFF13-2021-0011.Notes and references
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- L. Xi, S. Pan, X. Li, Y. Xu, J. Ni, X. Sun, J. Yang, J. Luo, J. Xi, W. Zhu, X. Li, D. Jiang, R. Dronskowski, X. Shi, G. J. Snyder and W. Zhang, J. Am. Chem. Soc., 2018, 140, 10785–10793 CrossRef CAS.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS.
- Materials Project, https://materialsproject.org/docs/calculations, accessed 30 October, 2018 Search PubMed.
- W. Ye, C. Chen, S. Dwaraknath, A. Jain, S. P. Ong and K. A. Persson, MRS Bull., 2018, 43, 664–669 CrossRef.
- T. Deng, J. Recatala-Gomez, M. Ohnishi, D. V. M. Repaka, P. Kumar, A. Suwardi, A. Abutaha, I. Nandhakumar, K. Biswas, M. B. Sullivan, G. Wu, J. Shiomi, S. W. Yang and K. Hippalgaonkar, Mater. Horiz., 2021, 8, 2463–2474 RSC.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Nat. Commun., 2017, 8, 15679 CrossRef CAS.
- A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054303 CrossRef.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220–6227 CrossRef CAS.
- A. Jain and T. Bligaard, Phys. Rev. B, 2018, 98, 214112 CrossRef.
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Sci. Adv., 2018, 4, eaaq1566 CrossRef.
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 3405 CrossRef PubMed.
- S. Kim, A. Jinich and A. Aspuru-Guzik, J. Chem. Inf. Model., 2017, 57, 657–668 CrossRef CAS PubMed.
- P. Gorai, D. Gao, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, Q. Lv, V. Stevanović and E. S. Toberer, Comput. Mater. Sci., 2016, 112, 368–376 CrossRef.
- Y. Katsura, M. Kumagai, T. Kodani, M. Kaneshige, Y. Ando, S. Gunji, Y. Imai, H. Ouchi, K. Tobita, K. Kimura and K. Tsuda, Sci. Technol. Adv. Mater., 2019, 20, 511–520 CrossRef CAS.
- C. K. H. Borg, E. S. Muckley, C. Nyby, J. E. Saal, L. Ward, A. Mehta and B. Meredig, Digital Discovery, 2023, 2, 327–338 RSC.
- G. S. Na and H. Chang, npj Comput. Mater., 2022, 8, 214 CrossRef.
- O. Sierepeklis and J. M. Cole, Sci. Data, 2022, 9, 648 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS.
- J. Recatala-Gomez, A. Suwardi, I. Nandhakumar, A. Abutaha and K. Hippalgaonkar, ACS Appl. Energy Mater., 2020, 3, 2240–2257 CrossRef CAS.
- G. Chen, Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons, Oxford University Press, MIT-Pappal., 2005 Search PubMed.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- F. Ricci, W. Chen, U. Aydemir, J. Snyder, G. Rignanese, A. Jain and G. Hautier, Sci. Data, 2017, 4, 170085 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- H. J. Goldsmid and J. W. Sharp, MIT-Pappalardo Series in Mechanical Engineering, Oxford University Press, 1999, vol. 28, pp. 1–4 Search PubMed.
- Z. M. Gibbs, H.-S. Kim, H. Wang and G. J. Snyder, Appl. Phys. Lett., 2015, 106, 022112 CrossRef.
- M. K. Y. Chan and G. Ceder, Phys. Rev. Lett., 2010, 105, 196403 CrossRef CAS PubMed.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420 CrossRef CAS.
- M. Topsakal and R. M. Wentzcovitch, Comput. Mater. Sci., 2014, 95, 263–270 CrossRef CAS.
- J. Osborne, Pract. Assess. Res. Evaluation, 2019, 15, 12 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS.
- A. Furmanchuk, J. E. Saal, J. W. Doak, G. B. Olson, A. Choudhary and A. Agrawal, J. Comput. Chem., 2018, 39, 191–202 CrossRef CAS PubMed.
- P. Pichanusakorn and P. Bandaru, Mater. Sci. Eng., R, 2010, 67, 19–63 CrossRef.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, npj Comput. Mater., 2017, 3, 1–6 CrossRef CAS.
- H. Zhu, G. Hautier, U. Aydemir, Z. M. Gibbs, G. Li, S. Bajaj, J.-H. Pöhls, D. Broberg, W. Chen, A. Jain, M. A. White, M. Asta, G. J. Snyder, K. Persson and G. Ceder, J. Mater. Chem. C, 2015, 3, 10554–10565 RSC.
- A. Suwardi, D. Bash, H. K. Ng, J. R. Gomez, D. V. M. Repaka, P. Kumar and K. Hippalgaonkar, J. Mater. Chem. A, 2019, 7, 23762–23769 RSC.
- J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 1–12 Search PubMed.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS.
- S. M. Lundberg and S.-I. Lee, in NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017, pp. 4768–4777 Search PubMed.
- J. Zhou, H. Zhu, T.-H. Liu, Q. Song, R. He, J. Mao, Z. Liu, W. Ren, B. Liao, D. J. Singh, Z. Ren and G. Chen, Nat. Commun., 2018, 9, 1721 CrossRef.
- Z. Jian, Z. Chen, W. Li, J. Yang, W. Zhang and Y. Pei, J. Mater. Chem. C, 2015, 3, 12410–12417 RSC.
- Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS.
- G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167 CrossRef CAS.
- Z. Bu, W. Li, J. Li, X. Zhang, J. Mao, Y. Chen and Y. Pei, Mater. Today Phys., 2019, 9, 100096 CrossRef.
- X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, Joule, 2020, 4, 986–1003 CrossRef CAS.
- M. Hong and Z.-G. Chen, Acc. Chem. Res., 2022, 55, 3178–3190 CrossRef CAS.
- J. Mao, J. Zhou, H. Zhu, Z. Liu, H. Zhang, R. He, G. Chen and Z. Ren, Chem. Mater., 2017, 29, 867–872 CrossRef CAS.
- S. Pandey and R. Vaze, in Proceedings of the 3rd IKDD Conference on Data Science, 2016, ACM, New York, NY, USA, 2016, pp. 1–2 Search PubMed.
- U. Chopra, M. Zeeshan, S. Pandey, R. Dhawan, H. K. Singh, J. van den Brink and H. C. Kandpal, J. Phys.: Condens.Matter, 2019, 31, 505504 CrossRef CAS.
- Y. Jin, Y. Xiao, D. Wang, Z. Huang, Y. Qiu and L.-D. Zhao, ACS Appl. Energy Mater., 2019, 2, 7594–7601 CrossRef CAS.
- A. Page, P. F. P. Poudeu and C. Uher, J. Mater., 2016, 2, 104–113 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens.Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens.Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- S. Guo, S. Anand, Y. Zhang and G. J. Snyder, Chem. Mater., 2020, 32, 4767–4773 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on methodology, Box–Cox transformations, machine learning models, and inverse design. See DOI: https://doi.org/10.1039/d3dd00131h |
| ‡ Equal contributors. |
| This journal is © The Royal Society of Chemistry 2024 |