Open Access Article
Open Access ArticleAccelerating nano-XANES imaging via feature selection†
Samantha
Tetef
 a,
Ajith
Pattammattel
a,
Ajith
Pattammattel
 b,
Yong S.
Chu
b,
Maria K. Y.
Chan
b,
Yong S.
Chu
b,
Maria K. Y.
Chan
 *c and
Gerald T.
Seidler
*c and
Gerald T.
Seidler
 *a
*a
aUniversity of Washington, Seattle, WA 98195, USA. E-mail: seidler@uw.edu
bNational Synchrotron Light Source II, Brookhaven National Laboratory, Upton, NY 11973, USA
cCenter for Nanoscale Materials, Argonne National Laboratory, Lemont, Illinois 60439, USA. E-mail: mchan@anl.gov
First published on 21st December 2023
Abstract
We investigate feature selection algorithms to reduce experimental time of nanoscale imaging via X-ray Absorption Fine Structure spectroscopy (nano-XANES imaging). Our approach is to decrease the required number of measurements in energy while retaining enough information to, for example, identify spatial domains and the corresponding crystallographic or chemical phase of each domain. We find sufficient accuracy in inferences when comparing predictions using the full energy point spectra to the reduced energy point subspectra recommended by feature selection. As a representative test case in the hard X-ray regime, we find that the total experimental time of nano-XANES imaging can be reduced by ∼80% for a study of Fe-bearing mineral phases. These improvements capitalize on using the most common analysis procedure – linear combination fitting onto a reference library – to train the feature selection algorithm and thus learn the optimal measurements within this analysis context. We compare various feature selection algorithms such as recursive feature elimination (RFE), random forest, and decision tree, and we find that RFE produces moderately better recommendations. We further explore practices to maintain reliable feature selection results, especially when there is large uncertainty in the system, thus requiring a more expansive reference library that results in high linear mutual dependence within the reference set. More generally, the class of spectroscopic imaging experiments that scan energy by energy (rather than collecting an entire spectrum at once) is well-addressed by feature selection, and our approach is equally applicable to the soft X-ray regime via Scanning Transmission X-ray Microscopy (STXM) experiments.
Introduction
As high-throughput experiments rise in prominence in all fields of science,1 advanced processing techniques – such as image overlay analysis – allow both humans and machines to utilize all information available.2 While the large amounts of data collected in these studies generate more opportunity for insight, these experiments often require quality control3 or feature selection tools4 to be both reliable and manageable. Feature selection is a machine learning technique that takes a set of observables, called features, corresponding to experimental parameters and determines the relative importance of the features in the context of targeted inference. In other words, the goal is to determine what measurement conditions (dictated by the experimental parameters) are needed to strongly retain the targeted information. Feature selection has the advantage of minimizing experimental time while simultaneously encouraging generalizability of learned predictions.5,6Here, we perform feature selection to choose the best measurements for a type of high-dimensional spectral imaging technique called nanoscale X-ray Absorption Near Edge Structure (nano-XANES).7–12 Nano-XANES is a scanning probe technique that contains a XANES spectrum at every pixel (with nanometer precision), by collecting 2D images usually at 50 to 100 energy points. While XANES experiments are popular in many fields of science,13–15 the prevalence of XANES imaging, especially in the hard X-ray regime, is on the rise due to synchrotron advances such as increased beam brightness,16 fast monochromator motors,17 and better spatial resolution18 due to fabrication of better nano-focusing optics.19 On the other hand, nanometer-scale XANES imaging in the soft X-ray regime, such as with Scanning Transmission X-ray Microscopy (STXM), is already a common experimental technique at synchrotrons.
However, hard X-ray spectroscopic imaging experiments are highly time-intensive (over 8 hours) and thus run into conflict with beamtime allocation limitations in addition to having risk of beam damage due to prolonged exposure to the X-ray beam. These time constraints limit expanding the measurement to higher dimensions – for example, expanding into a fourth dimension for in situ time-dependence studies of chemical kinetics.
A common bottleneck for XANES imaging studies is the number of energy measurements in each spectrum, contingent upon the specific experimental beamline. Given this difficulty, we hypothesize that feature selection can help reduce the number of energy points necessary in nano-XANES studies while retaining scientific purpose, such as statistically reliable inferences about the spatial distribution of mineral phases. This approach differs from previous work20,21 that has instead selected spatial regions of interest to gather full spectra, thus compromising global spatial information rather than spectral information. Even though there have been recent advances that accelerate XANES imaging22,23 from an implementation perspective, we find that feature selection can, for the representative test case of mineral phase identification of Fe-rich compounds, decrease total measurement time by ∼80%.
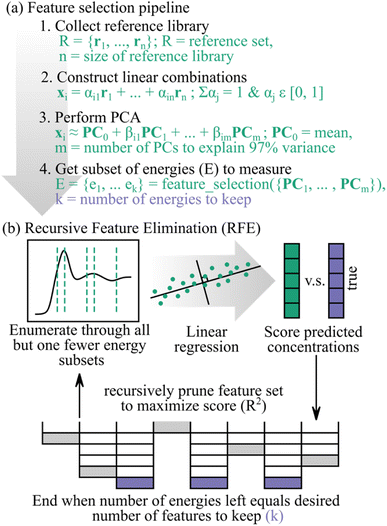
Fig. 1a shows how we incorporated feature selection into our pipeline. Details on the processing can be found in the Methods section, but of importance, we chose a subset of energies to measure in the context of a reference library. We also compare several different feature selection algorithms, namely recursive feature elimination (RFE), decision tree, random forest, and linear regression. Specifically, we find advantageous performance and heuristic merits for RFE,24 a wrapper-based supervised method, as our feature selection routine. Thus, Fig. 1b demonstrates RFE, which we highlight in this manuscript.
As the name suggests, the RFE model decides which input features are the most important by recursively pruning the feature space such that the least important features are removed first. The algorithm decides the importance of each feature by using one of a few possible options. For example, the RFE can correlate a subset of features to the accuracy of predicted target labels by training a base machine learning estimator on that specific feature subset. Or, in the case of linear regression, the RFE can rank the model weights which correspond to each input feature such that the feature with the largest weight is deemed most important and the feature corresponding to the smallest weight is least important. The RFE algorithm will then recursively retrain the base machine learning model on smaller and smaller feature subsets until a desired number of features remains. The recursive nature of RFE has potential benefits over linear regression, random forest, and decision trees if the importance of features change when fewer of them are considered.
In this work, we find that feature selection algorithms provide energy measurement recommendations that produce reduced energy point spectra, which we call subspectra, with enough information to maintain sufficient analysis accuracy. However, when training the feature selection algorithms, we found unwanted sensitivity to spectral correlations and thus pre-processing the spectral training set with principal component analysis (PCA) stabilized the feature selection algorithms (Fig. 1a). Additionally, appropriate normalization of subspectra is critical for accurate results. While our results are generally applicable for any supervised regression feature selection algorithm, we emphasize results using recursive feature elimination (RFE) for which there are conceptual benefits that suggest its modest superiority here may be generic for this class of application.
Methods
The sample and experimental data is the same as it appeared in A. Pattammattel, et al.25 and S. Tetef, et al.26 See those works for the experimental details. Briefly, the sample was composed of stainless steel (SS), lithium iron phosphate (LFP), pyrite (Pyr), and hematite (Hem) nanoparticles. We prepared this sample with prior knowledge to optimize data analysis workflows for spectromicroscopy analysis. Fe K-edge XANES mapping data were collected in about 24 hours at the Hard X-ray Nanoprobe (HXN) Beamline at National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory.18,19 Our reference library is the same as in A. Pattammattel, et al.12 and S. Tetef, et al.,26 which includes the four known phases – stainless steel, LFP, pyrite, and hematite – and seven additional ones – HFO (hydrous ferric oxyhydroxide), goethite, maghemite, magnetite, Fe3P, Fe(III)PO4, and Fe(III)SO4.Training data for the feature selection and machine learning models was generated by linear combinations of reference spectra (Fig. 1a), where a random dropout was included such that after the concentrations were sampled, some contributions were then randomly set to zero and the collection of concentrations were renormalized to sum to one. This dropout parameter enforced sparsity, allowing us to favor fewer references contributing to any one generated spectrum. We then generated validation sets using the same method – random linear combinations of the reference spectra. Because generating each set uses the same dropout parameter, we do not enforce uniqueness, as well as the draws being random, the sets should fall within the same space, and thus our validation set is equivalent as setting aside part of the training dataset.
All feature selection methods, including recursive feature elimination (RFE), random forest (RF), decision tree (DT), and linear regression (LR), are implemented using the sklearn python package. The RFE algorithm was trained on a dataset composed of 1000 linear combinations of references (without additional noise) and with linear regression as the base estimator. We then apply principal component analysis (PCA) to the reference library and project the 1000 generated linear combinations using the principal component vectors obtained from the reference library; the number of principal components was determined such that the principal components explained 99% of the variance in the reference spectra. The PCA-projected spectra were similarly given as training input to the feature selection models, with the PCA-projected coefficients as the target (or output) variables.
We keep the most important energies, which were selected as most important from a dataset of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 linear combinations of reference spectra that were subsequently PCA-projected, where the RFE ranked all energies (it stopped when only one energy was left). The number of energies kept was largely based on the degrees of freedom in the reference library, which we determined by the number of principal components it took to explain 97% of the variance in the reference set. We then choose three additional energies ad hoc to ensure proper normalization of spectra – two in the far pre-edge (maximally spaced) and one in the post-edge (highest energy available). Using normalization and test LCF results, we ultimately kept a total of 16 energies from the original 74 energies experimentally measured – 13 chosen by feature selection and 3 added as hoc for normalization. See results and discussion for more details.
000 linear combinations of reference spectra that were subsequently PCA-projected, where the RFE ranked all energies (it stopped when only one energy was left). The number of energies kept was largely based on the degrees of freedom in the reference library, which we determined by the number of principal components it took to explain 97% of the variance in the reference set. We then choose three additional energies ad hoc to ensure proper normalization of spectra – two in the far pre-edge (maximally spaced) and one in the post-edge (highest energy available). Using normalization and test LCF results, we ultimately kept a total of 16 energies from the original 74 energies experimentally measured – 13 chosen by feature selection and 3 added as hoc for normalization. See results and discussion for more details.
To normalize subspectra, we fit a line to the first two energies in each spectrum (energies which we added for that purpose) and subtracted that line. We then fit another background post-edge line to all energies above 7150 eV; this value created the most consistent normalized spectra, and it was selected based on the post-edge spectral features in the reference set. We found the maximum of the subspectra to determine edge location (rather than the maximum in the derivative, as is commonly done with full spectra) and generated “flattened” spectra by dividing by the post-edge line in the region past the edge so that the post-edge features on average fall along the μ(E)x = 1 line.
As a baseline, we obtain “true” linear combination fitting (LCF) results using the full-energy experimental spectra by performing pixel-by-pixel non-negative least squares linear combination fitting (NNLS-LCF) onto a smaller reference library composed of only the four known phases (SS, Hem, Pyr, LFP). The standard LCF utilizes stepwise regression (regression on enumeration of subsets of the reference library) on every pixel. Instead, here we utilize least absolute selection and shrinkage operator (LASSO) regression to encourage sparsity in fits, as originally presented in Jahrman, et al.27 Details of the alternative LCF approach – LASSO-LCF via manifold projection image segmentation (MPIS) – are in S. Tetef, et al.26 In short, we use Uniform Manifold Approximation and Projection (UMAP)28 and dbscan clustering29 to globally group spectra together and then perform LCF on the cluster-averaged spectra rather than pixel-by-pixel analysis.
Results and discussion
Recursive feature elimination (RFE) training, recommendations, and validation
Because RFE is a supervised feature selection routine, we synthesize a training dataset of linear combinations of reference spectra corresponding to possible mineral phases in our sample. Moreover, this training dataset incorporates prior knowledge of our system and mirrors post-experimental analysis, particularly by inverting the analysis process of linear combination fitting (LCF) onto a reference library. However, the accuracy of this library's composition is, of course, subject to the experimenter's prior knowledge. Here, we knew our sample was made of stainless steel (SS), lithium iron phosphate (LFP), pyrite (Pyr), and hematite (Hem) – see the Methods section. However, to represent a typical user uncertainty, we add other iron-containing mineral phases to the reference library. Specifically, we supplement the library with HFO (hydrous ferric oxyhydroxide), goethite, maghemite, magnetite, Fe3P, Fe(III)PO4, and Fe(III)SO4.12,26The size of the reference library is well known to be a nontrivial issue in linear combination fitting (LCF), or any other method of inference, when working with XANES data.27 Specifically, as the number of spectra in the reference library increases, the relative linear independence of the ensemble of spectra almost always decreases; often, the decrease is dramatic. This poses a core dilemma – if the spectra in the reference library have only weak linear independence, then any LCF fit results will be highly degenerate as there will be multiple solutions with almost identical goodness of fit parameters.
The same issue of the lack of linear independence in the reference library also impacts any feature selection algorithm. The choice of reference spectra, or generically the choice of basis vectors that are used to generate linear combinations for a training dataset, plays a critical role in the reliability of the feature selection results. For example, we randomly selected 50 experimental spectra as a basis set to generate linear combinations for the training data to simulate real-time feature selection during an experiment in the case entire spectra are collected at a time. However, using experimental spectra as a basis creates too little linear independence for the RFE algorithm to discern a solution; the base machine learning model at the center of the RFE learns unreliable solutions. We find that, in this case, the RFE produces recommendations that are contrary to our intuition by selecting energies (features) with low spectral variance (Fig. S1†). By contrast, the RFE results match our intuition – identifying regions with high variance as important – when the basis vectors are chosen to be linearly independent (shown below). For illustrative purposes, the RFE matches human intuition for the synthetic case where distinct Gaussian distributions act as the basis vectors for training the RFE (Fig. S2†). This pattern is equivalently present for the other feature selection algorithms we compared: linear regression, decision tree, and random forest.
However, if we relax the goal of inferring only from linear combinations of compositions but instead focus on information retention for the feature selection algorithms, we can circumvent the lack of linear independence issue. To do so, we recommend applying principal component analysis (PCA)30 to the reference library and then projecting the generated linear combination spectral training dataset onto these principal components. This pre-processing step forces feature inputs and target outputs to be linearly independent and thus obtain unique solutions for the feature selection model to learn. To be precise, the resulting unique solutions will be in terms of weighting coefficients of the principal components, not the reference spectra. Mathematically, we generate the linear combination spectra via
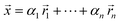 | (1) |
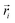 is a normalized spectrum in a reference library of size n, and where ∑iαi = 1. We then project spectra using PCA as
is a normalized spectrum in a reference library of size n, and where ∑iαi = 1. We then project spectra using PCA as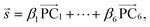 | (2) |
It then remains the experimentalist's task to address the lack of linear independence in the reference library when performing linear combination fitting on the final experimental data (taken with a reduced number of energy points), even though enforcing linear independence helps for feature selection. The distinct task of speeding up the experiment with feature selection is separate from performing analysis via linear combination fitting. The goal here is to perform feature selection that retains sufficient information. The subsequent data analysis gets no easier, but if we succeed in retaining (nearly) all information, then the analysis does not get more difficult, yet the experiment is accelerated.
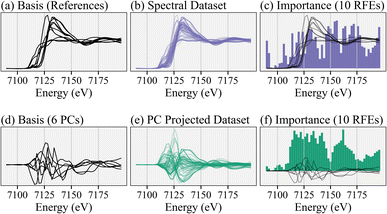
To illustrate the benefits of the PCA-based training dataset, Fig. 2 compares the RFE recommendations using the linearly dependent reference spectra versus the linear independent principal components as the basis for training data. Similar results occur with the other feature selection algorithms. Specifically, the first row uses the reference library (Fig. 2a) to make linear combinations (Fig. 2b) to train an ensemble of 10 RFE models and obtain a collective importance of every energy (Fig. 2c). On the other hand, the second row uses the first few principal components as a basis (Fig. 2d) for both the references and training dataset (Fig. 2e), to achieve RFE results (Fig. 2f). The RFE recommendations for both focus on the rising- and post-edge regions and result in similar prediction accuracies even though the energies are not the same. Fig. S3† quantitatively compares the results of training the RFE on the linear dependent versus linearly independent pairs of basis and target variables. The key observation is that the linear independence of both the input basis vectors and output coefficients help.
While an appropriate choice in a small but comprehensive reference library might mitigate the effects of linear dependence of the basis set when training the RFE model, applying PCA first is a flexible procedure that allows for inclusion of a larger reference library, thus providing robustness against incorrect or incomplete priors for composition. Again, it remains the experimentalist's task to address the lack of linear independence in the reference library when performing linear combination fitting on the final experimental data (taken with a reduced number of energy points), even though enforcing linear independence helps for feature selection; there is a clear separation of tasks between speeding up the experiment with feature selection and performing analysis via linear combination fitting. The goal here is to perform feature selection that retains sufficient information. The subsequent data analysis gets no easier, but if we succeed in retaining (nearly) all information, then the analysis does not get more difficult yet the experiment is accelerated.
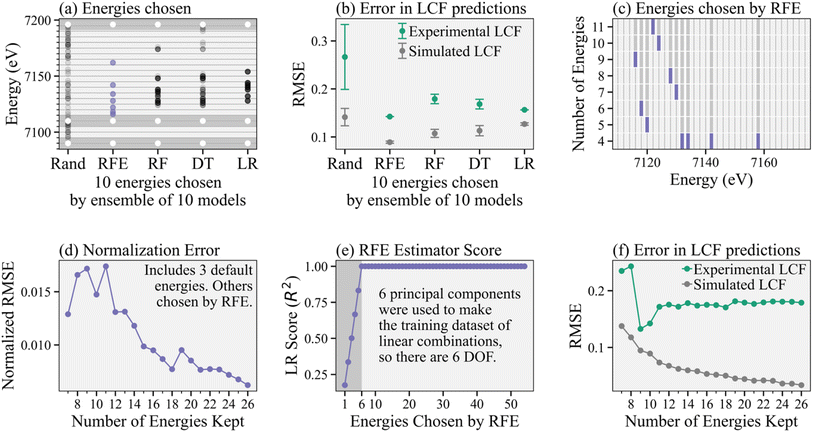
Continuing our analysis based on the PC-constructed training dataset, Fig. 3a shows the results for four different feature selection models, i.e., RFE, random forest (RF), decision tree (DT), and linear regression (LR), and compares them to a random selection of energies. We show the combined results of an ensemble of 10 instances (each with a corresponding randomly generated training dataset to demonstrate changes in results based on different input data) for each feature selection model (including 10 random draws), where each model selects the top 10 (arbitrarily chosen number) energies. We then add the same three energies to ensure normalization, as indicated by white points in the dark gray regions, for a total of 13 energies kept. We chose 10 instances of each model to show the variation of each model to different random samplings of the training data.
Fig. 3b shows the corresponding average and standard deviation of LASSO-LCF predictions given the energy selections for each feature selection model, where LCF is predicting the α coefficients corresponding to the reference spectra rather than the β coefficients corresponding to principal components. We compare the errors on both the simulated LCF (using a generated test dataset of linear combinations of references) and the actual experimental spectra. For the experimental spectra, we determine the “true” coefficients by performing non-negative least squares (NNLS) onto the four known reference spectra using the full energy point spectra. For each reduced energy point subspectrum, we perform LASSO regression onto the references (also reduced in energy points) to obtain the predicted coefficients. We focus on RFE in this paper since it produces moderately better subspectra with lower errors in predictions, likely due to the recursive nature of the algorithm, but the other feature selection algorithms may also be worth considering when exploring other systems.
Fig. 3c shows the consecutive energies discarded by the RFE as fewer energies are kept. Of note, the same energies are kept during each retraining of the RFE, where in each retraining the RFE picks fewer energies. This pattern is demonstrated by the purple stopping points and indicates that the RFE recommendations are consistent, regardless of the hyperparameter determining the number of features (or energies) to keep.
Fig. 3d shows the error in normalizing XANES spectra using the reduced energy point subspectra. Specifically, the normalized root mean squared error (RMSE/number of energies chosen) is shown, where the error is calculated between subspectra that are normalized after energy cuts from the raw experimental spectra and the spectra normalized first using the full energy spectra and then sliced by energy to make the subspectra. Because there is no spectral variation in the far pre-edge, the RFE does not choose energies in that region. However, normalization of real experimental data requires fitting a line in that region to account for stray elastic and Compton scattering of the primary beam or tails of fluorescence from other elements, for example. Thus, we add two default energies in the far pre-edge (to ensure this line can be appropriately determined) as well as another high energy point to similarly help with normalization. We see the error in normalization is reasonably small when more than 15 total energies are kept (12 chosen by the RFE plus the three default ones). However, we recommend taking further care to determine the number of energy points needed to ensure normalization.
Fig. 3e shows the score (coefficient of determination, or R2) of the base estimator inside the RFE, in this case linear regression (LR), as more and more energies are chosen by the RFE. Because each spectrum has six degrees of freedom (DOF) – one for each of the principal components the spectra are projected onto – the score for the base estimator is imperfect when fewer than six energies are kept, exactly because the system of equations is underdetermined in that regime. Thus, we recommend keeping enough energy points such that number of energies is greater than the number of principal components required to explain 99% variance of the reference set. Increasing uncertainty in the system by including a larger reference library31 slowly affects the number of principal components needed to reach 99% variance, see Fig. S4.† Finally, Fig. 3f compares errors in LCF predictions (on both the simulated linear combinations and experimental data) using different number of energies in the subspectra. Again, we have added three default energies to ensure normalization, so the RFE algorithm is recommending between 4 and 23 energies for a total of 7 to 26 energies kept, as shown. We see that errors in LCF predictions on the experimental spectra converge once 11 energies total are kept, providing a lower bound on our subspectra size. The slight drop in error at 9 and 10 energies kept is likely due to differences in normalization.
Reliability of inferences using measurements chosen by RFE
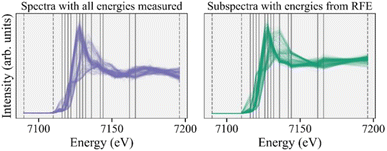
As emphasized above, the goal of feature selection is to reduce the number of measurements while retaining sufficient information for the desired analysis. We now transition to inferences on the reduced energy point experimental subspectra and demonstrate that the inferences are consistent when performed on the subspectra dataset guided by feature selection and the original dataset with all energy points.Following the recommendations above, we select the 13 most important energies recommended by the RFE algorithm and then add three ad hoc energies to ensure normalization, thus keeping a total of 16 energy points in our subspectra. We then take energy cuts of the experimental and reference spectra using these 16 energies and renormalize all subspectra independently. We attempt to combat any systematic errors in normalization in the experimental subspectra by renormalizing the reference subspectra as well. The full experimental spectra and 16-energy subspectra are shown in Fig. 4, with the solid gray lines indicating the RFE recommended energies and the dashed lines indicating the energies we added for normalization. Fig. S5† shows correlation matrices for both the full reference spectra and reference subspectra and Fig. S6† shows scree plots for the experimental dataset for the full spectra and subspectra. Both of those figures support our assertion that most of the information in the full spectra is retained in our subspectra.
Next, we apply manifold projection image segmentation (MPIS) to cluster spectra in the nano-XANES image and then performed linear combination fitting (LCF) via LASSO-LCF, as detailed in S. Tetef, et al.26 and originally presented in Jahrman, et al.27 Briefly, MPIS applies PCA to the spectra and then nonlinear dimensionality reduction, in the form of UMAP, to the projections onto the principal components. Then dbscan clustering groups spectra together such that cluster-average spectra are used to perform LASSO-LCF. See Fig. S7–S9† for the first four principal components, PCA triangle plot, and dbscan clustering on the UMAP space.
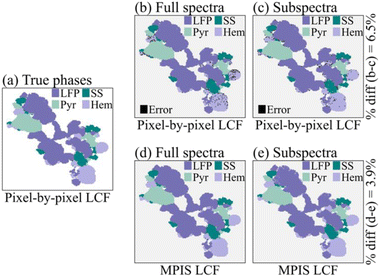
The end results for LASSO-LCF via MPIS are shown in Fig. 5. We calculate the “true results” (Fig. 5a) via pixel-by-pixel non-negative least squares linear combination fitting (NNLS-LCF) regression using just the four known phases as our reference library. We then compare the standard analysis procedure – pixel-by-pixel NNLS-LCF – using the full reference library on the full-energy spectra (Fig. 5b) versus the 16-energy subspectra (Fig. 5c). The dark speckles in these images are pixels where NNLS-LCF reported phases that were not one of the true phases, i.e., where it was distracted by the lack of linear independence in the reference set. The percentage of pixel difference between Fig. 5b and c is about 6.5%.
Finally, we compare these results instead using LASSO-LCF via MPIS on the full-energy spectra (Fig. 5d) and the 16-energy point subspectra (Fig. 5e). The results for the MPIS on the subspectra (Fig. 5e) are almost identical to the full-spectra results (Fig. 5d) – the percent difference is about 3.9% – indicating the 16-energy subspectra retained enough information to maintain accurate inferences of composition. Moreover, using the MPIS before performing LASSO-LCF removed the NNLS-LCF errors in Fig. 5b and c.
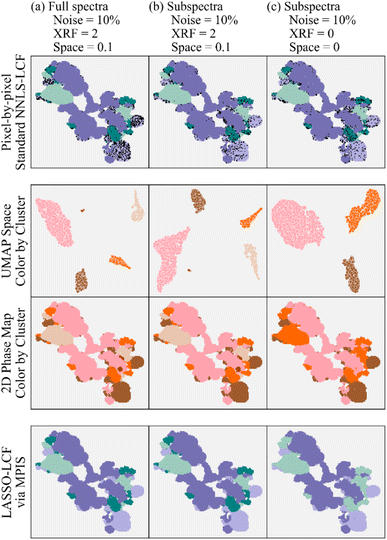
However, other experiments with larger noise would be more sensitive to incorrect results when fewer energy points are measured. To further reduce sensitivity to noise, we encode two additional modes of information into the MPIS analysis – the spatial location of each spectrum as well as the elemental composition of every pixel, specifically sulfur, phosphorus, and chromium using the X-ray fluorescence (XRF) intensities. The benefits of this approach are shown in Fig. 6, where Fig. 6a has the results for noisy full energy spectra (Gaussian noise with a standard deviation of 10% of the spectral intensity at each energy is added to the experimental spectra). We include augmented information by tuning the strength of the encoding of the XRF data and spatial location of every pixel using the “XRF” and “Space” weighting hyperparameters, respectively. The detail of this encoding is explained in S. Tetef, et al.26 To view the overall effects of varying the two hyperparameters in MPIS that control spatial segregation – strength of the encoding of spatial location and the number of neighbors in UMAP – see Fig. S10.† In summary, the UMAP space is a two-dimensional representation of the spectra and shows clustering of the experimental data; the details of the morphology of those clusters are not important here.
Fig. 6b shows the results for the same augmented information except using the 16-energy point subspectra. The MPIS generates similar phase maps for both the full spectra and subspectra with the additional information encoded. However, performing MPIS on the subspectra without the augmented information (Fig. 6c) fails to appropriately separate out two of the four phases (plus a small cluster of outliers), indicated by the UMAP space only containing three large clusters rather than four. Thus, the extra information encoded into the MPIS pipeline helped to recover the extra cluster, distinguishing hematite from stainless steel when noise levels are high. Also of note, the black dots represent incorrect LCF results at that pixel. The pixel-by-pixel LCF on the subspectra likely has fewer incorrect pixels because of the decrease in correlation of the reference subspectra (Fig. S5†), due to the increase in information density of the subspectra compared to the full spectra.
In general, feature selection, such as RFE, can be highly beneficial for any high-throughput experiment that produces high-dimensional spectra, not just nano-XANES imaging. For example, as an extension of our work here, feature selection would be applicable to imaging experiments in the soft X-ray regime, called Scanning Transmission X-ray Microscopy (STXM); similar to nano-XANES imaging in the hard X-ray regime, STXM scans over a sample energy by energy rather than taking full spectra at every spatial location. Moreover, while we applied feature selection to a system with a relatively small reference library here, it can also be applied on a representative set of collected experimental spectra rather than reference spectra, although more analysis and validation would be required. For example, the experimenter might perform a quick, coarse-grained study of the sample using all energies and use feature selection before performing a higher resolution scan with fewer energy points. However, feature selection requires careful evaluation, especially how the constrained experiment effects spectral normalization, so that reliable results can be maintained before performing the constrained experiment. We also recommend a variety of feature selection algorithms to be explored, not just RFE, even though we demonstrated feature selection results with RFE here. Furthermore, while we achieved 80% reduction in experimental time for this system, for other systems where variations are smaller and less distinct, such as 4d K-edge and 5d L3-edge rather than the 3d K-edge nano-XANES here, more energies will likely be needed to maintain sufficient accuracy and thus there will be less improvement in experimental efficiency.
Conclusions
We have shown that feature selection can be used to select the most important measurements in a nanoscale X-ray Absorption Near Edge Structure (nano-XANES) imaging study; this selection can accelerate high-dimensional spectroscopy experiments that spatially image a sample one energy at a time. We demonstrate the utility of feature selection, highlighting recursive feature elimination (RFE) to introduce this algorithm to the field, on a nano-XANES image of iron-containing mineral phases. However, the benefits of feature selection can equivalently be applied to other imaging spectroscopy techniques such as Scanning Transmission X-ray Microscopy (STXM) experiments.32We observed that there are three key considerations to determining the minimum number of energy points to measure. First, ensuring energies are chosen such that proper normalization can occur is critical in maintaining reliable analysis results, specifically linear combination fitting (LCF). Second, we recommend keeping the number of additional energies to measure at least equal to the degrees of freedom of the reference library, where principal component analysis (PCA) can be utilized to parameterize the number of linearly independent components in the library and thus quantify the uncertainty in the system. Finally, when implementing RFE or any feature selection algorithm, we recommend pre-processing the training dataset of linear combinations of references with PCA to ensure that input and output vectors are linearly independent and thus the learned solutions are unique. The PCA pre-processing step for feature selection, in this context, creates more robust recommendations for larger reference libraries, which are inherently more prone to linear dependence within the set and can thus cause a feature selection algorithm to make unreliable recommendations. Given these considerations, we were successfully able to use feature selection to maintain sufficient information in greatly reduced energy point subspectra, decreasing experiment time by 80% while maintaining similar analysis results.
Data availability
Data and processing scripts for this paper, including XANES and XRF images as well as the reference library, are available at https://github.com/stetef/nano-XANES-microscopy-of-Fe at https://doi.org/10.5281/zenodo.8209040.Author contributions
S. Tetef led the investigation, formal analysis, methodology, and writing effort. A. Pattammattel collected data and assisted with investigation. Y. S. Chu supported investigation. M. K. Y. Chan contributed to conceptualization and supervision. G. T. Seidler contributed to conceptualization, supervision, project administration, and writing effort.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank P. Lam and M. Marcus for sharing their Fe K-edge XANES reference library. We also thank M. Marcus and B. Toner for their beneficial discussions regarding STXM. Finally, we thank S. Rojsatien, N. Kumar, and M. Bertoni for their discussion on feature selection for XANES spectra. This work is supported by the U.S. Department of Energy (DOE) Office of Science Scientific User Facilities project titled “Integrated Platform for Multimodal Data Capture, Exploration and Discovery Driven by AI Tools”. M.K.Y. Chan acknowledges the support from the BES SUFD Early Career award. This research used Hard X-ray Nanoprobe beamline (HXN, 3-ID) of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract no. DE-SC0012704. Work performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract no. DE-AC02-06CH11357. All code is available through GitHub at github.com/stetef/nano-XANES-microscopy-of-Fe.References
- L. F. Li,
et al., High-throughput imaging: Focusing in on drug discovery in 3D, Methods, 2016, 96, 97–102 CrossRef CAS PubMed
.
- M. Blackwell,
et al., An Image Overlay system for medical data visualization, Med. Image Anal., 2000, 4(1), 67–72 CrossRef CAS PubMed
.
- N. Le Meur,
et al., Data quality assessment of ungated flow cytometry data in high throughput experiments, Cytometry Part A, 2007, 71A(6), 393–403 CrossRef PubMed
.
- W. J. Chen,
et al., High-throughput Image Analysis of Tumor Spheroids: A User-friendly Software Application to Measure the Size of Spheroids Automatically and Accurately, J. Vis. Exp, 2014, 89, e51639 Search PubMed
.
- R.-C. Chen,
et al., Selecting critical features for data classification based on machine learning methods, J. Big Data, 2020, 7(1), 52 CrossRef
.
- J. D. Li,
et al., Feature Selection: A Data Perspective, ACM Comput. Surv., 2018, 50(6), 1–45 CrossRef
.
- I. Nakai,
et al., Chemical speciation of geological samples by micro-XANES techniques, J. Trace Microprobe Tech., 1998, 16(1), 87–98 CAS
.
- R. Belissont,
et al., Germanium Crystal Chemistry in Cu-Bearing Sulfides from Micro-XRF Mapping and Micro-XANES Spectroscopy, Minerals, 2019, 9(4), 227 CrossRef CAS
.
- M. Cusack,
et al., Micro-XANES mapping of sulphur and its association with magnesium and phosphorus in the shell of the brachiopod, Terebratulina retusa, Chem. Geol., 2008, 253(3–4), 172–179 CrossRef CAS
.
- M. Bonnin-Mosbah,
et al., Micro X-ray absorption near edge structure at the sulfur and iron K-edges in natural silicate glasses, Spectrochim. Acta B: At. Spectrosc., 2002, 57(4), 711–725 CrossRef
.
- L. Mino,
et al., Iron oxidation state variations in zoned micro-crystals measured using micro-XANES, Catal. Today, 2014, 229, 72–79 CrossRef CAS
.
- A. Pattammattel,
et al., High-sensitivity nanoscale chemical imaging with hard x-ray nano-XANES, Sci. Adv., 2020, 6(37), eabb3615 CrossRef CAS PubMed
.
-
A. A. Hummer and A. Rompel, Chapter Eight – X-Ray Absorption Spectroscopy: A Tool to Investigate the Local Structure of Metal-Based Anticancer Compounds In Vivo, in Advances in Protein Chemistry and Structural Biology, ed. C. Z. Christov, Academic Press, 2013, pp. 257–305 Search PubMed
.
- M. Fernandez-Garcia, Xanes analysis of catalytic systems under reaction conditions, Catal. Rev.: Sci. Eng., 2002, 44(1), 59–121 CrossRef CAS
.
- M. Nicholls,
et al., The contribution of XANES spectroscopy to tribology, Can. J. Chem., 2007, 85(10), 816–830 CrossRef CAS
.
- M. D. Tully,
et al., BioSAXS at European Synchrotron Radiation Facility - Extremely Brilliant Source: BM29 with an upgraded source, detector, robot, sample environment, data collection and analysis software, J. Synchrotron Radiat., 2023, 30, 258–266 CrossRef PubMed
.
- J. Stötzel, D. Lützenkirchen-Hecht and R. Frahm, A new flexible monochromator setup for quick scanning x-ray absorption spectroscopy, Rev. Sci. Instrum., 2010, 81(7), 073109 CrossRef PubMed
.
- E. Nazaretski,
et al., Design and performance of an X-ray scanning microscope at the Hard X-ray Nanoprobe beamline of NSLS-II, J. Synchrotron Radiat., 2017, 24(6), 1113–1119 CrossRef CAS PubMed
.
- H. Yan,
et al., Multimodal hard x-ray imaging with resolution approaching 10 nm for studies in material science, Nano Futures, 2018, 2(1), 011001 CrossRef
.
- N. Mölders,
et al., X-ray Fluorescence Mapping and Micro-XANES Spectroscopic Characterization of Exhaust Particulates Emitted from Auto Engines Burning MMT-Added Gasoline, Environ. Sci. Technol., 2001, 35(15), 3122–3129 CrossRef PubMed
.
- M. Grafe,
et al., Speciation of metal(loid)s in environmental samples by X-ray absorption spectroscopy: A critical review, Anal. Chim. Acta, 2014, 822, 1–22 CrossRef CAS PubMed
.
- B. E. Etschmann,
et al., Speciation mapping of environmental samples using XANES imaging, Environ. Chem., 2014, 11(3), 341–350 CrossRef CAS
.
- U. Boesenberg,
et al., Fast XANES fluorescence imaging using a Maia detector, J. Synchrotron Radiat., 2018, 25, 892–898 CrossRef CAS PubMed
.
- H. Jeon and S. Oh, Hybrid-Recursive Feature Elimination for Efficient Feature Selection, Appl. Sci., 2020, 10(9), 3211 CrossRef CAS
.
- A. Pattammattel,
et al., Multimodal X-ray nano-spectromicroscopy analysis of chemically heterogeneous systems, Metallomics, 2022, 14(10), mfac078 CrossRef PubMed
.
- S. Tetef, A. Pattammattel, Y. S. Chu, M. K. Y. Chan and G. T. Seidler, Manifold Projection Image Segmentation for Nano-XANES Imaging, APL Mach. Learn., 2023, 1, 046119 CrossRef
.
- E. P. Jahrman,
et al., Assessing arsenic species in foods using regularized linear regression of the arsenic K-edge X-ray absorption near edge structure, J. Anal. At. Spectrom., 2022, 37(6), 1247–1258 RSC
.
- T. Sainburg, L. McInnes and T. Q. Gentner, Parametric UMAP Embeddings for Representation and Semisupervised Learning, Neural Comput., 2021, 33(11), 2881–2907 Search PubMed
.
- M. Hahsler, M. Piekenbrock and D. Doran, dbscan: Fast Density-Based Clustering with R, J. Stat. Software, 2019, 91(1), 1–30 Search PubMed
.
- S. Wold, K. Esbensen and P. Geladi, Principal component analysis, Chemom. Intell. Lab. Syst., 1987, 2(1), 37–52 CrossRef CAS
.
- M. A. Marcus and P. J. Lam, Visualising Fe speciation diversity in ocean particulate samples by micro X-ray absorption near-edge spectroscopy, Environ. Chem., 2014, 11(1), 10–17 CrossRef CAS
.
- M. A. Marcus, Data analysis in spectroscopic STXM, J. Electron Spectrosc. Relat. Phenom., 2023, 264, 147310 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00146f |
| This journal is © The Royal Society of Chemistry 2024 |