Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automatic mechanism generation involving kinetics of surface reactions with bidentate adsorbates†
Bjarne
Kreitz‡
 *a,
Katrín
Blöndal‡
a,
Kirk
Badger
a,
Richard H.
West
*a,
Katrín
Blöndal‡
a,
Kirk
Badger
a,
Richard H.
West
 b and
C. Franklin
Goldsmith
b and
C. Franklin
Goldsmith
 *a
*a
aSchool of Engineering, Brown University, Providence, RI 02912, USA. E-mail: bjarne_kreitz@brown.edu; franklin_goldsmith@brown.edu
bDepartment of Chemical Engineering, Northeastern University, Boston, MA 02115, USA
First published on 6th December 2023
Abstract
The open-source Reaction Mechanism Generator (RMG) has been enhanced with new features to handle multidentate adsorbates. New reaction families have been added based upon ab initio data from 26 reactions involving CxOyHz bidentate adsorbates with two heavy atoms on Pt(111). Additionally, the estimation routines for thermophysical properties were improved and extended towards bidentate species. Non-oxidative dehydrogenation of ethane over Pt(111) is used as a case study to demonstrate the effectiveness of these new features. RMG not only discovered the pathways from prior literature but also uncovered new elementary steps involving abstraction reactions. Various mono- and bimetallic catalysts for this process were screened using linear scaling relations within RMG, where a unique mechanism is generated for each catalyst. These results are consistent with prior literature trends, but they add additional insight into the rate-determining steps across the periodic table. With these additions, RMG can now explore more intricate reaction mechanisms of heterogeneously catalyzed processes for the conversion of larger molecules, which will be particularly important in fuel synthesis.
Introduction
The elucidation of reaction mechanisms on transition metal surfaces is the first step in the construction of microkinetic models for heterogeneously catalyzed reactions. This process is often performed on an ab initio basis using density functional theory (DFT) calculations. First-principles-based microkinetic models can be used to tailor catalytic materials and, when combined with multiscale models, can enhance reactor design and performance.1,2 With the advancement in computational power, investigating mechanisms for the conversion of larger molecules is now a common task. For example, Zijlstra et al.3 created a microkinetic model for the Fischer–Tropsch synthesis with a first-principles-based description of the C3 chemistry. Microkinetic models for the conversion of these large molecules necessarily involve highly unsaturated hydrocarbon adsorbates with multiple heavy atoms (here defined to be any element larger than hydrogen). When these large, unsaturated molecules adsorb, they can form multiple covalent bonds with the surface to form a stable, closed shell adsorbate. Species that bind to the surface through more than one atom are referred to as multidentate/polydentate adsorbates. Practically any reaction mechanism that involves adsorbates with two or more heavy atoms can contain multidentate species.Additionally, processes with large molecules encompass extensive reaction networks with numerous possible intermediates and elementary steps. Constructing the reaction mechanisms manually requires considerable chemical knowledge to compile an extensive list of possible elementary steps in the vast reaction space. Software tools are available to help with this task by compiling lists of elementary steps from an initial pool of species.4–6 However, it remains the researcher's responsibility (and challenge) to identify the kinetically relevant pathways with DFT calculations or (first-principles-based) estimation routines. Due to the high computational cost associated with electronic structure calculations for heterogeneous systems and limited computational resources, some chemical pathways remain unexplored. Thus, the determination of kinetic pathways is subject to bias. The Reaction Mechanism Generator (RMG)7–9 creates microkinetic models automatically containing only kinetically relevant pathways using a rate-based algorithm, while probing the entire chemical reaction space of a system. This selection is achieved through an on-the-fly parameterization of all possible elementary steps and intermediates based on ab initio databases and estimation routines.
RMG is a well-established tool to construct gas-phase mechanisms for complex systems, e.g., the pyrolysis of jet fuel.10 Functionalities for heterogeneous catalysts, in contrast, have been added relatively recently.11 Previous studies on the catalysis branch of RMG have focused on expanding the thermophysical adsorbate database,12,13 improving kinetics databases and rate rules of surface reaction families,13,14 and developing important features such as linear scaling relations.15 With these advancements, RMG has successfully generated microkinetic models for the CO2 methanation on Ni(111)14,16,17 and the oxidation of light hydrocarbons.12,13,15 It was also possible to include rigorous quantification of correlated uncertainties in the generation procedure.14,17,18 However, these studies have primarily focused on the chemistry of small molecules. Although RMG was able to construct mechanisms involving larger hydrocarbons, the reliability of its predictions for the C2 chemistry and beyond have not yet been thoroughly explored. One of the reasons for the limitations of RMG in dealing with larger molecules is its lack of functionalities for multidentate adsorbates, which was only previously achieved by providing precompiled reaction libraries.13 This limitation can cause the software to miss pathways that involve multidentate surface species, which are crucial in many important catalytic processes.
Bidentate species are central to the reaction mechanism for the dehydrogenation of light alkanes, which is becoming increasingly important to convert large amounts of shale gas to valuable alkenes.19 The dehydrogenation of light alkanes can happen under either oxidative or non-oxidative conditions.19–21 Although the oxidative route is energetically favorable, it requires O2 and produces H2O as a byproduct; non-oxidative dehydrogenation (NDH), in contrast, leads to valuable H2 as a side product.21 The endothermic NDH is carried out over Pt or CrOx-based catalysts at temperatures of 500 to 600 °C.22–24 A common problem for dehydrogenation is the identification of catalysts that can achieve a high alkane conversion while maintaining a high selectivity towards alkenes and high resistance to coke formation. The desired features can be obtained by alloying Pt or Pd with a range of other transition metals.19,25–27 A promising candidate that is used already at the industrial scale is Pt3Sn.28
Expanding the features of RMG to accommodate multidentate species is necessary to explore the complex dehydrogenation chemistry over the intricate active site motifs and aid in the elucidation of the reaction mechanism. In this study, we present new functionalities for multidentate adsorbates that enhance RMG's ability to explore reaction mechanisms for the conversion of larger molecules. These updates require (i) improved estimation routines for the thermophysical properties of multidentate species and (ii) new reaction families with accurate rate rules. We performed ab initio calculations for 26 reactions involving H/C/O-containing bidentate species on Pt(111) to create Brønsted(Bell)–Evans–Polanyi (BEP) relations for the new families. The updated software is then applied to investigate the NDH of ethane over Pt(111) as a representative test case for larger molecules. Further, we use linear scaling relations to screen across the periodic table, including bimetallic alloys, to demonstrate RMG's capabilities in identifying more active and selective catalysts. The significant updates to RMG greatly improve the exploration of all possible pathways of a mechanism, facilitating the automated discovery of more intricate reaction systems.
Methods
Electronic structure theory
DFT calculations were performed with the plane-wave code Quantum ESPRESSO29,30 using the vdW-DF-cx functional.31,32 SG15 Optimized Norm-Conserving Vanderbilt (ONCV) pseudopotentials, generated with the ONCVPSP code,33,34 were used. The optimized lattice constant with the vdW-DF-cx functional was found to be 3.93 Å for Pt in good agreement with the experimental value. The adsorbate-Pt(111) systems were modeled using a 4-layer Pt(111) slab with a 3 × 3 unit cell and 17 Å of vacuum between the top of the slab and the bottom of the repeated image. A step-wise approach was employed in the geometry optimizations. In the first step, the adsorbates were relaxed on the surface with all atoms fixed in their bulk geometry. In the second step, the bottom two layers of the surface atoms were held fixed, while the top two layers were relaxed with the adsorbates. A plane-wave cutoff of 50 Ry and (5 × 5 × 1) k-point grid was used for both steps and the Marzari–Vanderbilt smearing method35 with a smearing width of 0.02 Ry. The LBFGS algorithm in the Atomic Simulation Environment (ASE)36 was used for geometry relaxations with a maximum force convergence criterion of 0.025 eV Å−1. Sella, an open-source saddle point optimizer,37 was used to find the transition states with a maximum force convergence criterion of 0.05 eV Å−1. In most cases, a robust constrained force interpolation method38 was used to obtain the initial guesses for Sella. Vibrational frequencies of the adsorbates were calculated via finite differences in ASE. A higher plane-wave cutoff of 60 Ry and a (5 × 5 × 1) k-point grid was used for the single-point energy calculations.New features in RMG for multidentate adsorbates
RMG version 3.0 (ref. 9) and its functionalities are described in greater detail in ref. 7, 8 and 39. Ref. 11 describes special features for generating mechanisms for heterogeneously catalyzed reactions. In this paper, we focus only on the parts that were updated: the database of thermophysical properties and the reaction families, including their kinetic estimation routines. This update is focused primarily on H/C/O-containing adsorbates; similar expansion for nitrogen functionality will be the subject of future work.| Xadsorbate = Xgas + ΔXadsorption | (1) |
The adsorption corrections are based on adsorbates in the Pt(111) database, which are organized in a hierarchical tree, with the most generic nodes at the top level and more specific child nodes. RMG replaces functional groups of the discovered adsorbate with wildcards R to find a suitable adsorption correction, and descends the tree to the most specific node that has data.
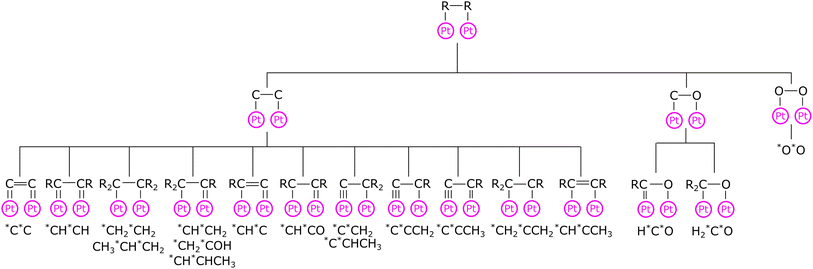
Previously, the corrections were created based on the thermochemistry database of adsorbates with no more than two heavy atoms on Pt(111).12 Since the publication of the RMG database paper,12 the Pt database has been extended to include 113 adsorbates containing many multidentate species,13,18 whereas the adsorption correction database remained unchanged. In the present work, we overhaul the adsorption correction tree for monodentate and bidentate species by providing new child nodes to provide more accurate thermophysical estimates for unknown species, especially for bidentate adsorbates. The adsorption corrections for every node are an average of all species or underlying child nodes at the higher levels. Fig. 1 shows the adsorption correction tree for bidentate adsorbates. Additionally, we created new trees for bidentate adsorbates with bridging atoms between the two adatoms and tridentate species.
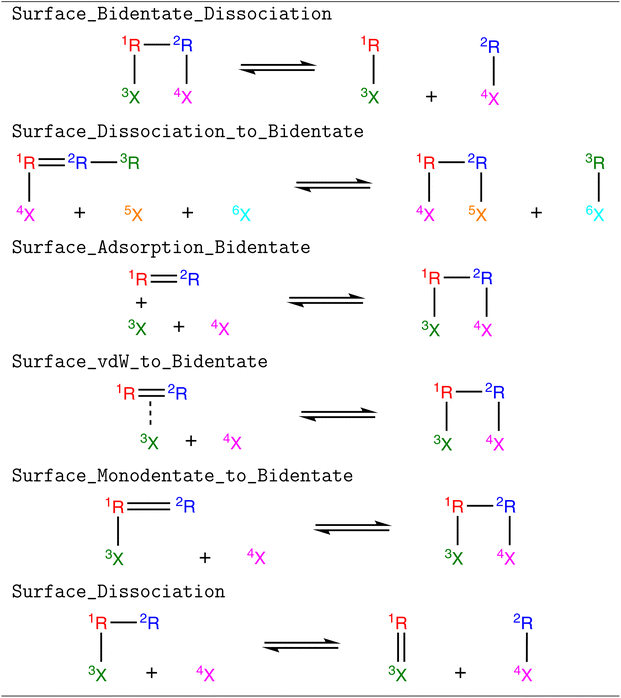
Five new reaction families were created to extend the capabilities of RMG to bidentate or multidentate adsorbates, which are shown in Table 1. We refer to them in a manner consistent with their names in the RMG database. Surface_Bidentate_Dissociation is a template to dissociate a bidentate adsorbate with a single bond into two monodentate species. A monodentate adsorbate can undergo bond scission from an R group to form a bidentate and a monodentate adsorbate, which is described with the Surface_Dissociation_to_Bidentate template. Physisorbed species with double or triple bonds can form bidentate adsorbates (Surface_Adsorption_Bidentate). A similar reaction can occur for monodentate species (Surface_Monodentate_to_Bidentate), where the species bends over to form an additional bond with the surface. Surface_Adsorption_Bidentate provides a recipe for the direct adsorption of a gas-phase molecule as a bidentate species, such as C2H4. Additionally, training data was generated for the dissociation of a bidentate species, where the product remains a bidentate. This bond-breaking recipe is grouped in the (Surface_Dissociation) family, which was introduced in the original development of RMG-Cat.11 Templates for the (Surface_Dissociation) family may not always involve a bidentate adsorbate.
Results and discussion
The DFT results for the energy barriers and reaction enthalpies for a set of 26 unique reactions belonging to the six considered reaction families are listed in Table 2. Raw DFT energies and vibrational modes for these reactions are provided in the ESI.† All data and scripts are made publicly available in ref. 41. Detailed potential energy diagrams for the reactions in the Surface_Bidentate_Dissociation, Surface_Dissociation, and Surface_Dissociation_to_Bidentate families are shown in the ESI in Fig. S1–S3,† respectively. The rate constants for the reactions with a well-defined energy barrier were computed assuming fixed (harmonic) transition state theory over a temperature range of 300 to 2000 K. The partition functions of the transition state Q‡ and initial state QR, as well as the subsequent rate constants kTST in the low-coverage limit, are calculated with in-house Python routines.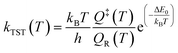 | (2) |
| No | ΔE0 (kJ mol−1) | ΔHrxn (kJ mol−1) | A (cm2 mol−1 s−1) or A (cm4 mol−2 s−1)† or A (s−1)‡ or A (1)¶ | E a (kJ mol−1) | |
|---|---|---|---|---|---|
| a These reactions are endothermic in the reported direction. By default, all reactions are specified in the exothermic direction in RMG's generated mechanism. Therefore, the reverse direction was parameterized with an Arrhenius approach and provided as training data in RMG (see ESI). The forward direction was used to construct the BEP relation. b This is a guess, assuming transition state theory with kBT/h = 1 × 1013 s−1. c Literature values for the adsorption of acetylene are obtained from Vattuone et al.42 and for ethylene from Brown et al.43 | |||||
| Surface_Bidentate_Dissociation | |||||
| 1a | *C*C ⇌ *C + *C | 103 | −77 | 4.22 × 1012‡ | 104 |
| 1b | *CH*C ⇌ *CH + *C | 78 | −80 | 1.30 × 1012‡ | 77 |
| 1c | *CH*CH ⇌ *CH + *CH | 88 | −49 | 7.93 × 1012‡ | 90 |
| 1d | *CH*CH2 ⇌ *CH + *CH2 | 135 | 0 | 2.74 × 1013‡ | 140 |
| 1ea | *CH2*CH2 ⇌ *CH2 + *CH2 | 218 | 71 | 2.61 × 1015‡ | 227 |
| 1fa | *CH*O ⇌ *CH + *O | 180 | 40 | 6.50 × 1012‡ | 183 |
| 1ga | *CH2*O ⇌ *CH2 + *O | 141 | 30 | 3.61 × 1013‡ | 145 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Surface_Dissociation | |||||
| 2a | *CH*CH2 + * ⇌ *CH*CH + *H | 68 | −7 | 9.5 × 1021 | 72 |
| 2b | *CH2*CH2 + * ⇌ *CH2*CH + *H | 55 | −6 | 4.45 × 1021 | 59 |
| 2c | *CH2*O + * ⇌ *CH*O + *H | 1 | −74 | 1.75 × 1021 | 2 |
| 2da | *C*CH2 + * ⇌ *C*CH + *H | 128 | 93 | 2.81 × 1022 | 134 |
| 2ea | *CH*CH + * ⇌ *C*CH + *H | 130 | 70 | 2.84 × 1022 | 137 |
| 2f | *CH*CH2 + * ⇌ *C*CH2 + *H | 44 | −17 | 9.69 × 1021 | 48 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Surface_Dissociation_to_Bidentate | |||||
| 3a | *CH2CH3 + 2* ⇌ *CH2*CH2 + *H | 42 | −41 | 1.67 × 1030† | 46 |
| 3b | *CHCH3 + 2* ⇌ *CH*CH2 + *H | 45 | −34 | 1.95 × 1030† | 49 |
| 3ca | *CH2OH + 2* ⇌ *CH2*O + *H | 50 | 1 | 2.47 × 1029† | 52 |
| 3da | *CCH3 + 2* ⇌ *C*CH2 + *H | 100 | 30 | 1.79 × 1030† | 103 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Surface_vdW_to_Bidentate | |||||
| 4a | CHCH* + * ⇌ *CH*CH | — | −156 | 1.0 × 1021b | — |
| 4b |
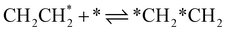
|
11 | −35 | 1.78 × 1021 | 12 |
| 4c | CH2O* + * ⇌ *CH2*O | — | −44 | 1.0 × 1021b | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Surface_Adsorption_Bidentate | |||||
| 5a | CHCH + 2* ⇌ *CH*CH | — | −255 | 0.83¶c | — |
| 5b | CH2CH2 + 2* ⇌ *CH2*CH2 | — | −148 | 0.69¶c | — |
| 5c | CH2O + 2* ⇌ *CH2*O | — | −69 | 0.2¶ | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Surface_Monodentate_to_Bidentate | |||||
| 6a | *CCH2 + * ⇌ *C*CH2 | — | −148 | 1.0 × 1021b | — |
| 6b | *CHCH2 + * ⇌ *CH*CH2 | 3 | −86 | 7.15 × 1020 | 3 |
| 6c | H*CO + * ⇌ H*C*O | — | 6 | 1.0 × 1021b | — |
For consistency with the convention in RMG of defining the exothermic direction as the forward direction, rate constants for reactions 1d–1g and 3c were calculated in the exothermic direction and the fitted Arrhenius parameters for them were used in the RMG training reactions database. Two of the Surface_vdW_to_Bidentate reactions, 4a and 4c, all the Surface_Adsorption_Bidentate reactions (5a, 5b and 5c), and reactions 6a and 6c of the Surface_Monodentate_to_Bidentate were found to have no potential energy barrier. Therefore, fixed transition-state theory could not be used to calculate the rate constants; a more rigorous variational analysis would be necessary. As an approximate solution, Arrhenius expressions with a pre-exponential factor of 1021 cm2 mol−1 s−1 and Ea = 0 kJ mol−1 are used in the RMG database for training reactions 4a, 4c, 6a, and 6c. The rate of adsorption reactions, including bidentate adsorption, is described in RMG with a sticking coefficient S0 in a modified Arrhenius-type equation
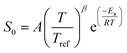 | (3) |
RMG can estimate the reaction kinetics for elementary steps discovered by the templates of the reaction families from either a set of training reactions or hand-crafted BEP relations. The training reactions can be provided in (modified) Arrhenius form, whereas the BEP relations read as
| Ea = E0a + αΔHrxn | (4) |
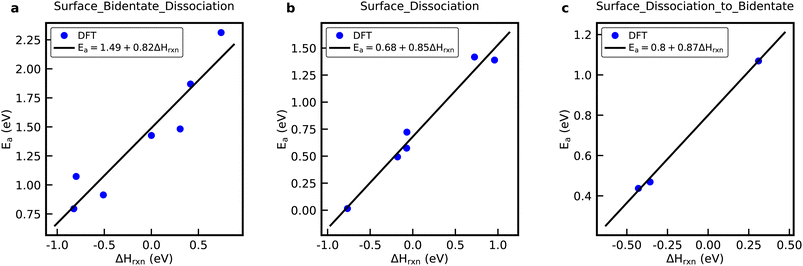 | ||
| Fig. 2 DFT data and BEP relations for the (a) Surface_Bidentate_Dissociation, (b) Surface_Dissociation, and (c) Surface_Dissociation_to_Bidentate reaction family. | ||
Fig. S5† shows the rate constants calculated from DFT versus the rate constants calculated using a general rate rule in RMG, shown by eqn (4) in the ESI,† for the Surface_Bidentate_Dissociation, Surface_Dissociation, and Surface_Dissociation_to_Bidentate families.
Example: ethane dehydrogenation on Pt(111)
The new features added to RMG are used to generate a mechanism for the NDH of ethane on Pt(111) to produce ethylene. RMG's core was initialized with 5% C2H6 in N2 with a vacant Pt(111) surface. This scenario is loosely based on the experiments of Riley et al.28 who investigated PtxSn catalysts supported on Al2O3 for non-oxidative ethane dehydrogenation. The reader is referred to ref. 7, 8, 11 and 39 for details on the automated mechanism generation procedure with RMG and to ref. 13 for a detailed description of the workflow for heterogeneously catalyzed systems.Mechanisms were generated using the ranged reactor feature in a temperature range of 623 to 973 K and a pressure of 1 bar. The maximum number of carbon atoms was set to 3 so as to expedite the mechanism generation process by avoiding larger species, and the maximum number of surface sites was set to 2 to focus on the bidentate chemistry. Gas-phase reactions were not considered, as they are not expected to be important around an operating temperature of 873 K (though RMG can simultaneously explore both gas and surface kinetics12). The mechanism expansion halts if the rate ratio (initial reaction rate divided by the rate of the expansion step) drops below a threshold of 10−7. We determined this threshold through convergence tests, systematically varying it and monitoring both the mechanism size and predictions (see Fig. S7†), similar to the approach detailed in ref. 13. An acceptable value is identified when further reductions do not change the predictions of the microkinetic model. Larger thresholds lead to smaller mechanisms, and tighter thresholds enlarge the microkinetic model. Alternatively, a target conversion or simulation time can be used as a termination criterion.7,8 However, these criteria may lead to extensive mechanisms if the reaction rates are slow, characteristic for a poorly performing catalyst. Further parameters for the mechanism generation are provided in Table 3. We rely solely on the general rate rules in the form of BEP relations instead of training reactions, since this approach has consistently led to excellent results in previous studies.13,14,18
| Property | Value |
|---|---|
| Temperatures | 623–973 K |
| nSim | 7 |
| Pressure | 1 bar |
| Active site | Pt(111) |
| Surface site density | 2.39 × 10−9 mol cm−2 |
| Specific surface area | 1 × 105 m2 m−3 |
| toleranceMoveToCore, εcore | 1 × 10−1 |
| toleranceKeepInEdge, εcore | 1 × 10−8 |
| terminationRateRatio, εrate | 1 × 10−7 |
| maximumCarbonAtoms | 3 |
| maximumSurfaceSites | 2 |
| maximumRadicalElectrons | 0 |
| Initial composition | 5% C2H6, 95% N2 |
| Initial coverage | Vacant site fraction = 1.0 |
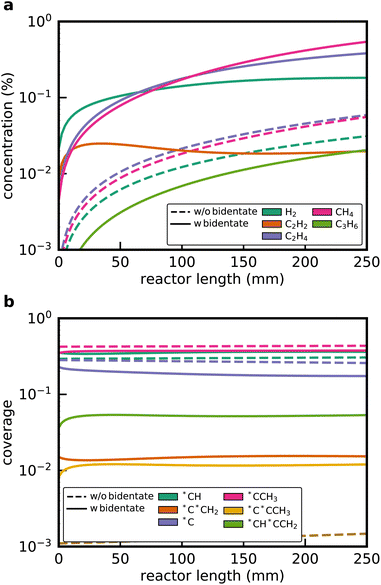
Mechanisms were generated with and without the newly added bidentate reaction families for the ethane dehydrogenation over Pt(111) to demonstrate the impact of the new software features. Without the new bidentate functionalities, the microkinetic mechanism contains 22 species and 64 reactions. RMG still discovers C2H4 as well as CH4, which demonstrates that there are both dehydrogenation and C–C cracking pathways involving only monodentate or physisorbed species. In contrast, when the new bidentate reaction families were included, the resulting microkinetic mechanism contains 52 species and 760 elementary steps. The size of the investigated reaction space is also significantly expanded, as reflected in the size of the edge mechanism (see Table 4). Additionally, the time to generate the mechanism is increased by more than a factor of 10. Both C2H2 and C3H6 are additional discovered gas-phase species for the case with bidentate functionalities, and there are many adsorbates containing 3 carbon atoms (adsorbates with 4+ heavy atoms were restricted by design). In the mechanism generated with the bidentate reaction families, 17 bidentate adsorbates were discovered, and 52 reactions were direct hits from the newly added reaction families and rate rules. If a bidentate adsorbate is discovered, RMG will apply all existing reaction templates as it would do with monodentate species, leading to 594 reactions of the discovered mechanism (≈80% of the reactions) involving bidentate adsorbates. These results highlight that the inclusion of bidentate functionalities leads to an exploration of a larger chemical reaction space. Therefore, the omission of bidentate reaction families neglects potentially kinetically relevant pathways.
Fig. 3a shows the simulated gas-phase concentration profiles along the reactor length for the microkinetic model from the default RMG run and with the new bidentate features. Without any bidentate functionalities, RMG still discovers pathways leading to the formation of C2H4 and CH4, but the overall activity of the catalyst is found to be extremely low. A C2H4 yield of 0.3% is obtained at the end of the reactor. The profiles change considerably when the new reaction families are included in the generation procedure. C2H4 and H2 formation is dominating at the entrance of the reactor, while CH4 formation via C–C cracking reactions gradually increases over the length of the reactor. At the end of the reactor, the C2H6 conversion reaches 14.3% with a selectivity towards C2H4 of 56.4%. Additionally, the formation of traces of C2H2 and C3H6 is predicted, which is also observed experimentally for Pt-containing catalysts.28
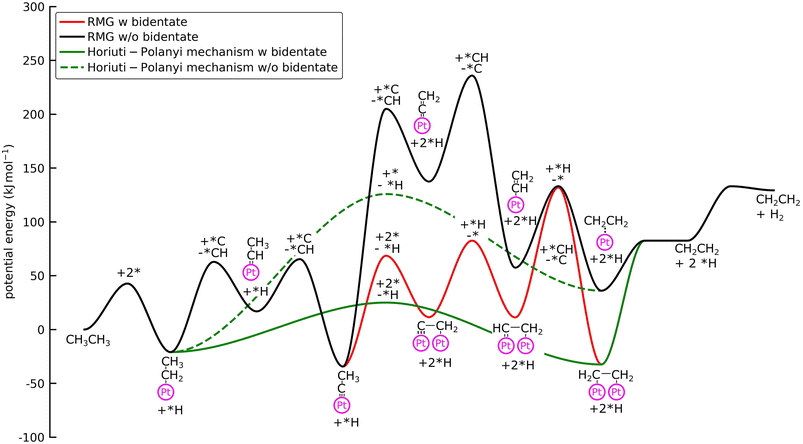
Surface coverages play a significant role in the dominating pathways and influence the composition of the product stream. Interestingly, the new reaction families do not change the coverage profiles (see Fig. 3b). The surface is mostly covered by (*CCH3), which is the most stable adsorbate, with the lowest free energy of formation (Fig. 4), methylidyne (*CH), and surface carbon (*C). This observation can be attributed to the fact that no bidentate species are involved in the formation of *CCH3 (see below). However, bidentate pathways are required to crack or dehydrogenate *CCH3 further. Yet, with bidentate features, new pathways were discovered that lead to deeply dehydrogenated species with 3 carbon atoms, such as *C*CCH3 and *CH*CCH2. These species are considered to be precursors for coke formation, a major challenge during NDH of ethane and propane.24,46,47 Without a truncation of the maximum chain length size, it would have been possible for RMG to discover even larger precursors for coke formation, thereby further expanding the considered reaction space.
 .
.
With bidentate features, the dissociation of the C–H bond in *CCH3 leads to the formation of *C*CH2, as discovered by the Surface_Dissociation_to_Bidentate family, which is considerably more stable than the monodentate counterpart (ΔEb = 1.3 eV) (see Fig. 4). Additionally, the barriers for the monodentate pathway are considerably higher, which explains the low reactivity seen in Fig. 3. This bidentate species is then hydrogenated to C2H4via bidentate vinyl (*CH*CH2) and di-σ ethylene (*CH2*CH2). Formation of acetylene occurs if the *C*CH2 is further dehydrogenated to *C*CH, followed by hydrogenation of the carbon atom.
All intermediates and pathways discussed in the literature were successfully discovered by RMG.25,45 Yet, the main pathways for C2H4 formation uncovered in the reaction path analysis are in disagreement with the proposed path in the literature. Hansen et al.25 showed that *CH2CH3 is directly dehydrogenated to a physisorbed  , following the proposed Horiuti–Polanyi mechanism.48 RMG discovered this elementary step and a similar elementary step, where a bidentate *CH2*CH2 is formed instead of the physisorbed species. As shown in Fig. 4, the reaction pathway with the physisorbed species has a large activation barrier compared to a relatively low activation barrier for the one-step formation of *CH2*CH2. It is debatable whether the assumption of physisorbed ethylene by Hansen et al.25 is justified, as the relaxed geometry clearly shows a bidentate species, which is usually more stable. The transition state calculation showed that bidentate *CH2*CH2 is stabilized by 0.4 eV and there is only a small barrier connecting the physisorbed and bidentate well, which makes it meta-stable, especially if the entropy increases at high temperatures. This fact might seem not relevant at first, but it has an impact on the reaction order, which changes from a first-order reaction with respect to vacant sites
, following the proposed Horiuti–Polanyi mechanism.48 RMG discovered this elementary step and a similar elementary step, where a bidentate *CH2*CH2 is formed instead of the physisorbed species. As shown in Fig. 4, the reaction pathway with the physisorbed species has a large activation barrier compared to a relatively low activation barrier for the one-step formation of *CH2*CH2. It is debatable whether the assumption of physisorbed ethylene by Hansen et al.25 is justified, as the relaxed geometry clearly shows a bidentate species, which is usually more stable. The transition state calculation showed that bidentate *CH2*CH2 is stabilized by 0.4 eV and there is only a small barrier connecting the physisorbed and bidentate well, which makes it meta-stable, especially if the entropy increases at high temperatures. This fact might seem not relevant at first, but it has an impact on the reaction order, which changes from a first-order reaction with respect to vacant sites 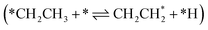 to a second-order reaction (*CH2CH3 + 2* ⇌ *CH2*CH2 + *H). The second-order reaction is orders of magnitude slower for the same amount of available vacant sites. Therefore, this pathway is too slow to occur on the highly covered Pt(111) surface in the generated microkinetic model.
to a second-order reaction (*CH2CH3 + 2* ⇌ *CH2*CH2 + *H). The second-order reaction is orders of magnitude slower for the same amount of available vacant sites. Therefore, this pathway is too slow to occur on the highly covered Pt(111) surface in the generated microkinetic model.
Admittedly, our treatment of coverage dependence for this intricate system is rather simplistic. A completely covered Pt surface is not possible since all these species exhibit strong repulsive interactions. For a more rigorous description, it would be necessary to subject all adsorbates that have a high coverage with lateral interactions as well as cross interactions, but that is beyond the scope of the present work.
Interestingly, most of the hydrogenation or dehydrogenation steps of the adsorbates occur through abstraction (or bimolecular-to-bimolecular) reactions by *C or *CH, respectively. Given the high coverages of these adsorbates, the pathways are actually reasonable and consistent within this study, albeit in disagreement with the literature. Abstraction reactions are often not considered in the literature for heterogeneously catalyzed reactions. Yet, abstraction reactions make up a significant portion of elementary steps in gas-phase reaction mechanisms. One notable exception are oxidative dehydrogenation steps during oxidation of, e.g., ethane.49 However, the abstraction to C and larger moieties is often not considered. This omission has multiple reasons, such as the increasing complexity of potential configuration on a facet as well as the increasing computational costs. Additionally, including all possible bimolecular reactions results in a combinatorial explosion of possible pathways.50 These facts contribute to the omission of these pathways and the dominance of dissociation reactions in the literature. We are currently in the process of improving the rate rules to provide better estimates for these reactions so that it is possible to elucidate the importance of these reactions with a higher certainty. It has also to be mentioned that the catalysts consists of a range of different facets, which can all contribute to the activity.47 This complex morphology has to be considered during the mechanism generation and multiscale modeling for a fair comparison with experiments.2,51
Ultimately, our goal with this study is not to provide conclusive new insights into the ethane dehydrogenation chemistry but to demonstrate that RMG can generate plausible mechanisms for systems involving bidentate species. With the newly added bidentate features, RMG discovers a mechanism that contains all the relevant intermediates and pathways that are discussed in the literature for the NDH of C2H6.25 The usage of RMG to generate a mechanism is just a starting point in the mechanism exploration. A better agreement can be achieved via iterative refinement of the most important energetic parameters identified by degree of rate control analysis13 or via rigorous uncertainty quantification in all possible parameters.14,18 The big advantage of RMG is the exhaustive exploration of all possible reactions. Thus, the software can uncover new pathways that are worth investigating with DFT calculations, e.g. the abstraction reactions.
Automated mechanism generation with linear scaling
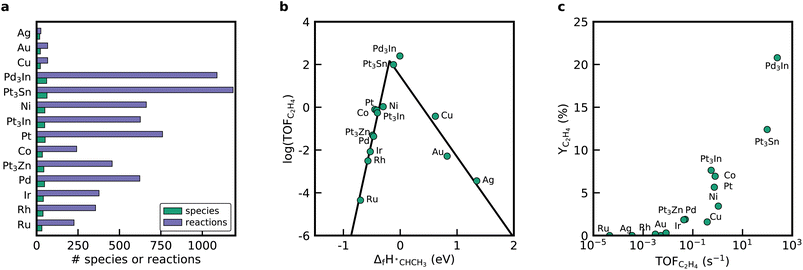
RMG can utilize linear scaling relations to scan the periodic table to reveal more active or selective materials.15 In the prior literature, when looking for an improved catalyst via linear scaling relations, a static mechanism with a fixed rate-determining step is often assumed.25,52–54 In contrast, RMG generates a new mechanism for every point in the descriptor space and does not rely on these simplifying assumptions. Thus, RMG can capture changes in the mechanism since only the kinetically relevant pathways are included due to the objective selection by the rate-based algorithm. To demonstrate RMG's ability to apply scaling relations for mechanisms involving bidentate adsorbates, we screened for improved dehydrogenation catalysts by considering other close-packed monometallic facets and bimetallic alloys. The selection of the catalyst in RMG is performed by either selecting metals from a pre-compiled database or by providing binding energies for the descriptor species, in this case, *C and *H. The binding energies for the monometallic facets are provided in RMG's database and can be called via the metal property tag. We confirmed that the linear scaling relations implemented in RMG are suitable to accurately determine the heats of formation of the bidentate species when scaling from a Pt(111) database, which is discussed in the ESI.†Fig. 5 shows the results from the mechanism generation for the monometallic close-packed surfaces. Every generated mechanism is unique and has its own set of elementary steps and intermediates, which is easily seen by looking at the mechanism metrics in Fig. 5a. Among the tested metals, noble metals like Ag, Cu, and Au have only very small mechanisms, whereas the largest reaction mechanisms were discovered for Pt, Ni, and Co. The time it takes to generate the mechanisms also varies significantly across the different metals. Reactor simulations conducted with the microkinetic models for all metals show only meager C2H6 conversion rates for Ag, Au, and Cu (see ESI†), which is why the mechanism expansion stops early. If the initial production rate is fast due to the adsorption of gas molecules on the surface, but the following reactions on the surface are slow, the threshold for the termination criterion (i.e. the rate ratio), will be reached quickly.
Fig. 5b shows a volcano diagram with the turnover frequency (TOF) for the ethylene production at the initial conditions of the reactor. As a simplification for the linear screening study, we assumed that the coverage dependence of *CCH3 is identical on all close-packed metal surfaces. Concentration profiles in the reactor are provided in Fig. S12.† Mapping the TOF as a function of the enthalpy of formation of *CHCH3 results in a volcano curve based on the monometallic facets. *CHCH3 is identified in the literature to be the selectivity and activity descriptor for NDH.25 The noble metals are located on the right-hand side of the volcano curve, binding *CHCH3 weakly. The rest of the metals are on the left-hand side and exhibit a strong binding energy for *CHCH3. Overall, the activity for ethylene formation at the inlet conditions of the reactor increases in the order Ru < Ag < Au < Rh < Ir < Pd < Cu < Co < Pt < Ni, which is in agreement with literature studies for these close-packed facets. The selectivity towards ethylene obtained at the end of the reactor is highest for Pt(111) and Co(0001).
To enhance the activity and selectivity of the catalyst for the NDH, alloying Pt and Pd with other transition metals is a common approach. In the literature, it was identified that Pt3Sn, Pt3Zn, Pt3In, and Pd3In are promising candidates.19 Accordingly, we generated mechanisms for these alloys using binding energies for *C and *H for the bimetallic catalysts derived from structures from Catalysis-Hub55 (see ESI†), which are based on the work of Hansen et al.25 These bimetallic catalysts align nicely onto the volcano curve created from the monometallic surface. The highest activity is obtained for the Pd3In(111) surface, followed by Pt3Sn(111). Both catalysts also show the highest C2H4 yields at the end of the reactor (see Fig. 5). Next to C2H4 and C2H2, RMG predicts that these catalysts also form propylene, propyne (CH3CCH) and allene (CH2CCH2). Riley et al.28 observed traces of propylene, supporting the results from the automatically generated mechanisms. Co(111) and Ni(111) also form small amounts of C3H6 (see Fig. S12†).
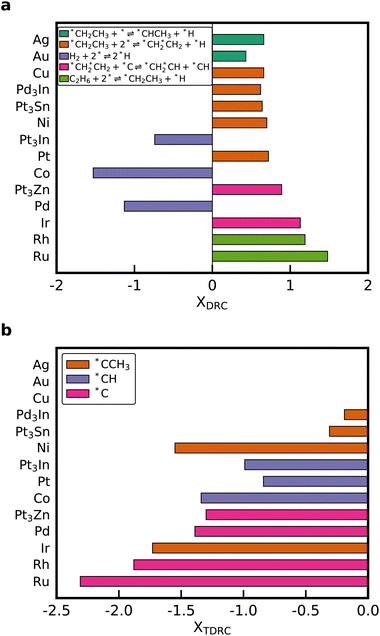
Degree of rate control (DRC) analysis was performed to determine the rate-controlling steps and intermediates.56,57 The elementary steps with the highest DRC for every catalyst are shown in Fig. 6a. Dissociation of *CH2CH3 to *CHCH3 is the elementary step with the highest DRC for the noble metals Au and Ag. The rate-controlling step of the Horiuti–Polanyi mechanism is the dehydrogenation of ethyl to ethylene (*CH2CH3 + 2* ⇌ *CH2*CH2 + *H), which is also obtained for Cu, Pt, Ni, Pt3Sn, and Pd3In. Dissociative adsorption of ethane is rate-limiting for the metals that bind carbon strongly. Interestingly, the production rate of C2H4 is reduced when the dissociative adsorption rate of H2 is increased on Pt3In, Pd and Co. However, for the other metals, a high positive DRC is observed for this reaction, which shows that increasing the adsorption rate of H2 can potentially increase the C2H4 formation rate. Therefore, co-feeding H2 during NDH can be used to accelerate ethane conversion and increase the selectivity towards C2H4.25,46 Similar results are obtained for the thermodynamic degree of rate control (TDRC) as seen in Fig. 6b. Adsorbates with a high thermodynamic degree of rate control are *C, *CH, and *CCH3. These species have a high coverage on the surface and participate in many of the abstraction reactions that lead to *CH2*CH2. Our result shows that it is not justified to assume a fixed rate-determining elementary step or rate-controlling intermediate when changing the binding strength of carbon by multiple eV to scale across the periodic table. A similar variability in the DRC was observed when perturbing the parameters of a microkinetic model within their correlated uncertainty space.14,18
Conclusions
We have enhanced the capabilities of the open-source software RMG for heterogeneously catalyzed reactions to cope with the complexity of multidentate adsorbates. New reaction families were added and generalized rate rules were parameterized with ab initio calculations. RMG was applied in a test case to automatically generate mechanisms for the non-oxidative dehydrogenation of C2H6 on Pt(111), an essential process for the formation of ethylene. A reaction mechanism that consisted of around 90% of elementary reactions involving bidentate species was discovered. Although the considered intermediates and species agree with the literature, the dominant pathway at the investigated temperature proceeds primarily via abstraction reactions pointing to further development directions for the catalysis branch of RMG. In conclusion, with the significant updates performed in this work, RMG can now explore reaction mechanisms for processes involving larger adsorbates.Data availability
The raw DFT data, the RMG database used for the mechanism generation, the generated mechanisms, all scripts used for the simulation and analysis in this paper as well as the scripts used to make the figures are available at https://zenodo.org/record/8341630 with DOI: https://doi.org/10.5281/zenodo.8341630.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank Chris Blais and Chao Xu for helpful suggestions. BK, KB and CFG gratefully acknowledge support by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award #0000232253 and #DE-SC0019441, as part of the Computational Chemical Sciences Program. BK acknowledges financial support from the Alexander von Humboldt Foundation. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357.References
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, First-Principles-Based Multiscale Modelling of Heterogeneous Catalysis, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- G. D. Wehinger, et al., Quo Vadis Multiscale Modeling in Reaction Engineering? – A Perspective, Chem. Eng. Res. Des., 2022, 184, 39–58 CrossRef CAS.
- B. Zijlstra, R. J. P. Broos, W. Chen, G. L. Bezemer, I. A. W. Filot and E. J. M. Hensen, The Vital Role of Step-Edge Sites for Both CO Activation and Chain Growth on Cobalt Fischer–Tropsch Catalysts Revealed through First-Principles-Based Microkinetic Modeling Including Lateral Interactions, ACS Catal., 2020, 10, 9376–9400 CrossRef CAS.
- S. Vernuccio and L. J. Broadbelt, Discerning Complex Reaction Networks Using Automated Generators, AIChE J., 2019, 65, e16663 CrossRef.
- S. Rangarajan, A. Bhan and P. Daoutidis, Language-Oriented Rule-Based Reaction Network Generation and Analysis: Description of RING, Comput. Chem. Eng., 2012, 45, 114–123 CrossRef CAS.
- S. Rangarajan, R. R. O. Brydon, A. Bhan and P. Daoutidis, Automated Identification of Energetically Feasible Mechanisms of Complex Reaction Networks in Heterogeneous Catalysis: Application to Glycerol Conversion on Transition Metals, Green Chem., 2014, 16, 813–823 RSC.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic Construction of Chemical Kinetic Mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- M. Liu, A. G. Dana, M. Johnson, M. Goldman, A. Jocher, A. M. Payne, C. Grambow, K. Han, N. W.-W. Yee, E. Mazeau, K. Blöndal, R. West, F. Goldsmith and W. H. Green, Reaction Mechanism Generator v3.0: Advances in Automatic Mechanism Generation, J. Chem. Inf. Model., 2021, 61, 2686–2696 CrossRef CAS PubMed.
- W. H. Green and R. H. West, RMG – Reaction Mechanism Generator Version 3.0, 2023, https://rmg.mit.edu/, accessed 2023-02-16 Search PubMed.
- F. H. Vermeire, S. U. Aravindakshan, A. Jocher, M. Liu, T.-C. Chu, R. E. Hawtof, R. Van de Vijver, M. B. Prendergast, K. M. Van Geem and W. H. Green, Detailed Kinetic Modeling for the Pyrolysis of a Jet A Surrogate, Energy Fuels, 2022, 36, 1304–1315 CrossRef CAS.
- C. F. Goldsmith and R. West, Automatic Generation of Microkinetic Mechanisms in Heterogeneous Catalysis, J. Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- K. Blöndal, J. Jelic, E. Mazeau, F. Studt, R. H. West and C. F. Goldsmith, Computer-Generated Kinetics for Coupled Heterogeneous/Homogeneous Systems: A Case Study in Catalytic Combustion of Methane on Platinum, Ind. Eng. Chem. Res., 2019, 58, 17682–17691 CrossRef.
- B. Kreitz, P. Lott, J. Bae, K. Blöndal, S. Angeli, Z. W. Ulissi, F. Studt, C. F. Goldsmith and O. Deutschmann, Detailed Microkinetics for the Oxidation of Exhaust Gas Emissions through Automated Mechanism Generation, ACS Catal., 2022, 12, 11137–11151 CrossRef CAS.
- B. Kreitz, K. Sargsyan, E. J. Mazeau, K. Blöndal, R. H. West, G. D. Wehinger, T. Turek and C. F. Goldsmith, Quantifying the Impact of Parametric Uncertainty on Automatic Mechanism Generation for CO2 Hydrogenation on Ni(111), JACS Au, 2021, 1, 1656–1673 CrossRef CAS PubMed.
- E. Mazeau, P. Satpute, K. Blöndal, F. Goldsmith and R. West, Automated Mechanism Generation Using Linear Scaling Relationships and Sensitivity Analyses Applied to Catalytic Partial Oxidation of Methane, ACS Catal., 2021, 11, 7114–7125 CrossRef CAS.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, in 30th European Symposium on Computer Aided Process Engineering, ed. Pierucci, S., Manenti, F., Bozzano, G. L. and Manca, D., Comput.-Aided Chem. Eng., Elsevier, 2020, vol. 48, pp. 529–534 Search PubMed.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, Microkinetic Modeling of the Transient CO2 Methanation with DFT-Based Uncertainties in a Berty Reactor, ChemCatChem, 2022, e202200570 CrossRef CAS.
- B. Kreitz, P. Lott, F. Studt, A. J. Medford, O. Deutschmann and C. F. Goldsmith, Automated Generation of Microkinetics for Heterogeneously Catalyzed Reactions Considering Correlated Uncertainties, Angew. Chem., Int. Ed., 2023, e202306514 CAS.
- J. J. H. B. Sattler, J. Ruiz-Martinez, E. Santillan-Jimenez and B. M. Weckhuysen, Catalytic Dehydrogenation of Light Alkanes on Metals and Metal Oxides, Chem. Rev., 2014, 114, 10613–10653 CrossRef CAS PubMed.
- L. M. Madeira and M. F. Portela, Catalytic oxidative dehydrogenation of n-butane, Catal. Rev., 2002, 44, 247–286 CrossRef CAS.
- H. Saito and Y. Sekine, Catalytic Conversion of Ethane to Valuable Products through Non-Oxidative Dehydrogenation and Dehydroaromatization, RSC Adv., 2020, 10, 21427–21453 RSC.
- D. Fairuzov, I. Gerzeliev, A. Maximov and E. Naranov, Catalytic Dehydrogenation of Ethane: A Mini Review of Recent Advances and Perspective of Chemical Looping Technology, Catalysts, 2021, 11, 833 CrossRef CAS.
- C. Samanta and R. K. Das, in Catalysis for Clean Energy and Environmental Sustainability: Petrochemicals and Refining Processes – Volume 2, ed. Pant, K. K., Gupta, S. K. and Ahmad, E., Springer International Publishing, Cham, 2021, pp. 149–204 Search PubMed.
- M. Huš, D. Kopač and B. Likozar, Kinetics of Non-Oxidative Propane Dehydrogenation on Cr2O3 and the Nature of Catalyst Deactivation from First-Principles Simulations, J. Catal., 2020, 386, 126–138 CrossRef.
- M. H. Hansen, J. K. Nørskov and T. Bligaard, First Principles Micro-Kinetic Model of Catalytic Non-Oxidative Dehydrogenation of Ethane over Close-Packed Metallic Facets, J. Catal., 2019, 374, 161–170 CrossRef CAS.
- V. Galvita, G. Siddiqi, P. Sun and A. T. Bell, Ethane dehydrogenation on Pt/Mg(Al)O and PtSn/Mg(Al)O catalysts, J. Catal., 2010, 271, 209–219 CrossRef CAS.
- S. Liu, B. Zhang and G. Liu, Metal-Based Catalysts for the Non-Oxidative Dehydrogenation of Light Alkanes to Light Olefins, React. Chem. Eng., 2021, 6, 9–26 RSC.
- C. R. Riley, A. De La Riva, I. L. Ibarra, A. K. Datye and S. S. Chou, Achieving High Ethylene Yield in Non-Oxidative Ethane Dehydrogenation, Appl. Catal., A, 2021, 624, 118309 CrossRef CAS.
- P. Giannozzi, et al., Quantum ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- K. Berland and P. Hyldgaard, Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412 CrossRef.
- K. Berland, C. A. Arter, V. R. Cooper, K. Lee, B. I. Lundqvist, E. Schröder, T. Tronhauser and P. Hyldgaard, van der Waals density functionals built upon the electron-gas tradition: facing the challenge of competing interactions, J. Chem. Phys., 2014, 140, A539 CrossRef PubMed.
- D. R. Hamann, Optimized norm-conserving Vanderbilt pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- M. Schlipf and F. Gygi, Optimization algorithm for the generation of ONCV pseudopotentials, Comput. Phys. Commun., 2015, 196, 36–44 CrossRef CAS.
- N. Marzari, D. Vanderbilt, A. De Vita and M. C. Payne, Thermal Contraction and Disordering of the Al(110) Surface, Phys. Rev. Lett., 1999, 82, 3296 CrossRef CAS.
- S. R. Bahn and K. W. Jacobsen, An object-oriented scripting interface to a legacy electronic structure code, Comput. Chem. Eng., 2002, 4, 56–66 CAS.
- E. D. Hermes, K. Sargsyan, H. N. Najm and J. Zádor, Accelerated Saddle Point Refinement through Full Exploitation of Partial Hessian Diagonalization, J. Chem. Theory Comput., 2019, 15, 6536–6549 CrossRef CAS PubMed.
- J. Bae, C. F. Goldsmith and A. A. Peterson, 2023, in preparation.
- M. S. Johnson, et al., RMG Database for Chemical Property Prediction, J. Chem. Inf. Model., 2022, 62, 4906–4915 CrossRef CAS PubMed.
- C. F. Goldsmith, Estimating the Thermochemistry of Adsorbates Based Upon Gas-Phase Properties, Top. Catal., 2012, 55, 366–375 CrossRef CAS.
- B. Kreitz, K. Blöndal, K. Badger, R. H. West and C. F. Goldsmith, Data for Automatic Mechanism Generation Involving Kinetics of Surface Reactions with Bidentate Adsorbates, 2023, DOI:10.5281/zenodo.8341630.
- L. Vattuone, Y. Y. Yeo, R. Kose and D. A. King, Energetics and kinetics of the interaction of acetylene and ethylene with Pd100 and Ni100, Surf. Sci., 2000, 447, 1–14 CrossRef CAS.
- W. A. Brown, R. Kose and D. A. King, Femtomole Adsorption Calorimetry on Single-Crystal Surfaces, Chem. Rev., 1998, 98, 797–832 CrossRef CAS PubMed.
- D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes, 2022, https://www.cantera.org, Version 2.6.0 Search PubMed.
- L. Skubic, J. Sovdat, N. Teran, M. Huš, D. Kopač and B. Likozar, Ab Initio Multiscale Process Modeling of Ethane, Propane and Butane Dehydrogenation Reactions: A Review, Catalysts, 2020, 10, 1405 CrossRef CAS.
- S. Saerens, M. K. Sabbe, V. V. Galvita, E. A. Redekop, M.-F. Reyniers and G. B. Marin, The Positive Role of Hydrogen on the Dehydrogenation of Propane on Pt(111), ACS Catal., 2017, 7, 7495–7508 CrossRef CAS.
- C. Fricke, B. Rajbanshi, E. A. Walker, G. Terejanu and A. Heyden, Propane Dehydrogenation on Platinum Catalysts: Identifying the Active Sites through Bayesian Analysis, ACS Catal., 2022, 12, 2487–2498 CrossRef CAS.
- I. Horiuti and M. Polanyi, Exchange Reactions of Hydrogen on Metallic Catalysts, Trans. Faraday Soc., 1934, 30, 1164 RSC.
- N. R. Peela, J. E. Sutton, I. C. Lee and D. G. Vlachos, Microkinetic Modeling of Ethane Total Oxidation on Pt, Ind. Eng. Chem. Res., 2014, 53, 10051–10058 CrossRef CAS.
- J. T. Margraf and K. Reuter, Systematic Enumeration of Elementary Reaction Steps in Surface Catalysis, ACS Omega, 2019, 4, 3370–3379 CrossRef CAS PubMed.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, Microkinetic Modeling of the CO2 Desorption from Supported Multifaceted Ni Catalysts, J. Phys. Chem. C, 2021, 125, 2984–3000 CrossRef CAS.
- A. J. Medford, A. C. Lausche, F. Abild-Pedersen, B. Temel, N. C. Schjødt, J. K. Nørskov and F. Studt, Activity and Selectivity Trends in Synthesis Gas Conversion to Higher Alcohols, Top. Catal., 2014, 57, 135–142 CrossRef CAS.
- G. Jones, F. Studt, F. Abild-Pedersen, J. K. Nørskov and T. Bligaard, Scaling Relationships for Adsorption Energies of C2 Hydrocarbons on Transition Metal Surfaces, Chem. Eng. Sci., 2011, 66, 6318–6323 CrossRef CAS.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, Degree of Rate Control Approach to Computational Catalyst Screening, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Catalysis-Hub.Org, an Open Electronic Structure Database for Surface Reactions, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- C. T. Campbell, Finding the Rate-Determining Step in a Mechanism, J. Catal., 2001, 204, 520–524 CrossRef CAS.
- C. T. Campbell, The Degree of Rate Control: A Powerful Tool for Catalysis Research, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- T.-C. Chu, Z. J. Buras, P. Oßwald, M. Liu, M. J. Goldman and W. H. Green, Modeling of aromatics formation in fuel-rich methane oxy-combustion with an automatically generated pressure-dependent mechanism, Phys. Chem. Chem. Phys., 2019, 21, 813–832 RSC.
- J. Bae, J. Hashemi, D. Yun, D. K. Kim, D. H. Choo, C. F. Goldsmith and A. A. Peterson, Non-oxidative methane conversion by Fe single site catalysts: quantifying temperature limitations imposed by gas-phase pyrolysis, Catal. Sci. Technol., 2022, 12, 6903–6919 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Transition state theory and BEP relation equations, enthalpy of reaction comparison, potential energy diagrams, electronic structure calculations results. See DOI: https://doi.org/10.1039/d3dd00184a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |