Open Access Article
Open Access ArticleStructure Seer – a machine learning model for chemical structure elucidation from node labelling of a molecular graph†
Denis Andzheevich
Sapegin
 *ab and
Joseph C.
Bear
*ab and
Joseph C.
Bear
 a
a
aDepartment of Chemical and Pharmaceutical Sciences, Kingston University, Penrhyn Rd, Kingston upon Thames KT1 2EE, UK. E-mail: D.Sapegin@kingston.ac.uk
bQuantori, 625 Massachusetts Ave, Cambridge, MA 02139, USA
First published on 20th December 2023
Abstract
The identification of a compound's chemical structure remains one of the most crucial everyday tasks in chemistry. Among the vast range of existing analytical techniques NMR spectroscopy remains one of the most powerful tools. As a step towards structure prediction from experimental NMR spectra, this article introduces a novel machine-learning (ML) Structure Seer model that is designed to provide a quantitative probabilistic prediction on the connectivity of the atoms based on the information on the elemental composition of the molecule along with a list of atom-attributed isotropic shielding constants, obtained via quantum chemical methods based on a Hartree–Fock calculation. The utilization of shielding constants in the approach instead of NMR chemical shifts helps overcome challenges linked to the relatively limited sizes of datasets comprising reliably measured spectra. Additionally, our approach holds significant potential for scalability, as it can harness vast amounts of information on known chemical structures for the model's learning process. A comprehensive evaluation of the model trained on the QM9 and custom dataset derived from the PubChem database was conducted. The trained model was demonstrated to have the capability of accurately predicting up to 100% of the bonds for selected compounds from the QM9 dataset, achieving an impressive average accuracy rate of 37.5% for predicted bonds in the test fold. The application of the model to the tasks of NMR peak attribution, structure prediction and identification is discussed, along with prospective strategies of prediction interpretation, such as similarity searches and ranking of isomeric structures.
1. Introduction
NMR spectroscopy allows for the characterization of the chemical environments of individual atoms, providing the possibility to determine the molecular structure. The concept behind NMR implies the determination of the energy required for the excitation of certain nuclei in the magnetic field1,2 by measuring their characteristic resonance frequency, which strongly depends on the electron environment around them and, hence, their relative position in a given molecule. Such features make NMR spectroscopy a benchmark analytical method, especially when establishing the structure of an unknown compound. However, extracting information about the chemical structure from the NMR spectra often poses a challenge. Spectral interpretation is usually approached by analyzing similar and/or reference compounds, comparing with the modelled (simulated) spectra,3 and, when possible, conducting a database search.4–7 While the first approach is more universal, it requires a significant amount of experience and skill. The second approach is restrained by the precision of the modelling and the initial information about the structure, whereas the third is limited by the completeness of the databases available. Due to these factors, careful consideration and expertise are necessary to interpret NMR spectra accurately.Recent advances in machine learning algorithms have inspired numerous researchers to apply them to tasks related to NMR spectra interpretation.8,9 A significant portion of these efforts are focused on spectra prediction.3,10–12 Accurate prediction of NMR spectra simplifies the interpretation of the spectra, especially when information about the studied compound's potential structure is available. This capability holds significant value for a wide array of specialists by simplifying the interpretation routine.1,2
However, a major obstacle in this field is the lack of extensive and comprehensive databases containing reliable spectral information. This limitation hampers the training capabilities of machine learning models and subsequently restricts their accuracy.
One potential solution to address this issue is to train machine learning models using simulated spectra. These simulated spectra can be obtained through quantum-mechanical atomistic simulation methods,13 providing a valuable alternative data source for training the predictive models. Nevertheless, it is crucial to acknowledge that the accuracy of the predictive models is constrained by the level of theory utilized in the dataset generation.
Despite the abundance of attempts at NMR spectra prediction, there have been only a few attempts at direct NMR spectra interpretation,14,15i.e., predicting the chemical structure of a compound solely from its NMR spectra. The limited success in this area may be attributed to:
- The relatively small size of reliable datasets containing spectral information,3–7,15 which limits the amount of diverse and comprehensive data available for training and validation.
- The non-representative nature of these datasets, which means they may not fully capture the wide variety of chemical structures encountered in practical applications.
Self-consistent field (SCF)16 calculation-assisted machine learning approaches appear to be highly promising based on these observations. SCF approaches enable the calculation of nuclei shielding constants, which define the chemical shifts observed in NMR spectra. Gao et al.12 demonstrated that shielding constants alone can significantly improve the precision of predicting NMR spectra for a given structure. This study suggests the possibility of utilizing SCF calculations to generate a representative dataset for training a machine learning algorithm to reconstruct the chemical structure from the complete list of isotropic shielding constants of the atoms. Moreover, if a complete list of shielding constants for atoms in a molecule can be generated from its NMR spectra, this approach allows for the prediction of the chemical structure based solely on the NMR data and, of course, the elemental composition of the molecule.
Considering the aforementioned points, this research project aims to investigate the efficiency and capability of machine learning in application to chemical structure reconstruction from a list of isotropic shielding constants assigned for corresponding atoms in the molecule. Based on the evaluation it is aimed to suggest a model architecture that will be capable of generating a chemical structure from the information about its elemental composition and a corresponding list of isotropic shielding constants.
2. Methodology
2.1 Preface
In general, the task of structure prediction from the full list of NMR shifts assigned for atoms of a known element can be formulated as predicting a molecular graph adjacency matrix from its node labelling. However, in practical applications, the most commonly studied nuclei are 1H and 13C, and it is often challenging, expensive, and sometimes impossible to acquire NMR spectra of other types of nuclei in the sample. Current research aims at exploring the use of isotropic shielding constants, which can be calculated computationally for all atoms in a given molecule, rather than relying on experimentally measured NMR shifts, for structure prediction. While this approach may have some limitations in its applicability, it allows for the employment of SCF-calculated isotropic shielding constants as equivalents of chemical shifts for our specific task.Furthermore, it is suggested that in organic molecules, where carbon is often the most abundant non-hydrogen element, shielding constants for all non-hydrogen atoms can be predicted with an acceptable level of accuracy using information from 13C NMR spectra, 1H spectra, or a combination of both. Therefore the final task of structure prediction from NMR spectra is divided into:
- Generation of the isotropic shielding constants for all (except hydrogen) atoms in the molecule from NMR spectra.
- Prediction of the structure from the complete list of generated shielding constants and elemental information.
This stage of the research aims to approach the second task as it appears more complex and crucial. NMR spectra are highly dependent on experimental conditions,1,2 while shielding constants represent a more general parameter, serving as a “bridge” between varying NMR results and the target structure. This influence of experimental conditions may be accounted for when generating a list of target shielding constants from the given NMR spectra.
It should be noted that the proposed approach is based on the assumption that the compound considered for prediction was isolated and purified prior to the measurement of the NMR spectra, meaning that all shifts observed in the spectra belong to a single molecule.
2.2 Unification of adjacency matrix representation
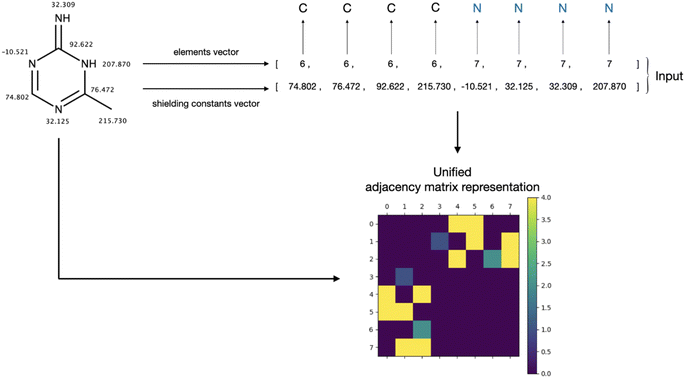
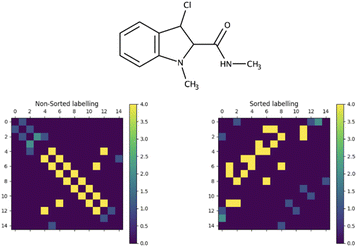
The generation of chemical structures in this research is proposed to be approached in a one-hot manner, wherein the primary task involves reconstructing the adjacency matrix of a molecular graph based on the labelling of its nodes. This labelling contains information about the element (atomic number) assigned to each node and its corresponding shielding constant. An illustration of the labelling and an example of the input to the designed model are presented in Fig. 1.The primary challenge in generating the adjacency matrix is that it is not an invariant for a given graph. For a given graph with G nodes, there are G! adjacency matrices that can describe its connectivity. To tackle this issue, the adjacency matrix representation needs to be unified. Typically, in the machine-readable representation of a molecule, its atoms are stored in the first-depth-tree traversal order.17 While this order contains information about the stored structure, it cannot be easily reconstructed when only the elemental composition of the molecule and the isotropic shielding constant for each atom are known. Since the shielding constant provides a unique characterization of an atom's chemical environment, it can be employed to standardize the representation of the adjacency matrix in conjunction with element information. This approach effectively addresses the multivariate problem of describing the graph connectivity with an adjacency matrix. To achieve this, atoms are ordered based on their atomic numbers. Subsequently, within each subset containing equal atomic numbers, the atoms are sorted according to their shielding constant values, resulting in unified node labelling vectors (Fig. 1, input vectors). This unification process guarantees a consistent representation of the molecular graph. Furthermore, this ordering can be effortlessly derived from the information enclosed in the target input vectors. The influence of this sorting process on the adjacency matrix appearance of a molecular graph representing 3-chloro-N,1-dimethylindole-2-carboxamide (stripped of hydrogens) is illustrated in Fig. 2.
As can be seen, the adjacency matrix corresponding to the first-depth-tree traversal order of the node labels has most of the bonds located just around the main diagonal, whereas the “sorted” appearance of the adjacency matrix has a more “random” character.
Given that there are 5 types of possible bonds between atoms (0 – absence of a bond, 1 – single bond, 2 – double bond, 3 – triple bond, and 4 – bond with aromatic character), the task can be treated as a multi-class classification problem for each potential bond location in the adjacency matrix. To address this task, we can use cross-entropy loss between three-dimensional representations of adjacency matrices (with the size of the number of atoms by the number of atoms by the number of bond types) as the objective function for optimization.
The desired adjacency matrix is obtained from the model's predictions, which contain scores for each possible class of bonds at each position in the adjacency matrix. The argmax operation is used to obtain the final adjacency matrix, representing the most probable bond type at each position.
Unlike previously reported applications of machine learning models to NMR spectra elucidation, the discussed approach aims not only at structure refinement14 but also at providing the possibility to predict the atom adjacencies for the target molecule, solely from the spectral and elemental information. Furthermore, its main focus is on reconstructing the complete molecular graph rather than solely evaluating the probabilities of substructure presence.15 This approach prevents the need to generate a multitude of potential structures to achieve a reliable prediction. Additionally, it enables working with significantly larger molecules without imposing a substantial burden on computational resources; however, it may be assisted by such algorithms.
2.3 Model architecture
| Hl+1 = ReLU(Lnorm·H(l)·W(l)) | (1.1) |
| Lnorm = D−1/2·A′·D−1/2 | (1.2) |
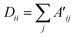 | (1.3) |
In order to propagate through the GCN layer while having only information about the nodes, it is proposed to generate the placeholder A′ by passing the element-shielding embedding through several fully connected layers with a sigmoid activation function, which enables obtaining the encoded graph representation from the element-shielding embedding only:
| A′l+1 = sigmoid(A′(l)·W(l) + b(l)) | (2.1) |
| A′0 = X | (2.2) |
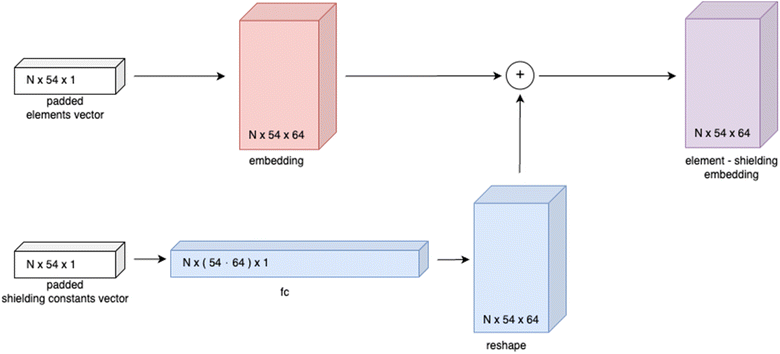
Based on the generic matrix – GCN approach a simple encoder–decoder “Structure Seer” architecture is proposed for adjacency matrix prediction. The architecture takes the element and shielding constants vectors as input and generates a predicted three-dimensional adjacency matrix with scores for each class of each bond. The model's architecture is illustrated in Fig. 4.
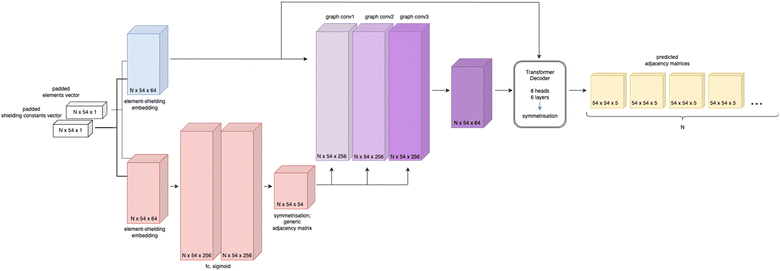 | ||
| Fig. 4 Schematic representation of the Structure Seer architecture, where N is the batch size (number of molecules in a batch). | ||
The Structure Seer model comprises two main components: a generic matrix – GCN encoder and a transformer decoder.20 The model features two separate element-shielding embeddings for node embedding and generic matrix generation with an embedding size of 64, three fully connected layers for generic matrix generation with a hidden size of 256, three GCN layers with a hidden size of 256 and a transformer decoder with 8 heads, six layers and a feedforward network model dimension of 2048. For learning facilitation the generic matrix (A′) used for graph convolution and final adjacency matrices are symmetrised, as proposed in:21
| Aout = AT + A | (3) |
The architecture of the Structure Seer model bears similarities to other GCN-based models used for diverse tasks involving molecular graphs.18,22 However, its distinctive design is centred around encoding the molecule solely based on node labelling, which allows for the generation of the complete adjacency matrix. This feature makes the considered architecture applicable to a broad range of atom adjacency reconstruction tasks.
3. Experimental
To assess the capabilities of the Structure Seer architecture, two different datasets were used for training. The first dataset utilized was the benchmark QM9 dataset,23,24 which was considered a good starting point due to its inclusion of optimized geometries. Furthermore, to evaluate the scalability of the approach, the model was also trained on a custom dataset comprising a larger number of elements and bigger structures extracted from the PubChem database.25 The models were implemented using the PyTorch library.263.1 SCF calculations
All SCF calculations were conducted using the Orca 4.0 software.27 The HF-3c method was chosen as the primary approach for calculating the shielding constants,28 owing to its low computational cost and relatively good accuracy. The choice of geometry for computing the shielding constants significantly influences the accuracy of predictions. Therefore, it is preferable to use accurate, yet resource-intensive DFT methods such as B3LYP with an appropriate basis set. However, for the geometry optimization of samples gathered from the PubChem database within the framework of this research, a less accurate but much less resource-demanding PM3 semi-empirical method29 was utilized.3.2 QM9 dataset preparation
Shielding constants for 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 structures, from the QM9 dataset, containing H, C, N, O and F atoms, with B3LYP/6-31G optimised geometries were calculated using the HF-3c method. The obtained dataset, with shielding constants for each atom calculated, was filtered to include structures with shielding constants not more than 1000 and not less than −1000, in order to exclude unreliable calculation results. All node labels in graph representations of the molecules were represented in a sorted manner. The atoms were sorted according to their atomic number, and according to their shielding constant within the same atomic number subset. Hydrogen atoms were stripped out from each structure, and shielding constants were normalised to be in the (0, 1) range.
885 structures, from the QM9 dataset, containing H, C, N, O and F atoms, with B3LYP/6-31G optimised geometries were calculated using the HF-3c method. The obtained dataset, with shielding constants for each atom calculated, was filtered to include structures with shielding constants not more than 1000 and not less than −1000, in order to exclude unreliable calculation results. All node labels in graph representations of the molecules were represented in a sorted manner. The atoms were sorted according to their atomic number, and according to their shielding constant within the same atomic number subset. Hydrogen atoms were stripped out from each structure, and shielding constants were normalised to be in the (0, 1) range.
The final refined dataset comprising 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 structures with shielding constants was split into training (110
685 structures with shielding constants was split into training (110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), validation (12
000), validation (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and test (11
000) and test (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683) folds. The distribution of samples within the dataset, based on the number of atoms and the number of bonds, is presented in Fig. 5a and b.
683) folds. The distribution of samples within the dataset, based on the number of atoms and the number of bonds, is presented in Fig. 5a and b.
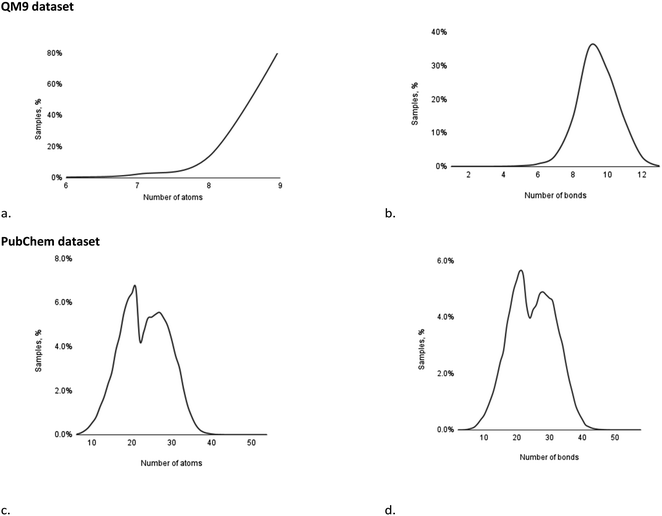 | ||
| Fig. 5 Distribution of samples in the QM9 and PubChem datasets by the number of atoms (a and c) and the number of bonds (b and d). | ||
Based on the distribution of the samples, it may be observed that the QM9 dataset mainly contains molecules comprising 8–9 atoms (97%) and/or with 8–11 bonds (93%), while other examples of molecules are represented by a significantly lower amount of samples.
3.3 PubChem dataset preparation
In order to create a suitable dataset for training 100 × 103 compounds that satisfied the following list of conditions, they were randomly selected from the PubChem database:- Have only the following elements in their structure: H, C, N, O, F, P, S, Cl, Br.
- Have not more than 60 atoms (including hydrogens).
- Have not more than 54 atoms (excluding hydrogens).
- Not charged.
The SMILES17 codes for the selected molecules were converted to rdkit-mol30 objects, sanitised and assigned preliminary 3D atom coordinates using the MMFF94 method. The geometry of the selected compounds was optimised via a semi-empirical PM3 method. The shielding constants for all the atoms in each molecule were calculated using PM3-optimised geometries via the HF-3c method. The obtained dataset, with shielding constants for each atom, was filtered to include structures with shielding constants in the range (−1000, 1000), in order to exclude unreliable calculation results. All node labels in graph representations of the molecules were represented in a sorted manner. The atoms were sorted according to their atomic number, and according to their shielding constant within the same atomic number subset. Hydrogen atoms were stripped out from each structure. The shielding constants were normalised to be in the (0, 1) range.
The final refined dataset comprised 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619 structures with shielding constants and was split into training (66
619 structures with shielding constants and was split into training (66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938), validation (8640) and test (9041) folds. The distribution of samples within the dataset, based on the number of atoms and the number of bonds, is presented in Fig. 5c and d.
938), validation (8640) and test (9041) folds. The distribution of samples within the dataset, based on the number of atoms and the number of bonds, is presented in Fig. 5c and d.
Unlike the case of the QM9 dataset, the PubChem collection features a more uniform distribution of samples over a number of atoms and bonds. Both distributions illustrate two major maxima of samples: the first, corresponding to samples comprising 19–21 atoms (19.2%) and containing 20–22 bonds (16.4%); and the second, corresponding to samples comprising 24–28 atoms (26.9%) and containing 27–31 bonds (23.7%).
3.4 Training procedure
The Structure Seer architecture underwent 200 epochs of training with a batch size of 32, using the AdamW optimizer with a cross-entropy loss function. The learning rate was gradually decreased in a cosine manner, starting from 6 × 10−4 and reaching 8 × 10−5 at epoch 32. Subsequently, the training continued at a constant learning rate. The training process utilized the Tesla T4 GPU accelerator. To demonstrate the efficiency of the proposed architecture, a transformers encoder–decoder architecture20 with a similar number of parameters (6 layers, 8 heads in the encoder; same decoder) was trained alongside the Structure Seer model under the same conditions, serving as a basis for comparison.3.5 Metrics
| Δp = |A1target − A1prediction|; Δex = |Atarget − Aprediction| | (4.1) |
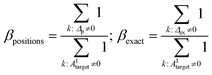 | (4.2) |
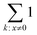 operation denotes the count of nonzero elements in x; βpositions is the fraction of “wrong” bonds (regardless of the type of the bond); βexact is the fraction of “wrong” bonds with account for their type.
operation denotes the count of nonzero elements in x; βpositions is the fraction of “wrong” bonds (regardless of the type of the bond); βexact is the fraction of “wrong” bonds with account for their type.
The “wrong” bond fraction was chosen over the accurate bond fraction because the latter has a tendency to take negative values when the number of incorrectly guessed bonds surpasses the total number of bonds in the molecule.
| Δ = A1target − A1prediction; | (5.1) |
 | (5.2) |
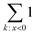 operation denotes the count of elements lower than zero in x; ε is the fraction of excess bonds in the predicted adjacency matrix.
operation denotes the count of elements lower than zero in x; ε is the fraction of excess bonds in the predicted adjacency matrix.
It is important to highlight that if the prediction does not contain any bonds, the total number of predicted bonds is considered equal to 1 to prevent the possibility of division by zero.
| HM = 1 − softmax(P, dim = 3)[:, :, 0] | (6.1) |
The predicted heatmap can be treated as a target adjacency matrix with noise, implying uncertainty. To characterize the similarity between the predicted noisy matrix and the target matrix, metrics for noise characterization, such as peak signal-to-noise ratio (PSNR), can be utilized. To assess the similarity of predictions to the target, a heatmap similarity measure is defined analogous to the PSNR as follows:
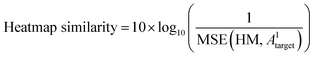 | (6.2) |
This measure serves as a criterion for evaluating the similarity of bond positions between the target and the prediction. The metric is calculated between the heatmaps of the target and predicted matrices, where heatmaps illustrate the probability of any bond type (1, 2, 3, or 4) over the absence of a bond (type 0).
4. Results and discussion
The evaluation results of both rival architectures, based on suggested metrics across three folds, are presented in Tables 1 and 2 (the metrics' values are averaged over the corresponding fold). While both models shared the same transformer decoder, the substitution of the transformer encoder with a generic matrix – a GCN-based one in the case of Structure Seer – led to a substantial improvement in terms of training efficiency and the achieved results. The average time per epoch for training a Structure Seer model is around 75% of that required for the transformers architecture while demonstrating significantly lower error rates in both bond positioning and exact prediction (lower by 8.4% for the QM9 dataset and by 5.5% for the PubChem dataset – test folds). It should be noted that both architectures exhibited similar error values in bond positioning (class 0 or any other) and exact prediction (class 0, 1, 2, 3, or 4) within the folds, which may indicate that the general optimization problem is well suited for the task.| Architecture | Structure Seer | |||||
|---|---|---|---|---|---|---|
| Dataset | Fold | Wrong bonds (position only), % | Wrong bonds, % | Excess bonds, % | Average heatmap similarity (PSNR), dB | Time per epoch, s |
| QM9 | Test | 62.14 | 62.47 | 23.63 | 26.106 | 137 |
| Validation | 63.04 | 63.42 | 24.52 | 26.036 | ||
| Training | 58.25 | 58.52 | 21.26 | 26.412 | ||
| PubChem | Test | 87.75 | 88.27 | 33.58 | 19.736 | 100 |
| Validation | 87.04 | 87.63 | 32.59 | 19.722 | ||
| Training | 80.29 | 80.65 | 24.06 | 20.165 | ||
| Architecture | Transformers | |||||
|---|---|---|---|---|---|---|
| Dataset | Fold | Wrong bonds (position only), % | Wrong bonds, % | Excess bonds, % | Average heatmap similarity (PSNR), dB | Time per epoch, s |
| QM9 | Test | 70.53 | 70.99 | 25.87 | 25.439 | 173 |
| Validation | 70.83 | 71.34 | 26.10 | 25.396 | ||
| Training | 69.68 | 70.15 | 25.23 | 25.501 | ||
| PubChem | Test | 93.26 | 93.72 | 36.03 | 19.388 | 139 |
| Validation | 92.06 | 92.57 | 34.29 | 19.431 | ||
| Training | 89.87 | 90.34 | 30.46 | 19.575 | ||
The averaged “wrong” bond-based metrics showed similar values across the folds, with slightly lower values observed for the training sets, as expected. This observation demonstrates the good generalization ability of both models. Importantly, the use of different levels of theory to calculate shielding constants in the QM9 dataset and PubChem dataset makes it incorrect to train a model on both datasets simultaneously.
The low values of the excess bonds fraction demonstrate that both models have a low tendency to predict non-existent bonds. Additionally, it can be noted that the Structure Seer architecture exhibits slightly lower values for both datasets, but only by 2–3%.
The heatmap similarity, defined as PSNR, can be interpreted as a relative “confidence” measure of the prediction, indicating how the probability of a bond at a target position is higher than the probabilities of the bond at positions around it. While the averaged values for the QM9 dataset are relatively good (25–26 dB), most ones for the PubChem dataset fall below the threshold considered acceptable for general image applications (20 dB).31 Several reasons could account for this observation:
- The size of the dataset may not be sufficient, especially given the significant size of the molecules and increased elemental vocabulary under consideration in the PubChem dataset compared to QM9.
- The PM3 semi-empirical geometry optimization may result in a low discretization and relatively high uncertainty of shielding constant values. This could lead to the shielding constants for two different types of atoms being too close to decide on their type accurately.
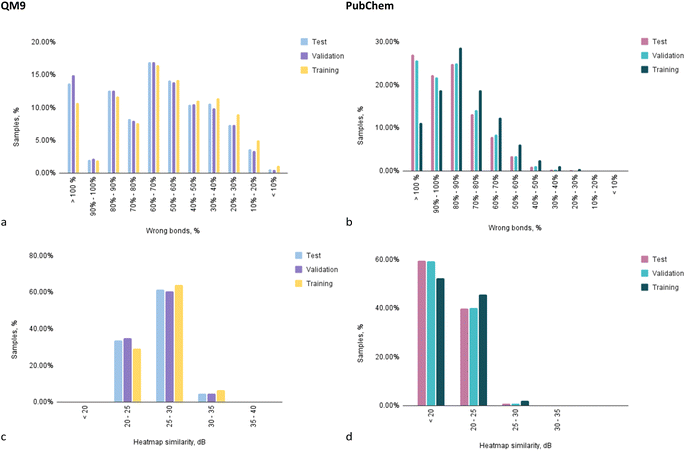
To examine the performance of Structure Seer in a more detailed manner, an evaluation of the distribution of predictions within characteristic intervals of metrics' values was conducted (Fig. 6). Upon analysing the prediction of adjacency matrices for samples from the QM9 dataset, it can be observed that half of the compounds had a relative number of correctly predicted bonds higher than 40% (Fig. 6a). Meanwhile, in the case of the PubChem dataset, only 5% of the compounds were predicted with that level of accuracy (Fig. 6b). Overall, over 63% of the structures for samples from QM9 were predicted with at least 30% correct bond accuracy, which is considered a good result, especially when taking into account the absence of any initial information about the adjacency of atoms.
On the other hand, the model trained on the PubChem dataset cannot be deemed accurate due to the fact that around 26% of the predictions for test and validation folds contained more wrongly guessed bonds than the total number of bonds in the molecule. As mentioned above, this may be caused by the dataset quality rather than model limitations. Nevertheless, given that for the optimisation of PubChem structures a significantly less accurate SCF method was applied, considering the complexity of the structures and a trade-off between computational cost and accuracy the results seem moderately favourable.
The charts illustrating the distribution of predictions between characteristic intervals of heatmap similarity values correspond to other observations and illustrate that in the case of QM9 (Fig. 6c) dataset training, all the predictions are of relatively good quality (20 dB and higher), while in case of the PubChem trained model (Fig. 6d) for most of the compounds, the “confidence” level is below 20 dB.
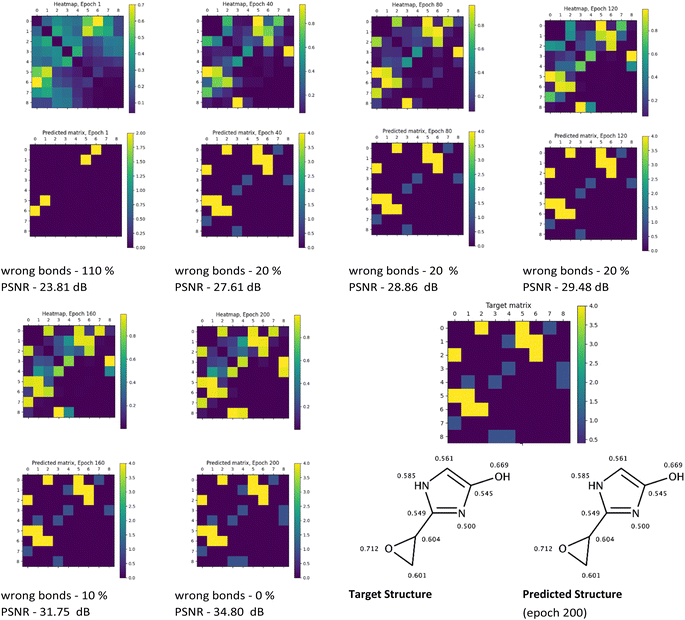
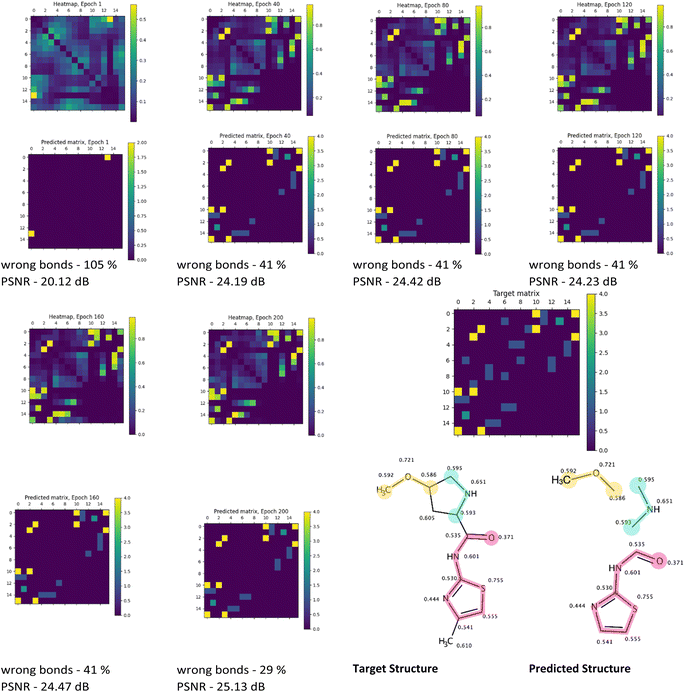
The visual analysis of the heatmaps and adjacency matrices predicted with high accuracy was conducted to assess the applicability of the trained model in real-world use cases. Additionally, this analysis aimed to gain a better understanding of the evaluated metrics' values. Fig. 7 and 8 present the evolution of the predicted adjacency matrices of two sample compounds during model training: 2-(oxiran-2-yl)-imidazol-4-ol (OIM-ol) (QM9 original ID – dsgdb9nsd_029301) from the test fold of the QM9 dataset, and 4-methoxy-N-(4-methyl-1,3-thiazol-2-yl)pyrrolidine-2-carboxamide (MTPC) (PubChem CID 61214160) from the test fold of the PubChem dataset. The training intervals are set at 40 epochs.
The evolution of the prediction of OIM-ol structure with the Structure Seer architecture throughout training on the QM9 dataset (Fig. 7) shows a gradual increase in “confidence” in the positioning of the bonds from epoch 1 to epoch 200. This increase is reflected in an increase in the heatmap similarity values from 24 to 35 dB and a decrease in the total number of incorrectly predicted bonds in the molecule from 110% to 0%. It is worth mentioning that the model starts to perceive the general pattern of the bonds quite well from epoch 40, as evidenced by the corresponding heatmap. An interesting observation is that the model recognized the aromaticity in the imidazole cycle, having information only about the elements comprising the molecule and corresponding isotropic shielding constants. The overall performance of the QM9-trained model demonstrates the applicability and great potential in generating adjacency matrices from information about the molecule's elemental composition and shielding constant values.
Similar to the case of training on the QM9 dataset, a gradual increase in heatmap similarity is observed during the PubChem training (Fig. 8) for the MTPC. However, the increase from 20 to 25 dB is noticeably less significant compared to the QM9 case (24–34 dB). Nonetheless, this progress is accompanied by a decrease in the “wrong” bonds fraction from 105% to 29%.
A closer examination of the predicted structure reveals that 3 fragments of the original molecule were predicted correctly (Fig. 8 – target structure and predicted structure). Notably, the bonds within all fragments were guessed faultlessly. Intriguingly, based on the general visual representation of the heatmaps from epoch 40 and onward, the overall areas of bond locations closely resemble the target positions of the bonds. While the fraction of the wrong bonds does not change significantly between epochs 40 and 200, the improvement in prediction quality can be observed in the increasing value of the heatmap similarity. The lower increase in prediction quality for the PubChem-trained model, apart from the size of the dataset, may be caused by the utilisation of the PM3 method for preliminary geometry optimization, leading to insufficient accuracy of the isotropic shielding constants computation, and uncertainty introduced by that. However, it should be noted that this uncertainty may be unavoidable if the shielding constants for two atoms with different chemical environments in the molecule are equal at the ground truth level.
As a result, it can be inferred that direct prediction of the exact adjacency between given atoms may pose challenges. However, gaining insights into probable bond locations and identifying fragments within the target molecule can still be highly valuable for researchers. These goals are more likely to be achievable with the current state of the QM9-trained model rather than the PubChem-trained one. Such insights into the most probable bond positions may be used for substructure search in general chemical databases, providing researchers with the possibility to search a database not with SMILES or other structure-based queries, but based on the NMR spectra and information on the elemental composition of the molecule. Additionally, these insights can be visualized comprehensively, facilitating NMR interpretation by the researcher. Predicted heatmaps also seem to be highly valuable in tasks of structure verification, where researchers need to attribute NMR signals to particular atoms in the known structure.
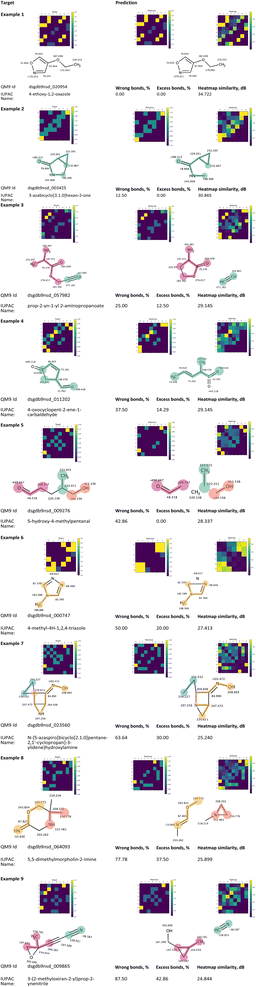
Fig. 9 presents a collection of representative predictions from the QM9 test fold, generated by the corresponding trained Structure Seer model. These illustrations exemplify the model's capabilities in predicting atom adjacencies and aim to offer a comprehensive illustration of its performance. Each sample was randomly selected from one of the characteristic intervals examined in Fig. 6a.
Each sample in Fig. 9 corresponds to one of the nine characteristic intervals shown in Fig. 6a, excluding the two intervals with a wrong bonds fraction of 90% and higher. Example 1, characterised by the “wrong” bonds fraction of 0%, illustrates that the developed model is capable of predicting the exact atom adjacencies accurately for some molecules. When considering the distribution of predictions based on the wrong bonds fraction, it is noteworthy that over 84% of the predictions are made with at least 10% of the bonds being accurately predicted. An intriguing observation emerges: regardless of the wrong bonds fraction value, the model consistently captures the distinct functional groups within the target molecule. For instance, in example 9, the nitrile and sp3 hybridised oxygen fragments are correctly identified; example 8 accurately identifies imine and ether fragments; example 7 pinpoints the hydroxyimine fragment and a cycle featuring sp3 hybridized nitrogen; example 6 faultlessly guesses the presence of aromatic bonds in the structure; example 5 captures hydroxy and aldehyde fragments; example 4 identifies sp2 hybridized carbon and oxygen fragments. Examples 1 to 3 are particularly remarkable, displaying high accuracy, with only a few incorrectly guessed or missed bonds.
Upon closer examination of predictions with relatively low accuracy, it becomes evident that despite the values for the wrong bonds fraction, these predictions offer a wealth of insightful information. In example 7, characterized by a wrong bonds fraction of 63.6%, the bonds within the large yellow fragment are accurately guessed, and the overall structure of the predicted molecule closely resembles the target. Notably, the structure in example 7 contains numerous carbon atoms with very similar shielding constant values (ranging from 204 to 234.5). This “low discretization” contributes to heightened uncertainty in determining precise bond positions, as indicated by the low heatmap similarity value (25.240 dB). In the case of example 6, where only 50% of the bonds are correctly guessed, the predicted adjacency matrix suggests that the bonds within the predicted cycle possess an aromatic nature. Despite this cycle comprising just four atoms, the prediction of aromatic bond character provides significant assistance to researchers with a chemical background in reconstructing the five-membered triazole ring. This can be achieved by closely examining both the predicted structure and its adjacency matrix. Furthermore, example 4 presents another intriguing scenario. Although the majority of the bonds are guessed correctly, the prediction includes a pentavalent carbon, which is undoubtedly incorrect. Upon conducting a more detailed analysis of the corresponding heatmap (Fig. 9, example 4, heatmap), it becomes apparent that the model assigns a bond score of 0.57 between atoms 1 and 7 and a score of 0.45 between atoms 2 and 7. Notably, atoms 1 and 2 possess highly similar shielding constant values (52.762 and 53.638). Similar to the situation in example 6, a careful examination of the predicted structure, adjacency matrix, and the associated heatmap could prove immensely valuable to a researcher in determining the target structure and attributing the observed chemical shifts in the spectra. In general, all the illustrated predictions bear noteworthy information about the structure under consideration.
The applicability of the developed solution was also assessed within the context of peak attribution, using the example task of attributing isotropic shielding constants to specific carbon atoms within a given molecule. The approach involved ranking all possible permutations of carbons based on the similarity of their adjacency matrix appearance to the model's predictions. The evaluation of predicted attributions, including the top 1 ranked candidate and the best candidate from the top 10 ranked candidates, for samples from the test fold of the QM9 dataset, is presented in Table 3.
| Considered candidates | Average accuracy, % (fraction of absolutely correct attributions) | Average absolute error in prediction, a.u. | Average relative error in prediction, % | Average number of incorrectly attributed carbons per molecule |
|---|---|---|---|---|
| Top 1 | 45.0% | 6.86 | 5.35% | 2.28 |
| Top 10 | 56.9% | 3.50 | 2.71% | 1.25 |
The QM9 trained model is able to precisely attribute the value of the shielding constant to a particular atom in the molecule in 45% of the cases when top-1 scored permutation is considered, and in almost 60% of structures, when considering the best candidate among top-10 scored permutations. Based on the average absolute and relative error values (6.86 a.u. and 5.35% correspondingly), it can be concluded that the model usually makes mistakes when attributing similar shielding values, which is consistent with the previous observations. The model's capacity to attribute atoms incorrectly is low, with an average of 2.3 incorrectly attributed atoms per molecule for the top-1 scored permutation, and only 1.25 for the best candidate from the top-10 permutations. Despite occasional inaccuracies in the assigned shielding constants, given the proximity of these values and the analysis of absolute and relative errors, the current state of the model could be deemed suitable for the task of peak attribution.
Despite the current limitations preventing the model from reliably predicting the whole set of precise atom adjacencies, it may serve as a valuable tool for researchers in peak attribution and structure identification. The model can significantly aid in these crucial tasks by accurately guessing distinctive structural fragments and offering information on the most probable bond locations. It is also considered that apart from a standalone usage the Structure Seer model can be enclosed into the framework along with the isomeric molecular graph generator.32,33 This integration may serve to facilitate the interpretation of the predicted adjacency matrices and to reshape the objective into a ranking procedure for all generated isomers, guided by the prediction, similar to an approach described by Huang et al.15
Based on several instances where the “low discretisation” of shielding constants has been observed to potentially result in a greater inaccuracy of the predicted adjacency matrix, a conclusion may be drawn. Alongside the augmentation of the dataset size, the substitution of the HF-3c method with the more precise yet resource-intensive B3LYP method for computing shielding constants has the potential to significantly enhance the model's accuracy and overall performance.
At this stage of development, our current approach exhibits several limitations. While the present implementation model accommodates a maximum of 54 atoms, it is important to note that the Structure Seer architecture can be configured to handle molecules of any size if trained using a dataset featuring larger examples. The primary constraint lies in the dimension of the model weights, which can be readily adjusted, albeit requiring retraining. However, the training process for Structure Seer, specifically for the interpretation of large molecules containing heavy atoms, poses a challenge owing to complexities in dataset preparation associated with vast computational resources necessary.
Another noteworthy limitation pertains to the applicability of Structure Seer in interpreting NMR spectra of mixtures with the aid of machine learning approaches.34,35 Despite the theoretical possibility of representing mixtures as non-fully connected molecular graphs, challenges arise during dataset preparation and training of the Structure Seer architecture for such tasks. Further detailed investigation is warranted in addressing these challenges.
While our manuscript predominantly focuses on employing the Structure Seer architecture for structure elucidation from NMR spectra, it is essential to highlight its versatility. The input vectors required for model predictions can be generated not only from NMR spectra but also from alternative data sources. This adaptability extends its applicability to a diverse array of tasks where the generation of molecular structures is essential.
5. Conclusion
A novel GCN-Transformer Structure Seer architecture has been introduced for the task of predicting molecular graph adjacency matrices based on atom labelling, which includes information about the element and the isotropic shielding constant of each atom. The usage of the GCN layer solely with atom labels is made possible by the introduction of generic-matrix generation layers. An approach for the unification of adjacency matrices representation based on element-shielding constants sorted labelling was suggested for overcoming the multivariate problem.The model was trained and evaluated using QM9 and PubChem-based datasets. Comparatively, the Structure Seer architecture outperformed a similar transformers encoder–decoder architecture in terms of accuracy and efficiency, requiring only 75% of the training time. The QM9-trained model demonstrated its capability to correctly predict nearly 40% of the bonds within the molecule for the majority of samples while being able to predict up to 100% of bonds correctly. Over 63% of the structures for samples from QM9 were predicted with at least 30% correct bond accuracy with the absence of any initial information about the adjacency of atoms. The overprediction was confined to a maximum of 24% of the bonds while shielding constants were calculated via the lightweight HF-3c method. The QM9-trained model in the current state was illustrated to be applicable to the task of attribution of an isotropic shielding constant value to a particular carbon in the molecule (a model task for 13C NMR spectra peak attribution).
The correlation between the difference in shielding constant for atoms within the same element subset and the relative confidence of prediction is observed, which indicates that the usage of more accurate but much more resource-consuming density functional theory methods for shielding constants computation may increase the accuracy of the model. The model has demonstrated significant potential in predicting atom adjacencies within relatively large structures (up to 54 non-hydrogen atoms), encompassing a wide variety of elements extracted from the PubChem dataset. However, enhancing the dataset through augmentation and implementing more dependable methods for geometry optimization are essential steps to substantially improve prediction accuracy.
The proposed model due to its graph-oriented design enables the prediction of bonds between specific atoms that possess corresponding labels. This capability allows the Structure Seer to predict the assignment of NMR spectra peaks to individual atoms within the target molecule. Considering the aforementioned points, the architecture holds significant promise in application to various tasks such as NMR peak attribution, structure identification, and structure prediction. To address practical challenges, an approach for reconstructing a list of shielding constants for each atom in the molecule from NMR spectra needs to be formulated and assessed, but this task seems less crucial due to tight theoretical connections between NMR signals and isotropic shielding constant values.
The predictions generated by the model do not require the generation of candidate molecular graphs for the obtainment of the suggested structure. This allows one to work with relatively big molecules without a drastic increase in computational resources necessary, thus demonstrating the scalability of the developed model to large molecules. However, the integration of the Structure Seer-based model with molecular graph generators or structure similarity search engines for working with small molecules presents a remarkable opportunity, laying the foundation for the development of an exceptionally accurate, efficient, and versatile machine learning framework capable of addressing diverse challenges within the realm of NMR spectra interpretation.
Data availability
The source code for data preparation, model implementation, training, and evaluation is available in the ESI.†Author contributions
D. A. Sapegin refined the idea, performed the investigation, and developed software for the model implementation and analysis, along with conceptualisation and writing of the original manuscript draft. J. C. Bear reviewed and edited the original draft, initiated discussions on the results, and contributed to the quality of the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors express their gratitude to Alexey V. Checkmachev for providing valuable consultations and insightful comments throughout the model's architecture development process. Additionally, the authors extend their deepest appreciation to Alexander Proutskiy and Todor Angelov for their meticulous review of the initial manuscript drafts and fruitful discussions.Notes and references
- N. E. Jacobsen, NMR Spectroscopy Explained, 2007, DOI:10.1002/9780470173350.
- NMR Spectroscopy: Basic Principles, Concepts and Applications in Chemistry, ed. H. Günther, Wiley-VCH, Weinheim, Germany, 3rd edn, 2013 Search PubMed.
- T. Bally and P. R. Rablen, Quantum-Chemical Simulation of 1H NMR Spectra. 2. Comparison of DFT-Based Procedures for Computing Proton–Proton Coupling Constants in Organic Molecules, J. Org. Chem., 2011, 76, 4818–4830, DOI:10.1021/jo200513q.
- Spectral Database for Organic Compounds, SDBSWeb, National Institute of Advanced Industrial Science and Technology, 07.08 2023, https://sdbs.db.aist.go.jp Search PubMed.
- N. Blonder and F. Delaglio, The NMR Spectral Measurement Database: A System for Organizing and Accessing NMR Spectra of Therapeutic Proteins, J. Res. Natl. Inst. Stand. Technol., 2021, 126, 126035, DOI:10.6028/jres.126.035.
- John Wiley & Sons, Inc., SpectraBase, https://spectrabase.com/about, accessed 07/08/ 2023.
- S. Kuhn and N. E. Schlörer, Facilitating Quality Control for Spectra Assignments of Small Organic Molecules: Nmrshiftdb2 - a Free in-House NMR Database with Integrated LIMS for Academic Service Laboratories, Magn. Reson. Chem., 2015, 53, 582–589, DOI:10.1002/mrc.4263.
- S. Kuhn, Applications of Machine Learning and Artificial Intelligence in NMR, Magn. Reson. Chem., 2022, 60, 1019–1020, DOI:10.1002/mrc.5310.
- D. Chen, Z. Wang, D. Guo, V. Orekhov and X. Qu, Review and Prospect: Deep Learning in Nuclear Magnetic Resonance Spectroscopy, Chem.–Eur. J., 2020, 26, 10391–10401, DOI:10.1002/chem.202000246.
- Y. Binev, M. M. B. Marques and J. Aires-de-Sousa, Prediction of 1H NMR Coupling Constants with Associative Neural Networks Trained for Chemical Shifts, J. Chem. Inf. Model., 2007, 47, 2089–2097, DOI:10.1021/ci700172n.
- E. Jonas and S. Kuhn, Rapid Prediction of NMR Spectral Properties with Quantified Uncertainty, J. Cheminf., 2019, 11, 50, DOI:10.1186/s13321-019-0374-3.
- P. Gao, J. Zhang, Q. Peng, J. Zhang and V.-A. Glezakou, General Protocol for the Accurate Prediction of Molecular 13C/1H NMR Chemical Shifts via Machine Learning Augmented DFT, J. Chem. Inf. Model., 2020, 60, 3746–3754, DOI:10.1021/acs.jcim.0c00388.
- M. O. Marcarino, M. M. Zanardi, S. Cicetti and A. M. Sarotti, NMR Calculations with Quantum Methods: Development of New Tools for Structural Elucidation and Beyond, Acc. Chem. Res., 2020, 53, 1922–1932, DOI:10.1021/acs.accounts.0c00365.
- Y.-H. Tsai, M. Amichetti, M. M. Zanardi, R. Grimson, A. H. Daranas and A. M. Sarotti, ML-J-DP4: An Integrated Quantum Mechanics-Machine Learning Approach for Ultrafast NMR Structural Elucidation, Org. Lett., 2022, 24, 7487–7491, DOI:10.1021/acs.orglett.2c01251.
- Z. Huang, M. S. Chen, C. P. Woroch, T. E. Markland and M. W. Kanan, A Framework for Automated Structure Elucidation from Routine NMR Spectra, Chem. Sci., 2021, 12, 15329–15338, 10.1039/d1sc04105c.
- K. Wolinski, R. Haacke, J. F. Hinton and P. Pulay, Methods for Parallel Computation of SCF NMR Chemical Shifts by GIAO Method: Efficient Integral Calculation, Multi-Fock Algorithm, and Pseudodiagonalization, J. Comput. Chem., 1997, 18, 816–825, DOI:10.1002/(sici)1096-987x(19970430)18:6<816::aid-jcc7>3.0.co;2-v.
- D. Weininger, SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36, DOI:10.1021/ci00057a005.
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. A. Langer, Compact Review of Molecular Property Prediction with Graph Neural Networks, Drug Discovery Today: Technol., 2020, 37, 1–12, DOI:10.1016/j.ddtec.2020.11.009.
- T. N. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks, arXiv, 2016, preprint, arXiv:1609.02907, DOI:10.48550/ARXIV.1609.02907.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Attention Is All You Need, arXiv, 2017, preprint, arXiv:1706.03762, DOI:10.48550/ARXIV.1706.03762.
- X. Gao, W. Hu and Z. Guo, Exploring Structure-Adaptive Graph Learning for Robust Semi-Supervised Classification, arXiv, 2019, preprint, arXiv:1904.10146, DOI:10.48550/ARXIV.1904.10146.
- J. Xia, C. Zhao, B. Hu, Z. Gao, C. Tan, Y. Liu, S. Li and S. Z. Li, Mole-BERT: Rethinking Pre-training Graph Neural Networks for Molecules, Proceedings of ICLR Conference, 2013, https://openreview.net/forum?id=jevY-DtiZTR Search PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875, DOI:10.1021/ci300415d.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Quantum Chemistry Structures and Properties of 134 Kilo Molecules, Sci. Data, 2014, 1, 140022, DOI:10.1038/sdata.2014.22.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, PubChem 2023 Update, Nucleic Acids Res., 2022, 51, D1373–D1380, DOI:10.1093/nar/gkac956.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, arXiv, 2019, preprint, arXiv:1912.01703, DOI:10.48550/ARXIV.1912.01703.
- F. Neese, Software Update: The ORCA Program System, Version 4.0, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 8, e1327, DOI:10.1002/wcms.1327.
- R. Sure and S. Grimme, Corrected Small Basis Set Hartree-Fock Method for Large Systems, J. Comput. Chem., 2013, 34, 1672–1685, DOI:10.1002/jcc.23317.
- G. B. Rocha, R. O. Freire, A. M. Simas and J. J. P. Stewart, RM1: A Reparameterization of AM1 for H, C, N, O, P, S, F, Cl, Br, and I, J. Comput. Chem., 2006, 27, 1101–1111, DOI:10.1002/jcc.20425.
- RDKit: Open-Source Cheminformatics, https://www.rdkit.org Search PubMed.
- D. R. Bull and F. Zhang, Digital Picture Formats and Representations, Intelligent Image and Video Compression, 2021, pp. 107–142, DOI:10.1016/b978-0-12-820353-8.00013-x.
- M. A. Yirik, M. Sorokina and C. Steinbeck, MAYGEN: An Open-Source Chemical Structure Generator for Constitutional Isomers Based on the Orderly Generation Principle, J. Cheminf., 2021, 13, 48, DOI:10.1186/s13321-021-00529-9.
- R. Gugisch, A. Kerber, A. Kohnert, R. Laue, M. Meringer, C. Rücker and A. Wassermann, MOLGEN 5.0, A Molecular Structure Generator, Adv. Math. Chem. Appl., 2014, 113–138, DOI:10.2174/9781608059287114010010.
- S. Kuhn, E. Tumer, S. Colreavy-Donnelly and R. M. Borges, A Pilot Study for Fragment Identification Using 2D NMR and Deep Learning, Magn. Reson. Chem., 2021, 60, 1052–1060, DOI:10.1002/mrc.5212.
- R. Reher, H. W. Kim, C. Zhang, H. H. Mao, M. Wang, L.-F. Nothias, A. M. Caraballo-Rodriguez, E. Glukhov, B. Teke, T. Leao, K. L. Alexander, B. M. Duggan, E. L. Van Everbroeck, P. C. Dorrestein, G. W. Cottrell and W. H. Gerwick, A Convolutional Neural Network-Based Approach for the Rapid Annotation of Molecularly Diverse Natural Products, J. Am. Chem. Soc., 2020, 142, 4114–4120, DOI:10.1021/jacs.9b13786.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00178d |
| This journal is © The Royal Society of Chemistry 2024 |