Open Access Article
Open Access ArticleGlobal geometry of chemical graph neural network representations in terms of chemical moieties
Amer Marwan
El-Samman
*a,
Incé Amina
Husain
 a,
Mai
Huynh
a,
Stefano
De Castro
a,
Mai
Huynh
a,
Stefano
De Castro
 a,
Brooke
Morton
a,
Brooke
Morton
 a and
Stijn
De Baerdemacker
a and
Stijn
De Baerdemacker
 ab
ab
aUniversity of New Brunswick, Department of Chemistry, 30 Dineen Dr, Fredericton, Canada. E-mail: aelsamma@unb.ca
bUniversity of New Brunswick, Department of Mathematics and Statistics, 30 Dineen Dr, Fredericton, Canada. E-mail: stijn.debaerdemacker@unb.ca
First published on 15th February 2024
Abstract
Graph neural nets, such as SchNet, [Schütt et al., J. Chem. Phys., 2018, 148, 241722], and AIMNet, [Zubatyuk et al., Sci. Adv., 2019, 5, 8] provide accurate predictions of chemical quantities without invoking any direct physical or chemical principles. These methods learn a hidden statistical representation of molecular systems in an end-to-end fashion; from xyz coordinates to molecular properties with many hidden layers in between. This naturally leads to the interpretability question: what underlying chemical model determines the algorithm's accurate decision-making? By analyzing the hidden layer activations of QM9-trained graph neural networks, also known as “embedding vectors” with dimension-reduction, linear discriminant analysis and Euclidean-distance measures we shed light on an interpretation. The result is a quantifiable geometry of these models' decision making that identifies chemical moieties and has a low parametric space of ∼5 important parameters from the fully-trained 128-parameter embedding. The geometry of the embedding space organizes these moieties with sharp linear boundaries that can classify each chemical environment within <5 × 10−4 error. Euclidean distance between embedding vectors can be used to demonstrate a versatile molecular similarity measure, comparable to other popular hand-crafted representations such as Smooth Overlap of Atomic Positions (SOAP). We also reveal that the embedding vectors can be used to extract observables that are related to chemical environments such as pKa and NMR. While not presenting a fully comprehensive theory of interpretability, this work is in line with the recent push for explainable AI (XAI) and gives insights into the depth of modern statistical representations of chemistry, such as graph neural nets, in this rapidly evolving technology.
1 Introduction
Neural networks have become common-use in our increasingly data-driven world. With the proliferation of giant computational chemistry databases, it is becoming more evident that chemistry can benefit from such techniques as well. For example, they can aid in drug and material discovery,2–13 speed up lengthy electronic structure calculations,14–16 or bypass them all together for the predictions of chemical properties.17–23 Their ability to provide on-par predictions with ab initio data is based on their ability to intricately fit such data. However, these fits are generally high-dimensional, non-linear, and hidden from the user of the algorithm. With this type of process, usually involving hundreds of parameters, it is not clear if the algorithm's predictions are due to an underlying reliable chemical model or are just a result of its sophisticated fitting techniques. There have increasingly been attempts to explain these models, also known as explainable-AI techniques (XAI).24–26 This has especially been the case for ML models that make risky autonomous decisions, such as those used in medicine or self-driving vehicle technology.27–38 For chemistry, explainability is becoming a way of gaining insights into complex chemical data which may be easily overlooked by traditional analysis.39–42We are specifically interested in providing interpretability to graph neural nets (GNN) that bypass the computation of chemistry's electronic properties. Such neural nets hold promise in statistically learning the solutions (or approximate solutions) of the costly Schrödinger equation, a feat that would tremendously speed up the exploration of chemical space.43–45
In this work, we narrow in on this new and rapidly progressing area of graph modelling of chemical data, using GNNs such as SchNet. By analyzing the graph neural network's activations in response to molecular input, we find that the activations (called “embeddings”) fit sharply within what is universally understood as chemical environments/moieties. Furthermore, we show that one can associate a Euclidean-distance measure to the hidden atomistic neural net activations, allowing for a straightforward molecular similarity measure in terms of Euclidean distances. This Euclidean-distance-preserving space of embeddings can be analyzed with Linear Discriminant Analysis (LDA) to show clear-cut boundaries between different chemical moieties.
1.1 Related work
Work on GNN interpretability in chemistry has been done before in other contexts. Letzgus et al.46 showed that SchNet uses the bond order concept to account for atomization energy contributions. They also showed that SchNet captures the expected trend of increasing energies with increasing bond order. In this work, we observe the concept of chemical moieties rather than bonds as another significant contributor to the model's decision-making.Early indications of this concept have been observed by Zubatyuk et al.47 and Smith et al.48 while validating the feature vectors of their AIMNet neural net and ANI-1x model, respectively, with t-distributed stochastic neighbor embedding (t-SNE). In both architectures, the learned feature vectors of their neural net naturally clustered into distinct regions representing distinct chemical environments found in the QM9 and ANI datasets. However, due to the distortions of the non-linear t-SNE projection used in their studies,49 it is not possible to further analyze and quantify this space as a representation of chemistry on its own with its own useful characteristics. More recently, Lederer et al. showed that a type-assignment matrix50 and adjacency matrix can be used to arrive at an unsupervised learning objective to assign atoms to their chemical moieties.51
In our work, we take a different approach. In the interest of revealing the hidden contents of a GNN model itself, we do not design a machine learning model or do any additional training. Instead, we analyze a pretrained GNN model of chemistry with Euclidean-distance-preserving techniques to show a representation of chemistry that already contains structural integrity in terms of chemical moieties without the need for more machine learning. A simple Linear Discriminant Analysis (LDA) model shows that a GNN model already contains a representation that divides boundaries between chemical moieties with high resolution (classification error of 3 × 10−4). In addition, the internal structure of the model can be analyzed with Euclidean-distance measurements which act as a similarity measure between these moieties. We also provide precursors on how this representation can be used for transfer learning purposes towards other local chemical properties such as pKa and NMR.
The approach we take in this work is a global one.52–55 We seek to understand the elementary decision-making and the variables that underlie the system's predictions as a whole. Whereas local explanations, such as feature-attribution methods, saliency maps, deep visualization and others56–65 can render case-by-case explanations, they are not aimed at providing an appreciable understanding that encapsulates the whole black-box model in one interpretable model. In many instances decision-trees are seen as global interpretable models since they can be thought of as performing a set of elementary decisions.66 The purpose of this work is to seek an interpretation on that level for GNNs: what is the system of decision-making that the model undergoes for a prediction and what are the variables at play that affect decisions (and predictions)? With that respect, we follow the subtle difference in definitions for interpretability and explainability from Roscher et al.,67 in which the former refers to a mapping of an internally learned abstract feature to a human-defined concept, such as moieties or functional groups in chemistry, whereas the latter employs features from the interpretable domain to explain the decision making of the model for specific examples.
1.2 Organization of paper
The remainder of the paper is organized as follows: in Section 2.1–2.3, we recapitulate how message-passing neural nets (MPNNs) generate their hidden representation and how we extracted this representation at a meaningful point in the network. In section 2.4, we provide a synopsis of t-distributed stochastic neighbor embedding (t-SNE),68 linear discriminant analysis (LDA),69 and principal component analysis (PCA)70 dimension-reduction techniques useful for this work. In Section 3.1, we extend Zubatyuk's analysis,47 to reveal a global and more refined visualization of moiety chemistry. We demonstrate the compactness of the embedding space and introduce the Euclidean distance in embedding space as a new measure of molecular similarity. In Section 3.2, we employ LDA to quantify the geometric organization of the embedding space, and extend the learned geometric representation to other chemical quantities in Section 3.3. We present our Conclusions and outlook in Section 4.2 Methods
2.1 MPNNs
Before the advent of message-passing neural nets (MPNN), the field was limited to standard feedforward architectures.17,18 The Cartesian xyz coordinates of the molecule would serve as the input and, typically, the potential energy of the system was the output. These neural nets were not transferable to other chemical properties nor size-extensive: their architecture was fixed to predict the potential energy surface of a particular compound with a fixed number of atoms over a variety of configurations. Moreover, these early neural nets did not adhere to the permutational symmetry of indices within a molecule, changing the order of atoms in the list incorrectly changed the energy.Behler and Parinello would solve these problems, proposing a neural network architectural design that is more compatible with molecular systems.71–73 Based on an atom-centered approach to predictions, Behler–Parinello neural nets partitioned each molecule into atoms. These atomistic neural nets contributed to a total potential energy by pooling all the predicted atomwise contributions. To include rotationally-invariant interatomic interactions between each atomwise partition, Behler and Parinello used manually-crafted symmetry functions of the interatomic distance as input. In other words, the neural net was not end-to-end (did not make predictions directly from xyz coordinates) but assumed an initial representation of interacting molecular systems via the symmetry functions.
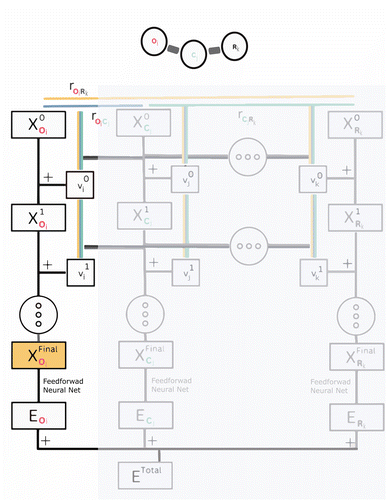
SchNet's architecture,19–22 and many other MPNNs,74–76 are similar to Behler–Parinello neural nets, see Fig. 1, particularly that they are often partitioned atomwise. However, MPNNs can have a completely end-to-end architecture and are thus not restricted to make hand-crafted assumptions about the interatomic interactions. Instead MPNNs derive their own representation of interacting atoms from the molecular graph. The messages between atomistic “nodes” can themselves be parameterized to fit the interatomic distances between the atoms and thus “fitted” to make an accurate prediction. After these interactions, a final representation for each atom in the molecule is stored in the so-called “embedding vector”. The embedding vector is the neural-network-representation of an atom-in-a-molecule. This internal representation is finally used to make a prediction of that atom's contribution to the total property by running it through a standard feedforward neural net. The atomwise properties are then summed to give a total molecular property. Throughout the process, the internal representation for each atom, and the entire molecule, remains a hidden feature of the algorithm, leaving the precise nature of the chemical model unknown. We seek to shed light on the type of chemical model that GNNs build using their embedding vectors, which allow them to achieve their accurate predictions.
2.2 SchNet's hidden representation
There are many intricate variations to how a GNN can be designed, with important advantages and disadvantages to each. Because of the many variations of architectures, We have chosen to describe one such variation, SchNet, in detail, and concisely summarize other architectures that come up. Nonetheless, ultimately the same methodology and interpretation holds regardless of the exact GNN architecture used, so long as the main features of a GNN, its embedding and graph interactions, are present. In SchNet, the “embedding vector” is an atom-in-molecule vector representation xil ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) D that is dependent on layer l and atom i with charge Zi (see Fig. 1 for a visual summary of the network's architecture). The dimension of the embedding vector D determines the information storage capacity of the embedding vectors, and should therefore be chosen sufficiently large by the user. During a feedforward pass through the network, the embedding vectors are updated after each individual layer l
D that is dependent on layer l and atom i with charge Zi (see Fig. 1 for a visual summary of the network's architecture). The dimension of the embedding vector D determines the information storage capacity of the embedding vectors, and should therefore be chosen sufficiently large by the user. During a feedforward pass through the network, the embedding vectors are updated after each individual layer l| xil+1 = xil + vil, | (1) |
2.3 Network training and dataset
For the analysis, we employed the QM9 dataset,77 a set of 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 small-sized organic molecules (∼5 Å to 10 Å in size) with optimized geometries at the B3LYP/6-31G(d,p) level of theory. The network was trained on total electronic energy at 0 K, although QM9 includes other associated properties such as dipole moment, enthalpy, etc. The algorithm used for training had six interaction layers and an embedding vector dimension D = 128. Other relevant parameters in the network are 128 convolutional filters, 50 Gaussians, and an interaction cutoff distance of 50 Å. The first 100
000 small-sized organic molecules (∼5 Å to 10 Å in size) with optimized geometries at the B3LYP/6-31G(d,p) level of theory. The network was trained on total electronic energy at 0 K, although QM9 includes other associated properties such as dipole moment, enthalpy, etc. The algorithm used for training had six interaction layers and an embedding vector dimension D = 128. Other relevant parameters in the network are 128 convolutional filters, 50 Gaussians, and an interaction cutoff distance of 50 Å. The first 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules of QM9 were used as training data points, the next 10
000 molecules of QM9 were used as training data points, the next 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 as validation data points, and the rest was left for testing. Gaussians were used for an initial expansion of the interatomic distances to provide a flexible starting representation for the model. The cutoff distance was purposely chosen to be very large (relative to QM9 molecules) so that all atoms were included in the interaction, giving the model freedom to have a global representation rather than force it into a local representation.78 Although generally expensive and often leading to an overfitted model, a balance was achieved between high accuracy and generalizability on QM9, as shown by the loss plot in Fig. 5 in the Appendix section which displays a final validation MAE of 0.020 eV. The generalizability of the SchNet model was verified explicitly by running an additional experiment in which training was performed on a QM9 data subset in which all alcohols were systematically removed, after which test set errors on both test sets with or without alcohols produced comparable results. Various embeddings sizes, such as 30, 60, along with the 128, gave similar results for the analysis. We present the analysis of the 128-embedding model.
000 as validation data points, and the rest was left for testing. Gaussians were used for an initial expansion of the interatomic distances to provide a flexible starting representation for the model. The cutoff distance was purposely chosen to be very large (relative to QM9 molecules) so that all atoms were included in the interaction, giving the model freedom to have a global representation rather than force it into a local representation.78 Although generally expensive and often leading to an overfitted model, a balance was achieved between high accuracy and generalizability on QM9, as shown by the loss plot in Fig. 5 in the Appendix section which displays a final validation MAE of 0.020 eV. The generalizability of the SchNet model was verified explicitly by running an additional experiment in which training was performed on a QM9 data subset in which all alcohols were systematically removed, after which test set errors on both test sets with or without alcohols produced comparable results. Various embeddings sizes, such as 30, 60, along with the 128, gave similar results for the analysis. We present the analysis of the 128-embedding model.
Using the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules test set extracted from the QM9 datable, the model was then evaluated and updated embedding vectors were extracted for all layers. No additional SchNet training was performed on these molecules. The fully-updated embeddings xfinali (as highlighted in orange in Fig. 1) were then analyzed using dimension-reduction techniques, linear discriminant analysis, and Euclidean distance measures. More specifically, the extracted embedding vectors were parsed into each element-type (e.g. all oxygen embedding vectors are isolated), and the analysis was performed on the set of all embedding vectors of a certain atom type, across all 10
000 molecules test set extracted from the QM9 datable, the model was then evaluated and updated embedding vectors were extracted for all layers. No additional SchNet training was performed on these molecules. The fully-updated embeddings xfinali (as highlighted in orange in Fig. 1) were then analyzed using dimension-reduction techniques, linear discriminant analysis, and Euclidean distance measures. More specifically, the extracted embedding vectors were parsed into each element-type (e.g. all oxygen embedding vectors are isolated), and the analysis was performed on the set of all embedding vectors of a certain atom type, across all 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules (one molecule can contribute multiple embedding vectors). More specifically, the analysis in the Results section is focused on the oxygen-type embedding vectors, but the methodology can be applied to any chosen element (see Appendix Table 5 for the LDA analysis on all element-types). The analysis for vil and xil for the intermediate layers (l ≠ final) can also be found in the Appendix section, Table 4, and produces very similar results to xfinali. The trained model and generated embedding vectors are freely available via a Dataverse Repository.1 The extracted embedding vectors in the dataset were also labelled with integers representing the various chemical environments found in QM9. For this, we manually surveyed the functional groups of QM9 and automated the labelling of them using the adjacency matrix extracted from the .mol files. It is important to note that for all datasets used in this study, the geometries are either optimized at the ground-state DFT level or experimentally determined (see Section 3.3), and therefore exclude transition-state, bond-breaking, or explicitly charged molecules (with the exception of a few ammoniums in the QM9 database).
000 molecules (one molecule can contribute multiple embedding vectors). More specifically, the analysis in the Results section is focused on the oxygen-type embedding vectors, but the methodology can be applied to any chosen element (see Appendix Table 5 for the LDA analysis on all element-types). The analysis for vil and xil for the intermediate layers (l ≠ final) can also be found in the Appendix section, Table 4, and produces very similar results to xfinali. The trained model and generated embedding vectors are freely available via a Dataverse Repository.1 The extracted embedding vectors in the dataset were also labelled with integers representing the various chemical environments found in QM9. For this, we manually surveyed the functional groups of QM9 and automated the labelling of them using the adjacency matrix extracted from the .mol files. It is important to note that for all datasets used in this study, the geometries are either optimized at the ground-state DFT level or experimentally determined (see Section 3.3), and therefore exclude transition-state, bond-breaking, or explicitly charged molecules (with the exception of a few ammoniums in the QM9 database).
To demonstrate generality of this method to other GNN architectures, we also extracted embedding vectors from a pretrained AIMNet ensemble model47 on the same 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 QM9 test molecules to compare the analysis with that of SchNet. This AIMNet ensemble model trained on ANI-1x data (includes molecular energies, atomic forces, and more) computed using ωB97x/def2-TZVPP level. AIMNet's embeddings (and GNN architecture) are built considerably different than SchNet's. First, AIMNet uses symmetry functions for input; which have both angular and radial parts.23,72 The symmetry functions are used as the features that describe the local environment around each atom. The radial and angular features are embedded via an outerproduct on an atomic feature vector space (AFV). In short, a trainable layer combines the flattened radial and angular tensors and learns a constant-sized embedding from them. This is how the embeddings in AIMNet are built. We extracted this embedding representation for the QM9 dataset using pretrained AIMNet Ensemble model.
000 QM9 test molecules to compare the analysis with that of SchNet. This AIMNet ensemble model trained on ANI-1x data (includes molecular energies, atomic forces, and more) computed using ωB97x/def2-TZVPP level. AIMNet's embeddings (and GNN architecture) are built considerably different than SchNet's. First, AIMNet uses symmetry functions for input; which have both angular and radial parts.23,72 The symmetry functions are used as the features that describe the local environment around each atom. The radial and angular features are embedded via an outerproduct on an atomic feature vector space (AFV). In short, a trainable layer combines the flattened radial and angular tensors and learns a constant-sized embedding from them. This is how the embeddings in AIMNet are built. We extracted this embedding representation for the QM9 dataset using pretrained AIMNet Ensemble model.
2.4 Dimension-reduction to analyze embeddings in MPNNs
While there are a plethora of sophisticated interpretability techniques at our disposal, most methods, such as variational autoencoders,79–82 and saliency maps,83–90 give predominantly local explanations of the model, providing insight into the decision making process on a case-by-case basis. In contrast, dimension-reduction techniques,91–94 are able to provide a global account of the decision making mechanism which can be more informative.49 In addition, they are convenient and useful in the context of MPNNs. Typically, each node in a MPNN is a high-dimensional vector space, in our case, a.k.a embedding vectors, and dimension-reduction allows us to explore a more tractable (and possibly visualizable) low-dimensional projection of that space.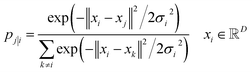 | (2) |
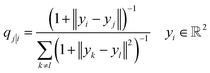 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–117
000–117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, not involved in SchNet training), the LDA model was then evaluated on the remaining 2500 molecule subset QM9 testset (the molecules indexed 117
500, not involved in SchNet training), the LDA model was then evaluated on the remaining 2500 molecule subset QM9 testset (the molecules indexed 117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–120
500–120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in QM9).
000 in QM9).
3 Results and discussion
3.1 Dimension-reduction on SchNet's trained embedding vectors
As a confirmation and extension of ref. 47, we begin our analysis with t-SNE on the embedding vectors of all oxygen atoms in the dataset. The result is a visualizable 2-dimensional plot of various clusters, see Fig. 2a. Information in these clusters is only revealed when we label the oxygen-associated embedding vectors with the moiety (or chemical environment) that the atom resides in. In the QM9 dataset, we found 20 moieties that are associated with oxygen atoms and labeled the embedding vectors accordingly (Fig. 2b shows the moiety key). As can be seen from the labeled t-SNE projection, the model distinguishes environments with fine detail, even when the representation of that environment in the data is scarce (e.g. nitrosos group which only contain 4 molecules in the test set and 574 in the entire QM9). Some chemical environments (such as those indexed 16 and 19 in Table 1) have less than 200 data points to represent them in the entire QM9.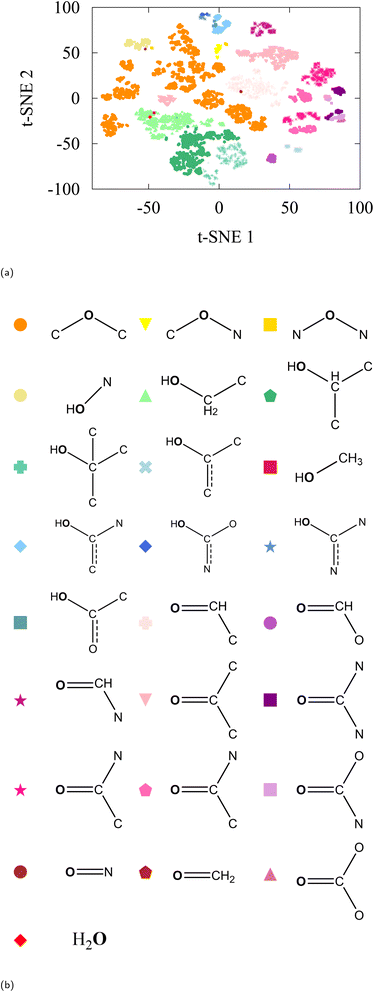 | ||
| Fig. 2 (a) t-SNE of oxygen-type embedding vectors of QM9-trained SchNet with labelling as defined in (b). | ||
Despite the caveats related to long-range distortions, one can already observe an intuitive organization between moieties in the t-SNE. For instance, all carbonyls (carboxylic acids, ketones, aldehydes, amides, and more) are grouped together in the bottom right; all primary, secondary, and tertiary alcohols in the center; and carbonates, carbamides, and carbamates on the top of the figure. It is evident that the pretrained SchNet model already contains enough information to distinguish chemical moieties.
To project a Euclidean-distance faithful representation, we move on to using linear PCA projection, which provides a minimally-distorted projection. Fig. 3 shows the 2D PCA projection on the oxygen-type embedding vectors of the QM9 test set labelled with the same chemical environments key shown in Fig. 2b.
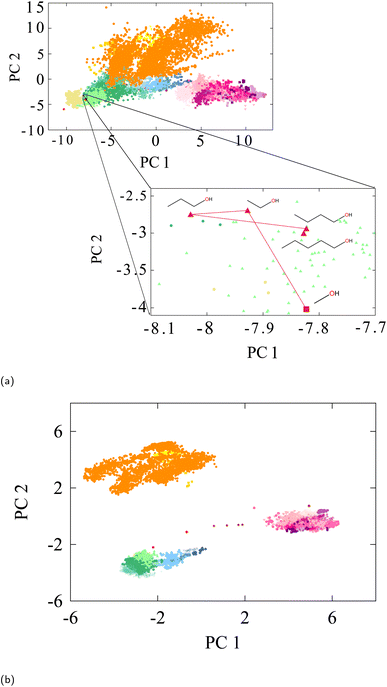 | ||
| Fig. 3 (a) PCA of Oxygen-type embedding vectors of QM9-trained SchNet labelled accorded to Fig. 2b. The focus is on straight-chain alcohols. It can be seen even in the 2D projection that distances between the alcohols' embeddings converge as the chain gets larger. The Euclidean distance does indeed decrease for each successively larger straight-chain alcohol in the full PCA space. In that space, the distances between methanol, ethanol, propanol, butanol, and pentanol are 3.98, 2.12, 1.45, and 0.98, respectively. (b) PCA of oxygen-type embedding vectors of pretrained AIMNet neural net tested on the same QM9 dataset labelled according to Fig. 2b. | ||
The projection reveals how the various chemical environments that are organized in the global embedding space are consistent with a notion of molecular similarity. For example, the projection consistently shows that carbonyls are “closer” to alcohols in a Euclidean sense than they are to hydroxylamines. This is a chemically intuitive result that cannot be faithfully reproduced in the distortions of the t-SNE projection. Moreover, Fig. 3a illustrates how embedding representations become increasingly closer to one another as the molecular environment of the associated atom becomes more similar. To illustrate this, we analyzed Euclidean-distances between the oxygen embedding vectors of several primary straight chain alcohols. As detailed in the figure, we indeed find a converging distance between the embedding vectors of the oxygens as the chain gets longer. Thus, all straight-chain or straight-chain-like alcohol groups will be grouped in the same region of embedding space within the primary alcohol cluster. Although Fig. 3a only provides a 2D projection of the principal components, the figure provides an approximate representation of how the full Euclidean distances, computed in full (D = 128) embedding space, relates the individual embedding vectors to one another.
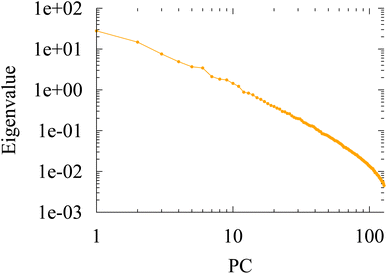
This suggests that only a few dimensions of the full 128-dimensional embedding space are truly relevant to capture the chemical identity of the associated atom. Indeed, the PCA eigenvalue spectrum, presented in Fig. 4, reveals that only a few significant eigenvalues (∼5–6) are required to account for 75% of the variance in the data. This is a remarkably low number compared with the dimension of the original embedding space, hinting at the possibility of determining low-dimensional chemical heuristics or rules for explaining the attributes of each of these individual dimensions.
For comparison, we also extracted AIMNet's QM9 embedding vectors and analyzed them with PCA projection. The result is shown in Fig. 3b. AIMNet's embedding are more compact than SchNet, as AIMNet was trained on a more diverse dataset (ANI-1x) obtained through active learning.96 This may be an explanation to why AIMNet's representation of QM9 is more compact as it must leave space for a wider representation. However, the relative positions of the various classes is strikingly similar even though AIMNet is a different GNN architecture and involves a significantly different embedding process briefly described in Section 2.4. This points to the notion of a weak universality in GNNs, as recently introduced by Chughtai et al.,97 in which universal underlying principles are shared by different GNNs, however in slightly different ways.
The existence of a Euclidean distance measure opens the opportunity to quantify the “closeness” of atoms from different moieties. In Fig. 5a, we chose a random molecule from the QM9 dataset (prop-2-yn-1-ol) and evaluated embedding vector distances with all other molecules in the dataset. Clearly, the closest molecules to prop-2-yn-1-ol are molecules of the same class and have similar structural motifs; primary alcohols with an α-alkyne group. Fig. 5b shows a close-up of distances to all other primary alcohols. As distance increases, the similarity is diminished but in a very gradual way. First, showing linear-like moieties with α-alkynes, then gradually moving the alkyne away to further parts of the molecule as embedding distance increases. This can be confirmed until molecules that do not contain any alkyne and do not resemble the reference primary alcohol anymore.
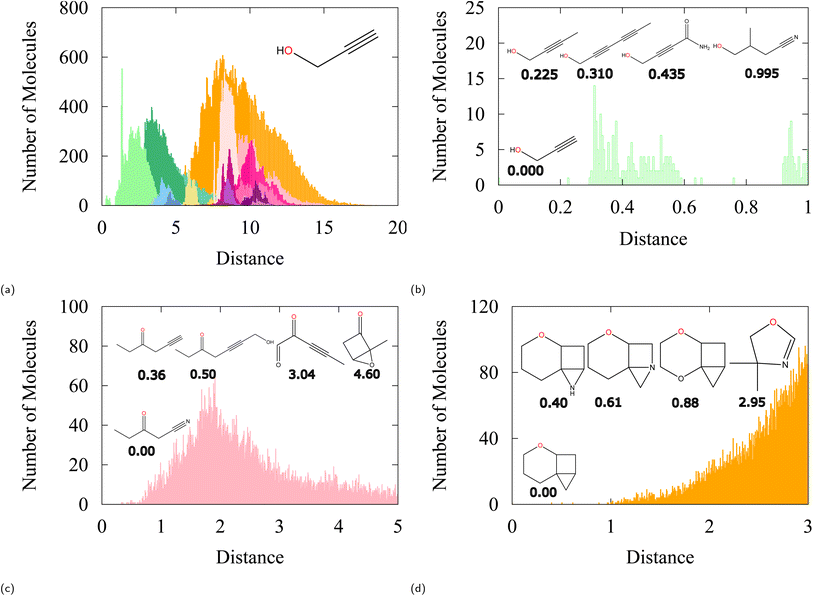 | ||
| Fig. 5 Euclidean distance analysis of chosen cases from QM9. (a) Overall distance distribution between embedding vector of the reference oxygen of prop-2-yn-1-ol to the rest of the oxygen embeddings in the dataset. The color key follows Fig. 2b. (b) Close-up of the nearest embeddings to prop-2-yn-1-ol which are also primary alcohols and additionally have similar structural motifs. (c) Same analysis on 3-oxopentanitrile and (d) on tri-ringed structure shown. | ||
The same analysis can be done on, e.g., 3-oxopentanenitrile (shown in Fig. 5c) where the presence of an alkyne is important for similarity, but one that is specifically at the α position to the ketone. Triple bonds that are right next to the ketone (i.e. not α) appear in more distant embedding vectors, after all the α-triple-bonded-ketones in the dataset. Lastly we show an example of the tri-ringed structure (Fig. 5d) which shows gradual change in the ring elements and ring structure with distance between the oxygen's embedding vectors.
3.2 Linear boundaries and Euclidean distance geometry of the embedding space
Ultimately, the use of visualization techniques such as t-SNE or PCA lacks precise quantification of the geometric space revealed. We can further quantify the embedding geometry along the lines of testing with concept activation vectors (TCAV) methodology.38 TCAV uses the idea of training another algorithm to intake embedding vectors and respond to their concept labels, in our case the chemical labels. In the spirit of using interpretable techniques, and in view of such a low-volume PCA projection, we may use linear discriminant analysis (LDA)69 to draw boundaries between the various embeddings and perform a chemical environment classification task on them. If this simple classification algorithm performs accurately, then we can conclude that the space is made up of well-defined clusters separated by thick boundaries, showing that the SchNet model contains enough information to capture the concept of chemical environments with a high degree of resolution.We performed LDA on the oxygen-type embedding vectors to get a minimum classification error of 3 × 10−4 for all classes defined in Table 1. See Table 1 for errors on individual classes. The confusion matrix of the predicted vs. true is dominantly diagonal. The excellent performance strongly supports the existence of distinct regions in high-dimensional space that are highly associated with chemical environments in the trained embeddings. To show the significance of this, we performed the same classification task on the smooth overlap of atomic positions (SOAP)98 representations, a popular method for molecular similarity measures, on the same set of oxygen atoms, the results are shown in Table 1. We performed two separate tests (SOAP1 & SOAP2) with two different sets of hyperparameters, the former consistent with a long cut-off range like the SchNet training (12 Å, beyond the sizes of the molecules in the QM9 dataset, 6 radial functions and 6 spherical harmonics), whereas the latter imposed a more local cut-off (6 Å, and 6 radial basis functions and 4 spherical harmonics). The classification results for SOAP1 and SOAP2 are given in Table 1. Whereas SOAP1 appears to struggle with distilling the local character of functional groups, imposing locality in SOAP2 produces perfect classification results. However, as the LDA only scales linearly in the number of data points, the memory requirements are significantly lighter than SOAP, for which only a 1000 molecules could be used for this test without requiring a large amount of memory (>2 GB). Therefore it is fair to state that embedding vectors are at least on par with coordinate-based features such as SOAP at capturing chemical environments in a compact representation, the catch being that all geometric considerations have already been encoded during the SchNet pretraining stage.
3.3 Transferability properties of the embedding space
An important question to ask is how useful is this global geometric interpretation for other chemical applications? Embedding vectors provide an atomwise representation of a molecule, so a direct comparison with other chemical observables than energy (on which the SchNet architecture has been trained) ideally involves chemical observables of atomic nature. For this reason, we focused on pKa values and NMR shifts in the present study.As a first test, we related the pKa values of certain atoms with their embedding vectors. More precisely, we addressed the assumption that moieties for which the embedding vectors are close in Euclidean distance should also have comparable pKa values. We employed a portion of the IUPAC pKa database,99 consisting of 600 clean and accurate pKa data points, and plotted the difference in pKa values between all possible pairs vs. the embedding distance between the pairs, see Fig. 6b. The triangular shape of the distribution confirms that chemical environments that are close in embedding space necessarily have pKa values that are also close. In Fig. 6a, we narrow in on the distribution by selecting a random carbamide oxygen found on 2H-1,2,4-triazine-3,5-dione from the database and plotting only relative distances with respect to this oxygen. From this figure, we can see how certain groups such as carbamides are closer in pKa to amides than they are to aldehydes and that they are significantly different from hydroxylamines. This is basic chemistry knowledge that a trained chemist may have, however the associated embedding space stemming from a learned representation allows for qualitative and quantitative organization of this chemical intuition.
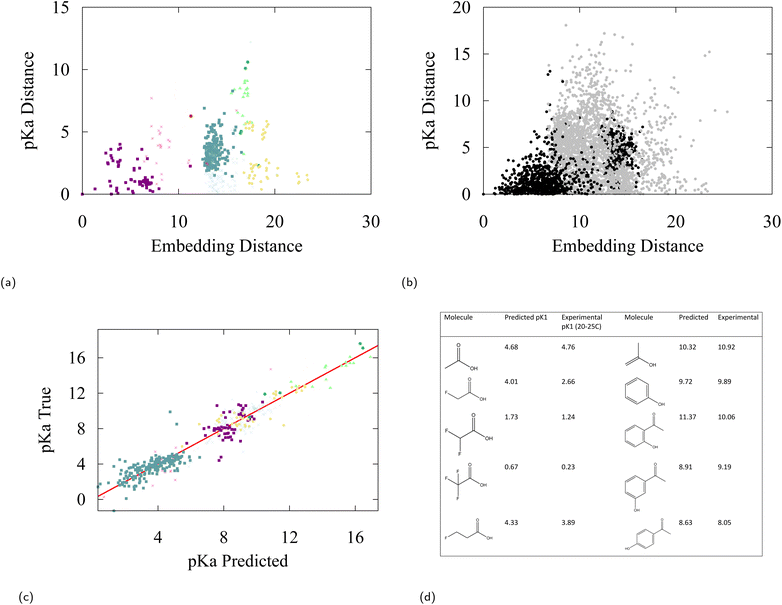 | ||
| Fig. 6 (a) pKa difference versus embedding vector distance from a reference carbamide oxygen found on 2H-1,2,4-triazine-3,5-dione to all other oxygens in the IUPAC pKa database. (b) pKa difference vs. embedding distance between all pairs of oxygen atoms in the IUPAC pKa database. The black labels are oxygens of the same class, the grey labels are oxygens of another class. (c) Truth versus linear regression predictions of oxygen pKa values of protic sites from 128 dimensional embedding vectors, the R2 value of the fit is 0.91. (d) Predicted vs. experimental pKa values for molecules affected by inductive and resonance effects, experimental data taken from ref. 101, pKa data taken from an IUPAC high confidence pKa molecular database.102 All oxygen labels are taken from Fig. 2b. | ||
A second test has been performed with 13C nuclear magnetic resonance (NMR) data, extracted from the NMRShiftDB2 model on a selection of 200 QM9 molecules.100 This model uses the Hierarchically Ordered Spherical Environment (HOSE) molecular descriptor to describe atomic neighborhoods. NMR shifts are particularly interesting to consider for our purpose as they are considered a sensitive fingerprint of atomic environments. Again, the differences in NMR shift between all possible carbon pairs have been plotted against the associated C-embedding distance between the pairs in Fig. 7b. Fig. 7a shows a selection of Fig. 7b in which only relative distances with respect to an ethane carbon are considered. The NMR distance can be taken to be a proxy to molecular similarity and we find that groups that are close in embedding space have similar NMR shifts.
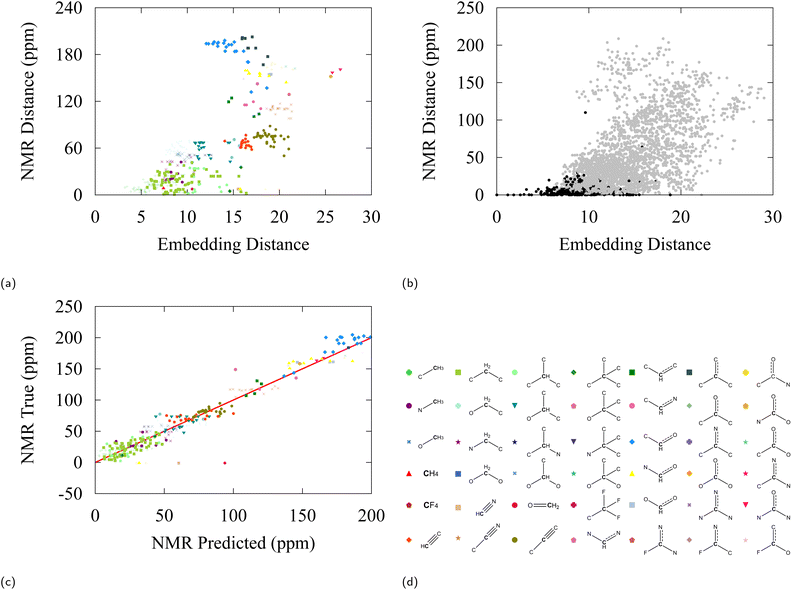 | ||
| Fig. 7 (a) 13C-NMR shift difference vs. embedding distance for carbon atoms with respect to a reference ethane carbon in the NMR dataset. (b) 13C-NMR shift difference vs. embedding distance between all pairs. Black labels are carbons of the same class, grey labels are carbons of another class. (c) Truth values versus linear regression predictions for 13C-NMR shifts from 128-dimensional embedding vectors, the R2 value of the fit is 0.95. (d) Carbon moiety labels. NMR values were found using NMRDShiftDB2 model100 applied on first 200 QM9 molecules. | ||
Finally, we explore the potential to use embedding vectors for transfer learning. We considered a simple linear regression model to predict pKa values and 13C-NMR shifts from pretrained embedding vectors of SchNet. As can be anticipated from our discussion, a linear regression model is relatively successful in predicting both observables from embedding space with a modest accuracy, giving a testing error of 1.48 and 23.3 ppm for pKa and 13C-NMR respectively (see Fig. 6c and 7c). It can be seen from the errors in Table 4 and the determination coefficient of the linear fit (R2 = 0.91), that some degree of induction and resonance effects on the pKa can be captured by the embeddings. Given the small sizes of the datasets used, these results provide a promising starting point for understanding transfer learning in GNNs, which we aim to address in future studies and applications.
An important hyperparameter in machine learning applications is data volume. More often than not, the amount of training data from computational or experimental studies is limited, potentially hampering the interpretability of the embedding vector representation. To this end, we investigated the effect of dataset size on the interpretability of the embedding vectors. We trained the same SchNet architecture as described in Section 2.3, however on different datasets with decreasing sizes (see Table 2). For the training sets, random molecules were chosen from the full QM9 data, with 10% additional data points for validation purposes. As is expected, we notice a sharp increase in validation error (MAE) when reducing the dataset from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules to 1000. In order to compare the classification capabilities, we extracted the embedding vectors of the same 10
000 molecules to 1000. In order to compare the classification capabilities, we extracted the embedding vectors of the same 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules employed in Section 3.1 and ran the LDA classification task on them. We observed a similar drop in accuracy moving into smaller training data as the MAE, however plateauing towards a 97% accuracy on the functional group classification. These numbers suggest that the model still succeeds in categorizing the training data into chemical moieties for smaller training data sets, however lacked the capability to reduce the uncertainty and refine the feature space for regression tasks. To further quantify this observation, we computed the ratio of the average radial width of all functional group clusters with respect to the average distance between the individual clusters, finding that the average size of the clusters grows relative to the average distance between the clusters (see Table 2).
000 molecules employed in Section 3.1 and ran the LDA classification task on them. We observed a similar drop in accuracy moving into smaller training data as the MAE, however plateauing towards a 97% accuracy on the functional group classification. These numbers suggest that the model still succeeds in categorizing the training data into chemical moieties for smaller training data sets, however lacked the capability to reduce the uncertainty and refine the feature space for regression tasks. To further quantify this observation, we computed the ratio of the average radial width of all functional group clusters with respect to the average distance between the individual clusters, finding that the average size of the clusters grows relative to the average distance between the clusters (see Table 2).
| Size | MAE (eV) | LDA mean error | ρ |
|---|---|---|---|
| 50 | 1.23 | 0.025 | 1.02 |
| 100 | 0.88 | 0.029 | 1.08 |
| 500 | 0.64 | 0.024 | 0.95 |
| 1000 | 0.78 | 0.024 | 0.77 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.02 | 3.0 × 10−4 | 0.45 |
4 Conclusions
We demonstrate how the embedding vectors of SchNet provide a chemically interpretable representation endowed with Euclidean-distance-preserving geometry. The model organizes chemical space into chemical environments or moieties, confirmed by sharp linear discriminant analysis (LDA) boundaries. Furthermore, principal component analysis (PCA) reveals that the model retains a small volume of information, up to 6 dimensions required to account for 75% the variance in the data. The chemical information contained in the embedding vectors is confirmed by confronting them with atomwise chemical observables such as pKa values or 13C-NMR shifts. This result holds promise that embeddings can be used for applications in transfer learning while providing an explainable framework for their predictions.One important open question leading from this study is to further pinpoint the algebraic properties and geometry of the embedding space, as well as identify the chemical role of each of the significant dimensions of the PCA. Another question that has been left untouched is the role of the underlying computational data. The SchNet GNN has been trained on electronic energies that have been computed at the density functional theory level. How much of the fundamental quantum mechanical ingredients that go in the computed energy data, in casu the densities or the B3LYP functional in the DFT computation, have been implicitly identified by the GNN and absorbed into the embedding vector representation. Can similar conclusions be drawn when pretrained on different chemical training data, such as enthalpies or dipole moments? These questions will be addressed in future studies.
A Appendix
A.1 Training and validation results and reproducibility of analysis
We repeated the analysis by retraining a SchNet neural network 10 times on QM9's potential energies at 0 K, with all validation errors reported in Table 3. The mean absolute error on validation dataset (molecules indexed 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–110
000–110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0000 in QM9) is 0.023 eV with standard deviation of 0.004 eV. Fig. 8 shows the training of model 1 (MAE = 0.020 eV).
0000 in QM9) is 0.023 eV with standard deviation of 0.004 eV. Fig. 8 shows the training of model 1 (MAE = 0.020 eV).
| Trial | MAE (eV) |
|---|---|
| 1 | 0.020 |
| 2 | 0.017 |
| 3 | 0.023 |
| 4 | 0.029 |
| 5 | 0.019 |
| 6 | 0.025 |
| 7 | 0.023 |
| 8 | 0.025 |
| 9 | 0.021 |
| 10 | 0.027 |
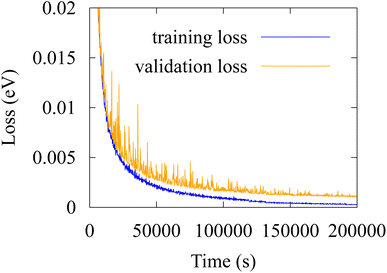 | ||
| Fig. 8 Training loss and validation loss of SchNet model with 128 atom basis, 128 gaussian filters, 50 gaussians, and a cutoff of 50 Å. | ||
A.2 Analysis of interaction layers, vl
Other than analyzing the fully updated atomwise embedding vectors xil, we also analyzed the intermediate layers,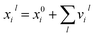 in a similar fashion. Table 4 below shows the mean absolute error of interaction updates on the embedding vector, the mean Euclidean distance between embedding vectors of different layers, the mean Euclidean distance between embedding of different classes, and lastly, the mean LDA accuracy on chemical classes using the intermediate layers.
in a similar fashion. Table 4 below shows the mean absolute error of interaction updates on the embedding vector, the mean Euclidean distance between embedding vectors of different layers, the mean Euclidean distance between embedding of different classes, and lastly, the mean LDA accuracy on chemical classes using the intermediate layers.
| Layer | 〈|vl|〉 | 〈Dist(xl − xl−1)〉 | 〈Dist(xfgl − xfgl)〉 | LDA mean error |
|---|---|---|---|---|
| x 0 | 0.25 | — | 0.00 | 9 × 10−1 |
| x 1 | 0.30 | 3.56 | 2.64 | 2 × 10−3 |
| x 2 | 0.28 | 4.29 | 3.90 | 5 × 10−4 |
| x 3 | 0.26 | 3.88 | 5.13 | 8 × 10−4 |
| x 4 | 0.28 | 3.64 | 5.74 | 2 × 10−3 |
| x 5 | 0.25 | 4.02 | 6.32 | 5 × 10−4 |
The interesting thing to note about the table is that while the interaction updates remain relatively the same over the layers (and so does the average distance between embeddings of different layers), the average distance between different moieties continues to increase over the interaction layers (Fig. 9).
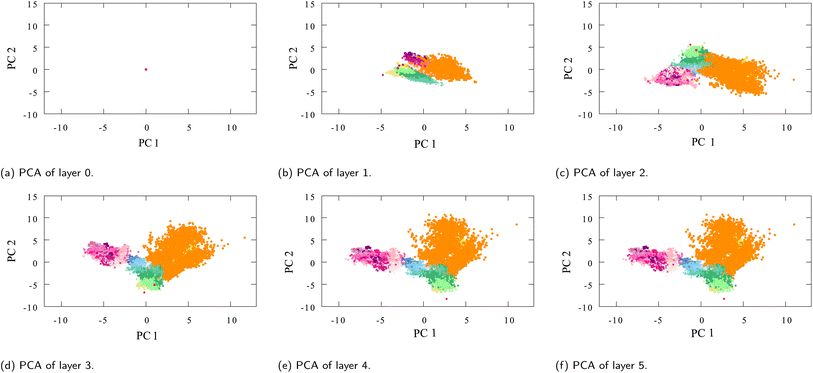 | ||
| Fig. 9 PCA plots of oxygen-type embeddings of each successive interaction layer l ≠ final (see Fig. 3 for the final layer l = final), (a) layer 0, containing the initialized embedding which is the same for all oxygens, (b–f) layers 1 to 5. | ||
A.3 Analysis on other heteroatoms
One can also perform a similar analysis on the embeddings of other elements than oxygen in the QM9 dataset. Table 5 below shows the LDA accuracy of chemical environment classification using embeddings of each element in QM9.| Element | LDA mean error |
|---|---|
| H | 5 × 10−3 |
| C | <1 × 10−5 |
| N | <1 × 10−4 |
| O | 3 × 10−4 |
| F | <1 × 10−3 |
Data availability
The Jupyter notebooks used to generate our research findings are available on the githubrepository, https://github.com/QuNB-Repo/DLCheM. The generated data set of “SchNet Model embedding vectors of QM9 atoms labeled according tofunctional group designation” on which the analysis have been published on UNB’s Dataverseserver, https://doi.org/10.25545/EK1EQA, IUPAC dataset of pKa values can be found at https://doi.org/10.5281/zenodo.7236452. NMRShiftDB2 model used to extract NMR predictions for QM9 database found at https://nmrshiftdb.nmr.uni-koeln.de/.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
AES, IAH, MH and SDB acknowledge NSERC, CFI, NBIF, and AARMS for financial support. SDB acknowledges the Canada Research Chair program. This research was enabled in part by software provided by the Digital Research Alliance of Canada (https://www.alliancecan.ca). Discussions with Niels Billiet, Guillaume Acke, Nicholas Touikan and Max Hennick about GNNs in all stages of the project are gratefully acknowledged.Notes and references
- A. M. El-Samman, SchNet Model Embedding Vectors of QM9 Atoms Labelled According to Functional Groups Designation, 2023, DOI:10.25545/EK1EQA.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, New J. Phys., 2013, 15, 095003 CrossRef CAS.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. Von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326 CrossRef CAS PubMed.
- K. Yao, J. E. Herr, S. N. Brown and J. Parkhill, J. Phys. Chem. Lett., 2017, 8, 2689 CrossRef CAS PubMed.
- T. B. Hughes, G. P. Miller and S. J. Swamidass, ACS Cent. Sci., 2015, 1, 168 CrossRef CAS PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, Front. Environ. Sci., 2016, 3, 80 Search PubMed.
- J. Ma, R. P. Sheridan, A. Liaw, G. E. Dahl and V. Svetnik, J. Chem. Inf. Model., 2015, 55, 263 CrossRef CAS PubMed.
- T. Unterthiner, A. Mayr, G. Klambauer, M. Steijaert, J. K. Wegner, H. Ceulemans and S. Hochreiter, Proceedings of the Deep Learning Workshop at NIPS, 2014, p. 1 Search PubMed.
- G. E. Dahl, N. Jaitly and R. Salakhutdinov, arXiv, 2014, preprint, arXiv:1406.1231, DOI:10.48550/arXiv.1406.1231.
- A. Korotcov, V. Tkachenko, D. P. Russo and S. Ekins, Mol. Pharm., 2017, 14, 4462 CrossRef CAS PubMed.
- T. Unterthiner, A. Mayr, G. Klambauer and S. Hochreiter, arXiv, 2015, preprint, arXiv:1503.01445, DOI:10.48550/arXiv.1503.01445.
- J. Wenzel, H. Matter and F. Schmidt, J. Chem. Inf. Model., 2019, 59, 1253 CrossRef CAS PubMed.
- M. Li, H. Zhang, B. Chen, Y. Wu and L. Guan, Sci. Rep., 2018, 8, 1 Search PubMed.
- K. Mills, M. Spanner and I. Tamblyn, Phys. Rev. A, 2017, 96, 042113 CrossRef.
- K. Yao and J. Parkhill, J. Chem. Theory Comput., 2016, 12, 1139 CrossRef CAS PubMed.
- R. T. McGibbon, A. G. Taube, A. G. Donchev, K. Siva, F. Hernández, C. Hargus, K.-H. Law, J. L. Klepeis and D. E. Shaw, J. Chem. Phys., 2017, 147, 161725 CrossRef PubMed.
- S. Lorenz, A. Groß and M. Scheffler, Chem. Phys. Lett., 2004, 395, 210 CrossRef CAS.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129 CrossRef CAS.
- K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, in Proceedings of Advances in Neural Information Processing Systems 30 (NIPS 2017), 2017, p. 992 Search PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- K. Schutt, P. Kessel, M. Gastegger, K. Nicoli, A. Tkatchenko and K.-R. Muüller, J. Chem. Theory Comput., 2018, 15, 448 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192 RSC.
- A. B. Arrieta, N. Díaz-Rodríguez, J. Del Ser, A. Bennetot, S. Tabik, A. Barbado, S. García, S. Gil-López, D. Molina and R. Benjamins, et al. , Inf. Fusion, 2020, 58, 82 CrossRef.
- W. Samek, A. Binder, G. Montavon, S. Lapuschkin and K.-R. Müller, IEEE Transact. Neural Networks Learn. Syst., 2016, 28, 2660 Search PubMed.
- W. Samek, G. Montavon, S. Lapuschkin, C. J. Anders and K.-R. Müller, Proc. IEEE, 2021, 109, 247 Search PubMed.
- M. Bojarski, P. Yeres, A. Choromanska, K. Choromanski, B. Firner, L. Jackel and U. Muller, arXiv, 2017, preprint, arXiv:1704.07911, DOI:10.48550/arXiv.1704.07911.
- R. Caruana, Y. Lou, J. Gehrke, P. Koch, M. Sturm and N. Elhadad, Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2015, p. 1721 Search PubMed.
- J. T. Leek, R. B. Scharpf, H. C. Bravo, D. Simcha, B. Langmead, W. E. Johnson, D. Geman, K. Baggerly and R. A. Irizarry, Nat. Rev. Genet., 2010, 11, 733 CrossRef CAS PubMed.
- C. Soneson, S. Gerster and M. Delorenzi, PLoS One, 2014, 9, 1 CrossRef PubMed.
- S. Lapuschkin, A. Binder, G. Montavon, K.-R. Muller and W. Samek, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, p. 2912 Search PubMed.
- G. B. Goh, N. O. Hodas, C. Siegel and A. Vishnu, arXiv, 2017, preprint, arXiv:1712.02034, DOI:10.48550/arXiv.1712.02034.
- W. Samek, T. Wiegand and K.-R. Müller, arXiv, 2017, preprint, arXiv:1708.08296, DOI:10.48550/arXiv.1708.08296.
- D. Castelvecchi, Nat. News, 2016, 538, 20 CrossRef CAS PubMed.
- D. Lei, X. Chen and J. Zhao, arXiv, 2018, preprint, arXiv:1805.08355, DOI:10.48550/arXiv.1805.08355.
- W. J. von Eschenbach, Phil. Technol., 2021, 34, 1607 CrossRef.
- R. Shwartz-Ziv and N. Tishby, arXiv, 2017, preprint, arXiv:1703.00810, DOI:10.48550/arXiv.1703.00810.
- B. Kim, M. Wattenberg, J. Gilmer, C. Cai, J. Wexler, F. Viegaset al., International Conference on Machine Learning, 2018, p. 2668 Search PubMed.
- K. Preuer, G. Klambauer, F. Rippmann, S. Hochreiter and T. Unterthiner, in Interpretable Deep Learning in Drug Discovery, ed. W. Samek, G. Montavon, A. Vedaldi, L. K. Hansen and K.-R. Müller, Springer International Publishing, Cham, 2019, p. 331 Search PubMed.
- F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Acc. Mater. Res., 2022, 3, 597 CrossRef CAS.
- R. Dybowski, New J. Chem., 2020, 44, 20914 RSC.
- N. Omidvar, H. S. Pillai, S.-H. Wang, T. Mou, S. Wang, A. Athawale, L. E. Achenie and H. Xin, J. Phys. Chem. Lett., 2021, 12, 11476 CrossRef CAS PubMed.
- P. Schwaller, A. C. Vaucher, R. Laplaza, C. Bunne, A. Krause, C. Corminboeuf and T. Laino, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1604 Search PubMed.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem, 2020, 4, 347 CrossRef PubMed.
- R. Ramakrishnan and O. A. von Lilienfeld, Rev. Comput. Chem., 2017, 30, 225 CAS.
- S. Letzgus, P. Wagner, J. Lederer, W. Samek, K.-R. Muller and G. Montavon, IEEE Signal Process. Mag., 2022, 39, 40 Search PubMed.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490 CrossRef CAS PubMed.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 134 CrossRef CAS PubMed.
- M. Wattenberg, F. Viégas and I. Johnson, Distill, 2016, 1, 2 Search PubMed.
- F. M. Bianchi, D. Grattarola and C. Alippi, International conference on machine learning, 2020, p. 874 Search PubMed.
- J. Lederer, M. Gastegger, K. T. Schütt, M. Kampffmeyer, K. R. Müller and O. T. Unke, Phys. Chem. Chem. Phys., 2023, 25(38), 26370–26379 RSC.
- R. Guidotti, A. Monreale, S. Ruggieri, F. Turini, F. Gianotti and D. Pedreschi, ACM Comput. Survey, 2018, 51, 1 Search PubMed.
- H. Lakkaraju, R. Caruana, E. Kamar and J. Leskovec, arXiv, 2017, preprint, arxiv:1707.01154v1, 10.1039/D3CP03845A.
- O. Bastani, C. Kim and H. Bastani, arXiv, 2019, preprint, arxiv:1705.08504, DOI:10.48550/arXiv.1705.08504.
- J. Jiménez-Luna, F. Grisoni and G. Schneider, Nat. Mach. Intell., 2020, 2, 573 CrossRef.
- S. Lundberg and S.-I. Lee, arXiv, 2017, preprint, arxiv:1705.07874, DOI:10.48550/arXiv.1705.07874.
- M. Sundararajan, A. Taly and Q. Yan, In Proceedings of the 34th International Conference on Machine Learning, 2017, vol. 70, p. 3319 Search PubMed.
- J. Jiménez-Luna, M. Skalic, N. Weskamp and G. Schneider, J. Chem. Inf. Model., 2021, 61, 1083 CrossRef PubMed.
- M. H. Rasmussen, D. S. Christensen and J. H. Jensen, SciPost Chem., 2023, 2, 2 CrossRef.
- D. Smilkov, N. Thorat, B. Kim, F. Viégas and M. Wattenberg, arXiv, 2017, preprint, arxiv:1706.03825, DOI:10.48550/arXiv.1706.03825.
- M. T. Ribeiro, S. Singh and C. Guestrin, KDD’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, p. 1135 Search PubMed.
- A. Shrikumar, P. Greenside and A. Kundaje, Proceedings of the 34th International Conference on Machine Learning, PMLR, 2017, p. 3145 Search PubMed.
- P. E. Pope, S. Kolouri, M. Rostami, C. E. Martin and H. Heiko, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, p. 10772 Search PubMed.
- J. Yosinski, J. Clune, A. Nguyen, T. Fuchs and H. Lipson, arXiv, 2015, preprint, arxiv:1506.06579, DOI:10.48550/arXiv.1506.06579.
- S. Riniker and G. A. Landrum, J. Cheminf., 2013, 5, 43 CAS.
- S. M. Lundberg, G. Erion, H. Chen, A. DeGrave, J. M. Prutkin, B. Nair, K. Ronit, J. Himmelfarb, N. Bansal and S.-i. Lee, Nat. Mach. Intell., 2020, 2, 56 CrossRef PubMed.
- R. Roscher, B. Bohn, M. Duarto and J. Garcke, IEEE Access, 2020, 8, 42200 Search PubMed.
- L. Van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579 Search PubMed.
- A. J. Izenman, Modern multivariate statistical techniques, 2013, p. 237 Search PubMed.
- H. Abdi and L. J. Williams, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2010, 2, 433 CrossRef.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930 RSC.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, p. 1263 Search PubMed.
- Y. Kwon, D. Lee, Y.-S. Choi, M. Kang and S. Kang, J. Chem. Inf. Model., 2020, 60, 2024 CrossRef CAS PubMed.
- J. Jo, B. Kwak, H.-S. Choi and S. Yoon, Methods, 2020, 179, 65 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 1 Search PubMed.
- T.-C. Nguyen, V.-Q. Nguyen, V.-L. Ngo, Q.-K. Than and T.-L. Pham, Comput. Mater. Sci., 2021, 200, 110784 CrossRef CAS.
- D. P. Kingma and M. Welling, arXiv, 2013, preprint, arXiv:1312.6114, DOI:10.48550/arXiv.1312.6114.
- Z. Kong and K. Chaudhuri, Adv. Neural Inf. Process. Syst., 2021, 34, 2400 Search PubMed.
- V. Svensson, A. Gayoso, N. Yosef and L. Pachter, Bioinformatics, 2020, 36, 3418 CrossRef CAS PubMed.
- Y. B. Varolgüneş, T. Bereau and J. F. Rudzinski, Mac. Learn.: Sci. Technol., 2020, 1, 015012 Search PubMed.
- A. A. Ismail, H. Corrada Bravo and S. Feizi, Adv. Neural Inf. Process. Syst., 2021, 34, 26726 Search PubMed.
- C. Etmann, S. Lunz, P. Maass and C.-B. Schönlieb, arXiv, 2019, preprint, arXiv:1905.04172, DOI:10.48550/arXiv.1905.04172.
- C. Olah, A. Satyanarayan, I. Johnson, S. Carter, L. Schubert, K. Ye and A. Mordvintsev, Distill, 2018, 3, e10 Search PubMed.
- K. Simonyan, A. Vedaldi and A. Zisserman, arXiv, 2013, preprint, arXiv:1312.6034, DOI:10.48550/arXiv.1312.6034.
- M. D. Zeiler and R. Fergus, European Conference on Computer Vision, 2014, p. 818 Search PubMed.
- A. Mahendran and A. Vedaldi, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, p. 5188 Search PubMed.
- J. T. Springenberg, A. Dosovitskiy, T. Brox and M. Riedmiller, arXiv, 2014, preprint, arXiv:1412.6806, DOI:10.48550/arXiv.1412.6806.
- C. Olah, A. Mordvintsev and L. Schubert, Distill, 2017, 2, e7 Search PubMed.
- H. A. Chipman and H. Gu, J. Appl. Stat., 2005, 32, 969 CrossRef.
- B. M. S. Hasan and A. M. Abdulazeez, J. Soft Computing Paradigm, 2021, 2, 20 Search PubMed.
- A. Bibal and B. Frénay, Safe Machine Learning Workshop at ICLR, 2019 Search PubMed.
- B. Hosseini and B. Hammer, Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 2020, p. 310 Search PubMed.
- L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- B. Chughtai, L. Chan and N. Nanda, arXiv, 2023, preprint, arxiv:2302.03025, DOI:10.48550/arXiv.2302.03025.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Zheng, IUPAC/Dissociation-Constants: v1.0, 2022, DOI:10.5281/zenodo.7236453.
- D. S. Wishart, Z. Sayeeda, Z. Budinski, A. Guo, B. L. Lee, M. Berjanskii, M. Rout, H. Peters, R. Dizon, R. Mah, C. Torres-Calzada and M. Hiebert-Giesbrecht, Nucleic Acids Res., 2022, 50, D665 CrossRef CAS PubMed.
- Chemical Book, 2023, https://www.chemicalbook.com/, accessed on 07 20, 2023.
- J. Zheng, IUPAC/Dissociation-Constants: v1.0, 2022, DOI:10.5281/zenodo.7236453.
| This journal is © The Royal Society of Chemistry 2024 |