Not as simple as we thought: a rigorous examination of data aggregation in materials informatics

Abstract

Recent Machine Learning (ML) developments have opened new perspectives on accelerating the discovery of new materials. However, in the field of materials informatics, the performance of ML estimators is heavily limited by the nature of the available training datasets, which are often severely restricted and unbalanced. Among practitioners, it is usually taken for granted that more data corresponds to better performance. Here, we investigate whether different ML models for property predictions benefit from the aggregation of large databases into smaller repositories. To do this, we probe three different aggregation strategies prioritizing training size, element diversity, and composition diversity. For classic ML models, our results consistently show a reduction in performance under all the considered strategies. Deep Learning models show more robustness, but most changes are not significant. Furthermore, to assess whether this is a consequence of a distribution mismatch between datasets, we simulate the data acquisition process of a single dataset and compare a random selection with prioritizing chemical diversity. We observe that prioritizing composition diversity generally leads to a slower convergence toward better accuracy. Overall, our results suggest caution when merging different data sources and discourage a biased acquisition of novel chemistries when building a training dataset.

---

1 Introduction

In recent years, following the increased availability of computational material databases,^1–3 Machine Learning (ML) and data-driven approaches have opened new frontiers for accelerating materials discovery. These aim at overcoming the limitations imposed by the expensive physical simulations adopted in density functional theory (DFT), which allow only for a narrow exploration of the chemical space. Furthermore, DFT suffers from systematic errors due to numerical approximations occurring in any solver.⁴ Besides the computational advantages, ML models can also discover novel patterns that are otherwise hard to identify by only leveraging traditional chemical knowledge.^5,6 While, on the one hand, such approaches have shown remarkable success,^7–10 it is important to acknowledge their limitations and potential downsides. One significant challenge is the difficulty in assessing the quality of performance outside the distribution of training data. As it happens, ML models can learn patterns that are too specific to the training data and fail to extrapolate to unseen data (overfitting).

Furthermore, these approaches are highly dependent on the size of the training dataset, and a shortage of data can result in models that have limited capabilities and make inaccurate predictions. Experimental datasets of specific chemical properties, such as thermoelectric properties,^11,12 are often unbalanced and rare throughout the literature. This is a consequence of the popular material repositories predominantly relying on DFT calculations,^1,2,13 which tend to provide a constrained selection of chemical attributes. This hampers the ability to effectively target specific material classes. Different approaches have been adopted to mitigate biases in materials data. For example, LOCO-CV¹⁴ has been proposed as a modification of the standard KFold evaluation strategy to measure the extrapolation error of ML models on unseen chemical clusters. Moreover, an entropy-based metric has been recently proposed to mitigate the imbalance of a crystal structures dataset by improving the diversity of underrepresented crystal systems.¹⁵

On a general level, three main strands are usually considered to improve the predictive accuracy of ML models:

• Better model: in a model-centric approach, the primary emphasis is on creating better algorithms to extract valuable insights from the available data. Lately, especially in the area of Deep Learning (DL), this is mostly done by designing novel architectures. Here, a popular approach is to strengthen the algorithm by tailoring the architecture to the specific application, usually by leveraging symmetries that exist in the data, e.g. crystal structures;¹⁶

• Better data: in a data-centric approach, the focus is instead on the quality of the inputs for the model. Notable examples are the refinement of the measurement strategy and preprocessing, e.g. data balancing or outlier filtering. Also falling under this category are methods that leverage domain knowledge to design better data features, more commonly known as ‘feature engineering’.^17,18

• More data: in this branch of the data-centric approach, the attention is shifted to increasing the number of data points. This is generally considered to be more significant in view of a better-performing statistical model^19,20 and a compelling alternative to vast domain knowledge.²¹

As this last point is generally taken for granted, little attention has been dedicated to it in the materials informatics literature. Given this and the limited availability of experimental data, it is natural for practitioners to consider the aggregation of diverse data sources.²² However, data aggregation in materials informatics presents unique challenges.²³ Unlike many other domains, datasets of chemical properties are often small in size, unbalanced towards common materials, and collected under diverse experimental conditions. In this scenario, the quantity and quality of data can easily conflict with each other. In fact, expanding the size of the dataset with external sources may affect the organicity of the dataset and the overall data quality. Adding to the complexity, the substantial diversity among material data entries, originating from the heterogeneity within the vast chemical space, presents an additional challenge in assessing the impact on training from individual data points. These challenges emphasize the need for careful consideration when aggregating different datasets in materials informatics research.

In this work, we deepen the aggregation of different datasets reporting chemical formulae and associated properties. In particular, we study whether the predictive accuracy of different ML models can benefit from the aggregation of local repositories with databases with larger availability. In order to do that, we consider three different aggregation strategies in which we prioritize training size, element diversity, and composition diversity. Our main findings are summarized as follows:

• We report that classical ML methods performance undergo a noticeable degradation subsequent to a concatenation with popular databases. Additionally, we show that the incorporation of data points focusing on maximizing chemical diversity also leads to a worsening in the performance of such models.

• We establish that DL models exhibit a much higher level of robustness. However, the majority of changes in the accuracy, whether improvements or degradations, are not statistically significant.

• We simulate the data acquisition process on a single dataset by utilizing both the DiSCoVeR algorithm and a random acquisition approach. We proceed to compare the results obtained from these two methods on both a randomly generated test set and a biased test set, which was previously constructed using DiSCoVeR. Notably, our observations demonstrate that a biased acquisition strategy for new stoichiometries deteriorates the learning process, regardless of the test set scenario.

The rest of the paper is structured as follows. In Sec. 2, we present the datasets and the downstream ML models that we use to support our claims; in Sec. 3, we evaluate different dataset aggregation strategies and discuss results; in Sec. 4, we present the result about prioritizing chemical diversity in progressive data acquisition; Sec. 5 concludes the paper with the final remarks.

2 Preliminaries

2.1 Datasets

In our experimental setting, we consider eight different datasets for eight different chemical properties:

• Electrical resistivity, electrical conductivity and Seebeck coefficient from the MRL dataset;¹¹

• Thermal conductivity from the Citrine platform;²⁴

• Band gap from ref. 25;

• DFT calculated bulk modulus and shear modulus from AFLOW.¹³

For each property, the respective dataset is aggregated with experimental data coming from the Materials Platform for Data Science (MPDS),³ retrieved by using the provided API. MPDS is one of the largest resources currently available for material scientists. It leverages the extensive data available in the Pauling File,²⁶ a comprehensive database of materials information reporting crystal structures chemical compositions and phase diagrams, to enable efficient exploration, analysis, and modeling of materials. For the two calculated datasets, we also consider the aggregation with calculated data from the Materials Project (MP) database.¹

Several steps of preprocessing are applied to the raw datasets. First, we filter out values outside ±15 K of the room temperature. We adopt this choice as the temperature information was not available for all the datasets under consideration. Therefore, to prioritize property diversity and to establish a homogeneous analysis, we have chosen a reasonable threshold for the temperature information, whenever reported. Furthermore, we filter out noble gases and radio-isotopes (atomic number (A) > 93). If input duplicates are found, we store their median. Finally, we discard all the data points outside 3 standard deviations from the overall mean. Fig. 1 compares the distributions of the mentioned local repositories with the corresponding dataset from which we gather the additional data. Except for sporadic cases, we observe a general agreement in shape between the considered pairs of datasets. As expected, local repositories generally cover a smaller range of values with respect to the data gathered from the archives. Further details about sizes and value range for all datasets are given in Table 1. With the only exception of the band gap datasets pair, the size of the archives' data are always larger.

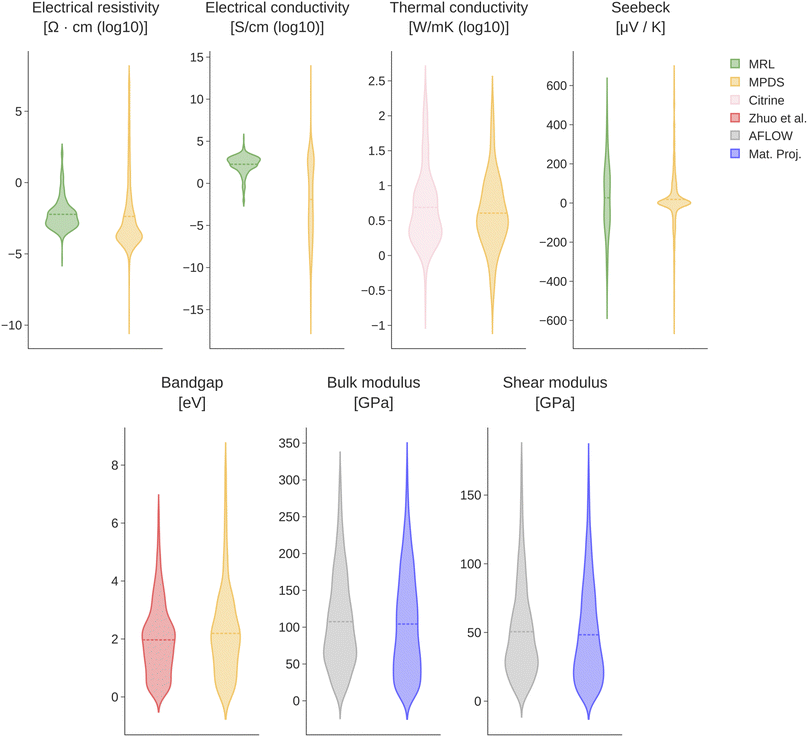Fig. 1 Violin plots of all pairs of datasets. Notably, archives' data covers a wider range of the target property.

Table 1 Dataset details. Datasets labeled with ‘A’ are the ones that will be increased through aggregation (denoted ‘A’) with points from dataset ‘B’

Property	Units	Dataset	Nature	Size	Minimum	Maximum	Aggregation label
Electrical resistivity	Ω cm	MRL	Exp.	400	−5.3 (log)	2.17 (log)	A
		MPDS	Exp.	6352	−10 (log)	7.6 (log)	B
Electrical conductivity	S cm^−1	MRL	Exp.	401	−2.17 (log)	5.3 (log)	A
		MPDS	Exp.	1489	−15 (log)	11 (log)	B
Thermal conductivity	W m^−1 K^−1	Citrine	Exp.	219	−0.70 (log)	2.37 (log)	A
		MPDS	Exp.	878	−0.85 (log)	2.30 (log)	B
Seebeck coefficient	μV K^−1	MRL	Exp.	416	−476.68	525.2	A
		MPDS	Exp.	2050	−640	674	B
Band gap	eV	Zhuo	Exp.	2287	0.02	6.43	A
		MPDS	Exp.	918	2 × 10^−4	8	B
Bulk modulus	GPa	AFLOW	Calc.	4822	0.66	312.94	A
		MP	Calc.	6221	0.73	324.70	B
		MPDS	Exp.	1367	2 × 10^−7	379.4	B
Shear modulus	GPa	AFLOW	Calc.	4747	0.65	175.81	A
		MP	Calc.	6073	0	174.12	B
		MPDS	Exp.	358	0.36	293	B

---

2.2 ML estimators

Throughout the paper, we evaluate data aggregation by comparing the performance of different ML estimators before and after increasing the dataset size. These models include baselines and state-of-the-art (SOTA) models for chemical properties prediction given the stoichiometry, with representatives of both classical and DL approaches. In more detail, we consider ridge regression as a simple baseline model, random forest regression as a robust model for low-data regimes,²¹Roost²⁷ as a DL model based on graph representations and CrabNet²⁸ as a transformer-based approach and representative of the SOTA. Performance is assessed through the ordinary procedure of train-test split and on the mean absolute error (MAE), a typical metric used for regression that quantifies the absolute deviation between models' predictions and true corresponding values.

Finally, we adopt a classification task, inspired by recent work investigating machine learning extrapolation capabilities in materials informatics.²⁹ We first label as extraordinary those materials associated to a chemical property value in the top 20% of the distribution. Here, the term ‘top’ is defined based on the specific property under consideration. In some cases, ‘top’ refers to the highest values, while in other cases, ‘top’ denotes the lowest values, depending on the tail of the distribution. We finally consider logistic regression as a simple binary classifier to differentiate ordinary from extraordinary materials.

The regularization strength for the ridge regression and logistic regression model is optimized via Cross Validation (CV) from a range of logarithmically spaced values between [10⁻⁴, 10³]. Finally, results are averaged across 5 iterations with different random seeds controlling the initialization of all stochastic components.

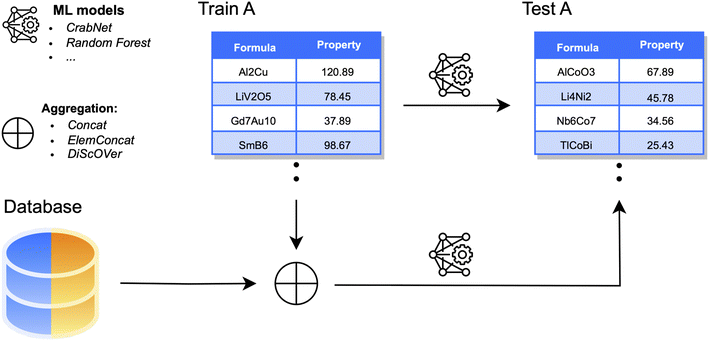
3 A–B data aggregation

As our first and main experiment, we consider the aggregation of each dataset A with data points collected from the respective dataset B (Fig. 2). To assess the benefits of the aggregation, we first evaluate the performance of ML estimators before integrating any new data points; this will be indicated as baseline setting. This is done, as usual, by training on a subset (80%) of dataset A and computing prediction errors on the corresponding test set (20%). For DL models, 10% of the training size is reserved for a validation set. In the aggregation process, data points collected from B only increase the size of the original training set (and validation, for DL) of A. For consistency, performance is always assessed on the original test set of A. We consider three different aggregation strategies:

Fig. 2 Data aggregation framework. For each chemical property, ML models are trained on a fraction of the available dataset (here indicated as Train set) and on the aggregation with part of a material database. The performance of ML models is always evaluated on the same Test set, which consists of a separate fraction of the original dataset.

3.1 Concatenation

A simple concatenation of all points from the train set of A with the whole dataset B. Duplicated instances are removed by taking the median across reported target properties. The primary advantage of this strategy is that the size of the resulting dataset is maximized. This is generally believed to strengthen the robustness of the estimators and potentially discover new patterns. However, a possible drawback is a saturation effect which arises from the compounded presence of redundant data points, hindering model learning and generalization. In particular, different associated values and experimental conditions may have the overall effect of increasing the degree of noise in the dataset.

3.2 Element-focused concatenation

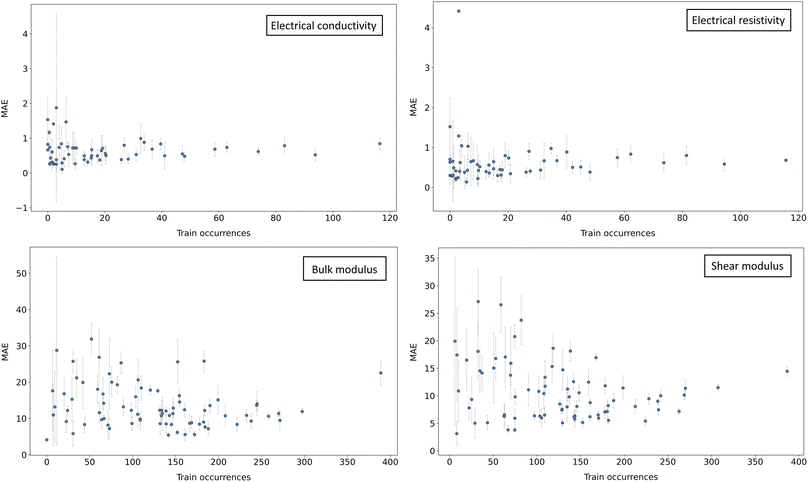
To introduce the next strategy, we consider the following illustrative example. In Fig. 3, the mean average error (MAE) of a Random Forest model³⁰ is plotted against the occurrences of the chemical elements in compositions of the training dataset A. Two main patterns can be observed: an increase in MAE as fewer representatives are available at the training stage, and an increase in variance (similar patterns are also observed with other models). As a consequence, one might expect to improve the overall accuracy by populating chemical regions with fewer representatives, while, at the same time, avoiding the introduction of noise that would alter the performances on the rest.

Fig. 3 Imbalance of MAE. For different datasets A in the baseline setting (see Sec. 3), the mean absolute error (MAE) of a Random Forest model is plotted against the occurrences of individual elements in compositions of the training set. Error bars represent 1σ over 5 different random seeds. It can be observed how larger errors and deviations are mostly found in correspondence with low train occurrences. Similar patterns can be observed for most other properties and models.

In order to do this, we identify the k = 5 elements with the smallest prevalence in A and, for each, we collect n = 10 data points at random containing such element from dataset B. This addresses the weakness of previous concatenation strategy. Although targeting specific classes of elements with a narrow prevalence may be attractive, the presence or absence of a certain single element is not a good proxy for the chemical composition. In fact, this approach ignores any high-level relationship between the involved stoichiometries.

3.3 DiSCoVeR

DiSCoVeR³¹ algorithm is a recently proposed ensemble of machine learning methods aimed at facilitating the identification of chemistries lying at the intersection between novelty and performance. In practice, DiSCoVeR can be used to provide novelty scores of a given pool of data with respect to another and it was recently employed to identify new chemically novel high-temperature superconductors.³² The framework employed by DiSCoVeR is structured as follows: first, a distance matrix between all compositions in the dataset is computed by using the Element Movers Distance,³³ a proposed metric which takes into account chemical similarities; subsequently, the obtained distance matrix is used to obtain 2D UMAP embeddings of all data points (A ∪ B); the likelihood of each point in B is computed with respect to the density of A, returning a quantitative measure of novelty (density score). Compositions in regions of low density are assigned with a higher novelty score. In the original DiSCoVeR implementation, a complementary score target score is calculated based on a specific property of interest. Subsequently, these two scores are combined using predetermined weighting factors to highlight materials that lie at the intersection of novelty and performance boundaries. We rely only on the density score to propose the 10% top candidates of B to be merged into the training set of A. To avoid merging a novel data block with all points similar to each other, we iteratively alternate the merging of a small number of candidates and an update of the novelty scores, until 10% of B is integrated into A.

3.4 Transfer learning

Transfer learning (TL) is a learning paradigm that involves transferring knowledge gained from a source task to a different, but related, target task.³⁴ In general, different flavors of TL are possible: the most commons consist of pre-training deep neural networks on large datasets, allowing the model to learn general patterns and features. Subsequently, pre-trained models can be employed as a starting point for training on datasets of interest, typically characterized by smaller sizes. As illustrated in ref. 35, various configurations can be employed in a TL approach. One option involves applying a deep neural network obtained from the source task to the target task, commonly known as fine-tuning. A slight modification of this involves randomly initializing the weights of the last layer of the network, referred to as modified fine-tuning. Alternatively, features can be extracted from the initial layers of a pre-trained model and used as input for a separate neural network. In the latter approach, a preference is given to selecting features within inner layers, because input representations deriving from outer layers have empirical shown to be less effective, potentially lacking generalizability in applications. TL approaches result particularly valuable in scenarios where labeled data for the target task is limited, expensive, or difficult to obtain. Therefore, it is natural to consider TL in the materials informatics domain,^35,36 where these challenges arise naturally. To investigate the advantages introduced by TL in the data aggregation process for the considered datasets, we initially pre-train the DL models under examination (Roost and CrabNet) by leveraging the information from dataset B. Subsequently, we adopt a modified fine-tuning approach using the train set of dataset A. This choice is motivated by findings in ref. 35, where the authors show that the adoption of modified fine-tuning leads to statistically-significant improvements over fine-tuning for the datasets examined in their study. Consequently, we operate a random reinitialization of the last layer in the residual neural networks within Roost and CrabNet, before applying the pretrained models on the train set of dataset A.

3.5 Discussion for A–B data aggregation

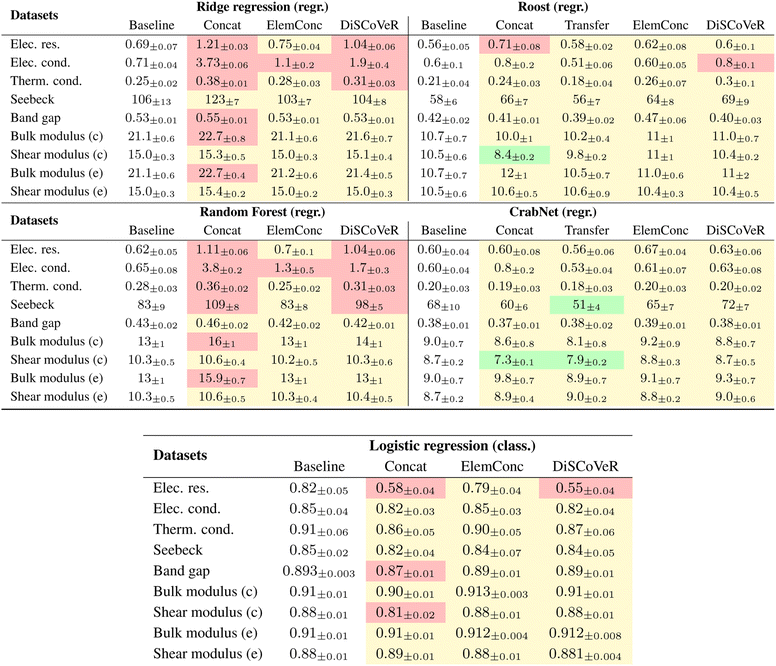
Table 2 shows the average testing errors on the original test of A obtained by training different ML estimators after different AB aggregation strategies. A color scheme is used to guide the interpretation.

Table 2 For each model–dataset pair, the MAE is reported before (baseline) and after 3 different data aggregation strategies (Concat, ElemConc, DiSCoVeR). For calculated datasets A, experiments are repeated using calculated (MP) and experimental (MPDS) dataset B. A green color represents an improvement above one standard deviation with respect to the Baseline setting, yellow indicates equivalent performance (variations could simply be attributed to random fluctuations) and red denotes a worsening above one standard deviation. Overall, different aggregation strategies fail to improve performance

---

Traditional ML. Our experiments reveal that classical ML approaches fail to leverage the advantages offered by any of the considered aggregation strategies. Among the strategies, the plain Concatenation performs the worst, followed by DiSCoVeR, and finally ElemConc. This observation suggests that the contamination in the original dataset increases as a function of the number of added points, irrespective of the aggregation strategy. Our analysis suggests that, for classical machine learning models, a smaller amount of data seems to yield better results. This observation can be explained by the challenges that more traditional approaches face in handling the noise and biases introduced when incorporating material entries from potentially diverse experimental conditions.

DL models. Contrary to classical ML approaches, DL models exhibit much greater stability. A possible explanation for this phenomenon can be attributed to the choice of the loss function employed at the training stage. Notably, both Roost and CrabNet utilize a customized variant of the L1 loss referred to as ‘robust’.^27,28 The rationale behind employing this modified loss function is the ability to capture and incorporate the inherent noise associated with individual data points. Therefore, this approach may facilitate a more robust and stable data aggregation process. Despite that, except for sporadic cases, improvements or degradations in accuracy are not significant. In contrast to conventional ML methods, determining that less data is better is not straightforward for the case of DL models.

Further investigation into the reasons behind this robustness could provide valuable insights for future research.

Computed-experimental. By comparing the results obtained for the calculated datasets (bulk modulus and shear modulus from AFLOW), we observe that maintaining consistency between the nature of datasets A and B led to slightly better performance. In fact, aggregating such calculated data with the calculated data from MP (c) leads to slightly better performance than aggregating with experimental data from the MPDS (e). This outcome is expected, considering the methodological differences that contribute to the observation of the respective data types.

Transfer learning. The experiments conducted on TL highlight a notable flexibility of this approach within the specified task. However, the achieved results do not exhibit substantial differences from the other considered baselines, with the notable exception of Seebeck coefficient in the case of CrabNet. The lack of significant differentiation can be attributed to the fact that TL has proven effective primarily in scenarios involving the pretraining of ML models on large datasets of source properties, followed by adaptation to target properties. This context is different from the conditions presented in the current study, where target and source property are the same. Moreover, our study presupposes the knowledge of stoichiometry alone, with a corresponding restricted pool of information, and potentially aggregate values reported under different experimental conditions. In light of these considerations and our experimental analysis, we posit that the information transferred from one dataset to another through transfer learning would not be substantial. In conclusion, different ML algorithms do not consistently benefit from any of the proposed aggregation strategies. Most interestingly, adding material entries targeting empty regions of the chemical space does not show a clear advantage. This can be attributed to the inherent challenges that ML models face in effectively fitting simultaneously diverse data points within a highly heterogeneous ambient space. In light of this consideration, data-aggregation driven by prioritizing chemical diversity cannot be considered as a good proxy for downstream ML models performance. Overall, our findings shed light on the strengths and limitations of different approaches in the context of dataset aggregation and provide valuable insights for future studies in this domain.

4 A–A data aggregation

In this section, we conduct a further experiment with the intent of decoupling our results from the use of the archives' data (MPDS and MP) as our resource for gathering additional data. In fact, the use of an external database does not guarantee that the experimental conditions in A are met in B, which can lead to heavy distribution shifts.³⁷ Instead, here, we simulate a progressive data acquisition of one single dataset. This is done by initially constricting dataset A to a random subset comprising only 5% of the original size. Subsequently, DiSCoVeR is used to integrate new candidates from the remaining 95%. Similarly to the previous experiment, the novelty scores are updated as new data points are continuously added in small batches, until the whole dataset is exhausted. The aforementioned strategy is compared with a random acquisition which iteratively adds random data points ignoring any novelty constraint. We assess the outcomes of the self-acquisition process on top of a test set created by holding out an amount corresponding to 20% of the original dataset: in one case such test set is created randomly; in the other case the DiSCoVeR algorithm is utilized to construct a biased test set with proportionate representatives of ordinary and extraordinary materials, with proportions 2/3 and 1/3. The primary objective is to evaluate whether a biased data acquisition approach facilitated by DiSCoVeR enhances the discovery of these new stoichiometries.

4.1 Discussion for A–A data aggregation

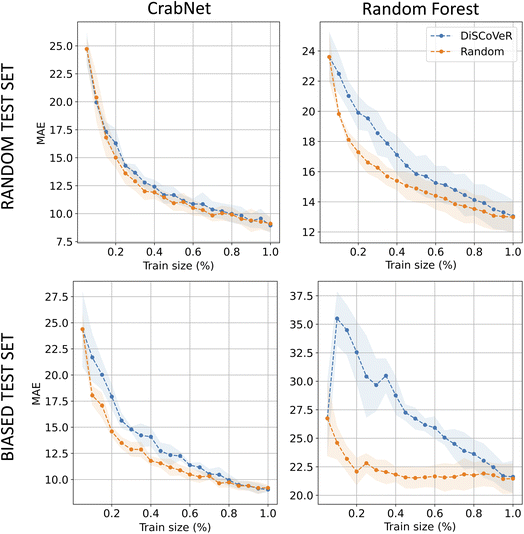
Fig. 4 shows the outcomes of the A–A aggregation process in the case of the bulk modulus, which is representative of the results observed across all datasets. As for the regression model, we limit here, for brevity, our presentation to the two SOTA for classic ML and DL methods, i.e. CrabNet (left) and random forest (right). The figure encompasses the two exposed test scenarios: the randomly selected test set (top) and a biased test set created using the DisCoVer algorithm (below). Notably, our analysis uncovers a consistent pattern across both test configurations. Contrary to our initial expectations, in both cases, where the tests are either random or biased, the application of DisCoVer-guided data acquisition leads to a deceleration in the model learning process with respect to a random acquisition strategy. This observation holds true for both CrabNet and the random forest model, though with a different intensity. These findings underscore an intriguing phenomenon: the incorporation of bias, even when guided by the DisCoVer algorithm, appears to impede the learning progress of the models. Furthermore, this suggests that the balancing of a dataset in terms of chemical diversity is not to be thought of in correspondence with better ML accuracies. Consequently, a thorough examination of the intricate interplay between data acquisition strategies, model architecture, and test set composition is warranted with the intent of gaining deeper insights and devising more effective approaches for model training and evaluation in the field.

Fig. 4 For the bulk modulus dataset, the plot tracks the MAE of CrabNet (left) and random forest (right) models under the A–A data integration setting. As explained in the text, the experiment is repeated for a random test set (top) and for a biased one (bottom).

5 Conclusions

In this paper, we have investigated the aggregation of different datasets in the field of materials informatics and its impact on the performance of ML models for property predictions. In our evaluation, we showed that classical ML models experienced a reduction in performance under all considered aggregation strategies, indicating that the aggregation of diverse datasets can introduce noise and hinder model learning and generalization. DL models exhibited more robustness, but most changes in accuracy were not statistically significant. This suggests that while deep learning models are less affected by the aggregation of datasets, they may not necessarily benefit significantly from it. Furthermore, we simulated a data acquisition process within a single dataset and compared a random data acquisition approach with one guided by the DiSCoVeR algorithm. Surprisingly, we found that prioritizing chemical diversity through the DiSCoVeR-guided approach did not lead to a faster convergence toward better accuracy but rather degraded performance. In line with recent work,³⁸ our findings highlight the challenges and limitations of data handling in materials informatics and emphasize the need for caution when merging different material datasets.

Future research efforts should focus on developing more effective approaches for dataset aggregation in materials informatics. As an example, supervised learning algorithms may be used to recognize and aggregate only chemical families with a higher impact on the validation error. This would allow a targeted integration of material entries with the goal of purely enhancing the performance of ML models. At the same time, this approach would not rely on prior assumptions, such as aiming solely to improve chemical diversity, as our study highlights that these solutions can be counterintuitive for practical applications. Furthermore, more advanced and robust transfer learning approaches can be designed for data-aggregation tasks. Finally, to facilitate the integration of diverse datasets and enhance the reproducibility and comparability of research outcomes, the community should consider revising data saving and storing standards, as well as creating automatic ML-driven detectors for nonsense identification. By addressing these challenges, we can enhance the quality, reliability, and efficiency of data aggregation in materials informatics, leading to improved ML models and accelerated materials discovery.

Code availability

The code accompanying this work can be found at the following link: https://github.com/fedeotto/data-aggregation-mi. Results are made reproducible by using fixed random seeds that control aggregation methods and, simultaneously, initializations of machine learning models.

Data availability

All publicly available datasets can be found at the same address as the code: https://github.com/fedeotto/data-aggregation-mi. In particular, AFLOW and MP data can be used to reproduce all aggregation results. As for the MPDS data, these are not openly accessible, but can be accessed via the related API, provided that a valid license has been acquired (see https://mpds.io/developer/ for more information).

Conflicts of interest

The authors have no competing interests to declare.

Acknowledgements

F. O. acknowledges Pilkington (NSG Group) and EPSRC under grant number EP/V026887 for funding this research. G. D. F. acknowledges the Beckers Group for funding this research. V. V. G. thank Leverhulme Trust for support via the Leverhulme Research Centre for Functional Materials Design and EPSRC under grant number EP/V026887. T. D. S. acknowledges support from NSF Grant No. 1936383 and 1651668 as well as the Royal Society Wolfson Visiting Fellowship program.

References

1. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards and S. Dacek, et al., The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 , http://link.aip.org/link/AMPADS/v1/i1/p011002/s1%26Agg=doi.
2. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak and M. Aykol, et al., The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1(1), 15010,  DOI:10.1038/npjcompumats.2015.10.
3. E. Blokhin and P. Villars, in The PAULING FILE Project and Materials Platform for Data Science: From Big Data Toward Materials Genome, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2018, pp. 1–26,  DOI:10.1007/978-3-319-42913-7_62-1.
4. G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys.: Mater., 2019, 2(3), 032001,  DOI:10.1088/2515-7639/ab084b.
5. A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper and F. Lin, et al., Machine learning directed search for ultraincompressible, superhard materials, J. Am. Chem. Soc., 2018, 140(31), 9844–9853.
6. A. Tewari, S. Dixit, N. Sahni and S. P. Bordas, Machine learning approaches to identify and design low thermal conductivity oxides for thermoelectric applications, Data-Centric Eng., 2020, 1, e8.
7. T. Wang, K. Zhang, J. Thé and H. Yu, Accurate prediction of band gap of materials using stacking machine learning model, Comput. Mater. Sci., 2022, 201, 110899 , https://www.sciencedirect.com/science/article/pii/S0927025621006078.
8. H. Khakurel, M. F. N. Taufique, A. Roy, G. Balasubramanian, G. Ouyang and J. Cui, et al., Machine learning assisted prediction of the Young's modulus of compositionally complex alloys, Sci. Rep., 2021, 11(1), 17149,  DOI:10.1038/s41598-021-96507-0.
9. Z. Cao, Y. Dan, Z. Xiong, C. Niu, X. Li and S. Qian, et al., Convolutional Neural Networks for Crystal Material Property Prediction Using Hybrid Orbital-Field Matrix and Magpie Descriptors, Crystals, 2019, 9(4), 191 , https://www.mdpi.com/2073-4352/9/4/191.
10. X. Li, Y. Dan, R. Dong, Z. Cao, C. Niu and Y. Song, et al., Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning, Appl. Sci., 2019, 9(24), 5510 , https://www.mdpi.com/2076-3417/9/24/5510.
11. M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Data-Driven Review of Thermoelectric Materials: Performance and Resource Considerations, Chem. Mater., 2013, 25(15), 2911–2920,  DOI:10.1021/cm400893e.
12. Y. Katsura, M. Kumagai, T. Kodani, M. Kaneshige, Y. Ando and S. Gunji, et al., Data-driven analysis of electron relaxation times in PbTe-type thermoelectric materials, Sci. Technol. Adv. Mater., 2019, 20(1), 511–520,  DOI:10.1080/14686996.2019.1603885.
13. S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii and R. H. Taylor, et al., AFLOW: An automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226 , https://www.sciencedirect.com/science/article/pii/S0927025612000717.
14. B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling and S. Paradiso, et al., Can machine learning identify the next high-temperature superconductor? Examining extrapolation performance for materials discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825,  10.1039/C8ME00012C.
15. H. Zhang, W. W. Chen, J. M. Rondinelli and W. Chen, et al., Entropy-targeted active learning for bias mitigation in materials data, Appl. Phys. Rev., 2023, 10(2), 021403,  DOI:10.1063/5.0138913.
16. A. Klipfel, Z. Bouraoui, Y. Fregier and A. Sayede, Equivariant Graph Neural Network for Crystalline Materials (Invited Paper), in STRL@IJCAI, 2022.
17. L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2(1), 16028,  DOI:10.1038/npjcompumats.2016.28.
18. S. Lee, C. Chen, G. Garcia and A. Oliynyk, Machine learning descriptors in materials chemistry: prediction and experimental validation synthesis of novel intermetallic UCd3, 2023.
19. I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016, Book in preparation for MIT Press, http://www.deeplearningbook.org.
20. D. Zha, Z. P. Bhat, K. H. Lai, F. Yang, Z. Jiang, S. Zhong, et al., Data-centric Artificial Intelligence: A Survey, 2023.
21. R. J. Murdock, S. K. Kauwe, A. Y. T. Wang and T. D. Sparks, Is Domain Knowledge Necessary for Machine Learning Materials Properties?, Integr. Mater. Manuf. Innov., 2020, 9(3), 221–227,  DOI:10.1007/s40192-020-00179-z.
22. S. K. Kauwe, T. Welker and T. D. Sparks, Extracting Knowledge from DFT: Experimental Band Gap Predictions Through Ensemble Learning, Integr. Mater. Manuf. Innov., 2020, 9(3), 213–220,  DOI:10.1007/s40192-020-00178-0.
23. L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Data-driven materials science: status, challenges, and perspectives, Adv. Sci., 2019, 6(21), 1900808.
24. R. Mullin, Citrine Informatics, C&EN Global Enterprise, 2017, 11, 95.
25. Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, Predicting the Band Gaps of Inorganic Solids by Machine Learning, J. Phys. Chem. Lett., 2018, 9(7), 1668–1673,  DOI:10.1021/acs.jpclett.8b00124.
26. P. Villars, M. Berndt, K. Brandenburg, K. Cenzual, J. Daams, F. Hulliger, et al., The Pauling File, in European Powder Diffraction EPDIC 8. vol. 443 of Materials Science Forum, Trans Tech Publications Ltd, 2004, pp. 357–360.
27. R. E. A. Goodall and A. A. Lee, Predicting materials properties without crystal structure: deep representation learning from stoichiometry, Nat. Commun., 2020, 11(1), 6280,  DOI:10.1038/s41467-020-19964-7.
28. A. Y. T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally restricted attention-based network for materials property predictions, npj Comput. Mater., 2021, 7(1), 77,  DOI:10.1038/s41524-021-00545-1.
29. S. K. Kauwe, J. Graser, R. Murdock and T. D. Sparks, Can machine learning find extraordinary materials?, Comput. Mater. Sci., 2020, 174, 109498 , https://www.sciencedirect.com/science/article/pii/S0927025619307979.
30. L. Breiman, Random Forests, Mach. Learn., 2001, 45(1), 5–32,  DOI:10.1023/A:1010933404324.
31. S. G. Baird, T. Q. Diep and T. D. Sparks, DiSCoVeR: a materials discovery screening tool for high performance, unique chemical compositions, Digital Discovery, 2022, 1, 226–240.
32. C. C. Seegmiller, S. G. Baird, H. M. Sayeed and T. D. Sparks, Discovering chemically novel, high-temperature superconductors, Comput. Mater. Sci., 2023, 228, 112358,  DOI:10.1016/j.commatsci.2023.112358.
33. C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32(24), 10610–10620,  DOI:10.1021/acs.chemmater.0c03381.
34. F. Zhuang, Z. Qi, K. Duan, D. Xi, Y. Zhu, H. Zhu, et al., A Comprehensive Survey on Transfer Learning, 2020.
35. V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao and A. Choudhary, et al., Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data, Nat. Commun., 2021, 12(1), 6595,  DOI:10.1038/s41467-021-26921-5.
36. M. L. Hutchinson, E. Antono, B. M. Gibbons, S. Paradiso, J. Ling and B. Meredig, Overcoming data scarcity with transfer learning, 2017.
37. O. Wiles, S. Gowal, F. Stimberg, S. Alvise-Rebuffi, I. Ktena, K. Dvijotham, et al., A fine-grained analysis on distribution shift, arXiv, 2021, preprint arXiv:2110.11328.
38. K. Li, D. Persaud, K. Choudhary, B. DeCost, M. Greenwood and J. Hattrick-Simpers, On the redundancy in large material datasets: efficient and robust learning with less data, 2023.

---

Footnotes

† Equal contribution.

‡ Work done while at Liverpool.

---