Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Data-driven representative models to accelerate scaled-up atomistic simulations of bitumen and biobased complex fluids†
Daniel
York
a,
Isaac
Vidal-Daza
ab,
Cristina
Segura
c,
Jose
Norambuena-Contreras
de and
Francisco J.
Martin-Martinez
 *a
*a
aDepartment of Chemistry, Swansea University, Swansea, SA2 8PP, UK. E-mail: f.j.martin-martinez@swansea.ac.uk
bGrupo de modelización y diseño molecular, Universidad de Granada, Granada, 18071, Spain
cUnidad de Desarrollo Tecnológico, Universidad de Concepción, Coronel 4191996, Chile
dLabMAT, Department of Civil and Environmental Engineering, University of Bío-Bío, Concepción 4051381, Chile
eMaterials and Manufacturing Research Institute, Department of Civil Engineering, Faculty of Science and Engineering, Swansea University, Bay campus, SA1 8EN, UK
First published on 16th April 2024
Abstract
Complex molecular organic fluids such as bitumen, lubricants, crude oil, or biobased oils from biorefineries are intrinsically challenging to model with molecular precision, given the large variety and complexity of organic molecules in their composition. Large scale atomistic simulations have been historically limited by this complexity, which has hampered the bottom-up molecular design of these materials, something especially relevant given the current surge of biobased fluids for sustainable applications and the cost of trial-and-error experimental developments. To address this limitation, we have developed an author-agnostic computational framework to generate data-driven representative models of any complex mixture of organic molecules directly from Gas Chromatography-Mass Spectrometry (GCMS) experimental characterisation, thus reducing human biases in model creation and providing a platform for self-driven digital development of molecular organic fluids. The method proposed generates statistically representative molecular samples that simplify the complexity of the fluid in a limited group of molecules, while capturing the critical chemical features needed to describe the overall properties of the mixture. As a case study, we generated a showcase of data-driven representative models from the GCMS characterisation of a bio-oil from the pyrolysis of pine bark, specially produced for this study. Pyrolytic biomass processing into bio-oils provides a waste valorisation route with applications in biorefinery products like asphalt additives and biofuel precursors. Our case study focuses on complex fluids such as bio-oils for asphalt rejuvenators for self-healing purposes or biofuel upgrading. Nevertheless, the general computational framework developed in this manuscript provides a platform for generating data-driven representative models of any bitumen or biobased organic fluid.
Introduction
At the dawn of artificial intelligence and self-driving laboratories for materials design, automated generation of unbiased atomistic models that capture the complexity of molecular fluids in a computationally efficient way is a persistent challenge.1,2 Complex molecular fluids like bitumen, lubricants, crude oil, or biobased oils from pyrolysis or hydrothermal liquefaction are intrinsically challenging to model with molecular precision, given the large variety and complexity of molecules in their composition. This limitation has hampered the development of computational platforms for bottom-up molecular design of bitumen-like materials in the biorefinery space, even though it has been an approach that has been proven extremely useful for decades in other areas of materials science like protein modelling, drug design or nanomaterials development. This lack of atomistic models is especially relevant with the surge of biobased fluids from biorefineries, e.g., biofuels, biobased lubricants, asphalt additives, and given the economic impact of these materials. Asphalt bitumen, a dark-coloured thermoplastic material composed of hydrocarbons derived from the distillation of petroleum, is the principal civil engineering material used for road construction worldwide. However, environmental conditions and traffic load contribute to premature cracking of the asphalt mixtures, reducing the durability of our roads.3,4 As a reference, in the UK alone, effectively maintaining a road network consisting of over 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 miles has required over £11 billion yearly since 2019.5 Among this, £100 million alone is dedicated to the filling of potholes, which fundamentally occur due to cracks propagating at the nanoscale because of a combination of asphalt ageing, water inclusion, and extreme temperatures. Improving asphalt's capacity to resist oxidation increases the functional lifetime of the material and helps mitigate cracking. To this end, bio-oils from pyrolysis of biomass waste are drawing attention as asphalt rejuvenators due to their ability to scavenge free radicals and hinder damage caused by oxidative ageing.6,7 Similarly, there is also strong interest in their use of bio-oils as precursors for transport fuels such as diesel, gasoline, or kerosene.8 Biofuel application requires total or partial upgrading to fluids compatible with traditional refinery streams, which implies full deoxygenation of the molecular components. However, despite the societal relevance of asphalt cracking or sustainable fuel production and the countless initiatives for biomass waste valorisation, there is still limited fundamental understanding of the structure–property relationships of bitumen-like materials like asphalt binders and bio-oils. One reason for this lack of knowledge is the limited availability of detailed molecular models for atomistic simulations. Current studies on bio-oils from pyrolysis, biocrude oils from hydrothermal processing, and petroleum asphalt are generally focused on the experimental production and chemical characterisation, with limited investigation of their properties at the nanoscale, or their reactivity towards aging or deoxygenation using computational approaches.9,10
000 miles has required over £11 billion yearly since 2019.5 Among this, £100 million alone is dedicated to the filling of potholes, which fundamentally occur due to cracks propagating at the nanoscale because of a combination of asphalt ageing, water inclusion, and extreme temperatures. Improving asphalt's capacity to resist oxidation increases the functional lifetime of the material and helps mitigate cracking. To this end, bio-oils from pyrolysis of biomass waste are drawing attention as asphalt rejuvenators due to their ability to scavenge free radicals and hinder damage caused by oxidative ageing.6,7 Similarly, there is also strong interest in their use of bio-oils as precursors for transport fuels such as diesel, gasoline, or kerosene.8 Biofuel application requires total or partial upgrading to fluids compatible with traditional refinery streams, which implies full deoxygenation of the molecular components. However, despite the societal relevance of asphalt cracking or sustainable fuel production and the countless initiatives for biomass waste valorisation, there is still limited fundamental understanding of the structure–property relationships of bitumen-like materials like asphalt binders and bio-oils. One reason for this lack of knowledge is the limited availability of detailed molecular models for atomistic simulations. Current studies on bio-oils from pyrolysis, biocrude oils from hydrothermal processing, and petroleum asphalt are generally focused on the experimental production and chemical characterisation, with limited investigation of their properties at the nanoscale, or their reactivity towards aging or deoxygenation using computational approaches.9,10
Some models for bio-oils exist when looking at upgrading methods and the evaluation of anti-oxidant performance, but only one full atomistic model is available to date for a biocrude oil derived from the hydrothermal liquefaction of algae.6,11,12 For asphalt material, an atomistic model suggested by Li and Greenfield has been accepted as a standard for molecular dynamics simulations and theoretical studies, providing substantial fundamental knowledge and highlighting the utility of molecular modelling in this area.13,14 Li–Greenfield's atomistic model expands some previously developed models, and it builds on the Yen–Mullins colloidal description of asphalt structure, in which asphaltenes form nanoaggregates and subsequently, clusters in a matrix of lighter molecules.15–18 Li and Greenfield followed this colloidal representation and leveraged experimental data to select model asphaltenes that match real-world asphalt systems, e.g., AAA-1, AAK-1 and AAM-1 asphalt blends, as described by the Strategic Highway Research Programme (SHRP).19 To complete the molecular composition of their atomistic model, they included molecules that are representative of the four solubility classes described by the known SARA analysis, i.e., Saturates, Aromatics, Resins and Asphaltenes.20 The resulting selection of molecules provided by strategies based on chemical intuition and personal selection yielded a starting point for computational studies that needed atomistic models, i.e., density functional theory (DFT) calculations and full-atomistic molecular dynamics simulations,21–26 and also for those coarse grain models developed from such selection of molecules.27–29
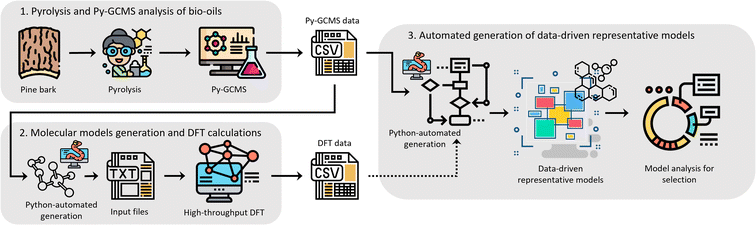
We believe that an author-agnostic platform will reduce human biases as our automated data-driven approach develops atomistic models of bitumen and biobased complex fluids based solely on experimental data and selection algorithms that are independent of the users end goals or specific case. We believe that this will boost the performance of data-driven atomistic simulations and allow for atomistic models to be generated via a predefined methodology rather than on a case-by-case basis. To this end, we have developed a platform (see Fig. 1) for model generation from experimental data, e.g., gas chromatography-mass spectrometry (GCMS), liquid chromatography-mass spectrometry (LCMS) or high-performance liquid chromatography (HPLC), with a subsequent high-throughput computation of molecular properties using DFT. The exponential growth of machine learning applications and the need for large data sets for training and validation add additional value to this automated generation of models and the performance of DFT calculations. Utilising these atomistic models for machine learning applications can accelerate a bottom-up design and property prediction of complex fluids, an approach that has been successfully used in synthetic biology, catalyst development and even controlled lithium deposition.30–32 Existing transformer models could also be utilised to suggest target molecules during the production of complex fluids, and to predict the properties of candidate molecules.33,34 Other similar areas that also use artificial intelligence to find solutions to complex problems could assist the further development of model generation methodologies and validation methods using adequate training data.35,36
The success of these applications, as well as the capacity the models developed here to describe real complex systems are constrained by the accuracy and detection limits of the GCMS/LCMS/HPLC analysis used to generate the raw data. Therefore, the most complete analysis possible that maximises the number of molecules identified would be ideal to provide the most extensive and accurate experimental characterisation of the complex fluid.
As a case study, the computational platform was tested with bio-oil from the pyrolysis of pine bark, produced ad hoc for this purpose, and chemically characterised using GCMS. Whilst pine bark-derived bio-oil is the selected case study for proof of concept, this general approach applies to other complex mixtures of organic molecules.
Experimental details
Raw material and pyrolysis experiments
Pinus radiata bark from 15 to 20 year-old trees was provided by a forest company located in Biobio Region (Chile). The proximate analysis and elemental compositions of bark are presented in Table 1. The elemental composition (CHNSO) of raw material was measured in a Leco CHNS 628 elemental analyser. The proximate analyses for moisture content (ISO 18134-2), volatile matter (ISO 18123) and ash content (ISO 18122) were performed in a muffle furnace (JSR JSMF-140H) by following the ISO standard methods. The pyrolysis experiments were performed in a continuous rotary kiln (280 mm diameter and 3000 mm length) coupled with a quench-type condenser to recover bio-oil. The details of the setup are given in our previous work.37 A mount of 70 kg of Pinus radiata bark with a particle size of 1–3 mm was fed by a feeder screw at a rate of 17 kg h−1 into the reactor. The reactor was heated indirectly by liquefied petroleum gas (LPG) burners, and the temperature was held to 450 °C. Pyrolysis products were initially collected and condensed by quenching with water and recirculating aqueous-phase bio-oil. The organic-phase bio-oil was decanted and separated.Bio-oil production and GCMS characterisation
The organic-phase bio-oil underwent fractionation through liquid–liquid extraction employing a methanol/n-hexane mixture. Two distinct fractions were isolated: one with a phenolic nature and the other characterised as wax. The process involved dissolving the organic-phase bio-oil in methanol at a 1/6.6 mass ratio. Subsequently, the extraction was performed using n-hexane at 25 °C, with a 1/1 mass ratio of the methanolic solution to n-hexane. The organic-phase bio-oil, phenolic fraction and wax were analysed by gas chromatography (GC-2010 Plus, Shimadzu) coupled to a quadrupole mass spectrometer (QP2010Ultra, Shimadzu). For organic-phase bio-oil and phenolic fraction a ZB-5ms capillary column (60 mm × 0.25 mm × 0.25 μm) was used with following parameters: high purity helium B (99.999%, Air Liquide, Chile) at flow rate 1.04 ml min−1 as carrier gas; sample port temperature set at 250 °C and splitting ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The column was initially set at 40 °C for 1 minute; the first stage was ramped up to 180 °C at a rate of 5 °C min−1 hold for 2 min, and the second stage was ramped up to 280 °C at a rate of 15 °C min−1 and hold for 20 min with the total run time of 58 min. For wax analysis, a ZB-1HT INFERNO capillary column (30 × 0.25 mm × 0.25 μm) was used with the following program: helium at a flow rate of 1 ml min−1 and injection port temperature of 300 °C. The GC oven temperature was set as follows: hold for 2 min at 60 °C, heat to 140 °C at a rate of 5°C min−1 and hold for 5 mi, heat to 300 °C at a rate of 3 °C and hold for 20 min with a total run time of 96 min. The MS was operated in full-scan mode, with a scan range of m/z 35–600, with electron ionisation voltage set at 70 eV. The eluted compounds were identified using the NIST library. The compounds identified for bio-oil, phenolic fraction and wax are presented in Table 2.
1. The column was initially set at 40 °C for 1 minute; the first stage was ramped up to 180 °C at a rate of 5 °C min−1 hold for 2 min, and the second stage was ramped up to 280 °C at a rate of 15 °C min−1 and hold for 20 min with the total run time of 58 min. For wax analysis, a ZB-1HT INFERNO capillary column (30 × 0.25 mm × 0.25 μm) was used with the following program: helium at a flow rate of 1 ml min−1 and injection port temperature of 300 °C. The GC oven temperature was set as follows: hold for 2 min at 60 °C, heat to 140 °C at a rate of 5°C min−1 and hold for 5 mi, heat to 300 °C at a rate of 3 °C and hold for 20 min with a total run time of 96 min. The MS was operated in full-scan mode, with a scan range of m/z 35–600, with electron ionisation voltage set at 70 eV. The eluted compounds were identified using the NIST library. The compounds identified for bio-oil, phenolic fraction and wax are presented in Table 2.
| Molecular subclasses | Molecule | Ph. (%) | Wx. (%) | Cp. (%) |
|---|---|---|---|---|
| Furans | Furfural | 2.12 | — | 1.41 |
| 5-Methyl-2-furancarboxaldehyde | 0.71 | — | — | |
| Phenols | Phenol | 5.74 | — | 3.82 |
| 2-Methylphenol | 9.89 | — | 6.59 | |
| 3-Methylphenol | 4.11 | — | 2.74 | |
| Catechol | 3.29 | — | 2.19 | |
| 2,4-Dimethylphenol | 5.16 | — | 3.43 | |
| 4-Ethylphenol | 3.53 | — | 2.35 | |
| 3,4-Dimethylphenol | 1.86 | — | 1.24 | |
| 2,5-Dimethylphenol | 1.06 | — | 0.71 | |
| 2,6-Dimethylphenol | 0.52 | 1.43 | 0.82 | |
| 2-Ethylphenol | 0.45 | — | 0.30 | |
| 4-Methy-1,2-benzenediol | 9.42 | — | 6.27 | |
| 2-Methoxyphenol | 2.27 | 1.04 | 1.85 | |
| 2-Methoxy-6-methylphenol | — | 0.22 | 0.07 | |
| 2-Methyl-1,3-benzenediol | 2.08 | — | 1.39 | |
| 4-(2-Propenyl)-phenol | 0.77 | — | 0.51 | |
| 2-Ethyl-5-methyl-phenol | 2.80 | — | 1.86 | |
| p-Cumenol | 0.88 | — | 0.59 | |
| 3,4,5-Trimethylphenol | 0.85 | — | 0.57 | |
| 2,3,6-Trimethylphenol | 0.52 | — | 0.35 | |
| 2,3-Dimethylhydroquinone | 5.87 | — | 3.91 | |
| 4-Ethylcatechol | 4.42 | — | 2.94 | |
| 2,6-Dimethyl-1,4-benzenediol | 1.63 | — | 1.09 | |
| 2-Methyl-1,4-benzenedicarboxaldehyde | 1.19 | — | 0.79 | |
| 2-Methyl-6-(2-propenyl)-phenol | 0.87 | — | 0.58 | |
| 2-Methoxy-4-vinylphenol | 3.35 | 0.48 | 2.39 | |
| 4-Ethyl-2-methoxyphenol | 2.60 | 0.50 | 1.90 | |
| 2-Methoxy-4-(1-propenyl)-phenol | 2.11 | 0.28 | 1.50 | |
| Apocynin | 1.14 | — | 0.76 | |
| Benzofurans | 2,3-Dihydrobenzofuran | 1.11 | — | 0.74 |
| Aliphatic molecules with oxygen heteroatoms (carboxylic acids, aldehydes, alcohols, esters) | Pentadecanoic acid | 1.44 | 0.45 | 1.11 |
| Hexadecenoic acid | — | 4.1 | 1.37 | |
| Palmitoleic acid | 0.92 | — | 0.61 | |
| cis-Vaccenic acid | 2.98 | 8.72 | 4.90 | |
| Octadecanoic acid | 0.79 | 3.84 | 1.81 | |
| Nonadecanoic acid | 1.0 | — | 0.66 | |
| Eicosanoic acid | — | 8.53 | 2.85 | |
| Tetracosanal | — | 0.58 | 0.19 | |
| Tetracosan-1-ol | — | 1.57 | 0.52 | |
| Tetracosanoic acid | — | 17.6 | 5.88 | |
| Hexacosanal | — | 0.43 | 0.14 | |
| Tetracosanoic acid methyl ester | — | 0.91 | 0.30 | |
| Hexacosanoic acid | — | 5.27 | 1.76 | |
| Hydrocarbons | 1-Undecene | — | 1.36 | 0.45 |
| 1-Dodecene | — | 0.94 | 0.31 | |
| Dodecane | — | 0.41 | 0.14 | |
| 1-Tridecene | — | 1.12 | 0.37 | |
| Tridecane | — | 0.48 | 0.16 | |
| 1-Tetradecene | — | 1.39 | 0.46 | |
| Tetradecane | — | 0.77 | 0.26 | |
| 1-Pentadecene | — | 1.52 | 0.51 | |
| Pentadecane | — | 0.65 | 0.22 | |
| Cetene | — | 1.69 | 0.56 | |
| Hexadecane | — | 0.51 | 0.17 | |
| 1-Heptadecene | — | 1.25 | 0.42 | |
| Heptadecane | — | 0.53 | 0.18 | |
| 1-Octadecene | — | 1.31 | 0.44 | |
| Octadecane | — | 0.46 | 0.15 | |
| 1-Nonadecene | — | 1.31 | 0.44 | |
| Nonadecane | — | 0.8 | 0.27 | |
| 3-Eicosene, (E) | — | 2.16 | 0.72 | |
| Eicosane | — | 0.57 | 0.19 | |
| 10-Henicosene | — | 1.03 | 0.34 | |
| Heneicosane | — | 1.47 | 0.49 | |
| 1-Docosene | — | 7.17 | 2.39 | |
| Docosane | — | 0.69 | 0.23 | |
| 1-Tricosene | — | 0.76 | 0.25 | |
| Tricosane | — | 1.23 | 0.41 | |
| 1-Tetracosene | — | 7.42 | 2.48 | |
| Tetracosane | — | 1.11 | 0.37 | |
| Pentacos-1-ene | 0.82 | — | 0.55 | |
| Heptacos-1-ene | — | 0.53 | 0.18 | |
| Sterols | Stigmast-4-en-3-one | — | 0.85 | 0.28 |
| Stigmast-5-ene, 3-beta-methoxy- | — | 2.54 | 0.85 |
Computational details
DFT calculations were performed using ORCA 4.2.1.38 Geometries of all molecular structures were fully optimised, and the electron density and the associated chemical properties for each molecule were calculated with the PBEh-3c functional. PBEh-3c implements the Perdew–Burke–Ernzerhoff (PBE) exchange and correlation functional within the generalised gradient approximation alongside a three-fold corrected (3c) Hartree–Fock method to adequately describe dispersion forces and correct the basis set superposition error.39,40 PBEh-3c is specially optimised in ORCA 4.2.1, and it has been evaluated as an efficient and accurate method for electronic structure calculations.40 In conjunction with PBEh-3c, the def2-TZVP basis set was used, a triple-zeta basis set with polarisation functions. Chemical properties like the dipole moment and polarizability, as well as the global chemical hardness (η) were calculated with this method. The global chemical hardness is a conceptual DFT reactivity descriptor that quantifies the tendency of a molecule to transfer electrons upon chemical reaction.41 In practice, η is estimated from the ionisation energy (I) and the electron affinity (A) following eqn (1). In an approximated way, the required values for I and A are calculated following Koopman's theorem, which states that the ionisation energy of a given molecule can be estimated from the energy of the highest occupied molecular orbital (HOMO) in its neutral electronic configuration, see eqn (2).42 Following the same rationale, the electron affinity is estimated from the energy of the lowest unoccupied molecular orbital (LUMO), as in eqn (3). This approximation bypasses the need for open-shell DFT calculations for the charged species of each molecule, accelerating the DFT high-throughput calculations.| η = (I − A)/2 | (1) |
| I = −EHOMO | (2) |
| A = −ELUMO | (3) |
Results and discussion
Bio-oil composition
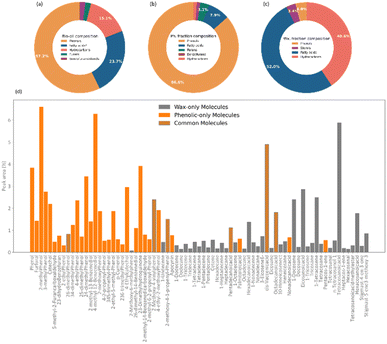
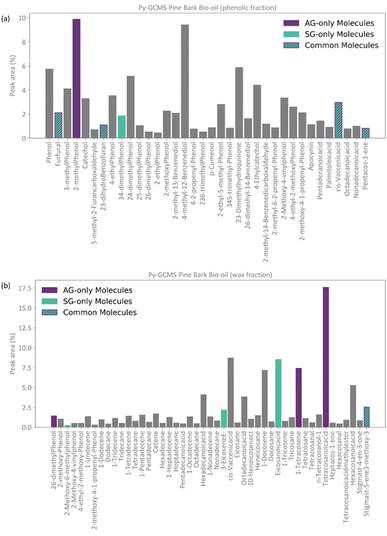
An analysis of the chemical composition of the complete bio-oil from the pyrolysis of pine bark is shown in Fig. 2. The main subclasses of molecules identified by GCMS were phenols, fatty acids, and a range of alkene and alkane hydrocarbons. Phenolic species accounted for over 50% of the bio-oil and were likely produced from the pyrolysis of condensed tannins, predominantly composed of catechins, and coniferyl alcohol, a monolignol building block of lignin. Fatty acids constituted the second most abundant molecular subclass, probably from the breakdown of triglycerides, and they account for almost 25% of the bio-oil, in agreement with previous studies.43,44When fractionated into lighter and heavier fractions, phenols formed more than 85% of the lighter fraction, which is now referred to as phenolic fraction. In comparison, fatty acids (up to 52%) and hydrocarbons (up to 40%) formed the heavier fraction, now called wax. As seen in Fig. 2d, some molecules were identified in both fractions.
Representative model development
Two different strategies for model development have been considered: (i) an abundancy-based system that selects a subset of molecules depending on their abundancy in the GCMS characterisation in relation to a defined threshold, and (ii) a molecular classification system that selects molecules after grouping them into molecular classes and subsequent subclasses using feature identification dependent on structural features and atomic composition. Within each of these strategies, two different methods were tested: (i) a fix-threshold (FT) method and a proportional threshold (PT) method for the abundancy-based system, and (ii) an abundancy grouping (AG) method, and a scored grouping (SG) method for the molecular classification system. Both methods are tested with GCMS data, which is limited by size of the database against which the compounds are identified, and the resolution of experimental equipment, i.e., GCMS detection limits. However, our methods for model generation are independent of the number of molecules characterised by the analytical equipment, and the same algorithms apply to any experimental data provided independently of the equipment's resolution, as long as the proportion of each component within the complex fluid is quantifiable.To implement the abundancy-based system, the proportion of each molecule Pi is defined following eqn (4), where ai is the abundance of a molecule in the model, and ∑aselected is the summative abundance of the selected molecules.
| Pi = ai/∑aselected | (4) |
For the molecular-classification system, an extra consideration is required as the selected molecules may vary vastly in their relative abundancies in GCMS data, creating disproportional representation of molecules within the models. To mitigate the effect of these disproportionate relative abundancies, a correction is implemented using eqn (5), where ∑asubclass is the summative abundancy of all the molecules within a molecular subclass, ∑aall molecules is the summative abundancy of all molecules in the GCMS data, and Pi is the calculated proportion of the molecule in question. This idea of a disproportionate influence is further explained in the ESI.†
| Pi = ∑asubclass/∑aall molecules | (5) |
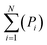 | (6) |
To analyse the accuracy and representativity of the resulting models, i.e., FT, PT, AG, and SG models, a control model that includes all the molecules characterised by GCMS was also created and is referred to as the all-molecule model. DFT calculations were performed for the all-molecule model, and weighted average molecular descriptors were calculated following eqn (7), where again Pi is the proportion of a molecule within the model, x the descriptor being averaged, xall the weighted average for such descriptor, and N the total number of molecules in the model.
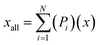 | (7) |
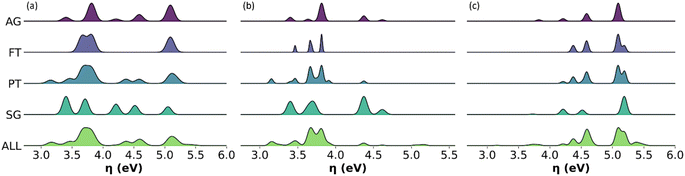
The molecular descriptors included the global chemical hardness, dipole moment, total energy, molecular weight, polarizability, and oxygen content. Special attention was given to the chemical reactivity, quantified by the global chemical hardness, given its relevance in oxidative processes during ageing and deoxygenation during upgrading. Given its significance, the weighted average, and the distribution of global chemical hardness across each representative model were monitored against the all-molecule model.
We also carry out an analysis of the omission of molecular subclasses in the all-molecule model of each fraction and their effect on the model's representability of the properties of the complete bio-oil was also performed to evaluate the necessity of including each individual molecular subclass.
Given the complexity of bio-oils, isolating individual molecules experimentally to create samples that mimic our computational models, is technically unachievable. An alternative could be the synthesis of molecular mixtures matching the composition of our models, although this generation of experimental mixtures would be dependent on the availability of the modelled compounds (i.e., cost or complexity of synthetic routes). Therefore, for further validation of our representative models, we intend to carry out molecular dynamics simulations to compare our model with available experimental data of the complete bio-oil.
Abundancy-based model generation system
As mentioned before, the abundancy-based system tested two methods for model generation: the FT and the PT. The FT method uses a predefined cut-off value of abundancy, using the selection criterion shown in eqn (8), where ai is the abundance of the molecule in question, and X is a predefined selection threshold. The PT method defines a selection threshold based on the number of unique molecules in a mixture following eqn (9), where ai is the abundance of the molecule in question, as is the sum of all abundancies, and N is the total number of characterised molecules.| ai > X | (8) |
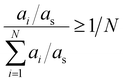 | (9) |
Fig. 3 summarises the procedure for the abundancy-based model generation system, indicating the FT method (pale purple), the PT method (pale green-blue) and its automation using Python code.
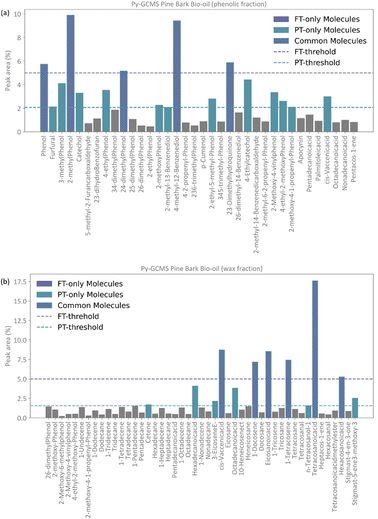
Conceptually, the FT method implements a locked selection rule, which is tailored to a specific bio-oil composition and abundancies of each compound. For the pine bark bio-oil case study, we defined 5% as the fixed abundancy selection criterion. On the other hand, the PT method considers the relative abundancy of each molecule in the mixture, allowing for a dynamic selection rule that is defined for an individual mixture on a case-by-case basis, as described in eqn (9). Fig. 4 shows the GCMS data and highlights the molecules that were selected using the FT method (in pale purple) and those selected using the PT method (in pale green-blue) for both the phenolic (Fig. 4a) and wax (Fig. 4b) fractions.
The PT method yields a detailed atomistic model that is a statistical representation of the mixture, whilst the FT aims to select the molecules that constitute the largest proportions in the composition of the bio-oil. Because of its definition, the PT model will typically include all those molecules that were considered in the FT model plus some additional ones unless a mixture is extremely diverse and there were no molecules abundant enough to be selected by a given fixed threshold (e.g., 5%), or if a threshold below the one defined by the PT method was chosen. Fig. 4 shows how, in our case study, all the molecules selected by the FT method are also selected by the PT one, and no “FT-only molecules” are highlighted in the plot.
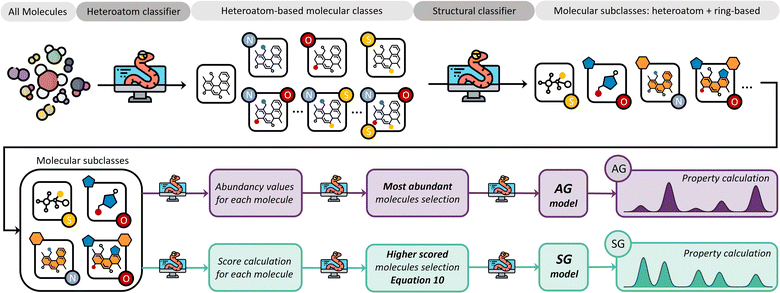
Molecular classification model generation system
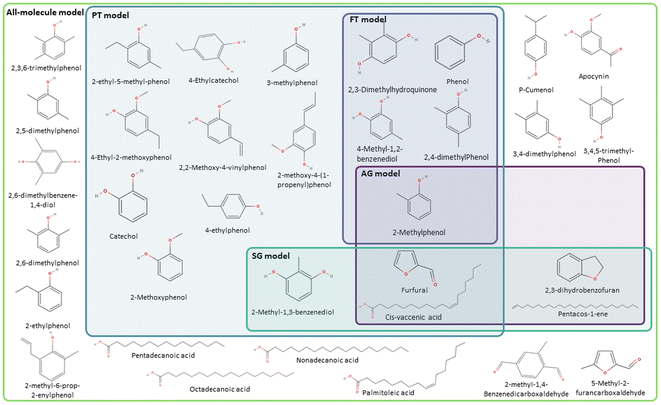
The core concept in the molecular classification system is that each molecular subclass is important in the mixture as each may be key to adequately describing the overall chemical properties, even if they are only present in trace amounts. Accordingly, molecules are classified using a feature identification algorithm based on their chemical structure and atomic composition, followed by either a selection of the most abundant ones from each subclass, i.e., AG method, or a selection based on a scoring function, i.e., SG method.Our feature identification algorithm focuses on general structures and heteroatom compositions of each molecule rather than specific criteria like type of functional groups or characteristics of branching, i.e., degree of branching, presence of π bonds in branches, and number of different branches. This approach is deliberately simple and aims to develop a generalized method for any mixture, whilst preventing over-classification which would increase the complexity of resulting models.
The SG method's scoring function quantifies how a given molecule's molecular properties match the weighted averages of each DFT-calculated molecular descriptor. The final expression for the scoring function is described by eqn (10), where xall, yall, etc., refer to the weighted averages of the properties, and x, y, etc., are the corresponding values of those properties for a molecule within the subclass under consideration. The molecules with the best score, i.e., closest to 1.0, are then selected to represent that subclass in the final atomistic model.
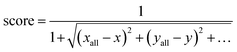 | (10) |
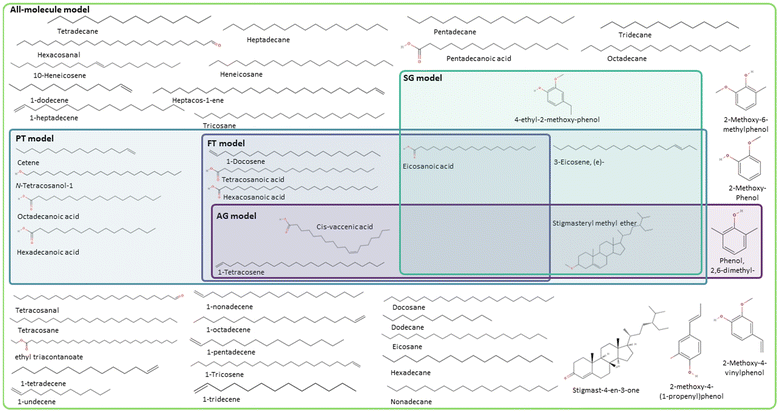
Fig. 5 summarises the procedure for the molecular classification system, indicating the AG (intense purple colour) and the SG (intense green-blue colour) methods considered and their automation using Python code.
In the case of pine bark, there are two molecular classes: molecules with no heteroatoms and those containing oxygen. Nevertheless, separate classes would have also been defined if the bio-oil had included other elements in the molecular composition. For example, if the bio-oil had also contained nitrogen and sulphur, classes of molecules containing all possible combinations of two heteroatoms in their structure would have been considered, as well as one class with the three of them. Once these heteroatom-containing classes are defined, the method defines subclasses based on chemical structure using feature identification, i.e., presence of rings and different ring sizes (Fig. 5).
Following the procedure described in Fig. 5, the classification algorithm generated five molecular subclasses for the phenolic fraction, i.e., furans, phenols, benzofurans, fatty acids and hydrocarbons, and four molecular subclasses in the wax fraction, i.e., phenols, fatty acids, sterols, and hydrocarbons, for the pine bark bio-oil. Fatty acids were the most common oxygen-containing aliphatic molecules in the wax fraction, although one aldehyde and one alcohol molecule were also included in the fatty acid molecular class. Nevertheless, this subclass will be referred to as the ‘fatty acid’ molecular subclass for ease of reference. Fig. 6 shows the GCMS data and highlights the molecules selected with the AG method (in intense purple) and those selected with the SG method (in intense green-blue) for both the phenolic (Fig. 6a) and wax (Fig. 6b) fractions.
For the phenolic fraction, the same molecules were selected by the AG and SG method for each molecular subclass, except for phenols. The phenolic subclass contained 28 different molecules, with the most abundant constituting 12.5% of this molecular subclass. In this case, the most abundant molecule did not dominate the composition (i.e., more than 50%) of the phenolic subclass and a different molecule was selected with the SG method that matched the weighted average descriptors more closely. For the wax fraction, only the sterol group is common across the selection from the AG and SG methods, with the other 3 molecular subclasses (phenols, fatty acids, and hydrocarbons) containing a wide range of molecules. In these large molecular subclasses, and similarly to the phenolic subclass in the phenol fraction, the most abundant molecule did not dominate the composition of the subclass since the SG method selected the molecule that yielded the best score.
Fig. 7 and 8 summarise the molecules selected by the FT, PT, AG, and SG methods for the phenolic and wax fractions to form the data-driven representative models, where different colour boxes were used, following the same colour code adopted across the manuscript. FT (pale purple colour), PT (pale green-blue colour), AG (intense purple colour), and SG (intense green-blue colour) model, together with the all-molecule model (pale green colour). For each model of the complete bio-oil and the phenolic and wax fractions, the number of unique molecules selected and the proportion of the bio-oil they represent is summarised in Table 3. The values reported in the table are calculated using eqn (4) for each representative model.
| Model | No. of molecules | % Fraction represented | ||||
|---|---|---|---|---|---|---|
| Ph. | Wx. | Cp. | Ph. | Wx. | Cp. | |
| All-molecule | 36 | 47 | 75 | 100.00 | 100.00 | 100.00 |
| FT | 5 | 6 | 3 | 36.08 | 54.71 | 18.73 |
| PT | 17 | 12 | 27 | 71.74 | 70.61 | 73.43 |
| AG | 5 | 4 | 5 | 16.92 | 20.11 | 17.20 |
| SG | 5 | 4 | 5 | 9.11 | 13.73 | 7.21 |
Comparative performance of data-driven representative models
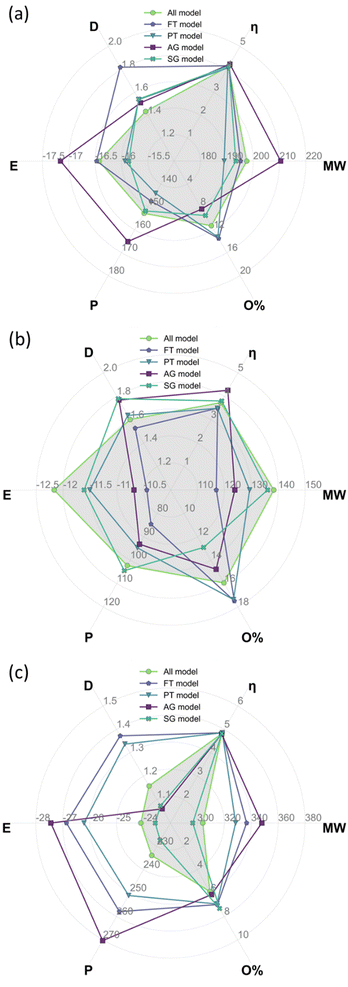
Table 4 summarises the weighted average descriptors for the complete bio-oil and the phenolic and wax fractions using the all-molecule model. These descriptors, calculated from DFT results, constitute the benchmark to compare the equivalent values from each of the representative molecular models developed in this work, i.e., FT, PT, AG, and SG. The results of the benchmark are shown in Fig. 9, where the radar plots graphically analyse the fitting of the values of global chemical hardness, dipole moment, total energy, molecular weight, polarizability, and oxygen contents for the FT, PT, AG, and SG models with respect to the all-molecule one (shadowed in grey in Fig. 9).| Model | M w (g mol−1) | η (eV) | Polarizability (a.u.) | Dipole moment (D) | Total energy (eV) | Atomic composition (%) | ||
|---|---|---|---|---|---|---|---|---|
| C | O | H | ||||||
| Cp. | 197.55 | 4.13 | 152.81 | 1.43 | −16426.84 | 77.74 | 11.30 | 10.96 |
| Ph. | 138.38 | 3.74 | 102.27 | 1.60 | −12165.78 | 73.96 | 17.93 | 8.11 |
| Wx. | 304.07 | 4.82 | 243.85 | 1.15 | −24098.27 | 80.84 | 5.86 | 13.30 |
Comparing the abundancy-based methods in Fig. 9, the PT model outperforms the FT model overall in all cases because a larger number of molecules are selected with the PT method. Nevertheless, the PT model slightly underestimates the total energy, the polarizability, and the oxygen context and slightly overestimates the dipole moment. In particular, the PT method performs exceptionally well for the complete bio-oil (Fig. 9a). It also matches most weighted average descriptors of the phenolic fraction (Fig. 9b), although it clearly underestimates the oxygen content. The proportion of molecules containing two oxygen atoms is 33% lower than it is in the all-molecule model as there are 8 molecules containing multiple oxygen atoms that do not meet the PT model criteria yet account for a combined abundancy of 8.5% within the phenolic fraction. However, it very accurately describes the reactivity, which is especially relevant in this type of material. Compared to the FT model, the performance of the PT model highlights the significance of creating a statistical representation of the bio-oil rather than just selecting the most abundant molecules in each mixture. Overall, the FT method performs best when modelling the phenolic fraction (Fig. 9b) because most molecules in the fraction are phenols (80%), and all molecules selected are from this molecular subclass. Conversely, the FT method performs worst when modelling the wax fraction (Fig. 9c) as the composition is much more diverse and more challenging to be encapsulated with a pre-defined selection rule. Generally, simpler, or more homogenous mixtures (i.e., most molecules belonging to the same molecular subclass) are more effectively modelled by the FT method.
Shifting the focus to the molecular classification system, the SG model outperforms the AG model in all cases, although the AG model seems to be better suited for less diverse mixtures where a molecule clearly dominates the composition of a molecular subclass. The consistent performance of the SG model indicates that the use of a scoring function provides a superior method for molecule selection among molecular subclasses, resulting in a better representation of weighted average descriptors. Like the PT models of each fraction (i.e. complete bio-oil, phenolic and wax), the SG one closely matches the weighted average global chemical hardness of the all-molecule benchmark in each case. It is also the most accurate describing molecular weight and oxygen content. This variation between the performance of the SG and AG methods occurs due to the existence of molecular subclasses with several molecules, i.e. the hydrocarbon, fatty acid, and phenolic subclasses. In these cases, different molecules are selected by each of the methods where the most abundant molecule, selected by the AG method, differs from that selected by the SG method. In these cases, the most abundant compound in the subclass does not represent the average descriptors of that subclass.
The AG method performed best when modelling the phenolic fraction (Fig. 9b), even though the SG model still performed better. This improved performance of the AG model is attributed to the most abundant molecules in many of the molecular subclasses being those that most closely match the average descriptors of that subclass – in these cases molecular subclasses are small or contain molecules with very similar properties (i.e. fatty acids of differing lengths). Only the molecule selected from the phenolic molecular subclass differs in the models generated for the phenolic fraction using the AG and SG methods.
From the analysis of Fig. 9, there is no clear champion model, but the most suitable method varies depending on the mixture being modelled, hence the development of an automatic platform for model generation and validation. In the case of the complete bio-oil and the phenolic fraction, the PT method performs best when comparing the model's weighted average descriptors against those of the all-molecule model. Differently, the SG method provides a better model for the wax fraction (Fig. 9c), even though the PT model contains three times as many molecules, highlighting the situations where each excels. The PT model performs better when the bio-oil fraction is dominated by a single molecular subclass (i.e. the characterisation identified the fraction to be comprised of 86.6% phenolic compounds) and a statistical sample of this subclass is optimal. Whereas the SG model triumphs where the bio-oil fraction is not solely dominated by a single molecular subclass, and it is more important to represent each class with the molecule that most closely matches the average descriptors for that class.
Distribution of chemical reactivity descriptors
Given the relevance of bio-oils for asphalt rejuvenators or upgrading to biofuels, we found important to describe the distribution of individual values of global chemical hardness across the sampled molecules in all the representative models, in addition to the average descriptors. Fig. 10 shows histograms with the distribution of values for global chemical hardness in the all-molecule model as well as in each of the representative models. Whilst the distribution of global chemical hardness across models is the most important for our uses, distributions of the other weighted descriptors, i.e., polarizability, dipole moment, and molecular weight, are also calculated and provided in the ESI.†As seen in Fig. 10, the FT model fails to represent the distribution of global chemical hardness in all cases (Fig. 10a–c), and unlike the PT method, it does not select enough molecules to reflect the diversity of values in the reactivity descriptor accurately. Whereas the AG and SG models include a much better distribution of global chemical hardness. For instance, in the case of the phenolic fraction (Fig. 10b), the AG and SG models include an extra peak that corresponds to the hydrocarbon subclass, which is not present in the FT or PT model histograms. This occurs as hydrocarbons are present in very small amounts in the bio-oil and do not meet the selection criteria of the FT and PT models but are included in the AG and SG models by design. A similar observation is seen where the FT and PT models fail to capture the distribution of global chemical hardness in the wax fraction (Fig. 10c), and the peak between 3.5 and 4 eV is absent in both models. This peak corresponds to the phenolic molecular subclass and, which again, is present in the AG and SG models by design, highlighting that the omission of phenols by the abundancy-based methods affects the description of the chemical properties of the mixture, particularly the description of their reactivity.
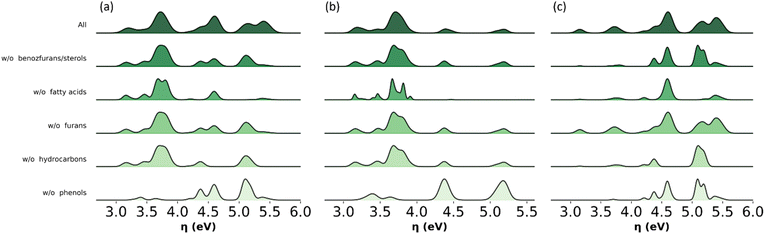
Model sensitivity analysis of omitted molecular subclasses
Since the omission of phenols by the abundancy-based methods when modelling the wax fraction has been highlighted to be relevant to the description of weighted average descriptors and weighted descriptors distribution, we implemented a model sensitivity analysis to analyse the effect that omissions of each molecular subclass have on the weighted descriptors distribution, and especially on the global chemical hardness. This helps provide information on which approach (i.e. abundancy-based model generation system or molecular classification model generation system) is most suitable for a given mixture. A breakdown of the molecular subclasses included in each representative model for the complete bio-oil and the phenolic and wax fractions is shown in Table 5. Fig. 11 shows the distribution of global chemical hardness where each different molecular class has been deliberately omitted from the all-molecule model for the complete bio-oil, the phenolic and wax fractions.| Molecular subclass | Complete bio-oil | Phenolic fraction | Wax fraction | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | FT | PT | AG | SG | All | FT | PT | AG | SG | All | FT | PT | AG | SG | |
| Phenols | O | O | O | O | O | O | O | O | O | O | O | X | X | O | O |
| Fatty acids | O | O | O | O | O | O | X | O | O | O | O | O | O | O | O |
| Hydrocarbons | O | X | O | O | O | O | X | X | O | O | O | O | O | O | O |
| Furans | O | X | O | O | O | O | X | O | O | O | — | — | — | — | — |
| Benzofurans/sterols | O | X | X | O | O | O | X | X | O | O | O | X | O | O | O |
The analysis shown in Fig. 11 identifies key molecular subclasses for the distribution of global chemical hardness in the bio-oil and the two main fractions. For example, this distribution in the phenolic fraction is mostly affected by the omission of phenols and fatty acids but nominally by the omission of benzofurans, furans and hydrocarbons (Fig. 11b) and in Fig. 9b the performance of the PT model is not affected by the exclusion of benzofurans and hydrocarbons. In the wax fraction only the omission of phenols affects the distribution (Fig. 11c). This analysis highlights phenols to be included in any model, and it supports the implementation of a molecular-classification system, which is more suited for modelling the wax fraction.
Representative models applicability to multi-scale atomistic simulations
The generation of data-driven representative models facilitates the scalability of atomistic simulations by describing average chemical properties and property distribution with a small number of selected molecules, hence dramatically reducing the number of interacting particles required to describe the overall behaviour of complex organic fluids. The implementation of these atomistic models is expected to accelerate ab initio and classical molecular dynamics simulations, as well as to enable less computationally demanding high-throughput DFT calculations.To quantify the minimum number of molecules and atoms required for an atomistic simulation, each component within a model must have the possibility of interacting with each of the other components and with itself simultaneously. Eqn (11) determines the number of unique molecule-to-molecule interactions within a molecular system or model where, n is the number of components and r is the number of components in each combination, which for simplicity we will restrict to r = 2, meaning that only bimolecular interactions happen simultaneously.
| c(n,r) = n!/(r! + (n − r)! | (11) |
For example, to represent each possible molecular interaction for molecule A in the FT model constituted by five molecules (FT model of the phenolic fraction), and only considering bimolecular interactions occurring simultaneously, at least six molecules of A would be required to allow for each possible interaction, i.e., the interaction of A with itself (two molecules of A required), and the interactions of A with each the other four molecules (4 molecules of A required). The same reasoning applies to the other four molecules different from A in the model, so in total, 30 molecules would be required, within the FT model, to consider all possible molecule-to-molecule interactions. However, this procedure assumes that all molecules are equally proportional in the mixture, which is not the case. To address this technicality, eqn (12) calculates the minimum number of molecules, but considering their relative proportions or stoichiometry, where ai is the abundancy of molecule i, as is the abundancy of the least abundant molecule, and N is the number of unique molecules. All concentrations are normalised with respect to as and scaled by a factor of N + 1 (the +1 accounting for the interaction with the molecule itself). The sum of these scaled values is the minimum number of molecules required whilst still retaining their relative proportions in the mixture. For example, the FT model of the phenolic fraction requires 41 molecules, 11 more than before, but more accurately describing the mixture.
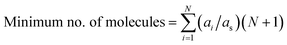 | (12) |
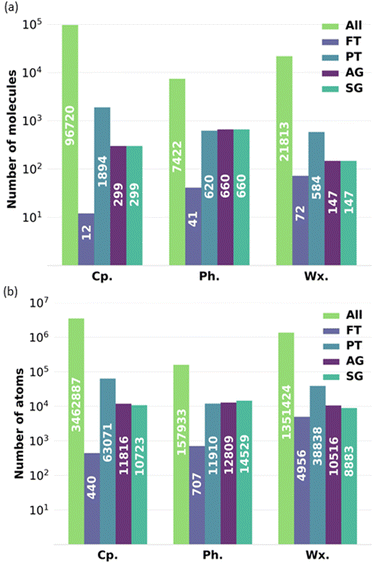
To exemplify the impact of reducing the number of molecules in a complex bio-oil, Fig. 12 shows the minimum number of molecules and atoms within that are required for each of the representative models to perform a full-atomistic molecular dynamics simulation while considering all possible intermolecular interactions resulting from all the molecules characterised by GCMS and retaining their relative proportions in the mixture. Fig. 12 shows data for the complete bio-oil for the pyrolysis of pine bark, as well as for the phenolic and wax fractions. The FT model requires the lowest number of atoms, but it oversimplifies the mixture. AG and SG models require similar numbers of atoms among them, but they need a lower number of atoms than the PT model, as fewer molecules are utilised to describe the overall properties. Conversely, the PT model of the phenolic fraction requires less atoms than its AG and SG models.
Generally, the all-molecule model requires 10–100 times more atoms than the FT, PT, AG, and SG models, without even considering the required increase in system size beyond the minimum in molecular dynamics simulations that aim to describe agglomeration and clustering of particles.45,46 In our case study, the number of atoms in the all-molecule model for the complete bio-oil is almost 3.5 million, which reduces to roughly 10 thousand for the SG model, potentially the best-performing representative model. It implies a scale-up in complexity of around 500 times for a molecular dynamics simulation that utilises the particle-mesh Ewald method, with its associated increase in computational time and computational resources required.47,48
The order of magnitude of the scale-up in complexity when using the all-molecule model concerning any other representative model considered is in a similar range for the particle-mesh Ewald method. Other methods, like the fast multipole method, scale linearly, following a O(N) function.49 The fast multipole method has been reported to outperform the particle mesh Ewald method in large systems with an inhomogeneous distribution of particles (i.e., water droplets in vacuum).50 Regardless of its performance with other methods when computing long-range interactions, the increase in time complexity for the fast multipole method is still more than 300 times higher if representative models are not adopted to reduce complexity.
Conclusions
The large variety and complexity of organic molecules in fluids like bitumen, crude oil, or biobased oils from pyrolysis or hydrothermal liquefaction has hampered the development of atomistic models for bottom-up molecular design of bitumen-like materials in the biorefinery space. Existing strategies for atomistic model development are based on chemical intuition and personal selection of the molecular components. We have developed an author-agnostic data-driven computational platform that reduces human biases in model generation from experimental data. Given bio-oils relevance for asphalt rejuvenators or upgrading to biofuels, we specifically focused on accurately describing the chemical reactivity. Two approaches were investigated: an abundancy-based system that selects the most abundant species within a mixture (FT and PT methods) and a molecular-classification system that categorises molecules into classes and subclasses based on heteroatom and similarities in chemical structure using a feature identification algorithm (AG and SG methods). In all cases, our platform analysed weighted average descriptors of several chemical properties and weighted descriptor distribution across the sample of molecules. As proof of concept, this computational platform was tested with bio-oil from the pyrolysis of pine bark, which was produced ad hoc for this purpose, although our approach is applicable to any complex mixture of organic molecules.There is no clear champion method for model generation, but the most suitable alternative varies depending on the mixture being modelled, hence the development of an automatic platform for model generation and validation. Nevertheless, among the different methods developed and tested, the abundancy-based PT method, and the molecular classification SG method performed particularly well when describing the complexity of the molecular mixture with a reduced sample of selected molecules. Their good performance highlights the importance of generating a statistically representative sample of molecules, and the convenience of implementing a scoring function for molecular selection. While the PT method excels when the composition of a mixture is dominated by a subclass of similar compounds (i.e., the complete bio-oil and phenolic fraction, which consist of 57.2% and 86.6% phenolic molecules, respectively), the SG method performs best when a mixture contains a diverse mixture of molecular subclasses, such as the wax fraction, as it provides a way to encapsulate each chemical group within a mixture.
The adoption of these data-driven representative models reduces the number of atoms required for molecular dynamics simulations by a factor of 10 to 100, which implies, for our case study, a reduction in time complexity by factors of between 100 to 1000 times for a molecular dynamics simulation that utilises the particle-mesh Ewald method, or the fast multipole method.
Given the societal relevance of asphalt cracking or sustainable fuel production, in addition to the countless initiatives for biomass waste valorisation, a platform for faster and accurate molecular dynamics simulations and high-throughput DFT calculations is essential to unlock structure–property relationships of bitumen-like materials like asphalt binders and bio-oils from biorefineries. Furthermore, at the dawn of self-driving laboratories, with an exponential growth of machine learning applications, and the need for large data sets for training and validation, innovative strategies for an automated generation of atomistic models that enable digital development of organic complex fluids using computational chemistry and multiscale modelling is especially relevant.
Data availability statement
The code for the generation of Data Driven Representative Models can be found at https://github.com/MMLabCodes/data-driven-representative-models-of-biobased-complex-fluids with https://doi.org/10.5281/zenodo.10356310.Author contributions
Daniel York: conceptualization (supporting), investigation (lead), formal analysis (equal), visualization (equal), software (lead), writing – original draft (equal). Isaac Vidal-Daza: investigation (supporting), software (supporting), writing – review and editing (supporting). Cristina Segura: investigation (equal); writing – review and editing (supporting). Jose Norambuena-Contreras: writing – review and editing (supporting). Francisco J. Martin-Martinez: conceptualization (lead), investigation (supporting), formal analysis (lead), visualization (equal), software (supporting), writing – review and editing (lead), project administration (lead), funding acquisition (lead).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Royal Society of Chemistry Enablement Grant (E21-7051491439), the Engineering and Physical Sciences Research Council's Industrial CASE ref. 220197 with Tata Steel, and the Chilean Economic Development Agency (CORFO) through the R&D project Prototype and Validation (grant number 19CVID-107445). The authors also acknowledge the support of the Supercomputing Wales project which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government, and the support of the Google Cloud Platform Credits program with the award GCP19980904. F. J. M.-M. acknowledges the support from the Google Cloud Research Innovators program.References
- A. Aspuru-Guzik, R. Lindh and M. Reiher, ACS Cent. Sci., 2018, 4, 144–152 CrossRef CAS PubMed
.
- A. Aspuru-Guzik, Digital Discovery, 2023, 2, 10–11 RSC
.
- J. Norambuena-Contreras, R. Serpell, G. Valdés Vidal, A. González and E. Schlangen, Constr. Build. Mater., 2016, 127, 369–382 CrossRef
.
- I. Gonzalez-Torre and J. Norambuena-Contreras, Constr. Build. Mater., 2020, 258, 119568 CrossRef CAS
.
- UK road spending 2023, https://www.statista.com/statistics/298667/united-kingdom-uk-public-sector-expenditure-national-roads/, accessed 21 August 2023.
- F. Pahlavan, A. Lamanna, K.-B. Park, S. F. Kabir, J.-S. Kim and E. H. Fini, Resour., Conserv. Recycl., 2022, 187, 106601 CrossRef CAS
.
- A. Bachs-Herrera, D. York, T. Stephens-Jones, I. Mabbett, J. Yeo and F. J. Martin-Martinez, iScience, 2023, 26, 106549 CrossRef PubMed
.
- G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044–4098 CrossRef CAS PubMed
.
- C. Pandit, S. Pandit, M. Pant, D. Ghosh, D. Agarwal, D. Lahiri, M. Nag and R. R. Ray, Chem. Afr., 2023, 6, 2237–2263 CrossRef CAS
.
- S. Jabeen, X. Gao, J. Hayashi, M. Altarawneh and B. Z. Dlugogorski, J. Environ. Chem. Eng., 2022, 10, 107953 CrossRef CAS
.
- M. M. Royko, S. M. Drummond, J. Boyt, S. M. Ghoreishian and J. Lauterbach, Front. Energy Res., 2022 DOI:10.3389/fenrg.2022.1088902
.
- D. López Barreiro, F. J. Martin-Martinez, C. Torri, W. Prins and M. J. Buehler, Algal Res., 2018, 35, 262–273 CrossRef
.
- D. D. Li and M. L. Greenfield, Fuel, 2014, 115, 347–356 CrossRef CAS
.
- F. J. Martín-Martínez, E. H. Fini and M. J. Buehler, RSC Adv., 2015, 5, 753–759 RSC
.
- M. L. Greenfield, Int. J. Pavement Eng., 2011, 12, 325–341 CrossRef CAS
.
- D. D. Li and M. L. Greenfield, Energy Fuels, 2011, 25, 3698–3705 CrossRef CAS
.
- L. Zhang and M. L. Greenfield, Energy Fuels, 2007, 21, 1712–1716 CrossRef CAS
.
- O. C. Mullins, H. Sabbah, J. Eyssautier, A. E. Pomerantz, L. Barré, A. B. Andrews, Y. Ruiz-Morales, F. Mostowfi, R. McFarlane, L. Goual, R. Lepkowicz, T. Cooper, J. Orbulescu, R. M. Leblanc, J. Edwards and R. N. Zare, Energy Fuels, 2012, 26, 3986–4003 CrossRef CAS
.
- O. C. Mullins, Energy Fuels, 2010, 24, 2179–2207 CrossRef CAS
.
- T. Fan and J. S. Buckley, Energy Fuels, 2002, 16, 1571–1575 CrossRef CAS
.
- H. Yao, Q. Dai and Z. You, Fuel, 2015, 164, 83–93 CrossRef
.
- H. Yao, J. Liu, M. Xu, J. Li, Q. Dai and Z. You, Adv. Colloid Interface Sci., 2021, 299, 102565 CrossRef PubMed
.
- F. Guo, J. Zhang, J. Pei, B. Zhou and Z. Hu, J. Mol. Model., 2019, 25, 365 CrossRef CAS PubMed
.
- P. Lu, Y. Ma, K. Ye and S. Huang, Constr. Build. Mater., 2022, 350, 128903 CrossRef CAS
.
- M. Su, C. Si, Z. Zhang and H. Zhang, Fuel, 2020, 263, 116777 CrossRef CAS
.
- D. Hu, X. Gu and B. Cui, Front. Struct. Civ. Eng., 2021, 15, 1261–1276 CrossRef
.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- J. Tang and H. Wang, Constr. Build. Mater., 2022, 314, 125605 CrossRef CAS
.
- S. Majumder and A. P. Liu, Phys. Biol., 2017, 15, 013001 CrossRef PubMed
.
- Z. Yang, J. Li, Y. Ling, Q. Zhang, X. Yu and W. Cai, ChemCatChem, 2017, 9, 3307–3313 CrossRef CAS
.
- X. Wang, Z. Chen, K. Jiang, M. Chen and S. Passerini, Adv. Energy Mater., 2024, 2304229 CrossRef
.
- R. K. Luu, M. Wysokowski and M. J. Buehler, Appl. Phys. Lett., 2023, 122, 234103 CrossRef CAS
.
- M. J. Buehler, J. Mech. Phys. Solids, 2023, 181, 105454 CrossRef
.
- B. Ni and M. J. Buehler, Extreme Mech Lett., 2024, 67, 102131 CrossRef
.
- A. Ghafarollahi and M. J. Buehler, arXiv, 2024, preprint, arXiv: 2402.04268, DOI:10.48550/arXiv.2402.04268.
- K. Mikula, G. Soja, C. Segura, A. Berg and C. Pfeifer, Processes, 2020, 8, 764 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS
.
- M. L. Senent and S. Wilson, Int. J. Quantum Chem., 2001, 82, 282–292 CrossRef CAS
.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed
.
- J. Luo, Z. Q. Xue, W. M. Liu, J. L. Wu and Z. Q. Yang, J. Phys. Chem. A, 2006, 110, 12005–12009 CrossRef CAS PubMed
.
- O. Pinto, R. Romero, M. Carrier, J. Appelt and C. Segura, J. Anal. Appl. Pyrolysis, 2018, 136, 69–76 CrossRef CAS
.
- P. A. Case, C. Bizama, C. Segura, M. Clayton Wheeler, A. Berg and W. J. DeSisto, J. Anal. Appl. Pyrolysis, 2014, 107, 250–255 CrossRef CAS
.
- S. Wang, Q. Cheng, Y. Gan, Q. Li, C. Liu and W. Sun, Molecules, 2022, 27, 4432 CrossRef CAS PubMed
.
- M. Rahmati, Chem. Phys. Lett., 2021, 779, 138847 CrossRef CAS
.
- A. C. Simmonett and B. R. Brooks, J. Chem. Phys., 2021, 154, 054112 CrossRef CAS PubMed
.
- H. G. Petersen, J. Chem. Phys., 1995, 103, 3668–3679 CrossRef CAS
.
- J. Kurzak and B. M. Pettitt, Mol. Simul., 2006, 32, 775–790 CrossRef CAS PubMed
.
- B. Kohnke, C. Kutzner and H. Grubmüller, J. Chem. Theory Comput., 2020, 16, 6938–6949 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00245d |
| This journal is © The Royal Society of Chemistry 2024 |