Open Access Article
Open Access ArticleA reproducibility study of atomistic line graph neural networks for materials property prediction†
Kangming
Li
 *a,
Brian
DeCost
*a,
Brian
DeCost
 b,
Kamal
Choudhary
b,
Kamal
Choudhary
 b and
Jason
Hattrick-Simpers
b and
Jason
Hattrick-Simpers
 acde
acde
aDepartment of Materials Science and Engineering, University of Toronto, 27 King's College Cir, Toronto, ON, Canada. E-mail: kangming.li@utoronto.ca; jason.hattrick.simpers@utoronto.ca
bMaterial Measurement Laboratory, National Institute of Standards and Technology, 100 Bureau Dr, Gaithersburg, MD, USA
cAcceleration Consortium, University of Toronto, 27 King's College Cir, Toronto, ON, Canada
dVector Institute for Artificial Intelligence, 661 University Ave, Toronto, ON, Canada
eSchwartz Reisman Institute for Technology and Society, 101 College St, Toronto, ON, Canada
First published on 30th April 2024
Abstract
Use of machine learning has been increasingly popular in materials science as data-driven materials discovery is becoming the new paradigm. Reproducibility of findings is paramount for promoting transparency and accountability in research and building trust in the scientific community. Here we conduct a reproducibility analysis of the work by K. Choudhary and B. Brian [npj Comput. Mater., 7, 2021, 185], in which a new graph neural network architecture was developed with improved performance on multiple atomistic prediction tasks. We examine the reproducibility for the model performance on 29 regression tasks and for an ablation analysis of the graph neural network layers. We find that the reproduced results generally exhibit a good quantitative agreement with the initial study, despite minor disparities in model performance and training efficiency that may be resulting from factors such as hardware difference and stochasticity involved in model training and data splits. The ease of conducting these reproducibility experiments confirms the great benefits of open data and code practices to which the initial work adhered. We also discuss some further enhancements in reproducible practices such as code and data archiving and providing data identifiers used in dataset splits.
1. Introduction
As science continues to evolve, it is transitioning towards what is now often referred to as its “fourth paradigm”, characterized by the pivotal role that data-driven approaches are playing in advancing our understanding of the natural world.1,2 In this landscape, machine learning (ML) has become an indispensable tool in materials science, where it aids in tasks ranging from materials discovery to property prediction.3–6 As the reach of ML expands, the issue of reproducibility has come to the forefront.7–10 Reproducibility is the cornerstone upon which scientific credibility is built; it fosters trust, transparency, and accountability in data-centric research. However, despite the growing support for sharing data, code, and workflows to facilitate replication,10–13 ensuring reproducibility is generally recognized as an ongoing issue in both the scientific14–17 and machine learning communities.7–10 So far, there has been a lack of systematic reproducibility assessments in the field of ML for materials science.18We present a case study aiming to reproduce the main results of K. Choudhary and B. DeCost centering on the development of Atomistic Line Graph Neural Network (ALIGNN).19 Indeed, among the variety of machine learning architectures, Graph Neural Networks (GNNs) have demonstrated state-of-the-art performance in capturing complex atomistic relationships and predicting material properties.20–25 As one of the first GNN architectures that account for many-body interactions, ALIGNN performs message passing on both the interatomic bond graph and its line graph corresponding to bond angles. This explicit inclusion of angle information was demonstrated to improve performance on multiple atomistic prediction tasks.19 While a number of advanced architectures (in particular equivariant GNNs)26–29 have been proposed with improved performance in some cases,30 it is still an open question whether equivariant GNNs have a substantial and systematic advantage over invariant ones.31 In addition, recent benchmarks show that ALIGNN model remains competitive with respect to other leading GNNs in terms of accuracy and robustness.32–34 As ALIGNN is often used as a representative GNN in many ML studies,32–36 we feel it is an important target for reproducibility assessment.
The original ALIGNN study incorporated an evaluation of the model's performance on 52 crystal and molecular properties across the JARVIS-DFT,37 Materials Project,38 and QM9 databases,39 supplemented by an ablation analysis of ALIGNN models trained on formation energy and band gap data from the JARVIS-DFT database. Here we focus on evaluating the reproducibility of (1) the model performance on all of the 29 regression tasks from the JARVIS-DFT database, and (2) of the ablation analysis using models trained on the formation energy data from the JARVIS-DFT database.
The remainder of this paper is organized as follows: Section 2 details the procedure to set up the model training. Section 3 and 4 present the reproducibility analysis of the model performance and ablation analysis, respectively. Finally, Section 5 is devoted to discussing the observed challenges and providing suggestions for better reproducibility.
2. Computational setup
2.1 Python environment setup and package installation
The ALIGNN model training code is provided as a Python package , registered on the Python package index (https://pypi.org/project/alignn/2023.5.3) with public source code available on GitHub at https://github.com/usnistgov/alignn including an installation guide. To avoid potential dependency conflicts, we first created a new
, registered on the Python package index (https://pypi.org/project/alignn/2023.5.3) with public source code available on GitHub at https://github.com/usnistgov/alignn including an installation guide. To avoid potential dependency conflicts, we first created a new  environment. We then followed the installation guide to install the
environment. We then followed the installation guide to install the  package with
package with  support on a Ubuntu 20.04 desktop equipped with an RTX 3080 Ti 12GB graphics processing unit (GPU). The
support on a Ubuntu 20.04 desktop equipped with an RTX 3080 Ti 12GB graphics processing unit (GPU). The 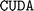 11.6 version and the
11.6 version and the 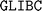 2.31 version were used during the installation.
2.31 version were used during the installation.
While no obvious warnings or errors occurred during the installation process, subsequent ALIGNN training with GPU support encountered errors linked to the 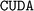 version of
version of 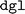 . The latter is the Deep Graph Library (DGL)40 utilized for the model's implementation. This issue might be attributable to the deprecated
. The latter is the Deep Graph Library (DGL)40 utilized for the model's implementation. This issue might be attributable to the deprecated 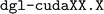 package name recommended in the
package name recommended in the 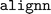 installation guide. On the other hand, updating to a newer
installation guide. On the other hand, updating to a newer 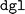 version induced installation errors due to dependency conflicts between
version induced installation errors due to dependency conflicts between 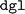 and
and 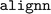 involving the
involving the 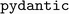 library used by
library used by 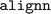 for configuration parsing and validation. Moreover, the training failure persisted. Upon further examination, it was found that the order of package installation was a critical factor: successful ALIGNN training could only be achieved when an updated version of
for configuration parsing and validation. Moreover, the training failure persisted. Upon further examination, it was found that the order of package installation was a critical factor: successful ALIGNN training could only be achieved when an updated version of 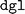 was installed prior to
was installed prior to 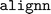 , and not vice versa. This sequence still generated dependency conflicts but these did not impede the ALIGNN training. The exact cause of this delicate dependency on the installation order is not exactly clear. However, our hypothesis is that the
, and not vice versa. This sequence still generated dependency conflicts but these did not impede the ALIGNN training. The exact cause of this delicate dependency on the installation order is not exactly clear. However, our hypothesis is that the 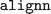 package installs the CPU-only version of
package installs the CPU-only version of 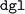 , so that the
, so that the  package manager skips installation of the explicitly-requested
package manager skips installation of the explicitly-requested 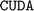 version of
version of  without providing a clear warning.
without providing a clear warning.
We chose to use the current version 2023.5.1 of  in our reproducibility study rather than using the specific revision from the original ALIGNN study due to ongoing updates in the codebase. Regardless, the modifications in training efficiency and model performance are anticipated to be minimal as there has been no major update in the relevant components.
in our reproducibility study rather than using the specific revision from the original ALIGNN study due to ongoing updates in the codebase. Regardless, the modifications in training efficiency and model performance are anticipated to be minimal as there has been no major update in the relevant components.
2.2 Data retrieval
The datasets used in the original ALIGNN study can be retrieved using the package,37 which is installed as a
package,37 which is installed as a  dependency for general utilities. Instructions to retrieve and import the data are provided on the
dependency for general utilities. Instructions to retrieve and import the data are provided on the  online documentation. Here we focus on the reproducibility of the results related to the JARVIS-DFT dataset. The database version utilized in the ALIGNN paper has been preserved as a snapshot and can be accessed under the database name
online documentation. Here we focus on the reproducibility of the results related to the JARVIS-DFT dataset. The database version utilized in the ALIGNN paper has been preserved as a snapshot and can be accessed under the database name 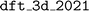 , facilitating our reproducibility study.
, facilitating our reproducibility study.
The interpretation of the retrieved data is generally straightforward with the provided property labels, albeit not always intuitively so. For instance, the retrieved data includes properties labeled as “magmom_oszicar” and “magmom_outcar”, and it is unclear which one corresponds to the magnetic moment data discussed in the paper. Nonetheless, the mean absolute deviation (MAD) of the data was provided in the original paper, which can be used to disambiguate the property labels' significance.
2.3 Model training setup
The package includes a
package includes a  script, with a training tutorial on the
script, with a training tutorial on the  GitHub webpage. The hyperparameters can also be readily configured via a
GitHub webpage. The hyperparameters can also be readily configured via a  configuration file, simplifying the entire training process, particularly for novice users. In this work, the same hyperparameters as in the original paper were used, and all the ALIGNN models were trained on a Ubuntu 20.04 desktop using a single GPU (RTX 3080 Ti 12GB) and 8 CPU cores (AMD Ryzen 9 5900X).
configuration file, simplifying the entire training process, particularly for novice users. In this work, the same hyperparameters as in the original paper were used, and all the ALIGNN models were trained on a Ubuntu 20.04 desktop using a single GPU (RTX 3080 Ti 12GB) and 8 CPU cores (AMD Ryzen 9 5900X).
3. Reproducibility of model performance
Here we aim to examine the reproducibility of the ALIGNN model performance on all the 29 regression tasks in the JARVIS-DFT dataset.37 For each task, we evaluated the model performance with a single 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 random train-validation-test split, which is the splitting strategy used in the ALIGNN paper. The precise allocation of specific materials across splits may not exactly match the original dataset partitions because the original manuscript relies on a specified random seed and the implementation details of the particular version of the random number generator used instead of specifying unambiguous identifiers for each training, validation, and test instance. For each property, we performed five independent model training runs using different random seeds for the model parameter initialization on the same train-validation-test split. For each run, we computed the deviation of the mean absolute error (MAE):
1 random train-validation-test split, which is the splitting strategy used in the ALIGNN paper. The precise allocation of specific materials across splits may not exactly match the original dataset partitions because the original manuscript relies on a specified random seed and the implementation details of the particular version of the random number generator used instead of specifying unambiguous identifiers for each training, validation, and test instance. For each property, we performed five independent model training runs using different random seeds for the model parameter initialization on the same train-validation-test split. For each run, we computed the deviation of the mean absolute error (MAE):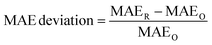 | (1) |
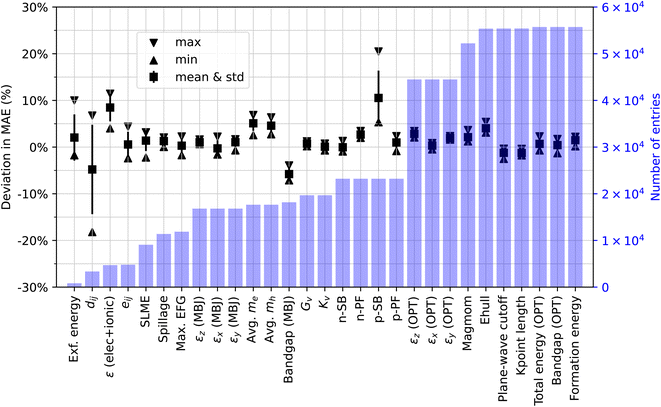
Fig. 1 presents the minimum, maximum, mean, and standard deviation of the MAE deviations for the selected properties, along with the corresponding total number of entries. Two general observations emerge from these results. Firstly, the variability in the reproduced MAE is more conspicuous for properties with fewer entries, with the exception of the models for predicting p-type Seebeck coefficients, which exhibit a relatively large MAE variance despite having over 20k entries. Since the MAE variance stems from the random seeds used for model parameter initialization and random batch construction for stochastic gradient optimization, this suggests that model performance on smaller datasets is more susceptible to parameter initialization and other sources of training variation. This is expected because model training with smaller datasets is expected to fall into the high variance regime and poses challenges for convergence towards a model with consistent predictive behavior. Furthermore, we anticipate that the variance could potentially increase if different data splits (even if the split ratio is the same) were employed. Secondly, the model performance reported in the original ALIGNN paper is reasonably well reproduced in this study. As can be seen from Fig. 1, the original MAE values are covered within the ranges of the reproduced MAE for 19 out of the 29 tasks. For the remaining 10 tasks whose reproduced MAEs do not cover the original ones, the minimum absolute MAE deviation is no more than 5%, which means that the original MAE can be matched within the 5% deviation by one of our independent runs.
4. Reproducibility of ablation analysis
An ablation study serves to assess the individual components' contributions to the overall model architecture. In the original paper, a layer ablation study was conducted to evaluate the contributions of the ALIGNN and Graph Convolution Network (GCN) layers to model performance and training cost.19 Here we followed the original paper's procedure by altering the numbers of the ALIGNN and GCN layers from 0 to 4, while keeping other parameters constant. We carried out the ablation analysis focusing on the JARVIS-DFT formation energy target.First, we note that the model performance on various properties in the previous section was obtained with 4 ALIGNN and 4 GCN layers. In particular, for the formation energy prediction, we obtained the same MAE (0.033 eV per atom) as in the original paper. We use this value as the baseline to normalize the MAEs obtained with different numbers of ALIGNN and GCN layers in the ablation analysis. The resulting normalized MAEs from the original paper and this work are shown in Table 1. Overall, similar effects of the layers on the model performance are reproduced, with a maximum deviation of 6% from the original value when using 1 ALIGNN and 1 GCN layer. Such a deviation is expected to be within the error bar of the performance, since here we performed only a single model training run with a fixed random seed for each layer combination due to the high training cost.
| Original paper | GCN-0 | GCN-1 | GCN-2 | GCN-3 | GCN-4 |
|---|---|---|---|---|---|
| ALIGNN-0 | 13.48 | 1.97 | 1.52 | 1.36 | 1.33 |
| ALIGNN-1 | 1.94 | 1.24 | 1.12 | 1.09 | 1.12 |
| ALIGNN-2 | 1.18 | 1.09 | 1.03 | 1.03 | 1.03 |
| ALIGNN-3 | 1.09 | 1.03 | 1.00 | 1.03 | 1.03 |
| ALIGNN-4 | 1.03 | 1.03 | 1.03 | 1.03 | 1.00 |
| This work | GCN-0 | GCN-1 | GCN-2 | GCN-3 | GCN-4 |
|---|---|---|---|---|---|
| ALIGNN-0 | 13.66 | 1.95 | 1.48 | 1.30 | 1.27 |
| ALIGNN-1 | 1.95 | 1.16 | 1.11 | 1.09 | 1.09 |
| ALIGNN-2 | 1.22 | 1.06 | 1.08 | 1.06 | 1.04 |
| ALIGNN-3 | 1.07 | 1.03 | 1.02 | 1.03 | 1.02 |
| ALIGNN-4 | 1.04 | 1.02 | 1.00 | 1.01 | 1.00 |
The original ALIGNN paper also documented the training time per epoch as a function of the number of layers. Since we did not use the same hardware as the original paper, it is not suitable to compare directly the training time. Instead, we normalize the training time per epoch with respect to that of the 4 ALIGNN + 4 GCN layer configuration and compare the normalized training cost as shown in Table 2. Compared to the effect of number of layers on the model performance, reproducing the effect on the training time proves more challenging. For instance, using no ALIGNN and GCN layer requires only 11% of the training cost of that using 4 ALIGNN and 4 GCN layers according to the original paper, whereas using no ALIGNN and GCN layer is found to require 19% of the training cost of that using 4 ALIGNN and 4 GCN layers in this work. In other words, the relative deviation of our reproduced effect of layers on the training cost can be as large as 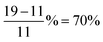 . This is not surprising because training time is sensitive to hardware and operating system configuration and using layer combination may induce varying system loads that could lead to discrepancies in training efficiency. Training efficiency for deep learning workloads in particular can be sensitive to memory bandwidth and the ability of the dataloading pipeline to saturate the GPU.
. This is not surprising because training time is sensitive to hardware and operating system configuration and using layer combination may induce varying system loads that could lead to discrepancies in training efficiency. Training efficiency for deep learning workloads in particular can be sensitive to memory bandwidth and the ability of the dataloading pipeline to saturate the GPU.
| Original paper | GCN-0 | GCN-1 | GCN-2 | GCN-3 | GCN-4 |
|---|---|---|---|---|---|
| ALIGNN-0 | 0.11 | 0.22 | 0.22 | 0.28 | 0.33 |
| ALIGNN-1 | 0.33 | 0.50 | 0.56 | 0.56 | 0.56 |
| ALIGNN-2 | 0.56 | 0.67 | 0.63 | 0.72 | 0.67 |
| ALIGNN-3 | 0.67 | 0.78 | 0.78 | 0.83 | 0.78 |
| ALIGNN-4 | 0.83 | 0.89 | 0.94 | 0.94 | 1.00 |
| This work | GCN-0 | GCN-1 | GCN-2 | GCN-3 | GCN-4 |
|---|---|---|---|---|---|
| ALIGNN-0 | 0.19 | 0.24 | 0.28 | 0.31 | 0.35 |
| ALIGNN-1 | 0.33 | 0.41 | 0.44 | 0.47 | 0.49 |
| ALIGNN-2 | 0.51 | 0.59 | 0.60 | 0.63 | 0.64 |
| ALIGNN-3 | 0.68 | 0.77 | 0.79 | 0.82 | 0.84 |
| ALIGNN-4 | 0.83 | 0.95 | 1.03 | 0.98 | 1.00 |
With the above results of the model performance and training time, we can construct an accuracy-cost Pareto plot as shown in Fig. 2. Deviations between the original and reproduced Pareto fronts occur when the normalized training time is below 0.6. On the other hand, the layer configurations on the Pareto fronts are largely the same: the original Pareto fronts include (0,1)-(0,2)-(0,3)-(0,4)-(1,1)-(1,2)-(1,4)-(1,3)-(2,2), with the first and second numbers indicating the numbers of the ALIGNN and GCN layers; the reproduced Pareto front includes (0,1)-(0,2)-(0,3)-(0,4)-(1,1)-(1,2)-(1,3)-(1,4)-(2,1). The sources of deviations include the uncertainty in the model performance related to the model parameter initialization and potential sensitivity of training efficiency to changes in memory bandwidth relative to the compute capability of the different GPUs. These factors may influence the performance ranking, training cost ranking, and ultimately the Pareto fronts.
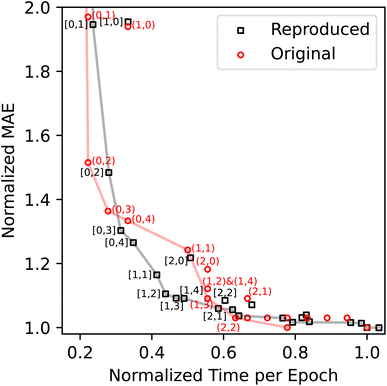 | ||
| Fig. 2 ALIGNN accuracy-cost ablation analysis for the JARVIS-DFT formation energy models. The values of the plotted normalized MAE and training time per epoch are given in Tables 1 and 2, respectively. The numbers in square brackets (or parentheses) indicate the corresponding numbers of the ALIGNN and GCN layers for the reproduced (or original) points. The solid lines indicate the original and reproduced Pareto fronts. | ||
5. Discussion
In this work, we examine the reproducibility of the model performance and the ablation analysis in the atomistic line graph network (ALIGNN) paper originally conducted by K. Choudhary and B. DeCost.19 The reproduced results generally exhibit a good quantitative agreement with the initial study. The relative ease to reproduce their work can be attributed to the adherence to the open data and code practices as their datasets, codes, and training scripts are readily found on the public repositories. A clear description of important details in the original work and documentation of model installation and training also contributed to the reproducibility experiments.Nonetheless, minor disparities in model performance and training times emerge. The variations observed in model performance likely stem from the innate variance associated with the random initialization of the model parameters and the stochastic training process. The discrepancy in training time, on the other hand, is likely attributable to external factors such as hardware configurations and operating system variances. In addition, we cannot completely dismiss the potential influence of updates to the codebase on these discrepancies. Indeed, in a practical setting it is recommended to re-optimize certain training pipeline hyperparameters, such as the batch size, to maximize training throughput on the available hardware. Typically this also requires re-tuning the learning rate and regularization hyperparameters, which works against the goal of using the same hyperparameters as in the original work.
From the perspective of reproducibility, it would be advantageous to make available a snapshot of the code and data version utilized in any published computational research. Primarily, this would eliminate the potential influence of codebase updates when determining the root causes of any discrepancies between the original and reproduced results. For instance, the Zenodo repository supports automated Github code release archiving that can be referenced with digital object identifiers (DOIs). As an example, the snapshot of the Github code used in this work is archived at https://zenodo.org/records/10042567 with a DOI of 10.5281/zenodo.10042567.
Additionally, providing the snapshots would simplify the task of correctly setting up the package installation. Indeed, the frequency of updates to the installation guide is typically less than that of codebase updates, and the compatibility checks between newer versions of dependencies are conducted less regularly. This could make the installation process more susceptible to unforeseen issues, which may be hard to solve for new users. For this work, we find that a smooth setup of a workable installation appears to be more challenging than reproducing the ALIGNN results; the latter is straightforwards by simply following the ALIGNN tutorial.
Another good practice would be to provide the data identifiers used in the training-validation-test splits, which can guarantee that exactly the same data splits are used in the model training and evaluation. While the effects of different random splits may be small especially for large data, using the same data splits can remove such uncertainty and enhance reproducibility, and is a common practice in the community benchmarks (due to the need for fair model comparison).22,24,25 Future ML work on existing datasets could use the same data splits as in those benchmarks to avoid this additional reporting task. Alternatively, it is straightforwards to generate such outputs in the ML pipeline and include them as a part of the ESI,† as is done in this work.
Another challenge surfaced in reproducing the ablation analysis when the model training failed due to the number of ALIGNN layers being set to zero. This failure was traced back to an inappropriate data type check in the latest  code. Although the remedy in this case required merely a one-line correction, it could prove challenging for users unfamiliar with the code or uncertain about potential side effects from making such modifications. Providing a snapshot of the version would therefore bolster the reproducibility study by mitigating such unforeseen issues that could emerge during the codebase update.
code. Although the remedy in this case required merely a one-line correction, it could prove challenging for users unfamiliar with the code or uncertain about potential side effects from making such modifications. Providing a snapshot of the version would therefore bolster the reproducibility study by mitigating such unforeseen issues that could emerge during the codebase update.
Ethical statement
Certain commercial products or company names are identified here to describe our study adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the products or names identified are necessarily the best available for the purpose.Data and code availability
The materials dataset used in this work can be retrieved using the package.37 The scripts used for the data retrieval and model training are available on Github at https://github.com/mathsphy/reproducibility-alignn. The generated output data and the python script to generate the figures and tables in this paper can be found on Zenodo at https://zenodo.org/records/10460493 with a DOI of 10.5281/zenodo.10460493.
package.37 The scripts used for the data retrieval and model training are available on Github at https://github.com/mathsphy/reproducibility-alignn. The generated output data and the python script to generate the figures and tables in this paper can be found on Zenodo at https://zenodo.org/records/10460493 with a DOI of 10.5281/zenodo.10460493.
Author contributions
K. L. and J. H.-S. conceived and designed the project. K. L. conducted replication experiment and analysis and wrote the manuscript. To ensure an independent regeneration of the results, B. D. and K. C (the original authors of the work replicated here) were excluded from replication experiment and analysis and participated only in the consultation of package installation and discussion of potential causes of discrepancies in the reproduced results. All authors reviewed of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was undertaken thanks in part to funding provided to the University of Toronto's Acceleration Consortium from the Canada First Research Excellence Fund (Grant Number: CFREF-2022-00042).References
- T. Hey, S. Tansley, K. Tolle and J. Gray, The Fourth Paradigm: Data-Intensive Scientific Discovery, Microsoft Research, 2009, available from: https://www.microsoft.com/en-us/research/publication/fourth-paradigm-data-intensive-scientific-discovery/ Search PubMed.
- A. Agrawal and A. Choudhary, Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science, APL Mater., 2016, 4(5), 053208 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559(7715), 547–555 CrossRef CAS PubMed.
- R. K. Vasudevan, K. Choudhary, A. Mehta, R. Smith, G. Kusne and F. Tavazza, et al., Materials science in the artificial intelligence age: High-throughput library generation, machine learning, and a pathway from correlations to the underpinning physics, MRS Commun., 2019, 9(3), 821–838 CrossRef CAS PubMed.
- D. Morgan and R. Jacobs, Opportunities and Challenges for Machine Learning in Materials Science, Annu. Rev. Mater. Res., 2020, 50, 71–103 CrossRef CAS.
- B. L. DeCost, J. R. Hattrick-Simpers, Z. Trautt, A. G. Kusne, E. Campo and M. Green, Scientific AI in materials science: a path to a sustainable and scalable paradigm, Mach. Learn.: Sci. Technol., 2020, 1(3), 033001 Search PubMed.
- J. Pineau, P. Vincent-Lamarre, K. Sinha, V. Larivière, A. Beygelzimer and F. d'Alché Buc, et al., Improving reproducibility in machine learning research (a report from the neurips 2019 reproducibility program), J. Mach. Learn. Res., 2021, 22(1), 7459–7478 Search PubMed.
- A. L. Beam, A. K. Manrai and M. Ghassemi, Challenges to the reproducibility of machine learning models in health care, J. Am. Med. Assoc., 2020, 323(4), 305–306 CrossRef PubMed.
- E. Raff A step toward quantifying independently reproducible machine learning research Advances in Neural Information Processing Systemsed. H. Wallach, H. Larochelle, A. Beygelzimer, F. d. Alch-Buc, E. Fox and R. Garnett, 2019, vol. 32 Search PubMed.
- R. Isdahl and O. E. Gundersen, Out-of-the-box reproducibility: A survey of machine learning platforms, in 2019 15th international conference on eScience (eScience), IEEE, 2019, pp. 86–95 Search PubMed.
- A. Y. T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo and J. Brgoch, et al., Machine learning for materials scientists: an introductory guide toward best practices, Chem. Mater., 2020, 32(12), 4954–4965 CrossRef CAS.
- M. D. Wilkinson, M. Dumontier, I. J. Aalbersberg, G. Appleton, M. Axton and A. Baak, et al., The FAIR Guiding Principles for scientific data management and stewardship, Sci. Data, 2016, 3(1), 1–9 Search PubMed.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, AiiDA: automated interactive infrastructure and database for computational science, Comput. Mater. Sci., 2016, 111, 218–230 CrossRef.
- O. S. Collaboration, Estimating the reproducibility of psychological science, Science, 2015, 349(6251), aac4716 CrossRef PubMed.
- M. Baker, 1,500 scientists lift the lid on reproducibility, Nature, 2016, 533, 452–454 CrossRef CAS PubMed.
- V. Stodden, M. McNutt, D. H. Bailey, E. Deelman, Y. Gil and B. Hanson, et al., Enhancing reproducibility for computational methods, Science, 2016, 354(6317), 1240–1241 CrossRef CAS PubMed.
- O. E. Gundersen and S. Kjensmo, State of the art: Reproducibility in artificial intelligence, in Proceedings of the AAAI Conference on Artificial Intelligence, 2018, vol. 32 Search PubMed.
- L. Pouchard, Y. Lin and H. Van Dam, Replicating machine learning experiments in materials science, in Parallel Computing: Technology Trends, IOS Press, 2020, pp. 743–755 Search PubMed.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 185 CrossRef.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31(9), 3564–3572 CrossRef CAS.
- R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal and A. Das, et al., The Open Catalyst 2022 (OC22) dataset and challenges for oxide electrocatalysts, ACS Catal., 2023, 13(5), 3066–3084 CrossRef CAS.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza and R. Cohn, et al., Recent advances and applications of deep learning methods in materials science, npj Comput. Mater., 2022, 8(1), 59 CrossRef.
- K. Choudhary, D. Wines, K. Li, K. F. Garrity, V. Gupta, A. H. Romero, et al., Large Scale Benchmark of Materials Design Methods, arXiv, 2023, preprint, arXiv:230611688, DOI:10.48550/arXiv.2306.11688.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm, npj Comput. Mater., 2020, 6(1), 1–10 CrossRef.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728 CrossRef PubMed.
- M. Geiger and T. Smidt, e3nn: Euclidean neural networks, arXiv, 2022, preprint, arXiv:220709453, DOI:10.48550/arXiv.2207.09453.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, MACE: Higher order equivariant message passing neural networks for fast and accurate force fields, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han and C. J. Bartel, et al., CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5(9), 1031–1041 CrossRef.
- J. Riebesell, R. E. Goodall, A. Jain, P. Benner, K. A. Persson and A. A. Lee, Matbench Discovery–An evaluation framework for machine learning crystal stability prediction, arXiv, 2023, preprint, arXiv:230814920, DOI:10.48550/arXiv.2308.14920.
- T. W. Ko and S. P. Ong, Recent advances and outstanding challenges for machine learning interatomic potentials, Nat. Comput. Sci., 2023, 3(12), 998–1000 CrossRef CAS PubMed.
- S. Gong, K. Yan, T. Xie, Y. Shao-Horn, R. Gomez-Bombarelli and S. Ji, et al., Examining graph neural networks for crystal structures: limitations and opportunities for capturing periodicity, Sci. Adv., 2023, 9(45), eadi3245 CrossRef PubMed.
- S. S. Omee, N. Fu, R. Dong, M. Hu and J. Hu, Structure-based out-of-distribution (OOD) materials property prediction: a benchmark study, arXiv, 2024, preprint, arXiv:240108032, DOI:10.48550/arXiv.2401.08032.
- H. Yu, M. Giantomassi, G. Materzanini and G. M. Rignanese, Systematic assessment of various universal machine-learning interatomic potentials, arXiv, 2024, preprint, arXiv:240305729, DOI:10.48550/arXiv.2403.05729.
- K. Li, D. Persaud, K. Choudhary, B. DeCost, M. Greenwood and J. Hattrick-Simpers, Exploiting redundancy in large materials datasets for efficient machine learning with less data, Nat. Commun., 2023, 14(1), 7283 CrossRef CAS PubMed.
- A. N. Rubungo, C. Arnold, B. P. Rand and A. B. Dieng, LLM-Prop: Predicting Physical And Electronic Properties Of Crystalline Solids From Their Text Descriptions, arXiv, 2023, preprint, arXiv:231014029, DOI:10.48550/arXiv.2310.14029.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi and A. R. Hight Walker, et al., The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6(1), 173 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards and S. Dacek, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1(1), 1–7 Search PubMed.
- M. Wang, D. Zheng, Z. Ye, Q. Gan, M. Li and X. Song, et al., Deep Graph Library: A Graph-Centric, Highly-Performant Package for Graph Neural Networks, arXiv, 2019, preprint, arXiv:190901315, DOI:10.48550/arXiv.1909.01315.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00064a |
| This journal is © The Royal Society of Chemistry 2024 |