Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Inverse design of metal–organic frameworks for direct air capture of CO2via deep reinforcement learning†
Hyunsoo
Park‡
 ab,
Sauradeep
Majumdar‡
ab,
Sauradeep
Majumdar‡
 b,
Xiaoqi
Zhang
b,
Xiaoqi
Zhang
 b,
Jihan
Kim
b,
Jihan
Kim
 *a and
Berend
Smit
*a and
Berend
Smit
 *b
*b
aDepartment of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: jihankim@kaist.ac.kr
bLaboratory of Molecular Simulation (LSMO), Institut des Sciences et Ingénierie Chimiques, Ecole Polytechnique Fédérale de Lausanne (EPFL), Sion, Valais, Switzerland. E-mail: berend.smit@epfl.ch
First published on 12th March 2024
Abstract
The combination of several interesting characteristics makes metal–organic frameworks (MOFs) a highly sought-after class of nanomaterials for a broad range of applications like gas storage and separation, catalysis, drug delivery, and so on. However, the ever-expanding and nearly infinite chemical space of MOFs makes it extremely challenging to identify the most optimal materials for a given application. In this work, we present a novel approach using deep reinforcement learning for the inverse design of MOFs, our motivation being designing promising materials for the important environmental application of direct air capture of CO2 (DAC). We demonstrate that our reinforcement learning framework can successfully design MOFs with critical characteristics important for DAC. The reinforcement learning framework uniquely integrates two separate predictive models within its structure, uncovering two distinct subspaces in the MOF chemical space: one with high CO2 heat of adsorption and the other with preferential adsorption of CO2 from humid air, with few structures having both characteristics. Our model can thus serve as an essential tool for the rational design and discovery of materials for different target properties and applications.
1. Introduction
Metal–organic frameworks (MOFs) are a class of crystalline nanomaterials known for their high internal surface areas, tunable chemistries, and wide range of pore sizes.1 The variety of features makes MOFs promising materials for a wide range of applications like carbon capture,2 methane storage,3 hydrogen storage,4 photocatalysis,5 drug delivery,6 conductivity,7 and so on. To date, there are more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experimentally reported MOF structures8–10 and millions of MOF structures that have been predicted in silico.2,11–18
000 experimentally reported MOF structures8–10 and millions of MOF structures that have been predicted in silico.2,11–18
From the perspective of material chemists, the holy grail is to design the most promising materials for a given application.19 Currently, the most commonly used strategy is to find the best materials through brute force screening of these materials library. However, as we are interested in a small subset of top-performing materials, most of the effort in these brute-force methods is spent on computing properties of those materials that are not interesting. As the number of structures in these databases has grown significantly, several groups have started taking a different approach in searching more efficiently within this infinite chemical space of MOFs, using methods such as diversity-driven searches,16,17,20 and active learning based searches.19,21
An alternative way to explore this enormous chemical design space is through the inverse design of materials possessing desired properties.22,23 The chemical design space of MOFs involves combining metal clusters and organic linkers with topologies, which gives us a highly complex design space. This complexity has led to a limited number of studies focusing on the inverse design of MOFs. One approach to tackle this challenge is a top-down strategy that employs an evolutionary algorithm,15,24–27 utilizing predefined molecular building blocks and topologies derived from existing MOF databases, such as the CoRE MOF database.9 Alternatively, a joint top-down/bottom-up approach can be adopted to construct MOFs with novel molecular building blocks. Yao et al.28 developed a deep-generative model with variational autoencoders for the inverse design of MOFs with desired properties by optimizing the latent space. The latent space optimization involved a reticular framework representation that incorporated a combination of SELFIES (for organic linkers) and categorical variables (for metal clusters and topologies). However, optimizing the materials with non-convex objective functions in such a high dimensional latent space can be challenging,29 which may introduce the risk of generating invalid organic linkers.
In this context, deep reinforcement learning offers a promising solution to address the limitations associated with the joint top-down/bottom-up approach and capitalize on its advantages in generating novel MOFs with desired properties. The introduction of novel topologies and metal clusters is restricted in practical and chemical aspects when generating MOFs due to constraints such as the complex chemistry associated with metal clusters. Hence, the de novo design of organic linkers is crucial for effectively navigating the intricate and high-dimensional landscape of MOF design space. Deep reinforcement learning is particularly adept at optimizing string representations like SMILES and SELFIES for organic linkers by leveraging existing knowledge. This is a distinct advantage of reinforcement learning over methods like Bayesian optimization and genetic algorithms, which might struggle with the nuanced optimization of string-based chemical structures. Furthermore, the inherent capacity of reinforcement learning algorithms to navigate the trade-off between exploration and exploitation within chemical domains positions them as particularly advantageous for addressing the inverse design challenges associated with complex crystalline architectures such as MOFs. This capability provides a distinct advantage over alternative methods such as VAEs. In the field of de novo drug design,30–32 this approach allows learning how to design molecules that maximize a reward function using deep learning models such as recurrent neural networks and generative adversarial networks.
Apart from molecule generation, Pan et al.33 demonstrated that the reinforcement learning approach could be extended to inorganic materials such as metal oxide. However, the complex crystal structure of MOFs, which typically contain more than 100 atoms per unit cell, presents a significant challenge for this approach. In this work, we propose a deep reinforcement learning framework designed for large crystalline materials such as MOFs, which can tackle the complexity of crystalline systems through reinforcement learning.
We apply this reinforcement learning framework to design MOFs for direct air capture (DAC). DAC has been developed to reduce the CO2 concentration in the atmosphere. As we have a large risk of overshooting these CO2 levels, DAC has become a very active area of research.34–36 The main challenge of DAC is the low concentration of CO2 in the air (compared to flue gas), and at such an extremely dilute concentration (∼400 ppm), one needs a material with a high CO2 enthalpy.36–38 Currently, a class of materials known as chemisorbents is used industrially to tackle this challenge. Chemisorbents can bind CO2 very strongly, which is reflected in its high heat of adsorption that can go up to 100 kJ mol−1.39,40 However, very high heat of adsorption could also lead to increased difficulty and costs in regenerating the materials. Using physisorbents for DAC could have the advantage of lower regeneration costs. Yet, one still needs them to have a sufficiently strong binding to compensate for the low concentration of CO2 in the air.
Although there is no agreed value of the CO2 heat of adsorption in literature to demarcate physisorbents from chemisorbents, the former usually have a CO2 heat of adsorption of <40 kJ mol−1. There have been reports, though, of few physisorbent structures having CO2 heat of adsorption higher than 50 kJ mol−1.41 Based on the heat of adsorption, Findley et al.37 computationally screened the CoRE2014 MOF database and several classes of zeolites to search for the best physisorbent MOF for DAC. However, from their analysis, they concluded that the materials they considered were not viable for DAC. This overall scenario motivated us to explore an important scientific question—can we design a library of physisorbent MOFs specifically for DAC?
The main objectives of this work are thus: (1) to illustrate the use of a reinforcement learning framework to inverse-design physisorbent MOFs with desired properties; (2) to highlight the use of these inverse-designed MOFs for an extremely important application like DAC. It is important to note that when we refer to physisorption, we refer to systems in which the binding does not involve charge transfer. Charge transfer is not something that we can model with our classical force fields, and, therefore, we do not include the amines interacting with CO2 through chemisorption in our screening study.
We first show the working of our reinforcement learning framework by inverse designing MOFs with CO2 heat of adsorption higher than 40 kJ mol−1. To make this design even more challenging, we must consider the effect of H2O. Depending on the climate, there are different levels of water vapor in the atmosphere, and most materials that strongly bind CO2 have a higher affinity for H2O. Hence, we must design MOFs that perform well in humid conditions.36 And for this reason, our second design criterion is that the material prefers CO2 above H2O (i.e., CO2/H2O selectivity to be higher than 1). The successful inverse design of MOFs for a challenging application like DAC could significantly advance the rational design and discovery of materials for a wide range of applications.
2. Results
2.1 Data representation of MOFs for inverse design
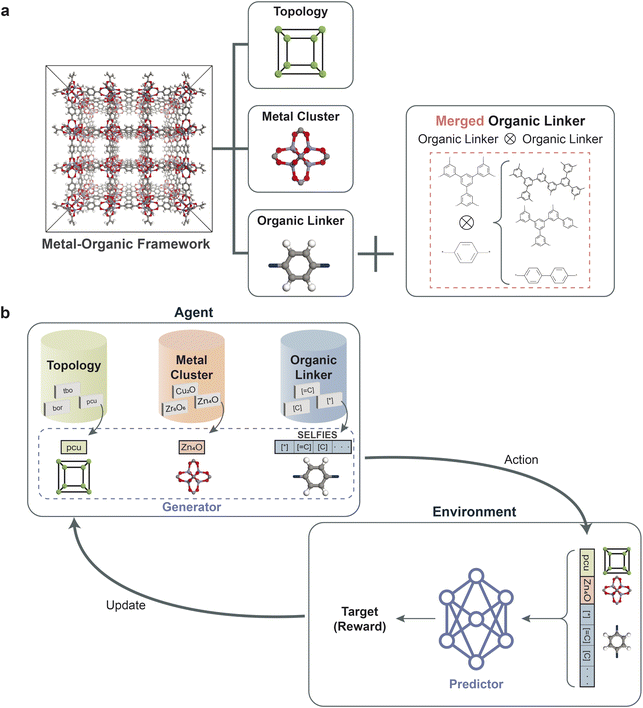
The data representation of MOFs for inverse design is crucial for successfully developing our reinforcement learning framework, as illustrated in Fig. 1a. A unique combination of metal clusters, organic linkers, and topologies represents each MOF structure in our database. Given that metal clusters in MOFs usually have constraints due to complex chemistry (such as oxidation states), we featurized the metal clusters and topologies (represented in RCSR using three-letter codes) with categorical variables. For the representation of organic linkers, a string representation known as SELFIES,42 which ensures the basic chemical rules such as SMILES, was adopted. The SELFIES representation was adopted because it has been shown to outperform SMILES within generative models such as VAE,43 GAN44 by generating more diverse and valid molecules. We used the building blocks and topologies of PORMAKE,15 where there are libraries of building blocks (from the CoRE MOF database9) and topologies (from the Reticular Chemistry Structure Resource (RCSR) Database45). Additional details of the MOF structure representation are provided in the Methods section. Moreover, PORMAKE was employed to construct MOF structures from the representation, enabling the computation of the properties for the generated MOF representations through simulation tools.2.2 Reinforcement learning framework
The overall schematic of the reinforcement learning framework is depicted in Fig. 1b, which comprises two key components: an agent and an environment. The agent, which serves as the generator, takes action by creating a data representation of a new MOF structure. At the same time, the predictor evaluates the action as the environment by predicting the property of the new MOF representation. The predictor, as a surrogate model, enables faster estimation of crucial properties, aiding in the efficient screening and iteration of structures during the reinforcement learning phase. This approach is key in high-throughput studies for the manageable and timely evaluation of a large number of generated structures. Based on the prediction, a reward is returned to update the agent for generating MOF structures to maximize the reward. The objective of reinforcement learning is to find the weights of the agent that maximize the expected return obtained from the environment. The details of the framework are provided in the Methods section.2.3 Results of reinforcement learning
We trained the reinforcement learning framework using the pre-training generator and predictors, with the aim of generating novel MOFs that exhibit high CO2 heat of adsorption and CO2/H2O selectivity. The performance of the optimized generator by the reinforcement learning algorithm was evaluated using three metrics: validity, scaffold, and uniqueness. The validity metric evaluates if the generator can generate MOFs which (1) match connection points of metal clusters and organic linkers for a given topology and (2) produce chemically valid organic linkers. To evaluate (2), we converted the generated SELFIES to canonical SMILES using the RDkit sanitizer. The scaffold metric measures whether the generated organic linkers contain a batch of scaffolds used as encoder inputs. Finally, the uniqueness metric assesses the proportion of distinct organic linkers generated. The performance was tested on a test set of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data used during the pre-training stage, and the performance was evaluated using metrics and rewards, as summarized in Table 1.
000 data used during the pre-training stage, and the performance was evaluated using metrics and rewards, as summarized in Table 1.
| Metric | CO2 heat of adsorption | CO2/H2O selectivity | ||||||
|---|---|---|---|---|---|---|---|---|
| Scratch | Round 1 | Round 2 | Round 3 | Scratch | Round 1 | Round 2 | Round 3 | |
| Validity | 0.69 | 0.69 | 0.70 | 0.68 | 0.69 | 0.72 | 0.73 | 0.71 |
| Scaffold | 0.96 | 0.75 | 0.79 | 0.61 | 0.96 | 0.60 | 0.62 | 0.68 |
| Uniqueness | 0.79 | 0.61 | 0.64 | 0.56 | 0.79 | 0.58 | 0.58 | 0.64 |
| Target | 19.16 | 26.44 | 28.52 | 33.52 | 1.74 | 3.38 | 3.64 | 4.14 |
| Reward | 0.32 | 0.44 | 0.48 | 0.56 | 0.17 | 0.34 | 0.36 | 0.41 |
As we have a relatively small number of structures with the desired properties, we carried out the reinforcement learning for three rounds. After each round, we used the top-performing MOFs to retrain the predictors for the next round. More details on the training of the reinforcement learning framework are provided in the Methods section. ESI Fig. S1† shows the parity plots of the predictors for each round. In Fig. 3, the property distributions of MOFs generated by the pre-training generator (i.e., scratch) and generators optimized by reinforcement learning for three rounds are illustrated, where the estimated property values are based on the predictors. Notably, we observe that the average target values increase as the rounds progress, and also, the overall distribution of our target properties shifts towards the desired high values. This also means that with each passing round, we get more structures that meet our target requirements. To the best of our knowledge, some of our reinforced structures have the highest calculated CO2 heat of adsorption and CO2/H2O selectivity values ever reported for physisorbent MOFs (see Table 2). This, thus, indicates the success of the reinforcement learning approach in optimizing the generator to produce MOFs with improved target properties. ESI Fig. S3† reveals that the property distribution improves significantly as training progresses within a particular round. Table 1 shows that the overall scaffold metric decreased after optimization compared to scratch because the optimized generator generated organic linkers without the scaffolds used as input to maximize rewards. After optimization, the metric for uniqueness also exhibits a decrease, suggesting that the generator favors generating organic linkers with desirable properties. Based on the predictors' estimations, the most frequently observed topologies, metal clusters, and organic linkers for rounds 1, 2, and 3 are presented in ESI Fig. S5, S6, and S7,† respectively. Also, ESI Fig. S4† show the attention scores of topology, metal cluster, and organic linker for the two targets. These attention scores have been computed using the attention rollout method.50 We find that the metal cluster has the highest attention score for both the targets, and this result agrees with previous findings in the literature regarding the role of metal clusters in low-pressure CO2 capture applications.16,20
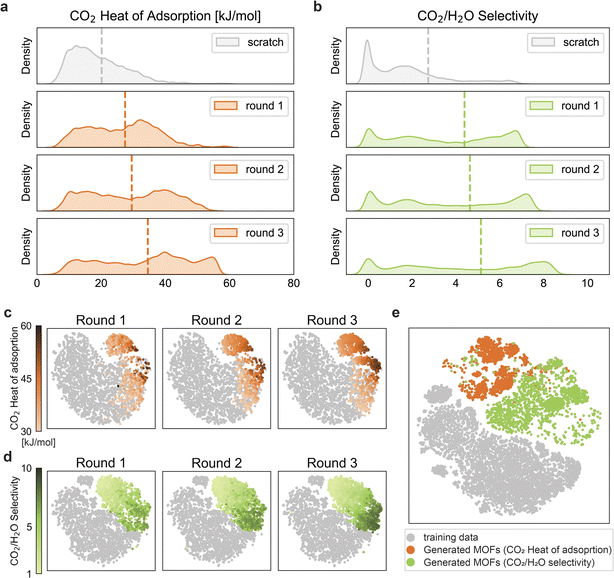 | ||
Fig. 3 Comparison of the distributions of (a) CO2 heat of adsorption and (b) CO2/H2O selectivity for scratch and optimized MOFs based on the predictor's estimated values. The scratch distributions show the property distributions of the MOFs generated by the pre-training generator before being optimized by the reinforcement learning algorithm. The optimized distributions show the property distributions of the MOFs generated by the generator after being optimized by the reinforcement learning algorithm. After each round, the final top-performing MOFs of that round were selected and added to the next round for retraining the predictor. And this updated predictor was then used in the training of the reinforcement learning for the next round. The evolution of the generated structures for (c) CO2 heat of adsorption and (d) CO2/H2O selectivity in the chemical space of MOFs. The gray points in (c) and (d) represent the training structures for CO2 heat of adsorption (∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and CO2/H2O selectivity (∼19 000) and CO2/H2O selectivity (∼19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) respectively. Orange points in (c) represent the generated structures for CO2 heat of adsorption (having values >30 kJ mol−1), green points in (d) represent the generated structures for CO2/H2O selectivity (having values >1). The color code represents the respective target properties as obtained from molecular simulations. Further details on the number of generated structures in each round are provided in ESI Fig. S2.† (e) The mapping of the overlapping training (∼15 000) respectively. Orange points in (c) represent the generated structures for CO2 heat of adsorption (having values >30 kJ mol−1), green points in (d) represent the generated structures for CO2/H2O selectivity (having values >1). The color code represents the respective target properties as obtained from molecular simulations. Further details on the number of generated structures in each round are provided in ESI Fig. S2.† (e) The mapping of the overlapping training (∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and generated structures from all three rounds for the two targets. 000) and generated structures from all three rounds for the two targets. | ||
| Name | CO2 heat of adsorption (kJ mol−1) | CO2 uptake, 400 ppm (mmol g−1) | CO2/H2O selectivity | Ref. |
|---|---|---|---|---|
| ARAHIM02_clean | 57.26 | 2.44 | 0.0012 | 41 |
| RUFMUA_clean | 56.65 | 3.19 | 0.025 | 37 |
| CDLGLU01_clean | 60.06 | 4.36 | 0.003 | 37 |
| AGESIP_clean | 41.17 | 0.016 | 2.33 | 37 |
| PEXBIF_clean | 39.33 | 0.01 | 9.67 | 37 |
| v1+tfz-d + N692 + 2546 | 39.05 | 0.005 | 7.37 | This work |
| v0+tfz-d + N131 + 290 | 59.72 | 4.59 | 2.79 × 10−6 | This work |
| v1+hex + N262 + 1184 | 29.15 | 33.4 × 10−4 | 7.91 | This work |
2.4 Chemical space analysis of the MOFs
We performed a chemical space analysis of the training and generated structures for the two targets, with t-distributed stochastic neighbor embedding (t-SNE).51 To visualize the evolution of the generated structures in the same reduced dimension space, we used the round 3 predictor of the corresponding target to obtain the latent vectors for training structures and generated structures of all the three rounds in Fig. 3c and d. Generated structures from three rounds with the heat of adsorption larger than 30 kJ mol−1 are highlighted in Fig. 3c. The ratio of structures with high heat of adsorption values (represented by darker orange points) over the generated structures increases with rounds, which is in the same trend of right-shifting of the peak in Fig. 3a, even though some structures are discarded during the molecular simulations. A similar plot for CO2/H2O selectivity (for structures having values greater than 1) is shown in Fig. 3d. Similarly, the evolution in Fig. 3d is consistent with Fig. 3b.In Fig. 3e, we projected the structures for both targets in the same chemical space to investigate if there are structures that satisfy both criteria. We gathered the overlapping training structures and all generated structures for the two targets and obtained their latent vectors by concatenating representations from the two third-round predictors. Fig. 3e further highlights the two separate subspaces occupied by these generated structures for the two targets. This corroborates the fact that structures having high CO2 heat of adsorption have characteristics quite different from structures having high CO2/H2O selectivity. Thus, they occupy relatively different subspaces in the MOF chemical space, with a small overlap. This fact is explained in more detail in the Discussion section. It is important to note that we still managed to generate a few structures simultaneously satisfying both targets (represented by the overlapping orange and green points).
2.5 Feasibility tests for the generated top-performing MOFs
To ensure that the structures generated from our reinforcement learning framework are reasonable, we employed different structure feasibility tests to narrow down the ideal MOF candidates for DAC (the workflows for the same are summarized in ESI Fig. S2†). For each of the three rounds, first, from the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 test set, the valid MOFs (the ones satisfying the validity metric) generated by the optimized generators with CO2 heat of adsorption higher than 30 kJ mol−1 and CO2/H2O selectivity greater than 1 were selected. Since few structures have their predicted CO2 heat of adsorption higher than 40 kJ mol−1, we went ahead with 30 kJ mol−1 as a temporary threshold so as to obtain a higher number of structures for the training of the subsequent rounds of reinforcement learning. Then, to estimate the synthesizability of the organic linkers, we computed the synthetic accessibility (SA) score.52 The SA score is based on molecular complexity; molecules with a low SA score are less complex and are expected to have an easier synthesis route compared to those more complex molecules with a high SA score. The MOFs with an SA score of organic linkers higher than 6 were dismissed.53 In addition, the number of generated structures was restricted through the topological root mean squared deviation (RMSD) of the atomic positions between the building block node vectors and the target topology node vectors.15 Lower topological RMSD values indicate that the strain between the two vectors is low, and the resultant MOF structure is more stable. Given that the MOFs created by the PORMAKE are typically feasible when the topological RMSD is lower than 0.3,15 the same constraint was adopted. Apart from these, the generated MOFs with more than 3000 atoms and higher than 60 Å cell lengths were also dismissed to avoid calculations on very large structures. Structure optimization and charge generation were then carried out to obtain further reasonable structures. The generated structures that passed all the above tests went through molecular simulations to estimate the respective “true” target values. The details of the molecular simulations are provided in the Methods section. Finally, after all the tests, we obtained 409/497/999 structures with CO2 heat of adsorption higher than 40 kJ mol−1 and 2215/2304/2426 structures with CO2/H2O selectivity higher than 1 based on RASPA simulations, in round 1/round 2/round 3, respectively.
000 test set, the valid MOFs (the ones satisfying the validity metric) generated by the optimized generators with CO2 heat of adsorption higher than 30 kJ mol−1 and CO2/H2O selectivity greater than 1 were selected. Since few structures have their predicted CO2 heat of adsorption higher than 40 kJ mol−1, we went ahead with 30 kJ mol−1 as a temporary threshold so as to obtain a higher number of structures for the training of the subsequent rounds of reinforcement learning. Then, to estimate the synthesizability of the organic linkers, we computed the synthetic accessibility (SA) score.52 The SA score is based on molecular complexity; molecules with a low SA score are less complex and are expected to have an easier synthesis route compared to those more complex molecules with a high SA score. The MOFs with an SA score of organic linkers higher than 6 were dismissed.53 In addition, the number of generated structures was restricted through the topological root mean squared deviation (RMSD) of the atomic positions between the building block node vectors and the target topology node vectors.15 Lower topological RMSD values indicate that the strain between the two vectors is low, and the resultant MOF structure is more stable. Given that the MOFs created by the PORMAKE are typically feasible when the topological RMSD is lower than 0.3,15 the same constraint was adopted. Apart from these, the generated MOFs with more than 3000 atoms and higher than 60 Å cell lengths were also dismissed to avoid calculations on very large structures. Structure optimization and charge generation were then carried out to obtain further reasonable structures. The generated structures that passed all the above tests went through molecular simulations to estimate the respective “true” target values. The details of the molecular simulations are provided in the Methods section. Finally, after all the tests, we obtained 409/497/999 structures with CO2 heat of adsorption higher than 40 kJ mol−1 and 2215/2304/2426 structures with CO2/H2O selectivity higher than 1 based on RASPA simulations, in round 1/round 2/round 3, respectively.
3. Discussion
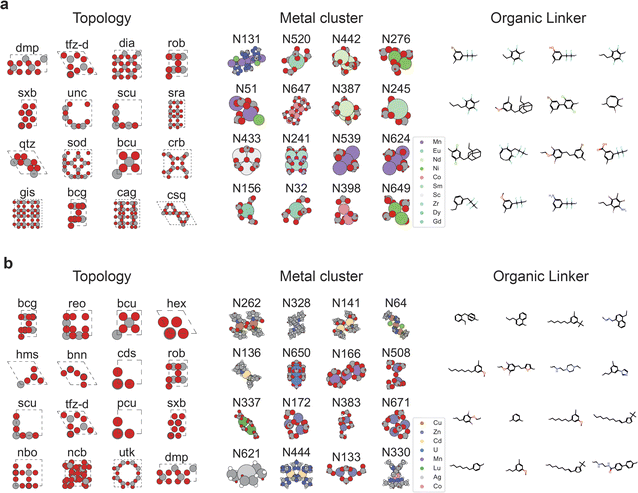
From a material chemist's perspective, it is interesting to know what makes a material good for DAC. Or in other words, what are the features or the genes of the top-performing materials for DAC? Our top-performing candidates' topologies, metal clusters, and organic linkers are shown in Fig. 4. When it comes to CO2 heat of adsorption, we find that the top-performing MOFs mostly contain the metal clusters Mn-based N131 and Eu-based N520 (see Fig. 4; the naming of all the metal clusters can be found in the PORMAKE paper.15). The Mn-based N131 cluster has an open metal site that strongly attracts the CO2 molecules towards the metal atom.54 Many structures built from this cluster have a CO2 heat of adsorption value higher than 40 kJ mol−1. One example of such a structure is shown in Fig. 5a. Other metal clusters within the high-performing MOFs include lanthanide metals (i.e., Nd, Sm, Dy) and transition metals (i.e., Ni, Co, and Zr). Apart from the metal cluster, the organic linkers of the top-performing MOFs have more abundant branches (i.e., functional groups) such as F, Cl, Br, and NH2. The top-performing candidates' topologies, metal clusters, and organic linkers for round 1 and 2 are summarized in ESI Fig. S8 and S9,† respectively.The top-performing MOFs with respect to the high selectivity of CO2/H2O, however, have different characteristics from the ones having high CO2 heat of adsorption, as shown in Fig. 4b. The metal clusters include metals frequently used for synthesizing MOFs such as Cu, Zn, Cd. In particular, metal clusters Cu-based N262,55 and Zn-based N328 (ref. 56) appear most frequently. Most metal nodes having open metal sites (like metal node N131) attract H2O more than CO2, and therefore the MOFs consisting of those metal nodes have low CO2/H2O selectivity. Also, the generated organic linkers of the top-performing MOFs, in this case, rarely include functional groups such as F, Cl, Br, NH2. This shows that it is indeed a challenge to find a MOF having a good balance between CO2 heat of adsorption and CO2/H2O selectivity.37
In our model, the topology of a MOF is described by the three-letter codes as defined in RCSR.45 The topology guides the underlying network connectivity of the metal nodes and organic linkers in a MOF. From Fig. 4a., we find that certain topologies such as dmp and tfz-d primarily dominate in structures with high CO2 heat of adsorption. If we then look into the features of the MOFs for high CO2/H2O selectivity, we find the presence of a different set of dominant topologies such as bcg and reo. Furthermore, from the attention score plots (see ESI Fig. S4†) we find that our model also considers topology while making its decision on property prediction. However, it is to be noted that the surface characteristics of a MOF (like pore diameters, surface areas, and other pore geometry characteristics) are determined by the combination of the topology along with the node and linker used to construct the MOF. At very low concentrations of CO2 such as in DAC, the chemistry of the MOF (type of metal nodes, organic linkers) usually plays a much stronger role than pore geometry characteristics in determining the CO2 adsorption.16,20,57
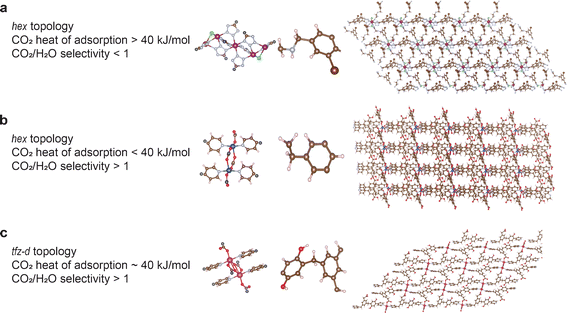
Fig. 5 highlights the structures of some of the top-performing MOFs for DAC application (inverse) designed in this work. Structure (a) has a high CO2 heat of adsorption (∼62 kJ mol−1) but a low CO2/H2O selectivity (<1) whereas structure (b) has a high CO2/H2O selectivity (>1) but a low CO2 heat of adsorption (∼29 kJ mol−1). And structure (c) has both high CO2/H2O selectivity (>1) and moderately high CO2 heat of adsorption (∼40 kJ mol−1).
In addition, we have listed some experimental MOFs studied for DAC from reported literature37,41 and some top-performing ones from our work in Table 2. The experimental cif files were obtained from the CoRE2019 MOF database9 as treated in our previous work.20 The structures in this table have been selected with the aim of covering a range of values for the different metrics. We find that for each of the considered metrics, we have managed to generate structures that compete strongly with the reported ones, with a few of our structures performing well across all the metrics. It is also important to note that structures having high CO2 heat of adsorption also tend to have high CO2 uptake at 400 ppm.
In a broader context, it is also interesting to note that all of the three categories of structures from Fig. 5 and Table 2 can be promising candidates for DAC, depending on the environment in which they are used. For example, if a particular industrial process configuration can have a dehumidifier unit before the adsorption step, then structure 5(a) can be potentially interesting despite its low CO2/H2O selectivity. This structure can also be promising in regions with very low water vapor content in the atmosphere. The stronger binding of CO2 to the MOF would become the more dominating factor in choosing this material. On the other hand, if there is no dehumidifier unit, and in regions with very high water vapor content in the atmosphere, structure 5(b) can be an interesting choice because of its preferential adsorption of CO2 in humid conditions. Structure 5(c), satisfying both requirements, is likely to be an interesting candidate in both scenarios: with and without humidity. Thus, it will be interesting to evaluate these materials one step further, on a process level, to get even more insights into these materials' performance and we are looking into it as future work.
It is important to note here that our reinforcement learning framework needs training data for at least ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials, which requires us to trade between computational expense and accuracy (i.e., Universal Force Field (UFF) and extended charge equilibration methods (EQeq)). The main aim of this article is to demonstrate that reinforcement learning can give us a library of structures with the desired properties. This illustration is, of course, independent of the details of the force field. However, it is important to ensure the accuracy of these predictions before giving a follow-up of this work. But as this only needs to be done for the top-performing structures, one can use, for example, DFT-derived charges.
000 materials, which requires us to trade between computational expense and accuracy (i.e., Universal Force Field (UFF) and extended charge equilibration methods (EQeq)). The main aim of this article is to demonstrate that reinforcement learning can give us a library of structures with the desired properties. This illustration is, of course, independent of the details of the force field. However, it is important to ensure the accuracy of these predictions before giving a follow-up of this work. But as this only needs to be done for the top-performing structures, one can use, for example, DFT-derived charges.
4. Conclusion
In this work, we have developed a deep reinforcement learning framework to inverse design MOFs. We illustrate this approach to design MOFs with important characteristics for direct air capture (DAC) of CO2. We successfully (inverse) designed a set of materials that have a high affinity towards CO2 (CO2 heat of adsorption >40 kJ mol−1). In addition, we generated a set of materials that preferentially adsorb CO2 from humid air. Subsequent analysis of the chemical design space shows that the top-performing structures populated two separate subspaces concerning the two target properties. Yet, few of our structures satisfy both requirements. We show that the top-performing structures generated in this work compete strongly against the top-performing MOFs reported in the literature for DAC, thereby providing the research community with more potential options for further investigation.The heat of adsorption is an important proxy for performance in a DAC process; it allows us to eliminate really poor structures and identify some of the most promising ones, thereby narrowing down the enormous MOF chemical search space effectively.
To gain further insights into the materials' performance in industrial setups, the next step of this work would be to evaluate the top-performing materials in a more detailed DAC process engineering design.58
5. Methods
5.1 Details of MOF structure representation
The building blocks from PORMAKE are composed of vertices (i.e., abstractions with more than two connection points) and edges (i.e., abstractions with two connection points).15 In this work, however, they were modified more intuitively into metal clusters and organic linkers depending on the presence of metal atoms in the building blocks. Thereby, 486 vertices containing metal atoms were used for the metal clusters. For organic linkers, there are 103 vertices and 175 edges that do not contain metal atoms. Apart from building blocks, we used 97 topologies extracted from the CoREMOF database by MOFkey,59 which is summarized in ESI Note S1.† It is important to note that data augmentation of the organic linkers is required to train with deep generative models, given the insufficient number of organic linkers. Hence, augmentation was implemented by merging the organic linkers, where the connection points of organic linkers were replaced with the other organic linkers. To this end, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 merged organic linkers were generated, and their validity was examined by the RDkit sanitizer.60 It is to be noted that these data representations can be used to reconstruct the MOF structures using PORMAKE.
642 merged organic linkers were generated, and their validity was examined by the RDkit sanitizer.60 It is to be noted that these data representations can be used to reconstruct the MOF structures using PORMAKE.
5.2 Computational details for molecular simulations
All structures for pre-training were optimized using the Universal Forcefield (UFF)61 with LAMMPS62 that can be implemented with multi-core processors, thereby facilitating calculations with a large number of structures. The input files for the same were generated using lammps_interface.63,64 The number of MOF structures generated via reinforcement learning was much less than the number used for pre-training, and these were optimized using the Universal Forcefield (UFF)61 as implemented in the Forcite Module of Materials Studio 2019.65 The EQEq (extended charge equilibration) method66,67 was used to generate the partial charges of the framework atoms of the MOFs. The lowest common oxidation states of the elements were chosen as their charge centers.16,20,68The cif files of the experimental structures used for comparison in Table 2 were obtained from the work of Moosavi et al.,20 where the partial charges were also generated using the EQEq method.
The Henry coefficient and heat of adsorption at infinite dilution, for CO2 and H2O, were computed using Widom's test particle insertion algorithm.69 All of the calculations were performed at 298.15 K using RASPA.70 We computed the CO2/H2O Henry's selectivity as the ratio of the respective Henry coefficients:
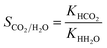 | (1) |
The CO2 uptake at DAC conditions (400 ppm, 1 bar, 298.15 K) was derived from the CO2 henry coefficient:
| uptakeCO2 = KHCO2 × p | (2) |
To prevent the insertion of gas molecules in inaccessible pores of the MOF during Monte Carlo simulations, artificial blocking is necessary to avoid overestimation of adsorption values.71,72 For this purpose, blocking spheres were calculated using the Zeo++ software.73
The framework atoms of the MOF structures were described by UFF.61 CO2 and H2O molecules were described by the TraPPE forcefield74 and TIP4P/2005 forcefield respectively.75 The gas–framework interactions were modeled using Lennard Jones potential, truncated at 12 Å, with tail corrections.76 The Lennard-Jones interactions between dissimilar atoms were approximated using Lorentz–Berthelot rules.77 The coulombic electrostatic interactions were computed using Ewald summation. The DAC properties for the experimental MOF structures were obtained using the same simulation protocol as mentioned above.
The RASPA simulations were employed to compute the properties of the initial training dataset for the predictors and to evaluate the top-performing MOFs predicted by the predictors.
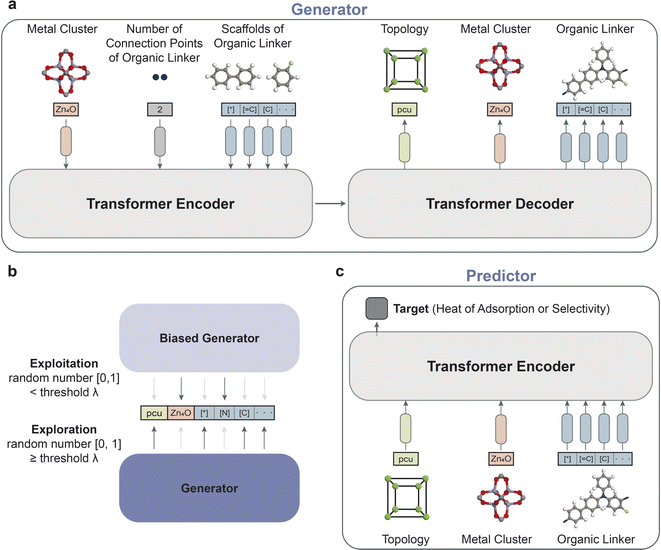
5.3 Details of reinforcement learning framework
In our reinforcement learning framework, the generator serves as the agent with the task of generating novel MOF representations. Each of these representations is defined as a sequence of state S with a maximum length T = 128, encapsulating the MOF structure. Specifically, a state S in our context is defined as S(topology, metalcluster, organiclinker), where the topology and metal cluster are categorical variables, and the organic linker is represented by a SELFIES string, limited to 126 characters to ensure the total length does not exceed T. At each step t, (0 < t < T), the generator takes state s1:t in previous steps as inputs and then determines probability distribution p of state st. Therefore, the state st is determined by sampling from the probability distribution of the previous step t − 1. At t = 0 and t = 1, the generator respectively determines topologies and metal clusters that are categorical variables. Then, it generates sequences of SELFIES for organic linker during 1 < t ≤ T. The predictor takes the data representations created by the generator as inputs and estimates the expected reward r(st). To refine the generator's performance in generating MOF representations that maximize the expected reward, the weights of the generator θ are updated. We employ a policy gradient method (REINFORCE algorithm)78 aimed at maximizing the expected cumulative reward (see Section 5 5.5). The policy's objective function, parameterized by θ, is expressed as: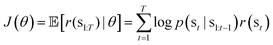 | (3) |
Regarding the initial state and the exploration strategy, at the commencement of training, θ is initialized using the weights from a pre-trained model of the generator to leverage prior knowledge. As mentioned in the ‘Exploration strategy’ section, we employed diverges from the epsilon-greedy method by incorporating a dual-generator approach. One generator remains static (biased) to exploit known good strategies, while the other is trainable and tasked with exploring the state space. The exploration is governed by a stochastic process that decides whether to exploit or explore at each step, thereby balancing between the two for efficient learning. This approach allows for more directed exploration and potentially faster convergence by leveraging the strengths of both exploitation and exploration.
5.4 Training details for pre-training
In the pre-training step, a dataset comprising 646![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 MOFs, generated using building blocks from the PORMAKE database, was utilized for the generator. Since these building blocks originate from the CoRE MOF database, this approach enables the generator to learn the patterns and chemistry inherent in existing MOFs. For organic linkers, we initially created a set of 30
907 MOFs, generated using building blocks from the PORMAKE database, was utilized for the generator. Since these building blocks originate from the CoRE MOF database, this approach enables the generator to learn the patterns and chemistry inherent in existing MOFs. For organic linkers, we initially created a set of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 merged organic linkers, each validated using the RDKit sanitizer. This initial step is represented in Fig. 1a, where we show examples of small linker fragments used as building blocks. These fragments were sourced from the PORMAKE database and then merged to form the comprehensive set of linkers. In the second step, the merged 30
642 merged organic linkers, each validated using the RDKit sanitizer. This initial step is represented in Fig. 1a, where we show examples of small linker fragments used as building blocks. These fragments were sourced from the PORMAKE database and then merged to form the comprehensive set of linkers. In the second step, the merged 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 organic linkers were decomposed into scaffold fragments with the BRICS algorithm, which allows the splitting of molecules into chemically semantic fragments. The batches of scaffolds were employed to train generators in the pre-training stage. If the decomposed fragments by the BRICS algorithm were a subset of other fragments for each organic linker, the subsets were dismissed. And the maximum number of scaffold fragments was set to four. The smaller fragments were omitted if a molecule was decomposed into more than four scaffold fragments. The scaffold fragments were randomly combined and joined in SELFIES to build a batch of scaffolds. Finally, a dataset of 1
642 organic linkers were decomposed into scaffold fragments with the BRICS algorithm, which allows the splitting of molecules into chemically semantic fragments. The batches of scaffolds were employed to train generators in the pre-training stage. If the decomposed fragments by the BRICS algorithm were a subset of other fragments for each organic linker, the subsets were dismissed. And the maximum number of scaffold fragments was set to four. The smaller fragments were omitted if a molecule was decomposed into more than four scaffold fragments. The scaffold fragments were randomly combined and joined in SELFIES to build a batch of scaffolds. Finally, a dataset of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540
540![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889/385
889/385![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 223/10
223/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (train/validation/test) was created for the generator. For the predictor, an additional set of ∼35
000 (train/validation/test) was created for the generator. For the predictor, an additional set of ∼35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs were generated using the PORMAKE database, following the same methodology as the generator. After conducting the Widom insertion simulations with RASPA, a total of ∼33
000 MOFs were generated using the PORMAKE database, following the same methodology as the generator. After conducting the Widom insertion simulations with RASPA, a total of ∼33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOF structures were utilized for training the predictor for CO2 heat of adsorption, and ∼24
000 MOF structures were utilized for training the predictor for CO2 heat of adsorption, and ∼24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures were used for the CO2/H2O selectivity predictor. Subsequently, these datasets were split in an 8
000 structures were used for the CO2/H2O selectivity predictor. Subsequently, these datasets were split in an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for training, validation, and testing sets, respectively. Comprehensive information regarding the dataset used for training the predictor, including specific quantities and their detailed distribution, is summarized in ESI Table S1.†
1 ratio for training, validation, and testing sets, respectively. Comprehensive information regarding the dataset used for training the predictor, including specific quantities and their detailed distribution, is summarized in ESI Table S1.†
The architectures of the generator and predictor were derived from the original transformer paper.46 For the generator, the transformer encoder and decoder consist of 3 layers, 4 heads, and a hidden size of 256. The maximum length of the data representations of MOFs is 128. The model was trained with a batch size of 128 during 50 epochs and AdamW79 optimizer with a learning rate of 10−4. The predictor, which is similar to the encoder of the generator, consists of 4 layers of the Transformer encoder. It was trained with a batch size of 128 during 100 epochs. The AdamW optimizer with a learning rate of 10−4 and weight decay of 10−2 was used for the predictor. The learning rate was warmed up during the first 5% of the total epoch and then linearly decayed to zero for the remaining epochs.
5.5 Training details for reinforcement learning
The reward functions used in reinforcement learning were assigned by the estimated values provided by the predictor. The reward functions of CO2 heat of adsorption and CO2/H2O selectivity are defined as eqn (4) and (5), respectively. It is important to note that these reward functions were calculated using two separate predictors, each independently trained to estimate these two different properties.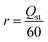 | (4) |
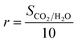 | (5) |
The policy gradient algorithm was trained with a batch size of 16 during 20 epochs where each epoch was constructed by randomly selecting 8000 data in the training dataset of the generator. The optimizer and scheduler were the same as those used in the training process of the generator.
The reinforcement learning was carried out for three rounds. After each round, the top-performing structures of that round were added to retrain the predictor for the next round. And, this updated predictor was then used in the training of the reinforcement learning for the next round.
Code availability
The reinforcement learning framework is available at https://github.com/hspark1212/MOFreinforce as open source so that it allows training the reinforcement learning with other target properties. Our GitHub source code will be updated. A consolidated version of our code used for this work has been exported to Zenodo at https://doi.org/10.5281/zenodo.7851250.81Data availability
The cif files and properties of the top-performing MOFs for CO2 heat of adsorption and CO2/H2O selectivity for each of the three rounds, the dataset used for pre-training the predictor, and some additional data are available on the Zenodo platform at https://doi.org/10.5281/zenodo.7853157.80Author contributions
H. P. developed the reinforcement learning framework and analyzed the results of reinforcement learning and the top-performing MOFs. S. M. conceived the idea of the project, performed molecular simulations, and analyzed the top-performing MOFs and the results of reinforcement learning. X. Z. performed the chemical space analysis of the MOF structures. J. K. and B. S. led the project and provided directions. The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the USorb-DAC Project, which is funded by a grant from The Grantham Foundation for the Protection of the Environment to RMI's climate tech accelerator program, Third Derivative. H. P. and J. K. acknowledge funding from National Research Foundation of Korea (NRF) under Project Number 2021M3A7C208974513. The authors would like to thank Kevin Maik Jablonka and Elias Moubarak for insightful discussions.Notes and references
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter and M. O'Keeffe,
et al., Systematic Design of Pore Size and Functionality in Isoreticular MOFs and Their Application in Methane Storage, Science, 2002, 295(5554), 469–472 CrossRef CAS PubMed
.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff and R. Bounds,
et al., Data-Driven design of Metal–Organic Frameworks for Wet Flue Gas CO2 Capture, Nature, 2019, 576(7786), 253–256 CrossRef CAS PubMed
.
- D. Gomez-Gualdron, O. Gutov, V. Krungleviciute, B. Borah, J. Mondloch and J. Hupp,
et al., Computational Design of Metal-Organic Frameworks Based on Stable Zirconium Building Units for Storage and Delivery of Methane, Chem. Mater., 2014, 26(19), 5632–5639 CrossRef CAS
.
- A. Ahmed, Y. Liu, J. Purewal, L. D. Tran, A. G. Wong-Foy and M. Veenstra,
et al., Balancing Gravimetric and Volumetric Hydrogen Density in MOFs, Energy Environ. Sci., 2017, 10(11), 2459–2471 RSC
.
- M. Fumanal, A. Ortega-Guerrero, K. M. Jablonka, B. Smit and I. Tavernelli, Charge Separation and Charge Carrier Mobility in Photocatalytic Metal-Organic Frameworks, Adv. Funct. Mater., 2020, 30(49), 2003792 CrossRef CAS
.
- J. Cao, X. Li and H. Tian, Metal-organic framework (MOF)-based drug delivery, Curr. Med. Chem., 2020, 27(35), 5949–5969 CrossRef CAS PubMed
.
- L. Sun, M. G. Campbell and M. Dincă, Electrically conductive porous metal–organic frameworks, Angew. Chem., Int. Ed., 2016, 55(11), 3566–3579 CrossRef CAS PubMed
.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney and P. A. Wood,
et al., Development of a Cambridge Structural Database Subset: A Collection of Metal-Organic Frameworks for Past, Present, and Future, Chem. Mater., 2017, 29(7), 2618–2625 CrossRef CAS
.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee and H. Zhang,
et al., Advances, updates, and analytics for the computation-ready, experimental metal–organic framework database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64(12), 5985–5998 CrossRef CAS
.
- D. Ongari, L. Talirz and B. Smit, Too Many Materials and Too Many Applications: An Experimental Problem Waiting for a Computational Solution, ACS Cent. Sci., 2020, 6(11), 1890–1900 CrossRef CAS PubMed
.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser and J. T. Hupp,
et al., Large-Scale screening of Hypothetical Metal-Organic Frameworks, Nat. Chem., 2021, 4, 83–89 CrossRef PubMed
.
- P. G. Boyd and T. K. Woo, A Generalized Method for Constructing Hypothetical Hanoporous Materials of Any Net Topology from Graph Theory, CrystEngComm, 2016, 18(21), 3777–3792 RSC
.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y. S. Chen and J. T. Hupp,
et al., Evaluating topologically diverse metal–organic frameworks for cryo-adsorbed hydrogen storage, Energy Environ. Sci., 2016, 9(10), 3279–3289 RSC
.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically Guided, Automated Construction of Metal-Organic Frameworks and Their Evaluation for Energy-Related Applications, Cryst. Growth Des., 2017, 17(11), 5801–5810 CrossRef
.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee and E. S. Cho,
et al., Computational screening of trillions of metal–organic frameworks for high-performance methane storage, ACS Appl. Mater. Interfaces, 2021, 13(20), 23647–23654 CrossRef CAS PubMed
.
- S. Majumdar, S. M. Moosavi, K. M. Jablonka, D. Ongari and B. Smit, Diversifying databases of metal organic frameworks for high-throughput computational screening, ACS Appl. Mater. Interfaces, 2021, 13(51), 61004–61014 CrossRef CAS PubMed
.
- J. Burner, J. Luo, A. White, A. Mirmiran, O. Kwon and P. G. Boyd,
et al., ARC–MOF: a diverse database of metal-organic frameworks with DFT-derived partial atomic charges and descriptors for machine learning, Chem. Mater., 2023, 35(3), 900–916 CrossRef CAS
.
- M. Gibaldi, O. Kwon, A. White, J. Burner and T. K. Woo, The HEALED SBU Library of Chemically Realistic Building Blocks for Construction of Hypothetical Metal–Organic Frameworks, ACS Appl. Mater. Interfaces, 2022, 14(38), 43372–43386 CrossRef CAS PubMed
.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Bias free multiobjective active learning for materials design and discovery, Nat. Commun., 2021, 12(1), 1–10 CrossRef PubMed
.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet and P. G. Boyd,
et al., Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11(1), 1–10 CrossRef PubMed
.
- A. Deshwal, C. M. Simon and J. R. Doppa, Bayesian optimization of nanoporous materials, Mol. Syst. Des. Eng., 2021, 6(12), 1066–1086 RSC
.
- B. Kim, S. Lee and J. Kim, Inverse design of porous materials using artificial neural networks, Sci. Adv., 2020, 6(1), eaax9324 CrossRef CAS PubMed
.
- M. Zhou and J. Wu, Inverse design of metal–organic frameworks for C2H4/C2H6 separation, npj Comput. Mater., 2022, 8(1), 256 CrossRef CAS
.
- Y. Bao, R. L. Martin, C. M. Simon, M. Haranczyk, B. Smit and M. W. Deem, In silico discovery of high deliverable capacity metal–organic frameworks, J. Phys. Chem., 2015, 119(1), 186–195 CAS
.
- Y. Lim, J. Park, S. Lee and J. Kim, Finely tuned inverse design of metal–organic frameworks with user-desired Xe/Kr selectivity, J. Mater. Chem. A, 2021, 9(37), 21175–21183 RSC
.
- J. Park, Y. Lim, S. Lee and J. Kim, Computational Design of Metal–Organic Frameworks with Unprecedented High Hydrogen Working Capacity and High Synthesizability, Chem. Mater., 2023, 35(1), 9–16 CrossRef CAS
.
- S. Han and J. Kim, Design and Screening of Metal–Organic Frameworks for Ethane/Ethylene Separation, ACS Omega, 2023, 8(4), 4278–4284 CrossRef PubMed
.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar and S. P. Collins,
et al., Inverse design of nanoporous crystalline reticular materials with deep generative models, Nat. Mach. Intell., 2021, 3(1), 76–86 CrossRef
.
- Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Optimization of molecules via deep reinforcement learning, Sci. Rep., 2019, 9(1), 1–10 CrossRef PubMed
.
- B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, Optimizing distributions over molecular space. An objective-reinforced generative adversarial network for inverse-design chemistry (ORGANIC), ChemRxiv, 2017, preprint, DOI:10.26434/chemrxiv.5309668.v3.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de-novo design through deep reinforcement learning, J. Cheminf., 2017, 9(1), 1–14 Search PubMed
.
- G. L. Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias and A. Aspuru-Guzik, Objective-reinforced generative adversarial networks (ORGAN) for sequence generation models, arXiv, 2017, preprint, arXiv:1705.10843, DOI:10.48550/arXiv.1705.10843.
-
E. Pan, C. Karpovich and E. Olivetti, Deep Reinforcement Learning for Inverse Inorganic Materials Design, arXiv, 2022, preprint, arXiv:2210.11931, DOI:10.48550/arXiv.2210.11931
.
- K. S. Lackner, S. Brennan, J. M. Matter, A. H. A. Park, A. Wright and B. van der Zwaan, The urgency of the development of CO2 capture from ambient air, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(33), 13156–13162 CrossRef CAS PubMed
.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston and S. Brown,
et al., Carbon capture and storage (CCS): the way forward, Energy Environ. Sci., 2018, 11(5), 1062–1176 RSC
.
- E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Direct capture of CO2 from ambient air, Chem. Rev., 2016, 116(19), 11840–11876 CrossRef PubMed
.
- J. M. Findley and D. S. Sholl, Computational screening of MOFs and zeolites for direct air capture of carbon dioxide under humid conditions, J. Phys. Chem. C, 2021, 125(44), 24630–24639 CrossRef CAS
.
- R. P. Lively and M. J. Realff, On thermodynamic separation efficiency: Adsorption processes, AIChE J., 2016, 62(10), 3699–3705 CrossRef CAS
.
- R. Veneman, N. Frigka, W. Zhao, Z. Li, S. Kersten and W. Brilman, Adsorption of H2O and CO2 on supported amine sorbents, Int. J. Greenhouse Gas Control, 2015, 41, 268–275 CrossRef CAS
.
- A. H. Berger and A. S. Bhown, Comparing physisorption and chemisorption solid sorbents for use separating CO2 from flue gas using temperature swing adsorption, Energy Procedia, 2011, 4, 562–567 CrossRef CAS
.
- P. M. Bhatt, Y. Belmabkhout, A. Cadiau, K. Adil, O. Shekhah and A. Shkurenko,
et al., A fine-tuned fluorinated MOF addresses the needs for trace CO2 removal and air capture using physisorption, J. Am. Chem. Soc., 2016, 138(29), 9301–9307 CrossRef CAS PubMed
.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation, Mach. learn.: Sci. Technol., 2020, 1(4), 045024 Search PubMed
.
- D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv, 2013, preprint, arXiv:1312.6114, DOI:10.48550/arXiv.1312.6114.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley and S. Ozair,
et al., Generative adversarial networks, Commun. ACM, 2020, 63(11), 139–144 CrossRef
.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, The reticular chemistry structure resource (RCSR) database of, and symbols for, crystal nets, Acc. Chem. Res., 2008, 41(12), 1782–1789 CrossRef PubMed
.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones and A. N. Gomez,
et al., Attention is all you need, Adv. Neural Inf. Process. Syst., 2017, 30, 6000–6010 Search PubMed
.
- J. Lim, S. Y. Hwang, S. Moon, S. Kim and W. Y. Kim, Scaffold-based molecular design with a graph generative model, Chem, 2020, 11(4), 1153–1164 CAS
.
- Y. Li, J. Hu, Y. Wang, J. Zhou, L. Zhang and Z. Liu, Deepscaffold: a comprehensive tool for scaffold-based de novo drug discovery using deep learning, J. Chem. Inf. Model., 2019, 60(1), 77–91 CrossRef PubMed
.
- J. Arús-Pous, A. Patronov, E. J. Bjerrum, C. Tyrchan, J. L. Reymond and H. Chen,
et al., SMILES-based deep generative scaffold decorator for de-novo drug design, J. Cheminf., 2020, 12(1), 1–18 Search PubMed
.
-
S. Abnar and W. Zuidema, Quantifying Attention Flow in Transformers, 2020 Search PubMed
.
- L. Van der Maaten and G. Hinton, Visualizing Data using t-SNE, J. Mach. Learn. Res., 2008, 9(11), 2509–2605 Search PubMed
.
- P. Ertl and A. Schuffenhauer, Estimation of synthetic
accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1(1), 1–11 Search PubMed
.
- M. Popova, O. Isayev and A. Tropsha, Deep reinforcement learning for de novo drug design, Sci. Adv., 2018, 4(7), eaap7885 CrossRef CAS PubMed
.
- I. Boldog, K. V. Domasevitch, I. A. Baburin, H. Ott, B. Gil-Hernández and J. Sanchiz,
et al., A rare alb-4, 8-Cmce metal–coordination network based on tetrazolate and phosphonate functionalized 1, 3, 5, 7-tetraphenyladamantane, CrystEngComm, 2013, 15(6), 1235–1243 RSC
.
- T. T. Lian and S. M. Chen, A new microporous Cu (II)-isonicotinate framework with 8-connected bcu topology, Inorg. Chem. Commun., 2012, 18, 8–10 CrossRef CAS
.
- T. Jacobs and M. J. Hardie, Construction of Metal–Organic Frameworks: Versatile Behaviour of a Ligand Containing Mono-and Bidentate Coordination Sites, Chem. - Eur. J., 2012, 18(1), 267–276 CrossRef CAS PubMed
.
- R. Anderson and D. A. Gómez-Gualdrón, Increasing topological diversity during computational “synthesis” of porous crystals: how and why, CrystEngComm, 2019, 21(10), 1653–1665, 10.1039/c8ce01637b
.
- C. Charalambous, E. Moubarak, J. Schilling, E. Sanchez Fernandez, J. Y. Wang and L. Herraiz, Shedding Light on the Stakeholders’ Perspectives for Carbon Capture, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-sn90q.
- B. J. Bucior, A. S. Rosen, M. Haranczyk, Z. Yao, M. E. Ziebel and O. K. Farha,
et al., Identification schemes for metal–organic frameworks to enable rapid search and cheminformatics analysis, Cryst. Growth Des., 2019, 19(11), 6682–6697 CrossRef CAS
.
-
G. Landrum, et al., Rdkit: Open-source cheminformatics software, 2016 Search PubMed
.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035 CrossRef
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown and P. S. Crozier,
et al., LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- P. G. Boyd, S. M. Moosavi, M. Witman and B. Smit, Force-Field Prediction of Materials Properties in Metal-Organic Frameworks, J. Phys. Chem. Lett., 2017, 8, 357–363 CrossRef CAS PubMed
.
- P. G. Boyd, S. M. Moosavi and M. Witman, LAMMPS Interface, Using August 1, 2019 release throughout this study, https://github.com/peteboyd/lammps_interface.
-
D. S. Biovia, Materials Studio. R2 (Dassault Systèmes) BIOVIA, San Diego, 2017 Search PubMed
.
- C. E. Wilmer, K. C. Kim and R. Q. Snurr, An Extended Charge Equilibration Method, J. Phys. Chem. Lett., 2012, 3, 2506–2511 CrossRef CAS PubMed
.
- D. Ongari, EQeq:Charge equilibration method for crystal structures, Using March 10, 2020 release throughout this study, https://github.com/danieleongari/EQeq.
- D. Ongari, P. G. Boyd, O. Kadioglu, A. K. Mace, S. Keskin and B. Smit, Evaluating Charge Equilibration Methods to Generate Electrostatic Fields in Nanoporous Materials, J. Chem. Theory Comput., 2018, 15(1), 382–401 CrossRef PubMed
.
-
D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, San Diego, vol. 1, 2002 Search PubMed
.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, RASPA: Molecular Simulation Software for Adsorption and Diffusion in Flexible Nanoporous Materials, Mol. Simul., 2016, 42(2), 81–101 CrossRef CAS
.
- P. Gomez-Alvarez, A. R. Ruiz-Salvador, S. Hamad and S. Calero, Importance of blocking inaccessible voids on modeling zeolite adsorption: revisited, J. Phys. Chem. C, 2017, 121(8), 4462–4470 CrossRef CAS
.
- D. Ongari, P. G. Boyd, S. Barthel, M. Witman, M. Haranczyk and B. Smit, Accurate Characterization of the Pore Volume in Microporous Crystalline Materials, Langmuir, 2017, 33(51), 14529–14538 CrossRef CAS PubMed
.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials, Microporous Mesoporous Mater., 2012, 149(1), 134–141 CrossRef CAS
.
- J. J. Potoff and J. I. Siepmann, Vapor–Liquid Equilibria of Mixtures containing Alkanes, Carbon Dioxide, and Nitrogen, AIChE J., 2001, 47(7), 1676–1682 CrossRef CAS
.
- J. L. Abascal and C. Vega, A general purpose model for the condensed phases of water: TIP4P/2005, J. Chem. Phys., 2005, 123(23), 234505 CrossRef CAS PubMed
.
- K. M. Jablonka, D. Ongari and B. Smit, Applicability of Tail Corrections in the Molecular Simulations of Porous Materials, J. Chem. Theory Comput., 2019, 15(10), 5635–5641 CrossRef CAS PubMed
.
- H. A. Lorentz, About the Application of the Virial Theorem in the Kinetic Theory of Gases, Ann. Phys., 1881, 248(1), 127–136 CrossRef
.
- R. S. Sutton, D. McAllester, S. Singh and Y. Mansour, Policy gradient methods for reinforcement learning with function approximation, Adv. Neural Inf. Process. Syst., 1999, 12, 1057–1063 Search PubMed
.
- I. Loshchilov and F. Hutter, Decoupled weight decay regularization, arXiv, 2017, preprint, arXiv:1711.05101, DOI:10.48550/arXiv.1711.05101.
-
H. Park, S. Majumdar, X. Zhang, J. Kim and B. Smit, Dataset for Inverse design of metal-organic frameworks for direct air capture of CO2 via deep reinforcement learning, Zenodo, 2023, DOI:10.5281/zenodo.7853157
.
-
H. Park, S. Majumdar, X. Zhang, J. Kim and B. Smit, hspark1212/MOFreinforce, Initial Release, Zenodo, 2023, DOI:10.5281/zenodo.7851250
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00010b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |