Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
ChemGymRL: A customizable interactive framework for reinforcement learning for digital chemistry
Chris
Beeler
abc,
Sriram Ganapathi
Subramanian
bd,
Kyle
Sprague
b,
Mark
Baula
b,
Nouha
Chatti
b,
Amanuel
Dawit
b,
Xinkai
Li
b,
Nicholas
Paquin
b,
Mitchell
Shahen
b,
Zihan
Yang
b,
Colin
Bellinger
c,
Mark
Crowley
 *b and
Isaac
Tamblyn
de
*b and
Isaac
Tamblyn
de
aDepartment of Mathematics and Statistics, University of Ottawa, Ottawa, ON, Canada. E-mail: christopher.beeler@uottawa.ca
bDepartment of Electrical and Computer Engineering, University of Waterloo, Waterloo, ON, Canada. E-mail: mark.crowley@uwaterloo
cDigital Technologies, National Research Council of Canada, Ottawa, ON, Canada. E-mail: colin.bellinger@nrc-cnrc.gc.ca
dVector Institute for Artificial Intelligence, Toronto, ON, Canada
eDepartment of Physics, University of Ottawa, Ottawa, ON, Canada. E-mail: isaac.tamblyn@uottawa.ca
First published on 20th February 2024
Abstract
This paper provides a simulated laboratory for making use of reinforcement learning (RL) for material design, synthesis, and discovery. Since RL is fairly data intensive, training agents ‘on-the-fly’ by taking actions in the real world is infeasible and possibly dangerous. Moreover, chemical processing and discovery involves challenges which are not commonly found in RL benchmarks and therefore offer a rich space to work in. We introduce a set of highly customizable and open-source RL environments, ChemGymRL, implementing the standard gymnasium API. ChemGymRL supports a series of interconnected virtual chemical benches where RL agents can operate and train. The paper introduces and details each of these benches using well-known chemical reactions as illustrative examples, and trains a set of standard RL algorithms in each of these benches. Finally, discussion and comparison of the performances of several standard RL methods are provided in addition to a list of directions for future work as a vision for the further development and usage of ChemGymRL.
1. Introduction
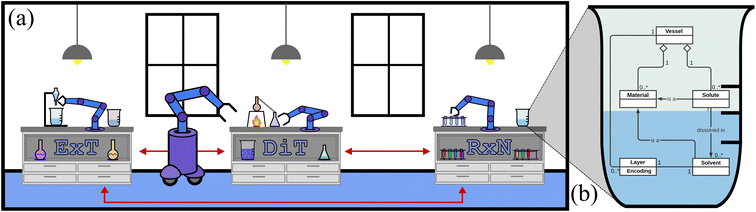
In material design, the goal is to determine a pathway of chemical and physical manipulation that can be performed on some starting materials or substances in order to transform them into a desired target material. The aim of this research is to demonstrate the potential of goal-based reinforcement learning (RL) in automated labs. Our experiments show that when given an objective (such as a target material) and a set of initial materials, RL can learn general pathways to achieve that objective. We postulate that well-trained RL chemist-agents could help reduce experimentation time and cost in these and related fields by learning to complete tasks that are repetitive, labour intensive and/or require a high degree of precision. With increased simulation complexity, well trained RL chemist-agents could potentially discover new materials and/or reaction pathways in this system as well. To support this, we share the ChemGymRL environment that allows scientists and researchers to simulate chemical laboratories for the development of RL agents.ChemGymRL is a collection of interconnected environments (or chemistry benches) that enable the training of RL agents for discovery and optimization of chemical synthesis. These environments are each a virtual variant of a chemistry “bench”, an experiment or process that would otherwise be performed in real-world chemistry labs. As shown in Fig. 1, the ChemGymRL environment includes reaction, distillation, and extraction benches on which RL agents learn to perform actions and satisfy objectives. Each bench could be a standalone environment (as the majority of RL environments are), this would counter the purpose of their inter-connectivity. While their inter-connectivity is not important for training a specific agent on a single bench, sharing an overarching framework for the benches ensures a compatibility between them, allowing the results of one experiment to be easily used as input to another bench's task. This makes inter-connectivity important if one wishes to perform a multi-task experiment, requiring several benches to be used in differing orders.
The need for a simulated chemistry environment for designing, developing, and evaluating artificial intelligence algorithms is motivated by the recent growth in research on topics, such as automated chemistry and self-driving laboratories,1–5 laboratory robots6–13 and digital chemistry for materials and drug discovery.14–22 Given RL's appropriateness for sequential decision making, and its ability to learn via online interactions with a physical or simulated environment without a supervised training signal, we see it as having a great potential within digital chemistry and self-driving laboratories. Within this context, recent work has demonstrated some successful applications of RL23,24 or methods inspired by parts of RL25 to automated chemistry. Nonetheless, it remains an understudied area of research. Our work aims to partially addresses this problem by sharing an easy to use, extensible, open source, simulated chemical laboratory. This serves to simplify the design and development of application specific RL agents.
Although RL agents could be trained online in physical laboratories, this approach has many limitations, particularly in early stages of the research before mature policies exist. Training agents in a robotic laboratory in real-time would be costly (in both time and supplies) and restrictive (due to potential safety hazards). Our simulated ChemGymRL environment remedies this by allowing the early exploration phase to occur digitally, speeding up the process and reducing the waste of chemical materials. It provides a mechanism to design, develop, evaluate and refine RL for chemistry applications and researcher, which cannot safely be achieved in a physical setting. We would also like to specifically highlight ChemGymRL as a unique testbed for RL research. Since ChemGymRL is open source and highly customizable, it provides a training environment to accelerate both chemical and RL research in several directions in addition to providing a useful training environment with real-world applications (more discussions in Section A.1).
The software is developed according to the Gymnasium† standard, which facilitates easy experimentation and exploration with novel and off-the-shelf RL algorithms. When users download it, they gain access to a standard gymnasium compatible environment that simulates chemical reactions using rate law differential equations, the mixing/settling of soluble and non-soluble solutions for solute extractions, the distillation of solutions, and a digital format for storing the state of the vessels used. In addition to this article, further detailed information about this software package, documentation and tutorials, including code and videos can be found at https://www.chemgymrl.com/.
In our experimental results, we illustrate how to setup and use each bench with two distinct classes of reactions, along with how they can be extended to new reaction types. We evaluate the capabilities of a wide cross-section of off-the-shelf RL algorithms for goal-based policy learning in ChemGymRL, and compare these against hand-designed heuristic baseline agents. In our analysis, we find that only one RL off-the-shelf RL algorithm, proximal policy optimization (PPO), is able to consistently outperform these heuristics on each bench. This suggests that the heuristics are a challenging baseline to compare to but that they are also far from optimal. Thus there is space for an optimization approach such as RL to achieve optimal behavior on each bench. Near the end of the paper, we discuss some of the challenges, limitations and potential improvements in RL algorithms required to learn better, more sample efficient policies for discovery and optimization of material design pathways.
The remainder of the paper is organized as follows. The next section describes the ChemGymRL environment, including the three primary benches: reaction, extraction and distillation. Section 3 provides an overview of reinforcement learning and Section 4 contains a case study of the Wurtz reaction and its use in each bench. Our experimental setup involves training off-the-shelf RL algorithms on each of the benches. The RL algorithms and hyper-parameters are discussed in Section 5 and the specific laboratory settings and objectives used in our experiments are described in Section 6. The results of the RL experiments are presented in Section 7 and the limitations of the simulations are discussed in Section 8 followed by our general conclusions and some ideas for future directions.
2. ChemGymRL
2.1 The laboratory
ChemGymRL is designed in a modular fashion so that new simulated benches can be added or modified with minimal difficulty or changes to the source code. The environment can be thought of as a virtual chemistry laboratory consisting of different stations or benches where a variety of tasks can be completed, represented in Fig. 1(a). The main 2 components of the laboratory are vessels and benches.Benches recreate a simplified version of a task in a material design pipeline and vessels contain materials and track the hidden internal state of their contents, as shown in Fig. 1(b). A bench must be able to receive a set of initial experimental supplies, possibly including vessels, and return the results of the intended experiment, also including modified vessels. A vessel is used to transfer the chemical state contained in one bench to another, allowing for continuation of experiments.
We provide some core elements of a basic chemistry lab which enable the simulation of essential materials experiments. Critically, each bench and the gym as a whole is extensible. Therefore there is no limit on the complexity and precision simulations can be implemented. In the following sections we describe each of these benches in term and demonstrate an example workflow.
These benches each have three crucial components required for operating them. The observation space is the possible set of observations which the agent (or human user) can use to learn the status of the bench and take appropriate actions. These observations are, a usually only partial, representation of the internal state of the system. The action space for a bench, is a set of actions the user can take on that bench. These actions are methods of modifying the state of the system or observation. Lastly, the reward function is a measure of success based on the states the system has been in and the actions that have been taken. Generally in RL, the goal is to maximize its expected outputs, known as rewards, over time. These rewards are usually discounted over time. An episode refers to a single play of a bench from starting materials until the agent stops. The total, cumulative expected reward over an entire episode is called the return.
2.2 Reaction bench (RxN)
The sole purpose of the reaction bench (RxN) is to allow the agent to transform available reactants into various products via a chemical reaction. The agent has the ability to control temperature and pressure of the vessel as well as the amounts of reactants added. The mechanics of this bench are quite simple in comparison to real-life, which enables low computational cost for RL training. Reactions are modelled by solving a system of differential equations which define the rates of changes in concentration (see Appendix).The goal of the agent operating on this bench is to modify the reaction parameters, in order to increase, or decrease, the yield of certain desired, or undesired, materials. The key to the agent's success in this bench is learning how best to allow certain reactions to occur such that the yield of the desired material is maximized and the yield of the undesired material is minimized. Therefore the reward in this bench is zero at all steps except the final step, at which point it is the difference in the number of mols of the desired material and undesired material(s) produced.
A main feature of ChemGymRL is its modularity. If one wanted to make the results of RxN more accurate and generalizable, they could replace the current system of differential equations with a molecular dynamics simulation without needing to change how the agent interacts with the bench or how the bench interacts with the rest of ChemGymRL. In its current state, this bench takes approximately 0.73 ms to initialize and 0.87 ms to perform an action.
2.3 Extraction bench (ExT)
Chemical reactions commonly result in a mixture of desired and undesired products. Extraction is a method to separate them. The extraction bench (ExT) aims to isolate and extract certain dissolved materials from an input vessel containing multiple materials through the use of various insoluble solvents. This is done by means of transferring materials between a number of vessels and utilizing specifically selected solvents to separate materials from each other.A simple extraction experiment example is extracting salt from an oil solvent using water. Suppose we have a vessel containing sodium chloride dissolved in hexane. Water is added to a vessel and the vessel is shaken to mix the two solvents. When the contents of the vessel settle, the water and hexane will have separated into two different layers. Sodium chloride is an ionic compound, therefore there is a distinct separation of charges when dissolved. Due to hexane being a non-polar solvent and water being a polar solvent, a large portion of the dissolved sodium chloride is pulled from the hexane into the water. Since water has a higher density than hexane, it is found at the bottom of the vessel and can be easily drained away, bringing the dissolved sodium chloride with it.
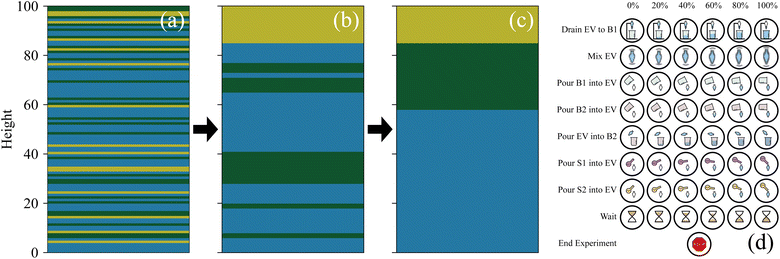
The mutually exclusive actions are: (1) mix the vessel or let it settle (i.e. wait), (2) add an amount of solvent to the vessel, (3) drain contents of the vessel into an auxiliary vessel bottom first, (4) pour contents of the vessel into a second auxiliary vessel, (5) pour contents of the first auxiliary vessel into the second, (6) pour contents of first auxiliary vessel into the second, (7) pour contents back into the original vessel, (8) end the experiment.
The multiplier for each action corresponds to either the duration (mix, wait), the amount to pour, or the amount to drain, with 5 discrete non-zero values each. These actions are depicted in Fig. 3(d).
Note that, for practical implementation purposes, the two-part action described above is flattened into a single discrete value to reduce redundancy in the action space.
The goal of the agent in this bench is to use these processes in order to maximize the purity of a desired solute relative to other solutes in the vessel. This means the agent must isolate the desired solute in one vessel, while separating any other solutes into the other vessels. Note that the solute's relative purity is not affected by the presence of solvents, only the presence of other solutes. Therefore the reward in this bench is zero at all steps except the final step, at which point it is the difference in the relative purity of the desired solute at the first and final steps.
As with RxN, the realism of ExT could be improved by replacing the separation equations with a physics-based simulation without needing to change how the agent interacts with the bench or how the bench interacts with the rest of ChemGymRL. In its current state, this bench takes approximately 0.87 ms to initialize and 0.47 ms to perform an action.
2.4 Distillation bench (DiT)
Similar to the ExT, the distillation bench (DiT) aims to isolate certain materials from a provided vessel containing multiple materials (albeit with a different process). This is done by means of transferring materials between a number of vessels and heating/cooling the vessel to separate materials from each other.A simple distillation example is extracting a solute dissolved in a single solvent. Suppose we have a vessel containing sodium chloride dissolved in water. If we heat the vessel to 100 °C, the water will begin to boil. With any added heat, more water will evaporate and be collected in an auxiliary vessel, leaving the dissolved sodium chloride behind to precipitate out as solid sodium chloride in the original vessel.
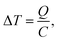 | (1) |
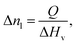 | (2) |
Similar to the ExT bench, these processes are mutually exclusive and each have a magnitude (temperature change, amount to pour). Thus, the same kind of (action, multiplier) definition is used for DiT bench. The actions can be one of the following four choices: (1) heat/cool by some amount, (2) pour from the distillation vessel into an auxiliary vessel, (3) pour from an one auxiliary vessel into another, or (4) end the experiment. Actions (1–3) each can have one of 10 multiplier values specifying magnitude. These actions are depicted in Fig. 4. Just as in ExT, the actions are returned by the agent are flattened into a single discrete value to reduce redundancy in the action space.
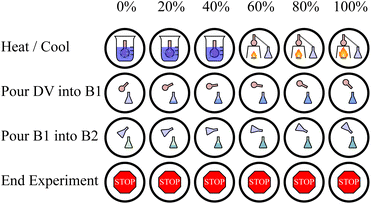 | ||
| Fig. 4 The icons representing each action and their multiplier values available in DiT. The distillation vessel (DV) is the primary vessel and B1/B2 are the auxiliary vessels in the experiment. | ||
The goal of the agent in this bench is to use these processes to maximize the absolute purity of a desired material in the vessel. This means the agent must isolate the desired material in one vessel, while separating any other materials into other vessels. Note that unlike ExT, the material's absolute purity is affected by the presence of all materials. Therefore the reward in this bench is zero at all steps except the final step, at which point it is the difference in the absolute purity of the desired material at the first and final steps. In its current state, this bench takes approximately 0.87 ms to initialize and 0.86 ms to perform an action.
2.5 Characterization bench
In general, it is impossible to determine the exact contents of a vessel just by looking at it. Techniques exist to help characterize the contents of a vessel, however each comes with a cost. The primary cost is the monetary cost to acquire/maintain/run the instrument used. In some cases, the sample of the vessel contents being measured is destroyed during the measurement, thus incurring a different type of cost. While these costs are not implemented in this version of ChemGymRL, they are important to consider when expanding the system.The characterization bench is the primary method to obtain insight as to what the vessel contains. The purpose of the characterization bench is not to manipulate the input vessel, but to subject it to analysis techniques that observe the state of the vessel, possibly including the materials inside it and their relative quantities. This does not mean that the contents of the input vessel cannot be modified by the characterization bench. This allows an agent or user to observe vessels, determine their contents, and allocate the vessel to the necessary bench for further experimentation.
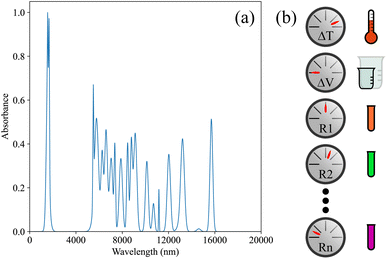
The characterization bench is the only bench that is not “operated”. A vessel is provided to the bench along with a characterization method and the results of said method on that vessel are returned. Currently, the characterization bench consists of a UV-vis spectrometer that returns the UV-vis absorption spectrum of the provided vessel. Each material in ChemGymRL has a set of UV-vis absorption peaks defined and the UV-vis spectrum for a vessel is the combination of the peaks for all materials present, weighted proportionally by their concentrations. In future versions of ChemGymRL we will expand the characterization bench to include other forms of partial observation.
3. Reinforcement learning
Reinforcement learning (RL)26 is one possible solution to a Markov decision process (MDP). MDPs are represented as a tuple 〈S, A, R, T, γ〉 where the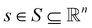 denotes the state space,
denotes the state space, 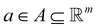 denotes the action space,
denotes the action space, 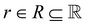 denotes the reward function and T = P(st+1|st, at) denotes the transition dynamics (or model) that provides the probability of state st+1 at the next time step given that the agent is in state st and performs action at. The objective for an RL agent is to learn a policy π(a|s) that maximizes the discounted sum of expected rewards provided by the equation
denotes the reward function and T = P(st+1|st, at) denotes the transition dynamics (or model) that provides the probability of state st+1 at the next time step given that the agent is in state st and performs action at. The objective for an RL agent is to learn a policy π(a|s) that maximizes the discounted sum of expected rewards provided by the equation 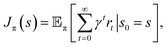 where γ ∈ [0, 1) is the discount factor.
where γ ∈ [0, 1) is the discount factor.
In the field of model-free RL on which we focus here, a major distinction between solution algorithms is between value optimization approaches and direct policy optimization approaches. A popular example of value optimization is Q-learning,27,28 where a state-value function Q(s,a):S × A → ℜ, is learned iteratively using the Bellman optimality operator 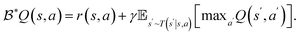 Here s and s′ denote the current and next state respectively, a and a′ denote the current and next action, respectively. After this process converges, an exact or approximate scheme of maximization is used to extract the greedy policy from the Q-function. These methods are often restricted to environments with discrete actions, although many generalizations exist to other formulations.29–31
Here s and s′ denote the current and next state respectively, a and a′ denote the current and next action, respectively. After this process converges, an exact or approximate scheme of maximization is used to extract the greedy policy from the Q-function. These methods are often restricted to environments with discrete actions, although many generalizations exist to other formulations.29–31
Direct policy optimization32 approaches are ones which iteratively improve the target policy directly. They may do this as the only optimization approach, or they may do it in combination with value-function optimization. Actor-critic33–35 methods are a currently popular approach for doing just that. In actor-critic methods, the algorithm alternates between estimating a value function Qπ (the “critic”) of a current policy via a partial policy evaluation routine using the Bellman operator on an initially random, stochastic policy π. The current policy π (the “actor”) is then improved by biasing it towards selecting actions that maximize the estimate maintained by the current Q-values and the value function for this improved policy is then re-estimated again. This family of methods can easily apply to both discrete and continuous action space environments, thus may be used on any bench in chemistry gym environment.
4. Case study
As a simple example, we outline how a particular chemical production process uses each of the benches.4.1. Wurtz reaction
Wurtz reactions are commonly used for the formation of certain hydrocarbons. These reactions are of the form: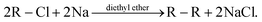 | (3) |
 | (4) |
 | (5) |
| Reaction | R1 | R2 | R1–R2 |
|---|---|---|---|
| 1 | 1-Chlorohexane | 1-Chlorohexane | Dodecane |
| 2 | 1-Chlorohexane | 2-Chlorohexane | 5-Methylundecane |
| 3 | 1-Chlorohexane | 3-Chlorohexane | 4-Ethyldecane |
| 4 | 2-Chlorohexane | 2-Chlorohexane | 5,6-Dimethyldecane |
| 5 | 2-Chlorohexane | 3-Chlorohexane | 4-Ethyl-5-methylnonane |
| 6 | 3-Chlorohexane | 3-Chlorohexane | 4,5-Diethyloctane |
Wurtz can be an interesting and challenging reaction because the yield varies greatly between each product, making it difficult to train an agent which can optimally make each of them.
4.2 Workflow
Suppose that we have the previously listed chlorohexanes, sodium, diethyl ether, and water available to us with the goal to produce dodecane. Using RxN we can add diethyl ether, 1-chlorohexane, and sodium to a vessel. With time, this will produce a vessel containing dodecane and sodium chloride dissolved in diethyl ether. The UV-vis spectrometer in the RxN can be used to measure the progression of the reaction.The vessel can then be brought to the ExT to separate dodecane from sodium chloride. Dodecane is non-polar, so if we add water to the vessel and mix, most of the sodium chloride will be extracted into the water while most of the dodecane will be left in the diethyl ether. We can then drain the water out of the vessel while keeping the diethyl ether. While it's impossible to get all of the sodium chloride out with this method, we can repeat this process to increase the purity of dodecane.
The vessel can then be brought to the DiT to separate the dodecane from the diethyl ether. Diethyl ether has a much lower boiling point than dodecane so it will boil first. Heating the vessel enough will cause all of the diethyl ether to vaporize, leaving the dodecane in the vessel with trace amounts of sodium chloride.
Alternatively, because dodecane has a much lower boiling point than sodium chloride, we can skip the ExT and bring the vessel to DiT right after RxN. As before, heating the vessel enough will cause all of the diethyl ether to vaporize, condensing into an auxiliary vessel. We can then put the collect diethyl ether elsewhere such that the auxiliary vessel collected the vaporized materials is now empty. If the vessel is heated up even further now, the dodecane will be vaporized and collected into the empty auxiliary vessel, leaving the sodium chloride behind. Our auxiliary vessel now contains pure dodecane, concluding the experiment.
While this example workflow uses the benches in a specific order, more complicated experiments may use them in a completely different order or even use each bench multiple times. Given specific goals, below we will outline how RL can be used to emulate this behavior for various cases.
5 RL details
In our discrete benches, proximal policy optimization (PPO),36 advantageous actor-critic (A2C)35 and deep Q-network (DQN)28 were used. In our continuous benches, soft actor-critic (SAC)37 and twin delayed deep deterministic policy gradient (TD3)38 were used instead of DQN.Unless otherwise specified, all RL agents were trained for 100 K time steps across 10 environments in parallel (for a total of 1 M time steps). Training was done by repeatedly gathering 256 time steps of experience (in each environment), then updating our policy and/or Q-function with this new experience. For the PPO and A2C algorithms, the updates happened directly with the 2560 steps of new experiences. In contrast, for the DQN, SAC, and TD3 algorithms, the standard training approach uses an experience replay buffer, in our case containing 1 M steps, which was sampled from for training. For the first 30 K steps of DQN training, a linear exploration schedule beginning at 1.0 and ending at 0.01 was used. Exploration remained at 0.01 afterwards. All of these RL algorithms were performed using the stable baselines 3 implementations.39
In this paper, we choose to use DQN as a representative of the Q-learning family of algorithms since it is a very standard benchmark in RL, and the central themes that were initially introduced in DQN by Mnih et al.28 led to an explosion of different RL techniques that emerged subsequently. DQN is known to overestimate the values for multiple states and double DQN (DDQN)40 was introduced to decouple action selection and action evaluation. However, the classic solution to this, DDQN, is not necessarily better than DQN in all settings. It has been shown that DDQN suffers from an underestimation bias that is equally bad for performance,41 so we did not use it in these experiments.
6 Laboratory setup
6.1 Reaction bench methodology
For the reaction bench (RxN), we consider two chemical processes. In both processes, each episode begins with a vessel containing 4 mols of diethyl ether, and operates for 20 steps. We chose 20 steps because it's long enough that the agent can explore the space to find the optimal behavior but short enough that the reward acquired at the end of the episode can be propagated back through the trajectory. In the first process, the agent has access to 1.0 mol each of 1, 2, 3-chlorohexane, and sodium, where the system dynamics are defined by the Wurtz reaction outlined above. Each episode, a target material is specified to the agent via length 7 one-hot vector where the first 6 indices represent the 6 Wurtz reaction products in Table 1 and the last represents NaCl. After the 20 steps have elapsed, the agent receives a reward equal to the molar amount of the target material produced.In the second experiment, we introduce a new set of reaction dynamics given by
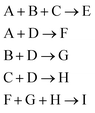 | (6) |
6.2 Extraction bench methodology
For the extraction bench (ExT), we consider a layer-separation process where the agent operates for up to 50 steps. We chose a larger number of steps in this experiment because the optimal solution is more complicated than the previous bench. Similar to the Wurtz reaction, the target material is specified via length 7 one-hot vector. Each episode begins with a vessel containing 4 mols of diethyl ether, 1 mol of dissolved sodium chloride, and 1 mol of one of the 6 Wurtz reaction products in Table 1. The Wurtz reaction product contained in the vessel is the same as the target material, unless the target material is sodium chloride, in which case dodecane is added since sodium chloride is already present. After the episode has ended, the agent receives a reward equal to the change in solute purity of the target material weighted by the molar amount of that target material, where the change in solute purity is relative to the start of the experiment. If the target material is present in multiple vessels, a weighted average of the solute purity across each vessel is used.Again, the PPO agents consistently outperform the A2C, SAC, and TD3 agents for all 5 target materials, however it is not as significant of a gap as in Wurtz RxN. Target materials with high returns across each algorithm (such as F, G, and H) appear to be easier tasks to learn, where target materials with less consistent return across each algorithm (such as E and I) appear to be more difficult tasks to learn.
As an example, consider when the target material is dodecane. In this experiment, the 1 mol of dissolved sodium chloride becomes 1 mol each of Na+ and Cl−, so the initial solute purity of dodecane is 1/3. Suppose we end the experiment with 0.7 mols of dodecane with 0.2 mols each of Na+ and Cl− in one vessel, and the remaining molar amounts in a second vessel. Dodecane has a solute purity of 7/11 and 3/19 in each vessel respectively. The final solute purity of dodecane would be 0.7 × 7/11 + 0.3 × 3/19 ≈ 0.493. Thus the agent would receive a reward of 0.159.
6.3 Distillation bench methodology
For the distillation bench (DiT), we consider a similar experimental set-up to the ExT one. Each episode begins with a vessel containing 4 mols of diethyl ether, 1 mol of the dissolved target material, and possibly 1 mol of another material. If the target material is sodium chloride, the additional material is dodecane, otherwise the additional material is sodium chloride. After the episode has ended, the agent receives a reward calculated similarly to the ExT, except using absolute purity rather than solute purity.7. RL results
7.1 Reaction bench
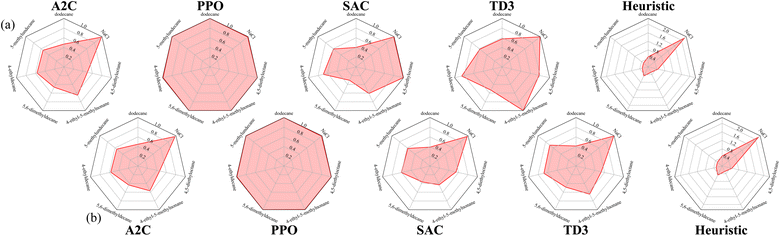
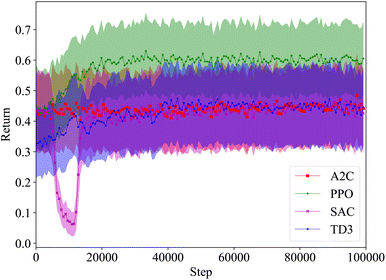
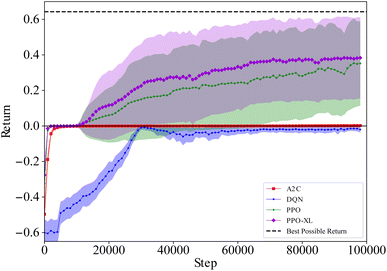
Since reaction bench (RxN) has a continuous action space, we trained SAC and TD3 in addition to A2C and PPO. For the first experiment, we are looking at the Wurtz reaction dynamics. Given that we know the system dynamics in this case, we have also devised a heuristic agent for the experiment, which we expect to be optimal. Since the Wurtz reaction is a single step process, the optimal behavior is quite simple. For target R1–R2, exclusively add R1 and R2 at step 1, and increase the temperature to speed up the reaction in order to produce as much of the target before the experiment ends. Thus the heuristic was designed to follow this behavior. This heuristic agent achieves an average return of approximately 0.62. Using the performance of this heuristic as a reference, the best and mean relative performances of the agents trained with each algorithm is shown in Fig. 5. Each algorithm can consistently give rise to agents that produce sodium chloride when requested. Since this is a by-product of all reactions in our set-up, it is the easiest product to create. While the other products are not hard to produce either, they require specific reactants, and in order to maximize the yield, they require the absence of other reactants. The PPO agents are able to match the heuristic agent for all targets, while some SAC and TD3 agents are able to come close on a few targets. A2C only comes close to the heuristic on producing sodium chloride.The average return as a function of training steps for each algorithm is shown in Fig. 6. On average, the agents trained with each algorithm are able to achieve a return of at least 0.4. This is expected as even an agent taking random actions can achieve an average return of approximately 0.44. The agents trained with A2C, SAC, and TD3 do not perform much better than a random agent in most cases, however the ones trained with PPO significantly outperform it. While on average, A2C, SAC, and TD3 have similar performance, we saw in Fig. 5 that the best performing SAC and TD3 agents outperformed the best A2C agents.
The second RxN experiment uses reaction dynamics more complicated than the Wurtz reaction. In the Wurtz reaction, the agent need only add the required reactants for the desired product all together. In this new reaction, this is still true for some desired products, however not all of them. Similarly to the previous experiment, we also devised a heuristic agent for this experiment, which achieves an average return of approximately 0.83. For target materials E, F, G, and H, the required reaction is a single step process like before. Therefore the optimal behavior is to exclusively add the required reactants at step 1, and increase the temperature to speed up the reaction in order to produce as much of the target before the experiment ends. For target material I, the required reaction is a two step process, allowing for variation in how to material is produced. While all four reactants are required to produce I, adding them all at once would also produce E, wasting needed materials. Hence the optimal behavior is not necessarily producing all intermediate products simultaneously. As any two of the three intermediates can be safely produced simultaneously, the heuristic policy is designed to add only the reactants required for two intermediates products (we arbitrarily choose F and G). Given the limited number possibilities it is easily determined by brute force that step 6 is the optimal step for the heuristic policy to add the reactants required to create the third intermediate products.
Using the performance of the heuristic agent as reference again, the best and mean relative performances of the agents trained with each algorithm are shown in Fig. 7. Once again, PPO consistently produces agents that can match the performance of the heuristic agent. The best performing policies produced by A2C, SAC, and TD3 are able to nearly match the heuristic agent for all desired products excluding I. This is not unexpected as producing I requires producing intermediate products at different times during the reaction. On average, the policies produced by SAC and TD3 however, are unable to match the heuristic agent when asked to produce E. This is also not unexpected, given that producing E is penalized for all other desired products.
Unlike PPO, the other algorithms used appear to be less reliable at producing these best performing agents. This could be due to PPO learning these policies much faster than the other algorithms, as seen in Fig. 8. Since PPO converges to optimal behavior so quickly, there's very little room for variation in the policy. The other algorithms however are slowly converging to non-optimal behaviors, leaving much more room for variation in the policies (and returns) that they converge to.
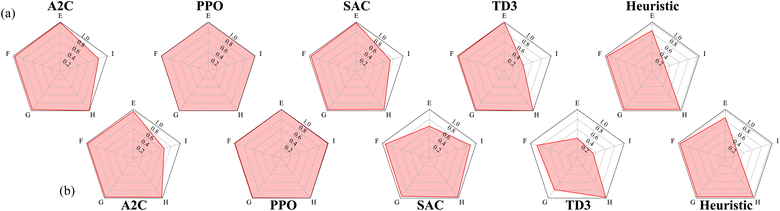
For the best performing agents produced by each algorithm, the average action values for each target are shown in Fig. 9. Looking at the heuristic policy, a constant action can be used for each target product, excluding I. When the target is I, the desired action must change after several steps have passed, meaning the agent cannot just rely on what the specified target is. Note that if all of a material has been added by step t, then it does not matter what value is specified for adding that material at step t + 1.
The best performing agent for each algorithm were all able to produce E when requested and Fig. 9 shows that they each have learned to add A, B, C, and not D. It can also be seen that all four algorithms learned to add two of A, B, or C in addition to D, then add the third one several steps later when I is the target product, mimicking the behavior of the heuristic policy. Note that even though the heuristic waits to add C, waiting to add A or B instead would be equally optimal. While each algorithm does this, PPO and A2C do so better than the others. PPO is also the only one that succeeds in both of these cases, showing that an RL agent can learn the required behavior in this system.
7.2 Extraction bench
With the results seen in the RxN tests, we now move onto the extraction bench (ExT) experiment. Regardless of the target material in our Wurtz extraction experiment, the optimal behavior is quite similar so we will not focus on the different cases as before. Since the ExT uses discrete actions, we replace SAC and TD3 with DQN. We also use what we call PPO-XL which is PPO trained with more environments in parallel. PPO-XL was not implemented for the RxN tests as regular PPO was able to achieve optimal results as it is, thus not justifying the increased computational cost associated with PPO-XL.Unlike the reaction bench, we do not have an analytic solution for this bench, therefore we have devised a heuristic policy for this experiment based on what an undergraduate chemist would learn. These lessons involve adding a solvent of opposite polarity to the existing solution (i.e., adding a non-polar solvent to a vessel containing a polar solvent solution or vice versa), mixing everything, letting it settle until distinct layers are formed, and separating the two solvents into separate vessels. The vessel containing the solvent with a similar polarity to the target material is kept while the other vessel is discarded. Thus, our heuristic policy is designed mimic this behavior. However, as the dynamics are more complex we do not necessarily expect it to be optimal.
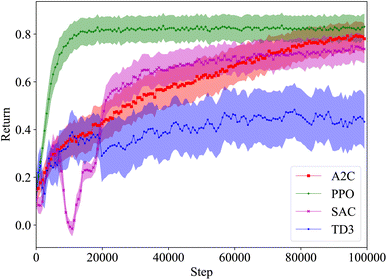
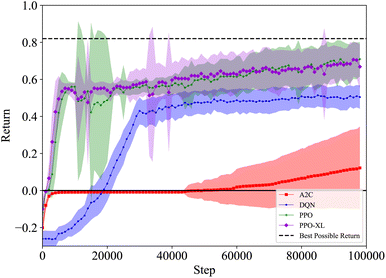
As seen in Fig. 10, the agents trained with A2C do not achieve a return above zero, while the agents trained with DQN ended up achieving a negative return. Not only do both PPO and PPO-XL produce agents that achieve significantly more reward than the other algorithms, they are able to outperform the heuristic policy as well. On average, the best performing agent trained with PPO-XL manages to achieve a return of approximately 0.1 higher than the heuristic (see Fig. 10), resulting in roughly a 10% higher solute purity. While there is a large variance in the final performance of the agents trained with PPO and PPO-XL, they consistently outperform the agents trained with the other algorithms.
As shown in Fig. 11, the action sequences of the policies learned from A2C, DQN, and PPO are quite different. The action sequences of the policies learned by PPO and PPO-XL are much more similar, as expected. The first half of these sequences are comparable to the heuristic, however the agents in both cases have learned a second component to the trajectory to achieve that extra return. Interestingly, both PPO and PPO-XL agents have learned to end the experiment when they achieve the desired results, whereas the A2C and DQN agents do not. PPO once again shows that an RL agent can learn the required behavior in this system.
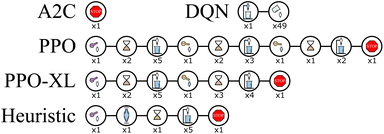 | ||
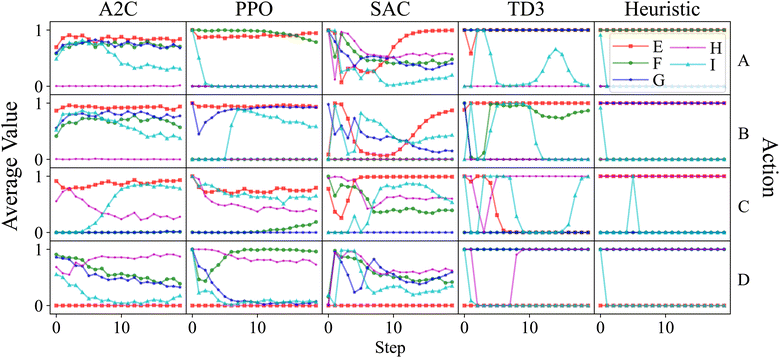
| Fig. 11 Wurtz ExT, the sequence of actions with the highest return when dodecane is the target material seen during the rollout of the best performing policy learned by each algorithm. Each picture represents an action and average value described by Fig. 3(d). The number beneath the image represents how many times that action was repeated. While it is more difficult to interpret these policies than with RxN, similarities can be seen between the PPO, PPO-XL, and heuristic policies, explaining their high performances. The A2C policy uses a similar action set, however in a different order, outlining the precision required by the agent. The DQN policy use many actions that either undo previous actions or do nothing in that specific state. | ||
7.3 Distillation bench
Lastly, we now move onto the final experiment, distillation bench (DiT). Similar to ExT, the desired target material in the Wurtz distillation experiment does not have much effect on the optimal behavior so we will not focus on the different target cases. Instead we will focus on the different cases of when salt is and is not present with another material in the initial distillation vessel. Note that a single agent operates on both of these cases, not two agents trained independently on each case.As before, we have devised a heuristic policy and as with the RxN experiments, we expect it to be optimal once again. In distillation, the optimal behavior is to heat the vessel until everything with a boiling point lower than the target material has boiled off, discarding the boiled off contents, then continuing to heat the vessel until just the target material has boiled off, condensing in a separate vessel. Our heuristic policy is designed to mimic this behavior.
In Fig. 12 we can see that on average, the algorithms (excluding A2C) converge faster than in the other experiments, however, there is much less variation in return compared to before. For the case when no salt is present in the distillation vessel, the best-performing agents trained with each algorithm learn a very similar policy to the heuristic one, as seen in Fig. 13. They heat the vessel until the solvent has boiled away, then end the experiment. For the case when salt and additional material are present, the best-performing agents trained with PPO and PPO-XL modify their actions similar to the heuristic policy, achieving the optimal return in both cases. The best-performing agent trained with A2C modifies their actions in a similar fashion, however, it does so in a way that also achieves a much lower return. The best-performing agent trained with DQN makes much more significant changes to their policy, however, it still achieves a return closer to optimal than A2C. This shows that the expected behavior in our final bench can also be learned by an RL agent.
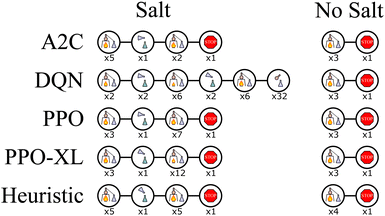 | ||
| Fig. 13 Wurtz DiT, the sequences of actions with the highest return produced by the best performing policy learned with each algorithm for two cases: when salt is and is not initially present in the distillation vessel with another material. Each picture represents an action and average value described by Fig. 4. The number beneath the image represents how many times that action was repeated. The PPO, PPO-XL, and heuristic policies are nearly identical in both cases, with only minor differences. When no salt is present, the A2C and DQN policies are similar to the others, however when salt is present they continue to behave as if it is not. | ||
8. Limitations
ChemGymRL has limitations; any reaction or material that one wishes to model must be predefined with all properties specified by the user. Additionally, the solvent dynamics are modeled using simple approximations and while they suffice for these introductory tests, they would not for real-world chemistry.As previously mentioned, the ChemGymRL framework was designed in a modular fashion for the ease of improvement. The differential equations used to model the reactions could be replaced with a molecular dynamics simulation. This would allow RxN to operate with on a more generalizable rule-set. Without having to manually define the possible reactions, the RxN could be used to discover new, more efficient reaction pathways by an RL agent. Currently, the reward metric used in RxN is the molar amount of desired material produced by the agent. If this metric was changed to reflect a certain desired property for the produced material, then the RxN could be used for drug discovery. Making similar improvements to ExT and DiT, the RL agent could then learn to purify these new discoveries.
9. Future work
In future work, we intend to try some more recent variants of DQN and study the performance improvements obtained as a function of computational cost when these methods are used in ChemGymRL. Dueling DQN42 is one such suggestion from the literature to improve upon DQN, where the Q-values are split into two parts, the value function and the advantage function. Though dueling DQN can show better performance than DQN, it is known to take vastly more training time and require larger networks as compared to DQN.43 Similarly, several enhancements to experience replay techniques, such as prioritized experience replay44 and hindsight experience replay,45 could improve performance but take a longer training time as compared to DQN.In terms of the ChemGymRL library itself, the next step is to create a lab manager environment which will be constructed to allow an RL agent to operate the entire system. Using pre-trained agents for the individual benches, the lab manager agent would decide which vessel to give to which bench while also specifying the desired goal to each bench, in order to achieve the lab manager's own goal. The lab manager agent would make proper use of the agentless characterization bench introduced here as well, which will have characterization methods with associated costs. In addition to this, the implementation of new benches will be explored, allowing more complicated experiments to be conducted and new insights into the benefits and challenges of the integration of RL into automated chemistry and self-driving labs.
10. Conclusions
We have introduced and outlined the ChemGymRL interactive framework for RL in chemistry. We have included three benches that RL agents can operate and learn in. We also include a characterization bench for making observations and presented directions for improvement. To show these benches are operational, we have successfully, and reproducibly, trained at least one RL agent on each of them. Included in this framework is a vessel state format compatible with each bench, therefore allowing the outputs of one bench to be the input to another.In the Wurtz RxN experiment, A2C, SAC, and TD3 were not able to show better performances than an agent taking random actions, where PPO was able to achieve optimal returns on all targets. In the second RxN experiment, A2C, SAC, and TD3 were able to show performances that achieves optimal returns for one of the two difficult tasks, whereas PPO was able to achieve optimal returns on both.
In the Wurtz ExT experiment, A2C and DQN were not able to produce agents that perform better than doing nothing, whereas PPO was able to achieve higher returns than the devised heuristics. In the Wurtz DiT experiment each algorithm was able to produce an agent that performs better than doing nothing and much better than an agent taking random actions.
Finally, we included discussions on other RL algorithms that can be tried in ChemGymRL and how this environment will be extremely valuable to the broader RL research community. We hope to see a wide adoption of ChemGymRL within the set of test-beds commonly used by researchers in the RL community.
A. Appendix
A.1 RL testbed
ChemGymRL can provide a new training environment for RL researchers in various fields to explore (especially pertaining to different RL sub-areas like hierarchical RL,46 model-based RL,47 distributional RL,48 curriculum learning,49 constrained RL,50 inverse RL51etc.) while the majority of prior RL environments have focused on computer game domains with specific challenges for the RL community,‡ ChemGymRL pertains to a comparatively large space of RL challenges since it is associated with a real-world problem having open world difficulties. From the perspective of an RL researcher, there is a critical need for new test beds based on real-world applications that can test the limits of modern RL algorithms, which will accelerate the development of RL. ChemGymRL will be highly beneficial to the RL community in this context.From the perspective of a RL researcher, ChemGymRL provides a very useful training environment on a problem having real-world impact. While majority of prior RL environments focus on games, researchers now acknowledge that RL has become a mature technology that can be useful in a variety of real-world applications.54 RL is growing rapidly and many new sub-fields within RL have emerged over the last five years.26 In this section we highlight the specific RL areas where we think ChemGymRL will be helpful, with the objective of encouraging the RL community to adopt this library within their suite of RL training environments.
Table 2 captures a set of RL paradigms (and associated algorithms) where we believe ChemGymRL will be impactful. In the previous sections, we considered a small set of RL algorithms to benchmark performances in ChemGymRL. However, there are a much larger class of RL sub-fields where ChemGymRL can be used as a testbed.
| Paradigm | Algorithm | Other testbeds | ChemGymRL application |
|---|---|---|---|
| Model-based RL47 | I2A55 | Sokoban52 | Learn a model for chemical reactions and plan using the model |
| ME-TRPO56 | Mujoco57 | ||
| Curriculum learning49 | OOCG58 | Half field offense59 | Generate a curriculum of tasks across benches |
| ScreenNet60 | Minecraft53 | ||
| H-DRLN61 | StarCraft-II62 | ||
| CM3 (ref. 63) | SUMO64 | ||
| Reward shaping66 | RCPO65 | Mujoco57 | Provide shaping rewards for intermediate steps |
| DPBA67 | Cartpole68 | ||
| Partial observability70 | DRQN69 | Atari28 | True state not observed as in extraction bench |
| DNC56 | POPGym71 | ||
| Distributional RL48 | C51 (ref. 48) | Atari28 | Policy based on distribution of reagents produced for every action |
| QR-DQN72 | Windy gridworld68 | ||
| Experience replay methods74 | HER73 | Montezuma's revenge28 | Sparse rewards only obtained at the end of the episode |
| ERO75 | Mujoco57 | ||
| Learning from demonstations77 | DQfD76 | Atari28 | Demonstrations from hueristic/human policies |
| NAC78 | GTA-V78 | ||
| Hierarchical RL80 | Option-critic79 | Atari28 | Hierarchical policy in terms of benches (options) and low-level actions |
| AOC81 | Four rooms domain80 | ||
| Constrained RL83 | IPO82 | Safety gym83 | Safe handing of chemical reagents |
| CPO84 | Mujoco57 |
Traditionally most RL methods are model-free, where the transition dynamics is neither known nor learned by the algorithms,26 and most algorithms we considered in this paper fall into the model-free category. Alternatively, another class of algorithms combines planning85 and RL. These algorithms explicitly learn the transition dynamics model and then use this model to arrive at the optimal policy (by planning). Such algorithms are classified as model-based RL algorithms.47 Depending on the domain, model-based RL methods can be significantly more sample efficient than their widely used model-free counterparts.86 In ChemGymRL, model-based approaches that learn the transition dynamics can effectively plan over all the different possible ways of obtaining higher amounts of the target products from the input reactants.
Another class of methods applicable to ChemGymRL is the curriculum learning methods in RL.49 In this paradigm, RL problems that are too hard to learn from scratch can be broken down into a curriculum of tasks which can then be tackled individually. Curriculum learning methods generally have 3 key elements: task generation, sequencing, and transfer learning. Task generation is the process of generating a good set of tasks that are neither trivial nor too hard to solve. Sequencing is the process of generating a sequence (in terms of difficulty, cost etc.) of available tasks. Transfer learning focuses on strategies to transfer knowledge from one task to another (so that the agent does not have to learn each task from scratch). Generating desired products from available reactants is a complex process that requires learning policies across multiple benches in ChemGymRL. This renders itself well to the curriculum learning framework. Closely related to curriculum learning is the hierarchical RL approach using the options framework.46 Transferring higher-level knowledge across tasks can take the form of partial policies of options. Options can be seen as temporally extended actions which allow learning/planning over a sequence of lower-level actions.
The default reward function in ChemGymRL is sparse. For example, in the RxN the agent only receives a reward equal to the molar amount of the target material produced at the end of the episode. Reward shaping methods66 provide small rewards in intermediate steps to help the agent learn and converge faster. It is possible for reward shaping to change the optimal behaviour and make agents learn unintended policies. Potential-based reward shaping methods are a special class of reward shaping methods that preserves the optimality order over policies and does not affect the converged optimal behaviour of the MDP.87,88 Such methods can be used in ChemGymRL.
The benches in ChemGymRL are typically partially observable. For example, the ExT had (partial) observations that do not show the amount of dissolved solutes present nor their distribution throughout the solvents. In this paper, we have considered benchmarks that assume that the observation obtained is the true state (such methods perform surprisingly well in partially observable domains too, in many cases69). Alternatively, using other algorithms such as DRQN69 or DNC56 that explicitly reason over partial observations, is guaranteed to provide better empirical performances.
RL algorithms traditionally aim to maximize the expected utility using the Q-function or the value function. However, in many environments considering the entire distribution of returns rather than just the expected value has been demonstrated to be helpful.48 This distributional perspective of RL has gained a lot of attention recently in the RL research community.89 Distributional algorithms can show good performances in the ChemGymRL environments since the returns are typically multi-modal (in the sense of distributions) with more than one product expected to be produced as a result of chemical reactions. Hence, these methods can also use ChemGymRL as a testbed.
The commonly used RL algorithms such as DQN28 and deep deterministic policy gradients DDPG90 use an experience replay technique for improving sample efficiency and removing correlations between successive data samples. Recently, there have been many advances in RL algorithms that aim to improve the efficiency of the experience replay technique, especially in sparse reward settings. Several such algorithms, including the popular human experience replay (HER)73 and experience replay optimization (ERO)75 methods can be tested in ChemGymRL.
Another paradigm of interest is the learning from demonstrations (LfD), which combines imitation-learning from external demonstrations with RL approach of learning from the environment.77 The objective is to make use of pre-existing policies or human knowledge to accelerate the training of RL agents, as opposed to learning from scratch which is highly sample inefficient. In ChemGymRL, for all the benches we have provided heuristic policies that can be used as the external demonstrator to train RL algorithms. Popular LfD techniques like deep Q-learning from demonstrations (DQfD)76 and normalized actor-critic (NAC)78 are of interest in ChemGymRL.
Finally, while handing chemical reagents, it is not only sufficient to learn the most optimal policy that provides higher quantities of the required products but also use safe techniques that do not cause any harm or injuries to agents or humans using these reagents. Such constraints in learning the optimal behaviour can be principally incorporated within the Constrained RL framework.83 The constrained RL techniques like interior-point policy optimization (IPO) and constrained policy optimization (CPO)84 impose constraints in the MDP that curtail an agent's ability to explore, so that it can perform safe exploration.91 Such methods are also expected to be successful in ChemGymRL.
We would like to highlight in Table 2 that many of the other testbeds used by prior works pertained to computer games, video games, or robotic simulations. In this context, ChemGymRL provides an excellent alternative testbed that pertains to a real-world problem and helps in evaluating the performance of a large class of RL algorithms.
A.2 Reactions
As an example, consider the reaction X + Y → Z. Its system of differential equations is defined as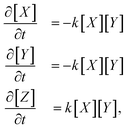 | (7) |
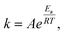 | (8) |
Chemical reactions of this form can be considered as special cases of the initial value problem:
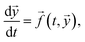 | (9) |
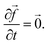 Note,
Note, ![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) are your concentrations and
are your concentrations and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) (t,
(t,![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) ) are your rates. The RK45 (Runge–Kutta–Fehlberg) method92 was used to solve these ODE equations and obtain new chemical concentrations as time passes.
) are your rates. The RK45 (Runge–Kutta–Fehlberg) method92 was used to solve these ODE equations and obtain new chemical concentrations as time passes.
A.3 Extractions
In the layer separation equations we present here, we consider the solvents settling as moving forward in time and mixing the contents of a vessel as moving backwards through time. This ExT uses Gaussian distributions to represent the solvent layers. For solvents L1, L2, …, Ln, the center of solvent Li, or mean of the Gaussian, is given by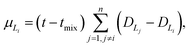 | (10) |
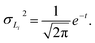 | (11) |
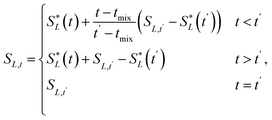 | (12) |
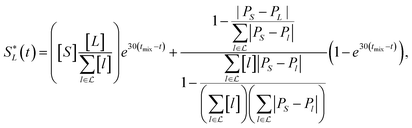 | (13) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is the set of all solvents in the vessel, and PX is the polarity of X.
is the set of all solvents in the vessel, and PX is the polarity of X.
Data availability
The code, training scripts, and analysis scripts supporting this article are available in the public github repository at the following URL: https://github.com/chemgymrl/chemgymrl.Author contributions
C. Beeler contributed to the conceptualization of this work, development of the ChemGymRL code used, source for background chemistry knowledge, development of project documentation, creation of figures, and writing of this article. S. Subramanian contributed to the conceptualization of this work, development of the ChemGymRL code used, source for background RL knowledge, RL experimentation, and writing of this article. K. Sprague contributed to the development of the ChemGymRL code used, development of project documentation, source of background RL knowledge, RL experimentation, creation of figures, and writing of this article. N. Chatti contributed to the conceptualization of this work and source for background RL knowledge. M. Shanen, N. Paquin, M. Baula, Z. Yang, and X. Li contributed to the development of the ChemGymRL code used. A. Dawit contributed to the development of project documentation. C. Bellinger, M. Crowley, and I. Tamblyn served as the principle investigators for this work, contributing to all aspects listed above.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. Beeler and C. Bellinger performed work at the National Research Council of Canada under the AI4D program. I. Tamblyn and M. Crowley received two research grants from the National Research Council under the NRC AI4D program and under the NRC-UW Collaboration Centre. Additional funding from the NSERC Discovery Grant program also contributed to this project for M. Crowley.Notes and references
- J. S. Manzano, W. Hou, S. S. Zalesskiy, P. Frei, H. Wang, P. J. Kitson and L. Cronin, Nat. Chem., 2022, 14, 1311–1318 CrossRef CAS PubMed.
- B. P. MacLeod, F. G. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney and N. Taherimakhsousi, et al. , Nat. Commun., 2022, 13, 995 CrossRef CAS PubMed.
- B. P. MacLeod, F. G. Parlane, A. K. Brown, J. E. Hein and C. P. Berlinguette, Accelerated Materials Discovery, De Gruyter, 2022, pp. 105–122 Search PubMed.
- M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. Morgan Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu and A. Aspuru-Guzik, Acc. Chem. Res., 2022, 55, 2454–2466 CrossRef CAS PubMed.
- M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait, C. Amador-Bedolla and A. Aspuru-Guzik, Curr. Opin. Green Sustainable Chem., 2020, 25, 100370 CrossRef.
- Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, Sci. Adv., 2022, 8, eabo2626 CrossRef CAS PubMed.
- S. She, N. L. Bell, D. Zheng, J. S. Mathieson, M. D. Castro, D.-L. Long, J. Koehnke and L. Cronin, Chem, 2022, 8, 2734–2748 CAS.
- D. Caramelli, J. M. Granda, S. H. M. Mehr, D. Cambié, A. B. Henson and L. Cronin, ACS Cent. Sci., 2021, 7, 1821–1830 CrossRef CAS PubMed.
- H. Fakhruldeen, G. Pizzuto, J. Glowacki and A. I. Cooper, 2022 International Conference on Robotics and Automation (ICRA), 2022, pp. 6013–6019 Search PubMed.
- M. B. Rooney, B. P. MacLeod, R. Oldford, Z. J. Thompson, K. L. White, J. Tungjunyatham, B. J. Stankiewicz and C. P. Berlinguette, Digital Discovery, 2022, 1, 382–389 RSC.
- R. J. Hickman, P. Bannigan, Z. Bao, A. Aspuru-Guzik and C. Allen, Matter, 2023, 6, 1071–1081 CrossRef CAS PubMed.
- J. A. Bennett and M. Abolhasani, Curr. Opin. Chem. Eng., 2022, 36, 100831 CrossRef.
- L. Porwol, D. J. Kowalski, A. Henson, D.-L. Long, N. L. Bell and L. Cronin, Angew. Chem., 2020, 132, 11352–11357 CrossRef.
- S. H. M. Mehr, D. Caramelli and L. Cronin, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2220045120 CrossRef CAS PubMed.
- A. Bubliauskas, D. J. Blair, H. Powell-Davies, P. J. Kitson, M. D. Burke and L. Cronin, Angew. Chem., 2022, 134, e202116108 CrossRef.
- G. Pizzuto, J. De Berardinis, L. Longley, H. Fakhruldeen and A. I. Cooper, 2022 International Joint Conference on Neural Networks (IJCNN), 2022, pp. 1–7 Search PubMed.
- E. O. Pyzer-Knapp, L. Chen, G. M. Day and A. I. Cooper, Sci. Adv., 2021, 7, eabi4763 CrossRef CAS PubMed.
- X. Li, P. M. Maffettone, Y. Che, T. Liu, L. Chen and A. I. Cooper, Chem. Sci., 2021, 12, 10742–10754 RSC.
- M. Fievez, N. Taherimakhsousi, B. P. MacLeod, E. P. Booker, M. Matheron, M. Manceau, S. Cros, S. Berson and C. P. Berlinguette, 2022 IEEE 49th Photovoltaics Specialists Conference (PVSC), 2022, pp. 1072–1072 Search PubMed.
- N. Yoshikawa, K. Darvish, A. Garg and A. Aspuru-Guzik, Digital pipette: Open hardware for liquid transfer in self-driving laboratories, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-nvxkg.
- H. Choubisa, J. Abed, D. Mendoza, H. Matsumura, M. Sugimura, Z. Yao, Z. Wang, B. R. Sutherland, A. Aspuru-Guzik and E. H. Sargent, Matter, 2023, 6, 605–625 CrossRef CAS.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. Yunker, J. E. Hein and A. Aspuru-Guzik, PLoS One, 2020, 15, e0229862 CrossRef CAS PubMed.
- A. A. Volk, R. W. Epps, D. T. Yonemoto, B. S. Masters, F. N. Castellano, K. G. Reyes and M. Abolhasani, Nat. Commun., 2023, 14, 1403 CrossRef CAS PubMed.
- S. K. Gottipati, B. Sattarov, S. Niu, Y. Pathak, H. Wei, S. Liu, S. Blackburn, K. Thomas, C. Coley, J. Tang, et al., International Conference on Machine Learning, 2020, pp. 3668–3679 Search PubMed.
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3, 1337–1344 CrossRef CAS PubMed.
- R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, MIT press, 2018 Search PubMed.
- C. J. Watkins, PhD thesis, King’s College, Cambridge, UK, 1989.
- V. Mnih, K. Kavukcuoglu, D. Silver, A. a. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg and D. Hassabis, Nature, 2015, 518, 529–533 CrossRef CAS PubMed.
- J. Xiong, Q. Wang, Z. Yang, P. Sun, L. Han, Y. Zheng, H. Fu, T. Zhang, J. Liu and H. Liu, arXiv, 2018, preprint, arXiv:1810.06394.
- M. Ryu, Y. Chow, R. Anderson, C. Tjandraatmadja and C. Boutilier, arXiv, 2019, preprint, arXiv:1909.12397, DOI:10.48550/arXiv.1909.12397.
- C. Gaskett, D. Wettergreen and A. Zelinsky, Australasian Joint Conference on Artificial Intelligence, 1999, pp. 417–428 Search PubMed.
- R. S. Sutton, D. McAllester, S. Singh and Y. Mansour, Policy gradient methods for reinforcement learning with function approximation, Advances in neural information processing systems 12, 1999 Search PubMed.
- V. Konda and J. Tsitsiklis, Advances in Neural Information Processing Systems, 1999 Search PubMed.
- J. Peters, S. Vijayakumar and S. Schaal, European Conference on Machine Learning, 2005, pp. 280–291 Search PubMed.
- V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. P. Lillicrap, T. Harley, D. Silver and K. Kavukcuoglu, Proceedings of The 33rd International Conference on Machine Learning (ICML), 2016, pp. 1928–1937 Search PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, preprint, arXiv:1707.06347, DOI:10.48550/arXiv.1707.06347.
- T. Haarnoja, A. Zhou, P. Abbeel and S. Levine, International Conference on Machine Learning, 2018, pp. 1861–1870 Search PubMed.
- S. Fujimoto, H. Hoof and D. Meger, International Conference on Machine Learning, 2018, pp. 1587–1596 Search PubMed.
- A. Raffin, A. Hill, A. Gleave, A. Kanervisto, M. Ernestus and N. Dormann, J. Mach. Learn. Res., 2021, 22, 12348–12355 Search PubMed.
- H. van Hasselt, A. Guez and D. Silver, Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, February 12-17, 2016, Phoenix, Arizona, USA, 2016, pp. 2094–2100 Search PubMed.
- Q. Lan, Y. Pan, A. Fyshe and M. White, 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020, 2020 Search PubMed.
- Z. Wang, N. de Freitas and M. Lanctot, arXiv, 2015, preprint, arXiv:1511.06581, DOI:10.48550/arXiv.1511.06581.
- Z. Zhu, C. Hu, C. Zhu, Y. Zhu and Y. Sheng, J. Mar. Sci. Eng., 2021, 9, 1267 CrossRef.
- T. Schaul, J. Quan, I. Antonoglou and D. Silver, 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, May 2–4, 2016, Conference Track Proceedings, 2016 Search PubMed.
- M. Andrychowicz, D. Crow, A. Ray, J. Schneider, R. Fong, P. Welinder, B. McGrew, J. Tobin, P. Abbeel and W. Zaremba, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4–9, 2017, Long Beach, CA, USA, 2017, pp. 5048–5058 Search PubMed.
- R. S. Sutton, D. Precup and S. Singh, Artif. Intell., 1999, 112, 181–211 CrossRef.
- T. M. Moerland, J. Broekens, A. Plaat and C. M. Jonker, et al. , Found. Trends® Mach. Learn., 2023, 16, 1–118 CrossRef.
- M. G. Bellemare, W. Dabney and R. Munos, International Conference on Machine Learning, 2017, pp. 449–458 Search PubMed.
- S. Narvekar, B. Peng, M. Leonetti, J. Sinapov, M. E. Taylor and P. Stone, J. Mach. Learn. Res., 2020, 21, 7382–7431 Search PubMed.
- Y. Liu, A. Halev and X. Liu, The 30th International Joint Conference on Artificial Intelligence (IJCAI), 2021 Search PubMed.
- A. Y. Ng and S. J. Russell, ICML, June 29–July 2, 2000, Stanford University, Stanford, CA, USA, 2000, pp. 663–670 Search PubMed.
- Y. Shoham and G. Elidan, Proceedings of the International Symposium on Combinatorial Search, 2021, pp. 191–193 Search PubMed.
- W. H. Guss, B. Houghton, N. Topin, P. Wang, C. Codel, M. Veloso and R. Salakhutdinov, arXiv, 2019, preprint, arXiv:1907.13440, DOI:10.48550/arXiv.1907.13440.
- G. Dulac-Arnold, N. Levine, D. J. Mankowitz, J. Li, C. Paduraru, S. Gowal and T. Hester, Mach. Learn., 2021, 1, 1–50 Search PubMed.
- S. Racanière, T. Weber, D. Reichert, L. Buesing, A. Guez, D. Jimenez Rezende, A. Puigdomènech Badia, O. Vinyals, N. Heess and Y. Li, et al. , Adv. Neural Inform. Process. Syst., 2017, 30, 5691 Search PubMed.
- T. Kurutach, I. Clavera, Y. Duan, A. Tamar and P. Abbeel, arXiv, 2018, preprint, arXiv:1802.10592, DOI:10.48550/arXiv.1802.10592.
- E. Todorov, T. Erez and Y. Tassa, 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012, pp. 5026–5033 Search PubMed.
- F. L. D. Silva and A. H. R. Costa, Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, 2018, pp. 1026–1034 Search PubMed.
- M. Hausknecht, P. Mupparaju, S. Subramanian, S. Kalyanakrishnan and P. Stone, AAMAS Adaptive Learning Agents (ALA) Workshop, 2016 Search PubMed.
- T.-H. Kim and J. Choi, arXiv, 2018, preprint, arXiv:1801.00904, DOI:10.48550/arXiv.1801.00904.
- C. Tessler, S. Givony, T. Zahavy, D. Mankowitz and S. Mannor, Proceedings of the AAAI Conference on Artificial Intelligence, 2017 Search PubMed.
- M. Samvelyan, T. Rashid, C. S. De Witt, G. Farquhar, N. Nardelli, T. G. Rudner, C.-M. Hung, P. H. Torr, J. Foerster and S. Whiteson, arXiv, 2019, preprint, arXiv:1902.04043, DOI:10.48550/arXiv.1902.04043.
- J. Yang, A. Nakhaei, D. Isele, K. Fujimura and H. Zha, arXiv, 2018, preprint, arXiv:1809.05188, DOI:10.48550/arXiv.1809.05188.
- P. A. Lopez, M. Behrisch, L. Bieker-Walz, J. Erdmann, Y.-P. Flötteröd, R. Hilbrich, L. Lücken, J. Rummel, P. Wagner and E. Wießner, 2018 21st International Conference on Intelligent Transportation Systems (ITSC), 2018, pp. 2575–2582 Search PubMed.
- C. Tessler, D. J. Mankowitz and S. Mannor, arXiv, 2018, preprint, arXiv:1805.11074, DOI:10.48550/arXiv.1805.11074.
- A. D. Laud, Theory and Application of Reward Shaping in Reinforcement Learning, University of Illinois, Urbana-Champaign, 2004 Search PubMed.
- A. Harutyunyan, S. Devlin, P. Vrancx and A. Nowé, Proceedings of the AAAI Conference on Artificial Intelligence, 2015 Search PubMed.
- R. Sutton and A. Barto, Reinforcement Learning: An Introduction, MIT Press, Cambridge, MA, 1998, vol. 9 Search PubMed.
- M. Hausknecht and P. Stone, 2015 Aaai Fall Symposium Series, 2015 Search PubMed.
- A. Graves, G. Wayne, M. Reynolds, T. Harley, I. Danihelka, A. Grabska-Barwińska, S. G. Colmenarejo, E. Grefenstette, T. Ramalho and J. Agapiou, et al. , Nature, 2016, 538, 471–476 CrossRef PubMed.
- S. Morad, R. Kortvelesy, M. Bettini, S. Liwicki and A. Prorok, arXiv, 2023, preprint, arXiv:2303.01859, DOI:10.48550/arXiv.2303.01859.
- W. Dabney, M. Rowland, M. Bellemare and R. Munos, Proceedings of the AAAI Conference on Artificial Intelligence, 2018, DOI:10.1609/aaai.v32i1.11791.
- M. Andrychowicz, F. Wolski, A. Ray, J. Schneider, R. Fong, P. Welinder, B. McGrew, J. Tobin, O. Pieter Abbeel and W. Zaremba, Adv. Neural Inform. Process. Syst., 2017, 30, 5049 Search PubMed.
- W. Fedus, P. Ramachandran, R. Agarwal, Y. Bengio, H. Larochelle, M. Rowland and W. Dabney, International Conference on Machine Learning, 2020, pp. 3061–3071 Search PubMed.
- D. Zha, K.-H. Lai, K. Zhou and X. Hu, arXiv, 2019, preprint, arXiv:1906.08387, DOI:10.48550/arXiv.1906.08387.
- T. Hester, M. Vecerik, O. Pietquin, M. Lanctot, T. Schaul, B. Piot, D. Horgan, J. Quan, A. Sendonaris, I. Osband, et al., Proceedings of the AAAI Conference on Artificial Intelligence, 2018 Search PubMed.
- B. Piot, M. Geist and O. Pietquin, Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2014, Nancy, France, September 15–19, 2014. Proceedings, Part II 14, 2014, pp. 549–564 Search PubMed.
- Y. Gao, H. Xu, J. Lin, F. Yu, S. Levine and T. Darrell, arXiv, 2018, preprint, arXiv:1802.05313, DOI:10.48550/arXiv.1802.05313.
- P.-L. Bacon, J. Harb and D. Precup, Proceedings of the AAAI Conference on Artificial Intelligence, 2017 Search PubMed.
- R. S. Sutton, D. Precup and S. Singh, Artif. Intell., 1999, 112, 181–211 CrossRef.
- R. Chunduru and D. Precup, arXiv, 2022, preprint, arXiv:2201.02628, DOI:10.48550/arXiv.2201.02628.
- Y. Liu, J. Ding and X. Liu, Proceedings of the AAAI Conference on Artificial Intelligence, 2020, pp. 4940–4947 Search PubMed.
- A. Ray, J. Achiam and D. Amodei, arXiv, 2019, preprint, arXiv:1910.01708, DOI:10.48550/arXiv.1910.01708.
- J. Achiam, D. Held, A. Tamar and P. Abbeel, International Conference on Machine Learning, 2017, pp. 22–31 Search PubMed.
- S. J. Russell, Artificial Intelligence a Modern Approach, Pearson Education, Inc., 2010 Search PubMed.
- T. Wang, X. Bao, I. Clavera, J. Hoang, Y. Wen, E. Langlois, S. Zhang, G. Zhang, P. Abbeel and J. Ba, arXiv, 2019, preprint, arXiv:1907.02057, DOI:10.48550/arXiv.1907.02057.
- A. Y. Ng, D. Harada and S. J. Russell, Proceedings of the Sixteenth International Conference on Machine Learning (ICML 1999), June 27–30, 1999, Bled, Slovenia, 1999, pp. 278–287 Search PubMed.
- E. Wiewiora, G. W. Cottrell and C. Elkan, Proceedings of the Twentieth International Conference of Machine Learning (ICML 2003), August 21-24, 2003, Washington, DC, USA, 2003, pp. 792–799 Search PubMed.
- M. G. Bellemare, W. Dabney and M. Rowland, Distributional Reinforcement Learning, MIT Press, 2023 Search PubMed.
- T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver and D. Wierstra, arXiv, 2015, preprint, arXiv:1509.02971, DOI:10.48550/arXiv.1509.02971.
- J. Garcıa and F. Fernández, J. Mach. Learn. Res., 2015, 16, 1437–1480 Search PubMed.
- E. Hairer, S. P. Nørsett and G. Wanner, Solving Ordinary Differential Equations. 1, Nonstiff Problems, Springer-Vlg, 1993 Search PubMed.
Footnotes |
| † The Gymnasium API https://github.com/Farama-Foundation/Gymnasium is the continuing development name of the original OpenAI Gym library for RL environments. |
| ‡ For example Sokoban-RL52 pertains to model-based RL, MineRL53 corresponds to curriculum learning etc., however ChemGymRL is a general testbed that can support a wide-variety of RL paradigms and algorithms. |
| This journal is © The Royal Society of Chemistry 2024 |