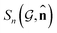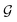Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A message passing neural network for predicting dipole moment dependent core electron excitation spectra†
Kiyou
Shibata
 * and
Teruyasu
Mizoguchi
* and
Teruyasu
Mizoguchi

Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan. E-mail: kiyou@iis.u-tokyo.ac.jp; Fax: +81-3-5452-6319; Tel: +81-3-5452-6320
First published on 26th March 2024
Abstract
Absorption near-edge structures in core electron excitation spectra reflect the anisotropy of orbitals in the final transition state and can be utilized for analyzing the local atomic environment, including its orientation. So far, the analysis of fine structures has primarily relied on fingerprint-matching with high-cost experimental or simulated spectra. If core electron excitation spectra, including their anisotropy, can be predicted at a low cost using machine learning, the application range of these spectra will be accelerated and extended to areas such as the orientation and electronic structure analysis of liquid crystals and organic solar cells at high spatial resolution. In this study, we introduce a message-passing neural network, named inversion symmetry-aware directional PaiNN (ISD-PaiNN) for predicting core electron excitation spectra using a unit direction vector in addition to molecular graphs as the input. Utilizing a database of calculated C K-edge spectra, we have confirmed that the network can predict core electron excitation spectra reflecting the anisotropy of molecules. Our model is expected to be expanded to other physical quantities in general that depend not only on molecular graphs but also on anisotropic vectors.
1 Introduction
Fine structures of core electron excitation spectra near the excitation edges, electron-energy loss near edge structure (ELNES) and X-ray absorption near edge structure (XANES or NEXAFS), have been widely used as some of the most effective fingerprints for determination of local atomic structures and electronic states. The fine structures reflect the excitation of an electron from an occupied core orbital to unoccupied orbitals. Since the fine structures differ depending on the symmetry of the orbital against the momentum transfer during the core electron excitation, orientation-dependence of the spectra can be used to analyze the local atomic environments including the anisotropic nature of orbitals. This kind of analysis has been applied for analyzing the orientation of molecules such as polymer films,1 liquid crystals2 and organic solar cells3,4 through analysis of orientation dependence of characteristic peaks corresponding to anisotropic orbitals. Meanwhile, quantitative analysis of fine structures has conventionally been performed by fingerprint matching of reference spectra obtained from standard samples with known structures, but it is difficult to apply to unknown structures.Recently, comparison with spectral shapes obtained by first-principles calculations has been used to analyze the experimental spectra.5–7 As the reference spectra can be obtained faster and on a larger scale with calculations than with experiments, databases of simulated core electron excitation spectra have been constructed and published.8–11 While experimental databases typically contain a few hundred spectra, simulated ones can include over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra. However, first-principles calculations are computationally expensive, and it is still difficult to obtain spectra exhaustively for a large number of candidate structures to identify unknown structures from experimental data without a priori structural information. It would be useful to develop a low-computational-cost alternative to first-principles calculations that can obtain spectra exhaustively for a large number of structures.
000 spectra. However, first-principles calculations are computationally expensive, and it is still difficult to obtain spectra exhaustively for a large number of candidate structures to identify unknown structures from experimental data without a priori structural information. It would be useful to develop a low-computational-cost alternative to first-principles calculations that can obtain spectra exhaustively for a large number of structures.
In this context, attempts have been made to predict spectra from molecular structures using machine learning models, and there have been several reports: prediction from molecular graphs using a message passing graph neural network (GNN),12 a deep neural network,13–15 and prediction using neural network ensemble through featurized local structural information.16 However, as far as the authors know, the prediction of core electron excitation spectra considering anisotropy according to the momentum transfer has not been proposed.
From the perspective of predicting physical quantities in general, many machine learning models for material science, not limited to the spectral example above have been proposed. Previous research in GNN architecture includes notable models such as DimeNet17 and GemNet18 that leverage invariance, both emphasizing the utilization of invariance properties. Exploring equivariance, PaiNN19 and NequIP20 have been proposed, employing strict equivariance constraints. Moreover, attempts to enhance expressive capabilities by slightly relaxing equivariance constraints and incorporating nonlinear transformations have been performed in SCN21 and eSCN.22 However, most models predict physical quantities that depend solely on the structure, overlooking the explicit integration of material anisotropy and directional dependencies. It is crucial to consider such directional dependencies when dealing with anisotropic physical quantities, including strain tensors, resistivity tensors, dielectric polarization, and phenomena like dipole transitions. These physical quantities and phenomena reflect the anisotropic nature of materials, and neglecting them in model construction could limit accurate predictions of material properties.
In this study, we developed a message passing neural network23 model named inversion symmetry-aware directional PaiNN (ISD-PaiNN) that can predict spectra due to the dipole transition. Our model can predict site-specific spectra which are dependent on not only the molecular graph but also the dipole moment direction relative to the molecular graph. Notably, our model consists of transformations that satisfy the physically required invariance of symmetric operations on the input pair of the molecular graph and dipole moment with respect to dipole transitions, ensuring an inductive bias with respect to the invariance.
2 Methods
2.1 Spatial symmetry constraints of dipole-transition spectra
In the limit of small angle electron scattering or long wavelength of the incident X-ray in ELNES and XANES, respectively, the core electron excitation process can be described in the form of a dipole transition. The transition matrix element for ELNES and XANES from an occupied initial state |ψi〉 to an unoccupied final state |ψf〉 is proportional to 〈ψi|q·r|ψf〉 and 〈ψi|![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ·r|ψf〉, respectively, where r is the relative position of the excited electron from the core, q is the momentum transfer, and
·r|ψf〉, respectively, where r is the relative position of the excited electron from the core, q is the momentum transfer, and ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) is the polarization vector. In either case, the generalized oscillator strength is proportional to the square of the transition matrix element, and the differential cross section of the energy loss spectrum can be expressed as a function of energy loss E as:
is the polarization vector. In either case, the generalized oscillator strength is proportional to the square of the transition matrix element, and the differential cross section of the energy loss spectrum can be expressed as a function of energy loss E as: | (1) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) is the unit directional vector parallel to the momentum transfer q or polarization vector
is the unit directional vector parallel to the momentum transfer q or polarization vector ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , and Ei and Ef are the energy eigenvalues of |ψi〉 and |ψf〉, respectively.
, and Ei and Ef are the energy eigenvalues of |ψi〉 and |ψf〉, respectively.
Based on eqn (1), we consider the constraints imposed on spectra associated with dipole transitions. Let 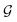 be the structural (molecular or crystal) graph defined by atomic numbers Zi and positions
be the structural (molecular or crystal) graph defined by atomic numbers Zi and positions 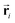 ,
, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the dipole vector, n site index as the input, and the target site-specific spectrum of n-th site in
the dipole vector, n site index as the input, and the target site-specific spectrum of n-th site in 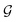 for the transition regarding
for the transition regarding ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ,
,  . The invariance of
. The invariance of 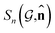 against symmetry operations are as follows:
against symmetry operations are as follows:
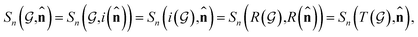 | (2) |
2.2 Model architecture
To satisfy the constraints in eqn (2), we employ the message passing neural network (MPNN)23 and referred to its variant, the polarizable atom interaction neural network (PaiNN).19The model takes atomic numbers 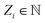 and atomic positions
and atomic positions 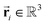 as inputs. Internally, it employs two node-wise features at each i-th site: an SO(3) equivariant 3D vector
as inputs. Internally, it employs two node-wise features at each i-th site: an SO(3) equivariant 3D vector 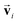 and an SO(3) invariant scalar si. The features
and an SO(3) invariant scalar si. The features 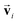 and si at the i-th site are initialized with zero vector
and si at the i-th site are initialized with zero vector 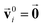 and embedded by atomic number Zi, respectively. Subsequently, they are updated by a message constructed with relative positional vectors between site i and j,
and embedded by atomic number Zi, respectively. Subsequently, they are updated by a message constructed with relative positional vectors between site i and j, 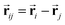 . The transformation of features
. The transformation of features 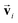 and si while preserving their equivariance and invariance, respectively, is achieved by properly constructed message and update functions.
and si while preserving their equivariance and invariance, respectively, is achieved by properly constructed message and update functions.
The design of the PaiNN implies a dependency of its model output solely on the input structural graph 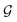 . Consequently, the PaiNN cannot incorporate additional information beyond
. Consequently, the PaiNN cannot incorporate additional information beyond 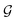 , such as directional information respective to
, such as directional information respective to 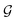 .
.
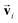 using a scaled vector constructed using the embedded representation specific to each elemental species:
using a scaled vector constructed using the embedded representation specific to each elemental species: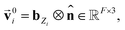 | (3) |
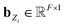 is the embedded representation for the Zi-th element, and F is the dimension of the embedded representation.
is the embedded representation for the Zi-th element, and F is the dimension of the embedded representation.
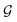 is satisfied by using translational invariant
is satisfied by using translational invariant 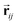 for the message block. The invariance and equivariance of features under R on both
for the message block. The invariance and equivariance of features under R on both 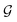 and
and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) are also satisfied by the message function in the PaiNN. However, the message function for
are also satisfied by the message function in the PaiNN. However, the message function for 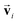 in the PaiNN is asymmetric under the inversion operation i on either
in the PaiNN is asymmetric under the inversion operation i on either 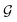 or
or ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , which also results in si being asymmetric under i due to the mixing of
, which also results in si being asymmetric under i due to the mixing of 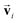 and si in the message and update functions. To satisfy the constraints concerning invariance against space inversion symmetry operation i, i.e.
and si in the message and update functions. To satisfy the constraints concerning invariance against space inversion symmetry operation i, i.e.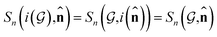 intrinsically, the message function for
intrinsically, the message function for 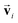 ,
, 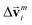 is modified slightly from one in the PaiNN as follows:
is modified slightly from one in the PaiNN as follows: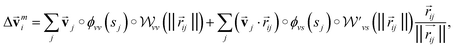 | (4) |
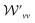 and
and 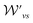 are the weight functions following eqn (8) in ref. 19. The modification is only on the second term and is just multiplying the inner product
are the weight functions following eqn (8) in ref. 19. The modification is only on the second term and is just multiplying the inner product 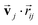 which is odd against
which is odd against 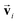 and
and 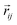 so that the overall message function is odd and even against the inversion operation i on
so that the overall message function is odd and even against the inversion operation i on 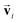 and
and 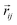 , respectively.
, respectively.
The other message function for si and the update functions are the same as those of the PaiNN. This modification makes si to be updated with 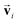 , which reflects the input direction
, which reflects the input direction ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) . As a result, si possesses even symmetry against i on
. As a result, si possesses even symmetry against i on 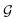 and
and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , which is the required invariance for
, which is the required invariance for 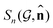 as described in eqn (2).
as described in eqn (2).
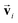 by using eqn (3) and the modified message function by using eqn (4) make si satisfy the required symmetry in eqn (2). The prediction of the site-specific spectrum is performed by converting si at the site of interest by using a multilayer perceptron consisting of two fully connected layers.
by using eqn (3) and the modified message function by using eqn (4) make si satisfy the required symmetry in eqn (2). The prediction of the site-specific spectrum is performed by converting si at the site of interest by using a multilayer perceptron consisting of two fully connected layers.
2.3 Dataset and training for evaluation
To validate the model, a spectral dataset that includes dipole vector dependent and site-specific oscillation intensity is needed. In this study, we validate our model with a simulated C K-edge spectral database of organic molecules,10 which is constructed by first-principles calculations based on density functional theory (DFT) and contains 117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 site-specific spectra for three typical directions of dipole vectors of symmetrically unique sites in 22
340 site-specific spectra for three typical directions of dipole vectors of symmetrically unique sites in 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 molecules with no more than eight non-hydrogen atoms (C, O, N, and F) in the QM9 database.24,25 We preprocessed the spectra with a Gaussian smearing of 0.5 eV in the energy range of 288–310 eV sampled equally spaced as 256 dimensional vectors for the objective variable. Spectral intensities were normalized by scaling the entire data set so that the averaged intensity of each spectrum in the energy range considered was 1, while preserving the relative magnitude relationship between the spectra at each site.
155 molecules with no more than eight non-hydrogen atoms (C, O, N, and F) in the QM9 database.24,25 We preprocessed the spectra with a Gaussian smearing of 0.5 eV in the energy range of 288–310 eV sampled equally spaced as 256 dimensional vectors for the objective variable. Spectral intensities were normalized by scaling the entire data set so that the averaged intensity of each spectrum in the energy range considered was 1, while preserving the relative magnitude relationship between the spectra at each site.
The model was developed by modifying the PaiNN implemented in the Open Catalyst Project's library opc26 with PyTorch Geometric27 and PyTorch,28 based on the description in Section 2.2.2–2.2.4. Mini-batch learning with a batch size of 32 molecular graphs was performed. The loss function is the mean squared error (MSE) between the predicted and reference spectra on carbon sites with available spectra. We used the Adam29 optimizer with a learning rate of 0.0001 for the learning process, implementing early stopping with a patience of 40 epochs.
3 Results and discussion
We evaluated the prediction performance using the processed C K-edge spectral dataset described in Section 2.3. The dataset was randomly divided: 80% for training and validation (in a ratio of 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2) and 20% for testing based on molecules. The number of anisotropic and site-specific spectra for training, validation, and testing were 221
0.2) and 20% for testing based on molecules. The number of anisotropic and site-specific spectra for training, validation, and testing were 221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274, 55
274, 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653, and 69
653, and 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477, respectively.
477, respectively.
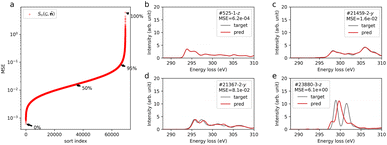
Fig. 1a shows the distribution of MSE, confirming that the over 95% data points have a MSE below 0.1. Fig. 1b–e show the predicted spectra (red line) and calculated results (gray line), sampled at typical percentiles at 0, 50, 95, and 100%, respectively as shown in Fig. 1a. For MSEs below 0.1 (Fig. 1b–d), the predicted spectra show good agreement with the calculated ones. Particularly, for the top 50% of MSEs, the predicted spectra closely resemble the calculated spectra. In the case of the worst-performing prediction (Fig. 1e), the general trend of peak distribution around 297 eV rising and falling at 305 eV is reproduced. However, accurate prediction of the major peaks is lacking. This specific spectrum corresponds to the trifluorocarbon site in molecule id #23880 (refer to ESI Fig. S7†). The poor prediction results might stem from the limited trifluorocarbon site data, consisting of only 87 sites within the 117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 sites in the database, and the distinct spectral features originating from chemical interactions with highly electronegative fluorine. Concerning the value of the MSE and metrics for spectral similarity, we evaluated the MSE and its use by comparing it with another metric by simulating spectra with added noise (see the ESI†).
340 sites in the database, and the distinct spectral features originating from chemical interactions with highly electronegative fluorine. Concerning the value of the MSE and metrics for spectral similarity, we evaluated the MSE and its use by comparing it with another metric by simulating spectra with added noise (see the ESI†).
Predictions account for relative intensity enables the derivation of molecular spectra by aggregating site-specific ones. Fig. 2 displays both the site-specific spectra and the molecular spectra of a representative molecule (id #10578) from QM9, which represents the median MSE for the molecular spectra (refer to the ESI†). Not only the site-specific spectra but the molecular spectra are also predicted correctly including their dipole moment direction dependence, which confirms potential applications for molecular structure analysis taking advantage of the anisotropic dipole transition.
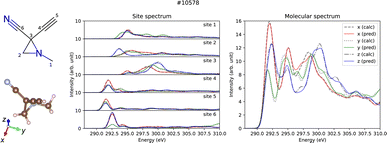 | ||
| Fig. 2 Prediction results of site-specific and molecular anisotropic C K-edge spectra for molecule id #10578 in QM9. The left panel shows the molecular structure formula and the three-dimensional structure drawn by RDKit30 and VESTA,31 respectively. Middle and right panels show the predicted (solid lines) and calculated (dotted lines) spectra for site-specific spectra for each C site and molecular spectra, respectively. | ||
In order to investigate the effectiveness of non-zero initialization of 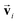 as given in eqn (3) and the modified message block outlined in eqn (4), we conducted ablation experiments by systematically altering these components and assessing the resulting prediction performances of the models (see the ESI†). The comparative analysis among the models reveals the crucial role of the non-zero initialization of
as given in eqn (3) and the modified message block outlined in eqn (4), we conducted ablation experiments by systematically altering these components and assessing the resulting prediction performances of the models (see the ESI†). The comparative analysis among the models reveals the crucial role of the non-zero initialization of 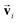 in accurate predictions. In addition, the utilization of the symmetrized message block demonstrates its effectiveness in improving overall prediction performance. We also evaluated the generalization performance of the model by scaffold splitting, a test on larger molecules, and prediction of orientation dependence of a specific molecule (see the ESI†). The results confirm the model's generalization ability to predict the spectra of molecules with different sizes and shapes. For the efficiency and speed of spectrum prediction, we also compared the computational cost of our model with that of first-principles calculations, and comfirmed that our model is 106 times faster than first-principles calculations (see the ESI†).
in accurate predictions. In addition, the utilization of the symmetrized message block demonstrates its effectiveness in improving overall prediction performance. We also evaluated the generalization performance of the model by scaffold splitting, a test on larger molecules, and prediction of orientation dependence of a specific molecule (see the ESI†). The results confirm the model's generalization ability to predict the spectra of molecules with different sizes and shapes. For the efficiency and speed of spectrum prediction, we also compared the computational cost of our model with that of first-principles calculations, and comfirmed that our model is 106 times faster than first-principles calculations (see the ESI†).
4 Conclusion
We propose a message passing neural network based on the PaiNN for predicting core electron excitation spectra considering its constraints on the physically required symmetry. We tested the model on C K-edge spectra of organic molecules, and it can predict the general shape of most of the site-specific spectra and molecular spectra including their dependence on the dipole moment direction.So far, analysis considering anisotropy of core electron excitation spectra requires a highly accurate reference, whether by calculations or an experiment. The cost of obtaining such a reference may become a bottleneck in the future, and our model, which is low-cost compared to first-principles calculations, will be useful for analyzing materials such as polymers, liquid cells, and organic solar cells.
Furthermore, the proposed model architecture is extended to be applied to targets other than ELNES/XANES by setting the required physical symmetry as an inductive bias to predict spectral data that physically depend on the orientation to molecules and crystals, which can advance GNN in materials science by explicitly incorporating directional dependencies in physical quantities alongside the representation of material graphs. This new approach complements the existing GNN paradigm by filling the gap in addressing directional aspects, fostering more accurate predictions in materials science. We anticipate that this novel strategy will contribute to an improved understanding of material anisotropy, offering innovative methodologies for detailed characterization.
Data availability
The code for the model IDS-PaiNN, scripts for training, and the data of the time comparison can be found at https://github.com/nmdl-mizo/isdpainn with https://doi.org/10.5281/zenodo.10554765. The simulated C-K edge spectral dataset for evaluation is originally published in ref. 10 and can be downloaded at https://doi.org/10.6084/m9.figshare.c.5494395.v1. The code of the dataset class for the C-K edge spectral dataset in PyTorch Geometric is available as a Python module C-K edge maker at https://github.com/nmdl-mizo/ck_edge_maker with https://doi.org/10.5281/zenodo.6352029. The weights of the trained model and MSEs for random split and scaffold split discussed in this paper are available at https://doi.org/10.5281/zenodo.10547719. The configuration, weights, and MSEs of the models for the ablation experiments are available at https://doi.org/10.5281/zenodo.10566201. The additional calculated data for evaluation of the amino acids and benzene rotation series are available on the NOMAD repository at https://doi.org/10.17172/NOMAD/2024.01.23-1 and https://doi.org/10.17172/NOMAD/2024.01.23-2, respectively.Author contributions
K. S.: conceptualization, data curation, formal analysis, investigation, methodology, software, writing. T. M.: project administration, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the Grant-in-Aid for Scientific Research (Grant No. 19H05787) from the MEXT and CREST (Grant No. JPMJCR1993) from the JST. The authors thank Kento Nishio, Naoto Kawaguchi, and Izumi Takahara for their helpful discussions.Notes and references
- M. G. Samant, J. Stöhr, H. R. Brown, T. P. Russell, J. M. Sands and S. K. Kumar, Macromolecules, 1996, 29, 8334–8342 CrossRef.
- N. Kawatsuki, Y. Taniguchi, M. Kondo, Y. Haruyama and S. Matsui, Macromolecules, 2015, 48, 2203–2210 CrossRef CAS.
- U. Aygül, D. Batchelor, U. Dettinger, S. Yilmaz, S. Allard, U. Scherf, H. Peisert and T. Chassé, J. Phys. Chem. C, 2012, 116, 4870–4874 CrossRef.
- H. Yao, L. Ye, H. Zhang, S. Li, S. Zhang and J. Hou, Chem. Rev., 2016, 116, 7397–7457 CrossRef CAS PubMed.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- J. Rehr and A. Ankudinov, Coord. Chem. Rev., 2005, 249, 131–140 CrossRef CAS.
- H. Ikeno and T. Mizoguchi, Microscopy, 2017, 66, 305–327 CAS.
- K. Mathew, C. Zheng, D. Winston, C. Chen, A. Dozier, J. J. Rehr, S. P. Ong and K. A. Persson, Sci. Data, 2018, 5, 180151 CrossRef CAS PubMed.
- Y. Chen, C. Chen, C. Zheng, S. Dwaraknath, M. K. Horton, J. Cabana, J. Rehr, J. Vinson, A. Dozier, J. J. Kas, K. A. Persson and S. P. Ong, Sci. Data, 2021, 8, 153 CrossRef CAS PubMed.
- K. Shibata, K. Kikumasa, S. Kiyohara and T. Mizoguchi, Sci. Data, 2022, 9, 214 CrossRef CAS PubMed.
- H. Guo, M. R. Carbone, C. Cao, J. Qu, Y. Du, S.-M. Bak, C. Weiland, F. Wang, S. Yoo, N. Artrith, A. Urban and D. Lu, Sci. Data, 2023, 10, 349 CrossRef CAS PubMed.
- M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401 CrossRef CAS PubMed.
- M. M. M. Madkhali, C. D. Rankine and T. J. Penfold, Phys. Chem. Chem. Phys., 2021, 23, 9259–9269 RSC.
- C. D. Rankine and T. J. Penfold, J. Chem. Phys., 2022, 156, 164102 CrossRef CAS PubMed.
- L. Watson, C. D. Rankine and T. J. Penfold, Phys. Chem. Chem. Phys., 2022, 24, 9156–9167 RSC.
- A. Ghose, M. Segal, F. Meng, Z. Liang, M. S. Hybertsen, X. Qu, E. Stavitski, S. Yoo, D. Lu and M. R. Carbone, Phys. Rev. Res., 2023, 5, 013180 CrossRef CAS.
- J. Gasteiger, J. Groß and S. Günnemann, Directional Message Passing for Molecular Graphs, arXiv, 2022, preprint, arXiv:2003.03123, DOI:10.48550/arXiv.2003.03123.
- J. Gasteiger, F. Becker and S. Günnemann, Universal Directional Graph Neural Networks for Molecules, arXiv, 2022, preprint, arXiv:2106.08903, DOI:10.48550/arXiv.2106.08903.
- K. T. Schütt, O. T. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, arXiv, 2021, preprint, arXiv:2102.03150, DOI:10.48550/arXiv.2102.03150.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- C. L. Zitnick, A. Das, A. Kolluru, J. Lan, M. Shuaibi, A. Sriram, Z. Ulissi and B. Wood, Spherical Channels for Modeling Atomic Interactions, arXiv, 2022, preprint, arXiv:2206.14331, DOI:10.48550/arXiv.2206.14331.
- S. Passaro and C. L. Zitnick, Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs, arXiv, 2023, preprint, arXiv:2302.03655, DOI:10.48550/arXiv.2302.03655.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Proceedings of the 34th International Conference on Machine Learning, 2017, pp. 1263–1272 Search PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- M. Fey and J. E. Lenssen, ICLR Workshop on Representation Learning on Graphs and Manifolds, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
- A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga and A. Lerer, 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 2017 Search PubMed.
- D. P. Kingma and J. Ba, A Method for Stochastic Optimization, arXiv, 2017, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- RDKit: Open-source cheminformatics, http://www.rdkit.org.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00021h |
| This journal is © The Royal Society of Chemistry 2024 |