Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bayesian optimisation for additive screening and yield improvements – beyond one-hot encoding†
Bojana
Ranković
 *a,
Ryan-Rhys
Griffiths
*a,
Ryan-Rhys
Griffiths
 b,
Henry B.
Moss
c and
Philippe
Schwaller
b,
Henry B.
Moss
c and
Philippe
Schwaller
 *a
*a
aLaboratory of Artificial Chemical Intelligence (LIAC), National Centre of Competence in Research (NCCR) Catalysis, Ecole Polytechnique Fédérale de Lausanne (EPFL), Switzerland. E-mail: bojana.rankovic@epfl.ch; philippe.schwaller@epfl.ch
bDepartment of Physics, University of Cambridge, UK
cDepartment of Applied Mathematics and Theoretical Physics, University of Cambridge, UK
First published on 2nd November 2023
Abstract
Reaction additives are critical in dictating the outcomes of chemical processes making their effective screening vital for research. Conventional high-throughput experimentation tools can screen multiple reaction components rapidly. However, they are prohibitively expensive, which puts them out of reach for many research groups. This work introduces a cost-effective alternative using Bayesian optimisation. We consider a unique reaction screening scenario evaluating a set of 720 additives across four different reactions, aiming to maximise UV210 product area absorption. The complexity of this setup challenges conventional methods for depicting reactions, such as one-hot encoding, rendering them inadequate. This constraint forces us to move towards more suitable reaction representations. We leverage a variety of molecular and reaction descriptors, initialisation strategies and Bayesian optimisation surrogate models and demonstrate convincing improvements over random search-inspired baselines. Importantly, our approach is generalisable and not limited to chemical additives, but can be applied to achieve yield improvements in diverse cross-couplings or other reactions, potentially unlocking access to new chemical spaces that are of interest to the chemical and pharmaceutical industries. The code is available at: https://github.com/schwallergroup/chaos.
1 Introduction
Artificial intelligence holds great promise to accelerate the chemical sciences.1–4 Over the last decade, we have witnessed ground-breaking advances in machine learning for de novo molecular design,5–10 synthesis planning,11–17 and reaction outcome prediction.18–26 Recently, research has focused on sequential model-based optimisation algorithms, particularly Bayesian optimisation (BO), to identify optimal conditions for chemical reactions effectively.27–38 As demonstrated in the space of chemical reactions, BO is particularly well suited for trading off exploration and exploitation in the low data regime. Surprisingly, most BO studies report one-hot encoding (OHE), that contains limited chemical information, to perform remarkably well.31,35 This recurring observation raises an important question: why does OHE, with its inherent simplicity manage to deliver competitive results? For instance, Shields et al.32 compared OHE to more elaborate reaction representations such as quantum mechanical (QM) descriptors. The study found no significant difference in optimisation performance stating these two representations “largely indistinguishable”. This conclusion emerges from evaluating BO across several reaction datasets including the optimisation of Buchwald Hartwig reactions. Consider the case of the Buchwald Hartwig dataset: five distinct reactions with 790 data points each, covering four variable components to optimise over – base, ligand, aryl halide and additive. Our study, while bearing similarities in examining four different Ni-catalysed photoredox decarboxylative arylations‡ reactions with 720 data points per reaction,39 has a distinguishing feature: all other reaction components remain fixed, except for the additive being screened. Consequently, the resulting OHE vectors create an orthogonal space where the number of dimensions equals the number of data points, making it difficult for any machine learning method to grasp valuable patterns. This inherent constraint forces us to think beyond OHE and leverage alternative representations to combine with BO and pinpoint the optimal additives for given chemical reactions. Accordingly, we have examined representations that not only address these limitations but also ensure computational efficiency on par with OHE.Additives are critical for altering the reactivity and outcome of chemical reactions.40,41 According to the IUPAC Gold Book definition, additives are “substances that can be added to a sample for any of a variety of purposes”.42 They are crucial in a range of chemical processes, including polymer synthesis, pharmaceutical development, and materials science.43–45 Identifying optimal additives can significantly enhance reaction efficiency, selectivity and yield, leading to cost-effective and sustainable chemical processes.46,47 In this study, we introduce a BO-based approach for efficient exploration of the additive§ search space. Subsequently, we explore a range of representation methods to determine the most appropriate ones for uncovering additive-induced yield improvements. This approach not only streamlines experimental design and optimisation but also holds immense promise for various applications within the field of chemistry. While Prieto Kullmer et al.39 screened these compounds using high-throughput experimentation (HTE), not all laboratories can access robotic platforms. Synthetic chemists, however, could highly benefit from using BO to discover the optimal additives, allowing them to improve a reaction without the need for exhaustive (and expensive) testing of all possible combinations (Fig. 1). Compared to existing applications of BO to chemical reactions (e.g., Buchwald–Hartwig reactions48), the additive dataset is substantially more challenging. Firstly, OHE is ill-suited for this task as it results in high-dimensional vectors, with only one active dimension per additive. The resulting extreme sparsity and lack of shared information make it difficult to address the complexities of the dataset. This kind of representation limits the use of machine learning models, which can struggle to extract valuable insights. While seemingly intuitive, we empirically confirm these shortcomings, with details in the results section. As we demonstrate, applying BO in this setting fails to improve over random search. Secondly, the additives in this paper exhibit greater structural diversity than the components screened in other HTE studies. This distinctiveness significantly increases the computational demands for generating human-labelled atomic or local QM descriptors. We overcome these limitations by using computationally efficient reaction and molecular representations with a maximal diversity initialisation scheme and flexible surrogate models. Finally, the inherent complexity of the dataset coupled with the limited predictive signal¶ between the representations and the output (yield) poses a significant challenge for optimisation. Existing research, however, suggests that the application of BO can still help reach promising results even in those scenarios.49 Despite these challenges, we demonstrate that augmenting BO with adequate reaction representations, initialisation schemes and appropriate surrogate models results in an efficient search towards the best-performing additives in less than 100 evaluations while using as little as ten initialisation reactions.
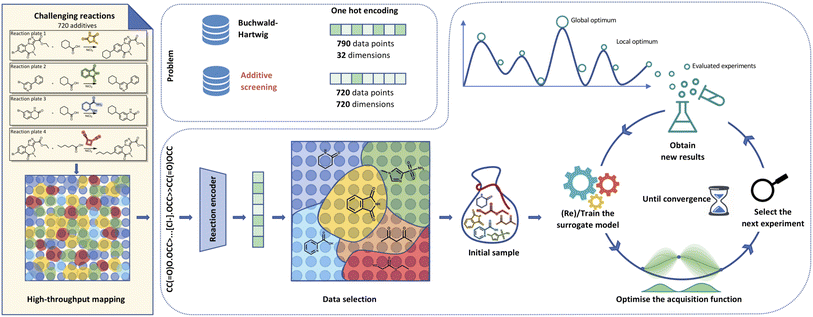 | ||
| Fig. 1 Visualisation of Bayesian optimisation pipeline for additive screening. Starting from the HTE dataset,39 we extract either additive smiles or reaction components to generate reaction smiles. We propagate these smiles through a molecular (i.e.) fingerprints, fragprints, xtb, cddd, mqn, chemberta or reaction encoder (rxnfp, drfp) into features. The built features allow us to select initial points leveraging methods like clustering to set up the Gaussian process surrogate model. The BO loop then runs for a predetermined number of iterations with the objective of reaching the global optimum that corresponds to the highest UV210 product area absorption. | ||
The structure of this paper is as follows: Section 2 details the data and the representations, Section 3 covers methodology, followed by a presentation and discussion of results in Section 4. We conclude and offer future directions in Sections 5 and 6.
2 Data
We obtained the data for this paper from a study by Prieto Kullmer et al.39 that explored the use of small organic additives to improve the reactivity of challenging Ni-catalysed photoredox decarboxylative arylation reactions in a high-throughput experimentation setup. They examined different cross-coupling reactions on separate reaction plates, each containing the same set of diverse additives. The aim was to determine additives that can further enhance the reaction efficiency of already highly reactive substrates. In total, the dataset consists of 720 additives used in four distinct reactions. We provide a brief description of each reaction below, with detailed explanations available in the ESI:†Reaction plate 1: investigates the impact of additives on the decarboxylative C–C coupling of Informer X2 (a highly reactive aryl halide substrate)50 and cyclohexanoic acid.
Reaction plate 2: explores the influence of additives on the coupling between 3-bromo-5-phenylpyridine and cyclohexanoic acid.
Reaction plate 3: examines the role of additives in the coupling of 7-bromo-3,4-dihydroquinolin-2(1H)-one with cyclohexanoic acid.
Reaction plate 4: assesses the effect of additives on the coupling between Informer X2 and hexanoic acid.
2.1 Data representation
Chemical reaction representations shape the reaction space and are therefore crucial in determining the success of the optimisation process.51–53 Different representations impact the efficiency and accuracy of optimisation by capturing unique chemical aspects. In each of the four reactions within the screening dataset, the additive stands out as the sole variable component, with all other components kept fixed.This property offers two primary ways to encode these reactions: one by isolating the additive and the other by considering the holistic reaction. The former pertains to molecular representations of the additive, while the latter could involve reaction fingerprints or global QM descriptors.
2.2 Molecular descriptors
Together with mqn descriptors,56–58 they offer representations summarising molecular structure. In our experiments, we leveraged both mqn descriptors and Morgan fingerprints (referred to as fingerprints henceforth). Additionally, we explored combining fingerprints with encoded fragments of a molecule (computed using RDKit59), essentially forming a more comprehensive representation (aptly coined fragprints60–63). The enriched fragprints provide insights into the overall structure and the specific constituents of the molecule. Though computationally efficient compared to descriptors involving intensive human labour or simulations, traditional cheminformatics descriptors might not capture the complexity of chemical interactions.
We focus on data-driven methods that utilise simplified molecular-input line-entry system (SMILES) representations.67 smiles codes are textual representations of molecules that encode the molecular graph structure in a simple string format. Their textual nature allows employing advanced machine learning models originally designed for natural language processing tasks.68 These models can interpret the ‘syntax’ and ‘grammar’ of smiles to extract chemically meaningful features leading to a multitude of data-driven representation methods.69–73 In this study, we specifically employ two data-driven molecular descriptors. First, CDDD (Continuous and Data-Driven molecular Descriptors), which translates between semantically equivalent but syntactically different molecular structures like smiles and InChI representations.70 Second, ChemBERTa, a BERT-based model pre-trained on a large corpus of chemical smiles strings using an optimised pretraining procedure.71,74,75
2.3 Reaction descriptors
Translating from molecular descriptors to reactions poses an interesting challenge. For instance, Schneider et al.76 computes the reaction fingerprint by subtracting the molecular fingerprints54,55 of the reactants from those of the products. Another approach is to concatenate different reaction components and create an information-rich final vector. Although this method offers considerable flexibility, it comes with the ‘curse of dimensionality’:77 concatenated vectors can quickly increase in size based on the number of reaction components. This property can limit their general applicability, as the variable number of reaction components creates variable-sized vectors, which are inconvenient for machine learning models. A straightforward yet effective alternative is one-hot encoding (OHE). This technique maps each component of the reaction to a unique binary vector, where a single active dimension indicates the presence of that specific component. To represent the entire reaction, we can concatenate these one-hot encoded vectors resulting in a fixed-size binary vector, serving as a surprisingly effective representation for Bayesian optimisation of chemical reactions, although, as already mentioned, less suitable for our use case.Recent approaches have looked to map reactions directly to a fingerprint, independent of the number of reaction components and the underlying representation. Schwaller et al.69 derived data-driven reaction fingerprints (RXNFP) directly from the reaction smiles by employing transformer models78 trained for reaction type classification tasks. Reaction smiles is an extension of the regular smiles notation that represents not just a single molecule, but entire chemical reactions. It includes the smiles strings of reactants and reagents on one side (separated by dots) and the product on the other side, separated by a special character “>>”. The benefit of this approach is its ability to map reactions to highly versatile continuous representations regardless of the number of reaction components. However, using rxnfp in this project's scope might not be adequate since additives play a relatively minor role in reaction type classification. On the other hand, Probst et al.79 introduced the differential reaction fingerprint (DRFP). This representation is based on the symmetric difference|| of two sets generated from the molecules listed left (reactants and reagents) and right (products) from the reaction arrow using a method that captures the environments around atoms in a radial manner, termed ‘circular molecular n-grams’. Their design makes them extremely flexible, effectively encoding the interplay of diverse reaction elements and maintaining a robust performance in scenarios where both a single or multiple reaction components may vary.
3 Methods
In this section, we detail our methodological approach to using Bayesian optimisation for the chemical dataset in question. We first describe the specific Bayesian optimisation framework employed, its necessary elements such as the surrogate model, acquisition functions and strategies employed to initialise the BO search.Several components play crucial roles in determining the outcome of BO-based search strategy. Firstly, the representation of chemical reactions dictates how the model interprets the data. Secondly, the kernel choice in the surrogate model shapes the learned relationships between data points. Thirdly, the initialisation strategy influences the starting point and path of the optimisation process. Lastly, the acquisition function guides the decision on where to sample next.
We applied BO on a dataset of 720 screened additives across four unique reactions aiming to maximise the UV210 product area absorption. To evaluate the BO approach, we initiate the search with a set of 10 starting points. The optimisation process runs for up to 100 iterations during which we monitor the performance against the remaining dataset, comprising over 600 data points. We measure the success of the optimisation by assessing how many of the top performing reactions we identify during these iterations. For this reason, we define a top-n neighbourhood metric as a set of n reactions with the highest yield for each reaction plate. The motivation behind the top-n neighbourhood search is to provide a diverse set of high-performing additives, giving researchers more flexibility in their choice based on factors such as availability, complexity, and price. This approach allows for a more flexible and pragmatic selection of additives and reflects the practical constraints and requirements of real-world applications. To find the optimal configuration, we carry out a grid search over combinations of parameters, namely data representation, kernel, initialisation strategy and acquisition function, repeating the runs across 20 different seed values to ensure robust findings. The limitation with one-hot encoding OHE on this dataset directed us towards the exploration of other molecular and reaction representations, both computationally and chemically reasonable, while steering away from the intensive demands of quantum molecular descriptors. For data representation, we extensively evaluated fingerprints, fragprints, mqn and xtb features, data-driven cddd and chemberta descriptors and holistic reaction representations such as rxnfp, drfp and OHE. We used a Gaussian process surrogate model and assessed the influence of different kernels (Matern, Tanimoto, Linear). To select the 10 starting points we used an initialisation strategy (random, clustering and maximising the minimum distance between the selected points) and for guiding the search towards promising regions we compared acquisition functions—upper confidence bound (UCB) and expected improvement (EI). The core objective of this study was to identify whether BO can emulate or even surpass the outcomes of HTE and if so, under which configuration. We used the first of the four available reactions to evaluate the combinations of parameters over 20 different seed-runs and finally carried out the optimisation loop for the remaining reactions using the best-performing setup.
Below, we delve deeper into each of the necessary BO elements (Table 1), explaining our choices and their implications.
| Variables | Values |
|---|---|
| Kernel | Matern, Tanimoto, Linear |
| Initialisation | Clustering, Maxmin, Random |
| Acquisition | ei, ucb |
| Representation | drfp, rxnfp, OHE, cddd, xtb, fingerprints |
| fragprints, mqn, chemberta |
3.1 Bayesian optimisation
We can define many problems in scientific discovery as a global optimisation task of the form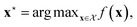 | (1) |
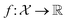 is a function over a design space
is a function over a design space 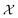 . As previously discussed, the molecular and reaction design space can be both discrete and continuous, and can consist of structured data representations such as graphs and strings. Eqn (1) is a black-box optimisation problem as we do not know the analytic form of f or its gradients and may only query f pointwise. Furthermore, evaluations of f require laboratory experiments and are high-cost and time-consuming. Lastly, our observations of f are subject to a (potentially heteroscedastic80,81) noise process. BO82 is an adaptive strategy that has recently emerged as a powerful solution method for black-box optimisation problems with proven success in applications including machine learning hyperparameter optimisation,83,84 chemical reaction optimisation,32 protein design,85 and as a sub-component in AlphaGo86 and Amazon Alexa.87 The ESI 1 provides pseudo-code for bo and more details on the algorithm.† The readers who wish to delve further into the mechanics and philosophy of Bayesian optimisation can refer to a vast collection of standout resources. For a more application-focused introduction, the documentation for Meta's Adaptive Experimentation (Ax) Platform offers a comprehensive yet accessible overview.88 Complementary, those seeking a rigorous understanding with mathematical foundations can refer to.89
. As previously discussed, the molecular and reaction design space can be both discrete and continuous, and can consist of structured data representations such as graphs and strings. Eqn (1) is a black-box optimisation problem as we do not know the analytic form of f or its gradients and may only query f pointwise. Furthermore, evaluations of f require laboratory experiments and are high-cost and time-consuming. Lastly, our observations of f are subject to a (potentially heteroscedastic80,81) noise process. BO82 is an adaptive strategy that has recently emerged as a powerful solution method for black-box optimisation problems with proven success in applications including machine learning hyperparameter optimisation,83,84 chemical reaction optimisation,32 protein design,85 and as a sub-component in AlphaGo86 and Amazon Alexa.87 The ESI 1 provides pseudo-code for bo and more details on the algorithm.† The readers who wish to delve further into the mechanics and philosophy of Bayesian optimisation can refer to a vast collection of standout resources. For a more application-focused introduction, the documentation for Meta's Adaptive Experimentation (Ax) Platform offers a comprehensive yet accessible overview.88 Complementary, those seeking a rigorous understanding with mathematical foundations can refer to.89
3.2 Surrogate model
The backbone of Bayesian optimisation is a surrogate model approximating the complex relationships and dependencies within the data. A surrogate model is a probabilistic method that acts as a replacement for the true objective function. For its role in BO, the surrogate must combine two primary components: a prediction model and uncertainty estimates. The prediction model produces the mean function value (subject to measurement noise) across the input space. The uncertainty estimates quantify the model's confidence in its predictions.This definition allows a variety of models to act as surrogate components in the Bayesian optimisation setup. Any model that can output predictions over the input space and confidence over predictions is a potential choice for a surrogate model. A favoured selection is often a Gaussian process because of its flexibility, simplicity, and ability to capture complex functions with relatively few hyperparameters to tune (admitting second-order optimisers such as L-BFGS-B,90 for the marginal likelihood loss function).
Gaussian processes easily adapt to different problem domains by changing the kernel function, which defines the covariance structure between input points. In Gaussian processes, kernel functions measure the similarity between data points in the input space. This similarity is then used to predict the function value for a new input by considering its proximity to previously evaluated data points. Different kernel functions can capture different types of relationships between data,91,92 and their choice plays a significant role in determining the properties of the surrogate model, such as smoothness, periodicity, and stationarity. Selecting kernel functions that are appropriate for the chosen reaction representations is essential in the context of reaction optimisation.
Among the kernels developed for chemical reactions, we find the Tanimoto kernel62,93,94 effective for binary representations due to its ability to quantify structural overlap. The Linear kernel is often sufficient if the descriptors are informative enough or the problem has a Linear nature. Additionally, we consider the Matern kernel for its flexibility in capturing varying degrees of smoothness in the data, making it a suitable choice for more complex reaction spaces.
3.3 Acquisition function
A flexible probabilistic surrogate model captures prior beliefs about the black-box objective f(x) guiding the acquisition function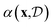 towards promising regions of the search space. The acquisition function balances between the exploration of uncertain regions and the exploitation of high-yield areas. More specifically, exploration refers to sampling points in the design space where the model's prediction uncertainty is high, while exploitation involves sampling points where the model predicts high function values. This trade-off is central to the success of Bayesian optimisation, as it ensures that the method does not prematurely converge to suboptimal solutions. From a computational standpoint, the acquisition function should be cheaper to evaluate and easier to optimise relative to the black-box function.95–98 In the context of chemical reaction optimisation, computational overhead from BO is often negligible compared to the time and resource drain of actual chemical experiments.
towards promising regions of the search space. The acquisition function balances between the exploration of uncertain regions and the exploitation of high-yield areas. More specifically, exploration refers to sampling points in the design space where the model's prediction uncertainty is high, while exploitation involves sampling points where the model predicts high function values. This trade-off is central to the success of Bayesian optimisation, as it ensures that the method does not prematurely converge to suboptimal solutions. From a computational standpoint, the acquisition function should be cheaper to evaluate and easier to optimise relative to the black-box function.95–98 In the context of chemical reaction optimisation, computational overhead from BO is often negligible compared to the time and resource drain of actual chemical experiments.
3.4 Design spaces: reaction versus BO configuration
In reaction optimisation, two design spaces serve distinct yet interlinked roles. The “reaction design space” covers the possible combinations of reaction components and conditions, and the “BO configuration design space” entails the model parameters and optimisation frameworks facilitating exploration of the reaction design space.Reaction design space contains potential combinations of additives, reactants, catalysts, solvents, and reaction conditions such as temperature, pressure and concentration. In this study, the focus narrows down to a set of possible additives.
On the other hand, Bayesian optimisation configuration design space includes model parameters and optimisation frameworks that enable effective exploration of the reaction design space. Here we explore parameters such as the choice of reaction representations, kernel functions and data initialisation methods. Understanding the interplay between these factors is key to achieving efficient search and optimisation. For example, kernel choice may depend on the reaction representation which, as a consequence, dictates the optimisation success.
3.5 Model initialisation
Initialising the BO algorithm with a diverse set of sample data is one of the determining factors for effective reaction optimisation.34 Using Gaussian processes as the surrogate models allows us to operate effectively within the low data regime due to their well-calibrated uncertainty estimates. For a detailed description of the Gaussian process in the context of structured inputs, ref. 61 and 62.In the domain of chemistry, operating within a low data regime is often the norm rather than the exception. Furthermore, chemists might face a dual incentive when empowered with BO solutions: starting the optimisation process early to save time and resources, while also needing a diverse set of data to initialise the optimisation models effectively.
A Gaussian process surrogate model, although well-suited to limited data settings, achieves a more comprehensive understanding of the underlying data function when initialised with a diverse set of data points incorporating prior knowledge of the design space.99–101 This selection leads to increased precision in uncertainty measurements, and subsequently, more accurate model predictions. To achieve this, we employ maximum diversity initialisation schemes that enable us to explore the structured search space of reactions and select a representative sample of points to accelerate the optimisation process. These schemes include clustering, maximal coverage, and random sampling baseline.
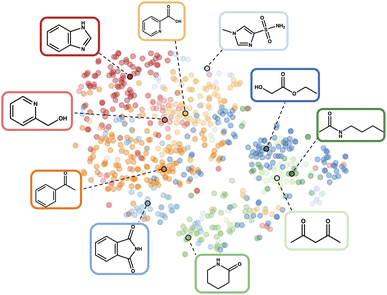 | ||
| Fig. 2 t-SNE visualisation102 of the fragprints representation of Reaction 1 in the latent space. The colours describe the clusters, highlighting the central additives with their corresponding molecular structures. We discover the phthalimide additive, identified as the best overall additive in the original study, within the initial clustering. This compelling side effect of the clustering demonstrates its ability to effectively describe the latent space and identify appropriate initial additives. | ||
4 Results & discussion
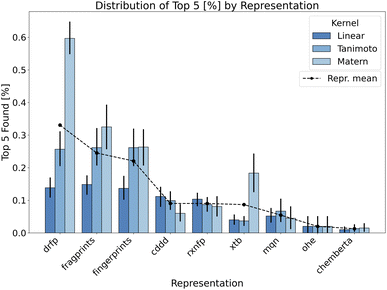
This segment provides a comprehensive assessment of the BO approach when applied to the additive screening dataset. With the established methodological procedures outlined in the Methods section, we now turn to the results obtained from varied configurations and parameters including reaction representations, surrogate model kernels, data initialisation strategies and acquisition functions.To reiterate, we focus on identifying the top-performing reactions within the evaluated BO iterations. This is measured using the top-n neighbourhood metric, aiming for a selective and diverse array of high-yield reactions. As a compromise between top one and top 10 discovered additives and aiming for a clear visualisation we show the percentage of top five performing additives discovered during the optimisation process across different representations in the Fig. 3. The same plot shows a significant importance of the reaction representation choice for the success of the BO strategy. Given the unique nature of additive screening, we can encode reactions using either reaction or molecular descriptors. As the additive is the only variable component in additive screening, it uniquely describes each data point per reaction in the dataset. However, reaction representations, like drfp, inherently capture more comprehensive information by considering the interplay of all reaction components. This representation emerged as particularly effective, especially when combined with Matern kernel, contrasting our expectations about the binary-tailored Tanimoto kernel. Moreover, Matern kernel dominates other alternatives over majority of representations highlighting its adaptability and robustness.
Focusing on the internal structure of additives only, both fingerprints and fragprints emerge as strong contenders. The slight advantage of fragprints suggests the potential relevance of molecular fragments in the context of evaluated additives. Among the continuous representations, data-driven feature-rich representations such as cddd underperform in BO tasks despite having higher validation scores in model fit related metrics (see Fig. 1 in ESI).† This outcome may be due to the overcomplexity of this representation (continuous 512-dimensional vectors) accompanied by the constraints of a low data regime. While cddd can capture intricate chemical features and relationships, it also introduces a high degree of complexity into the model which can be challenging to decipher with only a small number of points in the initialisation.
Importantly, we are often inclined to associate the complexity of the feature with its dimensionality. While the connection can be made for continuous representation, in binary representations, the high dimensionality often takes on a different meaning due to the nature of the input space. As a consequence, binary data translates to “practical” dimensionality that is generally lower than what one might encounter in a Euclidean space. For example, binary representations in our experiments, such as fingerprints and drfp, form 512-dimensional design spaces (Table 2), but the complexity they introduce to the model is significantly lower compared to the 512-dimensional continuous cddd representations, enhancing the BO performance as a result.
| Repr. | Dimension | Type |
|---|---|---|
| drfp | 512 | Binary |
| fragprints | 597 | Binary |
| fingerprints | 512 | Mixed |
| cddd | 512 | Continuous |
| rxnfp | 256 | Continuous |
| xtb | 11 | Continuous |
| mqn | 42 | Continuous |
| ohe | 722 | Binary |
| chemberta | 768 | Continuous |
Another data-driven reaction representation such as rxnfp shares similar path to cddd as shown in Fig. 4. We can use the same argument based on low-data rich-features coupling setup as with cddd, yet with a considerable difference in the encoded information between the two representations. rxnpf allow us to encode the whole reaction with interrelation between additives and other reaction components. However, the design of rxnfp may not be well-suited for task at hand. Out of the box, the rxnfp representation aims to capture the global information of a reaction including all reactants, reagents, and the transformation itself. They encode information valuable for distinguishing reaction types. In the unique setup of additive screening, where the only variable component is the additive, this global reaction information may dilute the effect of the additive, considering their limited role in this task and therefore undermine the performance of BO.
Xtb features, on the other hand, include properties related to the additive's electronic structure and molecular properties and result in low-dimensional continuous representations. However, similar to drfp, they show an increased sensitivity to the choice of kernel. The discovery of the phthalimide ligand additive in the original study and the consequent mechanistic understanding it provided39 served as initial reasoning why xtb features might be an effective representation for BO search in this paper. The specific electronic properties of phthalimide, such as its electron-withdrawing capacity, significantly influence the oxidative addition step. These properties play a crucial role in facilitating the reaction by stabilising the transition state or the reactive intermediates. The xtb features, capturing these electronic properties, should provide a detailed and nuanced representation of the additive. In scenarios where the additive's electronic structure is the primary determinant of its performance, xtb features might offer a significant advantage, but they omit other crucial information. Moreover, xtb demand for custom calculations, and they might not be ideal in cases where other factors, such as steric effects, define the reaction outcome.
The remaining representations—mqn, chemberta and as anticipated, OHE—show below-par performance, indicating their limited utility in BO search. Given its inherent design we expected OHE to result in poor exploitability of the data and therefore limit the model in learning from this representation. As a consequence, the outcome is often worse than random search as shown in Fig. 4. Similarly, mqn and chemberta perform on par with random search.
Following on the influence of various reaction representations, we evaluated the remaining parameters and represented the results in the Table 3. Alongside the data representation, the choice of kernel, initialisation strategy and acquisition function further dictate the success of the Bayesian optimisation process. The table provides an aggregate overview of the performance of each of these parameters, measured in terms of the percentage rate of identifying the top one and top five additives and the validation R2 score evaluated on the remaining 610 additives after the 100 BO iteration starting from the 10 initial compounds. The Matern kernel stands out, achieving the highest success rate in identifying valuable additives, albeit with noticeable variance. Tanimoto and Linear kernels, display lower success rates and inability to adapt to diverging underlying data distribution coming from different reaction representation alternatives. Moreover, the Linear kernel, while having the highest R2 score, performs the least in terms of identifying top additives. As mentioned, this result confirms the premise that the best-performing combination in terms of Gaussian process regression, does not necessarily yield the best results in a Bayesian optimisation setting. This observation underscores the importance of considering the interplay between representations, initialisation strategies, and the broader optimisation context when evaluating performance. The choice of initialisation which determines the starting points for the BO process impacts the trajectory towards the optimal values. Cluster-based initialisation, possibly due to its capability to capture diverse regions of the search space, achieves better BO performance scores. The ucb acquisition function slightly outperforms EI for the BO metrics. However, the R2 score is noticeably higher for EI, signalising that this acquisition function tends to uncover points that improve the surrogate model fit, but fails on leading towards optimal values in the search space. For a more comprehensive evaluation of different parameters and their influence on BO search, refer to Table 1 in the ESI.†
| Param. | Type | Top 1 [%] ↑ | Top 5 [%] ↑ | Valid. R2 ↑ |
|---|---|---|---|---|
| Kernel | Matern | 0.20 ± 0.40 | 0.19 ± 0.31 | −0.02 ± 0.18 |
| Tanimoto | 0.08 ± 0.28 | 0.13 ± 0.24 | −0.02 ± 0.18 | |
| Linear | 0.02 ± 0.14 | 0.09 ± 0.15 | 0.03 ± 0.14 | |
| Init. | Clusters | 0.14 ± 0.34 | 0.18 ± 0.28 | 0.01 ± 0.17 |
| Random | 0.10 ± 0.30 | 0.13 ± 0.23 | 0.01 ± 0.15 | |
| MaxMin | 0.07 ± 0.26 | 0.11 ± 0.21 | −0.02 ± 0.19 | |
| Acq. | UCB | 0.11 ± 0.31 | 0.15 ± 0.25 | −0.04 ± 0.19 |
| EI | 0.09 ± 0.29 | 0.12 ± 0.23 | 0.04 ± 0.14 |
In summary, the combined influence of reaction representation, kernel choice, initialisation strategy and acquisition function shapes the BO's ability to efficiently navigate the search space and identify high-yield additives. The results emphasise the importance of rational parameter selection in achieving the full potential of BO for chemical optimisation.
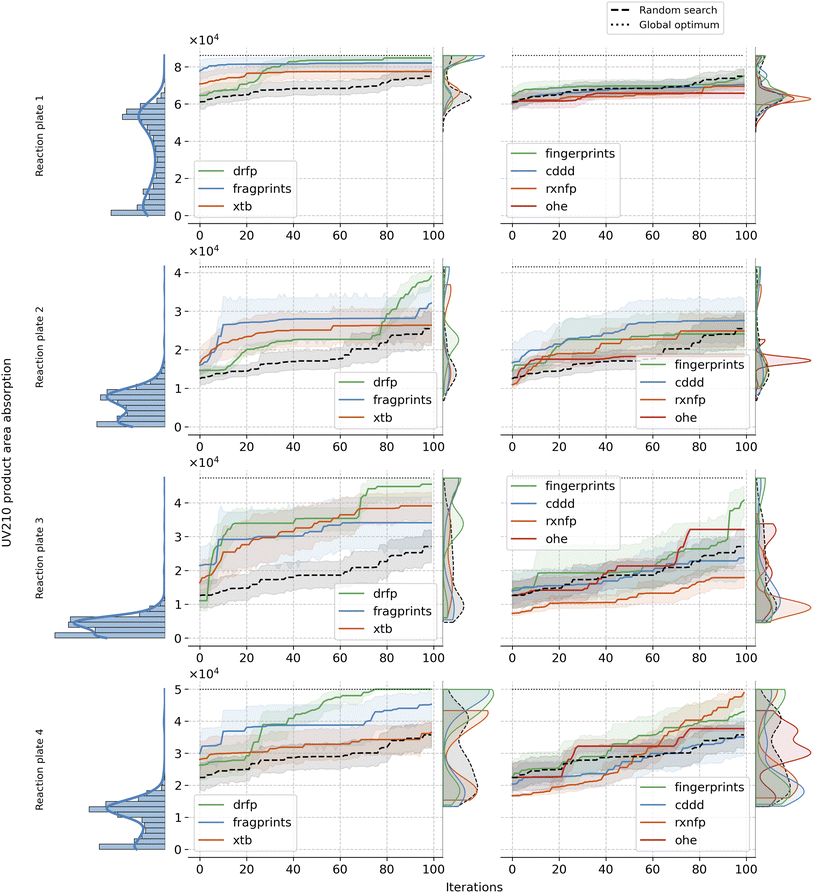
Building up on our analysis, we proceeded to fix the optimal choices for kernel, acquisition function, and initialisation strategy. Specifically, we employed the Matern kernel, ucb acquisition function, and clustering initialisation method. With these choices set, we observed the Bayesian optimisation paths over 100 iterations, averaged across 20 seeds, for each of the representations and reaction plates. Fig. 4 reveals resulting patterns and illustrates the strengths and limitations of each representation in the given setup. fragprints, combined with clustering initialisation, begin the optimisation at a substantially higher level but tend to plateau more quickly. Similarly, clustering initialisation works well for xtb, but they have limited success in reaching optimal additives. Impressively, however, both of these representation tend to uncover additives from the higher end of the complex long-tailed target distribution early in the BO loop, facilitated by the clustering of the design space. On the other hand drfp, even though starting from a set of additives with lower objective values, exhibits consistent growth, eventually steering towards the optimum. cddd representation fails to reach the high-yielding regions of the search space underscoring the idea that it is not ideally suited for the optimisation task at hand. The fingerprints representation, despite its third-place position in the previous analysis (see Fig. 3), show mixed results across reaction plates in this specific setup, often performing similarly to random search. This result highlights the sensitivity of BO to the alignment of representation and chosen parameters as the best configuration for this representation included EI as the acquisition function and Tanimoto kernel for the surrogate model. Meanwhile, rxnfp, in combination with Matern kernel lags behind, reinforcing the notion of its optimal pairing with simpler kernels. As expected, OHE consistently performs among the worst, underperforming even against a random search. Its inherent sparsity and lack of inter-data point information render it ill-suited for the task. As a comparison, we also evaluated reaction-level representations: OHE, rxnfp and drfp on Buchwald–Hartwig dataset. Interestingly, OHE has been reported to perform particularly well on this data. Notably, in line with the findings from our primary study, drfp exhibited consistent and robust performance, showcasing its universal applicability in Bayesian optimisation scenarios across datasets with differing requirements and constraints. For more details on the results on this dataset, refer to the Section A.5 in the ESI.†
5 Conclusion
Bayesian optimisation is a powerful optimisation method that steers the exploration of the search space towards more promising regions. It is especially valuable in chemistry, where it saves time and resources while uncovering high-yielding chemical reactions.32 This study showcases the effectiveness of BO supported by appropriate reaction representations, initialisation strategies and surrogate model specification in guiding the discovery of optimal additives in chemical reactions. The results highlight the importance of selecting suitable priors for optimal BO performance. We observed that drfp, when combined with the clustering initialisation method and a robust and adaptive Matern kernel, consistently outperformed both the one-hot encoding and random search baselines in identifying top-performing additives. Other representations have their merits, such as molecular fingerprints complemented with encoded fragments benefiting from the clustering and uncovering points on the higher end of the target distribution during the initialisation stage of BO. Similarly, xtb features facilitate clustering but show mixed performance across different reactions, emphasising their narrower application. Data-driven representations, although rich and expressive, demonstrated difficulties performing with limited data.6 Future work
This research underscores the potential of using BO for accelerating additive discovery in chemical reactions, paving the way for more efficient experimental design and optimisation in the field of chemistry. The reaction type and its unique chemical features influence the performance of specific chemical representations in the optimisation process. In addition, devising methods to evaluate the fit of different representations for distinct sets of reactions could enhance the optimisation process, leading to more accurate and reliable results.Future research should focus on determining the optimal reaction representation, or possibly a dynamic combination of representations for employing bo on different reaction types while incorporating domain knowledge. For example, switching from one reaction representation to another during the BO search. This strategy would allow to incorporate benefits of initialising the search at higher objective values while also reaching the optimum; or incorporating data-driven descriptors only once we have collected enough data for their optimal performance.
In this regard, several factors warrant further development. Firstly, potential biases in the dataset and assumptions made in the modelling could impact the generalisability of the results to other chemical reactions. Future work should focus on validating the methodology using diverse datasets and reaction types to ensure robustness and applicability across different contexts. Secondly, while this study investigated several reaction representations and initialisation strategies, additional research should explore alternative representations and strategies that may further improve the performance of BO in additive discovery by adapting to specific reaction types. For example, data-driven representations, although powerful, failed to deliver encouraging results in BO in this study. They could benefit from custom specifically designed surrogates or fine-tuning strategies on the datasets at hand.
By addressing these future research directions and refining the BO methodology, the chemical research community can benefit from further advancements in the powerful optimisation approach, ultimately contributing to a more efficient and comprehensive understanding of chemical reactions and their optimisation potential. The research can also extend to a broader range of chemical reactions and applications, such as high-throughput settings where batches of reactions can be evaluated simultaneously.103,104
Data availability
This study was carried out using publicly available data from https://doi.org/10.1126/science.abn1885. The code for all models and plots can be found at https://github.com/schwallergroup/chaos.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BR and PS acknowledge support from the NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation.Notes and references
- C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 22858–22893 CrossRef CAS.
- K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Nat. Rev. Chem, 2021, 5, 240–255 CrossRef CAS PubMed.
- P. Schwaller, A. C. Vaucher, R. Laplaza, C. Bunne, A. Krause, C. Corminboeuf and T. Laino, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1604 Search PubMed.
- N. David, W. Sun and C. W. Coley, Nat. Comput. Sci., 2023, 3, 362–364 CrossRef CAS.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS.
- M. H. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS.
- R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586 RSC.
- F. Grisoni, B. J. Huisman, A. L. Button, M. Moret, K. Atz, D. Merk and G. Schneider, Sci. Adv., 2021, 7, eabg3338 CrossRef CAS.
- A. Grosnit, R. Tutunov, A. M. Maraval, R.-R. Griffiths, A. I. Cowen-Rivers, L. Yang, L. Zhu, W. Lyu, Z. Chen, J. Wang, et al., arXiv, 2021, preprint, arXiv:2106.03609, DOI:10.48550/arXiv.2106.03609.
- M. H. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604–610 CrossRef CAS.
- T. Klucznik, B. Mikulak-Klucznik, M. P. McCormack, H. Lima, S. Szymkuć, M. Bhowmick, K. Molga, Y. Zhou, L. Rickershauser and E. P. Gajewska, et al. , Chem, 2018, 4, 522–532 CAS.
- C. W. Coley, D. A. Thomas III, J. A. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers and H. Gao, et al. , Science, 2019, 365, eaax1566 CrossRef CAS.
- P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Chem. Sci., 2020, 11, 3316–3325 RSC.
- A. Thakkar, T. Kogej, J.-L. Reymond, O. Engkvist and E. J. Bjerrum, Chem. Sci., 2020, 11, 154–168 RSC.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminf., 2020, 12, 1–9 Search PubMed.
- B. Mikulak-Klucznik, P. Gołębiowska, A. A. Bayly, O. Popik, T. Klucznik, S. Szymkuć, E. P. Gajewska, P. Dittwald, O. Staszewska-Krajewska and W. Beker, et al. , Nature, 2020, 588, 83–88 CrossRef CAS.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS.
- M. H. Segler and M. P. Waller, Chem.–Eur. J., 2017, 23, 5966–5971 CrossRef CAS.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef CAS PubMed.
- P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC.
- R.-R. Griffiths, P. Schwaller and A. A. Lee, 2021, preprint, arXiv:2105.02637, DOI:10.48550/arXiv.2105.02637.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS.
- P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Mach. Learn.: Sci. Technol., 2021, 2, 015016 Search PubMed.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- N. S. Eyke, W. H. Green and K. F. Jensen, React. Chem. Eng., 2020, 5, 1963–1972 RSC.
- K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem.: Methods, 2021, 1, 116–122 CAS.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen, E. Liles, J. E. Hein and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2021, 2, 035021 Search PubMed.
- A. Pomberger, A. P. McCarthy, A. Khan, S. Sung, C. Taylor, M. Gaunt, L. Colwell, D. Walz and A. Lapkin, React. Chem. Eng., 2022, 1368–1379 RSC.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96 CrossRef CAS.
- P. Müller, A. D. Clayton, J. Manson, S. Riley, O. S. May, N. Govan, S. Notman, S. V. Ley, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 987–993 RSC.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007 CrossRef CAS.
- R. Hickman, J. Ruža, L. Roch, H. Tribukait and A. García-Durán, React. Chem. Eng., 2023, 8, 2284–2296 RSC.
- D. S. Wigh, M. Tissot, P. Pasau, J. M. Goodman and A. A. Lapkin, J. Phys. Chem. A, 2023, 127, 2628–2636 CrossRef CAS PubMed.
- J. Guo, B. Ranković and P. Schwaller, Chimia, 2023, 77, 31 CrossRef CAS.
- C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger, G. Chessari, C. N. Johnson and A. A. Lapkin, ACS Cent. Sci., 2023, 957–968 CrossRef CAS.
- C. N. Prieto Kullmer, J. A. Kautzky, S. W. Krska, T. Nowak, S. D. Dreher and D. W. MacMillan, Science, 2022, 376, 532–539 CrossRef PubMed.
- A. Bellomo, J. Zhang, N. Trongsiriwat and P. J. Walsh, Chem. Sci., 2013, 4, 849–857 RSC.
- J. C. Vantourout, H. N. Miras, A. Isidro-Llobet, S. Sproules and A. J. Watson, J. Am. Chem. Soc., 2017, 139, 4769–4779 CrossRef CAS PubMed.
- I. U. of Pure and A. Chemistry, IUPAC Compendium of Chemical Terminology – The Gold Book, 2009, https://goldbook.iupac.org/ Search PubMed.
- E. M. Vogl, H. Gröger and M. Shibasaki, Angew. Chem., Int. Ed., 1999, 38, 1570–1577 CrossRef CAS.
- L. Hong, W. Sun, D. Yang, G. Li and R. Wang, Chem. Rev., 2016, 116, 4006–4123 CrossRef CAS PubMed.
- R. F. Grossman and J. T. Lutz Jr, Polymer modifiers and additives, CRC Press, 2000 Search PubMed.
- T. Gensch, M. Teders and F. Glorius, J. Org. Chem., 2017, 82, 9154–9159 CrossRef CAS PubMed.
- K. D. Collins and F. Glorius, Nat. Chem., 2013, 5, 597–601 CrossRef CAS.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS.
- G. Tom, R. J. Hickman, A. Zinzuwadia, A. Mohajeri, B. Sanchez-Lengeling and A. Aspuru-Guzik, Digital Discovery, 2023, 759–774 RSC.
- P. S. Kutchukian, J. F. Dropinski, K. D. Dykstra, B. Li, D. A. DiRocco, E. C. Streckfuss, L.-C. Campeau, T. Cernak, P. Vachal and I. W. Davies, et al. , Chem. Sci., 2016, 7, 2604–2613 RSC.
- P. van Gerwen, A. Fabrizio, M. D. Wodrich and C. Corminboeuf, Mach. Learn.: Sci. Technol., 2022, 3, 045005 Search PubMed.
- D. S. Wigh, J. M. Goodman and A. A. Lapkin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1603 Search PubMed.
- B. Cheng, R.-R. Griffiths, S. Wengert, C. Kunkel, T. Stenczel, B. Zhu, V. L. Deringer, N. Bernstein, J. T. Margraf and K. Reuter, et al. , Acc. Chem. Res., 2020, 53, 1981–1991 CrossRef CAS PubMed.
- R. E. Carhart, D. H. Smith and R. Venkataraghavan, J. Chem. Inf. Comput. Sci., 1985, 25, 64–73 CrossRef CAS.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- M. Awale and J.-L. Reymond, Bioorg. Med. Chem., 2012, 20, 5372–5378 CrossRef CAS PubMed.
- M. Awale, R. Van Deursen and J.-L. Reymond, MQN-mapplet: visualization of chemical space with interactive maps of DrugBank, ChEMBL, PubChem, GDB-11, and GDB-13, 2013 Search PubMed.
- K. T. Nguyen, L. C. Blum, R. Van Deursen and J.-L. Reymond, ChemMedChem, 2009, 4, 1803–1805 CrossRef CAS.
- G. Landrum, P. Tosco, B. Kelley, R. Vianello, N. Schneider, D. Cosgrove, E. Kawashima, A. Dalke, D. N. G. Jones, B. Cole, M. Swain, S. Turk, A. Savelyev, A. Vaucher, M. Wójcikowski, I. Take, D. Probst, K. Ujihara, V. F. Scalfani, A. Pahl, F. Berenger, J. L. Varjo and D. Gavid, 2022.
- R.-R. Griffiths, J. L. Greenfield, A. R. Thawani, A. R. Jamasb, H. B. Moss, A. Bourached, P. Jones, W. McCorkindale, A. A. Aldrick and M. J. Fuchter, et al. , Chem. Sci., 2022, 13, 13541–13551 RSC.
- H. B. Moss and R.-R. Griffiths, arXiv, 2020, preprint, arXiv:2010.01118, DOI:10.48550/arXiv.2010.01118.
- R.-R. Griffiths, L. Klarner, H. Moss, A. Ravuri, S. T. Truong, B. Rankovic, Y. Du, A. R. Jamasb, J. Schwartz, A. Tripp, G. Kell, A. Bourached, A. Chan, J. Moss, C. Guo, A. Lee, P. Schwaller and J. Tang, ICML 2022 2nd AI for Science Workshop, 2022 Search PubMed.
- A. R. Thawani, R.-R. Griffiths, A. Jamasb, A. Bourached, P. Jones, W. McCorkindale, A. A. Aldrick and A. A. Lee, 2020, preprint, arXiv:2008.03226, DOI:10.48550/arXiv.2008.0322.
- K. Jorner, Chimia, 2023, 77, 22 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- P. Schwaller, B. Hoover, J.-L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2021, 7, eabe4166 CrossRef PubMed.
- P. Schwaller, D. Probst, A. C. Vaucher, V. H. Nair, D. Kreutter, T. Laino and J.-L. Reymond, Nat. Mach. Intell., 2021, 3, 144–152 CrossRef.
- R. Winter, F. Montanari, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 1692–1701 RSC.
- S. Chithrananda, G. Grand and B. Ramsundar, 2020, preprint, arXiv:2010.09885, DOI:10.48550/arXiv.2010.09885.
- S. Wang, Y. Guo, Y. Wang, H. Sun and J. Huang, Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, 2019, pp. 429–436 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- J. Devlin, M. Chang, K. Lee and K. Toutanova, Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2019, pp. 4171–4186 Search PubMed.
- Y. Liu, M. Ott, N. Goyal, J. Du, M. Joshi, D. Chen, O. Levy, M. Lewis, L. Zettlemoyer and V. Stoyanov, 2019, preprint, arXiv:1907.11692, DOI:10.48550/arXiv.1907.11692.
- N. Schneider, D. M. Lowe, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 39–53 CrossRef CAS PubMed.
- R. Bellman, Dynamic Programming, Dover Publications, 1957 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural Inf. Process., 2017, 30, 5998–6008 Search PubMed.
- D. Probst, P. Schwaller and J.-L. Reymond, Digital Discovery, 2022, 1, 91–97 RSC.
- R.-R. Griffiths, A. A. Aldrick, M. Garcia-Ortegon and V. Lalchand, et al. , Mach. Learn.: Sci. Technol., 2021, 3, 015004 Search PubMed.
- A. Makarova, I. Usmanova, I. Bogunovic and A. Krause, Adv. Neural Inf. Process., 2021, 34, 17235–17245 Search PubMed.
- R. Garnett, Bayesian optimization, Cambridge University Press, 2023 Search PubMed.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Proc. IEEE, 2015, 104, 148–175 Search PubMed.
- A. I. Cowen-Rivers, W. Lyu, R. Tutunov, Z. Wang, A. Grosnit, R.-R. Griffiths, A. M. Maraval, H. Jianye, J. Wang, J. Peters and H. Bou-Ammar, J. Artif. Intell. Res., 2022, 74, 1269–1349 CrossRef.
- H. Moss, D. Leslie, D. Beck, J. Gonzalez and P. Rayson, Adv. Neural Inf. Process., 2020, 33, 15476–15486 Search PubMed.
- Y. Chen, A. Huang, Z. Wang, I. Antonoglou, J. Schrittwieser, D. Silver and N. de Freitas, 2018, preprint, arXiv:1812.06855, DOI:10.48550/arXiv.1812.06855.
- H. B. Moss, V. Aggarwal, N. Prateek, J. González and R. Barra-Chicote, ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2020, pp. 7639–7643 Search PubMed.
- Bayesian Optimization: Ax, https://ax.dev/docs/bayesopt.html, accessed on 09/07/2023 Search PubMed.
- P. I. Frazier, 2018, preprint, arXiv:1807.02811, DOI:10.48550/arXiv.1807.02811.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- R.-R. Griffiths, J. Jiang, D. J. Buisson, D. Wilkins, L. C. Gallo, A. Ingram, D. Grupe, E. Kara, M. L. Parker and W. Alston, et al. , Astrophys. J., 2021, 914, 144 CrossRef.
- R.-R. Griffiths, 2023, preprint, arXiv:2303.14291, DOI:10.17863/CAM.93643.
- T. Tanimoto, An Elementary Mathematical Theory of Classification and Prediction, International Business Machines Corporation, 1958 Search PubMed.
- L. Ralaivola, S. J. Swamidass, H. Saigo and P. Baldi, Neural Netw., 2005, 18, 1093–1110 CrossRef PubMed.
- J. Wilson, F. Hutter and M. Deisenroth, Adv. Neural Inf. Process., 2018, 31, 9884–9895 Search PubMed.
- A. Grosnit, A. I. Cowen-Rivers, R. Tutunov, R.-R. Griffiths, J. Wang and H. Bou-Ammar, J. Mach. Learn. Res., 2021, 22, 160–161 Search PubMed.
- A. M. Schweidtmann, D. Bongartz, D. Grothe, T. Kerkenhoff, X. Lin, J. Najman and A. Mitsos, arXiv, 2020, preprint, arXiv:2005.10902, DOI:10.1007/s12532-021-00204-y.
- A. Grosnit, A. I. Cowen-Rivers, R. Tutunov, R.-R. Griffiths, J. Wang and H. Bou-Ammar, J. Mach. Learn. Res., 2021, 22, 7183–7260 Search PubMed.
- M. T. Morar, J. Knowles and S. Sampaio, Data Science meets Optimization Workshop: CEC2017 & CPAIOR 2017: DSO 2017, 2017 Search PubMed.
- A. Ramachandran, S. Gupta, S. Rana, C. Li and S. Venkatesh, Knowl.-Based Sys., 2020, 195, 105663 CrossRef.
- J. Kim, S. Kim and S. Choi, 2017, preprint, arXiv:1710.06219, DOI:10.48550/arXiv.1710.06219.
- L. Van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- S. Vakili, H. Moss, A. Artemev, V. Dutordoir and V. Picheny, Adv. Neural Inf. Process., 2021, 34, 5631–5643 Search PubMed.
- H. B. Moss, S. W. Ober and V. Picheny, International Conference on Artificial Intelligence and Statistics, 2023, pp. 5213–5230 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00096f |
| ‡ “Ni-catalysed photoredox decarboxylative arylation” refers to a chemical reaction where a nickel catalyst, combined with light energy, enables the removal of a carboxyl group from a molecule while introducing an aryl group. Common in organic synthesis, this methodology allows crafting molecules with specific chemical attributes. |
| § The term “additive” refers to a single selection from a set of 720 examined additives. |
| ¶ The term “limited signal” refers to the low validation scores indicating poor alignment between the data representations and the desired output in the low data regime. This complexity results in a challenging modelling scenario. |
| || The symmetric difference encapsulates elements that are in either set, but not in the intersection. |
| ** The k-medoids method is similar to k-means but uses the most centrally located data point in a cluster (medoid) to represent that cluster. This method can employ various distance metrics, allowing it to be more flexible based on the data representation type. |
| This journal is © The Royal Society of Chemistry 2024 |