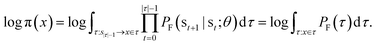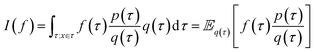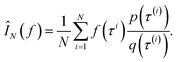Open Access Article
Open Access ArticleTowards equilibrium molecular conformation generation with GFlowNets†
Alexandra
Volokhova‡
 *a,
Michał
Koziarski‡
*a,
Alex
Hernández-García
*a,
Michał
Koziarski‡
*a,
Alex
Hernández-García
 a,
Cheng-Hao
Liu
b,
Santiago
Miret
a,
Cheng-Hao
Liu
b,
Santiago
Miret
 c,
Pablo
Lemos
d,
Luca
Thiede
c,
Pablo
Lemos
d,
Luca
Thiede
 e,
Zichao
Yan
a,
Alán
Aspuru-Guzik
a and
Yoshua
Bengio
e,
Zichao
Yan
a,
Alán
Aspuru-Guzik
a and
Yoshua
Bengio
 f
f
aMila, Université de Montréal, Canada. E-mail: alexandra.volokhova@mila.quebec; michal.koziarski@mila.quebec
bMila, McGill University, Canada
cIntel Labs, USA
dMila, Université de Montréal, Ciela Institute, Flatiron Institute, Canada
eVector Institute, University of Toronto, Canada
fMila, Université de Montréal, CIFAR Fellow, Canada
First published on 29th April 2024
Abstract
Sampling diverse, thermodynamically feasible molecular conformations plays a crucial role in predicting properties of a molecule. In this paper we propose to use GFlowNets for sampling conformations of small molecules from the Boltzmann distribution, as determined by the molecule's energy. The proposed approach can be used in combination with energy estimation methods of different fidelity and discovers a diverse set of low-energy conformations for drug-like molecules. We demonstrate that GFlowNets can reproduce molecular potential energy surfaces by sampling proportionally to the Boltzmann distribution.
1 Introduction
Molecules exist in the three-dimensional space as a distribution of atomic positions, referred to as conformations. Given the temperature of the system, the probability of each conformation to occur is defined by its formation energy, and follows a Boltzmann distribution.1 In many computational drug-discovery processes, it is crucial to know the set of most probable, i.e. low-energy, conformations to predict properties of interest.2,3 In addition, exploring the potential energy surface by sampling proportionally to the Boltzmann distribution can give key chemical insights such as transition pathways and electron transfer.4,5Among computational chemistry methods, molecular dynamics simulation is the standard approach, where methods such as CREST have shown feasibility to accurately access numerous low-energy conformations.6 However, it remains computationally expensive for high throughput applications and large compounds. Faster alternatives with knowledge-based algorithms, such as distance-geometry methods like ETKDG,7 cannot sample in accordance to the Boltzmann distribution and quickly deteriorate with increasing molecular size.
Machine learning (ML) generative models shown great promise for conformation generation of molecules.8–10 However, they are traditionally focused on maximum likelihood training with a fixed dataset, which does not guarantee sampling proportionally to the Boltzmann distribution. Several recent works such as Boltzmann generators are approaching this problem,10–13 but none of them has yet demonstrated sufficient generality (see Section 2 for more details).
In this paper, we use generative flow networks (GFlowNets) for sampling molecular equillibrium conformations from the Boltzmann distribution. We focus on sampling torsion angles of a molecule, as they contain most of the variance of the conformation space while bond lengths and angles can be efficiently generated by fast rule-based methods. A recent work on continuous GFlowNets14 presented a proof of concept to demonstrate the capability of GFlowNet to sample from a distribution defined on a two-dimensional torus. Here, we extend this work to a more realistic setting of an arbitrary number of torsion angles. Furthermore, we train GFlowNets with several energy estimation methods of varying fidelity. We experimentally demonstrate that the proposed approach can sample molecular conformations from the Boltzmann distribution, producing diverse, low-energy conformations for a wide range of drug-like molecules with varying number2–12 of torsion angles.
2 Related works
2.1 Conventional approaches
The most accurate way to get a set of low-energy conformers is based on molecular-dynamics (MD) simulation,15 which is a computational method for studying the time evolution of physical systems. This method integrates a Newtonian equation of motion with forces obtained by differentiating the potential energy function of the system and employs metadynamics to discover multiple minima of the energy landscape. However, this accuracy comes with high computational costs, despite simplifications of the energy function, making this method not suitable for high-throughput applications and large molecules.16Alternatively, cheminformatics methods are a fast and popular approach for conformer generation. They utilize structures from experimental reference datasets, chemical rules and heuristics to generate plausible 3D structures given a molecular graph. While significantly faster than MD simulations, these methods tend to lack accuracy and generalization. ETKDG is the most widely used cheminformatics method for conformer generation7 implemented in the open-source library RDKit. OMEGA17 is a popular commercial software implementing cheminformatics methods.
2.2 Machine learning and reinforcement learning approaches
Several deep learning approaches have been developed for conformer generation. Recent advancements include GeoMol,8 GeoDiff,9 and Torsional Diffusion.10 These methods show good results on the popular benchmark of drug-like molecules GEOM,16 demonstrating a decent performance and allowing for faster generation than MD simulations. However, a recently proposed simple clustering algorithm on top of the conformations generated by RDKit outperforms many of these approaches.18 Notably, these machine learning methods are mainly trained for maximizing the likelihood of the conformations present in the training dataset and therefore not suitable for sampling proportionally to the Boltzmann distribution. In contrast, the GFlowNet framework utilizes information about the Boltzmann weights of the conformations by querying the reward function and allows for generating conformations proportionally to the Boltzmann distribution.Another promising avenue in the realm of conformer generation is the application of machine learning to model the force fields.19–22 This approach involves training a machine learning model for predicting forces in the system. Then, molecular dynamics equations are unrolled to sample conformations from the local minima of the energy function based on the forces (gradients of the energy) provided by the model. Machine learning models allow for faster computation of the forces giving a speed advantage compared to MD with an energy function based on the first principles. However, molecular dynamics integration with estimated force fields presents significant stability challenges due to the error accumulation during integration,23 which limits the applicability of this approach.
Reinforcement learning (RL) is another class of machine learning algorithms which cast the generation of molecular structures into a Markov decision process. Well-known examples include TorsionNet24 which sequentially alters the molecular conformation via updating all torsion angles at every step. The algorithm employs proximal policy optimization25 and learns by querying a force-fields energy estimation. While TorsionNet and other RL methods do not rely on existing molecular conformation dataset—a setup similar to our method—they lack the theoretical guarantee of exploring the broader ensemble space of molecular conformation, and indeed,26 shows that they fail at recovering a diverse set of conformations.
2.3 Boltzmann generators
A closely relevant direction of work is Boltzmann generators11,12 – machine learning models aimed at generating samples from the Boltzmann distribution. Many of the existing approaches are based on normalising flows,11,12 which are known to have limited expressivity and require training a separate model for each molecular graph. The torsional diffusion model10 incorporated annealed importance sampling into the training of the diffusion model allowing for sampling from the target distribution. However, importance sampling brings additional variance into the gradients and becomes challenging with higher dimensions which limits applicability of this approach. Recent work by13 also attempted to make diffusion models sample from the Boltzmann distribution. Authors pretrained the score model, constraining it to both follow the Fokker–Plank equation and match the energy gradient and then trained it on the dataset of conformations with the standard maximum-likelihood objective. This approach allows to incorporate information about energies into the model but does not have theoretical guarantees for sampling from the Boltzmann distribution. Another recent approach27 approximates Boltzmann distribution as a product of independent distributions for each intrinsic coordinate (a mixture of von-Mises distribution for each torsion angle, unimodal Gaussian distribution for bond lengths and angles). This work shows promising results on the molecules with up to 64 atoms, but the independence assumption can be limiting for modeling larger molecules with long-range interactions.3 GFlowNet for conformation generation
GFlowNets were originally introduced as a learning algorithm for amortized probabilistic inference in high-dimensional discrete spaces28 and a generalisation to continuous or hybrid spaces was recently introduced.14 The method is designed for sampling from an unnormalised probability density which is often represented as a reward function R(x) over the sample space x ∈ X.As shown in Fig. 1, the sampling process starts from a source state s0 and continues with a trajectory of sequential updates τ = (s0 → s1 → … → sn = x) according to a trainable forward policy pF(st|st−1; θ), which defines probability of the forward transition st−1 → st. Once the termination transition sn−1 → x is sampled, the reward function R(x) provides a signal for computing the training objective. In addition to the trainable forward policy, GFlowNet can learn a backward policy pB(st−1|st; θ) for modelling the probability of the backward transitions st → st−1. It gives additional flexibility to the forward policy pF allowing to model a rich family of distributions over X.
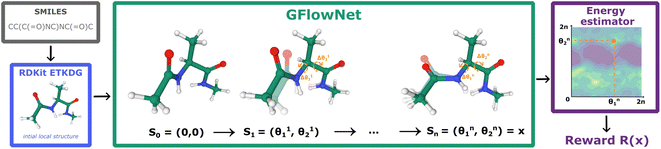 | ||
| Fig. 1 GFlowNet for molecular conformation generation. First, RDKit samples the initial conformation given the molecular graph encoded as a SMILES string. Then, we fix bond lengths and angles and set initial values of rotatable torsion angles to zero. Finally, GFlowNet sequentially updates rotatable torsion angles providing the final sample according to the Boltzmann reward (eqn (2)). | ||
In this paper, we propose the use of GFlowNets as a generative model to sample molecular conformations in the space of torsion angles. Formally, we can describe the space of d torsion angles of a molecule as the hyper-torus defined in X = [0,2π)d. To sample trajectories τ with GFlowNets that satisfy the required theoretical assumptions,14 we establish a fixed number of steps n and include the step number into the state. This yields a state space S = {s0} ∪ [0,2π)d × {1,2…n}. In order to learn expressive distributions on the hyper-tori, we parameterized independently the forward and backward policies pF and pB and trained the GFlowNets with the Trajectory Balance objective29 defined as:
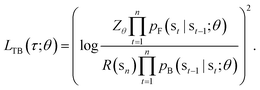 | (1) |
In eqn (1), Zθ is the (trainable) partition function and R(sn) is the reward function, evaluated on the terminating states of the trajectories, sn = x ∈ X.
Both forward and backward policies are parameterized with a multilayer perceptron (MLP) which outputs parameters for a mixture of von Mises distribution. Note that in this setting we need to train an individual GFlowNet for every molecule as different molecules may have different numbers of torsion angles. We discuss possibility to generalise this approach in the Section 5.
In order to sample from the Boltzmann distribution, we define the reward function using the energy of the molecular conformation in the following way:
| R(x) = e−E(C(x))β, | (2) |
The energy function is computed as an approximation of quantum mechanical density-functional theory (DFT) and we consider several estimators of different fidelity in our experiments. We use the molecule's potential energy in vacuum for the scope of our work, but the method can be applied to any energy function of interest.
4 Empirical evaluation
We conducted an experimental study aimed at addressing several research questions: whether the proposed approach can sample conformations proportionally to the Boltzmann distribution; its capacity to generate diverse low-energy conformations; and how the choice of the energy estimator impacts the performance. Additionally, we examined how the proposed approach scales with an increasing number of torsion angles. Firstly, we conducted experiments on molecules with only two considered torsion angles to perform a more in-depth analysis of the results which was not possible in higher dimensions. Then, we scaled up our study, considering a broader range of molecules with varying numbers of torsion angles. Training details can be found in Appendix A.1.4.1 Set-up
Conformation generation is conditioned for an input molecular graph encoded as a SMILES string. We first process SMILES with RDKit library30 which uses ETKDG to generate an initial conformation. This defines bond lengths and angles and non-rotatable torsion angles. Then, GFlowNet generates rotatable torsion angles and their values are updated accordingly in the conformation (see Fig. 1).4.2 Two-dimensional setting
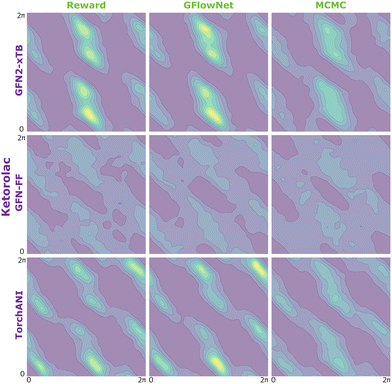
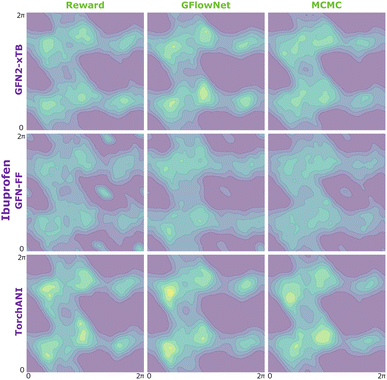
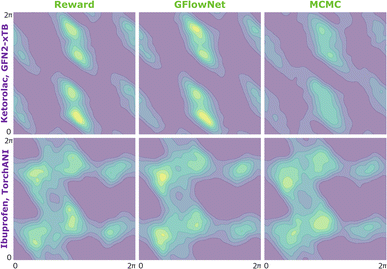
We begin by investigating the performance of GFlowNet in simple, well-studied molecular systems in two dimensions: alanine dipeptide, ibuprofen, and ketorolac.35,36 In this experiment, we aim to assess how well the proposed approach can learn to sample from the target distribution and analyze the impact of the energy estimator.The low dimensionality allows us to visualize the kernel density estimation and evaluate the performance numerically using an unbiased estimation of the Jensen–Shannon divergence (JSD). We used nested sampling37 to produce reference ground-truth energy surfaces, and compared the proposed approach with MCMC as an example of an unamortized method for sampling from an unnormalized probability distribution.
In Fig. 2, we present the obtained potential energy surfaces of ketorolac and ibuprofen. Comparable analysis for all three molecules and proxies, as well as the computed JSD values, can be found in Appendix A.5 Fig. 8–10 and Table 1. As can be seen, while the choice of the energy estimator can influence the overall shape of the energy surface, both considered methods accurately reproduce the ground truth energy surface for all estimators. Interestingly, GFlowNet outperformed MCMC in some cases, producing energy surfaces more closely resembling the ground truth.
4.3 Scaling to multiple torsion angles
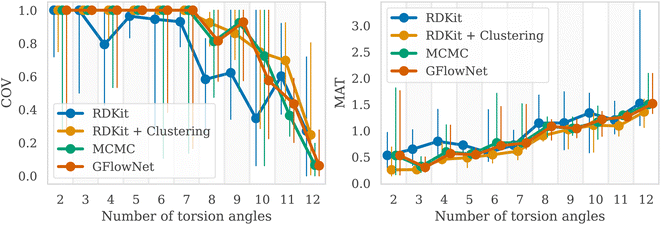
We then examined a setting with a higher number of torsion angles, up to 12. For each number of torsion angles we selected 5 different molecules from the GEOM-Drugs dataset, and trained GFlowNet using GFN2-xTB energy estimator separately for each one of them. We compared our method with several baselines: MCMC, RDKit ETKDG,7 as well as a recent approach combining ETKDG with clustering,18 which has shown to outperform many of the existing machine learning methods in the low energy conformation generation task. Note that both ETKDG-based approaches perform a qualitatively different task of generating optimized, low-energy conformers, whereas GFlowNet and MCMC aim at sampling from the underlying Boltzmann distribution. In this experiment, we investigate whether diverse low-energy conformations are present among the GFlowNet samples.In Fig. 3, we report the COV and MAT metrics (Appendix A.3.1), which evaluate the proportion of the reference conformations among samples (COV) and the proximity of the sampled conformations to the reference onces (MAT). We use a set of 1000 generated conformations for all methods to compute the metrics. We repeated experiment five times with different molecules for each number of torsion angles. As can be seen, GFlowNet outperforms vanilla RDKit, and achieves performance comparable to MCMC and RDKit-clustering, indicating that it can sample low-energy conformations that closely match the ground-truth dataset. In this experiment, both GFlowNet and MCMC use GFN2-xTB energy estimator.
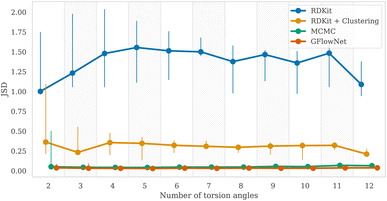
4.4 Sampling from the Boltzmann distribution
To measure the discrepancy between model sampling distribution and the target distribution, we estimated Jensen-Shannon divergence (JSD) between sampling and Boltzmann distribution given by GFN2-xTB energy function (see Appendix A.3.2 for more details). As one can see from the Fig. 4 and 6, both GFlowNet and MCMC samples are much closer to the Boltzmann distribution compared to RDKit and RDKit + clustering methods. In this experiment, both GFlowNet and MCMC use GFN2-xTB energy estimator.Finally, to provide additional evaluation of GFlowNet's scalability to higher dimensions, we examined the correlation between the estimated probability to sample a conformation with a GFlowNet (Appendix A.4) and its energy. We performed this analysis for GFlowNet exclusively because other methods do not provide a straightforward way for estimating sample probability. For the sake of this comparison, we considered all TorchANI, GFN-FF and GFN2-xTB energy estimators. The results are presented in Fig. 5. As can be seen, while the correlation declines with the increasing number of torsion angles, it remains relatively high throughout the considered range, serving as a further indication that the proposed approach sample according to the Boltzmann distribution in the high dimensions. Interestingly, the higher correlation in higher dimensions with GFN2-xTB and GFN-FF may suggest that their energy landscape is easier to learn than TorchANI, possibly because of the more accurate modelling of the energy surface.
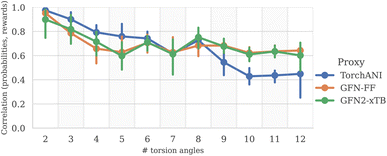 | ||
| Fig. 5 Correlation between estimated sample probability and its reward, as a function of the number of torsion angles (higher is better). | ||
5 Discussion and future work
In this paper, we have proposed a method for sampling molecular conformations using GFlowNet, which samples proportionally to the Boltzmann distribution. We experimentally evaluated the proposed approach and demonstrated that it can sample diverse, low-energy conformations, can be used in combination with energy estimators of different fidelity, and scales well to a higher number of torsion angles.While the proposed method still requires training individually for every molecule, the described work can be treated as a stepping stone towards developing a generalised GFlowNet model, which could be trained on a large data set of molecules and sample torsion angles for an arbitrary molecule conditioned on its molecular graph. This can potentially allow us to amortize the computational costs of sampling proportionally to the Boltzmann distribution.
Code and data availability
The code used to carry out the experiments of this paper, alongside with instructions for their reproduction, is open-sourced and available on the GitHub repository https://github.com/GFNOrg/conf-gfn. The GEOM dataset used in this work is publicly available at https://github.com/learningmatter-mit/geom.Conflicts of interest
The authors declare no conflicts of interests relevant to this research.A Appendix
A.1 Experimental details
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random conformations, based on them estimated the minimum and maximum energy values, and normalized all of the estimated energy values to a [0; 1] range. Furthermore, to remove outliers we clamped the values between 1st and 99th quantile of the energy values observed in the initial random sample.
000 random conformations, based on them estimated the minimum and maximum energy values, and normalized all of the estimated energy values to a [0; 1] range. Furthermore, to remove outliers we clamped the values between 1st and 99th quantile of the energy values observed in the initial random sample.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, and used Adam optimizer with learning rate of 0.0001 for the policy and 0.01 for Zθ. Batches consisted of 80 on-policy trajectories with probability of random sampling equal to 0.1, and 20 trajectories from replay buffer of best trajectories seen so far, with a total buffer capacity of 1000.
000 iterations, and used Adam optimizer with learning rate of 0.0001 for the policy and 0.01 for Zθ. Batches consisted of 80 on-policy trajectories with probability of random sampling equal to 0.1, and 20 trajectories from replay buffer of best trajectories seen so far, with a total buffer capacity of 1000.
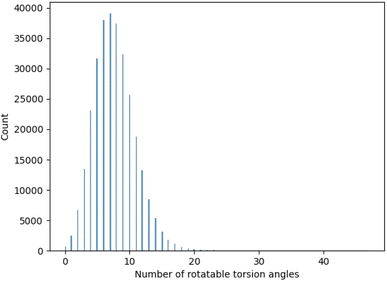
A.2 GEOM-DRUGS torsion angle distribution
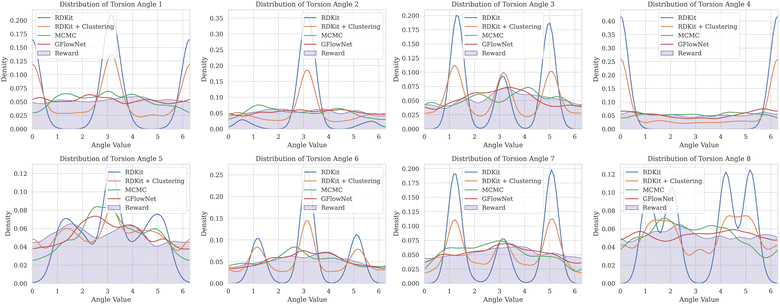
One important consideration for the experimental study was the range of evaluated torsion angles. To chose an appropriate range we analysed the distribution of torsion angles for molecules contained in GEOM-DRUGS, as presented in Fig. 7. As can be seen, the considered range of 2 to 12 torsion angles faithfully represents the dataset, with majority of molecules contained in it.A.3 Evaluation
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) it can be defined as:
it can be defined as: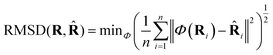 | (3) |
Coverage (COV) and matching (MAT) are two metrics incorporating RMSD. Given a set of reference low-energy conformations Sr, they measure to what extent generated samples Sg cover the reference dataset (COV), and how closely do they resemble the reference conformations (MAT):
 | (4) |
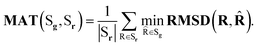 | (5) |
Note that COVMAT metrics were traditionally used in the task of low-energy molecular conformation generation, with the assumption that all the generated conformations Sg are designed to closely approximate the local energy optima. This does not hold when sampling from Boltzmann distribution, and can produce unfavourable results. Because of that we adjusted the procedure by sampling more conformations than typically seen in the literature, as described in the main text.
We follow the literature18,22,41 and set δ to 1.25 Å in our experiments.
For estimating marginal JSD, we first discretized each dimension into K bins. Then, we sampled M d-dimensional vectors of torsion angles from the uniform distribution over X. Then, we computed their Boltzmann weights w(x) = exp(−ε(C(x))β) and used them to estimate Boltzmann probability for each bin:
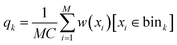 | (6) |
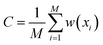 and the indicator function [condition] = 1 when condition is true and [condition] = 0 otherwise. After that, we sampled M samples from the model and estimated sampling probability in each bin as a standard histogram:
and the indicator function [condition] = 1 when condition is true and [condition] = 0 otherwise. After that, we sampled M samples from the model and estimated sampling probability in each bin as a standard histogram: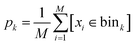 | (7) |
Finally we computed discrete marginal JSD using estimated qk and pk:
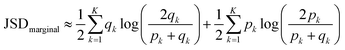 | (8) |
And took the average over dimensions
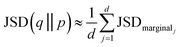 | (9) |
In our analysis, we used M = 1000 and K = 25. Note that this estimation is biased as in practice torsion angles are not independent from each other.
A.4 Estimation of the log-likelihood of sampling a terminating state x
The log-probability of sampling a terminating state x according to the GFlowNet policy π(x) can be expressed as follows:Note that we simplify notation in favour of readability in the domain of the integral of the right-most equation, which should be identical to the previous integral's. While computing the integral (or even the corresponding sum, if the state space is discrete but very large) in the above expression is intractable in general, we can efficiently estimate it with importance sampling, by using the backward transition probability distribution PB(τ|x) as the importance proposal distribution. Let us recall the core aspects of importance sampling, which is a kind of Monte Carlo simulation method.
Monte Carlo simulation methods can be used to estimate integrals 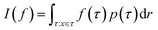 , as well as very large sums, by drawing N independent and identically distributed (i.i.d.) samples {τ(i)}i=1N and computing an estimate
, as well as very large sums, by drawing N independent and identically distributed (i.i.d.) samples {τ(i)}i=1N and computing an estimate 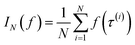 which converges to I(f) as N → ∞. Importance sampling introduces an importance proposal distribution q(τ) whose support includes the support of the target distribution p(τ), such that we can express the integral I(f) as an expectation over the proposal distribution:
which converges to I(f) as N → ∞. Importance sampling introduces an importance proposal distribution q(τ) whose support includes the support of the target distribution p(τ), such that we can express the integral I(f) as an expectation over the proposal distribution:
By drawing N i.i.d. samples from the proposal distribution q(τ) we can compute the estimate
Returning to the original problem of estimating the log-probability of sampling x with a GFlowNet, we have that the target density is the forward transition probability distribution (p(τ) = PF(τ)), the importance proposal distribution is the backward transition probability distribution given x (q(τ) = PB(τ|x)), and the function under the intergal is simply one (f(τ) = 1). Therefore:
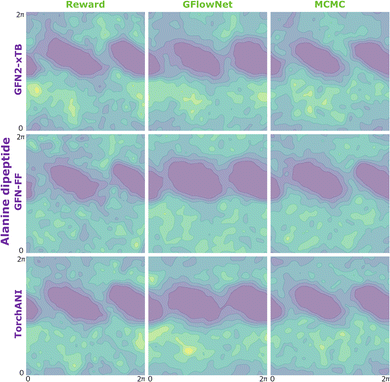
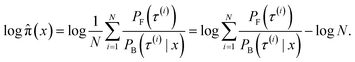 | (10) |
A.5 Two-dimensional results
This section presents additional results for the experiments in section 4.2. The JSD metric reported here is estimated differently from the Section 4.4. and Appendix A.3.2. Here, it was possible to compute an unbiased estimation of the JSD due to the low dimentionality of the problem. First, we computed kernel density estimation (KDE) on the samples from the model and on the samples from the reward distribution drawn with rejection sampling. Then, we used the obtained KDEs to compute probabilities on a dence grid of torsion angles in the interval [0, 2π). Finally, we computed discrete JSD using the probabilities of the points on the grid.| Method | Proxy | Alanine dipeptide | Ibuprofen | Ketorolac |
|---|---|---|---|---|
| MCMC | TorchANI | 0.0056 | 0.0055 | 0.0172 |
| GFN-FF | 0.0076 | 0.0175 | 0.0123 | |
| GFN2-xTB | 0.0090 | 0.0074 | 0.0143 | |
| GFlowNet | TorchANI | 0.0077 | 0.0055 | 0.0070 |
| GFN-FF | 0.0166 | 0.0182 | 0.0078 | |
| GFN2-xTB | 0.0073 | 0.0075 | 0.0059 |
 | ||
| Fig. 8 KDE on samples from the reward function (left) GFlowNet (centre) and MCMC (right) for ketorolac for the three proxies: GFN2-xTB (top), GFN-FF (middle) and TorchANI (bottom). | ||
 | ||
| Fig. 9 KDE on samples from the reward function (left) GFlowNet (centre) and MCMC (right) for ibuprofen for the three proxies: GFN2-xTB (top), GFN-FF (middle) and TorchANI (bottom). | ||
 | ||
| Fig. 10 KDE on samples from the reward function (left) GFlowNet (centre) and MCMC (right) for alanine dipeptide for the three proxies: GFN2-xTB (top), GFN-FF (middle) and TorchANI (bottom). | ||
Acknowledgements
We thank Léna Néhale-Ezzine an Prudencio Tossou for their contributions to our discussions. We thank Will Hua for his contribution in the code development at the initial stages of the project. We acknowledge computational support from Intel Labs and Mila compute resources for necessary experiments. We acknowledge Mila's IDT team support. We would like to express our gratitude to the CIFAR (Canadian Institute for Advanced Research), IVADO-PRF3; Genetech-Mila partnership; Amgen-Mila partnership and Intel-Mila partnership for their generous support in funding this research project. Cheng-Hao Liu thanks Vanier Scholarship for supporting their work in this project. In addition, we acknowledge material support from NVIDIA Corporation in the form of computational resources.References
- D. A. McQuarrie and J. D. Simon, Physical Chemistry: A Molecular Approach, University Science Books, Sausalito, CA, 1997, ch. 17 Search PubMed.
- D. D. Boehr, R. Nussinov and P. E. Wright, The role of dynamic conformational ensembles in biomolecular recognition, Nat. Chem. Biol., 2009, 5(11), 789–796 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading, J. Comput. Chem., 2010, 31(2), 455–461 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/jcc.21334.
- H. B. Schlegel, Exploring potential energy surfaces for chemical reactions: An overview of some practical methods, J. Comput. Chem., 2003, 24(12), 1514–1527 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/jcc.10231.
- A. C. Benniston and A. Harriman, Charge on the move: how electron-transfer dynamics depend on molecular conformation, Chem. Soc. Rev., 2006, 35, 169–179, 10.1039/B503169A.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192, 10.1039/C9CP06869D.
- S. Riniker and G. A. Landrum, Better informed distance geometry: using what we know to improve conformation generation, J. Chem. Inf. Model., 2015, 55(12), 2562–2574 CrossRef CAS PubMed.
- O. Ganea, L. Pattanaik, C. Coley, R. Barzilay, K. Jensen and W. Green, et al., Geomol: Torsional geometric generation of molecular 3d conformer ensembles, Adv. Neural Inf. Process. Syst., 2021, 34, 13757–13769 Search PubMed.
- M. Xu, L. Yu, Y. Song, C. Shi, S. Ermon and J. Tang, Geodiff: A geometric diffusion model for molecular conformation generation, arXiv, 2022, preprint, arXiv:220302923, DOI:10.48550/arXiv:2203.02923.
- B. Jing, G. Corso, J. Chang, R. Barzilay and T. Jaakkola, Torsional diffusion for molecular conformer generation, Adv. Neural Inf. Process. Syst., 2022, 35, 24240–24253 Search PubMed.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning, Science, 2019, 365(6457), eaaw1147 CrossRef PubMed.
- J. Köhler, A. Krämer and F. Noé, Smooth normalizing flows, Adv. Neural Inf. Process. Syst., 2021, 34, 2796–2809 Search PubMed.
- S. Zheng, J. He, C. Liu, Y. Shi, Z. Lu, W. Feng, et al., Towards Predicting Equilibrium Distributions for Molecular Systems with Deep Learning, arXiv, 2023, preprint, arXiv:230605445, DOI:10.48550/arXiv.2306.05445.
- S. Lahlou, T. Deleu, P. Lemos, D. Zhang, A. Volokhova, A. Hernández-Garcıa, et al., A theory of continuous generative flow networks, In International Conference on Machine Learning, PMLR, 2023, pp. 18269–18300 Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22(14), 7169–7192 RSC.
- S. Axelrod and R. Gomez-Bombarelli, GEOM, energy-annotated molecular conformations for property prediction and molecular generation, Sci. Data, 2022, 9(1), 185 CrossRef CAS PubMed.
- P. C. Hawkins, A. G. Skillman, G. L. Warren, B. A. Ellingson and M. T. Stahl, Conformer generation with OMEGA: algorithm and validation using high quality structures from the Protein Databank and Cambridge Structural Database, J. Chem. Inf. Model., 2010, 50(4), 572–584 CrossRef CAS PubMed.
- G. Zhou, Z. Gao, Z. Wei, H. Zheng and G. Ke, Do Deep Learning Methods Really Perform Better in Molecular Conformation Generation?, arXiv, 2023, preprint, arXiv:230207061, DOI:10.48550/arXiv.2302.07061.
- J. Wang, S. Olsson, C. Wehmeyer, A. Pérez, N. E. Charron and G. De Fabritiis, et al., Machine learning of coarse-grained molecular dynamics force fields, ACS Cent. Sci., 2019, 5(5), 755–767 CrossRef CAS PubMed.
- M. Arts, V. G. Satorras, C. W. Huang, D. Zuegner, M. Federici, C. Clementi, et al., Two for one: Diffusion models and force fields for coarse-grained molecular dynamics, arXiv, 2023, preprint, arXiv:230200600, DOI:10.48550/arXiv.2302.00600.
- P. Thölke and G. De Fabritiis, Equivariant transformers for neural network based molecular potentials, in International Conference on Learning Representations, 2021 Search PubMed.
- C. Shi, S. Luo, M. Xu and J. Tang, Learning gradient fields for molecular conformation generation, in International conference on machine learning, PMLR, 2021, pp. 9558–9568 Search PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli, et al., Forces are not enough: Benchmark and critical evaluation for machine learning force fields with molecular simulations, arXiv, 2022, preprint, arXiv:221007237, DOI:10.48550/arXiv:2210.07237.
- T. Gogineni, Z. Xu, E. Punzalan, R. Jiang, J. Kammeraad and A. Tewari, et al., Torsionnet: A reinforcement learning approach to sequential conformer search, Adv. Neural Inf. Process. Syst., 2020, 33, 20142–20153 Search PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, Proximal Policy Optimization Algorithms, CoRR, 2017, 06347 Search PubMed.
- Y. Patel and A. Tewari, RL Boltzmann Generators for Conformer Generation in Data-Sparse Environments, arXiv, 2022, preprint, arXiv:221110771, DOI:10.48550/arXiv.2211.10771.
- K. Swanson, J. L. Williams and E. M. Jonas, Von mises mixture distributions for molecular conformation generation, In International Conference on Machine Learning, PMLR, 2023, pp. 33319–33342 Search PubMed.
- E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, Flow network based generative models for non-iterative diverse candidate generation, Adv. Neural Inf. Process. Syst., 2021, 34, 27381–27394 Search PubMed.
- N. Malkin, M. Jain, E. Bengio, C. Sun and Y. Bengio, Trajectory balance: Improved credit assignment in gflownets, Adv. Neural Inf. Process. Syst., 2022, 35, 5955–5967 Search PubMed.
- G. Landrum. RDKit: open-source cheminformatics, 2016, 3, 8, https://www.rdkit.org/.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theor. Comput., 2019, 15(3), 1652–1671 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht and J. Seibert, et al., Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(2), e1493 CAS.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, TorchANI: A free and open source PyTorch-based deep learning implementation of the ANI neural network potentials, J. Chem. Inf. Model., 2020, 60(7), 3408–3415 CrossRef CAS PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk and O. Isayev, et al., Extending the applicability of the ANI deep learning molecular potential to sulfur and halogens, J. Chem. Theory Comput., 2020, 16(7), 4192–4202 CrossRef CAS PubMed.
- R. Vargas, J. Garza, B. P. Hay and D. A. Dixon, Conformational Study of the Alanine Dipeptide at the MP2 and DFT Levels, J. Phys. Chem. A, 2002, 106(13), 3213–3218, DOI:10.1021/jp013952f.
- J. Zeng, Y. Tao, T. J. Giese and D. M. York, QDπ: A quantum deep potential interaction model for drug discovery, J. Chem. Theory Comput., 2023, 19(4), 1261–1275, DOI:10.1021/acs.jctc.2c01172.
- J. Buchner, Nested sampling methods, Statistic Surveys., 2023, 17, 169–215 Search PubMed.
- J. Torrado and A. Lewis, Cobaya: Bayesian analysis in cosmology, Astrophysics Source Code Library, 2019, 1910 Search PubMed.
- J. Torrado and A. Lewis, Cobaya: Code for Bayesian Analysis of hierarchical physical models, J. Cosmol. Astropart. Phys., 2021, 2021(05), 057 CrossRef CAS.
- A. Gelman and D. B. Rubin, Inference from iterative simulation using multiple sequences, Stat. Sci., 1992, 7(4), 457–472 Search PubMed.
- M. Xu, S. Luo, Y. Bengio, J. Peng and J. Tang, Learning neural generative dynamics for molecular conformation generation, arXiv, 2021, preprint, arXiv:210210240, DOI:10.48550/arXiv.2102.10240.
Footnotes |
| † AI for Materials Design Workshop at 37th Conference on Neural Information Processing Systems (Neurips 2023). |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1COc2ccc(C(
C1COc2ccc(C(