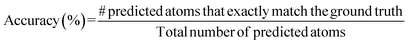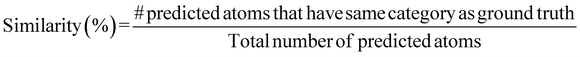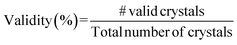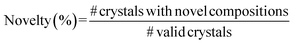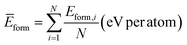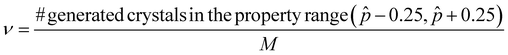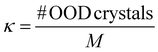Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Learning conditional policies for crystal design using offline reinforcement learning†
Prashant
Govindarajan
 *a,
Santiago
Miret
*a,
Santiago
Miret
 b,
Jarrid
Rector-Brooks
c,
Mariano
Phielipp
b,
Janarthanan
Rajendran
c and
Sarath
Chandar
a
b,
Jarrid
Rector-Brooks
c,
Mariano
Phielipp
b,
Janarthanan
Rajendran
c and
Sarath
Chandar
a
aMila-Quebec AI Institute, Polytechnique, Montréal, Canada. E-mail: prashant.govindarajan@mila.quebec
bIntel Labs, USA
cMila-Quebec AI Institute, Université de Montréal, Canada
First published on 29th February 2024
Abstract
Navigating through the exponentially large chemical space to search for desirable materials is an extremely challenging task in material discovery. Recent developments in generative and geometric deep learning have shown promising results in molecule and material discovery but often lack evaluation with high-accuracy computational methods. This work aims to design novel and stable crystalline materials conditioned on a desired band gap. To achieve conditional generation, we: (1) formulate crystal design as a sequential decision-making problem, create relevant trajectories based on high-quality materials data, and use conservative Q-learning to learn a conditional policy from these trajectories. To do so, we formulate a reward function that incorporates constraints for energetic and electronic properties obtained directly from density functional theory (DFT) calculations; (2) evaluate the generated materials from the policy using DFT calculations for both energy and band gap; (3) compare our results to relevant baselines, including behavioral cloning and unconditioned policy learning. Our experiments show that conditioned policies achieve targeted crystal design and demonstrate the capability to perform crystal discovery evaluated with accurate and computationally expensive DFT calculations.
1 Introduction
The widespread enthusiasm in exploiting artificial intelligence (AI) for scientific discovery1 has resulted in various methodologies to integrate existing scientific knowledge and large databases to design and test new hypotheses more quickly. Recently, AI has shown favorable results in expediting the discovery of new chemical structural entities (e.g., small molecules, materials, and polymers).2–5 While several studies have focused on small molecule design for applications in drug discovery, there has also been an upsurge in attention for AI-based material discovery.6–9 Among solid-state materials, crystalline substances are abundant in nature and are extensively used in industry for designing batteries, semiconductors, and photovoltaic systems. The set of known and experimentally observed crystalline materials is an infinitesimally tiny fraction (around 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) of the exponentially large chemical space spanning over 100 elements in the periodic table and 230 space groups in 3 dimensions.10,11 Determining a way to navigate through this large space to select chemical candidates with desired properties would be immensely beneficial for a plethora of applications like designing energy-efficient semiconductors and combatting climate change.
000) of the exponentially large chemical space spanning over 100 elements in the periodic table and 230 space groups in 3 dimensions.10,11 Determining a way to navigate through this large space to select chemical candidates with desired properties would be immensely beneficial for a plethora of applications like designing energy-efficient semiconductors and combatting climate change.
Besides the complex nature of the chemical space, designing stable crystalline materials using computational chemistry is a long-standing challenge primarily due to the time-consuming density functional theory (DFT) calculations to estimate energetic and electronic properties of materials. Previous works have utilized generative adversarial networks (GANs),12 diffusion models,13,14 and reinforcement learning (RL),15,16 in addition to advanced crystal representation schemes for generating crystals.17,18 However, we identify two major gaps in the existing literature for AI-based material discovery. Firstly, most methods do not incorporate quantum mechanics-based first-principles calculations in the learning model, and instead use ML approximators. Studies that incorporate DFT computations in their ML pipeline for material design usually focus on smaller and very specific chemical systems (with limited number of elements or constraints on the space group) that might not generalize well to diverse chemical systems.15,19 Secondly, state-of-the-art generative AI methods, such as diffusion models, predict the identities and positions of all atoms simultaneously, which is orthogonal to sequence based RL methods that also have more established exploration methods applicable to vast search spaces.
In this work, we develop a model that learns to sequentially construct crystal skeleton graphs by optimizing for both lower formation energy and desired band gap value (energy gap between the valence and conduction bands in solids), as computed by DFT. In our case, the crystal lattice parameters and positions of atomic sites are known beforehand (crystal skeleton), and the task is to learn a conditional policy that can sequentially fill atoms to generate a stable and valid crystal with a desired band gap energy. To alleviate the issue of time-consuming DFT calculations when integrated into the scientific discovery loop, we apply offline reinforcement learning using the conservative Q-learning (CQL) approach,20 which is known to mitigate overestimation and out-of-distribution issues when agents are trained with static datasets in an offline manner. We construct a state transition dataset from high-quality nonmetallic crystal structures present in the Materials Project database. The reward function is carefully formulated to penalize high energies and large deviations from the desired band gap. Further, we leverage an expressive graph neural network (GNN) for crystal representation that ensures invariance to periodicity, translation, and rotation. Through our work, we aim to accelerate the process of high-throughput virtual screening (HTVS) for materials,21 where usually elements are combinatorially substituted in a known crystal structure and optimized using DFT calculations. Overall, our contributions are three-fold, as follows:
(1) DFT evaluation of crystals designed with reinforcement learning: our targeted formulation of the reward function for offline RL is crafted from formation energy (per atom) and band gap values computed using first-principles DFT calculations, widely used in computational chemistry. The reward function penalizes high energy and large deviations from the desired band gap, resulting in a policy conditioned on a target band gap value.
(2) Conservative offline reinforcement learning approach: using CQL as our offline RL framework, we show that conservatism, combined with the right amount of importance for the energy and band gap terms in the reward function, can result in an intuitive approach for generating crystals with a favorable shift in the distribution of properties of interest. Considering our task has a very sparse reward scheme, allows no exploration, and has a high dimensional action space and limited data, we highlight the important challenges that could be addressed in the future.
(3) Open-source crystal structure design trajectory data: to ensure consistency in our reward calculation, we evaluate ∼20k crystal structures using the Quantum Espresso22 package for DFT calculation and subsequently construct offline RL trajectories based on the data. We release the dataset of trajectories and calculations as part of the paper to enable research to further improve our work. We use an open-source DFT calculator that is highly reproducible and consistent for all the structures evaluated. Prior work used different types of proprietary DFT software, which is difficult for the research community to reproduce.
2 Related works
2.1 Automated materials design
Prior work has explored the application of various types of methods to crystal structure design, including evolutionary algorithms, simulated annealing, particle swarm optimization, and high-throughput screening.23–25 Machine learning based methods have been more recently applied, primarily to molecular design problems, but also to periodic crystal structures.17,26 Moreover, there have been notable works using machine learning based methods to approximate the evaluation of material properties and behaviors.8,27 This includes approximating DFT outputs directly for different systems, such as ground-state crystal structures for a variety of applications, such as catalysts.28,29 The recent progress in graph neural networks and generative models has led to their successful application in materials design.29,30 GANs have been well explored for crystal structure design.12,19,31 However, these approaches restrict the complexity of the problem to a fixed crystal system or a smaller chemical space.11 proposed a physics-guided GAN model using convolutional layers to learn the generative distribution of stable crystals, and the evaluation of generated crystals was done using DFT. CDVAE13 introduced a diffusion-based framework with highly expressive graph representation learning techniques to generate stable and valid crystal structures in 3 dimensions.32 used their Distributional Graphormer to generate structures of carbon polymorphs with the desired band gap.15 focused on building an online RL framework with DFT integrated reward function for surface reconstructions. However, they use the tight-binding version of DFT (DFTB), whose accuracy is lower than full DFT calculations. Other relevant works include ref. 33–35 and 362.2 Offline reinforcement learning
Offline RL37,38 enables for learning an optimal policy directly from existing trajectories, making it possible to utilize knowledge from known crystal structures. The ability to learn from previously determined crystal structures reduces the need for costly DFT calculations during training, which are necessary for online RL methods. Many recently proposed offline RL methods focus on managing distribution shift between the offline data and the learned policy,39–41 with Conservative Q-Learning (CQL)20 proving to be a particularly robust approach. CQL has shown success in training large capacity models and performing better with suboptimal data, which makes it a particularly good fit for our crystal structure design case.3 Background
3.1 Crystals
Solid-state crystals are characterized by ordered and periodic arrangement of atoms in 3 dimensional space. They consist of unit cells, which are the smallest group of atoms that form the repeating pattern of the crystal. A crystal's composition and arrangement of atoms give rise to distinct electronic properties usually determined by experimental or simulation-based density functional theory (DFT) calculations. In 3 dimensions, we can mathematically express the unit cell U as follows.| U = {w1l1 + w2l2 + w3l3|0 ≤ wi < 1}, | (1) |
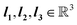 are primitive translation vectors that define the periodic translation symmetry of the crystal. Discrete linear transformations can be performed to obtain unit cells at different locations with ∇ = c1l1 + c2l2 + c3l3, where c1, c2, and c3 are integers, thus generating the entire 3-dimensional lattice. Therefore, a 3-dimensional lattice Λ is defined as all integral combinations of the lattice basis vectors.
are primitive translation vectors that define the periodic translation symmetry of the crystal. Discrete linear transformations can be performed to obtain unit cells at different locations with ∇ = c1l1 + c2l2 + c3l3, where c1, c2, and c3 are integers, thus generating the entire 3-dimensional lattice. Therefore, a 3-dimensional lattice Λ is defined as all integral combinations of the lattice basis vectors.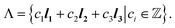 | (2) |
For a crystal with N atoms, where the atom positions are given by X = {x0, …, xN−1}, the corresponding position of atom u in a unit cell translated by c1l1 + c2l2 + c3l3 is given by
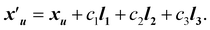 | (3) |
Further, there are 230 space groups in the 3-dimensional space, each of which describes a specific crystal symmetry. Every crystal in the database is associated with one space group number (1–230) depending on the arrangement of atoms in the crystal lattice. The order is based on the increasing complexity of symmetry elements and their combinations. For instance, space group number 1 is the simplest and least symmetric crystal system (triclinic), and 230 has the highest degree of symmetry (cubic).
3.2 Crystal representation
A natural way to represent crystals is using graphs, with atoms as nodes and edges that connect neighboring or bonded atoms. However, using simple graphs is often not expressive enough to incorporate the inherent periodicity in crystals. In this work, we adopt multigraphs, following42 to represent crystal structures. In multigraphs, two nodes can be connected by more than one type of edge. In the context of crystals, consider a graph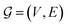 with nodes (atoms) V = {v0, …, vN−1} and edges (neighboring atoms)
with nodes (atoms) V = {v0, …, vN−1} and edges (neighboring atoms) 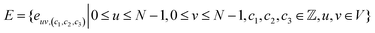 . Here, euv,(c1,c2,c3) is a directed edge from atom u to atom v in a unit cell translated by c1l1 + c2l2 + c3l3. If c1 = c2 = c3 = 0, it corresponds to an edge between u and v in the same unit cell. Likewise, if c1 = 1, c2 = c3 = 0 it corresponds to an edge between atom u in the original unit cell and atom v in a unit cell translated by l1. This way, multigraphs carry information about the entire 3 dimensional structure of crystals.
. Here, euv,(c1,c2,c3) is a directed edge from atom u to atom v in a unit cell translated by c1l1 + c2l2 + c3l3. If c1 = c2 = c3 = 0, it corresponds to an edge between u and v in the same unit cell. Likewise, if c1 = 1, c2 = c3 = 0 it corresponds to an edge between atom u in the original unit cell and atom v in a unit cell translated by l1. This way, multigraphs carry information about the entire 3 dimensional structure of crystals.
3.3 Offline reinforcement learning
While online RL methods demand frequent agent-environment interactions, offline RL exploits existing data,38 which is useful when receiving rewards or feedback from the environment is computationally expensive or physically implausible. As previously mentioned, our reward formulation depends on the energies and band gaps of crystals computed by DFT. Given that the time it takes to perform DFT simulation ranges between 6 seconds to more than 20 minutes for each input, depending on its size and type, it is highly infeasible to train an online reinforcement learning algorithm for this problem. Additionally, the high dimensional action space and the extremely complex reward landscape with narrow modes demand large amounts of exploration while learning in an online manner. Offline RL aims to learn from a static dataset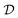 consisting of state transitions, i.e., (st, at, st+1, rt+1) obtained from a behavioral policy πβ(a|s) to learn an offline policy πo(a|s). However, directly adopting popular RL (e.g., deep Q-learning) approaches in a data-driven manner causes two major issues – (1) the learned policy becomes out-of-distribution from the behavioral policy, and (2) values of some states are over-estimated. Both these issues go hand-in-hand. Addressing these issues,20 proposed conservative Q-learning (CQL), which regularizes Q-values by concurrently optimizing for the Bellman error to learn a conservative and lower-bound Q function. The optimization objective of the DQN43 version (discrete action space) of CQL is given below
consisting of state transitions, i.e., (st, at, st+1, rt+1) obtained from a behavioral policy πβ(a|s) to learn an offline policy πo(a|s). However, directly adopting popular RL (e.g., deep Q-learning) approaches in a data-driven manner causes two major issues – (1) the learned policy becomes out-of-distribution from the behavioral policy, and (2) values of some states are over-estimated. Both these issues go hand-in-hand. Addressing these issues,20 proposed conservative Q-learning (CQL), which regularizes Q-values by concurrently optimizing for the Bellman error to learn a conservative and lower-bound Q function. The optimization objective of the DQN43 version (discrete action space) of CQL is given below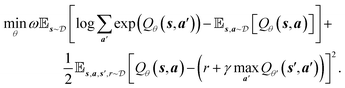 | (4) |
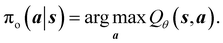 | (5) |
3.4 Density functional theory
DFT is a quantum mechanics-based simulation model that is used to compute the electronic structure of multi-atom systems, thereby estimating several properties including total energy, formation energy, and band gap. This is achieved by iteratively solving the Kohn–Sham equations.44 For evaluating crystal structures, we make use of the open-source Quantum Espresso software suite22 to perform self-consistent field (SCF calculations) using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional. However, the PBE functional is known for its systematic underestimation of band gap energies,45 and is less accurate than functionals like HSE06 (ref. 46) or other self-energy approximations like GW.47 Nevertheless, we used PBE because of its lower computational costs and superiority over DFTB. The output produced by the DFT simulation consists of two important properties that we are interested in – total energy (in Rydberg) and band gap (in eV units). Using total energy, we can also compute the formation energy (in eV per atom units). We also faced multiple new crystals failing to complete DFT simulation due to unknown properties (e.g., spin, magnetization) as part of our evaluation. Details about failure handling are provided in Section A.1.6.1.4 Methods
4.1 RL formulation
The RL formulation of our problem follows a MDP defined as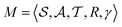 , where
, where 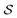 denotes the state space,
denotes the state space, 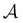 denotes the action space,
denotes the action space, 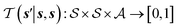 is the environment transition probability function,
is the environment transition probability function, 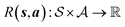 is the reward function, and γ ∈ [0, 1] is a discount factor denoting the preference for long term rewards over short term rewards. In our setup, the state space consists of empty, partially or fully filled multigraphs
is the reward function, and γ ∈ [0, 1] is a discount factor denoting the preference for long term rewards over short term rewards. In our setup, the state space consists of empty, partially or fully filled multigraphs 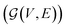 of crystal structures. The action space
of crystal structures. The action space 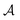 consists of atomic elements from which the agent has to choose to assign an atom at a given atomic site in a unit cell. Starting with initial state s0, which is the graph
consists of atomic elements from which the agent has to choose to assign an atom at a given atomic site in a unit cell. Starting with initial state s0, which is the graph 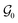 of an empty crystal skeleton, the sequential construction of a crystal of N atoms can be represented as a trajectory, as shown in Fig. 1a.
of an empty crystal skeleton, the sequential construction of a crystal of N atoms can be represented as a trajectory, as shown in Fig. 1a.
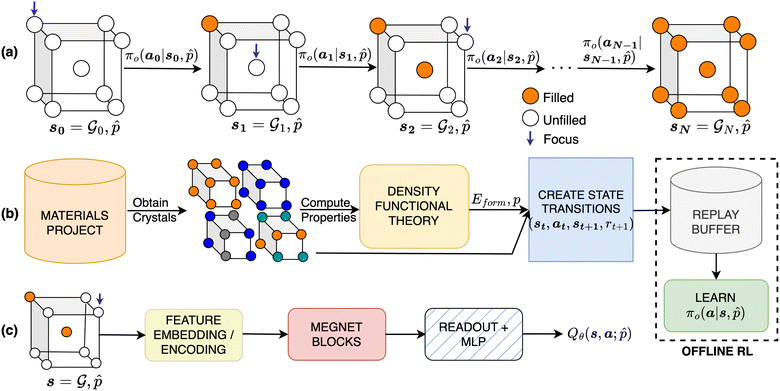 | ||
| Fig. 1 (a) Our design approach centers on filling in the composition of predefined crystal using an RL policy. (b) To successfully train an RL policy, we obtain data from Materials Project,48 recompute relevant property values using open-source DFT (Quantum Espresso22) and create trajectories for offline RL. (c) We train a graph neural network based policy based on MEGNet49 to achieve property-conditioned crystal generation. | ||
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) . In the context of training an offline RL agent with batches of transitions, we aim to minimize the deviation between the ground truth property p of the crystal and
. In the context of training an offline RL agent with batches of transitions, we aim to minimize the deviation between the ground truth property p of the crystal and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) (desired property). This bi-objective optimization can be addressed by using a linear combination of terms that individually optimize for lower energy and desired property. In other words, for a crystal with N atoms, the terminal reward, which is also equal to the return in this case, can be expressed in terms of its formation energy Eform and ground truth property p as follows.
(desired property). This bi-objective optimization can be addressed by using a linear combination of terms that individually optimize for lower energy and desired property. In other words, for a crystal with N atoms, the terminal reward, which is also equal to the return in this case, can be expressed in terms of its formation energy Eform and ground truth property p as follows.rN(Eform,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ,p) = α1gE(Eform) + α2gp(p, ,p) = α1gE(Eform) + α2gp(p,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ). ). | (6) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ) enforces p and
) enforces p and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) to be close (e.g. distance function), and α1 and α2 are design parameters that control the importance of each of the terms. We use the exponentials of the negative formation energy of the crystal and the distance between the true and desired properties, yielding a terminal reward as follows:
to be close (e.g. distance function), and α1 and α2 are design parameters that control the importance of each of the terms. We use the exponentials of the negative formation energy of the crystal and the distance between the true and desired properties, yielding a terminal reward as follows: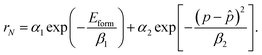 | (7) |
This introduces more design parameters β1, and β2, which essentially influence the sharpness of the mode of the exponential function; lower value of {βi}i=1,2 results in a higher level of sharpness.2
4.2 Q-Network and state representation
Our conditional Q-network Qθ(s,a;![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ) consists of two components: (1) a graph neural network that extracts meaningful state representation of the input multigraph; (2) linear layers for computing Q-values from this representation. To represent and process multigraphs in an expressive manner, we adopt the MEGNet model,49 a universal graph machine learning framework for molecules and materials. MEGNet provides an effective way of iterative information exchange among node, edge and state features, which is particularly useful for chemical entities. For a crystal graph
) consists of two components: (1) a graph neural network that extracts meaningful state representation of the input multigraph; (2) linear layers for computing Q-values from this representation. To represent and process multigraphs in an expressive manner, we adopt the MEGNet model,49 a universal graph machine learning framework for molecules and materials. MEGNet provides an effective way of iterative information exchange among node, edge and state features, which is particularly useful for chemical entities. For a crystal graph 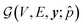 conditioned on the desired property
conditioned on the desired property ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , V and E are sets of nodes and edges, and y corresponds to the global state-level feature. For the N atoms in a unit cell, the categorical feature of the nodes
, V and E are sets of nodes and edges, and y corresponds to the global state-level feature. For the N atoms in a unit cell, the categorical feature of the nodes 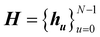 denote the one-hot encoding of the atom type in each of the nodes. It includes an additional dimension to indicate whether the node is currently filled or unfilled with an atom. Edges connect neighboring atoms based on the CrystalNN scheme proposed by50 for determining the presence and type (i.e., (c1, c2, c3) triplet) of edges. The set of edge features
denote the one-hot encoding of the atom type in each of the nodes. It includes an additional dimension to indicate whether the node is currently filled or unfilled with an atom. Edges connect neighboring atoms based on the CrystalNN scheme proposed by50 for determining the presence and type (i.e., (c1, c2, c3) triplet) of edges. The set of edge features 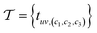 represents the Gaussian distance between the position of atom u in the reference unit cell and atom v in a unit cell shifted by c1l1 + c2l2 + c3l3.
represents the Gaussian distance between the position of atom u in the reference unit cell and atom v in a unit cell shifted by c1l1 + c2l2 + c3l3.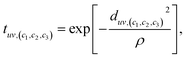 | (8) |
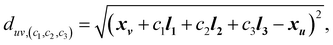 | (9) |
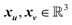 are the positions (Cartesian coordinates) of atoms u and v in the reference unit cell. The state-level feature y is expressed as follows:
are the positions (Cartesian coordinates) of atoms u and v in the reference unit cell. The state-level feature y is expressed as follows:y = [z‖f],z = [a,b,c,ϕ1,ϕ2,ϕ3,S,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ], ], | (10) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) is the desired property that the policy is conditioned on, and f is a categorical feature, which we refer to as focus – it instructs the policy which unfilled node to focus on for atom type prediction in the following step. The categorical features H and f are passed through embedding layers to obtain embedded feature maps
is the desired property that the policy is conditioned on, and f is a categorical feature, which we refer to as focus – it instructs the policy which unfilled node to focus on for atom type prediction in the following step. The categorical features H and f are passed through embedding layers to obtain embedded feature maps ![[H with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0048_0303.gif) ,
,![[f with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0066_0303.gif) . Numerical features
. Numerical features 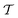 and y are passed through multilayer perceptrons (MLPs)
and y are passed through multilayer perceptrons (MLPs)ỹ = MLP([z‖![[f with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0066_0303.gif) ]). ]). | (11) |
A graph 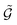 with embedded and encoded features is then passed through K MEGNet layers, followed by a readout layer (Appendix A.1.4) to obtain a graph-level representation, which is then passed through an MLP to obtain conditioned Q-values for all actions in
with embedded and encoded features is then passed through K MEGNet layers, followed by a readout layer (Appendix A.1.4) to obtain a graph-level representation, which is then passed through an MLP to obtain conditioned Q-values for all actions in 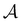 .
.
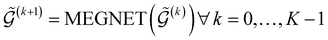 | (12) |
 | (13) |
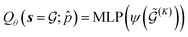 | (14) |
4.3 Dataset
For this study, we used a subset of the Materials Project database, referred to as MP-20, that was previously used by.13 MP-20 consists of ∼45k metallic and nonmetallic crystals with different structures and compositions, covering 88 elements in the periodic table. All of them have at most 20 atoms. For our experiments, we excluded metallic crystals with zero band gap.‡ Metals constituted more than 60% of the data, leading to class imbalance challenges while conditioning the model with a nonzero band gap. Next, we used Quantum Espresso to determine the formation energies and band gaps of all nonmetallic crystals in the training and validation set. In the end, our training set included 8832 crystals, and our validation set included 2486 crystals.4.4 State transitions for offline RL
As shown in Fig. 1, we generated a static dataset for training the offline policy using episodic trajectories consisting of (st, at, st+1, rt+1) transitions from MP-20 crystals. We applied a deterministic policy πβ(a|s), where the actions correspond to the original element identities of the atom at a specific position of interest in an empty or partially constructed crystal skeleton graph. Each trajectory of an episode starts with the initial state s0, which is a graph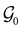 of a crystal skeleton, where all atom identities are hidden. Through the focus feature f, we are explicitly providing the order of traversal through the nodes of the graph, thereby simplifying the problem further. To mitigate the effects of bias due to this order dependency, we obtain up to 5 trajectories for each crystal by varying the order of nodes with breadth-first traversals of the graph from different source nodes. This way, we obtained ∼520k transitions to train our offline RL policies.
of a crystal skeleton, where all atom identities are hidden. Through the focus feature f, we are explicitly providing the order of traversal through the nodes of the graph, thereby simplifying the problem further. To mitigate the effects of bias due to this order dependency, we obtain up to 5 trajectories for each crystal by varying the order of nodes with breadth-first traversals of the graph from different source nodes. This way, we obtained ∼520k transitions to train our offline RL policies.
5 Experiments
In this study, we focus on training conditional CQL (c-CQL) models to design stable (i.e., low formation energy) crystals that have a desired band gap (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ) of 1.12 eV, 2 eV, 3 eV, and 4 eV, which fall within the semiconductor range. To determine the amount of conservatism required for better performance, we varied ω using weights of 1 and 5, with the latter being more conservative than the former. After an initial hyperparameter sweep, we choose the coefficients as follows: α1 = 1, α2 = 10, β1 = 5, β2 = 3. Our baselines are (1) random policy, (2) behavioral cloning (BC)§, and (3) Unconditional CQL (u-CQL) Policy (where
) of 1.12 eV, 2 eV, 3 eV, and 4 eV, which fall within the semiconductor range. To determine the amount of conservatism required for better performance, we varied ω using weights of 1 and 5, with the latter being more conservative than the former. After an initial hyperparameter sweep, we choose the coefficients as follows: α1 = 1, α2 = 10, β1 = 5, β2 = 3. Our baselines are (1) random policy, (2) behavioral cloning (BC)§, and (3) Unconditional CQL (u-CQL) Policy (where ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) is removed in the state feature vector and the reward is only in terms of Eform). For evaluating the model, we start with an empty crystal skeleton graph
is removed in the state feature vector and the reward is only in terms of Eform). For evaluating the model, we start with an empty crystal skeleton graph 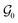 as the initial state s0, and perform a rollout using the learned conditional offline policy πo(a|s,
as the initial state s0, and perform a rollout using the learned conditional offline policy πo(a|s,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ) to sequentially fill atoms in the crystal. We then perform a pre-simulation assessment of the generated crystals using the following metrics – (1) compositional validity: a generated crystal is valid if it has an overall neutral charge, as computed by SMACT,51 (2) accuracy, which is the fraction of correctly predicted atoms, (3) similarity, which measures the similarity of the predicted atoms with the ground truth, i.e., two atoms are similar if they belong to the same class of elements¶, and (4) novelty, which measures the fraction of valid crystals whose composition is not present already in the Materials Project database. Our results are shown in Table 1.
) to sequentially fill atoms in the crystal. We then perform a pre-simulation assessment of the generated crystals using the following metrics – (1) compositional validity: a generated crystal is valid if it has an overall neutral charge, as computed by SMACT,51 (2) accuracy, which is the fraction of correctly predicted atoms, (3) similarity, which measures the similarity of the predicted atoms with the ground truth, i.e., two atoms are similar if they belong to the same class of elements¶, and (4) novelty, which measures the fraction of valid crystals whose composition is not present already in the Materials Project database. Our results are shown in Table 1.
| Accuracy (%) | Similarity (%) | Validity (%) | Novelty (%) | |||||
|---|---|---|---|---|---|---|---|---|
| CQL weight | ω = 1 | ω = 5 | ω = 1 | ω = 5 | ω = 1 | ω = 5 | ω = 1 | ω = 5 |
| Random | 0.0115 | 0.1254 | NaN | NaN | ||||
| BC | 49.37 | 69.04 | 81.84 | 51.34 | ||||
| u-CQL | 46.30 | 48.69 | 67.73 | 68.64 | 79.17 | 80.78 | 51.15 | 48.26 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 1.12 eV) = 1.12 eV) |
43.31 | 47.72 | 65.66 | 69.24 | 78.75 | 80.66 | 63.51 | 50.95 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 2 eV) = 2 eV) |
42.73 | 47.97 | 65.35 | 68.87 | 80.23 | 79.99 | 65.57 | 51.18 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 3 eV) = 3 eV) |
43.59 | 48.16 | 65.95 | 69.67 | 79.15 | 81.15 | 65.08 | 50.11 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 4 eV) = 4 eV) |
43.40 | 46.63 | 65.92 | 68.29 | 79.87 | 78.29 | 65.55 | 51.03 |
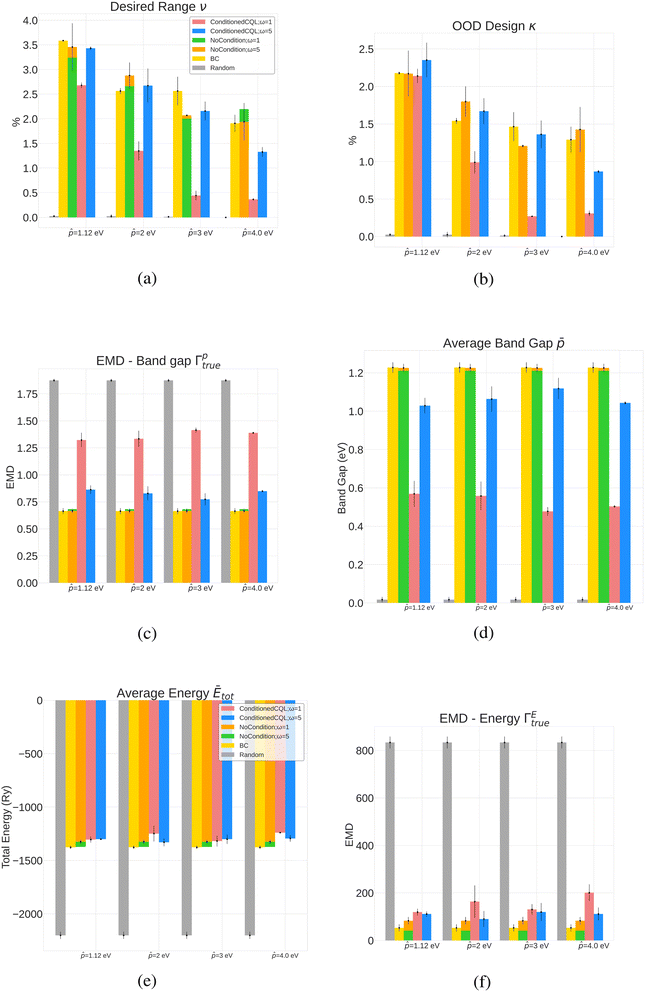
Next, we performed DFT simulation for all the valid crystals to estimate the total energy and band gap. The post-simulation metrics are (1) Average Formation Energy per atom Ēform of the policy-generated crystals (2) Earth Mover Distance (EMD) between the generated and true band gap distributions (Γptrue), (3) Earth Mover Distance between the generated and true formation energy distributions (ΓEtrue), (4) % of crystals that have the band gap value in the desired range (ν), which in our case is from ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) − 0.25 eV to
− 0.25 eV to ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) + 0.25 eV, and (5) Out-of-distribution (OOD) design (κ) – % of generated crystals that have band gaps in the desired range but whose corresponding ground truth crystals have band gaps outside the desired range. The results are shown in Fig. 2. Our initial set of experiments incorporated total energy (Etot) in the reward formulation instead of formation energy, where we also tuned the design parameters. The results of the same are detailed in Appendix A.3.
+ 0.25 eV, and (5) Out-of-distribution (OOD) design (κ) – % of generated crystals that have band gaps in the desired range but whose corresponding ground truth crystals have band gaps outside the desired range. The results are shown in Fig. 2. Our initial set of experiments incorporated total energy (Etot) in the reward formulation instead of formation energy, where we also tuned the design parameters. The results of the same are detailed in Appendix A.3.
 | ||
Fig. 2 Results for conditioned CQL policies on four band gap design targets (1.12 eV, 2 eV, 3 eV and 4 eV) with formation energy in the reward function (eqn (7)). Conditioned and more conservative policies perform well in the κ and ν metric when the target is lower, while unconditioned policies, including behavioral cloning, perform better at reproducing the original distribution. Random policies fail to reproduce the original distribution and achieve desired properties. (a) % Desired range for the four band gaps targets for various policies. Conditioned policies outperform random policy and compete with unconditional policies in designing crystal in the desired property range (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) − 0.25, − 0.25, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) + 0.25). (b) % of generated crystals with property in the desired range with corresponding ground truth crystals outside the desired range. Conditioned policies outperform baselines for lower band gap targets (1.12 eV and 2 eV). (c) Band gap EMD (generated vs. true) for various policies showing that unconditioned policies reproduce the original dataset better. Lower value indicates more resemblance to the true distribution. (d) Formation energy EMD (generated vs. true) for various policies showing that unconditioned policies reproduce the original dataset better. Lower value indicates more resemblance to the true distribution. (e) Average formation energy for various policies yielding valid crystals with energy below 0. The average formation energy of randomly generated crystals is high and positive. Lower is better. + 0.25). (b) % of generated crystals with property in the desired range with corresponding ground truth crystals outside the desired range. Conditioned policies outperform baselines for lower band gap targets (1.12 eV and 2 eV). (c) Band gap EMD (generated vs. true) for various policies showing that unconditioned policies reproduce the original dataset better. Lower value indicates more resemblance to the true distribution. (d) Formation energy EMD (generated vs. true) for various policies showing that unconditioned policies reproduce the original dataset better. Lower value indicates more resemblance to the true distribution. (e) Average formation energy for various policies yielding valid crystals with energy below 0. The average formation energy of randomly generated crystals is high and positive. Lower is better. | ||
5.1 Analysis of pre-simulation metrics
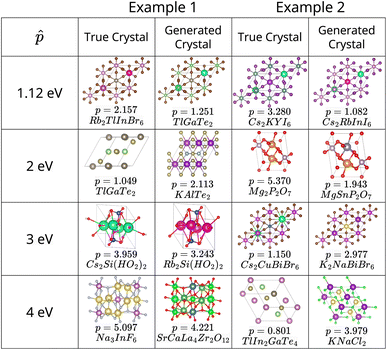
For all band gap targets, as seen in Table 1, the more conservative models (i.e., ω = 5) generally perform better in terms accuracy, similarity, and validity. The metrics were also influenced by the magnitude of the reward function – the higher the magnitude, lower the accuracy, and in most cases, the lower the validity of generated structures (pre-simulation results with total energy in Tables 2 and 3). This is interesting because when the magnitude of the reward is lower or ω is higher, the conservative term in the CQL objective in eqn (4) becomes dominant, resulting in the net maximization of Q-values of state-action pairs present in the dataset. Higher ω also results in lower novelty scores. Behavioral cloning (BC), trained with no reward signal, performed the best in accuracy and validity (Table 1), which can be attributed to BC's better prediction capacities attributed to supervised learning. However, this might not be helpful from the perspective of property-driven crystal design where the CQL-based policies outperform BC in ν and κ in some cases, as described next in Section 5.2 outlining relevant case studies.5.2 Band gap design case studies: targeting 1.12 eV, 2 eV, 3 eV & 4 eV
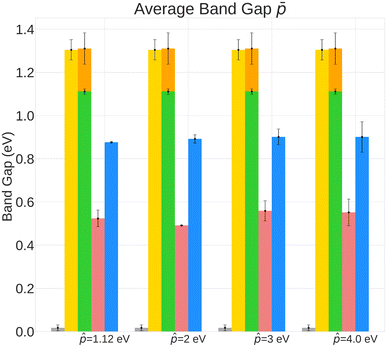
The results in Fig. 2, which include a well-performing policy for all the design cases, show some clear trends: (1) for lower band gap targets (i.e. 1.12 eV, 2 eV), conditioned policies (with ω = 5) generate more materials in the desired property range when the corresponding true materials have properties outside the desired range (Fig. 2a). Examples of such materials are shown in Fig. 3. (2) Greater conservatism leads to more materials in the desired range as shown by the fact that ω = 5 outperforms ω = 1 in all design cases. (3) Unconditioned policies manage to recreate the original distributions better than conditioned distributions. This is shown by better performance in Fig. 2c and d, holding for both band gap and formation energy. (4) Random policies are not effective in generating valid and desired crystal structures. It is likely that the random policy generated a small subset of valid metal-like crystals given the close to zero average band gap shown in Appendix A.1.3. Random policy generates many unrealistic crystals with high and positive formation energies (Fig. 2e), and many of the DFT runs validating the crystals failed (Table 2). Results of pre-simulation metrics included in Table 1 also show poor performance of random policy. As shown in Fig. 2, the higher values of![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) are more challenging because: (1) most samples in the dataset have a lower band gap value (Appendix A.2) making the number of samples with a higher band gap that get exposed to the model while training a very small fraction, (2) underestimation of band gaps by DFT, which causes an unfavorable shift from the expected band gap distribution.
are more challenging because: (1) most samples in the dataset have a lower band gap value (Appendix A.2) making the number of samples with a higher band gap that get exposed to the model while training a very small fraction, (2) underestimation of band gaps by DFT, which causes an unfavorable shift from the expected band gap distribution.
6 Limitations
The important limitations of this work are that the scope is limited to predicting only the atom types, given all other information about the skeleton of the crystal and the order of traversal, and the training data is small and limited to nonmetals. Considering computational challenges attributed to DFT calculations, we had to restrict our design parameter space to a very small set, but it would be interesting to see the results after an extensive analysis after training models with several values of ω, α1, α2, β1 and β2. A recent study showed that the performance of offline RL algorithms is influenced by the bias of the dataset generated by the behavioral policy and the strength of the reward signals.52 These aspects should be analyzed in the context of the crystal design problem with DFT-based reward signals for choosing the most appropriate offline RL algorithm and design parameters. Due to the significant underestimation of band gaps by DFT, many of the generated crystals had an estimated band gap value of 0.0, which severely hindered our evaluation and analyses. This explains the very low fraction of generated crystals having a greater band gap. Further, resolving the imbalance in the data due to the large number of samples in the lower band gap regions could help in learning better policies for generating crystals with higher band gap.7 Conclusion
We show that it is possible to train reinforcement learning based policies that can design valid crystal compositions conditioned on a crystal structure skeleton and a target property, such as the band gap, evaluated on precise and expensive computational chemistry engines, such as DFT. We demonstrate that offline RL methods can be used to learn distributions of design trajectories for valid crystal structures and provide tuning based on desired properties. While our results suggest that one can train policies for materials design problems, there is still significant space for future work to improve the performance, robustness, and capabilities of the RL policies. First, our approach can be extended to include additional design variables, such as crystal lattice parameters and atomic positions, for greater design flexibility to design more performant materials. Second, the dataset we used for offline RL is still limited in size given the large cost of generating the dataset in a consistent manner and evaluating the reward function for structures generated by the policy. This leaves significant room for future work in creating large pretraining datasets and accelerating the evaluation of crystal structures through more optimized high-throughput DFT or machine learning based approximators. Third, much algorithmic work remains in designing better policies for material design that can further improve the performance of conditional design.Data availability
The source code and models for this work can be obtained from https://github.com/chandar-lab/crystal-design. The offline trajectory datasets can be obtained from https://zenodo.org/records/10626005.Conflicts of interest
The authors declare no conflicts of interests.A Appendices
A.1 Experimental details
A.1.1.1 Accuracy. Accuracy is measured as the percentage of predicted atoms that match the ground truth. Note that the accuracy in this case is computed globally across atoms predicted in all the crystals present in the validation dataset.
We can also measure the fraction of crystals that were reconstructed to match the ground truth exactly. However, this was a very small percentage (∼2–7%) for all the models.
A.1.1.2 Similarity. While accuracy measures the fraction of exact matches, our similarity metric considers a prediction as a match if the predicted atom and the ground truth atom belong to the same category. The categories are defined as follows.
(1) Group 1: Li, Na, K, Rb, Cs
(2) Group 2: Be, Mg, Ca, Sr, Ba
(3) Transition metals: Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, Hf, Ta, W, Re, Os, Ir, Pt, Au, Hg
(4) Nonmetals: H,B, C, N, O, Si, P, S, As, Se, Te
(5) Halogens: F, Br, Cl, I
(6) Noble: Xe, Ne, Kr, He
(7) Lanthanides: La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu
(8) Actinides: Ac, Th, Pa, U, Np, Pu
A.1.1.3 Compositional validity. We follow13 and compute the compositional validity of crystals using SMACT.51
A.1.1.4 Novelty. To assess the novelty aspect of our approach, we compute the fraction of valid generated crystals whose compositions are novel, i.e., when the compositions are not present in the Materials Project Database.48 We utilised the API of Materials Project (
 function) to retrieve crystals with matching compositions. Note that our novelty percentage is conditioned on the valid crystals, and we do not query invalid compositions. Hence, in Table 1, while other metrics are computed by dividing the total number of crystals in the validation set, novelty is computed by dividing the number of valid crystals generated by the model.
function) to retrieve crystals with matching compositions. Note that our novelty percentage is conditioned on the valid crystals, and we do not query invalid compositions. Hence, in Table 1, while other metrics are computed by dividing the total number of crystals in the validation set, novelty is computed by dividing the number of valid crystals generated by the model.A.1.2.1 Average formation energy. Following Appendix A.1.7, the formation energy was calculated for all the generated and valid crystals that successfully underwent DFT simulation. The average formation energy if therefore,
where N is the number of valid crystals whose formation energy values were computed successfully using DFT.
A.1.2.2 EMD (band gap). The Earth Mover's Distance (EMD) was computed to determine the distributional distance between the properties of generated crystals and the ground truth crystals in the validation dataset. For band gap, the Γptrue was calculated as follows.
Γptrue = EMD({pi}Mi = 1,{![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) j}Nj = 1) j}Nj = 1) |
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) j is the property value of the jth valid crystal generated by the model.
j is the property value of the jth valid crystal generated by the model.
A.1.2.3 EMD (formation energy). Similar to Γptrue, EMD between the true and generated formation energy distributions, ΓEtrue were computed as follows.
| ΓEtrue = EMD({Eform,i}Mi = 1,{Ẽform,j}Nj = 1) |
A.1.2.4 Desired range. The desired range metric (ν) is the fraction of generated crystals whose property (here, band gap) lies between
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) − 0.25 and
− 0.25 and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) + 0.25, where
+ 0.25, where ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) is the target property. For simplicity and easier analysis, the denominator of this fraction is the total number of crystals in the validation set. This way, the metric provides a way to quantitatively compare the corresponding percentages across different models.
is the target property. For simplicity and easier analysis, the denominator of this fraction is the total number of crystals in the validation set. This way, the metric provides a way to quantitatively compare the corresponding percentages across different models.Here, M is the number of crystals in the validation set.
A.1.2.5 OOD design. Through the κ metric, we compared the number of crystals generated (from the validation set) whose property value lies in the desired range, i.e., (
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) − 0.25,
− 0.25,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) + 0.25), but the corresponding ground truth property is outside the desired range (hence, OOD crystals). This indicates that the model has learned to place atoms such that the property shifts from a value outside the desired range to within the range. Similar to ν, the denominator is M, the number of crystals in the validation set.
+ 0.25), but the corresponding ground truth property is outside the desired range (hence, OOD crystals). This indicates that the model has learned to place atoms such that the property shifts from a value outside the desired range to within the range. Similar to ν, the denominator is M, the number of crystals in the validation set.• Number of MEGNet blocks: 3
• Node embedding dimensions: 16
• Edge embedding dimensions: 1
• State embedding dimensions: 8
• READOUT Function: order-invariant set2set53
• Number of steps trained: 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000
• Discount factor: 0.99
• Batch size: 1024
• Learning rate: 3 × 10−4
• Soft target network update rate: 5 × 10−3
• Optimizer: Adam
• Calculation: SCF
• Pseudopotentials: solid-state pseudopotentials (SSSP) version 1.3.0 obtained from https://www.materialscloud.org/discover/sssp/table/efficiency
• Tolerance: 10−6
• Number of bands: 256
• k-points: (3–3–3)
• Occupations: fixed (since our training set consists only of nonmetallic crystals)
• Diagonalization: David
• ecutrho: 245
• ecutwfc: 30
• mixing_beta: 0.7
• degauss: 0.001
• Default charge: 0
• Maximum iterations: 1000
A.1.6.1 Handling failures. It is important to note that DFT can be best leveraged once we know certain properties of the crystals – for example, charge, magnetization, and metallicity. Considering the difficulty in determining these properties for completely unknown crystals, we standardized the evaluation procedure by using the same DFT configuration for all crystals (except for the crystal-specific parameters like number of atoms, species, and pseudopotentials directory). However, this resulted in multiple crystals failing DFT simulation. Some of the errors are explained below.
• Charge is wrong. Smearing is needed: this error mainly occurs because of unpaired electrons in the system, and can be resolved by changing the occupation to ‘smearing’ instead of ‘fixed’. However, doing so will not help in determining the band gap of crystals, as it will only output the Fermi energy. Another way is to set the ‘nspin’ parameter to 2 and specify the total magnetization value as an additional input to Quantum Espresso. This helped us resolve most of the failures for the MP-20 crystals in the training and validation set because the total magnetization value is retrievable from the Materials Project, but for the newly generated crystals, we had to ignore those that failed because of this error. The error could also occur if the generated crystal is metallic, and this property is also difficult to identify directly from the structure and composition.
• NOT converged in 1000 iterations: for some crystals, the DFT simulation did not converge even after 1000 iterations. These crystals were ignored while constructing the offline dataset, and also when evaluating the policy-generated crystals.
• Time limit exceeded: for constructing the offline dataset using known crystals, we used a flexible time limit to ensure none of the crystals were discarded because of time restrictions. However, while performing DFT simulation for the policy-generated crystals, due to the high-throughput nature of our evaluation pipeline, we had to ignore crystals that did not converge in 15 minutes.
• Too few bands: this error occurs when the number of bands specified, through ‘nbnds’ parameter is insufficient for the crystal system being simulated. This error was largely resolved by specifying a higher number of bands. In our case, we used 256 bands for all crystals.
Overall, during evaluation of generated crystals, only 50–70% of the valid crystals successfully underwent DFT simulation to output the energy and band gap (Table 2), and the rest failed because of the above errors.
A.1.6.2 % DFT success. Table 2 shows the percentage of policy-generated crystals that successfully underwent DFT simulation based on failure handling strategies discussed in Appendix A.1.6.1.
| % DFT success | ||
|---|---|---|
| CQL weight | ω = 1 | ω = 5 |
| Random | 15.18 | |
| BC | 68.25 | |
| u-CQL | 68.97 | 70.29 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 1.12 eV) = 1.12 eV) |
58.59 | 66.82 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 2 eV) = 2 eV) |
56.04 | 67.99 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 3 eV) = 3 eV) |
56.55 | 68.38 |
c-CQL (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = 4 eV) = 4 eV) |
55.64 | 66.19 |
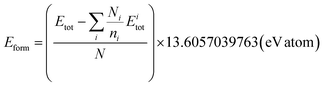 | (15) |
A.2 True distributions of properties
This section shows the true distribution of the band gaps and total energies for both training and validation data (Fig. 5).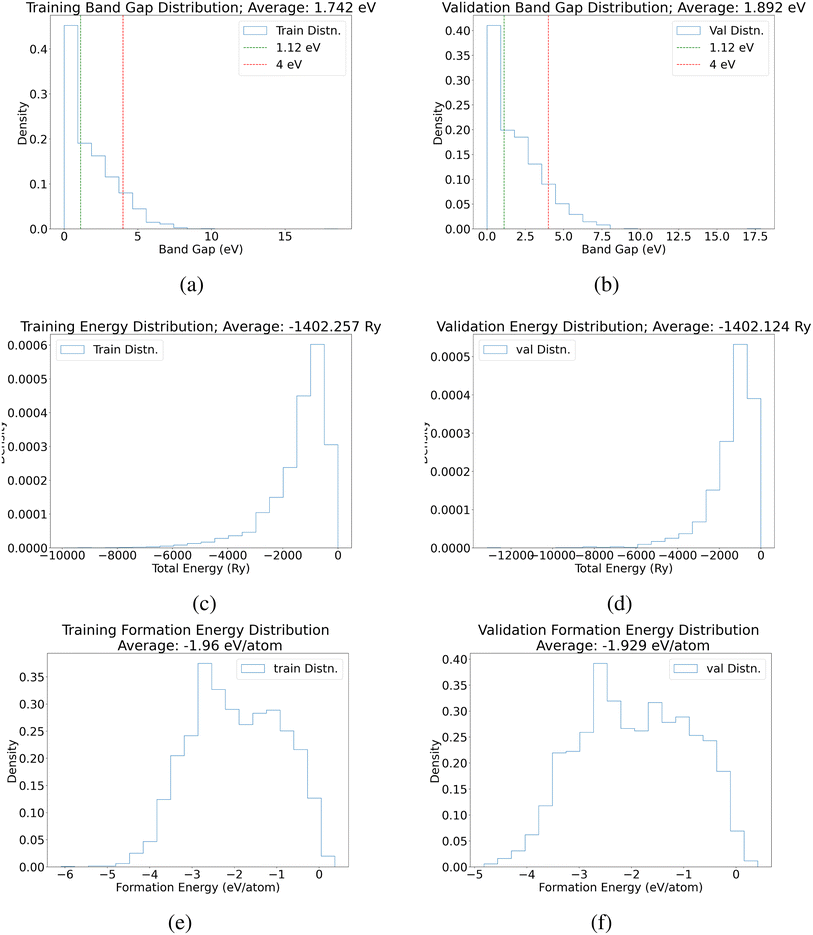 | ||
| Fig. 5 Distribution of band gap (eV), total energy (Ry), and formation energy (eV per atom) for training and validation datasets. | ||
A.3 Experiments with total energy
As part of our initial analysis, we performed the experiments with total energy (Etot) in the reward formulation instead of formation energy, with the aim of designing crystals that are generally considered stable (in an absolute sense), so they can be used for practical purposes. However, total energy is less meaningful when it comes to comparing the stability of different crystals, while energy above hull is the best-known metric to compare thermodynamic stability.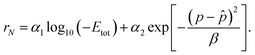 | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps.
000 steps.
| Accuracy (%) | Similarity (%) | Validity (%) | ||||
|---|---|---|---|---|---|---|
| CQL weight | ω = 1 | ω = 5 | ω = 1 | ω = 5 | ω = 1 | ω = 5 |
| Random | 0.0115 | 0.1254 | NaN | |||
| BC | 52.26 | 71.98 | 85.00 | |||
| uCQL | 49.77 | 51.53 | 70.85 | 71.26 | 81.50 | 82.54 |
| (0 − 5 − 1) | 38.64 | 48.85 | 61.23 | 69.38 | 69.99 | 77.84 |
| (0 − 5 − 3) | 43.02 | 46.43 | 65.01 | 67.04 | 73.57 | 78.44 |
| (0 − 10 − 1) | 36.54 | 43.72 | 59.3 | 65.18 | 73.33 | 80.81 |
| (0 − 10 − 3) | 35.16 | 42.42 | 57.48 | 64.15 | 71.20 | 81.30 |
| (1 − 5 − 1) | 42.11 | 47.72 | 64.00 | 68.12 | 75.62 | 80.29 |
| (1 − 5 − 3) | 40.59 | 47.57 | 63.70 | 67.26 | 72.93 | 76.51 |
| (1 − 10 − 1) | 35.02 | 43.18 | 58.63 | 65.13 | 67.82 | 75.14 |
| (1 − 10 − 3) | 35.38 | 43.81 | 57.23 | 65.58 | 61.87 | 77.19 |
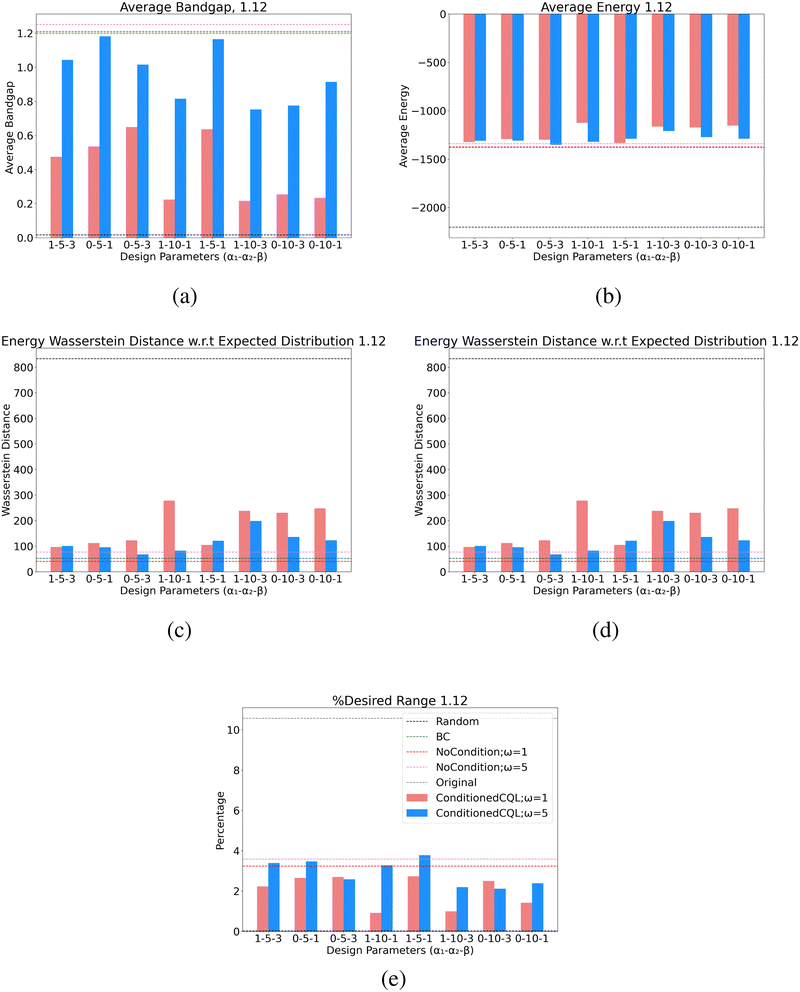 | ||
| Fig. 7 Full design parameter values for all learned policies for the band gap design case of 1.12 eV. Nomenclature of the table is (α1 − α2 − β) corresponding to the terms of the reward function in eqn (16). | ||
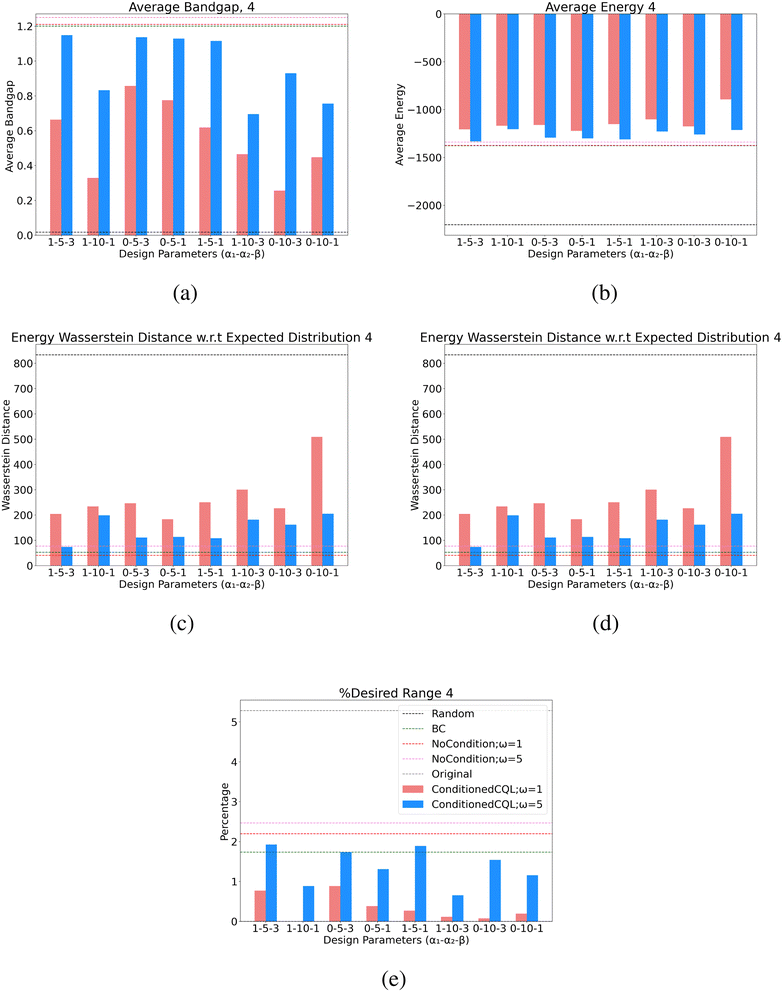 | ||
| Fig. 8 Full design parameter values for all learned policies for the band gap design case of 4.0 eV. Nomenclature of the table is (α1 − α2 − β) corresponding to the terms of the reward function in eqn (16). | ||
| Accuracy (%) | Similarity (%) | Validity (%) | ||||
|---|---|---|---|---|---|---|
| CQL weight | ω = 1 | ω = 5 | ω = 1 | ω = 5 | ω = 1 | ω = 5 |
| Random | 0.0115 | 0.1254 | NaN | |||
| BC | 52.26 | 71.98 | 85.00 | |||
| uCQL | 49.77 | 51.53 | 70.85 | 71.26 | 81.50 | 82.54 |
| (0 − 5 − 1) | 41.82 | 48.09 | 64.34 | 68.82 | 80.21 | 82.18 |
| (0 − 5 − 3) | 39.46 | 47.61 | 61.59 | 68.24 | 74.46 | 80.09 |
| (0 − 10 − 1) | 33.24 | 39.42 | 60.78 | 53.42 | 62.39 | 67.82 |
| (0 − 10 − 3) | 35.24 | 41.47 | 57.14 | 64.06 | 64.40 | 75.54 |
| (1 − 5 − 1) | 38.80 | 46.79 | 60.09 | 68.77 | 70.80 | 80.17 |
| (1 − 5 − 3) | 42.06 | 47.49 | 63.36 | 68.35 | 78.32 | 81.0 |
| (1 − 10 − 1) | 36.52 | 42.21 | 59.57 | 65.07 | 76.55 | 74.41 |
| (1 − 10 − 3) | 35.94 | 42.91 | 56.8 | 64.2 | 68.95 | 77.63 |
Acknowledgements
We would like to thank Pierre-Paul De Breuck and Rajesh Raju for their valuable domain-related inputs. We acknowledge and thank the people responsible for the smooth functioning of the compute resources of Mila and Compute Canada. We also wish to acknowledge funding from Intel and CIFAR. Janarthanan Rajendran is supported by IVADO postdoctoral fellowship. Sarath Chandar is supported by the Canada CIFAR AI Chairs program, the Canada Research Chair in Lifelong Machine Learning, and the NSERC Discovery Grant.References
- H. Wang, T. Fu, Y. Du, W. Gao, K. Huang and Z. Liu,
et al., Scientific discovery in the age of artificial intelligence, Nature, 2023, 620(7972), 47–60 CrossRef CAS PubMed
.
-
M. Jain, S. C. Raparthy, A. Hernandez-Garcia, J. Rector-Brooks, Y. Bengio, S. Miret, et al., Multi-objective gflownets, in International Conference on Machine Learning, PMLR, 2023, pp. 14631–14653 Search PubMed
.
- M. Xu, X. Yuan, S. Miret and J. Tang, ProtST: Multi-Modality Learning of Protein Sequences and Biomedical Texts, in Proceedings of the 40th International Conference on Machine Learning, ed. A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato and J. Scarlett, Proceedings of Machine Learning Research, 2023, vol. 202, pp. 38749–38767, available from: https://proceedings.mlr.press/v202/xu23t.html Search PubMed.
- A. M. Bran, S. Cox, A. D. White and P. Schwaller, ChemCrow: Augmenting large-language models with chemistry tools, arXiv, 2023, preprint, arXiv:230405376, DOI:10.48550/arXiv.2304.05376.
-
M. Sim, M. G. Vakili, F. Strieth-Kalthoff, H. Hao, R. Hickman, S. Miret, et al., ChemOS 2.0: an orchestration architecture for chemical self-driving laboratories, 2023 Search PubMed
.
- S. Miret, M. Skreta, B. Sanchez-Lengelin, S. P. Ong, Z. Morgan-Chan and A. Aspuru-Guzik, AI4Mat: AI for Accelerated Materials Design NeurIPS 2022 Workshop, 2022, available from: https://sites.google.com/view/ai4mat Search PubMed.
-
Y. Song, S. Miret and B. Liu, MatSci-NLP: Evaluating Scientific Language Models on Materials Science Language Tasks Using Text-to-Schema Modeling, in Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics, ACL, 2023 Search PubMed
.
- K. L. K. Lee, C. Gonzales, M. Nassar, M. Spellings, M. Galkin and S. Miret, MatSciML: A Broad, Multi-Task Benchmark for Solid-State Materials Modeling, in AI for Accelerated Materials Design – NeurIPS 2023 Workshop, 2023, available from: https://openreview.net/forum?id=josIqIStKs Search PubMed.
-
S. Miret, K. L. K. Lee, C. Gonzales, M. Nassar and M. Spellings, The Open MatSci ML Toolkit: A Flexible Framework for Machine Learning in Materials Science, Transactions on Machine Learning Research, 2023, available from: https://openreview.net/forum?id=QBMyDZsPMd Search PubMed
.
- J. S. Rutherford, Crystal Structure, in Encyclopedia of Condensed Matter Physics, ed. F. Bassani, G. L. Liedl and P. Wyder, Elsevier, Oxford, 2005, pp. , pp. 289–294, available from: https://www.sciencedirect.com/science/article/pii/B0123694019006860 Search PubMed.
- Y. Zhao, E. M. D. Siriwardane, Z. Wu, N. Fu, M. Al-Fahdi and M. Hu,
et al., Physics guided deep learning for generative design of crystal materials with symmetry constraints, npj Comput. Mater., 2023, 9(1), 38 CrossRef
.
- A. Nouira, N. Sokolovska and J. Crivello, Crystalgan: learning to discover crystallographic structures with generative adversarial networks, arXiv, 2018, preprint, arXiv:181011203, DOI:10.48550/arXiv.1810.11203.
- T. Xie X. Fu O. E. Ganea R. Barzilay and T. JaakkolaCrystal Diffusion Variational Autoencoder for Periodic Material Generation, in International Conference on Learning Representations 2022, available from: https://openreview.net/forum?id=03RLpj-tc_ Search PubMed.
- R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu, et al., Crystal Structure Prediction by Joint Equivariant Diffusion, in Thirty-seventh Conference on Neural Information Processing Systems, 2023, available from: https://openreview.net/forum?id=DNdN26m2Jk Search PubMed.
- S. A. Meldgaard, H. L. Mortensen, M. S. Jørgensen and B. Hammer, Structure prediction of surface reconstructions by deep reinforcement learning, J. Phys.: Condens. Matter, 2020, 32(40), 404005 CrossRef CAS PubMed
.
-
E. Zamaraeva, C. M. Collins, D. Antypov, V. V. Gusev, R. Savani, M. S. Dyer, et al., Reinforcement Learning in Crystal Structure Prediction, 2023 Search PubMed
.
- J. Damewood, J. Karaguesian, J. R. Lunger, A. R. Tan, M. Xie and J. Peng,
et al., Representations of materials for machine learning, Annu. Rev. Mater. Res., 2023, 53(1), 399–426 CrossRef CAS
.
- A. Duval, V. Schmidt, S. Miret, Y. Bengio, A. Hernández-García and D. Rolnick, PhAST: Physics-Aware, Scalable, and Task-specific GNNs for Accelerated Catalyst Design, in AI for Accelerated Materials Design NeurIPS 2022 Workshop, 2022, available from: https://openreview.net/forum?id=hHercGKiXvP Search PubMed.
- Y. Zhao, M. Al-Fahdi, M. Hu, E. M. Siriwardane, Y. Song and A. Nasiri,
et al., High-throughput discovery of novel cubic crystal materials using deep generative neural networks, Advanced Science, 2021, 8(20), 2100566 CrossRef CAS PubMed
.
- A. Kumar, A. Zhou, G. Tucker and S. Levine, Conservative q-learning for offline reinforcement learning, Adv. Neural Inf. Process., 2020, 33, 1179–1191 Search PubMed
.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, What is high-throughput virtual screening? A perspective from organic materials discovery, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car and C. Cavazzoni,
et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens.Matter, 2009, 21(39), 395502 CrossRef PubMed
.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—Evolutionary crystal structure prediction, Comput. Phys. Commun., 2006, 175(11–12), 713–720 CrossRef CAS
.
- K. Doll, J. Schön and M. Jansen, Structure prediction based on ab initio simulated annealing for boron nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(14), 144110 CrossRef
.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 183(10), 2063–2070 CrossRef CAS
.
- J. Li, K. Lim, H. Yang, Z. Ren, S. Raghavan and P. Y. Chen,
et al., AI applications through the whole life cycle of material discovery, Matter, 2020, 3(2), 393–432 CrossRef
.
- S. Miret, K. L. K. Lee, C. Gonzales, M. Nassar and M. Spellings, The Open MatSci ML Toolkit: A Flexible Framework for Machine Learning in Materials Science, Transactions on Machine Learning Research, 2023, available from: https://openreview.net/forum?id=QBMyDZsPMd Search PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi and M. Riviere,
et al., Open catalyst 2020 (OC20) dataset and community challenges, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS
.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728 CrossRef PubMed
.
- A. A. Duval, V. Schmidt, A. Hernandez-Garcia, S. Miret, F. D. Malliaros, Y. Bengio, et al., FAENet: Frame Averaging Equivariant GNN for Materials Modeling, in Proceedings of the 40th International Conference on Machine Learning, ed. A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato and J. Scarlett, PMLR, vol. 202, 2023, pp. , pp. 9013–9033, available from: https://proceedings.mlr.press/v202/duval23a.html Search PubMed.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, Generative Adversarial Networks for Crystal Structure Prediction, ACS Cent. Sci., 2020, 6(8), 1412–1420, DOI:10.1021/acscentsci.0c00426
.
- S. Zheng, J. He, C. Liu, Y. Shi, Z. Lu, W. Feng, et al., Towards Predicting Equilibrium Distributions for Molecular Systems with Deep Learning, arXiv, 2023, preprint, arXiv:230605445, DOI:10.48550/arXiv.2306.05445.
- E. Pan, C. Karpovich and E. Olivetti, Deep Reinforcement Learning for Inverse Inorganic Materials Design, in AI for Accelerated Materials Design NeurIPS 2022 Workshop, 2022, available from: https://openreview.net/forum?id=V-DQd_iX1xJ Search PubMed.
- F. Sui, R. Guo, Z. Zhang, G. X. Gu and L. Lin, Deep reinforcement learning for digital materials design, ACS Mater. Lett., 2021, 3(10), 1433–1439 CrossRef CAS
.
- J. N. Law, S. Pandey, P. Gorai and P. C. St John, Upper-Bound Energy Minimization to Search for Stable Functional Materials with Graph Neural Networks, JACS Au, 2022, 3(1), 113–123 CrossRef PubMed
.
- B. Zheng, Z. Zheng and G. X. Gu, Designing mechanically tough graphene oxide materials using deep reinforcement learning, npj Comput. Mater., 2022, 8(1), 225 CrossRef
.
-
S. Levine, A. Kumar, G. Tucker and J. Fu, Offline Reinforcement Learning: Tutorial, Review. and Perspectives on Open Problems, 2020, vol. 5 Search PubMed
.
-
R. F. Prudencio, M. R. Maximo and E. L. Colombini, A survey on offline reinforcement learning: Taxonomy, review, and open problems, IEEE Transactions on Neural Networks and Learning Systems, 2023 Search PubMed
.
- A. Nair, M. Dalal, A. Gupta and S. Levine, {AWAC}: Accelerating Online Reinforcement Learning with Offline Datasets, 2021, available from: https://openreview.net/forum?id=OJiM1R3jAtZ Search PubMed.
- I. Kostrikov, A. Nair and S. Levine, Offline Reinforcement Learning with Implicit Q-Learning, in International Conference on Learning Representations, 2022, available from: https://openreview.net/forum?id=68n2s9ZJWF8 Search PubMed.
- T. Yu, A. Kumar, R. Rafailov, A. Rajeswaran, S. Levine and C. Finn, Combo: Conservative offline model-based policy optimization, Adv. Neural Inf. Process., 2021, 34, 28954–28967 Search PubMed
.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed
.
- V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness and M. G. Bellemare,
et al., Human-level control through deep reinforcement learning, nature, 2015, 518(7540), 529–533 CrossRef CAS PubMed
.
- S. Kurth, M. A. L. Marques and E. K. U. Gross, Density-Functional Theory, in Encyclopedia of Condensed Matter Physics, ed. F. Bassani, G. L. Liedl and P. Wyder, Elsevier, Oxford, 2005, pp. , pp. 395–402, available from: https://www.sciencedirect.com/science/article/pii/B0123694019004459 Search PubMed.
- A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Generalized Kohn-Sham schemes and the band-gap problem, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(7), 3764 CrossRef CAS PubMed
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215 CrossRef CAS
.
- F. Aryasetiawan and O. Gunnarsson, The GW method, Rep. Prog. Phys., 1998, 61(3), 237 CrossRef CAS
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards and S. Dacek,
et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef
.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31(9), 3564–3572 CrossRef CAS
.
- H. Pan, A. M. Ganose, M. Horton, M. Aykol, K. A. Persson and N. E. Zimmermann,
et al., Benchmarking coordination number prediction algorithms on inorganic crystal structures, Inorg. Chem., 2021, 60(3), 1590–1603 CrossRef CAS PubMed
.
- D. W. Davies, K. T. Butler, A. J. Jackson, J. M. Skelton, K. Morita and A. Walsh, SMACT: Semiconducting materials by analogy and chemical theory, J. Open Source Softw., 2019, 4(38), 1361 CrossRef
.
- A. Li, D. Misra, A. Kolobov and C. A. Cheng, Survival Instinct in Offline Reinforcement Learning, in Thirty-seventh Conference on Neural Information Processing Systems, 2023, available from: https://openreview.net/forum?id=shePL2nbwl Search PubMed.
- O. Vinyals, S. Bengio and M. Kudlur, Order matters: Sequence to sequence for sets, arXiv, 2015, preprint, arXiv:151106391, DOI:10.48550/arXiv.1511.06391.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00024b |
| ‡ Metallic crystals, being conductors, have a zero band gap because of the overlapping conduction and valence bands. |
| § Trained with supervised classification loss. |
| ¶ Classes – transition metals, post-transition metals, group 1 metals, group 2 metals, nonmetals, lanthanides, actinides, halogens, and noble elements (Appendix A.1.1.2). |
| This journal is © The Royal Society of Chemistry 2024 |