Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
EGraFFBench: evaluation of equivariant graph neural network force fields for atomistic simulations†
Vaibhav
Bihani‡
 a,
Sajid
Mannan‡
a,
Sajid
Mannan‡
 a,
Utkarsh
Pratiush‡
a,
Tao
Du
b,
Zhimin
Chen
b,
Santiago
Miret
a,
Utkarsh
Pratiush‡
a,
Tao
Du
b,
Zhimin
Chen
b,
Santiago
Miret
 c,
Matthieu
Micoulaut
d,
Morten M.
Smedskjaer
c,
Matthieu
Micoulaut
d,
Morten M.
Smedskjaer
 b,
Sayan
Ranu
*a and
N. M. Anoop
Krishnan
b,
Sayan
Ranu
*a and
N. M. Anoop
Krishnan
 *a
*a
aIndian Institute of Technology Delhi, Hauz Khas, 110016, New Delhi, India. E-mail: vaibhav.bihani525@gmail.com; cez218288@civil.iitd.ac.in; utkarshp1161@gmail.com; sayanranu@cse.iitd.ac.in; krishnan@iitd.ac.in
bAalborg University, 9220 Aalborg, Denmark. E-mail: dutao220@gmail.com; zhiminc@bio.aau.dk; mos@bio.aau.dk
cIntel Labs, Santa Clara, CA, USA. E-mail: santiago.miret@intel.com
dSorbonne University, Paris, France. E-mail: matthieu.micoulaut@gmail.com
First published on 4th March 2024
Abstract
Equivariant graph neural network force fields (EGraFFs) have shown great promise in modelling complex interactions in atomic systems by exploiting the graphs' inherent symmetries. Recent works have led to a surge in the development of novel architectures that incorporate equivariance-based inductive biases alongside architectural innovations like graph transformers and message passing to model atomic interactions. However, a thorough evaluation of these deploying EGraFFs for the downstream task of real-world atomistic simulations is lacking. To this end, here we perform a systematic benchmarking of 6 EGraFF algorithms (NequIP, Allegro, BOTNet, MACE, Equiformer, TorchMDNet), with the aim of understanding their capabilities and limitations for realistic atomistic simulations. In addition to our thorough evaluation and analysis of eight existing datasets based on the benchmarking literature, we release two new benchmark datasets, propose four new metrics, and three challenging tasks. The new datasets and tasks evaluate the performance of EGraFF on out-of-distribution data, in terms of different crystal structures, temperatures, and new molecules. Interestingly, evaluation of the EGraFF models based on dynamic simulations reveals that having a lower error on energy or force does not guarantee stable or reliable simulation or faithful replication of the atomic structures. Moreover, we find that no model clearly outperforms other models on all datasets and tasks. Importantly, we show that the performance of all the models on out-of-distribution datasets is unreliable, pointing to the need for the development of a foundation model for force fields that can be used in real-world simulations. In summary, this work establishes a rigorous framework for evaluating machine learning force fields in the context of atomic simulations and points to open research challenges within this domain.
1 Introduction
Graph neural networks (GNNs) have emerged as powerful tools for learning representations of graph-structured data, enabling breakthroughs in various domains such as social networks, mechanics, drug discovery, and natural language processing.1–7 In the field of atomistic simulations, GNN force fields have shown significant promise in capturing complex interatomic interactions and accurately predicting the potential energy surfaces of atomic systems.8–11 These force fields can, in turn, be used to study the dynamics of atomic systems—that is, how the atomic systems evolve with respect to time—enabling several downstream applications such as drug discovery, protein folding, stable structures of materials, and battery materials with targeted diffusion properties.Recent work has shown that GNN force fields can be further enhanced and made data-efficient by enforcing additional inductive biases, in terms of equivariance, leveraging the underlying symmetry of the atomic structures. This family of GNNs, hereafter referred to as equivariant graph neural network force fields (EGraFFs), have demonstrated their capability to model symmetries inherent in atomic systems, resulting in superior performance in comparison to other machine-learned force fields. This is achieved by explicitly accounting for symmetry operations, such as rotations and translations, and ensuring that the learned representations in EGraFFs are consistent under these transformations.
Traditionally, EGraFFs are trained on the forces and energies based on first principles simulation data, such as density functional theory. Recent work has shown that low training or test error does not guarantee the performance of the EGraFFs for the downstream task involving atomistic or molecular dynamics (MD) simulations.12 Specifically, EGraFFs can suffer from several major issues such as (i) unstable trajectory (the simulation suddenly explodes/becomes unstable due to high local forces), (ii) poor structure (the structure of the atomic system including the coordination, bond angles, and bond lengths is not captured properly), (iii) poor generalization to out-of-distribution datasets including simulations at different temperatures or pressures of the same system, simulations of different structures having the same chemical composition—for example, crystalline (ordered) and glassy (disordered) states of the same system, or simulations of different compositions having the same chemical components—for example, Li4P2S6 and Li7P3S11. Note that these are realistic tasks for which a force field that is well-trained on one system can generalize to other similar systems. As such, an extensive evaluation and comparison of EGraFFs is needed, which requires standardized datasets, well-defined metrics, and comprehensive benchmarking, that capture the diversity and complexity of atomic systems.
An initial effort to capture the performance of machine-learned force fields was made.12 In this work, the authors focused on existing datasets and some metrics, such as radial distribution functions and diffusion constants of atomic systems. However, the work did not cover the wide range of EGraFFs that has been newly proposed, many of which have shown superior performance in common tasks. Moreover, the metrics in ref. 12 were limited to stability, mean absolute error of forces radial distribution function, and diffusivity. While useful, these metrics either do not capture the variations during the dynamic simulation (e.g., how the force or energy error evolves during simulation) or require long simulations (such as diffusion constants, which requires many steps to reach the diffusive regime). Further, the work does not propose any novel tasks that can serve as a benchmark for the community developing new force fields.
With the increasing interest in EGraFFs for atomic simulations, we aim to address the gap in benchmarking by performing a rigorous evaluation of the quality of simulations obtained using modern EGraFF force fields. To this extent, we evaluate 6 EGraFFs on 10 datasets, including two new challenging datasets that we contribute, and propose new metrics based on real-world simulations. By employing a diverse set of atomic systems and benchmarking metrics, we aim to objectively and rigorously assess the capabilities and limitations of EGraFFs. The main contributions of this research paper are as follows:
• EGraFFs: We present a benchmarking package to evaluate 6 EGraFFs for atomistic simulations. As a byproduct of this benchmarking study, we release a well-curated codebase of the prominent equivariant GNN force fields in the literature enabling easier and streamlined access to relevant modeling pipelines https://github.com/M3RG-IITD/MDBENCHGNN.
• Challenging benchmark datasets: We present 10 datasets, including two new datasets, namely GeTe and LiPS20. The datasets cover a wide range of atomic systems, from small molecules to bulk systems. The datasets capture several scenarios, such as compounds with the same elements but different chemical compositions, the same composition with different crystal structures, and the same structure at different temperatures. This includes complex scenarios such as melting trajectories of crystals.
• Challenging downstream tasks: We propose several challenging downstream tasks that evaluate the ability of EGraFFs to model the out-of-distribution datasets described earlier.
• Improved metrics: We propose additional metrics that evaluate the quality of the atomistic simulations regarding the structure and dynamics with respect to the ground truth.
2 Preliminaries
Every material consists of atoms that interact with each other based on the different types of bonds (e.g., covalent and ionic). These bonds are approximated by force fields that model the atomic interactions. Here, we briefly describe atomistic simulations and the equivariant GNNs used for modeling these systems.2.1 Atomistic simulation
Consider a set of N atoms represented by a point cloud corresponding to their position vectors (r1, r2, …, rN) and their types ωi. Specifically, the potential energy of a system can be written as the summation of one-body U(ri), two-body U(ri, rj), three-body U(ri, rj, rk), up to N-body interaction terms as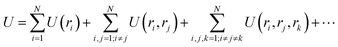 | (1) |
Since the exact computation of this potential energy is challenging, they are approximated using empirical force fields that learn the effective potential energy surface as a function of two-, three-, or four-body interactions. In atomistic simulations, these force fields are used to obtain the system's energy. The forces on each particle are then obtained as Fi = −∂U/∂ri. The acceleration of each atom is obtained from these forces as Fi/mi where mi is the mass of each atom. Accordingly, the updated position is computed by numerically integrating the equations of motion using a symplectic integrator. These steps are repeated to study the dynamics of atomic systems.
2.2 Equivariant GNN force fields (EGraFF)
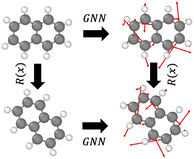
GNNs are widely used to model the force field due to the topological similarity to atomic systems. Specifically, nodes are considered atoms, the edges represent interactions/bonds, and the energy or force is predicted as the output at the node or edge levels. Equivariant GNNs employ a message passing scheme that is equivariant to rotations, that is, G(Rx) = RG(x), where R is a rotation and G is an equivariant transformation (see Fig. 1). This enables a rich representation of atomic environments equivariant to rotation. Notably, while the energy of an atomic system is invariant to rotation (that is, a molecule before and after rotation would have the same energy), the force is equivariant to rotation (that is, the forces experienced by the molecules due to the interactions also get rotated when the molecule is rotated).3 Models studied
All EGraFFs employed in this work rely on equivariance in the graph structure. All models use a one-hot encoding of the atomic numbers Zi as the node input and the position vector ri as a node or edge input. Equivariance in these models is ensured by the use of spherical harmonics along with radial basis functions. The convolution or message-passing implementation differs from model to model. Further hyperparameter details for all models are tabulated in ESI Section A† and Tables S1 to S11† along with the model's code version information in Table S16.†NequIP,13 based on the tensor field networks, employs a series of self-interaction, convolution, and concatenation with the neighboring atoms. The convolution filter 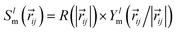 represented as a product of radial basis function R and spherical harmonics Ylm ensures equivariance. This was the first EGraFF proposed for atomistic simulations based on spherical harmonics.
represented as a product of radial basis function R and spherical harmonics Ylm ensures equivariance. This was the first EGraFF proposed for atomistic simulations based on spherical harmonics.
Allegro14 merges the precision of recent equivariant GNNs with stringent locality, without message passing. Its inherent local characteristic enhances its scalability for potentially more extensive systems. In contrast to other models, Allegro predicts the energy as a function of the final edge embedding rather than the node embeddings. All the pairwise energies are summed to obtain the total energy of the system. Allegro features remarkable adaptability to data outside the training distribution, consistently surpassing other force fields in this aspect, especially those employing body-ordered strategies.
BOTNet15 is a refined body-ordered adaptation of NequIP. While maintaining the two-body interactions of NequIP in each layer, it increments the body order by one with every iteration of message passing. Unlike NequIP, BOTNet uses non-linearities in the update step.
MACE16 offers efficient equivariant messages with high body order computation. Due to the augmented body order of the messages, merely two message-passing iterations suffice to attain notable accuracy. This contrasts with the usual five or six iterations observed in other GNNs, rendering MACE both scalable and amenable to parallelization.
TorchMDNet17 introduces a transformer-based GNN architecture, utilizing a modified multi-head attention mechanism. This modification expands the traditional dot-product attention to integrate edge data, which can enhance the learning of interatomic interactions.
Equiformer18 is a transformer-based GNN architecture, introducing a new attention mechanism named ‘equivariant graph attention’. This mechanism equips conventional attention used in the transformers with equivariance.
PaiNN10 is a polarizable atom interaction neural network consisting of equivariant message passing architecture that takes into account the varying polarizability of atoms in different chemical environments, allowing for a more realistic representation of molecular behavior.
DimeNeT++19 is a directional message passing neural network where each rotationally equivariant message is associated with a direction in coordinate space.
4 Benchmarking evaluation
In this section, we benchmark the above-mentioned architectures and distill the insights generated. The evaluation environment is detailed in ESI Section A.8.† The codebase and datasets are made available at https://github.com/M3RG-IITD/MDBENCHGNN.4.1 Datasets
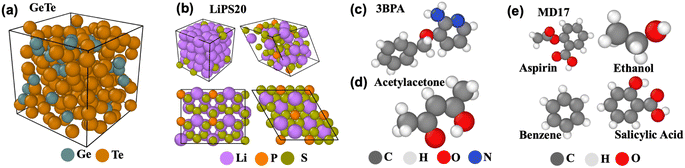
Since the present work focuses on evaluating EGraFFs for molecular dynamics (MD) simulations, we consider only datasets with included time dynamics—i.e., all the datasets represent the dynamics of an atom (see Fig. 2). We consider a total of 10 datasets (see Table S1 and Section A.1 in the ESI†). The data splits are tabulated in Table S17 in the ESI.†MD17 is a widely used12,13,15–18 dataset for benchmarking ML force fields. It was proposed by ref. 20 and constitutes a set of small organic molecules, including benzene, toluene, naphthalene, ethanol, uracil, and aspirin, with energy and forces generated by ab initio MD (AIMD) simulations. Here, we select four molecules, namely aspirin, ethanol, naphthalene, and salicylic acid, to cover a range of chemical structures and topology. Further, zero-shot evaluation is performed on benzene. We train the models on 950 configurations and test them on 50.
3BPA contains a large flexible drug-like organic molecule, 3-(benzyloxy)pyridin-2-amine (3BPA), sampled from different temperature MD trajectories.21 It has three consecutive rotatable bonds leading to a complex dihedral potential energy surface with many local minima, making it challenging to approximate using classical or ML force fields. The models can be trained either on 300 K snapshots or on mixed temperature snapshots sampled from 300 K, 600 K, and 1200 K. In the following experiments, we train models on 500 configurations sampled at 300 K and test 1669 configurations sampled at 600 K.
LiPS consists of lithium, phosphorous, and sulfur (Li6.75P3S11), and is used in similar benchmarking analysis,12 as a representative system for the MD simulations to study kinetic properties in materials. Note that LiPS is a crystalline (ordered structure) material that can potentially be used in battery development. We have adopted this dataset from ref. 13 and benchmarked all models for their force and energy errors. The training and testing datasets have 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 1000 configurations, respectively.
000 and 1000 configurations, respectively.
Acetylacetone (AcAc): The dataset was generated by conducting MD simulations at both 300 K and 600 K using the Langevin thermostat.15 The uniqueness of this dataset stems from the varying simulation temperatures and the range of sampled dihedral angles. While the training set restricts sampling to dihedral angles below 30°, our models are tested on angles extending up to 180°. The model must effectively generalize on the Potential Energy Surface (PES) for accurate generalization at these higher angles. This challenge presents an excellent opportunity for benchmarking GNNs. The dataset consists of 500 training configurations and 650 testing configurations.
GeTe is a new dataset generated by Car-Parrinello MD (CPMD) simulations22 of Ge and Te atoms, which builds on a density functional theory (DFT) based calculation of the interatomic forces, prior to a classical integration of the equations of motion. It consists of 200 atoms, of which 40 are Ge and 160 are Te, i.e., corresponding to the composition GeTe4 whose structural properties have been investigated in detail and reproduce a certain number of experimental data in the liquid and amorphous phase from neutron/X-ray scattering23,24 and Mössbauer spectroscopy.25 As GeTe belongs to the promising class of phase-change materials,26 it is challenging to simulate using classical force fields because of the increased accessibility in terms of time and size. Thus, an accurate force field is essential to understand the structural changes in GeTe during the crystalline to disordered phase transitions. Here, our dataset consists of 1500 structures in training, 300 in test, and 300 in validation.
LiPS20 is a new dataset generated from AIMD simulations of a series of systems containing Li, P, and S elements, including both the crystalline and disordered structures of elementary substances and compounds, such as Li, P, S, Li2P2S6, β-Li3PS4, γ-Li3PS4, and xLi2S-(100 − x)P2S5 (x = 67, 70, 75, and 80) glasses using the CP2K package.27 Details of dataset generation, structures, and compositions in this dataset are given in ESI Section A.2 and Table S2.†
4.2 Evaluation metrics
Ideally, once trained, the forward simulations by EGraFFs should be close to the ground truth (first principles simulations) both in terms of the atomic structure and dynamics. To this extent, we propose four metrics. Note that these metrics are evaluated based on the forward simulation, starting from an arbitrary structure for n steps employing the force fields, a task for which it is not explicitly trained. All the forward simulations were performed using the Atomic Simulation Environment (ASE) package.28 The simulations were conducted in the canonical (NVT) ensemble, where the temperature and timesteps were set in accordance with the sampling conditions specified in the respective datasets. See details in ESI Section A.3 and Table S3.†4.2.1.1 Wright's factor (WF), Rχ. Ref. 29 represents the relative difference between the radial distribution function (RDF) of the ground truth atomic structure (gref(r)) and the structure obtained from the atomistic simulations employing the EGraFFs (g(r)) as
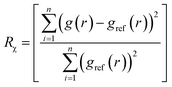 | (2) |
RDF essentially represents the local time-averaged density of atoms at a distance r from a central atom (see ESI Section A.4 and Fig. S1†). Hence, it captures the structure simulated by a force field concisely and one-dimensionally. A force field is considered acceptable if it can provide a WF less than 9% for bulk systems.30
4.2.1.2 Jensen–Shannon divergence (JSD) of the radial distribution function. Jensen–Shannon Divergence (JSD)31,32 is a useful tool for quantifying the difference or similarity between two probability distributions in a way that overcomes some of the limitations of the KL divergence.33 Since the RDF is essentially a distribution of the atomic density, the JSD between two predicted RDF and ground truth RDF can be computed as:
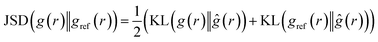 | (3) |
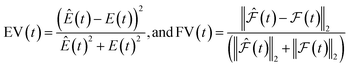 | (4) |
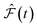 and
and 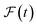 are the predicted and ground truth forces. Note that this metric ensures that the energy and the force violation errors are bounded between 0 and 1, with 0 representing exact agreement with the ground truth and 1 representing no agreement. Further, we compute the geometric mean of EV(t) and FV(t) over the trajectory to represent the cumulative EV and FV.
are the predicted and ground truth forces. Note that this metric ensures that the energy and the force violation errors are bounded between 0 and 1, with 0 representing exact agreement with the ground truth and 1 representing no agreement. Further, we compute the geometric mean of EV(t) and FV(t) over the trajectory to represent the cumulative EV and FV.
4.3 Results
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | PaiNN | DimeNET++ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | F | E | F | E | F | E | F | E | F | E | F | E | F | E | F | |
| Acetylacetone | 1.38 | 4.59 | 0.92 | 4.4 | 2.0 | 10.0 | 2.0 | 8.0 | 4.0 | 4.0 | 1.0 | 5.0 | 4.92 | 7.73 | 102.39 | 15.28 |
| 3BPA | 3.15 | 7.86 | 4.13 | 10.0 | 5.0 | 14.0 | 4.0 | 12.0 | 6.0 | 7.0 | 3.0 | 11.0 | 36.67 | 40.41 | 796.74 | 46.72 |
| Aspirin | 6.84 | 13.89 | 5.00 | 9.17 | 7.99 | 14.06 | 8.53 | 14.01 | 6.15 | 15.29 | 5.33 | 8.97 | 41.49 | 12.41 | 133.24 | 22.07 |
| Ethanol | 2.67 | 7.49 | 2.34 | 5.01 | 2.60 | 6.80 | 2.36 | 3.19 | 2.66 | 9.73 | 2.67 | 5.93 | 7.77 | 11.81 | 149.55 | 17.19 |
| Naphthalene | 5.70 | 6.20 | 5.14 | 2.64 | 6.67 | 6.07 | 6.26 | 1.98 | 3.88 | 7.01 | 2.55 | 4.03 | 10.56 | 4.07 | 175.04 | 19.65 |
| Salicylic acid | 5.78 | 8.42 | 5.76 | 6.30 | 5.56 | 10.21 | 5.34 | 4.24 | 5.22 | 12.39 | 6.85 | 7.19 | 24.15 | 11.12 | 169.18 | 25.48 |
| LiPS | 165.43 | 5.04 | 31.75 | 2.46 | 28.0 | 13.0 | 30.0 | 15.0 | 83.20 | 51.10 | 67.0 | 61.0 | 128.80 | 112.43 | 55.22 | 42.23 |
| LiPS20 | 26.80 | 3.04 | 33.17 | 3.31 | 24.59 | 5.51 | 14.05 | 4.64 | 3274.93 | 57.63 | 20.47 | 57.19 | — | — | — | — |
| GeTe | 1780.951 | 244.40 | 1009.4 | 253.45 | 3034.0 | 258.0 | 2670.0 | 247.0 | 666.34 | 363.17 | 2613.0 | 371.0 | 884.28 | 330.05 | 51704.65 | 222.39 |
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | PaiNN | DimeNET++ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | |
| Acetylacetone | 28.24 | 24.55 | 29.63 | 22.17 | 30.61 | 26.04 | 31.07 | 22.90 | 29.86 | 21.78 | 29.34 | 22.49 | 26.97 | 22.33 | 66.0 | 143.36 |
| 3BPA | 0.82 | 6.02 | 1.13 | 7.98 | 1.07 | 7.13 | 0.98 | 8.36 | 0.94 | 7.44 | 0.87 | 7.31 | 1.39 | 6.65 | 6.87 | 89.97 |
| Aspirin | 0.133 | 30.66 | 0.108 | 23.29 | 0.122 | 27.36 | 0.111 | 18.92 | 0.120 | 23.58 | 0.131 | 23.99 | 0.03 | 4.0 | 0.31 | 167.48 |
| Ethanol | 0.526 | 18.34 | 0.450 | 15.89 | 0.360 | 15.57 | 0.494 | 17.93 | 0.549 | 23.48 | 0.464 | 17.70 | 0.78 | 9.42 | 3.75 | 205.75 |
| Naphthalene | 0.089 | 20.96 | 0.082 | 19.44 | 0.093 | 24.65 | 0.095 | 22.89 | 0.090 | 26.72 | 0.081 | 19.25 | 0.02 | 2.52 | 0.23 | 130.40 |
| Salicylic acid | 0.077 | 16.95 | 0.124 | 27.58 | 0.076 | 14.65 | 0.097 | 19.35 | 0.072 | 14.17 | 0.077 | 16.12 | 0.08 | 7.63 | 0.50 | 208.95 |
| LiPS | 0.0 | 3.89 | 0.0 | 3.57 | 0.0 | 3.93 | 0.0 | 3.66 | 0.0 | 1.97 | 0.0 | 1.49 | 0.0 | 0.51 | 0.0 | 28.55 |
| LiPS20 | 0.001 | 14.92 | 0.001 | 18.32 | 0.001 | 17.08 | 0.001 | 17.70 | — | — | 0.006 | 41.70 | — | — | — | — |
| GeTe | 0.0 | 2.78 | 0.0 | 2.06 | 0.0 | 2.03 | 0.0 | 2.02 | — | — | 0.0 | 2.80 | 0.0 | 2.29 | 0.0 | 16.77 |
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | PaiNN | DimeNET++ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | F | E | F | E | F | E | F | E | F | E | F | E | F | E | F | |
| Acetylacetone | 0.960 | 0.709 | 0.820 | 0.710 | 0.923 | 0.713 | 0.813 | 0.710 | 0.810 | 0.711 | 0.836 | 0.713 | 2.129 | 0.705 | 1.043 | 0.705 |
| (0.361) | (0.042) | (0.275) | (0.041) | (0.331) | (0.041) | (0.275) | (0.041) | (0.276) | (0.043) | (0.282) | (0.042) | (0.457) | (0.042) | (0.353) | (0.041) | |
| 3BPA | 0.810 | 0.711 | 0.729 | 0.710 | 0.680 | 0.711 | 0.760 | 0.710 | 0.803 | 0.709 | 0.814 | 0.710 | 0.893 | 0.716 | 1.92 | 0.707 |
| (0.394) | (0.032) | (0.292) | (0.033) | (0.248) | (0.032) | (0.281) | (0.032) | (0.310) | (0.032) | (0.30) | (0.032) | (0.446) | (0.031) | (0.367) | (0.032) | |
| Aspirin | 1.068 | 0.626 | 1.009 | 0.625 | 1.083 | 0.627 | 1.004 | 0.628 | 1.023 | 0.637 | 1.096 | 0.626 | 2.908 | 0.662 | 1.188 | 0.680 |
| (0.351) | (0.081) | (0.358) | (0.085) | (0.337) | (0.078) | (0.338) | (0.075) | (0.36) | (0.083) | (0.352) | (0.077) | (0.598) | (0.061) | (0.265) | (0.055) | |
| Ethanol | 3.287 | 0.684 | 3.497 | 0.686 | 3.239 | 0.698 | 3.579 | 0.690 | 3.252 | 0.698 | 3.420 | 0.686 | 4.828 | 0.687 | 3.071 | 0.708 |
| (1.275) | (0.071) | (1.209) | (0.071) | (1.206) | (0.078) | (1.255) | (0.076) | (1.245) | (0.072) | (1.327) | (0.074) | (1.133) | (0.070) | (0.719) | (0.073) | |
| Naphthalene | 2.45 | 0.624 | 2.305 | 0.603 | 2.524 | 0.599 | 2.59 | 0.604 | 2.593 | 0.616 | 2.700 | 0.604 | 4.071 | 0.661 | 1.778 | 0.693 |
| (0.685) | (0.073) | (0.688) | (0.062) | (0.644) | (0.063) | (0.663) | (0.072) | (0.675) | (0.075) | (0.688) | (0.070) | (0.839) | (0.061) | (0.520) | (0.059) | |
| Salicylic acid | 2.135 | 0.625 | 1.955 | 0.604 | 2.042 | 0.621 | 2.14 | 0.610 | 1.996 | 0.616 | 2.146 | 0.594 | 4.107 | 0.687 | 2.15 | 0.694 |
| (0.468) | (0.068) | (0.465) | (0.064) | (0.45) | (0.072) | (0.444) | (0.063) | (0.477) | (0.065) | (0.529) | (0.062) | (0.696) | (0.056) | (36.01) | (0.058) | |
| LiPS | 87.52 | 0.711 | 97.64 | 0.710 | 100.07 | 0.712 | 100.30 | 0.765 | 78.93 | 0.718 | 160.60 | 0.712 | 662.431 | 0.705 | 222.94 | 0.699 |
| (36.342) | (0.054) | (39.990) | (0.053) | (36.839) | (0.053) | (39.041) | (0.053) | (47.28) | (0.050) | (76.441) | (0.049) | (89.605) | (0.042) | (42.777) | (0.052) | |
| LiPS20 | 45.10 | 0.720 | 32.79 | 0.721 | 27.99 | 0.726 | 41.47 | 0.722 | — | — | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108.75 108.75 |
0.834 | — | — | — | — |
| (14.206) | (0.043) | (8.09) | (0.040) | (8.201) | (0.039) | (8.613) | (0.039) | — | — | (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106.23) 106.23) |
(0.065) | — | — | — | — | |
| GeTe | 495.30 | 0.800 | 294.39 | 0.756 | 351.86 | 0.764 | 352.46 | 0.765 | — | — | 346.44 | 0.779 | 175.928 | 0.77 | 3914.07 | 0.807 |
| (36.945) | (0.064) | (23.563) | (0.063) | (27.139) | (0.072) | (27.055) | (0.073) | — | — | (25.362) | (0.060) | (80.01) | (0.052) | (181.98) | (0.081) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, has the largest per epoch training time. Since MD simulations are generally performed on CPUs, we report inference time as a mean over five simulations for 1000 steps performed on a CPU. TorchMDNet is significantly fast on all the datasets while Allegro and MACE show competitive performance. A visual analysis of the models on these metrics is given in ESI section A.7.†
000, has the largest per epoch training time. Since MD simulations are generally performed on CPUs, we report inference time as a mean over five simulations for 1000 steps performed on a CPU. TorchMDNet is significantly fast on all the datasets while Allegro and MACE show competitive performance. A visual analysis of the models on these metrics is given in ESI section A.7.†
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | I | T | I | T | I | T | I | T | I | T | I | |
| Acetylacetone | 0.66 | 3.18 | 0.17 | 1.94 | 0.11 | 1.90 | 0.04 | 2.66 | 0.52 | 9.98 | 0.11 | 1.79 |
| 3BPA | 1.07 | 7.07 | 1.80 | 4.92 | 0.12 | 4.46 | 0.06 | 4.18 | 0.68 | 19.25 | 0.13 | 4.83 |
| Aspirin | 5.23 | 2.93 | 1.61 | 1.68 | 0.21 | 1.76 | 0.14 | 2.45 | 0.85 | 13.04 | 0.15 | 1.41 |
| Ethanol | 5.49 | 2.05 | 1.62 | 0.68 | 5.03 | 1.07 | 1.15 | 1.28 | 0.81 | 5.70 | 0.14 | 0.80 |
| Naphthalene | 5.26 | 3.75 | 2.11 | 1.07 | 13.47 | 1.27 | 4.728 | 2.28 | 0.85 | 14.67 | 0.14 | 1.37 |
| Salicylic acid | 5.24 | 3.30 | 1.61 | 0.87 | 11.68 | 1.26 | 3.858 | 2.29 | 0.82 | 9.79 | 0.14 | 1.17 |
| LiPS | 89.91 | 35.83 | 20.89 | 13.91 | 4.82 | 10.29 | 3.61 | 6.52 | 18.51 | 46.34 | 3.18 | 6.95 |
| LiPS20 | 2.78 | 25.51 | 0.76 | 11.42 | 0.36 | 15.187 | 0.18 | 6.75 | 1.86 | 56.59 | 0.21 | 5.12 |
| GeTe | 7.22 | 105.62 | 4.49 | 220.43 | 2.07 | 78.2 | 0.58 | 26.75 | 9.33 | 143.91 | 1.55 | 21.67 |
4.4 Challenging tasks on EGraFF
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | F | E | F | E | F | E | F | E | F | E | F | ||
| Acetylacetone | 300 K | 0.959 | 0.7092 | 0.817 | 0.7110 | 0.924 | 0.7131 | 0.813 | 0.7096 | 0.810 | 0.7113 | 0.836 | 0.7128 |
| 600 K | 1.806 | 0.7145 | 1.912 | 0.7137 | 1.893 | 0.7140 | 2.215 | 0.7127 | 2.169 | 0.7137 | 1.996 | 0.7120 | |
| 3BPA | 300 K | 0.809 | 0.7106 | 0.708 | 0.7102 | 0.677 | 0.7109 | 0.759 | 0.7097 | 0.803 | 0.7089 | 0.814 | 0.7097 |
| 600 K | 1.180 | 0.7095 | 1.603 | 0.7092 | 1.607 | 0.7102 | 1.214 | 0.7087 | 1.319 | 0.7104 | 1.160 | 0.7121 | |
| NequIP | Allegro | BOTNet | MACE | Equiformer | TorchMDNet | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | JSD | WF | ||
| Acetylacetone | 300 K | 28.244 | 24.552 | 29.628 | 22.166 | 30.612 | 26.038 | 31.072 | 22.904 | 29.863 | 21.783 | 29.335 | 22.485 |
| 600 K | 18.868 | 31.480 | 21.068 | 26.178 | 18.332 | 26.620 | 19.295 | 28.708 | 17.938 | 27.414 | 19.054 | 29.626 | |
| 3BPA | 300 K | 0.821 | 6.024 | 1.130 | 7.986 | 1.069 | 7.129 | 0.976 | 8.358 | 0.923 | 6.991 | 0.874 | 7.309 |
| 600 K | 0.758 | 6.202 | 0.596 | 5.137 | 0.778 | 5.861 | 0.683 | 5.120 | 1.053 | 6.648 | 0.859 | 6.985 | |
4.4.2.1 Unseen crystalline structures. Crystal structures are stable low-energy structures with inherent symmetries and periodicity. Predicting their energy accurately is an extremely challenging task and a cornerstone in materials discovery. Here, we train the models on liquid (disordered) structures and test them on the out-of-distribution crystalline structures to evaluate their generalizability capabilities. Table 7 shows that BOTNet performs appreciably well with almost the same energy and force error on crystal structures as the obtained training error. Both the transformer models have poor performance on the LiPS20 system, in terms of both the training and testing datasets. TorchMDNet has significantly high energy and force errors, whereas Equiformer exhibits instability during the forward simulation.
| NequIP | Allegro | BOTNet | MACE | TorchMDNet | ||
|---|---|---|---|---|---|---|
| Train structures | E | 45.100 | 32.786 | 27.997 | 41.475 | 15108.747 |
| F | 0.719 | 0.721 | 0.726 | 0.722 | 0.834 | |
| Crystal structures | E | 108.842 | 197.276 | 27.159 | 50.380 | 40075.532 |
| F | 0.717 | 0.720 | 0.726 | 0.722 | 0.886 | |
| Test structure | E | 15439.338 | 16803.125 | 117.531 | 99.390 | 59906.813 |
| F | 0.763 | 0.766 | 0.729 | 0.723 | 0.902 | |
4.4.2.2 Generalizability to unseen composition. The LiPS20 dataset consists of 20 different compositions with varying system sizes and cell geometries (see ESI Section A.2†). In Tables 7 and 8, we show the results on the test structures that are not present in the training datasets. The test dataset consists of system sizes up to 260 atoms, while the models were trained on system sizes with <100 atoms. It tests the models' generalization as well as inductive capability. We observe that MACE and BOTNet have the lowest mean energy, force violation, and low WF. NequIP and Allegro have significantly higher test errors.
| NequIP | Allegro | BOTNet | MACE | TorchMDNet | ||
|---|---|---|---|---|---|---|
| Train structures | JSD | 0.001 | 0.001 | 0.001 | 0.001 | 0.006 |
| WF | 14.920 | 18.318 | 17.076 | 17.697 | 41.703 | |
| Crystal structures | JSD | 0.0 | 0.0 | 0.0 | 0.0 | 0.006 |
| WF | 7.909 | 8.7305 | 10.525 | 12.661 | 61.201 | |
| Test structures | JSD | 0.009 | 0.01 | 0.002 | 0.001 | 0.0159 |
| WF | 37.974 | 35.747 | 14.234 | 14.936 | 70.133 | |
5 Concluding insights
In this work, we present EGraFFBench, a benchmarking suite for evaluating machine-learned force fields. The key insights drawn from the extensive evaluation are as follows.(1) Dataset matters: there was no single model that performed the best on all the datasets and all the metrics. Thus, the selection of the model depends highly on the nature of the atomic system, whether it is a small molecule or a bulk system, for instance.
(2) Structure is important: Low force or energy error during model development does not guarantee faithful reproduction of the atomic structure. Conversely, models with higher energy or force error may provide reasonable structures. Accordingly, downstream evaluation of atomic structures using structural metrics is important in choosing the appropriate model.
(3) Stability during dynamics: Models exhibiting low energy or force errors during the model development on static configurations do not guarantee low errors during forward simulation. Thus, the energy and force violations during molecular dynamics should be evaluated separately to understand the stability of the simulation.
(4) Out-of-distribution is still challenging: Discovery of novel materials relies on identifying hitherto unknown configurations with low energy. We observe that the models still do not perform reliably on out-of-distribution datasets, leaving an open challenge in materials modeling.
(5) Fast to train and fast on inference: We observe that some models are fast on training, while others are fast on inference. For instance, TorchMDNet is slow to train but fast on inference. While MACE is fast both on training and inference, it does not give the best results in terms of structure or dynamics. Thus, in cases where larger simulations are required, the appropriate model that balances the training/inference time and accuracy may be chosen.
5.1 Limitations and future work
Our research clearly points to developing a foundation model trained on large datasets. Further, improved training strategies that (i) ensure the learning of gradients of energies and forces, (ii) take into account the dynamics during simulations, and (iii) reproduce the structure faithfully need to be developed. This suggests moving away from the traditional training approach only on energy and forces and instead focusing on the system's dynamics. Further strategies combining experimentally observed structures and simulated dynamics can be devised through experiment–simulation fusion to develop reliable force fields that are faithful to both experiments and simulations. Another interesting aspect is the empirical evaluation of which particular architectural feature of a model helps in giving a superior performance for a given dataset or system (defined by the type of bonding, number of atoms, crystalline vs. disordered, etc.). Such a detailed analysis can be a guide to designing improved architecture while also providing thumb rules toward the use of an appropriate architecture for a given system.Data availability
The code for the study reported in this article can be found in the GitHub repository at https://github.com/M3RG-IITD/MDBENCHGNN and the data is available at https://doi.org/10.5281/zenodo.10678029.Author contributions
Vaibhav Bihani-investigation, software, methodology, visualisation, writing – original draft, Sajid Mannan-Investigation, software, methodology, visualisation, writing – original draft, Utkarsh Pratiush-investigation, software, methodology, visualisation, writing – original draft, Tao Du- methodology, data curation, Zhimin Chen-methodology, data curation, Santiago Miret-review & editing, Matthieu Micoulaut – data curation, review & editing, Morten M. Smedskjaer-methodology, review & editing, Sayan Ranu-conceptualization, supervision, writing – review & editing, N. M. Anoop Krishnan-conceptualization, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
N. M. A. Krishnan and S. Ranu acknowledges the financial support for this research provided by Intel, and Google Research Scholar Award. N. M. A. Krishnan acknowledges the financial support from BRNS YSRA (53/20/01/2021-BRNS). The authors thank the IIT Delhi HPC facility for providing computational and storage resources. S. Mannan acknowledges the financial support from the Prime Minister's Research Fellowship (PMRF), Ministry of Education, Government of India.References
- B. Perozzi, R. Al-Rfou and S. Skiena, Deepwalk: Online learning of social representations, In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, 2014, pp. 701–710 Search PubMed.
- Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and S. Y. Philip, A comprehensive survey on graph neural networks, IEEE Trans. Neural Netw. Learn. Syst., 2020, 32(1), 4–24 Search PubMed
.
- M. Zhang and Y. Chen, Link prediction based on graph neural networks, Adv. Neural Inf. Process., 2018, 31 DOI:10.48550/arXiv.1802.09691
.
- J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz and N. M. Donghia,
et al., A deep learning approach to antibiotic discovery, Cell, 2020, 180(4), 688–702 CrossRef CAS PubMed
.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang and Z. Liu,
et al., Graph neural networks: A review of methods and applications, AI open, 2020, 1, 57–81 CrossRef
.
- S. Miret, K. L. K. Lee, C. Gonzales, M. Nassar and M. Spellings, The Open MatSci ML Toolkit: A Flexible Framework for Machine Learning in Materials Science, Transactions on Machine Learning Research, 2023, Available from: https://openreview.net/forum?id=QBMyDZsPMd Search PubMed.
- K. L. K. Lee, C. Gonzales, M. Nassar, M. Spellings, M. Galkin and S. Miret, MatSciML: A Broad, Multi-Task Benchmark for Solid-State Materials Modeling, arXiv, preprint, arXiv:230905934, 2023 Search PubMed.
- C. W. Park, M. Kornbluth, J. Vandermause, C. Wolverton, B. Kozinsky and J. P. Mailoa, Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture, npj Comput. Mater., 2021, 7(1), 73 CrossRef
.
- A. Sanchez-Gonzalez, J. Godwin, T. Pfaff, R. Ying and J. Leskovec and P. Battaglia, Learning to simulate complex physics with graph networks, In International conference on machine learning, PMLR, 2020, pp. 8459–8468 Search PubMed.
-
K. Schütt, O. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, In International Conference on Machine Learning, PMLR, 2021, pp. 9377–9388 Search PubMed
.
- Z. Qiao, A. S. Christensen, M. Welborn, F. R. Manby, A. Anandkumar and T. F. Miller III, Unite: Unitary n-body tensor equivariant network with applications to quantum chemistry, arXiv, preprint, arXiv:210514655, 2021, DOI:10.48550/arXiv.2105.14655.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli, et al., Forces are not Enough: Benchmark and Critical Evaluation for Machine Learning Force Fields with Molecular Simulations, Transactions on Machine Learning Research, 2023, Survey Certification, Available from: https://openreview.net/forum?id=A8pqQipwkt Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa and M. Kornbluth,
et al., E (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13(1), 2453 CrossRef CAS PubMed
.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen and M. Kornbluth,
et al., Learning Local Equivariant Representations for Large-Scale Atomistic Dynamics, Nat Commun., 2023, 14(1), 579 CrossRef CAS PubMed
.
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. C. Simm, R. Drautz, et al., The Design Space of E(3)-Equivariant Atom-Centered Interatomic Potentials, arXiv, preprint, arXiv:2205.06643, 2022 Search PubMed.
- I. Batatia, D. P. Kovacs, G. N. C. Simm, C. Ortner and G. Csanyi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, In Advances in Neural Information Processing Systems, ed. A. H. Oh, A. Agarwal, D. Belgrave and K. Cho, 2022, Available from: https://openreview.net/forum?id=YPpSngE-ZU Search PubMed.
- P. Thölke and G. D. Fabritiis, Equivariant Transformers for Neural Network based Molecular Potentials, In International Conference on Learning Representations, 2022, Available from: https://openreview.net/forum?id=zNHzqZ9wrRB Search PubMed.
- Y. L. Liao and T. Smidt, Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs, In: International Conference on Learning Representations, 2023. Available from: https://openreview.net/forum?id=KwmPfARgOTD Search PubMed.
- J. Gasteiger, S. Giri, J. T. Margraf and S. Günnemann, Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules, In: Machine Learning for Molecules Workshop, NeurIPS, 2020 Search PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K. R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3(5), e1603015 CrossRef PubMed
.
- D. P. Kovács, O. Cvd, J. Kucera, A. E. Allen, D. J. Cole and C. Ortner,
et al., Linear atomic cluster expansion force fields for organic molecules: beyond rmse, J. Chem. Theory Comput., 2021, 17(12), 7696–7711 CrossRef PubMed
.
- J. Hutter, Car–Parrinello molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(4), 604–612 CAS
.
- M. Micoulaut, M. V. Coulet, A. Piarristeguy, M. Johnson, G. J. Cuello and C. Bichara,
et al., Effect of concentration in Ge-Te liquids: A combined density functional and neutron scattering study, Phys. Rev. B, 2014, 89(17), 174205 CrossRef
.
- K. Gunasekera, P. Boolchand and M. Micoulaut, Effect of mixed Ge/Si cross-linking on the physical properties of amorphous Ge-Si-Te networks, J. Appl. Phys., 2014, 115(16), 164905 CrossRef
.
- M. Micoulaut, K. Gunasekera, S. Ravindren and P. Boolchand, Quantitative measure of tetrahedral-s p 3 geometries in amorphous phase-change alloys, Phys. Rev. B, 2014, 90(9), 094207 CrossRef CAS
.
- W. Zhang, R. Mazzarello, M. Wuttig and E. Ma, Designing crystallization in phase-change materials for universal memory and neuro-inspired computing, Nat. Rev. Mater., 2019, 4(3), 150–168 CrossRef CAS
.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald and F. Stein,
et al., CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103 CrossRef PubMed
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen and M. Dułak,
et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed
.
- D. I. Grimley, A. C. Wright and R. N. Sinclair, Neutron scattering from vitreous silica IV. Time-of-flight diffraction, J. Non-Cryst. Solids, 1990, 119(1), 49–64 CrossRef CAS
.
- M. Bauchy, Structural, vibrational, and elastic properties of a calcium aluminosilicate glass from molecular dynamics simulations: the role of the potential, J. Chem. Phys., 2014, 141(2), 024507 CrossRef CAS PubMed
.
-
T. M. Cover and J. A. Thomas, Network information theory, Elements of information theory, 1991, pp. 374–458 Search PubMed
.
- C. E. Shannon, A mathematical theory of communication, Bell Syst. Tech. J., 1948, 27(3), 379–423 CrossRef
.
- S. Kullback and R. A. Leibler, On information and sufficiency, Ann. Math. Stat., 1951, 22(1), 79–86 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00027g |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |