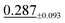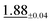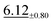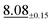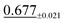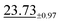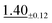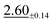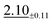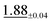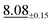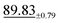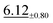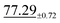Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CoDBench: a critical evaluation of data-driven models for continuous dynamical systems†
Priyanshu
Burark
a,
Karn
Tiwari
a,
Meer Mehran
Rashid
b,
Prathosh
A. P.
*a and
N. M. Anoop
Krishnan
 *b
*b
aIISc Bangalore Bengaluru, 560012, India. E-mail: priyanshub@iisc.ac.in; karntiwari@iisc.ac.in; prathosh@iisc.ac.in
bIIT Delhi, New Delhi, 110016, India. E-mail: meermehran777@gmail.com; krishnan@iitd.ac.in
First published on 18th April 2024
Abstract
Continuous dynamical systems, characterized by differential equations, are ubiquitously used to model several important problems: plasma dynamics, flow through porous media, weather forecasting, and epidemic dynamics. Recently, a wide range of data-driven models has been used successfully to model these systems. However, in contrast to established fields like computer vision, limited studies are available analyzing the strengths and potential applications of different classes of these models that could steer decision-making in scientific machine learning. Here, we introduce CoDBench, an exhaustive benchmarking suite comprising 12 state-of-the-art data-driven models for solving differential equations. Specifically, we comprehensively evaluate 4 distinct categories of models, viz., feed forward neural networks, deep operator regression models, frequency-based neural operators, and transformer architectures against 10 widely applicable benchmark datasets encompassing challenges from fluid and solid mechanics. We conduct extensive experiments, assessing the operators' capabilities in learning, zero-shot super-resolution, data efficiency, robustness to noise, and computational efficiency. Interestingly, our findings highlight that current operators struggle with the newer mechanics datasets, motivating the need for more robust neural operators. All the datasets and codes are shared in an easy-to-use fashion for the scientific community. We hope this resource will be an impetus for accelerated progress and exploration in modeling dynamical systems. For codes and datasets, see: https://github.com/M3RG-IITD/cod-bench.
1 Introduction
Nature is in a continuous state of evolution. “Rules” governing the time evolution of systems in nature, also known as dynamics, can be captured mathematically through partial differential equations (PDEs). In the realm of science and engineering, PDEs are widely used to model and study several challenging real-world systems, such as fluid flow, deformation of solids, plasma dynamics, robotics, mechanics, and weather forecasting, to name a few.1–3 Due to their highly non-linear and coupled nature, these PDEs can be solved analytically only for trivial or model systems. Thus, accurate numerical solutions for the PDEs are the cornerstone in advancing scientific discovery. Traditionally, the PDEs are solved using classical numerical methods such as finite difference, finite volume, or finite element methods.4 However, these numerical methods exhibit major challenges in realistic systems in terms of system size, timescales, and numerical instabilities. Specifically, simulating the systems for longer timescale or for large domains is extremely computationally intensive to the extent that performing them in real-time for decision-making is a major challenge. Further, in the case of large/highly non-linear fields, these simulations often exhibit numerical instabilities, rendering them ineffective.5The recent surge in artificial intelligence-based approaches suggests that neural models can efficiently capture continuous dynamical systems in a data-driven fashion.6 These models are extremely time-efficient in comparison to traditional solvers and can capture highly non-linear input–output relationships. Earlier approaches in this direction relied directly on learning the input–output map through multilayer perceptrons (MLPs), convolutional neural networks, or graph neural networks. However, these approaches faced challenges in terms of generalizing to unseen initial or boundary conditions, geometries, or resolutions. This could be attributed to the fact that the neural models essentially learn the input–output relationship in a finite-dimensional approximation. To address this challenge, a seminal theory, extending the universal approximation theorem of neural networks7 to neural operators was proposed, namely, the universal operator approximation theory.8 This theory unveiled the neural networks' prowess in handling infinite-dimensional inputs and outputs.
Theoretically, directly learning the solution operator through specialized neural network architectures offers several key advantages. (i) They can directly learn input–output function mappings from data, thereby obviating the necessity for prior knowledge of the underlying PDE. (ii) They offer significantly improved time efficiency compared to traditional numerical solvers. (iii) They exhibit zero-shot generalizability, extending their applicability to systems of larger scale and complexity than those encompassed within the training dataset. (iv) They provide superior approximations of the solution operator compared to existing neural architectures, spanning from feed-forward networks to specialized models like convolutional networks and conditional generative adversarial networks (GANs). Thus, the neural operators attempt9 to combine the best of both data-driven and physics-based numerical models.
This motivated the exploration of neural operator architectures,10,11 capable of directly learning the solution operator. For instance, consider DeepONet,12 which leverages the universal approximation theorem introduced by Chen and Chen to directly address PDEs. On a different front, FNO,13 one of the most widely used Neural Operators, focuses on parameterizing the integral kernel within Fourier space. Moreover, a noteworthy study14 highlights the notion that all transformers are essentially operators. This insight has sparked endeavors to create operator transformers. Given their proven effectiveness in sequence-to-sequence learning tasks, these transformer-based designs open avenues for enhancing the approximation of spatiotemporal PDEs. Prior studies, such as those by ref. 15 and have delved into the realm of PINNs16 and some neural operator architectures, like DeepONet, FNO, and their variants.
However, unlike fields like computer vision, comprehensive comparative evaluations of these neural operators are absent. Such evaluations are pivotal to discerning the distinctive advantages of diverse architectural paradigms, especially when addressing equations from a wide spectrum of scientific domains (Fig. 1). The challenging nature of these comparative evaluations is amplified by variations and incompatibilities among different architectures. While there have been several attempts at repositories, such as,17–19 featuring implementations of various neural operators, their scope remains limited (refer to ESI Table 2†).
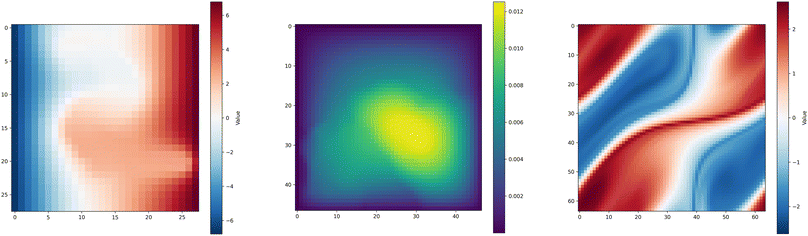 | ||
| Fig. 1 A glimpse of the data diversity under consideration. From left to right, we present visual representations of three distinct datasets — Biaxial, Darcy flow, and Navier–Stokes. | ||
This study aims to bridge this gap by rigorously evaluating data-driven models that encompass a wide range of classes and methods, including the foundational deep operator regression model, frequency domain parameterization models, and transformer-based architectures, to achieve state-of-the-art performance comparison on selected PDE datasets. Moreover, we integrate conventional neural architectures to underscore the merits of PDE-specialized structures. Our dataset selection is methodical, designed to challenge each model with equations from various scientific disciplines. We incorporate five prevalent equations from fluid dynamics and five standard differential equations from solid mechanics into the neural operator domain, ensuring a holistic comparison within the realm of neural operators.
1.1 Our contribution
In this work, we critically analyze 12 data-driven models, including operators and transformers, on 10 PDE datasets. The major contributions of our research are as follows:(1) CoDBench: we present a package that allows seamless analysis of several data-driven approaches on PDEs. We thoroughly assess state-of-the-art data-driven neural models for solving PDE datasets across diverse scientific realms, such as fluid and solid mechanics, shedding light on their precision and efficacy.
(2) Super-resolution: we analyze the ability of neural operators' to generalize to systems of different resolutions than that of their training sets' discretizations.
(3) Data efficiency and robustness to noise: we critically assess the efficiency of these models to learn from small amounts of data or noisy data. This is an important aspect since the data available can be scarce and noisy in practical applications.
(4) Out-of-distribution task: a novel task to gain insights into what these models are truly learning to determine whether the underlying operator is genuinely being learned or if the training dataset is simply being fitted. Two closely related stress and strain datasets are interchanged during training and testing to dig deeper into whether the solvers are actually operators.
2 Preliminaries
This section provides a concise mathematical framework to illustrate how traditional PDE solving can be transitioned and addressed using data-driven methodologies via neural networks.(1) Function domains: consider a bounded open set  , which serves as the coordinate space. Within this domain, we define
, which serves as the coordinate space. Within this domain, we define 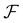 and
and 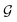 as separable Banach spaces corresponding to the input and output functions. They are denoted by
as separable Banach spaces corresponding to the input and output functions. They are denoted by 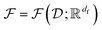 and
and 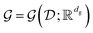 . Here,
. Here, 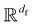 and
and 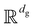 represent the ranges of functions in
represent the ranges of functions in 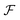 and
and 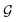 , respectively.
, respectively.
(2) The solution operator: n our exploration, we introduce 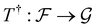 , a mapping that is typically nonlinear. This mapping emerges as the solution operator for PDEs, playing a pivotal role in scientific computations. Refer to ESI Appendix A.2† for examples of
, a mapping that is typically nonlinear. This mapping emerges as the solution operator for PDEs, playing a pivotal role in scientific computations. Refer to ESI Appendix A.2† for examples of 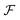 ,
, 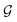 and T† in the context of PDEs.
and T† in the context of PDEs.
(3) Data generation: for training purposes, models utilize PDE datasets constructed as 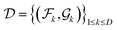 , where
, where 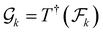 . Given the inherent challenges in directly representing functions as inputs to neural networks, the functions are discretized using mesh generation algorithms20 over domain
. Given the inherent challenges in directly representing functions as inputs to neural networks, the functions are discretized using mesh generation algorithms20 over domain 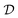 . For the input function
. For the input function 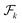 , we discretize it on a mesh {xi ∈ Ω}1≤i≤R, and the discretized
, we discretize it on a mesh {xi ∈ Ω}1≤i≤R, and the discretized 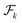 is {(xi,fik)}1≤i≤R, where
is {(xi,fik)}1≤i≤R, where 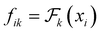 . Similarly, For the solution function
. Similarly, For the solution function 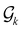 , we discretize it on a mesh {yi ∈ Ω}1≤i≤R, and the discretized
, we discretize it on a mesh {yi ∈ Ω}1≤i≤R, and the discretized 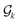 is {(yi,gik)}1≤i≤R, where
is {(yi,gik)}1≤i≤R, where 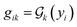 . While the majority of datasets included in the study sample both input and output functions on a uniform grid to ensure compatibility with all selected solvers, we also incorporate datasets sampled on irregular grids. This addition allows us to assess the capability of solvers to handle complex real-life applications.
. While the majority of datasets included in the study sample both input and output functions on a uniform grid to ensure compatibility with all selected solvers, we also incorporate datasets sampled on irregular grids. This addition allows us to assess the capability of solvers to handle complex real-life applications.
(4) Objective: the overarching goal for each model is to craft an approximation of T†. This is achieved by developing a parametric mapping, denoted as 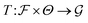 or, in an equivalent form,
or, in an equivalent form, 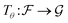 , where θ ∈ Θ, is a parameter space.
, where θ ∈ Θ, is a parameter space.
(5) Metric: evaluating the efficacy of the parametric mapping involves comparing its outputs, 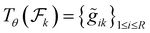 , with the actual data, aiming to minimize the relative L2 loss:
, with the actual data, aiming to minimize the relative L2 loss:
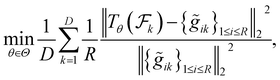 | (1) |
3 Model architectures
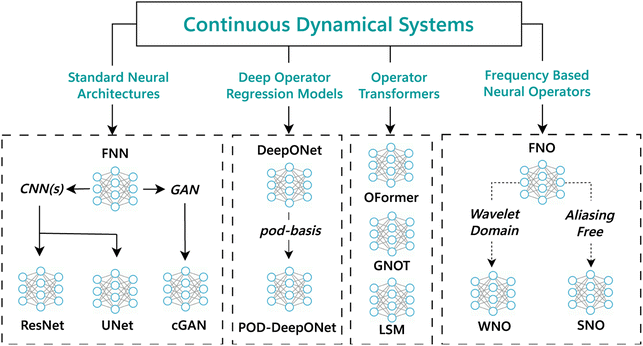
We systematically select 12 data-driven models, encompassing four distinct categories (refer to Fig. 2). We incorporate standard neural network architectures to establish a baseline for all neural operators, while deep operator regression models serve as foundational elements. Advanced state-of-the-art contributions emerge in frequency-based operators, with FNO representing a milestone model. Including frequency-based models enhances the benchmark's utility. Notably, 2023 introduces three major transformer-based neural operator architectures, exhibiting state-of-the-art performance in error rates. We include transformer-based models to compare the latest research in neural operators with previously established approaches.3.1 Standard neural network architectures
UNet, delineated in ref. 21, employs a U-shaped encoder–decoder design augmented by skip connections, facilitating the capture of granular and abstract features. ResNet, described in ref. 22, consists of a series of residual blocks and are commonly used in computer vision tasks.23 Conditional Generative Adversarial Networks (cGAN), introduced in ref. 24, are an evolution of the GAN framework, facilitating conditional generation via the incorporation of label information in both the generator and discriminators. FNN is a foundational element for all machine learning models. Meanwhile, ResNet and UNet exhibit promising results, with UNet demonstrating competitive error rates among leading neural operators. cGAN features a distinctive generative-adversarial architecture, showing promise in learning PDE datasets. Including these models in the benchmark study reflects their simple architecture yet notable performance in addressing partial differential equations.3.2 Deep operator-based regression models
Neural Operators represent a novel ML paradigm, predominantly employed in scientific machine learning to decipher PDEs. These operators rely solely on data and remain agnostic to the underlying PDE. DeepONet bifurcates into two sub-networks: the branch net, which encodes the input function at fixed sensor locations, and the trunk net, encoding solution function locations.12 The solution emerges from the inner product of the outputs from these nets. In POD-DeepONet, the bases are determined by executing proper orthogonal decomposition (POD) on training data, replacing the self-learned basis of output functions.25 This POD basis forms the trunk net, leaving only the branch net as the trainable component, which discerns the coefficients of the POD basis. These models exemplify a direct application of the universal operator approximation theory, highlighting the capacity of neural networks in learning and embodying operators.3.3 Frequency-based operators
Frequency-based solvers like FNO employ a finite-dimensional parameterization using truncated Fourier modes.13 By integrating this with an integral operator restricted to convolution and instantiated via a linear transformation in the Fourier domain, the FNO operator is conceived. WNO, or Wavelet Neural Operator, amalgamates the prowess of wavelets in time-frequency localization with an integral kernel. By learning the kernel in the wavelet domain, convolution operates on wavelet decomposition coefficients rather than direct physical space convolution.26 SNO, the Spectral Neural Operator, addresses the often-overlooked aliasing error in the Fourier Neural Operator. By representing both input and output functions using coefficients in truncated Fourier or Chebyshev series, SNO offers an aliasing-free approach.27 Any transformation between these coefficients can be executed using neural networks, and methods employing these series are termed spectral neural operators. Their approach utilizes a straightforward, feed-forward neural network architecture in the complex domain. Although multiple variants of FNO demonstrate commendable performance, the selected models above are chosen to exemplify the most diverse yet effective approaches in solving partial differential equations (PDEs) within the frequency domain.3.4 Transformer operators
GNOT introduces the Heterogeneous Normalized (linear) Attention (HNA) block and a geometric gating mechanism, specifically tailored for enhanced performance on PDE datasets.28 This architecture effectively performs a soft domain decomposition,29 treating each decomposed domain independently and subsequently integrating them using a mixture-of-experts approach to predict the underlying truth. In contrast, the OFormer model builds upon the seminal work presented in ref. 30. It incorporates random Fourier projection to counteract spectral bias, enhancing its efficacy on PDEs.31 Another recent advance in the field of the neural operator comes with the Latent Spectral Model. It maps the high-dimensional coordinate space to a compact latent space and learns the solution operator in latent space. An attention-based neural network is instantiated to learn the mapping from coordinate to latent space and vice versa.32 Despite sharing a common foundational architecture, all the aforementioned models approach the task of learning partial differential equations (PDEs) differently. Their varied methodologies and consistent state-of-the-art performance across multiple datasets make them ideal candidates for inclusion in the evaluation of data-driven PDE solvers.4 Datasets
Here, we briefly describe the 10 datasets used in the present. While previous approaches have mostly focussed on fluid datasets, here we present 5 datasets on fluid flow and 5 on the deformation of solids; for complete dataset details, refer A.2.(1) Burgers equation: this dataset models the one-dimensional flow of a viscous fluid. The input is the fluid's initial velocity distribution at time t = 0, and the output is the fluid's velocity at a time t > 0.19
(2) Darcy flow equation: the Darcy flow dataset describes the steady-state flow of a fluid through a porous medium in two dimensions. The input is the spatial distribution of the medium's resistance to flow (viscosity), and the output is the fluid's velocity distribution across the domain at steady-state.19
(3) Navier Stokes: this dataset models the time evolution of a 2D viscous, incompressible fluid. The input includes the fluid's initial swirling motion (vorticity) and external forces acting on the fluid. The output is the fluid's velocity distribution over a specified time period.19
(4) Shallow water equation: the shallow-water equations simulate the behavior of water that flows over a shallow surface in 2D. The input consists of the initial water depth and velocity distribution, and the output predicts the water flow dynamics in response to gravitational forces and varying underwater terrain (bathymetry).19
(5) Stress dataset: this dataset models the stress distribution in a 2D binary composite material subjected to mode-I tensile loading. The input is the material microstructure (distribution of two materials), and the output is the stress field (stress) distribution of the digital composite.33
(6) Strain dataset: the strain dataset describes the deformation of a 2D binary composite material subjected to mode-I tensile loading. The input is the material microstructure, and the output is the resulting strain fields (strain).33
(7) Shear dataset: part of the mechanical MNIST collection, this dataset simulates the deformation of a heterogeneous material block when forces are applied parallel to its surface (shear). The input is the material microstructure, and the output captures element-wise displacements subjected to shear loading.34
(8) Biaxial dataset: another subset of the mechanical MNIST experiments, this dataset models the material's response when stretched equally in two perpendicular directions (equibiaxial loading). The input is the material microstructure, and the output records the full field displacement under biaxial stretching.34
(9) Elasticity dataset: for this dataset, an external tension is exerted on an incompressible material featuring an arbitrary void at its center. The input to the system is characterized by the material's structure, which is highly irregular and provided in the form of point clouds. The output is the inner stress within the material.35
(10) Airfoil dataset: the dataset characterizes the transonic flow of a fluid over an airfoil. Input to the system comprises the locations of mesh points configured in an irregularly structured mesh. The output corresponds to the captured Mach number associated with these specific locations.35
5 Benchmarking results
We present the results of rigorous experimentation on PDE solvers across six tasks, each designed to elucidate the unique capabilities and strengths of the models. The diversity of the selected PDEs, sourced from,19,33–35 encompasses both time-dependent and time-independent challenges, capturing the intrinsic computational complexity inherent to these tasks. Additionally, irregular grid datasets are included to evaluate the models' capabilities in handling datasets with real-life, general geometries, as opposed to uniform grids. The experiments conducted on novel mechanical datasets not previously encountered by the solvers offer invaluable insights for the broader scientific community.In alignment with established experimental protocols, the dataset was split as follows: ∼80% for training, ∼10% for validation, and ∼10% for testing (refer to ESI Table 3† for more details). We ensured a level playing field for each operator by defining a hyperparameter range and selecting the best subset for experimentation (see ESI Table 4†). Model optimization was achieved using Adam36 and AdamW37 optimizers (refer to ESI Table 5†). Depending on the specific task, we employed either step-wise or cycle learning rate scheduling.38 While we have attempted to standardize the comparison by tuning on multiple optimizers, schedulers, different learning rates, scheduler hyperparameters as well as architectural hyperparameters, we acknowledge that additional techniques such as regularization could further level the playing field.
The training was conducted under optimal hyperparameter configurations, introducing variability through distinct random seeds and data splits. All experiments adhered to a fixed batch size of 20 and were executed on 1–8 NVIDIA A6000 GPUs, with memory capacities of 48 GBs. To ensure fairness and accuracy in results, each experiment was replicated thrice with different seeds, and we report the mean and deviation in r relative L2 error.
5.1 Accuracy
Table 1 shows the performance of the models on the eight datasets. FNO architecture stands out on the majority of datasets. Subsequently, GNOT and LSM showcase exemplary performance on a significant proportion (5/8) of datasets. Similar results are observed in experiments conducted on irregular grid datasets.FNO's strength lies in its frequency space transformation. By capturing and transforming the lower frequencies present in the data, the FNO can approximate the solution operators of scientific PDEs. This approach, which uses the integral kernel in the Fourier space, facilitates a robust mapping between input and output function spaces, making it particularly adept at handling the complexities of the datasets in this study. GNOT employing a mixture-of-experts approach and its unique soft domain decomposition technique divides the problem into multiple scales, allowing it to capture diverse features of the underlying PDE. Each expert or head in the model focuses on a different aspect of the PDE, and their combined insights lead to a comprehensive understanding, especially for challenging datasets like shear and biaxial.
In contrast to other transformer-based approaches, LSM initially projects high-dimensional input data into a compact latent space, eliminating redundant information before learning the underlying partial differential equation (PDE). It utilizes a neural spectral block to learn the solution operator within this low-dimensional latent space, leveraging universal approximation capacity with favorable theoretical convergence guarantees. By employing attention for efficient data projection to and from the latent space and employing theoretically sound methods to learn the PDE from a lower-dimensional space, LSM consistently achieves low error rates.
The OFormer architecture that employs an innovative approach to solving spatio-temporal PDEs, exhibits best results in Navier Stokes dataset. It efficiently forwards the time step dynamics in the latent space by unrolling in the time dimension and initiating with a reduced rollout ratio. This method conserves significant space during training on time-dependent datasets while achieving high accuracy.
Among the models, only four inherently support datasets with irregular grids (refer to Table 2). To facilitate a comprehensive comparison, we introduce variants of LSM (Geo-LSM) and FNO (Geo-FNO). Notably, GNOT, tailored for practical applications involving irregular meshes, excels on both datasets. It utilizes MLP for initially encoding data into feature embeddings and leverages transformers to handle diverse input structures. While FNO and LSM demonstrate proficiency in handling uniform grid datasets, their effectiveness is maintained when an additional geometric layer learns the transformation from irregular input domains to a uniform transformed domain. However, this approach has limitations, particularly in tasks where efficient transformation from the input grid to a uniform grid space is challenging to learn.
Interestingly, most models, with the notable exception of GNOT, struggle to accurately learn the underlying PDE for the biaxial and shear datasets. The simpler FNN architecture demonstrates significant proficiency in learning these datasets. Interestingly, architectures like cGAN, originally designed for 2D image data analysis with its U-Net encoder, demonstrate impressive performance across tasks. This underscores the versatility of such architectures, even when they aren't explicitly designed as operators.
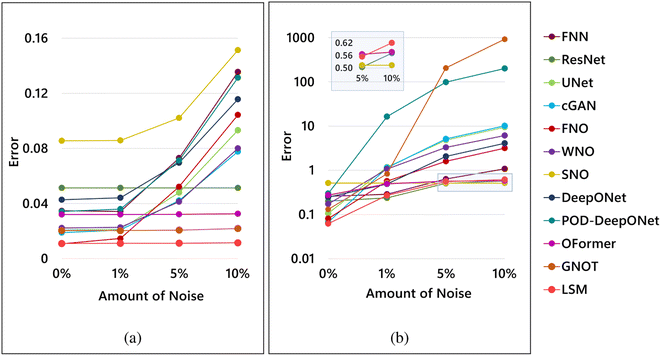
5.2 Robustness to noise
In practical applications, it's common to encounter noise in measurements. We simulated conditions with noisy data to understand how various neural operators handle such real-world challenges. We intentionally introduced corrupted input function data to each model during our testing phase. The goal was to see how well these models could still predict the ground truth amidst this noise.Fig. 3 shows the performance of the models on noisy data. Transformer-based architectures have shown commendable performance on the Darcy dataset. Even when noise is introduced, these models continue to perform well. However, the resilience of OFormer and GNOT is tested when faced with the Stress dataset. In scenarios where they already find it challenging to learn the underlying PDEs, the addition of noise exacerbates their performance issues.
On the other hand, SNO shows superior robustness to noise. While its performance in a noise-free environment is far from the best, it performs remarkably when exposed to noisy datasets, especially on the stress dataset. This resilience can be attributed to its unique approach: unlike other frequency-based methods that transition between the time and frequency domains, SNO exclusively processes data in the frequency domain. This design choice allows it to filter out noise, identifying it as a high-frequency disturbance.
A similar scenario is evident in the performance of LSM, as it remains largely unaffected by noisy input when tested on the Darcy dataset. Even when subjected to the demanding stress dataset, LSM consistently ranks among the best-performing models. This resilience is attributed to its projection into a compact latent space, eliminating redundant information, including the noise introduced from the coordinate space.
5.3 Data efficiency
We utilized the Darcy dataset with 1700 samples of 47 × 47 dimensions for the data-efficiency experiments. To assess the data efficiency of the models, we trained all models on reduced subsets: 25% (425 samples) and 50% (850 samples) of the original dataset.The exceptional performance of frequency-based methods, notably FNO and WNO, even with limited data, is rooted in their operation within the frequency domain (see Table 3). The notable capability of these methods to capture the essential dynamics of the underlying PDEs through the lower frequencies present in the data enables data-efficient learning, a crucial feature for realistic data where the number of observations may be limited.
Transformer-based neural operator architectures have demonstrated potential in approximating operators. However, their efficacy diminishes when data is sparse. GNOT, which typically excels with a rich dataset, struggles to outperform even basic neural network architectures in a data-limited scenario. On the other hand, LSM consistently remains the second best model in terms of error rates. However, more than a two-fold increase in the error shows the data dependence of the attention-based projection method used within the model. This trend underscores the inherent data dependency of transformer architectures, highlighting the challenges faced by many models, except frequency-based operators, when trained on limited data.
5.4 Out-of-distribution generalization
The equations for stress and strain are intrinsically linked, differing primarily by the coefficient of elasticity, commonly known as Young's modulus. Given that our training and testing processes utilize normalized data, it's reasonable to anticipate that the models trained on the stress dataset should be adept at predicting strain in the material microstructures and vice versa. This expectation is particularly true for neural operators that grasp the underlying partial differential equations (PDEs) governing such relationships. Table 4 shows the OOD evaluation on all the models. Interestingly, for SNO, the error on the strain test dataset remains consistent, whether it was trained on the strain or stress datasets. The same holds when tested on the stress dataset. This consistency underscores SNO's ability to learn the underlying PDE. In stark contrast, other models don't exhibit this adaptability. Their accuracy levels decline when the testing set is swapped, indicating a potential limitation in their ability to generalize across closely related tasks.5.5 Zero-shot super-resolution
Directly approximating the solution operator offers a theoretical advantage: the potential for a mesh invariant continuous dynamical system. Once trained, such a system can ideally maintain accuracy even when applied to larger systems than those it was trained on. This capability is termed “zero-shot super-resolution”.Note that FNO and GNOT enables zero shot super-resolution without any modifications. Upon closer examination, other models, such as SNO and DeepONet, cannot have a straightforward application on zero-shot super-resolution. Instead, they lean on certain workarounds to achieve the desired results. While these modifications might enable super-resolution in practice, they diverge from the concept of zero-shot super-resolution from an architectural perspective.
Accordingly, we consider only FNO and GNOT for our evaluation. Tests on both Darcy and strain datasets are conducted, with the original training data having a lower resolution, and the neural operators are evaluated on higher resolution data.
The inherent architecture of FNO fails to respect the continuous-discrete equivalence, leading to aliasing errors.39 These errors exacerbate as the test data resolution differs from the training data; see Table 5. Although GNOT performs slightly better, its results are still suboptimal. Further theoretical research is necessary to comprehend the mathematical foundations of learning a discretized version of PDE using transformer-based architectures and the limitation and scope of improvement regarding generalization capability to continuous domains.
| Dataset | Resolution | Models | |
|---|---|---|---|
| FNO | GNOT | ||
| Darcy | 47 × 47 | 1.08 ±0.06 | 2.04 ±0.05 |
| 64 × 64 | 60.50±5.49 | 55.32±5.65 | |
| 128 × 128 | 59.99±5.48 | 55.42±5.68 | |
| Strain | 48 × 48 | 5.61 ±0.23 | 9.99 ±0.62 |
| 104 × 104 | 16.92±0.36 | 20.26±0.65 | |
| 200 × 200 | 18.74±0.24 | 20.89±0.20 | |
5.6 Time efficiency
Neural operators are gaining traction over traditional numerical solvers due to their promise of rapid inference once trained. For this assessment, we've bench-marked various continuous dynamical systems on two criteria: the duration required to train on the Darcy dataset and the time needed to predict output function values for 200 test samples, each mapped on a uniform 47 × 47 grid. As anticipated, the FNN, with its straightforward architecture, stands out by requiring the least time for training and inference. However, when we delve into the other models, those based on deep operator regression methods show training duration on par with some complex but standard neural network architectures. For better visualization, see Fig. 4. When considering inference time, a pivotal metric in practical applications, the narrative shifts. While FNO is relatively efficient during training, it, along with the transformer-based models, takes a longer inference stride. While LSM outperforms other transformer-based architectures in both metrics, in the broader context of assessed operators, it doesn't rank as a highly time-efficient model in either training or inference time. Though all these models show promising performance on different metrics, inference time efficiency remains challenging. In stark contrast, most other models edge closer to offering real-time inference, highlighting the inherent time complexity trade-offs one must consider when opting for a particular neural operator.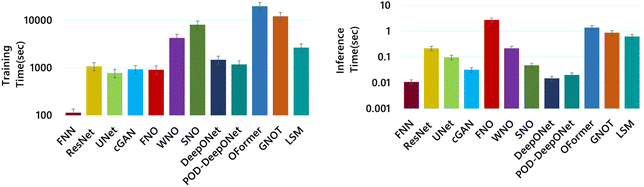 | ||
| Fig. 4 Time efficiency: we report the time taken by each model during training (on left) and inference time on test set (on right). Results are collected during the training on Darcy dataset. | ||
6 Concluding insights
The key insights drawn from this work are as follows.(1) Operator and transformer: FNO, GNOT and LSM emerge as the superior models across various metrics, suggesting that the architectural novelty in these models can indeed capture the maps between infinite-dimensional functional spaces.
(2) SNOs' promise to generalize: despite modest overall performance, SNO stands alone in demonstrating remarkable adaptability to related datasets. Its exceptional generalization is facilitated by singular Fourier and inverse Fourier transformations, mapping input to output entirely in the frequency domain.
(3) Spectral resilience to noise: LSM and SNO demonstrate robust predictions in the face of noise through a transformation to reduced dimensional space. By employing effective approaches for dimensionality reduction even before the prediction process begins, they efficiently eliminate noise as redundant information.
(4) Attention alone is not enough: OFormer, employing the attention-based transformer architecture, showcases notable advantages on the Navier Stokes dataset. It also demonstrates commendable results on specific PDEs like Burgers, Darcy. However, a glaring limitation surfaces when these architectures are applied to other PDEs, whether of comparable complexity or even simpler ones. They fail to generalize. This shortcoming starkly contrasts with one of the primary advantages anticipated from data-driven PDE solvers: the capacity to discern the solution operator solely from data, independent of prior knowledge of the underlying PDE.
(5) Data-driven models work: surprisingly, the cGAN, a standard architecture for image tasks, excels in performance, even though it isn't inherently an operator. This prowess, however, wanes during cross-dataset evaluations, underscoring the importance of truly learning the underlying PDE rather than merely excelling on a given dataset.
(6) Challenges with shear and biaxial datasets: The collective struggle of most operators with the shear and biaxial datasets underscores the importance studying complex deformation patterns. Specifically, it suggests clear and well-defined operator failure modes where future works can be focused.
(7) Time efficiency should be improved: while the models give reasonable performance, they grapple with time efficiency. Significantly, the best-performing models, such as transformer-based architectures, are time-intensive during training and inference, FNO is relatively swift in training but still intensive in inference.
6.1 Future work
Although FNO, GNOT and LSM exhibit consistent superior results, their results in cross-dataset evaluations and zero-shot super-resolution raise the questions of whether they are truly learning approximate solutions to the underlying PDE (see App. A.8). Similarly, although resilient to noise and OOD, the internal neural network architecture of SNO remains largely unexplored and often yields subpar outcomes. Future endeavors leveraging SNO might pave the way to operators with improved robustness. Failure modes of operators in datasets require further investigations to build more robust operators that can capture complex shear deformations. Finally, the model's inference time requires improvement to be applied to large-scale real-world problems.Data availability
For codes and datasets, see: https://github.com/Priyanshu-bee/cod-bench.Conflicts of interest
There are no conflicts to declare.References
- L. Debnath and L. Debnath, Nonlinear partial differential equations for scientists and engineers, Springer, 2005 Search PubMed.
- S. Nakamura, Computational methods in engineering and science, with applications to fluid dynamics and nuclear systems, John Wiley and Sons, Inc., New York, 1977 Search PubMed.
- D. Robert, Partial Differential Equations and Applications, Sémin. Congr., 2007, 15, 181–250 Search PubMed.
- G. Sewell, Analysis of a finite element method: PDE/PROTRAN, Springer Science & Business Media, 2012 Search PubMed.
- P. Ŝolín, Partial differential equations and the finite element method, John Wiley & Sons, 2005 Search PubMed.
- S. L. Brunton and J. N. Kutz, Data-driven science and engineering: Machine learning, dynamical systems, and control, Cambridge University Press, 2022 Search PubMed.
- G. Cybenko, Approximation by superpositions of a sigmoidal function, Math. Control Signals Syst., 1989, 2(4), 303–314 CrossRef.
- T. Chen and H. Chen, Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems, IEEE Trans. Neural Netw., 1995, 6(4), 911–917 CrossRef CAS PubMed.
- N. Kovachki, Z. Li, B. Liu, K. Azizzadenesheli, K. Bhattacharya, A. Stuart and A. Anandkumar, Neural operator: Learning maps between function spaces with applications to pdes, J. Mach. Learn. Technol., 2023, 24(89), 1–97 Search PubMed.
- K. Bhattacharya, B. Hosseini, N. B. Kovachki and A. M. Stuart, Model reduction and neural networks for parametric PDEs, SMAI J. Comput. Math., 2021, 7, 121–157 CrossRef.
- N. H. Nelsen and A. M. Stuart, The random feature model for input-output maps between banach spaces, SIAM J. Sci. Comput., 2021, 43(5), A3212–A3243 CrossRef.
- L. Lu, P. Jin, G. Pang, Z. Zhang and G. E. Karniadakis, Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators, Nat. Mach. Intell., 2021, 3(3), 218–229 CrossRef.
- Z. Li, N. Kovachki, K. Azizzadenesheli, B. Liu, K. Bhattacharya, A. Stuart, A. Anandkumar, Fourier neural operator for parametric partial differential equations, arXiv, 2020, preprint, arXiv:2010.08895, DOI:10.48550/arXiv.2010.08895.
- S. Cao, Choose a transformer: Fourier or galerkin, Adv. Neural Inf. Process. Syst., 2021, 34, 24924–24940 Search PubMed.
- Z. Hao, S. Liu, Y. Zhang, C. Ying, Y. Feng, H. Su, J. Zhu, Physics-informed machine learning: A survey on problems, methods and applications, arXiv, 2022, preprint, arXiv:2211.08064, DOI:10.48550/arXiv.2211.08064.
- M. Raissi, P. Perdikaris and G. E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys., 2019, 378, 686–707 CrossRef.
- L. Lu, X. Meng, Z. Mao and G. E. Karniadakis, DeepXDE: A deep learning library for solving differential equations, SIAM Rev., 2021, 63(1), 208–228 CrossRef.
- S. M. S. Hassan, A. Feeney, A. Dhruv, J. Kim, Y. Suh, J. Ryu, et al., BubbleML: A Multiphase Multiphysics Dataset and Benchmarks for Machine Learning, Advances in Neural Information Processing Systems, 2024, vol. 36 Search PubMed.
- M. Takamoto, T. Praditia, R. Leiteritz, D. MacKinlay, F. Alesiani and D. Pflüger, et al., PDEBench: An extensive benchmark for scientific machine learning, Adv. Neural Inf. Process. Syst., 2022, 35, 1596–1611 Search PubMed.
- J. R. Tristano, S. J. Owen and S. A. Canann, Advancing front surface mesh generation in parametric space using a riemannian surface definition, in IMR, 1998, pp. 429–445 Search PubMed.
- O. Ronneberger, P. Fischer, and T. Brox, U-net: Convolutional networks for biomedical image segmentation, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, Springer, 2015, pp. 234–241 Search PubMed.
- S. Jian, H. Kaiming, R. Shaoqing and Z. Xiangyu, Deep residual learning for image recognition, in IEEE Conference on Computer Vision & Pattern Recognition, 2016, pp. 770–778 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778 Search PubMed.
- M. Mirza and S. Osindero, Conditional generative adversarial nets, arXiv, 2014, preprint, arXiv:1411.1784, DOI:10.48550/arXiv:1411.1784.
- L. Lu, X. Meng, S. Cai, Z. Mao, S. Goswami and Z. Zhang, et al., A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data, Comput. Methods Appl. Mech. Eng., 2022, 393, 114778 CrossRef.
- T. Tripura and S. Chakraborty, Wavelet neural operator for solving parametric partial differential equations in computational mechanics problems, Computer Methods in Applied Mechanics and Engineering, 2023, 404, 115783 CrossRef.
- V. Fanaskov and I. Oseledets, Spectral neural operators, in , Doklady Mathematics, Pleiades Publishing, Moscow, 2023, vol. 108, 2, pp. S226–S232 Search PubMed.
- Z. Hao, Z. Wang, H. Su, C. Ying, Y. Dong, S. Liu, et al., Gnot: A general neural operator transformer for operator learning, in International Conference on Machine Learning, PMLR, 2023, pp. 12556–12569 Search PubMed.
- A. D. Jagtap and G. E. Karniadakis, Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations, Commun. Comput. Phys., 2020, 28(5), 2002–2041 CrossRef.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, et al., Attention is all you need, Advances in Neural Information Processing Systems, 2017, vol. 30 Search PubMed.
- Z. Li, K. Meidani, A. B. Farimani, Transformer for partial differential equations' operator learning, arXiv, 2022, preprint, arXiv:2205.13671, DOI:10.48550/arXiv:2205.13671.
- H. Wu, T. Hu, H. Luo, J. Wang, M. Long, Solving high-dimensional pdes with latent spectral models, arXiv, 2023, preprint, arXiv:2301.12664, DOI:10.48550/arXiv:2301.12664.
- M. M. Rashid, T. Pittie, S. Chakraborty and N. A. Krishnan, Learning the stress-strain fields in digital composites using Fourier neural operator, iScience, 2022, 105452 CrossRef PubMed.
- E. Lejeune, Mechanical MNIST: A benchmark dataset for mechanical metamodels, Extreme Mech. Lett., 2020, 36, 100659 CrossRef.
- Z. Li, D. Z. Huang, B. Liu and A. Anandkumar, Fourier neural operator with learned deformations for pdes on general geometries, J. Mach. Learn. Technol., 2023, 24(388), 1–26 CAS.
- D. P. Kingma, J. Ba, Adam: A method for stochastic optimization, arXiv, 2014, preprint arXiv:1412.6980, DOI:10.48550/arXiv:1412.6980.
- I. Loshchilov and F. Hutter, Decoupled weight decay regularization, arXiv, 2017, preprint arXiv:1711.05101, DOI:10.48550/1711.05101.
- L. N. Smith and N. Topin, Super-convergence: Very fast training of neural networks using large learning rates, in Artificial intelligence and machine learning for multi-domain operations applications, SPIE, 2019, vol. 11006, pp. 369–386 Search PubMed.
- F. Bartolucci, E. de Bézenac, B. Raonić, R. Molinaro, S. Mishra, R. Alaifari, Are neural operators really neural operators? frame theory meets operator learning, arXiv, 2023, preprint, arXiv:2305.19913, DOI:10.48550/arXiv:2305.19913.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00028e |
| This journal is © The Royal Society of Chemistry 2024 |