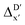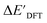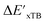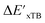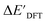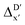Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailoring phosphine ligands for improved C–H activation: insights from Δ-machine learning†
Tianbai
Huang
a,
Robert
Geitner
 *b,
Alexander
Croy
*a and
Stefanie
Gräfe
*b,
Alexander
Croy
*a and
Stefanie
Gräfe
 *a
*a
aInstitute for Physical Chemistry (IPC) and Abbe Center of Photonics, Friedrich Schiller University Jena, Helmholtzweg 4, 07743 Jena, Germany. E-mail: alexander.croy@uni-jena.de; s.graefe@uni-jena.de
bInstitute of Chemistry and Bioengineering, Technical University Ilmenau, Weimarer Str. 32, 98693 Ilmenau, Germany. E-mail: robert.geitner@tu-ilmenau.de
First published on 28th May 2024
Abstract
Transition metal complexes have played crucial roles in various homogeneous catalytic processes due to their exceptional versatility. This adaptability stems not only from the central metal ions but also from the vast array of choices of the ligand spheres, which form an enormously large chemical space. For example, Rh complexes, with a well-designed ligand sphere, are known to be efficient in catalyzing the C–H activation process in alkanes. To investigate the structure–property relation of the Rh complex and identify the optimal ligand that minimizes the calculated reaction energy ΔE of an alkane C–H activation, we have applied a Δ-machine learning method trained on various features to study 1743 pairs of reactants (Rh(PLP)(Cl)(CO)) and intermediates (Rh(PLP)(Cl)(CO)(H)(propyl)). Our findings demonstrate that the models exhibit robust predictive performance when trained on features derived from electron density (R2 = 0.816), and SOAPs (R2 = 0.819), a set of position-based descriptors. Leveraging the model trained on xTB-SOAPs that only depend on the xTB-equilibrium structures, we propose an efficient and accurate screening procedure to explore the extensive chemical space of bisphosphine ligands. By applying this screening procedure, we identify ten newly selected reactant–intermediate pairs with an average ΔE of 33.2 kJ mol−1, remarkably lower than the average ΔE of the original data set of 68.0 kJ mol−1. This underscores the efficacy of our screening procedure in pinpointing structures with significantly lower energy levels.
1. Introduction
Organometallic compounds have been extensively applied in homogeneous catalytic processes, owing to their versatile redox properties that can be easily tuned and optimized to the specific chemical process of interest. This tunability is achieved through the alteration of the metal center, and more importantly, through structural modification of the ligand sphere. For example, by precisely designing the ligand architecture, Ir- and Rh-based complexes can be applied for the hydrogenation of CO2 (ref. 1) and olefins,2 the oxidation of water,3 the activation of hydrocarbon halides,4,5 the dehydrogenation of alkanes,6,7 as well as the carbonylation of alkanes and benzene.6,8 Notably, variation in the efficiencies has been observed in the dehydrogenation reaction of alkanes mediated by Rh complexes featuring different ligands.7 This emphasizes the important role of ligand selection in determining the efficiency of organometallic catalysts.Computational chemistry serves as a potent tool for ligand design for organometallic catalysts. Reaction energies and activation barriers can readily be obtained by analyzing the energy profiles of molecular configurations on the potential energy (hyper-)surface, calculated by quantum chemical (QC) methods, such as density functional theory (DFT). These values can be linked to the reaction rate by means of the transition state theory.9 Moreover, with the aid of QC methods, the key intermediates and transition states (TSs) of the catalytic reaction can be identified. Once the ligand sphere of the transition metal complex is specified, this process can also be accomplished via automated exploration of the chemical reaction network (CRN).10–16 However, the massive number of possible combinations of the building blocks of the ligands leads to a vast chemical space with varying properties.17 Due to the high computational cost, QC methods become impractical to screen thousands of key intermediates and TSs for the reaction of interest to find an optimized ligand structure.
By virtue of high computational efficiency, machine learning (ML) techniques have emerged as complements to QC methods, and have been successfully applied in drug discovery,18,19 as well as in screening the properties of metal–organic frameworks20 and transition metal complexes.21 ML techniques are also widely applied in the investigation of chemical reactions.22 For instance, Choi et al.23 predicted the activation barriers of reactions from the RMG-py12 database with a mean absolute error (MAE) of 1.95 kcal mol−1. Ye et al.24 predicted the activation barriers of a reductive elimination step of Pd-catalyzed C–N coupling reactions with a MAE of 0.48 kcal mol−1. In addition, the activation barriers in the CRN of formamide, aldol, and unimolecular decomposition of 3-hydroperoxypropanal were accurately predicted using an artificial neural network (ANN) model.25 It is noteworthy that the ML models used in these studies incorporated the thermodynamic properties of the products and reactants as descriptors for the reaction, aligning with the Bell–Evans–Polanyi principle26 and leading to high prediction accuracy. The utilization of QC-free molecular descriptors was also proven to be successful in predicting the activation barriers of glutathione adduct formation27 and dihydrogen activation.28
Despite the successes in predicting the activation energy of elementary reactions, the prediction of energy differences between the reactant and the intermediates in the entire catalytic cycle, which is important for multistep catalytic reactions, is uncommon in literature. The challenge remains in effectively modeling the reaction energy ΔE, namely, the energy difference between the reactant and the intermediate within the same elementary reaction. This challenge may stem from the large number of conformers of both reactants, intermediates, and products, making it difficult to pair the proper reactant-product or reactant–intermediate pairs. Consequently, the improper pairing can lead to inaccuracies in the training data that are fed into the ML models.
The present study aims to predict the energy difference, denoted as ΔE, between the 6-coordinated metal alkyl-hydride (Rh(PLP)(Cl)(CO)(H)(alkyl)) and the 4-coordinated precursor (Rh(PLP)(Cl)(CO)) featuring different bidentate phosphine ligands PLP. According to the theoretical and experimental mechanistic studies,29–31 the Rh complex undergoes a series of transformations including CO dissociation, C–H activation, CO recombination, C–C coupling and reductive elimination, where C–H activation is identified to be the one of the rate-limiting steps. According to the Bell–Evans–Polanyi principle, the activation energy ΔE‡ is highly correlated to the reaction energy. A complex with low ΔE for the C–H activation usually features a low ΔE‡ of this step, which benefits the entire catalytic cycle. In addition, the 6-coordinated intermediate is one of the relatively stable intermediates after the C–H activation and CO recombination, which can proceed with a subsequent C–C formation step in the carbonylation process. In this regard, lowering the ΔE could also increase the equilibrium concentration of the 6-coordinated intermediate, accelerating the subsequent C–C coupling reaction. Therefore, to minimize ΔE of the C–H activation by varying the ligand structure of the complexes is the primary objective for designing a complex with high catalytic activity. In this context, an efficient screening scheme of ΔE between the 4-coordinated reactant and the 6-coordinated intermediate is of great importance.
We demonstrate in the present study that the Δ-ML approach,32 which has been successfully applied in predicting the activation barriers and reaction enthalpies of the “breaking two bonds, forming two bonds” type reactions,33 is a possible way for the reaction energy prediction. By training on diverse sets of descriptors, the Δ-ML models can obtain a well-balanced performance between the efficiency and the accuracy of the prediction. We demonstrate that this screening approach allows us to identify ten new bisphosphine ligands, which correspond to ten reactant–intermediate pairs with an average ΔE remarkably lower than the average ΔE of the original data set. Thus, we are able to identify ten new promising Rh-bisphosphine catalysts for C–H activation.
2. Methodology
2.1. The Δ-ML approach for prediction of driving force
The primary objective of the original Δbt-model32 was to predict the target (t) value based on a baseline (b) value as a reference, accompanied by a correction obtained through an ML approach. More specifically, to predict the molecular property Pt(Rt) at the geometry Rt, which is determined at an advanced level of theory, the model primarily relies upon a related molecular property![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) b(Rb), calculated at a low level of theory with the geometry Rb, as the main constituent of the approximation. Furthermore, the correction is performed utilizing an ML-optimized function FML(σ(Rb)) that depends on the molecular descriptors σ(Rb) evaluated at the geometry Rb. Therefore, the molecular property Pt(Rt) acquired at the target level of theory can be approximated as32
b(Rb), calculated at a low level of theory with the geometry Rb, as the main constituent of the approximation. Furthermore, the correction is performed utilizing an ML-optimized function FML(σ(Rb)) that depends on the molecular descriptors σ(Rb) evaluated at the geometry Rb. Therefore, the molecular property Pt(Rt) acquired at the target level of theory can be approximated as32ΔPt(Rt) ≈ Δbt(Rb) = ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) b(Rb) + FML(σ(Rb)). b(Rb) + FML(σ(Rb)). | (1) |
In our study, we have employed this Δ-ML methodology to investigate reaction energies associated with the C–H activation process mediated by Rh complexes. In this context, the properties obtained at the DFT level serve as the target values to be predicted while those obtained at the computationally much more efficient semi-empirical GFN2-xTB34 level of theory (further denoted as xTB throughout this study) are used as the baseline values.
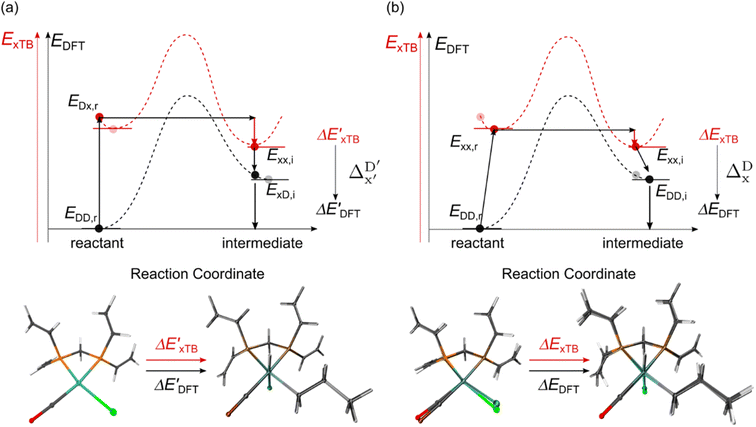
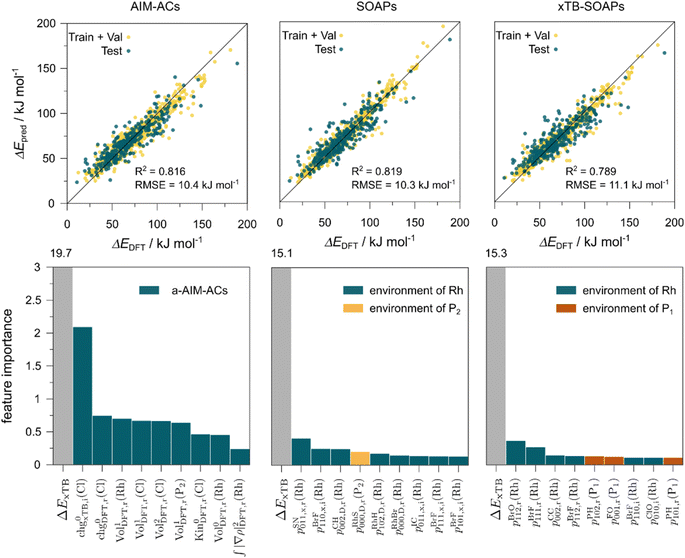
Firstly, to account for the errors that are solely introduced by the different levels of theory, namely DFT vs. xTB, we examine the upper bound of the reaction driving force, denoted as 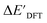 (see Fig. 1a). We denote the corresponding Δbt-model as
(see Fig. 1a). We denote the corresponding Δbt-model as 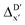 . The prediction task can be formulated as follows,
. The prediction task can be formulated as follows,
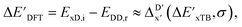 | (2) |
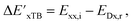 | (3) |
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) b(Rb), as indicated in eqn (1); instead, we incorporate the baseline property as an additional feature for the ML model, as indicated in eqn (2).
b(Rb), as indicated in eqn (1); instead, we incorporate the baseline property as an additional feature for the ML model, as indicated in eqn (2).
Beyond the baseline value 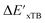 , the feature vector σ of the reactant–intermediate pair is constructed by incorporating the structural information from both reactant and intermediate. In this context, we define σ as σ(RDFT,r,RxTB,i), which helps to account for the difference between
, the feature vector σ of the reactant–intermediate pair is constructed by incorporating the structural information from both reactant and intermediate. In this context, we define σ as σ(RDFT,r,RxTB,i), which helps to account for the difference between 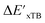 and
and 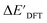 . Referring to Fig. 1a, RDFT,r and RxTB,i represent the geometries of the DFT-equilibrium reactant and xTB-equilibrium intermediate, respectively. Topological-based descriptors, such as autocorrelation functions (ACs)35,36 or position-based descriptors, such as smooth overlap atomic positions (SOAPs),37,38 can be used to construct the feature vector σ. If electronic information is also taken into consideration, the feature vector can be further expanded as σ = σ(RDFT,r, RxTB,i, ρDFT,r, ρxTB,r, ρxTB,i), where ρ depends on the electron density information obtained at different level of theories (see AIM-AC in Section 2.2 for details).
. Referring to Fig. 1a, RDFT,r and RxTB,i represent the geometries of the DFT-equilibrium reactant and xTB-equilibrium intermediate, respectively. Topological-based descriptors, such as autocorrelation functions (ACs)35,36 or position-based descriptors, such as smooth overlap atomic positions (SOAPs),37,38 can be used to construct the feature vector σ. If electronic information is also taken into consideration, the feature vector can be further expanded as σ = σ(RDFT,r, RxTB,i, ρDFT,r, ρxTB,r, ρxTB,i), where ρ depends on the electron density information obtained at different level of theories (see AIM-AC in Section 2.2 for details).
Secondly, another Δbt-model, denoted as ΔDx-model, is trained to predict the reaction energy ΔEDFT (see Fig. 1b)
| ΔEDFT = EDD,i − EDD,r ≈ ΔDx(ΔExTB, σ), | (4) |
| ΔExTB = Exx,i − Exx,r. | (5) |
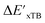 .
.
2.2. Features used in the description of reactant–intermediate pairs of Rh complexes
 | (6) |
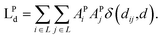 | (7) |
Furthermore, ACs can be evaluated on a specified atom i, which helps to describe the atomic environment. This is defined as the atom-specific ACs (a-ACs):
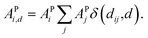 | (8) |
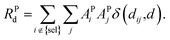 | (9) |
The illustrations of standard ACs, rest-ACs, l-ACs and a-ACs are shown in Fig. S1.† To offer a detailed description that focuses on the local reaction site, the a-ACs of selected atoms (Rh, P1, P2, Cl, R11, R12, R21, R22, L1, L2) were employed to construct the feature vector for the reactant, while a broader set of atoms (Rh, P1, P2, Cl, R11, R12, R21, R22, L1, L2, H, C) was used for the intermediate (see Fig. S3† for details). The chemical environment of the reaction site, i.e., Rh and Cl ions in our study, is expected to undergo significant changes before and after reacting with the C–H bond. Therefore, including the a-ACs of these specified atoms, which emphasizes the description of the atomic environment, is deemed beneficial for characterizing the reactant–intermediate pairs and the associated reaction energy. In addition, we also incorporated the global information of the Rh complex, by including the rest-ACs and l-ACs. All ACs are solely dependent on the graph structures of the complex, therefore the feature vectors in both 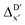 - and ΔDx-models take the form of σ(Rr,Ri).
- and ΔDx-models take the form of σ(Rr,Ri).
In the framework of AIM theory,40,41 the nuclei in a molecule are naturally separated in atomic basins Ω, the boundary of which is defined by a zero-flux surface in the gradient vector field of the electron density. The partitioning of the molecular space into atomic basins enables the assignment of the molecular properties to individual atoms. Details of the atomic properties used in this study are listed in Table S1 and explained in the ESI.† The AIM analysis, as implemented in Multiwfn (3.8),42 can be applied to both, the DFT and xTB calculations. Consequently, including the AIM-ACs of the reactant calculated at DFT level of theory provides additional information for describing the reaction energy. In this context, both feature vectors for 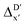 - and ΔDx-models not only depend on geometries RDFT,r, RxTB,i and RxTB,r, but also on the electron information ρDFT,r, ρxTB,r and ρxTB,i.
- and ΔDx-models not only depend on geometries RDFT,r, RxTB,i and RxTB,r, but also on the electron information ρDFT,r, ρxTB,r and ρxTB,i.
Given SOAPs' ability to capture the 3D structure of the molecules, SOAPs evaluated on the xTB-equilibrium reactant are included to account for the energy difference caused by the change in geometry, when predicting the reaction energy ΔEDFT (recall Fig. 1b). Consequently, the feature depends on RDFT,r, RxTB,r and RxTB,i in the ΔDx-model, whereas in the 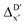 -model, the feature vector of the reactant–intermediate pair depends only on RDFT,r and RxTB,i, given that RDFT,r and RxTB,r are equivalent.
-model, the feature vector of the reactant–intermediate pair depends only on RDFT,r and RxTB,i, given that RDFT,r and RxTB,r are equivalent.
2.3. Computational exploration of reaction energies
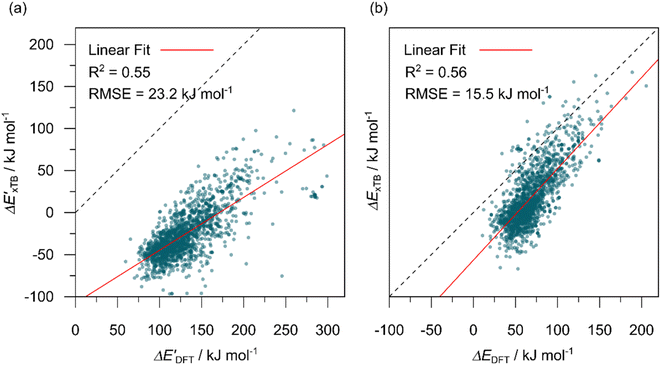
The computational protocol used in this work is illustrated in Fig. 2.The geometry guesses required to optimize the reactant and intermediate states were generated using a combination of RDKit (2022.03)45 and OpenBabel (3.0).46 We initiated the construction of reactants and intermediates geometries from an octahedral Rh(PLP)(Cl)4 prototype, where the linkers L, as well as the residual groups R1 and R2 were selected from a comprehensive set of 19 different linkers and 62 residual groups (see Fig. S5†). To address potential conformational variations, conformer searches using CREST47 were performed within a subset of prototypes. In addition to the conformer with the lowest energy, several other minima on the xTB potential energy (hyper)surface (PES) were identified in the conformer search processes. Each of these minima represented different prototypic molecules, and would subsequently serve as individual data points for ML analysis.
After the prototypes were optimized at GFN2-xTB (6.6.1)34 level of theory, the initial guesses of 4-coordinated reactants Rh(PLP)(Cl)(CO) were achieved by removing the excess chloride ions in the axial positions. Furthermore, one additional chloride ion in the equatorial plane is replaced by CO. Additionally, the initial geometries of 6-coordinated intermediates Rh(PLP)(Cl)(CO)(H)(propyl) were generated by substituting one chloride ion in the axial position with H, and two equatorial chloride ions with a propyl group and a CO, respectively.
Calculations at density functional of theory (DFT), as well as at xTB level of theory, were carried out sequentially for every system, to obtain the target values ΔEDFT and 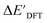 , as well as the baseline values ΔExTB and
, as well as the baseline values ΔExTB and 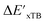 for our ML objectives.
for our ML objectives.
Firstly, xTB optimizations were performed on the initial guesses of reactants and intermediates, yielding the xTB single point energies Exx,r and Exx,i. Subsequently, both xTB-optimized species were further optimized at the level of DFT, yielding the single-point DFT energies EDD,r and EDD,i, respectively.
The DFT calculations, employing the range-separated ωB97XD functional48 and the def2-SVP basis set, along with the respective effective core potential,49 were carried out in the Gaussian 16 software package.50 A vibrational analysis was carried out for DFT-equilibrium structures to verify that a minimum was obtained on the PES. Furthermore, the DFT single-point energies ExD,i, were obtained by performing a calculation for each xTB-optimized intermediate while the xTB single-point energies EDx,r, were obtained for each DFT-optimized intermediate. Recall that ExD,i is used to calculate the target upper bound of reaction energy 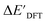 (eqn (2)), and EDx,r is used to calculate the corresponding baseline value
(eqn (2)), and EDx,r is used to calculate the corresponding baseline value 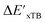 (eqn (3)). Structural assessments were performed on reactants and intermediates optimized at both DFT and xTB levels of theory, to validate that the coordination numbers of Rh ion are 4 and 6 in reactant and intermediate states, respectively. In addition, the phosphine ligands of both reactant and intermediate states of the molecules are ensured to be in cis-position.
(eqn (3)). Structural assessments were performed on reactants and intermediates optimized at both DFT and xTB levels of theory, to validate that the coordination numbers of Rh ion are 4 and 6 in reactant and intermediate states, respectively. In addition, the phosphine ligands of both reactant and intermediate states of the molecules are ensured to be in cis-position.
2.4. Machine learning models trained on the ACs, AIM-ACs and SOAPs
After examining the structure of the reactants and intermediates, three sets of feature vectors based on ACs, AIM-ACs, and SOAPs of complexes were calculated for the Δ-ML study. To decrease the training time and complexity51 for the non-linear model, a feature selection based on an extra-trees regressor,52 as implemented in scikit-learn,53 was performed to reduce the dimension of the feature vectors. In this selection method, the extra-tree models were trained to predict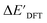 and ΔEDFT merely with the ACs, AIM-ACs or SOAPs features, i.e., in the absence of the
and ΔEDFT merely with the ACs, AIM-ACs or SOAPs features, i.e., in the absence of the 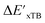 and ΔExTB, respectively. The features with importance lower than 0.0003 were considered unimportant and discarded, and by this filtering, the dimensionality of the feature vectors was considerably decreased. The dimensionalities of the various feature sets before and after reduction are summarized in Table S2.†
and ΔExTB, respectively. The features with importance lower than 0.0003 were considered unimportant and discarded, and by this filtering, the dimensionality of the feature vectors was considerably decreased. The dimensionalities of the various feature sets before and after reduction are summarized in Table S2.†
The artificial neural network (ANN) implemented within the NeuralFastAI54 framework, was employed to train the two types of Δ-ML models on the features after dimensionality reduction. The ANN models utilize the rectified linear functions (ReLU) to capture potential nonlinear relationships between the features on the target values. For optimization, the Adam optimizer,55 a method for efficient stochastic optimization, was employed to fit the parameters of the model. Hyperparameters, including the network architectures, embedding layers dropout rate, linear layers dropout rate, and number of epochs were optimized efficiently using the Bayesian optimization56,57 in an automated fashion, as implemented in the AutoGluon package (1.0).58 Other classical ML models, such as XGBoost59 and CatBoost,60 are also available in the AutoGluon package and can be implemented conveniently in an automated fashion as well.
Furthermore, the permutation importance61,62 of the features was assessed on the best-performing model, in order to gain insights into the relationships between the descriptors and the deviation of the baseline values from the target values.
3. Results and discussion
3.1. Predictions on the upper bound of reaction energy 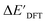
In this study, 1743 reactant–intermediate pairs were successfully optimized, and the corresponding target values 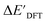 and ΔEDFT were obtained. Fig. 3a provides a visual representation of the disparity between the baseline model and the target model, where the baseline values
and ΔEDFT were obtained. Fig. 3a provides a visual representation of the disparity between the baseline model and the target model, where the baseline values 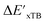 range from −96.6 to 121.4 kJ mol−1 while the target values
range from −96.6 to 121.4 kJ mol−1 while the target values 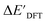 range from 59.7 to 298.9 kJ mol−1. Directly applying linear regression to the baseline values for predicting the target values yields significant errors, with a root mean squared error (RMSE) of 23.2 kJ mol−1 and a coefficient of determination (R2) of only 0.55. This deviation of baseline and target values is exclusively introduced by the disparities stemming from the choice of different calculation levels.
range from 59.7 to 298.9 kJ mol−1. Directly applying linear regression to the baseline values for predicting the target values yields significant errors, with a root mean squared error (RMSE) of 23.2 kJ mol−1 and a coefficient of determination (R2) of only 0.55. This deviation of baseline and target values is exclusively introduced by the disparities stemming from the choice of different calculation levels.
To account for the difference arising from the different calculation levels, 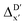 -models were trained using AIM-ACs and ACs of varying depths as molecular descriptors. The dataset of 1743 reactant–intermediate pairs were split into training, validation and test sets with a ratio of 64
-models were trained using AIM-ACs and ACs of varying depths as molecular descriptors. The dataset of 1743 reactant–intermediate pairs were split into training, validation and test sets with a ratio of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 in two steps: first, 20% of the total data were randomly selected to form the test set for all models in our study. The remaining data were randomly split into training and validation set with a ratio of 8
20 in two steps: first, 20% of the total data were randomly selected to form the test set for all models in our study. The remaining data were randomly split into training and validation set with a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (64% and 16% of all data, respectively) during the automated training procedure as implemented in the Autogluon package.58 The performance of the
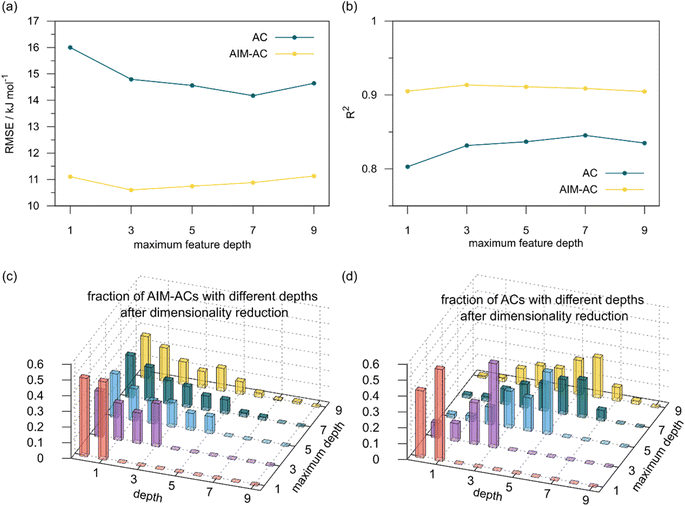
2 (64% and 16% of all data, respectively) during the automated training procedure as implemented in the Autogluon package.58 The performance of the 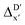 -models is depicted in Fig. 4. Having comprised the electron information computed at both DFT and xTB levels of theory, all models trained on AIM-ACs with varying maximum depths dmax exhibited notably good performance, with a RMSE of approximately 11.0 kJ mol−1 and a R2 exceeding 0.90. When increasing the maximum feature depth from 1 to 3, the RMSE decreased from 11.1 kJ mol−1 to 10.6 kJ mol−1, and the R2 increased from 0.905 to 0.913. The optimal performing model, achieved with dmax = 3, had 4 hidden layers with 1042, 367, 150, 121 neurons, respectively, along with an embedding layer dropout rate of 0.651, linear layer dropout rate of 0.002 and 24 epochs. The hyperparameter sets and other detailed results of the optimal models trained on different dmax are summarized in Table S2.† Besides the ANN models, the identical training set was also fed to other models, such as XGBoost59 and CatBoost.60 The results for these models are summarized in Table S3.† The performance of the ANN model is slightly better than these classical ML models. Therefore, we mainly focus on the discussion of the performance of ANN models throughout this study. Further increasing the maximum feature depth did not improve the performance of the
-models is depicted in Fig. 4. Having comprised the electron information computed at both DFT and xTB levels of theory, all models trained on AIM-ACs with varying maximum depths dmax exhibited notably good performance, with a RMSE of approximately 11.0 kJ mol−1 and a R2 exceeding 0.90. When increasing the maximum feature depth from 1 to 3, the RMSE decreased from 11.1 kJ mol−1 to 10.6 kJ mol−1, and the R2 increased from 0.905 to 0.913. The optimal performing model, achieved with dmax = 3, had 4 hidden layers with 1042, 367, 150, 121 neurons, respectively, along with an embedding layer dropout rate of 0.651, linear layer dropout rate of 0.002 and 24 epochs. The hyperparameter sets and other detailed results of the optimal models trained on different dmax are summarized in Table S2.† Besides the ANN models, the identical training set was also fed to other models, such as XGBoost59 and CatBoost.60 The results for these models are summarized in Table S3.† The performance of the ANN model is slightly better than these classical ML models. Therefore, we mainly focus on the discussion of the performance of ANN models throughout this study. Further increasing the maximum feature depth did not improve the performance of the 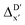 -models. This suggests that the discrepancy between
-models. This suggests that the discrepancy between 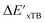 and
and 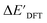 can be attributed to the difference in description of electron information in the short range (d = 0, 1, 2, 3). Fig. 4c provides insight into the fraction of AIM-ACs with different dmax after dimensionality reduction. As dmax increased from 3 to 9, the fraction of AIM-ACs of d = 0, 1, 2, 3 remained consistently over 0.72. This observation supports the conclusion that including AIM-AC features with larger dmax (dmax > 3) does not provide additional information for addressing the difference between
can be attributed to the difference in description of electron information in the short range (d = 0, 1, 2, 3). Fig. 4c provides insight into the fraction of AIM-ACs with different dmax after dimensionality reduction. As dmax increased from 3 to 9, the fraction of AIM-ACs of d = 0, 1, 2, 3 remained consistently over 0.72. This observation supports the conclusion that including AIM-AC features with larger dmax (dmax > 3) does not provide additional information for addressing the difference between 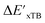 and
and 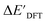 .
.
Although 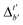 -models trained on AIM-ACs have exhibited excellent performance, it is important to note that the calculations for AIM-based atomic properties are computationally demanding, rendering AIM-ACs less practical in accelerating high-throughput screening for the desired catalysts. In contrast, the original ACs based on the isolated atomic properties demand significantly lower computational costs.
-models trained on AIM-ACs have exhibited excellent performance, it is important to note that the calculations for AIM-based atomic properties are computationally demanding, rendering AIM-ACs less practical in accelerating high-throughput screening for the desired catalysts. In contrast, the original ACs based on the isolated atomic properties demand significantly lower computational costs.
In our study, a substantial number of isolated atomic properties derived from DFT calculations with a ωB97XD functional48 and the parameters used in xTB calculations were used to construct the ACs (see ESI†). However, in comparison to AIM-ACs, the 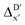 -models trained on ACs generally had poorer performance in predicting the
-models trained on ACs generally had poorer performance in predicting the 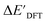 . The best performing model was obtained at dmax = 7, with a RMSE of 14.2 kJ mol−1 and a R2 of 0.845. Fig. 4d illustrates the importance of including the atomic properties with larger dmax. As dmax increased from 1 to 7, the peak of the fraction also moves towards a higher d values, with d = 5 and d = 6 contributing the largest fraction (0.23 and 0.24, respectively) to the entire feature vector. On the contrary, ACs of d = 0 and d = 1 were less important and discarded via the dimensionality reduction procedure as dmax increased.
. The best performing model was obtained at dmax = 7, with a RMSE of 14.2 kJ mol−1 and a R2 of 0.845. Fig. 4d illustrates the importance of including the atomic properties with larger dmax. As dmax increased from 1 to 7, the peak of the fraction also moves towards a higher d values, with d = 5 and d = 6 contributing the largest fraction (0.23 and 0.24, respectively) to the entire feature vector. On the contrary, ACs of d = 0 and d = 1 were less important and discarded via the dimensionality reduction procedure as dmax increased.
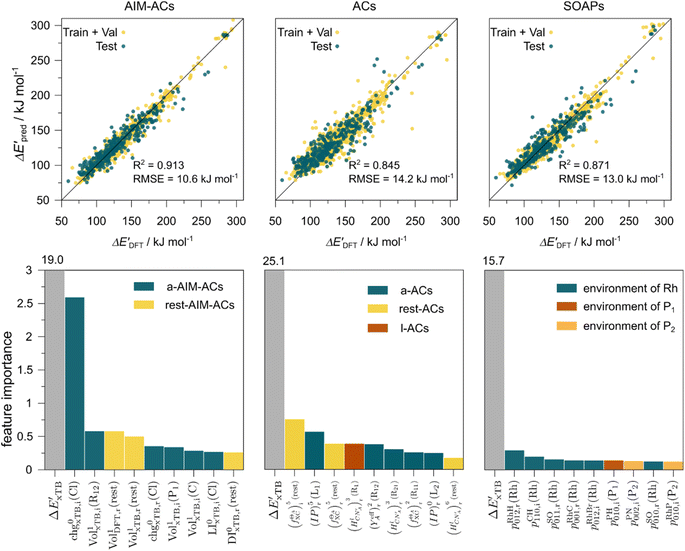
The details of the best performing models trained on AIM-ACs (dmax = 3) and ACs (dmax = 7), along with the corresponding feature importance analysis, are presented in Fig. 5. Regarding the model trained on AIM-ACs with dmax = 3, data points in the test and training sets were distributed evenly around the y = x line in the parity plot. Compared to the prediction performance using the pure baseline value 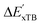 (as shown in Fig. 3a), this
(as shown in Fig. 3a), this 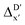 -model displays a notable enhancement, with the RMSE decreasing from 23.2 to 10.6 kJ mol−1. Feature importance analysis indicates that the a-AIM-ACs contributed the most to the improvement, among a total of 364 features. On the contrary, the l-AIM-ACs, which are designed to describe the ligands, play less crucial roles in improving the model. Although this optimal model was trained on the AIM-ACs with dmax = 3, features of d = 0 and 1 exhibited the strongest predictive power, with AIM-ACs of d = 2, 3 contributing only minor corrections to the model.
-model displays a notable enhancement, with the RMSE decreasing from 23.2 to 10.6 kJ mol−1. Feature importance analysis indicates that the a-AIM-ACs contributed the most to the improvement, among a total of 364 features. On the contrary, the l-AIM-ACs, which are designed to describe the ligands, play less crucial roles in improving the model. Although this optimal model was trained on the AIM-ACs with dmax = 3, features of d = 0 and 1 exhibited the strongest predictive power, with AIM-ACs of d = 2, 3 contributing only minor corrections to the model.
Compared to AIM-ACs, 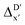 -model trained on ACs exhibited lower accuracy, and notable deviating points were observed in both test and training sets. This disparity could be attributed to the inherent inflexibility of ACs compared to AIM-ACs, as the distribution of ACs in
-model trained on ACs exhibited lower accuracy, and notable deviating points were observed in both test and training sets. This disparity could be attributed to the inherent inflexibility of ACs compared to AIM-ACs, as the distribution of ACs in 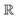 is much sparser than that of AIM-ACs. Nevertheless, when compared to the pure baseline model, the performance of the
is much sparser than that of AIM-ACs. Nevertheless, when compared to the pure baseline model, the performance of the 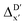 -model trained on ACs has substantially improved at a considerably lower cost. In contrast to the model trained on AIM-ACs, the ACs of d = 0 or d = 1 barely provided distinctive information for different complexes. Consequently, ACs of greater depth (d = 2 ∼ 6) have higher predictive power in addition to the baseline value
-model trained on ACs has substantially improved at a considerably lower cost. In contrast to the model trained on AIM-ACs, the ACs of d = 0 or d = 1 barely provided distinctive information for different complexes. Consequently, ACs of greater depth (d = 2 ∼ 6) have higher predictive power in addition to the baseline value 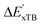 . It is noteworthy that the features with high importance are dependent on the xTB parameters, particularly the anisotropic XC scaling parameter fXCθA, which is parametrized to describes the quadrupole expansion of the electron density of a specific element and account for the anisotropic exchange-correlation effect.34
. It is noteworthy that the features with high importance are dependent on the xTB parameters, particularly the anisotropic XC scaling parameter fXCθA, which is parametrized to describes the quadrupole expansion of the electron density of a specific element and account for the anisotropic exchange-correlation effect.34
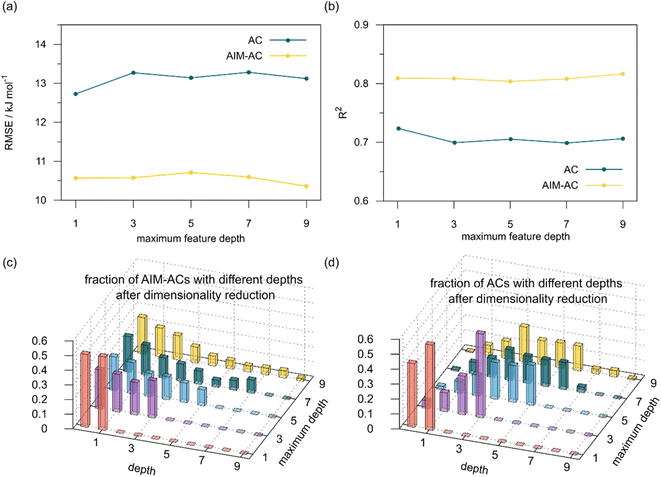
In addition to the topology-based features such as AIM-ACs and ACs, the 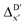 -model was also trained on the position-based feature set, such as SOAPs, which can be computed very efficiently in the describe43,44 package. Compared to the model trained on ACs, the model trained on SOAPs exhibited superior prediction performance, with a RMSE of 13.0 kJ mol−1 and a R2 of 0.871. The optimal set of hyperparameters is summarized in Table S2.† In contrast to the model trained on AIM-ACs features, where the xTB charge of the Cl ion in the intermediate (chg0xTB(Cl)) emerged as the most important feature, the atomic environments around Rh (p(Rh)) played the most significant role among a total of 463 features, in enhancing the predictive performance of the model trained on SOAPs.
-model was also trained on the position-based feature set, such as SOAPs, which can be computed very efficiently in the describe43,44 package. Compared to the model trained on ACs, the model trained on SOAPs exhibited superior prediction performance, with a RMSE of 13.0 kJ mol−1 and a R2 of 0.871. The optimal set of hyperparameters is summarized in Table S2.† In contrast to the model trained on AIM-ACs features, where the xTB charge of the Cl ion in the intermediate (chg0xTB(Cl)) emerged as the most important feature, the atomic environments around Rh (p(Rh)) played the most significant role among a total of 463 features, in enhancing the predictive performance of the model trained on SOAPs.
In summary, the 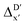 -models trained on AIM-ACs exhibit strong predictive performance. However, it is important to note that the calculation of the AIM properties demands high computational power (roughly equivalent to a single point calculation), due to the heavy numerical integration of the electron density. Nevertheless, by comprising the electron information into the feature sets, these models point out that the charge in the Cl basin calculated at the xTB level of theory (chg0xTB(Cl)) is the most relevant feature accounting for the difference between
-models trained on AIM-ACs exhibit strong predictive performance. However, it is important to note that the calculation of the AIM properties demands high computational power (roughly equivalent to a single point calculation), due to the heavy numerical integration of the electron density. Nevertheless, by comprising the electron information into the feature sets, these models point out that the charge in the Cl basin calculated at the xTB level of theory (chg0xTB(Cl)) is the most relevant feature accounting for the difference between 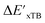 and
and 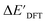 . Alternatively, ACs and SOAPs provide a much faster route to predict
. Alternatively, ACs and SOAPs provide a much faster route to predict 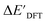 with relatively high accuracies. In the case of ACs, features with higher d value have stronger predictive power while in the case of SOAPs, the atomic environments of Rh play significant roles in enhancing the performance of the model.
with relatively high accuracies. In the case of ACs, features with higher d value have stronger predictive power while in the case of SOAPs, the atomic environments of Rh play significant roles in enhancing the performance of the model.
3.2. Predictions on the reaction energy ΔEDFT
The Δ-ML strategy has been further adapted to predict the reaction energy ΔEDFT, which plays a significant role in determining the relative concentration of the intermediate and reactant in equilibrium. Therefore, finding a suitable ligand architecture that can reduce the reaction energy ΔEDFT would be advantageous for facilitating the C–H activation and subsequent functionalization. Fig. 3b illustrates the difference between the baseline values ΔExTB and the target values ΔEDFT, where the values span from of −66.8 to 167.0 kJ mol−1, and from 10.8 to 205.5 kJ mol−1, respectively. The results of ΔDx-models trained on AIM-ACs and ACs with different dmax values are presented in Fig. 6. The best performing models were achieved when trained on dmax = 9 and dmax = 1, with RMSEs of 10.4 and 12.5 kJ mol−1, respectively. However, compared to corresponding the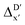 -models, ΔDx-models exhibited lower R2 values, which suggests that the features have a limitation in predicting the difference between ΔEDFT and ΔExTB. This arises from two aspects, the different levels of theory and the changes in geometries. In addition to the information provided by AIM-ACs of d = 0, 1, 2, 3, which mainly accounts for the difference in calculation levels (as discussed in Section 3.1), including the information of greater depths can further enhance the performance of the model. The proportion of AIM-ACs of d = 7, 8, 9 is also comparably larger in this model than in the
-models, ΔDx-models exhibited lower R2 values, which suggests that the features have a limitation in predicting the difference between ΔEDFT and ΔExTB. This arises from two aspects, the different levels of theory and the changes in geometries. In addition to the information provided by AIM-ACs of d = 0, 1, 2, 3, which mainly accounts for the difference in calculation levels (as discussed in Section 3.1), including the information of greater depths can further enhance the performance of the model. The proportion of AIM-ACs of d = 7, 8, 9 is also comparably larger in this model than in the 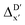 -model, with a fraction of 0.11 vs. 0.02, respectively (refer to Fig. 6cvs.Fig. 4c). The presence of non-zero AIM-AC features of greater depth (d = 7, 8, 9) typically suggests that the complex possesses a large and bulky ligand, which may introduce more significant deviation between the xTB- and DFT-equilibrium structures. Therefore, including the AIM-ACs of greater depths can potentially account for the difference due to the change in geometries.
-model, with a fraction of 0.11 vs. 0.02, respectively (refer to Fig. 6cvs.Fig. 4c). The presence of non-zero AIM-AC features of greater depth (d = 7, 8, 9) typically suggests that the complex possesses a large and bulky ligand, which may introduce more significant deviation between the xTB- and DFT-equilibrium structures. Therefore, including the AIM-ACs of greater depths can potentially account for the difference due to the change in geometries.
The ΔDx-models trained on ACs generally exhibit lower accuracies than the models trained on AIM-ACs. Unexpectedly, the best performing model was obtained at dmax = 1, with a RMSE of 12.7 kJ mol−1 and a R2 of 0.723. Fig. 6d illustrates that the fraction of ACs of d = 0, 1 dropped drastically as dmax increases. However, in contrast to the 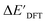 prediction, including the AC features with d > 1 does not improve the accuracy of the model.
prediction, including the AC features with d > 1 does not improve the accuracy of the model.
Details and the feature importance analysis of the ΔDx-model trained on AIM-ACs with dmax = 9 are shown in Fig. 7. Data points in the test and training sets were distributed uniformly around the y = x line in the parity plot, with only a few notably deviating points present in the high energy region where ΔEDFT exceeds 100 kJ mol−1. The corresponding feature importance analysis reveals that a-AIM-ACs are the most significant contributors to the high predictive performance of the model. Among these features, the electron information around Cl and Rh ions are of the highest significance among a total of 507 features, particularly the AIM-charge of Cl in the intermediate calculated at xTB level of theory (chg0xTB,i(Cl)). As discussed in Section 3.1, this feature primarily accounts for the difference arising from the different calculation levels of theory. In contrast to the 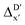 -model, where electronic information from xTB calculations plays a more prominent role, DFT information from the reactant is more important in this model, in addition to the already known importance of chg0xTB,i(Cl). Note that the changes in geometries in both reactants and intermediates can introduce errors independently to the prediction in the energy difference. The structural change of the reactants can be captured by the AIM analysis on the DFT-equilibrium structure and xTB-equilibrium structure of the reactant, namely, on RDFT,r and RxTB,r, respectively. However, the change in geometries of the intermediates remains hard to describe solely through the AIM analysis of RxTB,i. Therefore, higher importance of the AIM-ACs which depend on the DFT calculations is observed. On the contrary, it is less practical to discuss the results for ΔDx-models trained on ACs due to their low prediction accuracy. Nevertheless, the parity plot and the corresponding feature importance ranking are shown in Fig. S6.†
-model, where electronic information from xTB calculations plays a more prominent role, DFT information from the reactant is more important in this model, in addition to the already known importance of chg0xTB,i(Cl). Note that the changes in geometries in both reactants and intermediates can introduce errors independently to the prediction in the energy difference. The structural change of the reactants can be captured by the AIM analysis on the DFT-equilibrium structure and xTB-equilibrium structure of the reactant, namely, on RDFT,r and RxTB,r, respectively. However, the change in geometries of the intermediates remains hard to describe solely through the AIM analysis of RxTB,i. Therefore, higher importance of the AIM-ACs which depend on the DFT calculations is observed. On the contrary, it is less practical to discuss the results for ΔDx-models trained on ACs due to their low prediction accuracy. Nevertheless, the parity plot and the corresponding feature importance ranking are shown in Fig. S6.†
Furthermore, the ΔDx-model was trained using SOAPs that depend on the structure of reactants optimized at both xTB and DFT levels of theory, as well as the structure of the intermediate optimized at the xTB level of theory. It is noteworthy that SOAPs can be calculated much more efficiently compared to AIM-ACs, and the performance of the model trained on these features even slightly exceeds that of the model trained on AIM-ACs, with a RMSE of 10.3 kJ mol−1 and a R2 of 0.819. Given that SOAPs are less accurate in predicting the difference in different levels of theory than the AIM-ACs, as demonstrated in the comparative study on the 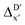 -models, this result suggests that SOAPs may have stronger predictive power regarding the change in geometries. Among all the SOAP features, the atomic environment of the Rh ions in DFT-equilibrium structures of the reactants and in xTB-equilibrium structures of the intermediates is the most significant factor for the accuracy of this ΔDx-model.
-models, this result suggests that SOAPs may have stronger predictive power regarding the change in geometries. Among all the SOAP features, the atomic environment of the Rh ions in DFT-equilibrium structures of the reactants and in xTB-equilibrium structures of the intermediates is the most significant factor for the accuracy of this ΔDx-model.
The SOAPs can be further simplified by excluding the information of the DFT structure, although it plays an important role according to the results of the feature ranking. In this manner, the energy difference of the reaction obtained at the DFT level of theory ΔEDFT can be predicted exclusively using the information from xTB calculations, which eliminates the need for computationally expensive structural optimizations at the DFT level of theory. This simplified feature set is denoted as xTB-SOAPs. The DFT calculation for a molecule containing 72 atoms typically requires more than two days of CPU time, while a xTB optimization for the same molecule requires less than one minute on the same machine. In addition, the generation of the SOAP features requires less than one second. In general, xTB-SOAPs can be generated very efficiently. Note that xTB-SOAPs only gain efficiency in predicting ΔEDFT but not 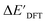 . This is due to the fact that xTB-SOAPs and SOAPs are identical for the prediction of
. This is due to the fact that xTB-SOAPs and SOAPs are identical for the prediction of 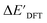 , since the energies of the complexes at xTB and DFT levels were evaluated for identical geometries. As expected, the performance of the ΔDx-model slightly deteriorated after excluding the information from DFT-equilibrium structures, with the RMSE increasing to 11.1 kJ mol−1, and the R2 reducing to 0.789. However, compared to the prediction from pure baseline values ΔExTB, this is already a considerable improvement with only a minor increase in computational cost. Although this result is less accurate than the predictive study of activation energies of different types of elementary reactions,23,24,28 where the errors range from 2.0 to 8.1 kJ mol−1, our study allows the prediction of energy differences between the reactant and intermediate. The structural difference between the reactant and the intermediate is greater than the difference between the reactant and the TS, because they are further apart on the 3N-6 potential energy surface. This could be the reason for the difficulties in predicting the reaction energy.
, since the energies of the complexes at xTB and DFT levels were evaluated for identical geometries. As expected, the performance of the ΔDx-model slightly deteriorated after excluding the information from DFT-equilibrium structures, with the RMSE increasing to 11.1 kJ mol−1, and the R2 reducing to 0.789. However, compared to the prediction from pure baseline values ΔExTB, this is already a considerable improvement with only a minor increase in computational cost. Although this result is less accurate than the predictive study of activation energies of different types of elementary reactions,23,24,28 where the errors range from 2.0 to 8.1 kJ mol−1, our study allows the prediction of energy differences between the reactant and intermediate. The structural difference between the reactant and the intermediate is greater than the difference between the reactant and the TS, because they are further apart on the 3N-6 potential energy surface. This could be the reason for the difficulties in predicting the reaction energy.
Without the information of the atomic environments of Rh obtained in the DFT-equilibrium structure, the feature ranking shows an increased importance of the environment around P1 in the reactant, which emphasizes information from the ligands. A large size and high bulkiness of a ligand usually implies a large deviation between DFT-equilibrium and xTB-equilibrium structures. Therefore, the importance of a more detailed description on the ligand structure is heightened, when the direct descriptions on the change in geometries, such as SOAPs evaluated on DFT-equilibrium structure, are absent.
In summary, the ΔDx-model trained on AIM-ACs and SOAPs exhibits good performance in predicting the energy difference ΔEDFT. However, these two feature sets may account for different aspects of the difference between the baseline value and the target value: AIM-ACs are more related to the difference in levels of theory, while SOAPs are more associated to the change in geometry. Furthermore, xTB-SOAPs features are highly recommended for efficient prediction of the energy difference, owing to the low computational costs for xTB optimization and SOAPs calculation.
3.3. High-throughput screening using the ΔDx-model trained on xTB-SOAPs
Utilizing the ΔDx-model trained on xTB-SOAPs, we propose an efficient two-step screening pipeline for exploring the chemical space of Rh complexes featuring bidentate phosphine ligands. First, 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 selected reactant and intermediate pairs undergo xTB optimization without conformer search. The baseline value ΔExTB, as well as the SOAP features were evaluated at the xTB equilibrium structure of reactants and intermediates. After the evaluation of ΔEML using the trained ΔDx-model, 60 pairs with lowest reaction energies are selected for a refined screening step. In a second step, the selected reactant–intermediate pairs undergo conformer search. ΔEML and SOAP features were obtained from the corresponding optimal conformer structures. Detailed information on the procedure is described in the ESI.† Implementing the two-step high-throughput screening procedure onto a vast chemical space with 27
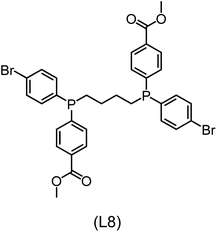
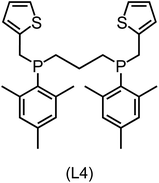
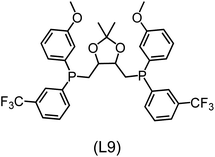
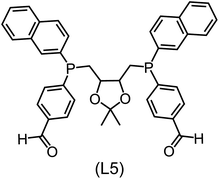
832 selected reactant and intermediate pairs undergo xTB optimization without conformer search. The baseline value ΔExTB, as well as the SOAP features were evaluated at the xTB equilibrium structure of reactants and intermediates. After the evaluation of ΔEML using the trained ΔDx-model, 60 pairs with lowest reaction energies are selected for a refined screening step. In a second step, the selected reactant–intermediate pairs undergo conformer search. ΔEML and SOAP features were obtained from the corresponding optimal conformer structures. Detailed information on the procedure is described in the ESI.† Implementing the two-step high-throughput screening procedure onto a vast chemical space with 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 data points, we identified ten reactant–intermediate pairs of Rh complexes with potentially the lowest ΔEML. These Rh complexes are promising catalysts for the C–H activation process. The Lewis structures of the bidentate phosphine ligands, the predicted energy difference of the reactant–intermediate pairs ΔEML, the baseline value ΔExTB, as well as the target value ΔEDFT as validation, are summarized in Table 1. The related activation energies and isomerization energies of the 6-coordinated intermediates are summarized in Table S5.† The RMSE evaluated on these 10 reactant–intermediate pairs is 10.8 kJ mol−1, where the errors of six of these structures are smaller than 5.0 kJ mol−1. Compared to the averaged reaction energy of the original dataset with 1743 data points (68.0 kJ mol−1), the average reaction energy of the ten newly proposed structures is 34.8 kJ mol−1 lower (33.2 kJ mol−1). In addition, the relationship between the activation energy and reaction energy of the reactant–intermediate pairs is demonstrated in Fig. 8. As expected, the reaction energy (ΔEDFT) and activation energy (ΔE‡DFT) are highly correlated. Compared to the 16 structures in our previous mechanistic study,30 the ten new structures have not only a lower ΔEDFT (33.2 vs. 61.8 kJ mol−1) but also a lower ΔE‡DFT (108.3 vs. 133.6 kJ mol−1). This outcome indicates that the ΔDx-model trained on xTB-SOAPs provides an efficient and reliable way for searching complexes with low reaction energies, which usually possess low activation energy as well. Recalling that the C–H activation is one of the rate-determining steps in an alkane carbonylation reaction as we have shown previously,30 our screening pipeline is effective in designing ligand structures with high catalytic efficacy.
832 data points, we identified ten reactant–intermediate pairs of Rh complexes with potentially the lowest ΔEML. These Rh complexes are promising catalysts for the C–H activation process. The Lewis structures of the bidentate phosphine ligands, the predicted energy difference of the reactant–intermediate pairs ΔEML, the baseline value ΔExTB, as well as the target value ΔEDFT as validation, are summarized in Table 1. The related activation energies and isomerization energies of the 6-coordinated intermediates are summarized in Table S5.† The RMSE evaluated on these 10 reactant–intermediate pairs is 10.8 kJ mol−1, where the errors of six of these structures are smaller than 5.0 kJ mol−1. Compared to the averaged reaction energy of the original dataset with 1743 data points (68.0 kJ mol−1), the average reaction energy of the ten newly proposed structures is 34.8 kJ mol−1 lower (33.2 kJ mol−1). In addition, the relationship between the activation energy and reaction energy of the reactant–intermediate pairs is demonstrated in Fig. 8. As expected, the reaction energy (ΔEDFT) and activation energy (ΔE‡DFT) are highly correlated. Compared to the 16 structures in our previous mechanistic study,30 the ten new structures have not only a lower ΔEDFT (33.2 vs. 61.8 kJ mol−1) but also a lower ΔE‡DFT (108.3 vs. 133.6 kJ mol−1). This outcome indicates that the ΔDx-model trained on xTB-SOAPs provides an efficient and reliable way for searching complexes with low reaction energies, which usually possess low activation energy as well. Recalling that the C–H activation is one of the rate-determining steps in an alkane carbonylation reaction as we have shown previously,30 our screening pipeline is effective in designing ligand structures with high catalytic efficacy.
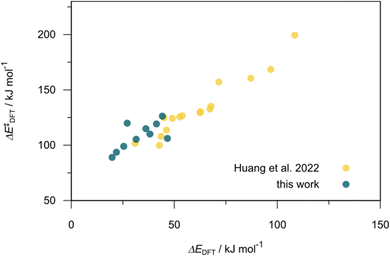 | ||
| Fig. 8 Relationship between the reaction energy (ΔEDFT) and activation energy ΔE‡DFT of C–H activation. Compared to the 16 structures from our previous study,30 the ten newly selected structures possess lower reaction energies as well as lower activation energies. | ||
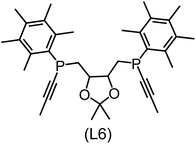
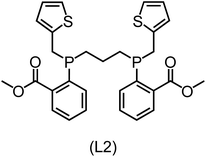
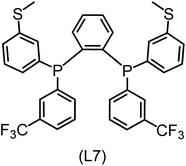
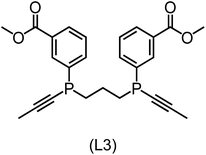
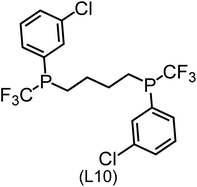
Regarding the structures of the ligands of the ten selected complexes, as can be seen from Table 1, the linker unit connecting the two coordinating phosphorous atoms varies and includes flexible alkyl chains but also more rigid aromatic or 2,3-O-isopropylidene-2,3-dihydroxy-1,4-bisbutyl structures. All structures have in common that the phosphorus atoms bear at least one aromatic substituent. A more in-depth analysis of geometric and electronic parameters based on the DFT-optimized [Rh(PLP)(CO)(Cl)] equilibrium structures reveals that the newly suggested ligand structures have larger buried B5 Sterimol parameters,63 as well as an on average lower dipole moment. In total 20 geometric and electronic descriptors exhibit significant differences between the original and the newly proposed bisphosphine set (see ESI†). Importantly, steric factors describing the accessibility of the Rh center such as the % buried volume64 are included in this descriptor set. The complexes with a lower predicted reaction energy also have a lower % buried volume, pointing to the fact that the Rh center is more accessible for the substrate. Overall, the dependence of the C–H activation reaction energy on the complex structure cannot be explained with a single factor, instead, multiple geometric and electronic parameters influence the C–H activation process. This underlines the complexity when searching for new C–H activation catalysts.
When looking at the synthetic accessibility of the suggest structures it can be concluded that although the ligands look complex at first, the structures can be realistically synthezised as both the linker as well as the substituted phosphine part can be independently synthezised. E.g. the 2,3-O-isopropylidene-2,3-dihydroxy-1,4-bisbutyl linker found in L1, L5, L6 and L9 can be synthezised following the procedure from Kagan and Dang,65 while the unsymmetric phosphines can be synthesized following Singh and Nicholas.66 Thus, the structures suggested in Table 1 can be synthezised and subsequently their performance can be experimentally validated.
4. Conclusion
In this study, an efficient and reliable prediction of the energy difference between the 4-coordinated Rh(PLP)(CO)(Cl) and 6-coordinated Rh(PLP)(CO)(Cl)(H)(propyl) was realized by employing the Δ-ML approach. On the one hand, the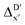 -model trained on autocorrelation functions based on atoms in molecules theory (AIM-ACs) achieved the best performance with a root-mean-squared error (RMSE) of 10.6 kJ mol−1 and a R2 of 0.913. This result underscores the superiority of AIM-ACs over the other two feature sets in accounting for errors due to the difference in the level of theory. On the other hand, the ΔDx-model trained on smooth overlap atomic position (SOAP) features achieved remarkable performance with an RMSE of 10.3 kJ mol−1 and an R2 of 0.819, which suggests that SOAPs have better performance in accounting for errors due to the change in geometry. Notably, the ΔDx-model trained on xTB-SOAPs alone excels not only in efficiently screening the chemical space of Rh complexes featuring bidentate phosphine ligands but also in accurately predicting the reaction energies ΔEDFT. With our approach, we were able to predict ten promising ligand structures that should feature a low C–H reaction energy and therefore, should be able to substantially accelerate the catalytic functionalization of alkanes.
-model trained on autocorrelation functions based on atoms in molecules theory (AIM-ACs) achieved the best performance with a root-mean-squared error (RMSE) of 10.6 kJ mol−1 and a R2 of 0.913. This result underscores the superiority of AIM-ACs over the other two feature sets in accounting for errors due to the difference in the level of theory. On the other hand, the ΔDx-model trained on smooth overlap atomic position (SOAP) features achieved remarkable performance with an RMSE of 10.3 kJ mol−1 and an R2 of 0.819, which suggests that SOAPs have better performance in accounting for errors due to the change in geometry. Notably, the ΔDx-model trained on xTB-SOAPs alone excels not only in efficiently screening the chemical space of Rh complexes featuring bidentate phosphine ligands but also in accurately predicting the reaction energies ΔEDFT. With our approach, we were able to predict ten promising ligand structures that should feature a low C–H reaction energy and therefore, should be able to substantially accelerate the catalytic functionalization of alkanes.
Data availability
The DFT optimized xyz files, the Gaussian16 log files as well as csv files used for training of the different models are available from Zenodo (https://doi.org/10.5281/zenodo.10529636, DOI: 10.5281/zenodo.10529636, Version used: 1.0). Additional detailed experiment descriptions, figures, as well as tables supporting the findings of the article can be found in the ESI.†Author contributions
R. G., A. C. and S. G. performed the conceptualization and the project-administration. T. H. and R. G. performed quantum chemical simulations, data analysis and machine learning. Figures and the original draft were prepared by T. H. All authors contributed to the writing by reviewing and editing of the original draft.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
T. H. and S. G. gratefully acknowledge funding from Carl-Zeiss-Stiftung “Durchbrüche”. S. G. highly acknowledges funding by the German Science Foundation DFG within the priority program SPP 2363 “Molecular Machine Learning”, GR4482/6. R. G. gratefully acknowledges funding from the “Bund-Länder Tenure-Track Programm” of the Federal Ministry of Education and Research (BMBF) as well as by an accompanying grant from the Free State of Thuringia (FKZ: 16TTP133). The major part of the calculations were performed at the Universitätsrechenzentrum of the Friedrich Schiller University Jena, while a minor part was performed at TU Ilmenau.References
- W.-H. Wang, Y. Himeda, J. T. Muckerman, G. F. Manbeck and E. Fujita, CO2 Hydrogenation to Formate and Methanol as an Alternative to Photo- and Electrochemical CO2 Reduction, Chem. Rev., 2015, 115, 12936–12973 CrossRef CAS PubMed.
- R. Crabtree, Iridium compounds in catalysis, Acc. Chem. Res., 1979, 12, 331–337 CrossRef CAS.
- M. D. Kärkäs, O. Verho, E. V. Johnston and B. Åkermark, Artificial Photosynthesis: Molecular Systems for Catalytic Water Oxidation, Chem. Rev., 2014, 114, 11863–12001 CrossRef PubMed.
- T. Shen, Q. Xie, Y. Li and J. Zhu, Aromaticity-promoted C− F Bond Activation in Rhodium Complex: A Facile Tautomerization, Chem.–Asian J., 2019, 14, 1937–1940 CrossRef CAS PubMed.
- Y. Li and J. Zhu, Achieving a favorable activation of the C–F bond over the C–H bond in five-and six-membered ring complexes by a coordination and aromaticity dually driven strategy, Organometallics, 2021, 40, 3397–3407 CrossRef CAS.
- X. Li, W. Ouyang, J. Nie, S. Ji, Q. Chen and Y. Huo, Recent Development on Cp* Ir (III)-Catalyzed C− H Bond Functionalization, ChemCatChem, 2020, 12, 2358–2384 CrossRef CAS.
- T. Sakakura, T. Sodeyama, K. Sasaki, K. Wada and M. Tanaka, Carbonylation of hydrocarbons via carbon-hydrogen activation catalyzed by RhCl (CO)(PMe3) 2 under irradiation, J. Am. Chem. Soc., 1990, 112, 7221–7229 CrossRef CAS.
- A. J. Kunin and R. Eisenberg, Photochemical carbonylation of benzene by iridium (I) and rhodium (I) square-planar complexes, Organometallics, 1988, 7, 2124–2129 CrossRef CAS.
- K. J. Laidler and M. C. King, The development of transition-state theory, J. Phys. Chem., 1983, 87, 2657–2664 CrossRef CAS.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Methods for exploring reaction space in molecular systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Computer Generated Pyrolysis Modeling: On-the-Fly Generation of Species, Reactions, and Rates, Ind. Eng. Chem. Res., 1994, 33, 790–799 CrossRef CAS.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- D. Rappoport, C. J. Galvin, D. Y. Zubarev and A. Aspuru-Guzik, Complex chemical reaction networks from heuristics-aided quantum chemistry, J. Chem. Theory Comput., 2014, 10, 897–907 CrossRef CAS PubMed.
- S. Habershon, Sampling reactive pathways with random walks in chemical space: Applications to molecular dissociation and catalysis, J. Chem. Phys., 2015, 143, 094106 CrossRef PubMed.
- M. Bergeler, G. N. Simm, J. Proppe and M. Reiher, Heuristics-guided exploration of reaction mechanisms, J. Chem. Theory Comput., 2015, 11, 5712–5722 CrossRef CAS PubMed.
- A. L. Dewyer and P. M. Zimmerman, Finding reaction mechanisms, intuitive or otherwise, Org. Biomol. Chem., 2017, 15, 501–504 RSC.
- D. H. Valentine Jr and J. H. Hillhouse, Electron-rich phosphines in organic synthesis II. Catalytic applications, Synthesis, 2003, 2003, 2437–2460 Search PubMed.
- H. Altae-Tran, B. Ramsundar, A. S. Pappu and V. Pande, Low data drug discovery with one-shot learning, ACS Cent. Sci., 2017, 3, 283–293 CrossRef CAS PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner, M. Steijaert, J. K. Wegner, H. Ceulemans, D.-A. Clevert and S. Hochreiter, Large-scale comparison of machine learning methods for drug target prediction on ChEMBL, Chem. Sci., 2018, 9, 5441–5451 RSC.
- Y. J. Colón and R. Q. Snurr, High-throughput computational screening of metal–organic frameworks, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- J. P. Janet and H. J. Kulik, Resolving transition metal chemical space: Feature selection for machine learning and structure–property relationships, J. Phys. Chem. A, 2017, 121, 8939–8954 CrossRef CAS PubMed.
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Machine learning activation energies of chemical reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1593 CAS.
- S. Choi, Y. Kim, J. W. Kim, Z. Kim and W. Y. Kim, Feasibility of activation energy prediction of gas-phase reactions by machine learning, Chem.–Eur. J., 2018, 24, 12354–12358 CrossRef CAS PubMed.
- Q. Ye, Y. Zhao and J. Zhu, Probing the origin of higher efficiency of terphenyl phosphine over the biaryl framework in Pd-catalyzed CN coupling: A combined DFT and machine learning study, Artif. Intell., 2023, 1, 100005 Search PubMed.
- I. Ismail, C. Robertson and S. Habershon, Successes and challenges in using machine-learned activation energies in kinetic simulations, J. Chem. Phys., 2022, 157, 014109 CrossRef CAS PubMed.
- M. Evans and M. Polanyi, Inertia and driving force of chemical reactions, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- F. Palazzesi, M. R. Hermann, M. A. Grundl, A. Pautsch, D. Seeliger, C. S. Tautermann and A. Weber, BIreactive: a machine-learning model to estimate covalent warhead reactivity, J. Chem. Inf. Model., 2020, 60, 2915–2923 CrossRef CAS PubMed.
- P. Friederich, G. dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Machine learning dihydrogen activation in the chemical space surrounding Vaska's complex, Chem. Sci., 2020, 11, 4584–4601 RSC.
- P. Margl, T. Ziegler and P. E. Bloechl, Reaction of methane with Rh (PH3) 2Cl: A dynamical density functional study, J. Am. Chem. Soc., 1995, 117, 12625–12634 CrossRef CAS.
- T. Huang, S. Kupfer, M. Richter, S. Gräfe and R. Geitner, Bidentate Rh (I)-Phosphine Complexes for the C− H Activation of Alkanes: Computational Modelling and Mechanistic Insight, ChemCatChem, 2022, 14, e202200854 CrossRef CAS.
- J. S. Bridgewater, T. L. Netzel, J. R. Schoonover, S. M. Massick and P. C. Ford, Time-Resolved Optical and Infrared Spectral Studies of Intermediates Generated by Photolysis of trans-RhCl (CO)(PR3) 2. Roles Played in the Photocatalytic Activation of Hydrocarbons1, Inorg. Chem., 2001, 40, 1466–1476 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Big data meets quantum chemistry approximations: the Δ-machine learning approach, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- Q. Zhao, D. M. Anstine, O. Isayev and B. M. Savoie, D2 machine learning for reaction property prediction, Chem. Sci., 2023, 14, 13392–13401 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- H. Wiener, Structural determination of paraffin boiling points, J. Am. Chem. Soc., 1947, 69, 17–20 CrossRef CAS PubMed.
- B. Hollas, An analysis of the autocorrelation descriptor for molecules, J. Math. Chem., 2003, 33, 91–101 CrossRef CAS.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- M. Ceriotti, M. J. Willatt and G. Csányi, in Handbook of Materials Modeling: Methods: Theory and Modeling, Springer, Cham, 2020, pp. 1911–1937 Search PubMed.
- J. Devillers, D. Domine, C. Guillon, S. Bintein and W. Karcher, Prediction of partition coefficients (log p oct) using autocorrelation descriptors, SAR QSAR Environ. Res., 1997, 7, 151–172 CrossRef CAS.
- R. Bader, Atoms in molecules: a quantum theoryOxford University Press, USA, 1994 Search PubMed.
- R. J. Boyd and C. F. Matta, The quantum theory of atoms in molecules: from solid state to DNA and drug design, Wiley-VCH Verlag GmbH & Co. KGaA, 2007 Search PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, DScribe: Library of descriptors for machine learning in materials science, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, Updates to the DScribe library: New descriptors and derivatives, J. Chem. Phys., 2023, 158, 234802 CrossRef CAS PubMed.
- G. A. Landrum, et al., RDKit: Open-Source Cheminformatics Software, version 2022_03_3 Search PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An open chemical toolbox, J. Cheminf., 2011, 3, 1–14 Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- I. Guyon and A. Elisseeff, An introduction to variable and feature selection, J. Mach. Learn. Res., 2003, 3, 1157–1182 Search PubMed.
- P. Geurts, D. Ernst and L. Wehenkel, Extremely randomized trees, Mach. Learn., 2006, 63, 3–42 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- J. Howard and S. Gugger, Fastai: A layered API for deep learning, Information, 2020, 11, 108 CrossRef.
- D. P. Kingma and J. Ba: A method for stochastic optimization, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Taking the human out of the loop: A review of Bayesian optimization, Proc. IEEE, 2015, 104, 148–175 Search PubMed.
- A. Klein, L. C. Tiao, T. Lienart, C. Archambeau and M. Seeger, Model-based asynchronous hyperparameter and neural architecture search, arXiv, preprint, arXiv: 2003.10865, DOI:10.48550/arXiv.2003.10865.
- N. Erickson, J. Mueller, A. Shirkov, H. Zhang, P. Larroy, M. Li and A. Smola: Robust and accurate automl for structured data, arXiv, preprint, arXiv: 2003.06505, DOI:10.48550/arXiv.2003.06505.
- J. H. Friedman, Greedy function approximation: a gradient boosting machine, Ann. Math. Stat., 2001, 1189–1232 Search PubMed.
- L. Prokhorenkova, G. Gusev, A. Vorobev, A. V. Dorogush and A. Gulin, CatBoost: unbiased boosting with categorical features, arXiv, preprint, arXiv: 1706.09516, DOI:10.48550/arXiv.1706.09516.
- A. Altmann, L. Toloşi, O. Sander and T. Lengauer, Permutation importance: a corrected feature importance measure, Bioinformatics, 2010, 26, 1340–1347 CrossRef CAS PubMed.
- L. Breiman, Random forests, Mach. Learn., 2001, 45, 5–32 CrossRef.
- T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D’Addario and M. S. Sigman, A comprehensive discovery platform for organophosphorus ligands for catalysis, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- L. Falivene, R. Credendino, A. Poater, A. Petta, L. Serra, R. Oliva, V. Scarano and L. Cavallo, SambVca 2. A web tool for analyzing catalytic pockets with topographic steric maps, Organometallics, 2016, 35, 2286–2293 CrossRef CAS.
- H. B. Kagan and T.-P. Dang, Asymmetric catalytic reduction with transition metal complexes. I. Catalytic system of rhodium (I) with (-)-2, 3-0-isopropylidene-2, 3-dihydroxy-1, 4-bis (diphenylphosphino) butane, a new chiral diphosphine, J. Am. Chem. Soc., 2002, 94, 6429–6433 CrossRef.
- S. Singh and K. M. Nicholas, A novel synthesis of unsymmetrical tertiary phosphines: selective nucleophilic substitution on phosphorus (III), Chem. Commun., 1998, 149–150 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00037d |
| This journal is © The Royal Society of Chemistry 2024 |