Open Access Article
Open Access ArticleA 3d convolutional neural network autoencoder for predicting solvent configuration changes in condensed phase biomass reactions†
Anjana
Puliyanda
 ,
Arul Mozhi
Devan Padmanathan
,
Arul Mozhi
Devan Padmanathan
 ,
Samir H.
Mushrif
,
Samir H.
Mushrif
 and
Vinay
Prasad
and
Vinay
Prasad
 *
*
Department of Chemical and Materials Engineering, 9211 116 Street NW, Edmonton, Alberta T6G 1H9, Canada. E-mail: vprasad@ualberta.ca
First published on 17th April 2024
Abstract
Configuration changes in the solvent or melt-phase (condensed phase reactions) molecules impact reaction thermodynamics and kinetics, making it vital to assess if solvent/melt-phase molecules need to be considered explicitly in first principles-based reactive molecular simulations. A basis for these configuration changes is established using MD simulations of melt-phase cellobiose decomposition. A 3d CNN autoencoder is trained to extract spatio-temporal features from coordinates of atomic positions in the MD trajectories of cellobiose decomposition. The differences between the encoded reactant and product features were fit to probability distributions, where larger configuration changes were found to be more probable at lower temperatures. The machine learning model then predicts changes in solvent orientation by using a distance-based classifier to assess the closeness between encoded features from reactant trajectories of cellobiose systems with larger configuration changes and those from the following systems: (i) fructose protonation in water–DMSO and, (ii) glucose isomerization via hydride transfer in water and methanol. The extent of solvent configuration changes in the fructose systems was predicted to increase with DMSO concentrations and was validated using trends in the difference between reaction free energies. For glucose isomerization, configurational changes in pure methanol were predicted to be higher than that in water, consistent with the high polarizability of methanol due to which the reaction free energy barrier is ∼50 kJ mol−1 higher than that in water. This work demonstrates a machine learning framework that has the potential to limit the computational cost and accelerate the deployment of molecular simulations in screening solvents for reactive chemical transformations.
1 Introduction
Solvents have been extensively used in biomass processing to achieve higher conversion rates or product selectivity1,2 for sustainable manufacturing of biofuels and commodity chemicals. Solvent effects can be categorized as: (i) physical solute–solvent solvation and, (ii) solvent effects on chemical thermodynamics/kinetics of bioconversion reactions. Physical interactions between solvents and reaction intermediates (reactants, transition state (TS), products, and catalysts) in the condensed phase can have promoting/inhibiting effects on the reaction.3 When the reactant is relatively better solvated than the products, the solvent has an inhibiting effect on the reaction. For instance, during the hydrogenation of phenol (reactant) to cyclohexanone over Pd/C in either alcohol or water (solvents),4 there are strong alcohol–phenol (solvent–reactant) interactions in the former, whereas in water, cyclohexanone (desired product) undergoes further hydrogenation to cyclohexanol, thus lowering product selectivity, because cyclohexanone is immiscible in water, and may not desorb quickly from the catalyst surface. Therefore, both physical and chemical solvation effects arising from solvent–reactant–product interactions impact reaction yields.In heterogeneous catalysis, solvent effects arise from competitive adsorption of solvents and reactants, changes in internal diffusion of porous catalysts, and entropic effects due to confinement or increasing catalyst stability/durability.2 Similarly, in the condensed phase with homogeneous catalysis, various chemical mechanisms are involved in changing the activation barrier by affecting the relative stabilization of the reactant and/or TS. The specific mechanism involved depends both on the type of solvents and the reaction. For example, the cracking of polystyrene between 350 °C and 400 °C depends heavily on the hydrogen donating ability of the solvent.5 Protic solvents inhibit chain-end scission while phenols promote random scission of polystyrene. Such solvent effects are also measured in thermochemical melting of cellulose6 above 450–500 K.7 High speed photography of cellulose pyrolysis on a catalytic surface captured a short-lived liquid intermediate before complete volatilization.8 In this “liquid cellulose”, cellulose is both the solvent and reactant–solute. Depending on the thermal expansion of the cellulose lattice (solvent), different mechanisms are promoted, as measured using millisecond-scale reaction kinetics,6,9 and supported by the calculated free energy barrier.10 It has been suggested that cellulose decomposes via chain-end scission at low temperatures and random scissions at high temperatures. Similarly, the cellulose lattice can also be penetrated by solvent induced chemical effects that could either be static or dynamic. Solvent statics refers to the de-/stabilization effect on reacting species along reaction coordinates. The free energy of activation is affected, and the reacting species (activated complex) are in equilibrium with the solvent. Here, either the reactant activation does not induce solvent reorganization or reactant activation involves conformational change and is slower than the induced solvent relaxation.11 On the other hand, solvent dynamics refers to the effects due to time-dependent solvent behavior including structural changes that occur in the solvent and the surrounding environment and also non-equilibrium solvation for reactions in a strong dipole or relatively slow relaxing solvent environment.12–14 Reactant activation has significant redistribution of charges and is faster than induced solvent relaxation.2 Glucose isomerization to fructose was more reactive in water compared to methanol because of the slow reorganization of larger and more polarizable methanol molecules during the rate determining hydride transfer step.15 Furthermore, acid catalyzed conversion of fructose to HMF involves various solvent (water) mediated hydride transfer and proton transfer steps. The microkinetic model was able to reproduce experimental kinetics only when the Marcus reorganization energy was included.16
Traditionally, macroscopic approaches have been used to study these solvent effects measured using their impact on reaction rates,17,18 reaction pathways, product selectivity,19–23 and catalyst durability.2,11 Parameters such as viscosity, dielectric constant,24,25 hydrogen (H) bond donor ability, H bond acceptor ability, polarity, polarizability, dipole moment, Lewis acidity and basicity4,26 are regressed against measured effects on reaction rates, product selectivity, or rate constants.27 However, microscopic parameters such as water enrichment in local domains, average H bond lifetime and fraction of the reaction surface occupied by functional groups also play a significant role in altering the relative stability of the reactant, TS, and products.27,28 This favors molecular simulations to derive kinetic and thermodynamic insights into solvent effects that may not be fully explained by macroscopic empirical parametrization that is limited by costly experiments. However, these simulations involve obtaining the energy and forces of atomic configurations achieved by computationally expensive biasing techniques and quantum mechanical (QM) calculations, making them intractable for systems with large numbers of atoms and longer time scales.29 This can be overcome either by coarse-graining atomic calculation methods using empiricism-based classical molecular mechanics, or by using machine learning (ML) to accelerate QM based (ab initio molecular dynamics (AIMD)) simulations.30 The acceleration of QM simulations encompasses: (a) ML for estimating the potential energy surface (PES) based on atomic coordinates, which speeds up MD simulations of chemical structures,31 (b) predictive ML using AIMD simulation data to develop computationally efficient property prediction models of molecular systems,32 and, (c) generative ML using AIMD data to learn probability distributions of molecular representations, given the macroscopic properties for advancing computer-aided molecular design,33 though it is still in its infancy.34 Hence, we proceed to discuss studies from the first two classes of ML models with respect to solvent effects and contextualize this paper and its novelty.
ML to accelerate QM calculations uses neural networks and regression techniques to extract features from the PES before fitting them to predict energy (machine learning potentials (MLPs)) or force fields (machine learning force fields (MLFFs)).32 MLPs as computationally tractable surrogates for ab initio calculations using neural network architectures to capture atomic interactions in Cartesian space via convolutions (SchNet) and physical symmetries via local frame coordinates (DeepPMD) are seen to speed up catalyst screening by efficiently computing reaction activation energies35 and modeling solid–liquid interfaces36 in heterogeneous catalysis. DeepPMD has demonstrated how ML can scale the accuracy of ab initio calculations in surface chemistry, from a system with 1000 atoms to that with 100 million atoms. This is achieved by expressing the total potential energy as a sum in parts of that of the local atomic environments using their extracted symmetrical spatio-temporal features, to assess whether or not solvent molecules dissociate at the interface.37 The high dimensionality of the data, typically 3N atomic coordinates for a system with N atoms, not only limits the use of ML to sample from QM simulations to construct the PES, but also causes the computational cost of reference data from density functional theory (DFT) calculations to scale cubically as the number of electrons in the system.38 This has been surmounted by using time-lagged autoencoders to learn low dimensional manifolds (collective variables) that reproduce the conformational dynamics by maximizing time-lagged autocorrelation within the original space.39
Deploying ML to derive interpretable insights from AIMD simulations by predicting the mechanism, rate and yield of chemical systems as functions of reaction thermodynamic properties has been recognized as one of the six grand challenges of the 21st century.40 Preserving physico-chemical intuition by supplying physically meaningful data representations such as molecular fingerprints or local environment descriptors29 facilitates the ML model to recognize meaningful correlations between the system properties and the features extracted from data. ML regression models trained on fingerprints extracted from MD simulations are shown to predict solvation free energy and partition coefficients that have been experimentally validated.41 However, such frameworks perform poorly when they encounter an atomic configuration not present in the training data. Hence, adaptive ML regression frameworks that query new configurations to retrain ML models on the fly have been shown to result in more reliable predictions.42 Aside from regression models, ML classifiers have been trained to extract features from AIMD data of the decomposition of dioxetane that correspond to either successful or frustrated dissociations.43 The emphasis on retaining physical intuition such as symmetry or translation invariance of atomic configurations in ML models has popularized the use of convolutional neural networks (CNNs) that capture spatio-temporal patterns via parameter sharing, thereby making predictive ML models more efficient.44 It can be seen that the density of water molecules stacked over time (3d grids), or the time-averaged density maps of water (2d grids) when fed into 3d CNNs and 2d CNNs respectively, efficiently capture spatio-temporal variation in water density while predicting the hydration free energy that rationalizes interfacial hydrophobicity in protein folding.45 However, catalytic biomass conversion involves polar aprotic cosolvents in addition to water, the volume ratio of which impacts the rate and yield of the reaction, that is regressed against voxel representations (density of water, the cosolvent and the reactant in discrete volume elements of the simulation box, across 3 separate channels) input to a CNN from MD simulation data to facilitate rapid high throughput screening via a ML surrogate.46 This pre-trained model (SolventNet) has also been used to predict reaction rates in mixed-solvent environments, with just 4 ns of classical MD (force-field-based) trajectories, thereby speeding up the screening of solvent compositions.47
The focus of this manuscript is not to accelerate AIMD directly, but instead to use a predictive ML model to inform simulations about the possible solvent reorganization/reorientation during reactive events. The computational cost involved in generating training data from MD simulations with their associated labels, and the cost of training a ML model itself, is projected to be significantly lower than having to explicitly perform uninformed first principles-based MD simulations on newer systems. Generating labels/targets to train predictive ML models such as reaction rates46 and dissociation time48 involves experiments or indirect sampling calculations from simulation data. In this work, we seek to overcome the cost of assigning labels using experiments or sampling calculations by proposing a self-supervised 3d CNN autoencoder to extract spatio-temporal features of trajectories of solvent molecules around the reactant and product that are supplied from multiple classical/AIMD simulations. The model can screen several new solvent systems by assessing the extent to which the solvent molecules may reorient by using only reactant trajectory simulations. Finally, should first principles simulation be performed on the product profiles of a system found to have lower solvent configuration changes, one could eliminate simulating explicit dynamics of solvent molecules. Reactant/product trajectories were generated for three case studies covering the direct effect of static and dynamic solvent reorganization in cellobiose and in water-DMSO systems, respectively, in addition to the indirect effect of solvent on catalyst–reactant interaction:
1. Glycosidic bond cleavage in ‘liquid cellulose’ during pyrolysis: cellulose kinetics are affected10,49 by the thermal change in the condensed phase.7 The equilibrium trajectories of the cellobiose high temperature melt (solvent) along with the reactant/product are generated using classical MD simulations, in combination with the thermodynamic integration method.10 These are equilibrium solvent trajectories and the corresponding activation barriers are calculated. Therefore, this is an example of solvent statics where the thermal change in hydrogen bonding has a destabilizing effect on the reactant.
2. Glucose to fructose isomerization in water/methanol: hydride transfer involving large asymmetric redistribution of charges is the rate-limiting step of this Lewis/Brønsted acid catalyzed reaction15 comprising non-equilibrium charge transfer, due to which solvent dynamics significantly impact reaction kinetics. Since the solvent is polarizable and the trajectories are generated using Car Parinello MD with metadynamics implementation, the slower solvent relaxation dynamics is captured and the TS ends up being in non-equilibrium solvation.
3. Dehydration of fructose to HMF in water/DMSO: conversion of sugars (glucose and fructose) to furanic compounds (HMF) is widely studied in condensed phase biomass processing.50,51 The solvent alters the interaction between the proton (catalyst) and fructose/HMF (reactant). Reactant/product trajectories are generated using classical MD simulations with metadynamics implementation. In this example the solvent dynamics are captured and the free energy landscape is evaluated as the proton moves towards and away from fructose/HMF.
This paper presents a self-supervised machine learning model by way of using a 3d convolutional neural network (CNN) autoencoder for spatio-temporal feature extraction from the molecular simulation trajectories of the configuration of solvent arrangement around reactant/product systems, the difference between the root mean square deviation (RMSD) of which is fit to a probability distribution via kernel density estimation (KDE) to assess solvent configuration changes. This subsequently informs the development of a Mahalanobis distance-based classifier to predict the extent of solvent reorganization in newer systems by assessing the distance of its reactant features from the distribution of those encoded in systems where the reorganization extent has already been quantified. The rationale behind the choice of this distance-based classifier was to avoid the training costs, as with neural network-based classifiers.52 This framework has the potential to reduce the cost of MD simulations and that of training ML models by predicting the extent of solvent configuration changes, as a basis to inform the consideration of solvent molecules explicitly or not, while simulating the final product configuration.
2 Methods
2.1 Molecular modeling methods
Simulation data for the 3 case studies are generated using molecular modeling methods specific to the systems. In the condensed phase kinetics of cellobiose, with ∼ 60 molecules in the melt, equilibrated MD simulations were performed prior to QM calculations (ConTS), followed by a relative solvation-based free energy correction (ReSolv).10 For the acid catalyzed fructose dehydration, force field-based MD (TIP3P for water; OPLS-AA for DMSO, fructose and HMF) and well-tempered metadynamics are performed to study the impact of structure and local ordering changes of solvent atoms on the interaction of fructose and HMF with the hydronium ion.53 Finally, for the glucose isomerization, the Car–Parrinello scheme with metadynamics was used to simulate solvent effects on reaction dynamics. Solvent molecules were treated quantum mechanically, and the details of the modeling techniques are provided in the ESI.†152.2 Self-supervised machine learning method
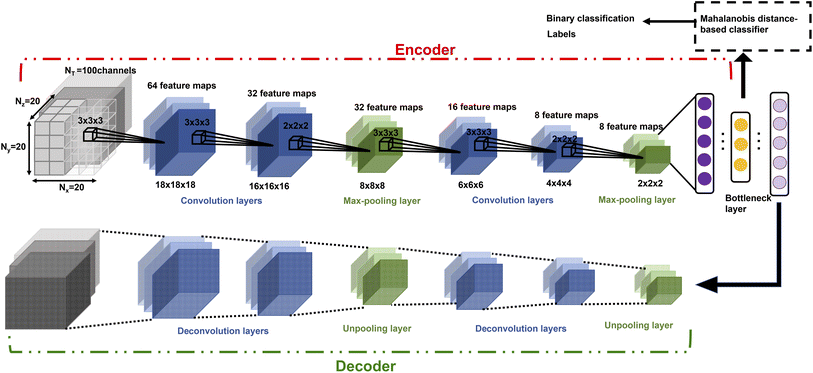
CNNs have been used to extract rotational and translation invariant features from a wide variety of data modalities that are represented as grids,54 and more recently have been applied to datasets from molecular simulations that can be expressed as grids. Coordinates of all the atoms stacked in x,y,z channels corresponding to the axes can be input to train a 1d CNN,55 but in systems with an arbitrary number of atoms, the input data would have to be padded or truncated accordingly, thereby impacting the patterns the CNN learns. Hence, the representation of atomic coordinates or molecular features extracted from the MD simulations before being fed into the CNN is vital. In the present work, we seek to use a voxel representation of the atomic configurations to train the 3d CNN autoencoder, where the x, y, z atomic coordinates with respect to the size of the simulation box are discretized into volume elements bound by grids.56 In order for the spatial location of the atoms to be invariant of the grid resolution, the density distribution of atoms in the voxels has been widely used as an input.44 Positional atomic densities from MD simulations have been supplied as x–y grids averaged across simulation time steps to train 2d CNNs, or as tensors where separate x–y grids generated for the water and hydrogen molecules have been stacked into channels along the simulation time steps to train 3d CNNs to predict interfacial hydrophobicity.45 Similarly, positional densities of atoms in the x–y–z space recovered from classical MD simulations, averaged across simulation time steps, have been supplied as tensors stacked into channels grouped by the category of the molecules viz., reactant, solvent and co-solvent, to train 3d CNNs to predict reaction rates.46 This work differs from those efforts in that the positional densities of the atoms in the x–y–z space from MD coordinate trajectories are represented as voxels that are stacked across several simulation time steps, shown in Fig. 1, to train a self-supervised 3d CNN autoencoder that extracts spatio-temporal features.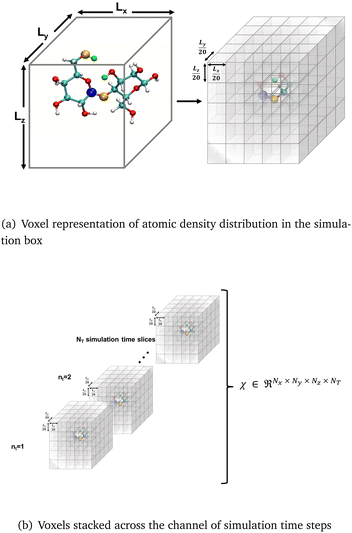 | ||
| Fig. 1 The atomic coordinates from MD simulation data are, (a) spatially represented as voxels at each time step, and (b) spatio-temporally represented as time-stacked voxels. | ||
The x–y–z atomic positions of cellobiose with respect to the simulation box of dimensions Lx × Ly × Lz is represented as a probability density distribution of the atoms existing in a certain discrete volume element of dimensions 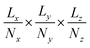 , where Nx, Ny, and Nz (all chosen to be 20 in the present work) are the number of grid elements that the simulation box is discretized into along each axis, as illustrated in Fig. 1(a). Since the voxels are discrete representations of point clouds of molecules in the simulation box, each of them must be of a size not smaller than the order of magnitude of the atomic radius, to avoid violating the continuum assumption and counterproductively increasing the computational costs of training a machine learning model. At the same time, choosing a voxel size that is larger than the average length-scale of molecular orientation changes for a given solute–solvent system may lead to the desired phenomena not being captured when training the machine learning model. Additionally, the size of the voxel is a hyperparameter that impacts how coarse-grained or fine-grained the data presented to the machine learning model would be, and therein impacts the network architecture of the 3d-CNN autoencoder. The voxel size can be varied independently of the solute–solvent system, with the aforementioned criteria in mind. Each simulation of the reactant and product configurations for the transglycosylation of cellobiose at four different temperatures (100 K, 500 K, 900 K, and 1200 K) has been performed over 8 ns using GROMACS,57 and the coordinate positions have been recorded every 1 ps. The positional voxel density representations of the atomic coordinates are stacked across NT = (100 ps) simulation time steps as shown in Fig. 1(b), to generate T = 80 spatiotemporal tensor samples
, where Nx, Ny, and Nz (all chosen to be 20 in the present work) are the number of grid elements that the simulation box is discretized into along each axis, as illustrated in Fig. 1(a). Since the voxels are discrete representations of point clouds of molecules in the simulation box, each of them must be of a size not smaller than the order of magnitude of the atomic radius, to avoid violating the continuum assumption and counterproductively increasing the computational costs of training a machine learning model. At the same time, choosing a voxel size that is larger than the average length-scale of molecular orientation changes for a given solute–solvent system may lead to the desired phenomena not being captured when training the machine learning model. Additionally, the size of the voxel is a hyperparameter that impacts how coarse-grained or fine-grained the data presented to the machine learning model would be, and therein impacts the network architecture of the 3d-CNN autoencoder. The voxel size can be varied independently of the solute–solvent system, with the aforementioned criteria in mind. Each simulation of the reactant and product configurations for the transglycosylation of cellobiose at four different temperatures (100 K, 500 K, 900 K, and 1200 K) has been performed over 8 ns using GROMACS,57 and the coordinate positions have been recorded every 1 ps. The positional voxel density representations of the atomic coordinates are stacked across NT = (100 ps) simulation time steps as shown in Fig. 1(b), to generate T = 80 spatiotemporal tensor samples 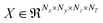 , from the simulation trajectory of either the reactant or product, for a given system. The molecular reorientation in time is captured by the spatio-temporal convolution across time-stacked voxels, without the need to rearrange system coordinates or fix the center of mass as a reference.
, from the simulation trajectory of either the reactant or product, for a given system. The molecular reorientation in time is captured by the spatio-temporal convolution across time-stacked voxels, without the need to rearrange system coordinates or fix the center of mass as a reference.
For the total number of N (=2T × number of systems modeled) input tensor samples from both the reactant and product trajectories of all systems, X(i) for i = {1, 2,⋯N}, a 3d CNN autoencoder is trained as a hierarchical model that uses a sequence of convolutional, activation, pooling, flattening and fully connected layers in the encoder (E), before symmetrically unrolling the sequence in the decoder (D) to reconstruct the input as ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) (i) = fD(fE(X(i),θE),θD). The parameters of the encoder and decoder functions (θ = {θE, θD}) of the self-supervised autoencoder network are learned by minimizing the following loss function:
(i) = fD(fE(X(i),θE),θD). The parameters of the encoder and decoder functions (θ = {θE, θD}) of the self-supervised autoencoder network are learned by minimizing the following loss function:
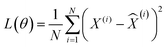 | (1) |
The number of parameters in the 3d CNN autoencoder scales with the choice of hyperparameters that govern the network architecture in the hierarchy of operations. The convolutional operation given by 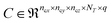 comprises a 3d kernel of dimensions (ncx × ncy × ncz) that performs convolutions across a stride of s voxels in each dimension over the NT time slices to produce q feature maps in the output
comprises a 3d kernel of dimensions (ncx × ncy × ncz) that performs convolutions across a stride of s voxels in each dimension over the NT time slices to produce q feature maps in the output 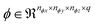 , as given by the following equation, where x1 ∈ {1, 2,…, nϕx}, x2 ∈ {1, 2,…, nϕy}, x3 ∈ {1, 2,…, nϕz}, j ∈ {1, 2⋯, q} and
, as given by the following equation, where x1 ∈ {1, 2,…, nϕx}, x2 ∈ {1, 2,…, nϕy}, x3 ∈ {1, 2,…, nϕz}, j ∈ {1, 2⋯, q} and 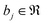 is the bias term.
is the bias term.
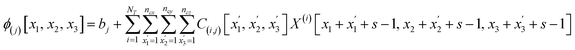 | (2) |
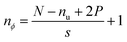 | (3) |
The dimensions of the output (nϕ) across any specific axis are impacted by the respective kernel dimension (nu), stride (s) and padding (P), if any, given an input of size N, as indicated by eqn (3). The purpose of padding is to preserve the input dimensions in the convolved output.58 However, since the convolutional operation is used to down sample the inputs for feature extraction, zero padding has been used in this work. The convolved features are then passed through a nonlinear activation function that does not modify the dimensions.
| f(ϕ) = max (0,ϕ) | (4) |
| v′ = f(Wfcv + bfc) | (5) |
As compared to activation functions such as the tanh and sigmoid, the rectified linear unit, given by eqn (4), is preferred as it does not suffer from gradient saturation in the event of large magnitude inputs, thereby increasing the sensitivity of the model to input representations.59 Following this, the pooling operation  is used to down sample the activated output, to make the encoded representations invariant to minor translations in the input,60 resulting in a pooled output
is used to down sample the activated output, to make the encoded representations invariant to minor translations in the input,60 resulting in a pooled output  . This follows the same lines as eqn (2) and (3), except that there is no bias translation and the 3d max pooling kernel of dimensions (npx × npy × npz) merely outputs a maximum valued scalar as it strides over s voxels at a time along the axes, for all the input feature maps. Several units comprising the aforementioned convolutional, activation and pooling operations can be hierarchically stacked to transform the input sample X(i) into a tensor
. This follows the same lines as eqn (2) and (3), except that there is no bias translation and the 3d max pooling kernel of dimensions (npx × npy × npz) merely outputs a maximum valued scalar as it strides over s voxels at a time along the axes, for all the input feature maps. Several units comprising the aforementioned convolutional, activation and pooling operations can be hierarchically stacked to transform the input sample X(i) into a tensor 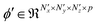 , of p feature maps, before finally flattening it to result in a vector
, of p feature maps, before finally flattening it to result in a vector 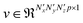 that is fed into a fully connected layer to result in an output feature vector
that is fed into a fully connected layer to result in an output feature vector 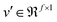 , given in eqn (5), where
, given in eqn (5), where 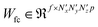 and
and 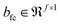 are the weights and biases, parametrizing the fully connected layer, respectively. There can be many such fully connected layers as indicated by the schematic in Fig. 2, to finally obtain f′ latent features in the bottleneck layer of the encoder. The structure of the decoder is seen to mirror that of the encoder in reconstructing the input from the features of the bottleneck layer via a series of upsampling operations such as deconvolution and unpooling. If theconvolutional operation is expressed as the multiplication of the Toeplitz block of strided kernel coefficients with the input, then the deconvolution can be expressed as its inverse, where upsampling is achieved by multiplication with the transpose Toeplitz block.61 Similarly, unpooling is performed by inserting the maximum values into their index positions, cached during the pooling operation.
are the weights and biases, parametrizing the fully connected layer, respectively. There can be many such fully connected layers as indicated by the schematic in Fig. 2, to finally obtain f′ latent features in the bottleneck layer of the encoder. The structure of the decoder is seen to mirror that of the encoder in reconstructing the input from the features of the bottleneck layer via a series of upsampling operations such as deconvolution and unpooling. If theconvolutional operation is expressed as the multiplication of the Toeplitz block of strided kernel coefficients with the input, then the deconvolution can be expressed as its inverse, where upsampling is achieved by multiplication with the transpose Toeplitz block.61 Similarly, unpooling is performed by inserting the maximum values into their index positions, cached during the pooling operation.
Once trained, the bottleneck layer of the encoder is used to extract latent features from the MD trajectories of the reactant that are plugged into the quadratic distance-based classifier, to predict whether or not the configurations of solvent molecules change significantly in the product profile. This is based on the key assumption that samples with the same label should have similar latent features extracted by the autoencoder.62 However, developing a classifier to discriminate between latent features is supervised, in that there is a requirement for ground truth labels, the generation of which is expensive and time consuming.63 This is surmounted by calculating the root mean square deviation between features of the product and reactant trajectory for a system, followed by using KDE to probabilistically assess systems with a higher extent of reorganization using a threshold, based on which labels are assigned to the features extracted from the reactant trajectory samples to develop the Mahalanobis classifier, a choice deliberately made to also eliminate the cost of training neural network classifiers.52
 | (6) |
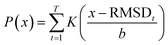 | (7) |
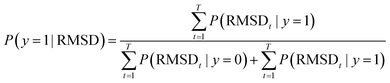 | (8) |
For a particular system, the 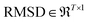 , pointing to the deviation of features of the product trajectory samples from the time average of features across the reactant trajectory samples, is given in eqn (6). The probability distribution of x ∈ [min (RMSD), max (RMSD)], for each of the systems is fit using kernel density estimation (eqn (7)), where the choice of the kernel function (K) and bandwidth (b) are guided by grid search optimization.64 The systems with the least and highest probabilistic mode of RMSD from the distributions are designated labels, y = {0, 1}, corresponding to a large and small extent of solvent reorganization, respectively. The posterior probability of the other systems being labelled 1, given their RMSDs and the assumption of equally likely priors, is determined using eqn (8).65 These encoded reactant and product trajectories in question are calculated for the cellobiose system, which is also the system on which the 3d CNN autoencoder is trained to learn the feature encodings. Hence, there are no assigned labels for the cellobiose systems until we proceed to look at the distribution describing the RMSD (eqn (7)), based on which the posterior probabilities of label assignment are computed using eqn (8). If the posterior probability of the cellobiose system exceeds a certain threshold, all the features corresponding to the samples in the reaction trajectory are designated a label 1, else 0, giving rise to labeled samples {fE(X(i)reactant),y(i)} for all i ∈ {1, 2,⋯N} supplied as reference data to a quadratic classifier based on the Mahalanobis distance. The classifier is trained to detect solvent reorganization patterns from a reduced set of encoded features of the reactant trajectories in a kernel space
, pointing to the deviation of features of the product trajectory samples from the time average of features across the reactant trajectory samples, is given in eqn (6). The probability distribution of x ∈ [min (RMSD), max (RMSD)], for each of the systems is fit using kernel density estimation (eqn (7)), where the choice of the kernel function (K) and bandwidth (b) are guided by grid search optimization.64 The systems with the least and highest probabilistic mode of RMSD from the distributions are designated labels, y = {0, 1}, corresponding to a large and small extent of solvent reorganization, respectively. The posterior probability of the other systems being labelled 1, given their RMSDs and the assumption of equally likely priors, is determined using eqn (8).65 These encoded reactant and product trajectories in question are calculated for the cellobiose system, which is also the system on which the 3d CNN autoencoder is trained to learn the feature encodings. Hence, there are no assigned labels for the cellobiose systems until we proceed to look at the distribution describing the RMSD (eqn (7)), based on which the posterior probabilities of label assignment are computed using eqn (8). If the posterior probability of the cellobiose system exceeds a certain threshold, all the features corresponding to the samples in the reaction trajectory are designated a label 1, else 0, giving rise to labeled samples {fE(X(i)reactant),y(i)} for all i ∈ {1, 2,⋯N} supplied as reference data to a quadratic classifier based on the Mahalanobis distance. The classifier is trained to detect solvent reorganization patterns from a reduced set of encoded features of the reactant trajectories in a kernel space 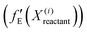 for a new system, by assessing their closeness to positively labelled trajectories of the cellobiose system, using the mean and covariances of their kernelized features as follows:
for a new system, by assessing their closeness to positively labelled trajectories of the cellobiose system, using the mean and covariances of their kernelized features as follows:
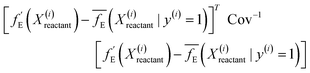 | (9) |
The loss function of the 3d CNN autoencoder is minimized by stochastic gradient descent, implemented using the Adam optimizer on PyTorch with a learning rate of 10−3. The process of gradient descent involves computing the gradient of the loss function with respect to the weights of the layers and is efficiently performed via the backpropagation algorithm. The distance-based classifier is then implemented to assess the extent of solvent reorganization in newer systems by measuring the distance between their features and the distribution of features extracted from the systems labelled as 1 (where larger RMSDs are more probable).
The saliency of the highest magnitude latent feature obtained by using the encoder to project the time aggregate of the data voxels from the reactant trajectory for a given system is calculated from eqn (10). The closeness of the encoded features of the reactant trajectory of a new system, to that of the low temperature cellobiose systems, is used as a basis to assess solvent configuration changes in this manuscript. Hence, saliency maps are an important tool to validate if the latent features of the reactant trajectory for the cellobiose systems duly sensitize the region of the simulation box containing the solvent molecules.
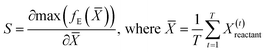 | (10) |
3 Results and discussion
Section 3.1 demonstrates the self-supervised ML framework to establish whether or not solvent configuration changes are significant, using the cellobiose systems as a reference. A 32 core HPC cluster takes ∼258 h of wall clock time (i.e., 258 × 32 = 8256 CPU-hours) to simulate just the reactant profile, at one of the temperatures for the cellobiose system. This amounts to a total wall time of ∼2064 h (i.e., 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 CPU-hours) to simulate both the reactant and product profiles across 4 temperatures for cellobiose. Training a 3d CNN autoencoder on all of the above simulation generated data of cellobiose, using an identical number of cores, takes ∼3 h of wall time. In Section 3.2, the insights drawn from the map between features of the reactant cellobiose profiles and the extent of solvent configuration changes are shown to generalize well across the different systems considered (fructose dehydration and glucose isomerization), when it comes to predicting the same from just the reactant profiles. This eliminates the need to explicitly account for the solvent molecules when simulating the product trajectories, thereby limiting the computational cost. The trends from the ML model predictions have been physically rationalized using saliency maps, and also validated using the trends in the thermodynamic free energy that accompany solvent configuration changes.
048 CPU-hours) to simulate both the reactant and product profiles across 4 temperatures for cellobiose. Training a 3d CNN autoencoder on all of the above simulation generated data of cellobiose, using an identical number of cores, takes ∼3 h of wall time. In Section 3.2, the insights drawn from the map between features of the reactant cellobiose profiles and the extent of solvent configuration changes are shown to generalize well across the different systems considered (fructose dehydration and glucose isomerization), when it comes to predicting the same from just the reactant profiles. This eliminates the need to explicitly account for the solvent molecules when simulating the product trajectories, thereby limiting the computational cost. The trends from the ML model predictions have been physically rationalized using saliency maps, and also validated using the trends in the thermodynamic free energy that accompany solvent configuration changes.
3.1 Training the ML model on the cellobiose systems
Pyrolytic decomposition of cellobiose in the condensed phase is primarily initiated by the glycosidic C–O bond cleavage (cf.Fig. 3). Gas phase DFT calculations carried out for isolated cellobiose decomposition showed that glycosidic cleavage via the transglycosylation mechanism (Fig. 3) exhibited the least enthalpic barrier. In addition to the C–O bond cleavage, diffraction and spectroscopic studies have shown that an anisotropic expansion of cellulose starts above 500 K with abrupt changes in H bonding.67–70 Supporting this, recent millisecond scale kinetic experiments have measured a difference in reaction kinetics6,9 at the transition (467 °C) between the low temperature crystalline and high temperature amorphous cellulose states. The neighboring molecules form the condensed phase in which the reactant molecules break down and the de-solvation (anisotropic expansion) effects would alter bond cleavage energetics. The configuration of molecules around the reacting species sheds light on how the condensed phase affects reaction energetics. Therefore, the changes in solvent orientation around the reactant cellobiose for the transglycosylation mechanism have been simulated at four different temperatures viz. 100 K, 500 K, 900 K and 1200 K. Previous studies examining cellulose activation failed to capture the observed shift in the kinetic regime, as measured in millisecond-scale kinetics experiments. However, through explicit modeling of the high-temperature reaction environment and considering finite-temperature effects in the condensed phase, we observe two distinct kinetic regimes, consistent with the millisecond-scale experiments.10 This suggests that the de-/stabilization effects arising from interactions with the melt-phase configuration, determined by hydrogen bond distribution and hydroxymethyl group conformations, play a significant role in determining the energetics of glycosidic bond cleavage. Molecular dynamics (MD) trajectories of the cellobiose melt-phase configuration (solvent) and its interaction with the reactant/product (solute) calculated from first principles are recorded at intervals of 500 simulation time steps over an 8 ns duration, resulting in reactant or product profiles. | ||
| Fig. 3 Glycosidic bond cleavage in the pyrolytic decomposition of cellobiose.66 | ||
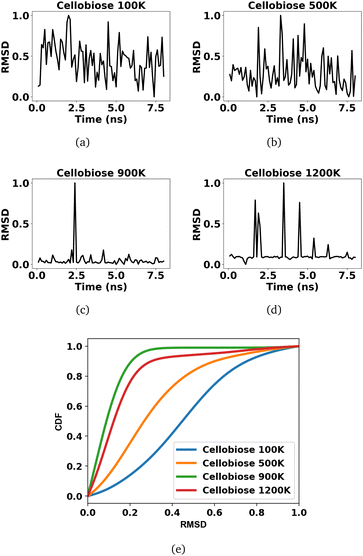
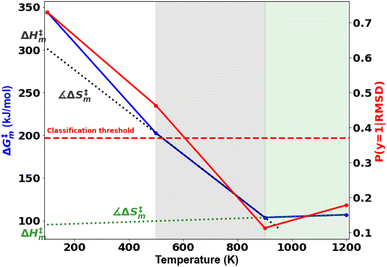
The voxels of atomic densities stacked over every 100 ps result in 80 samples each, from the reactant and product profiles, at each finite temperature simulation of cellobiose. This leads to a total of 640 temporal voxels of data samples across all 4 temperatures that are used to train the 3d CNN, with 80% used for training while the remaining 20% is used as a validation set for early stopping. A 3d CNN autoencoder with a structure as given in Fig. 2 is trained on these samples to extract encoded feature representations in the bottleneck layer. The root mean square deviation (RMSD) between these features of the samples in the product profiles and the average of the encoded features across all samples in the reactant profiles are indicated in Fig. 4(a)–(d), across the four temperatures. Since the encoded features are extracted from equilibrium simulations of the cellobiose systems, it is permissible to average the encoded features across all samples in the reactant trajectory, as a reference against which the encoded features of the product trajectory are compared, when defining the RMSD. The use of RMSD as a descriptor of the extent of solvent reorganization circumvents the need for expensive sampling strategies45 to compute metrics from the simulation data. It can be seen from Fig. 4(c) and (d) that solvent configuration changes are less prominent at higher temperatures. A kernel density estimation is used to quantify the probability distributions of the RMSDs in accordance with eqn (7) using a Gaussian kernel (K). The bandwidth chosen by grid search cross validation is found to be optimal at 0.1 and results in cumulative density distributions given in Fig. 4(e), from which the cellobiose 100 K system and the cellobiose 900 K system are seen to have the most (class 1) and least probable (class 0) solvent configuration changes, respectively. The density distributions of the cellobiose 100 K and 900 K systems are then used to quantify the posterior probability of a system being recognized as significantly reorganized, conditioned on its RMSD, as outlined in eqn (8). The average of the posterior probabilities across all the cellobiose systems is then used as a threshold as shown in Fig. 5, to recognize if significant solvent reorganization has been observed in a system or not. This threshold is used to assign labels only to the cellobiose systems, on the basis of which solvent configuration changes in newer test systems will later be assessed.
A probability distribution is fit to the RMSD fluctuations at each temperature shown in Fig. 4(a)–(d) using kernel density estimation (KDE). A kernel can be understood as a function describing a smooth symmetric curve characterized by a shape factor, for instance, a Gaussian bell curve is a kernel, and its shape factor is the standard deviation that characterizes the spread of the probability distribution that the curve is an estimate of. In KDE, each data point is modeled using a kernel, and the contribution to the estimated probability density at a certain RMSD is the weighted contribution from the kernels fit to all datapoints within a window of that specific RMSD value. Hence, KDE helps in estimating the probability distribution of data when the true underlying distribution is unknown. The cumulative density function from the probability distributions fit to the RMSDs is shown in Fig. 4(e). The solvent configuration changes are then quantified on the basis of the RMSD distributions. The posterior probability of a system with large reorganization calculated from the RMSD distribution is presented in Fig. 5. At 100 K and 500 K, there is a higher probability for temperature-induced orientation of the condensed cellobiose molecules (i.e. the melt-phase analogous to a solvent). In the earlier MD work published by the authors,10 free energy barriers for glycosidic bond cleavage in cellobiose were calculated. These reaction barriers include the enthalpic activation of the condensed phase owing to static solvent reorganization and the finite temperature entropic contributions. The trend of the probability for solvent reorganization calculated here using the 3d convolutional neural network autoencoder seems to be consistent with trends in the Gibbs free energy barrier for the transglycosylation mechanism of the reacting cellobiose molecules in the melt phase across the four different temperatures, as given by Fig. 5. The free energy barrier (FEB) decreases almost linearly with increasing temperatures and asymptotes above 900 K, at a constant value of ∼105 kJ mol−1. The reduction in the FEB going from 100 K to 900 K is 267.76 kJ mol−1 and suggests a strong impact of the temperature of the cellobiose melt environment on the glycosidic bond cleavage. The slope and the y-intercept of the free energy vs. temperature plot give the entropic and enthalpic contributions, respectively. The constant slope of the FEB curve at low temperature is indicative of the constant gain in entropy 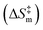 for the decomposition of the cellobiose melt to LGA. At higher temperatures the FEB flattens indicating that the entropic contribution to the barrier is zero, making it an enthalpy-controlled regime. Hence, the linear slopes of the low temperature and the high temperature curves form distinct decomposition regimes, also measured using millisecond scale kinetics experiments.71 The temperature-induced conformational changes in the molecules going from the crystal to the melt-phase influence cellulose chemistry. At low temperatures, cellulose exists in its crystalline state with an ordered intermolecular H bonding network which makes it energy intensive for the twisting and breaking of cellulose chains. At higher temperatures, the cellulose matrix expands taking a low-density state and disrupts the ordered H bonding network. As seen in Fig. 5, the free energy barrier is high which decreases with temperatures to eventually settle above 900 K. This is in coherence with the condensed phase reorganization probability predictions. At 100 K/500 K, the probability for reorganization is high as the neighboring molecules are close by and they would have to reorient breaking other H bonds to accommodate the reaction, whereas, at 900 K/1200 K, the temperature-induced shift in crystallinity pushes the neighboring molecules away cleaving H bonds and reducing the extent of their involvement in the reaction. Therefore, the free-energy barrier calculated using molecular modelling, supports and validates the qualitative trends in the RMSD probability distributions when it comes to using ML to decipher the extents of melt configuration changes in the decomposition of cellobiose across different temperatures (Fig. 5), from which it can be concluded that the barrier for glycosidic cleavage in the condensed phase is heavily influenced by the reorganization energy of the solvent.
for the decomposition of the cellobiose melt to LGA. At higher temperatures the FEB flattens indicating that the entropic contribution to the barrier is zero, making it an enthalpy-controlled regime. Hence, the linear slopes of the low temperature and the high temperature curves form distinct decomposition regimes, also measured using millisecond scale kinetics experiments.71 The temperature-induced conformational changes in the molecules going from the crystal to the melt-phase influence cellulose chemistry. At low temperatures, cellulose exists in its crystalline state with an ordered intermolecular H bonding network which makes it energy intensive for the twisting and breaking of cellulose chains. At higher temperatures, the cellulose matrix expands taking a low-density state and disrupts the ordered H bonding network. As seen in Fig. 5, the free energy barrier is high which decreases with temperatures to eventually settle above 900 K. This is in coherence with the condensed phase reorganization probability predictions. At 100 K/500 K, the probability for reorganization is high as the neighboring molecules are close by and they would have to reorient breaking other H bonds to accommodate the reaction, whereas, at 900 K/1200 K, the temperature-induced shift in crystallinity pushes the neighboring molecules away cleaving H bonds and reducing the extent of their involvement in the reaction. Therefore, the free-energy barrier calculated using molecular modelling, supports and validates the qualitative trends in the RMSD probability distributions when it comes to using ML to decipher the extents of melt configuration changes in the decomposition of cellobiose across different temperatures (Fig. 5), from which it can be concluded that the barrier for glycosidic cleavage in the condensed phase is heavily influenced by the reorganization energy of the solvent.
The ratio of probabilities of an observed RMSD (change in molecular configurations in the product trajectory from the average of the configuration changes in the reactant profiles), evaluated from the kernel density estimates of the two cellobiose systems at the extremes of melt configuration changes (100 K and 900 K), is called the posterior (eqn (8)). It quantifies the probability of a cellobiose system having a similar extent of solvent/condensed phase reorganization in the product (after the conformational changes have equilibrated) as compared to the reactant, at a temperature of 100 K. Its trend is similar to the activation free energy barrier with temperature, indicating that the reorganization of the melt-phase from the reactant to the product governs the reaction kinetics. At lower temperatures, the cellobiose melt is more ordered and interacts with the reactant cellobiose via H bonds and hence reorients largely to accommodate the structural changes when the reactant goes to its TS. However, at high temperatures the condensed phase matrix is already broken and its density is lower, because of which the melt-phase molecules need not reorient significantly between the reactant and its TS. Hence, prominent reorganization of solvent molecules at lower temperature results in larger entropy differences, as compared to higher temperatures.
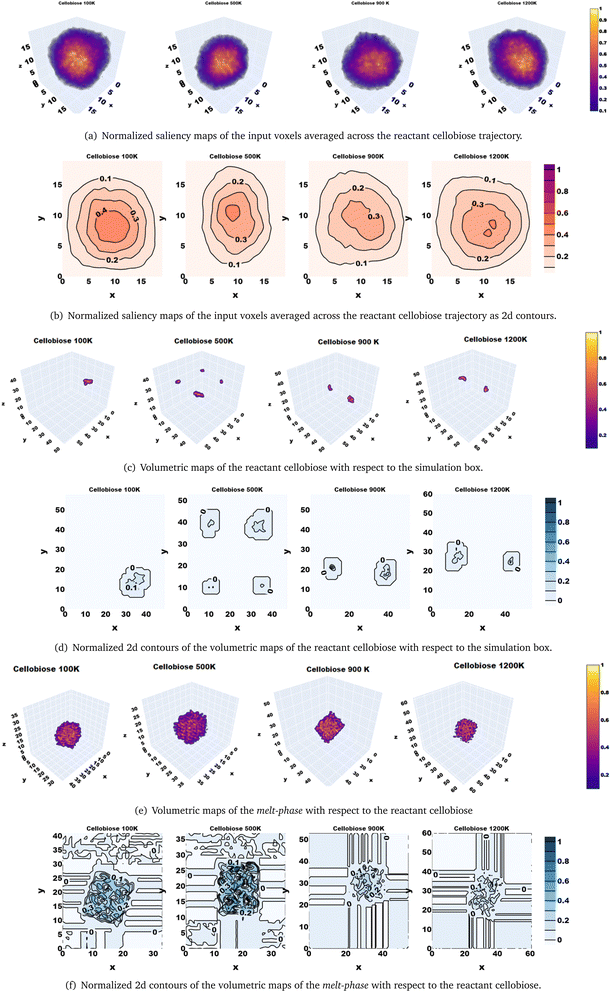
Thus far, the predictions from the ML model have been rationalized by the physics of the reactive systems. However, it is difficult to physically interpret the bottleneck features of the 3d CNN autoencoder that inherently capture signatures mapping to solvent configuration changes. Explainability in CNNs that capture spatial information has been demonstrated using saliency maps that comprise gradient information of the loss function with respect to the input data and hence hold information about regions of the input space that are sensitized while minimizing a certain loss, in making target predictions for supervised machine learning tasks.72 Since we developed a 3d-CNN autoencoder as a self-supervised ML model in this work, the saliency maps have been analyzed as gradients of the strongest activated neuron in the bottleneck layer with respect to the averaged input data voxels. Inspection of the time-averaged saliency maps reveals that the 3d-CNN autoencoder is sensitized by a locally centered domain of the simulation voxel (Fig. 6(a)) of the trajectories of the solvent molecules around the reactant cellobiose, whose 2d contours are also shown in Fig. 6(b). The activated intensities of the 3d-CNN in the central region of the simulation box do not overlap with the reactant cellobiose (Fig. 6(c) and (d)), but coincide with the regions occupied by the condensed phase (Fig. 6(e) and (f)). It can be deduced that the 3d-CNN autoencoder is sensitized by the melt-phase configuration changes in the bulk, rather than in the vicinity of the reactant because the saliency maps corresponding to the strongly activated feature in the bottleneck layer that is used as a basis for distance-based classification are seen to build on the spatio-temporal features extracted from the Cartesian coordinates of atoms in the condensed melt-phase (solvent). Ultimately, the reorganization of the bulk melt-phase impacts the temperature-induced conformational changes in the reactant cellobiose, and it has been validated that the ML model captures the same by means of the feature saliency maps.
3.2 Testing the ML model predictions on fructose dehydration and glucose isomerization
This section focuses on using the ML model trained on the cellobiose systems to make predictions about the solvent configuration changes in two other systems: (i) glucose isomerization and (ii) fructose dehydration, using the reactant simulation trajectories in different solvent environments. This is proposed to be achieved by obtaining the spatio-temporal encoded features from the trajectory of solvent molecules around the reactant molecules of different systems, from the 3d-CNN autoencoder before classifying them using the Mahalanobis classifier in terms of the distance of the features of these systems from the distributions of features from the cellobiose systems at lower temperatures, viz. 100 K and 500 K (established as systems with significant melt-phase configuration changes). Hydride transfer is the rate limiting step in glucose isomerization and involves charge transfer in the reactant. Thereby, solvent polarizability has a dominant effect on the associated reaction activation free energy barrier. In the dehydration of fructose, polar aprotic solvents such as dimethylsulfoxide (DMSO) are known to result in higher reactivities. The stability of the catalyst (hydronium ion) in the first solvation shell of fructose as compared to the bulk of the solvent is seen to differ across the composition ratios of the solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosolvent, thereby impacting the reaction kinetics in the conversion of fructose.
cosolvent, thereby impacting the reaction kinetics in the conversion of fructose.
Simulations for hydride transfer in glucose isomerization were performed using two different solvents viz., water and methanol and have been recorded over 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 45
000 and 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation time steps, respectively of 0.0964 fs each. The solvation dynamics of these non-equilibrium simulations indicate an increase in the carbon–hydrogen bond length due to hydride transfer, commencing after ∼8000 and 10
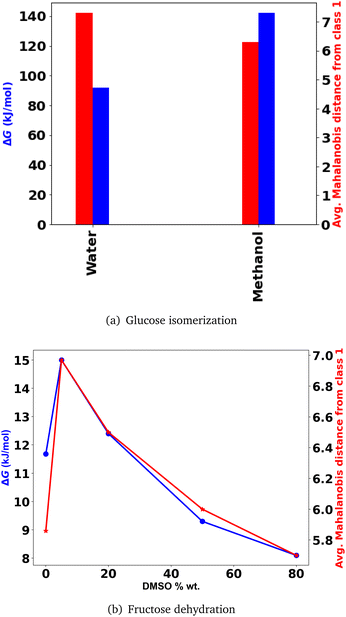
000 simulation time steps, respectively of 0.0964 fs each. The solvation dynamics of these non-equilibrium simulations indicate an increase in the carbon–hydrogen bond length due to hydride transfer, commencing after ∼8000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps, for the water and methanol systems, respectively. For the purpose of prediction using our trained ML model, these initial time steps will be treated as the reactant configurations.15 A voxel sample over every 100 time steps i.e. 9.64 fs would lead to 80 and 100 samples, for the reactant trajectories in water and methanol, respectively. The spatio-temporal 3d CNN provides encoded latent features for these samples from the reactant trajectories. When we are interested in quantifying the overall solvent configuration changes of the system as a whole using these simulations, it must be noted that even highly reoriented systems may have points in their trajectories where configurations do not change much and vice versa for lower reoriented systems. Therefore, the average of the Mahalanobis distance of each of the sample encoded features, from the distributions of features of the low temperature cellobiose systems at 100 K and 500 K, is used to assess solvent configuration changes, as shown in Fig. 7(a). This indicates that methanol reorients to a greater extent than water during the hydride transfer reaction in glucose isomerization. This is substantiated by the fact that a change in the charge structure of glucose during the hydride shift has the tendency to polarize methanol to a larger extent than water because of which its activation free energy barrier (ΔG (kJ mol−1)) for the hydride transfer is 50 kJ mol−1 higher15 (Fig. 7(a)). The large electronic polarization of methanol results in its significant reorientation during the hydride transfer and much slower relaxation dynamics resulting in the non-equilibrium solvation of the transition state, while water undergoes lower electronic polarization and subsequently reorients to a lesser extent because of which its relaxation dynamics is near equilibrium solvation in going from the transition state to the product, both of which are better solvated by water and result in lower activation energy of hydride transfer.
000 time steps, for the water and methanol systems, respectively. For the purpose of prediction using our trained ML model, these initial time steps will be treated as the reactant configurations.15 A voxel sample over every 100 time steps i.e. 9.64 fs would lead to 80 and 100 samples, for the reactant trajectories in water and methanol, respectively. The spatio-temporal 3d CNN provides encoded latent features for these samples from the reactant trajectories. When we are interested in quantifying the overall solvent configuration changes of the system as a whole using these simulations, it must be noted that even highly reoriented systems may have points in their trajectories where configurations do not change much and vice versa for lower reoriented systems. Therefore, the average of the Mahalanobis distance of each of the sample encoded features, from the distributions of features of the low temperature cellobiose systems at 100 K and 500 K, is used to assess solvent configuration changes, as shown in Fig. 7(a). This indicates that methanol reorients to a greater extent than water during the hydride transfer reaction in glucose isomerization. This is substantiated by the fact that a change in the charge structure of glucose during the hydride shift has the tendency to polarize methanol to a larger extent than water because of which its activation free energy barrier (ΔG (kJ mol−1)) for the hydride transfer is 50 kJ mol−1 higher15 (Fig. 7(a)). The large electronic polarization of methanol results in its significant reorientation during the hydride transfer and much slower relaxation dynamics resulting in the non-equilibrium solvation of the transition state, while water undergoes lower electronic polarization and subsequently reorients to a lesser extent because of which its relaxation dynamics is near equilibrium solvation in going from the transition state to the product, both of which are better solvated by water and result in lower activation energy of hydride transfer.
For the fructose systems, MD simulations have been carried out at different solvent compositions and have been recorded every 200 time steps for a duration of 10 ns. Hence, a voxel sample over every 100 ps would lead to 100 samples from each of these trajectories. The average of the Mahalanobis distance of each of these 100 fructose features from the distributions of features of the cellobiose systems at 100 K and 500 K is shown in Fig. 7(b). The results are seen to concur with the trends of the relative stability of hydronium ions at different DMSO concentrations given by the difference (ΔG) in the free energy surface (FES) minimum corresponding to the hydronium ion in the first solvation shell of fructose and that of the FES minimum corresponding to the hydronium ion in the bulk solvent,53 as shown in Fig. 7(b). The increase in ΔG when DMSO goes from 0 to 5% wt can be attributed to the instability of DMSO molecules in the bulk solvent, generating a rich local domain of DMSO molecules near fructose while the water (solvent) molecules in the bulk stabilize the hydronium ion. However, as the DMSO concentrations increase from 5 to 80% wt a clear descending trend is observed in ΔG and the average distance from the strongly reoriented cellobiose systems (class 1), suggesting that the relative stability of hydronium ions in the first solvation shell of fructose increases. Brønsted acid catalysis of biomass components in water and co-solvent had a higher proportion of water in the first solvation shell compared to the bulk. Such water enriched local domains are formed with an increase in the co-solvent concentration around the hydroxyl groups of reactants, promoting proton transfer,18,73–77 making the reaction highly dependent on the water concentration in the first solvation shell. Aprotic solvents such as DMSO have been reported to drastically increase the HMF selectivity and fructose conversion78–82 owing to the furanose conformation83 that stabilizes the TS84,85 and induces hydroxyl (fructose) interactions with water.3 Moreover, with an increase in the DMSO concentration acid-catalysis is enhanced as the relative stability of the proton near fructose (reactant) and HMF (product), increases and decreases, respectively.77 In polar aprotic solvents, the free energy of H+ solvation decreases by 24 kJ mol−1 compared to water.11 Recombination of protons was promoted, leading to decreased dehydration rates suggesting that polar aprotic solvents significantly destabilize the proton. In the case of glucose dehydration to HMF, glucose hydroxyl groups and solvents compete for the proton. Addition of DMSO as co-solvent improved the conversion, because of its lower affinity for protons.86,87
It must be noted that the free energy barriers indicate different aspects in both of the systems discussed above. Hence, an identical trend in the free energy barrier is not observed across both the systems as they get closer in distance to the low temperature cellobiose systems where the melt phase is found to reorganize significantly. In the water and methanol systems, the charge distribution in the reactant glucose due to the hydride transfer polarizes the solvent molecules, and leads to higher reaction energy barrier in more polar solvents such as methanol that reorient to a greater extent by virtue of the reaction, therefore found to lie at a closer distance to the highly reorganizing lower temperature melt-phase cellobiose systems. However, in fructose systems, the relative concentrations of the protic solvent (water) and the aprotic co-solvent (DMSO) govern the instability of the hydronium ion in the bulk, thereby providing a driving force for it to migrate towards the first solvation shell of fructose in the presence of large concentrations of aprotic DMSO. The free energy difference in this case is a measure of the thermodynamic instability in the first solvation shell as opposed to the bulk. Hence, lower free energy corresponds to a decline in the relative instability, i.e., an increase in stability of the first solvation shell, prompting solvent reorientation that subsequently facilitates the reactive transformation of fructose into HMF, and is consistent with the decrease in distance from the lower temperature cellobiose systems (denoted as class 1 in ML classifier terminology).
4 Conclusions
In this study, three systems have been evaluated for configuration changes in solvent molecules that are known to impact reaction thermodynamics. The term solvent molecules broadly encompasses the melt-phase in condensed cellobiose glycosidic bond cleavage, polarizable solvents (water and methanol) in glucose isomerization via hydride transfer, and water along with organic co-solvent molecules in the acid catalyzed dehydration of fructose. Cellobiose pyrolysis kinetics are impacted by the melt temperature, while the hydride transfer in glucose isomerization involving charge transfer in the reactant is impacted by polarity of the solvents, and finally the proton affinity of the solvent/co-solvent is seen to impact the dehydration of fructose. We have demonstrated the effectiveness of a self-supervised framework for training predictive machine learning models to assess solvent configuration changes, which are seen to arise from different factors in each of the three systems presented. The ML model is not only computationally efficient to train but can also inform the decision of whether the solvent molecules ought to be considered explicitly when performing molecular dynamics simulations or not, thereby limiting the computational cost.A 3d-CNN autoencoder for spatio-temporal feature extraction is trained on both the simulation trajectories of the solvent molecules surrounding the reactant and product molecules in the condensed phase transglycosylation reaction of cellobiose at different temperatures. The probability distributions across the RMSD of the features between the product and the reactant profiles are seen to show a higher probability of solvent configuration changes for the lower temperature finite simulations at 100 K and 500 K. These findings are consistent with the linear decrease in the free energy barrier with increasing temperatures, supporting that the reaction kinetics is impacted by the reorganization of the melt-phase from the reactant to the product. To assess the extent of solvent configuration changes in newer systems, a quadratic classifier based on the Mahalanobis distance metric is then used to calculate the average distance between features from the trajectory of the solvent molecules around the reactant in test systems; and the distribution of features from the reactant trajectory of the strongly reorganizing low temperature cellobiose systems (100 K and 500 K). The ML model assesses methanol to reorient to a greater extent than water and is consistent with the prior findings in the literature where the changes in the charge structure due to hydride transfer in glucose have a tendency to polarize methanol to a greater extent than water, because of which the reaction activation free energy is ∼50 kJ mol−1 higher in methanol. For the fructose dehydration systems, the average Mahalanobis distance from the cellobiose systems at 100 K and 500 K is seen to increase at first and then decrease almost linearly with increasing concentrations of DMSO, consistent with the trends in the difference between the free energy surface minima that point to a larger impact of solvent configuration changes on reaction kinetics with increasing DMSO concentrations. It has been demonstrated that the ML framework can generalize well when it comes to predicting the extent of solvent reorganization across different systems by using their reactant trajectory simulations. Hence, it can be used to limit computational efforts when simulating product trajectories in systems where solvent configuration changes are found to be lower, by eliminating the dynamics of the said molecules and/or eliminating the necessity for an explicit condensed phase environment. Consequently, if a library of solvents is to be screened for their suitability in chemical reactions using molecular simulations, one could assess whether or not to explicitly simulate the solvent molecules with the aid of the ML framework presented in this paper.
Data availability
All the datasets and codes used to reproduce the results of the manuscript have been publicly hosted on the GitHub repository https://github.com/Anjana-T-Puliyanda/3dCNN-Autoencoder-for-solvent-configuration-changes/tree/main.Conflicts of interest
There is no conflict of interest for the authors to declare.Acknowledgements
Anjana Puliyanda and Vinay Prasad would like to acknowledge funding from Alberta Innovates (currently Innotech), the MITACS Globalink Graduate Fellowship, and funding from the Natural Sciences and Engineering Research Council of Canada (NSERC) for support in the form of a scholarship. Vinay Prasad also acknowledges support from the Jaffer Professorship in Process Systems and Control Engineering. Samir H. Mushrif and Arul Mozhi Devan Padmanathan acknowledge financial support from NSERC and the Canada First Research Excellence Fund as part of the University of Alberta's Future Energy Systems research initiative. Samir H. Mushrif also acknowledges computational support from the Digital Research Alliance of Canada.References
- P. Kolář, J.-W. Shen, A. Tsuboi and T. Ishikawa, Fluid Phase Equilib., 2002, 194, 771–782 CrossRef
.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC
.
- S. H. Mushrif, S. Caratzoulas and D. G. Vlachos, Phys. Chem. Chem. Phys., 2012, 14, 2637–2644 RSC
.
- G. Feng, Z. Liu, P. Chen and H. Lou, RSC Adv., 2014, 4, 49924–49929 RSC
.
- S. Sato, T. Murakata, S. Baba, Y. Saito and S. Watanabe, J. Appl. Polym. Sci., 1990, 40, 2065–2071 CrossRef CAS
.
- C. Krumm, J. Pfaendtner and P. J. Dauenhauer, Chem. Mater., 2016, 28, 3108–3114 CrossRef CAS
.
- V. Agarwal, G. W. Huber, W. C. Conner and S. M. Auerbach, J. Chem. Phys., 2011, 135, 134506 CrossRef PubMed
.
- P. J. Dauenhauer, J. L. Colby, C. M. Balonek, W. J. Suszynski and L. D. Schmidt, Green Chem., 2009, 11, 1555–1561 RSC
.
- C. Zhu, C. Krumm, G. G. Facas, M. Neurock and P. J. Dauenhauer, React. Chem. Eng., 2017, 2, 201–214 RSC
.
- A. M. D. Padmanathan and S. H. Mushrif, React. Chem. Eng., 2022, 7, 1136–1149 RSC
.
- L. Shuai and J. Luterbacher, ChemSusChem, 2016, 9, 133–155 CrossRef CAS PubMed
.
- R. Cukier and D. Nocera, J. Chem. Phys., 1992, 97, 7371–7376 CrossRef CAS
.
- S. Chakrabarti, M. Liu, D. H. Waldeck, A. M. Oliver and M. N. Paddon-Row, J. Phys. Chem. A, 2009, 113, 1040–1048 CrossRef CAS PubMed
.
- M. Tachiya, Radiat. Phys. Chem., 1996, 47, 43–46 CrossRef CAS
.
- S. H. Mushrif, J. J. Varghese and C. B. Krishnamurthy, Phys. Chem. Chem. Phys., 2015, 17, 4961–4969 RSC
.
- N. Nikbin, S. Caratzoulas and D. G. Vlachos, ChemCatChem, 2012, 4, 504–511 CrossRef CAS
.
- M. A. Mellmer, D. M. Alonso, J. S. Luterbacher, J. M. R. Gallo and J. A. Dumesic, Green Chem., 2014, 16, 4659–4662 RSC
.
- M. A. Mellmer, C. Sener, J. M. R. Gallo, J. S. Luterbacher, D. M. Alonso and J. A. Dumesic, Angew. Chem., Int. Ed., 2014, 53, 11872–11875 CrossRef CAS PubMed
.
- Y. Román-Leshkov, J. N. Chheda and J. A. Dumesic, Science, 2006, 312, 1933–1937 CrossRef PubMed
.
- Z. Wei, Y. Li, D. Thushara, Y. Liu and Q. Ren, J. Taiwan Inst. Chem. Eng., 2011, 42, 363–370 CrossRef CAS
.
- M. Mellmer, J. Gallo, D. M. Alonso, J. Dumesic, D. Alonso and J. Dumesic, Selective production of levulinic acid from furfuryl alcohol in THF solvent systems over H-ZSM-5, ACS Catal., 2015, 5, 3354–3359 CrossRef CAS
.
- Y. J. Pagan-Torres, T. Wang, J. M. R. Gallo, B. H. Shanks and J. A. Dumesic, ACS Catal., 2012, 2, 930–934 CrossRef CAS
.
- T. Zhang, R. Kumar and C. E. Wyman, RSC Adv., 2013, 3, 9809–9819 RSC
.
- P. Maurel, J. Biol. Chem., 1978, 253, 1677–1683 CrossRef CAS PubMed
.
- R. P. Mariella, R. R. Raube, J. Budde and C. E. Moore, J. Org. Chem., 1954, 19, 678–682 CrossRef CAS
.
- J. Catalán, J. Phys. Chem. B, 2009, 113, 5951–5960 CrossRef PubMed
.
- T. W. Walker, A. K. Chew, H. Li, B. Demir, Z. C. Zhang, G. W. Huber, R. C. Van Lehn and J. A. Dumesic, Energy Environ. Sci., 2018, 11, 617–628 RSC
.
-
C. Reichardt and T. Welton, Solvents and solvent effects in organic chemistry, John Wiley & Sons, 2011 Search PubMed
.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed
.
- N. V. Orupattur, S. H. Mushrif and V. Prasad, Comput. Mater. Sci., 2020, 174, 109474 CrossRef CAS
.
- M. Rupp, M. R. Bauer, R. Wilcken, A. Lange, M. Reutlinger, F. M. Boeckler and G. Schneider, PLoS Comput. Biol., 2014, 10, 1–8 CrossRef PubMed
.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed
.
- A. S. Alshehri, R. Gani and F. You, Comput. Chem. Eng., 2020, 141, 107005 CrossRef CAS
.
- T. Morawietz and N. Artrith, J. Comput.-Aided Mol. Des., 2021, 35, 557–586 CrossRef CAS PubMed
.
- J. Xu, X.-M. Cao and P. Hu, Phys. Chem. Chem. Phys., 2021, 23, 11155–11179 RSC
.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed
.
-
W. Jia, H. Wang, M. Chen, D. Lu, L. Lin, R. Car, W. E and L. Zhang, Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning, 2020 Search PubMed
.
- L. Böselt, M. Thürlemann and S. Riniker, J. Chem. Theory Comput., 2021, 17, 2641–2658 CrossRef PubMed
.
- Y. Wang, J. M. Lamim Ribeiro and P. Tiwary, Curr. Opin. Struct. Biol., 2020, 61, 139–145 CrossRef CAS PubMed
.
- A. Aspuru-Guzik, R. Lindh and M. Reiher, ACS Cent. Sci., 2018, 4, 144–152 CrossRef CAS PubMed
.
- J. Gebhardt, M. Kiesel, S. Riniker and N. Hansen, J. Chem. Inf. Model., 2020, 60, 5319–5330 CrossRef CAS PubMed
.
- V. Botu and R. Ramprasad, Int. J. Quantum Chem., 2015, 115, 1074–1083 CrossRef CAS
.
- F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, J. Phys.: Conf. Ser., 2020, 1412, 042003 CrossRef
.
- S. Jiang and V. M. Zavala, AIChE J., 2021, 67, e17282 CrossRef CAS
.
- A. S. Kelkar, B. C. Dallin and R. C. Van Lehn, J. Phys. Chem. B, 2020, 124, 9103–9114 CrossRef CAS PubMed
.
- A. K. Chew, S. Jiang, W. Zhang, V. M. Zavala and R. C. Van Lehn, Chem. Sci., 2020, 11, 12464–12476 RSC
.
- T. W. Walker, A. K. Chew, R. C. Van Lehn, J. A. Dumesic and G. W. Huber, Top. Catal., 2020, 63, 649–663 CrossRef CAS
.
- F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, Chem. Sci., 2019, 10, 2298–2307 RSC
.
- V. Maliekkal, S. Maduskar, D. J. Saxon, M. Nasiri, T. M. Reineke, M. Neurock and P. Dauenhauer, ACS Catal., 2019, 9, 1943–1955 CrossRef CAS
.
- F. S. Asghari and H. Yoshida, Ind. Eng. Chem. Res., 2007, 46, 7703–7710 CrossRef CAS
.
- P. Carniti, A. Gervasini, S. Biella and A. Auroux, Catal. Today, 2006, 118, 373–378 CrossRef CAS
.
-
F. Babiloni, L. Bianchi, F. Semeraro, J. del R Millan, J. Mourino, A. Cattini, S. Salinari, M. G. Marciani and F. Cincotti, 2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2001, vol. 1, pp. 651–654 Search PubMed
.
- J. C. Velasco Calderón, S. Jiang and S. H. Mushrif, ChemPhysChem, 2021, 22, 2222–2230 CrossRef PubMed
.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed
.
- V. K. Ramaswamy, S. C. Musson, C. G. Willcocks and M. T. Degiacomi, Phys. Rev. X, 2021, 11, 011052 CAS
.
-
R. Singh, A. Sharma, O. R. Bingol, A. Balu, G. Balasubramanian, D. D. Johnson and S. Sarkar, 3D Deep Learning with voxelized atomic configurations for modeling atomistic potentials in complex solid-solution alloys, 2018 Search PubMed
.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed
.
-
K. O'Shea and R. Nash, An Introduction to Convolutional Neural Networks, 2015 Search PubMed
.
-
T. Szandała, in Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks, ed. A. K. Bhoi, P. K. Mallick, C.-M. Liu and V. E. Balas, Springer Singapore, Singapore, 2021, pp. 203–224 Search PubMed
.
-
I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed
.
- P. C. Hansen, Numer. Algorithms, 2002, 29, 323–378 CrossRef
.
-
D. Bank, N. Koenigstein and R. Giryes, Autoencoders, 2021 Search PubMed
.
-
R. Yamashita, M. Nishio, R. K. G. Do and K. Togashi, Insights into Imaging, 2018, 9, 611–629 Search PubMed
.
-
S. Węglarczyk, ITM Web Conf., 2018, vol. 23 Search PubMed
.
- A. K. Ghosh, P. Chaudhuri and D. Sengupta, Technometrics, 2006, 48, 120–132 CrossRef
.
- V. Seshadri and P. R. Westmoreland, J. Phys. Chem. A, 2012, 116, 11997–12013 CrossRef CAS PubMed
.
- M. W. Nolte and M. W. Liberatore, Energy Fuels, 2010, 24, 6601–6608 CrossRef CAS
.
- A. Pictet and J. Sarasin, Helv. Chim. Acta, 1918, 1, 87–96 CrossRef
.
- X. Zhou, M. W. Nolte, H. B. Mayes, B. H. Shanks and L. J. Broadbelt, Ind. Eng. Chem. Res., 2014, 53, 13274–13289 CrossRef CAS
.
- A. Demirbas and G. Arin, Energy Sources, 2002, 24, 471–482 CrossRef CAS
.
- C. Krumm, J. Pfaendtner and P. J. Dauenhauer, Chem. Mater., 2016, 28, 3108–3114 CrossRef CAS
.
-
K. Simonyan, A. Vedaldi and A. Zisserman, Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps, 2014 Search PubMed
.
- W. J. Cheong and P. W. Carr, Anal. Chem., 1988, 60, 820–826 CrossRef CAS
.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422 CrossRef CAS PubMed
.
- M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794 CrossRef CAS
.
- C. Kalidas, G. Hefter and Y. Marcus, Chem. Rev., 2000, 100, 819–852 CrossRef CAS PubMed
.
- J. C. Velasco Calderón, S. Jiang and S. H. Mushrif, ChemPhysChem, 2021, 22, 2222–2230 CrossRef PubMed
.
- R. Weingarten, A. Rodriguez-Beuerman, F. Cao, J. S. Luterbacher, D. M. Alonso, J. A. Dumesic and G. W. Huber, ChemCatChem, 2014, 6, 2229–2234 CrossRef CAS
.
- J. He, M. Liu, K. Huang, T. W. Walker, C. T. Maravelias, J. A. Dumesic and G. W. Huber, Green Chem., 2017, 19, 3642–3653 RSC
.
- M. Tucker, R. Alamillo, A. Crisci, G. Gonzalez, S. Scott and J. Dumesic, ACS Sustainable Chem. Eng., 2013, 1, 554–560 CrossRef CAS
.
- A. H. Motagamwala, K. Huang, C. T. Maravelias and J. A. Dumesic, Energy Environ. Sci., 2019, 12, 2212–2222 RSC
.
- X. Qi, M. Watanabe, T. M. Aida and R. L. Smith Jr, Green Chem., 2008, 10, 799–805 RSC
.
- M. Bicker, D. Kaiser, L. Ott and H. Vogel, J. Supercrit. Fluids, 2005, 36, 118–126 CrossRef CAS
.
- J. M. R. Gallo, D. M. Alonso, M. A. Mellmer and J. A. Dumesic, Green Chem., 2013, 15, 85–90 RSC
.
- L. Qi, Y. F. Mui, S. W. Lo, M. Y. Lui, G. R. Akien and I. T. Horvath, ACS Catal., 2014, 4, 1470–1477 CrossRef CAS
.
- X. Qian and D. Liu, Carbohydr. Res., 2014, 388, 50–60 CrossRef CAS PubMed
.
- X. Qian, J. Phys. Chem. A, 2011, 115, 11740–11748 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00049h |
| This journal is © The Royal Society of Chemistry 2024 |