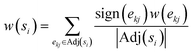Open Access Article
Open Access ArticleSolvmate – a hybrid physical/ML approach to solvent recommendation leveraging a rank-based problem framework†
Jan
Wollschläger
 * and
Floriane
Montanari‡
* and
Floriane
Montanari‡
Machine Learning Research, Bayer Pharmaceuticals, Müllerstr. 178, Berlin, 13353, Germany. E-mail: jan.wollschlaeger@bayer.com
First published on 30th July 2024
Abstract
The solubility in a given organic solvent is a key parameter in the synthesis, analysis and chemical processing of an active pharmaceutical ingredient. In this work, we introduce a new tool for organic solvent recommendation that ranks possible solvent choices requiring only the SMILES representation of the solvents and solute involved. We report on three additional innovations: first, a differential/relative approach to solubility prediction is employed, in which solubility is modeled using pairs of measurements with the same solute but different solvents. We show that a relative framing of solubility as ranking solvents improves over a corresponding absolute solubility model across a diverse set of selected features. Second, a novel semiempirical featurization based on extended tight-binding (xtb) is applied to both the solvent and the solute, thereby providing physically meaningful representations of the problem at hand. Third, we provide an open-source implementation of this practical and convenient tool for organic solvent recommendation. Taken together, this work could be of benefit to those working in diverse areas, such as chemical engineering, material science, or synthesis planning.
1 Introduction
The solubility in a given organic solvent is a key parameter in the synthesis, analysis and chemical processing of an active pharmaceutical ingredient (API).1–4 Therefore, it is a vital consideration reaching from initial drug discovery to final manufacturing.5,6 Hence, the development of a practical and reliable organic solvent recommendation system promises a reduction in both material costs and time-to-market.5,7Modelling of solubility can be roughly divided into physical, data-driven and hybrid approaches. Physical approaches aim to describe actual physical interactions involved in the observed solubility from first principles.8 Purely data-driven approaches lie on the other end of the spectrum and aim to employ statistical models without a priori knowledge of the physical effects involved. Due to its importance in drug discovery considerations, aqueous solubility prediction has been a major subject of focus. Hence, a plethora of approaches such as fragment-based,9 molecular-dynamics,10 general-solubility equation,11–13 Hansen solubility parameters and Hildebrandt solubility parameters,14,15 and first principle ab initio calculations have been reported.16–19 More recently, we see a switch of focus towards quantitative structure property relationships (QSPR) via statistical techniques.20–24 The Open Notebook Science challenge25 is one of the few data sources of organic solubility (i.e., solubility in solvents other than water), but has received little attention in comparison to the aqueous case.26,27
Vermeire et al.28 reported on a combined physical/ML approach that is applicable to a wide range of organic solvents and temperatures (RMSE ≈ 0.89, MAE ≈ 0.62). A recent communication29 reported on a hybrid approach towards organic solubility, that combines machine learning (ML) and ab initio calculations. In this study, a focused set of 14 physicochemical descriptors were chosen based on their significance in influencing the dissolution process. These descriptors encompass both properties derived from ab initio computations as well as the experimentally determined melting point. With this setup, an error of RMSE(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) ≈ 0.7 was obtained, which is close to the experimental accuracy of 0.7–1.0 log units for drug-like molecules.5,30 While this work does illustrate the advantages of hybrid physical/ML modelling, it is still somewhat restricted from a practical point of view: it requires expensive ab initio calculations, supports a limited set of solvents (acetone, benzene, and ethanol), and requires the experimental melting point.
S) ≈ 0.7 was obtained, which is close to the experimental accuracy of 0.7–1.0 log units for drug-like molecules.5,30 While this work does illustrate the advantages of hybrid physical/ML modelling, it is still somewhat restricted from a practical point of view: it requires expensive ab initio calculations, supports a limited set of solvents (acetone, benzene, and ethanol), and requires the experimental melting point.
Vassileiou et al.31 further support the observation that hybrid physical/ML approaches lead to improved predictive performance. Here, the conductor-like screening model for real solvents (COSMO-RS) with RMSE(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) ≈ 1.0 is critically compared against machine learning on 2D descriptors (RMSE(log
S) ≈ 1.0 is critically compared against machine learning on 2D descriptors (RMSE(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) ≈ 0.92), as well as hybrid models thereof, with hybrid models (RMSE(log
S) ≈ 0.92), as well as hybrid models thereof, with hybrid models (RMSE(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) ≈ 0.8) giving the best results. While the set of solvents was extended over ref. 29, it is still restrained to a limited set, and also shares the requirement of an experimental melting point as well as expensive electronic structure calculations.
S) ≈ 0.8) giving the best results. While the set of solvents was extended over ref. 29, it is still restrained to a limited set, and also shares the requirement of an experimental melting point as well as expensive electronic structure calculations.
In our quest to implement a more convenient solvent recommendation tool, we thus asked ourselves two questions:
Could the expensive ab initio calculations be replaced by faster approximate methods?
Are experimental melting points strictly required to produce accurate QSPR solubility predictions?
To replace the expensive ab initio models, a computationally efficient yet accurate solvation model based on the analytical linearized Poisson–Boltzmann (ALPB) parameterized for the extended tight binding (xtb) method32 was selected as a replacement for the more expensive COSMO-RS used in prior studies. The proposed method performs well over a broad range of systems and applications. For hydration free energies of small molecules, xtb(ALPB) is reaching the accuracy of sophisticated explicitly solvated approaches, with a mean absolute deviation of only 1.4 kcal mol−1 compared to experiment.32 While this compares favorably against COSMO (MAE = 2.19 kcal mol−1), it is worse than the computationally more elaborate COSMO-RS (MAECOSMO-RS = 0.52 kcal mol−1).33
But logarithmic octanol/water partitioning coefficients are computed with a MAE ≈ 0.65 log units,32 which is comparable to the performance of COSMO-RS with MAE ≈ 0.57.34 This indicates that xtb gives a consistent description of differential solvent effects,32 which we regarded as crucial for hybrid physics/ML descriptors in organic solvent recommendation. Concerning the second question, it has to be noted that the solubility of molecules in their solid state depends not only on the energy gained by solvation, but also upon the energy required for breaking up the crystal lattice in the solid.30 Therefore, including these solid state effects into the solubility modelling would likely lead to significant improvements. However, the modelling of the solid–solid interactions proves to be exceptionally difficult, as it depends on the minute details of the geometrical arrangement of the molecules in the crystal lattice.30 This can also be seen by the large errors in melting point prediction RMSE(ΔTmp) ≈ 40 − 50 °C, even though the experimental error is probably less than 5 °C.35,36 Although prohibitively computationally expensive at the moment, it seems quite likely that ab initio crystal structure prediction (CSP) could be involved to model the solid state crystal lattice energy contribution to solubility phenomena in the long term.37 As solubility differences between polymorphs (2-fold) are considerably lower than errors in solubility prediction (5- to 10-fold), it might not even be required to identify the correct polymorphic form.38 However, for the time remaining for such CSP tools to become feasible for routine use, the exact structure of the crystal phase remains elusive.
This raises the question whether it is possible to pose the solubility problem in a manner that eliminates the need for a description of the solid state, motivating the main idea behind the present work: modelling organic solubility/solvent selection as a ranking problem.
2 Methods
2.1 Data curation: general
Solubility data was collected from the Open Notebook Science Challenge,25§ as well as from a publication on solvent selection for crystallization, hereafter referred to as .39
.39
Temperature variations are ignored, and hence contribute to the overall error of the model. But, with a temperature span of 20–30 °C, with most data points recorded at 25 °C, we believe the system to be well-calibrated to typical lab room temperature conditions.
As  only provides qualitative labels for solubility, the following ordinal encoding was applied: partially soluble: (1), thermally soluble: (2), kinetically soluble: (3), readily soluble: (4). Entries where either solubility information, solvent SMILES or solute SMILES are missing were removed. Data from Bayer's internal solvent screening lab is also qualitative, and was converted into an ordinal numbering encoding in the same manner as the source
only provides qualitative labels for solubility, the following ordinal encoding was applied: partially soluble: (1), thermally soluble: (2), kinetically soluble: (3), readily soluble: (4). Entries where either solubility information, solvent SMILES or solute SMILES are missing were removed. Data from Bayer's internal solvent screening lab is also qualitative, and was converted into an ordinal numbering encoding in the same manner as the source  .
.
Next, only those data points were kept that contain measurements in at least 3 different solvents. The distribution of solvents after this preprocessing is shown in Table 1 of the ESI.† Only the most frequent 60 solvents were selected to ensure a sensible coverage within the training data and removal of unusual solvents.
2.2 Data curation: filtering for COSMO-RS calculations
Owing to the prohibitive computational demands associated with COSMO + COSMO-RS calculations, for all experiments involving COSMO-RS as a baseline, the dataset underwent a filtering process to arrive at a largely reduced dataset. For this, only solutes with five or more measurements in distinct solvents were retained to optimize the utilization of computational resources effectively. Furthermore, any data points for which COSMO-RS calculations failed (e.g. exceeding the timeout) were omitted from the dataset and not considered in the subsequent analysis outlined in the main text. This exclusion was vital to ensure a fair comparison between COSMO-RS and the other features. Throughout our discussion in the main text, we exclusively address findings derived from this reduced dataset. The dataset after this processing is provided as a CSV file in the ESI.†However, similar results are obtained (see ESI,† evaluation on full dataset) on the full dataset. Models provided in the open source package are trained on the full dataset ( +
+  ).
).
2.3 Data curation: processing of pairwise data for relative models
It was noticed that a few solutes account for many measurements in different solvents, and would consequently dominate in the pairwise data due to the quadratic scaling. Therefore, a square root-based downsampling was applied to entries with more than 50 solvent pairs (roughly more than 7 measurements for a single solute compound). For example, if a compound was measured 100 times, then instead of considering all 100 × 99/2 = 4950 pairs, only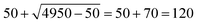 pairs would be considered at random. Pairs that differ by less than 0.01 log
pairs would be considered at random. Pairs that differ by less than 0.01 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S units or with the same qualitative solubility assignment are filtered out to prevent a ranking on pairs that are indistinguishably close in solubility. All models (relative and absolute) are evaluated on the same ranking test set.
S units or with the same qualitative solubility assignment are filtered out to prevent a ranking on pairs that are indistinguishably close in solubility. All models (relative and absolute) are evaluated on the same ranking test set.
2.4 Chemoinformatics processing
The OPSIN package was used to convert solvents specified in IUPAC nomenclature into SMILES.40 The RDKit41 was used for the initial 3D conformer generation, utilizing the experimental-torsion distance geometry with knowledge-terms (ETKDGv3) approach.42 The protonation and charge states are taken to be as defined by the SMILES string. All molecules in the training set are net-neutral, although 34 molecules contain ionized groups, 32 of which are nitro groups. For the two salts in the examples section of the ESI,† both parent ion and counter ion are embedded together as-is using the ETKDGv3 approach, without special treatment concerning the counterion position. ECFP calculations were performed using RDKit with radius 2 and 2048 bit-length.2.5 QM calculations
All xtb calculations were performed with version 6.5.1 using the GFN2-xtb/ALPB parameter file.43 COSMO-RS44 calculations are performed with the open-COSMO-RS implementation,45,46 using the accompanied open-source QM pipeline.¶ An infinite dilution assumption is approximated by screening for three different molar fractions of the solute (Xsolute ∈ 0.1, 0.01, 0.001), and concatenating all properties computed with open-COSMO-RS (total logarithmic activity coefficient, all partial molar and average interaction terms) into a single feature vector. Owing to the prohibitive computational demands associated with COSMO + COSMO-RS calculations, a timeout threshold of 48 hours was enforced.2.6 Feature selection
Extremely randomized trees (ET) trained on the following features were compared:cddd: continuous and data-driven molecular descriptors47 were selected because of the generality of this molecular representation, as well as the fact that the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D helper task applied during training of cddd is chemically strongly related to the challenge of relative solubility.
D helper task applied during training of cddd is chemically strongly related to the challenge of relative solubility.
cosmors: the conductor-like screening model for real solvents44 as implemented in open-COSMO-RS45 was selected because it is a de facto standard in organic solubility prediction.
ecfp_bit/count: extended-connectivity fingerprints in both bit-based and count-based flavors were considered as another commonly used molecular representation baseline.
rand: a uniform random real input, thus representing a random coin toss. Has no information about the problem and should thus exhibit no predictive performance.
prior: a random enumeration of the solvent classes, corresponding to the prior baseline (order all solvents according to their overall solubility on all datapoints, e.g. DMSO > hexane).
vermeire: the model described recently by Vermeire et al.28 is used as a baseline for current state-of-the-art performance in organic solubility prediction. Refers to a distinct model.
xtb: at last, we compare an ET trained on our proposed hybrid physical/ML features, as described in the section “XTB hybrid features”.
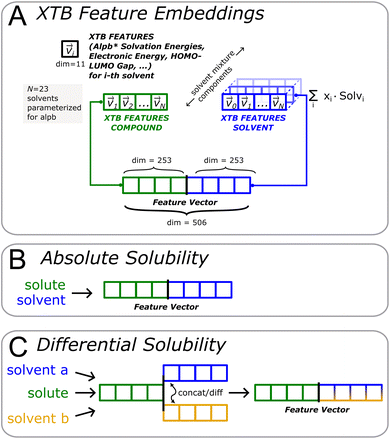
For each of these features, three different types of solubility relation were considered (where applicable): absolute refers to an absolute solubility model, while relative_concat and relative_diff describe relative solubility models employing concatenation or subtraction as the reduction operation (refer to Fig. 4).
2.7 Data splits
Spearman's rank correlation coefficient ρ is considered for the following evaluation scenarios:ρ (rand): random splits that take the solute SMILES column into account, such that every solute compound is assigned into a single CV-fold.
ρ (Butina): Taylor–Butina clustering is based on exclusion spheres at a given Tanimoto similarity level.48,49 The way the clusters are built allows all of the molecules belonging to each cluster to have a Tanimoto value above or equal to the similarity cutoff used. During each iteration, molecules are visited and labeled as either cluster centroid or as a cluster member. As such, it is an unsupervised non-hierarchical clustering algorithm that guarantees that every cluster contains molecules which are within a distance cutoff of the centroid molecule, and was chosen here as a method to generate more challenging splits that also take the chemical similarity into account. Butina clustering was performed using the RDKit with distance_threshold = 0.4.
ρ (solvent): random splits on the solvent SMILES column have been performed in such a way that each solvent is randomly assigned to one CV-split, beginning with the most frequent solvents first to balance the size of the CV-folds. This provides a very challenging generalization task, as predictions have to be made on solvents that have not been encountered during training.
ρ (ood, nova): an out-of-distribution evaluation was performed on a qualitatively-labelled dataset available in the public domain by Pillong et al.39
ρ (ood, bayer): an out-of-distribution evaluation was performed on a qualitatively-labelled Bayer-internal dataset.
2.8 Model development and evaluation
Models, as implemented in the scikit-learn framework,50 were evaluated within an outer 5-fold cross-validation utilizing one of the data splitting strategies described above. A hyperparameter search was conducted for all models on an inner three-fold cross validation (CV) using the HalvingRandomSearchCV of the scikit-learn API.51 For the RandomForestRegressor algorithm, the number of estimators (400, 700, and 1000) and maximum depth (30 and 50) were explored. The Lasso algorithm was tested with different values of alpha (0.01, 0.1, 1, and 10). For the ExtraTreesRegressor algorithm, the number of estimators (100, 200, and 300), maximum depth (none, 10, and 20), and minimum samples split (2, 5, and 10) have been varied. For the GradientBoostingRegressor algorithm, the number of estimators (100, 200, and 300), learning rate (0.01, 0.1, and 0.2), and maximum depth (3, 5, and 7) were optimized.All reported results (except vermeire) refer to extremely randomized trees (ET) regressor models, evaluated within an outer five-fold cross-validation. Error bars correspond to the variation across CV folds.
3 Results and discussion
3.1 Problem formulation: solubility as ranking
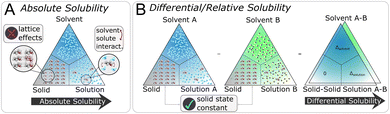
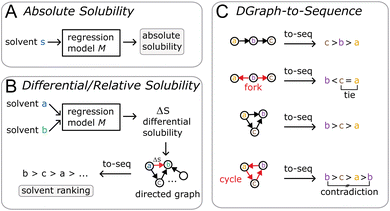
In this work, we introduce a different perspective on the problem of organic solubility. Instead of looking at the absolute value of the solubility, we frame solubility in organic solvents as a ranking problem. We envision the following scenario: a user|| specifies both the solute to be dissolved as well as a list of acceptable solvents all identified only via their chemical structure (e.g. given as SMILES strings), and expects from the solvent recommendation a ranking of the provided organic solvents by suitability (highest solubility first) as output. We immediately notice a few things: first, in our experience, it is most commonly the case that the structure of the solute is fixed, so the only variable at the hand of the practitioner is the solvent choice. Secondly, while the absolute solubility values are of ultimate interest, the relative solvent ranking is already of great practical utility to reduce the number of trial-and-error solvent screening experiments. Intuitively, by removing the requirement of modelling the absolute solubility, we greatly simplify the problem at hand. Considering the triangle (see Fig. 1) of the three phases—solid state, solvent, solution—that are involved in the dissolution process, we can disregard the solid phase as a constant (ignoring kinetic effects) in the ranking of solvents as the solute is kept fixed. It is therefore not necessary to estimate the crystal lattice energy, that is, as noted above, commonly regarded to be one of the largest contributing factors to the overall error of (absolute) solubility estimation.30,52 In addition, the relative solubility viewpoint also opens up additional datasets that only contain qualitative solubility assignments (e.g. the dataset). Fig. 2 illustrates the differences between an absolute and our differential/relative solubility model. To predict absolute solubility (Fig. 2A), a regression model M is called for each supported solvent s ∈ Solvents. In contrast, the relative recommender system (Fig. 2B) considers pairs of solvents sa, sb ∈ Solvents × Solvents such that sa ≠ sb. For each such pair, the differential solubility is computed through the regression model M and subsequently forms an edge of the directed solvent graph (dgraph) for this compound. We chose the convention that an edge points from the lower solubility to the higher one. The next step is to convert such a graph into a linear sequence of solvents, in order to obtain a ranking. This is referred to as “to-seq” in Fig. 2B and C. The resolution is non-trivial, as a fork in the graph would lead to ties in the final ranking, while a cycle would culminate in a contradiction. Therefore, the implementation of the to-seq part has to resolve both cycles and forks in the graphs. In our work, we chose to resolve ties randomly, while contradictions were handled by taking into account edge weights by applying the mean procedure outlined next. It is not expected that the strategy of randomly resolving ties should lead to problems in practice, as not a single hard tie was encountered.
dataset). Fig. 2 illustrates the differences between an absolute and our differential/relative solubility model. To predict absolute solubility (Fig. 2A), a regression model M is called for each supported solvent s ∈ Solvents. In contrast, the relative recommender system (Fig. 2B) considers pairs of solvents sa, sb ∈ Solvents × Solvents such that sa ≠ sb. For each such pair, the differential solubility is computed through the regression model M and subsequently forms an edge of the directed solvent graph (dgraph) for this compound. We chose the convention that an edge points from the lower solubility to the higher one. The next step is to convert such a graph into a linear sequence of solvents, in order to obtain a ranking. This is referred to as “to-seq” in Fig. 2B and C. The resolution is non-trivial, as a fork in the graph would lead to ties in the final ranking, while a cycle would culminate in a contradiction. Therefore, the implementation of the to-seq part has to resolve both cycles and forks in the graphs. In our work, we chose to resolve ties randomly, while contradictions were handled by taking into account edge weights by applying the mean procedure outlined next. It is not expected that the strategy of randomly resolving ties should lead to problems in practice, as not a single hard tie was encountered.
3.2 Linear ranking: the “to-seq” step
The differential solubility framing leads to a directed graph of solubility differences, that need to be converted into a linear order of the solvents as the final ranking output of the solvent recommender.A simple way to establish such a ranking that adheres to the outlined requirements is to compute the mean of the signed edge weights over each node. For each solvent node the weight of each incoming edge is added while all outgoing edge weights are subtracted, and finally divided by the overall number of edges:
This simple yet effective algorithm was compared against the ranked pairs53 and the PageRank54 algorithms as two alternatives for establishing a linear ranking.
Both alternatives showed degraded predictive performance (see Fig. S6 and ESI†) over the simple procedure outlined above. Hence, we focused on the simple mean method outlined here.
We acknowledge that deeper investigation into the details of these algorithms (e.g. optimizing the damping factor) might improve the performance so that the superiority of the mean algorithm can not be finally concluded.
3.3 Datasets
Solubility data was collected from the Open Notebook Science Challenge solubility dataset ( ). Only the top 60 solvents are kept, to remove data points corresponding to highly unusual solvents.
). Only the top 60 solvents are kept, to remove data points corresponding to highly unusual solvents.
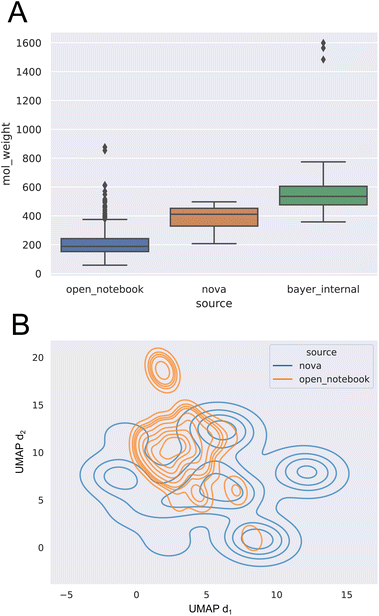
Analysis of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values show that the range in water is −11.7 to 1.01 with a mean of −3.05, while the log
S values show that the range in water is −11.7 to 1.01 with a mean of −3.05, while the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S-range of organic (non-water) solvents reaches from −7.30 to 1.11, with a mean of −0.826. Molecular weight (MW) of the open notebook dataset was found to be largely normally distributed centered on MW ≈ 200.
S-range of organic (non-water) solvents reaches from −7.30 to 1.11, with a mean of −0.826. Molecular weight (MW) of the open notebook dataset was found to be largely normally distributed centered on MW ≈ 200.
This low molecular weight average already indicates that  does not reflect the typical chemical space of active pharmaceutical ingredients.
does not reflect the typical chemical space of active pharmaceutical ingredients.
In order to obtain a more realistic comparison for drug-like chemical space, it was therefore decided to include two additional datasets: a qualitatively-labelled organic solubility dataset,39 referred to as  for the remainder of this text, and a Bayer-internal organic solubility dataset, referred to as
for the remainder of this text, and a Bayer-internal organic solubility dataset, referred to as  hereafter. Table 1 summarizes the three different data sources used in this work. A more detailed listing of the solvents can be found in the ESI.† There are no overlaps between the different datasets except for one solute with the SMILES
hereafter. Table 1 summarizes the three different data sources used in this work. A more detailed listing of the solvents can be found in the ESI.† There are no overlaps between the different datasets except for one solute with the SMILES 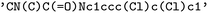 that is contained in both
that is contained in both  and
and  . Known drug-like chemical space encompasses compounds with MW ≤ 800 g mol−1.55 In accordance with this, both pharmaceutical datasets exhibit significantly larger average molecular weights, as shown in Fig. 3A. Furthermore, a 2D uniform manifold approximation and projection (UMAP) analysis56 (see Fig. 3B) on the count-ECFP representation shows that the
. Known drug-like chemical space encompasses compounds with MW ≤ 800 g mol−1.55 In accordance with this, both pharmaceutical datasets exhibit significantly larger average molecular weights, as shown in Fig. 3A. Furthermore, a 2D uniform manifold approximation and projection (UMAP) analysis56 (see Fig. 3B) on the count-ECFP representation shows that the  dataset covers only a small part of the drug-like chemical space of the
dataset covers only a small part of the drug-like chemical space of the  dataset.
dataset.
Which raised the question: Is it possible to train models on the large, but low MW,  training corpus that generalize towards broader (high MW) chemical space as exemplified by the drug-like datasets
training corpus that generalize towards broader (high MW) chemical space as exemplified by the drug-like datasets  and
and  ?
?
3.4 XTB hybrid features
To tackle the challenge of finding models that generalize from the low-molecular-weight regime of the training corpus towards larger compounds in the two drug-like datasets, we took inspiration from the QM/ML hybrid approach described in ref. 29 and follow their physical descriptors identified via feature importance analysis. However, we decided to replace the computationally more expensive ab initio calculations by the analytical linearized Poisson–Boltzmann (ALPB) model parameterized for the extended tight-binding (xtb).32,43 The method was shown to perform well over a broad range of systems and applications, covering conformational energetics, transition-metal complexes, intermolecular interactions, and even supramolecular association reactions.32 For hydration free energies, the method reaches a mean absolute error of 1.4 kcal mol−1, and is thus competitive with sophisticated explicitly solvated approaches.32 Furthermore, logarithmic octanol/water partitioning coefficients are computed with MAE ≈ 0.65 log units,32 indicating a consistent description of differential solvent effects, which we regarded as crucial for hybrid physics/ML descriptors in organic solvent recommendation.
training corpus towards larger compounds in the two drug-like datasets, we took inspiration from the QM/ML hybrid approach described in ref. 29 and follow their physical descriptors identified via feature importance analysis. However, we decided to replace the computationally more expensive ab initio calculations by the analytical linearized Poisson–Boltzmann (ALPB) model parameterized for the extended tight-binding (xtb).32,43 The method was shown to perform well over a broad range of systems and applications, covering conformational energetics, transition-metal complexes, intermolecular interactions, and even supramolecular association reactions.32 For hydration free energies, the method reaches a mean absolute error of 1.4 kcal mol−1, and is thus competitive with sophisticated explicitly solvated approaches.32 Furthermore, logarithmic octanol/water partitioning coefficients are computed with MAE ≈ 0.65 log units,32 indicating a consistent description of differential solvent effects, which we regarded as crucial for hybrid physics/ML descriptors in organic solvent recommendation.
One challenge that we encountered is that only a limited set of solvents is supported, and that the method cannot be trivially expanded towards a broader solvent selection.
To work around this limitation, we decided (see Fig. 4A) to compute 11 physical properties as exposed by alpb-xtb for all 23 solvents supported. Most important properties include energy of solvation Gsolv, partial contributions Ghb, Gsasa thereof, HOMO–LUMO gap ΔHOMO/LUMO, and dipole moment μsolu,solv (see ESI† for a listing of all features). Thus, a 11 × 23 = 253-dimensional vector is obtained for the solute and solvent part, respectively. As an added advantage, this formulation gives us a simple approximative way of representing solvent mixtures: as a linear combination of the vector representation of each mixture component with their corresponding fraction in the mixture as multiplicative coefficient.
Both solvent and solute components are concatenated to yield a feature vector totalling 506 dimensions. For the absolute solubility recommender (see Fig. 4B), the feature vector is used as-is. For the differential solubility, an edge (solvent a, solvent b) is represented by either subtracting or concatenating the solvent parts of the feature vector, thus arriving at a differential feature representation for the solvent pair (see Fig. 4C).
The same construction was also applied to all other features (e.g. ecfp, cddd), to obtain relative_diff and relative_concat flavors of these features in the same manner.
3.5 Evaluation of the ranking performance
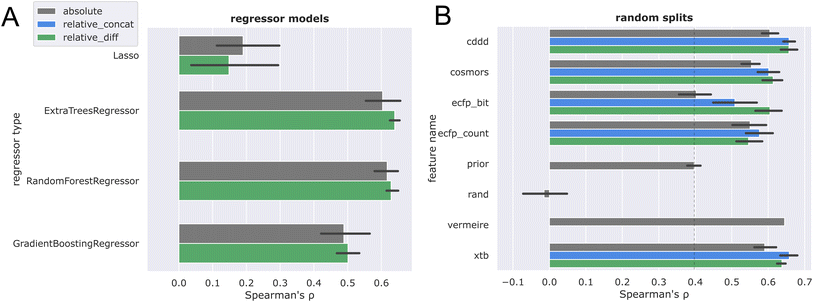
Different regressor types were screened (Fig. 5A), with extremely randomized trees (ET) showing the best performance, in agreement with observations made in ref. 29.One possible explanation could be that random feature splits characterizing the ET lead to smoother regression outcomes, as compared to bagging approaches.57 Based on these results, we chose extremely randomized trees (ET) as the regression model for all other experiments. Next, ETs with different feature types and solubility relations were evaluated within different data splits (see Methods section for additional details). The results of the performance evaluation are summarized in Table 2. Throughout the table, the best performing models have been highlighted in bold typeface, under consideration of the reported errors.
| Feature | Relation | ρ (rand) | ρ (Butina) | ρ (solvent) | ρ (ood, nova) | ρ (ood, bayer) |
|---|---|---|---|---|---|---|
| a Refers to a distinct model. | ||||||
| rand | absolute | −0.015 ± 0.1 | 0.021 ± 0.1 | −0.043 ± 0.1 | −0.018 ± 0.1 | −0.087 ± 0.2 |
| prior | absolute | 0.397 ± 0.03 | 0.386 ± 0.05 | 0.03 ± 0.09 | 0.293 ± 0.02 | 0.582 ± 0.01 |
| ecfp_bit | absolute | 0.403 ± 0.08 | 0.282 ± 0.1 | 0.091 ± 0.2 | 0.263 ± 0.05 | 0.312 ± 0.06 |
| relative_concat | 0.509 ± 0.08 | 0.484 ± 0.1 | 0.575 ± 0.1 | 0.662 ± 0.07 | 0.361 ± 0.09 | |
| relative_diff | 0.605 ± 0.05 | 0.481 ± 0.1 | 0.464 ± 0.3 | 0.715 ± 0.02 | 0.578 ± 0.04 | |
| ecfp_count | absolute | 0.55 ± 0.08 | 0.463 ± 0.06 | 0.273 ± 0.1 | 0.296 ± 0.03 | 0.581 ± 0.03 |
| relative_concat | 0.576 ± 0.05 | 0.53 ± 0.06 | 0.482 ± 0.4 | 0.74 ± 0.01 | 0.589 ± 0.03 | |
| relative_diff | 0.546 ± 0.05 | 0.509 ± 0.02 | 0.469 ± 0.3 | 0.733 ± 0.01 | 0.618 ± 0.03 | |
| cosmors44,45 | absolute | 0.554 ± 0.04 | 0.484 ± 0.03 | 0.474 ± 0.09 | 0.327 ± 0.02 | — |
| relative_concat | 0.602 ± 0.04 | 0.567 ± 0.06 | 0.542 ± 0.2 | 0.673 ± 0.04 | — | |
| relative_diff | 0.614 ± 0.03 | 0.569 ± 0.04 | 0.562 ± 0.1 | 0.641 ± 0.01 | — | |
| vermeire28a | absolute | 0.645 | — | — | 0.554 | 0.612 |
| cddd 47 | absolute | 0.605 ± 0.04 | 0.569 ± 0.03 | 0.279 ± 0.2 | 0.345 ± 0.04 | 0.608 ± 0.01 |
| relative_concat | 0.657 ± 0.02 | 0.608 ± 0.06 | 0.594 ± 0.2 | 0.744± 0.01 | 0.638 ± 0.01 | |
| relative_diff | 0.657 ± 0.03 | 0.602 ± 0.06 | 0.569 ± 0.3 | 0.733± 0.01 | 0.628 ± 0.01 | |
| xtb | absolute | 0.591 ± 0.05 | 0.554 ± 0.07 | 0.5 ± 0.06 | 0.322 ± 0.02 | 0.602 ± 0.01 |
| relative_concat | 0.658 ± 0.03 | 0.604 ± 0.08 | 0.572 ± 0.3 | 0.736± 0.01 | 0.644 ± 0.01 | |
| relative_diff | 0.638 ± 0.02 | 0.612 ± 0.06 | 0.578 ± 0.2 | 0.703 ± 0.02 | 0.647 ± 0.01 | |
The most significant observation is that relative models outperform the absolute solubility models throughout all features and evaluation scenarios considered.
We will now discuss the results of the different evaluation scenarios in more detail.
First, we consider the evaluation within random solute splits. In Fig. 5B, the ranking performance on random splits is shown for different features, which corresponds to column ρ (rand) of Table 2.
A random null model trained on a uniform random variable ( ) has no information about the outcome. Consequently, it exhibited the lowest performance, as it cannot possibly arrive at a sensible ranking decision. With the solvent prior order, a sharp jump of 40 percent points was seen, as compared to a random coin toss. This aligns with chemical intuition, as some solvents are intrinsically more suited than others (e.g. DMSO is in general a better organic solvent than hexane). The highest performing features are cddd, xtb and the vermeire model. However, for vermeire, leakage of the test data has to be considered, as 54.4% of solute compounds considered here were part of the SolProp dataset58 used in training this model.28 Therefore, the reported ρvermeire,rand = 0.645 provides an optimistic upper bound of the true performance. At first sight, it might seem surprising that the fast approximative xtb features lead to better results than the more sophisticated/computationally expensive COSMO-RS. However, we would like to point out, as noted before, that the alpb/xtb combination already reaches competitive accuracy with regards to differential solubility.32 Furthermore, the observation that pure machine learning models outperform COSMO-RS on a similar task31 are in agreement with this finding.
) has no information about the outcome. Consequently, it exhibited the lowest performance, as it cannot possibly arrive at a sensible ranking decision. With the solvent prior order, a sharp jump of 40 percent points was seen, as compared to a random coin toss. This aligns with chemical intuition, as some solvents are intrinsically more suited than others (e.g. DMSO is in general a better organic solvent than hexane). The highest performing features are cddd, xtb and the vermeire model. However, for vermeire, leakage of the test data has to be considered, as 54.4% of solute compounds considered here were part of the SolProp dataset58 used in training this model.28 Therefore, the reported ρvermeire,rand = 0.645 provides an optimistic upper bound of the true performance. At first sight, it might seem surprising that the fast approximative xtb features lead to better results than the more sophisticated/computationally expensive COSMO-RS. However, we would like to point out, as noted before, that the alpb/xtb combination already reaches competitive accuracy with regards to differential solubility.32 Furthermore, the observation that pure machine learning models outperform COSMO-RS on a similar task31 are in agreement with this finding.
Overall, the most significant trend is that the relative solubility framing consistently improves performance across all features.
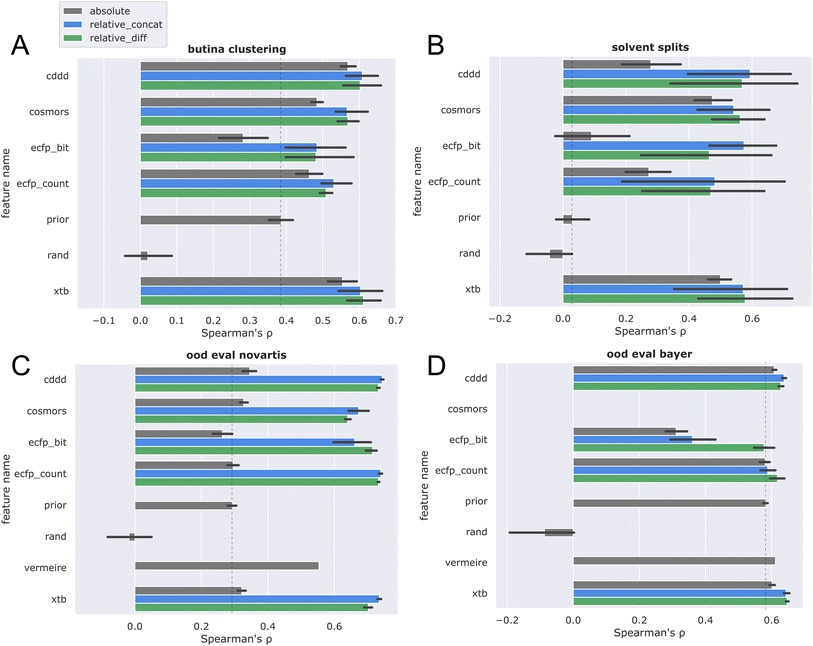
Next, Butina clustering was employed to obtain more challenging CV splits (see Fig. 6A). Similar trends were observed, with the differential frame again outperforming the absolute solubility frame. Comparing these results with the random splits, a more significant drop in performance is registered for the ecfp features, while cddd, cosmors, and xtb seem to generalize better across chemical space.
To investigate the generalization capability towards novel solvents, a split was performed by randomly assigning solvents towards different CV folds (Fig. 6B). This solvent split provides a very challenging generalization task, as models are required to train on one set of solvents and then predict towards a new set of solvents. Again, the differential solubility models trained on xtb and cddd features performed best, and largely retained the ranking performance on novel solvents as compared to random splits. The higher variance observed for the solvent split could be attributed to a mixture of two effects: firstly, the fact that some solvents exhibit more unique solubility characteristics, thereby introducing more variation. Secondly, the varying amount of training data available for each solvent (see Table S1 and ESI†). The first explanation seems more likely, because data was stratified in such a way that the top solvents are equally distributed among the splits. This is further corroborated by the observation that solvents with unique solubility characteristics contribute positively to the prediction accuracy in the more detailed per-solvent error analysis (vide infra).
The final two plots compare the ranking performance when training on the low-MW  dataset and evaluating on the higher-MW
dataset and evaluating on the higher-MW 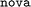 (Fig. 6C) and
(Fig. 6C) and 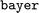 (Fig. 6D) datasets.
(Fig. 6D) datasets.
Referring back to Fig. 3A, it is apparent that dataset 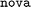 is chemically more similar to
is chemically more similar to 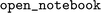 while the bayer data is characterized by a even larger distance in the mean MW.
while the bayer data is characterized by a even larger distance in the mean MW.
It is therefore reasonable that most models outperformed the prior on the nova ood evaluation (Fig. 6C), while only minor improvements over the prior were observed for the bayer data (Fig. 6D). While the large difference of over 300 g mol−1 between  and
and  provides a reasonable explanation for the low generalization performance, it is nonetheless important to acknowledge that discrepancies in data quality between the two out-of-distribution datasets cannot be discounted. Due to the high runtime requirements combined with the fact that the COSMO/COSMO-RS calculations failed for many inputs, the evaluation discussed here is restricted on the subset of datapoints where COSMO-RS calculations were successful, to ensure a fair comparison. However, the evaluation on the full dataset (see ESI, p. 3†) shows the same overall trends. In the end, the xtb + relative_concat was chosen, as it is the best performing feature combination in general, and furthermore also performed best in the ood evaluations, which are arguably the practically most relevant evaluation scenarios.
provides a reasonable explanation for the low generalization performance, it is nonetheless important to acknowledge that discrepancies in data quality between the two out-of-distribution datasets cannot be discounted. Due to the high runtime requirements combined with the fact that the COSMO/COSMO-RS calculations failed for many inputs, the evaluation discussed here is restricted on the subset of datapoints where COSMO-RS calculations were successful, to ensure a fair comparison. However, the evaluation on the full dataset (see ESI, p. 3†) shows the same overall trends. In the end, the xtb + relative_concat was chosen, as it is the best performing feature combination in general, and furthermore also performed best in the ood evaluations, which are arguably the practically most relevant evaluation scenarios.
Overall, when summarizing the results across all evaluation scenarios, the most significant enhancement arises from the relative solubility framework. This framework consistently boosts ranking performance across a diverse array of feature selections. Notably, it is remarkable to observe that a variety of features, including sparse fingerprints (ecfp_bit, ecfp_count), dense pretrained embeddings (cddd), and physical descriptors (cosmors, xtb), consistently exhibit improved ranking performance within the relative solubility frame. This observation reinforces the initial concept (see Fig. 1) that excluding the solute/solid state from the solubility equation offers a practical and widely applicable approximation.
3.6 Error analysis by solvent
To investigate the question whether some solvents are more challenging to rank than others, we evaluated the ranking performance with and without each of the top 60 solvents, yielding the result shown in Fig. S4.† In alignment with chemical intuition, it is observed that solvents with unique solubility characteristics like water, dimethylsulfoxide, hexane, or tetrahydrofuran have a positive impact on the ranking performance, so including them in the evaluation leads to positive increases in the Spearman rank correlation. Less unique solvents like the alcohols or chlorinated solvents have many similar potential substitutives (e.g. 2-butanol ↔ 1-butanol, methylene chloride ↔ 1,2-dichloroethane), thus making ranking more challenging.3.7 Error analysis by solubility difference threshold
One difficulty with the assessment of the ranking performance of solubility models lies in the fact that the recommender is forced to make decisions on solvent pairs that may be very close in terms of solubility. In the extreme, we might require a ranking to be performed on a solvent pair where Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S lies below the experimental error, thus artificially lowering the ranking performance in the evaluation of the model.
S lies below the experimental error, thus artificially lowering the ranking performance in the evaluation of the model.
From another perspective, the question can be formulated: What solubility differences Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S can we sensibly require to be ranked? To answer this question, a minimum solubility threshold, Δlog
S can we sensibly require to be ranked? To answer this question, a minimum solubility threshold, Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Smin, was defined. Then, all measurements for which there exists another measurement for the same solute, such that Δlog
Smin, was defined. Then, all measurements for which there exists another measurement for the same solute, such that Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S < Δlog
S < Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Smin, have been removed from the test set at random. Thus, for each solute that is to be ranked, similar solvents below the threshold do not need to be ranked with regards to each other. Thereby, the ranking task is simplified as it only focuses on solvents with significant solubility differences.
Smin, have been removed from the test set at random. Thus, for each solute that is to be ranked, similar solvents below the threshold do not need to be ranked with regards to each other. Thereby, the ranking task is simplified as it only focuses on solvents with significant solubility differences.
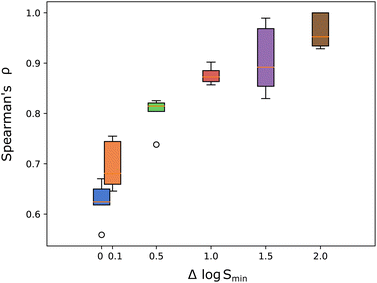
As shown in Fig. 7, most of the improvement in the ranking performance is seen from Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Smin = 0.0 → 1.0 which fits to the experimental solubility errors of 0.7–1.0 log units.30,59
Smin = 0.0 → 1.0 which fits to the experimental solubility errors of 0.7–1.0 log units.30,59
It can be concluded that the ranking performance without any Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S filtering are pessimistic, lower-bound, estimates. Furthermore, thresholds in the range Δlog
S filtering are pessimistic, lower-bound, estimates. Furthermore, thresholds in the range Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Smin = 0.5 − 1.0 should be applied, below which the models ranking performance degrades significantly.
Smin = 0.5 − 1.0 should be applied, below which the models ranking performance degrades significantly.
3.8 Solvmate: a solvent recommendation web application
We introduce Solvmate, a web application that provides our fully automated solvent recommender solution (see Fig. 8). On the input side, it requires only two pieces of information from the user: firstly, the solute structure, which can be either pasted as SMILES or drawn interactively in a molecule editor. Secondly, the list of all solvents as SMILES or IUPAC names, that are parsed with the help of the Open Parser for Systematic IUPAC nomenclature (OPSIN).40 These solvent sets can be saved with a descriptive name for later reuse.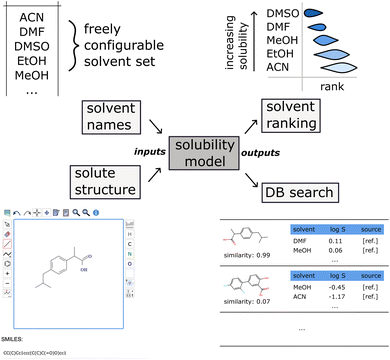 | ||
| Fig. 8 Schematic overview of the Solvmate solvent recommendation web app taking the list of solvents as IUPAC names and the solute structure as input, and producing a solvent ranking by solubility together with the most similar database matches (in the training dataset) as output. The OPSIN software40 is used for parsing IUPAC names into chemical structures. Solutes are either entered as SMILES or via a molecular structure editor. | ||
On the output side, a ranking of the solvents is shown as box plot, ordered from best solvent on the top to worst solvent on the bottom. The estimated uncertainty is obtained from the variance of an ensemble of five model instances trained on bootstrapped subsamples of the training data.
Furthermore, the recommender also displays the matching solubility data points in the training corpus that are closest in the feature space.
3.9 Solvent recommendation examples
Here, two examples of solvent recommendation outputs are discussed, that indicate current weaknesses of the model. For diclofenac (Fig. 9A), the top three solvents acetophenone, acetone, and ethyl acetate are correctly identified. However, the alcohols ethanol, methanol, 1-octanol, and propionic acid are not correctly ordered. This is sensible as these solvents are structurally similar, and furthermore protic solvents with strong hydrogen bonds that are difficult to model. For dioxopromethazine hydrochloride (Fig. 9B), only the solubility in acetic acid has been heavily underestimated. The degraded performance for salts can be attributed to the fact that no ionic compounds are present in the training dataset. To give the reader a broader impression of the resulting organic solvent recommendations, the ESI† displays the output for 12 additional solutes. In one case, a larger solvent set of around fifty solvents is utilized to give an example how screens of many solvents can be performed at once. Overall, the examples show chemically intuitive rankings—even for structurally unusual compounds. Systematic structural modifications of the solutes lead to sensible changes in the resulting solvent rankings. However, the examples also highlight weaknesses of the current model: as the prior of sorting solvents according to their overall suitability as a solvent is highly informative, the recommender tends to stick to rankings that align with the prior. Furthermore, solvents that are structurally similar tend to be confused.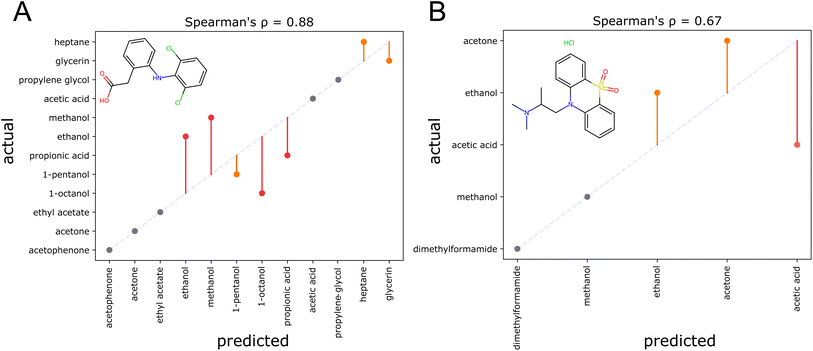 | ||
| Fig. 9 Two examples showcasing problems encountered when producing solvent rankings. Parity plots for the solvent ranking of diclofenac (A), as reported in ref. 60 and dioxopromethazine HCl (B), as reported in ref. 61. Correct ranking positions are shown in gray, errors by one position in orange, and errors by more than one position in red. An ideal ranking would yield the dotted diagonal line. | ||
4 Conclusions
In this work, we propose a new organic solvent recommender system, trained on publicly available organic solvent solubility data. We found that framing the problem as a relative/differential question, i.e. predicting the change in solubility for a given solute and a pair of solvents, allows us to build robust and generalizable models. It is remarkable to observe that a wide variety of features, including sparse fingerprints, dense embeddings, and physical descriptors consistently exhibit improved ranking performance within this relative solubility framework. We rationalize this finding by the fact that aspects related to the solid state of the solute can be ignored, a central problem when predicting absolute solubility. Hence, a experimental melting point measurement is not required. We additionally develop a new featurization protocol that brings the advantage of physics-based descriptors without the cost in speed or the limitation in supported solvents. For this, we use xtb upon which fast physical/ML hybrid models are constructed. In particular, we encode physical descriptors for both solvent and solute against a common set of 23 different solvent environments. Solvent mixtures can be handled by applying a linear combination (weighted by mixture proportions) of the constituent parts' representations. It was found that CDDD pretrained embeddings exhibit similar ranking performance at even lower computational cost. Analysis of the model reveals that most of the solvent ranking errors come from pairs with small solubility differences (below 0.5–1.0 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S), which is in agreement with the reported experimental error.30,59 To ease access to our methods, we release a web application that allows users to conveniently upload a solute and a list of solvents to rank, and obtain a solvent ranking fully automatically. This is, to the best of our knowledge, the first freely accessible solvent ranking recommender system, designed with the user in mind. We envision that it will be of benefit to the day-to-day work of lab workers in diverse areas, such as chemical engineering, material science, or synthesis planning.
S), which is in agreement with the reported experimental error.30,59 To ease access to our methods, we release a web application that allows users to conveniently upload a solute and a list of solvents to rank, and obtain a solvent ranking fully automatically. This is, to the best of our knowledge, the first freely accessible solvent ranking recommender system, designed with the user in mind. We envision that it will be of benefit to the day-to-day work of lab workers in diverse areas, such as chemical engineering, material science, or synthesis planning.
Consent for publication
All authors read and approved the final manuscript.Data availability
All source code is provided. All training and validation data stem from public sources, except the data used for validating the in-house performance on Bayer compounds. The code is open source and can be found under the following URL: https://github.com/Bayer-Group/solvmate. Trained model files are also available on the github repository.
data used for validating the in-house performance on Bayer compounds. The code is open source and can be found under the following URL: https://github.com/Bayer-Group/solvmate. Trained model files are also available on the github repository.
Author contributions
Conceptualization – J. W., F. M.; data curation – J. W.; exploratory analysis – J. W.; methodology – J. W., F. M.; supervision – F. M.; writing, original draft – J. W., writing, review & editing – F. M. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Olaf Nimz, Adiran Garaizar Suarez, and Sadra Kashef Ol Gheta for interesting discussions. Special thanks goes to Michal Sowa and Tia Jacobs for helping in the assembly of the internal solvent screening dataset, and Varia Nikolayenko for feedback on the app. We thank the ARTIDA LSC Project for funding.References
- L. J. Diorazio, D. R. Hose and N. K. Adlington, Org. Process Res. Dev., 2016, 20, 760–773 CrossRef CAS.
- G. Panapitiya, M. Girard, A. Hollas, J. Sepulveda, V. Murugesan, W. Wang and E. Saldanha, ACS Omega, 2022, 7, 15695–15710 CrossRef CAS PubMed.
- J. Wang and T. Hou, Comb. Chem. High Throughput Screening, 2011, 14, 328–338 CrossRef CAS PubMed.
- C. Loschen and A. Klamt, J. Pharm. Pharmacol., 2015, 67, 803–811 CrossRef CAS PubMed.
- W. L. Jorgensen and E. M. Duffy, Adv. Drug Delivery Rev., 2002, 54, 355–366 CrossRef CAS PubMed.
- T. Welton and C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, John Wiley & Sons, 2011 Search PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 1997, 23, 3–25 CrossRef CAS.
- K. Ge and Y. Ji, Ind. Eng. Chem. Res., 2021, 60, 9259–9268 CrossRef CAS.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- L. Li, T. Totton and D. Frenkel, J. Chem. Phys., 2017, 146, 214110 CrossRef PubMed.
- Y. Ran and S. H. Yalkowsky, J. Chem. Inf. Comput. Sci., 2001, 41, 354–357 CrossRef CAS PubMed.
- Y. Ran, Y. He, G. Yang, J. L. Johnson and S. H. Yalkowsky, Chemosphere, 2002, 48, 487–509 CrossRef CAS PubMed.
- J. Ali, P. Camilleri, M. B. Brown, A. J. Hutt and S. B. Kirton, J. Chem. Inf. Model., 2012, 52, 420–428 CrossRef CAS PubMed.
- C. M. Hansen, Hansen solubility parameters: a user's handbook, CRC press, 2007 Search PubMed.
- J. H. Hildebrand and R. L. Scott, The Solubility of Nonelectrolytes, Dover Publications, 1964 Search PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, F. Eckert, M. Hornig, M. E. Beck and T. Bürger, J. Comput. Chem., 2002, 23, 275–281 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- J. S. Delaney, Drug Discovery Today, 2005, 10, 289–295 CrossRef CAS PubMed.
- X. Yu, X. Wang, H. Wang, X. Li and J. Gao, QSAR Comb. Sci., 2006, 25, 156–161 CrossRef CAS.
- P. R. Duchowicz and E. A. Castro, Int. J. Mol. Sci., 2009, 10, 2558–2577 CrossRef CAS PubMed.
- J. Huuskonen, M. Salo and J. Taskinen, J. Chem. Inf. Comput. Sci., 1998, 38, 450–456 CrossRef CAS PubMed.
- A. Lusci, G. Pollastri and P. Baldi, J. Chem. Inf. Model., 2013, 53, 1563–1575 CrossRef CAS PubMed.
- H. Lim and Y. Jung, J. Cheminf., 2021, 13, 1–10 Search PubMed.
- J.-C. Bradley, C. Neylon, R. Guha, A. Williams, B. Hooker, A. Lang, B. Friesen, T. Bohinski, D. Bulger and M. Federici, et al. , Nat. Preced., 2010 DOI:10.1038/npre.2010.4243.3.
- A. Llinàs, R. C. Glen and J. M. Goodman, J. Chem. Inf. Model., 2008, 48, 1289–1303 CrossRef PubMed.
- A. Llinas and A. Avdeef, J. Chem. Inf. Model., 2019, 59, 3036–3040 CrossRef CAS PubMed.
- F. H. Vermeire, Y. Chung and W. H. Green, J. Am. Chem. Soc., 2022, 144(24), 10785–10797 CrossRef CAS PubMed.
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- D. S. Palmer and J. B. Mitchell, Mol. Pharm., 2014, 11, 2962–2972 CrossRef CAS PubMed.
- A. D. Vassileiou, M. Robertson, B. G. Wareham, M. Soundaranathan, S. Ottoboni, A. J. Florence, T. Hartwig and B. F. Johnston, Digital Discovery, 2023, 2, 356–367 RSC.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- A. Klamt and M. Diedenhofen, J. Phys. Chem. A, 2015, 119, 5439–5445 CrossRef CAS PubMed.
- J. Warnau, K. Wichmann and J. Reinisch, J. Comput.-Aided Mol. Des., 2021, 35, 813–818 CrossRef CAS PubMed.
- N. M. O'Boyle, D. S. Palmer, F. Nigsch and J. B. Mitchell, Chem. Cent. J., 2008, 2, 1–15 CrossRef PubMed.
- L. D. Hughes, D. S. Palmer, F. Nigsch and J. B. Mitchell, J. Chem. Inf. Model., 2008, 48, 220–232 CrossRef CAS PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle and G. R. Desiraju, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CrossRef CAS PubMed.
- D. S. Palmer, A. Llinàs, I. Morao, G. M. Day, J. M. Goodman, R. C. Glen and J. B. Mitchell, Mol. Pharm., 2008, 5, 266–279 CrossRef CAS PubMed.
- M. Pillong, C. Marx, P. Piechon, J. G. Wicker, R. I. Cooper and T. Wagner, CrystEngComm, 2017, 19, 3737–3745 RSC.
- D. M. Lowe, P. T. Corbett, P. Murray-Rust and R. C. Glen, J. Chem. Inf. Model., 2011, 51, 739–753 CrossRef CAS PubMed.
- G. Landrum, RDKit: A Software Suite for Cheminformatics, Computational Chemistry, and Predictive Modeling, 2013 Search PubMed.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- A. Klamt, V. Jonas, T. Bürger and J. C. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- T. Gerlach, S. Müller, A. G. de Castilla and I. Smirnova, Fluid Phase Equilib., 2022, 560, 113472 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- R. Winter, F. Montanari, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 1692–1701 RSC.
- D. Butina, J. Chem. Inf. Comput. Sci., 1999, 39, 747–750 CrossRef CAS.
- R. Taylor, J. Chem. Inf. Comput. Sci., 1995, 35, 59–67 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, V. Niculae, P. Prettenhofer, A. Gramfort, J. Grobler, R. Layton, J. VanderPlas, A. Joly, B. Holt and G. Varoquaux, ECML PKDD Workshop: Languages for Data Mining and Machine Learning, 2013, pp. 108–122 Search PubMed.
- D. Mathieu, Chemosphere, 2017, 182, 399–405 CrossRef CAS PubMed.
- T. M. Zavist and T. N. Tideman, Soc. Choice Welf., 1989, 6, 167–173 CrossRef.
- L. Page, S. Brin, R. Motwani and T. Winograd, Technical report, Stanford University, 1998 Search PubMed.
- R. Bade, H.-F. Chan and J. Reynisson, Eur. J. Med. Chem., 2010, 45, 5646–5652 CrossRef CAS PubMed.
- L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, 1802.03426, arXiv.1802.03426, DOI:10.48550/arXiv.1802.03426.
- P. Geurts, D. Ernst and L. Wehenkel, Mach. Learn., 2006, 63, 3–42 CrossRef.
- F. Vermeire, Y. Chung and W. Green, SolProp Dataset for: Predicting Solubility Limits of Organic Solutes for a Wide Range of Solvents and Temperatures (v1.2), 2022, DOI:10.1021/jacs.2c01768.
- C. A. Bergström and A. Avdeef, ADMET and DMPK, 2019, 7, 88–105 CrossRef PubMed.
- J. Barra, M.-A. Peña and P. Bustamante, Eur. J. Pharm. Sci., 2000, 10, 153–161 CrossRef CAS PubMed.
- Q.-S. Li, Z.-M. Yi, M.-G. Su, S. Wang and X.-H. Wu, J. Chem. Eng. Data, 2008, 53, 301–302 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional statistics about the different datasets, example ranking outputs, xtb configuration, and the feature importance analysis. Furthermore, datasets used in this study are uploaded as .csv-files to facilitate reuse. See DOI: https://doi.org/10.1039/d4dd00138a |
| ‡ Current affiliation: OWKIN, Paris, France. |
| § Dataset available under the url: https://figshare.com/articles/dataset/Open_Notebook_Science_Challenge_Solubility_Dataset/1514952. |
| ¶ Found here: https://github.com/TUHH-TVT/openCOSMO-RS_conformer_pipeline. |
| || Possible users of the system include chemists, pharmacists, chemical engineers, material scientists, lab technicians, …. |
| This journal is © The Royal Society of Chemistry 2024 |