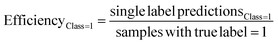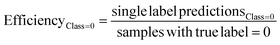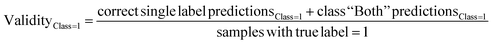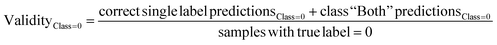Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A methodology to correctly assess the applicability domain of cell membrane permeability predictors for cyclic peptides†
Gökçe
Geylan
 *ab,
Leonardo
De Maria
*ab,
Leonardo
De Maria
 c,
Ola
Engkvist
c,
Ola
Engkvist
 ad,
Florian
David
b and
Ulf
Norinder
efg
ad,
Florian
David
b and
Ulf
Norinder
efg
aMolecular AI, Discovery Sciences, BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden. E-mail: gokce.geylan@astrazeneca.com
bDivision of Systems and Synthetic Biology, Department of Life Sciences, Chalmers University of Technology, Gothenburg, Sweden
cMedicinal Chemistry, Research and Early Development, Respiratory & Immunology, BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden
dDepartment of Computer Science and Engineering, Chalmers University of Technology and University of Gothenburg, Gothenburg, Sweden
eDepartment of Computer and Systems Sciences, Stockholm University, Kista, Sweden
fMTM Research Centre, School of Science and Technology, Örebro University, Örebro, Sweden
gDepartment of Pharmaceutical Biosciences, Uppsala University, Uppsala, Sweden
First published on 30th July 2024
Abstract
Being able to predict the cell permeability of cyclic peptides is essential for unlocking their potential as a drug modality for intracellular targets. With a wide range of studies of cell permeability but a limited number of data points, the reliability of the machine learning (ML) models to predict previously unexplored chemical spaces becomes a challenge. In this work, we systemically investigate the predictive capability of ML models from the perspective of their extrapolation to never-before-seen applicability domains, with a particular focus on the permeability task. Four predictive algorithms, namely Support-Vector Machine, Random Forest, LightGBM and XGBoost, jointly with a conformal prediction framework were employed to characterize and evaluate the applicability through uncertainty quantification. Efficiency and validity of the models' predictions with multiple calibration strategies were assessed with respect to several external datasets from different parts of the chemical space through a set of experiments. The experiments showed that the predictors generalizing well to the applicability domain defined by the training data, can fail to achieve similar model performance on other parts of the chemical spaces. Our study proposes an approach to overcome such limitations by the means of improving the efficiency of models without sacrificing the validity. The trade-off between the reliability and informativeness was balanced when the models were calibrated with a subset of the data from the new targeted domain. This study outlines an approach to enable the extrapolation of predictive power and restore the models' reliability via a recalibration strategy without the need for retraining the underlying model.
1. Introduction
Therapeutic peptides are a promising modality in drug discovery and development due to their high specificity, low toxicity, low immunogenicity, as well as for modulating protein–protein interactions (PPI).1 With the potential of regulating PPIs on the traditionally considered undruggable interaction interfaces, such as shallow pockets or large surfaces of target proteins, peptides now offer a promising step towards these uncharted target spaces.2 Cyclic peptides, in particular, have various notable structural advantages: with their reduced conformational flexibility, they have a higher metabolic stability and can display better membrane permeation profiles compared to their linear counterparts. Additionally, cyclized structures can be used to mimic the active loops that mediate PPIs.3 As a beyond-the-rule-of-5 modality, one of the key challenges to design a cyclic peptide as a standalone drug to address intracellular targets is its cell membrane permeation capability.4 Various strategies such as stereochemical modifications, backbone N-methylation, heterocycle incorporation or using non-natural amino acids have been utilized to improve the cell permeability of cyclic peptides.2,4 The identification of widely applicable set of rules has, however, proven elusive considering the intricate interplay between the structure and function.Integrating ML into drug discovery and development allows more complex challenges to be tackled and has the potential of accelerating the pipeline of drug projects. ML approaches could uncover patterns and help predict the impact of a set of design ideas on permeability across a diverse set of peptide sequences. Training predictive models for cell permeability have been previously investigated with peptide sequence data often including peptides conjugated to other molecules such as small molecules and antisense oligonucleotides. This has led to models that are either built specific to peptides with a certain conjugation partner or indifferent to the influence of any conjugate, posing a challenge in accurate profiling of the cell permeability of individual peptides.4–6 Therefore, there is still an existing need to have a permeability predictor that can predict the membrane permeability of peptides.
The peptidic chemical space has not been explored thoroughly with in silico methods compared to the small molecule space and the availability of comprehensive peptide data sources is rather limited and even more so for cyclic peptides. However, there are a considerable number of studies that have been published on traversing biological barriers for individual cyclic peptides. These studies generally provide the design strategies or methods on target peptide sequences and experimentally validate the achieved permeability upon modifications.7–10 Collecting data from different publications gives rise to two noteworthy considerations. First, the permeability values reported are predominantly on the design strategies that improve permeability. Therefore, compiling datasets from such studies lead to class imbalance towards positive instances for ML purposes. Secondly, combining data from multiple sources requires other assessments such as the risk of data leakage. Data leakage occurs when the model is presented with additional information in the training data about what it will predict.11 This leads to overoptimistic training performance while models suffer from generalizability during application. Data leakage was shown to be a widespread problem when training models and being one of the main causes for the “reproducibility crisis”.11,12 Some good preprocessing practices include not having duplicated entries across or within the training, validation, and test sets, collecting the same assay type, and splitting the test set to represent a never-before-seen external data from separate data sources.11 These preprocessing practices are preferred for the reproducibility and utilization of the models.11 Nevertheless, the advantage of training models with a compiled dataset is to have a robust predictive performance that can generalize across different parts of the chemical space.
The applicability domain of a predictive model is defined as the chemical space learned during training that determines the extent of acquiring reliable predictions. As the test samples move further away from this part of the chemical space and become less similar to the training data, the reliability of the model's predictions decreases, ultimately defining its applicability domain.13 Being informed of the model's boundaries allows the researchers to interpret the predictions as reliable or not and enables an efficient navigation in the explored chemical space. Therefore, acquiring insight on the applicability domain is necessary to have a valid and reliable decision-making process with respect to model predictions. One way to assign reliability to characterize model predictions is uncertainty quantification.14
Conformal prediction (CP) is a mathematical framework, used in conjunction with a previously trained model to provide uncertainty quantification on the model's predictions by utilizing calibration examples.15 The inductive CP methodology produces regression intervals, or prediction sets from point predictions for regression and classification, respectively.15 The CP methodology assumes the training and test data to be exchangeable, implying that the datapoints are not related to each other, in other words, independent.15 The CP application begins with the proper training set to train the predictor and the calibration set to generate the nonconformity scores. The nonconformity scores describe how different a data point is to the previously observed examples. After the model is trained, the calibration set is used to establish the mapping between these nonconformity scores and how confident the model is with its predictions.16 Upon training and calibrating, the model can be tested for its predictive performance by providing never-before-seen test data. If the predicted values are determined to have high nonconformity scores, this is translated to high dissimilarity to the calibration set examples and will be associated with a lower confidence, expressed as p-values. The predictions produced by the model depend on the user-specified significance level (α) which limits the error rate of the predictions. Intuitively, the significance level sets the model's confidence by providing prediction intervals for regression models or one of the prediction sets for classification models.15,17 In a binary classification case, the conformal prediction framework outputs one of the four label sets as opposed to two class labels: positive and negative. The labels are determined by comparing the class-specific p-values of the predicted data point and calibration set examples. If the model either cannot make a reliable prediction under the defined significance level or assigns similar confidences to both classes, the assigned label is “Empty” (a no-label prediction) or “Both”, (a two-label prediction), respectively. In other cases, for a predicted sample, the class having a higher p-value than the set significance level either is assigned a positive or a negative label (a single-label prediction). With the mathematical nature of the CP framework, the method aims to yield valid and meaningful predictions at a user-determined significance level.17
Traditionally, the training set is used to generate the proper training and the calibration sets. When the trained model is used to make predictions on new data that is dissimilar to the training data, the exchangeability assumption between the calibration and test data may be compromised leading to lower validity than expected.18 One approach to overcome such a situation is adding a fraction of the external test set examples to the calibration set to make them more exchangeable. The incorporation of some of the test set samples to the calibration set was argued to restore the confidence of the models on never-before-seen data. To demonstrate this, the models trained on public toxicity data were shown to have low validity on both more recent time-split or propriety data as the external test set until this recalibration strategy was applied.18,19 The models can make valid predictions on a space outside of the applicability domain through recalibrating with an “updated” calibration set.18 This strategy was, in another study on toxicity prediction, shown to be more effective then retraining the model with the external test data.19 While more effective in producing reliable predictions, it was comparably more efficient as it requires less computational resources than training from scratch.19 Heyndrickx et al. used conformal prediction in a federated learning setting across pharmaceutical companies. In this work, efficiency was established as a metric to assess the extent of the applicability domain and the reliability of predictions on unseen molecule datasets.20 Inspired by the previous small molecule-focused methods, we aim to explore various recalibration strategies on beyond-the-rule-of-5 molecules and to extend the proposed methodology to peptides.
In this study, we conduct a series of experiments to extend the recalibration strategies and show their influence on the model performance and confidence on its predictions. The study follows a systematic investigation of building predictors with various calibration strategies and later, evaluate the impact of the calibration on model's predictions on external test sets, with a particular focus on peptide permeability. The external test sets were selected from never-before-seen data from different data sources to assess the limitations of the predictive models on the diverse beyond-the-rule-of-5 data. The study aims to exhibit a predictive modelling approach for building predictors that can provide reliable predictions with a predefined expected error on new applicability domains, without the need of retraining the model.
2. Methods
2.1. Dataset description and data preparation
For this study, data was collected from the Cyclic Peptide Membrane Permeability Database (CycPeptMPDB).21 CycPeptMPDB contains experimental results of cell permeability measurements from 47 different sources for cyclic peptides and peptidic macrocycles, made up of 312 different types of monomers. The database contains data from 4 different assays: Caco-2, Madin-Darby canine kidney cell line (MDCK), Ralph Russ canine kidney cells (RRCK) based permeability and parallel artificial membrane permeability assay (PAMPA). 6941 non-conjugated cyclic peptide entries with PAMPA assay results were downloaded and standardized with RDKit v. 2022.03.2.22 After canonicalization with chirality, classification labels were assigned to data points where permeability (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pexp): greater than −6 is labelled with a positive permeability label and the remaining entities with a negative permeability label. Next, any duplicated peptide with same label was removed from the dataset as well as any peptide with conflicting labels due to variation in the measurements from different labs.
Pexp): greater than −6 is labelled with a positive permeability label and the remaining entities with a negative permeability label. Next, any duplicated peptide with same label was removed from the dataset as well as any peptide with conflicting labels due to variation in the measurements from different labs.
The data processing yields 6876 data points, with cycle size ranging between 12 to 46 atoms, from 35 different sources with four of these comprising approximately 90% of the data (Table 1). The processed data was imbalanced with 67.6% of it containing permeable entries. The sparsity of the data sources varied as some sources contained diverse peptides while others were composed of a set of cyclic peptides where stereochemical modifications were introduced to the wild-type amino acid sequence. The principal component analysis and visualizations of the chemical space covered were conducted with ChemPlot.26
2.2. Experiments and data splitting
In Experiment 4, we aimed to refine the calibration strategy by also representing the chemical space of the external test set in the calibration set. This was achieved by integrating a portion of the external test set into the calibration process in each case. To facilitate this, we divided the external test set into five parts, or folds, using stratified cross-validation, ensuring each fold to preserve the overall distribution of the Permeability labels. In each of the five iterations, one fold, or 20% of the external test set, was added to the calibration set, updating it. Employing the models built in Experiment 1, we have calibrated the models with the updated calibration set to test models' adaptability to the unseen chemical space. The remaining four folds were kept as the external test set, allowing the assessment of any changes in the efficiency and validity of the predictions of the recalibrated models. This procedure was repeated for each fold, and the results were aggregated by averaging these metrics to obtain a more stable estimate of the models' performances.
In Experiment 5, the same strategy as in Experiment 4 was followed to assess another recalibration strategy for the models. For this calibration set, instead of concatenating a fold to the pre-existing calibration set, we utilized each fold as a standalone calibration set for five iterations. During the recalibration, the models were not retrained as the proper training set was kept unchanged. The model performance on the remaining four folds were assessed with the conformal prediction metrics to detect any changes in models' reliability. The impact of the strategies in Experiment 4 and 5 were reported as the change of the efficiency and validity values from the respective values in Experiment 3. The difference in the efficiency scores with a value greater than 0 indicated an improvement of model's efficiency due to the recalibration strategy. Any validity score above 0.8 was levelled to 0.8 before the change is computed. This adjustment was to mitigate potential bias due to the inflated validity as we defined the models' confidence to be 80%. Therefore, any validity scores above 0 signified an improvement towards the specified confidence level while any difference below 0 indicated deterioration of validity.
Lastly, Experiment 6 consisted of an evaluation between the outcomes of the Experiment 4 and 5 where the two recalibration strategies were compared based on their potential improvement of efficiency and validity scores from the traditional conformal prediction established as the baseline in Experiment 3.
In the next scenario, the data splitting and the construction of cross-validation folds were achieved with stratification on both the data sources and the permeability label. During the stratification processes, the data from each source was placed to distinct sets or folds where data from a particular source can only be found in a particular fold. This case will be referred to as “Case 2: split on data sources” for the remainder of this study.
In the third and the final scenario, the splitting strategy was implemented with stratification on the canonical group labels assigned to the peptides. These labels were determined by removing the stereochemistry, canonicalizing the SMILES and checking if this yields identical representations. The groups with identical representation were distributed to folds making sure that the instances belonging to the same group were kept together. The singleton data entries were later added to the respective datasets as 20% calibration and 80% proper training set after stratification on the permeability label. This model will be referred to as “Case 3: split on canonical groups”. The experiments are summarized in Fig. 1.
 | ||
| Fig. 1 The workflow of the Experiments 1–7. Experiment 1 and 2 evaluate the trained model on the internal validation set and the external test set, respectively. Experiment 3, 4 and 5 in order, applies conformal prediction with the calibration set split from the training set, the calibration set augmented by a subset of the external test set and using a part of the external test set alone. Experiment 6 compares the three calibration strategies compares based on the prediction efficiency and validity on the external test set. Lastly, Experiment 7 explores various cross-validation strategies during model building. A summary table can be found in ESI Table 1.† | ||
2.3. Modelling
2048-bit Morgan fingerprints were used as molecular representation with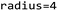 ,
, 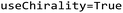 and
and  .27 This descriptor was chosen due to its established robust performance in predictive tasks for both small molecules and peptides.28,29 The molecular fingerprints were fed to baseline ML algorithms. We utilized a kernel-based algorithm (Support Vector Machine), a tree-based algorithm (Random Forest), and two gradient-boosting methods with distinct tree-growth strategies (depth-wise with XGBoost and leaf-wise with LightGBM), aiming to represent a baseline machine learning portfolio. Random Forest (RF) and Support Vector Machine (SVM) models were built using scikit-learn v.1.1.1.30 XGBoost (XGB) was implemented with
.27 This descriptor was chosen due to its established robust performance in predictive tasks for both small molecules and peptides.28,29 The molecular fingerprints were fed to baseline ML algorithms. We utilized a kernel-based algorithm (Support Vector Machine), a tree-based algorithm (Random Forest), and two gradient-boosting methods with distinct tree-growth strategies (depth-wise with XGBoost and leaf-wise with LightGBM), aiming to represent a baseline machine learning portfolio. Random Forest (RF) and Support Vector Machine (SVM) models were built using scikit-learn v.1.1.1.30 XGBoost (XGB) was implemented with 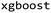 v.1.7.5 package and LightGBM was applied by using Microsoft's implementation of
v.1.7.5 package and LightGBM was applied by using Microsoft's implementation of 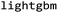 v.3.3.5.31 The hyperparameter optimization was performed using the Bayesian search function (BayesSearchCV) in scikit-optimize32 with predefined search spaces for all the models. 10-fold cross-validation was conducted using StratifiedKFold on permeability labels and the optimized model was obtained with the cross-validation results. The same methodology was employed for the Case 1: baseline to train a model with the whole data set as in Experiment 4 and 5. The 10-fold cross-validation during hyperparameter optimization was conducted in a more complex manner for Case 2: split on groups. In this case, the cross-validation was performed with StratifiedGroupKFold similarly on the proper training set where the stratification was based on the permeability labels and previously mentioned group labels.
v.3.3.5.31 The hyperparameter optimization was performed using the Bayesian search function (BayesSearchCV) in scikit-optimize32 with predefined search spaces for all the models. 10-fold cross-validation was conducted using StratifiedKFold on permeability labels and the optimized model was obtained with the cross-validation results. The same methodology was employed for the Case 1: baseline to train a model with the whole data set as in Experiment 4 and 5. The 10-fold cross-validation during hyperparameter optimization was conducted in a more complex manner for Case 2: split on groups. In this case, the cross-validation was performed with StratifiedGroupKFold similarly on the proper training set where the stratification was based on the permeability labels and previously mentioned group labels.
2.4. Uncertainty estimation
Conformal prediction is a mathematical methodology used as to assess the predictive performance of the algorithm based on a user-specified confidence level. The methodology uses a calibration set to recalibrate the predictions of the test set to analyze the uncertainty associated with these predictions.The 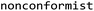 v.2.1.0 package was used to build the conformal prediction framework.33 The conformal prediction adapted to classification tasks was employed. The inductive conformal predictor (ICP) with Mondrian classification, where the nonconformity scores are generated for each class independently, was utilized to prevent error rate shifts due to class imbalances. Next, 10 ICPs were used as an ensemble and aggregated with the aim of enhancing the calibration of prediction intervals by pooling the predictions of the ensemble members. After the conformal prediction structure was completed, the calibration set was used together with the trained model to calculate the nonconformity scores. The fitted conformal predictor was later deployed to obtain predictions on the external test set. The predictions of new data points were carried out without specifying a significance level and the p-values were obtained as the output. The model performance was analyzed by investigating both conformal prediction metrics calculated using the p-values and classical model evaluation metrics from scikit-learn.
v.2.1.0 package was used to build the conformal prediction framework.33 The conformal prediction adapted to classification tasks was employed. The inductive conformal predictor (ICP) with Mondrian classification, where the nonconformity scores are generated for each class independently, was utilized to prevent error rate shifts due to class imbalances. Next, 10 ICPs were used as an ensemble and aggregated with the aim of enhancing the calibration of prediction intervals by pooling the predictions of the ensemble members. After the conformal prediction structure was completed, the calibration set was used together with the trained model to calculate the nonconformity scores. The fitted conformal predictor was later deployed to obtain predictions on the external test set. The predictions of new data points were carried out without specifying a significance level and the p-values were obtained as the output. The model performance was analyzed by investigating both conformal prediction metrics calculated using the p-values and classical model evaluation metrics from scikit-learn.
2.5. Performance metrics
The predictive models were evaluated using common metrics such as balanced accuracy (BA), precision, specificity, sensitivity, and Matthew's correlation coefficient (MCC). The model's conformal prediction performance was assessed with conformal prediction specific metrics by using the significance level at 0.20 in all experiments. The chosen significance level is commonly used as it generally demonstrates a good balance between efficiency and validity.34,35 Efficiency describes the fraction of single-labelled predictions of each class. Another metric is validity which explains the fraction of accurate predictions including the correct single label prediction as well as “Both” label to all the predictions of that class. The evaluations of the models' performances were conducted comprehensively by considering all the conformal prediction metrics.In Experiment 7, the model evaluation metrics were calculated for the single-label predictions of the test sets at the significance level of 0.20 additionally. The formulae for the conformal prediction metrics are provided below.
where the efficiency and validity of each class, permeable (class = 1) and non-permeable (class = 0), are calculated separately. The subscript defines the true class of the data points, i.e. single label predictions define the number of correct or incorrect single-label predictions on the peptides with the class denoted in the respective subscripts.
3. Results
In the following section, we will examine predictive performances of the different models built and optimized for permeability prediction for cyclic peptides. In the first step of the study, consisting of Experiments 1–6, the model building was performed under different scenarios where four of the largest data sources in the CycPeptMPDB were used as external test sets to investigate whether these data sources are exchangeable. The principal component analysis of the molecular representation space shows the preprocessed data with the sources used as the external test set (Fig. 2). 2013 Chugai23 and 2021 Kelly24 data sources were found to be dissimilar to the rest of the external test sets as well as the data used as the training set for model built to predict this data source. This can be interpreted as the data sources with the largest distances to their respective training data if were held out as the external test set. Thus, these peptides from these sources were hypothesized to be the hardest tasks for out-of-domain prediction.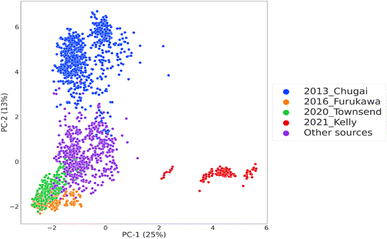 | ||
| Fig. 2 The chemical space visualization of the processed data obtained from CycPeptMPDB,21 coloured by the sources adapted as external test sets and the remaining data serving as the common training data instances in all experiments. The axes indicate the principal components and the percentage of explained variance. | ||
To provide context for the need to address the challenges of building predictive models from different data sources, Experiments 1 and 2 were aimed to showcase the outcome of traditional model building practices and to establish the model performance on the validation set and external test sets, respectively. In Experiment 3, the conformal prediction was applied to the models built in Experiment 1 and the model performance on the external test sets were re-evaluated through uncertainty quantification. The applicability domain of the model was investigated through two calibration strategies; expanding the calibration set with a portion of the external test set (Experiment 4) and using only a part of the external test set as the calibration set (Experiment 5) to recalibrate the underlying models. Chemical spaces spanned by the training, calibration and external test sets utilized in the first five experiments are visualized in ESI Fig. 1.† The influence of the calibration strategies on the efficiency and restoring validity of the models were compared in Experiment 6. Lastly, training models with the entire data with different cross-validation strategies was tackled to analyze the reliability of the model in the studied chemical space in its entirety.
3.1. Experiment 1: model building and performance on the internal validation set
In the initial phase of the model performance evaluation, we employed the baseline practices of hyperparameter optimization with 10-fold cross-validation and testing each optimized model on the assigned validation set. The data preprocessing and train-validation set splits were conducted separately for each dataset remained after holding out four external test sets. After the preprocessing, four models were built and validated on their respective training and validation sets. The validation sets consisted of data similar to the chemical spaces each model was trained on as the validation sets were stratified from the same data sources that constituted the respective training data. Therefore, the predictive task was expected to achieve better results compared to a predictive task on an external test data spanning a different chemical space than, or distant to, the training data. Fig. 3 displays the model performance metrics obtained from predictions on the validation sets. The models were trained and tested on the data that remained after the external test data was removed and almost all models except for the holdout case of “2021 Kelly24” showed similar results. The balanced accuracy was above 0.70 with averages of 0.76 (±0.04), 0.77 (±0.03), 0.77 (±0.09) for the models trained on the data remaining after setting aside the holdout cases of 2016 Furukawa,9 2013 Chugai23 and 2020 Townsend,25 respectively. The balanced accuracies were much lower, on average 0.60 (±0.11), for models trained on data from “2021 Kelly24” case. This case was not excluded from the remaining experiments to observe the relative differences on model performance under confidence pressure. Instead, this dataset was used as the most distant applicability domain extension task (ESI Fig. 1†).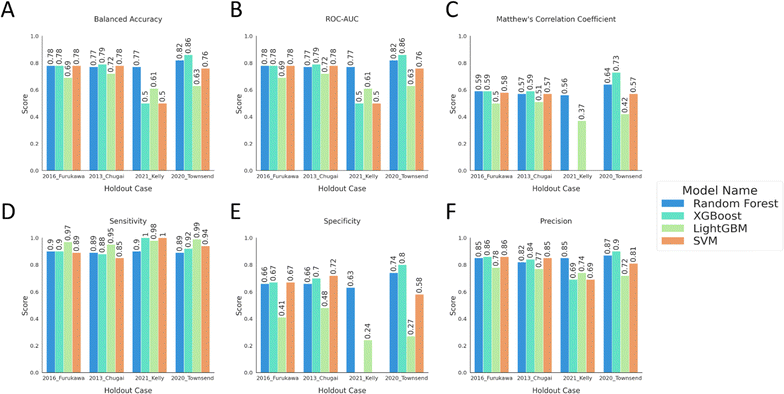 | ||
| Fig. 3 The model performance metrics on the internal validation data. The bar plots show (A) balanced accuracy, (B) ROC-AUC, (C) MCC, (D) sensitivity, (E) specificity, and (F) precision scores for the models, coloured as described in the legend. The models and the performance metrics are labelled with the external data set they will be evaluated on in the next experiment, Experiment 2. The purpose of this labelling is that the models designated by the same labels are built on the same training data and the training data contains all the data sources except for the holdout case label. Scores below or equal to 0 are not visualized in the plot and the tabular data for all the metrics can be found in ESI Table 2.† | ||
The models except for the “2021 Kelly24” case, generally produced higher sensitivity around 0.90 and lower specificity around 0.60. This reflects the influence of data imbalance on model performance even though the validation data was selected from the same data sources as in the training data where the model would be more confident. All the models showed Matthew's correlation coefficient above 0.50 implying that the predictions from the models correlate with the actual values and the binary predictors could separate the two classes efficiently. However, with the consideration of sensitivity and specificity, the models were more prone to predict the “Positive” or the “Permeable” class. Overall, this experiment shows how a model trained on a specific chemical space performs well on the same space. The models produced predictions with high balanced accuracy with an effective decision boundary separating the two classes while still affected by the data distribution. Since the internal validation data was later used as the calibration set data to apply conformal prediction framework, this experiment also aims to highlight the similarity of the calibration set to the data the models were built on.
3.2. Experiment 2: evaluation of model performance on the external test set
The predictive capabilities of the built models were further assessed on the independent test sets. The predictions on the external test sets for each holdout case showed similar results for all the performance metrics considered (Fig. 4). The models were less accurate and thus unsuccessful in predicting never-before-seen data as both the balanced accuracy and ROC-AUC showed an average decrease of 0.20 (±0.11) compared to the predictions on the corresponding validation set. Also, the decision boundary had significantly lower ability to separate the binary classes and the randomness of predicting class labels increased with the declining Matthew's correlation coefficient score compared to Experiment 1 with an average of 0.43 (±0.22) (Fig. 4). The higher sensitivity and the drastic drop in specificity indicate the increase in the fraction of false positives with much lower number of false negatives when the predictive performances were compared between Experiment 1 and 2. Models trained on the holdout case of “2021 Kelly24” show similar but more extreme performance changes with higher sensitivity, around 1.0, lower sensitivity ranging between 0 to 0.12 and lower precision compared to the predictions on the validation set. For this holdout case the model could only assign the positive label to all predictions which is the majority (“Permeable”) class label which was also reflected in the lower precision values.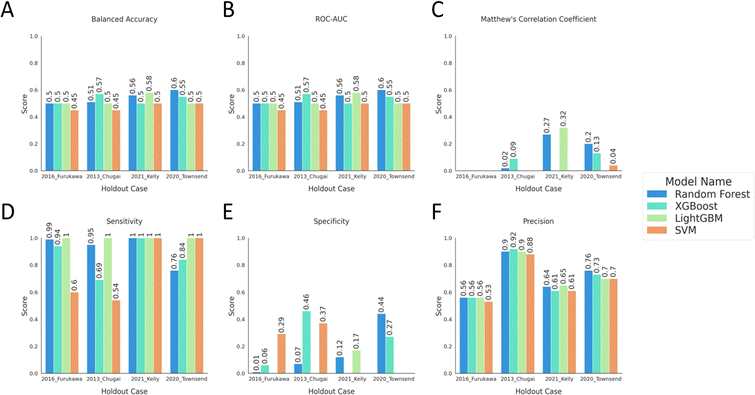 | ||
| Fig. 4 The model performance metrics on the external test sets. The bar plots show (A) balanced accuracy, (B) ROC-AUC, (C) MCC, (D) sensitivity, (E) specificity, and (F) precision scores for the models, coloured as described in the legend. The scores are reported on each model, with distinct colour, and labelled with the name of the external test set. Scores below or equal to 0 are not shown on the plot and the tabular data for the bar plots can be found in ESI Table 3.† | ||
The increase of the difference between sensitivity and specificity demonstrates the models' predictions to be heavily biased towards the “Permeable” class. Thus, when predictive models are applied on the extrapolated applicability domains, their inherent biases are more pronounced. The change in the predictive power translates into the reduction of the models' abilities to generalize to data outside of its applicability domain.
3.3. Experiment 3: applying conformal prediction framework
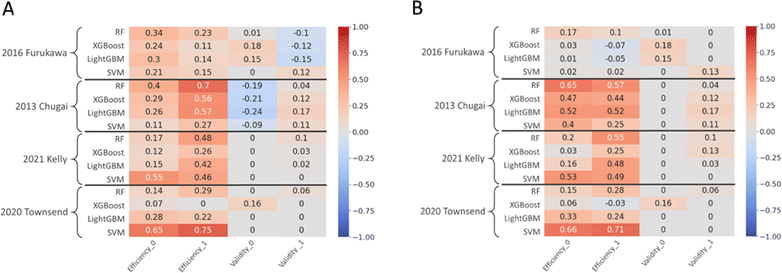
The conformal prediction methodology was applied by using the calibration data that was set aside for each model building scenario for recalibrating the holdout cases. The conformal prediction metrics were calculated at the defined significance level and compared for different algorithms on external test sets. The results in Fig. 5 show high validity, above 0.70, for both classes with comparably lower efficiency in most cases indicating that most of the valid predictions stem from two-label (“Both”) predictions. Except for the “2021 Kelly24” case, there were no significant differences in the efficiencies of “Permeable” and “Non-permeable” classes, even though the training data was imbalanced with a minority class of “Non-permeable” peptides. The low efficiencies but high validities display the models' generalizability as the model assigns a “Both” class to a fraction of instances with the indication that the model recognizes the instance to be similar to the applicability domain of the calibration set. However, the model cannot distinguish between the binary classes for these instances under the mandated error rate of 20%.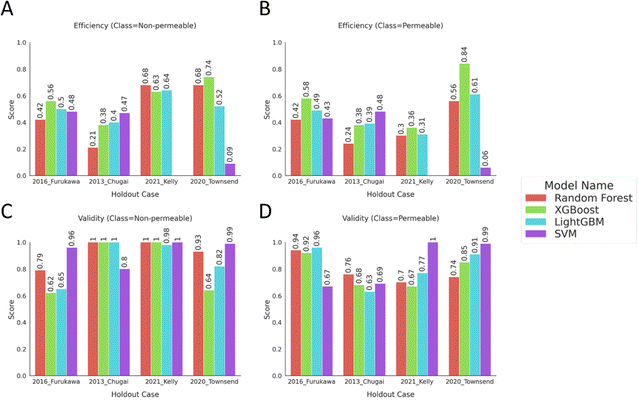 | ||
| Fig. 5 Bar plots show conformal prediction metrics; efficiency and validity, calculated on the external test sets predicted by the calibrated models. The metrics were computed at significance level = 0.2, mandating the model to produce predictions with 80% confidence. The efficiency of the instances with true labels of (A) “Non-permeable” and (B) “Permeable”, the validity scores of the instances with true labels of (C) “Non-permeable” and (D) “Permeable” were displayed. The tabular data of the plots can be found in ESI Table 4.† | ||
The “2021 Kelly24” case stands out with a much higher efficiency and validity for the “Non-permeable” class compared to the “Permeable” class. From the previous experiments, we have observed a predictive bias for the models of this case label to overpredict the majority “Permeable” class. Using conformal prediction, we can further characterize these models and conclude that the minority class examples on the external test set were comparably closer to the calibration set examples than the majority class for these models. Thus, the model can provide comparably more accurate single-label predictions for the “Non-permeable” class.
For the rest of the holdout cases, the low efficiency values imply that decision-making for assigning either one of the classes to the predictions was often not possible at the 80% confidence level. Nevertheless, some of the models showed high validity, above 0.75, for the binary classes while the majority of the models did not achieve this goal with one of the binary classes having a lower score than their counterpart. As the class with higher validity also was not, in general, accompanied by a higher efficiency compared to the other class, it is indicative that the models are producing two-label predictions for these classes (Fig. 5). The valid but inefficient predictions display the model's inability to make accurate single-label predictions for the independent test sets or strengthening the generalizability argument of the training and external sets from Experiment 2.
3.4. Experiment 4: recalibrating the model by augmenting the calibration set with a subset of the external test set
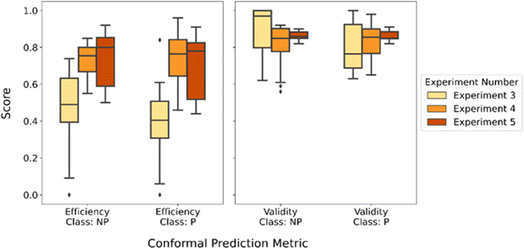
To explore whether the predictive power can be influenced by extending the calibration set with some portion of the external test set, the calibration set was updated with 20% of the external set, as described in Methods Section 3.2.1. The external data was added to the calibration set in a 5-fold cross validation manner to evaluate the influence of any potential improvements on the models' performance. The conformal prediction methodology was re-built on top of the trained models on Experiments 1 and 2 with the updated calibration set. The mean of the conformal prediction metrics from 5-fold augmentation process were calculated for the predictions on the remaining instances of the external test sets. The results were compared with the corresponding conformal prediction scores from the original calibration results from Experiment 3 (Fig. 6A). In Experiment 4 and 5, the pre-set significance level was 0.2, demanding 80% confidence in models' predictions. Therefore, any validity scores above 0.8 implies that the model is over-confident. The validity values above this threshold can be ignored as the task defined for the model entails only 80% accurate results. Hence, we only considered the scores below the specified confidence to conduct a comparison. The main goal of adopting an augmented calibration set was to improve the model's ability to provide single-label predictions under the user-defined confidence level without compromising the validity of the binary classes to a greater extent. In line with this purpose, the recalibration of the model resulted in an increase in efficiency for almost all models, for both binary classes and for all the holdout cases with mean absolute change in efficiency of 0.31 (±0.17) (Fig. 6A).The validity scores showed either no change or minor increase for the holdout cases of “2021 Kelly24” and “2020 Townsend25”. However, the validity of the “Non-permeable” class increases while the scores for “Permeable” class decreases for all but SVM model for “2016 Furukawa9” and vice versa for “2013 Chugai23”. These external test sets contain 56.4% and 89.9% “Permeable” class, respectively (Table 1). The increase or decrease of the imbalance of the external test sets influences the imbalance in the augmented calibration set. As the imbalance of the classes of the calibration set resembles the external test set, the validity of the classes shifts accordingly. While the validity scores exhibited mixed and distribution-dependent changes across model–data pairs, the mean absolute change in validity was 0.01 (±0.08). Additionally, the changes in validity scores on average for both classes did not show significant reduction with this recalibration strategy. The exact conformal prediction metrics with standard deviations for the recalibration experiment can be found in the ESI Table 5.†
The boost in the efficiency without drastic changes in validity indicates the model achieving better reliability as the nonconformity scores were also calculated partly on the external data set during calibration. The augmented calibration does not provide more valid predictions however, under the pre-set error rate, it makes more efficient predictions without the need of retraining the underlying model. This signifies that the model has shifted from two-label predictions, or predicting “Both” class, from Experiment 3 to provide more single-label predictions of “Permeable” and “Non-permeable”.
3.5. Experiment 5: recalibrating the model only with a subset of the external test set
The importance of the choice of calibration set to obtain reliable model predictions was reinforced by the previous experiments. However, using an augmented calibration set might still have its own drawbacks. The updated calibration can set still suffer from the applicability domain predominated by the original calibration set. The over-represented chemical space of the training data can lead to reduced performance on efficiency. In Experiment 4, the augmented calibration set is composed of 2 data sets. First, the data spanning the same or similar chemical space as the proper training set and secondly, a subset of the data of interest which spans a chemical space not necessarily in proximity with the space spanned by the proper training set. The imbalance of these two components could potentially impact the recalibration process. In the current experiment, we will explore if we can mitigate the influence of the original calibration data by adopting a new recalibration strategy.The recalibration in this experiment was merely done with the subsets of the external test set on the models from Experiment 1 and 2 and without the original calibration set samples from Experiment 3. Similar to the previous recalibration experiment, the calibration was conducted 5 times with individual folds from the 5-fold stratified split of the external test set. The remaining four folds in each case was kept as the external test set and means of the conformal prediction metrics are calculated on predictions on the remaining external test set instances. The conformal prediction metrics with standard deviations for this experiment can be found in the ESI Table 6.†
Almost all the models again showed improvements in efficiency for both “Permeable” and “Non-permeable” classes except for “2016 Furukawa9” case (Fig. 6B). For the rest of the models, we see a clear increase in the efficiency where the models provided more single-label predictions. Moreover, the validity scores were either preserved or in some cases improved for both classes. The validities of the “Permeable” classes were generally increased as well as the efficiency indicating that the models provided both more valid and efficient, or simply more accurate single-label, predictions to the external test set samples. The “Non-permeable” class generally showed no change in the validity but comparably greater increase in efficiency from the traditional calibration method in Experiment 3 (Fig. 6B). Therefore, the models' performance on both classes were strengthened compared to prediction results from Experiment 3.
Improving efficiency of the models' predictions without sacrificing validity was demonstrated in this experiment by using a subset of the external test set as a calibration set alone to recalibrate the models. This recalibration strategy was able to expand the reliability of the predictions to the never-before-seen applicability domains under the assumptions that the training data and the external test data are noticeably varied.
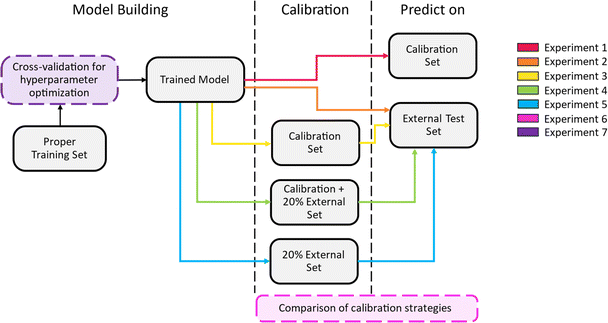
3.6. Experiment 6: comparison between the recalibration strategies from Experiments 4 and 5
In the previous two experiments, we have explored two recalibration strategies and compared the conformal predictions scores on the external test set predictions to the models from the traditional calibration set from Experiment 3. In this section, we will assess the recalibration strategies and perform a comparative analysis of the outcomes of the same underlying models with the calibration sets from Experiments 4 and 5. In these experiments, 16 models were kept constant as we employed the conformal prediction frame with different calibration sets. The first recalibration strategy from Experiment 4 was using the calibration set augmented with 20% of the external test set in each holdout case. The second recalibration strategy was using only the 20% of the external test set as the calibration set from Experiment 5. The conformal prediction metrics calculated from the predictions on the external test sets through both strategies were evaluated together and the distributions of the scores from the experiments are illustrated in Fig. 7. The efficiencies of both recalibration strategies were previously observed to be better than the baseline from Experiment 3, the traditional conformal prediction method. The median of the efficiency scores from the first recalibration strategy was lower compared to the second strategy. Even though the spread, or the interquartile range, of the efficiency scores from the second experiment was wider, the total range of the data was still more compact compared to the first recalibration strategy.The span of the validities for both classes are more similar for both recalibration strategies compared to our baseline. The models' predictive performance was balanced between the binary classes when we diverged from the traditional calibration methods using only the calibration set parsed from the training set. Additionally, there was consistency between the medians of both recalibration strategies as the spread of the validity scores are narrower for the predictions coming from models calibrated by the external test set alone.
In Experiments 4 and 5, the validity scores were compared with values from Experiment 3 after all the scores were bounded to 0.8, the pre-defined confidence level. The validity scores for the first recalibration strategy were spreading a range around 0.8 and below the baseline experiment for “Non-permeable” class while the validities for the second one was only having scores above 0.8. This implies that threshold at 0.8 was exceeded in all the model and external test sets for each holdout cases for the latter recalibration strategy. Therefore, the validity scores from models calibrated with the external test sets alone were able to protect the validity from being compromised with the exchange of better efficiency. The trade-off between efficiency and validity was optimized better when using the calibration set only representative of the extrapolated applicability domain. Considering the size of the datasets, “2016 Furukawa9” and “2013 Chugai23” were smaller and thus, the subset of 20% of these cases entailed a smaller calibration set. Since the major recovery of the validity scores between the two experiments were in these holdout cases, the influence of the original calibration set was clearly more prominent when the augmentation was achieved with smaller datasets.
3.7. Experiment 7: model building with the entire data sets
Building a predictive model with data composed of different data sources is cumbersome as one needs to be aware of data commonalities. In this final experiment, we explored another aspect of building predictive models which is the cross-validation strategies. Case 1: baseline uses a stratification strategy on the permeability label while Case 2: split on data sources utilizes both the permeability labels and the information on data sources. The third case, Case 3: split on canonical groups, was investigated on stratified splits on permeability label as well as the canonical structures in the data.The predictive models built with these cross-validation strategies were generally found to yield models with high efficiency (>0.7) and high validity (>0.8) for both classes (Table 2). The high efficiency and validity show that the training, calibration, and test sets are generated in an exchangeable manner. The training data are now, to a large extent, coming from the large size data sources and the external test sets utilized in the previous experiments as holdout cases are now placed in the training set. Therefore, training and test sets are more representative of the entire chemical space covered, contributing to the generalizability of the model.
| Case | Significance level = 0.2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Split cases | Model name | Efficiency 0 | Efficiency 1 | Validity 0 | Validity 1 | Balanced accuracy | Precision | Sensitivity | Specificity | MCC |
| Baseline | RF | 0.80 | 0.82 | 0.80 | 0.84 | 0.78 | 0.87 | 0.80 | 0.75 | 0.54 |
| XGBoost | 0.86 | 0.85 | 0.83 | 0.83 | 0.80 | 0.89 | 0.80 | 0.80 | 0.57 | |
| LightGBM | 0.74 | 0.76 | 0.85 | 0.85 | 0.80 | 0.89 | 0.80 | 0.79 | 0.57 | |
| SVM | 0.77 | 0.77 | 0.88 | 0.84 | 0.82 | 0.91 | 0.79 | 0.85 | 0.60 | |
| Split on data sources | RF | 0.77 | 0.79 | 0.89 | 0.86 | 0.84 | 0.92 | 0.83 | 0.86 | 0.66 |
| XGBoost | 0.78 | 0.77 | 0.87 | 0.86 | 0.82 | 0.91 | 0.81 | 0.83 | 0.62 | |
| LightGBM | 0.86 | 0.80 | 0.87 | 0.82 | 0.81 | 0.90 | 0.77 | 0.84 | 0.59 | |
| SVM | 0.72 | 0.66 | 0.91 | 0.85 | 0.82 | 0.92 | 0.76 | 0.88 | 0.62 | |
| Split on canonical groups | RF | 0.76 | 0.76 | 0.87 | 0.84 | 0.81 | 0.91 | 0.79 | 0.83 | 0.59 |
| XGBoost | 0.80 | 0.82 | 0.80 | 0.84 | 0.78 | 0.87 | 0.80 | 0.75 | 0.54 | |
| LightGBM | 0.86 | 0.85 | 0.83 | 0.83 | 0.80 | 0.89 | 0.80 | 0.80 | 0.57 | |
| SVM | 0.74 | 0.76 | 0.85 | 0.85 | 0.80 | 0.89 | 0.80 | 0.79 | 0.57 | |
Case 2: split on data sources shows similar efficiency scores and slightly higher validity scores than for Case 1: baseline. This yields more “Both” class predictions, showing that the model learns the chemical space more comprehensively and can be leveraged for more single-label predictions by lowering the significance level. Moreover, the rest of the explored metrics show similar results between the baseline and the split methodologies we have employed in the earlier experiments. This draws focus to the question of whether all the data sources are distinctly diverse from each other. To ensure that the chemical space is learned exhaustively during model building, we explored a third cross-validation scenario where the data points were grouped according to their stereochemical counterparts. Removing stereochemical information from the structures of cyclic peptides during canonicalization, allowed a new grouping strategy. The cyclic peptides were stereochemical variants of each other were kept in the same folds. The models were built with cross-validation where the folds contain diverse analogous peptide sequences, disregarding which data source they were part of. The peptides that were not grouped were later mixed in equal distributions to the generated folds. Models built with this setup, Case 3: split on canonical groups, was expected to be cross-validated on a harder task and thus, comprehensively explore the chemical space during training. The efficiency on both “Permeable” and “Non-permeable” classes show similar scores, but slightly higher for the “Permeable” class, for the models of this case compared to the models from Case 2. However, the validity of the binary classes was either on par or slightly lower with Case 2 although still above 0.8, the pre-defined confidence level. These results indicate that Case 2 models would need lower significance level to utilize the models for efficient predictions whereas Case 3 can be used for more single-label predictions with a slight drop in validity. Since both cases exhibit similar performances overall considering the trade-off between efficiency and validity, the models learned the chemical space similarly and could assign accurate and reliable single-label predictions at the set uncertainty level regardless of the splitting strategy.
Across cross-validation strategies, the comparison is not based on the models trained on the same training set or predicting the same test set. Therefore, one might question the fairness of a such comparison. However, the aim is to look at how confident these models are with respect to the conditions they were trained and validated on as well as to highlight the importance of considering the diversity of the descriptor space in addition to focusing only on data sources. The cross-validation split strategies were introduced to provide a starting point for different model building processes. In addition to the calibration set selection, the predictive models built on different data sources with the proposed methodologies can be used to produce reliable predictions for their respective applicability domain. Furthermore, these models can also be extrapolated to uncharted applicability domains with good performance.
4. Discussion
Cyclic peptides have been receiving increased attention for their therapeutic potential. Various studies focused on how their cell membrane permeability can be improved as this is the key for this type of compounds to emerge as an independent new modality. Predictive models for a range of properties are needed to accelerate the drug discovery process. The lack of large and diverse datasets for peptides and peptidic molecules, compared to small molecules, presents a challenge for the practical use of predictive models, in particular when models are expected to generalize to external data. This study establishes predictive modelling practices in the peptide domain using multiple source data to build predictors applicable to real-world use cases of drug discovery pipelines. In this study, we conducted a series of experiments to explore the applicability domain of the baseline ML models to predict membrane permeability for various external test sets. In line with the modelling practices, we have also investigated cross-validation and calibration strategies in conformal prediction framework in terms of generalizability to never-before-seen cyclic peptides.When building a predictive model, the data is split into training and validation datasets spanning overlapping or similar domains. The model trained on the training set is then, typically used to predict the validation set to assess the model's performance. Even though this shows that the model performs well to the applicability domain spanned by the training set, it does not establish the model's generalizability to its full potential. In our first experiment, we have shown that the trained permeability predictors perform well on the validation set spanning similar chemical spaces with the training set with high balanced accuracy and MCC. However, these models did not exhibit the same predictive power when it comes to an unseen data from a new data source, different from the learned chemical space. The performance metrics in Experiment 2, indicate that the model's predictions are more random with the drastic decline in all the metrics with balanced accuracy around 0.5 and MCC around 0. Since the class imbalance in the training data and the external data are different, the model provides predictions with the distribution it learned where the “Permeable” class dominates rather than the learned intricacy of the chemical space. This was reiterated when we explored the reliability of a model's predictions through conformal prediction in Experiment 3. Conformal prediction methodology allows the uncertainty to be investigated through a user-defined confidence where the predictions are evaluated on how valid and efficient they are. We have calibrated our models from with the validation set and predicted the external test sets. Under 80% confidence level, the predictions had poor efficiency scores but not inflated validity. This suggests that the models were not able to distinguish between the classes as a good portion of the peptides were predicted to be the “Both” class. The first three experiments highlight the importance of understanding the applicability domain and the generalizability of the model before relying on any predictions on new peptides in design-make-test-analyze cycle. If one wants to obtain efficient predictions, the only option for these models would be lowering the required confidence level as the validity becomes compromised. This compromise puts the practical applicability of the model at risk. To mitigate this risk, we evaluated new calibration strategies to make the external data more exchangeable with the calibration set and therefore, re-assessed the reliability of the model.
Experiment 4 and 5 focus on two calibration strategies where the underlying trained models were kept constant, and the confidence defined for the models was not sacrificed. The first recalibration strategy was augmenting the calibration set in Experiment 3 with a subset of the external set and the second one was employing a portion of the external test set alone as the calibration set. Both recalibration strategies extended the reliability of the models' predictions by improving the exchangeability of the calibration and test sets. This enhanced the models' efficiency without necessarily sacrificing the validity of predictions compared to the original calibration strategy. We conclude, in Experiment 6, that using only a portion of the external test set to calibrate the model resulted in more reliable predictions as the validity was preserved or improved across all the external test sets of different sizes and class imbalances. Additionally, the importance of the choice of calibration set was evident as the influence of the original calibration instances decreased the validity and in turn reliability for both classes. Consequently, we have established a proof-of-concept study for building uncertainty-aware predictive models for peptides and described the methodology through permeability prediction. In the real-world use, predictors trained on the public data can be used to predict proprietary or more recent public data by characterization of a small portion of the targeted chemical space. The newly characterized data can be leveraged as the calibration set to recalibrate the model to later provide predictions on the remaining part of the data. This methodology enables to make full use of the model with the confidence of its applicability domain. Additionally, the recalibration is less resource intensive as the underlying models do not need to be trained. Exploring additional factors such as the sizes of the calibration or the training set, selecting the calibration set with distinct compositions or the choice of nonconformity measure in subsequent research could provide new insights on the impact of the variations in conformal prediction framework on efficiency and validity.
In the final experiment, fold splitting strategies in cross-validation were examined. As the data used in this study is a compilation from diverse permeability studies of peptides, the previous experiments were assessing the reliability of building a model on data from these studies and predicting data from a different source. In these experiments, cyclic peptides contained stereochemical information impacting their permeability thus, chirality was not removed during the preprocessing. Grouping based on their canonical representations, without the chirality, resulted in groups of peptides with the same stereo-agnostic representation. Using this grouping as fold splitting strategy in Experiment 7, resulted in preserving highly similar peptides from various data sources together during cross-validation. Models built with this strategy had similar balanced accuracy and validity, but slightly higher efficiency compared to constructing the splits on the permeability labels. However, the models' performances were later observed to be on par with grouping on the data sources. As these models provide more informative or single-label predictions, they generalize better to the provided chemical space. This result also showcases the importance of considering the data sources in such cases as much as the structural commonalities during model building. Building on the insights gained, future studies can investigate how to assess the applicability domain across different types of molecules such as whether a model trained on small molecules can be applied on peptides. Furthermore, the modelling approaches such as transfer learning with conformal prediction can be explored to potentially expand the model's applicability through domain adaptation. The three-party similarities of the source, target and test domains and the impact of these on the model performance would have to be carefully assessed by quantifying the reliability of predictions.
5. Conclusions
In this work, the process of building the model and using it for the prediction of cyclic peptides outside of its applicability domain was assessed through the well-established uncertainty quantification framework of conformal prediction. The systematic exploration of fold splitting in cross-validation and the choice of calibration set examples were conducted by various experiments primarily focusing on permeability prediction for beyond-the-rule-of-5 molecules, cyclic peptides. The experiments illustrated various models' ability to provide high accuracy predictions on the peptidic chemical spaces in proximity to the training data. However, these models were later shown to fail in generalizing to cyclic peptides outside of their applicability domain. The non-exchangeability of the calibration and test data was further demonstrated using conformal prediction with calibration sets parsed from the training data. Later, two recalibration strategies were employed to evaluate whether the models' confidence can be extrapolated to overcome the displayed limitations: recalibration by augmentation and by replacement, respectively. Efficiency was important to define how informative the model predictions are while the validity defined the limitations of model's reliability. Recalibration by using only a subset of the never-before-seen test data exhibited better performance in improving the efficiency without violating the validity of the models' predictions. Finally, we also demonstrated that acquiring data from multiple resources requires a careful examination of the unified chemical space. Exploring the stereochemical variations of the cyclic peptides, the cross-validation with folds that keep the canonically similar structures together were shown to generalize better for the given confidence level to splitting on task labels while on par with grouping by data sources.Balancing the trade-off between the efficiency and validity is essential for the practical applications of predictive models to produce correct and informative predictions. After training a model that learns the provided chemical space, the choice of calibration set was shown to be important for extension of the models' reliability to new domains of interest. The use of various algorithms and test sets in this study through a set of experiments suggests a generic approach for probing the applicability domains. In conclusion, this study offers a methodology to attain flexible applicability profile for predictive models where the models can provide reliable membrane permeability predictions on unseen or uncharted peptidic chemical spaces.
Data availability
The data used to train cell permeability predictive models for cyclic peptides are publicly available in CycPeptMPDB: http://cycpeptmpdb.com/download/. The preprocessed data also publicly available in Zenodo: https://zenodo.org/records/10708332. The preprocessed data contains the amino acid sequence and SMILES for cyclic peptides, the annotation of the data source, the PAMPA experimental measurements and the permeability class labels. The codes for this study, including data splitting, model building, and conformal prediction codes, are also included in the Zenodo link provided above. Moreover, the trained and calibrated predictive models in each experiments and for each of the holdout cases are provided in the Zenodo link: https://zenodo.org/records/10708486.Author contributions
G. G. and U. N., and O. E. designed and conceptualized the project. G. G. performed the experiments. G. G. and U. N. analyzed the results. G. G. wrote the manuscript. All authors discussed the results and reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been partially funded by the Swedish Foundation for Strategic Research (SSF) through an industrial PhD studentship for GG.Notes and references
- L. Wang, N. Wang, W. Zhang, X. Cheng, Z. Yan, G. Shao, X. Wang, R. Wang and C. Fu, Signal Transduction Targeted Ther., 2022,(7), 1–27 Search PubMed.
- N. Tsomaia, Eur. J. Med. Chem., 2015, 94, 459–470 CrossRef CAS PubMed.
- H. Huang, J. Damjanovic, J. Miao and Y. S. Lin, Phys. Chem. Chem. Phys., 2021, 23, 607 RSC.
- L. K. Buckton, M. N. Rahimi and S. R. McAlpine, Chem.–Eur. J., 2021, 27, 1487–1513 CrossRef CAS PubMed.
- J. M. Wolfe, C. M. Fadzen, Z. N. Choo, R. L. Holden, M. Yao, G. J. Hanson and B. L. Pentelute, ACS Cent. Sci., 2018, 4, 512–520 CrossRef CAS PubMed.
- E. C. L. de Oliveira, K. Santana, L. Josino, A. H. Lima e Lima and C. de Souza de Sales Júnior, Sci. Rep., 2021, 11(1), 1–15 CrossRef PubMed.
- M. R. Naylor, A. M. Ly, M. J. Handford, D. P. Ramos, C. R. Pye, A. Furukawa, V. G. Klein, R. P. Noland, Q. Edmondson, A. C. Turmon, W. M. Hewitt, J. Schwochert, C. E. Townsend, C. N. Kelly, M. J. Blanco and R. S. Lokey, J. Med. Chem., 2018, 61, 11169–11182 CrossRef CAS PubMed.
- S. Ono, M. R. Naylor, C. E. Townsend, C. Okumura, O. Okada and R. S. Lokey, J. Chem. Inf. Model., 2019, 59, 2952–2963 CrossRef CAS PubMed.
- A. Furukawa, C. E. Townsend, J. Schwochert, C. R. Pye, M. A. Bednarek and R. S. Lokey, J. Med. Chem., 2016, 59, 9503–9512 CrossRef CAS PubMed.
- G. Bhardwaj, J. O'Connor, S. Rettie, Y. H. Huang, T. A. Ramelot, V. K. Mulligan, G. G. Alpkilic, J. Palmer, A. K. Bera, M. J. Bick, M. Di Piazza, X. Li, P. Hosseinzadeh, T. W. Craven, R. Tejero, A. Lauko, R. Choi, C. Glynn, L. Dong, R. Griffin, W. C. van Voorhis, J. Rodriguez, L. Stewart, G. T. Montelione, D. Craik and D. Baker, Cell, 2022, 185, 3520–3532 CrossRef CAS PubMed.
- S. Kapoor and A. Narayanan, Patterns, 2023, 100804 CrossRef PubMed.
- S. Kaufman, S. Rosset, C. Perlich and O. Stitelman, ACM Trans. Knowl. Discov. Data, 2012, 6(4), 1–21 CrossRef.
- K. Roy, S. Kar and P. Ambure, Chemom. Intell. Lab. Syst., 2015, 145, 22–29 CrossRef CAS.
- U. Norinder, L. Carlsson, S. Boyer and M. Eklund, J. Chem. Inf. Model., 2014, 54, 1596–1603 CrossRef CAS PubMed.
- G. Shafer and V. Vovk, J. Mach. Learn. Res., 2008, 9, 371–421 Search PubMed.
- V. Vovk, A. Gammerman and G. Shafer, Algorithmic Learning in a Random World, 2nd edn, 2022, pp. 1–476 Search PubMed.
- J. Alvarsson, S. Arvidsson McShane, U. Norinder and O. Spjuth, J. Pharm. Sci., 2021, 110, 42–49 CrossRef CAS PubMed.
- A. Morger, M. Garcia de Lomana, U. Norinder, F. Svensson, J. Kirchmair, M. Mathea and A. Volkamer, Sci. Rep., 2022,(12), 1–13 Search PubMed.
- A. Morger, F. Svensson, S. Arvidsson McShane, N. Gauraha, U. Norinder, O. Spjuth and A. Volkamer, J. Cheminf., 2021, 13, 1–14 Search PubMed.
- W. Heyndrickx, A. Arany, J. Simm, A. Pentina, N. Sturm, L. Humbeck, L. Mervin, A. Zalewski, M. Oldenhof, P. Schmidtke, L. Friedrich, R. Loeb, A. Afanasyeva, A. Schuffenhauer, Y. Moreau and H. Ceulemans, Artif. Intell. Life Sci., 2023, 3, 100070 CAS.
- J. Li, K. Yanagisawa, M. Sugita, T. Fujie, M. Ohue and Y. Akiyama, J. Chem. Inf. Model., 2023, 63(7), 2240–2250 CrossRef CAS PubMed.
- RDKit, http://www.rdkit.org/.
- S. Kariyuki, T. Iida, M. Kojima, R. Takeyama, M. Tanada, T. Kojima, H. Iikura, A. Matsuo, T. Shiraishi and T. Emura, Peptide-Compound Cyclization Method, WO2013100132A1, 2013.
- C. N. Kelly, C. E. Townsend, A. N. Jain, M. R. Naylor, C. R. Pye, J. Schwochert and R. S. Lokey, J. Am. Chem. Soc., 2021, 143, 705–714 CrossRef CAS PubMed.
- C. Townsend, E. Jason, M. R. Naylor, C. R. Pye, J. A. Schwochert, Q. Edmondson and R. S. Lokey, ChemRxiv, 2020, preprint, DOI:10.26434/CHEMRXIV.13335941.V1.
- M. C. Sorkun, D. Mullaj, J. M. V. A. Koelman and S. Er, Chem. Methods, 2022, 2, e202200005 CrossRef.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- F. Miljković, R. Rodríguez-Pérez and J. Bajorath, J. Med. Chem., 2020, 63, 8738–8748 CrossRef PubMed.
- C. K. Schissel, S. Mohapatra, J. M. Wolfe, C. M. Fadzen, K. Bellovoda, C. L. Wu, J. A. Wood, A. B. Malmberg, A. Loas, R. Gómez-Bombarelli and B. L. Pentelute, Nat. Chem., 2021, 13(10), 992–1000 CrossRef CAS PubMed.
- F. Pedregosa, V. Michel, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, J. Vanderplas, D. Cournapeau, F. Pedregosa, G. Varoquaux, A. Gramfort, B. Thirion, O. Grisel, V. Dubourg, A. Passos, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Advances in neural information processing systems 30 (NIP 2017), 2017, pp. 3149–3157 Search PubMed.
- T. Head, M. Kumar, H. Nahrstaedt, G. Louppe and I. Shcherbatyi, Zenodo, 2018, DOI:10.5281/ZENODO.4014775.
- donlnz/nonconformist, Python implementation of the conformal prediction framework, https://github.com/donlnz/nonconformist, accessed 22 November 2023 Search PubMed.
- F. Svensson, N. Aniceto, U. Norinder, I. Cortes-Ciriano, O. Spjuth, L. Carlsson and A. Bender, J. Chem. Inf. Model., 2018, 58, 1132–1140 CrossRef CAS PubMed.
- I. Cortés-Ciriano and A. Bender, Artif. Intell. Drug Discovery, 2020 10.1039/9781788016841-00063.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00056k |
| This journal is © The Royal Society of Chemistry 2024 |