Stability and transferability of machine learning force fields for molecular dynamics applications

Abstract

In this study, we focus on simplifying the generation of Machine Learning Force Fields (MLFFs) for Molecular Dynamics (MD) simulations of inorganic materials, with an emphasis on sustainable use of computational resources. We evaluate the efficiency and accuracy of existing state-of-the-art graph neural network (GNN) models and introduce new benchmarks that go beyond conventional mean absolute error on forces and energies. We showcase our methodology on the example of lithium-ion conductor materials, paving the way to a broader screening of ionic conductors for batteries and fuel cells.

---

Introduction

Molecular dynamics (MD) is one of the most important computer simulation methods in chemistry, biology, materials science, pharmaceutical, etc.^1,2 It involves solving Newton's equations of motion for a system of particles, allowing us to observe the detailed trajectories and interactions of atoms and molecules over time. One of the primary drawbacks of ab initio MD (AIMD) simulations is their exhaustive demand for computational resources.^3,4

To address these computational challenges, the integration of machine learning techniques with MD simulations has emerged as a transformative approach. Machine Learning Force Fields (MLFF) are designed to predict the forces and potential energies in molecular systems based on their atomic configurations.⁵ Unlike traditional force fields, which rely on predetermined functional forms and parameters, MLFF are trained directly from designated quantum mechanical calculations, allowing them to capture complex interactions and chemical environments with high precision.

MLFFs are typically based on Graph Neural Network (GNN) models due to their ability to effectively encode the 3D structural and complex interactions in atomic systems. Atoms are represented as nodes in a graph, while bonds or interactions are modeled as edges. This allows GNNs to respect the permutation invariance and locality of atomic environments, making them particularly well-suited for predicting material properties from diverse databases, such as the Materials Project⁶ or Open Catalyst Project.^7,8 Most of the materials GNN models show excellent capability in predicting general properties of static optimized structures, like total energy, band gap, and formation energy.⁹ However, MLFFs, which utilize GNNs, are primarily designed to predict dynamic properties such as forces and potential energies, which are critical for accurately simulating the time-dependent behavior of materials. For applications like the discovery of Li superionic conductors, dynamic properties of the systems in question are crucial, and there is a need for datasets that incorporate these properties for training MLFFs. Moreover, the immense resources required for such endeavors are often beyond the reach of the typical research group and no universal MLFF dedicated to ionic diffusion has been reported to date.

In our paper, we focus on generating MLFFs with limited resources. By concentrating on common elements scheme (Fig. 1), we aim to create transferable MLFFs that do not require extensive training, making the development of effective MLFFs more accessible to a broader range of researchers, with only hours of training on a single consumer-grade GPU. Our methodology not only simplifies the process but also maintains a high level of accuracy and applicability, demonstrating that machine learning applications in materials science can be highly effective in accurately predicting material properties, scalability across different material systems, leading to advancements in materials design and discovery, as we demonstrate on Li ion diffusion example.

Fig. 1 Illustration of the training and test structures. Different colors represent different elements (Li, P, Ge, S), with colored arrows showing the pairwise interactions learned by the GNN model. The identical color arrows represent the transferable learned interactions between atoms that the model applies to the test structure.

Results and discussion

Benchmarking datasets

In order to study the reliability, transferability, and stability of GNN models in performing MD simulations, we introduced known ionic conductors which have shared elements of Li, Ge, P, and S. This includes a superionic LGPS (Li₁₀GeP₂S₁₂),¹⁰ a borderline good ionic conductor Li₃PS₄,¹¹ and a poor ionic conductor Li₄GeS₄.¹² These initial configurations were obtained from the Materials Project and were used as is (Fig. 2).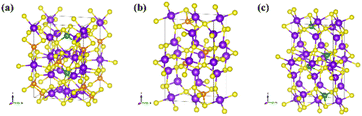

Fig. 2 Superionic conductors as benchmarking data in this work, (a) Li₁₀GeP₂S₁₂, (b) Li₃PS₄, (c) Li₄GeS₄. Color for Li: purple, Ge: green, P: orange, and S: yellow.

For reference dataset generation, we performed an AIMD simulation for each conductor to obtain sets of distinctive trajectories at five different temperatures, ranging from 800 to 1200 K. Each system was repeated three times to ensure good statistical distribution of the dataset. Ultimately, we successfully obtained 1.125 million AIMD snapshots from the simulation. We randomly selected portions of the trajectories to serve as the training set and the validation set as detailed in the Methods section.

Training machine learning models

In this work we compared side-by-side all state-of-the-art GNN models, including CGCNN,⁹ SchNet,^13–15 DimeNet,¹⁶ DimeNet++,¹⁷ GNS-TAT,¹⁸ DeeperGATGNN,¹⁹ SCN,²⁰ eSCN,²¹ ForceNet,²² Equiformer,²³ and LeftNet,²⁴ each of which has an extensively proven track record in materials predictions.

It should be noted that some models are not specifically designed for performing extensive energy/force prediction tasks. Even when they are, they often lack coverage across diverse MD systems and feature varied data generation processes. Additionally, previous models typically exhibit significant diversity, being customized for specific use cases and utilizing different data generation processes, which complicates the comparison of various ML models and datasets.

To address these challenges, we developed the Graph Neural Network Force Field (GraNNField) simulation package. This package is designed to implement existing state-of-the-art materials GNN models for energy and force prediction tasks, as well as MD calculations. It includes a built-in calculator and offers integration with external LAMMPS software²⁵ for enhanced simulation scenarios. Within the GraNNField suite, these models share data processing and training tools, enabling us to clearly distinguish the impact of the ML model from that of the data and MD trajectory propagation (Table 1).

Table 1 Models benchmarked in this work. The translation/rotation symmetries are respected by the feature representation at every layer. Number of parameters on the Li₁₀GeP₂S₁₂ training dataset are reported

Model	Symmetry	#Parameters	#Epochs	MD time (ns per day)
AIMD (reference)	N/A	N/A	N/A	0.034
CGCNN	E(3)-invariant	0.25 M	70	45.0
SchNet	E(3)-invariant	0.49 M	48	22.5
DimeNet	E(3)-invariant	1.11 M	5	1.4
DimeNet++	E(3)-invariant	1.49 M	17	6.0
GNS-TAT	E(3)-invariant	1.97 M	28	10.0
DeeperGATGNN	E(3)-invariant	0.22 M	19	30.0
SCN	SO(3)-equivariant	20.44 M	5	2.8
eSCN	SO(2)-equivariant	34.28 M	5	8.1
ForceNet	Translation-invariant	11.37 M	20	25.7
Equiformer	SE(3)/E(3)-equivariant	7.84 M	14	3.0
LeftNet	SE(3)/E(3)-equivariant	2.12 M	25	11.3

---

As we are focusing on minimizing the computational resources needed to generate MLFFs and ensuring transferability between different materials sharing the same chemical species, we chose the four-element Li₁₀GeP₂S₁₂ as the sole training dataset. Therefore, we will then evaluate the transferability performance in Li₃PS₄ and Li₄GeS₄, which share some elements with training. All training was limited to ten hours irrespective of the GNN model and number of epochs. Learning curves, their respective training and validation loss, and validation mean absolute error of energy and forces as criterion are shown in Fig. S1–S11a and b.† The checkpoints with the lowest validation error were used to represent the models.

Direct prediction of energy and forces

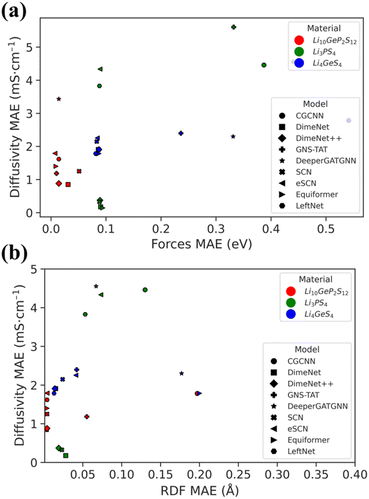
After ten hours of the model's training, we used the model's representations to directly predict the energy and forces on 2000 randomly chosen structures from an unseen portion of the dataset. The full details of the errors on energy and forces are visualized in Fig. S1–S11c–e† for energy and Fig. S1–S11f–n† for forces, respectively. From the results, most of the GNN models show good predictions of energy and forces on unseen portion of training Li₁₀GeP₂S₁₂ dataset with high R² (>0.98) on forces. On the other hand, for the transferability testing on a test dataset, the results varied. Energy predictions were ignored in all cases due to the model's lack of information about their absolute energies. At the very least, most of the models were able to distinguish between high- and low-energy structures, regardless of the absolute total energy value.

From the results, most of the models achieved moderately high R² scores (greater than 0.96 for Li₃PS₄ and Li₄GeS₄). The exceptions were CGCNN, SchNet, and DeeperGATGNN, which showed clearly incorrect force predictions in multiple dimensions. At this stage, one might believe that all models, except for those three, should produce reliable and transferable dynamic trajectories. However, we show below that this is not the case. Even accurate energy and force predictions can lead to catastrophic dynamic trajectories, which can be dangerous if one is not aware of this.

Machine learning force field molecular dynamics (MLFF-MD) and their structural integrity study using radial distribution function (RDF)

To go beyond forces and energies, we conducted a series of MD simulations with the trained models. All of MLFF-MD computations were carried out under the same conditions as their AIMD counterparts, with a minimum of six repetitions to ensure statistical robustness. In addition, we incorporated radial distribution function (RDF) analysis into model validation to ensure a more comprehensive assessment of its capabilities in capturing the essential physical and chemical properties of materials. The RDF, g(r), illustrates how particle density varies with distance, providing insights into the local arrangement of particles within a substance.²⁶ A precise RDF analysis is vital, as discrepancies between predicted and actual RDF values can indicate fundamental issues within the model, affecting its ability to accurately simulate real-world phenomena.

We categorized radial distribution functions (RDFs) as stable or unstable, based on visual observations and the mean absolute error (MAE) value. As illustrated in Fig. 3, a satisfactorily matched RDF typically results in a relatively low MAE (<0.02) compared to those deemed unstable. We observed two distinct types of RDF failure modes: lattice mismatch and atom fusion. The full details of the errors on energy, forces, and RDF are reported in Tables S1–S3 and Fig. S12–S22.†

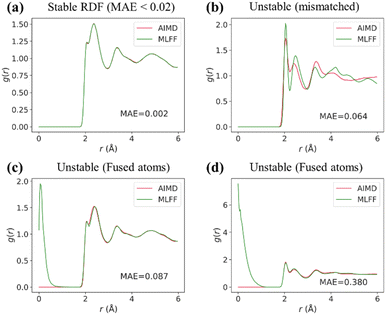Fig. 3 Comparative analysis of RDFs: (a) stable RDF with low MAE; (b) moderately unstable RDF, mismatch lattice; (c) and (d) severely unstable RDFs, fusion of atoms observed.

Surprisingly, even models with exceptional energy and force accuracy (Tables S1–S3†) failed to preserve structural integrity, as reflected in unstable RDF plots. Certain models delivered reliable RDFs only for the training material Li₁₀GeP₂S₁₂, but not for the test materials, including SchNet, eSCN, Equiformer, and LeftNet. Others failed even for the trained materials, such as CGCNN, GNS-TAT, DeeperGATGNN, and ForceNet. Eventually, only DimeNet, DimeNet++, and SCN were left for further assessment.

Diffusivity and ionic conductivity predictions

The diffusivity of each ionic conductor was derived from its single-temperature MLFF-MD trajectory. The negative logarithm of the ionic conductivity was then determined from the diffusivity at multiple temperatures, extrapolated to room temperature conductivity (298 K). The results are presented in Table 2, with detailed information in Tables S4–S6.† After eliminating most models through a series of evaluation criteria, it is notable that DimeNet and DimeNet++ still show the best room-temperature ionic conductivity predictions compared to the values obtained from AIMD. These observations are also consistent with the forces and RDF MAEs, as shown in Fig. 4. Although there is still a slight mismatch in conductivity values, a consistent trend can be observed with these models. Conversely, SCN and other models appear to fail in predicting ionic conductivity.

Table 2 The negative logarithms of the ionic conductivity predictions at multiple temperatures from MLFF-MD simulations employing various GNN models, extrapolated to 300 K

Model	Li10GeP2S12	Li3PS4	Li4GeS4
AIMD	−1.41	0.84	13.59
CGCNN	0.269	5.96	−2.41
SchNet	−1.31	N/A	N/A
DimeNet	−0.51	0.33	8.00
DimeNet++	−1.10	0.24	6.42
GNS-TAT	−0.99	6.89	46.81
DeeperGATGNN	−2.70	−2.06	2.13
SCN	−0.85	−0.72	75.95
eSCN	−0.81	5.17	76.73
ForceNet	21.03	8.67	8.67
Equiformer	−1.06	0.332	3.97
LeftNet	−1.25	1.72	3.33

---

Fig. 4 Comparison of (a) forces and (b) RDF MAE across various GNN models and different materials.

Furthermore, given that both DimeNet variants are E(3)-invariant, they outperformed the most recent state-of-the-art equivariant models in terms of the reliability and accuracy of ionic conductivity predictions.

This also serves as a proof of concept that models trained exclusively on entirely different materials can be transferable to other materials with common elements, ultimately proving useful for MLFF-MD computations and predicting dynamic properties such as diffusivity and ionic conductivity.

Lastly, even with diffusivity results that seem promising, one critical aspect remains to be considered: the diffusion path. We analyzed the diffusion paths of Li ions from their initial configurations to their final snapshots at 50 ps (Fig. S23–S25†) and found that GNN models do not necessarily perfectly replicate the diffusion behavior observed in AIMD. Alarmingly, some models suggest diffusion that does not occur through the proper channels but instead results from the random movement of atoms or the movement of the entire unit cell, as observed for SCN, eSCN, ForceNet, Deeper-GATGNN, and LeftNet. Some models indicated movement of Li within the unit cell but slightly different diffusion path than that observed in AIMD. It is imperative to further investigate the reliability of MLFF-MD results, particularly whether this divergence in diffusion paths could undermine the overall credibility of MLFF-MD diffusivity predictions.

Conclusions

While we have demonstrated that the concept of a transferable MLFF for common elements can be achieved, with dynamic diffusion predicted in good agreement with AIMD references, several questions remain to be investigated. In particular, the reliability of the MLFF-MD trajectory needs further examination, especially due to the differences in diffusion behavior compared to AIMD counterparts. Furthermore, the importance of equivariant models to the reliability of MLFF models remains questionable. As we stand on the point of these technological advancements, further research should delve into refining these computational models, with an emphasis on improving their accuracy and transferability. Such efforts will pave the way for more robust and reliable simulations that could revolutionize material design and discovery.

Methods

Datasets

The reference ab initio molecular dynamics (AIMD) dataset was constructed using Vienna Ab initio Simulation Package (VASP). The temperature was initially set at 100 K and then ramped up over a time span of 5 ps to the target temperature using velocity scaling. This was followed by a 50 ps simulation for equilibration, utilizing a Nosé–Hoover thermostat in the NVT ensemble. The simulations were performed with a 2 fs time step. For the analysis of diffusivity and related properties, the first 15 ps of the simulation are discarded to account for equilibration. From the remaining 35 ps, we compute the diffusivity using the ‘DiffusionAnalyzer’ module within the pymatgen package. We generated three trajectories per temperature per structure to ensure the integrity of the datasets. The final dataset consists of 25 000 snapshots (recorded every simulation step) per temperature per structure, resulting in a total of 1.125 million AIMD snapshots.

Diffusivity determination

The mean square displacement (MSD) of Li ions was used to calculate the diffusivity from molecular dynamics simulations. Then, the self-diffusion coefficient is obtained using the Einstein relation. From this, the ionic conductivity of the material, σ, can be calculated using the Nernst–Einstein equation. By applying the Arrhenius relation, the ionic conductivity at different temperatures can be used to extrapolate the room temperature conductivity.

Machine learning models

GraNNField was used to training state-of-the-art materials graph neural network models includes CGCNN, SchNet, DimeNet, DimeNet++, GNS-TAT, DeeperGATGNN, SCN, eSCN, ForceNet, Equiformer, and LeftNet. Due to the various models implementing different parameters, and the challenges in maintaining equal fairness in the model learning space, we endeavored to standardize model parameters as much as possible. This included setting the embedding layers of atomic features to 128, limiting max neighbors to 500, and setting the cut-off distance to 6.0 Å. All models were trained using multi-temperature AIMD trajectories of Li₁₀GeP₂S₁₂. We randomly selected 6000 snapshots per temperature, with 2000 from each different run, resulting in a total of 30 000 training structures. For validation, we chose 500 snapshots from each temperature, totaling 7500 snapshots. The same split was used in all the models' training processes. The loss function was weighted with a 1 : 1000 ratio for energy to forces. All models were allowed to train for 10 hours, and the final checkpoints will be used for evaluation. Every training session was performed on a single NVIDIA RTX 4090 GPU.

MD simulations using machine learning force field

MLFF-MD simulations were performed using the GraNNField-LAMMPS interface, wherein the pretrained model provides the energy and force values to LAMMPS. The MLFF-MD simulations were carried out under the same conditions as the AIMD dataset to ensure comparability and interpretability. Each MLFF-MD simulation was conducted on a single NVIDIA RTX 4090 GPU with a minimum of six repetitions.

Data availability

Data for this article are available at Figshare, AIMD trajectories at https://doi.org/10.6084/m9.figshare.26089474, MLFF trajectories at https://doi.org/10.6084/m9.figshare.26089486, and pre-trained machine learning model at https://doi.org/10.6084/m9.figshare.26089618. The code for GraNNField can be found at https://github.com/Voznyy-Clean-Energy-Lab-UToronto/GraNNField.

Author contributions

S. D.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, and the writing of the original draft and review & editing. D.-S. S.: co-acquired funding, provided project administration support, shared supervision responsibilities, and contributed to the writing and editing of the manuscript. O. V.: equally contributed to conceptualization and investigation, supported formal analysis, led funding acquisition, project administration, and resource gathering, supervised the project, and equally contributed to the writing and editing of both the original draft and the review.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This research was funded by the Natural Sciences and Engineering Research Council of Canada Discovery program (grant 2019-04897). S. D. acknowledges a scholarship from the University of Toronto's Acceleration Consortium funded by the Canada First Research Excellence Fund (grant number – CFREF-2022-00042).

References

1. J. A. McCammon, B. R. Gelin and M. Karplus, Nature, 1977, 267, 585–590.
2. M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652.
3. N. J. J. de Klerk, E. van der Maas and M. Wagemaker, ACS Appl. Energy Mater., 2018, 1, 3230–3242.
4. M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189,  DOI:10.1016/B978-044451719-7/50084-6.
5. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186.
6. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
7. C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728.
8. L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072.
9. T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301.
10. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030.
11. Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978.
12. S. Amaresh, K. Karthikeyan, K. J. Kim, Y. G. Lee and Y. S. Lee, Nanoscale, 2014, 6, 6661–6667.
13. K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890.
14. K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, arXiv, 2017, preprint, arXiv:1706.08566,  DOI:10.48550/arXiv.1706.08566.
15. K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722.
16. J. Gasteiger, J. Groß and S. Günnemann, arXiv, 2020, preprint, arXiv:2003.03123,  DOI:10.48550/arXiv.2003.03123.
17. J. Gasteiger, S. Giri, J. T. Margraf and S. Günnemann, arXiv, 2020, preprint, arXiv:2011.14115,  DOI:10.48550/arXiv.2011.14115.
18. S. Zaidi, M. Schaarschmidt, J. Martens, H. Kim, Y. Whye Teh, A. Sanchez-Gonzalez, P. Battaglia, R. Pascanu and J. Godwin, arXiv, 2022, preprint, arXiv:2206.00133,  DOI:10.48550/arXiv.2206.00133.
19. S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Patterns, 2022, 3, 100491.
20. C. L. Zitnick, A. Das, A. Kolluru, J. Lan, M. Shuaibi, A. Sriram, Z. Ulissi and B. Wood, arXiv, 2022, preprint, arXiv:2206.14331,  DOI:10.48550/arXiv.2206.14331.
21. S. Passaro and C. L. Zitnick, arXiv, 2023, preprint, arXiv:2302.03655,  DOI:10.48550/arXiv.2302.03655.
22. W. Hu, M. Shuaibi, A. Das, S. Goyal, A. Sriram, J. Leskovec, D. Parikh and C. L. Zitnick, arXiv, 2021, preprint, arXiv:2103.01436,  DOI:10.48550/arXiv.2103.01436.
23. Y.-L. Liao and T. Smidt, arXiv, 2022, preprint, arXiv:2206.11990,  DOI:10.48550/arXiv.2206.11990.
24. W. Du, Y. Du, L. Wang, D. Feng, G. Wang, S. Ji, C. Gomes and Z.-M. Ma, arXiv, 2023, preprint, arXiv:2304.04757,  DOI:10.48550/arXiv.2304.04757.
25. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
26. X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, arXiv, 2022, preprint, arXiv:2210.07237,  DOI:10.48550/arXiv.2210.07237.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00140k

---