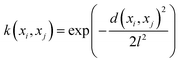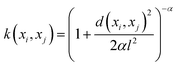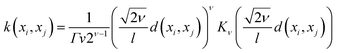Self-optimizing Bayesian for continuous flow synthesis process

Abstract

The integration of artificial intelligence (AI) and chemistry has propelled the advancement of continuous flow synthesis, facilitating program-controlled automatic process optimization. Optimization algorithms play a pivotal role in the automated optimization process. The increased accuracy and predictive capability of the algorithms will further mitigate the costs associated with optimization processes. A self-optimizing Bayesian algorithm (SOBayesian), incorporating Gaussian process regression as a proxy model, has been devised. Adaptive strategies are implemented during the model training process, rather than on the acquisition function, to elevate the modeling efficacy of the model. This algorithm facilitated optimizing the continuous flow synthesis process of pyridinylbenzamide, an important pharmaceutical intermediate, via the Buchwald–Hartwig reaction. Achieving a yield of 79.1% in under 30 rounds of iterative optimization, subsequent optimization with reduced prior data resulted in a successful 27.6% reduction in the number of experiments, significantly lowering experimental costs. Based on the experimental results, it can be concluded that the reaction is kinetically controlled. It provides ideas for optimizing similar reactions and new research ideas in continuous flow automated optimization.

---

Introduction

The synthesis of active pharmaceutical ingredients (APIs) and fine chemicals is gradually transitioning from traditional batch production to more efficient continuous flow production, driven by continuous manufacturing technology.^1–5 Continuous flow production systems provide smaller reaction systems, better temperature control, and superior mixing to traditional batch reactors. Safe, efficient, and sustainable chemical synthesis is gaining increasing popularity.^6–11 The optimization of continuous flow synthesis processes benefits significantly from the flexible adjustment of parameters.¹² However, as parameter tuning becomes more precise, the search space expands, resulting in more possible parameter combinations and increased optimization costs. Traditional methods like control variable and orthogonal experiment method often require many experiments, which can be resource-intensive and inefficient. Analyzing high-dimensional parameter space poses challenges for human researchers due to limitations in efficiency and subjective bias. Some response conditions may go unnoticed by humans, highlighting the need for new approaches to assist researchers in obtaining the most suitable process parameters and analyzing experimental data more efficiently.^13,14 In recent years, the convergence of chemistry and information science has facilitated the utilization of continuous flow synthesis for autonomous parameter selection and reaction optimization through programmatic approaches.¹² The optimization algorithm is crucial in this process. Developing a highly accurate regression algorithm and robust generalization capabilities can significantly improve optimization efficiency and reduce experimental costs. Bayesian optimization, an uncertainty-driven approach, has become a powerful tool for optimizing complex objective functions. It is especially effective in continuous flow synthesis and can be applied to automated optimization systems.^15–26 Bayesian algorithms commonly utilize Gaussian process regression (GPR) as a surrogate model to create a posterior distribution based on prior data, enabling optimization of the objective function through algorithmic guidance.^27,28

In previous cases, some adaptive strategies have been adopted and applied to acquisition functions. Acquisition functions calculate the mean and variance through a surrogate model to determine the next point to explore. The next point to explore is obtained by balancing the exploitation of the objective function, the exploration of unknown areas of the space, and the prediction of risk and uncertainty.²⁹ For instance, Bourne et al. employed an adaptive expected improvement strategy when dealing with continuous variable optimization problems, while Clayton et al. used the same strategy for mixed variable optimization.^15,30 This dynamically adjusted expected improvement strategy, achieved by modifying the implicit binding to the underlying model, allows the model to efficiently acquire the next target data for acquisition while ensuring accuracy. Similarly, Dragonfly's Bayesian optimization tool utilizes a lower confidence bound-based acquisition function, encouraging the algorithm to explore unknown regions by adjusting hyperparameters.^17,31 These self-optimizing strategies applied to acquisition functions have been successfully used in the optimization of continuous flow synthesis. However, adaptive strategies for kernel functions, which are the core of GPR models, are lacking. In previous cases, GPR algorithms often employed a single kernel with fixed hyperparameters for model training. Although this approach is effective for reaction optimization, its fixed model structure may lead to inaccurate or inefficient predictions. Therefore, this study explores the application of adaptive strategies to the model training process, constructing an adaptive strategy for kernel functions to obtain a self-optimizing Bayesian optimization algorithm and unleash more potential between continuous flow synthesis process optimization and automatic control. To verify the feasibility of the designed self-optimizing Bayesian algorithm, this study only adopts adaptive strategies during model training and does not design acquisition functions. Instead, it directly outputs the next objective function by traversing sample points throughout the entire search space.

This study optimizes the continuous flow synthesis process for nitrogen-containing heterocyclic amides, widely found in pharmaceuticals, proteins, and functional materials. Pyridinylbenzamide, a vital drug intermediate, was chosen due to its versatility in synthesizing diverse active compounds, such as luciferase inhibitors³² and anti-ulcer drugs.³³ The synthesis of pyridinylbenzamide via the Buchwald–Hartwig reaction, offering higher selectivity and conversion rates, was demonstrated.^34–36 Given the inherent efficiency, safety, and stability of continuous flow synthesis in producing APIs, it becomes imperative to integrate the synthesis of pyridinylbenzamide into this methodology. In this study, the Buchwald–Hartwig reaction was employed for the synthesis of pyridyl benzamide, efficiently synthesizing pyridyl benzamide using 2-bromopyridine and 4-methoxybenzamide (anisamide) as reactants. Gaussian process regression was utilized as a surrogate model to construct a Bayesian optimization algorithm for predicting yields through regression and outputting corresponding reaction parameters. By iteratively using different kernels, combined with n-fold cross-validation and Bayesian hyperparameter optimization, adaptive strategies were applied during model training to achieve self-optimization of the algorithm. Using 14 sets of prior data, optimal process parameters and yield were obtained after 15 iterations. Subsequently, optimization was performed using 5 sets of prior data with shorter retention times selected from the initial 14 datasets. Remarkably, the same optimization results were achieved after 16 iterations. The experiment results indicate that the self-optimizing Bayesian optimization algorithm performs well with small-scale datasets and efficiently optimizes process parameters to achieve a yield of 79.1% while reducing the number of experiments by 27.6%.

Experimental

Raw materials for experiments

2-Bromopyridine (98% purity), 4-methoxybenzamide (purity >98%), 1,8-diazabicyclo[5.4.0]undec-7-ene (99% purity) purchased from Shanghai Aladdin Biochemical Technology Co. 4,5-Bis(diphenylphosphino)-9,9-dimethylxanthene (purity >98%), palladium acetate (99.9% purity) purchased from Shanghai Adamas Reagent Co. N,N-Dimethylformamide (AR), isopropanol (AR) purchased from Tianjin Komeo Chemical Reagent Co. All reagents were used without additional purification.

Continuous flow experiments

The experiments were conducted using a Vapourtec R-series flow synthesizer. The experiments utilized a Vapourtec standard PFA coil reactor (1 mm ID), connected to a standard column reactor, R2 pump, and 100 psi backpressure valve, as shown in Fig. S1.† Positions B and D were equipped with two R2 type pumps. Position P2 contained a standard PFA coil reactor, while position P4 contained a standard column reactor filled with 200–300 mesh silica gel. A 100 psi backpressure valve was added to the end of the line. During the experiments, the software automatically switched the pipeline using a magnetron valve. The pipeline was equipped with functions for warming, cleaning, and product collection. After each experiment, the filled silica gel was replaced, and the pipeline was cleaned with isopropyl alcohol.

Reaction assessment

The concentration of 2-bromopyridine was tracked using Agilent 1260 infinity II HPLC (mobile phase: 90% water, 10% methanol at 0 min, 100% methanol at 12 min, gradient elution). The samples were analyzed by HPLC after a 10-fold dilution with methanol.

Self-optimizing Bayesian algorithm

The Bayesian optimization algorithm uses GPR as a proxy model and is implemented based on the Python platform using the scikit-learn library to develop the GPR model, and the Bayesian hyperparameter optimizer is implemented based on BayesSearchCV of the scikit-optimize library. Divide all data into a training set and a test set, where the ratio of the test set is 0.1. The algorithm defines four kernels as radial basis function kernel (RBF), matern kernel, rational quadratic kernel (RQ), and DotProduct kernel, and the program iterates through these four kernels and finally selects the kernel with the strongest generalization ability to make predictions. The Bayesian hyperparametric optimizer selects the learning rate and the maximum number of restarts as optimization objectives, with the learning rate sampled using logarithmic averaging (alpha optimization range 1 × 10⁻² to 1 × 10⁻⁶; n_restarts_optimizer optimization range 5–20). The number of Bayesian hyperparametric optimizer samples is 10, 5-fold cross-validation is used (4-fold cross-validation for 5 sets of prior data), the random state is set to 42, and the Bayesian hyperparametric optimizer evaluates the model based on the MSE.

Results and discussion

Construction of optimization experiments for continuous flow synthesis

Ensuring clear lines and continuous liquid flow is essential in continuous flow synthesis. The Buchwald–Hartwig reaction, catalyzed by palladium, requires pairing a ligand with a base to participate in the synthesis. When strong inorganic bases like NaOH and KOH are used, insoluble halogenated salts will form,³⁶ thereby hindering continuous flow synthesis. Hence, soluble organic bases are preferred. 1,8-Diazabicyclo[5.4.0]undec-7-ene (DBU) has demonstrated effectiveness in the sequential Buchwald–Hartwig reaction without causing precipitation,³⁷ making it a suitable choice for this study. Employing 4,5-bis(diphenylphosphino)-9,9-dimethylxanthene (xantphos) as a bisphosphine ligand bound to palladium facilitates cross-coupling reactions. It has been reported that when combined with DBU, amide coupling reactions can be carried out.³⁶ Palladium acetate is a precatalyst in the cross-coupling reaction and is reduced in situ to a palladium (0-valent) catalyst.³⁸ Dimethylformamide (DMF) is a high polarity aprotic solvent commonly used in cross-coupling reactions, which can facilitate this reduction process. In situ generated anionic complex catalysts are more suitable for existing in polar solvents.³⁹

The flow synthesis route involves pumping a solution of bromopyridine, anisamide, palladium acetate, and xantphos in DMF through one line, while a separate line delivers DBU dissolved in DMF at the specified concentration (Fig. 1a). These two fluids were combined using a mixer and then introduced into a standard PFA coiled tube reactor with a holding capacity of 10 mL for the heating reaction. Following the PFA coil reactor, a column reactor filled with silica gel is attached to filter out palladium from the system and cool it to terminate the reaction.

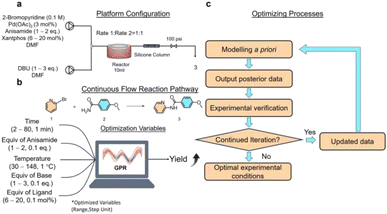Fig. 1 Experiments on the flow synthesis of pyridinylbenzamide. (a) Platform configuration. (b) Continuous flow reaction path and optimized variables. (c) Bayesian optimized synthesis process flow.

The independent variables for optimization included reaction temperature, retention time, and equivalents of anisamide, DBU, and xantphos, with yield as the objective function (Fig. 1b). The concentration of palladium acetate, as the catalyst feedstock for the Buchwald–Hartwig reaction, significantly affects the reaction. However, higher concentrations of palladium result in increased costs. Typically, the range of equivalents for palladium catalysts is 2–6 mol%.⁴⁰ Instead of adjusting the equivalent of palladium acetate, a lower equivalent of palladium (3 mol%) was chosen to reduce costs and better assess the impact of the optimized 5 independent variables on the reaction. No additional constraints were imposed on the algorithm to avoid the influence of manual decision-making on its optimization. The optimization range was widely set to maximize yields. More accurate parameter combinations were obtained by refining the parameter optimization step, resulting in a parameter space of 257 712 000, consisting of 118 × 10 × 78 × 20 × 140. The liquid retention time in a standard PFA coiled-tube reactor with a 10 mL capacity is represented by ‘time’, with an optimization range of 2–80 minutes and a step of 1 minute. ‘Equiv of anisamide’ represents the equivalents of 4-methoxybenzamide, with an optimization range of 1–2 eq. and a step of 0.1 eq. The ‘temperature’ refers to the reaction temperature in the standard PFA coiled-tube reactor. The optimization range is 30–148 °C with a step of 1 °C. The ‘equiv of base’ is the equivalent of DBU, with an optimization range of 1–3 eq. and a step of 0.1 eq. The ‘equiv of ligand’ is the equivalent of xantphos, with an optimization range of 6–20 mol% and a step of 0.1 mol%. The algorithm will search for the optimal parameters within this parameter space combination.

The optimization flow for the process parameters of flow synthesis is shown in Fig. 1c. Initially, the GPR model is trained using a prior dataset. The algorithm then predicts the optimal yield and corresponding experimental conditions by selecting the best model based on the minimum mean square error (MSE). The experimental data obtained are used as parameters for the next round of flow synthesis experiments, and the actual experimental yields of the predicted parameters are obtained. Subsequently, the predicted yield's consistency with the actual yield is assessed. If the predicted yield matches the actual yield or the algorithm provides unchanged predictions of the experimental parameters four consecutive times, it will be recognized as the end of the optimization process. Conversely, the prior dataset will be updated, and the newly obtained experimental parameters with the actual yield will be incorporated into the prior dataset along with the previous experimental data for the next round of training until the end of optimization. Given the specific challenges associated with training on small datasets, a GPR model was chosen for the regression model algorithm. This choice was complemented by implementing an n-fold cross-validation method to mitigate the potential drawbacks of limited training data, which could otherwise undermine the model's generalization capabilities. Additionally, Bayesian hyperparametric optimization was utilized to ensure the model's optimal state, enhancing its generalization ability. The importance of the kernel as the core component of the GPR model for model training and prediction is significant. The prediction kernel is chosen from the ergodic radial basis function (RBF) kernel, the rational quadratic (RQ) kernel, the matern kernel, and the DotProduct kernel. To the best of our knowledge, at the time of writing, these four kernels encompass all the options available in the scikit-optimize library for kernel-based optimization. The selection is based on the MSE criterion. The selected kernel exhibits the most accurate prediction and the strongest generalization ability for the current dataset. With this design, the model implements a self-optimizing function in iterative optimization and data modeling.

Prior data selection and analysis of optimization results

The selection of prior data is crucial as it directly impacts the subsequent optimization training process. More prior data incurs higher costs, but a larger amount of prior data may reduce the number of subsequent optimization iterations, while a smaller amount may increase them. However, it is the total number of experiments that directly affects the overall optimization cost, and the influence of the amount of prior data on the total number of experiments remains unclear.

To verify whether the designed GPR model is suitable for small sample datasets and to explore the model's adaptability to even less prior data, we investigate the effects of different amounts of prior data on the subsequent optimization process by varying the initial number of prior data points. In previous cases, methods such as full factorial design, Latin hypercube sampling, and maximum coverage initialization have often been used to design prior data. Adopting such global prior data design strategies can enhance optimization efficiency and avoid falling into local extrema traps.

Although better prior data sampling methods facilitate the optimization process, the algorithm should not rely excessively on more uniform prior data sampling. In research, scientists may directly use existing data for reaction optimization. However, such data may have issues like missing information or uneven distribution, making it unsuitable as high-quality training data. Redesigning experiments for reactions to obtain high-quality training data inevitably incurs higher experimental costs. Training with varying quality data poses greater challenges, but it is more aligned with practical reaction optimization goals and cost reduction.

To fully demonstrate the effectiveness of the designed self-optimization algorithm, adaptive strategies are applied only during the model training phase, and an acquisition function is not designed. The optimal experimental parameters are obtained by traversing the entire parameter space within the best model. This approach aims to test the effectiveness of the self-optimization algorithm and the feasibility of not using an acquisition function.

The experiment involved synthesizing under 14 randomly generated parameter conditions, with yields measured and used directly as prior data without undergoing iterative processes. Efficient optimization should also minimize the time cost in the initial data acquisition phase. Therefore, a further selection of 5 datasets with the shortest retention time from the 14 sets of prior data was made for comparison in optimization experiments (refer to Tables S1 and S2†). These 5 datasets may contain less information about the feature parameters, posing a challenge for model optimization. The impact of the quantity of prior data on subsequent optimization is examined by comparing the results of optimization performed using 14 sets of prior data with those using only 5 sets of prior data separately.

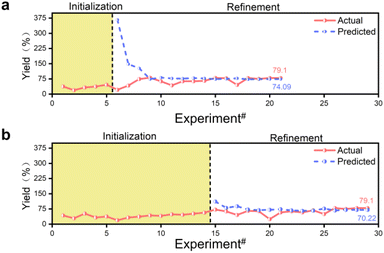
The model's predicted values gradually converge to the true values through successive iterations, a process known as convergence. However, exceptionally high or low predicted values may occur during this process. Even if the predicted value matches the true value at a given point, it may be due to locally extreme values rather than indicating a globally optimal solution. The model is considered to be converged only when the predicted values match the actual values or the same reaction conditions are output for four consecutive times. Fluctuations in the model's predicted yields are normal during this process. The optimization experiment started with 14 sets of prior data, running 29 experiments to determine the best experimental parameters. In comparison, the optimization experiment started with 5 sets of prior data, running 21 experiments to determine the best experimental parameters (Fig. 2). Both sets of prior data converged to the same reaction conditions, resulting in an actual yield of 79.1% at a retention time of 80 min, a reaction temperature of 148 °C, an anisamide equivalent of 1.9 eq., a base equivalent of 2.9 eq., and a ligand equivalent of 19.9 mol%. The inexpensive palladium acetate catalyst was limited in this process, and no special anaerobic treatment was applied to the reaction system. The optimal parameters were efficiently screened out using the constructed Bayesian algorithm with a self-optimization function, and high yields were obtained. When conducting reactions of the same type, the yield is typically observed to range from 10% to 75%, while our final yield was achieved at 79.1%.^36,41 The synthesis of pyridinylbenzamide was achieved efficiently in this reaction without the need for a special palladium catalyst and in a relatively closed environment provided by continuous flow synthesis. Thus, selecting the palladium catalyst and creating an anaerobic environment are not crucial factors that determine this reaction.

Fig. 2 Overview of the overall optimization. Dot line plot of optimized actual yields versus Gaussian process regression model predicted yields with the number of experiments for (a) 5 sets and (b) 14 sets of prior data.

The convergence process of the algorithm is analyzed. The initially predicted yield was 111.62% for 14 sets of prior data, while the corresponding experimental value was 71.6%. For 5 sets of prior data, the initially predicted yield was 366.35%, but the corresponding experimental value was 21.2% (Tables S3 and S4†). The initial model predicted a yield exceeding 100% due to the algorithm not being pre-trained. The discrepancy is attributed to the limited training data, especially the optimization with 5 sets of prior data, resulting in a significant error, poor generalization ability and inaccurate yield prediction. The algorithm converged the yield to within 100% in 1 iteration optimization with 14 sets of prior data, while it required 3 iterations with 5 sets of prior data due to the smaller training dataset. 14 Sets of prior data were optimized for 29 experiments over 15 iterations, and 5 sets of prior data were optimized for 21 experiments over 16 iterations. The 14 sets of prior data required one fewer iteration to optimize than the 5 sets of prior data, but resulted in 8 more experiments (Fig. 2). Despite the fewer experiments conducted with 5 sets of prior data compared to 14 sets, both achieved the same reaction conditions. Having more prior data can reduce the number of iterations but may not necessarily decrease the overall experimental costs, including the construction of the prior dataset. Although the same experimental conditions were obtained, the predicted yields are different. With 14 sets of prior data, the final algorithm converged the yield to 70.22%, whereas with 5 sets of prior data, it reached 74.09%, while the actual yield was 79.1%. Although more training data did not improve predictive accuracy, and the MSE output during model training did not significantly outperform the results obtained from training with a smaller amount of data, they can output the same experimental parameters, indicating the dynamic adjustment capabilities of the algorithm, allowing for self-optimization during successive iterations of the optimization process.

Fig. 3 demonstrates the progress of two sets of optimization experiments. During the design of these optimization experiments, the prior data for both sets were not evenly distributed across the entire parameter space but were instead concentrated in one corner of the space. Taking the 14 sets of prior data as an example, the prior data only contained experimental information with shorter retention times. However, after the first training prediction, the algorithm captured the information that longer retention times are beneficial for increasing yield, without limiting the search to the region of low retention times. As the optimization progressed, the model searched different corners of the entire parameter space and gradually identified the impact of various features on the objective function. The 5 sets of prior data provided less information compared to the 14 sets, posing a greater challenge for model training. During optimization with 5 sets of prior data, the algorithm did not accurately recognize the impact of retention time and reaction temperature on yield as it did with 14 sets of prior data. For example, reaction parameters such as lower temperature and shorter reaction time are provided. Nevertheless, as the optimization progressed, the algorithm actively explored the corners of the parameter space and ultimately achieved the same optimization results as with 14 sets of prior data. This also demonstrates the effectiveness of applying an adaptive strategy to model training. Additionally, even without using an adaptive acquisition function, the unknown objective function can be captured by traversing the parameter space within the model, thanks to our special design of hyperparameters during model training.

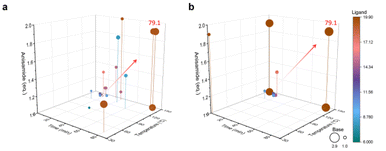Fig. 3 Buchwald–Hartwig reaction optimization results. (a) Reaction profile optimized with 14 sets of prior data. (b) Reaction profile optimized with 5 sets of prior data.

Logical analysis of self-optimizing Bayesian algorithms

Hyperparameters and kernels are pivotal components in GPR algorithms. Fixed hyperparameters and a single kernel can result in poor generalization and underfitting when faced with different training data. To address this issue, a self-optimizing Bayesian algorithm was developed. In designing the function for self-optimizing hyperparameters, ‘alpha‘’ and ‘n_restart_optimizer’ were chosen as hyperparameters. ‘Alpha’ is the value added to the diagonal of the kernel matrix during the fitting process. It guarantees that the computed values form a positive definite matrix, avoiding potential numerical issues during the fitting process. It can also be interpreted as the variance of the Gaussian measurement noise associated with the training observations. Smaller values of ‘alpha’ lead to better fitting of the model's predictions to the new data, as the kernel function becomes less smooth. Conversely, larger values of ‘alpha’ result in a smoother kernel function but poorer fitting of the model's predictions to new data. ‘n_restart_optimizer’ represents the number of optimizer restarts utilized to determine the kernel parameters that maximize the log marginal likelihood. The GPR model is a non-convex optimization problem, so that it may become trapped in local minima. The value of ‘n_restart_optimizer’ affects the number of optimizer restarts and the model's training time. A larger value may result in a better global optimal solution, while a smaller value may lead to local minima. It is important to find the right balance between the two. The iterative process of the Bayesian hyperparameter optimizer selects the best hyperparameters using MSE as a criterion to ensure the best algorithmic model is trained. To address the challenges faced by algorithms during training on small datasets, the method of n-fold cross-validation was incorporated into model training. By dividing the training data, data utilization was effectively improved, and a more active role was played in model tuning and hyperparameter selection, reducing the impact of overfitting or underfitting to some extent. Through the above hyperparameter settings, it is feasible to shift the traditional adaptive strategy from the acquisition function to the model training process, obtaining a model with strong generalization ability during the training phase.

The kernel function is a crucial element in GPR modeling, defining the similarity between data points and influencing the model's predictive and generalization capabilities. By mapping the data points in the input space to a high-dimensional feature space, the kernel function better reflects the distances between the data points and their similarities. In a GPR model, the algorithm utilizes the kernel function to calculate kernel function values for each data point. These kernel function values are then used as inputs to predict the output of new data points. RBF kernel is commonly used for GPR models. However, when dealing with higher dimensional data, the distance between data points may be small, which can result in poor generalization ability of the GPR model constructed by the RBF kernel. To address this issue, we allow the algorithm to iterate through four kernels during successive training sessions to improve generalization ability. The RBF kernel, RQ kernel, Matern kernel, and DotProduct kernel were selected. The algorithm traverses the four kernels during each training session, utilizing a different kernel for each training session and testing on a test set. Ultimately, the algorithm selects the model with the strongest generalization ability based on MSE and determines the kernel and corresponding hyperparameters. Fig. 4a shows the frequency of different kernels becoming the best when optimization starts with 14 sets of prior data versus 5 sets of prior data. The RQ kernel is the best performing kernel in both cases, followed by the Matern kernel and the dot product kernel, while the traditional RBF kernel performs the worst (Tables S3 and S4†).

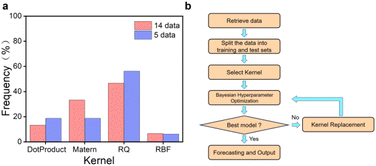Fig. 4 Bayesian optimization algorithm. (a) Frequency of using different kernels in GPR modeling optimization. (b) Flowchart of running GPR model.

The mathematical expression for the RBF kernel is provided below:

where d(x_i,x_j) is the Euclidean distance between x_i and x_j, l is the length feature parameter.

The mathematical expression for the RQ kernel is provided below:

where d(x_i,x_j) is the Euclidean distance between x_i and x_j, l is the length feature parameter, and α is the mixing scale parameter. The RQ kernel is a scaled mixture (infinite sum) of RBF kernels with different feature length scales. It gives the rational quadratic kernel a better generalization ability to nonlinear relations than the RBF kernel.

The mathematical expression for the Matern kernel is provided below:

where d(x_i,x_j) is the Euclidean distance between x_i and x_j, l is the length feature parameter, ν is the smoothness parameter, Γ is the Gamma function, and K_ν is the Bessel function. By controlling the kernel's smoothness, the model can better generalize and more accurately fit the underlying function.

The mathematical expression for the DotProduct kernel is provided below:

k(x_i,x_j) = σ₀² + x_i × x_j

The DotProduct kernel differs from the RBF kernel, the RQ kernel, and the Matern kernel because it is a non-stationary kernel. It is parameterized by σ₀² and represented as a dot product of two vectors. During the algorithm iteration, the most optimal kernel is selected. The radial basis kernel is preferred for regression problems due to its lower computational complexity and focus on calculating feature distances, making it suitable for high-dimensional data. By adjusting the smoothness of the radial basis function and combining it with other radial basis functions of varying scales, the function can be more accurately tailored to real-world applications.

The algorithm was benchmarked and compared to the advanced Dragonfly algorithm. The tests were conducted on a chemical reaction model based on the Arrhenius equation, proposed by Jensen et al. (For detailed information, please refer to the “computerized benchmarking of algorithms” in the ESI†).¹⁷ Different prior data sampling methods were chosen for the tests, including random sampling across the entire parameter space, sampling within a localized parameter space, and Latin hypercube sampling across the entire parameter space. By optimizing with 10 sets of prior data, it was found that neither random sampling nor Latin hypercube sampling had a significant impact on model optimization. The SOBayesian algorithm accurately captured the influence of features on the model, providing reasonable prediction results. Additionally, the impact of experimental errors on the model was verified. A training dataset with a manually introduced 5% error was used. Compared to optimization using correct values, SOBayesian provided the same optimization scheme but with a slight difference in yield prediction (4.56%). This indicates that the designed SOBayesian algorithm can, to some extent, mitigate the influence of experimental errors. It also demonstrates that the algorithm is suitable for both precise, fully automated machine experiments and batch experiments conducted by researchers for reaction optimization. Furthermore, compared to the Dragonfly algorithm, a random seed was set to ensure the reproducibility of optimization.

Characterization and analysis of reaction parameters

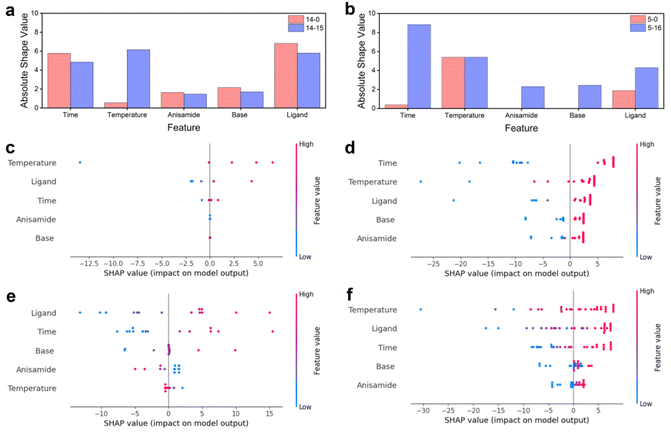
The impact of each feature on the model's prediction and the effect of reaction parameters on the reaction were analyzed by calculating the SHAP values for each feature in each sample (Fig. 5). In both sets of optimization experiments, all five reaction parameters showed a positive correlation with the increase in reaction yield. The top three important factors were ‘time’, ‘temperature’, and ‘ligand’, followed by ‘base’, while ‘anisamide’ had the least effect on the reaction. They increase the reaction temperature and extend the retention time, leading to higher yields. They are kinetic influencing factors and dominate, indicating that this reaction is primarily governed by kinetics. An increased reactant concentration thermodynamically contributes to a positive equilibrium shift and kinetically enhances the reaction rate. However, the experiment results show that the increase in anisamide equivalent had a minimal effect on the reaction yield. It indicates that the concentration of amide does not significantly influence the kinetics of this reaction, and the thermodynamic factor of chemical equilibrium is not a critical factor in this reaction. It indirectly shows that, in this reaction, the change in the reaction rate coefficient greatly influences the reaction rate. Moreover, increasing the temperature can enhance the reaction rate coefficient and consequently boost the reaction rate, aligning with the previously mentioned notion that temperature is one of the main influencing factors of the reaction rate. The equivalence of the ligand xantphos is another important factor, as xantphos is used to synthesize the zero-valent palladium catalyst in situ. Palladium acetate was a precatalyst reduced to zero-valent palladium by bidentate phosphine ligands (xantphos). The resulting palladium participated in the coordination process to form the coupling reaction catalyst. Thus, a higher concentration of xantphos favored the generation of the catalyst, resulting in an increased reaction rate. The base equivalent is also positively correlated with yield. Increasing the base concentration facilitates the departure of halogen atoms on the aromatic ring, but there is no significant benefit to improving the yield by increasing the base concentration. It suggests that the departure rate of halogen atoms on the aromatic ring is not the limiting factor for the overall reaction rate in the Buchwald–Hartwig reaction. Combined with the minimal impact of amide equivalent on the reaction, it can be concluded that the oxidative addition of aryl halide to the zero-valent palladium ligand is the rate-determining step in the overall reaction.

Fig. 5 SHAP values for optimization experiments. The mean absolute SHAP values of each feature parameter before iteration and after the final iteration for (a) 5 sets and (b) 14 sets of prior data. SHAP values of each feature parameter for 5 sets of prior data (c) before and (d) after optimization and for 14 sets of prior data (e) before and after (f) optimization.

The influence of different sets of prior data on model training varied. Utilizing 5 sets of prior data for prediction, reaction temperature, xantphos equivalents, and retention time were found to positively influence yield, while anisamide and DBU equivalents had no significant effect on yield prediction (Fig. 5c). Following 16 iterations of optimization, each feature positively affected the yield (Fig. 5d). The initial prediction with 14 sets of prior data showed a negative effect of reaction temperature and anisamide equivalents on yield. However, after 15 iterations of optimization, each feature demonstrated a positive effect on yield prediction, aligning with the performance of the final optimization result starting from 5 sets of prior data. Less training data may negatively impact the model's ability to generalize. For instance, training on only 5 data sets resulted in no discernible impact on anisamide and base equivalents. Similarly, training with only 14 data sets showed no effect on base equivalents. However, after optimization using 21 and 29 sets of data, respectively, both models exhibited positive effects for all features. The initial prediction using 14 sets of prior data showed a negative effect of reaction temperature and anisamide equivalents on yield, attributed to outliers in the 14 data sets, which experimental errors may cause. Ultimately, each feature had a positive impact because the normal training data far outnumbers the anomalous training data, enabling model correction. As optimization progressed, the algorithm addressed the negative impact of human error in the experiment. However, it is crucial to emphasize the importance of data quality. High-quality data can significantly reduce the time and cost associated with training and optimization, thereby facilitating the development of an accurate model.

The importance of each feature before and after optimization using 5 sets and 14 sets of prior data was assessed. With 5 sets of prior data, all features exhibited increased importance after optimization, indicating a growing contribution of each feature to the model's prediction as the optimization proceeds, and the model's ability to fit the model improves with the increase in data. Reaction time contributed the most to the predictions, followed by reaction temperature. With 14 sets of prior data, the contribution of the other four features decreased after optimization, except for reaction temperature, which contributed the most at the end of the optimization, followed by xantphos equivalents. This phenomenon aligns with the results of parameter optimization.

Algorithms with higher feature contributions will generally produce higher predicted values during prediction. The GPR model, constructed by introducing n-fold cross-validation, hyperparameter optimization, and kernel iteration, is suitable for regression prediction in small data sets. This model exhibits good accuracy and generalization ability. In particular, employing a self-optimizing Bayesian algorithm for optimization with 5 and 14 sets of prior data yielded consistent optimization results while reducing the total number of experiments by 27.6%. This significant improvement in efficiency can significantly enhance the optimization of computer-aided continuous flow processes, unlocking further potential for subsequent process optimization in continuous flow synthesis.

Conclusions

Continuous flow synthesis is one of the important means of synthesizing active pharmaceutical ingredients, and the efficient and rapid optimization of its process parameters has attracted much attention. To address this issue, a self-optimizing Bayesian algorithm is proposed. The Gaussian process regression model, developed for small datasets, dynamically adjusts its structure, self-optimizes, and performs as well as or better than current advanced algorithms. By applying adaptive strategies to the model training process, performing kernel iterations during previous optimizations, and integrating n-fold cross-validation with Bayesian hyperparameter optimization, the model's generalization ability is enhanced. The algorithm does not set an acquisition function and only traverses the entire parameter space during the algorithm, which also avoids falling into local extrema traps. Taking the Buchwald–Hartwig reaction to synthesize pyridyl benzamide as an example, the algorithm is used to optimize its continuous flow synthesis process parameters. Optimizations using 14 and 5 sets of prior data, respectively, converge to the same reaction conditions, and using fewer prior data can reduce the number of experiments by 27.6%. Under optimal reaction conditions, the actual yield reaches 79.1%. Overall, our proposed algorithm provides a reference solution for parameter optimization in continuous flow synthesis, contributing to the development of more efficient and sustainable chemical synthesis processes.

Data availability

The data supporting this article can be found in the ESI.† The code is open source at the following URL: https://github.com/Billy-Liu-DUT/SOBayesian.git.

Author contributions

R. L., Z. W.: conceptualization, data curation, formal analysis, investigation, methodology, software, writing. W. Y., J. C., S. T.: project administration, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the support of this research by the National Natural Science Foundation of China (No. 22272017, 22372025), Dalian High-Level Talent Innovation Program (No. 2022RQ005), the Fundamental Research Funds for the Central Universities (No. DUT22LAB607).

Notes and references

1. N. Zaquen, M. Rubens, N. Corrigan, J. Xu, P. B. Zetterlund, C. Boyer and T. Junkers, Prog. Polym. Sci., 2020, 107, 101256.
2. A. A. Folgueiras-Amador, K. Philipps, S. Guilbaud, J. Poelakker and T. Wirth, Angew. Chem., Int. Ed., 2017, 56, 15446–15450.
3. N. Hartrampf, A. Saebi, M. Poskus, Z. P. Gates, A. J. Callahan, A. E. Cowfer, S. Hanna, S. Antilla, C. K. Schissel, A. J. Quartararo, X. Ye, A. J. Mijalis, M. D. Simon, A. Loas, S. Liu, C. Jessen, T. E. Nielsen and B. L. Pentelute, Science, 2020, 368, 980–987.
4. J. Britton and T. F. Jamison, Nat. Protoc., 2017, 12, 2423–2446.
5. G. M. Martins, F. C. Braga, P. P. de Castro, T. J. Brocksom and K. T. de Oliveira, Chem. Commun., 2024, 60, 3226–3239.
6. M. Baumann, T. S. Moody, M. Smyth and S. Wharry, Org. Process Res. Dev., 2020, 24, 1802–1813.
7. D. J. C. Constable, P. J. Dunn, J. D. Hayler, G. R. Humphrey, J. J. L. Leazer, R. J. Linderman, K. Lorenz, J. Manley, B. A. Pearlman, A. Wells, A. Zaks and T. Y. Zhang, Green Chem., 2007, 9, 411–420.
8. M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893.
9. B. Gutmann, D. Cantillo and C. O. Kappe, Angew. Chem., Int. Ed., 2015, 54, 6688–6728.
10. H. Lin, C. Dai, T. F. Jamison and K. F. Jensen, Angew. Chem., Int. Ed., 2017, 56, 8870–8873.
11. J. Yu, J. Liu, C. Li, J. Huang, Y. Zhu and H. You, Chem. Commun., 2024, 60, 3217–3225.
12. C. P. Breen, A. M. K. Nambiar, T. F. Jamison and K. F. Jensen, Trends Chem., 2021, 3, 373–386.
13. A.-C. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann, J. Torosian, B. Yue, K. F. Jensen and T. F. Jamison, Science, 2018, 361, 1220–1225.
14. S. Chatterjee, M. Guidi, P. H. Seeberger and K. Gilmore, Nature, 2020, 579, 379–384.
15. A. D. Clayton, E. O. Pyzer-Knapp, M. Purdie, M. F. Jones, A. Barthelme, J. Pavey, N. Kapur, T. W. Chamberlain, A. J. Blacker and R. A. Bourne, Angew. Chem., Int. Ed., 2023, 62, e202214511.
16. M. Kondo, H. D. P. Wathsala, M. S. H. Salem, K. Ishikawa, S. Hara, T. Takaai, T. Washio, H. Sasai and S. Takizawa, Commun. Chem., 2022, 5, 148.
17. A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, ACS Cent. Sci., 2022, 8, 825–836.
18. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96.
19. N. Sugisawa, H. Sugisawa, Y. Otake, R. V. Krems, H. Nakamura and S. Fuse, Chem. Methods, 2021, 1, 484–490.
20. G.-N. Ahn, J.-H. Kang, H.-J. Lee, B. E. Park, M. Kwon, G.-S. Na, H. Kim, D.-H. Seo and D.-P. Kim, Chem. Eng. J., 2023, 453, 139707.
21. J. H. Dunlap, J. G. Ethier, A. A. Putnam-Neeb, S. Iyer, S.-X. L. Luo, H. Feng, J. A. Garrido Torres, A. G. Doyle, T. M. Swager, R. A. Vaia, P. Mirau, C. A. Crouse and L. A. Baldwin, Chem. Sci., 2023, 14, 8061–8069.
22. R. van de Schoot, S. Depaoli, R. King, B. Kramer, K. Märtens, M. G. Tadesse, M. Vannucci, A. Gelman, D. Veen, J. Willemsen and C. Yau, Nat. Rev. Methods Primers, 2021, 1, 1.
23. J. Ohyama, Y. Tsuchimura, H. Yoshida, M. Machida, S. Nishimura and K. Takahashi, J. Phys. Chem. C, 2022, 126, 19660–19666.
24. C. Horvatits, J. Lee, E. A. Kyriakidou and E. A. Walker, J. Phys. Chem. C, 2020, 124, 19174–19186.
25. W. Hashimoto, Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2020, 124, 9958–9970.
26. L. Gundry, S.-X. Guo, G. Kennedy, J. Keith, M. Robinson, D. Gavaghan, A. M. Bond and J. Zhang, Chem. Commun., 2021, 57, 1855–1870.
27. V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141.
28. Y. An and S. A. Deshmukh, Chem. Commun., 2020, 56, 9312–9315.
29. Y. Wu, A. Walsh and A. M. Ganose, Digital Discov., 2024, 3, 1086–1100.
30. N. Aldulaijan, J. A. Marsden, J. A. Manson and A. D. Clayton, React. Chem. Eng., 2024, 9, 308–316.
31. A. Slattery, Z. Wen, P. Tenblad, J. Sanjosé-Orduna, D. Pintossi, T. den Hartog and T. Noël, Science, 2024, 383, eadj1817.
32. T. Nakatsu, S. Ichiyama, J. Hiratake, A. Saldanha, N. Kobashi, K. Sakata and H. Kato, Nature, 2006, 440, 372–376.
33. R. B. Moffett, A. Rober and L. L. Skaletzky, J. Med. Chem., 1971, 14, 963–968.
34. L. Malet-Sanz and F. Susanne, J. Med. Chem., 2012, 55, 4062–4098.
35. R. Porta, M. Benaglia and A. Puglisi, Org. Process Res. Dev., 2016, 20, 2–25.
36. S. K. Kashani, J. E. Jessiman and S. G. Newman, Org. Process Res. Dev., 2020, 24, 1948–1954.
37. R. E. Tundel, K. W. Anderson and S. L. Buchwald, J. Org. Chem., 2006, 71, 430–433.
38. J. Sherwood, J. H. Clark, I. J. S. Fairlamb and J. M. Slattery, Green Chem., 2019, 21, 2164–2213.
39. R. Chinchilla and C. Nájera, Chem. Rev., 2007, 107, 874–922.
40. M. M. Heravi, Z. Kheilkordi, V. Zadsirjan, M. Heydari and M. Malmir, J. Organomet., 2018, 861, 17–104.
41. C. C. D. Wybon, C. Mensch, C. Hollanders, C. Gadais, W. A. Herrebout, S. Ballet and B. U. W. Maes, ACS Catal., 2018, 8, 203–218.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting information provides reaction parameters and benchmarking data from the SOBayesian optimization experiments. See DOI: https://doi.org/10.1039/d4dd00223g

---