Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sorting polyolefins with near-infrared spectroscopy: identification of optimal data analysis pipelines and machine learning classifiers†‡
Bradley P.
Sutliff
 a,
Peter A.
Beaucage
a,
Peter A.
Beaucage
 b,
Debra J.
Audus
b,
Debra J.
Audus
 a,
Sara V.
Orski
a,
Sara V.
Orski
 a and
Tyler B.
Martin
a and
Tyler B.
Martin
 *a
*a
aMaterials Science and Engineering Division, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA. E-mail: tyler.martin@nist.gov
bNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA
First published on 15th October 2024
Abstract
Polyolefins (POs) are the largest class of polymers produced worldwide. Despite the intrinsic chemical similarities within this class of polymers, they are often physically incompatible. This combination presents a significant hurdle for high-throughput recycling systems that strive to sort various types of plastics from one another. Some research has been done to show that near-infrared spectroscopy (NIR) can sort POs from other plastics, but they generally fall short of sorting POs from one another. In this work, we enhance NIR spectroscopy-based sortation by screening over 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 machine-learning pipelines to enable sorting of PO species beyond what is possible using current NIR databases. These pipelines include a series of scattering corrections, filtering and differentiation, data scaling, dimensionality reduction, and machine learning classifiers. Common scattering corrections and preprocessing steps include scatter correction, linear detrending, and Savitzky–Golay filtering. Dimensionality reduction techniques such as principal component analysis (PCA), functional principal component analysis (fPCA) and uniform manifold approximation and projection (UMAP) were also investigated for classification enhancements. This analysis of preprocessing steps and classification algorithm combinations identified multiple data pipelines capable of successfully sorting PO materials with over 95% accuracy. Through rigorous testing, this study provides recommendations for consistently applying preprocessing and classification techniques without over-complicating the data analysis. This work also provides a set of preprocessing steps, a chosen classifier, and tuned hyperparameters that may be useful for benchmarking new models and data sets. Finally, the approach outlined here is ready to be applied by the developers of materials sortation equipment so that we can improve the value and purity of recycled plastic waste streams.
000 machine-learning pipelines to enable sorting of PO species beyond what is possible using current NIR databases. These pipelines include a series of scattering corrections, filtering and differentiation, data scaling, dimensionality reduction, and machine learning classifiers. Common scattering corrections and preprocessing steps include scatter correction, linear detrending, and Savitzky–Golay filtering. Dimensionality reduction techniques such as principal component analysis (PCA), functional principal component analysis (fPCA) and uniform manifold approximation and projection (UMAP) were also investigated for classification enhancements. This analysis of preprocessing steps and classification algorithm combinations identified multiple data pipelines capable of successfully sorting PO materials with over 95% accuracy. Through rigorous testing, this study provides recommendations for consistently applying preprocessing and classification techniques without over-complicating the data analysis. This work also provides a set of preprocessing steps, a chosen classifier, and tuned hyperparameters that may be useful for benchmarking new models and data sets. Finally, the approach outlined here is ready to be applied by the developers of materials sortation equipment so that we can improve the value and purity of recycled plastic waste streams.
1 Introduction
Polyolefins (PO) are widely used in many areas, from automotive parts to single use plastics and beyond.1–3 The subset of plastics made from polymerizing simple olefins/alkenes, POs have a general formula of (CH2CHR)n, where R is a simple alkyl group, see Fig. S1‡ for examples.4,5 Academic and industrial research has engineered a wide variety of material properties by varying PO molecular architecture, i.e., the frequency, length, and connectivity of side chain branches off the backbone. These differences in architecture affect how the long molecular structures interact with one another, in turn affecting their bulk properties such as crystallinity, rheology, and toughness.1,2,6 High-density polyethylene (HDPE) is characterized by a linear carbon backbone, with minimal branching. Polypropylene (PP) also displays a consistent backbone, but the propylene monomer results in a methyl pendant on every other backbone carbon. This methyl pendant introduces stereochemistry, however most commercial PP is isotactic.7 Low-density polyethylene (LDPE) is constructed with a long carbon backbone, but can vary widely in both the length and frequency of its side chains.1 If the side chains are consistently short (≤6 carbons), then the PO is considered to be linear low-density polyethylene (LLDPE).1,8–11 Medium density polyethylene (MDPE) may also be used as a label for samples exhibiting a density somewhere between HDPE and LDPE. Each of these architectures provides a range of mechanical and physical properties, such as improved processability, toughness, durability, tensile strength, opacity, or melting temperature.1,12,13While this flexibility in POs has been industrially and societally transformative, their widespread use has introduced additional challenges, including environmental impacts.14,15 Unfortunately, incompatibility in mixed PO materials drastically impedes recycling and reuse efforts (e.g., multilayer films containing multiple PO species, additives, or poor separation techniques can lead to processing issues, poor mechanical properties, poor appearance, and phase separation in recycled parts).15,16 Given that industrial users of post consumer resins (PCR) are looking to avoid such challenges, efficient sorting of POs would enable materials recycling facilities (MRFs) and secondary recyclers to sell more reliable material feedstocks for resin manufacturers, leading to more reliable PCR. The higher the purity of the recycled material, the more valuable it is to users due to a promise of consistent processability. However, when dealing with post-consumer waste, the myriad of shapes, sizes, colors, and other additives can inhibit sortation. Technologies such as recycling codes, near-infrared radiation (NIR), and hyperspectral imaging (HSI) have been developed to help both humans and machines separate various types of plastics, such as polystyrene (PS), polyethylene terephthalate (PET), and POs. While beneficial for speeding up sortation, both simple recycling codes and NIR/HSI technologies have fallen short of enabling rapid and accurate sortation of PO species. Recycling codes are not present on all items, and can be difficult for both machines and humans to find and read, limiting their speed enhancement. NIR and HSI can be employed rapidly, but they struggle to distinguish the various grades of PE from one another, due to the similarity of their vibrational spectra.17–22
To enable better plastic sorting, there is a great deal of literature using analytical chemistry, chemometrics, and machine learning (ML) to provide rapid answers to the identity of any given plastic that may show up on a post-consumer conveyor belt.17–23 Using mid-IR (MIR),21 NIR,22,23 and NIR-based HSI,17,19,20 previous research has explored a wide variety of signal correction, normalization, signal smoothing, and differentiation processes to enable their classification techniques to apply to a broader range of samples.20–23 These techniques have included the standard normal variate method, mean centering, and detrending for scattering correction, as well as smoothing and differentiation techniques such as the Savitzky–Golay filter. Additionally, various forms of normalization and scaling approaches have been used to better represent the data to ML algorithms. All of these techniques seek to “clean” the data, removing various forms of noise and instrument artifacts from the signal or focusing data analysis on signal derivatives rather than the signal itself. Many of these techniques show promise for enabling ML algorithms to distinguish between polymer spectra, but no consensus exists for when a given method should be used.
Additionally, many of the ML techniques have focused on dimensionality reduction through compared ratios of selected NIR peaks,22 principal component analysis (PCA) of NIR or MIR signals,19–21,23 or partial least squares discriminant analysis (PLS-DA) of NIR or MIR signals.18,19,21,23 Other techniques have included classifiers such as the soft independent modelling by class analogy (SIMCA),20,21 support vector machines (SVM), k-nearest neighbors (KNN), random forest (RF), linear discriminant analysis (LDA), and multilayer perceptrons (MLP).21 These models have generally been successful in discriminating between chemically dissimilar materials such as PS, PET, PP, polyethylenes (PE), and polyamides (PA).17–23 However, when it comes to classifying the subclasses of POs, these techniques have stopped at differentiating PP from PE, generally failing or not attempting to sort HDPE from LDPE.17–20,22 This failure to sort PEs likely stems from the fact that the major spectroscopically detectable difference between POs is the ratio of methyl, methylene, and methine stretches. PP has numerous methine and methyl groups that may distinguish it from PE, but LDPE and LLDPE have far fewer of these pendants, making it likely those vibrations are largely hidden by the vibrations of the methylene groups. A notable exception is the work of Rani et al., where they reported using urban plastic waste and distinguished HDPE from LDPE with perfect accuracy using PLS-DA. However, their PLS-DA model required additional training on just the PE materials, and that work excluded black colored polymers.23 Additional research is also necessary to consider LLDPE, MDPE, and various form factors such as pellets, flake, or powders (something that may become more relevant with the increase in powder-based additive manufacturing techniques). These form factors can alter the spectra by selectively reflecting different wavelengths depending on the relative size scales of grains or textures.24,25
Here we aim to expand upon previous work to overcome these challenges in recycling POs, using a data-driven approach. Given the diverse methods and plethora of possible combinations that may be applied to analyzing and differentiating these polymers, the current work is intended to act as a resource for understanding many of the preprocessing and machine learning techniques used in plastic classification pipelines. Additionally, this work seeks to provide a benchmarking data set and series of recommended analysis steps to produce rapid, effective, and broadly applicable classification pipelines. We outline a step-wise, reasoned approach to down selection of the computationally intractable number of combinations of preprocessing pipelines, classifiers, and hyperparameters. To accomplish this goal, we first outline our overall approach, then provide brief descriptions of the techniques used at each step of our analysis. Next, this work builds on a previously published National Institute of Standards and Technology (NIST) data set,26 approximately doubling the number of POs to include powders, colored materials, and additional post-consumer resins and uses this data set to evaluate over 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 classification pipelines. This set of pipelines is then carefully down selected to identify a single hyperparameter-tuned pipeline that can be reproduced and implemented by other researchers to benchmark their models and processes.
000 classification pipelines. This set of pipelines is then carefully down selected to identify a single hyperparameter-tuned pipeline that can be reproduced and implemented by other researchers to benchmark their models and processes.
2 Machine learning pipeline components
An overview of our process is represented in Fig. 1 and described as follows. First (Fig. 1a), the expanded data set was preprocessed using 1152 combinations of scattering corrections, smoothing, differentiation, normalization, and dimensionality reduction steps. The output of each of these preprocessing pipelines was used to train and test 11 different classification algorithms with default hyperparameters to assess both the benefit of certain preprocessing steps and the ability of each classifier to consistently provide accurate classifications. While simultaneous cross-validation (CV) and hyperparameter tuning on all 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 full models (preprocessing pipelines + classifiers) considered in this study would be ideal, it was not computationally tractable in a reasonable timeframe. Instead, we carry out several, partial optimizations that allow us to reduce the size of the search space before applying full cross-validated optimization and tuning. This began with analyzing the scores of these default classifiers to down select the preprocessing steps, Fig. 1b. Next, the best performing preprocessing steps were used with a nested cross-validation (nested-CV) approach to tune hyperparameters of a random forest classifier (RFC). The RFC was trained and tested to enable selection of the most consistently high scoring pipeline for converting a raw NIR signal to a reliable label (Fig. 1c). Based on the result of the nested-CV-RFC study, the most consistent preprocessing pipeline was then used with another nested-CV to tune hyperparameters, train, and test 9 classification algorithms (Fig. 1d). This identified the most consistent and best performing classification algorithm for our data. Next, the selected preprocessing steps and classifier were evaluated using another nested-CV, this time using a leave-one-group-out CV (logoCV) to both tune the hyperparameters and evaluate the ability of the classifier to classify individual resins that it has not been trained on. Finally, using the hyperparameters suggested from the logoCV, the model was trained and evaluated with a 10-fold stratified shuffle split. The predictions from each split were then concatenated to produce an overview confusion matrix to identify any potential trends in model inaccuracies (Fig. 1e).
672 full models (preprocessing pipelines + classifiers) considered in this study would be ideal, it was not computationally tractable in a reasonable timeframe. Instead, we carry out several, partial optimizations that allow us to reduce the size of the search space before applying full cross-validated optimization and tuning. This began with analyzing the scores of these default classifiers to down select the preprocessing steps, Fig. 1b. Next, the best performing preprocessing steps were used with a nested cross-validation (nested-CV) approach to tune hyperparameters of a random forest classifier (RFC). The RFC was trained and tested to enable selection of the most consistently high scoring pipeline for converting a raw NIR signal to a reliable label (Fig. 1c). Based on the result of the nested-CV-RFC study, the most consistent preprocessing pipeline was then used with another nested-CV to tune hyperparameters, train, and test 9 classification algorithms (Fig. 1d). This identified the most consistent and best performing classification algorithm for our data. Next, the selected preprocessing steps and classifier were evaluated using another nested-CV, this time using a leave-one-group-out CV (logoCV) to both tune the hyperparameters and evaluate the ability of the classifier to classify individual resins that it has not been trained on. Finally, using the hyperparameters suggested from the logoCV, the model was trained and evaluated with a 10-fold stratified shuffle split. The predictions from each split were then concatenated to produce an overview confusion matrix to identify any potential trends in model inaccuracies (Fig. 1e).
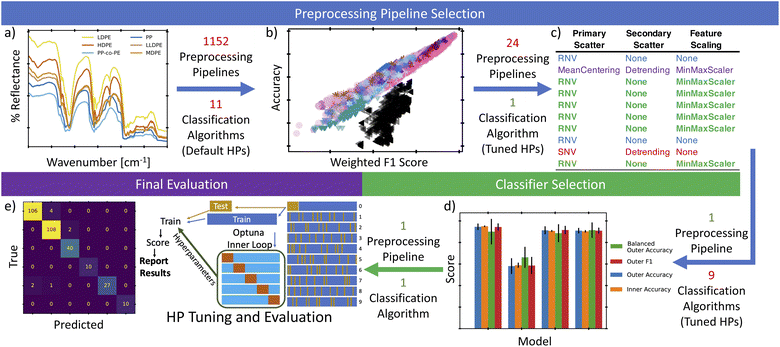 | ||
| Fig. 1 An overview of our analysis, with original figure and table numbers listed after each step. (a) Initial NIR data was collected from a variety of polymers. Then 1152 combinations of common preprocessing steps were used to correct/transform the data (expanded in Fig. 2). (b) Each of these was then fed into 11 different classification algorithms, using default parameters, and the accuracy and F1 scores were compared (Fig. 3). Based on the top scoring models, the 1152 preprocessing combinations were reduced to a set of 24 combinations that were assumed to produce consistent results (expanded in Fig. 4). (c) These 24 combinations were then evaluated with a nested CV technique and a random forest classification algorithm that could be readily tuned using the Optuna package (expanded in Table 3). (d) The most consistently high-scoring preprocessing combination was then selected for use in another nested CV loop to select the best of 9 Classifiers that could be readily tuned with Optuna (expanded in Fig. 5). (e) Finally, the selected preprocessing combination and the selected classifier were evaluated using a leave-one-group-out adaptation of the nested-CV approach and the corresponding confusion matrix (expanded in Fig. 7). | ||
2.1 Preprocessing
Preprocessing steps are those performed before the data are given to the ML algorithms. Generally, these steps are meant to remove signal artifacts and noise while also massaging the data so that it is in an ideal form for a given ML algorithm.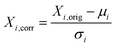 | (1) |
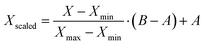 | (2) |
In terms of data visualization, a noteworthy weakness of both PCA and UMAP as described, is that they are unsupervised techniques, meaning that the new dimensions they construct separate the data itself, not the classes or labels we may actually want to sort. This means that samples with varying form factors, thermal history, or additives may be separated more effectively than those of different PO classes. When attempting to visualize data differences, it may be more beneficial to use techniques such as a supervised version of UMAP, or the latent variables that are created during some classification algorithms such as PLS-DA, linear discriminant analysis (LDA), and quadratic discriminant analysis (QDA). These techniques use the data labels (polymer class) to reduce the data in a way that maximizes the separation between classes, rather than every data point. However, supervised dimensionality reduction should only be used with great care. If the real-world variety is not sufficiently represented by the training data, it greatly increases the chances of overfitting the model to the training data and providing overly optimistic scores when compared to real-world testing.
2.2 Classification algorithms
Once the data are properly preprocessed, it is fed into a classification algorithm as training and testing data sets. A brief description of the supervised algorithms used in this paper is provided below to help the reader understand the differences in the methods. This includes every classification algorithm in the scikit-learn documentation at the time of writing, with the addition of some field-specific models. For reference, the features are the wavenumbers that correspond with the collected NIR intensities.2.2.1.1 Partial least squares-discriminant analysis (PLS-DA). PLS-DA is one of the most commonly used discriminant techniques, but it relies on regression-based prediction of labels, leading to much confusion throughout the literature.37,38 The algorithm takes an m by n data array (X) and a “label” array of m by l numerical or binary labels (Y, or y if l = 1), where m is the number of samples, n is the number of features, and l is either the number of labels or the number of labels minus one. For additional clarity, a sample labeled as HDPE may be represented in Y as [1, 0, 0] to indicate that it is labeled as HDPE, but not labeled as LDPE or LLDPE. A regression model is then performed between X and Y, to enable prediction of a number between 0 and 1 for each column/variable of Y. During this process, latent space components consisting of loadings and scores are created, such that the weighting vector maximizes covariance between the two arrays. Similar to PCA, the latent variables are constructed such that the first loading vector accounts for the most variation, and subsequent vectors are created from the using the residuals of the prior latent variable for X and Y.39 The number of components used in the final prediction can be down selected, where more components describe the data more fully but can also increase the chance of overfitting. It is important to again note that PLS-DA is not a true classification technique, it is a regression technique providing a coefficient vector that can be used to predict an unknown sample's label (in-class or not in-class). Since this is regression-based, the predicted label requires some level of post-prediction decision boundary to convert the prediction to a class label. In the case of Y composed of binary labels (0/false or 1/true for each label), the algorithm must convert decimals between 0 and 1 to a set of class labels. This means a sample's true label may be [0, 1, 0] but may have a predicted label of [0.1, 0.7, 0.2] or [0.5, 0.5, 0.5]. These decimals then must be rectified to produce a final label such as HDPE, LDPE, or LLDPE. It should be noted that each prediction coefficient is effectively unrelated to one another, meaning [0.1, 0.7, 0.2] does not represent a blend of polymers nor anything similarly percentage based. They are independent numerical values to represent where a given sample falls relative to the extremes of in-class (1) and not in-class (0), for each possible class label. A simple method to rectify these vectors into a single label is to round values to the nearest integer, but this may cause issues for samples labeled similarly to [0.5, 0.5, 0.5], as a sample is unlikely to be in all three categories at once. In the scikit-learn distribution, there are two types of PLS-DA.33 PLS1-DA is designed to handle a dichotomy of classes (y), while PLS2-DA is designed to handle multiple classes (Y). PLS1-DA can still be used with multiple classes, but generally requires multiple PLS1-DA classifiers to be trained in a one-vs.-rest manner. This further complicates analysis, as additional rules must be made to rectify the multiple classifiers into a single prediction. PLS2-DA is capable of predicting multiple outputs with the previously mentioned series of in-class versus not in-class comparisons. This creates a new regression for each label, increasing flexibility. However, it faces issues with the weighting of X, potentially penalizing larger groups if the labels are not equally distributed across samples.37 To combat this, the X can be weighted for each variable of Y, but this can be complicated to implement.37 For a more in-depth understanding of PLS-DA, readers are directed to ref. 37, 38 and 40.
2.2.1.2 Linear discriminant analysis (LDA). LDA functions similarly to PLS-DA such that PLS-DA using all latent variables should provide the same decision function as LDA, at least for a 2-class system.41 However, LDA measures distances using the Mahalanobis distance instead of the Euclidean distance.37 During this calculation, a single covariance matrix is generated to describe the variance of each class with respect to its features. With this technique, LDA is more readily able to handle features that may be of widely different scales as well as multi-class problems.37 However, despite these advantages, the decision boundary that LDA provides is still linear, meaning that it may not provide good results for class separation if the classes are not linearly separable.33
2.2.1.3 Quadratic discriminant analysis (QDA). To combat challenges with non-linearly separable data, QDA offers a more flexible decision boundary. Instead of applying a linear decision boundary to discriminate between classes, QDA uses a quadratic function. This is made possible by applying a different covariance matrix to each class, rather than one matrix that effectively averages the covariance across classes.42 While this may be more computationally expensive, it yields much more flexibility for data that may not be linearly separable.
2.2.7.1 Random forest (RF). RF classifiers rely on an ensemble of decision trees to vote on the correct label. Multiple trees are created simultaneously with different sets of sample data and with different splitting decisions. When a new sample is introduced, it is classified by each tree and the class with the most votes is returned as the final class prediction. The size and shape of the individual trees can be controlled, as well as the number of trees used to create the forest.33
2.2.7.2 AdaBoost. AdaBoost classifiers function similarly to RFs, but generate new decision trees using information from the previous trees. As new trees are created, weights are introduced to penalize inaccurate classifications and to focus training on avoiding such errors. The result is a forest of trees that have weighted votes when predicting new sample labels. Trees that performed poorly will have less weight to their vote than trees that performed well. Additionally, AdaBoost traditionally uses decision “stumps” instead of decision trees, meaning that each tree only splits the data once.33 While tuneable, this default tree size can play a large role in both the speed and accuracy of the final model.
2.3 Code specifications
3 Experimental methods
3.1 Materials
For this study, 31 POs, representing commercial plastic samples (including 11 PCRs), were used along with 9 PO samples from the Hawaii Pacific University Polymer Kit 1.0.53 Additionally, National Institute of Standards and Technology (NIST) PE Standard Reference Materials® 1473, 1474 and 1476 were included. This data includes 19 polymers characterized in ref. 26 and 24 new materials. For ML training purposes, supplier labels of PO type were assumed to be accurate labels. A summary of the samples and their sources is provided in Table 1. Table S2‡ contains information on the physical state and presence of color in the samples.| Source | HDPE | MDPE | LDPE | LLDPE | PP | PP-co-PE |
|---|---|---|---|---|---|---|
| Commercial polymers | 12 | 0 | 11 | 3 | 3 | 2 |
| Hawaii Pacific University | 2 | 1 | 3 | 2 | 1 | 0 |
| NIST | 1 | 0 | 2 | 0 | 0 | 0 |
| Total | 15 | 1 | 16 | 5 | 4 | 2 |
3.2 Near-infrared spectroscopy
NIR measurements were collected on a Nicolet iS50 NIR module, Thermo Fischer Scientific (Waltham, MA), at 4 cm−1 resolution and an accumulation of 32 scans with an integrating sphere, a sapphire window, calcium fluoride (CaF2) beam splitter, a gold internal reference, and an indium gallium arsenide (InGaAs) detector.54 Internal background and dark corrections were applied to the measurements. Pellets were used as received and filled at least halfway in a 10 mL or 20 mL VWR borosilicate glass scintillation vial as a representative aliquot of the sample resin. Each sample was measured 7 times, where the vial was shaken between scans in an attempt to redistribute the pellets in the vial and account for local composition variations. The vial was then placed flat on the NIR module, centered above the beam path. Additionally, changes in sample vial and vial lids were confirmed not to alter the reflected NIR signal significantly.3.3 Data analysis
Data analysis was performed using the Python coding language and freely available open-source packages. The code and the raw data used for this study are made available on the NIST Data Repository and GitHub.54 ML cross validation (CV) methods are described in detail in Section 5.4 Results and discussion
4.1 Preprocessing
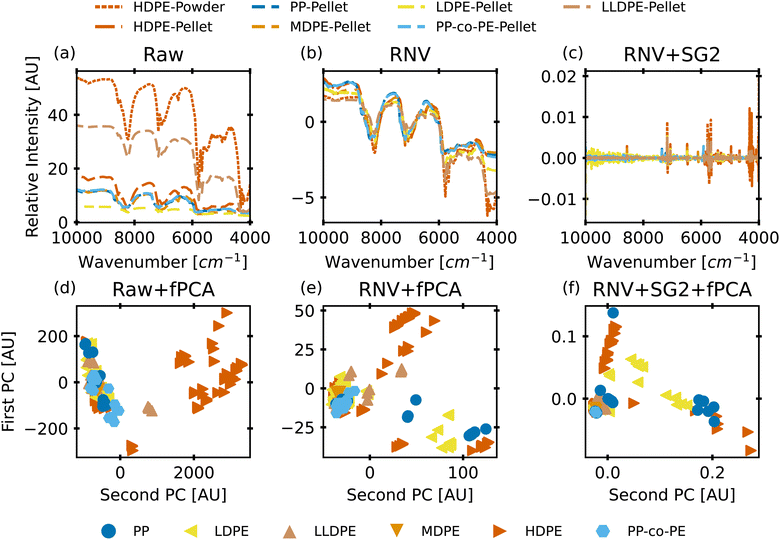
To evaluate the myriad of possible preprocessing and classifier combinations, it was necessary to design a systematic approach to test as many combinations of preprocessing steps and classification algorithms as possible. This was accomplished by splitting preprocessing steps into a maximum sequence of 6 functions: basic scatter corrections (mean centering, SNV, RNV), detrending, Savitzky–Golay filtering (and derivatives), spectra normalization (L1 and L2 norms), feature normalization (StandardScaler, MinMaxScaler), and dimensionality reduction (PCA, fPCA, UMAP). With each step of the preprocessing pipeline also having a “no correction” level, this creates a total of 1152 possible preprocessing combinations. A small selection of how these preprocessing techniques affect the data can be seen in the plots of Fig. 2. In this figure, the top row is the “spectra” view, while the bottom row is a reduced visualization using fPCA to demonstrate the potential for separation of the data with those corrections applied. From left to right, it shows the otherwise unprocessed data, the RNV corrected data, and the RNV corrected data with a second-derivative SG filter (SG′′) applied. This figure clearly demonstrates how impactful preprocessing can be on the final results of a machine learning algorithm, especially with unsupervised techniques like fPCA. The variation in reduced data stems from the removal of different sources of variation in the provided data, allowing different features/wavenumbers, and trends to stand out.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 different classification models and corresponding scores. During this step, each classifier was initiated using predominantly the default parameters, with no hyperparameter tuning. A summary of the parameters that were set to non-default parameters is shown in Table 2, and the default parameters for each model are presented in Tables S3 through S5.‡ These models were then trained and tested using a stratified train-test split, withholding 33% of the data for testing. Classifiers were compared by their accuracy (eqn (3)) and their weighted F1-score (eqn (6)). Accuracy provides a simple metric of how many samples were correctly labeled, while the weighted F1 score attempts to add penalties for models that systematically mislabel a class due to limited sample numbers. In these equations, n is the number of samples, y is the vector of true labels, ŷ is the vector of predicted labels, 1(x) is the indicator function, L is the set of possible labels, yl is the subset of y with the label l, and
672 different classification models and corresponding scores. During this step, each classifier was initiated using predominantly the default parameters, with no hyperparameter tuning. A summary of the parameters that were set to non-default parameters is shown in Table 2, and the default parameters for each model are presented in Tables S3 through S5.‡ These models were then trained and tested using a stratified train-test split, withholding 33% of the data for testing. Classifiers were compared by their accuracy (eqn (3)) and their weighted F1-score (eqn (6)). Accuracy provides a simple metric of how many samples were correctly labeled, while the weighted F1 score attempts to add penalties for models that systematically mislabel a class due to limited sample numbers. In these equations, n is the number of samples, y is the vector of true labels, ŷ is the vector of predicted labels, 1(x) is the indicator function, L is the set of possible labels, yl is the subset of y with the label l, and 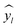 is the subset of ŷ with the label l. The weighted F1-score is a weighted harmonic mean of the precision (eqn (4)) and recall (eqn (5)) scores, thus reducing precision and recall to a single axis. For the scikit-learn implementation of eqn (4) and (5), if the denominators are 0, then P and R are set to 0. For more information on scoring criteria, readers are directed to Section 2.4 of scikit-learn's user guide.33
is the subset of ŷ with the label l. The weighted F1-score is a weighted harmonic mean of the precision (eqn (4)) and recall (eqn (5)) scores, thus reducing precision and recall to a single axis. For the scikit-learn implementation of eqn (4) and (5), if the denominators are 0, then P and R are set to 0. For more information on scoring criteria, readers are directed to Section 2.4 of scikit-learn's user guide.33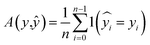 | (3) |
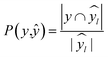 | (4) |
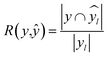 | (5) |
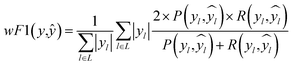 | (6) |
| Common name | Classifier | Source | Parameters |
|---|---|---|---|
| PLS-DA | PLSRegression | scikit-learn 1.2 | n_components = 3 |
| PLS-DA | PLSRegression | scikit-learn 1.2 | n_components = 5 |
| MLPC | MLPClassifier | scikit-learn 1.2 | max_iter = 2000 |
| SIMCA | SIMCA_classifier | Custom code adapted from ref. 21 and 56 | simca_type = ‘SIMCA’ cat_encoder = OneHotEncoder (**) **sparse_output = false, **handle_unknown = ‘ignore’ |
Fig. 3 presents the results of this initial study, organizing models by their weighted F1 score and their accuracy. While most models follow a similar linear relationship between their accuracy and F1 score, the SIMCA model differs from the trend. This is most likely due to the “soft” nature of the model, allowing it to give multiple labels to a single sample, where the other algorithms output one label per sample. With the applied accuracy metric, any sample that has multiple labels will automatically be scored as incorrect, since the true label has only one classification. Since SIMCA is largely designed to produce multi- or “soft” labels, it is understandable that the SIMCA algorithm is systematically penalized with the chosen metric.
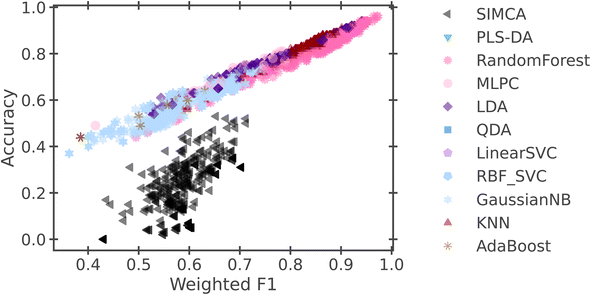 | ||
Fig. 3 The accuracy and weighted F1 scores for 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 models that were trained with default parameters. 672 models that were trained with default parameters. | ||
An ideal preprocessing pipeline should enable multiple ML models to score highly on both accuracy and F1 tests. Fig. 4 focuses on the models that scored above 90% for both metrics, and highlights them based on which preprocessing steps were used for each stage of the pipeline. The highest accuracy model was preprocessed with RNV, no detrending, no SG filtering, an L1 normalization step, a StandardScaler step, and no dimensionality reduction.
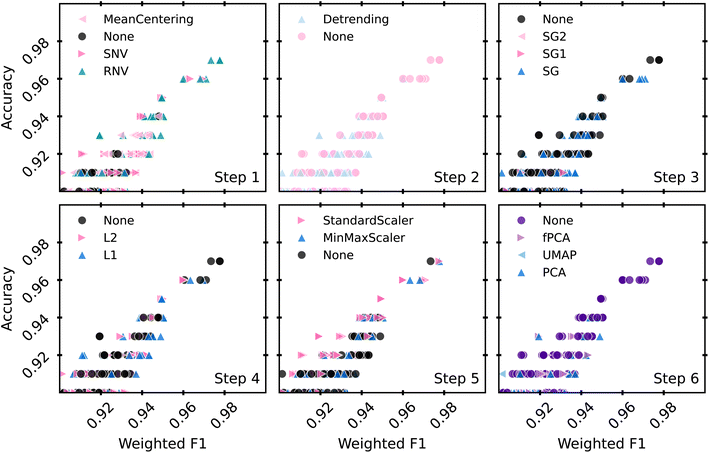 | ||
| Fig. 4 An alternative view of the high scoring models, including those with warnings. Models are highlighted by their preprocessing technique at each of the 6 preprocessing steps. | ||
Fig. 4 provides an opportunity to limit the preprocessing steps used with our models through elimination of steps that systematically add computation time without increasing scores. Limiting preprocessing steps or levels of those steps frees up computational power to tune hyperparameters and identify a more robust model. To reduce the available preprocessing steps, a few assumptions were made. Predominantly, if one of the 6 steps did not provide obvious improvement, but did add complexity to the model, we would not use any levels of that step. For example, Savitzky–Golay filtering relies on a set of parameters that can be arbitrarily set, such as window length, polynomial order, and sample spacing. These parameters can drastically change the results of the fit, necessitating a standard method to apply the filter. Since noisy and smoothed samples performed similarly in our tests, this step can be removed. Similarly, we remove the spectra normalization (step 4, lower left) step. Both RNV and SNV already perform some level of spectra normalization, further making this step partially redundant. Dimensionality reduction (step 6, lower right) displayed a marked decrease in performance, so it was also eliminated. Feature scaling (step 5, lower center) was kept, as many models in the scikit-learn package are documented to rely heavily on feature scaling for accurate results.33,57 This provides 24 possible pipelines, combinations of steps 1, 2 and 5, which can be used to tune a classification model to identify the most robust preprocessing pipeline.
To further reduce the 24 pipelines down to 1, a random forest model was trained and tuned using a nested-cross validation (CV) approach58 and the Optuna Python package.59 For this approach, the raw data was preprocessed by each of the 24 preprocessing pipelines, and the Optuna loop was able to select from the pipeline steps while also tuning the random forest model hyperparameters for the selected preprocessing pipeline. In the tuning step, Optuna uses a Tree-structured Parzen Estimator (by default) to rapidly and effectively tune provided hyperparameters of a given model.60
The nested-CV used a 10-fold stratified shuffle split as the outer loop, and a 5-fold CV inside the Optuna objective function as the inner loop. The inner loop enables careful tuning of the hyperparameters and preprocessing steps, while the outer loop holds an additional set of testing data that are hidden from every iteration of the inner loop's training steps. For each iteration of the inner loop, the Optuna study used 1000 trials to identify the best set of preprocessing steps and random forest hyperparameters, based on the mean accuracy of the 5-fold CV score. This set of tuned model parameters and preprocessing steps was then used in the outer loop to train a new RF model on all the data from the inner loop, and tested on data reserved from the initial 10-fold stratified shuffle split. The general workflow for this nested approach can be seen in Fig. 1e. It should be noted that the RF classifier was chosen for this step because it demonstrated a strong distribution of high weighted F1 scores across most of the initial 1152 preprocessing pipelines. The distribution of scores for each classifier is presented as a violin plot in Fig. S2.‡
The results of each outer loop are reported in Table 3. The results of the initial nested-CV show that RNV alone performed the best out of all the iterations. However, it was only selected by the inner loop a single time. In favor of a robust model, RNV with a MinMaxScaler (RNV-MMS) step was chosen as the final preprocessing pipeline, since it was selected by the inner loop for 6 of the 10 outer loop iterations. Additionally, since some ML models benefit strongly from feature scaling, the additional MinMaxScaler step should enable those algorithms to perform their best.33,57 The RNV-MMS data can now be used to tune a wide variety of scikit-learn classification models.
| Primary scatter | Secondary scatter | Feature scatter | Inner accuracy | Outer accuracy | Outer F1 |
|---|---|---|---|---|---|
| RNV | None | None | 94.8% | 100.0% | 100.0% |
| MeanCentering | Detrending | MinMaxScaler | 93.3% | 87.1% | 86.8% |
| RNV | None | MinMaxScaler | 94.8% | 96.8% | 95.2% |
| RNV | None | MinMaxScaler | 95.2% | 93.5% | 92.1% |
| RNV | None | MinMaxScaler | 94.4% | 93.5% | 92.7% |
| RNV | None | MinMaxScaler | 93.7% | 93.5% | 92.1% |
| RNV | None | MinMaxScaler | 95.6% | 93.5% | 92.0% |
| RNV | None | None | 95.2% | 90.3% | 89.1% |
| SNV | Detrending | None | 93.7% | 90.3% | 88.5% |
| RNV | None | MinMaxScaler | 94.4% | 90.3% | 88.8% |
4.2 Model evaluation
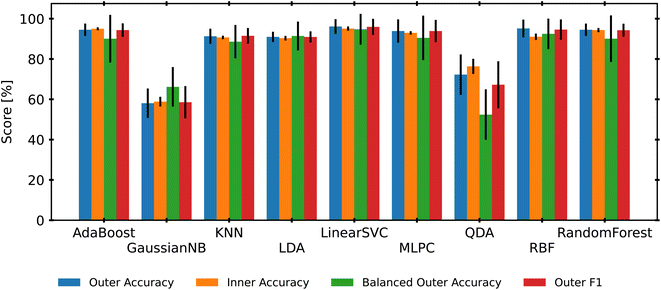
To isolate a single classification model as the best candidate for a benchmark study, we use another nested-CV approach to select the best candidate. Using the selected RNV-MMS preprocessed data, we create a new nested CV that loops through 9 different scikit-learn classifiers, tunes the hyperparameters with an Optuna study, and then evaluates the final results. This process repeats for another 10 iterations, providing mean accuracies and standard deviations for each classifier. It should be noted that both SIMCA and PLS-DA were removed from this analysis. This choice was made due to the additional need for post-model rectification of labels. Additionally, Fig. 3 revealed that both SIMCA and PLS-DA consistently returned some of the lowest accuracy scores. Finally, to ensure that classes with lower sample numbers (MDPE, PP, and PP-co-PE) were not consistently misclassified, this analysis began using weighted or balanced accuracy scores along with traditional accuracy. This method adds a weighting factor based on the support (number of samples) for each class. This is to say that providing an incorrect label to a class with fewer samples is more detrimental than providing an incorrect label to a class with more samples. The averaged results of this step are presented in Fig. 5. Most models performed well, with only KNN (89%), GaussianNB (66%), and QDA (52%) having lower than 90% accuracy when adjusted for data set imbalance (balanced accuracy score). LinearSVC held the highest mean balanced-accuracy score (95%) and was selected as the best classifier for this work.4.3 Leave one group out (LOGO)
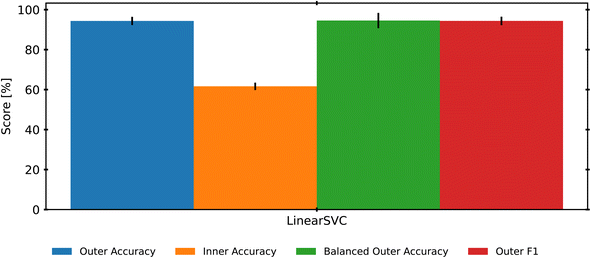
While the previous analysis evaluates the strength of LinearSVC to differentiate various types of known POs, it does not address how LinearSVC performs when it needs to categorize a new polymer, such as a new batch of HDPE. One way to test this robustness is to remove one polymer species (all replicates) from the training set, and instead use that polymer to test the model. Repeating this for each polymer species in our data set enables a leave-one-group-out cross validation (LOGO). Fig. 6 demonstrates the results of using a LOGO approach for the inner loop, selecting hyperparameters for the LinearSVC based on LOGO scores. In this version of the nested-CV approach, the data are split normally with a 10-fold stratified shuffle split, then all the replicates of one polymer species are used for the testing set of the inner (Optuna) loop. The outer loop is then used to evaluate if the same hyperparameters can be used to retrain the model with the new data, but without re-tuning the model. Ideally, this reflects the process that would be used by a commercial facility, as re-tuning the model's hyperparameters whenever a new polymer is identified would be much more computationally expensive than retraining the model with the same hyperparameters. For reference, the full LOGO-CV script took approximately 12 hours to run and optimize hyperparameters on a Windows desktop computer equipped with an Intel Core i7 13700KF processor and 32 GB of 5600 MHz DDR5 RAM.54 However, training on 90% of our data set, with the optimized hyperparameters completed in under 4 seconds, and predictions of the remaining 10% testing set were complete in under 1 ms.The inner accuracy score reflects how poorly the model can classify these “unknown” samples, averaging approximately 60% success across the loops. However, given the imbalance in this data set, the 60% may be surprisingly accurate when considering that the MDPE category only has 1 polymer species, and the PP-co-PE only has 2 species. This means that when the single MDPE polymer is removed, there is no MDPE data to train the LinearSVC on. This guarantees complete failure when the model is asked to classify the MDPE polymer that has been held out – the model will not know the MDPE class at all but will be expected to correctly label the 7 MDPE samples as MDPE. Similarly, the PP-co-PE samples vary significantly since they are copolymers, and having only one example of a copolymer in the data set likely hampers the test results. While these sample-limited classes could be removed to improve results, retaining them reflects the potential for novel materials and the potential impact on an industrial facility. Despite this challenge, when the resultant hyperparameters are used to retrain the model on all polymer species, the LinearSVC performs with 95% accuracy again.
This finding is particularly promising given that there is much research on innovative chemistries that are producing new polymers and new mixtures of polymers. When a recycling facility identifies a new polymer that may be causing issues in the sorting process, they will likely need to retrain their sorting model to identify the new polymer. However, retraining a model on new data is much quicker if the hyperparameters can remain the same.
4.4 Final model analysis
For the final analysis, we average the hyperparameter values chosen by the 10 iterations of Optuna trained via LOGO to suggest a generalized model that can be employed without the tuning step. For LinearSVC the hyperparameters are as follows.33C is the regularization parameter, meant to scale the loss function with relation to the penalty term. penalty is the penalty term that penalizes the optimization function for misclassifying a sample. multi_class determines if the SVC algorithm uses a one-vs.-rest approach to generate one SVC per class or tries to create one SVC that tries to separate all classes at once. class_weight enables adjusting C for each class, based on class size. max_iter limits how many iterations the models used to optimize the support vectors before it is forced to stop. dual determines what level of optimization the model uses. tol is the tolerance level for misclassification errors. The values obtained from both the initial nested-CV and the LOGO nested-CV can be seen in Table 4. The values for C and tol were taken as the mean from the 10 iterations. The max_iter argument was increased to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to guarantee convergence of the model, and all other arguments were the mode of the 10 iterations.
000 to guarantee convergence of the model, and all other arguments were the mode of the 10 iterations.
| Parameter name | Nested-CV value | LOGO value |
|---|---|---|
| C | 57 | 110 |
| penalty | “l1” | “l1” |
| multi_class | “ovr” | “ovr” |
| class_weight | Balanced | None |
| max_iter | 500 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| dual | “Auto” | “Auto” |
| tol | “0.012” | 0.015 |
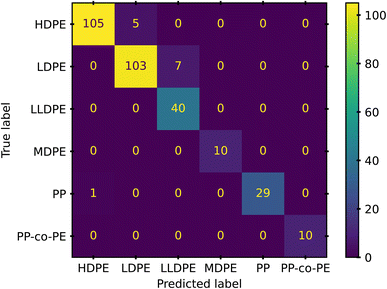
For a final evaluation of this model we conduct a 10-fold cross validation, using the StratifiedShuffleSplit method of scikit-learn. With a training set of 10% of the total data for each shuffle, we obtained an average weighted accuracy score of 98%. The confusion matrix generated from the cross validation study is presented in Fig. 7. The confusion matrix enables a view into where the final model struggles. Despite the limited amount of PP, PP-co-PE, and MDPE samples, we see only one misclassification from all the 10 iterations. Such a success with samples that have only had minimal support during training is likely due to the emphasis on a weighted or balanced accuracy metric. These metrics limit a model's incentive to “cover-up” failures by classifying questionable samples as the majority class. Instead, the errors lie with the majority classes of HDPE and LDPE.
Further investigation into the misclassifications revealed that 6 of the 7 LDPE misclassifications came from one polymer, and 4 of the 5 HDPE misclassifications arose from a black colored HDPE. The singular PP misclassification was from a black PP. This finding demonstrates that classification via NIR still struggles with black colorants.16,23 However, it also offers promise, as 16 of the 21 black samples were still properly classified. This indicates that there is potential for proper identification if there is enough data available to properly train models to recognize or ignore portions of the spectra that are altered by various additives. A larger study with more samples and a systematic representation of common additives may provide this level of refinement. The remaining 2 poor predictions arose from the recycled HDPE and LDPE samples. In both cases, the polymers could have degradation or contaminant artifacts from the recycling process. This seems especially likely for the LDPE that was consistently misclassified as LLDPE.
5 Conclusions
While more work must be done to build open and accessible databases to enable better sortation of polymeric waste, this work demonstrates the potential for a robust approach that can be applied easily by interested stakeholders. This work has thoroughly reviewed a wide variety of data preprocessing techniques to demonstrate that a simple RNV scattering correction and MinMaxScaler operation can successfully clean NIR spectra well enough to enable multiple machine learning algorithms to distinguish the highly similar PO classes with greater than 95% accuracy. This should enable more investigations, with more repeatable results, given that it eliminates overly complex or subjective corrections.Additionally, this work has demonstrated that multiple classification algorithms can be tuned to enable rapid sortation of POs. This work chose LinearSVC as the preferred model due to its simplicity and high balanced accuracy scores. By using a LOGO CV method to tune the model, a more robust set of hyperparameters could be chosen to avoid both overfitting and enable generalizability. Our approach to refining the many variables in this study can also be used as a template for further research to limit the computational strain. This method enables a broad parameter search while avoiding wasted computational resources on unpromising parameter sets.
Example code and the data that were used to produce this work has been made public to enable further advances in the challenge of waste sortation.26 We hope this approach to tuning classification models will be taken up by sortation equipment developers and applied by recyclers to improve the value and reuse of plastic waste recycling streams.
Data availability
The code and data for this manuscript can be found at https://github.com/usnistgov/ECAPS release 1.0.0. Additionally, the data used for this manuscript is being added to https://data.nist.gov/ (DOI: https://doi.org/10.18434/mds2-3022) and should be release version 1.2.0 or 2.0.0.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the NIST Circular Economy program for financial support and Dr Kathryn Beers for helpful conversations. BPS thanks the NIST-NRC postdoctoral fellowship program and the NIST Information Technology Laboratory for support. The authors thank Dr Shailja Goyal and Rosine Yao for measurement data and kind assistance with characterization.References
- P. Liu, et al., A comprehensive review on controlled synthesis of long-chain branched polyolefins: Part 1, single catalyst systems, Macromol. React. Eng., 2016, 10(3), 156–179, DOI:10.1002/mren.201500053.
- G. Usanase, et al., Determination of short chain branching in LLDPE by rheology, Macromol. Chem. Phys., 2022, 223(20), 2200150, DOI:10.1002/macp.202200150.
- B. D. Vogt, K. K. Stokes and S. K. Kumar, Why is Recycling of Postconsumer Plastics so Challenging?, ACS Appl. Polym. Mater., 2021, 3(9), 4325–4346, DOI:10.1021/acsapm.1c00648.
- Wikipedia contributors, Polyolefin, https://en.wikipedia.org/wiki/Polyolefin, accessed: 24-09-2024 Search PubMed.
- P. Werner, 3 – Polyolefins, in Applied Plastics Engineering Handbook, ed. M. Kutz, William Andrew Publishing, Oxford, 2011, pp. 23–48, DOI:10.1016/B978-1-4377-3514-7.10003-0, isbn: 9781437735147.
- A. Van Belle, et al., Microstructural Contributions of Different Polyolefins to the Deformation Mechanisms of Their Binary Blends, Polymers, 2020, 12(5), 1171, DOI:10.3390/polym12051171.
- V. Busico and R. Cipullo, Microstructure of polypropylene, Prog. Polym. Sci., 2001, 26(3), 443–533, DOI:10.1016/S0079-6700(00)00046-0.
- B. P. Sutliff, et al., Correlating near-infrared spectra to bulk properties in polyolefins, Macromolecules, 2024, 1520–5835, DOI:10.1021/acs.macromol.3c02290.
- S. L. Aggarwal and O. J. Sweeting, Polyethylene: Preparation, Structure, And Properties, Chem. Rev., 1957, 57(4), 665–742, DOI:10.1021/cr50016a004.
- D. W. Sauter, M. Taoufik and C. Boisson, Polyolefins, a Success Story, Polymers, 2017, 9(6), 185, DOI:10.3390/polym9060185.
- D. B. Malpass and E. Band, Introduction to Industrial Polypropylene: Properties, Catalysts Processes, John Wiley & Sons, 2012. isbn: 9781118062760 Search PubMed.
- S. V. Orski, et al., Design and Characterization of Model Linear Low-Density Polyethylenes (LLDPEs) by Multidetector Size Exclusion Chromatography, Macromolecules, 2020, 53(7), 2344–2353, DOI:10.1021/acs.macromol.9b02623.
- W. Wen-Jun, et al., Triple-detector GPC characterization and processing behavior of long-chain-branched polyethylene prepared by solution polymerization with constrained geometry catalyst, Polymer, 2004, 45(19), 6495–6505, DOI:10.1016/j.polymer.2004.07.035.
- A. H. Westlie, et al., Polyolefin Innovations toward Circularity and Sustainable Alternatives, Macromol. Rapid Commun., 2022, 43(24), e2200492, DOI:10.1002/marc.202200492.
- S. Yin, et al., Mechanical reprocessing of polyolefin waste: A review, Polym. Eng. Sci., 2015, 55(12), 2899–2909, DOI:10.1002/pen.24182.
- Z. O. G. Schyns and M. P. Shaver, Mechanical Recycling of Packaging Plastics: A Review, Macromol. Rapid Commun., 2021, 42(3), e2000415, DOI:10.1002/marc.202000415.
- S. Serranti, A. Gargiulo and G. Bonifazi, Classification of polyolefins from building and construction waste using NIR hyperspectral imaging system, Resour., Conserv. Recycl., 2012, 61, 52–58, DOI:10.1016/j.resconrec.2012.01.007.
- S. Serranti, et al., An innovative recycling process to obtain pure polyethylene and polypropylene from household waste, Waste Manage., 2015, 35, 12–20, DOI:10.1016/j.wasman.2014.10.017.
- S. Serranti, et al., “Characterization of microplastic litter from oceans by an innovative approach based on hyperspectral imaging”. en, Waste Manage., 2018, 76, 117–125, DOI:10.1016/j.wasman.2018.03.003.
- C. Vidal and C. Pasquini, A comprehensive and fast microplastics identification based on near-infrared hyperspectral imaging (HSI-NIR) and chemometrics, Environ. Pollut., 2021, 285, 117251, DOI:10.1016/j.envpol.2021.117251.
- X. Yan, et al., An ensemble machine learning method for microplastics identification with FTIR spectrum, J. Environ. Chem. Eng., 2022, 10(4), 108130, DOI:10.1016/j.jece.2022.108130.
- H. Masoumi, S. M. Safavi and Z. Khani, Identification and classification of plastic resins using near infrared reflectance, Int. J. Mech. Ind. Eng., 2012, 6, 213–220 Search PubMed.
- M. Rani, et al., Miniaturized Near-Infrared (MicroNIR) Spectrometer in Plastic Waste Sorting, Materials, 2019, 12(17), 2740, DOI:10.3390/ma12172740.
- I. S. Helland, T. Næs and T. Isaksson, Related versions of the multiplicative scatter correction method for preprocessing spectroscopic data, Chemom. Intell. Lab. Syst., 1995, 29(2), 233–241, DOI:10.1016/0169-7439(95)80098-T.
- Å. Rinnan, F. van den Berg and S. B. Engelsen, Review of the most common pre-processing techniques for near-infrared spectra, TrAC, Trends Anal. Chem., 2009, 28(10), 1201–1222, DOI:10.1016/j.trac.2009.07.007.
- B. P. Sutliff, S. Goyal, T. B. Martin, B. Tyler, P. A. Beaucage, D. J. Audus and S. V. Orski, Correlating Near-Infrared Spectra to Bulk Properties in Polyolefins, National Institute of Standards and Technology, 2023, DOI:10.18434/mds2-3022, accessed 2024-07-03.
- Q. Guo, W. Wu and D. L. Massart, The robust normal variate transform for pattern recognition with near-infrared data, Anal. Chim. Acta, 1999, 382(1), 87–103, DOI:10.1016/S0003-2670(98)00737-5.
- R. J. Barnes, M. S. Dhanoa and S. J. Lister, Standard normal variate transformation and DE-trending of near-infrared diffuse reflectance spectra, Appl. Spectrosc., 1989, 43(5), 772–777, DOI:10.1366/0003702894202201.
- D. Iacobucci, et al., Mean centering helps alleviate “micro” but not “macro” multicollinearity, Behav. Res. Methods, 2016, 48(4), 1308–1317, DOI:10.3758/s13428-015-0624-x.
- W. H. Press and S. A. Teukolsky, Savitzky-Golay Smoothing Filters, Comput. Phys., 1990, 4(6), 669–672, DOI:10.1063/1.4822961.
- A. Savitzky and M. J. E. Golay, Smoothing and differentiation of data by simplified least squares procedures, Anal. Chem., 1964, 36(8), 1627–1639 CrossRef CAS.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- scikit-learn, https://scikit-learn.org/stable/index.html, accessed: 2023-10-27.
- F. Corradini, et al., Predicting soil microplastic concentration using vis-NIR spectroscopy, Sci. Total Environ., 2019, 650(Pt 1), 922–932, DOI:10.1016/j.scitotenv.2018.09.101.
- E. R. Kai Neo, et al., A review on chemometric techniques with infrared, Raman and laser-induced breakdown spectroscopy for sorting plastic waste in the recycling industry, Resour., Conserv. Recycl., 2022, 180, 106217, DOI:10.1016/j.resconrec.2022.106217.
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- R. G. Brereton and G. R. Lloyd, Partial least squares discriminant analysis: taking the magic away, J. Chemom., 2014, 28(4), 213–225, DOI:10.1002/cem.2609.
- A. L. Pomerantsev and O. Y. Rodionova, Multiclass partial least squares discriminant analysis: Taking the right way—A critical tutorial, J. Chemom., 2018, 32(8), e3030, DOI:10.1002/cem.3030.
- L. C. Lee, C.-Y. Liong and A. J. Abdul, Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: a review of contemporary practice strategies and knowledge gaps, Analyst, 2018, 143(15), 3526–3539, 10.1039/c8an00599k.
- D. Ruiz-Perez, et al., So you think you can PLS-DA?, BMC Bioinf., 2020, 21(Suppl 1), 2, DOI:10.1186/s12859-019-3310-7.
- B. Ghojogh and M. Crowley, Linear and Quadratic Discriminant Analysis: Tutorial, arXiv, 2019, preprint, arXiv:1906.02590, DOI:10.48550/arXiv.1906.02590.
- Y. Qin, A review of quadratic discriminant analysis for high-dimensional data, Wiley Interdiscip. Rev. Comput. Stat., 2018, 10(4), e1434, DOI:10.1002/wics.1434.
- L. Wang, Support Vector Machines: Theory and Applications, Springer Science & Business Media, 2005, isbn: 9783540243885 Search PubMed.
- V. Kecman, Support Vector Machines – An Introduction, in Support Vector Machines: Theory and Applications. Studies in fuzziness and soft computing, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 1–47, DOI:10.1007/10984697\_1.
- A. Rácz, et al., Is soft independent modeling of class analogies a reasonable choice for supervised pattern recognition?, RSC Adv., 2017, 8(1), 10–21, 10.1039/C7RA08901E.
- O. Galtier, et al., Comparison of PLS1-DA, PLS2-DA and SIMCA for classification by origin of crude petroleum oils by MIR and virgin olive oils by NIR for different spectral regions, Vib. Spectrosc., 2011, 55(1), 132–140, DOI:10.1016/j.vibspec.2010.09.012.
- S. Wold and M. Sjöström, SIMCA: A Method for Analyzing Chemical Data in Terms of Similarity and Analogy, in Chemometrics: Theory and Application, ACS Symposium Series, American Chemical Society, 1977, vol. 52, pp. 243–282, isbn: 9780841203792. doi: DOI:10.1021/bk-1977-0052.ch012.
- A. Kelly and M. A. Johnson, Investigating the Statistical Assumptions of Naive Bayes Classifiers, in 2021 55th Annual Conference on Information Sciences and Systems (CISS), IEEE, 2021, pp. 1–6, DOI:10.1109/CISS50987.2021.9400215.
- L. B. Almeida, Multilayer perceptrons, in Handbook of Neural Computation, CRC Press, 2020, pp. C1–C2 Search PubMed.
- A. J. Myles, et al., An introduction to decision tree modeling, J. Chemom., 2004, 18(6), 275–285, DOI:10.1002/cem.873.
- P. Virtanen, et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272, DOI:10.1038/s41592-019-0686-2.
- C. Ramos-Carreño, et al., scikit-fda: A Python Package for Functional Data Analysis, arXiv, 2022, preprint, arXiv:2211.02566, DOI:10.48550/arXiv.2211.02566.
- Hawai'i Pacific University Center for Marine Debris Research, Polymers Kit 1.0, https://www.hpu.edu/cncs/cmdr/products-and-services.html, accessed: 2023-5-30.
- Any identification of software, equipment, instruments, companies, or materials in this work is done so for the express purposes of completeness and understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
- Q. Duan and L. Jia, Classification of Common Household Plastic Wastes Combining Multiple Methods Based on Near-Infrared Spectroscopy, ACS ES&T Eng., 2021, 1(7), 1065–1073, DOI:10.1021/acsestengg.0c00183.
- X. Yan, et al., An ensemble machine learning method for microplastics identification with FTIR spectrums, 2023, https://github.com/lyheiyu/An-ensemble-learning-for-microplastcs-identification-with-FTIR/.
- M. Manjurul Ahsan, et al., Effect of Data Scaling Methods on Machine Learning Algorithms and Model Performance, Technologies, 2021, 9(3), 52, DOI:10.3390/technologies9030052.
- S. Bates, T. Hastie and R. Tibshirani, Cross-validation: What does it estimate and how well does it do it?, J. Am. Stat. Assoc., 2023, 1–12, DOI:10.1080/01621459.2023.2197686.
- T. Akiba, et al., Optuna: A Next-generation Hyperparameter Optimization Framework, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD’19, Anchorage, AK, USA, Association for Computing Machinery, 2019, pp. 2623–2631, DOI:10.1145/3292500.3330701, isbn: 9781450362016.
- Optuna Contributors, Efficient Optimization Algorithms – Optuna 3.6.1 documentation, accessed: 2024-4-3.
Footnotes |
| † Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00235k |
| This journal is © The Royal Society of Chemistry 2024 |