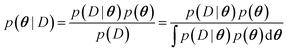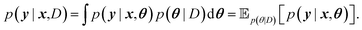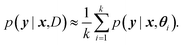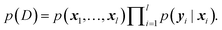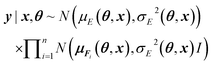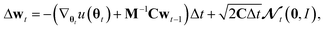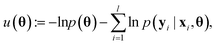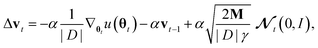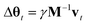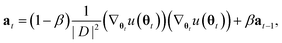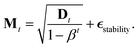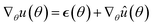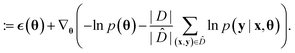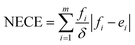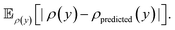Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High accuracy uncertainty-aware interatomic force modeling with equivariant Bayesian neural networks†
Tim
Rensmeyer
 *a,
Ben
Craig
b,
Denis
Kramer
a and
Oliver
Niggemann
a
*a,
Ben
Craig
b,
Denis
Kramer
a and
Oliver
Niggemann
a
aHelmut-Schmidt University Hamburg, Germany. E-mail: rensmeyt@hsu-hh.de
bUniversity of Southampton, UK
First published on 15th October 2024
Abstract
Ab initio molecular dynamics simulations of material properties have become a cornerstone in the development of novel materials for a wide range of applications such as battery technology and catalysis. Unfortunately, their high computational demand can make them unsuitable in many applications. Consequently, surrogate modeling via neural networks has become an active field of research. Two of the major obstacles to their practical application in many cases are assessing the reliability of the neural network predictions and the difficulty of generating suitable datasets to train the neural network in the first place. Bayesian neural networks offer a promising framework for modeling uncertainty, active learning and improving data efficiency and robustness by incorporating prior physical knowledge. However, due to the high computational demand and slow convergence of the gold standard approach of Monte Carlo Markov Chain (MCMC) sampling methods, variational inference via Monte Carlo dropout is currently the only sampling method successfully applied in this domain. Since MCMC methods have often displayed a superior quality in their uncertainty quantification, developing a suitable MCMC method in this domain would be a significant advance in making neural network-based molecular dynamics simulations more practically viable. In this paper, we demonstrate that convergence for state-of-the-art models with high-quality MCMC methods can still be achieved in a practical amount of time by introducing a novel parameter-specific adaptive step size scheme. In addition, we introduce a new stochastic neural network model based on the NequIP architecture and demonstrate that, when combined with our novel sampling algorithm, we obtain predictions with state-of-the-art accuracy as well as a significantly improved measure of uncertainty over Monte Carlo dropout. Lastly, we show that the proposed algorithm can even outperform deep ensembles while sampling from a single Markov chain.
1 Introduction
Despite the fact that the laws of quantum mechanics, which underly chemistry, were discovered almost a century ago, their application for the ab initio prediction of many chemical and material properties such as stress-strain relationships or catalytic activity remains a formidable task.1,2 This is in large part a result of the sheer computational complexity involved in solving these equations numerically.1,2Molecular Dynamics (MD), where the time evolution of atomic systems is investigated, is particularly affected by this challenge because each time step requires the numerical calculation of the forces acting on the atoms. While computational methods such as Density Functional Theory (DFT) have been developed that can calculate interatomic forces with very high accuracy, these methods are in general computationally expensive and scale badly with growing system sizes. Thus, it remains very difficult to model larger systems with high accuracy and a large enough time horizon.
To circumvent these difficulties, the prediction of interatomic forces via machine learning models such as neural networks has become a highly active area of research.3 However, the cost of generating training data from ab initio simulations prevents the generation of large training sets commonly required to construct sufficiently predictive neural networks. Recent innovations in neural network designs have already made it possible to learn highly accurate interatomic force fields for simple molecules and materials with limited data by incorporating hard constraints in the form of symmetry properties and energy conservation into neural network architectures.4–9 However, several open problems remain, for neural network-based force fields to become a practical tool for computational material scientists and chemists.
The first problem is the training of a suitable machine learning model. As a consequence of the vastness of the space of possible atomic configurations, training models to have chemical accuracy for entire classes of compounds requires large amounts of data10 and such models still don't reach a satisfactory accuracy for many applications computational material scientists are interested in. For example, leading models on the Open Catalyst 20 benchmark still have a prediction error that is more than ten times larger than the stated target accuracy of that benchmark.11 Hence, a material scientist attempting to investigate a system of interest will oftentimes have to train a machine-learning model for that specific system. However, the generation of suitable training datasets represents a major challenge. For example, in solid–gas interfaces, gas molecule adsorbates on the surface of the solid can cause the surface to restructure on an atomic level to make the total surface-adsorbate system more energetically favorable.12 Suppose that a material scientist attempts to investigate this process with a neural network model. A suitable training dataset would have to contain many intermediate configurations of this restructuring process to ensure the accuracy of the neural network during that transition. However, it is not known beforehand what these intermediate structures are because otherwise the neural network model would not be needed in the first place. Additionally, the space of apriori plausible intermediate structures will be unpractically large. The selection of configurations to label for the training dataset therefore will be very difficult, especially considering the high computational cost of labeling each configuration. The creation of predictive models is, therefore, still a challenging task.
The second challenge is, that the existing state-of-the-art models generally lack a measure of uncertainty in their prediction,3,13 which makes it impossible to tell which of the predictions are reliable. This limits the applicability of active learning strategies, where uncertainty can be used to select useful training data from the large configuration space more efficiently14–18 by only labeling configurations with a high predictive uncertainty and energies that are accessible at the target temperature. Further, for a deployed model detected outliers can be recomputed on-the-fly in DFT to ensure the accuracy of a neural network-based MD trajectory.
Deep ensembles, where several neural networks are trained from scratch with different weight initializations, are a popular method for quantifying uncertainty by measuring the disagreement between the neural network predictions.18 However, training several models from scratch can become very time-consuming with limited GPU hardware. Furthermore, they do not offer a solution to the final challenge we want to make progress toward in this work:
It would be very desirable to not have to train models from scratch but to instead fine-tune existing pre-trained neural network models to the specific system of interest since such fine-tuning can be vastly more data-efficient than training from scratch.19 Such models could have been pre-trained either on large-scale databases of different molecules and materials labeled in DFT or on data of the system of interest simulated with a lower accuracy method that is less computationally demanding. However, a practical fine-tuning strategy would most likely still have to be integrated with an active learning approach as the previous case study illustrates. This requires the development of a suitable framework to merge active learning with fine-tuning. Furthermore, most publicly available models don't quantify the uncertainty in their predictions and the training time of a single model on large material databases will already require larger GPU clusters.11 Therefore, it will not be a viable solution for many material scientists to pre-train a deep ensemble on such a database themself and then fine-tune it on the system they are interested in. How to fine-tune such uncertainty unaware, publicly available pre-trained models and simultaneously assess the predictive uncertainty during the fine-tuning process, therefore, represents a major difficulty.
Bayesian Neural Networks (BNNs) have a robust measure of uncertainty and offer a promising framework for fine-tuning pre-trained models via the Bayesian prior distribution.20,21 Additionally, constructing a prior from a single pre-trained model would still allow for the sampling of several models from the posterior which could in principle enable the assessment of uncertainty via their disagreement, even if the pre-trained model itself was uncertainty unaware.
Unfortunately, BNNs sometimes display a suboptimal accuracy22 and recent work has found that this is also the case for neural network-based force fields.23 However, the sampling approach used in that work has recently been demonstrated to have convergence issues.24 Therefore, whether BNNs can achieve state-of-the-art accuracy in this domain remains an open question.
Additionally, sampling the Bayesian posterior for commonly used modern neural network architectures comes with particular difficulties, as even with classical gradient descent-based optimizers the training on just a single compound to full convergence can already take days and for sampling the true posterior artificial noise has to be added to the gradients via Monte Carlo Markov Chain (MCMC) methods, further prolonging convergence times. Additionally, we found that current off-the-shelf MCMC methods are either unsuited for dealing with the vastly different gradient scales that different parameter groups exhibit in modern models or come with a significant increase in computational demand. This results in an unpractically slow traversal through the parameter space to the point where no convergence is achievable in reasonable amounts of time, which explains their current lack of use. Consequently, successful applications of Bayesian neural networks in practically relevant systems have so far all involved approximate inference via Monte Carlo dropout25,26 which often underperforms on uncertainty quantification metrics when compared with MCMC methods but is currently less computationally demanding.
The central research question investigated in this paper is, whether combining high-quality MCMC-based Bayesian neural network approaches and state-of-the-art neural network architectures is practically viable.
We measure viability on the following three conditions. First of all, the approach has to yield an improved quality of uncertainty over more basic BNN methods such as MC-Dropout. Furthermore, there has to be no significant loss in accuracy compared to classical non-Bayesian methods. Lastly, because the main purpose of the machine learning model is to speed up simulations for computational chemists and material scientists, it would be desirable if the training times remain reasonable on hardware available to those groups (e.g. no more than a few GPU days on a single small molecule dataset with a single modern GPU). Otherwise, training times could become a limiting factor in the speed-up that can be reached with the machine learning model.
The contributions of this paper are the following:
• We develop a new stochastic neural network model based on the NequIP architecture7 for uncertainty-aware interatomic force modeling with state-of-the-art accuracy.
• We introduce a novel Bayesian MCMC algorithm that produces high-quality samples of the posterior density in a practical amount of time.
• We show that the sampling algorithm produces models with state-of-the-art accuracy and high-quality uncertainty quantification, significantly outperforming Monte Carlo dropout.
• We discuss shortcomings as well as possible further improvements and research directions based on the results of the proposed neural network model and sampling algorithm.
Notation commonly used in this paper is summarized in Table 1.
1.1 Related work
While BNNs to date have found very few applications in this context, some use cases exist in the literature.23,25–27 However, in two of them25,26 Monte Carlo dropout was used for Bayesian inference. While this method can in some instances be interpreted as Bayesian variational inference,28 it yields only a local approximation of the true posterior distribution. Due to this fact, it can result in poorer uncertainty quantification compared to MCMC methods.29 While a much more accurate Bayesian algorithm was used by Thaler and Zavadlav,27 the use case was very limited in scope to diatomic systems. Further, all of the above instances were limited to very small fully connected neural networks while we utilize a state-of-the-art graph neural network-based architecture. We only found one attempt to generate samples from the true posterior of a graph neural network-based architecture in the literature by Thaler et al.23 who used the Preconditioned Stochastic Gradient Langevin Dynamics (PSGLD) sampler.30 In that work, they did not get competitive results when compared to non-Bayesian optimization in terms of accuracy. However, it was recently shown that this sampler suffers from serious convergence problems, causing it to converge to a suboptimal distribution.24A different Bayesian inference method, that has a long history in modeling interatomic forces and energies are Gaussian processes.17,31–35 In these approaches, the posterior distribution is explicitly modeled over the space of functions instead of the model parameters. The drawback of those models is, that, unlike neural networks, they do not scale well to large-scale datasets. This makes pre-training on large-scale databases unfeasible. Furthermore, while they yielded comparable accuracies to neural network potentials several years ago,36 neural network architectures have progressed significantly since then,4–9 substantially increasing their data efficiency and accuracy. Nonetheless, Gaussian processes have become a well-established approach for molecular dynamics modeling. Lastly, more recently deep evidential regression has been applied to molecular property prediction, including energy predictions.37 These methods model more sophisticated distributions than regular single-model uncertainty quantifiers and have shown promising results.
2 The base model
2.1 The formal setting
The aim of the neural network-based interatomic force model is to map a configuration of atoms x = {(r1, z1), …, (rn, zn)}, where ri denotes the position of the nucleus of atom i and zi refers to its nuclear charge, to the forces {F1, …, Fn} acting on the individual nuclei. These forces are then used to simulate the movement of the nuclei based on Newton's equations of motion via a solver for Ordinary Differential Equations (ODEs) (Fig. 1).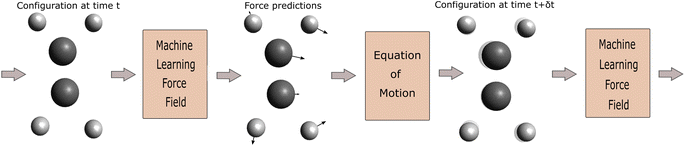 | ||
| Fig. 1 An illustration of a molecular dynamics workflow with neural network predictions for the forces. | ||
One important aspect of this form of data is that the order in which the atoms are enumerated is arbitrary. A suitable neural network model should therefore be equivariant under a reordering of the data. Another important constraint is, that these forces are conservative and can therefore be derived as the negative gradients of a single potential energy surface
| Fi = −∇riE((r1, z1), …, (rn, zn)). |
The potential energy surface itself is invariant under any distance-preserving transformation of the atomic coordinates. This was at first incorporated into neural network models by using only the interatomic distances rij and nuclear charges as input, which have these invariances themself. Even though it is in principle possible to extract directional information from the set of interatomic distances, in practice incorporating directional information explicitly can improve data efficiency and accuracy quite a lot13 and has become a key feature of many state-of-the-art neural network models.4–9
2.2 The NequIP model
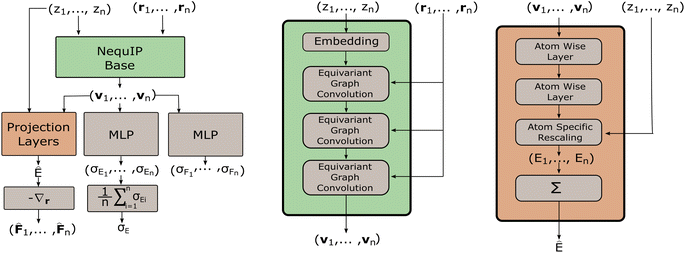
One of the most powerful neural network models for interatomic force modeling that currently exists is the NequIP model7 (Fig. 2). This model takes all the previous considerations into account and consists of a model base and projection layers. The model base maps an atomic configuration {(r1, z1), …, (rn, zn)} to a set of high dimensional latent feature vectors {v1, …, vn} that are invariant under distance-preserving transformations. The projection layers then map {(v1, z1), …, (vn, zn)} to (virtual) atomic energies {E1, …, En}.The potential energy E is then calculated as the sum of the atomic energies. Finally, the forces acting on the nuclei are then calculated as the negative gradients of the potential energy with respect to the nuclear coordinates.
3 Solution
3.1 Bayesian neural networks
The main difference between BNNs and regular neural networks is, that in the former the parameters, i.e. weights and biases, are modeled probabilistically. To keep the notation simple, we use θ to denote a vector containing a complete set of neural network parameters. For BNNs, it is assumed that some prior knowledge exists about what constitutes a good set of parameters, which is expressed in the form of a prior density p(θ). This prior density then gets refined through the training data D = {(x1, y1), …, (xl, yl)} by invoking Bayes rule for calculating the posterior density:A prediction on a new data point (x, y) can now be made via:
For BNNs, this integral is almost always analytically intractable. However, by generating samples θ1, …, θk from p(θ|D) it can be estimated through the law of large numbers as:
3.2 The stochastic model
In order to achieve state-of-the-art accuracy combined with a good measure of predictive uncertainty in modeling interatomic forces, a new stochastic neural network model is required, which we will introduce in this section.To build a stochastic model of the data, we make the following assumptions on the conditional independence of the data:
More specifically we model the conditional densities
| p(y|x, θ) = p(E, F1, …, Fn|(r1, z1), …, (rn, zn), θ) |
where y|x, θ denotes y conditioned on x and θ, x = {(r1, z1), …, (rn, zn)}, the means μE(θ, x) and μFi(θ, x) are the regular point predictions of the NequIP model, the standard deviations σE(θ, x) and σFi(θ, x) are predicted by two separate Multi-Layer Perceptrons (MLPs) from the outputs of the NequIP base v1, …, vn and I denotes the identity matrix (Fig. 2). Note that a single invariant standard deviation is calculated for all three force components to ensure equivariance of the predicted density under any distance-preserving transformation of the atomic coordinates.
We include the potential energy E here as an additional dependent training variable because it is calculated as a byproduct of force calculations in DFT anyway. Lastly, we use the simple Gaussian mean field prior θ ∼ N(0, I).
3.3 Sampling the posterior
Generating high-quality sample weights from the posterior distribution is usually done via the simulation of a Markov chain which converges in distribution to the posterior. While several Markov chain methods have been constructed for neural network applications, we found them unsuitable for this use case. The main difficulty we encountered was, that the scale of the gradients with respect to the different sets of parameters corresponding to the different layers of the neural network vary by several orders of magnitude. This makes the use of a single step size for all parameters impossible, as it would cause the sets of parameters with smaller gradients to be frozen during the optimization. In practice, we found that this causes the training and validation loss to become stuck at values several times higher than what can be achieved with modern (non-Bayesian) neural network optimizers, who circumvent this problem through an adaptive step size for each parameter.38 However, the use of adaptive step size is only possible to a very limited degree for Markov chains39 without changing the distribution to which they converge. Furthermore, this typically requires the calculation of higher-order derivatives39 which is computationally expensive‡, especially in light of the already slow convergence of SOTA architectures with classical optimizers. To deal with these challenges, we develop here a new approach to sampling the posterior distribution based on the Stochastic Gradient Hamiltonian Monte Carlo (SGHMC) algorithm introduced by Chen et al.40 In its basic form, the algorithm is given by the Markov chain| Δθt = M−1wtΔt. |
M−1 and C are vectors containing strictly positive values, Δt ≪ 1 is the step size and
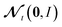 denotes a random variable with a multivariate standard normal distribution. To keep the notation simple, we use the convention here, that all operations on vectors (multiplication, inversion, etc.) are to be taken element-wise. The auxiliary variable wt has the same dimension as θt.
denotes a random variable with a multivariate standard normal distribution. To keep the notation simple, we use the convention here, that all operations on vectors (multiplication, inversion, etc.) are to be taken element-wise. The auxiliary variable wt has the same dimension as θt.
From a non-Bayesian machine learning perspective, wt represents a momentum term similar to the ones used in many modern neural network optimizers.38 In fact, Chen et al. used some substitutions which lead to a Bayesian analog to stochastic gradient descent with momentum,40 but we will make somewhat different substitutions that lead to a natural way to include adaptive step sizes: α = ΔtM−1C, γ = (Δt)2|D|α−1 and vt = γ−1Δtwt which yields:
where |D| is the size of the dataset D.
This is up to the noise term 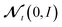 equivalent to the updates of the Adam optimizer.41
equivalent to the updates of the Adam optimizer.41
Unfortunately, the mass term M used in the standard Adam optimizer can vary a lot even during later stages of the training and this variation depends on the value of θt at the previous time steps. As a consequence, the resulting process (θt, vt) would not even be a Markov chain, and the Bayesian posterior would most likely no longer be the distribution θt converges to.39 For many neural network architectures, timely convergence to the posterior can be achieved by simply setting M = I. However, the vastly varying gradient scales of the different parameter groups in the model make this approach not feasible. As a solution, we introduce now a new adaptive step size method for the SGHMC algorithm which still converges to the posterior distribution without requiring the computation of higher-order derivatives. In order to achieve this, we set M as the denominator of the AMSGrad algorithm42 during the first phase of the optimization:
| Dt = max(Dt−1, at), |
Here, max(Dt−1, at) is the element-wise maximum,
 is a stability constant and β is a hyperparameter used in computing the running average at and is typically set between 0.99 and 0.9999.
is a stability constant and β is a hyperparameter used in computing the running average at and is typically set between 0.99 and 0.9999.
Because this mass term is still time- and path-dependent, θt can not, in general, be expected to converge exactly to the posterior distribution during this phase. However, because Mt is not based on a running average of squared gradients like most adaptive step size methods are, but instead on the maximum of such a running average, it typically changes very little during the later stages of the optimization. As a result, the process will already become fairly close in distribution to the Bayesian posterior during this stage of the optimization. Furthermore, because Mt already remains almost constant after a while, we can keep it entirely constant after a certain amount of steps without causing instabilities, at which point the process θt becomes a regular SGHMC process which is known to converge to the Bayesian posterior for sufficiently small step sizes.40
Because deep learning datasets are usually very large, evaluating ∇θu(θ) exactly is typically very time-consuming. Practical implementations instead estimate ∇θu(θ) on a smaller, randomly sampled subset ![[D with combining circumflex]](https://www.rsc.org/images/entities/char_0044_0302.gif) ⊂ D via
⊂ D via
The resulting algorithm is summarized in Algorithm 1. Here 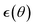 is the error in the estimation of ∇θu(θ) with
is the error in the estimation of ∇θu(θ) with 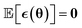 .
.
As long as 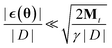 it is clear that this additional noise does not have a large effect on the dynamic as the Gaussian noise term will dominate. This can always be achieved by choosing an appropriate batch size and step size γ. Because the proposed algorithm becomes a regular SGHMC process once Mt remains constant, the same convergence analysis that was introduced by Chen et al.40 is also valid for this algorithm.
it is clear that this additional noise does not have a large effect on the dynamic as the Gaussian noise term will dominate. This can always be achieved by choosing an appropriate batch size and step size γ. Because the proposed algorithm becomes a regular SGHMC process once Mt remains constant, the same convergence analysis that was introduced by Chen et al.40 is also valid for this algorithm.
4 Empirical evaluation
4.1 The benchmarks
To assess our models' accuracy and predicted uncertainty we utilize three different datasets. To analyze our model's performance with varying amounts of Monte Carlo samples and under domain shift, we used a dataset consisting of PEDOT polymers, which are conducting polymers, that due to their chemical stability and tuneable properties43 have been used for a wide range of applications including sensors,44 supercapacitors,45 battery electrodes,46 bioelectronics, solar cells, electrochromic displays, electrochemical transistors,47 and spintronics.48 The dataset consists of polymers of lengths 8, 12 and 16, where only the shorter chains were used for training (see ESI Section A† for details). The total training set contained only 100 configurations, 50 of length 8 polymers and 50 of length 12 polymers. Equivalently a small validation set of size 30 was constructed.The second dataset used is the RMD17 dataset49 consisting of long molecular dynamics trajectories of several small organic molecules from the MD17 dataset50 recalculated at higher resolution in DFT. Because dropout is by far the most common Bayesian method used for interatomic force modeling and one of the most common methods for uncertainty quantification in this domain in general, we will compare our algorithms' performance to a dropout-based version of the proposed stochastic model on this dataset (see ESI Section A† for details).
For each compound, we used 1000 randomly sampled configurations during training and the rest for testing. Of the 1000 configurations sampled, 30 were reserved as a small validation set, and the remaining ones comprised the actual training set. The same samples were used as training, validation and test sets for our proposed model and the dropout-based model.
To include a stronger baseline than Monte Carlo Dropout and to demonstrate our methods' capability to model interatomic forces at very high accuracies we included a third benchmark consisting of a dataset from an ethanol molecule dataset simulated with coupled cluster methods and introduced by Bogojeski et al.51. This simulation method is typically more accurate than DFT although considerably more computationally expensive. On this benchmark, we compare our algorithm with a deep ensemble consisting of 8 of our proposed stochastic NequIP neural network models trained on the same dataset with different initializations of the weights. Deep ensembles generally have a high quality of uncertainty quantification52 but are computationally demanding to train since several neural networks have to be trained from scratch. We use 100 randomly sampled configurations for training and 1000 configurations as a test set. All neural networks for the deep ensemble were trained using early stopping on a validation set of 30 configurations.
The details of the neural network architectures and sampling procedures can be found in ESI Section A.†
4.2 Evaluation metrics
To measure prediction accuracy, we evaluate both the Mean Absolute Error (MAE) as well as the Root Mean Square Error (RMSE). In the evaluation, we use the expectation value under the estimated posterior density as a point prediction. I.e.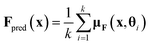 . One metric used to evaluate and compare the predicted uncertainties are the Mean Log Likelihoods (MLLs) of the forces and energies. Since in the most common applications, the main task of the uncertainty measure is outlier detection, we further evaluate the ROC AUC scores for detecting force components with an error larger than 1 kcal (mol Å)−1 on the basis of the variance of the predicted distribution of those force components. Because of the relatively small size of the PEDOT dataset, we only evaluate the outlier detection on the other datasets.
. One metric used to evaluate and compare the predicted uncertainties are the Mean Log Likelihoods (MLLs) of the forces and energies. Since in the most common applications, the main task of the uncertainty measure is outlier detection, we further evaluate the ROC AUC scores for detecting force components with an error larger than 1 kcal (mol Å)−1 on the basis of the variance of the predicted distribution of those force components. Because of the relatively small size of the PEDOT dataset, we only evaluate the outlier detection on the other datasets.
Lastly, to evaluate if the proposed model is properly calibrated we utilize a normalized version of the Expected Calibration Error (NECE)53 as well as a visual inspection of the predicted and observed error densities of the force components (Fig. 4) (see ESI Section A† for details). To calculate a NECE, the predictions yi are divided into m bins of equal width δ. The NECE is then calculated as
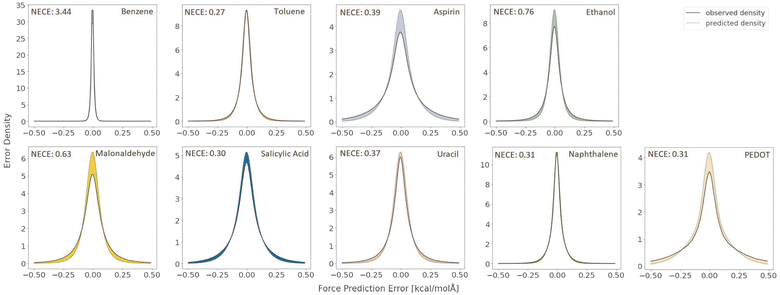 | ||
| Fig. 4 Observed and predicted error densities of the force components in kcal (mol Å)−1 with k = 8 Monte Carlo samples on the RMD17 datasets and the length 16 PEDOT polymer dataset. | ||
4.3 Results
| Chain length | k = 1 sample | k = 8 samples | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | NECE | MLL | MAE | RMSE | NECE | MLL | |
| 16 | 0.222 | 0.385 | 0.649 | −1.79 | 0.210 | 0.371 | 0.313 | −0.20 |
| 12 | 0.184 | 0.276 | 0.652 | −0.87 | 0.169 | 0.254 | 0.317 | 0.14 |
| 8 | 0.151 | 0.221 | 0.619 | −0.28 | 0.139 | 0.203 | 0.215 | 0.44 |
A slight improvement in the accuracy is observed when going from one to eight Monte Carlo samples. Further, it can be seen from Table 2, that a single Monte Carlo sample does not yield good uncertainty estimates for the forces which vastly improves when using eight Monte Carlo samples.
Even though no polymer chains of length 16 were included in the training set, we find that the model still achieves high accuracy (Table 2). Again we see much poorer uncertainty quantification for a single Monte Carlo sample when compared to the case of k = 8 Monte Carlo samples (Table 2). A complete histogram of predicted and actual force components can be found in ESI Section A.† We observe some overconfidence even in the k = 8 case (Fig. 4).
| Number of samples k | Proposed algorithm | |||
|---|---|---|---|---|
| MAE | RMSE | NECE | MLL | |
| 1 | 0.222 | 0.385 | 0.649 | −1.79 |
| 2 | 0.219 | 0.381 | 0.473 | −0.87 |
| 4 | 0.216 | 0.378 | 0.376 | −0.44 |
| 8 | 0.210 | 0.371 | 0.313 | −0.20 |
| 16 | 0.201 | 0.356 | 0.254 | 0.00 |
| Molecule | Dropout | Proposed algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MLL | AUC-ROC | MAE | RMSE | MLL | AUC-ROC | |
| Aspirin | 0.215 | 0.340 | −1.85 | 0.800 | 0.144 | 0.229 | 0.22 | 0.952 |
| Ethanol | 0.078 | 0.147 | 0.74 | 0.897 | 0.064 | 0.115 | 1.03 | 0.993 |
| Uracil | 0.082 | 0.141 | 0.71 | 0.888 | 0.085 | 0.138 | 0.83 | 0.986 |
| Malonaldehyde | 0.145 | 0.259 | −0.18 | 0.824 | 0.099 | 0.170 | 0.49 | 0.983 |
| Salicylic acid | 0.108 | 0.199 | 0.14 | 0.809 | 0.109 | 0.182 | 0.63 | 0.977 |
| Naphthalene | 0.044 | 0.069 | 1.19 | 0.902 | 0.043 | 0.069 | 1.63 | 0.995 |
| Toluene | 0.052 | 0.084 | 1.11 | 0.894 | 0.051 | 0.082 | 1.43 | 0.995 |
| Benzene | 0.020 | 0.032 | 1.50 | NA | 0.010 | 0.016 | 3.06 | NA |
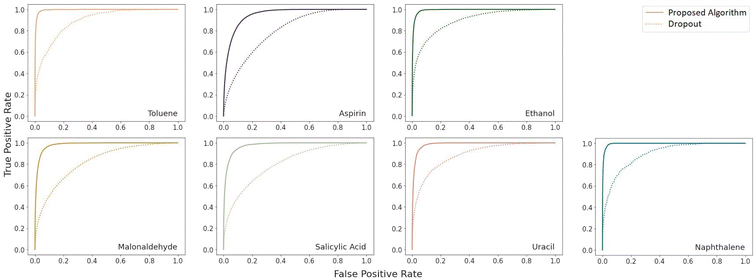
A very large difference in the performance of the models is found in the outlier detection task where the proposed algorithm consistently achieves ROC AUC scores much closer to the optimal score of 1 (Table 4). The benzene dataset was not included in this comparison because there were no instances of force prediction errors of the necessary scale for the proposed algorithm. A complete plot of the receiver operating characteristic curves is given in Fig. 3. As can be seen there, the proposed model is much more reliable at detecting outliers.
Lastly, as is evident from Fig. 4 the resulting model is not accurately calibrated in the case of 8 Monte Carlo samples and has a tendency for overconfidence.
A table with additional results for the energy predictions can be found in ESI Section A.†
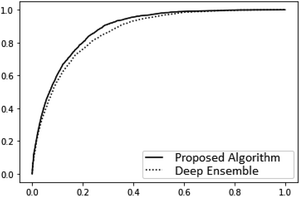 | ||
| Fig. 5 Receiver operating characteristic curves on the coupled cluster level ethanol force predictions for the deep ensemble and our proposed algorithm with k = 8 Monte Carlo samples. | ||
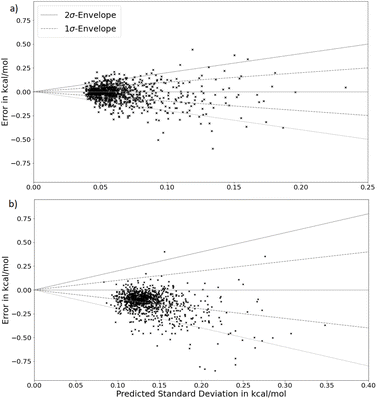
A significant difference in performance is found in the energy prediction task, where the proposed BNN model significantly outperforms the deep ensemble for the MAE (0.069 kcal mol−1vs. 0.142 kcal mol−1), RMSE (0.097 kcal mol−1vs. 0.191 kcal mol−1) and MLL (0.978 vs. 0.327).
As can be seen in Fig. 6, a clear trend for higher error variance for increasing predicted uncertainty is present. However, again a tendency for overconfidence is evident in both models, illustrated by an unusually high amount of points outside of the 2σ envelope. Lastly, a clear bias in the energy predictions is visible for the deep ensemble but not for the BNN, with energy predictions having a bias for being too low.
5 Conclusion and outlook
As the results demonstrate, the proposed Bayesian neural network model achieves all three conditions we used to assess the viability of combining state-of-the-art neural network architectures for interatomic force modeling with high-quality MCMC-based BNNs. Contrary to the results of Thaler et al.23 we found no evidence of reduced accuracy for models sampled from the Bayesian posterior, suggesting that the suboptimal performance in that work is due to the convergence issues of PSGLD.24 Instead, the accuracy is very consistent with what is achievable with non-Bayesian state-of-the-art neural networks. The proposed sampling algorithm appears to converge to the posterior distribution in a reasonable amount of time and maintains a fairly swift traversal through the parameter space afterward. Most importantly, the resulting model can detect outliers much more reliably than the commonly used dropout method while sampling parameters from the same Markov chain. Furthermore, on the coupled cluster-level ethanol benchmark, it outperforms a deep ensemble on all metrics. While the comparison to deep ensembles is limited to this benchmark due to the computational cost of generating deep ensembles, it provides evidence that our proposed method performs at least as well, if not better. In particular, the results on the energy predictions on that benchmark are quite promising, where a substantial performance difference was found. The reason for this might be, that the training dataset is fairly small and even though early stopping was used in the training of the ensemble models, overfitting might still be a problem. This would also explain the better result of the BNN, as BNNs are more robust to overfitting due to the noise added to the gradients.These results open up new possibilities for Bayesian active learning procedures for learning interatomic forces. Another interesting opportunity that could be built on top of these results is the principled incorporation of additional datasets in the Bayesian prior distribution. These datasets might have been created with lower accuracy but faster simulations or might be publicly available datasets from different molecules but labeled with the same simulation method. This might substantially improve the computational demand of creating machine learning force fields while simultaneously maintaining high-quality uncertainty quantification. While that approach is not widely studied in the literature, there are some papers where such methods yielded promising results.20,21
Even though the proposed model already achieves good results, some improvements could still be made.
While convergence to the posterior distribution becomes feasible with the proposed algorithm, in practice we find that it still takes a few days to reach convergence and generate all Monte Carlo samples (see ESI Section A† for more details on training times). However, given the time it takes to generate a suitable training dataset, such training times will not constitute a computational bottleneck in most applications. Furthermore, while it was useful for demonstrative purposes of the convergence properties of the proposed sampler, much faster convergence can most likely be achieved by simply reducing the injected gradient noise and the batch size during the initial phases of the optimization. An interesting aspect here is also that quick convergence was achieved without a locally adaptive step size for each parameter despite significant vanishing gradient problems of the neural network architecture. This is a promising sign, that the (global) parameter-specific adaptive step size approach we introduced here can also work in other BNN applications where vanishing gradients are an issue without the additional computational cost and convergence issues of locally adaptive methods.24
Of course, the inference time of eight Monte Carlo samples will be eight times as large as a single model prediction unless parallel implementations are used. However, even without parallel implementations, inference times can almost always be neglected when compared to the time of creating a training dataset.
Further, the stochastic model could potentially still be improved by adequate incorporation of covariances between atoms and also between force components. However, both of these covariances are challenging to include. For covariance between force components, the main challenge is to maintain rotation equivariance of the predicted density. For the incorporation of interatomic covariances, a dense covariance matrix will very quickly become impractical for larger molecules, as the evaluation of the log-likelihoods becomes a computational bottleneck. While a sparse covariance matrix might be adequate due to the mostly local nature of interatomic forces, a way to parameterize sparse covariance matrices would be needed, which is not trivial and which we could not find in the existing literature.
Lastly, we found that the predicted uncertainties are not always properly calibrated and have a tendency for overconfidence. This might be a result of sampling from the same Markov chain, where the models can never be completely independently sampled from each other. This can lead to a reduced predictive variance between the sampled models and hence increased confidence. Here it might be beneficial to recalibrate the uncertainties on a validation set.
Data availability
All datasets used for training and evaluating the neural network models in this paper as well as source code and in-depth illustrations on how the neural networks were trained and evaluated are available. The PEDOT datasets, source code and jupyter notebook files illustrating how the training and evaluation of the different models is done are included in the ESI file†. The RMD17 dataset is available at https://figshare.com/articles/dataset/Revised_MD17_dataset_rMD17_/12672038. The coupled cluster-level ethanol dataset is available at http://www.quantum-machine.org/gdml/data/npz/ethanol_ccsd_t.zip.Author contributions
T. R., O. N. and D. K. conceptualized the project. B. C. performed the DFT calculations for the PEDOT dataset. T. R. developed the MCMC sampling approach and performed the analysis under the supervision of O. N. T. R. wrote the original draft and D. K. and O. N. helped with reviewing and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research as part of the project CouplteIT! is funded by dtec.bw – Digitalization and Technology Research Center of the Bundeswehr which we gratefully acknowledge. dtec.bw is funded by the European Union – NextGenerationEU.Notes and references
- P. Atkins and R. Friedman, Molecular Quantum Mechanics, OUP Oxford, Oxford, 2011 Search PubMed.
- M. Gastegger and P. Marquetand, Machine Learning Meets Quantum Physics, 2020, vol. 1, pp. 233–252 Search PubMed.
- E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 2022, 73, 163–186 CrossRef CAS PubMed.
- J. Klicpera, F. Becker and S. Günnemann, Proceedings of the 35th International Conference on Neural Information Processing Systems, 2021, pp. 6790–6802 Search PubMed.
- O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Nat. Commun., 2021, 12, 7273, DOI:10.1038/s41467–021–27504–0.
- K. Schütt, O. Unke and M. Gastegger, Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 9377–9388 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453, DOI:10.1038/s41467–022–29939–5.
- M. Haghighatlari, J. Li, X. Guan, O. Zhang, A. Das, C. J. Stein, F. Heidar-Zadeh, M. Liu, M. Head-Gordon, L. Bertels, H. Hao, I. Leven and T. Head-Gordon, Digital Discovery, 2022, 1, 333–343 RSC.
- Z. Qiao, A. S. Christensen, M. Welborn, F. R. Manby, A. Anandkumar and T. F. Miller, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2205221119 CrossRef CAS PubMed.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi, Y. Asano, T. Onodera, T. Ishii, T. Kudo, H. Ono, R. Sawada, R. Ishitani, M. Ong, T. Yamaguchi, T. Kataoka, A. Hayashi, N. Charoenphakdee and T. Ibuka, Nat. Commun., 2022, 13, 2991, DOI:10.1038/s41467–022–30687–9.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- B. Hammer and J. Nørskov, Impact of Surface Science on Catalysis, Academic Press, 2000, vol. 45, pp. 71–129 Search PubMed.
- P. AU Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans, T. Sommer and P. Friederich, Commun. Mater., 2022, 3, 93, DOI:10.1038/s43246–022–00315–6.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- E. V. Podryabinkin, E. V. Tikhonov, A. V. Shapeev and A. R. Oganov, Phys. Rev. B, 2019, 99, 064114 CrossRef CAS.
- K. Gubaev, E. V. Podryabinkin, G. L. Hart and A. V. Shapeev, Comput. Mater. Sci., 2019, 156, 148–156 CrossRef CAS.
- R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, J. Phys. Chem. Lett., 2020, 11, 6946–6955 CrossRef CAS PubMed.
- A. Shapeev, K. Gubaev, E. Tsymbalov and E. Podryabinkin, Machine Learning Meets Quantum Physics, 2020, vol. 1, pp. 309–329 Search PubMed.
- J. I. T. Falk, L. Bonati, P. Novelli, M. Parrinello and M. pontil, Proceedings of the Thirty-seventh Conference on Neural Information Processing Systems, 2023, pp. 29783–29797 Search PubMed.
- C. H. Chen, P. Parashar, C. Akbar, S. M. Fu, M.-Y. Syu and A. Lin, IEEE Access, 2019, 7, 130168–130179 Search PubMed.
- R. Shwartz-Ziv, M. Goldblum, H. Souri, S. Kapoor, C. Zhu, Y. LeCun and A. G. Wilson, First Workshop on Pre-training: Perspectives, Pitfalls, and Paths Forward at ICML, 2022, https://openreview.net/forum?id=ao30zaT3YL Search PubMed.
- P. Izmailov, S. Vikram, M. D. Hoffman and A. G. G. Wilson, Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 4629–4640 Search PubMed.
- S. Thaler, G. Doehner and J. Zavadlav, J. Chem. Theory Comput., 2023, 4520–4532, DOI:10.1021/acs.jctc.2c01267.
- T. Rensmeyer and O. Niggemann, arXiv, 2024, preprint, arXiv:2403.08609, DOI:10.48550/arXiv.2403.08609.
- M. Wen and E. B. Tadmor, npj Comput. Mater., 2020, 6, 124 CrossRef.
- S.-H. Lee, V. Olevano and B. Sklénard, Solid-State Electron., 2022, 108508 Search PubMed.
- S. Thaler and J. Zavadlav, MATHMOD 2022 Discussion Contribution Volume, 2022, DOI:10.11128/arep.17.a17046.
- Y. Gal and Z. Ghahramani, Proceedings of the 33rd International Conference on International Conference on Machine Learning, 2016, pp. 1050–1059 Search PubMed.
- J. Yao, W. Pan, S. Ghosh and F. Doshi-Velez, Proceedings of the 36th International Conference on Machine Learning: Workshop on Uncertainty & Robustness in Deep Learning (ICML), 2019, https://finale.seas.harvard.edu/sites/scholar.harvard.edu/files/finale/files/quality_of_uncertainty_quantification_for_bayesian_neural_network_inference.pdf Search PubMed.
- C. Li, C. Chen, D. E. Carlson and L. Carin, Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, 2016, pp. 1788–1794 Search PubMed.
- O.-P. Koistinen, F. B. Dagbjartsdóttir, V. Ásgeirsson, A. Vehtari and H. Jónsson, J. Chem. Phys., 2017, 147, 152720 CrossRef PubMed.
- B. Kolb, P. Marshall, B. Zhao, B. Jiang and H. Guo, J. Phys. Chem. A, 2017, 121, 2552–2557 CrossRef CAS PubMed.
- J. Cui and R. V. Krems, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 224001 CrossRef.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- J. Vandermause, S. B. Torrisi, S. L. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, npj Comput. Mater., 2019, 6, 1–11 Search PubMed.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
- A. P. Soleimany, A. Amini, S. Goldman, D. Rus, S. N. Bhatia and C. W. Coley, ACS Cent. Sci., 2021, 7, 1356–1367 CrossRef CAS PubMed.
- S. Ruder, arXiv, 2017, preprint, arXiv:1609.04747, DOI:10.48550/arXiv.1609.04747.
- Y.-A. Ma, T. Chen and E. Fox, Proceedings of the 28th International Conference on Neural Information Processing Systems – Volume 2, 2015, pp. 2917–2925 Search PubMed.
- T. Chen, E. Fox and C. Guestrin, Proceedings of the 31st International Conference on Machine Learning, 2014, pp. 1683–1691 Search PubMed.
- D. P. Kingma and J. Ba, arXiv, 2015, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- S. J. Reddi, S. Kale and S. Kumar, arXiv, 2018, preprint, arXiv: 1904.09237, DOI:10.48550/arXiv.1904.09237.
- M. N. Gueye, A. Carella, N. Massonnet, E. Yvenou, S. Brenet, J. Faure-Vincent, S. Pouget, F. Rieutord, H. Okuno, A. Benayad, R. Demadrille and J.-P. Simonato, Chem. Mater., 2016, 28, 3462–3468 CrossRef CAS.
- T.-H. Le, Y. Kim and H. Yoon, Polymers, 2017, 9, 150, DOI:10.3390/polym9040150.
- M. N. Gueye, A. Carella, J. Faure-Vincent, R. Demadrille and J.-P. Simonato, Prog. Mater. Sci., 2020, 108, 100616 CrossRef CAS.
- N. S. Hudak, J. Phys. Chem. C, 2014, 118, 5203–5215 CrossRef CAS.
- I. Zozoulenko, A. Singh, S. K. Singh, V. Gueskine, X. Crispin and M. Berggren, ACS Appl. Polym. Mater., 2019, 1, 83–94 CrossRef CAS.
- K. Ando, S. Watanabe, S. Mooser, E. Saitoh and H. Sirringhaus, Nat. Mater., 2013, 12, 622–627 CrossRef CAS PubMed.
- A. S. Christensen and O. A. von Lilienfeld, Mach. Learn.: Sci. Technol., 2020, 1, 045018 Search PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2019, 11, 5223 CrossRef PubMed.
- M. Henne, A. Schwaiger, K. Roscher and G. Weiss, Proceedings of the Workshop on Artificial Intelligence Safety, SafeAI 2020, 2020, DOI:10.24406/publica–fhg–407174.
- M. P. Naeini, G. F. Cooper and M. Hauskrecht, Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, 2015, pp. 2901–2907 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00183d |
| ‡ Several MCMC algorithms have been proposed that use adaptive step sizes without using those higher-order derivative terms. However, none of them converge close to the correct distribution as was shown in ref. 24. |
| This journal is © The Royal Society of Chemistry 2024 |

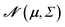
![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif)