Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis, magnetic and NMR spectroscopic properties of the MAl5Pt3 series (M = Ca, Y, La–Nd, Sm–Er)†
Stefan
Engel
 a,
Elias C. J.
Gießelmann
a,
Elias C. J.
Gießelmann
 a,
Lars
Schumacher
a,
Lars
Schumacher
 b,
Yuemei
Zhang
b,
Yuemei
Zhang
 c,
Frank
Müller
d and
Oliver
Janka
c,
Frank
Müller
d and
Oliver
Janka
 *a
*a
aInorganic Solid State Chemistry, Saarland University, Campus C4 1, 66123 Saarbrücken, Germany. E-mail: oliver.janka@uni-saarland.de
bInstitut für Anorganische und Analytische Chemie, Universität Münster, Corrensstrasse 28/30, 48149 Münster, Germany
cDepartment of Chemistry and Physics, Warren Wilson College, Swannanoa, NC 28778, USA
dExperimental Physics and Center for Biophysics, Saarland University, Campus E2 9, 66123 Saarbrücken, Germany
First published on 24th June 2024
Abstract
Following recent investigation in the ternary system Sr–Al–Pt led to the discovery of SrAl5Pt3 which crystallizes in the orthorhombic YNi5Si3 type (Pnma) structure. Interestingly, only two more aluminum representatives, CeAl5Pt3 and EuAl5Pt3, have been reported to adopt this structure type. Therefore, we decided to investigate the existence range of compounds adopting the YNi5Si3 type structure. Besides the already known Sr, Ce and Eu members, the series could be extended to Ca, Y and La–Nd as well as Sm–Er. All compounds were synthesized from the elements and characterized by powder X-ray diffraction. While for CaAl5Pt3 and LaAl5Pt3 also the respective M2Al16Pt9 members were observed, the other compounds could be obtained either as X-ray pure materials or with small amounts of Al3Pt2 as a side phase. The structure of ErAl5Pt3 could be refined from single crystal data, verifying that also the small rare-earth elements adopt the YNi5Si3 type structure. Selected members of the series were furthermore characterized by magnetization and susceptibility measurements. Since YAl5Pt3 could be obtained as a phase pure material and exhibits no paramagnetic behaviour it was investigated by 27Al MAS NMR investigations. Also, XPS measurements were conducted on this compound to gain an insight into the charge distribution. Finally, quantum-chemical calculations supported the NMR measurements and gave an insight into the chemical bonding and the charge distribution.
1 Introduction
Cerium, europium and ytterbium intermetallics often exhibit interesting physical properties due to their two possible oxidation states. For cerium Ce3+ ([Xe] 4f1) and Ce4+ ([Xe] 4f0) are known while europium exhibits Eu3+ ([Xe] 4f6) and Eu2+ ([Xe] 4f7) and ytterbium Yb3+ ([Xe] 4f13) and Yb2+ ([Xe] 4f14). Of these, Ce4+ and Yb2+ are diamagnetic due to their empty and full 4f shell, respectively.1,2 Eu2+ has a half-filled 4f shell (S = 7/2, isoelectronic to Gd3+) and therefore exhibits a high magnetic moment of μtheo = 7.94μB. For Eu3+ (S = 3, L = 3) in total seven states of the multiplet 7FJ exist with the ground state being 7F0. The ground state is diamagnetic due to spin–orbit coupling. However, the lowest state is only solely considered when the separation of the multiplet components is sufficiently large compared to kBT. Therefore, the contributions of the different components of the multiplet have to be taken into account for higher temperatures. The paramagnetic susceptibility can be expressed with the help of the Van Vleck theory.3 The availability of a second oxidation state, however, can result in numerous interesting physical phenomena. Static mixed valence states can be found (Eu3O4,4–6 Eu3S4,7 or EuPPt8) as well as intermetallic valence fluctuation materials (e.g. CeAl3,9,10 Yb4Ga24Pt9,11 CeMo2Si2C,12 CeAlRu1−xNix,13 Ce2Sn5Rh3,14 CeCu2Si2,15 EuCu2Si2,15,16 YbCu2Si2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15). A rather rare feature is a temperature or pressure dependent valence phase transition. Well known transitions of this type are e.g. the ones from metallic α-Ce to γ-Ce,17 where electron localization takes place, accompanied by a drastic volume effect. In EuPPt,18 EuCo2As2 and YbAl3 pressure dependent shifts of the Eu/Yb valence are observed.19,20 Finally, CeNi1−xCoxSn,21 and Yb1−xInxCu222–24 exhibit at least partial temperature dependent valence phase transitions. EuSi2Pd2,25,26 EuSi2(Ir1−xPdx)2,27 EuSi2(Pd1−xAux)2,28 Eu2Al15Pt6
15). A rather rare feature is a temperature or pressure dependent valence phase transition. Well known transitions of this type are e.g. the ones from metallic α-Ce to γ-Ce,17 where electron localization takes place, accompanied by a drastic volume effect. In EuPPt,18 EuCo2As2 and YbAl3 pressure dependent shifts of the Eu/Yb valence are observed.19,20 Finally, CeNi1−xCoxSn,21 and Yb1−xInxCu222–24 exhibit at least partial temperature dependent valence phase transitions. EuSi2Pd2,25,26 EuSi2(Ir1−xPdx)2,27 EuSi2(Pd1−xAux)2,28 Eu2Al15Pt6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 and YbAl3Pd2
29 and YbAl3Pd2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 all show valence phase transitions in different expressions. Some review articles summarize at least some aspects of intermetallic cerium,31–36 europium37 and ytterbium38 intermetallics.
30 all show valence phase transitions in different expressions. Some review articles summarize at least some aspects of intermetallic cerium,31–36 europium37 and ytterbium38 intermetallics.
Recently, we reported on a new compound in the ternary system Sr–Al–Pt, SrAl5Pt3,39 which adopts the orthorhombic YNi5Si3 type structure (Pnma).40 It is furthermore isostructural to CeAl5Pt3 and EuAl5Pt3. The europium compound shows antiferromagnetic ordering and an interesting change in electronic states under pressure.41 Since three compounds are known to crystallize in the same structure type, the question arose if other rare-earth or alkaline-earth members can be synthesized. Here we report that the series could be extended to Ca, Y and La–Nd as well as Sm–Er. All compounds were synthesized from the elements and characterized by powder X-ray diffraction. The structure of ErAl5Pt3 was refined from single crystal data, YAl5Pt3 was investigated by 27Al MAS NMR measurements. Furthermore, XPS measurements were conducted on YAl5Pt3 and Al3Pt2 and quantum-chemical calculations supported the NMR measurements and gave an insight into the chemical bonding and the charge distribution.
2 Experimental
2.1 Synthesis
All members of the MAl5Pt3 series were prepared from the elements using calcium pieces (Onyxmet), rare earth ingots (Onyxmet), platinum (Agosi AG) and aluminum pieces (Onyxmet), all with stated purities above 99.5%. Samples were prepared on a 100 to 150 mg scale. The early rare earth elements were stored under an argon atmosphere in a dry box (MBraun, Garching, Germany). In all cases, the starting materials were arc-melted42 in a custom build arc-melting apparatus in a water-cooled copper hearth under 800 mbar argon pressure using the ideal ratios of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt (1
Pt (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). To achieve homogeneous samples, the arc-melting was repeated three times and the buttons were turned over in between. For calcium and europium, the pieces were wrapped in aluminum foil (Alujet, Mammendorf, Germany). In all cases, no significant evaporation was observed, as determined by weighing the arc-melted beads after the reaction. The argon gas was purified over a titanium sponge (873 K), molecular sieves, activated carbon and silica gel prior to the use. Subsequently, the samples were enclosed in evacuated silica tubes and annealed in muffle furnaces. They were heated to 973 K within two hours and then kept at this temperature for 14 days. Afterwards they were cooled to room temperature with 2 K h−1. All samples are metallic, ground powders (particle size >100 μm) are grey and insensitive to air over months.
3). To achieve homogeneous samples, the arc-melting was repeated three times and the buttons were turned over in between. For calcium and europium, the pieces were wrapped in aluminum foil (Alujet, Mammendorf, Germany). In all cases, no significant evaporation was observed, as determined by weighing the arc-melted beads after the reaction. The argon gas was purified over a titanium sponge (873 K), molecular sieves, activated carbon and silica gel prior to the use. Subsequently, the samples were enclosed in evacuated silica tubes and annealed in muffle furnaces. They were heated to 973 K within two hours and then kept at this temperature for 14 days. Afterwards they were cooled to room temperature with 2 K h−1. All samples are metallic, ground powders (particle size >100 μm) are grey and insensitive to air over months.
2.2 X-ray diffraction
The pulverized samples were investigated at room temperature on a D8-A25-Advance diffractometer (Bruker, Karlsruhe, Germany) in Bragg–Brentano θ–θ-geometry (goniometer radius 280 mm) with Cu Kα-radiation (λ = 154.0596 pm). Diffraction patterns were recorded between 6 and 130° 2θ with a step size of 0.013° and a total scan time of 1 h. A 12 μm Ni foil working as Kβ filter and a variable divergence slit were mounted at the primary beam side. A LYNXEYE detector with 192 channels was used at the secondary beam side. The recorded data was evaluated using the Bruker TOPAS 5.0 software,43 with the observed reflections being treated via single-line fits. The refined lattice parameters are given in Table 1. Powder patterns of all samples are depicted in Fig. S1–S12.†| Compound | a (pm) | b (pm) | c (pm) | V (nm3) | Ref. |
|---|---|---|---|---|---|
| a This work; L literature data; P powder data; SC single crystal data. | |||||
| CaAl5Pt3 | 2050.3(1) | 409.0(1) | 736.4(1) | 0.6175 | |
| SrAl5Pt3L,SC | 2065.04(7) | 413.74(1) | 738.98(3) | 0.6314 | 39 |
| SrAl5Pt3L,P | 2067.07(6) | 414.16(2) | 739.88(3) | 0.6334 | 39 |
| YAl5Pt3P | 2052.8(1) | 406.7(1) | 728.7(1) | 0.6084 | |
| LaAl5Pt3P | 2068.7(1) | 415.5(1) | 732.2(1) | 0.6293 | |
| CeAl5Pt3L | 2065.1(4) | 413.81(8) | 728.42(15) | 0.6225 | 40 |
| CeAl5Pt3P | 2063.9(1) | 414.0(1) | 730.1(1) | 0.6239 | |
| PrAl5Pt3P | 2061.4(2) | 413.0(1) | 729.6(1) | 0.6212 | |
| NdAl5Pt3P | 2059.9(1) | 412.1(1) | 729.3(1) | 0.6190 | |
| SmAl5Pt3P | 2057.0(1) | 410.2(1) | 728.5(1) | 0.6148 | |
| EuAl5Pt3L | 2066.2(3) | 412.58(6) | 738.16(11) | 0.6293 | 41 |
| GdAl5Pt3P | 2055.3(2) | 408.7(1) | 728.3(2) | 0.6117 | |
| TbAl5Pt3P | 2052.9(1) | 407.7(1) | 728.2(1) | 0.6095 | |
| DyAl5Pt3P | 2051.5(1) | 406.7(1) | 728.5(1) | 0.6079 | |
| HoAl5Pt3P | 2050.4(1) | 405.9(1) | 729.1(1) | 0.6067 | |
| ErAl5Pt3P | 2048.4(1) | 405.1(1) | 729.3(1) | 0.6052 | |
| ErAl5Pt3SC | 2045.82(6) | 404.40(1) | 728.45(2) | 0.6027 | |
| CaGa5Pt3L | 2082.5(4) | 406.05(8) | 739.2(1) | 0.6251 | 44 |
| SrGa5Pt3L | 2092.3(1) | 413.16(2) | 740.88(3) | 0.6404 | 45 |
| BaGa5Pt3L | 2104.8(2) | 420.15(4) | 747.7(1) | 0.6612 | 44 |
| BaGa5Pt3L | 2104.3(2) | 420.11(5) | 747.80(8) | 0.6611 | 45 |
| EuGa5Pt3L | 2085.5(5) | 412.75(9) | 738.7(1) | 0.6359 | 44 |
Lath shaped crystal fragments of ErAl5Pt3 were obtained from the as-cast buttons. The crystals were glued to glass fibers using beeswax. An intensity data set of a suitable crystal was collected at room temperature using a Bruker X8 APEX2 diffractometer (Bruker, Karlsruhe, Germany). A multi-scan absorption correction using SadABS46 was applied to the data set. All relevant crystallographic data, deposition and details of the data collection and evaluation are listed in Tables 2–4.
| CSD number | 2349082 |
| Sum formula | ErAl5Pt3 |
| Formula weight, g mol−1 | 887.4 |
| Lattice parameters | see Table 1 |
| Calcd density, g cm−3 | 9.78 |
| Crystal size, μm3 | 120 × 40 × 30 |
| Diffractometer | Bruker X8 APEX2 |
| Wavelength; λ, pm | 0.71073 |
| Absorption correction | Multi-scan |
| Bruker SadABS | |
| Abs. coefficient, mm−1 | 83.8 |
| F(000), e | 1468 |
| θ range, ° | 2.97–33.15 |
| Range hkl | −31, +21; ±6; −10, +11 |
| Total no. reflections | 8867 |
| Independent reflections/Rint | 1279/0.0636 |
| Reflections I > 3σ(I)/Rσ | 950/0.0494 |
| Data/parameters | 1279/56 |
| Goodness of fit on F2 | 1.09 |
| R 1/wR2 for I > 3σ(I) | 0.0291/0.0594 |
| R 1/wR2 (all data) | 0.0457/0.0650 |
| Extinction coefficient | 31(7) |
| Extinction scheme | Lorentzian isotropic47 |
| Larg. diff. peak/hole, e Å−3 | +3.64/−2.64 |
| Atom | x | z | U 11 | U 22 | U 33 | U 13 |
U
eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|---|---|---|---|---|---|---|---|
| a The isotropic displacement parameter Ueq is defined as: Ueq = 1/3 (U11 + U22 + U33) (pm2); U12 = U23 = 0. Standard deviations are given in parentheses. | |||||||
| Er | 0.36014(3) | 0.87991(8) | 81(3) | 74(3) | 101(3) | 7(2) | 85(3) |
| Al1 | 0.0076(2) | 0.3702(5) | 57(2) | 67(2) | 71(3) | −1(2) | 65(2) |
| Al2 | 0.2011(2) | 0.6766(5) | 54(2) | 60(2) | 82(2) | 1(2) | 65(2) |
| Al3 | 0.2081(2) | 0.0610(5) | 70(2) | 50(2) | 69(2) | 1(2) | 63(2) |
| Al4 | 0.3809(2) | 0.3553(5) | 55(17) | 54(18) | 68(18) | −5(13) | 59(18) |
| Al5 | 0.4842(2) | 0.6168(5) | 70(17) | 79(19) | 47(18) | −6(13) | 65(18) |
| Pt1 | 0.07482(2) | 0.65917(7) | 73(17) | 36(18) | 78(19) | 16(14) | 62(18) |
| Pt2 | 0.08523(2) | 0.08160(7) | 24(16) | 18(16) | 76(18) | 5(13) | 39(17) |
| Pt3 | 0.25819(2) | 0.36976(7) | 57(17) | 69(18) | 87(19) | −1(14) | 71(18) |
| Er | 2 | Pt3 | 315.5 | Al1 | 1 | Pt1 | 251.4 |
| 2 | Pt1 | 316.2 | 1 | Pt2 | 263.4 | ||
| 2 | Pt2 | 317.2 | 2 | Pt1 | 264.1 | ||
| 1 | Al5 | 318.0 | 2 | Al5 | 274.3 | ||
| 2 | Al2 | 321.4 | 2 | Al1 | 278.6 | ||
| 1 | Al3 | 337.8 | 1 | Al4 | 306.9 | ||
| 2 | Al1 | 337.8 | Al2 | 1 | Pt3 | 252.1 | |
| 2 | Al3 | 338.2 | 1 | Pt1 | 258.9 | ||
| 1 | Al4 | 348.9 | 2 | Pt3 | 260.0 | ||
| 1 | Al1 | 352.4 | 1 | Al3 | 280.4 | ||
| 1 | Al2 | 357.3 | 2 | Al3 | 287.1 | ||
| Pt1 | 1 | Al5 | 246.9 | 2 | Al4 | 293.3 | |
| 1 | Al1 | 251.4 | Al3 | 1 | Pt3 | 247.2 | |
| 1 | Al2 | 258.9 | 1 | Pt2 | 251.9 | ||
| 2 | Al4 | 263.6 | 2 | Pt3 | 255.0 | ||
| 2 | Al1 | 264.1 | 1 | Al2 | 280.4 | ||
| 1 | Pt2 | 308.4 | 2 | Al2 | 287.1 | ||
| Pt2 | 2 | Al5 | 248.4 | 2 | Al4 | 310.7 | |
| 1 | Al3 | 251.9 | Al4 | 1 | Pt3 | 251.3 | |
| 1 | Al5 | 252.2 | 2 | Pt1 | 263.6 | ||
| 1 | Al1 | 263.4 | 2 | Pt2 | 269.9 | ||
| 2 | Al4 | 269.9 | 1 | Al5 | 284.4 | ||
| 1 | Pt1 | 308.4 | 2 | Al2 | 293.3 | ||
| Pt3 | 1 | Al3 | 247.2 | 1 | Al1 | 306.9 | |
| 1 | Al4 | 251.3 | 2 | Al3 | 310.7 | ||
| 1 | Al2 | 252.1 | 2 | Al5 | 342.7 | ||
| 2 | Al3 | 255.0 | Al5 | 1 | Pt1 | 246.9 | |
| 2 | Al2 | 260.0 | 2 | Pt2 | 248.4 | ||
| 1 | Pt2 | 252.2 | |||||
| 2 | Al5 | 272.1 | |||||
| 2 | Al1 | 274.3 | |||||
| 1 | Al4 | 284.4 |
CSD 2349082 contains the supplementary crystallographic data for this paper.†
2.3 Scanning electron microscopy
The powdered bulk samples of NdAl5Pt3, GdAl5Pt3 and ErAl5Pt3 were attached to a sticky carbon tape and semiquantitatively analyzed in a JEOL 7000F (Jeol, Freising, Germany) scanning electron microscope (SEM) equipped with an EDAX Genesis 2000 energy-dispersive X-ray spectroscopy (EDX) detector (EDAX, Unterschleissheim, Germany). Results are listed in Table 5.| Compound | RE (at%) | Al (at%) | Pt (at%) |
|---|---|---|---|
| Ideal composition | 11.1 | 55.6 | 33.3 |
| NdAl5Pt3 | 10 | 55 | 35 |
| GdAl5Pt3 | 11 | 53 | 36 |
| ErAl5Pt3 | 11 | 55 | 34 |
2.4 Magnetic measurements
Annealed pieces or powder of the respective X-ray pure REAl5Pt3 (RE = Y, Ce–Nd, Gd–Ho) samples were attached to the sample holder rod of a Vibrating Sample Magnetometer (VSM) using Kapton-foil or PE capsules for measuring the magnetization M(H,T) in a Quantum Design Physical Property Measurement System (PPMS2) or a Quantum Design PPMS DynaCool system. All samples were investigated in the temperature range of 3–300 K or 1.9–300 K with applied external magnetic fields of up to 80/90 kOe. The results of the magnetic measurements are given in Table 6.| Compound | T N (K) | μ eff (μB) | μ theo (μB) | θ P (K) | H crit (kOe) | μ sat (μB/RE3+) | g J × J (μB/RE3+) |
|---|---|---|---|---|---|---|---|
| a 1.8 K, 90 kOe. b 3 K, 80 kOe. | |||||||
| YAl5Pt3 | Pauli-paramagnetic, non-superconducting, χ(300 K) = +8.63(1) × 10−5 emu mol−1 | ||||||
| CeAl5Pt3 | — | 2.76(1) | 2.54 | −41(1) | — | 0.99(1)a | 2.14 |
| PrAl5Pt3 | — | 3.69(1) | 3.58 | −13(1) | 4.4(1) | 2.28(1)b | 3.20 |
| NdAl5Pt3 | 5.1(1) | 3.82(1) | 3.62 | +18(1) | 26.7(1) | 2.98(1)a | 3.27 |
| GdAl5Pt3 | 8.7(1) | 7.99(1) | 7.94 | −7(1) | — | 2.98(1)a | 7 |
| TbAl5Pt3 | 15.3(1) | 9.49(1) | 9.72 | +16(1) | 33.2(1) | 5.36(1)a | 9 |
| DyAl5Pt3 | 5.8(1) | 10.83(1) | 10.65 | +9(1) | 9.8(1) | 7.85(1)b | 10 |
| HoAl5Pt3 | 2.4(1) | 10.95(1) | 10.61 | +19(1) | 5.1(1) | 8.78(1)a | 10 |
2.5 27Al solid-state NMR spectroscopy
The 27Al MAS-NMR spectra of YAl5Pt3 were recorded at 104.31 MHz on an Avance III 400 WB spectrometer (Bruker, Billerica, US; 9.4 T) using magic-angle spinning (MAS) conditions. The sample was ground to a fine powder and mixed with an appropriate amount of NaCl (sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaCl = 1
NaCl = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9), to reduce the density and the electrical conductivity of the sample. The diluted sample was loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with a frequency of 10/13 kHz. A single-pulse experiment with a typical pulse length of 0.83 μs and a relaxation delay of 1 s was conducted. Resonance shifts were referenced to aqueous 1 molar AlCl3 solutions. The NMR-spectra were recorded using the Bruker TOPSPIN software,48 the analysis was performed with the help of the DMFIT program package.49 The extracted data is compiled in Table 7.
9), to reduce the density and the electrical conductivity of the sample. The diluted sample was loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with a frequency of 10/13 kHz. A single-pulse experiment with a typical pulse length of 0.83 μs and a relaxation delay of 1 s was conducted. Resonance shifts were referenced to aqueous 1 molar AlCl3 solutions. The NMR-spectra were recorded using the Bruker TOPSPIN software,48 the analysis was performed with the help of the DMFIT program package.49 The extracted data is compiled in Table 7.
| Site | δ | FWHM | C Q,calc | η Q,theo |
|---|---|---|---|---|
| Signal 1 | 693 | 31 | — | — |
| Signal 2 | 642 | 24 | — | — |
| Signal 3 | 602 | 13 | — | — |
| Signal 4 | 567 | 17 | — | — |
| Signal 5 | 510 | 14 | — | — |
| Al1 (4c) | — | — | −2484 | 0.771 |
| Al2 (4c) | — | — | −1642 | 0.523 |
| Al3 (4c) | — | — | −2302 | 0.425 |
| Al4 (4c) | — | — | +3819 | 0.519 |
| Al5 (4c) | — | — | +5487 | 0.690 |
2.6 X-ray photoelectron spectroscopy (XPS)
For XPS experiments an ESCALab Mk II spectrometer by Vacuum Generators with non-monochromatic Al-Kα radiation (ħω = 1486.6 eV) was used. The original 150°-type hemispherical analyzer with a three channeltron detector system was replaced by a 180°-type PreVac EA 15 analyzer with a multichannelplate detector. All spectra were recorded in normal emission mode (polar angle ϑ = 0°) at a pass energy of 50 eV for survey spectra and 20 eV for detail spectra. The step widths in binding energy were 1.0 eV for survey spectra and 100 meV for detail spectra.Powders of Al3Pt2 and YAl5Pt3 were pressed to pellets (diameter approx. 4 mm) and glued by a conductive carbon tape on an Al sample holder (diameter slightly lower than 4 mm to avoid spectral features from the sample holder and the tape). Due to the strong charging of the Al3Pt2 and YAl5Pt3 samples the C 1s peak was used for calibration of the binding energy EB, i.e. all spectra were shifted in binding energy by Δ = EB(C 1s) − EB(C 1sHOPG) with EB(C 1sHOPG) = 284.3 eV as probed on an in situ cleaved HOPG sample (Highly Oriented Pyrolytic Graphite). Pt 4f and Al 2s reference spectra were recorded on a sample from a Pt foil (cleaned by Ar ion etching) and an Al sheet (with the oxide only partially removed by Ar ion etching), respectively.
2.7 Quantum-chemical calculations
Density functional theory (DFT) calculations of YAl5Pt3 were performed using the projector augmented wave method (PAW) of Blöchl50,51 coded in the Vienna ab initio simulation package (VASP).52,53 All VASP calculations employed the generalized gradient approximation (GGA) with exchange and correlation treated by Perdew-Burke-Enzerhof (PBE).54 The cut-off energy for the plane wave calculations was set to 500 eV and the Brillouin zone integration was carried out using 3 × 15 × 9 k-point meshes. NMR parameters were evaluated through the field gradient tensor calculations in VASP with the nuclear quadrupole moment of 146.6 mb for 27Al. The Bader charge analysis was based on VASP calculations with subsequent calculations using the Bader program developed by the Henkelman group.55–57 Results of the Bader charge calculations are listed in Table 8. Chemical bonding was assessed via crystal orbital Hamiltonian population (COHP) analysis using the Stuttgart version of the tight-binding, linear muffin-tin orbital (TB-LMTO) method with the atomic spheres approximation.58 Within TB-LMTO, exchange and correlation were treated using the von Barth-Hedin local density approximation (LDA). All relativistic effects except for spin–orbit coupling were taken into account using a scalar relativistic approximation.59 The basis sets were 5s/(5p)/4d/(4f) for Y, 6s/6p/5d/(5f) for Pt, and 3s/3p/(3d) for Al, with orbitals in parentheses down-folded.60 The Brillouin zone was sampled by 280 k-points. Results of bonding analysis are summarized in Table 9.| YAl5Pt3 | Y | Al1 | Al2 | Al3 | Al4 | Al5 | Pt1 | Pt2 | Pt3 |
|---|---|---|---|---|---|---|---|---|---|
| Charge | +1.25 | +0.76 | +0.79 | +0.91 | +0.93 | +0.93 | −1.80 | −1.80 | −1.98 |
| Interaction | Counts | Distance | ICOHP/bond | ICOHP/f.u. |
|---|---|---|---|---|
| Y–Pt1 | 2 | 318.1 | −0.65 | −1.30 |
| Y–Pt2 | 2 | 319.2 | −0.65 | −1.30 |
| Y–Pt3 | 2 | 318.2 | −0.62 | −1.23 |
| Y–Al1 | 2 | 339.3 | −0.40 | −0.81 |
| 1 | 353.3 | −0.30 | −0.30 | |
| Y–Al2 | 2 | 322.5 | −0.51 | −1.02 |
| 1 | 358.5 | −0.29 | −0.29 | |
| Y–Al3 | 2 | 336.4 | −0.48 | −0.95 |
| 1 | 339.8 | −0.37 | −0.37 | |
| Y–Al4 | 1 | 347.6 | −0.36 | −0.36 |
| Y–Al5 | 1 | 319.0 | −0.46 | −0.46 |
| Sum | −8.40 (14.3%) | |||
| Pt1–Al1 | 1 | 251.9 | −2.19 | −2.19 |
| 2 | 264.8 | −1.74 | −3.48 | |
| Pt1–Al2 | 1 | 259.3 | −1.96 | −1.96 |
| Pt1–Al4 | 2 | 263.7 | −1.91 | −3.81 |
| Pt1–Al5 | 1 | 246.2 | −2.25 | −2.25 |
| Pt2–Al1 | 1 | 264.0 | −1.80 | −1.80 |
| Pt2–Al3 | 1 | 252.5 | −2.36 | −2.36 |
| Pt2–Al4 | 2 | 270.8 | −1.73 | −3.47 |
| Pt2–Al5 | 2 | 249.1 | −2.17 | −4.35 |
| 1 | 252.1 | −2.05 | −2.05 | |
| Pt3–Al2 | 1 | 252.9 | −2.07 | −2.07 |
| 2 | 261.2 | −1.81 | −3.63 | |
| Pt3–Al3 | 1 | 247.7 | −2.21 | −2.21 |
| 2 | 255.8 | −1.98 | −3.97 | |
| Pt3–Al4 | 1 | 250.2 | −2.32 | −2.32 |
| Sum | −39.6 (67.4%) | |||
| Pt1–Pt2 | 1 | 306.5 | −0.65 | −0.65 |
| Sum | −0.65 (1.10%) | |||
| Al1–Al1 | 2 | 279.5 | −1.09 | −2.19 |
| Al1–Al4 | 1 | 306.8 | −0.63 | −0.63 |
| Al1–Al5 | 2 | 275.2 | −1.14 | −2.29 |
| Al2–Al3 | 1 | 282.4 | −0.84 | −0.84 |
| 2 | 288.7 | −0.84 | −1.68 | |
| Al2–Al4 | 2 | 292.5 | −0.80 | −1.61 |
| Al3–Al4 | 2 | 314.0 | −0.41 | −0.82 |
| Al4–Al5 | 2 | 284.8 | −0.98 | −1.95 |
| 1 | 344.0 | −0.07 | −0.07 | |
| Al5–Al5 | 2 | 272.9 | −0.11 | −0.22 |
| Sum | −10.1 (17.2%) | |||
| Overall ICOHP | −58.8 |
3 Results
3.1 Powder X-ray diffraction
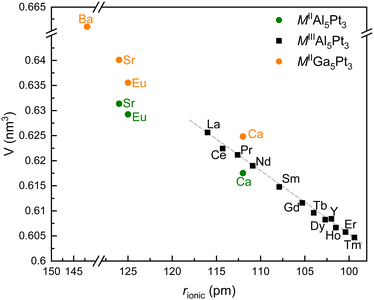
All samples were prepared with the nominal composition of MAl5Pt3 (M = Ca, Y, La–Nd, Sm–Er) in analogy to SrAl5Pt3,39 EuAl5Pt3,41 and CeAl5Pt3.40 The powder X-ray diffraction patterns clearly indicate the formation of the title compounds as well as them being isostructural to their Sr/Eu/Ce analogues. Most of the compounds could be obtained as X-ray pure materials crystallizing in the orthorhombic YNi5Si3 type structure (Pnma).61 But especially for lanthanum and calcium, orthorhombic M2Al16Pt9 (Immm, Ce2Al16Pt9 type)62 could be identified as a side phase. In some cases, also trigonal Al3Pt2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, Al3Ni2 type)63,64 was observed as binary by-product. In many cases, annealing led to X-ray pure samples or a drastic reduction of the Al3Pt2 amounts to <2 mass%. Fig. 1 depicts the trend of the unit cell volumes plotted versus the ionic radius of the respective metal ions. Most of the rare earth cations exhibit a trivalent oxidation state, however, europium and the alkaline earth metals are divalent in these compounds as can be seen from the significantly larger unit cell volumes. Also, the isostructural MGa5Pt3 (M = Ca, Sr, Eu, Ba)44,45 exhibit slightly larger unit cells as shown in Table 1 and Fig. 1.
m1, Al3Ni2 type)63,64 was observed as binary by-product. In many cases, annealing led to X-ray pure samples or a drastic reduction of the Al3Pt2 amounts to <2 mass%. Fig. 1 depicts the trend of the unit cell volumes plotted versus the ionic radius of the respective metal ions. Most of the rare earth cations exhibit a trivalent oxidation state, however, europium and the alkaline earth metals are divalent in these compounds as can be seen from the significantly larger unit cell volumes. Also, the isostructural MGa5Pt3 (M = Ca, Sr, Eu, Ba)44,45 exhibit slightly larger unit cells as shown in Table 1 and Fig. 1.
3.2 Single crystal X-ray diffraction and structure refinement
Analysis of the obtained single crystal X-ray diffraction data of ErAl5Pt3 revealed an orthorhombic lattice and space group Pnma was found to be correct. The structure was solved using the charge flipping algorithm of Superflip65 and a least squares refinement on F2 using the program Jana2006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66,67 was carried out. All atomic positions were refined with anisotropic displacement parameters and as a check for correct compositions, the occupancy parameters were refined in a separate series of least-square refinements. All sites were fully occupied within three standard deviations leading to the targeted compositions. Final difference Fourier syntheses were contour less. From the Pearson database,68 isotypism with CeAl5Pt3
66,67 was carried out. All atomic positions were refined with anisotropic displacement parameters and as a check for correct compositions, the occupancy parameters were refined in a separate series of least-square refinements. All sites were fully occupied within three standard deviations leading to the targeted compositions. Final difference Fourier syntheses were contour less. From the Pearson database,68 isotypism with CeAl5Pt3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 adopting the YNi5Si3 type61 was deduced. In contrast to UFe5As3 and related compounds no twinning was observed.69 Details of the structure determination, atomic parameters and interatomic distances can be found in Tables 2–4. When looking at the refined anisotropic displacement parameters (ADP) of the atoms, Er exhibits a value of 85 pm2, which is larger than the one of Pt and Al. This might be explained by the fact that ErAl5Pt3 is the last compound of this series, leading to the assumption that the Er atoms rattle inside the cavities of the polyanionic framework, leading to an increased ADP.
40 adopting the YNi5Si3 type61 was deduced. In contrast to UFe5As3 and related compounds no twinning was observed.69 Details of the structure determination, atomic parameters and interatomic distances can be found in Tables 2–4. When looking at the refined anisotropic displacement parameters (ADP) of the atoms, Er exhibits a value of 85 pm2, which is larger than the one of Pt and Al. This might be explained by the fact that ErAl5Pt3 is the last compound of this series, leading to the assumption that the Er atoms rattle inside the cavities of the polyanionic framework, leading to an increased ADP.
CSD 2349082 contains the supplementary crystallographic data for this paper.†
3.3 Crystal chemistry
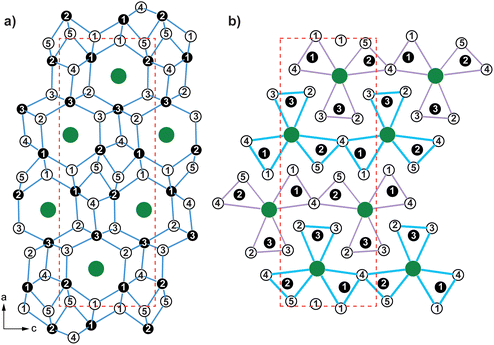
All members of the MAl5Pt3 series crystallizes in the orthorhombic crystal system with space group Pnma (oP36, c9) and are isostructural with the aluminum representatives CeAl5Pt3, EuAl5Pt3 and SrAl5Pt3.39–41 Besides the aluminum compounds also several gallium compounds MGa5Pt3 (M = Ca–Ba, Eu)44,45 have been reported, having the corresponding composition. These compounds, however, should not be considered isostructural to the prototypic YNi5Si3 structure,61 but rather isopointal. Especially since the [Ni5Si3]δ− polyanion exhibits a different transition metal to main group element ratio, compared to the respective platinides of aluminum and gallium.
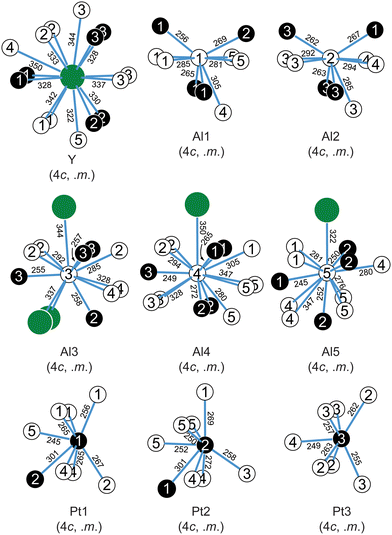
Fig. 2a exemplarily depicts the crystal structure of YAl5Pt3 as projection along [010]. The Y atoms exhibit a slightly distorted hexagonal prismatic coordination environment with an alternating arrangement of the Al and Pt atoms within the hexagon, but a congruent arrangement of top and bottom face is observed (Fig. 3). The Y@Al6Pt6 form strands along [010] via condensation of their hexagonal faces. Within the prism, the interatomic Y–Al distances range between 322 and 342 pm, while the Y–Pt distances are between 328 and 330 pm. Both, the Y–Al and Y–Pt distances are in line with the ones found in binary intermetallics e.g. YAl2 (MgCu2 type, 325–340 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70), YAl3 (Mg3Cd type, 302–310 pm
70), YAl3 (Mg3Cd type, 302–310 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71), YPt2 (MgCu2 type, 314–328 pm
71), YPt2 (MgCu2 type, 314–328 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70) or YPt3 (Cu3Au type, 288 pm
70) or YPt3 (Cu3Au type, 288 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72) as well as with the sum of the covalent radii (Y + Al = 162 + 125 = 287 pm; Y + Pt = 162 + 129 = 291 pm
72) as well as with the sum of the covalent radii (Y + Al = 162 + 125 = 287 pm; Y + Pt = 162 + 129 = 291 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73). Similar distances can be observed in ternary compounds of the Y–Al–Pt system like YAlPt (TiNiSi type, Y–Al: 308–336 pm; Y–Pt: 257–267 pm),74 YAl2Pt (MgAl2Cu type, Y–Al: 287–305 pm; Y–Pt: 287–308 pm),75 Y4Al24Pt9 (own type, Y–Al: 304–321 pm; Y–Pt: 328–336 pm),76 YAl3Pt2 (own type, Y–Al: 329–348 pm; Y–Pt: 301–316 pm),77 YAl2Pt5 (ZrAl5Ni2 type, Y–Al: no contacts; Y–Pt: 288–302 pm),78 Y4AlPt (Gd4InRh type, Y–Al: 324–348 pm; Y–Pt: 281–347 pm)79 or Y10Al3Pt (Y10Cd3Ru type, Y–Al: 324–348 pm; Y–Pt: 275 & 349 pm).80
73). Similar distances can be observed in ternary compounds of the Y–Al–Pt system like YAlPt (TiNiSi type, Y–Al: 308–336 pm; Y–Pt: 257–267 pm),74 YAl2Pt (MgAl2Cu type, Y–Al: 287–305 pm; Y–Pt: 287–308 pm),75 Y4Al24Pt9 (own type, Y–Al: 304–321 pm; Y–Pt: 328–336 pm),76 YAl3Pt2 (own type, Y–Al: 329–348 pm; Y–Pt: 301–316 pm),77 YAl2Pt5 (ZrAl5Ni2 type, Y–Al: no contacts; Y–Pt: 288–302 pm),78 Y4AlPt (Gd4InRh type, Y–Al: 324–348 pm; Y–Pt: 281–347 pm)79 or Y10Al3Pt (Y10Cd3Ru type, Y–Al: 324–348 pm; Y–Pt: 275 & 349 pm).80
The [Al5Pt3]δ− polyanion is formed by five crystallographically independent aluminum and three platinum sites (Fig. 2). All Pt sites exhibit a coordination number of seven with a highly asymmetrical coordination environment and interatomic Al–Pt distances between 247 and 270 pm. These agree well with those in binary (AlPt: 248–273 pm;81,82 Al2Pt: 256 pm;83 Al3Pt2: 255–286 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63,64) and ternary intermetallics (YAlPt: Al–Pt 308–336 pm,74 YAl2Pt: Al–Pt 287–305 pm,75 YAl3Pt2: Al–Pt: 329–348 pm
63,64) and ternary intermetallics (YAlPt: Al–Pt 308–336 pm,74 YAl2Pt: Al–Pt 287–305 pm,75 YAl3Pt2: Al–Pt: 329–348 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77) as well as with the sum of the covalent radii (Pt + Al = 129 + 125 = 254 pm
77) as well as with the sum of the covalent radii (Pt + Al = 129 + 125 = 254 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73). The respective homoatomic distances (YAl5Pt3: Pt–Pt: 306 pm; Al–Al: 273–293 pm) agree with what is observed in elemental Al (286 pm
73). The respective homoatomic distances (YAl5Pt3: Pt–Pt: 306 pm; Al–Al: 273–293 pm) agree with what is observed in elemental Al (286 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84), therefore suggesting partial bonding contributions while the Pt–Pt distances are significantly longer compared to the distances found in the elemental Pt (277 pm
84), therefore suggesting partial bonding contributions while the Pt–Pt distances are significantly longer compared to the distances found in the elemental Pt (277 pm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85) or the sum of the covalent radii (Al: 250 pm; Pt: 258 pm).73 Another possibility to describe the YNi5Si3 type structure, especially when compared to other structure types of the same stoichiometry MT5X3 such as the UFe5As3, the LaCo5P3, the UCo5Si3 or the YCo5P3 type structures, is to use trigonal prisms surrounding the As, P or Si atoms. These X@M2T4 prisms condense via common M2 or T2 edges to form “shamrock” like structures that are further condensed. One possibility is to form chains are linear in the case of the YNi5Si3 type structure (Fig. 2b). A more detailed description can be found in a recent publication.69
85) or the sum of the covalent radii (Al: 250 pm; Pt: 258 pm).73 Another possibility to describe the YNi5Si3 type structure, especially when compared to other structure types of the same stoichiometry MT5X3 such as the UFe5As3, the LaCo5P3, the UCo5Si3 or the YCo5P3 type structures, is to use trigonal prisms surrounding the As, P or Si atoms. These X@M2T4 prisms condense via common M2 or T2 edges to form “shamrock” like structures that are further condensed. One possibility is to form chains are linear in the case of the YNi5Si3 type structure (Fig. 2b). A more detailed description can be found in a recent publication.69
3.4 Scanning electron microscopy
Powders of NdAl5Pt3, GdAl5Pt3 and ErAl5Pt3 were investigated by SEM-EDX. The average of three point measurements are given in Table 5 and are in good agreement with the ideal composition (11.1 at% M, 55.6 at% Al, 33.3 at% Pt). The slight deviations can be explained by the irregular sample surface and the not perfect perpendicular orientation of the powder towards the beam. No impurity elements heavier than sodium (detection limit of the instrument) were detected.3.5 Magnetic measurements
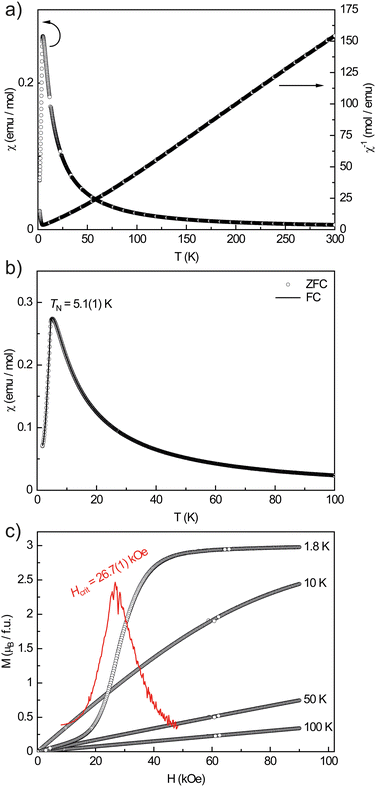
YAl5Pt3 is, as expected, a Pauli-paramagnetic material with a positive susceptibility since the Pauli contribution originating from the conduction electrons overcompensates the intrinsic diamagnetism. No superconductivity was observed at 20 Oe down to 2.5 K.All other X-ray pure members of the REAl5Pt3 series (RE = Y, Ce–Nd, Gd–Ho) exhibit an open-shell 4f electron configuration leading to paramagnetic behavior. Their effective magnetic moments calculated from modified Curie–Weiss fits indicate a stable trivalent oxidation state in all cases in good agreement with the expected moments for the free RE3+ cations (Table 6). Fig. 4 exemplarily depicts the magnetic behavior of NdAl5Pt3. The magnetic susceptibility data recorded between 1.8 and 300 K in zero-field-cooled mode (ZFC) at 10 kOe already shows a maximum at low temperatures indicating an antiferromagnetic transition (Fig. 4a). From the inverse susceptibility, the experimental magnetic moment was calculated to be μexp = 3.82(1)μB, in line with Nd3+ (μeff = 3.62μB). The positive Weiss constant of θP = 18(1) K points towards ferromagnetic interactions in the paramagnetic temperature regime and could be a sign of so called A-type antiferromagnetism in which each layer orders ferromagnetically but antiparallel to adjacent layers.86 The low field data (100 Oe) was recorded in zero-field-cooled and field-cooled (ZFC/FC) mode between 1.8 and 100 K (Fig. 4b). At TN = 5.1(1) K a clear maximum can be observed, originating from the antiferromagnetic ordering which causes the magnetic susceptibility to drop below the Néel temperature. Since the ZFC and FC curves are on top of each other, ferromagnetic impurities can be excluded. The magnetization isotherms are finally shown in Fig. 4c. The isotherms recorded at 50 and 100 K are linear up to 90 kOe, indicating Curie paramagnetism at these temperatures. The 10 K isotherm is slightly curved due to the proximity of the magnetic phase transition. The 1.8 K isotherm finally shows a pronounced S-shape indicating a meta-magnetic step. While at low magnetic fields the antiparallel orientation of the spins persists, a spontaneous reorientation is observed at a critical field of Hcrit = 26.7(1) kOe. The infliction point is determined by the first derivative dM/dH. The saturation magnetization at 1.8 K and 90 kOe reaches μsat = 2.98(1)μB which is close to the theoretical saturation magnetization according to gJ × J of 3.27μB and in line with the almost horizontal trace.
Since the interatomic M–M distances in the whole MAl5Pt3 series are rather large (>550 pm), RKKY (Ruderman-Kittel-Kasuya-Yosida) interactions between the rare-earth atoms are expected. In this case, the magnetic ordering temperatures, in this case the Néel temperatures, should scale with the de Gennes factor G [(gJ − 1)2J(J + 1)]. Fig. 5 shows the obtained correlation between TN and G, clearly indicating a deviation from the expected behavior. This points towards crystal field influences in the REAl5Pt3 series. Similar results have been observed for example in the RE2InT2 (RE = La–Nd, Sm, Gd–Lu; T = Ni, Cu, Pd) series.87–89
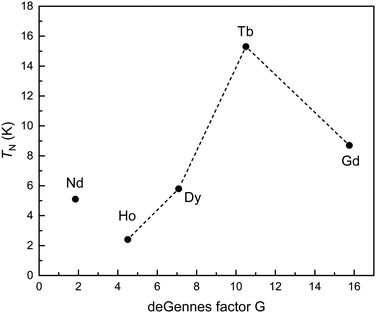 | ||
| Fig. 5 Plots of the ordering temperatures versus the de Gennes factor (gJ − 1)2J(J + 1) for the REAl5Pt3 series. | ||
Finally, for some of the other samples, the determined saturation magnetizations (Table 6) are significantly different to the values according to gJ × J which can either be explained by crystal field effects (see de Gennes scaling) or the polycrystalline nature of the samples.
3.6 27Al solid-state NMR spectroscopy
Solid-state MAS NMR spectroscopy is a powerful tool to support crystallography. Besides a plain confirmation of the crystal structure (number of sites equals number of signals) also structural distortions or the presence of solid solutions can be probed based on the shape of the e.g.27Al NMR signal.78,90–93Fig. 6 depicts the results of the 27Al MAS-NMR spectroscopic investigations on YAl5Pt3. Consistent with its crystal structure, the spectrum confirms the presence of five crystallographically independent Al sites. However, only the intense central line originating from the |+1/2〉 ↔ |−1/2〉 transitions of the five Al sites can be modelled with a Gauss-Lorentz fit. Since no significant broadening is observed, one can conclude that the electric quadrupolar couplings CQ are rather small (in a range <5 MHz) and second order quadrupole effects (SOQE) are not dominant, in line with the results from the quantum-chemical calculations (Table 7). The resonances of these five signals are significantly shifted compared to the standard of an aqueous solution of Al3+ (AlCl3), however, they are in line with the reported shifts for intermetallic aluminum compounds. The drastic shift, typically in the range of 200–1200 ppm,90 is caused by the s-electron spin density at the Fermi level as probed by the 27Al nuclei and dominated by the Knight shift contribution.90 Under magic angle spinning (MAS) conditions one can potentially observes a wide spinning sideband pattern originating from the outer satellite transitions, |±1/2〉 ↔ |±3/2〉 and |±3/2〉 ↔ |±5/2〉, however, this is not the case here.
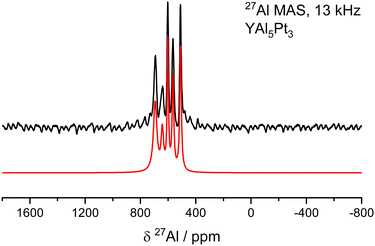 | ||
| Fig. 6 27Al MAS-NMR spectra (black) of YAl5Pt3 (YNi5Si3 type) along with the fit of the central transitions (red). | ||
3.7 XPS
X-ray photoelectron spectra have been recorded to investigate the electronic properties in the synthesized compounds from an experimental point of view. The 4f core levels of, e.g., Pt are very sensitive towards the electronic structure at the respective atom, allowing a spectroscopic approach to analyze the charge transfer in these intermetallic compounds. For intermetallic alkaline earth or rare-earth aluminum compounds with late transition metals, especially with 5d elements, an electron transfer from the AE/RE and Al atoms to the platinum atoms can be observed. This has been shown for quite some instances, e.g., Ba3Al4Pt4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 94 and the REAl3Pt2 (RE = Y, Dy–Tm) series.77 Since the most electronegative elements acquire additional electron density, shifts of the binding energies of the Pt 4f lines towards lower binding energies can be observed in the respective XPS measurements.94–97 In general, the Pt 4f states can be chosen as a reference as they are intense and sharp enabling the detection of already small shifts. However, it has to be mentioned that the Pt 4f and Al 2p levels have almost the same binding energy.98
94 and the REAl3Pt2 (RE = Y, Dy–Tm) series.77 Since the most electronegative elements acquire additional electron density, shifts of the binding energies of the Pt 4f lines towards lower binding energies can be observed in the respective XPS measurements.94–97 In general, the Pt 4f states can be chosen as a reference as they are intense and sharp enabling the detection of already small shifts. However, it has to be mentioned that the Pt 4f and Al 2p levels have almost the same binding energy.98
Fig. 7a depicts the XPS spectra of the Pt 4f lines of elemental Pt (black), YAl5Pt3 (red) and Al3Pt2 (blue). For the Pt reference (Pt foil) a binding energy of BE(Pt) = 71.0(1) eV was observed, in line with the literature.98 For YAl5Pt3 and Al3Pt2 shifts of +0.23 and +0.76 eV were obtained (BE(YAl5Pt3) = 71.23 eV; BE(Al3Pt2) = 71.76 eV). In contrast to what is intuitionally expected and described before, the shift of the Pt lines to higher binding energies indicates a formal formation of cationic Pt species in both compounds. Given the drastic electronegativity differences (χ(Pt) = 2.28 and χ(Al) = 1.61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73), a shift towards lower binding energies, in line with an anionic character, is expected. However, a recent HAXPES study has shown, that, although a charge transfer towards an anionic Pt species is expected based on quantum-chemical data, shifts towards formal cationic Pt are visible in binary aluminum platinides.99 The authors could show, that the QTAIM charges on the Pt atoms correlate with the positive shifts of the Pt 4f binding energies. This was attributed to changes in the Pt 5d orbital occupancies preventing an easy interpretation only based on the shifts of the Pt 4f binding energies in this binary system. Therefore the question arises if this is also applicable in the system reported here.
73), a shift towards lower binding energies, in line with an anionic character, is expected. However, a recent HAXPES study has shown, that, although a charge transfer towards an anionic Pt species is expected based on quantum-chemical data, shifts towards formal cationic Pt are visible in binary aluminum platinides.99 The authors could show, that the QTAIM charges on the Pt atoms correlate with the positive shifts of the Pt 4f binding energies. This was attributed to changes in the Pt 5d orbital occupancies preventing an easy interpretation only based on the shifts of the Pt 4f binding energies in this binary system. Therefore the question arises if this is also applicable in the system reported here.
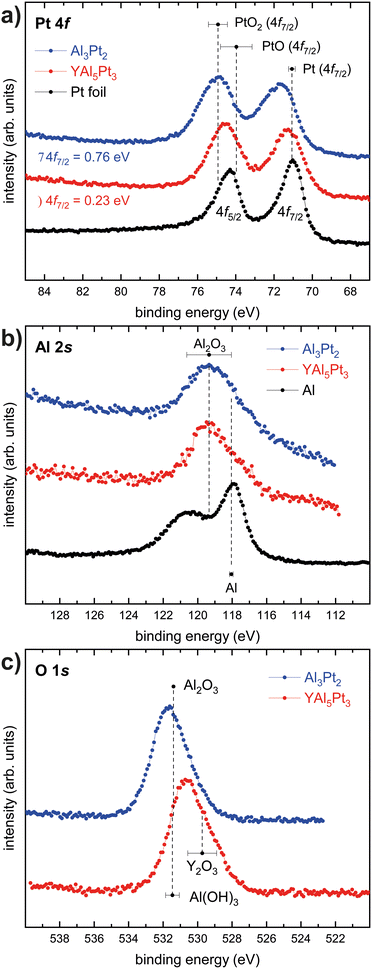 | ||
| Fig. 7 (a) Pt 4f spectra of YAl5Pt3 (red) and Al3Pt2 (blue) and Pt (black); (b) Al 2s spectra of YAl5Pt3 (red) and Al3Pt2 (blue) and Al (black); (a) O 1s spectra of YAl5Pt3 (red) and Al3Pt2 (blue). Mean values of binding energies and standard deviations are obtained by averaging over all entries in the NIST XPS database for the compounds specified in (a)–(c).101 | ||
When looking at the intensities of the 4f7/2 and 4f5/2 peaks, however, only the elemental Pt reference shows the expected 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio.98 For YAl5Pt3 and Al3Pt2, the 4f5/2 peaks seem to be equally high if not higher compared to the 4f7/2 peak. This is probably either due to at least a second set of Pt 4f levels. For Al, a shift towards higher binding energies, corresponding to a cationic character, is expected. Fig. 7b shows the XPS spectra of the Al 2s lines of elemental Al (black), YAl5Pt3 (red) and Al3Pt2 (blue). Here, the expected shift can be observed, however, the main peak corresponds to the one of trivalent Al as in Al2O3. Subsequently, XPS spectra of the oxygen 1s lines were conducted (Fig. 7c). Here, a signal corresponding to the expected value of Al2O3 can be observed for Al3Pt2, for YAl5Pt3, two overlapping lines can be observed that originate from Al2O3 and Y2O3. This suggests that the surface of the powder particles used for the XPS investigations is oxidized. This leads to the conclusion, that although these XPS investigations show an effect similar to what has been observed and reported for the binary Al–Pt system in literature, here a fully oxidized surface is present. Therefore, the shifts to higher binding energies in line with the literature are probably a mere coincidence. In the investigated samples, Pt atoms in an Al2O3 matrix rather than in the intermetallic compounds YAl5Pt3 and Al3Pt2 were probed in the XPS-accessible subsurface range. Studies on Al containing metallic glasses have shown a similar effect. Here, Al was oxidized throughout the material while all other metals were only oxidized within the first 5 nm below the surface.100
3 ratio.98 For YAl5Pt3 and Al3Pt2, the 4f5/2 peaks seem to be equally high if not higher compared to the 4f7/2 peak. This is probably either due to at least a second set of Pt 4f levels. For Al, a shift towards higher binding energies, corresponding to a cationic character, is expected. Fig. 7b shows the XPS spectra of the Al 2s lines of elemental Al (black), YAl5Pt3 (red) and Al3Pt2 (blue). Here, the expected shift can be observed, however, the main peak corresponds to the one of trivalent Al as in Al2O3. Subsequently, XPS spectra of the oxygen 1s lines were conducted (Fig. 7c). Here, a signal corresponding to the expected value of Al2O3 can be observed for Al3Pt2, for YAl5Pt3, two overlapping lines can be observed that originate from Al2O3 and Y2O3. This suggests that the surface of the powder particles used for the XPS investigations is oxidized. This leads to the conclusion, that although these XPS investigations show an effect similar to what has been observed and reported for the binary Al–Pt system in literature, here a fully oxidized surface is present. Therefore, the shifts to higher binding energies in line with the literature are probably a mere coincidence. In the investigated samples, Pt atoms in an Al2O3 matrix rather than in the intermetallic compounds YAl5Pt3 and Al3Pt2 were probed in the XPS-accessible subsurface range. Studies on Al containing metallic glasses have shown a similar effect. Here, Al was oxidized throughout the material while all other metals were only oxidized within the first 5 nm below the surface.100
3.8 Quantum-chemical calculations
The chemical bonding within YAl5Pt3 was investigated through crystal orbital Hamiltonian population (COHP) analysis. The integrated COHP (ICOHP) values, as listed in Table 9, highlights the predominant role of Al–Pt bonds, contributing over 65% to the total ICOHP value. Following these, the interactions of Al–Al are notable, while those involving Y–Al, Y–Pt, and Pt–Pt are relatively weaker. Particularly, the differences in the strengths between Al–Pt (−1.73 to −2.36 eV) and Al–Al interactions (−0.07 to −1.14 eV), in contrast to the Y–Pt (−0.62 to −0.65 eV) and Y–Al (−0.29 to −0.51 eV) ones, suggest the presence of a polyanionic [Al5Pt3]δ− network, with Yδ+ cations occupying the resulting cavities.The electronic structure of YAl5Pt3 was analyzed using density functional theory (DFT) calculations. The electron density of states (DOS) curves for YAl5Pt3 are depicted in Fig. 8. Notably, there exists a significant density of states at the Fermi level, indicative of metallic behavior, consistent with the observed silver to grey metallic appearance. The calculated Bader effective charges for YAl5Pt3 are detailed in Table 8. Each of the five crystallographically independent Al atoms exhibits positive charges. Moreover, the deviation of all Al atom charges from +3 (with values from +0.76 to +0.93) suggests that the Al–Pt interactions possess a predominantly covalent character than ionic. This observation aligns with the large negative Al–Pt ICOHP values and supporting the presence of a polyanionic [Al5Pt3]δ− network. Conversely, all Pt atoms demonstrate negative charges. Yttrium (Y) is observed to possess a positive charge of +1.25, which is notably less than a trivalent oxidation state. This suggests significant electron delocalization and robust Y–Pt and Y–Al covalent/metallic interactions, consistent with the noteworthy negative ICOHP values. These findings support the metallic character of YAl5Pt3.
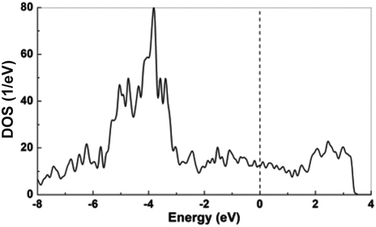 | ||
| Fig. 8 Total density of states of YAl5Pt3 from non-spin-polarized DFT calculation, dotted line indicates the Fermi level. | ||
4 Conclusion
The MAl5Pt3 series with M = Sr, Ce, Eu could be significantly extended to M = Ca, Y and La–Nd as well as Sm–Er. All compounds were synthesized from the elements using arc-melting and subsequent annealing and were characterized by powder X-ray diffraction. For CaAl5Pt3 and LaAl5Pt3 also the respective M2Al16Pt9 members were observed, however, the other compounds could be obtained either as X-ray pure materials or with small amounts of Al3Pt2 as side phase. Single-crystal X-ray diffraction studies on ErAl5Pt3 verified that also the small rare-earth elements adopt the YNi5Si3 type structure. For selected members of the series (M = Y, Ce–Nd, Gd–Ho) magnetization and susceptibility measurements were conducted. YAl5Pt3 is Pauli-paramagnetic while all other compounds are Curie paramagnets with the RE atoms in the trivalent oxidation state. For M = Nd, Gd–Ho, antiferromagnetic ordering was observed. Since YAl5Pt3 was obtained as phase pure material 27Al MAS NMR investigations were conducted. Five signals were observed, in line with the five crystallographic Al positions in the structure. Also, XPS measurements were conducted on this compound to gain an insight into the charge distribution. However, XPS cannot come up with this task due to the oxidation of the surface and the subsurface bulk. Finally, quantum-chemical calculations supported the NMR measurements and gave an insight into the chemical bonding and the expected charge distribution with the Pt atoms being the formal anions while the Y and Al atoms are cationic in nature.Author contributions
All authors have accepted responsibility for the entire content of this submitted manuscript and approved the submission.Data availability
The data supporting this article have been included as part of the ESI.† Crystallographic data for ErAl5Pt3 has been deposited at The Cambridge Crystallographic Data Centre (CCDC) under 2349082.†Conflicts of interest
The authors declare no conflicts of interest regarding this article.Acknowledgements
Instrumentation and technical assistance for this work were provided by the Service Center X-ray Diffraction, with financial support from Saarland University and German Research Foundation (project numbers INST 256/506-1 and INST 256/349-1) and by the Service Center NMR with financial support from Saarland University and German Research Foundation DFG (project number INST 256/384-1). The magnetometer was funded the by German Science Foundation DFG through INST 211/1034-1. Funding is provided by the Deutsche Forschungsgemeinschaft DFG (JA 1891-10-1, INST 211/1034-1, INST 256/349-1 and INST 256/506-1) and partially by the Collaborative Research Center CRC/SFB 1027. All DFT calculations used Expanse at SDSC through allocation CHE210062 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296.References
- J. Jensen and A. R. Mackintosh, Rare earth magnetism: Structures and excitations, Clarendon Press, Oxford, 1991 Search PubMed.
- H. Lueken, Magnetochemie, B. G. Teubner, Stuttgart, Leipzig, 1999 Search PubMed.
- J. H. van Vleck, The Theory Of Electric And Magnetic Susceptibilities, Oxford At The Clarendon Press, 1932 Search PubMed.
- H. Bärnighausen and G. Brauer, Acta Crystallogr., 1962, 15, 1059 CrossRef.
- R. Rau, Acta Crystallogr., 1966, 20, 716–723 CrossRef CAS.
- F. F. Y. Wang, Phys. Status Solidi, 1966, 14, 189–192 CrossRef CAS.
- F. L. Carter, J. Solid State Chem., 1972, 5, 300–313 CrossRef CAS.
- N. Lossau, H. Kierspel, J. Langen, W. Schlabitz, D. Wohlleben, A. Mewis and C. Sauer, Z. Phys. B: Condens. Matter, 1989, 74, 227–232 CrossRef CAS.
- K. H. J. Buschow and H. J. Vandall, Solid State Commun., 1970, 8, 363–365 CrossRef CAS.
- K. H. Mader and W. M. Swift, J. Phys. Chem. Solids, 1968, 29, 1759–1764 CrossRef CAS.
- O. Sichevych, Y. Prots, Y. Utsumi, L. Akselrud, M. Schmidt, U. Burkhardt, M. Coduri, W. Schnelle, M. Bobnar, Y.-T. Wang, Y.-H. Wu, K.-D. Tsuei, L. H. Tjeng and Y. Grin, Inorg. Chem., 2017, 56, 9343–9352 CrossRef CAS PubMed.
- U. B. Paramanik, Anupam, U. Burkhardt, R. Prasad, C. Geibel and Z. Hossain, J. Alloys Compd., 2013, 580, 435–441 CrossRef CAS.
- O. Niehaus, U. C. Rodewald, P. M. Abdala, R. S. Touzani, B. P. T. Fokwa and O. Janka, Inorg. Chem., 2014, 53, 2471–2480 CrossRef CAS PubMed.
- M. B. Gamża, R. Gumeniuk, U. Burkhardt, W. Schnelle, H. Rosner, A. Leithe-Jasper and A. Ślebarski, Phys. Rev. B, 2017, 95, 165142 CrossRef.
- B. C. Sales and R. Viswanathan, J. Low Temp. Phys., 1976, 23, 449–467 CrossRef CAS.
- E. R. Bauminger, D. Froindlich, I. Nowik, S. Ofer, I. Felner and I. Mayer, Phys. Rev. Lett., 1973, 30, 1053–1056 CrossRef CAS.
- D. C. Koskenmaki and K. A. Gschneidner, Handbook on the Physics and Chemistry of Rare Earths, 1978, vol. 1, pp. 337–377 Search PubMed.
- M. Akihiro, M. Shigeki, U. Masafumi, W. Hirofumi, M. Kazuyuki, U. Yoshiya, M. Masaichiro, K. Naomi, N. Kiyofumi, H. Naohisa, O. Yasuo and I. Naoki, J. Phys.: Condens. Matter, 2018, 30, 105603 CrossRef PubMed.
- R. S. Kumar, A. Svane, G. Vaitheeswaran, V. Kanchana, E. D. Bauer, M. Hu, M. F. Nicol and A. L. Cornelius, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075117 CrossRef.
- X. Tan, G. Fabbris, D. Haskel, A. A. Yaroslavtsev, H. Cao, C. M. Thompson, K. Kovnir, A. P. Menushenkov, R. V. Chernikov, V. O. Garlea and M. Shatruk, J. Am. Chem. Soc., 2016, 138, 2724–2731 CrossRef CAS PubMed.
- D. T. Adroja, B. D. Rainford, J. M. de Teresa, A. del Moral, M. R. Ibarra and K. S. Knight, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12790–12797 CrossRef PubMed.
- I. Felner and I. Nowik, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 617–619 CrossRef CAS PubMed.
- I. Felner, I. Nowik, D. Vaknin, U. Potzel, J. Moser, G. M. Kalvius, G. Wortmann, G. Schmiester, G. Hilscher, E. Gratz, C. Schmitzer, N. Pillmayr, K. G. Prasad, H. de Waard and H. Pinto, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6956–6963 CrossRef CAS PubMed.
- H. Müller, E. Bauer, E. Gratz, K. Yoshimura, T. Nitta and M. Mekata, J. Magn. Magn. Mater., 1988, 76, 159–160 CrossRef.
- E. V. Sampathkumaran, L. C. Gupta, R. Vijayaraghavan, K. V. Gopalakrishnan, R. G. Pillay and H. G. Devare, J. Phys. C: Solid State Phys., 1981, 14, L237 CrossRef CAS.
- M. Croft, J. A. Hodges, E. Kemly, A. Krishnan, V. Murgai and L. C. Gupta, Phys. Rev. Lett., 1982, 48, 826–829 CrossRef CAS.
- L. Fournes, B. Chevalier, B. Lloret and J. Etourneau, Z. Phys. B: Condens. Matter, 1989, 75, 501–505 CrossRef CAS.
- C. U. Segre, M. Croft, J. A. Hodges, V. Murgai, L. C. Gupta and R. D. Parks, Phys. Rev. Lett., 1982, 49, 1947–1950 CrossRef CAS.
- M. Radzieowski, F. Stegemann, T. Block, J. Stahl, D. Johrendt and O. Janka, J. Am. Chem. Soc., 2018, 140, 8950–8957 CrossRef CAS PubMed.
- F. Stegemann, J. Stahl, M. Bartsch, H. Zacharias, D. Johrendt and O. Janka, Chem. Sci., 2019, 10, 11086–11094 RSC.
- O. Janka, O. Niehaus, R. Pöttgen and B. Chevalier, Z. Naturforsch., 2016, 71b, 737–764 CrossRef.
- R. Pöttgen and B. Chevalier, Z. Naturforsch., 2015, 70b, 289–304 CrossRef.
- R. Pöttgen and B. Chevalier, Z. Naturforsch., 2015, 70b, 695–704 CrossRef.
- R. Pöttgen, O. Janka and B. Chevalier, Z. Naturforsch., 2016, 71b, 165–191 CrossRef.
- S. F. Matar, Prog. Solid State Chem., 2013, 41, 55–85 CrossRef CAS.
- S. Gupta and K. G. Suresh, J. Alloys Compd., 2015, 618, 562–606 CrossRef CAS.
- S. Engel, E. C. J. Gießelmann, R. Pöttgen and O. Janka, Rev. Inorg. Chem., 2023, 43, 571–582 CrossRef CAS.
- S. Engel, E. C. J. Gießelmann, M. K. Reimann, R. Pöttgen and O. Janka, ACS Org. Inorg. Au, 2024, 4, 188–222 CrossRef CAS PubMed.
- S. Engel, J. Bönnighausen, F. Stegemann, R. S. Touzani and O. Janka, Z. Naturforsch., 2022, 77, 367–379 CrossRef CAS.
- A. I. Tursina, N. G. Bukhan'ko, A. V. Gribanov, V. A. Shchelkunov and Y. V. Nelyubina, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, E61, i285–i286 CrossRef.
- T. Koizumi, F. Honda, Y. J. Sato, D. Li, D. Aoki, Y. Haga, J. Gouchi, S. Nagasaki, Y. Uwatoko, Y. Kaneko and Y. Ōnuki, J. Phys. Soc. Jpn., 2022, 91, 043704 CrossRef.
- R. Pöttgen, T. Gulden and A. Simon, GIT Labor-Fachz., 1999, 43, 133–136 Search PubMed.
- Topas, Version 5 Version 5, Bruker AXS Inc., Karlsruhe (Germany), 2014 Search PubMed.
- J. Bönnighausen, S. Seidel, S. Klenner and R. Pöttgen, Z. Kristallogr., 2021, 236, 293–300 Search PubMed.
- D. Langen, Dissertation, Universität zu Köln, 1997.
- G. M. Sheldrick, SADABS University of Göttingen, Germany, 1996.
- P. J. Becker and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1974, 30, 129–147 CrossRef.
- Topspin Version 2.1, Bruker Corp., Karlsruhe, 2008 Search PubMed.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- O. K. Andersen, R. W. Tank and O. Jepsen, TB-LMTO-ASA version 4.7, Max-Planck-Institut für Festkörperforschung, Stuttgart (Germany), 1998 Search PubMed.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107 CrossRef CAS.
- W. R. L. Lambrecht and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 2439–2449 CrossRef CAS PubMed.
- L. G. Akselrud, V. I. Yarovets, O. I. Bodak, Y. P. Yarmolyuk and E. I. Gladyshevskii, Kristallografiya, 1976, 21, 383–386 CAS.
- A. I. Tursina, E. V. Murashova, H. Noël, N. G. Bukhan'ko and Y. D. Seropegin, Intermetallics, 2009, 17, 780–783 CrossRef CAS.
- J. Comer, Acta Crystallogr., 1964, 17, 444–445 CrossRef CAS.
- M. Ellner, U. Kattner and B. Predel, J. Less-Common Met., 1982, 87, 305–325 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Jana2006. The crystallographic computing system Institute of Physics, Praha (Czech Republic), 2006 Search PubMed.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352 Search PubMed.
- P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds release 2023/24, ASM International®, Materials Park, Ohio, USA, 2023 Search PubMed.
- N. Zaremba, M. Krnel, Y. Prots, M. König, L. Akselrud, Y. Grin and E. Svanidze, Inorg. Chem., 2024, 63, 4566–4573 CrossRef CAS PubMed.
- V. B. Compton and B. T. Matthias, Acta Crystallogr., 1959, 12, 651–654 CrossRef CAS.
- T. M. Gumenyuk, Y. B. Kuz'ma and B. M. Stel'makhovych, J. Alloys Compd., 2000, 299, 213–216 CrossRef CAS.
- B. Erdmann and C. Keller, J. Solid State Chem., 1973, 7, 40–48 CrossRef CAS.
- J. Emsley, The Elements, Clarendon Press, Oxford University Press, Oxford, New York, 1998 Search PubMed.
- A. E. Dwight, J. Less-Common Met., 1984, 102, L9–L13 CrossRef CAS.
- M. Radzieowski, F. Stegemann, C. Doerenkamp, S. F. Matar, H. Eckert, C. Dosche, G. Wittstock and O. Janka, Inorg. Chem., 2019, 58, 7010–7025 CrossRef CAS PubMed.
- V. M. T. Thiede, B. Fehrmann and W. Jeitschko, Z. Anorg. Allg. Chem., 1999, 625, 1417–1425 CrossRef CAS.
- F. Eustermann, S. Gausebeck, C. Dosche, M. Haensch, G. Wittstock and O. Janka, Crystals, 2018, 8, 169 CrossRef.
- C. Benndorf, F. Stegemann, H. Eckert and O. Janka, Z. Naturforsch., 2015, 70b, 101–110 CrossRef.
- S. Engelbert and O. Janka, Intermetallics, 2018, 96, 84–89 CrossRef CAS.
- C. Benndorf, H. Eckert and O. Janka, Dalton Trans., 2017, 46, 1083–1092 RSC.
- K. Schubert, W. Burkhardt, P. Esslinger, E. Günzel, H. G. Meissner, W. Schütt, J. Wegst and M. Wilkens, Naturwissenschaften, 1956, 43, 248–249 CrossRef CAS.
- K. Schubert, H. Breimer, W. Burkhardt, E. Günzel, R. Haufler, H. L. Lukas, H. Vetter, J. Wegst and M. Wilkens, Naturwissenschaften, 1957, 44, 229–230 CrossRef CAS.
- E. Zintl, A. Harder and W. Haucke, Z. Phys. Chem., Abt. B, 1937, 35, 354–362 Search PubMed.
- A. W. Hull, Phys. Rev., 1917, 10, 661–696 CrossRef CAS.
- A. W. Hull, Trans. Am. Inst. Electr. Eng., 1919, 38, 1445–1466 Search PubMed.
- E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545–563 CrossRef CAS.
- M. Giovannini, H. Michor, E. Bauer, G. Hilscher, P. Rogl and R. Ferro, J. Alloys Compd., 1998, 280, 26–38 CrossRef CAS.
- I. R. Fisher, Z. Islam and P. C. Canfield, J. Magn. Magn. Mater., 1999, 202, 1–10 CrossRef CAS.
- Y. Tyvanchuk, S. Baran, T. Jaworska-Gołąb, R. Duraj, Y. M. Kalychak and A. Szytuła, Acta Phys. Pol., A, 2012, 121, 678–681 CrossRef CAS.
- C. Benndorf, H. Eckert and O. Janka, Acc. Chem. Res., 2017, 50, 1459–1467 CrossRef CAS PubMed.
- C. Benndorf, O. Niehaus, H. Eckert and O. Janka, Z. Anorg. Allg. Chem., 2015, 641, 168–175 CrossRef CAS.
- S. Engel, E. C. J. Gießelmann, L. E. Schank, G. Heymann, K. Brix, R. Kautenburger, H. P. Beck and O. Janka, Inorg. Chem., 2023, 62, 4260–4271 CrossRef CAS PubMed.
- E. C. J. Gießelmann, S. Engel, J. Baldauf, J. Kösters, S. F. Matar, G. Kickelbick and O. Janka, Inorg. Chem., 2024, 63, 8180–8193 CrossRef PubMed.
- F. Stegemann, C. Benndorf, T. Bartsch, R. S. Touzani, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2015, 54, 10785–10793 CrossRef CAS PubMed.
- F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2017, 56, 1919–1931 CrossRef CAS PubMed.
- F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Z. Anorg. Allg. Chem., 2017, 643, 1379–1390 CrossRef CAS.
- C. Benndorf, F. Stegemann, S. Seidel, L. Schubert, M. Bartsch, H. Zacharias, B. Mausolf, F. Haarmann, H. Eckert, R. Pöttgen and O. Janka, Chem. – Eur. J., 2017, 23, 4187–4196 CrossRef CAS PubMed.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-Ray Photoelectron Spectroscopy, Physical Electronics, Minnesota, 1995 Search PubMed.
- I. Antonyshyn, O. Sichevych, U. Burkhardt, A. M. Barrios Jiménez, A. Melendez-Sans, Y.-F. Liao, K.-D. Tsuei, D. Kasinathan, D. Takegami and A. Ormeci, Phys. Chem. Chem. Phys., 2023, 25, 31137–31145 RSC.
- J. Heinrich, R. Busch, F. Müller, S. Grandthyll and S. Hüfner, Appl. Phys. Lett., 2012, 100, 071909 CrossRef.
- NIST X-ray Photoelectron Spectroscopy Database, NIST Standard Reference Database Number 20, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2000, (retrieved Dec. 17th 2023), DOI:10.18434/T4T88K.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2349082. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt01296h |
| This journal is © The Royal Society of Chemistry 2024 |