Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
pKaH values and θH angles of phosphanes to predict their electronic and steric parameters†
Marta-Lisette
Pikma
 ,
Sofja
Tshepelevitsh
,
Sofja
Tshepelevitsh
 ,
Sigrid
Selberg
,
Sigrid
Selberg
 ,
Ivari
Kaljurand
,
Ivari
Kaljurand
 ,
Ivo
Leito
,
Ivo
Leito
 and
Agnes
Kütt
and
Agnes
Kütt
 *
*
Institute of Chemistry, University of Tartu, Ravila 14a, Tartu 50411, Estonia. E-mail: agnes.kutt@ut.ee
First published on 5th August 2024
Abstract
Phosphanes play an important role in various applications, serving as a class of organic bases with basicities spanning more than 30 orders of magnitude. Accessing comprehensive basicity data for phosphanes has been challenging due to scattered information across multiple sources and notable gaps in the existing data. In this report, we present basicities (pKaH values) of a diverse set of phosphanes, both newly measured or calculated and collected from the literature. We demonstrate that pKaH values can serve as an alternative to Tolman electronic parameters (TEP values) in evaluating the electronic properties of phosphanes. Additionally, we suggest parameters for assessing the steric properties of phosphanes without the need for preparation or calculation of metal-ligand complexes.
Introduction
The adaptable reactivity of phosphanes makes them indispensable across various chemistry disciplines, spanning organic synthesis, materials science, pharmaceuticals, and beyond. Phosphanes are widespread ligands in homogeneous transition metal catalysis, facilitating a wide range of organic transformations such as hydrogenation, cross-coupling reactions (e.g., Heck reaction, Buchwald-Hartwig amination, Suzuki-Miyaura coupling, etc.), olefin metathesis, three-component coupling reactions, polymerization, asymmetric synthesis, Michael addition, Wittig reactions, etc.1–9 Bulky phosphanes are also commonly employed in frustrated Lewis pair (FLP) systems as Lewis bases for activating small molecules and non-transition metal catalysis.10Phosphanes offer several advantages over possible alternative reagents (e.g., N-heterocyclic carbenes,11 nitrogen-containing ligands,12etc.): they are straightforward to synthesize, many are stable under ordinary environmental conditions, and are often commercially available. Furthermore, their properties can be adjusted to suit the requirements of a particular catalytic transformation, rendering them a favored option for ligands. To facilitate extensive ligand screening for catalytic transformations, several databases have been developed, such as the Ligand Knowledge Base (LKB), which comprises computed properties for a wide range of phosphanes, as well as the Kraken discovery platform, among others.13,14
Although phosphanes are primarily used in metal complexes, some of them, particularly those substituted with aromatic rings carrying para/ortho MeO groups, have found independent applications as catalysts as well, owing to their basic characteristics.15,16 Given the widespread application of phosphanes as nucleophiles and the possibility to predict their related properties based on their basicity,17 phosphanes as bases have been well studied, resulting in the availability of numerous reported pKaH values.18–20 However, despite these advancements, there are still notable gaps in this field, emphasizing the need for further investigations.
In the current work, we present self-consistent experimental pKaH values of 25 phosphanes, measured using relative UV-Vis and NMR methods. Some of the phosphanes are known to have high basicity but their exact pKaH values are presented for the first time. COSMO-RS method was used to predict pKaH values for the 21 phosphanes that were not studied experimentally.
The basicity of a base B in a solvent is defined by equilibrium (1); the pKaH value of a base B is equivalent to the pKa of its conjugate acid BH+ and is the negative logarithm of the conjugated acid's dissociation constant Ka (eqn (2)).
 | (1) |
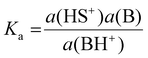 | (2) |
The gas-phase basicity (GB) of a neutral base B refers to the following equilibrium:
 | (3) |
GB of a base is the negative of Gibbs free energy change (−ΔGb) on protonation of the base according to equilibrium (3). Differently from proton affinity (PA), GB values include the entropy factor.
Electronic and steric parameters of ligands, a concept first introduced by C.A. Tolman in the 1970s, have been used to describe phosphanes.21,22 The Tolman electronic parameter (TEP) and Tolman cone angle are still the most commonly used characteristics in ligand chemistry.
TEP values of phosphanes as ligands are often determined by the infrared vibration of the CO group in ligand-Ni(CO)3 complexes (ν(CO)). While widely accepted and frequently applied to characterize new types of phosphanes due to their effectiveness in delineating electron-donating and accepting attributes of ligands, reliance on Ni(CO)4 as a required starting compound poses challenges, as it is a toxic gas not readily available in most research laboratories. Additionally, computational determination of ν(CO) values for solvent-phase metal–ligand complexes can be resource-intensive and highly influenced by the solvent, rendering computational gas-phase values less reliable without a suitable reference system. Several alternatives exist for assessing ligands’ electron-donating and -accepting properties in metal complexes. These alternatives include, e.g., NBO analysis,23 Hard-Soft Acid-Base (HSAB) Theory,24 Local Vibrational Mode,25 X-ray Crystallography,26etc.
Tolman cone angles were originally measured from metal-ligand complexes relatively robustly, using space-filling models and a specialized ruler; the distance from phosphorus to the metal was fixed to a length in the model equal to 2.28 Å on the molecular level.22,27 This method undoubtedly involved generalizations concerning both the ligand conformation and the metal position. Tolman initially utilized the tightest conformer, a choice later contested by others as potentially inaccurate.28,29 Hence, criticism has been directed towards the Tolman cone angle, and other approaches have been proposed.30 For example, these include exact cone angles,30 solid angles,31 percent buried volumes (%VBur),32,33 the He8 steric descriptor in Ligand Knowledge Base (LKB),13,34 angular symmetric deformation coordinate (S4′),35,36etc. Tolman cone angles have been recomputed for various phosphane ligands, which were obtained from three different transition metal coordination environments using the lowest-energy conformer geometry with MM/DFT methodology.37 Steric parameters have been also derived not directly from the metal-ligand complex but from implied methods, e.g. by NMR spectroscopy,38 organic reactivity,39,40etc.41
While modern parameters may offer greater precision in absolute values, they often prove inconvenient to obtain when only a rapid comparison of ligands is required. Therefore, employing a steric measure derived from a free ligand for preliminary screening holds promise for substantial resource savings.
While a number of parameters have been proposed to assess the electronic and steric properties of phosphanes, they are all derived from metal-ligand complexes, which is why the present study intended to investigate the feasibility of substituting these with alternative, more readily computed parameters for simple phosphanes as free ligands.
Results and discussion
In this work, experimental pKaH values in acetonitrile were obtained for 12 phosphanes. Each compound was measured against at least 3 reference bases using a relative measurement method based on the UV-Vis or NMR spectra (see below).42,43 In addition, pKaH(MeCN) and GB values were calculated for a diverse set of phosphanes (see below and ESI†). The results from this work, in addition to values from the literature, are presented in Table 1. The structures of selected substituents are shown in Fig. 1.| No | Compound | pKaH(MeCN) experimental | pKaH(MeCN) computational | GB [kcal mol−1] | TEP | θ CPC [°] | θ H [°] | θ Tolman [°] | θ Pd [°]i |
|---|---|---|---|---|---|---|---|---|---|
| a Experimental value from this work (NMR). b Experimental value from this work (UV-Vis). c Experimental value from ref. 17. d Experimental value from ref. 18. e Experimental value from ref. 41. f NPN angles. g Including CPH angles. h Including CPCl angles. i In the case the angles for two conformers are available, the average angle is presented. | |||||||||
| 1 | P(pyrr)3 | 20.35a | 19.5 | 241.8 | 111.7f | 218 | |||
| 2 | P[2,4,6-(MeO)3-C6H2]3 | 19.66b | 21.4 | 261.5 | 114.8 | 275 | |||
| 3 | P(dma)3 | 18.9a | 17.1 | 234.5 | 2061.9 | 111.6f | 223 | 157 | |
| 4 | PAd3 | 18.5 | 246.2 | 115.0 | 244 | ||||
| 5 | P(t-Bu)3 | 17.3 | 238.1 | 2056.1 | 114.8 | 244 | 182 | 187.6 | |
| 6 | P[2,6-(MeO)2-C6H3]3 | 17.23b | 18.2 | 254.2 | 114.8 | 273 | |||
| 7 | PCy3 | 16.70a | 16.6 | 240.3 | 2056.4 | 112.7 | 229 | 170 | |
| 8 | P[2,4,6-(MeO)3-C6H2]2Ph | 15.87b | 16.5 | 252.6 | 114.0 | 252 | |||
| 9 | P(i-Pr)3 | 15.7 | 233.1 | 2059.2 | 112.6 | 227 | 160 | 173.1 | |
| 10 | PMe2Et | 15.6 | 223.5 | 111.2 | 187 | 123 | 133.0 | ||
| 11 | PMe3 | 15.48d | 15.6 | 221.4 | 2064.1 | 111.0 | 163 | 118 | 120.4 |
| 12 | P(i-Pr)2Me | 15.3 | 228.6 | 111.9 | 219 | 146 | 160.1 | ||
| 13 | PMeEt2 | 15.1 | 225.4 | 111.4 | 187 | 127 | 141.4 | ||
| 14 | P(n-Pr)3 | 15.0 | 229.5 | 111.6 | 215 | 132 | |||
| 15 | PEt3 | 14.8 | 226.8 | 2061.7 | 111.5 | 212 | 132 | 152.4 | |
| 16 | P(n-Bu)3 | 14.7 | 230.0 | 2060.3 | 111.5 | 213 | 132 | 152.8 | |
| 17 | P(t-Bu)2Ph | 14.7 | 236.1 | 114.3 | 243 | 170 | 186.7 | ||
| 18 | P(i-Bu)3 | 13.8 | 229.7 | 110.9 | 250 | 143 | 213.8 | ||
| 19 | PCy2Ph | 13.1 | 235.1 | 112.4 | 225 | 159 | |||
| 20 | PMes3 | 12.87b | 13.0 | 239.5 | 115.9 | 302 | 212 | ||
| 21 | PNp3 | 12.8 | 231.3 | 110.0 | 284 | 180 | |||
| 22 | PEt2Ph | 12.7 | 228.2 | 2063.7 | 111.7 | 218 | 136 | 163.0 | |
| 23 | P(n-Bu)2Ph | 12.6 | 231.8 | 111.7 | 219 | 136 | 153.1 | ||
| 24 | PMe2Ph | 12.64d | 12.2 | 224.4 | 2065.3 | 111.2 | 198 | 122 | 148.5 |
| 25 | P[2,4,6-(MeO)3-C6H2]Ph2 | 11.76b | 11.5 | 241.5 | 113.2 | 237 | |||
| 26 | P(t-Bu)Ph2 | 11.4 | 232.6 | 113.6 | 241 | 157 | |||
| 27 | PCyPh2 | 10.23b | 10.0 | 231.3 | 112.4 | 232 | 152 | ||
| 28 | PEtPh2 | 10.1 | 227.3 | 2066.7 | 111.8 | 224 | 140 | 159.6 | |
| 29 | P(4-MeO-C6H4)3 | 10.06d | 10.5 | 239.5 | 2066.1 | 111.9 | 216 | 145 | 170.9 |
| 30 | PMePh2 | 9.97e | 9.5 | 226.5 | 2067.0 | 111.4 | 202 | 136 | 151.4 |
| 31 | P(2-MeO-C6H4)3 | 9.8 | 241.4 | 2058.3 | 110.7 | 248 | |||
| 32 | PBn3 | 9.3 | 229.1 | 2066.2 | 112.0 | 250 | 165 | ||
| 33 | P(4-Me-C6H4)3 | 8.7 | 234.8 | 2066.7 | 111.7 | 216 | 145 | 170.7 | |
| 34 | P(2-Me-C6H4)3 | 7.8 | 230.7 | 2066.6 | 111.7 | 277 | 194 | 191.9 | |
| 35 | PPh3 | 7.62d | 7.1 | 228.6 | 2068.9 | 111.6 | 218 | 145 | 170.0 |
| 36 | P(1-Napht)Ph2 | 7.29b | 7.0 | 230.0 | 111.6 | 229 | |||
| 37 | P(3-MeO-C6H4)3 | 7.25b | 7.7 | 234.6 | 111.5 | 229 | |||
| 38 | P[3,5-(MeO)2-C6H3]3 | 7.19b | 7.7 | 237.9 | 111.5 | 233 | |||
| 39 | P(4-F-C6H4)3 | 6.7 | 224.0 | 2071.3 | 111.6 | 216 | 145 | 170.8 | |
| 40 | P(1-Napht)3 | 6.55e | 6.3 | 232.3 | 111.6 | 247 | |||
| 41 | P(2-F-C6H4)Ph2 | 6.11c | 5.9 | 227.5 | 111.3 | 222 | |||
| 42 | P(2,6-F2-C6H3)Ph2 | 5.17c | 5.5 | 226.3 | 112.3 | 224 | |||
| 43 | P(4-Cl-C6H4)3 | 4.9 | 223.3 | 2072.8 | 111.4 | 215 | 145 | 170.2 | |
| 44 | PPh2H | 4.7 | 216.7 | 2073.3 | 110.8g | 187 | 128 | 146.3 | |
| 45 | P(2-F-C6H4)2Ph | 4.56c | 4.5 | 225.3 | 111.1 | 227 | |||
| 46 | P(2-F-C6H4)3 | 3.01c | 3.0 | 224.1 | 110.7 | 231 | |||
| 47 | P(C6F5)Ph2 | 2.54c | 2.7 | 219.9 | 2074.8 | 112.2 | 225 | ||
| 48 | P(2,6-F2-C6H3)2Ph | 2.50c | 2.5 | 224.9 | 112.7 | 235 | |||
| 49 | P(2,6-Cl2-C6H3)3 | 1.70c | 1.7 | 225.5 | 115.4 | 277 | |||
| 50 | P(2,6-F2-C6H3)3 | 0.5 | 222.0 | 113.5 | 255 | ||||
| 51 | P[CH2CH(CF3)2]3 | 0.0 | 201.9 | 109.0 | 256 | ||||
| 52 | PPh2Cl | −0.2 | 212.5 | 2080.7 | 111.0h | 202 | 138 | 156.3 | |
| 53 | P(C6F5)2Ph | −2.0 | 211.1 | 112.3 | 234 | ||||
| 54 | P[3,5-(CF3)2-C6H3]3 | −2.2 | 200.5 | 111.4 | 221 | ||||
| 55 | P(CH2CF3)3 | −3.3 | 194.6 | 111.1 | 228 | ||||
| 56 | P(C6F5)3 | −7.0 | 201.8 | 2090.9 | 113.0 | 253 | 184 | ||
As is seen from Table 1, electron-donating groups increase the basicity of phosphanes, whereas electron-accepting groups lower it. The elevation of basicity induced by the former arises from the stabilization of the protonated form, rendering the phosphane more inclined to accept a proton. In addition, despite the limited conjugation between the lone pair of phosphorus and the aromatic ring due to orbital positioning, a slight resonance effect remains, and electron-donating groups increase the accessibility of the lone pair on phosphorus in aromatic phosphanes.
Methoxy substituents in ortho and para positions increase the basicity of aryl-substituted phosphanes and lower it when in the meta position compared to PPh3 (pKaH value of PPh3 is 7.62).18,44 This is expected as the methoxy group is a resonance-donating group, and it increases the electron density in para and ortho positions (i.e., increasing the electron density on the phosphorus, making the electron pair more available and also stabilizing the protonated phosphane). At the same time, the methoxy group is also an induction-acceptor group, thereby lowering the basicity when in the meta position.
Replacing unsubstituted phenyl rings with 2,4,6-methoxy substituted rings increases the basicity considerably. The basicity increase upon trimethoxy-substitution of one phenyl ring (PPh3 (35) vs. P[2,4,6-(MeO)3-C6H2]Ph2 (25)) is 4.14 pKaH units; substituting the second phenyl (25vs. P[2,4,6-(MeO)3-C6H2]2Ph (8)) causes about the same basicity increase (4.11 pKaH units) and substituting the third phenyl (8vs. P[2,4,6-(MeO)3-C6H2]3 (2)) increases the pKaH by another 3.79 units (Scheme 1). The minor reduction in the basicity increase for the latter is attributable to a saturation effect. Both P[2,4,6-(MeO)3-C6H2]2Ph (8) and P[2,6-(MeO)2-C6H3]3 (6) feature six methoxy groups; however, the latter exhibits a higher pKaH value by approximately 1.5 units. This discrepancy suggests that the extra ortho-methoxy groups have an advantage over extra para-methoxy groups, as the former exert a more significant influence on basicity owing to their proximity to the protonation center in addition to the stabilization of the protonated form caused by the spatial proximity of the oxygen atoms to the proton.
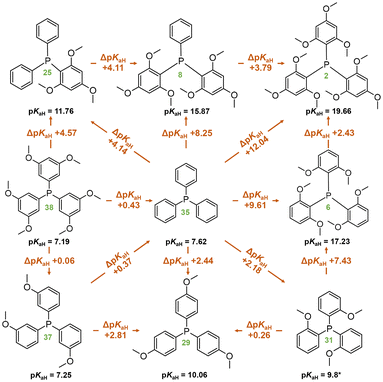 | ||
| Scheme 1 Comparison of compounds with methoxyphenyl groups in terms of pKaH(MeCN) values. Compound numbers, according to Table 1, are marked in green below the corresponding structures. *Predicted pKaH(MeCN) value. | ||
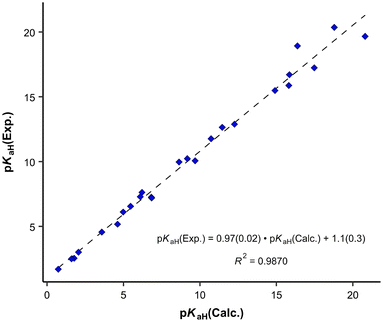
For the predicted pKaH(MeCN) values presented in Table 1, the theoretical pKaH values were initially computed with the COSMO-RS method45,46 and then subsequently corrected using available experimental data pertaining to other phosphanes (calculation method described below). Different versions of COSMO-RS parameterizations may rely on distinct datasets, and while newer iterations generally demonstrate overall enhancement, their performance across predicted properties and compound classes can vary. Hence, it is beneficial to assess different parameterizations for a particular task. It was observed that the quality of the correlation between the calculated pKaH(Calc.) (output of COSMOtherm software without additional corrections) and the experimental pKaH(Exp.) depended markedly upon the COSMO-RS parameterization employed at a given level (TZVPD_FINE). Unexpectedly, more recent parameterizations yielded inferior results, both in terms of absolute values and the quality of correlation with the experiment. To discern the optimal parameterization, pKaH(Calc.) values were computed with 8 parameterizations (Table 2).
| Parameterization | Slope | R 2 | S | RMSD |
|---|---|---|---|---|
| The standard deviation for slope is in brackets. S – standard error for the correlation; RMSD – root mean square deviation between pKaH(Calc.) and pKaH(Exp.). | ||||
| BP_TZVPD_FINE_23 (2023) | 1.32 (0.07) | 0.941 | 1.43 | 3.82 |
| BP_TZVPD_FINE_20 (2020) | 1.27 (0.06) | 0.943 | 1.40 | 3.68 |
| BP_TZVPD_FINE_18 (2018) | 1.34 (0.06) | 0.956 | 1.24 | 4.06 |
| BP_TZVPD_FINE_C30_1701 (2017) | 0.97 (0.02) | 0.987 | 0.67 | 1.05 |
| BP_TZVPD_FINE_ C30_1601 (2016) | 1.00 (0.03) | 0.980 | 0.84 | 0.84 |
| BP_TZVPD_FINE_ C30_1501 (2015) | 1.00 (0.03) | 0.979 | 0.86 | 0.83 |
| BP_TZVPD_FINE_ C30_1401 (2014) | 1.02 (0.04) | 0.969 | 1.03 | 1.10 |
| BP_TZVPD_FINE_HB2012_C30_1201 (2012) | 1.04 (0.04) | 0.964 | 1.12 | 1.30 |
The parameterization BP_TZVPD_FINE_C30_1701 from 2017 demonstrated the best correlation with experimental values and was consequently employed for the determination of predicted pKaH values in this study. Nevertheless, in instances where the objective is the direct utilization of calculated values, the 2015 parameterization proves more advantageous, given its ability to yield a reduced root mean square deviation (Table 2). The correlation between calculated (pKaH(Calc.)) and experimental (pKaH(Exp.)) pKaH values using BP_TZVPD_FINE_C30_1701 parameterization is depicted in Fig. 2. The correlation coefficient is reasonably high, and the slope of the correlation is statistically indistinguishable from 1. To obtain the predicted pKaH values from computational pKaH values for phosphanes, the following equation is used:
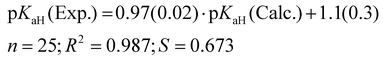 | (4) |
It was also examined whether employing all conformers for pKaH calculations yields significantly different results compared to using only the most stable conformer (denoted as c0). The average difference between these two is 0.08 units, and the largest deviating point (34) differs by around one pKaH unit in absolute values. The correlation in Fig. 2 remains practically the same when using only the c0 conformer (Fig. 3). Considering the overall standard deviation of the correlation eqn (4), the predicted pKaH values are not derived with substantially higher precision when using all conformers compared to using only the most stable one. Thus, in the case of predicting pKaH values of phosphanes in MeCN, conformer searches at a lower level of theory and complete geometry calculation (geometry optimization at BP-TZVP level, frequency calculation, and single-point calculation at BP-TZVPD level) only for the most stable structures (neutral and cation) can be considered to be sufficient.
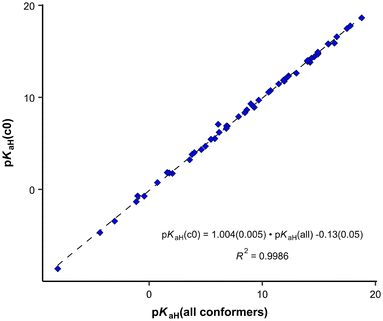 | ||
| Fig. 3 Correlation between calculated pKaH values using only the most stable conformer (c0) and all conformers. | ||
The pKaH value, a measure of the acidity of a hydrogen atom in a molecule, primarily reflects the electronic factors influencing the acidity/basicity center and is less affected by steric hindrance caused by more distant substituents. However, with substituents close to the protonation site, steric effects can sometimes significantly impact the stability of the protonated form and the accessibility of the hydrogen atom. For instance, in aromatic phosphanes, ortho-substitutions might engage in intramolecular hydrogen bonding with the proton, thereby significantly affecting the pKaH value. Even in the absence of a hydrogen bond, ortho-substituents may offer additional stabilization of the protonated form. In the calculated structure of protonated P[2,6-(MeO)2-C6H3]3 (6), the distance between the proton and the oxygens in MeO groups is smaller (∼2.45 Å) than the sum of their van der Waals radii (2.6 Å), suggesting the presence of some stabilizing effect, e.g., electrostatic stabilization. However, this cannot be called a true intramolecular hydrogen bond as the H–O distance is too large and the P–H–O angle is very narrow (around 91°). Consequently, while pKaH values offer insights into the electronic properties of compounds, they may not fully encompass the steric and structural factors.
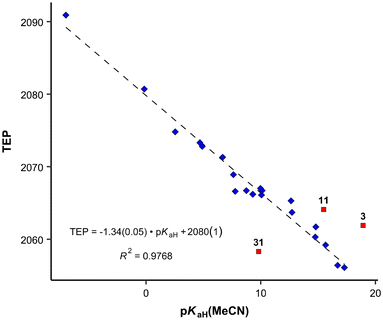
Previously, the basicities of phosphanes and other ligands have already been utilized to predict electronic parameters and have been correlated with TEP values.47,48 However, the dataset used was considerably limited in size. Given the ample availability of pKaH values in our work, we can assess how effectively they mirror the donor and acceptor properties similar to TEP values (Fig. 4), eliminating the necessity to calculate or synthesize the actual metal-ligand complex. The correlation between pKaH(MeCN) values and available TEP values (excluding three outliers, see below) is expressed by the following equation:
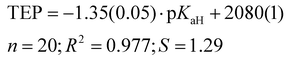 | (5) |
From the data available, three points stand out according to Grubbs's test as outliers – PMe3 (11), P(2-MeO-C6H4)3 (31) and P(dma)3 (3). The latter has a P–N bond, unlike all other phosphanes in Fig. 4, which may be the cause for the deviation. In the case of P(2-MeO-C6H4)3, it is possible that the ortho-MeO group forms a specific interaction with Ni-metal, leading inductively to a considerable decrease in TEP value (around 20 cm−1), or the ν(CO) measurements are somehow erroneous. PMe3 is the smallest of the studied ligands. The correlation with all points included is presented in the SI. The differences of the correlation coefficients are minor. However, the identities of the outliers give useful information regarding the limits of using this correlation for predictions.
Computational gas-phase proton affinity (PA), similar to the gas-phase basicity (GB) utilized in this study, and HOMO energies have been employed to estimate the suitability of phosphine ligands.13 However, our findings indicate that gas-phase computational results demonstrate a markedly weaker correlation with solution-phase values like TEP. We observe a considerably weaker correlation between GB and TEP (R2 = 0.807) compared to pKaH values and TEP (R2 = 0.977). Moreover, when comparing our calculated parameters to other parameters from the literature (e.g., Tolman cone angle), the correlation tends to be inferior for gas-phase values.
Another crucial factor in ligand screening involves considering the size of a ligand. The range of angles attributed to a single ligand can be quite extensive. This diversity is demonstrated in Fig. 6, where vertical bars represent the ranges of various cone angles reported in the literature, including solid cone angle.9,30,37
Tolman described that the steric demand of phosphane ligands is poorly characterized by their valence angles (in this work θCPC).49 However, we wanted to test whether the CPC angle, determined through a simple and straightforward “three-click method”, could offer any reasonable possibility to predict the steric demand of a phosphane and if this simplified method may suffice for preliminary screening purposes. The CPC angle used in this work represents the average of three angles from the most stable conformer of the protonated phosphane (the single CPC angle is depicted in Fig. 5). We opted for the protonated rather than neutral form because it may better represent the structure of the ligand in the metal complex, given the potential influence of the lone pair. However, the CPC angle can also be determined from a neutral phosphane, as it correlates well with the angle observed in its corresponding cation. θCPC is part of the deformation coordinate S4′,36 however, the correlation is weak between these two values.
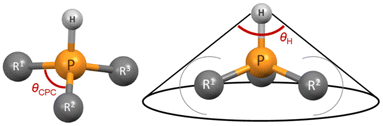 | ||
| Fig. 5 Single CPC angle (left); the average CPC angle used in this work is calculated using all three single CPC angles. θH angle (right) of a phosphane. | ||
It is apparent that the correlation involving all available compounds would be relatively poor (Fig. 6). We eliminated the most deviating compounds from the correlation. For instance, P(2-Me-C6H4)3 (34) stands apart from the main group, manifesting a smaller CPC angle than expected. This can be attributed to the orientation of ortho methyl groups towards the proton, which allows for the phenyl groups to be compressed (see below). It is conceivable that phosphanes with rigid, sterically cumbersome substituents need to be treated separately from others, although there is not enough data in this study to elaborate on this point. Additionally, it is evident that the CPC and cone angles may not correlate for flexible ligands – significant deviation is observed primarily for PNp3 (21) and, to a lesser extent, for PBn3 (32). Simultaneously, accounting for the diversity reflected in the literature data, as denoted by the vertical bars in Fig. 6, we observe that most of the points fall within the range of various ligand cone angles. The prediction error (RMSD) produced by eqn (6) (composed excluding outliers) over the whole dataset (incl. outliers) is 17 degrees.
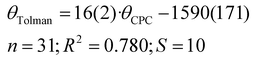 | (6) |
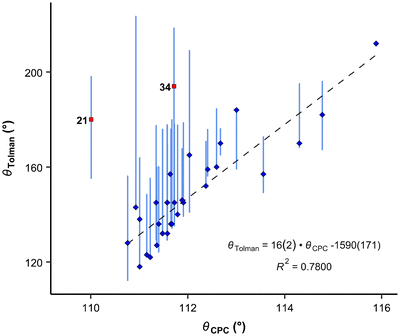 | ||
| Fig. 6 Correlation between CPC and Tolman angles. Blue diamonds: datapoints included in the correlation denoted by a dashed line; red squares: points omitted from the correlation (outliers according to the Grubbs test). Vertical bars show ranges of various cone angles reported in the literature, including solid cone angle.9,30,37 | ||
Moreover, the CPC angle may hold significance as a property for ligands. It has been shown that PNp3 (21) and P(t-Bu)3 (5) exhibit similar ligand cone angles (180° and 182°, respectively) and electronic properties, but they demonstrate markedly different catalytic properties, particularly concerning bulky substrates.28
We see that the CPC method necessitates distinct treatment for different phosphanes. Therefore, we also propose an alternative option that utilizes the exact cone angle concept.30 In this approach, we calculate the cone angle for the most stable protonated conformer obtained using the COSMO model, utilizing the proton as the apex (Fig. 5); the distance between P and H atoms comes from the optimized structure and is between 1.409 to 1.422 Å. This angle is denoted as θH. Since the proton lies within the van der Waals sphere of phosphorus, phosphorus is, by necessity, ignored in the calculation. Alternatively, the virtual apex point can be moved to the suitable distance along the P–H line. We found the results of both methods to have similar predictive capacity.
The θH values correlate relatively well with Tolman cone angle. The θH angle of most stable conformer yields to the correlation equation (eqn (7) and Fig. 7):
 | (7) |
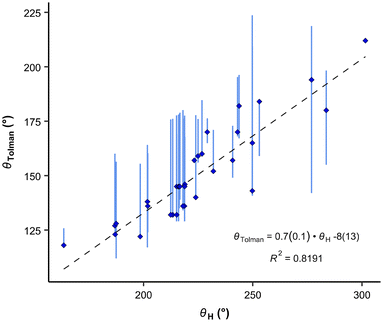 | ||
| Fig. 7 Correlation between the Tolman cone angles and the exact cone angle of the cation with hydrogen as the apex. Vertical bars show the range of various cone angles reported in the literature, including solid cone angle.9,30,37 | ||
It is interesting, that the conformers with the smallest θH values give only very slightly improved R2 for the correlation (0.827), but the conformers with the highest energy and largest θH angles considerably worsen correlations (R2 = 0.689 and 0.625, respectively). This demonstrates again, that for fast ligand screening, only the most stable conformer needs to be found.
Our results exhibit a good correlation with the exact cone angles reported in ref. 30 which were calculated for Pd-complexes (denoted in ref. 30 as θ° (Pd) and here as θPd). In cases where an exact cone angle was provided for two conformers – with maximum and minimum cone angles – the average values were used for the correlation. The correlation is presented in Fig. 8.
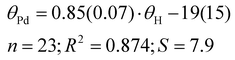 | (8) |
 | ||
| Fig. 8 Correlation between the average exact cone angle of palladium complexes and the exact cone angle of the cation with hydrogen as the apex. Vertical bars show the range of various cone angles reported in the literature, including solid cone angle.9,30,37 | ||
In the correlation in Fig. 8 and eqn (8), the maximum θPd angle, not the average, was used for P(2-Me-C6H4)3 (34), as the average θPd angle does not correlate as well with the θH angle of the most stable conformer. The average θPd angle of 34 is heavily influenced by the tightest, energetically unfavoured conformer, as it exhibits a more than 40° smaller θH angle (Table 3). A similar effect can be observed for the Tolman cone angle (Fig. 6), where 34 is an outlier when the θCPC angle of the most stable conformer is used. However, if we were to use the tightest conformer, where all Me groups point away from the phosphorus (Table 3), then it would align well with the correlation. For 34, the variability of the literature values is also high, which comes from the involvement of different conformers. In principle, this can be the case with all asymmetrically ortho-substituted triphenylphoshanes, which have to be treated with caution. Energies and angles for different conformers of 34 are presented in Table 3.
| All Me groups towards P | Two Me groups towards P | One Me group towards P | No Me groups towards P | |
|---|---|---|---|---|
| a BP86/def-TZVP/COSMO//BP86/def2-TZVPD/COSMO. b Ref. 30. c Ref. 49; exact conformer not known. | ||||
ΔEH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [kcal mol−1] a [kcal mol−1] |
0 | 1.7 | 4.7 | 7.8 |
| θ CPC [°] | 111.7 | 113.1 | 114.4 | 115.7 |
| θ H [°] | 276.9 | 264.2 | 252.7 | 236.3 |
| ΔEPd [kcal mol−1]b | 0 | — | — | 12.9 |
θ
Pd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b [°] b [°] |
208.2 | — | — | 175.6 |
| θ Tolman [°] | 194c | |||
Conclusions
This work provides previously unpublished experimental basicity values for 12 phosphanes measured using either UV-Vis or NMR methods. Computational pKaH values for 56 phosphanes are provided. Furthermore, self-consistent pKaH values of 13 additional phosphanes from the literature are presented. In total, these data cover pKaH(MeCN) values spanning almost 30 orders of magnitude. Steric parameters are also calculated for all 56 phosphanes.A framework for evaluating the electronic and steric properties of phosphanes is proposed. It is suggested that the conventional Tolman Electronic Parameters (TEP values) could be replaced with pKaH values based on the correlation between the two. The pKaH values are more accessible due to the availability and ease of calculations – obtaining the computational pKaH values is relatively straightforward with the COSMO-RS method, requiring only the identification and optimization of the most stable conformers of neutral and protonated forms. This approach enables facile ligand screening, which considerably simplifies the assessment of phosphanes as potential ligands.
The CPC angles or the exact cone angles of protonated phosphanes (θH), depending on the set of phosphanes, may be used instead of various previously utilized cone angles for preliminary screening purposes. The CPC angle serves as the most user-friendly property for ligand size, readily obtainable from the computational or crystal structure of a phosphane. However, it has some limitations, particularly with branched phosphanes. In cases where the CPC angle proves inadequate, θH can be employed as an alternative.
This prospective adjustment could streamline ligand screening processes in the future, thereby circumventing the necessity for the computation or preparation of metal-ligand complexes.
Experimental
Instruments and materials
1H spectra for measuring pKaH values of P(dma)3, P(pyrr)3, and PCy3 were recorded on a Bruker Avance III HD spectrometer (700 MHz) in CH3CN. Bruker Topspin software version 3.2 was used for spectrum processing. 1H chemical shifts were calibrated relative to the solvent peak: CH3CN/CD3CN 1H 1.94 ppm. All other pKaH(MeCN) measurements were carried out using UV-Vis spectrometer Lambda 40. The calculations were done using the following software: Avogadro 1.95.0, Tmolex 23.0.0, Turbomole 7.7, COSMOconf 21.0, COSMOtherm 23.0.0, R 4.3.2, and RStudio 2023.12.0. Air- and moisture-sensitive substances were handled in the Vigor SG1200/750TS glovebox. Karl Fischer titration was carried out on the Mettler Toledo DL32 coulometer to determine water content. Acetonitrile (Romil 190 SpS far UV/gradient quality) was used as a solvent for pKaH measurements after drying on molecular sieves (3 Å) for at least 12 hours, which ensured a water content under 6 ppm. All reagents were obtained from commercial sources and used without further purification. The following phosphanes were prepared according to previously described procedures: PMes3,50,51 P[2,4,6-(MeO)3-C6H2]Ph2, P[2,4,6-(MeO)3-C6H2]2Ph and P[2,4,6-(MeO)3-C6H2]3,52,53 P(3-MeO-C6H4)3,54 P[3,5-(MeO)2-C6H3]3,55,56 PCyPh2,57 P(1-Napht)Ph2,58 and P[2,6-(MeO)2-C6H3]3.52,53,55 Synthesis, purification, and identification of the used noncommercial reference bases are described in ref. 59, 60 and 61. The obtained spectral data corresponded to that previously reported. The preparation of the reference base 4-(Ph-N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-C6H4-N
N)-C6H4-N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P1(dma)2Ph is detailed in the ESI.†
P1(dma)2Ph is detailed in the ESI.†
pKaH measurements
A relative pKaH measurement method was employed to obtain the pKaH values of phosphanes.44,62,63 In this approach, a base under examination was titrated alongside a reference base within a single solution to ascertain the difference in pKaH values (ΔpKaH).NMR titration method
Inside a glovebox, three solutions were prepared in vials: (1) basic titrant t-Bu-N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P(pyrr)3, (2) acidic titrant CH3SO3H, and (3) the substance under investigation + reference(s). Typically, two references were concurrently employed, and the comparison of the obtained difference in pKaH values between these references with the difference of their pKaH values in ref. 44 served as an additional criterion for validating the method. Dry acetonitrile was used as the solvent (CD3CN was used for PCy3), and the concentrations were in the order of n × 10−3 M for the measured substances and in the order of n × 10−2 M for titrants. The solution containing the bases of interest (0.5 ml) was pipetted into three NMR tubes: two of them were standard NMR tubes, where 0.5 equiv. of basic titrant was added to one and 1.2–1.5 equiv. of acidic titrant to the other to obtain the corresponding (de)protonated forms. The third tube was a J Young NMR guard tube with a 1.5 ml vial cap (with a septum), where titration was later conducted at the NMR machine. Parafilm was applied to all vials and NMR tubes around the caps.
P(pyrr)3, (2) acidic titrant CH3SO3H, and (3) the substance under investigation + reference(s). Typically, two references were concurrently employed, and the comparison of the obtained difference in pKaH values between these references with the difference of their pKaH values in ref. 44 served as an additional criterion for validating the method. Dry acetonitrile was used as the solvent (CD3CN was used for PCy3), and the concentrations were in the order of n × 10−3 M for the measured substances and in the order of n × 10−2 M for titrants. The solution containing the bases of interest (0.5 ml) was pipetted into three NMR tubes: two of them were standard NMR tubes, where 0.5 equiv. of basic titrant was added to one and 1.2–1.5 equiv. of acidic titrant to the other to obtain the corresponding (de)protonated forms. The third tube was a J Young NMR guard tube with a 1.5 ml vial cap (with a septum), where titration was later conducted at the NMR machine. Parafilm was applied to all vials and NMR tubes around the caps.
Initially, the spectra of the (de)protonated forms of the bases were measured with NMR, followed by the titration process. Prior to each measurement, shimming was carried out using the MeCN peak to ensure the optimal quality of the peaks. The first spectrum was acquired without the titrant. Titrant was drawn into the syringe from a sealed vial through a septum and added to the NMR tube also through a septum to minimize water content (water content was checked after titration in randomly selected samples and was typically below 10 ppm and never higher than 150 ppm; CD3CN used for PCy3 had a higher water content than regularly used CH3CN). The titrant was added in increments of 2–10 drops depending on the previous spectrum and dissociation levels of the bases. As the peaks of some phosphanes broaden during titration and their chemical shifts cannot always be precisely determined due to overlapping with additional peaks, caution must be exercised during titrant addition to obtain a sufficient number of data points at appropriate dissociation levels.
To calculate the ΔpKaH values, the chemical shifts of the fully protonated forms (δB1H+ and δB2H+), the fully deprotonated forms (δB1 and δB2), and the chemical shifts of the investigated compounds at intermediary states (δ1 and δ2) were used (eqn (9)).43δ1 and δ2 were acquired for each titration point where the chemical shifts correspond to equilibrium mixtures of protonated and deprotonated forms at a given pH (exact pH value is irrelevant). The final ΔpKaH value was averaged over at least three titration points (usually five or more) where (δ − δB)/(δBH+ − δB) was between 0.1 and 0.9 for both bases.
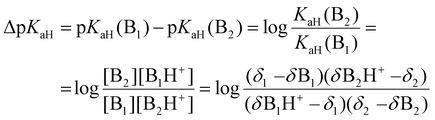 | (9) |
UV-Vis spectrophotometric titration method
UV-Vis spectrophotometric titration method and setup used in this work is previously published by Saame et al.63 In essence, each base, both the reference and the one under investigation, is individually titrated to obtain UV-Vis spectra for their fully protonated and deprotonated forms. Subsequently, a titration is conducted using a mixture containing both bases. By analyzing the spectral data acquired from this mixture at various wavelengths and employing multilinear regression analysis, the dissociation levels α = [B]/([B] + [BH+]) of the protonated forms for both bases are determined across all titration mixtures. These α values are then used to calculate the differences of the pKaH(MeCN) values (ΔpKaH) of the two bases according to the following equation: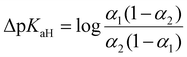 | (10) |
The pKaH(MeCN) values were obtained as a result of ΔpKaH measurements against at least three different reference bases. The concentrations of bases in all the solutions were in the order of n × 10−5 M, and the concentrations of the acidic (CH3SO3H) and basic (t-Bu-N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P(pyrr)3) titrant were in the order of n × 10−3 M.
P(pyrr)3) titrant were in the order of n × 10−3 M.
Calculations
Gas-phase calculations were conducted following the method outlined in ref. 19. Results are presented in ESI.† For HOMO/LUMO energies, single point calculation was carried out at MP2/def2-TZVPP level of theory for the geometries optimized at BP86/def2-TZVP level.Basicities in solution were estimated by calculating the pKaH values with the COSMO-RS64–66 method and correcting them using existing experimental data17,18,67,68 for analogous compounds. In order to calculate the pKaH values with the COSMO-RS method, first, DFT calculations were conducted for multiple conformers of neutral and protonated forms in an ideal conductor, yielding the total energies of the structures alongside partial charge distributions on the molecular surface. These results were then employed as input for statistical thermodynamic calculations, determining the energies of intermolecular interactions within liquid mixtures, as well as the total Gibbs energies of molecules within the liquids.
The conformational search was carried out with COSMOconf69 software using the def-TZVP basis set (B86 functional) with the COSMO model. Reaching energy minima during geometry optimization was confirmed by calculating the vibrational spectra and ensuring that imaginary frequencies were absent or very small – wavenumbers were in the range of −5 to −36 cm−1 for 11 compounds (15 conformers). The effect of remaining imaginary frequencies was less than 0.1 units to the pKaH values. Subsequently, a single point calculation was conducted for all geometries using the def2-TZVPD basis set (BP86 functional), COSMO model, and Fine cavity parameter. QM calculations were carried out using TURBOMOLE V7.7.70 pKaH(MeCN) values were computed using COSMOtherm71 software (see ESI†). The parameterizations listed in Table 2 were compared for the prediction of pKaH values of phosphanes in acetonitrile. The BP_TZVPD_FINE_C30_1701 parametrization was applied to compute the pKaH(Calc.) values in MeCN, which were then correlated to derive the predicted pKaH(MeCN) values. Every older parameterization used in this work is available with COSMOtherm newer versions. All unique conformers with relative energy below 3 kcal mol−1 (when compared to the most stable conformer c0) were considered when calculating the pKaH values.
θ H angles were calculated numerically by finding the vector of the cone axis using an optimization function (the used code in R language72 is available in ESI†). The van der Waals radii of the elements were taken from ref. 30.
Data availability
The data that support the findings of this study are available in the ESI† of this article and in Data DOI repository at https://datadoi.ee/handle/33/604 (https://doi.org/10.23673/re-461).73Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grant PRG1736 from the Estonian Research Council and by the grant TK210 from the Estonian Ministry of Education and Research. Research was carried out using the instrumentation at the Estonian Center of Analytical Chemistry (TT4, https://www.akki.ee). The quantum-chemical computations were carried out in the High Performance Computing Center of the University of Tartu.73References
- F. R. Hartley, in Organophosphorus Compounds, John Wiley & Sons, Ltd, Chichester, UK, 1990, pp. 1–8 Search PubMed.
- B. T. Elie, C. Levine, I. Ubarretxena-Belandia, A. Varela-Ramírez, R. J. Aguilera, R. Ovalle and M. Contel, Eur. J. Inorg. Chem., 2009, 2009, 3421–3430 CrossRef PubMed.
- J. Broggi, C. A. Urbina-Blanco, H. Clavier, A. Leitgeb, C. Slugovc, A. M. Z. Slawin and S. P. Nolan, Chem. – Eur. J., 2010, 16, 9215–9225 CrossRef CAS PubMed.
- D. Amoroso, J. L. Snelgrove, J. C. Conrad, S. D. Drouin, G. P. A. Yap and D. E. Fogg, Adv. Synth. Catal., 2002, 344, 757–763 CrossRef CAS.
- R. A. Findeis and L. H. Gade, Eur. J. Inorg. Chem., 2003, 2003, 99–110 CrossRef.
- S. T. Nguyen and T. M. Trnka, in Handbook of Metathesis, ed. R. H. Grubbs, Weinheim, 2003, pp. 61–85 Search PubMed.
- M.-L. Pikma, M. Ilisson, R. Zalite, D. Lavogina, T. Haljasorg and U. Mäeorg, Chem. Heterocycl. Compd., 2022, 58, 206–216 CrossRef CAS.
- W. G. Whitehurst, J. Kim, S. G. Koenig and P. J. Chirik, J. Am. Chem. Soc., 2022, 144, 4530–4540 CrossRef CAS PubMed.
- W. Matsuoka, Y. Harabuchi, Y. Nagata and S. Maeda, Org. Biomol. Chem., 2023, 21, 3132–3142 RSC.
- D. W. Stephan, Chem, 2020, 6, 1520–1526 CAS.
- M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496 CrossRef CAS PubMed.
- F. Fache, E. Schulz, M. L. Tommasino and M. Lemaire, Chem. Rev., 2000, 100, 2159–2232 CrossRef CAS PubMed.
- N. Fey, A. C. Tsipis, S. E. Harris, J. N. Harvey, A. G. Orpen and R. A. Mansson, Chem. – Eur. J., 2006, 12, 291–302 CrossRef CAS PubMed.
- T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- K. Yoshimoto, H. Kawabata, N. Nakamichi and M. Hayashi, Chem. Lett., 2001, 30, 934–935 CrossRef.
- M. Fevre, J. Vignolle, V. Heroguez and D. Taton, Macromolecules, 2012, 45, 7711–7718 CrossRef CAS.
- L. Greb, S. Tussing, B. Schirmer, P. Oña-Burgos, K. Kaupmees, M. Lõkov, I. Leito, S. Grimme and J. Paradies, Chem. Sci., 2013, 4, 2788–2796 RSC.
- K. Haav, J. Saame, A. Kütt and I. Leito, Eur. J. Org. Chem., 2012, 2167–2172 CrossRef CAS.
- M.-L. Pikma, M. Lõkov, S. Tshepelevitsh, J. Saame, T. Haljasorg, L. Toom, S. Selberg, I. Leito and A. Kütt, Eur. J. Org. Chem., 2023, e202300453 CrossRef CAS.
- K. Vazdar, D. Margetić, B. Kovačević, J. Sundermeyer, I. Leito and U. Jahn, Acc. Chem. Res., 2021, 54, 3108–3123 CrossRef CAS PubMed.
- C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2953–2956 CrossRef CAS.
- C. A. Tolman, Chem. Rev., 1977, 77, 313–348 CrossRef CAS.
- G. A. Ardizzoia and S. Brenna, Phys. Chem. Chem. Phys., 2017, 19, 5971–5978 RSC.
- D. S. Coll, A. B. Vidal, J. A. Rodríguez, E. Ocando-Mavárez, R. Añez and A. Sierraalta, Inorg. Chim. Acta, 2015, 436, 163–168 CrossRef CAS.
- R. Kalescky, E. Kraka and D. Cremer, Inorg. Chem., 2014, 53, 478–495 CrossRef CAS PubMed.
- T. E. Müller and D. M. P. Mingos, Transition Met. Chem., 1995, 20, 533–539 CrossRef.
- C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2956–2965 CrossRef CAS.
- S. M. Raders, J. N. Moore, J. K. Parks, A. D. Miller, T. M. Leißing, S. P. Kelley, R. D. Rogers and K. H. Shaughnessy, J. Org. Chem., 2013, 78, 4649–4664 CrossRef CAS PubMed.
- T. E. Barder and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 12003–12010 CrossRef CAS PubMed.
- J. A. Bilbrey, A. H. Kazez, J. Locklin and W. D. Allen, J. Comput. Chem., 2013, 34, 1189–1197 CrossRef CAS PubMed.
- D. White, B. C. Taverner, P. g. l. Leach and N. J. Coville, J. Comput. Chem., 1993, 14, 1042–1049 CrossRef CAS.
- A. C. Hillier, W. J. Sommer, B. S. Yong, J. L. Petersen, L. Cavallo and S. P. Nolan, Organometallics, 2003, 22, 4322–4326 CrossRef CAS.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
- J. Jover, N. Fey, J. N. Harvey, G. C. Lloyd-Jones, A. G. Orpen, G. J. J. Owen-Smith, P. Murray, D. R. J. Hose, R. Osborne and M. Purdie, Organometallics, 2010, 29, 6245–6258 CrossRef CAS.
- B. J. Dunne, R. B. Morris and A. G. Orpen, J. Chem. Soc., Dalton Trans., 1991, 653–661 RSC.
- K. D. Cooney, T. R. Cundari, N. W. Hoffman, K. A. Pittard, M. D. Temple and Y. Zhao, J. Am. Chem. Soc., 2003, 125, 4318–4324 CrossRef CAS PubMed.
- J. Jover and J. Cirera, Dalton Trans., 2019, 48, 15036–15048 RSC.
- B. Staskun, J. Org. Chem., 1981, 46, 1643–1646 CrossRef CAS.
- D. White and N. J. Coville, in Advances in Organometallic Chemistry, ed. F. G. A. Stone and R. West, Academic Press, 1994, vol. 36, pp. 95–158 Search PubMed.
- M. Charton, J. Am. Chem. Soc., 1975, 97, 1552–1556 CrossRef CAS.
- T. L. Brown and K. J. Lee, Coord. Chem. Rev., 1993, 128, 89–116 CrossRef CAS.
- A. Kütt, I. Leito, I. Kaljurand, L. Sooväli, V. M. Vlasov, L. M. Yagupolskii and I. A. Koppel, J. Org. Chem., 2006, 71, 2829–2838 CrossRef PubMed.
- E. Parman, M. Lõkov, R. Järviste, S. Tshepelevitsh, N. A. Semenov, E. A. Chulanova, G. E. Salnikov, D. O. Prima, Y. G. Slizhov, I. Leito and A. V. Zibarev, ChemPhysChem, 2021, 22, 2329–2335 CrossRef CAS PubMed.
- S. Tshepelevitsh, A. Kütt, M. Lõkov, I. Kaljurand, J. Saame, A. Heering, P. G. Plieger, R. Vianello and I. Leito, Eur. J. Org. Chem., 2019, 6735–6748 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, F. Eckert and W. Arlt, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 101–122 CrossRef CAS PubMed.
- M. N. Golovin, M. M. Rahman, J. E. Belmonte and W. P. Giering, Organometallics, 1985, 4, 1981–1991 CrossRef CAS.
- S. Joerg, R. S. Drago and J. Sales, Organometallics, 1998, 17, 589–599 CrossRef CAS.
- C. A. Tolman, Chem. Rev., 1977, 77, 313–348 CrossRef CAS.
- B. I. Stepanov, E. N. Karpova and A. I. Bokanov, J. Gen. Chem. USSR, 1969, 39, 1514–1519 Search PubMed.
- J. F. Blount, D. Camp, R. D. Hart, P. C. Healy, B. W. Skelton and A. H. White, Aust. J. Chem., 1994, 47, 1631–1639 CrossRef CAS.
- I. S. Protopopov and M. Y. Kraft, Zh. Obshch. Khim., 1963, 33, 3050–3052 CAS.
- M. Wada, S. Higashizaki and A. Tsuboi, J. Chem. Res., Synop., 1985, 38–39 CAS.
- L. Lamza, J. Prakt. Chem., 1964, 25, 294–300 CrossRef CAS.
- K. R. Dunbar and S. C. Haefner, Polyhedron, 1994, 13, 727–736 CrossRef CAS.
- D. Sinou, D. Maillard, A. Aghmiz and A. M. Masdeu i-Bultó, Adv. Synth. Catal., 2003, 345, 603–611 CrossRef CAS.
- S. O. Grim, E. F. Davidoff and T. J. Marks, Z. Naturforsch., B: Anorg. Chem., Org. Chem., Biochem., Biophys., Biol., 1971, 26, 184–190 CrossRef CAS.
- Y.-L. Zhao, G.-J. Wu, Y. Li, L.-X. Gao and F.-S. Han, Chem. – Eur. J., 2012, 18, 9622–9627 CrossRef CAS PubMed.
- T. Rodima, V. Mäemets and I. Koppel, J. Chem. Soc., Perkin Trans. 1, 2000, 2637–2644 RSC.
- T. Rodima, I. Kaljurand, A. Pihl, V. Mäemets, I. Leito and I. A. Koppel, J. Org. Chem., 2002, 67, 1873–1881 CrossRef CAS PubMed.
- S. Selberg, T. Rodima, M. Lõkov, S. Tshepelevitsh, T. Haljasorg, S. Chhabra, S. A. Kadam, L. Toom, S. Vahur and I. Leito, Tetrahedron Lett., 2017, 58, 2098–2102 CrossRef CAS.
- A. Kütt, S. Selberg, I. Kaljurand, S. Tshepelevitsh, A. Heering, A. Darnell, K. Kaupmees, M. Piirsalu and I. Leito, Tetrahedron Lett., 2018, 59, 3738–3748 CrossRef.
- J. Saame, T. Rodima, S. Tshepelevitsh, A. Kütt, I. Kaljurand, T. Haljasorg, I. A. Koppel and I. Leito, J. Org. Chem., 2016, 81, 7349–7361 CrossRef CAS PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- I. Kaljurand, A. Kütt, L. Sooväli, T. Rodima, V. Mäemets, I. Leito and I. A. Koppel, J. Org. Chem., 2005, 70, 1019–1028 CrossRef CAS PubMed.
- K. Kaupmees, R. Järviste and I. Leito, Chem. – Eur. J., 2016, 22, 17445–17449 CrossRef CAS PubMed.
- BIOVIA COSMOconfX (version 21.0) Dassault Systèmes, 2021 Search PubMed.
- TURBOMOLE V7.7 2022, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
- BIOVIA COSMOtherm (version 23.0.0) Dassault Systèmes, 2023 Search PubMed.
- R Core Team (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/ Search PubMed.
- University of Tartu “UT Rocket” share.neic.no, DOI:10.23673/PH6N-0144.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01430h |
| This journal is © The Royal Society of Chemistry 2024 |