Structure and size of complete hydration shells of metal ions and inorganic anions in aqueous solution

Abstract

The structures of nine hydrated metal ions in aqueous solution have been redetermined by large angle X-ray scattering to obtain experimental data of better quality than those reported 40–50 years ago. Accurate M–O_I and M–(O_I–H)⋯O_II distances and M–O_I(H)⋯O_II bond angles are reported for the hydrated magnesium(II), aluminium(III), manganese(II), iron(II), iron(III), cobalt(II), nickel(II), copper(II) and zinc(II) ions; the subscripts I and II denote oxygen atoms in the first and second hydration sphere, respectively. Reported structures of hydrated metal ions in aqueous solution are summarized and evaluated with emphasis on a possible relationship between M–O_I–O_II bond angles and bonding character. Metal ions with high charge density have M–O_I–O_II bond angles close to 120°, indicative of a mainly electrostatic interaction with the oxygen atom in the water molecule in the first hydration shell. Metal ions forming bonds with a significant covalent contribution, as e.g. mercury(II) and tin(II), have M–O_I–O_II bond angles close to 109.5°. This implies that they bind to one of the free electron pairs in the water molecule. Comparison of M–O bond distances of hydrated metal ions in the solid state with one hydration shell, and in aqueous solution with in most cases at least two hydration shells, shows no significant differences. On the other hand, the X–O bond distance in hydrated oxoanions increases by ca. 0.02 Å in aqueous solution in comparison with the corresponding X–O distance in the solid state. A linear correlation is observed between volume, calculated from the van der Waals radius of the hydrated ion, and the ionic diffusion coefficient in aqueous solution. This correlation strongly indicates that monovalent metal ions, except lithium and silver(I), and singly-charged monovalent oxoanions have a single hydration shell. Divalent metal ions, bismuth(III) and the lanthanoid(III) and actinoid(III) ions have two hydration shells. Trivalent transition and tetravalent metal ions have two full hydration shells and portion of a third one. Doubly charged oxoanions have one well-defined hydration shell and an ill-defined second one.

---

Introduction

Hydrated metal ions and anions bind different number of water molecules in aqueous solution depending on their size and charge. The number of water molecules close to an ion with different measurable physico-chemical parameters to those of bulk water molecules can be regarded as the hydration number. Except for the most weakly hydrated ions with only one hydration shell, these can be divided into hydration shells where on average one water molecule in an inner shell forms hydrogen bonds to two or three water molecules in the next shell, Fig. 1. Strongly polarized water molecules bound to a highly charged metal ion and thus having a depleted charge on hydrogen, bind two water molecules in the second hydration shell, Fig. 1 left panel. When the water molecules are less polarized, each water molecule accepts one and donates two hydrogen bonds to other water molecules outside, as in the second hydration shell of a metal ion and in the hydration shells of anions, Fig. 1.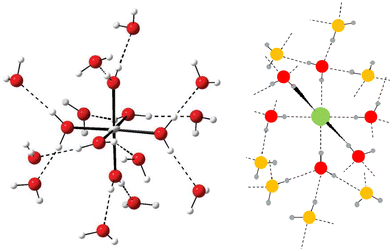

Fig. 1 Left panel: Principle structure of a highly charged metal ion coordinating two hydration shells. The figure has been prepared from the crystallographic data in ref. 7. Right panel: Principle structure of a monoatomic anion coordinating a complete first hydration shell (red oxygen atoms) and portion of a second one (orange oxygen atoms).

As part of this study the structures of nine hydrated metal ions have been redetermined in aqueous solution by large angle X-ray scattering (LAXS) to provide improved data to be placed in a general context. LAXS and large angle neutron scattering are more or less the only experimental structure methods that accurately determine long distances and thus can define to determine the broad distance distributions of the second and third hydration shells of hydrated ions in aqueous solution. Furthermore, second hydration shells or portions of them have only been described in very few cases in the solid state, vide infra. Therefore, the structure determination of hydration shells outside the first one is necessarily performed in aqueous solution. Extended X-ray Absorption Fine Structure (EXAFS) cannot be used to determine such distances as both increasing distance and the large Debye–Waller coefficient, σ², strongly damp the EXAFS signal as discussed in detail elsewhere.¹

Double difference infrared (DDIR) spectroscopy in aqueous solution containing 8% HDO, can be used to determine the O–D bond strength of the water molecules not in the aqueous bulk but bound to the ions in an electrolyte.² The value of the O–D stretching vibration in the HDO molecule, bound to an ion, reflects the strength of the M–O(–D) or X⋯D(–O) bonds, and can be compared to the O–D bond in HDO bulk water, observed at 2509 cm⁻¹.² If the M–O(–D) or X⋯D(–O) bond is stronger than the (D–)O⋯D(–O) one in the aqueous bulk, the D–O stretching vibration will have a value less than 2509 cm⁻¹. Conversely, when the M–O(–D) or X⋯D(–O) bond is weaker than the intermolecular hydrogen bond in bulk water, the O–D stretching frequency will be higher than 2509 cm⁻¹. The lower the O–D stretching frequency, the stronger M–O(–D) or X⋯D(–O) bond, and vice versa. The X⋯D(–O) bond strength is proportional to the polarization power of anions, while for M–O(–D) bonds the O–D stretching frequencies have specific values, ca. 2535, 2420 and 2200 cm⁻¹.² These correspond to water in the hydration shell of weakly hydrated metal ions and the outermost hydration shell when several hydration shells are present, in the first hydration shell of metal(II) ions, lanthanoid(III) and bismuth(III) ions or the second hydration shell of tri- and tetra-positive metal ions, and in the first hydration shell of tri- and tetra-positive metal ions, respectively.² Similar observations have been made for a recently developed vibrational spectroscopic technique, Raman difference with simultaneous curve fitting (RD-SCF).³ RD-SCF uses the O–H stretching vibration in non-bulk water where bands at ca. 3600 and 3300 cm⁻¹ are compared with the corresponding value of bulk water at 3420 cm⁻¹. The bands at ca. 3600 and 3300 cm⁻¹ correspond to weakly bound water, and more strongly bound water molecules in e.g. the first hydration shell of di-and trivalent metal ions, respectively.³ The information from these methods determines whether a metal ion has structure making or breaking properties.⁴

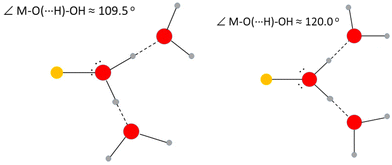
The positions relative to the metal ion of the oxygen atoms in the first and second hydration spheres give the M–O_I⋯O_II angle. This may be taken to indicate the bonding character of the M–O bond to the water molecules in the first hydration shell. Metal ions involved in an essentially electrostatic interaction are expected to have an M–O_I⋯O_II angle close to 120°, while metal ions forming significant covalent interactions will bind to one of the free electron-pairs on the water oxygen. This angle is expected to be close to the tetrahedral angle, 109.5°, due to the sp³ hybridization of the water oxygen, Fig. 2.

Fig. 2 Left panel: Structure of a water molecule bound to a metal ion forming M–O bonds with a high degree of covalency; right panel: structure of a water molecule bound to a metal ion forming essentially electrostatic M–O bonds.

A series of publications from Voigt et al.^5–7 has provided crystal structures of hydrated metal ions containing more water than normally found in solid structures due to crystallization at low temperature. These include MgCl₂·12H₂O,⁵ CaBr₂·9H₂O,⁶ AlCl₃·15H₂O, AlBr₃·15H₂O and AlI₃·17H₂O.⁷ AlI₃·17H₂O has two complete hydration shells with each water in the first hydration shell hydrogen binding two water molecules in the second one with a mean O_I–(H)⋯O_II distance of 2.663 Å.⁷ In the compounds MgCl₂·12H₂O and CaBr₂·9H₂O, portions of a second hydration shell are observed with mean O_I–(H)⋯O_II distances of 2.783 and 2.774 Å, respectively.^5,6

The present LAXS studies have been performed on 1.5 mol dm⁻³ aqueous solutions of metal perchlorates in perchloric acid to avoid hydrolysis. This is a compromise between the aim to collect data with as large contribution from the hydrated metal ion to the LAXS signal as possible, and to have sufficient amount of water for complete hydration and thereby limit the interactions between the solute ions. The results show that the hydrated metal ions bind the amount of water they require for complete hydration, while there may be some deficit of water for complete hydration of the perchlorate ions.

One aim of the present study was to collect LAXS data of nine hydrated metal ions in aqueous solution of better quality than data collected 40–50 years ago. While the previously reported M–O bond distances have been largely substantiated, the limited and somewhat scattered estimates of distances to the second hydration sphere, if reported, have been considerably improved. Another aim was to use these data to augment the general knowledge of reported structures of hydrated metal ions and inorganic anions in aqueous solution, with special emphasis on a possible relationship between the M–O_I–O_II bond angle and bonding character of the metal ion. To support the information from LAXS data, reported vibrational spectroscopy data on O–D or O–H stretching frequencies in water molecules in the first and second hydration spheres have been used as well as reported theoretical simulations of hydrated metal ions in aqueous solution. The correlation between the size of a hydrated ion and its ionic diffusion coefficient is discussed as a means of providing further information about the number of water molecules with different physico-chemical properties to bulk water surrounding an ion.

Experimental

Chemicals

Hexaaquamagnesium(II) perchlorate (Thermo Scientific, 99%), [Mg(H₂O)₆](ClO₄)₂, nonaaquaaluminum(III) perchlorate (Thermo Scientific, 99%), [Al(H₂O)₆](ClO₄)₃·3H₂O, hexaaquamanganese(II) perchlorate (Aldrich, 99%), [Mn(H₂O)₆](ClO₄)₂, hexaaquairon(II) perchlorate (Merck, 99%), [Fe(H₂O)₆](ClO₄)₂, hexaaquairon(III) perchlorate (Aldrich, 99%), [Fe(H₂O)₆](ClO₄)₃, hexaaquacobalt(II) perchlorate (Fluka, 99%), [Co(H₂O)₆](ClO₄)₂, hexaaquanickel(II) perchlorate (GFS Chemicals, 99%), [Ni(H₂O)₆](ClO₄)₂, hexaaquacopper(II) perchlorate (GFS Chemicals, 99%), [Cu(H₂O)₆](ClO₄)₂, hexaaquazinc(II) perchlorate (GFS Chemicals, 99%), [Zn(H₂O)₆](ClO₄)₂, and perchloric acid (Merck, 70 weigh%,) HClO₄, were used as purchased. All water used was deionized and MilliQ filtered, resistivity >18.2 MΩ cm.

Solutions

The solutions were prepared by dissolving weighed amounts of the salts in either 0.1 or 1.0 mol dm⁻³ perchloric acid for divalent or trivalent metal ion salts, respectively. The concentrations, densities and absorption coefficients of the perchloric acidic aqueous solutions used in the large angle X-ray scattering measurements are summarized in Table 1. Dissolution in perchloric acid was made to avoid hydrolysis reactions.

Table 1 Compositions (in mol dm⁻³), densities (ρ), and linear absorption coefficients of Mo-Kα radiation (μ) of the acidified aqueous solutions used in the LAXS experiments

Solute	[M^n+]	[ClO4^−]	[H^+]	[H2O]	ρ/g cm^−3	μ/cm^−1
Mg(ClO4)2	1.5008	3.0767	0.0751	48.6588	1.2086	2.709
Al(ClO4)3	1.5036	5.2107	0.6999	45.3949	1.3754	3.732
Mn(ClO4)2	1.5024	3.0778	0.0730	44.4087	1.1887	5.331
Fe(ClO4)2	1.5002	3.0719	0.0715	48.8097	1.2687	5.793
Fe(ClO4)3	1.5000	5.2000	0.7000	40.4582	1.3306	6.650
Co(ClO4)2	1.5019	3.0748	0.0710	49.6912	1.2896	6.342
Ni(ClO4)2	1.4999	3.0728	0.0730	49.1668	1.2795	6.650
Cu(ClO4)2	1.4864	3.0473	0.0745	50.2400	1.3027	7.386
Zn(ClO4)2	1.5060	3.0850	0.0730	49.1101	1.2901	8.027

---

Large angle X-ray scattering

A large-angle θ–θ diffractometer was used to measure the scattering of Mo Kα radiation, λ = 0.7107 Å, from the free surface of the aqueous solutions. The solutions were contained in a Teflon cuvette inside a radiation shield with beryllium windows. After monochromatization of the scattered radiation, by means of a focusing LiF crystal, the intensity was measured at 450 discrete points in the range 1 < θ < 65° (the scattering angle is 2θ). A total of 100 000 counts was accumulated at each angle and the whole angular range was scanned twice, corresponding to a statistical uncertainty of about 0.3%. The divergence of the primary X-ray beam was limited by 1° or 1/4° slits for different θ regions with overlap of some parts of the data for scaling purposes. All data treatment was carried out using the KURVLR program,⁸ which has been described in detail previously.⁹ The experimental intensities were normalized to a stoichiometric unit of volume containing one metal atom, using the scattering factors ƒ for neutral atoms, including corrections for anomalous dispersion, Δƒ′ and Δƒ′′,¹⁰ and values for Compton scattering.^11,12 For a better alignment of the intensity function, a Fourier back-transformation was applied to eliminate spurious (unrelated to any interatomic distances) peaks below 1.2 Å in the radial distribution function.¹³ Least-squares refinements of the model parameters were performed by means of the STEPLR program¹⁴ to minimize the error squares sum U = ∑w(s)·[i_exp(s) − i_cal(s)]².

Results

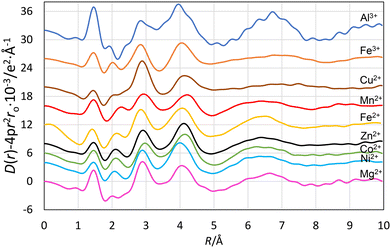
The new radial distribution functions (RDFs) from LAXS measurements for acidic aqueous solutions of magnesium(II), aluminum(III), manganese(II), iron(II), iron(III), cobalt(II), nickel(II), copper(II) and zinc(II) perchlorate show marked similarities with peaks at ca. 1.0, 1.5, 1.9–2.2, 2.9 and ca. 4.1 Å, Fig. 3. The peak at 1.0 Å corresponds to O–H bond distances in the water molecule, and the peak at 2.9 Å to the O_aq–(H)⋯O_aq distance in the aqueous bulk, and distance between the oxygens the first and second hydration shells, O_I–(H)⋯O_II, in the hydrated metal ion. The peaks at 1.9–2.2 Å and ca. 4.1 Å correspond to the M–O_I bond and the M–(O_I–H)⋯O_II distances in the hydrated metal ions. The peak at 1.45 Å, and the shoulder at 2.4 Å correspond to the Cl–O and O⋯O distances in the perchlorate ion. The fits of the individual systems are shown in Fig. 4, 5 and S1–S7,† and the refined structure parameters are summarized in Table 2. The structures of these and previously reported structures of hydrated metal ions are discussed in detail in the Discussion section, vide infra.

Fig. 3 RDFs of the hydrated metal ions in this study, magnesium(II) (no offset), nickel(II) (offset: +4), cobalt(II) (offset: +6), zinc(II) (offset: +8), iron(II) (offset: +12), manganese(II) (offset: +16), copper(II) (offset: +20), iron(III) (offset: +26) and aluminum(III) (offset: +32).

Fig. 4 (Top) LAXS radial distribution curves for a 1.50 mol dm⁻³ aqueous perchloric acidic solution of aluminum(III) perchlorate. Upper part: Separate model contributions (offset: 15) of the hydrated aluminum(III) ion (yellow line), the hydrated perchlorate ion (green line) and aqueous bulk (purple line). (Middle) Experimental RDF: D(r) − 4πr²ρ_o (black line); sum of model contributions (red line); difference (blue line). (Bottom) Reduced LAXS intensity functions s·i(s) (black line); model s·i_calc(s) (red line).

Fig. 5 (Top) LAXS radial distribution curves for a 1.50 mol dm⁻³ aqueous perchloric acidic solution of copper(II) perchlorate. Upper part: Separate model contributions (offset: 15) of the hydrated copper(II) ion (yellow line), the hydrated perchlorate ion (green line) and aqueous bulk (purple line). (Middle) Experimental RDF: D(r) − 4πr²ρ_o (black line); sum of model contributions (red line); difference (blue line). (Bottom) Reduced LAXS intensity functions s·i(s) (black line); model s·i_calc(s) (red line).

Table 2 Mean distances, d/Å, number of distances, N, and temperature coefficients, b/Ų, in the LAXS studies of the acidified aqueous magnesium(II), aluminum(III), manganese(II), iron(II), iron(III), cobalt(II), nickel(II), copper(II) and zinc(II) perchlorate solutions in the LAXS experiments at room temperature. The estimated standard deviations given within parenthesis include only statistical errors. The mean M–O bond distances in the [M(H₂O)₆]ⁿ⁺ complexes in the solid state, d(M–O) cryst./Å, are taken from Table S1 (ESI†)

Species/interaction	N	d/Å	b/Å^2	d(M–O) cryst./Å
[Mg(H2O)6(H2O)12]^2+
Mg–OI	6	2.069(5)	0.0061(4)	2.066
Mg(–OI–H)⋯OII	12	4.075(5)	0.0248(7)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.832(2)	0.0274(3)
Cl–O	4	1.452(2)	0.0026(2)
[Al(H2O)6(H2O)12(H2O)n]^3+
Al–OI	6	1.891(5)	0.0039(5)	1.883
Al(–OI–H)⋯OII	12	4.036(6)	0.0199(4)
Al(–OI–H⋯OII–H)⋯OIII	12	6.70(3)	0.030(4)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.820(2)	0.0302(3)
Cl–O	4	1.453(2)	0.0024(2)
[Mn(H2O)6(H2O)12]^2+
Mn–OI	6	2.174(2)	0.0059(5)	2.174
Mn(–OI–H)⋯OII	12	4.258(7)	0.0352(11)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.825(3)	0.0255(4)
Cl–O	4	1.451(2)	0.0025(2)
[Fe(H2O)6(H2O)12]^2+
Fe–OI	6	2.124(4)	0.0057(3)	2.120
Fe(–OI–H)⋯OII	12	4.092(7)	0.0317(8)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.832(2)	0.0282(9)
Cl–O	4	1.452(2)	0.0025(2)
[Fe(H2O)6(H2O)12]^3+
Fe–OI	6	1.999(2)	0.0040(3)	1.995
Fe(–OI–H)⋯OII	12	4.012(5)	0.0307(8)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.794(4)	0.0283(9)
Cl–O	4	1.454(2)	0.0026(2)
[Co(H2O)6(H2O)12]^2+
Co–OI	6	2.090(2)	0.0060(5)	2.087
Co(–OI–H)⋯OII	12	4.072(7)	0.0325(12)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.825(3)	0.0256(6)
Cl–O	4	1.452(2)	0.0026(2)
[Ni(H2O)6(H2O)12]^2+
Ni–OI	6	2.057(2)	0.0053(3)	2.055
Ni(–OI–H)⋯OII	12	3.981(6)	0.0304(10)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.834(2)	0.0266(4)
Cl–O	4	1.453(2)	0.0025(2)
[Cu(H2O)6(H2O)8]^2+
Cu–Oeq	4	1.965(5)	0.0040(3)	1.980
Cu–Oax1	1	2.161(9)	0.0043(12)	2.230
Cu–Oax2	1	2.29(1)	0.025(1)	2.36
Cu(–O–H)⋯O	8	4.094(4)	0.0277(10)
Oeq(–H)⋯OII and Oaq⋯Oaq	2	2.835(2)	0.0257(3)
Cl–O	4	1.451(2)	0.0023(2)
[Zn(H2O)6(H2O)12]^2+
Zn–OI	6	2.091(5)	0.0058(3)	2.088
Zn(–OI–H)⋯OII	12	4.100(5)	0.0318(8)
OI(–H)⋯OII and Oaq⋯Oaq	2	2.828(3)	0.0256(5)
Cl–O	4	1.452(2)	0.0024(2)

---

Discussion

The new LAXS data given above, and previously reported data on other metal ions and anions, can now be placed within the context of what is known broadly of the hydration characteristics of both cations and anions.

Hydrated alkali metal ions

A large number of experimental and theoretical simulation studies has been reported on the hydrated lithium ion in aqueous solution.^15–19 However, the spread in the reported results is very large, mainly due to the very weak scattering power of lithium in X-ray experiments and there is a large uncertainty in the experimental data. The hydrated lithium ion has been proposed to have tetrahedral or octahedral configuration in aqueous solution or a mixture of both. Tetrahedral coordination is predominant in the solid state with a mean Li–O bond distance of 1.941 Å for 53 structures, Table S1a (ESI†). A single structure each has been reported for the hydrated lithium ion in five- or six-coordination, giving mean Li–O bond distances of 2.044 and 2.144 Å, respectively, Table S1a (ESI†). Several different crystalline polyatomic lithium ion hydrates have described where lithium is in tetrahedral four-coordination, Table S1a (ESI†). The conclusion from these observations in both the solid state and aqueous solution is that the hydrated lithium ion prefers tetrahedral four-coordination with a mean Li–O bond distance of 1.95 Å. Four-coordination of the hydrated lithium ion is also supported by a vibrational spectroscopy study.²⁰ The presence of two O–D stretching bands belonging to the hydrated lithium ion in HDO, one below and one above the O–D stretching frequency in bulk HDO, at 2438 and 2530 cm⁻¹, respectively,² indicates that the hydrated lithium ion has two hydration shells. This is further supported by a RD-SCF study reporting two O–H stretching frequencies at ca. 3300 and 3600 cm⁻¹, due to water molecules in the first and second hydration sphere, respectively.³ Only one probable Li–(O_I–D)⋯O_II distance has been reported of 4.2 Å, with the corresponding Li–O and Li–(O)–D distances refined to 1.97 and 2.64 Å, respectively, giving an Li–O–D angle of ca. 125°.²⁰

DDIR spectroscopy has shown that the hydrated sodium, potassium, rubidium and cesium ions all have an O–D stretching frequency higher than in bulk water.² A RD-SCF study only detected O–H frequencies similar to those in bulk water.³ This shows that the M–O bonds are weaker than the O–H/D⋯·O–H/D bonds in bulk water. It is therefore not expected that any second hydration sphere is present around these ions in aqueous solution as the first hydration sphere is not sufficiently polarized to form a second hydration sphere with physical properties different from those in bulk water. LAXS studies have shown that the hydrated sodium, potassium, rubidium and cesium ions have octahedral six-coordinate, irregular seven-coordinate, square antiprismatic eight-coordinate and square antiprismatic eight-coordinate configurations in aqueous solution with mean M–O bond distances of 2.43, 2.79, 2.98 and 3.08 Å, respectively.^21,22 The structure determinations of these hydrated ions in aqueous solution do not provide any evidence of a well-defined second hydration shell.^21,22 Several experimental structure determinations and theoretical simulations of the hydrated alkali metal ions have been reported, but the spread in M–O bond distances and coordination numbers is large.²³ The sodium ion retains its first hydration shell on crystallization with reported di-, tetra-, penta-, hexa- and octahydrates as well as several kinds of polymeric structures where the sodium ion in most cases is octahedrally coordinated, Table S1b (ESI†). The most common sodium hydrate in the solid state is [Na(H₂O)₆]⁺ with octahedral coordination and a mean Na–O bond distance of 2.417 Å (28 structures), Table S1b (ESI†). Salts containing potassium, rubidium and cesium ions do crystallize either as anhydrous materials or with a number of water molecules significantly smaller than observed in aqueous solution, Tables S1c–e (ESI†).²¹

Alkaline earth metal ions

The structure of the hydrated beryllium(II) ion in aqueous solution has been described in a couple of studies.^24,25 The reported Be–O bond distances, 1.67 and 1.6 Å, are slightly different from the mean Be–O bond distance in the [Be(H₂O)₄]²⁺ ion in the solid state, 1.613 Å (20 structures), Table S1f (ESI†). The studies in aqueous solution report also the presence of a second hydration sphere, most likely with eight water molecules, with a Be–(O_I–H)⋯O_II distance of 3.7–3.8 Å.^24–26 A number of theoretical simulations have been reported,^27–30 of which that of D'Incal et al. is in close agreement with the experimental studies with Be–O_I and Be–(O_I–H)⋯O_II distances of 1.61 and 3.70 Å, respectively. A vibrational spectroscopic analysis strongly supports the results of the X-ray scattering and simulation studies.³¹

The Mg–O_I bond and Mg–(O_I–H)⋯O_II distances in the hydrated magnesium(II) ion were refined to 2.069(10) and 4.077(10) Å, respectively, Table 2; the fitted RDF and intensity functions are given in Fig. S1 (ESI†). This Mg–O_I bond distance is in close agreement with the mean Mg–O_I bond distance in solids containing a hexaaquamagnesium(II) ion, of 2.066 Å, an average of 521 structures, Table S1g (ESI†). The mean value of the O_I(–H)⋯O_II (55.5%) and O_aq(–H)⋯O_aq (44.5%) distances was refined to 2.832(5) Å, Table 2. The O_I(–H)⋯O_II distance was estimated as 2.785 Å from such distances in solid compounds,⁵vide supra, and from the refined mean value of the O_I(–H)⋯O_II and O_aq(–H)⋯O_aq distances; the O_aq(–H)⋯O_aq distance in dilute aqueous solutions of electrolytes is ca. 2.89 Å.²¹ The mean Mg–O_I⋯O_II angle becomes 113.4°, a result in good agreement with previously reported X-ray and neutron scattering and theoretical simualtions of the hydrated magnesium(II) ion in aqueous solution.^26,32–35 Smirnov and Trostin reviewed structural studies on the hydrated magnesium(II) ion in aqueous solution up to 2007.²⁶ They concluded that the hydrated magnesium(II) ion binds six water molecules in octahedral fashion with a mean Mg–O bond distance of 2.1 Å, also having a second hydration shell with twelve water molecules at 4.1 Å. Since then, several theoretical simulation studies have been reported supporting the experimental results in this and previous studies.^29,32–35 There is a small difference in the results reported in the experimental and simulation studies, the Mg–(O_I–H)⋯O_II distance being 4.1 and 4.2 Å, respectively, corresponding to Mg–O_I⋯O_II angles of ca. 115 and 120°, respectively. The simulations seem to result in a Mg–O bond with a higher degree of electrostatic bonding than observed experimentally. The O–D and O–H stretching frequencies of the hydrated magnesium(II) ion in aqueous solution clearly indicates the presence of two hydration shells.^2,3

LAXS studies of aqueous solutions of calcium(II) chloride, bromide and iodide, where the salts are fully dissociated, have shown that the hydrated calcium ion is eight-coordinate in square antiprismatic fashion with mean Ca–O_I and Ca–(O_I–H)⋯O_II distances of 2.46 and 4.58 Å, respectively.³⁶ The mean Ca–O bond distance in eight-coordinate hydrated calcium(II) ions in the solid state is 2.476 Å (11 structures), while it is significantly shorter in six- and seven-coordinate species present in crystalline hydrates at 2.324 and 2.401 Å (15 and 18 structures), Table S1h (ESI†), respectively.¹⁵ Earlier LAXS studies gave the same Ca–O_I and Ca–(O_I–H)⋯O_II distances but in some cases with lower coordination numbers.^23,37 A DFT simulation of the hydrated calcium(II) ion in aqueous solution has given a coordination number close to eight, and indicated the presence of a second hydration shell.³⁰

A combined LAXS and EXAFS study of aqueous strontium(II) perchlorate and chloride solutions has defined eight-coordination in a square antiprismatic fashion with mean Sr–O_I and Sr–(O_I–H)⋯O_II distances of 2.62 and 4.78 Å, respectively.¹ Another LAXS study reported a Sr–O_I bond distance of 2.64 Å, but a much longer Sr–(O_I–H)⋯O_II distance of 4.90 Å.³⁸ The mean Sr–O bond distance in the octaaquastrontium(II) ion in the solid state is 2.617 Å (20 structures), while the mean Sr–O bond distances in hexa- and nonaaquastrontium(II) ions are 2.496 Å (3 structures) and 2.658 Å (1 structure), Table S1i (ESI†). The Sr–O bond distance observed in aqueous solution indicates that hydrated strontium ion is eight-coordinate square antiprismatic. A combined MD simulation and EXAFS study supports eight-coordination, but with a shorter Sr–O bond distance, 2.57 Å, than the LAXS studies.³⁹

A LAXS study of an aqueous barium(II) perchlorate solution provided Ba–O_I and Ba–(O_I–H)⋯O_II distances of 2.82 and 4.90 Å, respectively.¹ The mean Ba–O bond distances in the octa- and nonaaquabarium(II) ions in the solid state are 2.777 and 2.832 Å (4 structures each), respectively, Table S1j (ESI†). The Ba–O bond distance observed in aqueous solution indicates that the hydrated barium ion is nine-coordinate, even though an equilibrium between eight- and nine-coordination species cannot be excluded. Two combined MD simulation and EXAFS studies provided a similar conclusion.^39,40

An RD-SCF study has detected two O–H stretching frequencies of the hydrated magnesium(II), calcium(II), strontium(II) and barium(II) ions both below and above the value of bulk water, showing the presence of two well-defined hydration shells.³ DDIR spectroscopy supports the presence of two hydration shells around all alkaline earth metal ions.²

Group 3 metal ions

The hydrated group 3 metal ions, scandium(III), yttrium(III) and lanthanum(III), differ in their coordination geometry being dicapped trigonal prismatic (8-coordination),⁴¹ square antiprismatic (8-coordination)⁴² and tricapped trigonal prismatic (9-coordination),⁴³ respectively, in both aqueous solution and the solid state. The hydrated scandium(III) ion binds six water molecules in a trigonal prism at 2.17 Å to which twelve water molecules are bound in a second hydration sphere at 4.27 Å.⁴¹ The mean value of the O_I(–H)⋯O_II (47.1%) and O_aq(–H)⋯O_aq (52.9%) distances was refined to 2.825(5) Å. Using this value the O_I(–H)⋯O_II distance was estimated as 2.752 Å using the O_aq(–H)⋯O_aq distance of 2.89 Å.²¹ The two water molecules in the capping positions are much more weakly bound at ca. 2.32 and 2.5 Å.⁴¹ As the capping water molecules are weakly bound, it is not expected that these are sufficiently polarized to form a second hydration shell with water molecules with different properties than bulk water. A summary of reported solid state structures containing a scandium(III) aqua ion is given in Table S1k (ESI†). It should be noted that the Sc–O bond distance in the capping positions are reported to be identical in some structure determinations. This is due to the fact that the compounds crystallize in space groups with higher symmetry than that of the [Sc(H₂O)₈]³⁺ complex.⁴¹

The hydrated yttrium(III) ion binds eight water molecules at 2.365 Å, and 16 water molecules in a second hydration sphere at 4.40 Å in aqueous solution.⁴² The mean Y–O bond distance in the octaaquayttrium(III) ion in solid state is 2.353 Å (21 structures), Table S1l (ESI†). No vibrational spectroscopic studies on the hydrated scandium(III) and yttrium(III) ions have been reported.

The hydrated lanthanum(III) ion binds six water molecules in the trigonal prismatic positions at 2.515 Å, and three in the capping positions at 2.66 Å in aqueous solution.⁴³ The water molecules in the prismatic positions hydrogen bind 12 water molecules in a second hydration sphere at 4.40 Å.⁴³ The mean La–O bond distance in the octa- and nonaaqualanthanum(III) ions in the solid state are 2.495 (2 structures) and 2.555 Å (19 structures), Table S1m (ESI†). The RD-SCF spectrum of the hydrated lanthanum(III) ion shows that the band related to weakly coordinated water molecules is more pronounced than, e.g., with the alkaline earth and transition metal ions.³ This means that the water molecules in the second hydration sphere and those in the capping positions have interactions that are weaker than the intermolecular hydrogen bonding in the aqueous bulk and indicates that any second hydration sphere is not present outside the water molecules in the capping positions. The strength of the hydrogen bonds between the first and second hydration spheres of lanthanum(III) is of the same order as that of divalent alkaline earth and transition metal ions,² and the O_I(–H)⋯O_II distance is estimated as 2.785 Å, vide supra.

Lanthanoid(III) and actinoid(IV) ions

The hydrated lighter lanthanoid(III) ions, Ce–Er, bind nine water molecules in tricapped trigonal prismatic fashion in aqueous solution and the solid state, while the heavier ones, Ho–Lu, have an increasing water deficit in the capping positions with creasing atomic number in both aqueous solution and the solid trifluoromethanesulfonate salts.⁴⁴ The Ln–O_p (prism) and Ln–O_c (capping) bond distances decrease with increasing atomic number, and the difference between the Ln–O_p and Ln–O_c bond distances increases with increasing atomic number.⁴⁴ The lanthanoid(III) ions with water deficit in the capping positions have different Ln–O_c bond distances, while for the lighter ones with all three capping positions filled, the Ln–O_c bond distances are the same.⁴⁴ The solid state structures containing a hydrated lanthanoid(III) ion are summarized in Tables S1n–S1z (ESI†). The RD-SCF spectra of the hydrated gadolinium, dysprosium(III) and lutetium(III) ions are similar to that of lanthanum(III).³ DDIR spectra of the hydrated lanthanoid(III) ions are more or less identical to the lanthanum(III) one.² A limited number of LAXS studies on hydrated lanthanoid(III) ions are reported^45,46 as summarized in Table 3. However, it can be assumed that all lanthanoid(III) ions are hydrated in a similar way with a second hydration shell outside the water molecules in the prismatic positions but with most likely no polarized water molecules outside the capping positions.

Table 3 Summary of results from LAXS and DDIR spectroscopy studies of hydrated metal ions in aqueous solution

Ion	CN	d(M–OI)	d(M(–OI))⋯OII	d(OI⋯OII)	∠M–OI–OII/°	ν(O–D)/cm^−1	Ref.
Li^+	4	1.95	4.0	2.85	114.1	2438 + 2530	2 and 15–20
Na^+	6	2.43				2534	2 and 21
K^+	7	2.79				2549	21
Rb^+	8	2.98				2560	21 and 22
Cs^+	8	3.08				2567	21
Be^2+	4	1.62	3.7	2.785	111.5		24–26
Mg^2+	6	2.069	4.077	2.785	113.4	2428	This work, ref. 2 and 26
Ca^2+	8	2.46	4.58	2.8	121.0	2540	2 and 36
Sr^2+	8	2.64	4.78	2.8	123.0	2529	1 and 2
Ba^2+	9	2.82	4.90	2.8	121.4	2537	1 and 2
Sc^3+	6 + 1 + 1	2.174 + 2.29 + 2.5	4.276	2.752	120.0		41
Y^3+	8	2.365	4.41	2.725	119.9		42
La^3+	6 + 3	2.527 + 2.60	4.63	2.785	121.2	2421	2 and 43
Ce^3+	6 + 3	2.516 + 2.58	4.56	2.785	118.6		45 and 46
Sm^3+	6 + 3	2.43 + 2.53	4.56	2.785	121.0		45
Tb^3+	6 + 3	2.40 + 2.53	4.50	2.785	120.1		45
Er^3+	6 + 2.9	2.36 + 2.48	4.45	2.785	119.7		45
Th^4+	6 + 3	2.454	4.547	2.725	122.8		47–49
U^4+	6 + 3	2.43	4.43	2.725	118.4		52
Al^3+	6	1.891	4.018	2.725	119.9	2200 + 2420	This work, ref. 2
Ga^3+	6	1.959	4.05	2.725	118.7		58
In^3+	6	2.131	4.13	2.725	116.0		58
Tl^3+	6	2.23	4.20	2.725	115.5		59
Tl^+	2 + 2	2.8 + 3.2					60
Sn^2+	3	2.204	4.126	2.785	111.1		61
Pb^2+	6	2.53	4.44	2.785	113.2		62
Bi^3+	8	2.411	4.47	2.745	120.1		64
Cr^3+	6	1.966	4.08	2.725	120.0	2200 + 2420	2, 58 and 65
Mn^2+	6	2.174	4.258	2.783	116.7	2420	This work, ref. 2 and 72
Fe^2+	6	2.124	4.092	2.785	112.2	2419	This work, ref. 2 and 77
Fe^3+	6	1.999	4.012	2.746	114.5		This work, ref. 77
Co^2+	6	2.090	4.072	2.788	112.4	2428	This work
Rh^3+	6	2.030	4.02	2.745	113.8	2200 + 2420	2 and 96–99
Ni^2+	6	2.057	3.981	2.788	109.6	2418 + 2530	This work, ref. 2, 71, 89, 90 and 101
Cu^2+	6	1.965 + 2.16 + 2.32	4.094	2.787	117.9	2400 + 2530	This work, ref. 2 and 109
Ag^+	2 + 2 + ?	2.33 + 2.59 + 4	4.65	2.89	125.6		118
Zn^2+	6	2.091	4.10	2.790	113.5	2418	This work, ref. 2 and 120–122
Cd^2+	6–7	2.302	4.284	2.788	114.4	2423	2 and 126–128
Hg2^2+	6	2.242	4.515	2.89	122.7		135
Hg^2+	6	2.342	4.198	2.785	109.6	2416	2 and 130
VO^2+	4 + 1	1.992 + 2.2	4.06	2.85	115.4		137
VO2^+	2 + 2	1.987 + 2.215	4.16 + 4.27	2.9	117.5 + 114.3		137
UO2^2+	5	2.421	4.37	2.85	111.7		138

---

The hydrated thorium(IV) ion hydrolyses very easily, and is only present in very acidic aqueous solution. Two LAXS and two EXAFS studies have shown that the mean Th–O bond distance in the hydrated thorium(IV) ion in acidic aqueous solution is ca. 2.46 Å.^47–50 The number of bound water molecules differs in the reported studies, mainly due to the difficulties in determining it from LAXS and EXAFS studies. The few reported homoleptic thorium complexes with oxygen donor ligands give mean Th–O bond distances of 2.40, 2.45 and 2.50 Å in eight-, nine- and ten-coordination, respectively,^47–51 Table S1aa (ESI†). The reported mean Th–O bond distance strongly indicates that the hydrated thorium(IV) ion binds ca. nine water molecules. The LAXS studies define a second hydration sphere of ca. 18 water molecules at 4.55–4.62 Å, and at least portions of a third hydration shell at 6.75–6.85 Å.^47–49 In the only homoleptic aquathorium(IV) complex known in the solid state, [Th(H₂O)₁₀]Br₄, thorium(IV) binds ten water molecules in bicapped square antiprismatic configuration with a mean Th–O bond distance of 2.50 Å.⁴⁹

The hydrated uranium(IV) ion binds ca. 8 water molecules at ca. 2.43 Å, and a second hydration shell at ca. 4.43 Å in acidic aqueous solution.⁵² A summary of reported solid state structures containing an aquauranium or an aquadioxouranium ion is given in Table S1ab (ESI†).

Group 13 metal ions

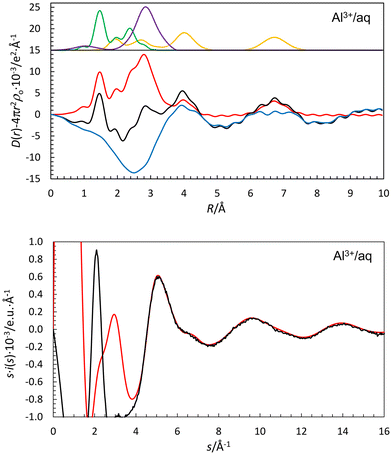
In the present work, the Al–O_I and Al–(O_I–H)⋯O_II distances obtained of 1.891(10) and 4.018(10) Å, respectively, Table 2, are in close agreement with previous LAXS studies.^53–55 In addition, portion of a third hydration shell is observed at ca. 6.7 Å, Fig. 3. The fits of the RDF and intensity functions are given in Fig. 4. The Al–O_I bond distance is in close agreement with the mean Al–O bond distance in solids containing the hexaaquaaluminum(III) ion, 1.882 Å (99 structures), Table S1af (ESI†). The mean value of both the O_I(–H)⋯O_II (60.0%) and O_aq(–H)⋯O_aq (40.0%) distances was refined to 2.791(5) Å, Table 2, and the O_I(–H)⋯O_II distance was estimated as 2.725 Å in the same way as described above, giving an Al–O_I⋯O_II bond angle of 119.9°. Most Al–O_I⋯O_II bond angles in solid AlI₃·17H₂O are in the range 120–125°.⁷ Theoretical simulation studies support the structure of the hydrated aluminum(III) ion in aqueous solution found in the experimental studies.^29,56 A vibrational spectroscopic analysis of the [Al(H₂O)₆(H₂O)₁₂]³⁺ complex in aqueous solution has shown the high symmetry of the hydrated aluminum(III) ion.⁵⁷ DDIR spectra show two bands of the hydrated aluminum(III) ion below the O–D stretching of bulk water, 2200 and 2420 cm⁻¹, identifying to HDO molecules in the first and second hydration shells, respectively.² The presence of significantly polarized water molecules in the second hydration shell strongly indicates the presence of at least parts of a third hydration sphere.

The hydrated gallium(III), indium(III) and thallium(III) ions bind six water molecules in octahedral fashion in the first hydration shell, and twelve in well-defined second hydration shells in aqueous solution.^58,59 The mean M–O_I and M–(O–H)⋯O_II distances are 1.959 and 4.05 Å, and 2.131 and 4.13 Å, for gallium(III) and indium(III) ions, respectively.⁵⁸ The Tl–O_I bond distance in the hydrated thallium(III) ion is reported to 2.236 Å, but a Tl–(O_I–H)⋯O_II distance was not reported even though a significant peak in the RDF was observed at 4.20 Å.⁵⁹ The mean M–O bond distances in solid compounds containing the hexaaquametal(III) ions are 1.946, 2.124 and 2.230 Å for gallium(III), indium(III) and thallium(III) as a mean of 13, 9 and 1 structures, respectively, Tables S1ag–S1ai (ESI†). No vibrational spectroscopic studies of the hydrated gallium(III), indium(III) and thallium(III) ions in aqueous solution have been reported.

The thallium(I) ion is weakly hydrated without any well-defined coordination number or figure.⁶⁰ It is not expected that any second hydration shell is present in aqueous solution.

Group 14 and 15 metal ions

The aqueous chemistry of group 14 and 15 metal ions is limited to the oxidation states +II and +III, respectively, which is two below the maximum one. These ions have d¹⁰s² electron configuration. The coordination chemistry of tin(II) and lead(II) is strongly affected by the electron configuration with at least partially filling of the Sn(5s)/Pb(6s)-ligand (np) anti-bonding orbitals causing a large gap in the coordination sphere.^61,62 The hydrated tin(II) ion binds three water molecules in a footstool-like configuration with a mean Sn–O_I bond distance of 2.21 Å, and a mean O_I–Sn–O_I bond angle of 78° in both aqueous solution and the solid state,^61,63 Table S1aj (ESI†). The mean Sn–O_I(–H)⋯O_II distance is 4.13 Å in aqueous solution. By assuming an O_I–(H)⋯O_II distance of 2.785 Å, as in most divalent metal ions, vide supra, the Sn–O_I–(H)⋯O_II bond angle becomes 111.1°.⁶¹

The hydrated lead(II) ion binds approximately six water molecules, but no detailed coordination geometry could be given.⁶² It can be expected that a large part of the coordination sphere is occupied by electrons in the anti-bonding orbital causing a gap in that sphere. The Pb–O_I and Pb–(O_I–H)⋯O_II distances are 2.53 and 4.44 Å, respectively, and assuming an O_I–(H)⋯O_II distance of 2.785 Å, the mean Pb–(O_I–H)⋯O_II angle becomes 113.4°.⁶²

The hydrated bismuth(III) ion binds eight water molecules in square antiprismatic fashion in aqueous solution with a mean Bi–O_I bond distance of 2.41 Å, and the Bi–(O–H)⋯O_II distance is 4.47 Å. Assuming an O_I–(H)⋯O_II distance of 2.785 Å, the mean Bi–(O_I–H)⋯O_II angle becomes 120.1°.⁶⁴ In the solid state, the hydrated bismuth(III) ion is nine-coordinate in a tricapped trigonal prismatic fashion in the trifluoromethanesulfonate salt with Bi–O_p and Bi–O_c bond distances of 2.435 and 2.595 Å, respectively.⁶⁴ No vibrational spectroscopic studies of the hydrated tin(II), lead(II) and bismuth(III) ions in aqueous solution have been reported.

Transition metal ions

The hydrated chromium(III) ion binds six water molecules in octahedral fashion at 1.966 Å, and twelve in a second hydration shell at 4.08 Å.^15,58,65 Assuming a mean Cr–(O_I–H)⋯O_II distance of 2.725 Å, as found for the trivalent aluminium ion, vide supra, the Cr–O_I–(H)⋯O_II bond angle becomes 120.0°. The mean Cr–O bond distance in hexaaquachromium(III) ions in crystalline compounds is 1.965 Å (24 structures), Table S1ap (ESI†). The results of combined MD simulation and EXAFS studies are in agreement with the LAXS studies.^66,67 DDIR spectroscopy shows that the hydrated chromium(III) ion has identical absorption bands to those of aluminum, vide supra, indicating the presence of at least part of a third hydration shell.² The LAXS studies of the hydrated chromium(III) ion in aqueous solution do however not show any well-defined Cr(–O_I–H⋯O_II–H)⋯O_III distance.^58,65

In the present study, the Mn–O_I and Mn–(O_I–H)⋯O_II distances were refined to 2.174(4) and 4.26(2) Å, respectively, Table 2. The fits of the RDF and intensity functions are given in Fig. S2 (ESI†). The mean value of the O_I(–H)⋯O_II (60.9%) and O_aq(–H)⋯O_aq (39.1%) distances was refined to 2.825(5) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.783 Å; the Mn–O_I⋯O_II angle becomes 116.7(2.0)°. The mean Mn–O bond distance in crystalline compounds containing a hexaaquamanganese(II) ion is 2.174 Å (166 structures), Table S1aq (ESI†). LAXS and EXAFS studies on the hydrated manganese(II) ion in aqueous solution have given Mn–O bond distances in the range 2.17–2.20 Å.^68–72 However, there is a large spread in the Mn–(O_I–H)⋯O_II distances of 4.17–4.43 Å. A theoretical simulation study of the hydrated manganese(II) ion in aqueous solution is good agreement with the experimental result in this study.⁷³ A vibrational spectroscopic analysis of the [Mn(H₂O)₆(H₂O)₁₂]²⁺ complex in aqueous solution has been reported,⁷⁴ and a DDIR spectroscopic study has given an O–D stretch of 2420 cm⁻¹ in agreement with the values for other divalent metal ions, showing two hydration shells around the manganese(II) ion in aqueous solution.²

The Fe–O_I and Fe–(O_I–H)⋯O_II distances in the hydrated iron(II) ion in aqueous solution have now been refined to 2.124(8) and 4.092(14) Å, respectively, Table 2. The fits of the RDF and intensity functions are given in Fig. S3 (ESI†). The mean value of the O_I(–H)⋯O_II (55.3%) and O_aq(–H)⋯O_aq (44.7%) distances was refined to 2.832(5) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.785 Å; the Fe–O_I⋯O_II angle becomes 112.2(1.0)°. The Fe–O bond distance is in close agreement with the mean Fe–O bond distance in crystalline compounds containing the hexaaquairon(II) ion of 2.120 Å (92 structures), Table S1ar (ESI†). LAXS, neutron scattering and EXAFS studies on the hydrated iron(II) ion in aqueous solution have given Fe–O bond distances in the range 2.10–2.13 Å.^75–77 The LAXS study gives a much longer Fe–(O_I–H)⋯O_II distance, 4.30–4.51 Å,⁷⁵ giving an unrealistically large Fe–O_I⋯O_II angle. This is also the case for two simulation studies of the hydrated iron(II) ion in aqueous solution.^78,79 DDIR spectroscopy gives an O–D stretching frequency at 2420 cm⁻¹ as found with other divalent metal ions, consistent with two hydration shells around the hydrated iron(II) ion.²

The Fe–O_I and Fe–(O_I–H)⋯O_II distances of the hydrated iron(III) ion have been refined to 1.999(4) and 4.012(10) Å, respectively, in this study, Table 2. The fits of the RDF and intensity functions are given in Fig. S4 (ESI†). The mean value of the O_I(–H)⋯O_II (66.7%) and O_aq(–H)⋯O_aq (33.3%) distances was refined to 2.794(5) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.746 Å, and an Fe-O_I⋯O_II angle of 114.5(0.7)°. The Fe–O bond distance is in close agreement with the mean Fe–O bond distance in crystals containing the hexaaquairon(III) ion of 1.995 Å (21 structures), Table S1ar (ESI†). LAXS and EXAFS studies on the hydrated iron(III) ion in aqueous solution give Fe–O bond distances in the range 1.99–2.05 Å.^77,80–86 One simulation study has given slightly longer Fe–O_I and Fe–(O_I–H)⋯O_II distances than in the experimental studies, with the Fe–O bonds deemed stronger than Al–O bonds due to a higher degree of covalency.⁷⁹ Another simulation study has given Fe–O_I and Fe–(O_I–H)⋯O_II distances in close agreement with the present LAXS data.⁸⁷

The Co–O_I and Co–(O_I–H)⋯O_II distances of the hydrated cobalt(II) ion in solution have now been refined to 2.090(4) and 4.072(14) Å, respectively, Table 2. The fits of the RDF and intensity functions are given in Fig. S5 (ESI†). The mean value of the O_I(–H)⋯O_II (54.4%) and O_aq(–H)⋯O_aq (45.6%) distances was refined to 2.835(5) Å, giving an estimated O_I(–H)⋯O_II distance of 2.788 Å and the Co–O_I⋯O_II angle becomes of 112.4(1.0)°. The Co–O bond distance is in close agreement with the mean Co–O bond distance in crystals containing a hexaaquacobalt(II) ion of 2.088 Å (446 structures), Table S1at (ESI†). Previous LAXS and EXAFS studies on the hydrated cobalt(II) ion in solution give Co–O bond distances in the range 2.08–2.14 Å but the Co–(O_I–H)⋯O_II distances are significantly longer, 4.20–4.28 Å,^88–91 than in this study resulting in unrealistically wide Co–O_I⋯O_II angles. Combined MD simulation and EXAFS studies give Co–O_I distances close to the LAXS studies of 2.09 Å.^92–95 However, several of the simulation studies gave significantly longer Co–(O_I–H)⋯O_II distances of ca. 4.4 Å, along with unrealistic Co–O_I⋯O_II angles,^91–93 while another gave 4.24 Å and a Co–O_I⋯O_II angle of 120°.⁹⁵ The contribution from the second hydration shell to the EXAFS signal was judged not to be significant.^92–95 DDIR spectroscopy has given an O–D stretching at 2428 cm⁻¹ in agreement with that of other divalent metal ions, indicative of two hydration shells around the cobalt(II) ion in solution.²

The hydrated rhodium(III) ion binds six water molecules in the first hydration shell at 2.03 Å, and twelve in a second hydration shell at 4.02 Å.^96–99 DDIR spectroscopy shows two O–D stretching bands at 2200 and 2420 cm⁻¹,² strongly indicating the presence of at least part of a third hydration shell. However, this was not confirmed in the reported LAXS studies.^96–98 The Rh–O bond distance is in close agreement with the mean Rh–O bond distance in crystals containing a hexaaquarhodium(III) ion of 2.022 Å (4 structures), Table S1au (ESI†).

The Ni–O_I and Ni–(O_I–H)⋯O_II distances in the hydrated nickel(II) ion in solution have been refined to 2.057(4) and 3.981(12) Å, respectively, in the present study, Table 2. The fits of the RDF and intensity functions are given in Fig. S6 (ESI†). The mean value of the O_I(–H)⋯O_II (54.9%) and O_aq(–H)⋯O_aq (45.1%) distances was refined to 2.834(5) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.788 Å and thereby a Ni–O_I⋯O_II angle of 109.6(0.7)°. The Ni–O bond distance is in close agreement with the mean Ni–O bond distance in crystals containing the hexaaquanickel(II) ion of 2.055 Å (386 structures), Table S1av (ESI†). LAXS and EXAFS studies on the hydrated nickel(II) ion in aqueous solution give Ni–O bond distances in the range 2.05–2.08 Å.^{71,89,90,100–107} The reported Ni–(O_I–H)⋯O_II distances are in the range 3.99–4.3 Å,^{71,89,90,100–107} thus, some are in close agreement with this study,^71,89,90,101 while others differ significantly with too long Ni–(O_I–H)⋯O_II distances for a realistic Ni–O_I⋯O_II angle. Combined MD simulation and EXAFS studies have given Ni–O_I distances close to that of the LAXS studies, 2.05 Å.^91,92,107 However, the simulations give significantly longer Ni–(O_I–H)⋯O_II distances of 4.27–4.4 Å and unrealistically large Ni–O_I⋯O_II angles.^92,93,108 The contribution from the second hydration shell to the EXAFS signal is not significant.^92,93,108 The DDIR spectrum showed an O–D stretch at 2418 cm⁻¹ similar to those of other divalent metal ions and indicating two hydration shells for the nickel(II) ion in solution.²

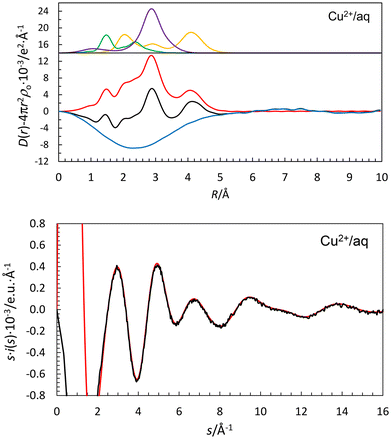
The RDF of the aqueous copper(II) perchlorate solution has a significantly different shape to those of the other hydrated metal ions in this study with significant contributions in the range 2.0–2.4 Å, Fig. 2 and 5. The peaks at 2.0 and 4.15 Å correspond to the Cu–O_I and Cu–(O_I–H)⋯O_II distances in the equatorial positions of the Jahn–Teller distorted hydrated copper(II) ion. The shoulders in the range 2.0–2.4 Å correspond to Cu–O bond distances to water molecules in the axial positions, Cu–O_ax, at different distances, as has been shown recently.^109,110 The Cu–O_I, Cu–O_ax1, Cu–O_ax2 and Cu–(O_I–H)⋯O_II distances were refined to 1.965(10), 2.16(2), 2.29(2) and 4.094(8) Å, respectively, which is in good agreement with EXAFS studies applying a model with two different axial bond distances,^109,110Table 2. The mean value of the O_I(–H)⋯O_II (53.3%) and O_aq(–H)⋯O_aq (46.7%) distances was refined to 2.835(5) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.787 Å and a Cu–O_I⋯O_II angle of 117.9(0.9)°. The water molecules in the weak Cu–O bonds in the axial positions are most likely not sufficiently polarized to form a second hydration shell in their vicinity.

The hexaaquacopper(II) complex has several different configurations in the solid state depending on the symmetry of space group in which the compound crystallizes. In space groups without a centre of symmetry or with one not located on copper in the Jahn–Teller distorted [Cu(H₂O)₆]²⁺ complex, different Cu–O_ax bond distances are observed; the mean Cu–O_I, Cu–O_ax1 and Cu–O_ax2 bond distances in the seven reported structures are 1.983, 2.298 and 2.362 Å, respectively.¹⁰⁹ In centrosymmetric space groups the axial Cu–O bond distances are equal and the mean Cu–O_I and Cu–O_ax bond distances in the 108 reported structures are 1.980 and 2.333 Å, the solid state structures containing a tetra-, penta- or hexaaquacopper(II) ion are summarized in Table S1ax (ESI†), respectively.¹⁰⁹ X-ray and neutron scattering, and studies on the hydrated copper(II) ion in aqueous solution have given Cu–O_I bond distances in the range 1.94–1.98 Å and Cu–O_ax bond distances of ca. 2.3 Å.^111–118 The Cu–(O_I–H)⋯O_II distances in the equatorial positions lie in the range 3.95–4.20 Å.^110–117 DDIR spectra show two O–D stretching bands at 2400 and 2530 cm⁻¹,² indicating a second hydration shell attached to the equatorially bound water molecules, while again the axially bound water molecules are most likely not sufficiently polarized to form a second hydration shell.

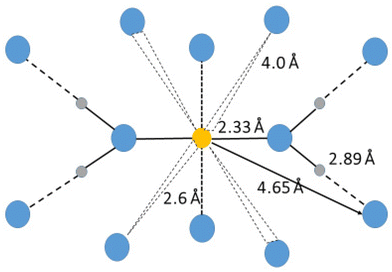
The hydrated silver(I) ion binds two water molecules in a linear fashion in the solid state with a mean Ag–O bond distance of 2.129 Å (6 structures), Table S1ay (ESI†). However, in aqueous solution the mean Ag–O bond distance is significantly longer, 2.33 Å, and a second hydration shell is apparent at 4.65 Å.¹¹⁹ In addition there are ca. two water molecules at ca. 2.6 Å, and another set of water molecules at ca. 4 Å, Fig. 6. The presence of these additional bound water molecules at long distances explains the significantly longer Ag–O bond distance in aqueous solution than in the solid state. The Ag–(O_I–H)⋯O_II angle of 125.6° is larger than observed for other hydrated metal ions, vide supra, and vide infra. The Ag–O_I–H_I angle was estimated as 130° in an EXAFS study supporting the result from the LAXS study.¹¹⁹ The loosely bound water molecules most likely repel the water molecules in the second hydration shell giving a larger Ag–(O_I–H)⋯O_II angle than observed for other hydrated metal ions, Table 3 and Fig. 5, even though the silver(I) ion has soft bonding characteristics. No vibrational spectroscopic studies on the hydrated silver(I) are reported.

Fig. 6 Proposed structure of the hydrated silver(I) ion in aqueous solution.

The Zn–O_I and Zn–(O_I–H)⋯O_II distances in the hydrated zinc(II) ion in solution have been refined to 2.091(10) and 4.100(10) Å, respectively, in the present study, Table 2. The mean value of the O_I(–H)⋯O_II (56.2%) and O_aq(–H)⋯O_aq (43.8%) distances was refined to 2.828(7) Å, Table 2, giving an estimated O_I(–H)⋯O_II distance of 2.780 Å and a Zn–O_I⋯O_II angle of 113.7(0.8)°. The fits of the RDF and intensity functions are given in Fig. S7 (ESI†). The Zn–O bond distance is in close agreement with the mean Zn–O bond distance in crystals containing the hexaaquazinc(II) ion, 2.088 Å (261 structures), Table S1ba (ESI†). LAXS and EXAFS studies on the hydrated zinc(II) ion in solution give Zn–O bond distances in the range 2.08–2.11 Å.^{90,91,120–122} Zn–(O_I–H)⋯O_II distances are in the range 3.95–4.26 Å.^{90,91,120–122} Simulation studies of the hydrated zinc(II) ion in solution are in good agreement with the experimental studies.^30,123–125 The DDIR spectrum shows an O–D stretch at 2418 cm⁻¹ in agreement with other divalent metal ion spectra, indicating two hydration shells around zinc(II) in solution.²

The Cd–O_I and Cd–(O–H)⋯O_II distances in the hydrated cadmium(II) ion are 2.30 and 4.28 Å.^126–128 The mean Cd–O bond distance in solids containing a hexaaquacadmium ion is 2.266 Å (57 structures), Table S1bb (ESI†), while no heptaaquacadmium(II) ion has been found in the solid state so far. There are indications that an equilibrium between hexa– and heptaaquacadmium(II) ions is present in aqueous solution.^126,127

The hexaaquamercury(II) ion has a regular octahedral coordination geometry in the solid perchlorate salt, crystallizing a trigonal space group with a Hg–O bond distance of 2.342 Å.¹²⁹ A combined LAXS and EXAFS study of the hydrated mercury(II) ion in acidic aqueous solution revealed a highly asymmetric bond distance distribution assigned to vibronic coupling of valence states in a so-called pseudo Jahn–Teller effect that induces a distorted configuration around six-coordinate mercury(II) complexes.¹³⁰ An EXAFS study of solid [Hg(H₂O)₆](ClO₄)₂ gave a mean Hg–O bond distance of 2.36 Å, while the peak maximum appears at 2.33 Å.¹³⁰ The corresponding values for a perchloric acid solution of mercury(II) gave mean and peak maximum Hg–O distances of 2.38 and 2.33 Å, respectively. The crystal structure of [Hg(OS(CH₃)₂)]₆(ClO₄)₂ shows three pair-wise Hg–O bond distances of 2.317, 2.320 and 2.376 Å,¹³¹ supporting a pseudo or second order Jahn–Teller distortion. By applying such a model to the hydrated mercury(II) ion in solution and in the solid perchlorate salt, the experimental observations are fully explained.¹³⁰ A LAXS study on a perchloric acidic solution of mercury(II) perchlorate gave a mean Hg–O bond distance of 2.34 Å, and a very large displacement factor implying a distribution at least 0.05 Å wider than that expected for a regular octahedral hydrated divalent transition metal ion.¹³⁰ A second hydration sphere is observed with a mean Hg–(O–H)⋯O_II distance of 4.20 Å.¹³⁰ Other EXAFS studies on the hydrated mercury(II) ion in solution have provided a mean Hg–O bond distance of 2.33 Å, and coordination number of seven.^132–134 However, seven-coordination of mercury(II) ion should result in a significantly longer Hg–O bond distance than the reported one.

Each mercury atom in the dimeric mercury(I) ion, [Hg–Hg]²⁺, binds three water molecules at 2.24 Å, and six water molecules in a second hydration shell at 4.52 Å in aqueous solution.¹³⁵ The Hg–Hg bond distance was found to be 2.524 Å. In the solid state, each mercury atom binds one water molecule at 2.135 Å, and the Hg–Hg bond distance is 2.501 Å (6 structures), Table S1bc (ESI†). A QMCF MD simulation study of the hydrated mercury(I) ion has provided somewhat longer Hg–Hg and Hg–O_I distances than determined experimentally.¹³⁶

Oxo- and dioxometal ions

The hydrated oxovanadium(IV) or vanadyl(IV) ion, VO²⁺, binds four water molecules in the equatorial plane almost perpendicular to the V=O double bond at 1.99 Å, and a second hydration shell is observed at 4.06 Å.¹³⁷ One water molecule is weakly bound trans to the V=O double bond at ca. 2.20 Å. This water molecule is most likely not sufficiently polarized to hydrogen bind to water molecules with different physical properties than bulk water. The V=O, V–O_cis and V–O_trans bond distances in the solid state are 1.580, 2.026 and 2.187 Å (10 structures), Table S1ao (ESI†).

The hydrated dioxovanadium(V) or vanadyl(V) ion VO₂⁺, has two V=O bonds in cis-configuration. Two water molecules trans to the V=O bonds are weakly bound at 2.22 Å, while the two cis-oxido atoms have a mean V–O bond distance of 1.99 Å, and a second hydration sphere at ca. 4.16 Å.¹³⁷

The hydrated dioxouranium(VI) or uranyl(VI) ion, UO₂²⁺, double-binds two oxygens, O=U=O, in a trans configuration, at 1.77 Å, and five water molecules perpendicular to the O=U=O unit at 2.42 Å with a second hydration sphere at 4.58 Å.¹³⁸ An early LAXS study reported similar results.¹³⁹ The mean U=O and U–O_I bond distances in crystals containing the pentaaquauranyl(VI) ion are 1.760 and 2.422 Å (7 structures), Table S1ab (ESI†). A combined simulation and EXAFS study reports U–O_aq and U–(O_aq–H)⋯O_II distances of 2.46 and 4.61 Å, respectively.¹⁴⁰

Degree of polarization of the second hydration shell of hydrated metal ions

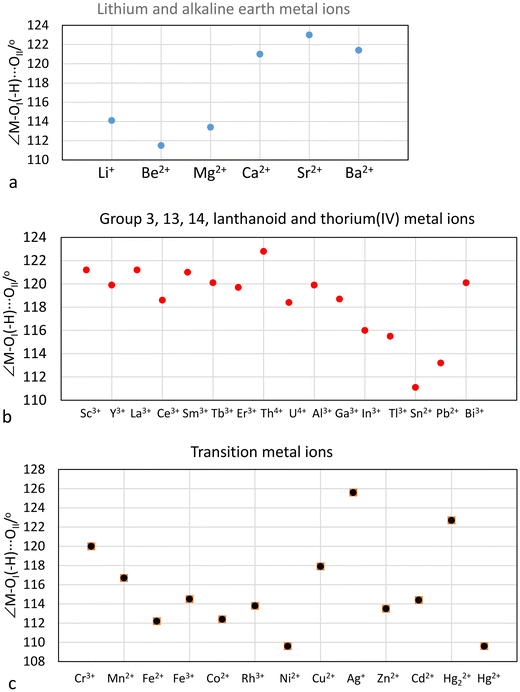
The M–O_I, M–(O_I–H)⋯O_II and O_I–(H)⋯O_II distances, the M–O_I–(H)⋯O_II bond angle, and the O–D stretching frequencies from DDIR measurements of hydrated metal ions in aqueous solution are summarized in Table 3. The large hydrated monovalent metal ions, Na⁺, K⁺, Rb⁺, Cs⁺ and Tl⁺, have an O–D stretching frequency higher than that of bulk HDO showing that the M–O bond is weaker than the intermolecular hydrogen bonds in bulk water.² These metal ions have most likely only a single hydration shell, Table 3. Furthermore, LAXS studies have not been able to prove the presence of second hydration sphere around these metal ions.^21,60 The lithium ion, all divalent metal ions and the trivalent lanthanoid(III) ions have an O–D stretching frequency of ca. 2420 cm⁻¹, showing that the M–O bond is stronger than the intermolecular hydrogen bonds in bulk water and the presence of two hydration shells,²Table 3. RD-SCF has detected two O–H stretching frequencies for these hydrated metal ions at 3300 and 3600 cm⁻¹ corresponding to the water molecules in the first and second hydration shell, respectively. This shows that the water molecules in the first hydration shell are sufficiently polarized to hydrogen bond to a second hydration shell. A second hydration shell has indeed been detected in LAXS and neutron scattering studies of these metal ions in aqueous solution, Table 3. Tri- and tertravalent metal ions, except lanthanum(III) and the lanthanoid(III) ions, show two O–D stretching frequencies below the one in bulk water, ca. 2200 and 2420 cm⁻¹, Table 3, strongly indicating the presence of at least portions of a third hydration shell. The third hydration shell is expected to have similar properties as the second hydration shell of divalent metal ions as they display similar O–D stretching frequencies, Table 3. At least portions of a third hydration shell has been detected for the aluminum(III) and thorium(IV) ions by LAXS, this work and ref. 47–49, while it is not sufficiently well-defined in the RDF's of the hydrated chromium(III), iron(III) and rhodium(III) ions.

The M–O_I–(H)–O_II angle is assumed to be an indicator of the M–O_I bond character, vide supra. The M–O_I–(H)–O_II angles of hydrated metal ions are summarized in Table 3 and Fig. 7. The small lithium, beryllium and magnesium(II)ions have M–O_I–(H)–O_II angles in the range 111–114°, indicating a covalent contribution in the M–O bonds, Fig. 7a. On the other hand, the larger alkaline earth metal ions, calcium, strontium and barium, have M–O_I–(H)–O_II angles close to 120° indicating mainly electrostatic M–O bonds, Fig. 7a. The group 3, 13, lanthanoid(III), thorium(IV) and bismuth(III) ions also have M–O_I–(H)–O_II angles close to 120°, Fig. 7b. The tin(II) and lead(II) ions have M–O_I–(H)–O_II angles close to 112° indicating a significant covalent contribution to the M–O bonds, Fig. 6b. The M–O_I–(H)–O_II angles in the hydrated first row transition metal ions decrease from 120 to 110° for chromium(III) to nickel(II), Fig. 7c. The Cu–O_I–(H)–O_II angle is surprisingly large, 118°. The d¹⁰ metal ions zinc and cadmium have M–O_I–(H)–O_II angles of 114°, while the mercury(II) ion, known to form bonds with a significant covalent contribution, has a Hg–O_I–(H)–O_II angle of 110°, Fig. 7c. The reason to the large Ag–O_I–(H)–O_II angle of 126°, is discussed vide supra.

Fig. 7 (a). The M–O_I–(H)–O_II angles of the hydrated lithium and alkaline earth metal ions. (b). The M–O_I–(H)–O_II angles of the hydrated group 3, 13, 14, lanthanoid(III) and thorium(IV) ions. (c). The M–O_I–(H)–O_II angles of the hydrated transition metal ions.

Hydration of inorganic anions in aqueous solution

The monovalent halide, oxohalo and oxometallate ions, except the fluoride ion, all have an O–D stretching frequency higher than that of bulk water, Table 4, showing that they are weakly hydrated. The di- and trivalent oxoanions have O–D stretching frequencies lower than that of bulk water, and thereby form bonds to water that are stronger than the intermolecular hydrogen bonds in bulk water. The presence of a second hydration should be possible but it has not been possible to detect any second hydration shell by structure methods, except for the vanadate ion.¹⁴⁹

Table 4 Summary of results from LAXS and DDIR spectroscopy studies of halide and oxoanions in aqueous solution

Ion	d(X–O)/Å	d(X–(O)⋯Oaq)/Å	d((X–)O⋯(H–)Oaq)/Å	X⋯O⋯Oaq/°	CN	ν(O–D)/cm^−1	Ref.
		d(X⋯(H)–Oaq)/Å
a Denotes estimated value.
F^−		2.7^a			4	2450	2 and 141–143
Cl^−		3.25			6	2530	2, 23 and 36
Br^−		3.36			6	2550	2, 23, 36 and 144
I^−		3.61			8	2570	2, 23, 36 and 145
NO3^−	1.28	3.61	3.02	107	9	2595	99, 128 and 146
ClO^−	1.662	3.85	3.045	106	3		147
ClO2^−	1.591	3.881	3.045	110	6		148
ClO3^−	1.501	3.770	3.021	108	9		148
ClO4^−	1.453	3.757	3.046	109	12	2630	2, 62 and 148
BrO3^−	1.671	4.068	2.987	119	6		148
IO3^−	1.829	4.27	3.013	122	6		148
IO4^−	1.781	4.243	3.009	123	8		148
MnO4^−	1.630	4.095	3.031	120	8	2610	149
ReO4^−	1.735	4.197	3.01	122	8	2592	149
SO3^2−	1.53	3.68	2.878	109	9		150
SO4^2−	1.495	3.61	2.85	108	12	2477	2 and 151
S2O3^2−	1.479	3.622	2.854	109	12		152
SeO3^2−	1.709	3.87	2.85	114	6–9	2478	153
SeO4^2−	1.657	3.94	2.85	120	8	2480	153
CrO4^2−	1.660	3.955	2.85	120	8	2472	149
MoO4^2−	1.775	4.010	2.85	118	8	2472	149
WO4^2−	1.797	4.024	2.85	118	8	2472	149
H2PO4^−	1.527	3.711	2.85	111	12	2478	154 and 155
HPO4^2−	1.531						154 and 155
PO4^3−	1.533					2434	154 and 155
H2AsO3^−	1.785	4.096	2.85	122	6		156
AsO3^3−	1.785						156
H2AsO4^−	1.707						156
HAsO4^2−	1.704						156
AsO4^3−	1.706	3.929	2.85	121	8		156
HVO4^2−	1.738	3.754	2.85	123	8		149
Cr2O7^2−	1.616 + 1.806						149

---

An interesting observation is the difference in the X–O⋯O_I angle of oxoanions as this angle also determines the number of water molecules binding to each oxygen atom in the oxoanion. The oxochloro, oxosulfur and oxophosphosphorus anions have X–O⋯O_I angles close to the tetrahedral angle, 109.5°, indicating that three water molecules bind to each oxygen, while for oxobromo, oxoiodo, oxoselenium, oxoarsenic and oxometallate anions, the X-O⋯O_I angle is close to 120°, indicating that only two water molecules bind to each anion oxygen, Table 4.

The X–O bond distance in all oxoanions studied, except the phosphate ion, increases by ca. 0.02 Å on hydration in aqueous solution in comparison to the X–O bond distance in the solid state. This shows that the hydration reduces the charge density of the oxoanion oxygens, and that this effect is independent of the total charge of the anion, Table 6. This lengthening of the X–O bond distance can also be expected for oxoanions such as nitrate and nitrite although there are no accurate structure determinations in aqueous solution due to the weak scattering power of nitrogen for X-rays.

Relationship between ionic diffusion coefficient and size of hydrated ions in aqueous solution

The larger the ion, the slower the expected diffusion rate in aqueous solution. Reported ionic diffusion coefficients are summarized in Table 6 together with structural information for hydrated metal ions and anions, and the estimated van der Waals radii. This has been calculated assuming a spherical model for all ions except for the linearly hydrated silver ion, where a cylindrical form has been applied. The relationship between ionic diffusion coefficient and size of hydrated ions in aqueous solution is shown in Fig. 8. The monovalent anions, monovalent metal ions, except sodium, and most divalent metal ions display a linear relationship with the assumed volume the hydrated ion. However, the volume of the aluminum(III), chromium(III) and iron(III) ions seems to be too large with three full hydration shells, but too small with two. This indicates that fractions of a third hydration shell are present around these ions, Fig. 8, as also indicated by the LAXS studies, vide supra. The volumes of the calcium(II), strontium(II), barium(II) and lead(II) ions are slightly larger than expected from the ionic diffusion coefficient-hydrated volume relationship, Fig. 8. This may indicate that the second hydration shells are not complete or that the water molecules in the second hydration shell are less stiff. This is supported by the increasing deviation from the linear relationship with increasing size/decreasing charge density of these ions, Fig. 8. The volumes of the divalent anions seem to be underestimated, indicating the presence of portion of a second hydration shell even though they have not been detected in LAXS studies. The ν(O–D) stretching frequencies of the first hydration shell being lower than in bulk water may indicate the possibility of portion of a second hydration shell, vide supra. The ionic diffusion coefficient-hydrated volume relationship strongly indicate that the sodium ion has two hydration shells even though neither the LAXS nor the DDIR studies indicate this (Table 5). The hydrated silver ion fits well into the size-ionic diffusion coefficient relationship assuming a cylindrical form.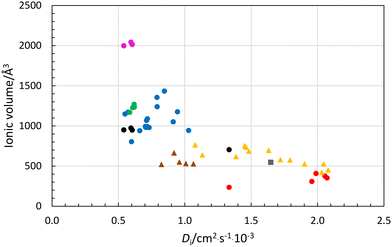

Fig. 8 Relationship between ionic diffusion coefficient, D_i, and volume of hydrated ion, ų, using experimental structure data in aqueous solution from Table 6; red circles-monovalent metal ions assuming one hydration shell, blue circles-divalent metal ions assuming two hydration shells, green circles-lanthanum(III) and lanthanoid(III) ions assuming two hydration shells, cerice circles-trivalent metal ions assuming three hydration shells, black circles-trivalent metal ions and sodium ion assuming two hydration shells, yellow triangles-monovalent anions with one hydration shell, and brown triangles-divalent anions assuming one hydration shell.

Table 5 Mean M–O bond distance, Å, in oxoanions in solid state (without strong bonds to the oxoanion oxygens) and aqueous solution, Tables S2 (ESI) and S4,† respectively

	d(M–O)(s)	d(M–O)(aq)	Diff.	Ref.
ClO2^−	1.573	1.591	0.018	148
ClO3^−	1.474	1.501	0.027	148
ClO4^−	1.430	1.453	0.023	2, 62 and 148
BrO3^−	1.652	1.671	0.019	148
IO3^−	1.807	1.829	0.022	148
IO4^−	1.756	1.781	0.025	148
MnO4^−	1.611	1.630	0.019	149
ReO4^−	1.710	1.735	0.025	149
SO3^2−	1.524	1.53	0.008	150
SO4^2−	1.475	1.495	0.020	151
SeO3^2−	1.692	1.709	0.017	153
SO3^2−	1.635	1.657	0.022	153
S2O3^2−	1.470 + 2.000	1.479 + 2.020	0.009 + 0.020	152
CrO4^2−	1.643	1.660	0.017	149
Cr2O7^2−	1.608 + 1.782	1.616 + 1.806	0.012 + 0.024	149
MoO4^2−	1.756	1.775	0.019	149
WO4^2−	1.776	1.797	0.021	149
PO4^3−	1.540	1.531	−0.009	154 and 155
AsO4^3−	1.678	1.704	0.026	156
VO4^3−	1.720	1.738	0.018	149

---

Table 6 Ionic diffusion coefficients at zero ionic strength, D_i, 10⁻³ m² s⁻¹, M–O_I bond distance, d(M–O) in hydrated metal ions, and X–(H)⋯O_I, or X–O(–H)⋯O_I distance in anions, Å, O_I(–H)⋯O_II distance in cations and O(–H)⋯O_I, Å, in oxoanions, Å, radius of hydrated ion including the hydration shells assuming a van der Waals radius of hydrogen of the water in the outer hydration shell of cations of 1.20 Å, and of oxygen in the outer hydration shell of anions, 1.40 Å, R, Å

Ion	D i ^a	d(M–O)	d(OI⋯OII)	d(M–(OI–H)⋯OII)	∠(M–OI⋯OII)	R	V
One hydration shell ions
Na^+	1.334	2.43				3.83	235
Na^+	1.334	2.43	2.95^c	4.67^c	120^c	5.52^c	704^c
K^+	1.957	2.79				4.19	308
Rb^+	2.072	2.98				4.38	352
Cs^+	2.056	2.43				4.48	377
Tl^+	1.989	2.8 + 3.2				4.6	407
Two hydration shell ions
Li^+	1.029	1.95	2.85^c	4.0	114.1	6.09	943
Be^2+	0.599	1.62	2.785^c	3.7	111.5	5.97	803
Mg^2+	0.706	2.069	2.785	4.08	113.4	6.17	983
Ca^2+	0.792	2.46	2.785	4.58	121.0	6.66	1239
Sr^2+	0.791	2.64	2.785	4.78	123.0	6.86	1355
Ba^2+	0.847	2.82	2.785	4.90	121.4	6.99	1433
Mn^2+	0.712	2.174	2.783	4.26	116.7	6.34	1068
Fe^2+	0.719	2.124	2.785	4.091	112.2	6.19	991
Co^2+	0.732	2.090	2.788	4.07	112.4	6.16	980
Ni^2+	0.661	2.057	2.787	3.981	109.6	6.08	940
Cu^2+	0.714	1.965	2.787	4.094	117.9	6.17	982
Ag^+	1.648	2.33	2.785	4.90	125.6	6.72; 3.6^b	547
Zn^2+	0.703	2.091	2.790	4.10	113.5	6.19	993
Cd^2+	0.719	2.302	2.785	4.284	114.4	6.38	1088
Hg^2+	0.913	2.33	2.785	4.198	109.6	6.31	1051
Pb^2+	0.945	2.53	2.785	4.44	113.2	6.55	1176
Sc^3+	0.574	2.174	2.752	4.276	120.0	6.35	1171
Y^3+	0.550	2.365	2.725	4.41	119.9	6.50	1149
La^3+	0.619	2.527	2.785	4.63	121.2	6.72	1269
Ce^3+	0.620	2.516	2.785	4.56	119.9	6.65	1234
Sm^3+	0.608	2.43	2.785	4.56	121.0	6.64	1227
Er^3+	0.585	2.36	2.785	4.45	120.1	6.54	1169
Al^3+	0.541	1.891	2.725	5.52	119.9	6.10^c	950^c
Cr^3+	0.595	1.966	2.725	5.58	120.0	6.15^c	974^c
Fe^3+	0.604	1.999	2.746	5.51	114.5	6.10^c	949^c
Three hydration shell ions
Al^3+	0.541	1.891	2.725	5.52	119.9	7.81	1999
Cr^3+	0.595	1.966	2.725	5.58	120.0	7.88	2042
Fe^3+	0.604	1.999	2.746	5.51	114.5	7.83	2014

---

Ion	D i	d(X–O)	d(X⋯OI)	d(O–(H)⋯OI)	d(X–(H)⋯OI)	R	V
a Ref. 157. b Length and radius of an applied cylindric model. c Denotes assumed value.
Cl^−	2.032		3.25			4.65	421
Br^−	2.080		3.36			4.76	452
I^−	2.045		3.61			5.01	527
NO3^−	1.902	1.28		3.02	3.61	5.01	527
ClO2^−	1.382	1.591		3.040	3.881	5.281	617
ClO3^−	1.72	1.501		3.021	3.770	5.170	579
ClO4^−	1.792	1.453		3.046	3.757	5.157	574
BrO3^−	1.483	1.671		2.987	4.068	5.468	685
IO3^−	1.078	1.829		3.013	4.270	5.670	764
IO4^−	1.451	1.781		3.009	4.243	5.643	753
MnO4^−	1.632	1.630		3.031	4.095	5.495	695
ReO4^−	1.462	1.735		3.010	4.197	5.597	734
CrO4^2−	1.132	1.660		2.85	3.940	5.340	637
WO4^2−	0.991	1.775		2.85	4.010	5.410	663
SO3^2−	0.959	1.53		2.878	3.68	5.080	549
SO4^2−	1.065	1.495		2.85	3.61	5.010	527
SeO4^2−	1.008	1.657		2.85	3.622	5.022	531
PO4^3−	0.824	1.537		2.815	3.588	4.988	520

---

Conclusions

The good correlation between calculated volume of the hydrated metal ions from the LAXS measurements and the ionic diffusion coefficients metal ions and anions at infinite dilution, summarized in Table 6 and Fig. 8, show that the hydrate structures studied in relatively concentrated solution are also representative for dilute solutions. It is possible that the outer hydration shells of both metal ions and inorganic anions becomes more well-defined in dilute solution where the competition of the available water molecules is very limited.

The results presented in this paper describe the arrangement of water molecules around metal ions and inorganic anions in aqueous solution. This information must be obtained in aqueous solution as at crystallization hydrate bonds weaker than hydrogen bonds in the aqueous bulk will transfer to the remaining aqueous bulk for bonding energy reasons. This can be partly overcome by crystallization at low temperatures as shown by Voigt and coworkers.^5–7 However, the magnesium(II) and calcium(II) ions have only portions a second hydration shell in the solid state,^5,6 and the aluminium(III) ion is completely lacking a third hydration shell.⁷ It is important to stress that hydrated metal ions and inorganic anions interact with significantly more water in aqueous solution than the amount observed in solid state structures. This is especially important at the analysis of reaction mechanisms and transport properties involving metal ions and anions in aqueous solution.

The alkali metal ions, except lithium, and the thallium(I) ion are weakly hydrated in aqueous solution and form only a single hydration shell with different physico-chemical properties to those of bulk water. However, the ionic diffusion coefficient-volume relationship supports the presence of two hydration shells around the sodium ion, Fig. 8. The lithium, silver(I), metal(II), scandium(III), yttrium(III), lanthanum(III) and lanthanoid(III) ions, and most likely the actinoid(III) ions, form two hydration shells with the second hydration shell water molecules having similar physico-chemical properties to those of the first hydration shell of the alkali and thallium(I) ions. The trivalent transition metal ions and the thorium(IV) and uranium(IV) ions form two well-defined hydration shells and portions of a third hydration shell. The M–O bond distances are not significantly affected by the presence of a second hydration shell, and M–O bond distances observed in solid compounds can be transferred to aqueous solution. On the other hand, the X–O bond distance in oxoanions, except phosphate, increase by ca. 0.02 Å in aqueous solution due to the hydration in comparison to the X–O bond distances in solid compounds where the anion is not bound to a metal ion other than the alkali metal ions. The monovalent anions have a single hydration shell, while the divalent anions form in addition portions of a second hydration shell, evidently in the lower ionic diffusion coefficients than expected for the size with a single hydration shell. The trivalent anions may have two hydration shells as experimentally observed for the vanadate ion.

Data availability

All experimental data are available upon request to author at E-mail: ingmar.persson@slu.se.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The support from the Department of Molecular Sciences, Swedish University of Agricultural Sciences, Uppsala, is gratefully acknowledged. Dr Lars Eriksson, Department of Materials and Environmental Chemistry, Stockholm University, is acknowledged for plotting the figure used in Fig. 1a and as TOC.

References

1. I. Persson, M. Sandström, H. Yokoyama and M. Chaudhry, Structures of the Solvated Barium and Strontium Ions in Aqueous, Dimethyl Sulfoxide and Pyridine Solution, and Crystal Structure of Strontium and Barium Hydroxide Octahydrate, Z. Naturforsch., A: Phys. Sci., 1995, 50, 21–37.
2. J. Stangret and T. Gampe, Ionic Hydration Behaviour Derived From Infrared Spectra in HDO, J. Phys. Chem. A, 2002, 106, 5393–5402.
3. A. Patra, S. Roy, S. Saha, D. K. Palit and J. A. Mondal, Observation of Extremely Weakly Interacting OH (∼3600 cm⁻¹) in the Vicinity of High Charge Density Metal Ions (M^z+; z = 1,2,3): A Structural Heterogeneity in the Extended Hydration Shell, J. Phys. Chem. C, 2020, 124, 3028–3036.
4. Y. Marcus, Effect of Ions on the Structure of Water: Structure Making and Breaking, Chem. Rev., 2009, 109, 1346–1370 , and references therein.
5. E. Hennings, H. Schmidt and W. Voigt, Crystal Structures of Hydrated of Simple Inorganic Salts. I. Water-rich Magnesium Halides MgCl₂·8H₂O, MgCl₂·12H₂O, MgBr₂·6H₂O, MgBr₂·9H₂O, MgI₂·8H₂O and MgI₂·9H₂O, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 1292–1300.
6. E. Hennings, H. Schmidt and W. Voigt, Crystal Structures of Hydrated of Simple Inorganic Salts. II. Water-rich Calcium Bromide and Iodide Hydrates: CaBr₂·9H₂O, CaI₂·8H₂O, CaI₂·7H₂O and CaI₂·6.5H₂O, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 876–881.
7. E. Hennings, H. Schmidt and W. Voigt, Crystal Structures of Hydrated of Simple Inorganic Salts. III. Water-rich Aluminium Halide Hydrates: AlCl₃·15H₂O, AlBr₃·15H₂O, AlI₃·17H₂O and AlBr₃·9H₂O, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 882–888.
8. G. Johansson and M. Sandström, Computer-programs for Analysis of Data on X-ray-Diffraction by Liquids, Chem. Scr., 1973, 4, 195–198.
9. C. M. V. Stålhandske, I. Persson, M. Sandström and E. Kamienska-Piotrowicz, A Large Angle Scattering and Vibrational Spectroscopic Study of the Solvated Zinc, Cadmium and Mercury(II) Ions in N,N-Dimethylthioformamide Solution, Inorg. Chem., 1997, 36, 3174–3182.
10. International Tables for X-ray Crystallography, Kynoch Press, Birmingham, U.K., 1974, vol. 4.
11. D. T. Cromer, Compton Scattering Factors for Aspherical Free Atoms, J. Chem. Phys., 1969, 50, 4857–4859.
12. D. T. Cromer and J. B. Mann, Compton Scattering Factors for Spherically Symmetric Free Atoms, J. Chem. Phys., 1967, 47, 1892–1893.
13. H. A. Levy, M. D. Danford and A. H. Narten, Data Collection and Evaluation with an X-ray Diffractometer Designed for the Study of Liquid Structure, Technical Report ORNL-3960, Oak Ridge National Laboratory, Oak Ridge, TN, 1966.
14. M. Molund and I. Persson, STEPLR - A Program for Refinements of Data on X-Ray Scattering by Liquids, Chem. Scr., 1985, 25, 197–197.
15. H. Ohtaki and T. Radnai, Structure and Synamics of Hydrated Ions, Chem. Rev., 1993, 93, 1157–1204 . and references therein.
16. P. R. Smirnov and V. N. Trostin, Structure of the Nearest Surrounding of the Li⁺ Ion in Aqueous Solutions of Their Salts, Russ. J. Gen. Chem., 2006, 76, 175–182 , and references therein.
17. P. R. Smirnov, Structure of the Li⁺ Ion Close Environment in Various Solvents, Russ. J. Gen. Chem., 2019, 89, 2443–2452 , and references therein.
18. Y. Kameda, T. Miyazaki, T. Otomo, Y. Amo and T. Usuki, Neutron Diffraction Study on the Structure of Aqueous LiNO₃ Solutions, J. Solution Chem., 2014, 43, 1588–1600.
19. Y. Kameda, T. Miyazaki, T. Otomo, Y. Amo, T. Usuki, K. Ikeda and T. Otomo, Neutron Diffraction Study on the Structure of Hydrated Li⁺ in Dilute Aqueous Solutions, J. Phys. Chem., 2018, 122, 1695–1701.
20. W. Rudolph, M. H. Brooker and C. C. Pye, Hydration of Lithium Ion in Aqueous Solution, J. Phys. Chem., 1995, 99, 3793–3797.
21. J. Mähler and I. Persson, A Study of the Hydration of the Alkali Metal Ions in Aqueous Solution, Inorg. Chem., 2012, 51, 425–438.
22. P. D'Angelo and I. Persson, On the Structure of the Hydrated and Dimethylsulfoxide Solvated Rubidium Ions in Solution, Inorg. Chem., 2004, 43, 3543–3549.
23. I. Persson, Structures of hydrated metal ions in solid state and aqueous solution, Liquids, 2022, 2, 210–242 , and references therein.
24. T. Yamaguchi, H. Ohtaki, E. Spohr, G. Pálinkás, K. Heinzinger and M. M. Probst, Molecular Dynamics and X-ray Diffraction Study of Aqueous Beryllium(II) Chloride Solutions, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1986, 41, 1175–1185.
25. P. E. Mason, S. Ansell, G. W. Neilson and J. W. Brady, Be²⁺ Hydration in Concentrated Aqueous Solutions of BeCl₂, J. Phys. Chem. B, 2008, 112, 1935–1939.
26. P. R. Smirnov and V. N. Trostin, Structural Patrameters of Hydration of Be²⁺ and Mg²⁺ in Aqueous Solution of Their Salts, Russ. J. Gen. Chem., 2008, 78, 1643–1649 , and references therein.
27. A. D'Incal, T. S. Hofer, B. R. Randolf and B. M. Rode, Be(II) in Aqueous Solution - An Extended ab initio QM/MM MD Study, Phys. Chem. Chem. Phys., 2006, 8, 2841–2847.
28. C. C. Pye, An Ab Initio Study of Beryllium(II) Hydration, J. Mol. Struct.: THEOCHEM, 2009, 913, 210–214.
29. J. M. Martínez, R. R. Pappalardo and E. Sánchez Marcos, First-Principles Ion-Water Interaction Potentials for Highly Charged Monatomic Cations. Computer Simulations of Al³⁺,Mg²⁺, and Be²⁺ in Water, J. Am. Chem. Soc., 1999, 121, 3175–3184.
30. M. Pavlov, P. E. M. Siegbahn and M. Sandström, Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory, J. Phys. Chem. A, 1998, 102, 219–228.
31. W. W. Rudolph, D. Fischer, D. Irmer and C. C. Pye, Hydration of Beryllium(II) in Aqueous Solutions of Common Inorganic Salts. A Combined Vibrational Spectroscopic and ab initio Molecular Orbital Study, Dalton Trans., 2009, 6513–6527.
32. D. Di Tommaso and N. H. de Leeuw, Structure and Dynamics of the Hydrated Magnesium Ion and of the Solvated Magnesium Carbonates: Insights From First Principles Simulations, Phys. Chem. Chem. Phys., 2010, 12, 894–901.
33. A. Bhattacharjee, A. B. Pribil, B. R. Randolf, B. M. Rode and T. S. Hofer, Hydration of Mg²⁺ and Its Influence on the Water Hydrogen Bonding Network via ab initio QMCF MD, Chem. Phys. Lett., 2012, 536, 39–44.
34. B. Das and A. Chandra, Ab Initio Molecular Dynamics Study of Aqueous Solutions of Magnesium and Calcium Nitrates: Hydration Shell Structure, Dynamics and Vibrational Echo Spectroscopy, J. Phys. Chem. B, 2022, 126, 528–544.
35. Y. Wang, G. Wang, D. T. Bowron, F. Zhu, A. C. Hannon, Y. Zhou, X. Liud and G. Shi, Unveiling the Structure of Aqueous Magnesium Nitrate Solutions by Combining X-ray Diffraction and Theoretical Calculations, Phys. Chem. Chem. Phys., 2022, 24, 22939–22949.
36. F. Jalilehvand, D. Spångberg, P. Lindqvist-Reis, K. Hermansson, I. Persson and M. Sandström, The Hydration of the Calcium Ion. An EXAFS, Large Angle X-Ray Scattering and Molecular Dynamics Simulation Study, J. Am. Chem. Soc., 2001, 123, 431–441.
37. T. Yamaguchi, S. Hayasshi and H. Ohtaki, X-ray Diffraction Study of Calcium(II) Chloride Hydrate Melts: CaCl₂·RH₂O (R = 4.0, 5.6, 6.0, and 8.6), Inorg. Chem., 1989, 28, 2434–2439.
38. R. Caminiti, A. Musinu, G. Paschina and G. Pinna, X-ray Diffraction Study of Aqueous SrCl₂ Solutions, J. Appl. Crystallogr., 1982, 15, 482–487.
39. R. R. Pappalardo, J. M. Martínez, D. Z. Caralampio and E. Sánchez Marcos, Hydration of Heavy Alkaline-Earth Cations Studied by Molecular Dynamics Simulations and X-ray Absorption Spectroscopy, Inorg. Chem., 2021, 60, 13578–13587.
40. V. Migliorati, A. Caruso and P. D'Angelo, Unraveling the Hydration Properties of the Ba²⁺ Aqua Ion: the Interplay of Quantum Mechanics, Molecular Dynamics, and EXAFS Spectroscopy, Inorg. Chem., 2019, 58, 14551–14559.
41. P. Lindqvist-Reis, I. Persson and M. Sandström, The Hydration of the Scandium(III) Ion in Aqueous Solution and Crystalline Hydrates Studied by XAFS Spectroscopy, Large Angle X-Ray Scattering and Crystallography, Dalton Trans., 2006, 3868–3878.
42. P. Lindqvist-Reis, K. Lamble, S. Pattanaik, M. Sandström and I. Persson, Hydration of the Yttrium(III) Ion in Aqueous Solution. An X-ray Diffraction and XAFS Structural Study, J. Phys. Chem. B, 2000, 104, 402–408.
43. J. Näslund, P. Lindqvist-Reis, I. Persson and M. Sandström, Steric Effects Control the Structure of the Solvated Lanthanum(III) Ion in Aqueous, Dimethyl Sulfoxide, and N,N’-Dimethylpropyleneurea Solution. An EXAFS and Large-Angle X-ray Scattering Study, Inorg. Chem., 2000, 39, 4006–4011.
44. I. Persson, P. D'Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Hydration of the Lanthanoid(III) Ions in Aqueous Solution and Crystalline Hydrates Studied by EXAFS Spectroscopy and Crystallography. The Myth of the “Gadolinium Break”, Chem. – Eur. J., 2008, 14, 3056–3066.
45. G. Johansson and H. Wakita, X-ray Investigation of the Coordination and Complex Formation of Lanthanoid Ions in Aqueous Perchlorate and Selenate Solutions, Inorg. Chem., 1985, 26, 3047–3052.
46. R. Caminiti, P. Cucca and A. D'Andrea, Hydration Phenomena in a Concentrated Aqueous Solution of Ce(NO₃)₃ - X-ray Diffraction and Raman Spectroscopy, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1983, 38, 533–539.
47. N. Torapava, I. Persson, L. Eriksson and D. Lundberg, Hydration and Hydrolysis of Thorium(IV) in Aqueous Solution and the Structures of Two Crystalline Thorium(IV) Hydrates, Inorg. Chem., 2009, 48, 11712–11723.
48. G. Johansson, M. Magini and H. Ohtaki, Coordination Around Thorium(IV) in Aqueous Perchlorate, Chloride and Nitrate Solutions, J. Solution Chem., 1991, 20, 775–792.
49. R. E. Wilson, S. Skanthakumar, P. C. Burns and L. Soderholm, Structure of the Homoleptic Thorium(IV) Aqua Ion [Th(H₂O)₁₀]Br₄, Angew. Chem., Int. Ed., 2007, 46, 8043–8045.
50. R. Spezia, C. Beuchat, R. Vuilleumier, P. D'Angelo and L. Gagliardi, Unravelling the Hydration Structure of ThX₄ (X = Br, Cl) Water Solutions by Molecular Dynamics Simulations and X-ray Absorption Spectroscopy, J. Phys. Chem. B, 2012, 116, 6465–6475.
51. N. Torapava, D. Lundberg and I. Persson, A Coordination Chemistry Study of Solvated Thorium(IV) Ions in Two Oxygen-Donor Solvents, Eur. J. Inorg. Chem., 2011, 5273–5278.
52. S. Pocev and G. Johansson, An X-ray Investigation of the Coordination of the Hydrolysis of the Uranium(IV) Ion in Aqueous Perchlorate Solutions, Acta Chem. Scand., 1973, 27, 2146–2160.
53. W. Bol and T. Welzen, The interpretation of X-ray diffraction by aqueous solutions of aluminum(III) nitrate and chromium(III) nitrate, Chem. Phys. Lett., 1977, 49, 189–192.
54. R. Caminiti, G. Licheri, G. Piccaluga, G. Pinna and T. Radnai, Order phenomena in aqueous AlCl₃ solutions, J. Chem. Phys., 1979, 71, 2473–2476.
55. R. Caminiti and T. Radnai, X-ray Diffraction Study of a Concentrated Al(NO₃)₃ Solution, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1980, 35, 1368–1372.
56. V. E. Barlette, L. C. G. Freitas, P. H. Guadagnini and C. A. A. Bertran, Hydration properties of Al³⁺ ion using empirical ion-water potential by Monte Carlo simulation, J. Braz. Chem. Soc., 2008, 19, 101–110.
57. W. W. Rudolph, R. Mason and C. C. Pye, Aluminium(III) hydration in aqueous solution. A Raman spectroscopic investigation and an ab initio molecular orbital study of aluminium(III) water clusters, Phys. Chem. Chem. Phys., 2000, 2, 5030–5040.
58. P. Lindqvist-Reis, S. Díaz-Moreno, A. Munoz-Páez, S. Pattanaik, I. Persson and M. Sandström, On the Structure of Hydrates Gallium, Indium and Chromium(III) Ions in Aqueous Solutions. A Large Angle X-ray Scattering and EXAFS Study, Inorg. Chem., 1998, 37, 6675–6683.
59. J. Glaser and G. Johansson, On the structures of the Hydrated Thallium(III) Ion and it Bromide Complexes in Aqueous Solution, Acta Chem. Scand., Ser. A, 1982, 36, 125–135.
60. I. Persson, F. Jalilehvand and M. Sandström, Structure of the Solvated Thallium(I) Ion in Aqueous, Dimethyl Sulfoxide, N,N′-Dimethylpopyleneurea and N,N-Dimethylthioformamide Solution, Inorg. Chem., 2002, 41, 192–197.
61. I. Persson, P. D'Angelo and D. Lundberg, Hydrated and Solvated Tin(II) Ions in Solution and the Solid State, and a Coordination Chemistry Overview of the d¹⁰s², Chem. – Eur. J., 2016, 22, 18583–18592.
62. I. Persson, K. Lyczko, D. Lundberg, L. Eriksson and A. Płaczek, A Coordination Chemistry Study of Hydrated and Solvated Lead(II) Ions in Solution and Solid State, Inorg. Chem., 2011, 50, 1058–1072.
63. E. Hennings, H. Schmidt, M. Köhler and W. Voigt, Crystal Structure of Tin(II) Perchlorate Trihydrate, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, 474–476.
64. J. Näslund, I. Persson and M. Sandström, Solvation of the Bismuth(III) Ion by Water, Dimethyl Sulfoxide, N,N’-Dimethylpropyleneurea, and N,N-Dimethylthioformamide. An EXAFS, Large-Angle X-ray Scattering, and Crystallographic Structural Study, Inorg. Chem., 2000, 39, 4012–4021.
65. R. Caminiti, G. Licheri, G. Piccaluga and G. Pinna, Hydration water–external water interactions around Cr³⁺ ions, J. Chem. Phys., 1977, 69, 1–4.
66. A. Muñoz-Páez, R. R. Pappalardo and E. Sánchez Marcos, Determination of the Second Hydration Shell of Cr³⁺ and Zn²⁺ in Aqueous Solutions by Extended X-ray Absorption Fine Structure, J. Am. Chem. Soc., 1995, 117, 11710–11720.
67. P. J. Merkling, A. Muñoz-Páez and E. Sánchez Marcos, Exploring the Capabilities of X-ray Absorption Spectroscopy for Determining the Structure of Electrolyte Solutions: Computed Spectra for Cr³⁺or Rh³⁺in Water Based on Molecular Dynamics, J. Am. Chem. Soc., 2002, 124, 10911–10920.
68. Y. Tajiri, N. Ichihashi, T. Mibuchi and H. Wakita, An X-Ray Diffraction Investigation of the Coordination Structure of Mn(II) Ions in Highly Concentrated Aqueous MnBr₂ and MnCl₂ Solutions, Bull. Chem. Soc. Jpn., 1986, 59, 1155–1159.
69. R. Caminiti, G. Cucca and T. Pintori, Hydration and ion-pairing in concentrated aqueous Mn(NO₃)₂ solutions. An X-ray and Raman Spectroscopy Study, Chem. Phys., 1984, 88, 155–161.
70. R. Caminiti, G. Marongiu and G. Paschina, A Comparative X-ray Diffraction Study of Aqueous MnSO₄ and Crystals of MnSO₄·5H₂O, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1982, 37, 581–586.
71. G. Licheri, G. Paschina, G. Piccaluga and G. Pinna, X–ray Diffraction Study of Aqueous Solutions of NiSO₄ and MnSO₄, J. Chem. Phys., 1984, 81, 6059–6063.
72. H. Konieczna, D. Lundberg and I. Persson, Solvation and Coordination Chemistry of Manganese(II) Ion in Solvents with Solvation Properties. A Transfer Thermodynamic, Complex Formation, EXAFS Spectroscopic and Crystallographic Study, Polyhedron, 2021, 195, 114961.
73. C. F. Schwenk, H. H. Loeffler and B. M. Rode, Structure and Dynamics of Metal Ions in Solution: QM/MM Molecular Dynamics Simulations of Mn²⁺ and V²⁺, J. Am. Chem. Soc., 2003, 125, 1618–1624.
74. W. W. Rudolph and G. Irmer, Hydration and Speciation Studies of Mn²⁺ in Aqueous Solution with Simple Monovalent Anions (ClO₄⁻, NO₃⁻, Cl⁻, Br⁻), Dalton Trans., 2013, 42, 14460–14472.
75. E. Kálmán, T. Radnai, G. Pálinkás, F. Hajdu and A. Vértes, Hydration of Iron(II) Ion in Aqueous Solutions, Electrochim. Acta, 1988, 33, 1223–1228.
76. G. Herdman and G. W. Neilson, Ferrous Fe(II) Hydration in a 1 Molal Heavy Water Solution of Iron Chloride, J. Phys.: Condens.Matter, 1992, 4, 649–653.
77. D. Lundberg, A.-S. Ullström, P. D'Angelo and I. Persson, A Structural Study of the Hydrated and the Dimethylsulfoxide, N,N′-dimethylpropyleneurea, and N,N-dimethylthioformamide Solvated Iron(II) and Iron(III) Ions in Solution and Solid State, Inorg. Chim. Acta, 2007, 360, 1809–1818.
78. A. M. Mohammed, Hydration Structure and Water Exchange Dynamics of Fe(II) Ion in Aqueous Solution, Bull. Chem. Soc. Ethiop., 2010, 24, 239–250.
79. S. T. Moin, T. S. Hofer, A. B. Pribil, B. R. Randolph and B. M. Rode, A Quantum Mechanical Charge Field Molecular Dynamics Study of Fe²⁺ and Fe³⁺ Ions in Aqueous Solutions, Inorg. Chem., 2010, 49, 5101–5106.
80. R. Caminiti and M. Magini, An X-ray diffraction study on the first and the second hydration shell of the Fe(III) ion in nitrate solutions, Chem. Phys. Lett., 1979, 61, 40–44.
81. G. Herdman and G. W. Neilson, Ferric (Fe(III) Coordination in Concentrated Aqueous Electyrolyte Solutions, J. Phys.: Condens.Matter, 1992, 4, 627–638.
82. R. Caminiti and T. Radnai, X–ray Diffraction Study of Ferric Chloride Solutions and Hydrated Melt. Analysis of the Iron(III)–Chloride Complexes Formation, J. Chem. Phys., 1979, 71, 4255–4262.
83. G. Piccaluga, X-ray Diffraction Study of the Coordination of Fe(III) in a Highly Hydrolyzed Solution of Iron(III) Chloride, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1982, 37, 154–157.
84. M. Magini and R. Caminiti, Structure of Highly Concentrated Iron(III) Salt Solutions, J. Inorg. Nucl. Chem., 1977, 39, 91–94.
85. R. Caminiti and M. Magini, An X-ray Diffraction Study on the First and the Second Hydration Shell of the Fe(III) in Nitrate Solutions, Chem. Phys. Lett., 1979, 61, 40–44.
86. M. Magini, An X-ray Investigation on the Structure of Iron(III) Perchlorate Solutions, J. Inorg. Nucl. Chem., 1977, 40, 43–48.
87. A. M. Mohammed, Structure of Co(III) and Fe(III) Transition Metal Ions in Aqueous Solution, Bull. Chem. Soc. Ethiop., 2006, 20, 121–131.
88. A. Musinu, G. Paschina, G. Piccaluga and M. Magini, X–ray Diffraction Study of CoCl₂−LiCl Aqueous Solutions, J. Chem. Phys., 1984, 80, 2772–2776.
89. M. Magini and G. Giubileo, Solute Structuring in Concentrated Aqueous Co(II) and Ni(II) Perchlorate Soutions, Gazz. Chim. Ital., 1981, 111, 449–454.
90. M. Magini, Hydration and Complex Formation Study on Concentrated MCl₂ solutions [M=Co(II), Ni(II), Cu(II)] by X–ray Diffraction Technique, J. Chem. Phys., 1981, 74, 2523–2529.
91. A. Corrias, A. Musinu and G. Pinna, EXAFS and X-ray Diffraction Study of a Mixed NiCl₂/CoCl₂ Solution, Chem. Phys. Lett., 1985, 120, 295–300.
92. P. D'Angelo, V. Barone, G. Chillemi, N. Sanna, W. Meyer-Klauke and N. V. Pavel, Hydrogen and Higher Shell Contributions in Zn²⁺, Ni²⁺, and Co²⁺ Aqueous Solutions: An X-ray Absorption Fine Structure and Molecular Dynamics Study, J. Am. Chem. Soc., 2002, 124, 1958–1967.
93. R. Spezia, M. Duvail, P. Vitorge, T. Catailler, J. Tortajada, G. Chillemi, P. D'Angelo and M. P. Gaigeot, A coupled Car-Parinello Molecular Dynamics and EXAFS Data Analysis Investigation of Aqueous Co²⁺, J. Phys. Chem. A, 2006, 110, 13081–13088.
94. P. D'angelo, M. Benfatto, S. Della Longa and N. V. Nicolae, Combined XANES and EXAFS Analysis of Co²⁺, Ni²⁺ and Zn²⁺ Aqueous Solutions, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 064209.
95. D. Z. Caralampio, B. Reeves, M. R. Beccia, J. M. Martínez, R. R. Pappalardo, C. den Auwer and E. Sánchez, Revisiting the Cobalt(II) hydration from Molecular Dynamics and X-ray Absorption Spectroscopy, Mol. Phys., 2019, 117, 3320–3328.
96. M. C. Read and M. Sandström, Second-Sphere Hydration of Rhodium(III) and Chromium(III) in Aqueous Solution. A Large Angle X-ray Scattering and EXAFS Study, Acta Chem. Scand., 1992, 46, 1177–1182.
97. R. Caminiti and P. Cucca, An X-ray Diffraction Study of Rh(III) Coordination in a Dilute Aqueous Solution of Rh(ClO₄)₃, Chem. Phys. Lett., 1984, 108, 51–57.
98. R. Caminiti, D. Atzei, P. Cucca, F. Squintu and G. Bongiovanni, Coordination of Rhodium(III) in Dilute Aqueous Solutions in Presence of Chloride Anion, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1985, 40, 1319–1328.
99. R. Caminiti, D. Atzei, P. Cucca, A. Anedda and G. Bongiovanni, Structure of Rhodium(III) Nitrate Aqueous Solutions - An Investigation by X-ray Diffraction and Raman Spectroscopy, J. Chem. Phys., 1986, 90, 238–243.
100. R. Caminiti, On Nickel–Sulfate Contacts and SO₄²⁻–H₂O Interactions in Aqueous Solutions, J. Chem. Phys., 1986, 84, 3336–3338.
101. R. Caminiti and P. Cucca, X-ray Diffraction Study on a NiBr₂ Aqueous Solution. Experimental Evidence of the Ni(II)-Br contacts, J. Chem. Phys., 1982, 89, 110–114.
102. E. Kálmán, I. Serke, G. Pálinkás, G. Johansson, G. Kabisch, M. Maeda and H. Ohtaki, Potentiometric and Calorimetric Studies on the Formation of Ethylenediamine Complexes of Nickel(II) Ion in Water and Dioxane-Water Mixtures, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1983, 38, 225–230.
103. R. Caminiti, Nickel and Cadmium Phosphates in Aqueous Solution - Cation Anion Complex Formation and Phosphate-H₂O Interactions, J. Chem. Phys., 1982, 77, 5682–5686.
104. R. Caminiti, G. Paschina and G. Piccaluga, Ni–Cl Bonding in Concentrated Ni(II) Aqueous Solutions at High Cl⁻/Ni²⁺ Ratios. An X–ray Diffraction Investigation, J. Chem. Phys., 1982, 76, 1116–1121.
105. J. R. Newsome, G. W. Neilson, J. E. Enderbyand and M. Sandström, Ni²⁺ Hydration in Perchlorate and Chloride Solutions, Chem. Phys. Lett., 1981, 82, 399–401.
106. B. Beagley, A. Eriksson, J. Lindgren, I. Persson, L. G. M. Pettersson, M. Sandström, U. Wahlgren and E. W. White, A Computational and Experimental Study on the Jahn-Teller Effect in the Hydrated Copper(II) Ion. Comparisons with Hydrated Nickel(II) Ions in Aqueous Solution and Solid Tutton's Salts, J. Phys.: Condens.Matter, 1989, 1, 2395–2408.
107. O. Kristiansson, I. Persson, D. Bobicz and D. Xu, A Structural Study of the Hydrated and the Dimethylsulfoxide, N,N′-Dimethylpropyleneurea, Acetonitrile, Pyridine and N,N-Dimethylthioformamide Solvated Nickel(II) Ion Solution and Solid State, Inorg. Chim. Acta, 2003, 344, 15–27.
108. P. D'Angelo, O. M. Roscioni, G. Chillemi, S. Della Longa and M. Benfatto, Detection of Second Hydration Shells in Ionic Solutions by XANES: Computed Spectra for Ni²⁺ in Water Based on Molecular Dynamics, J. Am. Chem. Soc., 2006, 128, 1853–1858.
109. I. Persson, D. Lundberg, É. G. Bajnoczi, K. Klementiev, J. Just and K. G. V. Sigfridsson Clauss, EXAFS Study on the Coordination Chemistry of the Solvated Copper(II) Ion in a Series of Oxygen Donor Solvents, Inorg. Chem., 2020, 59, 9538–9550 , and references therein.
110. P. Frank, M. Benfatto and M. Qayyum, [Cu(aq)]²⁺ is Structurally Plastic and the Axially Elongated Octahedron Goes Missing, J. Chem. Phys., 2018, 148, 204302.
111. I. Persson, P. Persson, M. Sandström and A.-S. Ullström, Structure of Jahn-Teller Distorted Solvated Copper(II) Ions in Solution, and in Solids with Apparently Regular Octahedral Coordination Geometry, J. Chem. Soc., Dalton Trans., 2002, 1256–1265.
112. P. S. Salmon and G. W. Neilson, The Coordination of Cu(II) in a Concentrated Copper Nitrate Solution, J. Phys.: Condens.Matter, 1989, 1, 5291–5295.
113. H. Ohtaki and M. Maeda, X-ray Diffraction Study of Hydrated Copper(II) in a Copper(II) Perchlorate Solution, Bull. Chem. Soc. Jpn., 1974, 47, 2197–2199.
114. M. Magini, Coordination of copper(II). Evidence of the Jahn-Teller Effect in Aqueous Perchlorate Solutions, Inorg. Chem., 1982, 21, 1535–1538.
115. M. Nomura and T. Yamaguchi, Concentration Dependence of Extended X-ray Absorption Fine Structure and X-ray Absorption Near-Edge Structure of Copper(II) Perchlorate Aqueous Solution - Comparison of Solute Structure in Liquid and Glassy States, J. Phys. Chem., 1988, 92, 6157–6160.
116. G. Licheri, A. Musinu, G. Paschina, G. Piccaluga and A. F. Sedda, Coordination of Cu(II) in Cu(NO₃)₂ Aqueous Solutions, J. Chem. Phys., 1984, 80, 5308–5311.
117. A. Musinu, G. Paschina, G. Piccaluga and M. Magini, Coordination of Copper(II) in Aqueous CuSO₄ Solution, Inorg. Chem., 1983, 22, 1184–1187.
118. W. Bol, G. J. A. Gerrits and C. L. van Panthaleon van Eck, The Hydration of Divalent Cations in Aqueous Solution. An X-ray Investigation with Isomorphous Replacement, J. Appl. Crystallogr., 1970, 3, 486–492.
119. M. Busato, A. Melchior, V. Migliorati, A. Colella, I. Persson, G. Mancini, D. Veclaniz and P. D'Angelo, The Elusive Coordination of the Ag⁺ Ion in Aqueous Solution: Evidence for a Linear Structure, Inorg. Chem., 2020, 59, 10291–10302.
120. D. H. Powell, P. M. N. Gullidge, G. W. Neilson and M. C. Bellissent-Funel, Zn²⁺ Hydration and Complexation in Aqueous Electrolyte Solutions, Mol. Phys., 1990, 71, 1107–1116.
121. S. P. Dagnall, D. N. Hague and A. D. C. Towl, X-ray Diffraction Study of Aqueous Zinc(II) Nitrate, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 2161–2167.
122. H. Wakita, G. Johansson, P. L. Goggin and H. Ohtaki, Structure Determination of Zinc Iodide Complexes Formed in Aqueous Solution, J. Solution Chem., 1991, 20, 643–668.
123. M. Xu, T. Zhu and J. Z. H. Zhang, Molecular Dynamics Simulation of Zinc Ion in Water with an ab Initio Based Neural Network Potential, J. Phys. Chem., 2019, 123, 6587–6595.
124. V. Migliorati, A. Zitolo, G. Chillemi and P. D'Angelo, Influence of the Second Coordination Shell on the XANES Spectra of the Zn²⁺ Ion in Water and Methanol, ChemPlusChem, 2012, 77, 234–239.
125. M. Q. Fatmi, T. S. Hofer, B. R. Randolf and B. M. Rode, An Extended ab initio QM/MM MD Approach to Structure and Dynamics of Zn(II) in Aqueous Solution, J. Chem. Phys., 2005, 123, 054514.
126. G. Chillemi, V. Barone, P. D'Angelo, G. Mancini, I. Persson and N. Sanna, Computational Evidence for a Variable First Coordination Shell of the Cadmium(II) Ion in Aqueous Solution, J. Phys. Chem. B, 2005, 109, 9186–9193.
127. R. Caminiti and G. Johansson, On the Structures of Cadmium Sulfate Complexes in Aqueous Solution, Acta Chem. Scand., Ser. A, 1981, 35, 373–381.
128. R. Caminiti, P. Cucca and T. Radnai, Investigation on the Structure of Cadmium Nitrate Aqueous Solutions by X-ray Diffraction and Raman Spectroscopy, J. Phys. Chem., 1984, 88, 2382–2386.
129. G. Johansson and M. Sandström, The crystal structure of hexaaquamercury(II) perchlorate, [Hg(H₂O)₆](ClO₄)₂, Acta Chem. Scand., Ser. A, 1978, 32, 109–113.
130. I. Persson, L. Eriksson, P. Lindqvist-Reis, P. Persson and M. Sandström, An EXAFS Spectroscopic, Large-Angle X-Ray Scattering, and Crystallographic Study of Hexahydrated, Dimethyl Sulfoxide and Pyridine 1-Oxide Hexasolvated Mercury(II) Ions, Chem. – Eur. J., 2008, 14, 6687–6696.
131. M. Sandström and I. Persson, Crystal and Molecular Structure of Hexakis(dimethylsulfoxide)mercury(II) Perchlorate, [Hg((CH₃)₂SO)₆](ClO₄)₂, Acta Chem. Scand., Ser. A, 1978, 32, 95–100.
132. G. Chillemi, G. Mancini, N. Sanna, V. Barone, S. Della Longa, M. Benfatto, N. V. Pavel and P. D'Angelo, Evidence for Sevenfold Coordination in the First Coordination Shell of Hg(II) aqua Ion, J. Am. Chem. Soc., 2007, 129, 5430–5436.
133. G. Mancini, N. Sanna, V. Barone, V. Migliorati, P. D'angelo and G. Chillemi, Structural and Dynamical Properties of the Hg²⁺ Aqua Ion: A Molecular Dynamics Study, J. Phys. Chem. B, 2008, 112, 4694–4702.
134. V. Migliorati, M. Busato and P. D'Angelo, Solvation Structure of the Hg(NO₃)₂ and Hg(TfO)₂ Salts in Dilute Aqueous and Methanol Solutions: An Insight Into the Hg²⁺ Coordination Chemistry, J. Mol. Liq., 2022, 363, 119801.
135. J. Rosdahl, I. Persson, L. Kloo and K. Ståhl, On the Solvation of the Mercury(I) Ion. A Structural, Vibration Spectroscopic and Quantum Chemical Study, Inorg. Chim. Acta, 2004, 357, 2624–2634.
136. T. S. Hofer, B. R. Randolph and B. M. Rode, The Hydration of the Mercury(I)-Dimer - A Quantum Mechanical Charge Field Molecular Dynamics Study, Chem. Phys., 2008, 349, 210–218.
137. J. Krakowiak, D. Lundberg and I. Persson, A Coordination Chemistry Study of Hydrated and Solvated Cationic Vanadium Ions in Oxidation States +III, +IV, and +V in Solution and Solid State, Inorg. Chem., 2012, 51, 9598–9609.
138. S. J. Edwards, D. T. Bowron and R. J. Baker, Insights into the solution structure of the hydrated uranyl ion from neutron scattering and EXAFS experiments, Dalton Trans., 2022, 51, 13631–13635.
139. M. Åberg, D. Feri, J. Glaser and I. Grenthe, Structure of the Hydrated Dioxouranium(VI) Ion in Aqueous Solution. An X-ray Diffraction and proton NMR Study, Inorg. Chem., 1983, 22, 3986–3989.
140. S. Pérez-Conesa, F. Torrico, J. M. Martínez, R. R. Pappalardo and E. Sánchez Marcos, A hydrated ion model of [UO₂]²⁺ in water: Structure, dynamics, and spectroscopy from classical molecular dynamics, J. Chem. Phys., 2016, 145, 224502.
141. A. H. Narten and S. Lindenbaum, Diffraction Pattern and Structure of the System Tetra–n–butylammonium Fluoride–Water at 25 °C, J. Chem. Phys., 1969, 51, 1108–1114.
142. C.-G. Zhan and D. A. Dixon, Hydration of the Fluoride Anion: Structures and Absolute Hydration Free Energy from First-Principles Electronic Structure Calculations, J. Phys. Chem. A, 2004, 108, 2020–2029.
143. T. S. Hofer, Solvation Structure and Ion–Solvent Hydrogen Bonding of Hydrated Fluoride, Chloride and Bromide—A Comparative QM/MM MD Simulation Study, Liquids, 2022, 2, 445–464.
144. P. D'Angelo, V. Migliorati and L. Guidoni, Hydration Properties of the Bromide Aqua Ion: the Interplay of First Principle and Classical Molecular Dynamics, and X-ray Absorption Spectroscopy, Inorg. Chem., 2010, 49, 4224–4231.
145. V. T. Pham, I. Tavernelli, C. J. Milne, R. M. van der Veen, P. D'Angelo, C. Bressler and M. Chergui, The solvent shell structure of aqueous iodide: X-ray absorption spectroscopy and classical, hybrid QM/MM and full quantum molecular dynamics simulations, Chem. Phys., 2010, 371, 24–29.
146. R. Caminiti, G. Licheri, G. Piccaluga and G. Pinna, NO₃-H₂O Interactions in aqueous-solutions, J. Chem. Phys., 1978, 68, 1967–1970.
147. L. Eklund, Hydration of Oxo Anions. A Combined Computational and Experimental Structure and Dynamics Study in Aqueous Solutions, doctoral thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2014 (available at https://pub.epsilon.slu.se/11192/).
148. L. Eklund, T. S. Hofer and I. Persson, I. Structure and water exchange of hydrated oxo halo ions in aqueous solution using QMCF MD simulation, large angle X-ray scattering and EXAFS, Dalton Trans., 2015, 44, 1816–1828.
149. M. Śmiechowski and I. Persson, Hydration of Oxometallate Ions in Aqueous Solution, Inorg. Chem., 2020, 59, 8231–8239.
150. L. Eklund, T. S. Hofer, A. B. Pribil, B. M. Rode and I. Persson, On the Structure and Dynamics of the Hydrated Sulfite Ion in Aqueous Solution – An ab initio QMCF MD Simulation and Large Angle X-ray Scattering Study, Dalton Trans., 2012, 41, 5209–5216.
151. V. Vchirawongkwin, B. M. Rode and I. Persson, Structure and Dynamics of Sulfate Ion in Aqueous Solution - An ab initio QMCF MD Simulation and Large Angle X-Ray Scattering Study, J. Phys. Chem. B, 2007, 111, 4150–4155.
152. L. Eklund, T. S. Hofer, A. K. H. Weiss, A. O. Tirler and I. Persson, Detailed structure elucidation of the hydrated thiosulfate ion using QMCF MD simulation and large angle X-ray scattering in aqueous solution, Dalton Trans., 2014, 43, 12711–12720.
153. L. Eklund and I. Persson, Structure and Hydrogen Bonding of the Hydrated Selenite and Selenate Ions in Aqueous Solution, Dalton Trans., 2014, 43, 6315–6321.
154. I. Persson, M. Trublet and W. Klysubun, Structure Determination of Phosphoric Acid and Phosphate Ions in Aqueous Solution Using EXAFS Spectroscopy and Large Angle X-ray Scattering, J. Phys. Chem. A, 2018, 122, 7413–7420.
155. M. Śmiechowski, E. Gojło and J. Stangret, Systematic Study of Hydration Patterns of Phosphoric(V) Acid and Its Mono-, Di-, and Tripotassium Salts in Aqueous Solution, J. Phys. Chem. B, 2009, 113, 7650–7661.
156. J. Mähler and I. Persson, Structure and Hydrogen Bonding of Arsenic Oxyacid Species in Aqueous Solution, Dalton Trans., 2013, 42, 1364–1377.
157. P. Vanýsek, Ionic conductivity and diffusion at infinite dilution, in Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Taylor Francis Group, Boca Raton, 96th edn, 2015–2016, pp. 5-76–5-78.

---

Footnote

† Electronic supplementary information (ESI) available: Fitted radial distribution and intensity functions from large angle X-ray scattering studies of aqueous solutions of magnesium(II), aluminium(III), manganese(II), iron(II), iron(III), cobalt(II), nickel(II), copper(II) and zinc(II) perchlorate, and summaries of reported crystal structures containing hydrated metal ions and oxoanions in solid state. See DOI: https://doi.org/10.1039/d4dt01449a

---