Open Access Article
Open Access ArticleAssessing the importance of nitric acid and ammonia for particle growth in the polluted boundary layer†
Ruby
Marten
 a,
Mao
Xiao
a,
Mingyi
Wang
b,
Weimeng
Kong
b,
Xu-Cheng
He
cd,
Dominik
Stolzenburg
ce,
Joschka
Pfeifer
fg,
Guillaume
Marie
g,
Dongyu S.
Wang
a,
Miriam
Elser
s,
Andrea
Baccarini
ah,
Chuan Ping
Lee
a,
Antonio
Amorim
i,
Rima
Baalbaki
c,
David M.
Bell
a,
Mao
Xiao
a,
Mingyi
Wang
b,
Weimeng
Kong
b,
Xu-Cheng
He
cd,
Dominik
Stolzenburg
ce,
Joschka
Pfeifer
fg,
Guillaume
Marie
g,
Dongyu S.
Wang
a,
Miriam
Elser
s,
Andrea
Baccarini
ah,
Chuan Ping
Lee
a,
Antonio
Amorim
i,
Rima
Baalbaki
c,
David M.
Bell
 a,
Barbara
Bertozzi
j,
Lucía
Caudillo
g,
Lubna
Dada
a,
Jonathan
Duplissy
a,
Barbara
Bertozzi
j,
Lucía
Caudillo
g,
Lubna
Dada
a,
Jonathan
Duplissy
 ck,
Henning
Finkenzeller
l,
Martin
Heinritzi
g,
Markus
Lampimäki
ck,
Henning
Finkenzeller
l,
Martin
Heinritzi
g,
Markus
Lampimäki
 c,
Katrianne
Lehtipalo
cd,
Hanna E.
Manninen
f,
Bernhard
Mentler
c,
Katrianne
Lehtipalo
cd,
Hanna E.
Manninen
f,
Bernhard
Mentler
 m,
Antti
Onnela
f,
Tuukka
Petäjä
m,
Antti
Onnela
f,
Tuukka
Petäjä
 c,
Maxim
Philippov
c,
Maxim
Philippov
 n,
Birte
Rörup
c,
Wiebke
Scholz
m,
Jiali
Shen
c,
Yee Jun
Tham
c,
António
Tomé
o,
Andrea C.
Wagner
glp,
Stefan K.
Weber
fg,
Marcel
Zauner-Wieczorek
g,
Joachim
Curtius
g,
Markku
Kulmala
n,
Birte
Rörup
c,
Wiebke
Scholz
m,
Jiali
Shen
c,
Yee Jun
Tham
c,
António
Tomé
o,
Andrea C.
Wagner
glp,
Stefan K.
Weber
fg,
Marcel
Zauner-Wieczorek
g,
Joachim
Curtius
g,
Markku
Kulmala
 c,
Rainer
Volkamer
l,
Douglas R.
Worsnop
cq,
Josef
Dommen
c,
Rainer
Volkamer
l,
Douglas R.
Worsnop
cq,
Josef
Dommen
 a,
Richard C.
Flagan
b,
Jasper
Kirkby
a,
Richard C.
Flagan
b,
Jasper
Kirkby
 fg,
Neil
McPherson Donahue
fg,
Neil
McPherson Donahue
 r,
Houssni
Lamkaddam
*a,
Urs
Baltensperger
a and
Imad
El Haddad
r,
Houssni
Lamkaddam
*a,
Urs
Baltensperger
a and
Imad
El Haddad
 *a
*a
aLaboratory of Atmospheric Chemistry, Paul Scherrer Institute, 5232 Villigen, Switzerland. E-mail: houssni.lamkaddam@psi.ch; imad.el-haddad@psi.ch
bCalifornia Institute of Technology, Division of Chemistry and Chemical Engineering 210-41, Pasadena, CA 91125, USA
cInstitute for Atmospheric and Earth System Research/Physics, Faculty of Science, University of Helsinki, 00014 Helsinki, Finland
dFinnish Meteorological Institute, FI-00560 Helsinki, Finland
eInstitute for Materials Chemistry, TU Wien, 1060 Vienna, Austria
fCERN, CH-1211 Geneva, Switzerland
gInstitute for Atmospheric and Environmental Sciences, Goethe University Frankfurt, 60438 Frankfurt am Main, Germany
hAtmospheric Processes and Their Impact, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
iCENTRA, FCUL, University of Lisbon, 1749-016 Lisbon, Portugal
jInstitute of Meteorology and Climate Research, Karlsruhe Institute of Technology, 76021 Karlsruhe, Germany
kHelsinki Institute of Physics (HIP)/Physics, Faculty of Science, University of Helsinki, 00014 Helsinki, Finland
lDepartment of Chemistry, CIRES, University of Colorado Boulder, 215 UCB, Boulder, 80309, CO, USA
mInstitute of Ion Physics and Applied Physics, University of Innsbruck, 6020 Innsbruck, Austria
nLebedev Physical Institute of the Russian Academy of Sciences, 119991, Leninsky prospekt, 53, Moscow, Russian Federation
oIDL-Universidade da Beira Interior, 6201-001 Covilhã, Portugal
pAerosol Physics Laboratory, Physics Unit, Tampere University, FI-33014 Tampere, Finland
qAerodyne Research, 01821 Billerica, MA, USA
rCenter for Atmospheric Particle Studies, Carnegie Mellon University, 1521 Pittsburgh, PA, USA
sEmpa, Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland
First published on 25th January 2024
Abstract
Aerosols formed and grown by gas-to-particle processes are a major contributor to smog and haze in megacities, despite the competition between growth and loss rates. Rapid growth rates from ammonium nitrate formation have the potential to sustain particle number in typical urban polluted conditions. This process requires supersaturation of gas-phase ammonia and nitric acid with respect to ammonium nitrate saturation ratios. Urban environments are inhomogeneous. In the troposphere, vertical mixing is fast, and aerosols may experience rapidly changing temperatures. In areas close to sources of pollution, gas-phase concentrations can also be highly variable. In this work we present results from nucleation experiments at −10 °C and 5 °C in the CLOUD chamber at CERN. We verify, using a kinetic model, how long supersaturation is likely to be sustained under urban conditions with temperature and concentration inhomogeneities, and the impact it may have on the particle size distribution. We show that rapid and strong temperature changes of 1 °C min−1 are needed to cause rapid growth of nanoparticles through ammonium nitrate formation. Furthermore, inhomogeneous emissions of ammonia in cities may also cause rapid growth of particles.
Environmental significanceUrban aerosol pollution is detrimental to human health, and can affect local climate and visibility. Current understanding of new particle formation, survival, and growth in polluted environments is incomplete, ambient measurements suggest that either scavenging of small particles is overestimated, or there is a missing growth mechanism. Rapid growth from ammonium nitrate formation can cause an increase in particle number concentration in polluted conditions. Since supersaturated conditions are required, it is unclear how this growth might occur in ambient urban conditions. We illustrate, using an experimentally validated temperature sensitive kinetic model of ammonium nitrate growth, that inhomogeneities typical of polluted environments cause sufficient supersaturation for rapid growth of nanoparticles and a resulting increase in particle number concentration. |
1 Introduction
Aerosols affect global and local climate by aerosol–radiation and aerosol–cloud interactions, where aerosol–cloud interactions are the larger forcing agent.1 Aerosols must grow into the 50–100 nm diameter size range to be able to act as cloud condensation nuclei (CCN).2 As well as acting as CCN, nucleation and growth of aerosols in urban environments can lead to persistent pollution, which is a leading cause of disability and death.3,4 Therefore, it is important to understand key drivers of nucleation and growth.Nucleation and growth in urban environments have been studied in depth through ambient measurements, chamber experiments, and models.5–9 In polluted conditions, the high number of large particles act as a high coagulation sink (CoagS), which is a large loss term for small particles (<10 nm) as they have high Brownian diffusivity and so collisions with larger particles are more frequent.2 In order for newly formed particles to escape scavenging by the CoagS, the growth rates need to outcompete the loss rates.10 Aerosols grow from condensation of supersaturated vapours and ambient measurements suggest that growth rates in cities are only up to a few times greater than those in clean environments, while coagulation sink values are much higher. Due to this, newly formed particles are not expected to be able to grow to large sizes in typical urban conditions. Nevertheless, new particle formation events have often been observed, with particle formation rates up to hundreds of times higher than in clean environments.11 Until recently there was no experimental evidence for an explanation of the persistence of high particle number concentrations sustained over a long time in the face of high loss processes. Wang et al. (2020)12 introduced a new mechanism of ammonium nitrate formation, which rapidly grows particles as small as a few nanometres to much larger sizes.12 Marten et al. (2022)13 showed that this growth was high enough to grow small particles through the most critical size range (the “valley of death” from nucleation until approximately 10 nm) even in the presence of high condensation sinks, thus sustaining particle number concentrations. They also presented evidence that small particles are efficiently scavenged by larger particles and therefore over-estimating of loss rates is not the reason for the discrepancy in particle survival.
The mechanism of growth via ammonium nitrate formation is extremely sensitive to temperature, as temperature strongly affects the saturation concentrations and therefore growth rates. Urban environments are inhomogeneous. In the troposphere, mixing is relatively fast, especially vertical mixing, which involves a rapid change in temperature.2,14 Furthermore, there are many sources with highly variable emission rates which result in varying gas phase concentrations.15 This may result in high supersaturation ratios of ammonia and nitric acid over particulate ammonium nitrate, which may rapidly grow nanoparticles. However, how long these supersaturations may be sustained for has not been quantified. Hence, the importance of ammonium nitrate on particle growth and survival remains unknown.
In this study we present results from the CLOUD experiment and modelled values of growth from ammonium nitrate at 5 °C and −10 °C, showing that the kinetic model is capable of replicating behaviour at different temperatures. Additionally, we use the kinetic model to assess how perturbations in temperature and concentration of NH3 affect the growth of ammonium nitrate, and whether ammonium nitrate could be supersaturated in typical urban conditions on a timescale relevant to make significant changes to the existing particle size distribution.
2 Methods
2.1 CLOUD experiments
The experiments presented were undertaken in the CLOUD chamber at CERN in 2018. The CLOUD chamber is a 26.1 m3 stainless steel nucleation chamber with controllable temperature, relative humidity, mixing speed, and irradiation.16–18 Gas concentrations are controlled by a state of the art injection system. Experiments were performed at 5 °C and −10 °C, at 60% relative humidity, all experiments were conducted without use of the 3.5 GeV/c secondary pion beam (π beam) from the CERN proton synchrotron. In order to onset nucleation, condensable gases such as sulfuric acid (H2SO4), ammonia (NH3), di-methyl amine, and organic oxidation products were generated. This was achieved via photolysis of ozone and/or HONO to generate OH radicals with UVA generated at 385 nm by a 400 W UVA LED saber and/or a 170 W quartz-clad high intensity Hg lamp. Rapid growth via ammonium nitrate formation was achieved by supersaturation of gas phase NH3 and HNO3, by injecting directly into the chamber, or producing HNO3via reaction of NO2 and OH radicals. All precursor gases are in steady state when the experiments are started by the onset of photolysis and optimal mixing in the chamber. For further experimental details see Marten et al. (2022).132.2 CLOUD chamber model
A kinetic model illustrating growth from ammonium nitrate formation was developed and presented in Marten et al. (2022).13 It was shown that the model could accurately replicate results from CLOUD experiments at 5 °C. The model was revised to conditions at −10 °C. The main changes are a new Kelvin diameter fit from CLOUD experiments at −10 °C, and adjusting other parameters that are temperature dependent, such as the saturation concentration of ammonium nitrate (Kp),19 the collision rate of particles, and the wall losses of particles.20| SAB,P = 10(dK10/dact) | (1) |
2.3 Ambient model
The model was further adapted to model ambient conditions. The wall and dilution losses of the chamber were replaced with diffusion losses. Diffusion losses were calculated using equations from Seinfeld and Pandis (2006),2 with literature deposition velocities for HNO3, NH3, and H2SO4.2,23 The height of the boundary layer used was 1 km. The production values of HNO3, NH3, and H2SO4 were calculated such that in the absence of a condensation sink, the values were at steady state. These calculations and examples of values used are shown in the ESI.† We also include a simulated condensation and coagulation sink (CondS = 0.005 s−1) typical of moderately polluted urban air,12 with an initial lognormal particle size distribution, which is centred at 200 nm. All model simulations are implied to have the same relative humidity of the experiments (60%). The effect of relative humidity is not covered in this model as it was not simulated in the CLOUD experiments and therefore would not have been experimentally validated. Nucleation rates (Jx) were calculated using a model based off of the general dynamic equation that is described in detail in Xiao et al. (2021).2,11Eqn (2) shows a simplified version of the equation, showing that loss rates (losses) are subtracted from the change in concentration of particles of a certain size x (Nx) over time (t). The units of Jx are particles per cm3 per s.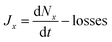 | (2) |
Both the parameterization in Xiao et al. (2021) and the experiments presented in this paper were undertaken in the presence of galactic cosmic rays (i.e. with the clearing field of the CLOUD chamber off). However, we have not considered the effect of varying ionization level during vertical transport. For the “air parcel rising” experiments, the nucleation rates used for these models were input rates of 1.7 nm particles, they are temperature dependent and typical of 1 × 107 molecules per cm3 H2SO4 with 3 ppbv NH3 and no amines as seen in previous CLOUD experiments and ambient studies, presented in Xiao et al. 2021.11,24,25 For the “concentration inhomogeneities” experiments, the nucleation rates were not constrained and kinetic nucleation rates were used, based on clusters of H2SO4 as in Marten et al. (2022).13
3 Results
3.1 Model validation at −10 °C using CLOUD chamber data
Experiments involving growth from ammonium nitrate formation were undertaken at 20 °C, 5 °C and −10 °C in the CLOUD chamber at CERN. The experiments were designed to use atmospherically relevant concentrations of all gases. Fig. 1a shows results from all of the CLOUD experiments as triangular points where the newly formed particles were activated by ammonium nitrate formation. We observe ammonium nitrate growth at 5 °C and −10 °C but not at 20 °C at the concentrations used in our study. At the lower temperature, lower gas-phase concentrations can result in higher growth rates. This is partially due to the fact that the saturation concentration of ammonium nitrate is lower at lower temperatures and therefore more NH3 and HNO3 can condense. Plotted with this data, as diamond points, are the growth rates obtained from model simulations with constrained gas phase concentrations of HNO3 and NH3 from CLOUD measurements. We use MCM21,22 to model the chemistry in the chamber, using measured gas-phase time-series, measured loss rates of vapours, and photolysis rates from CLOUD.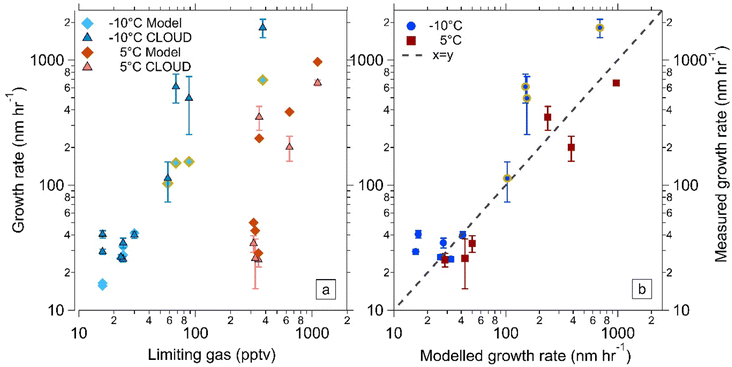 | ||
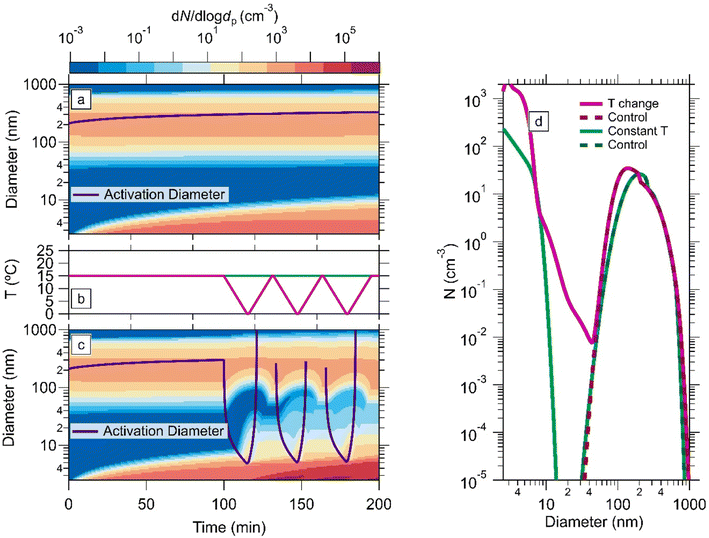
| Fig. 1 Comparison of measured and modelled growth rates at 5 °C and −10 °C. (a) Measured (triangles with error bars) and modelled (diamonds) growth rates at 5 °C and −10 °C, 60% RH, versus the limiting gas for ammonium nitrate condensation, which is either ammonia or nitric acid and is experiment dependent. The CLOUD measured growth rates were determined using the 50% appearance time method.26 The modelled data points were determined using the same method on output from the kinetic model, constrained by measured gas-phase concentrations from CLOUD experiments. The modelled values at −10 °C also included modelled N2O5 concentrations which may have contributed to growth, those with a thick golden border had 10 s to 100 s of pptv of N2O5. All measured data points and modelled data points at 5 °C were previously presented in Wang et al. (2020)12 and Marten et al. (2022).13 (b) Modelled growth rates versus measured growth rates at 5 °C and −10 °C for all the experiments shown in (a). | ||
The measured and modelled growth rates are plotted against the limiting gas for ammonium nitrate formation, which is either NH3 or HNO3. The limiting gas determines the amount of NH4NO3 that can condense on particles, thus the growth rate increases with increasing concentration. However, this relationship is not strictly linear as the growth also depends on which gas is limiting condensation (see Marten et al. (2022)13 ESI† for full explanation); it is used here only to display the data. Fig. 1b directly compares the measured CLOUD growth rates and model growth rates shown in Fig. 1a, a dashed line of x = y is also shown. From these two plots, it is clear that the kinetic model is capable of replicating CLOUD results not only at 5 °C but also at −10 °C.
For the points indicated in Fig. 1a at −10 °C by a thick golden border, we calculated that there were tens to hundreds of pptv of N2O5. Due to differing chemistries, the remaining experiments had negligible N2O5 concentration (Table S1†). Original model results using HNO3 concentrations alone (Fig. S1†) resulted in some simulations with growth rates that were much lower than the experimental results. The results were parameterised for N2O5 uptake by including additional HNO3, which resulted in better agreement between the experiment and model results. The uptake of N2O5 into small ammonium nitrate particles is not well characterized. Uptake rates determined from ambient measurements are approximately a few percent, but strongly increase with the aerosol water content. Without N2O5 measurements, modelling the condensation flux of N2O5 is subject to substantial uncertainties, because (1) the uptake rate coefficient of N2O5 onto small ammonium nitrate particles has not been previously determined, and (2) the wall loss behaviour of N2O5 in the CLOUD chamber is unknown. For our modelled values, we considered a kinetic condensation of the N2O5 as an upper limit and a complete loss of N2O5 onto the walls, which would yield a lowest estimate of N2O5 concentrations, which may explain why the growth rates are still under-predicted. N2O5 concentrations calculated without wall loss are also significantly higher and are shown in Table S1.† Under these assumptions, model to measurement discrepancy decreases from a factor of 10 to factor of 2.5. We concluded, albeit with uncertainty, that N2O5 may be a missing gas contributor to growth, but more experiments would be needed to measure the N2O5 uptake rates as a function of particle size and chemical composition.
3.2 Effect of temperature change during vertical transport
Using our experimentally validated model, we explored the effect of the changing temperature of a rising air parcel in a city on the overall size distribution. In these experiments, we also include an initial particle size distribution, which is lognormal and centred around 200 nm, in order to simulate a condensation sink of 0.005 s−1. Fig. 2 shows the size distribution versus time of an air parcel with constant temperature (Fig. 2a), an air parcel with several decreases and subsequent increases in temperature (Fig. 2c) and the respective temperature profiles plotted in Fig. 2b. The activation diameter (dact) is defined as the critical size at which ammonium nitrate can condense on particles and is dependent on the temperature, gas phase concentrations of NH3 and HNO3, and the Kelvin diameter. dact is plotted as a black line in both Fig. 2a and c. During each temperature drop the activation diameter decreases, and particles as small as 5 nm can rapidly grow from ammonium nitrate formation. The largest newly formed particles start to rapidly grow from less than 10 nm to around 50 nm. When the temperature increases as the air parcel returns to ground level, part of the NH4NO3 evaporates, resulting in a slight shrinking in the size distribution of the original condensation sink and the newly growing particles. However, this shrinkage does not result in a complete re-evaporation of the new particles and the net effect of the temperature change is the formation of new Aitken mode particles. Fig. 2d shows the size distributions at the end of the experiments with and without a change in temperature, and a control experiment for each, with the same condensation sink and temperature profiles but without new particle formation. In the case of constant temperature, there are two distinct modes, with a minimum particle concentration around 20 nm, i.e. the size that the new particles were able to grow to. By contrast, in the experiment with changing temperature the lower mode has grown as high as 50 nm and has considerably larger particle number concentrations. These results show that vertical mixing in a typical urban environment can stimulate growth from ammonium nitrate formation. This may help to increase the particle number of larger sizes and aid in survival of newly formed particles through the valley of death, even after returning to surface temperature and sub-saturated conditions. We acknowledge that this is a simplistic model and in reality, a decrease in temperature will also result in an increase in relative humidity and deliquescence of particles. If the effect of water were taken into account, the dissociation constant would be affected by the change of state and most likely result in more condensation of ammonium nitrate, therefore resulting in a larger effect on the particle size distribution than simulated here.We assessed the conditions required for ammonium nitrate to activate nucleated particles through sensitivity tests. We observed that a larger and faster temperature change results in more pronounced activation (Fig. S2 and S3†). At lower nucleation rates the effect of ammonium nitrate on growth is lessened, since fewer particles are present for activation (Fig. S4†). We also show that higher initial temperatures will result in a much larger change in supersaturated ammonia and nitric acid concentrations, which will be available for rapid particle growth (Fig. S5 and S6†). Therefore, the occurrence of this process requires sufficient pre-existing particles above the activation diameter and sufficient ammonium nitrate concentration above the saturation concentration. Such conditions are promoted by higher nucleation rates, higher boundary layer temperatures, and higher and faster changes in temperature.
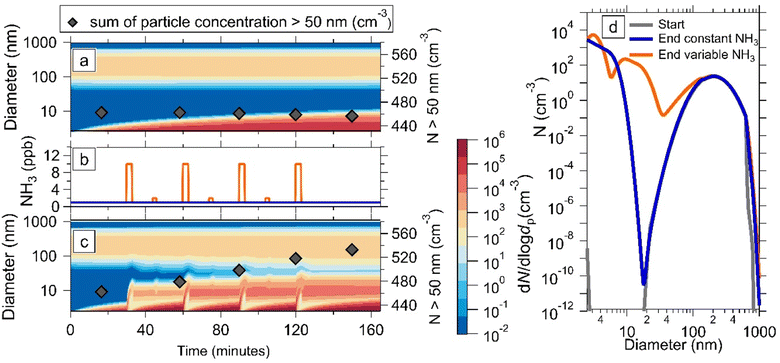
3.3 Effect of inhomogeneity of NH3 concentrations in cities
In typical urban environments air parcels will experience temporal inhomogeneities in gas-phase concentrations in addition to vertical mixing. Therefore, we set up a simulation with a variable ammonia time-series, meant to represent an area close to a source with large, sporadic variations in ammonia, such as traffic.15 We also include the same initial particle size distribution as in Fig. 2. Fig. 3a shows an experiment with fixed production rates of HNO3, NH3, and H2SO4, where newly formed particles have grown to ∼20 nm by the end of the simulation. The production values of NH3, HNO3, and H2SO4 were calculated such that in the absence of condensation, the concentrations were 1 ppbv, 0.2 ppbv, and 1 × 107 molecules per cm3 respectively. The concentrations were chosen as typical background concentrations, resulting in an activation diameter of 200 nm for ammonium nitrate growth. In Fig. 3c the simulation in Fig. 3(a) is repeated but with a variable NH3 time-series, with alternate “spikes” of 10 ppbv and 2 ppbv and a background concentration of 1 ppbv. The NH3 time-series is presented in Fig. 3(b). We observe that the newly formed particles have grown much larger than in Fig. 3(a), reaching the size of the original condensation sink. The concentration of particles above 50 nm, represented by black diamonds in Fig. 3(a) and (c), increases in Fig. 3(c) as new particles grow, whereas it slowly but steadily decreases in Fig. 3(a). Fig. 3d shows the size distributions corresponding to the first and last diamond points in Fig. 3(a) and (c). The blue trace, representing the final diamond in Fig. 3(a), differs from the starting size distribution with the appearance of the nucleation mode up to around 20 nm and by growth of the largest particles as the second mode shifts right. In addition to these changes, the orange trace, which represents the end diamond in Fig. 3(c), has dramatically increased particle number concentration up to 200 nm. From this we conclude that inhomogeneities in NH3 emissions can sustain particle number by causing temporary supersaturation of ammonium nitrate, and growing particles through the valley of death.In all of the simulations presented, we also model the particle composition throughout. Fig. S7† shows examples of plots with the relative concentrations of ammonium nitrate and ammonium sulfate. These results show that the fraction of NH4NO3 is only significant during the supersaturated periods and above the activation diameter. Once sub-saturated conditions resume, the ammonium nitrate quickly evaporates. However, Fig. 2 and 3 show that even after NH4NO3 evaporates into gas phase NH3 and HNO3, the edge of the growing particle size distribution still survives at larger sizes than before activation. This is because NH4NO3 condensation, even if it is brief and reversible, increases the survival rate of newly formed particles, making them less susceptible to coagulation loss.
4 Discussion and conclusions
In light of these results, it may be puzzling that similar size distributions as in Fig. 3 have not been frequently observed in ambient measurements. Experiments in the CLOUD chamber involved supersaturated conditions of ammonia and nitric acid, resulting in rapid particle growth, allowing the chemistry and particle microphysics of ammonium nitrate growth in the nanoparticle range to be verified. In the real atmosphere ammonium nitrate will mostly be found in equilibrium with its gas-phase counterparts, resulting in no particle growth. The model was therefore designed to simulate ambient atmospheric scenarios that would result in a short perturbation of equilibrium. We observe that in these conditions of high heterogeneities, although short-lived, rapid growth due to ammonium nitrate formation can occur.To the best of our knowledge, the rapid particle growth from ammonium nitrate formation has not been previously reported. One of the many reasons for the lack of ambient observations of this phenomenon could be the low resolution of particle size distribution measurements. Fig. S8† shows the same size distribution as in Fig. 3c, but with a lower time resolution of 5 minutes, and a diameter resolution and range of a typical scanning mobility particle sizer. The features are not as distinguished as those presented from the model results. In the simulations presented in Fig. 3c the inhomogeneities lasted only 2–3 minutes, which would be challenging to capture on an instrument with a 5 minutes resolution. This results in less obvious changes in the size distribution, with some features that could be interpreted as noise. In addition, more than one particle sizing instrument would be required to measure the diameter range and resolution presented from model results. Furthermore, at sustained concentrations of NH4NO3 in the absence of inhomogeneities, equilibrium is rapidly reached, and the required supersaturation for rapid growth is no longer present. Finally, these measurements would need to take place near to a large source of NH3 or HNO3, such as traffic, and background sites would therefore not measure such distributions. Additionally, direct particle emissions also result in pulses of primary particles, especially with high time resolution measurements, further blurring the interpretation of new particle formation events. The effect of the condensation sink on particle survival was presented in Marten et al. (2022) and revealed that even under condensation sinks over 0.01 s−1 [NH3] × [HNO3] concentrations higher than 1.2 ppb2 led to survival rates close to unity.13 In the experiments simulated in this paper, [NH3] × [HNO3] values were around 4 ppb2, which means that particle survival is relatively independent of the condensation sink. To summarise, although it is likely that this mechanism may occur in urban ambient air, it is hard to identify and it needs specific conditions with high heterogeneity coming from either large differences in temperatures or large emissions of ammonia (>10 ppbv).
It is important to point out that this model does not take into account the effect of relative humidity on the ammonium nitrate system. Since all of the experiments were performed with a relative humidity lower than the deliquescence relative humidity (DRH) of ammonium nitrate (62% at 25 °C, and higher at lower temperatures2), it might be considered a solid. However, as the efflorescence of NH4NO3 is below 40% (ref. 27) and since atmospheric aerosols are typically multicomponent in nature, it is likely that under most conditions, at least a fraction of NH4NO3 will be present in an aqueous solution. Although in the conditions presented in this paper water most likely does not affect ammonium nitrate growth, there are other conditions where water may play a larger role. Ambient, wet, conditions are even more likely to be supersaturated than corresponding dry conditions. Due to the Kelvin effect, water is less likely to condense on smaller particles, and therefore small particles will tend to contain less water than larger particles. Ammonium nitrate ionic strength also affects the dissociation constant, where Kp decreases with increasing ionic strength. In summary, larger particles in wet conditions will be liquid, and since this affects the dissociation constant, more ammonium nitrate should be able to condense on particles and increase the effect of NH4NO3 growth on the particle size distribution. This effect should be verified with further chamber experiments at higher relative humidity.
Our results highlight additional gaps in understanding the effect of temperature changes and inhomogeneous emissions on particle growth. At −10 °C, calculated N2O5 concentrations correlated with a growth rate enhancement in 4 out of 10 experiments. Whether N2O5 is the cause of this enhancement could not be corroborated experimentally, and warrants further investigation, especially for sub-10 nm particles. Changes in temperature will also have additional effects on nucleation and growth from other vapours in urban atmospheres. For example, anthropogenic low-volatility organic compounds (LVOCs) may increasingly condense at lower temperatures, which has not yet been fully assessed experimentally. Finally, future experimental and modelling studies should take the effect of relative humidity and water uptake on the condensation of ammonium nitrate into account.
We have shown that rapid particle growth through ammonium nitrate formation requires a large and rapid change in temperature, a sufficient pre-existing particle distribution, and high enough gas-phase concentrations of NH3 and HNO3. In the absence of a temperature change, inhomogeneous emissions of ammonia can also cause rapid growth. This phenomenon could occur close to emission sources, but observation would require high time- and size-resolved particle measurements. It is possible that such phenomena have not been observed due to factors such as location and time or diameter resolution.
Author contributions
Conceptualization: R. M., M. X., M. W., J. Dommen, J. K., N. M. D., H. L., U. B. and I. E. H., resources, prepared the CLOUD facility or measuring instruments: R. M., M. W., W. K., X.-C. H., D. S., J. P., G. M., D. S. W., A. B., C. P. L., A. A., D. M. B., R. B., L. C., L. D., J. Duplissy, H. F., M. H., K. L., H. E. M., B. M., T. P., M. P., B. R., W. S., J. S., Y. J. T., A. T., A. C. W., S. K. W., M. Z.-W., J. K., H. L., and I. E. H. Investigation: R. M., M. X., M. W., W. K., X.-C. H., D. S., J. P., G. M., D. S. W., A. B., C. P. L., R. B., D. M. B., B. B., L. C., L. D., J. Duplissy, H. F., M. H., M. L., H. E. M, B. M., W. S., J. S., Y. J. T., A. C. W., S. K. W., M. Z.-W., J. K., H. L., and I. E. H. Formal analysis: R. M., M. W., W. K., X. H., D. S., J. P., G. M., D. S. W., S. K. W., H. L., and I. E. H. Scientific discussion: R. M., M. X., M. W., W. K., X.-C. H., D. S., D. B., L. D., K. L., J. Dommen, R. C. F., J. K., N. M. D., H. L., U. B., and I. E. H. Writing: R. M., M. W., W. K., X.-C. H., D. S., J. Dommen, J. K., N. M. D., H. L., U. B., and I. E. H.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the European Organization for Nuclear Research (CERN) for supporting CLOUD with technical and financial resources and for providing a particle beam from the CERN Proton Synchrotron. This research has received funding from the European Community (EC) Seventh Framework Programme and the European Union (EU) H2020 programme (Marie Skłodowska Curie ITN CLOUD-TRAIN grant number 316662 and CLOUD-MOTION grant number 764991); European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 895875 (“NPF-PANDA”); the Swiss National Science Foundation (no. 200021 169090, 200020 172602, 20FI20 172622, and 200021 213071); the US National Science Foundation (NSF; grant numbers AGS1801574, AGS-NUC-1801897, and AGS132089); the German Ministry of Science and Education (project CLOUD-16, 01LK1601A), ACCC Flagship funded by the Academy of Finland grant number 337549; Academy professorship funded by the Academy of Finland (grant no. 302958); Academy of Finland projects no. 325656, 316114, 314798, 325647, 341349 and 349659; “Quantifying carbon sink, CarbonSink+ and their interaction with air quality” INAR project funded by Jane and Aatos Erkko Foundation; Jenny and Antti Wihuri Foundation project “Air pollution cocktail in Gigacity”, European Research Council (ERC) project ATM-GTP Contract No. 742206; the Arena for the gap analysis of the existing Arctic Science Co-Operations (AASCO) funded by Prince Albert Foundation Contract No. 2859; and the Portuguese Science Foundation, FCT, project CERN/FIS-COM/0028/2019. This research was performed before the invasion of Ukraine by Russia on 24 February 2022.References
- T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. M. Midgeley, Climate Change 2013 The Physical Science Basis, Intergovernmental Panel on Climate Change (IPCC), 2013 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics, John Wiley & Sons, 2nd edn, 2006 Search PubMed.
- WHO, Methods and Data Sources for Country-Level Causes of Death 2000-2019, World Health Organisation, 2020 Search PubMed.
- WHO, Methods and Data Sources for Global Burden of Disease Estimates 2000-2019, World Health Organisation, 2020 Search PubMed.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan, J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361, 278–281 CrossRef CAS PubMed.
- S. Xiao, M. Y. Wang, L. Yao, M. Kulmala, B. Zhou, X. Yang, J. M. Chen, D. F. Wang, Q. Y. Fu, D. R. Worsnop and L. Wang, Strong atmospheric new particle formation in winter in urban Shanghai, China, Atmos. Chem. Phys., 2015, 15, 1769–1781 CrossRef.
- Z. B. Wang, M. Hu, J. Y. Sun, Z. J. Wu, D. L. Yue, X. J. Shen, Y. M. Zhang, X. Y. Pei, Y. F. Cheng and A. Wiedensohler, Characteristics of regional new particle formation in urban and regional background environments in the North China Plain, Atmos. Chem. Phys., 2013, 13, 12495–12506 CrossRef.
- D. Bousiotis, M. Dall'Osto, D. C. S. Beddows, F. D. Pope and R. M. Harrison, Analysis of new particle formation (NPF) events at nearby rural, urban background and urban roadside sites, Atmos. Chem. Phys., 2019, 19, 5679–5694 CrossRef CAS.
- Z. Wang, Z. Wu, D. Yue, D. Shang, S. Guo, J. Sun, A. Ding, L. Wang, J. Jiang, H. Guo, J. Gao, H. C. Cheung, L. Morawska, M. Keywood and M. Hu, New particle formation in China: Current knowledge and further directions, Sci. Total Environ., 2017, 577, 258–266 CrossRef CAS.
- V.-M. Kerminen and M. Kulmala, Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 2002, 33, 609–622 CrossRef CAS.
- M. Xiao, C. R. Hoyle, L. Dada, D. Stolzenburg, A. Kürten, M. Wang, H. Lamkaddam, O. Garmash, B. Mentler, U. Molteni, A. Baccarini, M. Simon, X.-C. He, K. Lehtipalo, L. R. Ahonen, R. Baalbaki, P. S. Bauer, L. Beck, D. Bell, F. Bianchi, S. Brilke, D. Chen, R. Chiu, A. Dias, J. Duplissy, H. Finkenzeller, H. Gordon, V. Hofbauer, C. Kim, T. K. Koenig, J. Lampilahti, C. P. Lee, Z. Li, H. Mai, V. Makhmutov, H. E. Manninen, R. Marten, S. Mathot, R. L. Mauldin, W. Nie, A. Onnela, E. Partoll, T. Petäjä, J. Pfeifer, V. Pospisilova, L. L. J. Quéléver, M. Rissanen, S. Schobesberger, S. Schuchmann, Y. Stozhkov, C. Tauber, Y. J. Tham, A. Tomé, M. Vazquez-Pufleau, A. C. Wagner, R. Wagner, Y. Wang, L. Weitz, D. Wimmer, Y. Wu, C. Yan, P. Ye, Q. Ye, Q. Zha, X. Zhou, A. Amorim, K. Carslaw, J. Curtius, A. Hansel, R. Volkamer, P. M. Winkler, R. C. Flagan, M. Kulmala, D. R. Worsnop, J. Kirkby, N. M. Donahue, U. Baltensperger, I. El Haddad and J. Dommen, The driving factors of new particle formation and growth in the polluted boundary layer, Atmos. Chem. Phys., 2021, 21, 14275–14291 CrossRef CAS.
- M. Wang, W. Kong, R. Marten, X.-C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada, A. Kürten, T. Yli-Juuti, H. E. Manninen, S. Amanatidis, A. Amorim, R. Baalbaki, A. Baccarini, D. M. Bell, B. Bertozzi, S. Bräkling, S. Brilke, L. C. Murillo, R. Chiu, B. Chu, L.-P. De Menezes, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, R. Guida, A. Hansel, V. Hofbauer, J. Krechmer, K. Lehtipalo, H. Lamkaddam, M. Lampimäki, C. P. Lee, V. Makhmutov, G. Marie, S. Mathot, R. L. Mauldin, B. Mentler, T. Müller, A. Onnela, E. Partoll, T. Petäjä, M. Philippov, V. Pospisilova, A. Ranjithkumar, M. Rissanen, B. Rörup, W. Scholz, J. Shen, M. Simon, M. Sipilä, G. Steiner, D. Stolzenburg, Y. J. Tham, A. Tomé, A. C. Wagner, D. S. Wang, Y. Wang, S. K. Weber, P. M. Winkler, P. J. Wlasits, Y. Wu, M. Xiao, Q. Ye, M. Zauner-Wieczorek, X. Zhou, R. Volkamer, I. Riipinen, J. Dommen, J. Curtius, U. Baltensperger, M. Kulmala, D. R. Worsnop, J. Kirkby, J. H. Seinfeld, I. El-Haddad, R. C. Flagan and N. M. Donahue, Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- R. Marten, M. Xiao, B. Rörup, M. Wang, W. Kong, X.-C. He, D. Stolzenburg, J. Pfeifer, G. Marie, D. S. Wang, W. Scholz, A. Baccarini, C. P. Lee, A. Amorim, R. Baalbaki, D. M. Bell, B. Bertozzi, L. Caudillo, B. Chu, L. Dada, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, A. Hansel, M. Heinritzi, V. Hofbauer, D. Kemppainen, A. Kürten, M. Lampimäki, K. Lehtipalo, V. Makhmutov, H. E. Manninen, B. Mentler, T. Petäjä, M. Philippov, J. Shen, M. Simon, Y. Stozhkov, A. Tomé, A. C. Wagner, Y. Wang, S. K. Weber, Y. Wu, M. Zauner-Wieczorek, J. Curtius, M. Kulmala, O. Möhler, R. Volkamer, P. M. Winkler, D. R. Worsnop, J. Dommen, R. C. Flagan, J. Kirkby, N. M. Donahue, H. Lamkaddam, U. Baltensperger and I. El Haddad, Survival of newly formed particles in haze conditions, Environ. Sci.: Atmos., 2022, 2, 491–499 CAS.
- K. Lu, H. Fuchs, A. Hofzumahaus, Z. Tan, H. Wang, L. Zhang, S. H. Schmitt, F. Rohrer, B. Bohn, S. Broch, H. Dong, G. I. Gkatzelis, T. Hohaus, F. Holland, X. Li, Y. Liu, Y. Liu, X. Ma, A. Novelli, P. Schlag, M. Shao, Y. Wu, Z. Wu, L. Zeng, M. Hu, A. Kiendler-Scharr, A. Wahner and Y. Zhang, Fast Photochemistry in Wintertime Haze: Consequences for Pollution Mitigation Strategies, Environ. Sci. Technol., 2019, 53, 10676–10684 CrossRef CAS.
- M. Elser, I. El-Haddad, M. Maasikmets, C. Bozzetti, R. Wolf, G. Ciarelli, J. G. Slowik, R. Richter, E. Teinemaa, C. Hüglin, U. Baltensperger and A. S. H. Prévôt, High contributions of vehicular emissions to ammonia in three European cities derived from mobile measurements, Atmos. Environ., 2018, 175, 210–220 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes, A. Kürten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- J. Duplissy, J. Merikanto, A. Franchin, G. Tsagkogeorgas, J. Kangasluoma, D. Wimmer, H. Vuollekoski, S. Schobesberger, K. Lehtipalo, R. C. Flagan, D. Brus, N. M. Donahue, H. Vehkamäki, J. Almeida, A. Amorim, P. Barmet, F. Bianchi, M. Breitenlechner, E. M. Dunne, R. Guida, H. Henschel, H. Junninen, J. Kirkby, A. Kürten, A. Kupc, A. Määttänen, V. Makhmutov, S. Mathot, T. Nieminen, A. Onnela, A. P. Praplan, F. Riccobono, L. Rondo, G. Steiner, A. Tome, H. Walther, U. Baltensperger, K. S. Carslaw, J. Dommen, A. Hansel, T. Petäjä, M. Sipilä, F. Stratmann, A. Vrtala, P. E. Wagner, D. R. Worsnop, J. Curtius and M. Kulmala, Effect of ions on sulfuric acid-water binary particle formation: 2. experimental data and comparison with QC-normalized classical nucleation theory, J. Geophys. Res.: Atmos., 2016, 121, 1752–1775 CrossRef CAS.
- J. Voigtländer, J. Duplissy, L. Rondo, A. Kürten and F. Stratmann, Numerical simulations of mixing conditions and aerosol dynamics in the CERN CLOUD chamber, Atmos. Chem. Phys., 2012, 12, 2205–2214 CrossRef.
- M. Mozurkewich, The dissociation constant of ammonium nitrate and its dependence on temperature, relative humidity and particle size, Atmos. Environ., Part A, 1993, 27, 261–270 CrossRef.
- A. C. K. Lai and W. W. Nazaroff, Modeling indoor particle deposition from turbulent flow onto smooth surfaces, J. Aerosol Sci., 2000, 31, 463–476 CrossRef CAS.
- C. Bloss, V. Wagner, M. E. Jenkin, R. Volkamer, W. J. Bloss, J. D. Lee, D. E. Heard, K. Wirtz, M. Martin-Reviejo, G. Rea, J. C. Wenger and M. J. Pilling, Development of a detailed chemical mechanism (MCM v3.1) for the atmospheric oxidation of aromatic hydrocarbons, Atmos. Chem. Phys., 2005, 24(5), 641–664 CrossRef.
- M. E. Jenkin, S. M. Saunders, V. Wagner and M. J. Pilling, Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part B): tropospheric degradation of aromatic volatile organic compounds, Atmos. Chem. Phys., 2003, 3(1), 181–193 CrossRef CAS.
- R. San Jose, F. J. Moreno and M. A. San Feliu, Field study on O3, SO2 and NH3 deposition over a suburban area: Madrid case study, Air Pollution and Visibility Measurements, Proc. SPIE, 1995, vol 2506, pp. 274–285 Search PubMed.
- H. Gordon, J. Kirkby, U. Baltensperger, F. Bianchi, M. Breitenlechner, J. Curtius, A. Dias, J. Dommen, N. M. Donahue, E. M. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, C. Frege, C. Fuchs, A. Hansel, C. R. Hoyle, M. Kulmala, A. Kürten, K. Lehtipalo, V. Makhmutov, U. Molteni, M. P. Rissanen, Y. Stozkhov, J. Tröstl, G. Tsagkogeorgas, R. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, C. Yan and K. S. Carslaw, Causes and importance of new particle formation in the present-day and preindustrial atmospheres, J. Geophys. Res.: Atmos., 2017, 122, 8739–8760 CrossRef.
- E. M. Dunne, H. Gordon, A. Kurten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipila, J. N. Smith, Y. Stozkhov, A. Tome, J. Trostl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Global atmospheric particle formation from CERN CLOUD measurements, Science, 2016, 354, 1119–1124 CrossRef CAS.
- D. Stolzenburg, L. Fischer, A. L. Vogel, M. Heinritzi, M. Schervish, M. Simon, A. C. Wagner, L. Dada, L. R. Ahonen, A. Amorim, A. Baccarini, P. S. Bauer, B. Baumgartner, A. Bergen, F. Bianchi, M. Breitenlechner, S. Brilke, S. Buenrostro Mazon, D. Chen, A. Dias, D. C. Draper, J. Duplissy, I. El Haddad, H. Finkenzeller, C. Frege, C. Fuchs, O. Garmash, H. Gordon, X. He, J. Helm, V. Hofbauer, C. R. Hoyle, C. Kim, J. Kirkby, J. Kontkanen, A. Kürten, J. Lampilahti, M. Lawler, K. Lehtipalo, M. Leiminger, H. Mai, S. Mathot, B. Mentler, U. Molteni, W. Nie, T. Nieminen, J. B. Nowak, A. Ojdanic, A. Onnela, M. Passananti, T. Petäjä, L. L. J. Quéléver, M. P. Rissanen, N. Sarnela, S. Schallhart, C. Tauber, A. Tomé, R. Wagner, M. Wang, L. Weitz, D. Wimmer, M. Xiao, C. Yan, P. Ye, Q. Zha, U. Baltensperger, J. Curtius, J. Dommen, R. C. Flagan, M. Kulmala, J. N. Smith, D. R. Worsnop, A. Hansel, N. M. Donahue and P. M. Winkler, Rapid growth of organic aerosol nanoparticles over a wide tropospheric temperature range, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 9122–9127 CrossRef CAS PubMed.
- C. Peng, L. Chen and M. Tang, A database for deliquescence and efflorescence relative humidities of compounds with atmospheric relevance, Fundam. Res., 2022, 2, 578–587 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ea00001j |
| This journal is © The Royal Society of Chemistry 2024 |