Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determining methane mole fraction at a landfill site using the Figaro Taguchi gas sensor 2611-C00 and wind direction measurements†
Adil
Shah
 *a,
Olivier
Laurent
a,
Grégoire
Broquet
*a,
Olivier
Laurent
a,
Grégoire
Broquet
 a,
Carole
Philippon
a,
Carole
Philippon
 a,
Pramod
Kumar
a,
Pramod
Kumar
 a,
Elisa
Allegrini
b and
Philippe
Ciais
a,
Elisa
Allegrini
b and
Philippe
Ciais
 a
a
aLaboratoire des Sciences du Climat et de l’Environnement (CEA-CNRS-UVSQ), Institut Pierre-Simon Laplace, Université Paris-Saclay, Site de l’Orme des Merisiers, 91191 Gif-sur-Yvette, France. E-mail: adil.shah@lsce.ipsl.fr
bSUEZ Air Solutions, 15-27 Rue de Port, 92000 Nanterre, France
First published on 26th February 2024
Abstract
Top-down (atmospheric measurement-based) methane fluxes from individual emitting facilities are needed to reduce uncertainties in the global methane budget. This typically requires in situ methane mole fraction ([CH4]), traditionally measured using high-precision optical sensors. We show that the semiconductor-based Figaro Taguchi Gas Sensor (TGS) is a cheaper alternative. Two TGS loggers were deployed near a landfill site. Logger-1 uses a pumped cell, containing one TGS 2602, two TGS 2611-C00 and one TGS 2611-E00; laboratory testing showed methane, ethane, carbon monoxide and hydrogen sulphide sensitivity for each TGS. Logger-2 uses an external fan, containing one TGS 2611-C00. The tested TGS 2611-C00 and TGS 2611-E00 units could yield [CH4] during landfill deployment, by first modelling a reference baseline resistance in field conditions, representative of background (reference) [CH4] sampling. Background sampling was identified using wind direction from a designated background segment, which yielded a baseline resistance model as a function of time (incorporating long-term background effects), water mole fraction and temperature. The ratio between measured TGS resistance and modelled baseline resistance was converted into [CH4], using a two-term modified power fit. Logger-1 methane fitting coefficients were derived during laboratory testing, while Logger-2 coefficients used a 1.49% field sampling subset, alongside a high-precision reference (HPR) instrument. Reconstructed minute-averaged Logger-2 [CH4] for TGS 2611-C00 was compared to the HPR up to 31.5 ppm [CH4] (excluding [CH4] fitting data), resulting in a ±0.55 ppm [CH4] root-mean squared error (RMSE), for 295.2 overall sampling days (excluding data gaps). Reconstructed Logger-1 [CH4] RMSE compared to the HPR was ±0.67 ppm and ±0.77 ppm for the two TGS 2611-C00 and ±1.17 ppm for the TGS 2611-E00, up to 29.3 ppm [CH4], for 147.9 overall sampling days. Field TGS 2611-C00 superiority above other Logger-1 sensors is supported by laboratory tests, which showed TGS 2611-C00 to be most methane-sensitive. In summary, we show that the TGS 2611-C00 is an ideal low-cost sensor to measure [CH4] from facility-scale sources, with a field RMSE below ±1 ppm. This work represents the first application of TGS resistance ratios to yield parts-per-million level [CH4] field measurements, using a dynamic baseline resistance model.
Environmental significanceMethane is a potent greenhouse gas,2 yet global background methane mole fraction ([CH4]) is increasing.57,58 Cheap and accurate [CH4] measurements are urgently required near to facility-scale sources to detect leaks and quantify emissions.5 Low-cost sensors, such as the Figaro Taguchi Gas Sensor (TGS), are designed to measure high [CH4] enhancements. Yet, we show that TGS sampling can be used to detect [CH4] with an accuracy of better than ±1 ppm, by using wind direction measurements to identify background sampling. We also show that TGS methane characterisation can either be conducted in the field or in the laboratory. Thus, we show that this low-cost sensor has great potential in helping to constrain the global methane budget. |
1. Introduction
Methane (CH4) is Earth's third most important greenhouse gas, after water and carbon dioxide (CO2),1,2 with a complex variety of natural and anthropogenic sources.3,4 As an example of the role of anthropogenic CH4, emissions from landfills and waste contribute towards approximately 9% of total global CH4 emissions according to recent (2017) bottom-up estimates.5 However, there remain large uncertainties in the global methane budget,6,7 especially due to difficulties in quantifying emissions from facility-scale sources such as landfill sites.8–11Extensive facility-scale top-down (atmospheric measurement-based) CH4 flux quantification could be used to support the improvement of bottom-up flux estimates.5,12 This typically requires in situ methane mole fraction ([CH4]) measurements near to emission sources.13,14 However, most traditional high-precision CH4 sensors targeted to monitor emissions from facility-scale sources with a sufficiently good measurement accuracy (defined here to be ±1 ppm [CH4] or better), rely on optical sensing techniques, which are expensive and cumbersome.15 Semiconductor-based metal oxide (SMO) sensors may serve as a cheaper alternative, with most CH4 SMO sensors using n-type semiconductors, which bear an excess of free electrons.16 Unlike optical sensors which detect electromagnetic radiation, SMO sensors detect CH4 through chemical reactions.17 With suitable calibration and testing, the low cost of SMO sensors may negate their nominally low precision and low sensitivity.18,19
To detect gas mole fraction changes, n-type SMO sensors first acquire a layer of surface-adsorbed oxygen, taken from the surrounding environment.20 This causes a residual SMO resistance, under a potential difference.21 Reducing gases (such as CH4) react with this surface-adsorbed oxygen, thereby releasing electrons back into the bulk material, hence causing a resistance decrease.22 SMO sensor selectivity to certain gases can be tuned by doping the metal oxide with noble metals,23,24 by using filters25 or even by introducing quantum structures.26,27
Figaro Engineering Inc. (Mino, Osaka, Japan) is a popular manufacturer of low-cost SMO sensors, composed of packed grains.28 We focus here on the Figaro Taguchi Gas Sensor (TGS) range, with an ultimate objective of measuring [CH4] with a sufficient parts-per-million level accuracy to detect CH4 emissions from facility-scale sources. Unlike many SMO sensors, the TGS can operate in ambient humidity conditions29 and, in contrast, functions abnormally in dry conditions.30 Nevertheless, TGS resistance is highly sensitive to water mole fraction ([H2O]) and ambient temperature (T) variations.29,31–33 Furthermore, TGS resistance may behave erratically following sharp [H2O] changes.34 TGS resistance is also influenced by supply voltage.31,34
A variety of TGS model types have been designed to interact with different ensembles of target gas species. The highly sensitive TGS 2600 responds to various reducing gases including hydrogen, CH4, carbon monoxide (CO), ethanol and iso-butane.35 Its high sensitivity has successfully been exploited in past work to detect hydrogen28 and CH4.30,32,36–38 Alternatively, the TGS 2611 is more CH4-selective with two varieties: the TGS 2611-E00 has a filter to improve CH4-selectivity,39 whereas TGS 2611-C00 has no filter, meaning that the latter offers heightened sensitivity and a faster response,40 at the expense of CH4 selectivity.19 Many previous TGS 2611-E00 studies have attempted to measure [CH4] by devising various algorithms based on TGS resistance and environmental measurements.31,34,41–43 On the other hand, the TGS 2611-C00 has featured in fewer CH4 studies but has delivered promising results, with [CH4] exhibiting a clear correlation against TGS resistance.19,29,44,45 Elsewhere, the TGS 2602 is not marketed as a CH4 sensor and is instead designed to detect odorous species including hydrogen sulphide (H2S) and ammonia, though it is also sensitive to hydrogen, ethanol and other volatile organic compounds.46 The TGS 2602 has nevertheless been used extensively in combination with other low-cost sensors to help to account for cross-sensitivities.19,47–50
Although the TGS 2611-E00 has featured more widely in previous [CH4] work, we believe that the TGS 2611-C00 may be more apt where CH4 is the dominant reducing gas species expected to be emitted in terms of volume, such as from landfill sites. If other reducing gas mole fractions remain relatively stable, the sensitivity advantage of the TGS 2611-C00 may be utilised to improve [CH4] measurement capability. Yet, Duan et al.51 suggest that a vast array of (non-CH4) trace gas species (of the order of 1% of total volume) may be emitted from landfill sites including sulphur compounds (such as dimethyl sulphide, methanethiol and H2S), aromatic hydrocarbons, aliphatic hydrocarbons (such as ethanol and propanol) and oxygenated compounds (such as ethanol). Thus, the non-CH4 TGS 2602 may also serve to enrich [CH4] measurement algorithms from potentially complex CH4 sources such as landfill sites, by helping to identify variations in other trace gas species, although this may require complex approaches beyond the scope of this work.
In this work, we aim to exploit TGS sampling to measure [CH4] with a targeted accuracy of ±1 ppm or lower. It is worth noting here that ±1 ppm is an aspirational TGS target for facility-scale CH4 emissions. [CH4] measurements at this accuracy are deemed to be sufficiently useful to detect emissions from most facility-scale CH4 sources. Yet, the necessary accuracy level also depends on whether or not [CH4] measurements will be used for flux quantification (and the specific nature of flux analysis), as well as the magnitude of [CH4] enhancements above the background from the specific CH4 source in question.37,52,53 The specific nature of each individual site, sensor placement and wind dynamics are all factors to consider. Sources producing large [CH4] spikes above the background may have lower [CH4] accuracy requirements.54
In order to derive [CH4] from a TGS field logger, an appropriate calibration approach is necessary. Yet, TGS laboratory calibration can be challenging as laboratory-derived models may not be applicable in field conditions.38,55 Shah et al.34 propose that this may be due to the composition of some testing gases being slightly different to that of natural air in ambient field conditions. For example, natural ambient air can result in a different TGS signal compared to clean synthetic air, despite both gas sources containing the same background quantity of CH4,34 where a background [CH4] level is defined to be 2 ppm from hereon.56,57 As a consequence, laboratory-derived TGS resistance models based on (non-CH4) environmental conditions have exhibited large discrepancies at background [CH4], compared to both laboratory31 and field34 sampling. It is difficult to speculate regarding the specific cause of this phenomenon, other than to propose that unidentified TGS-sensitive gas species are present in different air sources.
Based on the challenges associated with laboratory calibrations, there is great interest in field calibrations of low-cost sensors.58 For example, several studies have conducted TGS field characterisations, using a high-precision reference instrument (HPR) for model training and refinement.38,47,48,54,55 Most of these previous studies modelled [CH4] directly using raw TGS resistance, without deriving a baseline resistance representative of sampling at a fixed (predefined) reference [CH4] level. The ability to derive a robust baseline TGS resistance at a reference [CH4] level, and from field sampling, would be a valuable asset in estimating [CH4] at a desired ±1 ppm [CH4] accuracy, by taking the resistance ratio between measured TGS resistance and this reference resistance.31,34,55 Furthermore, using a resistance ratio is recommended by the manufacturer,39,40 although this fundamental approach is less easy to implement if baseline resistance is influenced by varying (non-gas mole fraction) environmental conditions.30,31 As far as we are aware only Jørgensen et al.55 successfully derived [CH4] using a baseline resistance during field sampling (where they set their reference [CH4] level to 0 ppm), although their baseline resistance was assigned a constant value specific to a certain set of environmental conditions. To our knowledge, it has not yet been possible to derive a dynamic baseline TGS resistance, as a function of varying (non-gas mole fraction) environmental conditions.
In this work, two TGS logging systems (summarised in Section 2) were placed at the edge of a landfill site, with both systems featuring the TGS 2611-C00. Logger-1 is a bespoke mains-powered logger with a pumped air inlet feeding a TGS cell, whereas Logger-2 is a commercially available solar powered logger with a simple fan blowing air towards the sensor. Thus, this work allowed us to evaluate whether a bespoke system with higher power demands would be more advantageous than a commercially available logging system. To derive [CH4] from both systems, a baseline resistance was first characterised from field sampling, as a function of [H2O] and temperature (see Section 4), using a reference [CH4] level at the natural atmospheric background (i.e. 2 ppm). Periods of background sampling for this baseline resistance were identified using wind direction measurements made by an on-site sonic anemometer, by assigning background sampling to wind directions coming away from the landfill site. The [CH4] response for Logger-2 was characterised using a co-located HPR (see Section 4). The [CH4] response of Logger-1 was characterised in the laboratory, where TGS sensitivity to other gases was also tested (Section 3). The outcomes of these laboratory tests are evaluated within Section 3. [CH4] model results from both logging systems and their comparison to the field HPR are presented in Section 5, where we discuss the overall utility of our TGS measurement and [CH4] reconstruction approach. Finally, we conclude the overall feasibility of our TGS [CH4] derivation method for the long-term monitoring of CH4 from facility-scale sources in Section 6.
2. Logging systems
Here we briefly describe the TGS logging systems. Logger-1 is a bespoke logger that was extensively laboratory-tested before field deployment. It contains one Figaro TGS 2602, two Figaro TGS 2611-C00 (labelled TGS 2611-C00 1A and TGS 2611-C00 1B) and one Figaro TGS 2611-E00, all sampling at 1 Hz. Air is pumped into a 0.1 dm3 cell at 1 dm3 min−1. Logger-2 is a ready-made logger that was permanently deployed in the field throughout this study. It contains a single TGS 2611-C00 (labelled TGS 2611-C00 2), providing minute-averaged measurements of 1 Hz data. Air is blown towards the TGS using a downwards-facing fan. Both loggers contain a temperature and relative humidity sensor (SHT85, Sensirion AG, Staefa, Switzerland). Logger-1 contains an additional pressure and temperature sensor (BMP280, Bosch Sensortec GmbH, Reutlingen, Germany). Logger-1 and Logger-2 are described in further detail in Section S1 in the ESI.†3. Laboratory testing
3.1 Sensor response to reducing gases
Before laboratory testing, it is first important to set out how the TGS responds to reducing gases, to design any laboratory experiments accordingly. Shah et al.34 proposed that TGS gas response can be characterised relative to TGS resistance measured in a specific standard reference gas (SRG) which contains reference levels of all reducing gases. This principle is based on observations from Jørgensen et al.55 who showed resistance decay with increasing [CH4] to be independent of (non-gas mole fraction) environmental conditions. The Shah et al.34 model relates each target reducing gas (g) to the ratio between measured resistance (R) and resistance in the standard reference gas (R0), using eqn (1). This equation assumes that the independent effect of multiple g reducing gases on R0 decrease can be multiplied directly.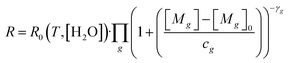 | (1) |
It follows that cg and γg can be derived for a single specific reducing gas by fitting the ratio between R and R0 to [Mg], at multiple levels of [Mg], if [Mg] is equal to [Mg]0 for all other reducing gases (as all other multiplicative gas terms equal unity). The combined effect of T and [H2O] on resistance are naturally accounted for in R0, thus allowing TGS gas response to be characterised independently.
3.2 Laboratory testing details
Individual tests were conducted to characterise TGS response to CH4, CO, ethane (C2H6) and H2S. These tests allowed each of the TGS types inside Logger-1 to be characterised simultaneously. These four testing gases were chosen as they are all reducing gases expected to influence TGS resistance. TGS response to CO2 was also tested as it is not a reducing gas and therefore, it is not expected to result in any TGS resistance change. Thus, this test was used to verify whether non-reducing gases in general can influence the TGS. Observing a null result for CO2 would also help to validate our overall testing methodology, ensuring that resistance changes in all other tests could be directly attributed to the additional presence of a reducing gas (and not some experimental artefact, for example). For each test, a specific testing gas was chosen, containing the target gas species. This testing gas was either sampled in multiple progressive steps (multiple-mole fraction tests), to characterise cg and γg (Sections 3.4 and 3.5), or in a single step (single-mole fraction tests), to compare how the three different TGS types respond to a fixed quantity of a certain species (Section 3.3). The key value of single-mole fraction tests is to qualitatively test the importance of each gas species and to compare how different TGS types respond to each gas.In each test, a SRG was selected, to best mirror the overall composition of the testing gas. Some tests used a gas cylinder filled with ambient air from outside our laboratory as a SRG. Alternatively, gas from a zero-air generator (UHP-300ZA-S, Parker Hannifin Manufacturing Limited, Gateshead, Tyne and Wear, UK) was used, which oxidises hydrocarbons and CO, resulting in 0.00 ppm carbon monoxide mole fraction ([CO]) and 0.00 ppm [CH4]. A third SRG option was to use a synthetic gas cylinder (Deuste Gas Solutions GmbH, Schömberg, Germany). These synthetic gas cylinders contain a natural balance of nitrogen, oxygen and argon (some cylinders also contain 0.3 ppm of nitrous oxide), to which other gas species are synthetically introduced.
All laboratory testing was conducted with a Picarro G2401 gas analyser (Picarro, Inc., Santa Clara, California, USA) drawing gas from upstream of Logger-1. The Picarro G2401 has a maximum sampling frequency of 0.2 Hz, with a flow rate of less than 0.3 dm3 min−1. It measures [CH4], [H2O], [CO] and carbon dioxide mole fraction ([CO2]) with a 0.2 Hz precision of less than ±0.001 ppm, ±0.003%, ±0.015 ppm and ±0.000005%, respectively.60 We used raw dry [CO] from the Picarro G2401, to which an offset correction was applied. A water correction was applied to all raw wet [CH4] and [CO2] measurements, using raw (reported) [H2O] from the Picarro G2401. When sampling at greater than 10 ppm [CH4], reported [H2O] was derived by applying a third order polynomial fit to Picarro G2401 (raw reported) [H2O] measurements from each experiment, as a function of time, when at less than 10 ppm [CH4]. This was required as spectral overlap between CH4 and water made Picarro G2401 [H2O] measurements unreliable at high [CH4]. This was deemed to be a sufficiently accurate [H2O] approximation for the purposes of this work, where minimal [H2O] changes were expected.
During laboratory testing, mass-flow controllers (Bronkhorst High-Tech B. V., AK Ruurlo, Netherlands) were used to create gas blends and to control overall gas flow to both the Picarro G2401 and Logger-1, ensuring a constant net flow rate of 1.5 dm3 min−1. Thus, there was always a surplus gas overflow. In addition, a dew-point generator (LI-610, LI-COR, Inc., Lincoln, Nebraska, USA) was placed directly downstream of the mass-flow controllers. This humidified any gas to a targeted 1.0% [H2O]. A sufficient water stabilisation time of at least 24 hours preceded each test; this is required as the TGS exhibits a prolonged resistance delay in response to small [H2O] changes.34 Furthermore, this delay paradoxically occurs in the opposite direction to the initial resistance change.
3.3 Description and results of single-mole fraction tests
Four single-mole fraction tests were conducted to quantify the fractional resistance drop observed for each sensor when sampling the testing gas, compared to sampling the SRG. These tests allowed the importance of a specific quantity of a specific gas species to be gauged, in terms of its effect on TGS resistance. These tests therefore allow the overall importance of each gas to be evaluated, on each TGS type, as there may be certain sampling field conditions when these gases may need to be accounted for. As these tests effectively treat resistance ratio (i.e. the right-hand side of eqn (1)) as a constant, they cannot be used to derive eqn (1)cg and γg coefficients (due to a single sampled target gas mole fraction).In each test, the SRG was sampled for at least 45 minutes. Then the testing gas was sampled for a fixed duration, with an average resistance value taken near the end of this sampling period (see Table 1 for averaging durations). The SRG was then sampled again. This was repeated multiple times for each test. A modelled set of R0 values, as a function of time, was derived by applying a third order polynomial fit to stable SRG sampling. The average resistance ratio between stable resistance (in the presence of the testing gas) and a corresponding R0 average is provided in Table 1 for each test. A resistance ratio of one corresponds to no TGS sensitivity, whereas a resistance ratio closer to zero corresponds to maximal sensitivity to a particular target gas (compared to the SRG).
| Test | Gas species of interest | Testing gas | SRG | Averaging period for each step (s) | Number of testing cycles | Average [H2O] (%) | Average T (K) | Average ratio between resistance in testing gas and R0 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TGS 2602 | TGS 2611-C00 1A | TGS 2611-C00 1B | TGS 2611-E00 | ||||||||
| Test 1 | Different sources of air containing the same 2 ppm [CH4] | Ambient laboratory air | Zero-air generator gas | 60 | 3 | 0.979 ± 0.002 | 311.4 ± 0.1 | 0.894 ± 0.007 | 0.798 ± 0.008 | 0.710 ± 0.016 | 0.735 ± 0.002 |
| Ambient air cylinder (2.0 ppm [CH4]; 0.11 ppm [CO]; 0.04% [CO2]; etc.) | 3 | 0.894 ± 0.007 | 0.798 ± 0.003 | 0.712 ± 0.006 | 0.729 ± 0.002 | ||||||
| Synthetic air cylinder (2.0 ppm [CH4]; 0.10 ppm [CO]; 0.10% [CO2]) | 3 | 0.964 ± 0.002 | 0.908 ± 0.001 | 0.897 ± 0.002 | 0.934 ± 0.001 | ||||||
| Test 2 | CO | Ambient air cylinder (2.2 ppm [CH4]; 0.17 ppm [CO]; 0.04% [CO2]; etc.), diluted with SRG to target 0.10 ppm [CO] | Ambient air cylinder (2.2 ppm [CH4]; 0.17 ppm [CO]; 0.04% [CO2]; etc.), passing through CO chemical scrubber | 120 | 6 | 0.993 ± 0.004 | 311.5 ± 0.1 | 0.975 ± 0.001 | 0.943 ± 0.002 | 0.901 ± 0.004 | 0.918 ± 0.003 |
| Test 3 | C2H6 | Synthetic air cylinder (50 ppm [C2H6]; 0.02 ppm [CH4] trace) | Zero-air generator gas | 300 | 4 | 0.997 ± 0.002 | 311.9 ± 0.2 | 0.89 ± 0.01 | 0.43 ± 0.02 | 0.43 ± 0.02 | 0.55 ± 0.02 |
| Test 4 | CO2 | Synthetic air cylinder (2.0 ppm [CH4]; 0.10 ppm [CO]; 0.10% [CO2]) | Synthetic air cylinder (2.0 ppm [CH4]; 0.10 ppm [CO]; 0.10% [CO2]), passing through CO2 chemical scrubber | 120 | 6 | 0.996 ± 0.003 | 311.5 ± 0.1 | 1.0014 ± 0.0013 | 1.0005 ± 0.0002 | 1.0006 ± 0.0002 | 0.9999 ± 0.0003 |
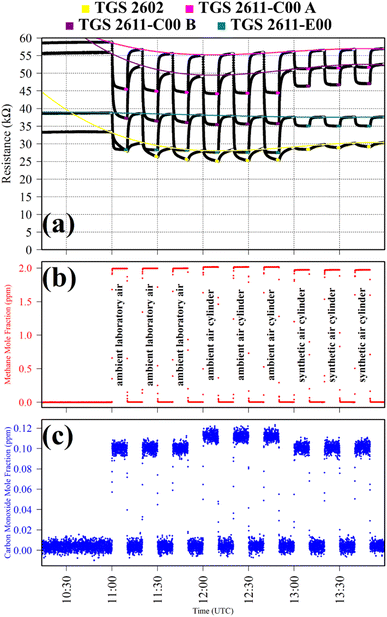
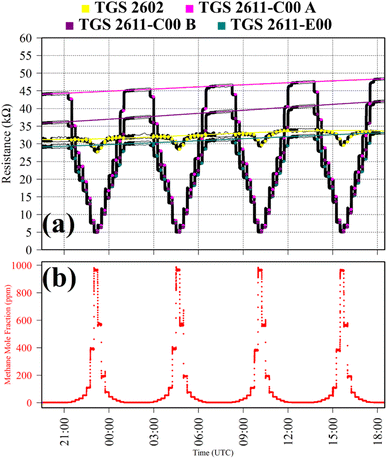
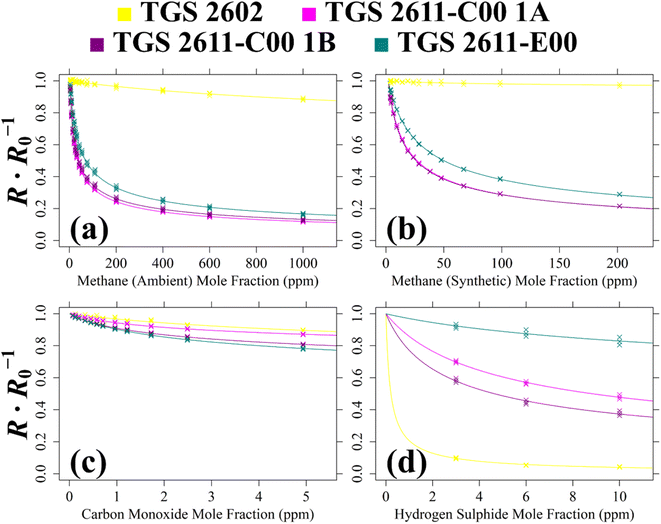
Test 1 sampled different gases containing the same CH4 quantity (2 ppm). Previous work has shown that the choice of SRG affects TGS 2611-E00 resistance, despite each SRG containing the same 2 ppm [CH4].34 This test was thus used to verify this behaviour for the three TGS types inside Logger-1. Using a zero-air SRG, ambient laboratory air was first sampled thrice. Then an ambient air cylinder was sampled thrice. Finally, a synthetic air cylinder containing 2 ppm [CH4] and 0.1 ppm [CO] was sampled thrice. Each gas was sampled for 10 minutes. TGS observations from Test 1 are presented in Fig. 1, along with corresponding Picarro G2401 measurements, which verify that all three testing gases contained a similar quantity of CH4 and CO.
Table 1 resistance ratio values confirm that the resistance of all three TGS types was consistently lower when sampling ambient air (both from the laboratory and from a cylinder filled with outside air) than synthetic air, compared to zero-air generator gas. This supports the hypothesis that there may be supplementary species in ambient air, causing an enhanced resistance decrease for each Logger-1 TGS. It is worth noting from Fig. 1 that TGS 2602 resistance did not fully stabilise within 15 minutes of gas exposure, meaning that the Table 1 resistance ratio values may be underestimated for this sensor, for this test. Nevertheless, the same qualitative conclusions can be inferred for this sensor, regarding the effect of different background gas compositions on resistance.
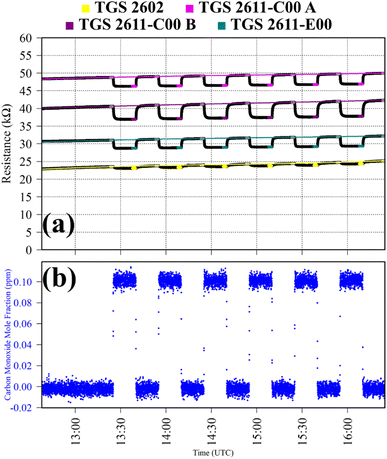
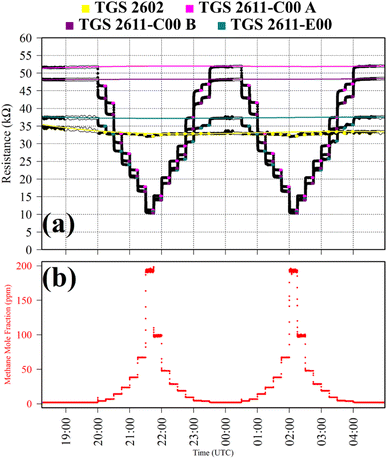
Test 2 was used to evaluate the influence on resistance decrease of a typical background [CO] level in ambient air. Ambient air cylinder gas was passed through a CO scrubber (Sofnocat 514, Molecular Products, Limited, Harlow, Essex, UK) to form a SRG. This was blended with pure gas (no CO scrubber) from the same cylinder, targeting 0.10 ppm [CO]. This was sampled in six 15 minutes intervals. TGS observations from Test 2 are presented in Fig. 2, along with corresponding Picarro G2401 measurements, which show [CO] alternating between 0.0 ppm and 0.1 ppm. Test 2 resistance ratio values in Table 1 show that 0.1 ppm [CO] causes a resistance drop for all four sensors, using an ambient air SRG. The fractional resistance decreases associated with the presence of CO for both the TGS 2611-E00 and the two TGS 2611-C00 are a similar order of magnitude. This is despite the fact that the TGS 2611-E00 incorporates an integrated filter to reduce sensitivity to (non-CH4) interfering gases.
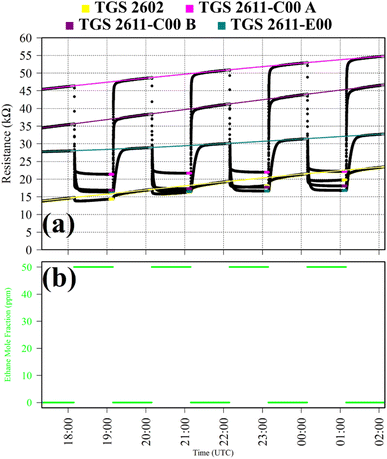
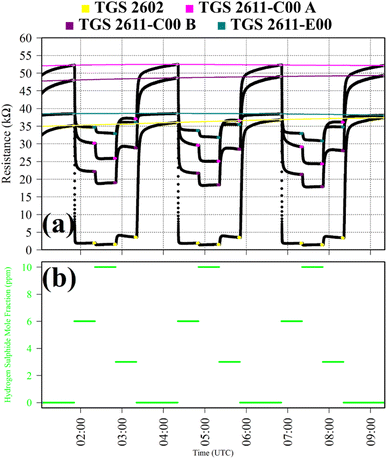
Test 3 assessed TGS response to C2H6, which is a reducing gas with similar chemical properties to CH4. Gas from the zero-air generator served as a SRG. A synthetic air cylinder containing 50 ppm ethane mole fraction ([C2H6]) and trace quantities of CH4 was sampled in four 1 hour intervals. This prolonged sampling period was necessary due to a delayed TGS resistance response. TGS observations from Test 3 are presented in Fig. 3, with C2H6 exposure periods also shown. Table 1 resistance ratio values show high TGS C2H6 sensitivity, yet the 11% resistance drop for the TGS 2602 is dwarfed by a 57%, 57% and 45% resistance drop for TGS 2611-C00 1A, TGS 2611-C00 1B and TGS 2611-E00, respectively. Thus, all sensors exhibit C2H6 sensitivity but at different levels.
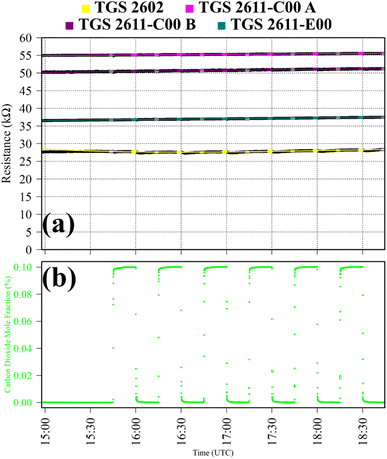
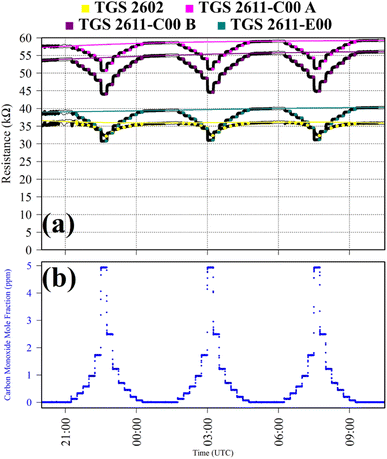
Test 4 was used to verify TGS CO2 insensitivity for all TGS types inside Logger-1, as previously observed for the TGS 2611-E00.34 Gas from a synthetic air cylinder containing 0.1% [CO2] passed through a chemical CO2 scrubber (Ascarite II, Thermo Fisher Scientific, Waltham, Massachusetts, USA), to serve as a SRG. Pure gas from the same cylinder was then sampled for six 15 minutes intervals. TGS observations from Test 4 are presented in Fig. 4, along with corresponding Picarro G2401 measurements, which show [CO2] to alternate between 0.0% and 0.1%. A resistance ratio of one for all four sensors (see Table 1) confirms that none of the TGS units exhibited CO2 sensitivity. This supports our understanding that TGS resistance decrease is caused by the additional presence of reducing gases.
It is worth noting here that for some of these tests, there was a gradually evolving baseline resistance. For example, for Test 3, Fig. 3 clearly shows baseline resistance to slowly increase over time. This cannot be attributed to temperature or water mole fraction changes which were small (see Table 1). The most likely cause was some form of memory effect from previous tests, causing the baseline resistance to take some time to stabilise. This was occasionally observed during this work following large changes in the overall composition of sampling gas. Nevertheless, the low standard deviation in average resistance ratio values given in Table 1 confirms that an evolving baseline is not an issue when evaluating a resistance ratio (as opposed to raw absolute resistance). Taking a resistance ratio can thus eliminate the influence of background baseline variability, allowing for independent analysis of the effect of reducing gas exposure.
In summary, these single-mole fraction tests allow us to qualitatively assess the importance of certain gases on each TGS type. Resistance ratio values also provide some additional quantitative insight for a specific mole fraction level of each gas, allowing for comparisons between different TGS types. These tests allow us to conclude that both 50 ppm of C2H6 and 0.1 ppm of CO effect all three TGS types. These tests also show that CO2 has no effect on any of the sensors, as expected, as it is not a reducing gas. Most importantly, Test 1 reinforces the significance of the effect of different SRGs on sensor response. Although different gas samples may contain the same quantity of CH4 and CO, other trace gas components in these different gas sources (synthetic versus ambient) clearly affect overall TGS resistance.
3.4 Description of multiple-mole fraction tests
Four multiple-mole fraction tests were conducted, by sampling a range of mole fractions of a single gas in each experiment. These tests were used to derive eqn (1)cg and γg coefficients by fitting decreasing TGS resistance ratio to increasing gas mole fraction. In each test, the SRG was sampled for at least 45 minutes. Then the testing gas was gradually introduced in multiple steps through dilution with the SRG, up to a maximum level and then back down again (see Table 2 for details). A 2 minutes average resistance was taken from the end of each sampling step. The SRG was then sampled again to complete the testing cycle. This cycle was repeated multiple times for each test. A modelled set of R0 values, as a function of time, was then derived by applying a third order polynomial fit to stable SRG sampling periods.| Test | Gas species of interest | Testing gas | SRG | Number of testing cycles | Average [H2O]a (%) | Average T (K) | Sensor | c g (ppm) | γ g | R 2 | RMSE (Ω Ω−1) | Inverted RMSE (ppm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Excluding any measurements above 10 ppm [CH4] due to spectral overlap between CH4 and water. | ||||||||||||
| Test 5 | CH4 | 10% [CH4] in argon cylinder | Ambient air cylinder (2.2 ppm [CH4]; 0.17 ppm [CO]; 0.04% [CO2]; etc.), passing through CO chemical scrubber | 4 | 0.978 ± 0.003 | 311.6 ± 0.1 | TGS 2602 | 618.89 ± 178.58 | 0.127 ± 0.026 | 0.9594 | ±0.0070 | ±45.4 [CH4] |
| TGS 2611-C00 1A | 9.06 ± 0.15 | 0.452 ± 0.003 | 0.9995 | ±0.0055 | ±17.2 [CH4] | |||||||
| TGS 2611-C00 1B | 9.22 ± 0.25 | 0.431 ± 0.005 | 0.9987 | ±0.0091 | ±36.0 [CH4] | |||||||
| TGS 2611-E00 | 17.62 ± 0.50 | 0.442 ± 0.006 | 0.9985 | ±0.0099 | ±29.7 [CH4] | |||||||
| Test 6 | CH4 | Synthetic air cylinder (202 ppm [CH4]; 0.1 ppm [CO]; 0.04% [CO2]) | Synthetic air cylinder (2.0 ppm [CH4]; 0.1 ppm [CO]; 0.10% [CO2]) | 2 | 0.977 ± 0.004 | 311.0 ± 0.1 | TGS 2602 | 26.09 ± 25.66 | 0.012 ± 0.007 | 0.4787 | ±0.0069 | ±57.2 [CH4] |
| TGS 2611-C00 1A | 7.30 ± 0.14 | 0.466 ± 0.004 | 0.9997 | ±0.0038 | ±3.2 [CH4] | |||||||
| TGS 2611-C00 1B | 6.64 ± 0.11 | 0.453 ± 0.004 | 0.9997 | ±0.0036 | ±2.3 [CH4] | |||||||
| TGS 2611-E00 | 13.36 ± 0.25 | 0.454 ± 0.005 | 0.9997 | ±0.0033 | ±2.2 [CH4] | |||||||
| Test 7 | CO | Synthetic air cylinder (5.0 ppm [CO]; 0.02 ppm [CH4] trace) | Zero-air generator gas | 2 | 0.987 ± 0.003 | 310.5 ± 0.1 | TGS 2602 | 2.59 ± 0.73 | 0.103 ± 0.021 | 0.9432 | ±0.0068 | ±0.2436 [CO] |
| TGS 2611-C00 1A | 0.69 ± 0.04 | 0.066 ± 0.002 | 0.9950 | ±0.0025 | ±0.0978 [CO] | |||||||
| TGS 2611-C00 1B | 0.57 ± 0.03 | 0.094 ± 0.002 | 0.9968 | ±0.0029 | ±0.0976 [CO] | |||||||
| TGS 2611-E00 | 0.76 ± 0.03 | 0.121 ± 0.003 | 0.9979 | ±0.0027 | ±0.0820 [CO] | |||||||
| Test 8 | H2S | Synthetic air cylinder (10 ppm [H2S]; 0.02 ppm [CH4] trace) | Zero-air generator gas | 3 | 0.995 ± 0.004 | 310.9 ± 0.1 | TGS 2602 | 0.14 ± 0.04 | 0.755 ± 0.061 | 0.9691 | ±0.0041 | ±0.794 [H2S] |
| TGS 2611-C00 1A | 2.58 ± 0.39 | 0.466 ± 0.040 | 0.9898 | ±0.0092 | ±0.413 [H2S] | |||||||
| TGS 2611-C00 1B | 1.30 ± 0.26 | 0.456 ± 0.044 | 0.9782 | ±0.0127 | ±0.571 [H2S] | |||||||
| TGS 2611-E00 | 5.29 ± 4.24 | 0.176 ± 0.095 | 0.8430 | ±0.0165 | ±1.448 [H2S] | |||||||
Test 5 was used to characterise CH4 TGS response, using ambient air cylinder gas as a SRG. Gas from a cylinder containing 10% [CH4] in argon (Air Products SAS, Saint Quentin Fallavier, France) was diluted with the SRG up to a 1000 ppm [CH4] target in 15 minutes steps. This cycle was repeated four times. A chemical CO scrubber (Sofnocat 514) was placed upstream of the dew-point generator during testing, resulting in a consistent [CO] level of 0 ppm throughout this test. TGS observations from Test 5 are presented in Fig. 5, along with corresponding [CH4] Picarro G2401 measurements. Resistance clearly decreased with increasing [CH4] for each TGS, as illustrated in Fig. 5. It is also interesting to note that all three sensors (except TGS 2602) reached a similarly low resistance level at high [CH4], regardless of the baseline resistance level, as the available activated oxygen on the SMO surface became saturated.
CH4 response was also characterised in Test 6, but instead, using synthetic air cylinder gas as a SRG; the SRG contained 2 ppm [CH4] and 0.1 ppm [CO]. This test was used to evaluate whether a similar fit could be derived for a single reducing gas (CH4 in this case) regardless of the choice of SRG, by compared to Test 5 which used an ambient air SRG. The synthetic SRG was blended with gas from another synthetic cylinder containing 202 ppm [CH4] and 0.1 ppm [CO] in 15 minutes steps, up to the maximum [CH4] level. This cycle was repeated twice. No CO scrubber was needed as both gas sources have a similar [CO] level. TGS observations from Test 6 are presented in Fig. 6, along with corresponding Picarro G2401 [CH4] measurements. Resistance clearly decreased for each TGS with increasing [CH4], as illustrated in Fig. 6. The decrease in resistance was less pronounced for the TGS 2602 with increasing [CH4]. However, sensor behaviour in general for Test 6 was similar to that of Test 5.
Test 7 was used to characterise TGS CO response at various [CO] levels. A key advantage of this test is that it allows us to test the applicability of eqn (1) to a single gas other than CH4. Gas from the zero-air generator served as a SRG. It was blended with gas from a synthetic air cylinder containing 5 ppm [CO] (and small traces of CH4) up to the maximum [CO], in 15 minutes steps. This cycle was repeated thrice. TGS observations from Test 7 are presented in Fig. 7, along with corresponding [CO] Picarro G2401 measurements. Resistance clearly decreased for each TGS with increasing [CO], as illustrated in Fig. 7. The magnitude of resistance change was similar for all of the sensors, except for the TGS 2602, which is clearly less sensitive to CO than the other sensors. Yet, this test shows that the TGS 2602 is far more sensitive to 10 ppm [CO] than 202 ppm [CH4] sampled during Test 6.
Test 8 was used to characterise TGS response to H2S, which is a potent reducing gas with potential to interact with SMO sensors. Gas from the zero-air generator was used as a SRG. It was blended with gas from a synthetic air cylinder containing 10 ppm hydrogen sulphide mole fraction ([H2S]), with trace quantities of CH4. [H2S] levels of 6 ppm, 10 ppm and 3 ppm were sampled in 30 minutes intervals. This cycle was repeated thrice. This longer 30 minutes sampling period was required for delayed sensor stabilisation in response to H2S. TGS observations from Test 8 are presented in Fig. 8, with each targeted [H2S] level. Resistance clearly decreased for each TGS with increasing [H2S], as illustrated in Fig. 8, although resistance variability was less pronounced for the TGS 2602. For the other three sensors, there was a more gradual resistance decrease with increasing [H2S], with greater resistance variability.
3.5 Results of multiple-mole fraction tests
TGS resistance measurements from Test 5, Test 6, Test 7 and Test 8 were used to derive eqn (1)cg and γg coefficients. First, the ratio between 2 minutes average measured resistance (in the presence of the testing gas) and a corresponding modelled R0 average (in the absence of the testing gas) was derived for each sensor. For each resistance ratio, corresponding gas mole fractions were also required. For CO, all [CO] measurements were taken from the Picarro G2401, sampling the same Logger-1 gas stream. For CH4, most [CH4] measurements were taken from the Picarro G2401. However, the Picarro G2401 can become unreliable at high [CH4] due to poor spectral fitting. Instead, [CH4] values above 150 ppm were estimated from mass-flow controller settings, considering the flow rate of each gas source into the overall gas mix. Based on mass-flow controller manufacturer-rated accuracy values, this results in a maximum uncertainty of ±0.6% for derived [CH4] values above 150 ppm, assuming the specified cylinder mole fraction to be accurate. [H2S] was also derived from mass-flow controller settings with a similar uncertainty, as no H2S gas analyser was used.The relationship between resistance ratio and gas mole fraction is plotted in Fig. 9 for the four multiple-mole fraction tests. For each plot, a non-linear least squares (NLS) regression was applied between resistance ratio and g gas mole fraction, following eqn (1), yielding cg and γg values for each Logger-1 TGS for each test (see Table 2). All NLS regressions referred to in this manuscript were derived using the “nls” function of R version 4.2.2.61 Standard deviation uncertainties in Table 2 for each cg and γg value were derived using rescaled covariances based on Hessian matrices, provided by R version 4.2.2.61 The coefficient of determination (R2) for each TGS resistance ratio fit is presented in Table 2, alongside the root-mean squared error (RMSE) in resistance ratio. An inverted RMSE in gas mole fraction is also provided, by using the original estimated cg and γg coefficients, but by inverting eqn (1) to make the target gas mole fraction the subject.
 | ||
| Fig. 9 The ratio between 2 minutes average measured TGS resistance and a modelled SRG R0 (coloured crosses) for Logger-1 (a) plotted against [CH4] with an ambient air SRG, (b) plotted against [CH4] with a synthetic air SRG, (c) plotted against [CO] with a synthetic air SRG and (d) plotted against [H2S] with a synthetic air SRG. Mole fraction values are fitted to resistance ratio, using eqn (1) coefficients (coloured curves). | ||
For Test 5, Fig. 9 shows that all four sensors are sensitive to CH4 in ambient sampling conditions including the TGS 2602, despite it not being marketed as a CH4 sensor. This figure shows that the TGS 2611-C00 is more CH4-sensitive than the TGS 2611-E00. This is probably due to the absence of an integrated filter, improving TGS 2611-C00 sensitivity. Although the TGS 2602 is poorly CH4-sensitive, an eqn (1) fit could still be derived. But realistically, TGS 2602 CH4 sensitivity may be difficult to observe in ambient conditions with cross-sensitivities due to the variation of other species, naturally present in ambient air. When comparing the Test 5 cg and γg estimates in Table 2, it is clear that both TGS 2611-C00 units yield similar eqn (1) fit values. However, estimated cg values vary significantly between the different TGS types, for example, cg for the TGS 2611-C00 is 9 ppm, whereas cg is 18 ppm for the TGS 2611-E00. The difference is even more stark for the TGS 2602.
For Test 6 which used a synthetic air SRG, Fig. 9 shows that the variability in sensitivity of the different TGS types is similar compared to that using an ambient air SRG (Test 5). This means to say that the TGS 2611-C00 is consistently more CH4-sensitive regardless of the choice of SRG, as expected. However, Table 2 also shows that the magnitude of the derived eqn (1) coefficients is different in the different SRGs. For TGS 2611-C00 for example, cg is 7 ppm in Test 6 (synthetic SRG) but it takes a higher value of 9 ppm in Test 5 (ambient SRG). This may, in part, be due to the different sampled [CH4] range in each test, yielding fits of a different nature. However, it may also be possible that there were other effects at play, making gas characterisation coefficients derived with an ambient air SRG potentially more reliable when applied to typical ambient field conditions.
When evaluating the quality of the eqn (1) fit for Test 5 and Test 6 using Table 2, the Test 5 inverted RMSE values are larger than Test 6 values (except for the TGS 2602) as Test 5 sampled over a wider [CH4] range. By limiting [CH4] to below 30 ppm, a reduced inverted RMSE can instead be acquired for Test 5 of ±33.6 ppm, ±0.495 ppm, ±0.830 ppm and ±0.906 ppm for TGS 2602, TGS 2611-C00 1A, TGS 2611-C00 1B and TGS 2611-E00, respectively. This shows that TGS 2611-C00 and TGS 2611-E00 can both provide [CH4] measurements at a parts-per-million accuracy level from Test 5 in ambient sampling conditions in principle, provided that a suitable R0 is derived as a first step. Following eqn (1), this also fundamentally requires mole fractions of other reducing gases to either be relatively stable or be independently measured, as only one unknown gas mole fraction can be derived from a resistance ratio.
For the CO analysis of Test 7, Fig. 9 shows all three TGS types to be CO-sensitive. The TGS 2602 and TGS 2611-C00 1A share a similar resistance ratio curve. Meanwhile, TGS 2611-C00 1B and the TGS 2611-E00 are both more CO-sensitive, with a lower resistance ratio curve. This is reflected in Table 2 values which show cg and γg for TGS 2611-C00 1A to differ considerably compared to values for TGS 2611-C00 1B. It is surprising that one of the TGS 2611-C00 units (TGS 2611-C00 1B) is almost equally CO-sensitive as the TGS 2611-E00, because the TGS 2611-E00 has a filter designed to reduce sensitivity to non-CH4 interfering gases. This result, combined with the single-mole fraction CO result from Test 2 (see Table 1), places doubt on the efficacy of this filter for CO. Yet, this test is still useful as it confirms that the eqn (1) resistance ratio decay model is valid for CO as well as for CH4, when tested separately. Thus, each tested TGS may, in principle, be used to make field [CO] measurements, assuming constant [CH4].
Finally Test 8 was used to characterise TGS H2S sensitivity. The Fig. 9 curves show all four sensors to be H2S-sensitive, with the TGS 2602 being the most sensitive. Thus, [H2S] may also be measured from TGS field sampling in principle, assuming other reducing gas mole fractions to remain constant. Yet, despite its high sensitivity, TGS 2602 resistance ratio decreases abruptly at low [H2S], making it more difficult to predict [H2S] from resistance ratio. Conversely, resistance ratio for the other sensors decreases more gradually across a larger [H2S] range. The TGS 2611-E00 is the least H2S-sensitive, perhaps due to its integrated filter.
To summarise these multiple-mole fraction tests, each Logger-1 TGS is sensitive to CH4, CO and H2S, exhibiting a decreasing resistance ratio (between measured resistance and R0) with increasing target gas mole fraction. Each test yielded eqn (1)cg and γg coefficients. Each fit (expect one) resulted in a R2 value of at least 0.8, given in Table 2. The only exception was the poor TGS 2602 fit for Test 6, with a R2 of 0.48, which was due to the [CH4] sampling range being insufficient to exhibit a significant resistance decrease compared to the baseline resistance for this (non-CH4) sensor. On the other hand, Test 5 which spanned a greater [CH4] range resulted in a R2 of 0.96 for the same sensor. Another key outcome from these tests is the overall difference between Test 5 and Test 6 coefficients, which shows that the choice of SRG may affect the nature of a gas response fit, making this an important consideration in future work.
4. Field deployment and testing
4.1 Site description
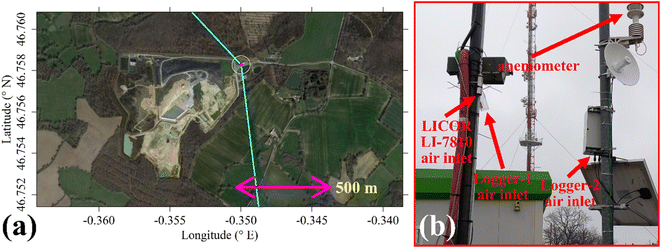
The two TGS logging systems were deployed at the SUEZ Amailloux landfill site in the west of Metropolitan France. The logger air inlets were on the site perimeter (+46.758281° N, −0.349997° E), approximately 2.5 m high and away from direct localised CH4 sources as illustrated in Fig. 10. This positioning allowed the sensors to sample the greater overall landfill emission plume. Logger-2 provided minute-average measurements between 1 April 2022 and 31 May 2023 with minor data transmission gaps. Logger-1 sampled at 1 Hz between 24 November 2022 (no later than 2 months after the start of laboratory testing) and 31 May 2023; these measurements were all subsequently minute-averaged. In the field, Logger-2 was solar powered while Logger-1 used mains power. As the Logger-2 fan air inlet was directly below the TGS, no lag time correction was needed. For Logger-1, there was a minor delay between the inlet and sensors (less than 20 s), so no lag time correction was applied.Shah et al.34 showed that brief instantaneous [H2O] changes cause an initial sharp jump in TGS resistance followed by a prolonged decay towards a stable resistance level in the opposite direction to the initial resistance change. To account for this, all TGS sampling following a sharp [H2O] change was omitted from further analysis. This procedure is described in full detail in Section S2 in the ESI,† resulting in an initial data loss of 10.69% for Logger-1 sampling and 9.24% for Logger-2 sampling. Any further analysis assumes this data to be removed from the original dataset. This left 243![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 022 remaining Logger-1 data points and 537
022 remaining Logger-1 data points and 537![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 remaining Logger-2 data points for the subsequent analysis, with each data point corresponding to 1 minute of sampling.
005 remaining Logger-2 data points for the subsequent analysis, with each data point corresponding to 1 minute of sampling.
The inlets for the two TGS loggers were co-located with a LICOR LI-7810 gas analyser (LI-COR, Inc., Lincoln, Nebraska, USA) air inlet. The LICOR LI-7810 uses optical feedback cavity-enhanced absorption spectroscopy to measure dry [CH4], dry [CO2] and [H2O] with a 1 Hz manufacturer-rated precision of ±0.0006 ppm, ±0.00035% and ±0.0045%, respectively.62 Following LICOR LI-7810 lag time correction, a supplementary water correction and laboratory calibration was applied to [CH4]. There were occasional data gaps for various reasons including power cuts and lack of data download (instrumental storage is limited to roughly 2 months). All available 1 Hz corrected LICOR LI-7810 [CH4] measurements were minute-averaged, with any average containing fewer than 59 data points discarded from further analysis. The maximum minute-averaged LICOR LI-7810 [CH4] during Logger-1 and Logger-2 sampling was 29.3 ppm and 31.5 ppm, respectively.
A two-dimensional sonic anemometer (MetPak Pro Weather Station, Gill Instruments Ltd, Lymington, Hampshire, UK) was also deployed on the site. It was originally aligned with True North and provided 1 Hz wind measurements which were subsequently minute-averaged. It was initially mounted onto a telescopic mast in the centre of the site. However, the mast occasionally twisted by up to approximately ±10°. The anemometer was therefore relocated to the air inlets on 22 November 2022 and mounted to a fixed pole. Thus, the combined dataset from both locations is valid with an uncertainty of ±10°.
4.2 Water mole fraction
[H2O] corresponding to each TGS minute-average measurement was calculated in two steps for both loggers. First, vapour pressure in each logger was derived as a function of minute-averaged SHT85 temperature measurements, using Tetens' equation, given by Murray.63 Vapour pressure was then converted into [H2O] using ambient pressure and minute-averaged SHT85 relative humidity measurements. For Logger-1, BMP280 minute-averaged pressure was used. With no Logger-2 pressure sensor, pressure was assigned a constant ambient value of 105 Pa. Pressure measurements from Logger-1 or the sonic anemometer were not applied to Logger-2, as each system sampled over a unique time range with specific data gaps. Thus, for a realistic atmospheric range of between 9.5 Pa and 10.5 Pa, using a fixed 105 Pa pressure results in a ±0.05% maximum [H2O] uncertainty, at 1% [H2O].4.3 Dynamic baseline resistance in a standard reference gas
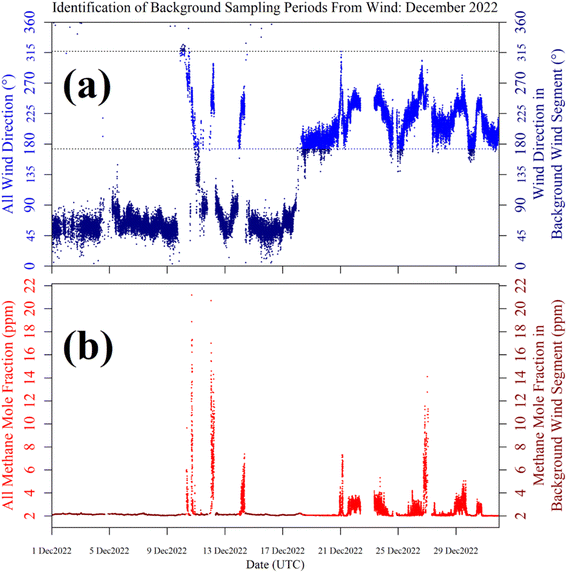
Shah et al.34 showed that applying a laboratory-derived R0 model to field sampling can result in poor correspondence with measured resistance. Therefore, a R0 baseline was instead derived from field sampling for both logging systems, by characterising TGS resistance measurements during background sampling. These periods of background sampling were identified using sonic anemometer wind direction. The basic principle was to collect as many TGS measurements as possible from air arriving from upwind of the landfill site, where it was likely that background air was being sampled. The objective was not to identify every single background measurement, but a sufficiently large ensemble of measurements with which to develop a field R0 model.Background assignment took advantage of TGS air inlet placement towards the North-East corner of the landfill site (see Fig. 10). Based on this particular configuration, sampling from three-fifths of wind directions (i.e. 216° out of 360°) in the opposite direction to the landfill (relative to TGS air inlet position) were classified as periods of background sampling. This corresponds to wind directions of between 317° and 173°, assuming 245° to be the direction of the centre of the landfill site (i.e. opposite to the background wind direction window). This background segment is shown by cyan lines in Fig. 10. As an additional step, good background status was only assigned to TGS measurements where at least 20 individual 1 Hz wind measurements contributed towards minute-average wind direction and where minute-average wind speed was at least 1 m s−1. As an example, the identification of periods of background sampling for December 2022 is presented in Fig. 11 for LICOR LI-7810 [CH4] measurements. Fig. 11 shows that wind direction is a valid tool to identify background sampling periods, as background-assigned [CH4] is typically 2 ppm in this figure (i.e. the natural atmospheric background). For the full datasets, the average LICOR LI-7810 [CH4] during background-assigned sampling periods was (2.06 ± 0.04) ppm and (2.05 ± 0.11) ppm for Logger-1 and Logger-2, respectively, corresponding to periods in which the loggers also recorded good data with stable [H2O]. This shows that thanks to favourable sensor air-inlet placement, periods of background sampling can successfully be identified from wind direction alone.
Next, a background model was derived from all TGS resistance measurements made during these background-assigned sampling periods, as a function of measured temperature and derived [H2O]. Shah et al.34 showed that the eqn (2) four-term model fit best characterises R0, without over-parametrisation, based on AIC and BIC tests performed on simplified eqn (2) models. Thus, a NLS regression was applied to all background-assigned TGS resistance, temperature and [H2O] values, following eqn (2), to yield these four parameters.
| R0 = A(t)·(1 − ([H2O]·(B − (T·C))) − (T·D)) | (2) |
After deriving an initial set of eqn (2)A, B, C, and D model parameters, temporal variability in A was characterised, while keeping B, C and D fixed. This temporal component was introduced to account for the variation of potential long-term factors that may slowly influence R0 over time (other than temperature and [H2O]) such as natural sensor drift, airflow variability or variability in the composition of other trace gas species in background air. A NLS regression was applied to all moving sets of 8 000 consecutive background-assigned resistance measurements spanning each TGS dataset (representing approximately 5.6 days of discontinuous background sampling), using eqn (2) with fixed B, C and D, to derive different A values as a function of R0 sampling time. This means to say that A was derived between background-assigned sampling point 1 and 8 000, between background-assigned sampling point 2 and 8 001, between background-assigned sampling point 3 and 8 002 and so on. Due to the discontinuous nature of background assignment, some sets of 8 000 measurements are very close in time and some are sparser, depending on wind directions and hence, background TGS assignment.
For each set of 8 000 background-assigned measurements, a corresponding average A time was derived. This average A time is different from the median time, as each set of 8 000 background-assigned measurements is not time-continuous. Then, the raw A values from the model output were linearly interpolated from the raw A time stamp (of median times) to the original full TGS dataset time stamp (including both background-assigned and non-background-assigned data). Thus, an initial set of A values was derived for the entire dataset, including non-background-assigned sampling periods. However, A values could not be interpolated to the ends of each TGS dataset, as the lowest and highest average A times corresponded to the average times of the first and last 8 000 background-assigned TGS data points.
Newly interpolated A values were then held fixed and new B, C and D values were generated following eqn (2), by applying a NLS regression to resistance measurements and corresponding interpolated A values, during background-assigned sampling periods only. This process was repeated through multiple cycles of refinement until the R2 reached a maximum level, to yield final values of A (as a function of sampling time), B, C and D, given in Table 3. An average value of A is given for the full dataset in Table 3; this average A value does not correspond to an average of the raw model outputs, as it applies to the timeseries of A after linear interpolation for each full TGS dataset (including all background-assigned and non-background-assigned sampling periods). These final baseline coefficients were then used to derive a full R0 baseline for each TGS. However, during this refinement procedure, it was not possible to resolve R0 model coefficients for the TGS 2602 as background-assigned resistance measurements could not be constrained by temperature and [H2O] alone, despite use of a dynamic A. This indicates that background-assigned sampling was influenced by other short-term effects, that a longer-term A value could not capture for this sensor. Therefore, an R0 baseline cannot be derived for the TGS 2602.
| Logging system | Sensor | B (%−1) | C (kK−1 %−1) | D (kK−1) | RMSE (kΩ) | R 2 | Refinement cycle | Average A (kΩ) |
|---|---|---|---|---|---|---|---|---|
| Logger-1 | TGS 2611-C00 1A | 0.770 | 2.00 | 1.51 | ±1.070 | 0.962 | 30 | 119 ± 2 |
| TGS 2611-C00 1B | 0.939 | 2.50 | 1.47 | ±0.942 | 0.962 | 21 | 100 ± 1 | |
| TGS 2611-E00 | 0.717 | 1.84 | 1.52 | ±0.697 | 0.956 | 24 | 78 ± 1 | |
| Logger-2 | TGS 2611-C00 2 | 0.432 | 1.18 | 1.95 | ±1.306 | 0.970 | 9 | 148 ± 8 |
During this R0 baseline modelling procedure, R0 for the entire dataset (for background-assigned and non-background-assigned periods alike) was modelled from available resistance measurements made exclusively during background-assigned sampling. The temporal component of baseline resistance was characterised by allowing the eqn (2)A offset to vary over time. Therefore, each raw derived A value was based only on available background-assigned resistance measurements. R0 was inferred for non-background-assigned sampling periods from surrounding background-assigned sampling periods. This procedure inherently requires a sufficient number of background-assigned data points, which is conducive to a larger background sampling wind direction window. It was assumed that any large time gap in background-assigned sampling was designated a suitable modelled A value from the available surrounding background-assigned measurements. This requires the time duration for significant A variability to be longer than the largest background-assigned resistance measurement gaps. Thus, there may be greater R0 baseline uncertainty during periods with fewer background-assigned measurements, which could be a fundamental limitation of this approach in situations with a highly variable A.
4.4 Deriving methane mole fraction
Next, [CH4] was derived from the ratio between R and R0, using eqn (3).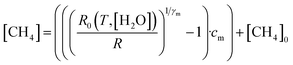 | (3) |
Eqn (3) is essentially an inversion of eqn (1), where [CH4]0 is the background methane mole fraction (set to precisely 2 ppm in this work), cm is the methane characteristic mole fraction and γm is the methane power. Use of this designated fixed 2 ppm background mole fraction is supported by the LICOR LI-7810 background-assigned average [CH4] values presented in Section 4.3, which are based on the origin of wind flow.
Eqn (3) assumes CH4 to be the only reducing gas with significant field mole fraction variability. This is a reasonable assumption for a typical landfill site where the two main emitted gases in terms of volume are CH4 and CO2,64–66 with trace quantities of other gases constituting a very small percentage of total landfill emissions.51,67–69 Consequently, this model requires for [CO] variability to be small, compared to its background level, making the effect of any [CO] variability on resistance ratio negligible compared to the effect of CH4. This is also usually a reasonable assumption at a landfill site which do not usually emit CO in significant quantities, although deep-seated fires at some sites may be a source of CO emissions due to incomplete combustion.70
To derive [CH4] for the TGS units inside Logger-1, cm and γm were taken from laboratory Test 5, which was conducted using an ambient air source (a gas cylinder filled with outside air) as a SRG, with a similar ambient air composition as expected at the landfill site. Although CO was absent during Test 5, the same ambient background [CO] level was assumed to be naturally present during both background-assigned sampling and non-background assigned sampling, meaning that any CO effect cancels out in the resistance ratio. The TGS 2602 produced no reconstructed [CH4] values as it was impossible to yield a baseline R0 fit (as described in Section 4.3) and, hence, no resistance ratio could be derived.
For the single TGS unit inside Logger-2, no laboratory testing was conducted as Logger-2 has no specific controlled air inlet. Therefore, to calculate [CH4], cm and γm for TGS 2611-C00 2 were derived from field sampling by comparing TGS resistance ratio not assigned as coming from a background wind direction with 8 000 corresponding minute-averaged LICOR LI-7810 [CH4] measurements of at least 3 ppm [CH4], taken from the middle of the dataset (representing 1.49% of Logger-2 sampling). This 1 ppm mole fraction enhancement limit avoided too much weight being applied to the abundance of low [CH4] measurements and instead focussed on identifying [CH4] spikes. A NLS regression was applied between these [CH4] measurements and resistance ratios following eqn (1), as illustrated in Fig. 12 up to 21.2 ppm [CH4], yielding cm of 5.26 ppm and γm of 0.349. This fit has a resistance ratio RMSE of ±0.0217 Ω Ω−1 and a R2 of 0.841. Applying the same initial estimated eqn (1)cm and γm coefficients and raw resistance ratios to eqn (3) (i.e. to make [CH4] the subject) revealed an inverted RMSE in [CH4] of ±0.593 ppm.
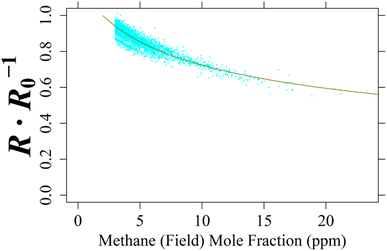 | ||
| Fig. 12 The ratio between measured resistance and modelled R0 (cyan dots) for TGS 2611-C00 2 inside Logger-2 plotted against 8 000 non-baseline-assigned corresponding minute-averaged LICOR LI-7810 [CH4] measurements, greater than 3 ppm [CH4], made at the SUEZ Amailloux landfill site. [CH4] measurements are fitted to resistance ratio, using derived eqn (1) coefficients (dark yellow curve). | ||
5. Methane mole fraction results and discussion
5.1 Modelled methane mole fraction
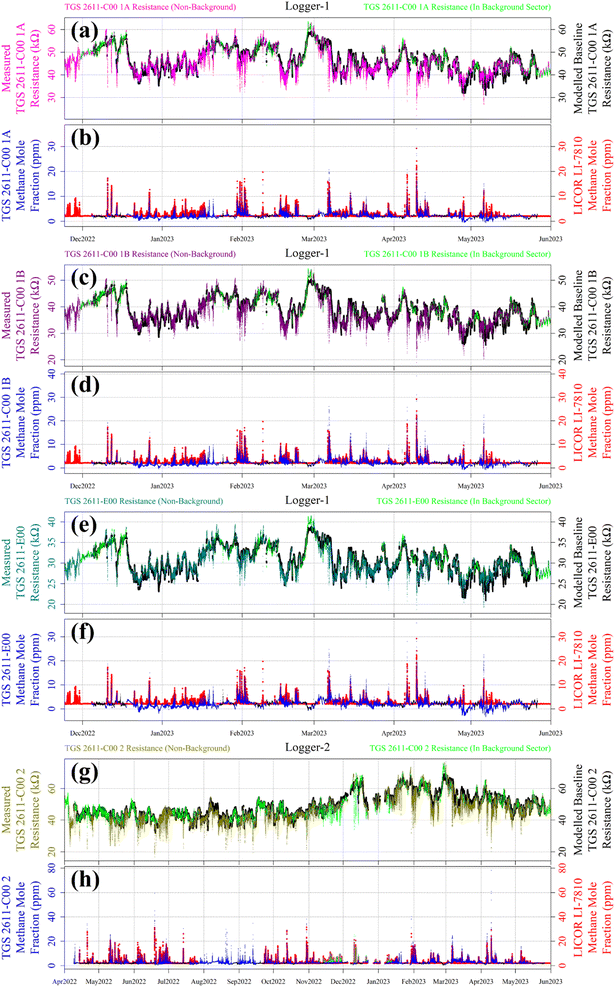
Reconstructed [CH4] measurements from TGS 2611-C00 1A, TGS 2611-C00 1B, TGS 2611-E00 and TGS 2611-C00 2 are presented in Fig. 13, with corresponding LICOR LI-7810 [CH4] measurements shown for reference, where available. For TGS 2611-C00 2 inside Logger-2, the measurements used to derive cm and γm are highlighted in cyan for distinction in Fig. 13. A R0 baseline could not be derived for TGS 2602 inside Logger-1 (as discussed in Section 4.3) and so, this sensor yielded no [CH4] estimates. Section S3 in the ESI† provides plots analogous to Fig. 13 but for each individual sampling month, allowing for a more detailed visual inspection of the reconstruction method for both loggers. Any [CH4] values in Fig. 13 (or the Section S3 plots†) of less than 2 ppm are a consequence of a resistance ratio greater than 1, which may ordinarily be discarded, but are included here (and throughout this manuscript) to demonstrate the aptitude of the overall [CH4] reconstruction approach. In addition, the correlation between TGS [CH4] and LICOR LI-7810 [CH4] measurements is shown in Fig. 14, for data where the LICOR LI-7810 and TGS loggers sampled simultaneously with a common timestamp. Sampling used to model cm and γm for TGS 2611-C00 2 (Logger-2) is excluded from Fig. 14.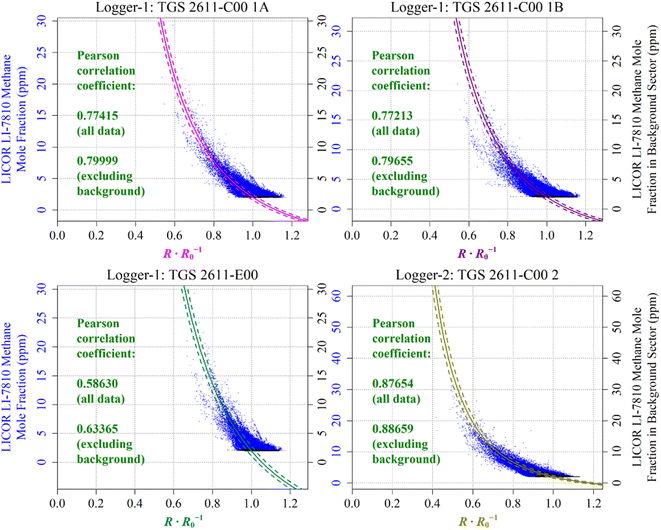 | ||
| Fig. 14 The correlation between reconstructed TGS [CH4] (coloured lines) and [CH4] measured by the LICOR LI-7810 HPR (blue dots), plotted as a function of the ratio between measured resistance and modelled baseline R0. Uncertainty ranges are plotted as dashed lines, which were derived by combining Table 1cm and γm uncertainty values and Table 3R0 RMSE values, where R0 was taken to be its average value for the duration of sampling for each sensor. TGS sampling in the background-assigned sampling segment is highlighted (black dots). | ||
The mean absolute error and the RMSE in reconstructed TGS [CH4] for the four sensors, compared to LICOR LI-7810 [CH4], is provided in Table 4. These values represent statistics derived from precisely 213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 and 425
019 and 425![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 minute-averaged Logger-1 and Logger-2 data points, respectively. This data corresponds to periods when reconstructed TGS [CH4] could be derived, when minute-averaged LICOR LI-7810 [CH4] was available and excluding periods used to derive cm and γm for TGS 2611-C00 2 in Logger-2. In total, this corresponds to 147.93 and 295.23 discontinuous sampling days for Logger-1 and Logger-2, respectively. Table 5 presents similar values to those in Table 4, but during common time periods when Logger-1, Logger-2 and the LICOR LI-7810 all yielded minute-average measurements with a common time stamp (and excluding Logger-2 sampling periods used to derive cm and γm for TGS 2611-C00 2). Table 5 values represent sampling from precisely 190
129 minute-averaged Logger-1 and Logger-2 data points, respectively. This data corresponds to periods when reconstructed TGS [CH4] could be derived, when minute-averaged LICOR LI-7810 [CH4] was available and excluding periods used to derive cm and γm for TGS 2611-C00 2 in Logger-2. In total, this corresponds to 147.93 and 295.23 discontinuous sampling days for Logger-1 and Logger-2, respectively. Table 5 presents similar values to those in Table 4, but during common time periods when Logger-1, Logger-2 and the LICOR LI-7810 all yielded minute-average measurements with a common time stamp (and excluding Logger-2 sampling periods used to derive cm and γm for TGS 2611-C00 2). Table 5 values represent sampling from precisely 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994 data points, equivalent to 132.63 discontinuous sampling days.
994 data points, equivalent to 132.63 discontinuous sampling days.
| Logging system | Sensor | Pearson correlation coefficient | Pearson correlation coefficient (excluding background-assigned sampling) | RMSE (ppm) | Mean absolute error (ppm) | Mean bias (ppm) |
|---|---|---|---|---|---|---|
| Logger-1 | TGS 2611-C00 1A | 0.774 | 0.800 | ±0.669 | ±0.500 | −0.267 |
| TGS 2611-C00 1B | 0.772 | 0.797 | ±0.766 | ±0.560 | −0.262 | |
| TGS 2611-E00 | 0.586 | 0.634 | ±1.170 | ±0.887 | −0.412 | |
| Logger-2 | TGS 2611-C00 2 | 0.877 | 0.887 | ±0.548 | ±0.357 | +0.059 |
| Logging system | Sensor | Pearson correlation coefficient | Pearson correlation coefficient (excluding background-assigned sampling) | RMSE (ppm) | Mean absolute error (ppm) | Mean bias (ppm) |
|---|---|---|---|---|---|---|
| Logger-1 | TGS 2611-C00 1A | 0.774 | 0.800 | ±0.645 | ±0.481 | −0.227 |
| TGS 2611-C00 1B | 0.775 | 0.800 | ±0.743 | ±0.539 | −0.215 | |
| TGS 2611-E00 | 0.588 | 0.634 | ±1.151 | ±0.865 | −0.351 | |
| Logger-2 | TGS 2611-C00 2 | 0.859 | 0.874 | ±0.677 | ±0.470 | +0.236 |
In order to evaluate the fit between the different data series, the Pearson correlation coefficient between measured LICOR LI-7810 [CH4] and reconstructed [CH4] from each TGS is also given in Table 4 (all available data) and Table 5 (common Logger-1 and Logger-2 data). Correlation was additionally quantified separately without background-assigned sampling (coming away from the landfill site), as these background-assigned sampling periods mostly correspond to measurements at 2 ppm [CH4], which should have a fixed resistance ratio of 1. However, due to uncertainty in the empirical R0 model, measured resistance was not precisely equal to the R0 baseline during these background-assigned periods. A component of R0 model uncertainty therefore contributes towards the full Pearson correlation coefficient. On the other hand, there should be improved correlation excluding periods of background-assigned sampling, as this correlation applies to the same full [CH4] range, but with less focus on the background. This fundamentally assumes that our [CH4] reconstruction method is able to model [CH4] spikes as observed by the HPR (as illustrated in Fig. 13 and Section S3 plots†), despite potential limitations in TGS [CH4] accuracy at a fixed [CH4] level. TGS [CH4] excluding background-assigned sampling is thus better correlated with the LICOR LI-7810 in Table 4.
5.2 Evaluation of methane mole fraction results
Here we evaluate our TGS [CH4] reconstruction approach both in terms of the ability to capture individual CH4 spikes and overall [CH4] correlation, compared to the LICOR LI-7810 HPR. The general performance of our technique compared to the HPR can be evaluated visually from the plots in Section S3† for each month and from Fig. 13 for all sampling data. These figures clearly show that each TGS could identify CH4 spikes during non-background-assigned sampling periods (i.e. when sampling at greater than 2 ppm [CH4]). Furthermore, Fig. 13 and Section S3† plots exhibit our ability to provide a reasonable [CH4] estimate for these spikes, which is supported by Fig. 14 correlation values, thus satisfying our broader objectives.However, when evaluating the reconstruction approach over time, Fig. 13 shows that Logger-1 [CH4] estimates were occasionally below the natural atmospheric background (for example, mid-December 2022 to mid-January 2023 and mid-April 2023 to mid-May 2023). This may be due to the persistent nature of winds during certain prolonged time intervals, which largely came from the direction of the landfill site, resulting in minimal background-assigned sampling. As a consequence, Logger-1 R0 modelling was poor during such periods. However, this was less of an issue for Logger-2 which sampled for a much longer overall duration, thus permitting better refinement of eqn (2)R0 model parameters, despite large gaps in background assignment periods. Comparing only the TGS 2611-C00 units, the R2 for the R0 fit is 0.962 inside Logger-1, whereas the R2 has a slightly improved level of 0.970 for Logger-2. This emphasises the complications in comparing measurements from different loggers sampling over different time windows, even if only comparing during common sampling periods.
Nevertheless, direct comparisons may be made between loggers, to some degree, by evaluating Table 5 RMSE and correlation values; this compares reconstructed TGS [CH4] to the HPR, only during simultaneous Logger-1 and Logger-2 sampling. However, alongside the caveat of the effect of different sampling windows on R0, different TGS units of the same type can also vary, especially if sourced from different batches.34,37,41,45 With these caveats in mind, and comparing only one TGS type (TGS 2611-C00) to the HPR, Table 5 shows that Logger-2 yielded a similar [CH4] RMSE (±0.677 ppm), as from Logger-1 (±0.645 ppm and ±0.743 ppm). However, correlation was a slightly improved for Logger-2 (0.859) compared to Logger-1 (0.774 and 0.775). It is thus difficult to form a clear conclusion when comparing between these two loggers, with both systems providing competitive [CH4] estimates.
Table 4 values reinforce the conclusions from Table 5, but instead apply to the full dataset, thus allowing for the overall evaluation of the [CH4] derivation approach, specific to different sampling windows. Despite different sampling durations, it is clear that the TGS 2611-C00 is a suitable sensor to measure [CH4] in both loggers, with a [CH4] RMSE of below ±0.8 ppm for TGS 2611-C00 1A, TGS 2611-C00 1B and TGS 2611-C00 2, with each sensor yielding a Pearson correlation coefficient of at least 0.7 compared to [CH4] from the HPR. This shows that the TGS 2611-C00 can be used in different CH4 characterisation approaches, endorsing the utility of both Logger-1 (laboratory CH4 calibration) and Logger-2 (field CH4 calibration) to derive [CH4]. Yet over each full sampling period, the two TGS 2611-C00 units inside Logger-1 had a mean overall bias of −0.267 ppm and −0.262 ppm compared to the HPR whereas the sensor inside Logger-2 had a much smaller bias of +0.059 ppm, which is probably a manifestation of longer overall Logger-2 sampling, resulting in a better R0 fit.
In terms of evaluating different TGS types, it is only possible to compare Logger-1 sensors, which sampled simultaneously, with the same caveat regarding the limited number of TGS units (see above). Yet it was clear that of the two Logger-1 TGS 2611-C00 units, both had a similar performance with a similar CH4 response when tested in the laboratory. They also yielded a similar field [CH4] RMSE compared to the HPR. The TGS 2602 could not be used to derive [CH4], not because of a lack of CH4 response (see Section 3.5, where there is clearly some CH4 sensitivity), but due to difficulties in dynamically characterising R0 as a function of temperature, [H2O] and R0 sampling time. This may be due to TGS 2602 sensitivity to a cocktail of interfering (non-landfill) background species, causing non-CH4 short-term resistance interference during background-assigned sampling periods.
Of the other TGS types simultaneously tested in Logger-1, the two TGS 2611-C00 were clearly superior to the TGS 2611-E00, which can clearly be visualised from the plots in Section S3,† resulting in better HPR field correlation coefficients (see Table 4). The same can said for [CH4] RMSE compared to the HPR, which was ±1.17 ppm for the TGS 2611-E00, while TGS 2611-C00 1A and TGS 2611-C00 1B resulted in an RMSE of ±0.669 ppm and ±0.766 ppm, respectively. This is contrary to the conclusions of others, who have overlooked or dismissed the utility of the TGS 2611-C00 to measure [CH4].19,31 The TGS 2611-C00 has no filter leading to improved CH4 sensitivity compared to the TGS 2611-E00, thus making the TGS 2611-C00 a suitable option for this landfill emission source.
5.3 General discussion
In this work we present a unique combination of TGS field characterisation, used to first derive a R0 baseline, and laboratory calibration, to characterise CH4 response. This approach enabled us to both dynamically characterise a R0 reference resistance as a function of environmental conditions, whilst precisely characterising TGS CH4 response through controlled Logger-1 laboratory testing, without need for a HPR in the field. Due to the lack of a controlled air inlet, Logger-2 could not be tested in the laboratory in this way. We therefore instead demonstrated Logger-2 CH4 characterisation with a HPR in field conditions, using 2.34% of non-background-assigned sampling above 3 ppm [CH4] (8 000 data points), resulting in a good model fit with a R2 of 0.84.Our approach of characterising TGS environmental response from field sampling has proved fruitful in similar previous work.32,33,54 However, environmental field sampling has never before been used to characterise a R0 baseline resistance representative of sampling at a reference [CH4] level (to our knowledge), with Jørgensen et al.55 instead fixing R0 from field sampling. By setting our reference [CH4] level to the natural atmospheric background, we could derive a TGS R0 baseline resistance model by assigning periods of TGS background sampling using wind direction measurements, which is unique to this work and a key development in TGS testing. This R0 approach requires no laboratory testing and no HPR. Only wind direction is required. Another key feature of our approach was to identify and remove TGS sampling following sharp [H2O] changes (see Section S2 in the ESI† for details) which can otherwise cause atypical TGS resistance response.34 This is a crucial step to enhance R0 baseline characterisation and also to improve the overall TGS resistance dataset, before deriving [CH4].
Our R0 approach therefore allows [CH4] to be derived from the ratio between measured resistance and R0, as temperature and [H2O] effects are incorporated into the four-term R0 model. Additionally, as eqn (2)A coefficients are empirically derived, unidentified causes of background-assigned resistance variation (such as long-term changes in levels of interfering trace gas species) are naturally incorporated into R0. Furthermore, introducing a temporal resistance component has been shown to improve TGS [CH4] estimation in the past,45,47 which has previously been attributed to sensor ageing, causing slow deterioration in sensitivity.30,37 By virtue of our successful R0 derivation method, we also demonstrated the successful applicability of eqn (1), first proposed by Shah et al.,34 to yield [CH4] from field resistance ratios, assuming variability in a single reducing gas.
R 0 modelling requires an ensemble of TGS measurements at the reference (background) [CH4] level. We conclude that using wind direction was a successful approach, with corresponding HPR [CH4] averages at our study site ((2.06 ± 0.04) ppm for Logger-1 sampling and (2.05 ± 0.11) ppm for Logger-2 sampling) being close to the natural atmospheric background.56,57 Uncertainty in identifying background periods of sampling may have been reduced further by minimising the size of the wind segment for background assignment. However, a 216° (60%) sized wind direction window of between 317° and 173° was chosen as a sensible compromise, as a larger ensemble of background-assigned measurements optimises R0 modelling. Although we fixed our reference [CH4] level to a background 2 ppm value, this level of background assignment precision may be unsuitable from certain sources where smaller [CH4] enhancements are expected, as subtle [CH4] variations may be undetectable. However, Fig. 3 shows that there was no issue in detecting [CH4] enhancements above the background from the landfill site in this study. Though we could have used the measured HPR background values to improve [CH4], we decided against this to best emulate autonomous TGS deployment without a HPR. This allowed us to robustly test the performance our [CH4] reconstruction technique.
During field deployment, our [CH4] method occasionally yielded less than 2 ppm. This is due to some natural error in our empirical R0 baseline resistance model (as discussed in Section 5.2) and thus, there were inevitably periods when R0 was less than measured resistance. Assuming a perfect R0 model and no measurement error, a measured resistance greater than R0 corresponds to [CH4] below the background level (i.e. less than 2 ppm in this work), according to eqn (3). In reality [CH4] did not drop below the 2 ppm background (see HPR measurements in Fig. 3) and these low [CH4] values were instead an artefact of an imperfect R0 baseline. Though such [CH4] estimates are clearly incorrect (and can realistically be omitted in real-world applications) they are included in this analysis to best demonstrate the aptitude of our [CH4] modelling approach in Fig. 13 and 14. Furthermore, this avoids TGS [CH4] from being artificially positively biased overall in Tables 4 and 5, as there should be periods when the dynamic R0 is both too high and too low over the full sampling duration.
When evaluating the different TGS types tested in this work, the TGS 2602 could not be used, as it was not possible to model R0 for this sensor. Both the TGS 2611-C00 and TGS 2611-E00 could be used to derive [CH4], though the TGS 2611-C00 units were better than the TGS 2611-E00. Due to its improved sensitivity, we conclude that the TGS 2611-C00 is better suited where emissions of other reducing gas species, such as CO, are unlikely to be an issue. In addition, laboratory Test 4 showed no TGS 2611-E00 selectivity advantage concerning CO interference, as TGS 2611-C00 1B was slightly more sensitive to 0.1 ppm [CO] than TGS 2611-E00, when using an ambient air SRG (see Table 1). From sources with a more complex variety of emission gases, the TGS 2611-E00 may be a safer option, at the expense of [CH4] sensitivity. We suggest that great care should be taken in future to evaluate the true benefits of the TGS 2611-E00 above the TGS 2611-C00 regarding CH4 selectivity, when selecting a TGS for field deployment. To verify the outcomes of this work, we recommend further TGS testing on more sensors from different batches, both in the laboratory and during prolonged field deployment.
Reconstructed TGS 2611-E00 and TGS 2611-C00 results from this work show that [CH4] with a parts-per-million level accuracy can be derived for a fraction of the cost of a high-precision gas analyser such as the LICOR LI-7810 (see correlation values in Table 4). Our approach can both reliably identify CH4 peaks (see Section S3 plots†) whilst offering reasonable [CH4] estimates. This transcends the stated manufacturer application of these sensors as CH4 alarms.39,40 Yet, a fundamental requirement of our approach is on-site wind measurements to identify sampling from a background-assigned wind direction window when deriving R0. Anemometer cost may be negated if installing a network of TGS logging systems on a single site, as only one anemometer is required per site. Furthermore, an anemometer is typically required in any CH4 emission detection or flux quantification work. Finally, an anemometer does not need to be highly precise for the purposes of assigning a large wind direction window, further minimising potential cost.
While each individual TGS costs less than 50 €, the entire Logger-1 system cost approximately 2000 € in raw materials (excluding labour and equipment costs). This is still an order of magnitude cheaper than a high-precision optical gas sensor. Furthermore, Logger-1 was overengineered with many supplementary features, such as multiple TGS units and complex electronic circuitry (see Section S1 for details†). This logging system cost would inevitably decrease in batch production. Logger-2 has a similar up-front cost to Logger-1, although data transmission costs should also be considered; we received complimentary Logger-2 data access in this study.
Both Logger-1 and Logger-2 have drawbacks, for example, unlike Logger-1, Logger-2 is ready to deploy with minor field installation work. Yet Logger-2 requires field calibration alongside an expensive HPR, such as the LICOR LI-7810, with laboratory calibration not possible due to the lack of an air inlet, as discussed above. Although this work only used 8 000 data points from the full dataset (i.e. 5.56 discontinuous sampling days), the full field characterisation period spanned 64.3 days, as background-assigned data was not used and a minimum 3 ppm [CH4] threshold was imposed. A sufficiently large [CH4] characterisation dataset is required for good eqn (1) model fitting, with enough [CH4] enhancements of a sufficient magnitude above the background. Thus, realistic net HPR field characterisation time depends on the specificities of the site and sensor placement; the CH4 characterisation period may be far shorter than 2 months if [CH4] spikes of a higher magnitude are intercepted more regularly. Furthermore, a CH4 field characterisation may simultaneously be applied to multiple loggers by first co-locating them all with a single HPR and then relocating the loggers after acquiring a sufficiently large gas characterisation dataset. Although Logger-1 was also characterised with a reference instrument, this was conducted in laboratory settings for a fixed duration, where there is greater logistical flexibility; [CH4] can be controlled using gas blends rather than relying on unpredictable field [CH4] enhancements.
Another advantage of Logger-1, is that it features a pump with a flow controller to precisely control sensor airflow, whereas Logger-2 uses a simple exterior fan. Yet, it is difficult to quantify the true value of using a pumped sampling cell in this work, as there were many other variables involved when comparing Logger-1 to Logger-2. Logger-2 fan speed may deteriorate over time, which will influence sensor behaviour,31 although our dynamic R0 should incorporate such effects. An advantage of the Logger-1 pumped cell, is that it remains warmer than its surroundings, therefore buffering sharp temperature changes. Nevertheless, the lack of a pump with its high power demands makes Logger-2 a competitive option, as it can be powered with a relatively small solar panel and battery. This allows Logger-2 deployment anywhere on a vast field site. On the other hand, Logger-1 requires up to 10 W, which would require a much larger solar panel and battery power system, which can be costly and may be more difficult to install at a logistically challenging field site. To summarise, it is not impossible to compare directly between Logger-1 and Logger-2 due to the different [CH4] characterisation methods used, the limited number of TGS units tested and the different sampling windows. Nevertheless, it can be concluded from this work that Logger-2 is a competitive option to derive [CH4] with a similar accuracy to Logger-1.
5.4 Future work and outcomes
Logger-1 combined with an anemometer has proved to be an effective [CH4] measurement system (see correlation values in Table 4). However, a limited Logger-1 sampling duration resulted in an inferior R0 fit compared to Logger-2 and, hence, occasional unrealistic [CH4] estimates below the natural atmospheric background, as shown in Fig. 13. Continued prolonged Logger-1 field deployment, alongside the LICOR LI-7810 HPR, would test the robustness of our [CH4] reconstruction approach over time and in a variety of meteorological conditions. It would also test whether our dynamic R0 baseline approach can overcome potential issues with TGS ageing or changes in background gas composition. It may be interesting to test other [CH4] derivation approaches with Logger-1 and Logger-2 data using more complex algorithms or machine learning techniques.29,48 Such approaches may be used in conjunction with the added insight gained from our work on characterising [CH4] using the Shah et al.34Eqn (1) adapted power fit and in conjunction with our work on R0, in particular, identifying periods of background sampling from wind direction. In addition, although the TGS 2602 could not be used due to our inability to derive a R0 baseline (see Section 4.3), it may be exploited in more complex [CH4] reconstruction models in future to identify the presence of species causing cross-sensitivities with other TGS units.19,50In our [CH4] reconstruction approach, a large accumulated dataset was required for a dynamic R0 baseline fit. As 8 000 background-assigned resistance values were used to yield each A value, A (and hence [CH4]) could not be derived from the ends of each dataset. We therefore waited to accumulate a large enough dataset before deriving [CH4], to minimise the proportion of data loss. In addition, a larger dataset improved B, C and D refinement for R0, with better constraint of A as a function of R0 sampling time. The requirement for a large dataset, with missing [CH4] at the ends, means that our current approach does not provide instantaneous [CH4]. Thus, future work must be conducted to test the feasibility of short-term [CH4] estimation, which will be essential if this approach is to be used for rapid identification of CH4 leaks. This will be invaluable when sampling from sources that require leak repair at short notice. We propose that this may be achieved using the last available A, B, C and D values to derive a rough initial value of R0, which may then be refined at a later stage.
In future landfill TGS sampling work, we propose that systems such as Logger-1 should be deployed along the entire site perimeter, following laboratory TGS [CH4] characterisation (avoiding a field-derived HPR [CH4] characterisation). In such a configuration, regardless of wind direction, a CH4 emission plume would always be intercepted. Sensor placement at a complex heterogeneous emission source (such as a landfill site or coal mine) is limited to the site perimeters, as deriving a R0 baseline at a background [CH4] reference level requires a significant portion of sampling in background-identifiable conditions. It would not therefore be possible to apply our [CH4] reconstruction approach to sampling from the middle of a complex heterogeneous area emission source, as emissions may occur from all directions, with many poorly defined and constantly changing non-localised sources. Yet our approach may permit greater flexibility in sensor placement where CH4 emissions occur from specific localised infrastructure with well-defined (fixed) positions. Examples of potential sites include anaerobic digestion facilities, wastewater treatment plants or oil and gas extraction sites, provided that specific site configuration is not overly complex (for example, with multiple overlapping point emissions sources or complex site topography). A dense enough network of Logger-1 systems, alongside an anemometer, would allow for the precise source of leaks to be targeted from specific localised infrastructure within such a site. We recommend roughly twice as many loggers are needed as identifiable emission sources, although this crude guide is highly dependent on the individual characteristics of the site in question. A dense sampling network would also benefit greatly from rapid [CH4] estimation, as discussed above.
To enable full flexibility for a field network of TGS logging systems, such as Logger-1, solar power will be of great use. Developing and testing a Logger-1 solar powered battery power source will be a critical next step. This power supply must be able to cope with the demands of a pump as well as deployment in mid-latitude winter, where days can last 8 hours and in fully overcast conditions (in Metropolitan France, for example). Internet availability is also a valuable consideration for remote data access.
To fully exploit the work presented in this manuscript, [CH4] measurements from an extensive network around a single site should be tested in flux quantification algorithms.54 As a first step, flux quantification can be attempted from the currently stationary sensor location. A suitable inversion flux approach may be applied to both TGS and LICOR LI-7810 [CH4] measurements for flux comparison. The ability to derive TGS CH4 emission fluxes would be a great step towards better regulation of anthropogenic CH4 emission sources. Cheap TGS networks would allow regulators and operators to take direct action to both identify and quantify CH4 emissions. By comparing top-down (atmospheric measurement-based) flux estimates to bottom-up (inventory based) flux estimates, efforts can be made to improve constraint of the global methane budget.
6. Conclusion
In this work, we set out to measure methane mole fraction ([CH4]) with a parts-per-million level accuracy, using the semiconductor-based Figaro Taguchi Gas Sensor (TGS). A bespoke logging system (Logger-1) costing approximately 2000 € (in terms of raw materials) was designed, containing the TGS 2602, TGS 2611-C00 (two units) and TGS 2611-E00. Logger-1 has a fixed flow rate, to regulate sensor cooling in the cell. Extensive laboratory tests revealed all of the sensors to be sensitive to methane, ethane, hydrogen sulphide and carbon monoxide. During testing, the TGS 2611-C00 units were more methane-sensitive than the TGS 2611-E00, as the TGS 2611-C00 lacks an integrated filter. Although this filter is designed to reduce interference from non-methane interfering gases, both sensor types were similarly sensitive to carbon monoxide.Logger-1 was deployed at a landfill site in France, yielding a total of 189 days of discontinuous field sampling. Another ready-made logging system (Logger-2) was also installed in the same location for 411 days of discontinuous sampling, containing a single TGS 2611-C00. As Logger-2 has no controlled air inlet, air was directed upwards to the sensor using a downwards facing fan. [CH4] was derived for both loggers by first modelling a baseline reference resistance, corresponding to resistance at a background [CH4] level. Periods of background air sampling were identified as coming from away from the landfill site using on-site wind direction measurements. A four-term baseline resistance fit was derived for both loggers based on temperature and water mole fraction. A dynamic time component was also incorporated into this fit, to account for supplementary background effects that could slowly affect sensor performance. A baseline resistance model could not be derived for the TGS 2602 so it could not be used to yield [CH4].
To derive [CH4] for the remaining sensors, the ratio between measured resistance and baseline reference resistance was used. This was applied to [CH4] fitting coefficients from Logger-1 laboratory testing. For Logger-2 with no laboratory testing, methane coefficients were instead derived using 1.49% of field sampling, which was compared to [CH4] measured by a co-located high-precision reference instrument. This reference instrument was then used to assess the aptitude of the two different [CH4] approaches. This revealed a root-mean squared error of ±0.67 ppm and ±0.77 ppm for the two TGS 2611-C00 units in Logger-1, ±1.17 ppm for the TGS 2611-E00 in Logger-1 and ±0.55 ppm for the TGS 2611-C00 in Logger-2, which sampled for a much longer duration. Logger-2 sampled up to 31.5 ppm [CH4] whereas Logger-1 sampled up to 29.3 ppm. This demonstrates that both the TGS 2611-C00 and TGS 2611-E00 can be used to derive [CH4]. This also demonstrates that [CH4] can be derived using a field calibration alongside a reference instrument, but can also be derived using a laboratory calibration, with no need for a reference instrument in the field. Finally, despite different [CH4] characterisation methods and the limited number of sensor units tested, we can conclude that Logger-2 is, at least, a competitive alternative to Logger-1.
In future, we recommend more testing on different TGS batches, to verify the outcomes of this work. Further stationary TGS sampling is also required, to test the robustness of our [CH4] derivation method over time and in different meteorological conditions, when compared to a reference instrument. To augment Logger-1 flexibility, a solar-powered battery system should be designed for better portability. Then, a network of pumped low-cost TGS logging systems can be deployed around the perimeter of a complex heterogeneous area emission source, such as a landfill site, to be able to intercept methane emission plumes from different wind directions. [CH4] measurements from a sampling network may be used in flux quantification algorithms, to quantify facility-scale methane emissions and thus, to help constrain the global methane budget.
Code availability
The code used to derive methane mole fraction from Logger-1 and Logger-2 sampling, in combination with sonic anemometer wind direction measurements, is available to access on the Internet.71Data availability
All Logger-1, Logger-2, sonic anemometer and LICOR LI7810 field sampling data from the SUEZ Amailloux landfill site is available to access on the Internet.72Author contributions
AS prepared an initial version of the manuscript which was edited and modified by GB, PC, EA, OL and PK. AS devised the methane mole fraction reconstruction method. AS and OL performed sensor field deployment and maintenance. AS processed field sampling data. EA facilitated site access. AS and CP conducted laboratory testing, in collaboration with OL who secured testing equipment and resources. AS designed Logger-1. PC secured funding for this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Chaire Industrielle TRACE (which is co-funded by the Agence Nationale de la Recherche (ANR) French National Research Agency (grant number: ANR-17-CHIN-0004-01), SUEZ, TotalEnergies – OneTech and Thales Alenia Space) and the Integrated Carbon Observation System (ICOS) National Network France. We thank ChampionX Corporation (The Woodlands, Texas, USA) for providing Logger-2 data access. We thank Mali Chariot, Timothé Depelchin, Luc Lienhardt and Mathis Lozano for support during sensor installation. We thank staff at the SUEZ Amailloux landfill site for facilitating site access and for on-site support.References
- J. F. B. Mitchell, Rev. Geophys., 1989, 27, 115–139, DOI:10.1029/rg027i001p00115.
- M. Etminan, G. Myhre, E. J. Highwood and K. P. Shine, Geophys. Res. Lett., 2016, 43, 12614–12623, DOI:10.1002/2016gl071930.
- Y. H. Chen and R. G. Prinn, J. Geophys. Res.: Atmos., 2006, 111, D10307, DOI:10.1029/2005jd006058.
- S. Kirschke, P. Bousquet, P. Ciais, M. Saunois, J. G. Canadell, E. J. Dlugokencky, P. Bergamaschi, D. Bergmann, D. R. Blake, L. Bruhwiler, P. Cameron-Smith, S. Castaldi, F. Chevallier, L. Feng, A. Fraser, M. Heimann, E. L. Hodson, S. Houweling, B. Josse, P. J. Fraser, P. B. Krummel, J. F. Lamarque, R. L. Langenfelds, C. le Quere, V. Naik, S. O'Doherty, P. I. Palmer, I. Pison, D. Plummer, B. Poulter, R. G. Prinn, M. Rigby, B. Ringeval, M. Santini, M. Schmidt, D. T. Shindell, I. J. Simpson, R. Spahni, L. P. Steele, S. A. Strode, K. Sudo, S. Szopa, G. R. van der Werf, A. Voulgarakis, M. van Weele, R. F. Weiss, J. E. Williams and G. Zeng, Nat. Geosci., 2013, 6, 813–823, DOI:10.1038/ngeo1955.
- M. Saunois, A. R. Stavert, B. Poulter, P. Bousquet, J. G. Canadell, R. B. Jackson, P. A. Raymond, E. J. Dlugokencky, S. Houweling, P. K. Patra, P. Ciais, V. K. Arora, D. Bastviken, P. Bergamaschi, D. R. Blake, G. Brailsford, L. Bruhwiler, K. M. Carlson, M. Carrol, S. Castaldi, N. Chandra, C. Crevoisier, P. M. Crill, K. Covey, C. L. Curry, G. Etiope, C. Frankenberg, N. Gedney, M. I. Hegglin, L. Höglund-Isaksson, G. Hugelius, M. Ishizawa, A. Ito, G. Janssens-Maenhout, K. M. Jensen, F. Joos, T. Kleinen, P. B. Krummel, R. L. Langenfelds, G. G. Laruelle, L. Liu, T. Machida, S. Maksyutov, K. C. McDonald, J. McNorton, P. A. Miller, J. R. Melton, I. Morino, J. Müller, F. Murguia-Flores, V. Naik, Y. Niwa, S. Noce, S. O'Doherty, R. J. Parker, C. Peng, S. Peng, G. P. Peters, C. Prigent, R. Prinn, M. Ramonet, P. Regnier, W. J. Riley, J. A. Rosentreter, A. Segers, I. J. Simpson, H. Shi, S. J. Smith, L. P. Steele, B. F. Thornton, H. Tian, Y. Tohjima, F. N. Tubiello, A. Tsuruta, N. Viovy, A. Voulgarakis, T. S. Weber, M. van Weele, G. R. van der Werf, R. F. Weiss, D. Worthy, D. Wunch, Y. Yin, Y. Yoshida, W. Zhang, Z. Zhang, Y. Zhao, B. Zheng, Q. Zhu, Q. Zhu and Q. Zhuang, Earth Syst. Sci. Data, 2022, 12, 1561–1623, DOI:10.5194/essd-12-1561-2020.
- E. G. Nisbet, M. R. Manning, E. J. Dlugokencky, R. E. Fisher, D. Lowry, S. E. Michel, C. Lund Myhre, M. Platt, G. Allen, P. Bousquet, R. Brownlow, M. Cain, J. L. France, O. Hermansen, R. Hossaini, A. E. Jones, I. Levin, A. C. Manning, G. Myhre, J. A. Pyle, B. H. Vaughn, N. J. Warwick and J. W. C. White, Global Biogeochem. Cycles, 2019, 33, 318–342, DOI:10.1029/2018gb006009.
- R. B. Jackson, M. Saunois, P. Bousquet, J. G. Canadell, B. Poulter, A. R. Stavert, P. Bergamaschi, Y. Niwa, A. Segers and A. Tsuruta, Environ. Res. Lett., 2020, 15, 071002, DOI:10.1088/1748-9326/ab9ed2.
- J. Bogner and E. Matthews, Global Biogeochem. Cycles, 2003, 17, 1065, DOI:10.1029/2002gb001913.
- C. Scheutz, P. Kjeldsen, J. E. Bogner, A. de Visscher, J. Gebert, H. A. Hilger, M. Huber-Humer and K. Spokas, Waste Manage. Res., 2009, 27, 409–455, DOI:10.1177/0734242X09339325.
- A. L. Ganesan, A. J. Manning, A. Grant, D. Young, D. E. Oram, W. T. Sturges, J. B. Moncrieff and S. O'Doherty, Atmos. Chem. Phys., 2015, 15, 6393–6406, DOI:10.5194/acp-15-6393-2015.
- J. Mønster, P. Kjeldsen and C. Scheutz, Waste Manage., 2019, 87, 835–859, DOI:10.1016/j.wasman.2018.12.047.
- E. Nisbet and R. Weiss, Science, 2010, 328, 1241–1243, DOI:10.1126/science.1189936.
- E. J Dlugokencky, E. G. Nisbet, R. Fisher and D. Lowry, Philos. Trans. R. Soc., A, 2011, 369, 2058–2072, DOI:10.1098/rsta.2010.0341.
- A. J. Turner, C. Frankenberg and E. A. Kort, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2805–2813, DOI:10.1073/pnas.1814297116.
- J. Hodgkinson and R. P. Tatam, Meas. Sci. Technol., 2013, 24, 012004, DOI:10.1088/0957-0233/24/1/012004.
- D. Kohl, J. Phys. D: Appl. Phys., 2001, 34, R125–R149, DOI:10.1088/0022-3727/34/19/201.
- T. Hong, J. T. Culp, K. J. Kim, J. Devkota, C. Sun and P. R. Ohodnicki, Trends Anal. Chem., 2020, 125, 115820, DOI:10.1016/j.trac.2020.115820.
- W. T. Honeycutt, M. T. Ley and N. F. Materer, Sensors, 2019, 19, 3157, DOI:10.3390/s19143157.
- D. Furuta, T. Sayahi, J. Li, B. Wilson, A. A. Presto and J. Li, Atmos. Meas. Tech., 2022, 15, 5117–5128, DOI:10.5194/amt-15-5117-2022.
- N. Barsan, D. Koziej and U. Weimar, Sens. Actuators, B, 2007, 121, 18–35, DOI:10.1016/j.snb.2006.09.047.
- A. Ponzoni, C. Baratto, N. Cattabiani, M. Falasconi, V. Galstyan, E. Nunez-Carmona, F. Rigoni, V. Sberveglieri, G. Zambotti and D. Zappa, Sensors, 2017, 17, 714, DOI:10.3390/s17040714.
- D. Kohl, Sens. Actuators, 1989, 1, 71–113, DOI:10.1016/0250-6874(89)87026-x.
- D. Kohl, Sens. Actuators, B, 1990, 1, 158–165, DOI:10.1016/0925-4005(90)80193-4.
- C. Wang, L. Yin, L. Zhang, D. Xiang and R. Gao, Sensors, 2010, 10, 2088–2106, DOI:10.3390/s100302088.
- H. Suto and G. Inoue, J. Atmos. Ocean. Technol., 2010, 27, 1175–1184, DOI:10.1175/2010jtecha1400.1.
- A. Das, V. Bonu, A. K. Prasad, D. Panda, S. Dharaa and A. K. Tyagia, J. Mater. Chem. C, 2014, 2, 164–171, 10.1039/c3tc31728e.
- M. Kooti, S. Keshtkar, M. Askarieh and A. Rashidibi, Sens. Actuators, B, 2019, 281, 96–106, DOI:10.1016/j.snb.2018.10.032.
- G. Ferri, C. Di Carlo, V. Stornelli, A. De Marcellis, A. Flammini, A. Depari and N. Jand, Sens. Actuators, B, 2009, 143, 218–225, DOI:10.1016/j.snb.2009.09.002.
- R. Rivera Martinez, D. Santaren, O. Laurent, F. Cropley, C. Mallet, M. Ramonet, C. Caldow, L. Rivier, G. Broquet, C. Bouchet, C. Juery and P. Ciais, Atmosphere, 2021, 12, 107, DOI:10.3390/atmos12010107.
- W. Eugster and G. W. Kling, Atmos. Meas. Tech., 2012, 5, 1925–1934, DOI:10.5194/amt-5-1925-2012.
- M. van den Bossche, N. T. Rose and S. F. J. De Wekker, Sens. Actuators, B, 2017, 238, 501–509, DOI:10.1016/j.snb.2016.07.092.
- A. Collier-Oxandale, J. G. Casey, R. Piedrahita, J. Ortega, H. Halliday, J. Johnston and M. P. Hannigan, Atmos. Meas. Tech., 2018, 11, 3569–3594, DOI:10.5194/amt-11-3569-2018.
- W. Eugster, J. Laundre, J. Eugster and G. W. Kling, Atmos. Meas. Tech., 2020, 13, 2681–2695, DOI:10.5194/amt-13-2681-2020.
- A. Shah, O. Laurent, L. Lienhardt, G. Broquet, R. Rivera Martinez, E. Allegrini and P. Ciais, Atmos. Meas. Tech., 2023, 16, 3391–3419, DOI:10.5194/amt-16-3391-2023.
- tgs2600_product information(fusa)_rev05.pdf, https://www.figarosensor.com/product/docs/tgs2600_productinformation%28fusa%29_rev05.pdf, accessed February 2023.
- L. Furst, M. Feliciano, L. Frare and G. Igrejas, Sensors, 2021, 21, 7456, DOI:10.3390/s21227456.
- S. N. Riddick, D. L. M. M. Celia, G. Allen, J. Pitt, M. Kang and J. C. Riddick, Atmos. Environ., 2020, 230, 117450, DOI:10.1016/j.atmosenv.2020.117440.
- J. J. Y. Lin, C. Buehler, A. Datta, D. R. Gentner, K. Koehler and M. L. Zamora, Environ. Sci.: Atmos., 2023, 3, 683–694, 10.1039/d2ea00100d.
- tgs2611-e00_product_information(fusa)_rev02.pdf, https://www.figarosensor.com/product/docs/tgs2611-e00_product_information%28fusa%29_rev02.pdf, accessed February 2023.
- tgs2611-c00_product information(fusa)rev01.pdf, https://www.figarosensor.com/product/docs/tgs2611-c00_productinformation%28fusa%29rev01.pdf, accessed February 2023.
- D. Bastviken, J. Nygren, J. Schenk, R. Parellada Massana and N. T. Duc, Biogeosciences, 2020, 17, 3659–3667, DOI:10.5194/bg-17-3659-2020.
- Y. Cho, K. M. Smits, S. N. Riddick and D. J. Zimmerle, Sens. Actuators, B, 2022, 355, 131276, DOI:10.1016/j.snb.2021.131276.
- A. Butturini and J. Fonollosa, Limnol. Oceanogr., 2022, 20, 710–720, DOI:10.1002/lom3.10515.
- J. Glöckler, C. Jaeschke, E. Tütüncü, V. Kokoric, Y. Kocaöz and B. Mizaikoff, Anal. Bioanal. Chem., 2020, 412, 4575–4584, DOI:10.1007/s00216-020-02705-6.
- R. A. Rivera Martinez, D. Santaren, O. Laurent, G. Broquet, F. Cropley, C. Mallet, M. Ramonet, A. Shah, L. Rivier, C. Bouchet, C. Juery, O. Duclaux and P. Ciais, Atmos. Meas. Tech., 2023, 16, 2209–2235, DOI:10.5194/amt-16-2209-2023.
- tgs2602_product information(fusa)_rev06.pdf, https://www.figarosensor.com/product/docs/tgs2602_productinformation%28fusa%29_rev06.pdf, accessed February 2023.
- A. M. Collier-Oxandale, J. Thorson, H. Halliday, J. Milford and M. Hannigan, Atmos. Meas. Tech., 2019, 12, 1441–1460, DOI:10.5194/amt-12-1441-2019.
- J. G. Casey, A. Collier-Oxandale and M. Hannigan, Sens. Actuators, B, 2019, 283, 504–514, DOI:10.1016/j.snb.2018.12.049.
- S. A. Mane, D. Y. Nadargi, J. D. Nadargi, O. M. Aldossary, M. S. Tamboli and V. P. Dhulap, Coatings, 2020, 10, 1148, DOI:10.3390/coatings10121148.
- E. M. Taguem, L. Mennicken and A. C. Romain, Sens. Actuators, B, 2021, 334, 129590, DOI:10.1016/j.snb.2021.129590.
- Z. Duan, C. Scheutz and P. Kjeldsen, Waste Manage., 2020, 119, 39–62, DOI:10.1016/j.wasman.2020.09.015.2020.
- D. R. Caulton, Q. Li, E. Bou-Zeid, J. P. Fitts, L. M. Golston, D. Pan, J. Lu, H. M. Lane, B. Buchholz, X. Guo, J. McSpiritt, L. Wendt and M. A. Zondlo, Atmos. Chem. Phys., 2018, 18, 15145–15168, DOI:10.5194/acp-18-15145-2018.
- A. Shah, J. R. Pitt, K. Kabbabe and G. Allen, Sensors, 2019, 19, 4705, DOI:10.3390/s19214705.
- R. A. Rivera Martinez, P. Kumar, O. Laurent, G. Broquet, C. Caldow, F. Cropley, D. Santaren, A. Shah, C. Mallet, M. Ramonet, L. Rivier, C. Juery, O. Duclaux, C. Bouchet, E. Allegrini, H. Utard, P. Ciais, Atmos. Meas. Tech. Discuss., DOI:10.5194/amt-2023-52, in review..
- C. J. Jørgensen, J. Mønster, K. Fuglsang and J. R. Christiansen, Atmos. Meas. Tech., 2020, 13, 3319–3328, DOI:10.5194/amt-13-3319-2020.
- E. J. Dlugokencky, L. P. Steele, P. M. Lang and K. A. Masarie, J. Geophys. Res., 1994, 99, 17021–17043, DOI:10.1029/94jd01245.
- Global Monitoring Laboratory - Carbon Cycle Greenhouse Gases, https://esrl.noaa.gov/gmd/ccgg/trends_ch4/, accessed March 2023.
- J. Kim, A. A. Shusterman, K. J. Lieschke, C. Newman and R. C. Cohen, Atmos. Meas. Tech., 2018, 11, 1937–1946, DOI:10.5194/amt-11-1937-2018.
- C. Yver-Kwok, C. Philippon, P. Bergamaschi, T. Biermann, F. Calzolari, H. Chen, S. Conil, P. Cristofanelli, M. Delmotte, J. Hatakka, M. Heliasz, O. Hermansen, K. Komínková, D. Kubistin, N. Kumps, O. Laurent, T. Laurila, I. Lehner, J. Levula, M. Lindauer, M. Lopez, I. Mammarella, G. Manca, P. Marklund, J. M. Metzger, M. Mölder, S. M. Platt, M. Ramonet, L. Rivier, B. Scheeren, M. K. Sha, P. Smith, M. Steinbacher, G. Vítková and S. Wyss, Atmos. Meas. Tech., 2021, 14, 89–116, DOI:10.5194/amt-14-89-2021.
- G2401 Analyzer Datasheet | Picarro, https://www.picarro.com/support/library/documents/g2401_analyzer_datasheet, accessed February 2024.
- R: The R Project for Statistical Computing, https://www.r-project.org/, accessed 8 August 2023.
- Trace Gas Analyzers | LI-COR Environmental, https://www.licor.com/env/products/trace_gas/LI-7810, accessed March 2023.
- F. W. Murray, J. Appl. Meteorol. Climatol., 1967, 6, 203–204, DOI:10.1175/1520-0450(1967)006<0203:otcosv>2.0.co;2.
- J. Bogner, K. Spokas, E. Burton, R. Swweney and V. Corona, Chemosphere, 1995, 31, 4119–4130, DOI:10.1016/0045-6535(95)80012-a.
- R. Pipatti and M. Wihersaari, Mitig. Adapt. Strateg. Glob. Change, 1997, 2, 337–358, DOI:10.1007/bf02437050.
- C. Scheutz, A. M. Fredenslund, J. Nedenskov, J. Samuelsson and P. Kjeldsen, Waste Manage., 2011, 31, 946–955, DOI:10.1016/j.wasman.2010.10.021.
- P. J. Young and A. Parker, Waste Manage. Res., 1983, 1, 213–226, DOI:10.1016/0734-242x(83)90004-6.
- C. Scheutz, J. Bogner, J. P. Chanton, D. Blake, M. Morcet, C. Aran and P. Kjeldsen, Waste Manage., 2008, 28, 1982–1908, DOI:10.1016/j.wasman.2007.09.010.
- D. C. Manheim, N. Yeşiller and J. L. Hanson, J. Indian Inst. Sci., 2021, 101, 625–657, DOI:10.1007/s41745-021-00234-4.
- S. Copping, C. Quinn and R. Greqory, Review and Investigation of Deep-Seated Fires within Landfill Sites, Bristol, United Kingdom, Environment Agency, 2007, ISBN: 978-1-84432-681-5 Search PubMed.
- AdilLSCE/Figaro, https://github.com/AdilLSCE/Figaro/, accessed September 2023.
- Figaro Taguchi Gas Sensor SUEZ Amailloux Data 2022-2023, https://zenodo.org/record/8350082, accessed September 2023.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ea00138e |
| This journal is © The Royal Society of Chemistry 2024 |