Open Access Article
Open Access ArticleWavelength-resolved quantum yields for vanillin photochemistry: self-reaction and ionic-strength implications for wildfire brown carbon lifetime†
Greg T.
Drozd
 *a,
Tate
Weltzin
a,
Samuel
Skiffington
a,
Dong
Lee
a,
Rashid
Valiev
b,
Theo
Kurtén
b,
Lindsey R.
Madison
a,
Yiheng
He
a and
Lydia
Gargano
a
*a,
Tate
Weltzin
a,
Samuel
Skiffington
a,
Dong
Lee
a,
Rashid
Valiev
b,
Theo
Kurtén
b,
Lindsey R.
Madison
a,
Yiheng
He
a and
Lydia
Gargano
a
aDepartment of Chemistry, Colby College, Waterville, Maine, USA. E-mail: gtdrozd@colby.edu
bDepartment of Chemistry, University of Helsinki, Helsinki 00014, Finland
First published on 28th February 2024
Abstract
The light absorbing component of organic aerosols, brown carbon (BrC), directly affects climate and can play a role in the oxidative aging of organic aerosols. Recent estimates suggest that globally BrC may have a warming potential that is approximately 20% that of black carbon, and photochemistry from BrC compounds can increase or transform aqueous SOA. Photobleaching of BrC is estimated to occur with a timescale of hours to days, a range that complicates estimates of the effects of BrC on climate and aerosol chemistry. The chemical environment (e.g. pH, ionic strength, and non-BrC organic content) of aqueous aerosols can also affect the reactivity of BrC, potentially altering absorption spectra and reactions of excited states formed upon irradiation. A range of solar illumination sources have been used in studying the photochemistry of BrC compounds, making direct comparisons between results difficult. Higher energy, single wavelength studies (e.g. 308 nm) show much larger quantum yields than broadband studies, indicating wavelength dependent quantum yields for a wide range of atmospherically relevant substituted aromatics. In this work we investigate the wavelength dependence of the quantum yield for loss of a prototypical BrC compound found in wildfire emissions, vanillin, using several narrow band UV-LEDs that span the 295–400 nm range. These wavelength dependent quantum yields will allow a more direct comparison between photochemical experiments with laboratory irradiation sources and actual actinic fluxes. Vanillin photochemical loss rates are concentration-dependent due to direct reaction between triplet excited state and ground state vanillin molecules. The quantum yield for photochemical loss of vanillin can be approximated by a Gaussian decay from 295 nm to ∼365 nm. This function is used to directly calculate the solar zenith angle (SZA) dependence for photochemical loss. Computational results show the presence of two π → π* transitions responsible for the observed UV-vis spectrum and that the rate of intersystem crossing has a wavelength dependence remarkably similar to that of the quantum yield for loss. A strong kinetic salt effect is observed, showing a doubling of the loss rate at high ionic strength.
Environmental significanceSolar radiation transforms organic materials in atmospheric aerosols, affecting how strongly aerosols absorb light and how quickly they oxidize. We studied the photochemistry of vanillin, an oxidized aromatic in wildfire emissions, using UV LEDs. These measurements can be directly generalized to the solar spectrum under any conditions (time/day/location). Vanillin photochemistry is faster as salt concentrations approach those of atmospheric aerosols. Generally, previous measurements require extrapolation to varying solar conditions and are limited to low salt concentrations. Our measurements reveal the wavelength dependence of photochemical efficiency (quantum yield), and calculations indicate that its origin is changing rates of electron processes after excitation by UV light (intersystem crossing). We demonstrate the importance of wavelength resolved measurements under conditions relevant to atmospheric aerosols. |
1 Introduction
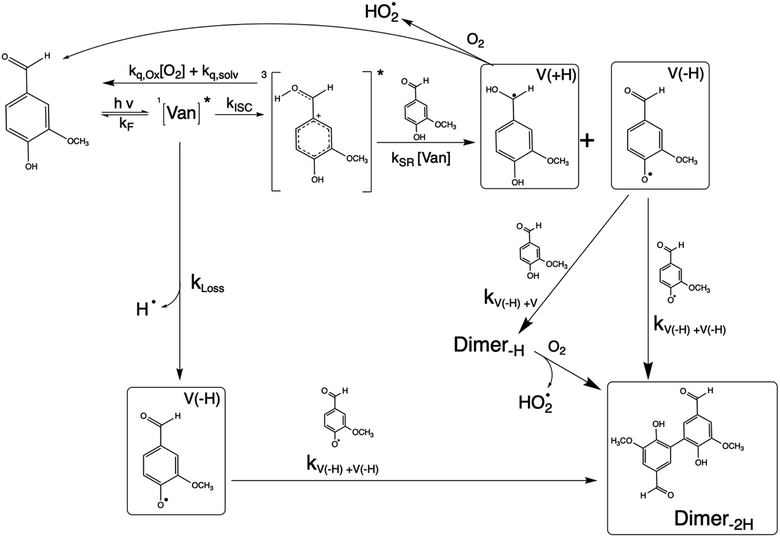
Phenolic carbonyls (PhC) are an important class of reactive compounds emitted from biomass burning, such as forest fires and domestic heating.1–5 In atmospheric aerosols and fog water, PhC can play key roles in processes that form both secondary organic aerosol (SOA) and light-absorbing organic compounds categorized as brown carbon (BrC).1,6–12 In addition to reaction with common atmospheric oxidants such as hydroxyl radicals and ozone, atmospheric PhC may act as photosensitizers, enabling unique oxidation pathways for organic aerosol components driven by exposure to solar radiation.9,13–16Atmospheric PhC span a wide range of structures, including oxidized derivatives of guaiacol and syringol, such as vanillin, syringaldehyde, and cinnamic acid.2 This diversity in PhC structures leads to complex properties and behaviors yet to be fully characterized.9,14,17,18PhC have moderate to strong absorption bands in the most photochemically active range of the solar spectrum (300–400 nm).4,13,14 Upon photon absorption and intersystem crossing in this range, PhC readily form triplet excited states that drive oxidation processes through a complex mechanism.9,14,19 The presence of multiple functional groups makes the photochemistry of oxidized PhC unique. In the case of vanillin, the carbonyl group along with the hydroxy and methoxy ring substituents enhance absorption in the photochemically active solar region, while the phenolic hydroxyl also serves as an efficient hydrogen atom donor for photo-redox chemistry. Triplet excited state PhC may thus abstract a hydrogen from ground state PhC through self-reaction, which further facilitates formation of dimeric or oligomeric PhC species, as was recently demonstrated for vanillin.9,18,20
The rate constant for photochemical loss, j, for an optically thin system and a simple reaction (e.g. isomerization) is
| j = ∫Φ(λ) × I0(λ) × ε(λ) × ldλ | (1) |
 , ε the base-e molar absorptivity (M−1 cm−1), and l pathlength (cm). While ε(λ) and I0(λ) are readily determined for any species and light source, the wavelength dependence of the quantum yield for loss of PhC species due to photochemical loss, Φloss(λ), is generally not known.15 Calculation of the photolysis rate constant using the explicit wavelength dependence avoids errors in extrapolating from measurements made at a single SZA. There is significant variation (20–100%) in the relative intensity of I0,sun(λ) between 0–60° SZA in the range 300–340 nm (Fig. S1†). The variation in the solar spectrum in this region may cause inaccuracies if only changes in total photon flux are used to predict the reaction rate as a function of solar zenith angle (SZA).
, ε the base-e molar absorptivity (M−1 cm−1), and l pathlength (cm). While ε(λ) and I0(λ) are readily determined for any species and light source, the wavelength dependence of the quantum yield for loss of PhC species due to photochemical loss, Φloss(λ), is generally not known.15 Calculation of the photolysis rate constant using the explicit wavelength dependence avoids errors in extrapolating from measurements made at a single SZA. There is significant variation (20–100%) in the relative intensity of I0,sun(λ) between 0–60° SZA in the range 300–340 nm (Fig. S1†). The variation in the solar spectrum in this region may cause inaccuracies if only changes in total photon flux are used to predict the reaction rate as a function of solar zenith angle (SZA).
The chemical environment in atmospheric aerosols introduces complex effects in terms of ionic strength, the range of hydrogen-atom donors/acceptors, and physical properties (e.g. viscosity).21–27 Dissolved oxygen in aqueous environments, whether fog or aerosols, provides multiple pathways to regenerate ground state PhC, while also forming reactive species (O2−/HO2/organic radicals) that may propagate oxidation of other species as well.14 Acid-base equilibria of the excited triplet states complicate the photochemistry of PhC, because excited state pKa values may differ significantly from those of the ground state.12,14,28 All these properties can affect PhC photochemistry and the rate of loss in atmospheric particles.
In this work, the photochemical loss of vanillin (Van) was studied as a function of excitation wavelength and concentration to determine Φ(λ,[Van]). Ionic strength was varied over a wide range (0–4 M), approaching aqueous aerosol conditions. Dissolved oxygen was also varied to constrain the effects of oxygen derived radicals and excited state quenching on photochemical loss of vanillin. The clear-sky variation in photochemical lifetime for vanillin was determined throughout the annual solar cycle, highlighting the importance of determining Φ(λ,[Van]).
2 Methods
2.1 Materials
All reagents including (vanillin; 99%, Na2SO4; 99% anhydrous, NaCl; 99% anhydrous, and HCl) were purchased from Sigma-Aldrich and used without further purification. HPLC solvents were prepared with 18 MΩ deionized water, acetonitrile (HPLC-Plus >99.9%), and formic acid (>95%). pH adjustments were made with HCl (1 N, Titripur).2.2 Illumination source characterization
7 UV-LEDs (Violumas) with nominal wavelengths of 295, 310, 325, 340, 365, 375, and 385 nm were used to illuminate aqueous vanillin samples. The LEDs are connected to a Tekpower TP1803D variable DC power supply with current controlled under 1 A. The LED spectral profiles are shown in Fig. 1, along with the solar spectrum at 0° and 60° SZA, and the base-e molar absorptivity of vanillin. The photon flux of each LED was determined using 2-nitrobenzaldehyde (NBA) as an actinometer which has a known and constant quantum yield (0.43) between 300–400 nm. The conversion of NBA to 2-nitrosobenzoic acid was monitored with an Agilent Cary 60 UV-vis Spectrometer over a period of 3 lifetimes (∼5% NBA remaining). Typical volume-averaged fluxes for LED varied between 3–9 × 1015 photon per cm3 sec. While photon fluxes were greater than the corresponding maximum solar flux at 0° SZA, the low concentrations of vanillin studied (≤25 μM) will preclude triplet–triplet interactions, due to the relatively short lifetime (<20 μs) of excited state vanillin.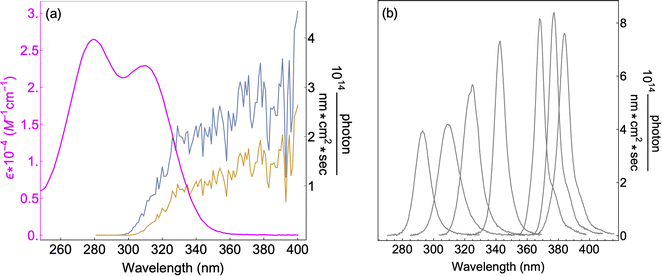 | ||
| Fig. 1 (a) Base-e molar absorptivity, ε, of vanillin (magenta), and solar irradiance at 0° (blue) and 60° (yellow) SZA. Solar spectrum data were obtained from the NCAR TUV Model (ozone: 300 DU, albedo: 0.1).16 (b) LED irradiance source profiles for nominal wavelengths of 295 nm, 310 nm, 325 nm, 340 nm, 365 nm, 375 nm, 385 nm. LED peak irradiance varied by experiment in the range of 3–9 × 1014 photon per nm cm2 sec. | ||
2.3 Photolysis experiments
Vanillin solution was added to a quartz vial (Technical Glass Products, 15 mm dia.) with UV LED illumination from below. To minimize internal screening, solution absorbance was kept below 0.2. The path length in the reaction vials was 0.88 cm per 1 mL of solution. The sample volume thus varied by experiment, depending on the initial [Van]. 1 mL was used for 5–25 μM, and 3 mL was used for 2 μM. For most experiments, fresh solution was used for each time point, rather than taking aliquots. For slower experiments (e.g. 2 μM) aliquots were removed for analysis, never reducing sample volume by more than a total of 10%. Evaporation was never observed, and for longer experiments, the vials were tightly sealed with a Teflon-lined screw cap. The laboratory temperature was 23 ± 2 °C. Internal screening, which reduces excitation illumination at greater solution depths relative to the illumination source, was calculated as the ratio of the actual light absorption at the top of the solution to the optically thin approximation (Section S2†). Screening factors ranged from 0.99 (3 mL sample, 2 μM, 340 nm) to 0.79 (1 mL sample, 25 μM, 295 nm).All samples were adjusted to pH = 2 with hydrochloric acid, as atmospheric particle pH is generally observed to be between 0 and 4, with an approximate range recently considered to span −1 to 5.29–32 Cloud or fog droplets generally have higher pH, approximately 2–7.30 At pH = 2, the excited triplet state will be fully protonated, forming 3*HVan+.14,17 Several tests with sulfuric acid did not change results compared to hydrochloric acid, showing no specific acid or anion effects.
For experiments with reduced dissolved oxygen concentration, 30 mL of sample was deoxygenated by bubbling with either argon or nitrogen for at least 30 minutes. Dissolved oxygen was monitored with a NeoFox fluorescence lifetime sensor with the FOSPOR oxygen probe (Ocean Insight). Initial oxygen levels for deoxygenated samples were less than 10% that of air-saturated levels. These solutions were capped during irradiation.
2.4 HPLC analysis
Eluents were ultrapure water (eluent A), and acetonitrile (eluent B) both with 0.1% formic acid. The solvent flow rate was 0.5 mL min−1. The mobile phase gradient was: starting with 0% B, isocratic for 2 min, followed by a gradient to 100% B in 5 minutes, a hold at 100% B for 1 minute, and a gradient to 0% B in 1 minute followed by a 3 minute hold at 0% B. The HPLC system was connected to the ToF-MS via a diode array detector (DAD) equipped with a 500 nL flow cell, 10 mm pathlength, using a reference wavelength of 500 nm. The electrospray ion source of the MS was operated using the following setup: nebulizer pressure 2400 mbar, drying gas flow 8 l min−1, dry gas temperature 325 °C, and spray voltage 3500 V.2.5 Kinetic analysis
The quantum yield for photochemical loss, Φloss, is defined as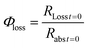 | (2) |
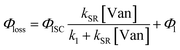 | (3) |
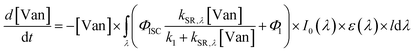 | (4) |
2.6 Computational and theoretical methods
The spin–orbit coupling matrix elements (SOCME) of the Pauli–Breit operator between the considered electronic states with different multiplicities were calculated using MOLSOC software.47 The nonadiabatic coupling matrix elements (NACME) and the oscillator strengths (f) between S0, S1, S2 and S3 were calculated at the TDDFT level of theory described above.48 All DFT calculations were done using Gaussian 16 (ref. 41) on the supercomputer resources at the CSC IT Center for Science in Espoo, Finland.
The rate constants for fluorescence (kr), intersystem crossing (kISC) and internal conversion (kIC) between the considered electronic states were calculated using time independent theory and the code described in the details of recent publications.49–52 This calculation takes NACME, SOCME, f, Hessians of initial and final electronic states and the energy gaps between the initial and final electronic states as the input parameters. One limitation of this model is that only the lowest vibronic state is considered for the initial electronic state. In this study, we address this limitation by considering the kISC calculation within a TD theory framework. We limit our analysis to kISC, as the ISC process plays the main role in the present work. A detailed description of the excited state dynamic calculations is given in Section S1.†
3 Results and discussion
3.1 Absorption spectrum and orbital transitions
The absorption spectrum of vanillin (Fig. 1) shows two strong absorption bands centered at 277 nm and 311 nm. We define the corresponding states as the S2 and S3 states, respectively (Fig. S3†). These excitation transitions are both characterized as π → π*, and the computed vertical excitation energies (269 nm and 303 nm) show good agreement with experiment. Our labeling scheme includes a dark state of lower energy with n → π* character as the S1 state. Natural transition orbitals (NTOs) were computed from the coefficients describing the particle–hole pair contributions to the excitations for the first two lowest allowed singlet transitions, both with oscillator strengths of approximately 0.2 (Fig. 2). NTOs convey how the electron density changes during an electronic transition, showing the aggregate electron–hole pairs that constitute a transition.42 The S2 excitation involves significant incorporation of both the methoxy and the hydroxy substituents in the originating NTO (Fig. 2a), while the S3 excitation is mainly influenced by the hydroxy substituent.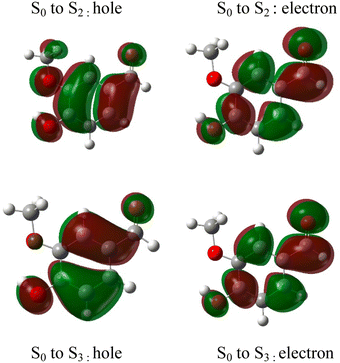 | ||
| Fig. 2 Natural transition orbitals (NTO) describing the π → π*excitations for the S0 to S2 and S0 to S3 transitions. | ||
3.2 Mechanism and product formation
The reaction between an excited triplet species, such as substituted aromatic carbonyls and phenols has been well characterized, showing catalytic production of hydrogen peroxide with loss of phenol in the presence of oxygen.14 Vanillin, and phenolic carbonyls in general, have both a carbonyl and a hydroxyl group, meaning the triplet excited state is reactive towards ground state vanillin. Recently the formation of a vanillin dimer and larger oligomers has been observed at millimolar levels of vanillin.18 Our HPLC-DAD results indicated the formation of only one product with strong UV absorption, and HR-ToF data identified that product to weigh 2 amu less than twice the molecular mass of vanillin (2 × MW − 2) (Fig. S4†). This indicates that the product formed is a dimer of vanillin, in agreement with previous experiments.9,18 We further verify that the dimer is the dominant, or only, product at these levels of photo-conversion through observation of two isosbestic points during irradiation (Fig. S5†). Notably, dimer formation was not reported for irradiation of the ketone analogue of vanillin, acetovanillone, at pH ∼ 6 within a similar wavelength range and much greater total photon fluxes.19
Scheme 1 shows a probable mechanism for dimer formation from vanillin, or PhC in general. Ground state vanillin is excited to a singlet state, with efficient ISC to the triplet excited state. Fluorescence (kF) and quenching by oxygen (kq,Ox) or solvent (kq,solv) may return the triplet state to the ground state. At pH = 2 the excited triplet state will be fully protonated, forming 3*HVan+.17 Bimolecular reaction between protonated triplet and ground state vanillin forms 2 radicals, a phenoxy and a ketyl, that differ in the number of hydrogens relative to vanillin, +1 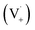 and −1
and −1 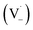 . At this point, multiple pathways can lead to dimer formation.
. At this point, multiple pathways can lead to dimer formation. 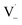 can add to
can add to 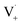 within its solvent cage, followed by the abstraction of 2 hydrogens.
within its solvent cage, followed by the abstraction of 2 hydrogens. 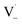 may also add to ground state vanillin, due to its relatively high concentration, followed by a single hydrogen abstraction. Combination of two
may also add to ground state vanillin, due to its relatively high concentration, followed by a single hydrogen abstraction. Combination of two 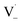 directly yields the dimer, likely the main route to dimer formation.9,20 In the presence of dissolved oxygen, hydrogen abstraction by O2 from
directly yields the dimer, likely the main route to dimer formation.9,20 In the presence of dissolved oxygen, hydrogen abstraction by O2 from 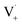 will regenerate vanillin, forming
will regenerate vanillin, forming 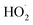 at low pH and reducing the observed quantum yield. Direct photolytic loss of a hydrogen, from either the singlet or triplet state (shown only for the singlet state in Scheme 1), has been suggested by Vione et al.9
at low pH and reducing the observed quantum yield. Direct photolytic loss of a hydrogen, from either the singlet or triplet state (shown only for the singlet state in Scheme 1), has been suggested by Vione et al.9
3.3 Concentration dependence of ΦLoss
The observed dependences of ΦLoss with varying initial vanillin concentration, [Van]init, for 295, 310, 325, and 340 nm LED irradiation are shown in Fig. 3. Loss was not observed for λ ≥ 365 nm. ΦLoss increases linearly with [Van]. This is consistent with the expression in eqn (3) for ΦLoss when k1 ≫ kSR[Van]. The expression for ΦLoss accounting for these factors is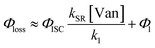 | (5) |
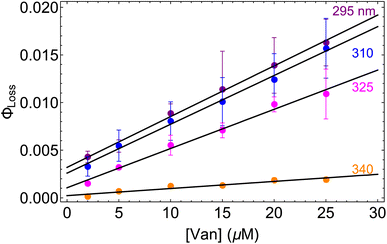 | ||
| Fig. 3 Φ loss as a function of initial [Van] at pH = 2 for 295 (purple), 310 (blue), 325 (magenta), and 340 nm (orange) irradiation. | ||
Eqn (5) is consistent with observations because ΦLoss ≪ 1. The presence of a y-intercept suggests that photochemical loss may proceed by a mechanism not involving ground state vanillin, such as direct photolytic loss of a hydrogen to form a phenoxy radical.9 Because self-reaction forms the same phenoxy radical as hydrogen loss, both pathways lead to the same final dimer product, consistent with our observation of an isosbestic point in UV spectra during irradiation. Self-reaction is efficient enough to be significant at all concentration ranges of atmospheric interest and consideration of PhC concentration will be important in determining photochemical loss of atmospheric phenolic carbonyls.2,9,10,17 Variation in the slopes in Fig. 3 indicates that the rate constants for intersystem crossing and/or self-reaction are a function of excitation wavelength. The highest energy excitation at 295 nm (purple) shows the greatest slope and the lowest energy excitation at 340 nm (orange) shows the smallest slope.
Fig. S6† compares ΦLoss as a function of [Van]init with 310 nm irradiation in air-saturated solution and when oxygenation is reduced to <10% of air saturation by bubbling with N2 or Ar. A linear trend is still observed, but ΦLoss values are significantly higher, and the apparent intercept is much smaller. These differences arise from the multiple steps affected by oxygen in the loss of vanillin. First, at lower [O2] the yield is expected to increase as quenching of Van3* is reduced. The greater lifetime of Van3* without oxygen increases its likelihood of reacting with a ground state vanillin and proceeding towards the product. At lower [O2] reduced regeneration of ground state vanillin via should also increase ΦLoss. Effects of other radicals formed involving O2, such as
should also increase ΦLoss. Effects of other radicals formed involving O2, such as  , will also be reduced at lower [O2], consistent with a smaller intercept.
, will also be reduced at lower [O2], consistent with a smaller intercept.
The values of (ΦISC × kSR) and Φ1 can be estimated using recent measurements by Felber et al. for the rates of triplet quenching of vanillin by the solvent (ksolv = 7.5 × 104 s−1) and oxygen kO2 = (2.7 × 109 M−1 s−1) at pH = 5.12 For an oxygen concentration of 300 μM in air-saturated water, we estimate k1 in eqn (5) to be 8.84 × 105 s−1. The values for (ΦISC × kSR) and Φ1 are shown in Table 1. (ΦISC × kSR) decreases at lower excitation energies, ranging from 0.7–4.7 × 108 M−1 s−1. Flash photolysis results from Vione et al. at a much greater [Van] (>1 mM) and higher pH (unadjusted) indicate a similar value of 4 × 108 M−1 s−1.8
| 295 nm | 310 nm | 325 nm | 340 nm | |
|---|---|---|---|---|
| Φ 1 × 103 | 3.2 ± 0.2 | 2.6 ± 0.3 | 1.1 ± 0.3 | 0.2 ± 0.2 |
| (ΦISC × kSR) × 10−8 (M−1 s−1) | 4.7 ± 0.1 | 4.5 ± 0.2 | 3.6 ± 0.2 | 0.7 ± 0.1 |
3.4 Wavelength and solar zenith angle dependence of ΦLoss
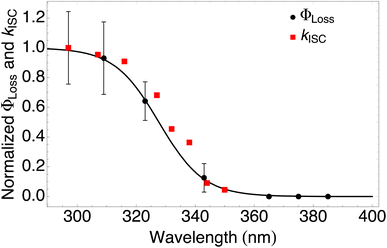 | ||
| Fig. 4 Measured ΦLoss as a function of wavelength at pH = 2 (black circles) and calculated kISC (red squares). All values are normalized to the maximum value which occurs at ∼295 nm for the wavelength range studied. The black curve is a fit to the measurements using eqn (6) with λm = 328 nm and w = 7.6 nm. | ||
The sigmoidal profile for ΦLoss can be modeled using the following function.53
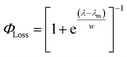 | (6) |
The fitting parameters for the curve shown in Fig. 4 were determined to be λm = 328 nm and w = 7.6 nm. Wavelength-resolved quantum yield measurements for analogous carbonyl compounds in solution phase are not available, but a comparison to the gas phase photolysis of the non-aromatic acetaldehyde suggests possible sources of structure and solvent effects. For vanillin, λm is slightly red-shifted by 8 nm relative to gas-phase acetaldehyde. This can be largely attributed to overall stabilization by an aromatic moiety and the difference in photochemical mechanism. Acetaldehyde undergoes bond scission in the gas phase, while for vanillin and other PhC a lower energy hydrogen abstraction process is dominant.9,20,54,55 The width parameter, w, of ΦLoss(λ) for vanillin is approximately twice that of acetaldehyde in the gas phase.56 For gas phase photochemical loss this width may be largely attributed to persistence of non-thermal conditions on short timescales leading to an energy dependence for open reaction channels,53 but in an aqueous system excited vanillin will be rapidly thermalized. The width in the fall-off for ΦLoss(λ) is likely due to the energy dependence of ΦISC, as discussed in Section 3.4.2. These differences between gas and solution phase photochemical loss highlight the need for Φ(λ) in the solution phase for a wide range of atmospherically relevant compounds.
According to our measurements, the yield of triplet-state products increases as the excitation wavelength decreases from 380 nm to 290 nm. The energy dependent ISC rate, kIsC(S2 → T2) derived above displays a similar behavior. Decreasing the excitation wavelength leads to an increase in the initial vibrational energy of the S2 state. This in turn leads to an increase in the density of final vibronic states.57 Because kISC depends on two factors: the spin orbit coupling matrix element, <Ψ(Si)|ĤSO|Ψ(Tj)>, and the density of final states, kISC(S2 → T2) increases as well. Our calculation of the dependence of kISC(S2 → T2) on the excitation energy is shown in Fig. 4. The theoretical curve matches the experimental results very well, in the sense that the computed rate coefficient, just like the experimental yield, increases by about a factor of 5 when the wavelength decreases from 340 to 300 nm. Quantitatively explaining the experimental results would require a competitive loss process for singlet excited vanillin, with a pseudo-unimolecular rate coefficient on the order of 1011 s−1 order to explain why excitation at longer wavelengths does not result in loss of vanillin.
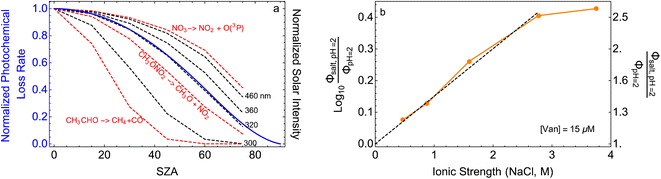 | ||
Fig. 5 (a) Solar zenith angle (SZA) dependence for j1 μM normalized to j(1 μM, 0°) (blue), the normalized intensity of several wavelengths of solar radiation (black, dashed), and three common gas-phase photochemical reactions (red, dashed). Solar spectra and photolysis rate data were obtained from the NCAR TUV Model.16 (b) Effect of ionic strength on the photochemical loss of 10 μM vanillin. The dashed line shows a linear fit to 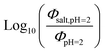 to derive the kinetic salting coefficient (b = 0.15 M−1). to derive the kinetic salting coefficient (b = 0.15 M−1). | ||
3.5 Ionic strength effects on ΦLoss
Aqueous aerosols in the atmosphere may have very high ionic strength, with supersaturated concentrations of inorganic as well as organic components that are greater than 6 M.25,58 Regarding vanillin photochemistry, ionic strength may affect the bimolecular reaction of 3*HVan+ + Van by differentially changing the thermodynamic activities of the reactants and the transition state. The photo-induced basicity of Van3* might also be affected by ionic strength and change the observed rate of reaction, because its protonated and unprotonated forms have different reaction rates.14,17 Ionic strength effects are parameterized empirically by the kinetic salting coefficient, and generally, reaction rates increase with ionic strength, even when one reactant is uncharged.58–60 For species of atmospheric relevance, experimental studies probing specific effects of ionic strength on photochemical mechanisms are uncommon, and they generally do not go to levels high enough to represent atmospheric aerosols.10,14,17,61Ionic strength has a significant effect on the rate of photochemical loss of vanillin, more than doubling its rate of loss at ionic strengths approaching that of atmospheric aerosols. The results of ΦLoss measurements with varying ionic strength are shown in Fig. 5b. Ionic strength was adjusted using NaCl, prepared at concentrations between 0.5–6 M. At concentrations this high, an effective ionic strength, accounting for ion pairing, was calculated using the expression:
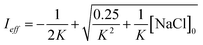 | (7) |
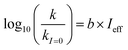 | (8) |
3.6 Atmospheric lifetime
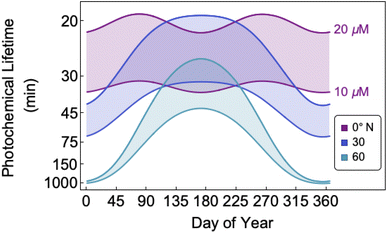
The bimolecular nature of vanillin's photochemical loss makes consideration of the lifetime complex. While an e-folding lifetime can be determined, it depends on the initial concentration. After reaching the e-folding lifetime, the approach to complete loss is much slower for bimolecular reactions than first order reactions. For brown carbon species, this will lead to increased integrated light absorption. Fig. 6 shows the range of photochemical lifetimes for vanillin with varying latitudes throughout the course of a year. Lifetimes are depicted as bands showing the range of lifetimes for 10–20 μM, and the y-axis has a decreasing, non-linear scale for clarity of presentation. The daily minimum SZA (highest Isun) was used, giving an estimate of the minimum daily lifetime. Across all latitudes vanillin has a short lifetime, increasing above 3 hours only at high latitudes within a month of the winter solstice. While the lifetime of vanillin is short, the dimer product absorbs at longer wavelengths and is persistent for longer periods. Studies of other PhC, e.g. coniferaldehyde, are known to have even shorter lifetimes, but product distributions and properties for reactions of other PhC are unknown.17,24The variation in the solar spectrum and its intensity with SZA complicates generalizing estimates of photochemical lifetime based on a measurement for a single SZA. Calculated lifetimes can be compared to the lifetimes for three SZA commonly reported in photochemical experiments (0°, 45°, 60°) for characteristic days for solar exposure (solstice and equinox) at specific latitudes (15°N: Cape Verde and 45°N: Milan). 15°N was chosen as significant amounts of BrC are predicted to lie in the tropics, and 45°N was chosen to show variation with latitude.27 These results are shown in Table S2,† both with and without a correction for differences in the intensity of solar radiation due to the difference between the actual SZA occurring on an equinox/solstice at a given latitude and the SZA reported in laboratory studies.
First, we compare our directly calculated lifetime and the lifetime calculated by extrapolating a measurement only by scaling according to the change in total solar photon flux. Extrapolating from a value reported at 45° SZA results in approximately 10% overestimation of the lifetime at 15°N or 45°N on the summer solstice or an equinox; agreement is slightly better extrapolating from a smaller SZA (<10%) and slightly worse (<20%) extrapolating from a larger SZA. Extrapolating to the winter solstice generally yields larger discrepancies (<50% for 0°SZA) that are underestimates of the lifetime calculated using our wavelength resolved quantum yields. If photon intensity is not considered, a much wider range in lifetime estimates is found,  . Furthermore, estimates based on scaling only with total photon fluxes assume that laboratory polychromatic sources can be related to solar radiation for a given SZA with good fidelity. This may not be possible with polychromatic light sources if the absorption cross-section and/or quantum yield of the molecule of interest and the utilized chemical actinometer span different wavelength ranges. Our lifetime analysis emphasizes the importance of considering the changing solar spectrum profile with SZA, not just its intensity, with wavelength resolved photochemical loss measurements.
. Furthermore, estimates based on scaling only with total photon fluxes assume that laboratory polychromatic sources can be related to solar radiation for a given SZA with good fidelity. This may not be possible with polychromatic light sources if the absorption cross-section and/or quantum yield of the molecule of interest and the utilized chemical actinometer span different wavelength ranges. Our lifetime analysis emphasizes the importance of considering the changing solar spectrum profile with SZA, not just its intensity, with wavelength resolved photochemical loss measurements.
4 Conclusions
Photochemical loss of vanillin highlights several important factors when considering the photochemistry of multiply substituted aromatic BrC molecules. In the case of PhC, self-reaction causes the rate of loss to be concentration dependent and leads to formation of dimer species that are more weakly absorbing but more photochemically stable. The wavelength dependence of ΦLoss for vanillin is not a sharp step function, but rather a gradual decay towards longer wavelengths, much broader than that observed for gas-phase photolysis reactions. This wavelength dependence appears to originate in wavelength dependent intersystem crossing, supported by the excellent agreement between the wavelength dependence of kISC(λ) and ΦLoss(λ); this may apply to PhC3* more broadly. Self-reaction of vanillin is slower than diffusion limitations alone, suggesting a significant, if small, reaction barrier and a temperature dependence to this reaction. Determining ΦLoss(λ) and ΦLoss(SZA) for BrC molecules is important for accurately assessing the lifetime of BrC molecules in the atmosphere and their effects on dimer/oligomer/SOA formation and their climate effects through absorption of solar radiation. Experimental values for the photochemical lifetimes of BrC species involving polychromatic light sources should include an estimate of the potential variation with SZA; this will reduce over/under-estimation of the photochemical lifetime to within 50% for all solar conditions. Finally, application of photochemical experiments to aerosol conditions needs to account for key aerosol properties, such as pH and ionic strength, as these factors can have significant effects on the rates of loss and product formation. These considerations will be important as the prevalence of oxidized aromatic emissions is likely to increase with greater annual wildfire size and frequency.Author contributions
Conceptualization: GTD. Formal analysis: GTD, TW, SS, DL, YH, LRM, RV, and TK. Funding acquisition: GTD. Investigation: GTD, TW, SS, DL, YH, LG, RV, TK and LRM. Methodology: GTD, TW, SS, DL, YH, and LG. Project administration: GTD. Visualization: GTD, RV, TK, and LRM. Writing – first draft: GTD, RV, and LRM. Writing – review & editing: GTD, LRM, RV, and TK.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Buck Lab for Environmental Science. We thank the CSC IT Center for Science in Espoo, Finland, for computational resources.References
- A. Akherati, Y. He, M. M. Coggon, A. R. Koss, A. L. Hodshire, K. Sekimoto, C. Warneke, J. De Gouw, L. Yee, J. H. Seinfeld, T. B. Onasch, S. C. Herndon, W. B. Knighton, C. D. Cappa, M. J. Kleeman, C. Y. Lim, J. H. Kroll, J. R. Pierce and S. H. Jathar, Environ. Sci. Technol., 2020, 54, 8568–8579 CrossRef CAS PubMed
.
- C. G. Nolte, J. J. Schauer, G. R. Cass and B. R. T. Simoneit, Environ. Sci. Technol., 2001, 35, 1912–1919 CrossRef CAS PubMed
.
- M. V. Misovich, A. Priyadarshani Silva Hettiyadura, W. Jiang, Q. Zhang and A. Laskin, ACS Earth Space Chem., 2021, 5, 1983–1996 CrossRef CAS
.
- R. F. Hems, E. G. Schnitzler, C. Liu-Kang, C. D. Cappa and J. P. D. Abbatt, ACS Earth Space Chem., 2021, 5, 722–748 CrossRef CAS
.
- L. T. Fleming, P. Lin, J. M. Roberts, V. Selimovic, R. Yokelson, J. Laskin, A. Laskin and S. A. Nizkorodov, Atmos. Chem. Phys., 2020, 20, 1105–1129 CrossRef CAS
.
- Y. L. Sun, Q. Zhang, C. Anastasio and J. Sun, Atmos. Chem. Phys., 2010, 10, 4809–4822 CrossRef CAS
.
- L. Yu, J. Smith, A. Laskin, C. Anastasio, J. Laskin and Q. Zhang, Atmos. Chem. Phys., 2014, 14, 13801–13816 CrossRef
.
- L. Yu, J. Smith, A. Laskin, K. M George, C. Anastasio, J. Laskin, A. M Dillner and Q. Zhang, Atmos. Chem. Phys., 2016, 16, 4511–4527 CrossRef CAS
.
- D. Vione, A. Albinet, F. Barsotti, M. Mekic, B. Jiang, C. Minero, M. Brigante and S. Gligorovski, Atmos. Environ., 2019, 206, 197–207 CrossRef CAS
.
- L. Ma, C. Guzman, C. Niedek, T. Tran, Q. Zhang and C. Anastasio, Environ. Sci. Technol., 2021, 55, 5772–5781 CrossRef CAS PubMed
.
- W. Jiang, M. V. Misovich, A. P. S. Hettiyadura, A. Laskin, A. S. McFall, C. Anastasio and Q. Zhang, Environ. Sci. Technol., 2021, 55, 5199–5211 CrossRef CAS PubMed
.
- T. Felber, T. Schaefer, L. He and H. Herrmann, J. Phys. Chem. A, 2021, 125, 5078–5095 CrossRef CAS PubMed
.
- S. Rossignol, K. Z. Aregahegn, L. Tinel, L. Fine, B. Nozière and C. George, Environ. Sci. Technol., 2014, 48, 3218–3227 CrossRef CAS PubMed
.
- C. Anastasio, B. C. Faust and C. Janakiram Rao, Environ. Sci. Technol., 1997, 31, 218–232 CrossRef CAS
.
- C. George, M. Ammann, B. D'Anna, D. J. Donaldson and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4218–4258 CrossRef CAS PubMed
.
- Ó. Guzmán-Méndez, M. M. Reza, B. Meza, J. Jara-Cortés and J. Peón, J. Phys. Chem. B, 2023, 127, 5655–5667 CrossRef PubMed
.
- J. D. Smith, H. Kinney and C. Anastasio, Atmos. Environ., 2016, 126, 36–44 CrossRef CAS
.
- T. A. Gawargy, B. Wang and J. C. Scaiano, Photochem. Photobiol., 2022, 98, 429–433 CrossRef CAS PubMed
.
- R. Ossola, R. Gruseck, J. Houska, A. Manfrin, M. Vallieres and K. McNeill, Environ. Sci. Technol., 2022, 56, 13449–13460 CrossRef CAS PubMed
.
- B. R. G. Mabato, Y. Lyu, Y. Ji, Y. J. Li, D. D. Huang, X. Li, T. Nah, C. H. Lam and C. K. Chan, Atmos. Chem. Phys., 2022, 22, 273–293 CrossRef CAS
.
- A. Laskin, J. Laskin and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4335–4382 CrossRef CAS PubMed
.
- H. Lignell, M. L. Hinks and S. A. Nizkorodov, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13780–13785 CrossRef CAS PubMed
.
- H. Herrmann, T. Schaefer, A. Tilgner, S. A. Styler, C. Weller, M. Teich and T. Otto, Chem. Rev., 2015, 115, 4259–4334 CrossRef CAS PubMed
.
- S. Net, E. G. Alvarez, N. Balzer, H. Wortham, C. Zetzsch and S. Gligorovski, ChemPhysChem, 2010, 11, 4019–4027 CrossRef CAS PubMed
.
- G. T. Drozd, K. Sun-Mi Brown and H. Q. Karp, ACS Earth Space Chem., 2022, 6, 1772–1781 CrossRef CAS
.
- K. J. Kiland, F. Mahrt, L. Peng, S. Nikkho, J. Zaks, G. V. Crescenzo and A. K. Bertram, ACS Earth Space Chem., 2023, 7, 1388–1400 CrossRef CAS
.
- E. G. Schnitzler, N. G. A. Gerrebos, T. S. Carter, Y. Huang, C. L. Heald, A. K. Bertram and J. P. D. Abbatt, Proc. Natl. Acad. Sci., 2023, 19, 2205610119 Search PubMed
.
-
N. J. Turro, Modern Molecular Photochemistry, Univ. Science Books, Sausalito, 4th edn, 1991, Ch. 2 Search PubMed
.
- R. J. Weber, H. Guo, A. G. Russell and A. Nenes, Nat. Geosci., 2016, 9, 282–286 CrossRef CAS
.
- H. O. T. Pye, A. Nenes, B. Alexander, A. P. Ault, M. C. Barth, S. L. Clegg, J. L. Collett, K. M. Fahey, C. J. Hennigan, H. Herrmann, M. Kanakidou, J. T. Kelly, I. T. Ku, V. Faye McNeill, N. Riemer, T. Schaefer, G. Shi, A. Tilgner, J. T. Walker, T. Wang, R. Weber, J. Xing, R. A. Zaveri and A. Zuend, Atmos. Chem. Phys., 2020, 20, 4809–4888 CrossRef CAS PubMed
.
- K. J. Angle, D. R. Crocker, R. M. C Simpson, K. J. Mayer, L. A. Garofalo, A. N. Moore, S. L. Mora Garcia, V. W. Or, S. Srinivasan, M. Farhan, J. S. Sauer, C. Lee, M. A. Pothier, D. K. Farmer, T. R. Martz, T. H. Bertram, C. D. Cappa, K. A. Prather and V. H. Grassian, Proc. Natl. Acad. Sci., 2021, 118, 2018397118 CrossRef PubMed
.
- G. Zheng, H. Su, S. Wang, M. O. Andreae, U. Pöschl and Y. Cheng, Science, 2020, 369, 1374–1377 CrossRef CAS PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed
.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 59, 1200–1211 CrossRef
.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed
.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 54103 CrossRef PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. M. Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed
.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS
.
-
R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, 2019 Search PubMed
.
-
M. E. Casida, in Recent Advances in Density Functional Methods Part I, 1995, pp. 155–192 Search PubMed
.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef
.
- O. K. Bazyl’, V. Ya. Artyukhov, G. V Mayer, P. P. Pershukevich, M. V Bel’kov, O. I. Shadyro and S. N. Samovich, Opt. Spectrosc., 2019, 127, 242–250 CrossRef
.
- S. G. Chiodo and M. Leopoldini, Comput. Phys. Commun., 2014, 185, 676–683 CrossRef CAS
.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed
.
- R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, G. V Baryshnikov, D. Sundholm, H. Ågren, B. F. Minaev and T. Kurtén, Phys. Chem. Chem. Phys., 2020, 22, 22314–22323 RSC
.
- R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2021, 23, 6344–6348 RSC
.
- R. R. Valiev, V. N. Cherepanov, G. V Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133 RSC
.
- R. R. Valiev, B. S. Merzlikin, R. T. Nasibullin, A. Kurtzevitch, V. N. Cherepanov, R. R. Ramazanov, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2023, 25, 6406–6415 RSC
.
- P. Warneck and G. K. Moortgat, Atmos. Environ., 2012, 62, 153–163 CrossRef CAS
.
- P. J. Wagner, P. A. Kelso and R. G. Zepp, J. Am. Chem. Soc., 1972, 94, 7480–7488 CrossRef CAS
.
- L. J. Johnston and J. C. Scaiano, Chem. Rev., 1989, 89, 521–547 CrossRef CAS
.
- G. K. Moortgat, H. Meyrahn and P. Warneck, ChemPhysChem, 2010, 11, 3896–3908 CrossRef CAS PubMed
.
-
E. S. Medvedev and V. I. Osherov, Radiationless Transitions in Polyatomic Molecules, Springer-Verlag, Berlin, 1995 Search PubMed
.
- H. Herrmann, Chem. Rev., 2003, 103, 4691–4716 CrossRef CAS PubMed
.
- F. A. Long and W. F. McDevit, Chem. Rev., 1951, 51, 119–169 CrossRef
.
- R. F. Cross, J. Phys. Chem., 1975, 79, 1822–1828 CrossRef CAS
.
- M. Mekic and S. Gligorovski, Atmos. Environ., 2021, 244, 117911 CrossRef CAS
.
- G. Loisel, M. Mekic, S. Liu, W. Song, B. Jiang, Y. Wang, H. Deng and S. Gligorovski, Atmos. Environ., 2021, 246, 118140 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ea00002a |
| This journal is © The Royal Society of Chemistry 2024 |