 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Lifetimes of pre-reactive complexes of peroxy radicals revisited: thermostat effects, temperature dependence and highly oxygenated molecules†
Christopher David
Daub
 *,
Robert
Skog
*,
Robert
Skog
 and
Theo
Kurtén
and
Theo
Kurtén
Department of Chemistry, University of Helsinki, P.O. Box 55, Helsinki 00014, Finland. E-mail: christopher.daub@helsinki.fi
First published on 23rd May 2024
Abstract
In recent work [Daub et al., ACS Earth Space Chem., 2022, 6, 2446] we have developed a simple model for describing the lifetime of pre-reactive complexes, and demonstrated its use for predicting the reactivity of barrierless reactions between peroxy radicals. Here, we modify and extend the method in three important ways. First, we compare the use of a Langevin thermostat for initial equilibration of the system with the Nosé–Hoover thermostat. Then, we show some new results for the lifetimes of complexes of secondary and tertiary ozonolysis and hydroxyl radical products from α-pinene. Finally, we use the method to measure the temperature dependence of complex lifetimes and compare them with available experimental results for reaction rates as a function of temperature.
Environmental significanceDespite a great deal of research work, peroxy radical reactions have been difficult to model theoretically. In particular, the accurate quantum chemical methods required are not tractable for the large peroxy radicals produced from volatile organic compounds (VOCs) known to be important in atmospheric new particle formation. Our work demonstrates that simple empirical force-field based methods can be used to predict the overall reactivity of peroxy radicals in cases where the tetroxide formation is barrierless, including the calculation of activation energies in good agreement with experiments. Our approach offers a computationally inexpensive way to predict the reactivity of other peroxy radicals which have not yet been (or cannot be) studied experimentally. |
1 Introduction
Reactions of volatile organic compounds (VOCs) with abundant atmospheric oxidizers (OH, O3) can initiate the formation of peroxy radicals (RO2).1–4 These radicals are comparatively long-lived, usually undergoing further reactions with NO or HO2, or, especially in less polluted regions, undergoing self- or cross-reactions with another peroxy radical.5 These latter reactions have attracted a great deal of recent research interest, since they can form larger accretion products such as ROOR or R(O)OR species which then can act as seeds for new particle formation leading to the growth of aerosols.3,6,7Our research group, among others, has long been involved in using theoretical chemistry methods to understand bi-molecular reactions between peroxy radicals.8–16 In particular, we have been attempting to extend our studies to include the dynamics of the reactions.13,14 In many cases, experimental results5,17–21 show a decrease in overall reactivity as temperature is increased, consistent with a negative activation energy Ea in the framework of an Arrhenius relation,
| k = Ae−Ea/RT. | (1) |
This negative Ea shows that any activation barrier in the reaction is either non-existent, or at least very small compared with the thermal energy of the system.
If a particular reaction is found to be effectively barrierless, then it suggests that expensive quantum chemical calculations to determine the entire potential energy surface and all of the possible reaction pathways may not always be needed. Instead, another approach is to use empirical force field models and molecular dynamics simulations to model the lifetime of the pre-reactive complex formation.
Even though tetroxide formation may be barrierless, it still will not occur unless the relative orientation of the two radicals is conducive to allowing the reaction. Over time, molecular vibrations within the complex should allow this particular geometry to be sampled, but only if the complex remains associated for a sufficient time. Therefore, under the assumption that the likelihood of reaction depends only on the complex lifetime, it should be possible to correlate between the simulated lifetime of the complexes and the experimental reactivity.
In our previous work,14 we have already demonstrated the success of this idea. We found that for a range of different peroxy radicals experimentally determined to have negative values of Ea, a strong correlation between the experimental reactivity and the simulated lifetime of the complex was established, with only one system (the cross-reaction between methyl peroxy and acetyl peroxy) being determined to be an outlier.
Since then, we have continued to develop our methods and apply them in new ways. In this work, we report on three of these developments. First, we have changed our equilibration method to use a Langevin thermostat, instead of the Nosé–Hoover thermostat we used previously. Second, we have extended the systems we studied to include some of the secondary and tertiary products of reactions between OH, ozone, O2 and α-pinene, including some of the interesting highly oxygenated molecules (HOMs) which can be produced as accretion products.22,23 Finally, we have done simulations at a range of temperatures, and have shown that the temperature dependence can be fit well by an Arrhenius equation with parameters in reasonable agreement with the available experimental data.
2 Methods and models
Most of the methods we used have been well-described in our recent papers.13,14 In the current work, we only give a brief summary, along with describing any differences in the methods used.Since we do not need to model bond-making and bond-breaking processes to describe pre-reactive complexes of peroxy radicals, we used computationally inexpensive empirical force-field models for our simulations. We used the OPLS force fields,24–26 with some small modifications required to model peroxy radicals instead of hydroperoxides.27
We used the LAMMPS software package to run our simulations.28 Each individual simulation started with two peroxy radicals, with centers of mass initially separated by 30 to 50 Å, depending on the size of the system. The energy and force calculation was cut off at a distance 5 to 10 Å less than the initial separation, so that there was no interaction between the systems during the equilibration phase. Each radical was given a randomized orientation, and a new random number seed was used each time to generate initial velocities. Some examples of LAMMPS input and data files we used are given in the ESI.†
Independent thermostats were used to equilibrate each molecule before initiating the collision. Recent work has given reasons for caution when using Nosé–Hoover thermostats in gas-phase systems.29 Therefore, we have rerun the complete set of simulations we previously used to establish a correlation between the lifetime of pre-reactive complexes and overall reactivity,14 using a Langevin thermostat for initial equilibration instead of a Nosé–Hoover thermostat. We also checked a few other possible issues, such as the duration of the equilibrations. In this work the equilibration was done for 0.75 × 106 timesteps (0.5 × 106 for MeOO). New random number seeds were also used in each simulation to initialize the random friction force generation in the Langevin thermostats.
After equilibration, the thermostats were removed and the rest of the simulation was run with constant total energy (NVE ensemble). One of the molecules' center of mass was given an initial velocity oriented in the direction of the other center of mass, chosen to match the relative velocity of two molecules of given mass at temperature T. This led to a collision after a few picoseconds. Different trajectories led to complex formation with variable association times. By running thousands of independent simulations, we were able to collect a histogram of association times.
In most cases, there was a peak in the histogram representing very short collisions which are effectively repulsive, and do not lead to complex formation. This would be difficult to include in our model for the association time histogram, so we did not attempt to fit the data at short times t < ts. For t > ts, we fit the association time histogram to a simple bi-exponential model with four parameters,
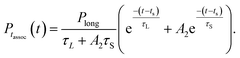 | (2) |
3 Results
3.1 Langevin thermostat vs. Nosé–Hoover thermostat
In addition to the systems we studied previously, we added one new system, (CH3)2C(OH)CH2O2, representing one of the possible butanol peroxy radicals (HOBuOO). The starting configuration for HOBuOO is shown in Fig. 2. Our results including fits to eqn (2) are shown in Table 1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 collisions (15
000 collisions (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for MeOO). Experimental data are from ref. 5 unless otherwise noted
000 for MeOO). Experimental data are from ref. 5 unless otherwise noted
| System | k expt/10−13 cm3 per molecule per s | P long | A 2 | τ S/ps−1 | τ L/ps−1 |
|---|---|---|---|---|---|
| MeOO | 3.5 | 0.421 | 7.0 | 2.8 | 15.9 |
| AcOO | 130 (ref. 19) | 0.726 | 7.6 | 3.5 | 64.9 |
| AceOO | 54 (ref. 20) | 0.801 | 3.4 | 4.7 | 53.1 |
| MeOO + AcOO | 200 (ref. 19) | 0.571 | 5.7 | 3.1 | 25.9 |
| MeOO + AceOO | 38 (ref. 20) | 0.616 | 3.3 | 3.1 | 20.8 |
| AcOO + AceOO | 50 (ref. 20) | 0.766 | 4.7 | 4.5 | 57.0 |
| ClCH2OO | 35 | 0.613 | 5.8 | 3.8 | 26.3 |
| HOEtOO | 22 | 0.751 | 3.5 | 4.8 | 33.0 |
| HOBuOO | 48 | 0.721 | 3.5 | 4.6 | 43.4 |
As in our previous paper,14 we then plotted our values for τLversus available experimental data for the overall rate coefficient k for the recombination of peroxy radicals (Fig. 1). We observe a strong correlation (with correlation coefficient r = 0.788) between τL and kexpt. A direct comparison between the new results and our previous results can be found in the ESI.† Even though the correlation coefficient is marginally lower than in our previous work (r = 0.845), we do not find this difference to be very significant. We note again that, even if our empirical force fields and the lifetime model of eqn (2) were perfect, and our simulations devoid of statistical error, due to the large uncertainties in the experimental reactivity kexpt (approximately a factor of two in some cases), we should not necessarily expect to see a stronger correlation. Therefore, a small difference in the correlation coefficient can likely be attributed to random chance.
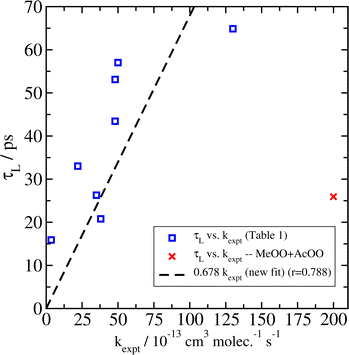 | ||
| Fig. 1 Correlation between τL determined from fits of the association lifetime histograms simulated at 300 K to eqn (2), and experimental data for overall reactivity kexpt for reactions between peroxy radicals. The MeOO + AcOO system (indicated by the red ×) was not included. | ||
Overall, there are not very large changes from our previous work, suggesting that, despite the equipartition issues arising from the use of the Nosé–Hoover thermostat, those results were still essentially correct. The main difference in the new data is a modest increase (ca. 5–10%) in the simulated association lifetimes, which seems to be general. Combined with the addition of the new HOBuOO system, the end result is a small increase in the correlation factor between τL and kexpt from 0.577 × 1013 to 0.678 × 1013, where kexpt is in units of cm−3 per molecule per s and τL is in units of ps. We suggest that this new value is likely to be more reliable than the one we published previously.
3.2 Secondary and tertiary products of α-pinene ozonolysis and hydroxy radical reactions
In our previous work,14 we ran collision simulations and the association lifetime analysis on three different peroxy radical products arising from atmospheric reactions of α-pinene with OH radicals and ozone,30 and we compared our results with some of the available experimental data for formation of ROOR′ accretion products from these.2 Here, we extend these simulations to a wider range of compounds, including highly oxidized molecules (HOMs) which can be formed by further reactions downstream from the initial formation of a peroxy radical.A scheme for such reactions based on experimental observations has been proposed by Berndt et al. (see Fig. 2 of ref. 1). We chose several of the products in this scheme to run our simulations on, and show optimized configurations of these in Fig. 2.
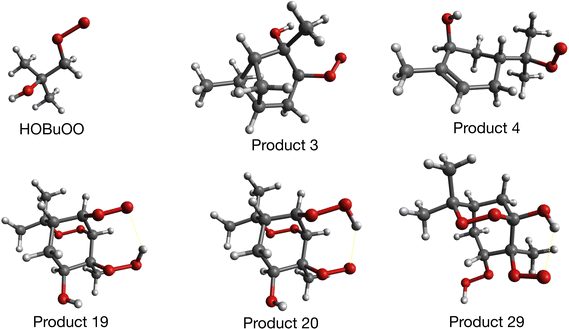 | ||
| Fig. 2 Configurations of butanol peroxy (HOBuOO), and 5 larger α-pinene derived peroxy radicals studied for this work. The product numbers given are taken from ref. 1. Products 3 and 4 come from reactions between one O2 molecule and the secondary alkyl radical generated by OH addition to α-pinene, while products 19, 20 and 29 come from further reactions with additional O2 to form HOMs. | ||
We ran between 2500 and 3000 separate collision trajectories for each system. Since these systems usually remained associated for significantly longer than smaller peroxy radical systems, we used a longer timestep (0.5 fs) and longer simulation times (5 ns) than previously. Association time histograms for these are shown in Fig. 3, and results of the fits to eqn (2) are tabulated in Table 2, including a prediction of the reaction rate kpred based on dividing τL by the correlation factor of 0.678 × 1013 determined as described in Section 3.1. We note that one of these systems (product 5) was studied in our previous work (system 1 in Fig. 3 and Table 2 of ref. 14); the new fit parameters are somewhat different, primarily due to our use of a Langevin thermostat instead of a Nosé–Hoover thermostat for equilibration as discussed in Section 3.1.
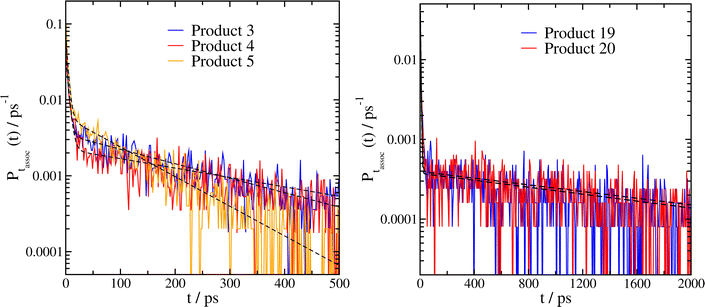 | ||
| Fig. 3 Association time histograms and fits to eqn (2) (dashed black lines) for complexes of two α-pinene derived peroxy radicals. The product numbers given are taken from ref. 1, for further details see the caption to Fig. 2 and the main text. Product 29 is not shown (see Table 2 and the text). | ||
| Product # | P long = P(>2 ps) | P(>100 ps) | P(>2 ns) | A 2 | τ s/ps−1 | τ L/ps−1 | k pred = τL/0.678 × 1013 |
|---|---|---|---|---|---|---|---|
| 3 | 0.877 | 0.512 | 0.004 | 6.6 | 4.2 | 228 | 3.36 × 10−11 |
| 4 | 0.896 | 0.578 | 0.034 | 11.3 | 4.7 | 351 | 5.18 × 10−11 |
| 5 | 0.796 | 0.274 | 0.0 | 6.9 | 3.8 | 111 | 1.64 × 10−11 |
| 19 | 0.876 | 0.721 | 0.336 | 109 | 3.1 | 1995 | 2.94 × 10−10 |
| 20 | 0.922 | 0.794 | 0.358 | 66 | 4.0 | 2072 | 3.05 × 10−10 |
| 29 | 0.909 | 0.837 | 0.764 | NA | NA | >2000 | >3 × 10−10 |
Several noteworthy results of this analysis stand out. First, we note that products 3 and 5 are very similar, differing only in the fact that the locations of the OH group and the peroxy radical group are swapped. However, the association time histograms and fits are surprisingly different, with the values of τL differing by a factor of two.
Secondly, the association times of HOMs resulting from reactions with additional O2 molecules (products 19, 20 and 29) are ∼10× longer than for the first generation peroxy radicals. For one of these systems, product 29, we were unable to fit the results to our model due to the fact that even after 5 ns, the majority of the trajectories remained bound in the complex. At the same time, there is still a significant chance (≈15–30%) of shorter association times, resulting from unfavourable initial collision geometries which do not form strong inter-molecular hydrogen bonds. Products 19 and 20, which are identical except for swapping the positions of the peroxy radical group and the hydroperoxide group, have nearly identical values of τL, even though the association time histograms for small values of t are measurably different.
Interpreting our analysis of the complex lifetimes in these larger peroxy radical systems should be done with caution. These are complicated molecules, and it is likely that in some cases, significant reaction barriers could exist, which would significantly lower the reactivity, regardless of the long lifetime of the pre-reactive complex. That caveat aside, these new results reinforce the claims made in the original experimental work of Berndt et al. that the overall reactivity between α-pinene peroxy radical products that have undergone one or more autoxidation events is collision limited;1 although collisions between them are rare in typical atmospheric conditions, if they do collide, they will stick together long enough to react.
3.3 Temperature dependence and fits to the Arrhenius equation
Experimentally, the temperature dependence of a reaction can be derived in a straightforward way, by simply measuring the reactivity at a series of different temperatures. In our approach, since we have established that the reaction rate coefficient k correlates with the complex lifetime parameter τL from eqn (2), we can similarly perform our MD simulations at a range of temperatures to get the temperature dependence.We have done this for five different systems, including complexes of two methyl peroxys (MeOO), two acetonyl peroxys (AceOO), two ethanol peroxys (HOEtOO), and two butanol peroxy compounds (HOBuOO), as well as the mixed AceOO + MeOO system. The histograms of complex lifetimes for the system of two AceOO molecules at temperatures T = 260, 280, 300, 320 and 340 K are shown in Fig. 4; similar plots for the other four systems are included in the ESI.† The fitted parameters for all five systems are given in Table 3. Finally, in Fig. 5 we plot the lifetime parameters τL and fit them to an Arrhenius equation (eqn (1)).
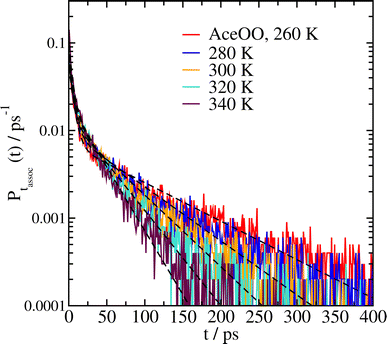 | ||
| Fig. 4 Association time histograms for complexes of two AceOO molecules at different temperatures, and fits of the data to eqn (2) (dashed black lines). | ||
| T/K | P long | A 2 | τ S/ps−1 | τ L/ps−1 |
|---|---|---|---|---|
| MeOO | ||||
| 255 | 0.487 | 4.81 | 2.62 | 16.76 |
| 270 | 0.464 | 4.76 | 2.52 | 15.37 |
| 285 | 0.442 | 4.87 | 2.40 | 13.89 |
| 300 | 0.421 | 7.02 | 2.77 | 15.90 |
| 315 | 0.397 | 4.71 | 2.20 | 12.10 |
| 330 | 0.389 | 3.44 | 1.87 | 9.56 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| AceOO | ||||
| 260 | 0.857 | 4.81 | 5.46 | 98.82 |
| 280 | 0.831 | 3.84 | 5.28 | 70.34 |
| 300 | 0.801 | 3.39 | 4.74 | 53.11 |
| 320 | 0.770 | 2.85 | 5.06 | 39.99 |
| 340 | 0.757 | 2.43 | 3.94 | 29.81 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| AceOO + MeOO | ||||
| 260 | 0.685 | 5.23 | 4.90 | 40.18 |
| 280 | 0.646 | 4.27 | 3.77 | 29.01 |
| 300 | 0.616 | 3.29 | 3.14 | 20.79 |
| 320 | 0.583 | 2.90 | 2.77 | 17.77 |
| 340 | 0.550 | 4.11 | 3.49 | 18.22 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| HOEtOO | ||||
| 260 | 0.807 | 3.99 | 6.45 | 58.86 |
| 280 | 0.782 | 3.19 | 5.28 | 40.89 |
| 300 | 0.751 | 3.48 | 4.83 | 33.02 |
| 320 | 0.714 | 4.05 | 5.49 | 29.95 |
| 340 | 0.676 | 3.14 | 5.09 | 23.41 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| HOBuOO | ||||
| 260 | 0.767 | 5.94 | 4.67 | 82.88 |
| 280 | 0.748 | 4.52 | 4.63 | 56.35 |
| 300 | 0.721 | 3.50 | 4.63 | 43.43 |
| 320 | 0.692 | 2.88 | 4.07 | 31.28 |
| 340 | 0.679 | 2.55 | 4.18 | 27.04 |
| 360 | 0.649 | 1.73 | 3.14 | 20.00 |
| 380 | 0.637 | 1.59 | 2.68 | 17.25 |
| 400 | 0.602 | 1.65 | 3.09 | 16.20 |
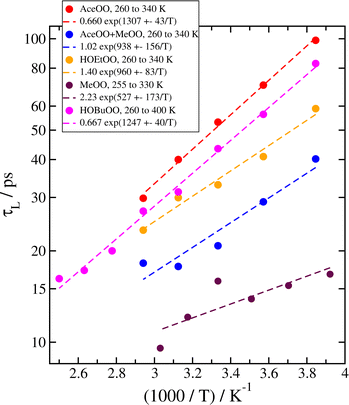 | ||
| Fig. 5 Arrhenius plots of the temperature dependence of values of τL for all five systems we studied. | ||
The Arrhenius relation agrees well with our data for all five systems, suggesting that it should be generally possible to determine the temperature dependence in the same way for all similar peroxy radical systems which feature a barrier–less reaction to form the tetroxide. In one case (AceOO), there is a very recent experimental result which we can directly compare with.18 Some other older experimental estimates, albeit with high uncertainties, are also available in the review by Orlando and Tyndall5 and/or the website of the IUPAC Task Group on Atmospheric Chemical Data Evaluation,21 or in other publications. We show comparisons between our results for the activation energy Ea/R determined from the Arrhenius equation fits and the available experimental data in Table 4.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τLversus 1/T, assuming the validity of the Arrhenius relation (eqn (1))
τLversus 1/T, assuming the validity of the Arrhenius relation (eqn (1))
In the more usual case where reactivity increases with temperature, in terms of the Arrhenius equation this arises due to an activation barrier with a characteristic activation energy Ea. However, when the temperature dependence is opposite, the interpretation is less clear. Even though a negative “activation energy” may be a strange concept, this is commonly done in experimental work in this field5,21 and so we do the same in order to compare our results with the experiments.
The experimental values of Ea/R we compare to have a large relative error. We have also reported the statistical error for our estimates; it is lower than in the experiments, however we also have significant systematic errors arising from uncertainties and limitations of the potential models and simulation methods we chose. Overall, our values agree rather well with the experimental data for barrierless reactions. We get similar high (negative) values of Ea/R for AceOO and HOBuOO, slightly lower for HOEtOO and the mixed AceOO + MeOO case, and the values of Ea/R for two MeOO are significantly lower in magnitude, in agreement with experiments. In some cases, we have some difficulty in separating the long and short decay regimes when τL ≲ 20 ps, which would make some of our data at high temperature less accurate, especially in the case of MeOO where τL < 20 ps at all temperatures we simulated.
We can finally also attempt to estimate the pre-exponential factor A in the Arrhenius equation, if we combine the correlation determined previously to relate τL to the rate coefficient k with the Arrhenius fits reported in Fig. 5. The pre-exponential factor determined by us (which we call τ0) has units of pico-seconds, but can be converted to a rate by dividing by the factor 0.678 × 1013 we obtained from the analysis in Fig. 1. A comparison of experimental and simulated values of A is shown in Table 5.
| System | τ 0/ps | A simul = τ0/0.678 × 1013 | A expt |
|---|---|---|---|
| MeOO | 2.23 | 3.28 × 10−13 | 0.95 × 10−13 |
| AceOO | 0.66 | 0.97 × 10−13 | 1.53 × 10−13 |
| AceOO + MeOO | 1.02 | 1.50 × 10−13 | 7.5 × 10−13 |
| HOEtOO | 1.40 | 2.06 × 10−13 | 0.78 × 10−13 |
| HOBuOO | 0.67 | 0.98 × 10−13 | 0.14 × 10−13 |
Determining A requires extrapolation of the results far outside of the temperature range measured, so it is not surprising that both experimental results and our simulated results should have large errors. Given this caveat, it is remarkable that our simulation-based determinations of A are at least within an order of magnitude of the experimental data.
4 Conclusions
We already have developed a procedure to use empirical force fields and molecular dynamics simulations of bimolecular collisions to study the formation and lifetime of pre-reactive complexes of two peroxy radicals.14 The goal of the current work was to modify and extend our methods in three important ways.First, we found that changing the equilibration method to use Langevin thermostats instead of Nosé–Hoover thermostats for temperature control had only a small effect, causing an increase of 5 to 10% in the simulated association lifetime. Despite the problems noted by others with using Nosé–Hoover thermostats for equilibration of gas-phase systems,29 in our case the practical effect was minor. Nevertheless, we would encourage researchers making use of our results to use our updated value for the correlation coefficient between our simulation-based association time decay constant τL and overall experimental reactivity k for peroxy radical recombination (see Fig. 1).
Second, we have run collision simulations of five additional secondary and tertiary products of OH addition and ozonolysis of α-pinene, including HOMs resulting from subsequent reactions between one of the products (product 4) and additional O2 molecules.1 The average association time between these radicals is significantly longer than it is between smaller peroxy radicals, consistent with the conclusion that reactions between aerosol-relevant highly oxidized peroxy radicals derived from VOCs are collision limited. For the HOMs, association times are an additional order of magnitude longer. Our detailed results predict significant differences in the dynamics of complex formation and breakup for very similar molecules. We are keen to see how the specificity of our methods can be combined with experimental results based on mass spectrometry for example, which are usually unable to distinguish between isomers of molecules with the same mass.
Finally, by running collision simulations with a range of initial temperatures, we demonstrated that we can predict the experimental activation energies Ea for barrierless reactions between peroxy radicals via the use of Arrhenius plots. In 4 of the 5 cases we studied, our predicted range for Ea/R overlaps with the experimental range of measured Ea/R. Additionally, we were also able to extrapolate to the infinite temperature limit in predicting the pre-exponential factor in the Arrhenius equation. While this extrapolation is somewhat lacking in predictive power, our predictions at least agree with experiments within one order of magnitude. It seems unlikely that this good agreement with the experimental data is simply a fluke, strongly suggesting that our method has pinpointed the lifetime of the pre-reactive complex as the main factor influencing the reactivity of RO2 + R′O2 systems where the reaction is effectively barrierless, including the temperature dependence.
Overall, while our method boasts smaller statistical errors compared with experiments, significant systematic errors remain due to uncertainty about the accuracy of the OPLS-based force fields used to describe the systems. As force field development continues, aided by e.g. machine learning methods, trajectory based methods such as the one we have developed can continue to be helpful to understand experimental trends in a broader range of different gas phase reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. R. Benny Gerber and Dr Imon Mandal at the Hebrew University in Jerusalem for their valuable input. C. D. D. and T. K. thank the Jane and Aatos Erkko Foundation for financial support. T. K. is also supported by the Academy of Finland (Centre of Excellence VILMA, grant number 346369). R. S. acknowledges the Doctoral Programme in Chemistry and Molecular Sciences (CHEMS) at the University of Helsinki. Computing resources were supplied by Finland's Center for Scientific Computing (CSC).Notes and references
- T. Berndt, S. Richters, T. Jokinen, N. Hyttinen, T. Kurtén, R. V. Otkjær, H. G. Kjaergaard, F. Stratmann, H. Herrmann, M. Sipilä, M. Kulmala and M. Ehn, Hydroxyl radical-induced formation of highly oxidized organic compounds, Nat. Commun., 2016, 7, 13677 CrossRef CAS PubMed.
- T. Berndt, B. Mentler, W. Scholz, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Accretion Product Formation from Ozonolysis and OH Radical Reaction of α-Pinene: Mechanistic Insight and the Influence of Isoprene and Ethylene, Environ. Sci. Technol., 2018, 52, 11069–11077 CrossRef CAS PubMed.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Highly Oxygenated Organic Molecules (HOM) from Gas-Phase Autoxidation Involving Peroxy Radicals: A Key Contributor to Atmospheric Aerosol, Chem. Rev., 2019, 119, 3472–3509 CrossRef CAS PubMed.
- M. Meder, O. Peräkylä, J. G. Varelas, J. Luo, R. Cai, Y. Zhang, T. Kurtén, M. Riva, M. Rissanen, F. M. Geiger, R. J. Thomson and M. Ehn, Selective deuteration as a tool for resolving autoxidation mechanisms in α-pinene ozonolysis, Atmos. Chem. Phys., 2023, 23, 4373–4390 CrossRef CAS.
- J. J. Orlando and G. S. Tyndall, Laboratory studies of organic peroxy radical chemistry: an overview with emphasis on recent issues of atmospheric significance, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Accretion Product Formation from Self- and Cross-Reactions of RO2 Radicals in the Atmosphere, Angew. Chem., Int. Ed., 2018, 57, 3820–3824 CrossRef CAS PubMed.
- O. Peräkylä, T. Berndt, L. Franzon, G. Hasan, M. Meder, R. R. Valiev, C. D. Daub, J. G. Varelas, F. M. Geiger, R. J. Thomson, M. Rissanen, T. Kurtén and M. Ehn, Large Gas-Phase Source of Esters and Other Accretion Products in the Atmosphere, J. Am. Chem. Soc., 2023, 145, 7780–7790 CrossRef PubMed.
- G. Ghigo, A. Maranzana and G. Tonachini, Combustion and atmospheric oxidation of hydrocarbons: Theoretical study of the methyl peroxyl self-reaction, J. Chem. Phys., 2003, 118, 10575–10583 CrossRef CAS.
- R. Lee, G. Gryn’ova, K. U. Ingold and M. L. Coote, Why are sec-alkylperoxyl bimolecular self-reactions orders of magnitude faster than the analogous reactions of tert-alkylperoxyls? The unanticipated role of CH hydrogen bond donation, Phys. Chem. Chem. Phys., 2016, 18, 23673–23679 RSC.
- R. R. Valiev, G. Hasan, V.-T. Salo, J. Kubečka and T. Kurtén, Intersystem Crossings Drive Atmospheric Gas-Phase Dimer Formation, J. Phys. Chem. A, 2019, 123, 6596–6604 CrossRef CAS PubMed.
- G. Hasan, V.-T. Salo, R. R. Valiev, J. Kubečka and T. Kurtén, Comparing Reaction Routes for 3(RO⋯OR′) Intermediates Formed in Peroxy Radical Self- and Cross-Reactions, J. Phys. Chem. A, 2020, 124, 8305–8320 CrossRef CAS PubMed.
- V.-T. Salo, R. Valiev, S. Lehtola and T. Kurtén, Gas-Phase Peroxyl Radical Recombination Reactions: A Computational Study of Formation and Decomposition of Tetroxides, J. Phys. Chem. A, 2022, 126, 4046–4056 CrossRef CAS PubMed.
- C. D. Daub, I. Zakai, R. Valiev, V.-T. Salo, R. B. Gerber and T. Kurtén, Energy transfer, pre-reactive complex formation and recombination reactions during the collision of peroxy radicals, Phys. Chem. Chem. Phys., 2022, 24, 10033–10043 RSC.
- C. D. Daub, R. Valiev, V.-T. Salo, I. Zakai, R. B. Gerber and T. Kurtén, Simulated pre-reactive complex association lifetimes explain trends in experimental reaction rates for peroxy radical recombinations with submerged barriers, ACS Earth Space Chem., 2022, 6, 2446–2452 CrossRef CAS.
- G. Hasan, V.-T. Salo, T. G. Almeida, R. R. Valiev and T. Kurtén, Computational Investigation of Substituent Effects on the Alcohol + Carbonyl Channel of Peroxy Radical Self- and Cross-Reactions, J. Phys. Chem. A, 2023, 127, 1686–1696 CrossRef CAS PubMed.
- V.-T. Salo, J. Chen, N. Runeberg, H. G. Kjaergaard and T. Kurtén, Multireference and Coupled-Cluster Study of Dimethyltetroxide (MeO4Me) Formation and Decomposition, J. Phys. Chem. A, 2024, 128, 1825–1836 CrossRef CAS PubMed.
- K. Zuraski, A. O. Hui, F. J. Grieman, E. Darby, K. H. Møller, F. A. F. Winiberg, C. J. Percival, M. D. Smarte, M. Okumura, H. G. Kjaergaard and S. P. Sander, Acetonyl Peroxy and Hydro Peroxy Self- and Cross-Reactions: Kinetics, Mechanism, and Chaperone Enhancement from the Perspective of the Hydroxyl Radical Product, J. Phys. Chem. A, 2020, 124, 8128–8143 CrossRef CAS PubMed.
- K. Zuraski, F. J. Grieman, A. O. Hui, J. Cowen, F. A. F. Winiberg, C. J. Percival, M. Okumura and S. P. Sander, Acetonyl Peroxy and Hydroperoxy Self- and Cross-Reactions: Temperature-Dependent Kinetic Parameters, Branching Fractions, and Chaperone Effects, J. Phys. Chem. A, 2023, 127, 7772–7792 CrossRef CAS PubMed.
- M. Assali and C. Fittschen, Rate Constants and Branching Ratios for the Self-Reaction of Acetyl Peroxy (CH3C(O)O2) and Its Reaction with CH3O2, Atmosphere, 2022, 13, 186 CrossRef CAS.
- M. Assali and C. Fittschen, Self-Reaction of Acetonyl Peroxy Radicals and Their Reaction with Cl Atoms, J. Phys. Chem. A, 2022, 126, 4585–4597 CrossRef CAS PubMed.
- IUPAC, IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation, https://iupac.aeris-data.fr.
- M. Rissanen, Anthropogenic Volatile Organic Compound (AVOC) Autoxidation as a Source of Highly Oxygenated Organic Molecules (HOM), J. Phys. Chem. A, 2021, 125, 9027–9039 CrossRef CAS PubMed.
- J. Zhang, J. Zhao, Y. Luo, V. Mickwitz, D. Worsnop and M. Ehn, On the potential use of highly oxygenated organic molecules (HOMs) as indicators for ozone formation sensitivity, Atmos. Chem. Phys., 2024, 24, 2885–2911 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, Potential energy functions for atomic-level simulations of water and organic and biomolecular systems, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS PubMed.
- J. Garrec, A. Monari, X. Assfeld, L. M. Mir and M. Tarek, Lipid Peroxidation in Membranes: The Peroxyl Radical Does Not “Float”, J. Phys. Chem. Lett., 2014, 5, 1653–1658 CrossRef CAS PubMed.
- S. J. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. Halonen, I. Neefjes and B. Reischl, Further cautionary tales on thermostatting in molecular dynamics: Energy equipartitioning and non-equilibrium processes in gas-phase simulations, J. Chem. Phys., 2023, 158, 194301 CrossRef CAS PubMed.
- MCM, Master Chemical Mechanism, MCM v3.3.1, http://mcm.york.ac.uk/.
- G. S. Tyndall, R. A. Cox, R. Lesclaux, G. K. Moortgat, M. J. Pilling, A. R. Ravishankara and T. J. Wallington, Atmospheric chemistry of small organic peroxy radicals, J. Geophys. Res., 2001, 106, 12157–12182 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: LAMMPS input files for some of the systems studied. Association time histograms at different temperatures for MeOO, HOEtOO, MeOO + AceOO and HOBuOO. See DOI: https://doi.org/10.1039/d4ea00037d |
| This journal is © The Royal Society of Chemistry 2024 |
