Open Access Article
Open Access ArticleInterplay of intercalation dynamics and lithium plating in monolithic and architectured graphite anodes during fast charging†
Aleksandar S.
Mijailovic‡
 a,
Seth
Waag-Swift‡
a,
Guanyi
Wang
b,
Bingyao
Zhou
b,
Mei
Luo
c,
Wenquan
Lu
c,
Qingliu
Wu
a,
Seth
Waag-Swift‡
a,
Guanyi
Wang
b,
Bingyao
Zhou
b,
Mei
Luo
c,
Wenquan
Lu
c,
Qingliu
Wu
 b and
Brian W.
Sheldon
b and
Brian W.
Sheldon
 *a
*a
aSchool of Engineering Brown University, Providence, RI, USA. E-mail: brian_sheldon@brown.edu
bWestern Michigan University, Kalamazoo, MI, USA
cArgonne National Laboratory, Lemont, IL, USA
First published on 4th October 2024
Abstract
Fast charging of high-capacity anodes is challenging due to lithium plating reactions, which lead to poor cycling performance and safety concerns. Thus, accurate predictions of plating onset and an understanding of this electrochemical process are crucial for robust battery design. However, the most commonly used models, based on porous electrode theory (e.g., the pseudo-2D model), are notoriously difficult to calibrate due to their complexity, limiting their predictive power. This work studies the process of lithium plating during fast charging of (small-particle) graphite half-cells by measuring local reaction progression and plating behavior using optical operando techniques. These experiments employ a realistic 1D graphite electrode geometry with commercially-relevant mass loading charged at fast charge rates. It is demonstrated that the local reaction progression and plating onset can not only be predicted accurately with a p2D numerical model, but that these processes follow a simple scaling law. Remarkably, the entire reaction histories of different electrodes charged at different rates (e.g., 160 μm thickness at 0.5C, 111 μm at 1C or 66 μm at 4C) were observed to have self-similar intercalation profiles. It is demonstrated that plating onset is in turn governed by the reaction profile which explains why both processes exhibit the same scaling behavior. Finally, operando measurements of local reaction dynamics are conducted for the first time in electrodes with channeled architectures, quantitatively determining how channels affect reaction uniformity and plating onset. Together, these results reveal underlying simplicity in the complex electrochemical environment of fast charging and lithium plating, improving understanding of this process. These fundamental insights are broadly applicable for design processes, modeling and experimental evaluation of lithium ion batteries.
Broader contextDevelopment of lithium ion batteries with high energy density and fast charging capability is essential for electrification of the transport sector and ultimately reducing carbon emissions. Mitigating lithium metal plating during fast charging is a central challenge in these efforts, as this parasitic reaction leads to poor cycle life and safety concerns. Thus, predicting when, where and how lithium plating occurs is of utmost importance for fast charging applications. Models have been developed to study and predict this process, but are notoriously difficult to calibrate and interpret due to their mathematical complexity. These issues are compounded in novel electrode designs that employ non-standard architectures. A simplified yet fundamental understanding of the processes of fast charging is therefore of great value to theorists and experimentalists. To this end, we demonstrate that the complex processes of plating onset and local reaction dynamics within graphite anodes can be understood through a simple scaling law, even under the harsh conditions of fast charging. These principles are demonstrated experimentally in both monolithic and architectured electrodes. |
1 Introduction
Electrification of the transportation sector is critical in efforts to curb carbon emissions worldwide. Consumer anxiety around range and charge time are primary obstacles to electric vehicle (EV) adoption, and they reflect two conflicting requirements for lithium ion batteries: namely energy density and fast charging capability. A central issue is that, at high rates (e.g., 4C or higher), lithium metal plating will occur on the anode prior to a “complete” charge.1–3 Irreversible lithium plating reactions degrade the battery through various mechanisms and ultimately lead to capacity fade and potential short circuit and thermal runaway.4–6 Thus mitigating lithium metal plating reactions entirely is an ambitious goal for designing robust electrodes capable of withstanding repeated fast charging cycles. Novel anode designs – including complex electrode architectures – are of high interest in an effort to control lithium plating by improving transport in the electrolyte phase.7–19 These have shown promise, and here geometric factors lead to additional challenges with understanding and predicting plating.7,12,19In the charging of porous anodes, lithium ions move from the cathode through the electrolyte and then react with the negative electrode, by intercalation in the case of graphite anodes (Fig. 1). However, at fast rates lithium plating reactions can become favorable locally in the electrode, occurring at particle surfaces long before the entire electrode is fully lithiated (Fig. 1A and B). Thus accurately assessing when initial plating onset occurs is essential for developing anodes with safe fast-charging operation.
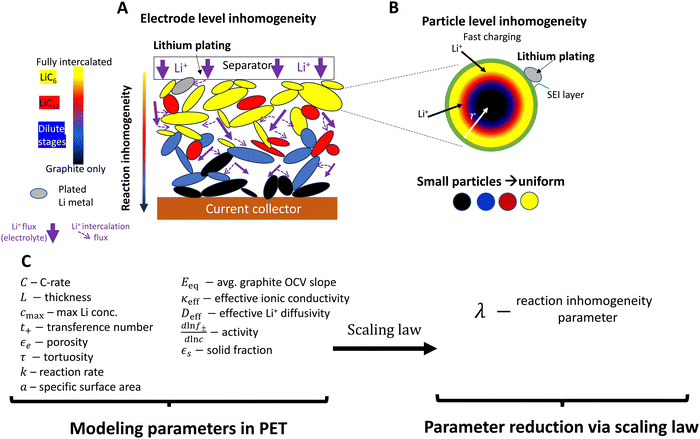 | ||
| Fig. 1 Schematic of reaction inhomogeneity (A) through the electrode thickness and (B) within individual graphite particles during fast charging. (A) There are through-plane gradients in intercalation (colors), with the higher local intercalation occurring near the separator surface leading to increased risk of lithium metal plating on particle surfaces (gray).11,20–23 Transport in the electrolyte is a major contributor to reaction gradients (purple arrows), partially due to high tortuosity in graphite electrodes.24,25 In-plane heterogeneity also occurs, with neighboring particles coexisting in separate phases. (B) Plating is favored at particle surfaces, and there may be intra-particle intercalation gradients, such as depicted in the “shrinking core” model here20,26,27 (or by intra-particle “intercalation waves”27,28). Sufficiently small particles have more uniform intercalation. (C) A large number of geometric, thermodynamic, kinetic, and (electrolyte/solid state) transport parameters are necessary for PET models. PET models are highly coupled and nonlinear, and have non-constant parameters whose reported magnitudes vary in the literature. A central question is whether simpler reduced order or scaling models can simplify the system without substantial loss of accuracy. Models that accurately predict when lithium metal plating occurs are of high interest. | ||
Unfortunately, prediction of plating onset requires precise information about the local electrochemical environment at the position where plating is first favorable (usually at the anode-separator interface).11,29–31 Plating during high C-rate charging in graphite is often attributed to inhomogeneous intercalation reactions at the electrode level (both through-plane and in-plane) and/or within particles, depending on the electrode structure and material composition (Fig. 1A and B). This is dictated by multiple transport processes (in the liquid electrolyte on the macroscale and within solid particles on the microscale), thermodynamic processes of the lithium reduction reaction, and the local interfacial reaction kinetics (Fig. 1A and B). Porous electrode theory (PET) models (e.g. the P2D model32) have been developed and employed extensively to predict this complex behavior, and can provide precise predictions of the local electrochemical environment and plating onset.31–33
However due to the large number of complex, coupled phenomena modeled, the material descriptions used in model input must be highly accurate to correctly describe plating onset (Fig. 1C). In practice, the inherent complexity due to coupled, nonlinear and multiscale nature of these models – and in particular the uncertainty associated with obtaining accurate values for many of these parameters34–36 – means that it is extremely difficult to accurately predict the onset of plating during fast charging, even for an unstructured electrode with 1D geometry. Assumed values of important modeling parameters can differ significantly in the literature (e.g., by over an order of magnitude for interfacial reaction kinetics7,11,29,35,37–41), potentially raising questions about accuracy of plating predictions between different studies. Thus, the common practice of model calibration by voltage alone (which is of high practical relevance)11,13,19,35,37,41–44 can also be inaccurate because different sets of parameters can create very similar voltage profiles (see Fig. S1, ESI†). This issue occurs because the voltage profile represents simply a sum of many processes within the electrode.40,41 While operando techniques can bypass this issue by providing more information about local intercalation, they are not typically used for model calibration due to the resources required as compared to voltage measurements. These calibration issues are compounded with difficulty interpreting electrochemical behavior due to the mathematical complexity of the model. As a consequence, optimization of electrode design can be reliant on iterative parametric simulations,7,16,19,36,37 which can be difficult to generalize between different studies. Introducing complex geometries such as architectured electrodes with electrolyte filled channels brings even more calibration issues and optimization parameters.7,16,19 Indeed, while models of architectured electrodes have been implemented, the local reaction behavior within those electrodes has never been directly measured. Clearly, developing these technologies requires a fundamental understanding of the relationship between electrode architecture, reaction progression, and lithium plating reactions. Together, these challenges can limit the utility of these models in designing electrodes that prevent lithium plating reactions during fast charging.
Several simplified models and scaling laws have been proposed to describe the processes of charging at the electrode and particle levels, providing important insights into fundamental behavior of porous electrodes and useful design strategies.11,27,45–51 However, applicability of these reduced order/scaling models to fast charging can be controversial, because the coupled, multiscale mechanisms in PET require a much larger number of modeling parameters than other physical systems (e.g., mechanical systems). Remarkably, one recent study has presented experimental evidence that, in small-particle graphite materials, plating onset can be accurately predicted in terms of a single non dimensional number – the reaction inhomogeneity parameter λ – derived from PET.11,45 It argues that the fast charging process can be quantitatively described more simply than has been previously published and generalizes the role of material and design variables on plating onset. The theory is grounded by the argument that the interplay of thermodynamics and electrolyte-level mass and charge transport dominate reaction dynamics and ultimately lead to accelerated plating onset during fast charging.11 However, studying this process within the electrode requires an involved set of experiments that must precisely measure how the local intercalation reaction and plating unfolds under a wide range of fast charging conditions.
Many sophisticated methods have been developed to acquire time-resolved local intercalation data,21,52,53 the most common and accessible being simple optical imaging to measure color changes in lithiated graphite.23,28,54–58 However, nearly all of these colorimetry studies use nonstandard electrode geometry that magnifies or enlarges the visible edge parallel to the direction of lithium flux, often employing a practically semi-infinite electrode relative to the diffusion length scale of the experiment.23,55,56,59,60 Those that do image at practical scales report a small number of experiments.57,58 In contrast, to accurately detect plating onset in situ, the perpendicular surface which normally faces the separator must be imaged, again necessitating drastic changes to the cell geometry to detect operando.61–63 Unfortunately, both of these modifications add an order of magnitude to the diffusion lengths involved, and/or fundamentally change the boundary conditions of the problem.
Using a similar colorimetric approach, the present study demonstrates that the complex physical and electrochemical phenomena of intercalation dynamics and lithium plating can be described by simple models and scaling laws. This is achieved using a comprehensive set of experiments that simultaneously quantify reaction inhomogeneity and lithium plating onset under fast charging conditions. Graphite with small particle size is used as the model system to decouple the electrode length scale mechanisms from intra-particle rate limitations (Fig. 1B). Operando colorimetry experiments via optical microscopy are used to quantify reaction profiles on the thin edge of graphite electrodes, providing a truly 1-D electrode geometry and a 2D cross section around architectured channels. These in situ studies are complemented with separate post-mortem imaging of coin cells where plating and through-thickness (and in plane) reaction profiles are be observed concurrently. The results demonstrate that a simple scaling law, which predicts reaction inhomogeneity with a nondimensional number (λ) can accurately describe reaction dynamics and plating onset during fast-charging. It is shown that the entire reaction history for two different electrodes charged under different conditions can be self-similar if the λ variable is constant. These results are verified with a p2D numerical model that is experimentally validated against both local intercalation and plating onset data. The experiments and model are then extended to study fast charging intercalation dynamics and plating in architectured electrodes.
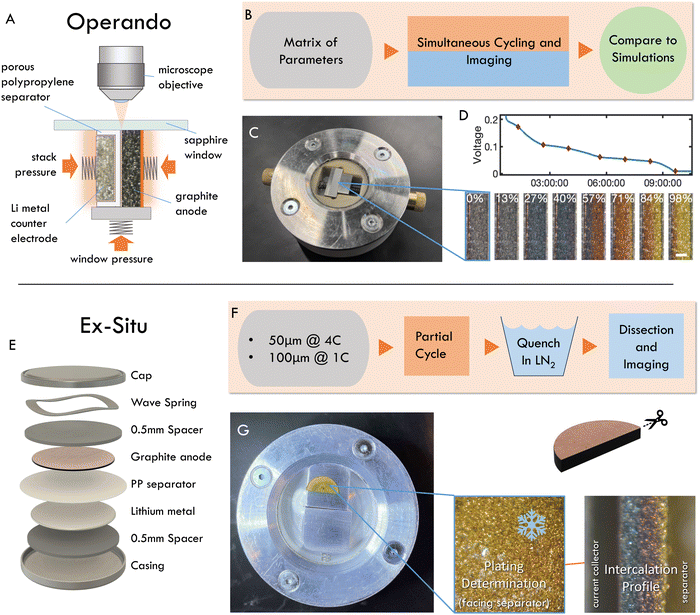
2 Imaging approaches
Two experimental methods were used to quantify reaction inhomogeneity and plating onset locally in a graphite anode during fast charging (lithiation): operando imaging in a custom made optical test cell, and ex situ (post mortem) imaging of electrodes cycled in coin cells (Fig. 2, see methods for details). In a departure from previous studies, these experiments used imaging with a visible light microscope to quantify the local reaction progress for practical electrode thicknesses (50–160 μm) in a truly 1-D cross section. Specifically, the operando experiments herein are used to obtain high-throughput observations of the entire time history of the reaction during fast charges (Fig. 2A–D). While these experiments are capable of measuring a wide range of charging conditions necessary to evaluate scaling behavior, they cannot identify plating onset, as it can occur anywhere on the graphite-separator surface. Thus a complementary “ex situ” imaging methodology was used. In these experiments, coin cells were fast charged to a range of SOC, abruptly quenched, then dissected post mortem to determine whether plating occurred, and to concurrently measure through-plane, and in-plane reaction heterogeneity (Fig. 2E–G).From the image data collected in these experiments, local electrode-scale dynamics of the intercalation reaction are measured optically via the color-changing properties of graphite intercalation compounds (GICs).23,28,54–58,64 Since the colors arise from thermodynamic phases, or “Stages”, in which lithium occupies specific galleries in the graphite layered structure (Fig. 3A), the observed colors can be used to infer the local state of charge at particle surfaces as shown in Fig. 3B (See Fig. S2 for further discussion of stoichiometry, ESI†).65–71 Small particles (D50 ≈ 6.5 μm) are used in these experiments to limit or eliminate gradients in intercalation within particle such that observed colors can be used to approximate the total state of charge locally, rather than that of only the particle surface. These data are then used to quantify the local state of charge SOCloc in the through-plane direction (Fig. 3B) via image processing, averaging of in-plane particle phase fraction, and an approximation of SOC corresponding to certain phase (See Fig. S2 for details on these approximations, ESI†). Finally, the calculated SOCloc data is averaged over the entire image to calculate an “particle average SOC” SOCapp, which represents the average state of charge of the particle surfaces in the entire imaged cross section (which can vary from the cell SOC). See Methods for a detailed description of the experimental procedures and calculations described here.
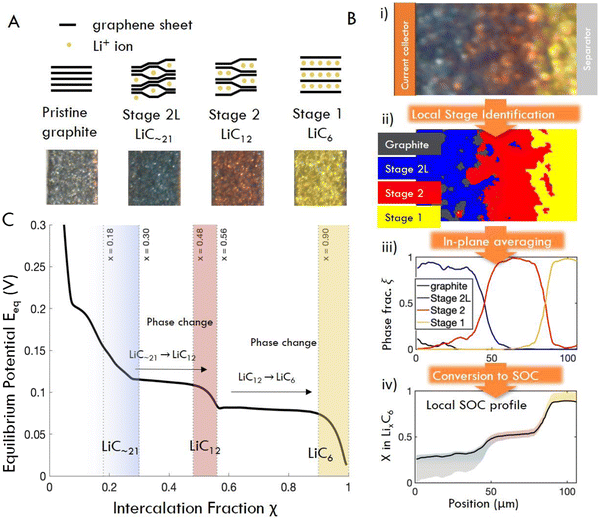 | ||
| Fig. 3 (A) Schematic structures and characteristic colors of GIC phases obtained operando. (B) Image processing workflow: raw image pixels (i) are assigned to phases (ii) by their distance in color space from the four “target” colors shown in (A). (iii) Phase fractions are obtained by summed pixels vertically, and (iv) converted to x in LixC6 (equivalently, local surface SOC) by multiplication with the chemical formula of each pure phase. Confidence region for SOC comes from the solid solution limits of each phase (see Fig. S2, ESI†). (C) Equilibrium potential curve of lithiation of graphite, obtained from C/40 cycle. Solid solution regions of each phase are shaded (after ref. 68). | ||
3 Results
3.1 Operando intercalation dynamics
To demonstrate the qualitative relationship between charge rates and through-plane reaction dynamics, representative operando images of one “slow” and one “fast” charge experiment are shown in Fig. 4A. At slow rates, the electrode converts to Stage 2L (blue) uniformly through the electrode depth, while the subsequent two phase transitions, Stage 2 (red) and Stage 1 (gold) begin adjacent to the separator (right) but rapidly propagate through the thickness before all particles are fully converted at the separator. In this wide transition region the particles undergo the phase transformations discretely and independently, generating the “mosaic” pattern previously reported.28,61,64 At high rates, all three phases initiate rapidly near the separator and travel in close succession through the electrode thickness (Fig. 4A). The boundaries between phases also become sharper, with less prominent “mosaic” patterns and a typical “wavelike” propagation of the phase boundaries.72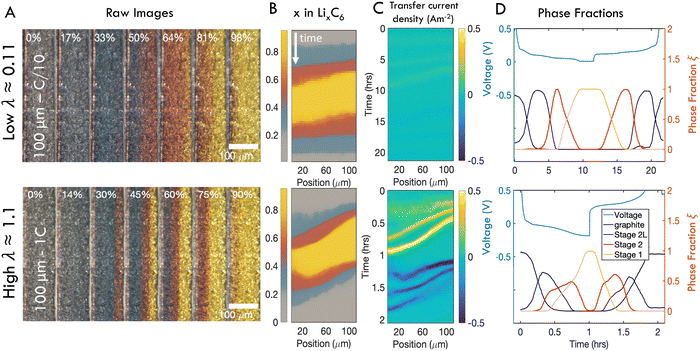 | ||
| Fig. 4 Representative operando results of “slow” (C/10) and “fast” (1C) charges of 100 μm thick electrodes. (A) Subset of photos taken during charge cycles. In each image, the current collector is located on the left and the separator is on the right. (B) Composite images showing distribution of phases in time and one spatial dimension over a full charge/discharge cycle. (C) Distribution of intercalation current. (D) Anode voltage vs. Li/Li+ alongside relative fractions of each phase anywhere in the imaged area as a function of time. At high λ, significant overpotentials are accompanied by coexistence of all three phases. Similar figures reporting data from all samples can be found in Fig. S3 and S4 (ESI†). | ||
The charge history at each rate is summarized with SOC maps, reaction rate maps, and phase fraction/voltage responses in Fig. 4B–D respectively (note that the latter show a full charge–discharge cycle at constant C-rate.) The SOC maps and raw images show that at fast rates, phase fronts advance more slowly compared to slow rates, relative to the timescale of the cycle, leading to coexistence of all three phases within the electrode (Fig. 4B and See Fig. S3 for all 30 experiments, ESI†). Indeed the localized transfer current is roughly an order of magnitude higher at high C-rates (Fig. 4C). Inspection of the concurrent voltage and cumulative phase fraction reveals that the staging plateaus, which occur during phase transitions at low rates, disappear at high charge rates, as the responses from all three phases are overprinted (Fig. 4D and See Fig. S4 for all 30 experiments, ESI†).
The total phase fractions of an entire imaged region were also used to calculate a “particle average SOC” (SOCapp). The SOCapp values approximately follow the cell state of charge as determined from the applied current on the entire cell, but with some fluctuations in time (Fig. S5–S6, ESI†). Since only small subsections of the electrode were observed in the operando experiments, these results suggest that local C-rates in the cell varied during the charge, presumably due to local in-plane inhomogeneities within the electrode (which will be discussed with the “ex situ” experimental data). However, these variations were typically transient, and provided an average C-rate close to that of the entire cell for most of the charge (Fig. S6, ESI†).
Next, the imaging data was used to calculate the position-dependent SOC profiles during the charge history to quantify local reaction heterogeneity. Fig. 5 shows selected snapshots of the calculated SOC as a function of through-plane position at a relatively “low” C-rate (Fig. 5A–C) and an order of magnitude higher C-rate (Fig. 5D–F) for six electrodes of three different thicknesses (66 μm, 111 μm, and 160 μm, all 30 operando experiments are shown in Table S1 and Fig. S7, ESI†). These local SOC measurements exhibit the same general trends described in Fig. 4, but can provide more quantitative information about reaction inhomogeneity and model validation. In all three cases, it is clear that “low” C-rates exhibit small gradients in SOC where phase changes span the thickness of the electrode, and the higher C-rates exhibit much steeper gradients, with Stage 1, 2 and 2L occurring simultaneously in the electrode. Reaction fronts are clearly associated with phase changes, but there is very uniform SOC during the (blue) dilute staging.
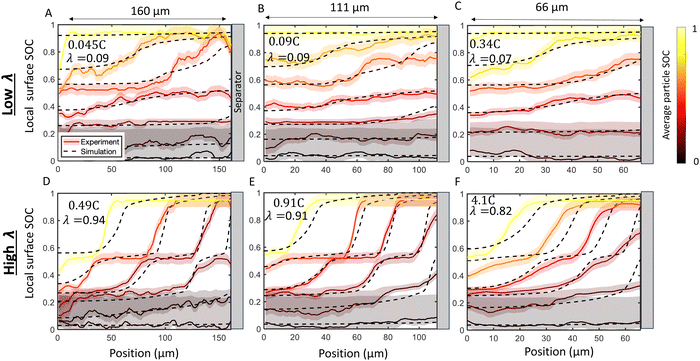 | ||
| Fig. 5 Comparison of SOC distribution between experiments (solid lines and shadow) and numerical simulations (dashed lines). Experimentally measured local surface SOC (SOCloc) is shown with colors and uncertainty highlighted with shaded regions. The colors represent the average in-plane particle surface SOC (SOCapp calculated from eqn (9)). Simulations at the same corresponding SOC are shown with dashed lines. Results are shown for a (A) 160 μm cell charged at 0.045C (B) 111 μm cell charged at 0.09C, (C) 66 μm cell charged at 0.34C, (D) 160 μm cell charged at 0.49C (E) 111 μm cell charged at 0.91C, and (F) 66 μm cell charged at 4.1C. There is agreement between experiment and simulation over the time history of charge in all cases. The top row (A)–(C) presents a “low” λ value roughly equivalent between cells, while the bottom row (D)–(F) presents a “high” λ which comprises of C-rates roughly ten times higher than the “low” rate. As predicted by the scaling law in eqn (2) the charging profiles are approximately self-similar for a constant λ, as seen by the consistency in the experimental and simulated SOC curves in (A)–(C) and in (D)–(F) Note that this self-similarity is observed with the abscissa representing normalized position, as depicted here with constant plot widths. Movies of the raw data in these plots is provided in ESI.† | ||
Next, p2D numerical simulations were validated against these experimental data (Fig. 5). Excellent agreement in local particle surface SOC was observed between the p2D numerical model with experiments during the entire time history of charge. The agreement with model and experiment is consistent over a large range of C-rates and cell thicknesses (Fig. 5 and see Fig. S8 for all experiments, ESI†). Since the model results suggest that lithium intercalation is constant within a given particle, the local surface SOC is assumed to be equivalent to the local average SOC, and is thus referred to as “local SOC” throughout this work. These results suggest that the p2D model can with accuracy capture average through-plane SOC over a wide range of conditions in this small-particle graphite system.
3.2 A scaling law for reaction inhomogeneity
A major goal of the operando imaging experiments was to evaluate the prediction that the inhomogeneity of a reaction is defined by a non-dimensional “reaction inhomogeneity parameter” λ. Previous works have demonstrated with theory and experiment that λ can accurately predict plating onset according to a “master curve” solution, which collapses charging behavior across variable electrode and electrolyte material, electrode structure and charging conditions to a single solution.11,45 In those works, it was theoretically predicted that the mechanism behind this scaling law is that the value of λ determines the reaction history during fast charging. This means that two electrodes (which may have different thickness, electrolyte, or charged at different C-rate) will have self-similar reaction profiles, and will as a result plate at the same SOC if they have the same λ value. This is a remarkable prediction due to the complexity of the reaction dynamics during fast charging, and verification of this is a primary motivation for the experiments reported here.The number λ is defined as
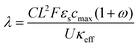 | (1) |
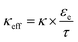 , where τ is tortuosity, and εe is porosity, and ω is a nondimensional number that is the ratio of lithium diffusion and ionic transport effects on reaction inhomogeneity (eqn (12)), and is explicitly defined in terms of electrolyte diffusivity, ionic conductivity, activity, and electrolyte concentration.73 Two electrodes with the same electrode material will have the same U and cmax, and will have the same ω and κ if the same electrolyte is used.
, where τ is tortuosity, and εe is porosity, and ω is a nondimensional number that is the ratio of lithium diffusion and ionic transport effects on reaction inhomogeneity (eqn (12)), and is explicitly defined in terms of electrolyte diffusivity, ionic conductivity, activity, and electrolyte concentration.73 Two electrodes with the same electrode material will have the same U and cmax, and will have the same ω and κ if the same electrolyte is used.
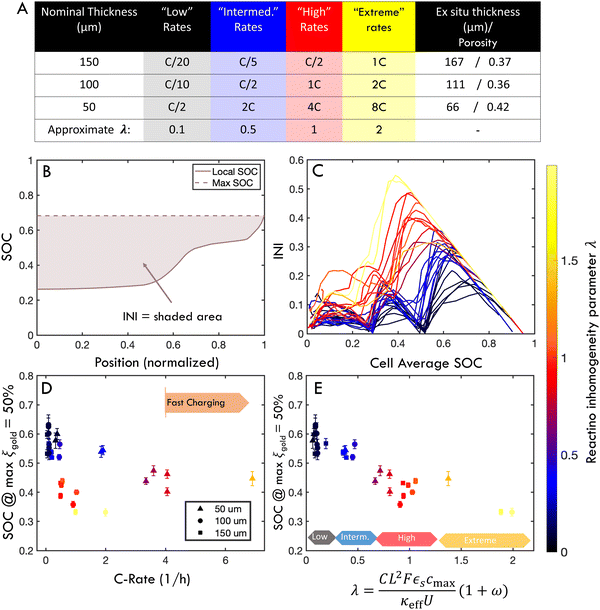
In the context of these experiments, a thin cell is charged at high C-rate is predicted to have the same intercalation history as a thicker cell charged a lower C-rate if λ is constant. To test this prediction, an experimental “parameter sweep” was conducted by fabricating electrodes of three thicknesses (nominally 150, 100, or 50 μm, with the same porosity), and cycling each set of electrodes at different C-rates. Since λ scales as
| λ ∼ CL2 | (2) |
Fig. 5 shows six experiments (and accompanying FEM simulations) that evaluates whether reaction inhomogeneity follows the scaling law of eqn (2). It is observed that the reaction profiles are roughly self similar for electrodes of different thickness when C-rates are scaled to have a constant λ. This self-similarity is observed at both “low” rates and “high” rates (Fig. 5A–C, D–F, respectively). Note that the abscissa in each of these plots is the same width even though the electrode thicknesses are different: the self-similarity of the reaction is with respect to the normalized position in the electrode. Fig. S7 (ESI†) shows results of all 30 operando experiments tested for various electrode thicknesses and rates.
To evaluate this scaling over a wider range of conditions, electrodes of 50, 100, or 150 μm nominal thickness were charged at “low”, “intermediate”, “high” or “extreme” rates (Fig. 6A and Table S1, ESI†). These rates were chosen to correspond to λ of approximately 0.1, 0.5, 1 or 2, respectively. However, a time-resolved figure of merit is necessary to compare this large parameter space. To this end, an “instantaneous inhomogeneity” (INI) parameter was defined as the area bounded by the SOC trace and the extrapolated maximum value anywhere in the electrode (Fig. 6B). (This metric is also of interest because it is related to plating onset as will be demonstrated with ex situ experiments.) Fig. 6C shows the INI for all 30 experiments over the entire charge cycle, with colors indicating different λ. Separate clusters of “low” “intermediate”, “high”, and “extreme” λ charging conditions are observed. During the charge history, three distinct peaks arise, as each new phase initiates at the separator. As λ increases, not only do absolute INI values increase, but the phase transformation peaks grow and shift earlier in the charge, representing consistently higher inhomogeneity (and plating risk). While INI can measure the inhomogeneity through an entire charge history, it does not provide easy quantitative comparison between various charging conditions.
Thus, to make a more quantitative evaluation of the λ scaling law for inhomogeneity, Fig. 6D and E measures the electrode SOC when the maximum local gold phase fraction in the electrode equals 50% (i.e., max(ξgold) = 50%). This definition was chosen as a representative benchmark for reaction inhomogeneity because it avoids high experimental noise near the extrema of the range (see Fig. 3). It is shown that the cell SOC when max(ξgold) = 50% is plotted as a function of C-rate, these values appear scattered because different trends emerge for different thicknesses (Fig. 6D). However, when the abscissa is normalized by λ, these values roughly collapse to a single trend (Fig. 6E), with clusters of colored points indicating regions of “low”, “intermediate”, “high” and “extreme” λ. There is some variability within these clusters, which may be due to in plane heterogeneity (see next sections), non-constant local C-rate (Fig. S6, ESI†) and experimental error. However, the results in Fig. 5 and 6 support the hypothesis of a scaling law between λ and reaction inhomogeneity in the through-thickness of the electrode. This mirrors previous experimental and theoretical work showing a scaling law between λ and plating onset,45 but additional experiments with post-mortem analysis are needed to connect the roles of reaction inhomogeneity and plating onset in a quantitative way.
3.3 Ex situ measurements of through-plane reaction inhomogeneity and plating onset
To bridge the gap between measurements of reaction homogeneity and plating onset, and to further validate the scaling law and numerical model, fast charging experiments in coin cells with ex situ imaging were conducted (Fig. 2E and F). These experiments concurrently measured local SOC profiles (Fig. 7A–C), plating onset (Fig. 7D and E), as well as in-plane reaction inhomogeneity (Fig. 7F) via post-mortem (i.e., ex situ) imaging of the surface (for plating) and cross section (for reaction profiles). By charging multiple samples to progressively higher SOC, the onset of lithium plating is determined within a 10% interval, along with the associated local SOC profiles. To this end, a 100 μm electrode was charged at 1C and a 50 μm electrode was charged at 4C. These conditions were chosen to achieve constant λ and thereby similar intercalation profiles and plating onset. Note that the actual measured thicknesses of the 50 μm and 100 μm cells were 54 and 102 μm, respectively, so the thinner cell had a slightly higher λ than the thicker cell.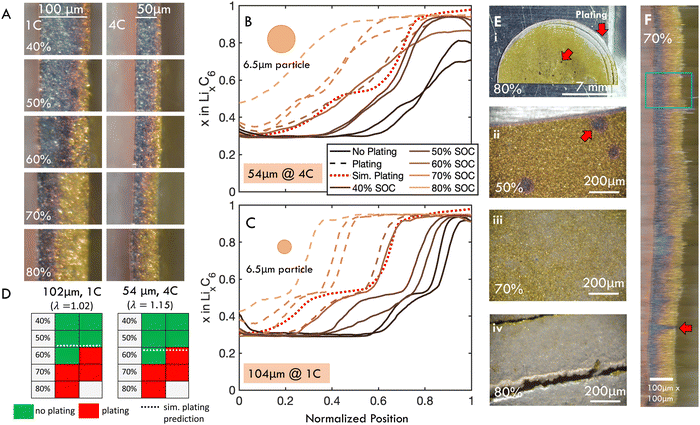 | ||
| Fig. 7 Post-mortem “ex situ” imaging of dissected coin cells was used to simultaneously measure reaction profile and identify plating for an approximately 50 μm thick graphite electrode charged at 1C and 100 μm thick electrode charged at 4C. C-rate was chosen to keep λ constant the cells, but actual thicknesses were 54 and 102 μm, measured post-mortem, meaning the thinner cells had slightly higher λ. (A) Representative sections of post mortem cross-sectional images. (B) and (C) Calculated local SOC (SOCloc) as a function of through-plane position from post-mortem imaging of a subsection of the electrode with (B) 54 and (C) 102 μm thickness. Dashed lines represent electrodes with observed plating, whereas solid lines indicate no plating. SOC profile at plating onset predicted by the p2D model is shown as red dotted line. D50 particle size is shown for reference of length scales. (D) Presence (red) or absence (green) of plating observed for cells charged to SOC indicated for data shown in (B) and (C). Each cell represents a different electrode imaged post mortem. For both electrode thicknesses, plating was first observed in half the cells charged to 60% SOC, and observed for all cells charged above 70% SOC. This agrees well with the p2D model, which predicted that plating was thermodynamically favorable at 59% and 63% SOC for the 54 and 102 μm cells, respectively (dotted lines). (E) Representative ex situ images of electrode surface, showing the various stages of plating development. Red arrows indicate location of presumed bubble formation and preferential plating near electrode edges. (F) Horizontally stretched composite image of entire electrode diameter. The blue rectangle illustrates extent of data analyzed in (B). Note that data presented in (B) and (C) is from a representative subsection of each electrode, and equivalent figures comprising data from the entire electrode diameters are included in Fig. S9 (ESI†). Full images of all ex situ samples included in Fig. S12 and S13 (ESI†). | ||
The local SOC profiles for the two electrodes are shown in Fig. 7B and C (54 and 102 μm, respectively). These profiles were analyzed from a subsection of the image (blue rectangle in Fig. 7F) to more clearly capture staging. The SOC measurements averaging the entire diameter of the cell are summarized in Fig. S9 (ESI†). While the staging is less pronounced in the thinner sample, the inhomogeneity is roughly equivalent, as predicted by the scaling law.
It follows that plating onset for the two cells occurs roughly at the same SOC (between 60 and 70% SOC), which was predicted by modeling to be 59% and 63% for the 54 and 102 μm cells (λ of 1.02 and 1.15), respectively (Fig. 7D and Tables S2, S3, ESI†). This plating onset range was determined by the observation that both electrodes could charge to 50% SOC without observable plating, exhibited plating in one of two samples charged up to 60% SOC, and plated in all cases when charged up to 70% SOC (Fig. 7D). The SOC profiles for experiments where plating was not observed (solid lines) and observed (dashed lines) are shown in Fig. 7B and C. The simulated reaction profile at plating onset (dotted line) agrees well with experiments. These results suggest that the finite element model can accurately capture both plating onset and reaction inhomogeneity, and that the scaling law dictates reaction inhomogeneity and plating onset simultaneously.
Further, an analytical model can be used to predict plating with λ, as described in ref. 11 and 45, with:
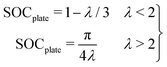 | (3) |
This analytical model predicts a cell SOC at plating onset of 0.62 and 0.66 for the 102 and 54 μm thick samples, as compared to the 0.59 and 0.63 predicted by the numerical model. These results agree well with experiments, and with previous work measuring plating onset by the “dOCV” method in this graphite material.45 In that previous work it was shown that, similarly to the inhomogeneity scaling results in Fig. 6E, the cell SOC at plating onset can be predicted by λ alone according to a “master curve”. In that work, the plating onset results under three C-rates (1, 2, and 4 C) and four electrode thicknesses (from roughly 20–100 μm) collapsed to a single curve predicted by eqn (3) and the same numerical model used herein. Together, these experimental results and that previous work provide evidence for the robustness of these models for generalizing the role of electrode geometry and charge rate on plating onset. This model establishes clear bounds to avoid lithium plating during fast charging procedures.
3.4 Physical picture
Models (validated via these experiments) can directly explain how plating onset and reaction inhomogeneity are related on the length scale of the electrodes, as shown in Fig. 8 (in small particle graphite). In short, plating occurs when the particles at the electrode–separator interface fully saturate with lithium. This occurs after LiC6 phase is present some finite distance into the electrode, as graphite particles have some capacity to intercalate lithium after LiC6 is formed.63 The resultant capacity loss is equal to the degree of inhomogeneity when the lithiated graphite/separator interface cannot appreciably absorb more lithium, which makes lithium metal plating favorable thermodyamically and kinetically. Indeed, eqn (3) calculates the cell capacity at plating onset as the cell state of charge when the graphite/separator interface is fully intercalated (using a simplified intercalation model).11,45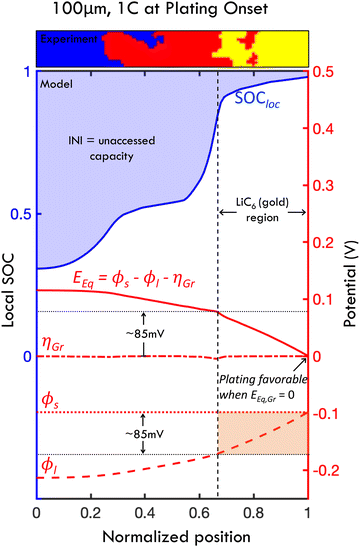 | ||
| Fig. 8 Mechanism of lithium plating from the interplay of transport effects and thermodynamic behavior, and relationship between reaction inhomogeneity and plating onset. Results shown from the p2D numerical model of a 100 μm thick graphite anode charged at 1C. The local SOC (blue line), equilibrium potential Eeq, overpotential ηGr, solid phase potential ϕs and liquid phase potential ϕl are shown at the instant when plating onset occurs in the simulation. Plating onset becomes thermodynamically favorable when Eeq → 0 (when ηGr is small), and consequently when SOCloc approaches 100% at the graphite/separator interface. Thus, the cell SOC at plating onset is defined by the reaction profile at this instant. At this point, INI, showed in shaded blue, represents the unaccessed capacity due to early onset plating, which explicitly defines the relationship between reaction inhomogeneity and plating mathematically. The reaction profile (i.e., local SOC) is determined directly from Eeq, and the level of inhomogeneity is equatable to the decrease of Eeq from the current collector (Z = 0) to the separator (Z = 1). With relatively fast interfacial reaction rates, this Eeq gradient is defined approximately by the change in ϕl which is defined directly from transport behavior (with large ϕl arising at high C-rates due to transport issues). Since plating occurs when SOC at the graphite-separator interface approaches 100% (i.e., full lithium saturation), a significant portion of the electrode appears gold due to LiC6 formation, which appears before full local saturation (Fig. 3C). A small slice of a processed (“ex situ”) experimental image of local particle partitioning is shown above in the plot to demonstrate this phenomenon at the first experimental observance of plating. Due to the thermodynamic behavior of lithiated graphite (see OCV in Fig. 3C), this gold region is present for all locations where Eeq < 85 mV, and corresponds to where ϕl drops by less than 85 mV (due to transport effects). Note that charging where polarization of ϕl is less than 85 mV will lead to little capacity loss (see Fig. S10, ESI†). | ||
To understand this mechanism on a physical and quantitative level, the local electrochemical environment must be considered. Specifically, the local potentials in the porous electrode – and their relationship to intercalation – explain the interplay of the thermodynamic, electrolyte transport and interfacial reaction phenomena leading to plating. Fig. 8 shows the simulated SOC, equilibrium potential (Eeq), overpotential for the graphite intercalation (ηLi), liquid phase potential (ϕl) and solid phase potential (ϕs) at the instant of plating onset for a 100 μm cell charged at 1C. In the mechanism, the applied current builds up a gradient in the liquid phase potential ϕl through the electrode thickness due to limitations in electrolyte mass transport. The graphite equilibrium potential (representing the chemical potential during graphite lithiation) is related to these via Eeq = ϕs − ϕl − ηGr; in this simulation, the graphite overpotential ηGr is small (i.e., interfacial reaction variable is small due to fast interfacial kinetics) and ϕs is roughly constant (due to high conductivity in graphite). It follows that gradients in equilibrium potential and liquid potential are roughly equivalent (∇Eeq = −∇ϕl). Physically, this means that the potential gradients due to sluggish transport are balanced by chemical potential gradients from resultant lithiation reactions. The resultant local SOC profile (SOCloc) is defined directly from the Eeq (see Fig. 3C), with the observed waves of intercalation occurring where the local Eeq reaches voltage plateaus at which phase transitions occur (because of the nonlinear mathematical relationship between equilibrium potential and degree of lithiation, i.e. due to staging). This electrochemical environment provides a mechanistic explanation of the scaling laws observed herein, because the reaction inhomogeneity parameter λ (which balances electrolyte transport and electrode thermodynamic properties) is used to directly define the relationships between ϕl, Eeq and χ (as derived from partial differential equations in ref. 11). Consequently, the profile of intercalation with respect to normalized position can be quantified for a given value of λ (as shown in the experiments in Fig. 5 and 7). It follows that λ also predicts plating onset because plating is directly related to local intercalation events within the electrode.
Plating is thermodynamically favorable when the lithium overpotential
| ηLi = Eeq + ηGr = 0. | (4) |
In these simulations, this occurs at the graphite–separator interface when graphite particles become fully saturated with lithium at that position, and, in turn, Eeq approaches zero (Fig. 8; see also Fig. 3C for relationship between χ and Eeq). With this information, it is clear that plating onset and reaction inhomogeneity are mathematically related to one another, as both are defined explicitly by the Eeq profile. Specifically, the amount of unaccessed capacity due to plating onset is equal to INI.
Based on this local electrochemical picture, the degree of accelerated plating can be quantitatively defined in terms of thermodynamic thresholds of the graphite material. Under the assumption of relatively fast reaction kinetics in the present model, there is a thermodynamic risk of plating before a complete charge when Eeq and ϕl drops across the cell exceed a threshold of 85 mV, since the LiC6 phase only occurs when the equilibrium potential is below this threshold (Fig. 3C). In Fig. 8, it is observed that only about 30% of the simulated electrode has formed LiC6 phase at the instant of plating onset; this is also observed in the representative slice of the ex situ experimental intercalation profile shown at the top of the figure (which is charged to 60% SOC, and is the earliest observed plating experiment). Conversely, if the ϕl drop is limited to less than 85 mV, via charge rate, electrode thickness or engineering of porosity or heterostructures, the entire cell can reach LiC6 phase, achieving a capacity of well over 80% without plating (Fig. S10, ESI†). It is important to note that this mechanism is based on a model that predicts relatively small overpotential variations ηGr relative to electrolyte potential variations (Fig. 8).
Graphite materials with sluggish interfacial reaction kinetics and solid electrolyte interphase (SEI) resistance can have a somewhat different potential landscape, and also affect intercalation. This condition is described in Fig. S11 (ESI†). Under these conditions, the overpotential barrier for lithium intercalation can lead to predictions of thermodynamically favored plating that are somewhat earlier that predicted with “fast” interfacial reaction kinetics, and have altered scaling behavior.11 Additionally, the intercalation “waves” observed during fast charging are predicted to be less pronounced with a more even reaction profile. However, as observed in Fig. S11 and ref. 11 (ESI†), the difference in capacity loss due to differences in interfacial reaction kinetics is secondary to the role of transport limitations (gradients in liquid phase potential). It is notable that the thinner samples for both operando (66 μm) and ex situ experiments (54 μm) described here had somewhat less pronounced intercalation gradients than thicker electrodes (100 > μm) (Fig. 5 and 7) which this may indicate that sluggish interfacial kinetics may be causing this. However, the thinner operando samples had slightly higher porosity (and lower tortuosity) than the thicker ones, resulting in a lower λ. Also, the D50 particle size for the graphite is 6.5 μm, which is on the order of the size of the reaction gradient Fig. 7, so these differences could also be attributed to continuum model assumptions, i.e. the optical “resolution” provided by the particles, which undergo phase transformations discretely. Future work is necessary to quantify these effects.
While the above analysis evaluates thermodynamic thresholds of plating, in reality there will be a kinetic barrier to local nucleation of plating on lithiated graphite particles, which further delays it by some amount. This kinetic barrier can be very significant, on the order of −100 mV, but has been difficult to accurately quantify.63
Finally, while small particle graphites are only considered here to simplify the understanding of local electrochemical environments, larger particle sizes will lead to differences in plating for local C-rates large enough to create intra-particle reaction inhomogeneity. As is true in both small and large particles, plating is expected to happen when particle surfaces at the graphite/separator interface saturate with lithium.63 However, since larger particles have less uniform intercalation, plating will always occur earlier on in the charge in comparison to smaller particles.74
3.5 In-plane reaction inhomogeneity and plating onset location
The ex situ methodology allows for inspection of in-plane reaction inhomogeneity through the entire electrode cross section as well as plating location on the graphite/separator surface. In the cross sectional view, it is evident that staging fronts advanced at somewhat different rates across the electrode diameter (Fig. 7F). This in-plane inhomogeneity is a well-documented phenomenon,53,54,64,75 and implies that there may be non-constant currents locally in the sample, even when a constant charge rate is applied to the entire sample. Thus, it is notable that the reaction profiles in Fig. 7B and C analyze only sub-area of the cross section (blue rectangle), and smaller sections were chosen to demonstrate the similarity in staging behavior between ex situ experiments and operando experiments. Indeed, the image-derived SOC of the operando experiments (which only imaged the anode locally) indicated variations of local intercalation current during fast charging (see Fig. S6, ESI†)These local charge rate inhomogeneities may raise questions whether conclusions based on local imaging are accurate. An analysis of the whole electrode (see Fig S9, ESI†) by averaging the intercalation profile across the entire imaged diameter did not show clear staging fronts due to in-plane inhomogeneity. However, the calculated values of imaged SOC and of reaction inhomogeneity of this sub-area fall within a few percent of the electrode bulk for all samples (Fig. S9, ESI†), meaning that the smaller subsets likely provide a good estimate to overall heterogeneity in the entire electrode. It is also notable that in some samples, isolated pockets of less lithiated phases are visible, both on the separator surface and in cross section (red arrows in Fig. 7E and F), which are attributed to gas bubbles formed during the fast charge cycle, a phenomenon observed infrequently in the in situ mode as well.
These experiments also investigated how plating progressed with increasing cell SOC. To observe this, the entire electrode surface was imaged after the charged electrode was disassembled. Plating initiation is known to be a highly localized process,29,30 and small patches of plating were observed initially. As SOC was increased, more uniform and severe plating occurred at higher cell SOC (Fig. 7E). Plating initiated preferentially at the edges of the electrode and at sites of other defects, as seen in Fig. 7E(i).76
3.6 Reaction dynamics and plating in architectured electrodes
To quantify the impact of architectured channels on reaction inhomogeneity, graphite electrodes with screen printed channels were imaged in cross section during fast charging using the operando experimental setup (Fig. 9). p2D simulations of the channel geometry were also conducted using the same material model as shown previously. The model idealized the geometry as an axisymmetric channel, which assumes that the channels do not interact because their large spacing of 400 μm (Fig. 9A).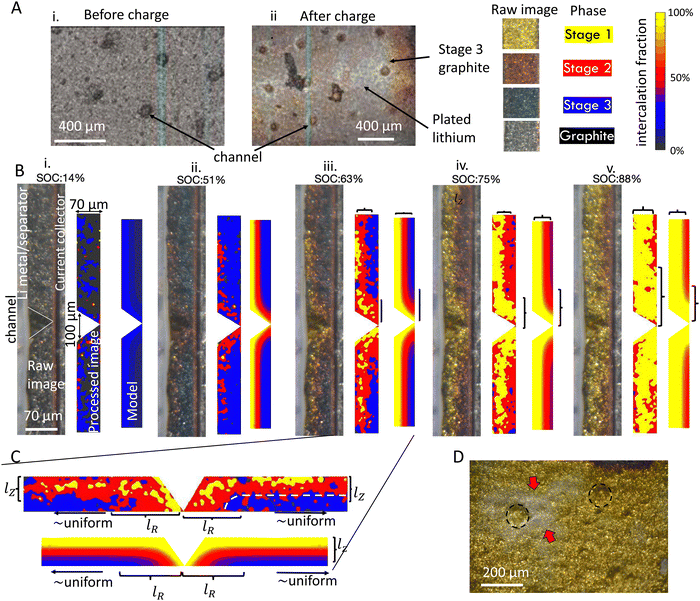 | ||
| Fig. 9 Reaction progression of graphite anode with a channeled architecture. (A) Electrode architecture. (B) Reaction progression for a 4C charge at increasing SOC ((i) through (v)). The raw image, processed image showing phases, and FEM simulation are shown on the left, center and right for each SOC. The colors in the processed image represent the discrete phases (graphite, Stage 1 etc.) whereas the colored contours in the simulation show the simulated SOC. The colors in the simulation were defined to represent the separate phases from the OCV in Fig. 3C, to facilitate comparison between simulation and experiment. (C) Zooming in to (iii) reveals that there is a characteristic length scale lR near the channel where the reaction is more uniform. Past this distance, the reaction is roughly uniform in the in-plane direction (horizontal direction in (C).). This is schematically shown when the reaction contours in the in-plane direction are parallel to the electrode surface (indicated by the white dashed line). (D) Preferential plating near channel edges occurred (arrows near dashed circles), as shown in this post mortem image of a coin half-cell charged to 90% at 2C. | ||
Fig. 9B(i)–(v) shows the reaction progression around a conical channel. This electrode had a thickness of 70 μm and was charged at 4C. The reaction progression is shown in the raw experimental image (left), a processed image indicating local stages (center), and the simulation (right) for 14% to 88% SOC (Fig. 9B(i)–(v)). The colors in the processed image represent the interpreted discrete phases (graphite, Stage 2L etc.) whereas the colored contours in the simulation show the simulated SOC with continuously varying concentration. In both experiment and simulation, there is a clear improvement in through-thickness reaction uniformity near the channel walls. This improvement is more significant at higher states of charge (Fig. 9B(iii)–(v)) than lower states of charge (Fig. 9B(i) and (ii)). This can be attributed to increase in inhomogeneity at higher states of charge due to staging (see Fig. 5). Examining these distributions closely, it is clear that there is a characteristic length scale lR defining the extent of the channel's effect on reaction distribution in the radial direction (Fig. 9C). Past this characteristic distance, the reaction is uniform in the in-plane direction, meaning that particles sufficiently far away are not affected by the channel. The increase in SOC near the channel decays nonlinearly from the channel wall outward (in-plane direction), similarly to what is observed in the through thickness direction (with length scale lZ). These results are consistent at other C-rates, as shown in Fig. S14 and Movies in ESI.†
Comparing simulations to experiment, there is reasonable agreement at 14% SOC (Fig. 9B(i)) and at higher states of charge (Fig. 9B(iii)–(v)). However, it is noteworthy that at approximately 50% cell state of charge (Fig. 9B(ii)), the simulation predicts significant progress of the stage 1 phase, while the experiment shows the presence of stage 2 and stage 2L only. Qualitatively, the image-derived state of charge in this experiment suggests an average particle state of charge significantly below 50%, which accounts for the substantial disagreement. This is likely due to long-range in-plane inhomogeneity as observed in ex situ results, which leads to variable local currents during the charging procedure, as discussed previously (See Fig. S6, ESI†).
Additional ex situ measurements were conducted, where these cells were charged in coin cells to the point of plating onset Fig. 9D. It was observed that plating occurred preferentially the edge of channel surfaces. This was predicted by the model as well, as the intercalation progressed the fastest at this point.
4 Discussion
Predicting lithium plating is highly relevant for design and optimization of conventional and architectured electrodes. However, fast charging of anodes and plating are complex coupled processes and mathematical models predicting this behavior are highly nonlinear and have a large number variables. Consequently, calibration and interpretation of results is difficult and potentially unreliable, as parameters describing these material systems vary largely between different works in the literature.Remarkably, this paper demonstrates, with extensive experimental and theoretical evidence, that reaction dynamics and the lithium plating process during fast charging can be understood through a simple scaling law, as demonstrated by self-similar reaction profiles between electrodes of different mass loadings, geometries and charge rates (Fig. 5). Further, these results suggest that plating onset is described directly from the reaction profile when local graphite near the separator fully saturates with lithium, and as a result both processes obey the same scaling law (Fig. 8). These observations imply that this scaling can be leveraged for parameter reduction not only for theoretical calculations11,45 but also for reducing the needed volume of experimental measurements. The principles described in these experiments are applied to architectured electrodes, where the degree of reaction uniformity due to electrolyte filled channels is quantified for the first time.
A key to elucidating the underlying simplicity in fast charging phenomena in this work is the decoupling of fast charging behavior on the electrode length scale vs. the intra-particle length scale. The present study achieved this decoupling by using small-particle graphite material, which reduced lithiation gradients within individual particles. In contrast, many previous works that have studied operando intercalation of graphite anodes have used large graphite particle sizes,21,56,57,62,64 which complicates analysis due to simultaneous reaction gradients within particles and through the electrode.44,74 However, Gao et al. recently conducted experiments on a single large particle (≈ 1 mm) to eliminate electrode-level effects on charging dynamics.63 Their operando colorimetry experiments provided strong evidence that saturation of the graphite particle surface with lithium was the dominant mechanism for plating onset, making it both thermodynamically and kinetically favorable for lithium metal nucleation. This study also shows that “full” saturation at the particle surface occurs after the gold LiC6 phase front extends a certain length scale into the particle; this can be explained because these particles can absorb some lithium (i.e., has some solid solution behavior) after LiC6 is first observed.68 These results in large single particles63 are strikingly similar to the electrode-level reaction dynamics and plating phenomena described herein. Indeed, it was shown that lithium saturation of graphite at the electrode–separator interface leads to plating onset (Fig. 8) (this is analogous to the plating when the single particle surface was saturated in Gao et al.). It was also experimentally observed that the LiC6 phase penetrated a certain length scale into the electrode prior to plating onset (Fig. 7), mirroring the results from the single particle study.63
In contrast to single particles, the charge-rate-limiting effect that dominates reaction inhomogeneity and ultimate plating on the whole electrode scale is due to the interplay of the liquid-phase transport and thermodynamics of graphite lithiation. This relationship is described in Fig. 8 and ref. 11, 45. It is shown that early onset plating occurs when transport limitations cause gradients in the electrolyte liquid phase potential to exceed approximately 85 mV across the electrode thickness, which leads to an incomplete reaction through the electrode when the graphite/separator interface is overcharged. It is the 85 mV height of the final plateau of graphite's equilibrium potential response (the Stage 2 to Stage 1 transition in Fig. 3C) that defines the electrode's thermodynamic tolerance to cell polarization from transport phenomena. Interfacial reaction kinetics may play a role as well at high C-rates (Fig. S10, ESI†), but the evidence here suggests that this limitation is secondary in comparison to transport limitations (at least in the graphite here which had only a small number of charging cycles). Further, it has been demonstrated with modeling that the scaling behavior based would differ from eqn (1) if kinetic limitations were a major factor in describing spatially dependent intercalation dynamics. It is also presumed that additional nucleation overpotential necessary for plating onset at particle surfaces (which can exceed −100 mV)63 would increase that tolerance to cell polarization. Yet, plating predictions based on the thermodynamic assumption have been demonstrated to be accurate experimentally (see Fig. 7 and ref. 45). Future work is necessary to better quantify the role of the nucleation barrier at fast charge rates in the context of electrode-level plating onset.
The robustness of the scaling laws in describing reaction dynamics and plating (both herein and elsewhere45) can provide important practical uses. First, these scaling laws provide bounds for safe charging without plating with respect to C-rate, mass loading, and electrode/electrolyte material properties. (It is noted that mass loading is defined by electrode thickness and porosity, and indirectly affects the tortuosity, all of which are defined in eqn (1)). Since it is shown here that the reaction inhomogeneity progression follows a trend that is described by λ (Fig. 6), this also implies that parameter reduction can be employed in the study of these systems. This can be applied to predict plating and reaction dynamics from a limited number of experiments. It may also present an additional means of PET model validation, which is in theory more prone to overfitting due to its large number of parameters. Additionally, parameter reduction can be used to develop simplified numerical models,11 which can aid in reducing the computation time of iterative (e.g., optimization) simulations. Previous theoretical work has shown that scaling laws for plating onset and reaction inhomogeneity are robust over a wide range of electrolyte (e.g., diffusivity, transference number) and electrode parameters (electrode thermodynamic behavior, lithium intercalation capacity).11,45 However, further experimental work is needed to test the robustness of these scaling laws across other electrolytes, anode materials (e.g., silicon, silicon-graphite blends, synthetic vs. natural graphite) and charging conditions (notably temperature). Similarly, theoretical work has shown that the scaling law for lithium plating was the same for both half-cells and full-cells (as long as there is no lithium ion depletion in the electrolyte),45 and additional experimental data is needed to confirm this. Further, previous theoretical work has demonstrated similar scaling relationships in cathodes undergoing fast charging, suggesting that the scaling law can be generalizable to other electrode materials.46,47 The scaling laws describing intercalation dynamics could in in principle be applied in solid state batteries where electrolyte is integrated within electrodes (e.g., cathode with catholyte) so long as porous electrode theory sufficiently describes these electrodes, and the assumptions described here are accurate.
Additionally, the p2D model used herein accurately predicted both local state of charge (Fig. 5, 7 and Fig. S8, ESI†) and plating onset (Fig. 7). It is emphasized that this validation contrasts with other studies due to the much larger number of operando experiments (e.g., ref. 57,58), and the fact that the model can predict the entire time history of the reaction profile with reasonable accuracy. This agreement is important, as the p2D is widely used but has known limitations. The first limitation is that electrodes are known to have local inhomogeneities due to their complex microstructure, leading to in-plane nonuniformities in reaction and localized plating (Fig. 7) not captured by the p2D model or other continuum PET models. Next, the p2D model does not well capture the phase separation behavior of graphite (see Section S1 for discussion, ESI†).63,77,78 These two effects are observed experimentally on small length scales, where individual particles can exist in one phase while neighboring particles exist in a different phase (i.e., the “mosaic pattern”). However, it is demonstrated here that the state of charge averaged over a large enough number of particles will be in between the states of charge of each the two phases. In other words particles can individually phase separate yet behave as a solid solution macroscopically. Thus, the continuum assumption in p2D (which treats lithiation as a solid solution) provides a reasonable description, at least for the small particle graphite described here.
In addition to defining design criteria for conventional cells, the relationship between plating onset and reaction inhomogeneity described here is essential for the design of architectured electrodes. Many studies have shown that fast charging performance is improved with architectured designs, compared to unstructured electrodes and that these architectures increase reaction uniformity in model simulations.7,8,15 However, the effect of the architectured electrodes on reaction profile has not been experimentally measured to our knowledge. This work has demonstrated that channels improve reaction uniformity for a specific length scale from the channel radially into the bulk (Fig. 9). This experimental quantification provides important information for model calibration of architectured electrodes, which can aid design. Future work with these operando or ex situ experiments can reveal how changes in porosity, channel size and spacing or other design factors can affect reaction uniformity. Importantly, it was shown here that plating onset occurs first near the channel entrance. It is therefore critical to fully understand intercalation around these heterostructures as they may have the potential to accelerate both lithiation and plating.
While the experimental results described herein are consistent with simulations, the potential sources of error in each experimental technique must be considered in the interpretation of these results. A thorough discussion of potential sources of error, as well as the experimental design and strategy to mitigate these errors, is discussed in Section S2 (ESI†). Finally, the role of temperature here was not considered for simplicity, and future work is needed to study temperature effects.
5 Conclusions
This work quantifies the related phenomena of reaction inhomogeneity and lithium plating during fast charging in graphite anodes, and demonstrates that these processes obey a simple scaling relationship. To study this process, local reaction behavior and plating onset were measured using operando and ex situ optical microscopy techniques and combined with modeling approaches. In departure from previous studies with similar microscopy techniques, a large number of high-throughput experiments were required, and practical electrode thicknesses (50–160 μm) were studied in a truly 1D geometry. Half-cells with a small particle graphite were chosen to reduce the effects of intra-particle reaction gradients, and thus study charging behavior on the electrode length scale independently. Both the observed reaction history and plating onset could be accurately predicted with a pseudo-2D finite element model developed for this material. It follows that the entire history of the local lithium intercalation reaction and plating onset obey a scaling law in terms of a nondimensional “reaction inhomogeneity parameter” λ, generalizing trends in charge rate, electrode mass loading and geometric parameters. Specifically, self-similar reaction profiles for different electrodes charged at different rates were observed if λ was constant, and plating occurred at the same cell state of charge. From a mechanistic standpoint, the evidence provided herein suggests that plating onset can occur when the graphite-separator interface is fully saturated with lithium, which happens after LiC6 is observed some finite distance into the electrode. Since plating onset is directly defined by local intercalation distribution, both exhibit the same scaling law. It is demonstrated with modeling that this can be quantified from the local electrochemical environment, where the interplay between anode thermodynamic behavior (gradients in equilibrium potential) and electrolyte transport (gradients in liquid phase potential) dictate reaction inhomogeneity and accelerated plating at high C-rates. The evidence herein suggests that interfacial reaction kinetics for graphite intercalation plays at most a secondary role in this process in the graphite material studied here. Finally, similar experiments and modeling elucidate the local intercalation behavior of electrodes with conical, electrolyte-filled channels. The results show that there is a characteristic length scale for which the channel decreases intercalation gradients.Together, these results provide a simplified, yet fundamental understanding of reaction dynamics and lithium plating during fast charging, establishing clear bounds on maximum “safe” charge rate based on mass loading and electrode structure. The models and scaling laws herein provide a framework for simplifying design processes, optimization processes, and experimental evaluation of high performing monolithic and architectured electrodes. Finally, the integrated experimental and modeling approaches here may be extended to a wide range of other battery chemistries (e.g., different electrolytes, Si-graphite anodes).
6 Methods
6.1 Electrode material
Sheets of anode material were prepared as follows. Graphite powders (P5), carbon black (C45, Timcal) and polyvinylidene difluoride (PVDF, Kureha 9300) were used as received from supplier in this study. To prepare the slurry, the graphite and carbon black were dispersed in the PVDF binder solution (8 wt% PVDF in N-methyl-2-pyrrolidone (NMP)) and well mixed by the slurry mixer (AR-100, Thinky). The homogenous slurry was coated onto Cu foil using the tape casting method and then dried at 40 °C for 2 hours following by drying at 80 °C under vacuum overnight. The dried electrodes with different mass loadings were calendared to targeted thicknesses with the same porosity for all electrodes. Three batches of electrodes were fabricated with the same porosity of 35% and different thickness of 50, 100 and 150 μm. All dried electrodes were composed of 92 wt% graphite, 2 wt% carbon black, and 6 wt% PVDF.6.2 Operando experiments
The graphite electrodes were cut into 1 cm squares with a fresh razor blade, weighed, and vacuum dried again at 90°C overnight. Half-cells were assembled under inert atmosphere in a glovebox. The electrode stack consisted of the graphite anode, a porous separator (alumina-coated polyolefin, Celgard) and a lithium metal counter electrode clamped together between two spring-loaded 316 stainless steel blocks. Care was taken such that the active materials protruded about 25 microns from the blocks before being inserted against the sapphire window in the custom optical test cell. This ensured good contact with the window and eliminated any alternate diffusion pathway or edge effects from an unconfined surface. The cell was then flooded with 0.7 mL electrolyte (1.2 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC(3
EMC(3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7), Tomiyama) and sealed, after which full stack pressure was applied.
7), Tomiyama) and sealed, after which full stack pressure was applied.
After resting for 4 hours, cells were cycled at room temperature on a potentiostat (VMP3, Biologic). After a single formation cycle, rate tests were performed. For the slow rate experiments, we are able to employ a standard CC/CV charge protocol with a cutoff voltage of 10 mV vs. Li/Li+. At higher rates, the ohmic drop combined with the high impedance of our test cell causes the lower limit to be reached much earlier in the charge. In these instances, the cells are permitted to drop to negative voltages (vs. Li/Li+) in order to prolong the constant current condition. Though this enters the regime where plating is thermodynamically possible, we maintain the constant current condition until reaching the capacity established during the formation cycle.
It is noted that the electrodes visibly expand primarily during the formation cycles, as observed in the movies provided in ESI† (possibly due to a combination of electrolyte absorption and SEI formation). Thus the thicknesses (and adjusted porosities) measured post-mortem are used for calculation of λ as well as simulation parameters (Table S1 lists condition for each experiment conducted herein, ESI†).
6.3 “Ex situ” imaging experiments
In coin cells, graphite anodes were cycled in a half-cell configuration at high rates of charge and then immediately frozen and dissected under argon to determine both the extent of lithium plating and the through-thickness distribution of intercalated lithium. Electrode sheets were punched into 14 mm discs before vacuum drying. Half-cells were assembled in CR2032 coin cell cases under inert atmosphere. The stack consisted of a 16 mm lithium metal disc, a porous separator (polyolefin, uncoated, Celgard), 3–5 drops of electrolyte, and the graphite anode, all sandwiched between two 0.5 mm spacers (to ensure planar contact) and a wave spring. Each cell underwent two formation cycles at C/10 (C/20 for 150 μm samples), after which the high rate tests were conducted. The actual cell capacity and high rate current was calculated from the discharge of the second formation cycle.All intercalation and plating/stripping processes were halted at varying SOCs by plunging the coin cell into a dewar of liquid nitrogen mid-cycle, and subsequently by rinsing the frozen electrodes 4–5 times in dimethyl carbonate once disassembled under argon in a glovebox. Upon disassembly, the electrolyte was observed to still be frozen. Electrodes were then placed into a second custom airtight visualization cell for imaging outside the glovebox. The electrode was thoroughly examined under magnification to identify plated lithium anywhere on the surface adjacent to the separator. The electrodes were also sliced precisely in half with a razor blade, and the cross section was imaged to capture the instantaneous intercalation profile.
6.4 Imaging
All images where captured using a digital single-lens reflex camera with an intervalometer (D5200, Nikon), and a long-working-distance microscope objective (M-plan Apo 20×, Mitutoyo) mounted to a 200 mm telephoto lens (Nikon) focused at infinity (Fig. S15, ESI†). The samples were illuminated from multiple angles with fiber optic light sources.Images were processed in Matlab, beginning with a registration step where the electrode/separator interface was fixed so that cyclic volume expansion due to intercalation had minimal confounding effects on the analysis. A small Gaussian blur was applied to each image to remove shadows between graphite particles. The blurred images were then dissected by assigning each pixel to a certain phase. The appropriate phase is identified by minimizing the Euclidean distances in CIELAB color space to each of four target colors:
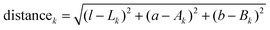 | (5) |
| k ∈ {graphite, Stage 2L, Stage 2, Stage 1} | (6) |
The phase fractions ξ as a function of depth in the electrode are found by summing the number of pixels assigned to each phase xj vertically in the image (in-plane direction).
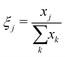 | (7) |
These phase fractions can easily be converted to local SOC, SOCloc by multiplication with the mean stoichiometry of each respective phase:
| SOCloc = 0.29ξBlue + 0.52ξRed + 0.95ξGold | (8) |
For each time in the charge, the “particle average SOC” SOCapp is calculated as
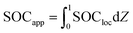 | (9) |
6.5 Modeling
The governing equations of the model are summarized in ref. 11. Since same graphite material and electrolyte were used, the present study used parameters as that described in ref. 45, except for the tortuosity correlation and the equilibrium potential. The equilibrium potential used herein was obtained using a C/40 charge in a coin cell (see Fig. S16, ESI†). The through-plane tortuosity correlation was empirically determined to be
| τZ = εe−1.5 | (10) |
Lithium plating onset was determined by the thermodynamic criteria. Lithium plating is thermodynamically possible when
| ϕs − ϕl = 0 | (11) |
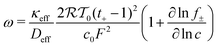 | (12) |
 is the activity coefficient, T0 is temperature and R is the universal gas constant.73 Temperature effects were not considered. The scaling described herein is robust when any of the electrolyte variables are varied over a range of relevant values, summarized in previous theoretical studies.45,73
is the activity coefficient, T0 is temperature and R is the universal gas constant.73 Temperature effects were not considered. The scaling described herein is robust when any of the electrolyte variables are varied over a range of relevant values, summarized in previous theoretical studies.45,73
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U. S. Department of Energy Office of Energy Efficiency and Renewable Energy (EERE) under the Advanced Manufacturing Office, award number DE-EE0009111.References
- Q. Liu, C. Du, B. Shen, P. Zuo, X. Cheng, Y. Ma, G. Yin and Y. Gao, Understanding undesirable anode lithium plating issues in lithium-ion batteries, RSC Adv., 2016, 6(91), 88683, 10.1039/c6ra19482f.
- A. M. Colclasure, A. R. Dunlop, S. E. Trask, B. J. Polzin, A. N. Jansen and K. Smith, Requirements for Enabling Extreme Fast Charging of High Energy Density Li-Ion Cells while Avoiding Lithium Plating, J. Electrochem. Soc., 2019, 166(8), A1412–A1424, DOI:10.1149/2.0451908jes.
- K. H. Chen, V. Goel, M. J. Namkoong, M. Wied, S. Muller, V. Wood, J. Sakamoto, K. Thornton and N. P. Dasgupta, Enabling 6C Fast Charging of Li-Ion Batteries with Graphite/Hard Carbon Hybrid Anodes, Adv. Energy Mater., 2021, 11, 2003336, DOI:10.1002/aenm.202003336.
- X. Feng, M. Ouyang, X. Liu, L. Lu, Y. Xia and X. He, Thermal runaway mechanism of lithium ion battery for electric vehicles: A review, Energy Storage Mater., 2018, 10, 246, DOI:10.1016/j.ensm.2017.05.013.
- M. Dubarry, B. Y. Liaw, M. S. Chen, S. S. Chyan, K. C. Han, W. T. Sie and S. H. Wu, Identifying battery aging mechanisms in large format Li ion cells, J. Power Sources, 2011, 196, 3420, DOI:10.1016/j.jpowsour.2010.07.029.
- V. Agubra and J. Fergus, Lithium ion battery anode aging mechanisms, Materials, 2013, 6, 1310, DOI:10.3390/ma6041310.
- W. Mai, F. L. E. Usseglio-Viretta, A. M. Colclasure and K. Smith, Enabling fast charging of lithium ion batteries through secondary-/dual- pore network: Part II - numerical model, Electrochim. Acta, 2020, 341, 136013, DOI:10.1016/j.electacta.2020.136013.
- Y. Qi, T. Jang, V. Ramadesigan, D. T. Schwartz and V. R. Subramanian, Is There a Benefit in Employing Graded Electrodes for Lithium-Ion Batteries?, J. Electrochem. Soc., 2017, 164(13), A3196–A3207, DOI:10.1149/2.1051713jes.
- V. Ramadesigan, R. N. Methekar, F. Latinwo, R. D. Braatz and V. R. Subramanian, Optimal porosity distribution for minimized ohmic drop across a porous electrode, J. Electrochem. Soc., 2010, 157, A1328, DOI:10.1149/1.3495992.
- S. Golmon, K. Maute and M. L. Dunn, A design optimization methodology for Li+ batteries, J. Power Sources, 2014, 253, 239, DOI:10.1016/j.jpowsour.2013.12.025.
- A. S. Mijailovic, G. Wang, Y. Li, J. Yang, W. Lu, Q. Wu and B. W. Sheldon, Analytical and numerical analysis of lithium plating onset in single and bilayer graphite electrodes during fast charging, J. Electrochem. Soc., 2022, 169, 060529, DOI:10.1149/1945-7111/ac73bb.
- K. H. Chen, M. J. Namkoong, V. Goel, C. Yang, S. Kazemiabnavi, S. Mortuza, E. Kazyak, J. Mazumder, K. Thornton, J. Sakamoto and N. P. Dasgupta, Efficient fast-charging of lithium-ion batteries enabled by laser-patterned three-dimensional graphite anode architectures, J. Power Sources, 2020, 471, 228475, DOI:10.1016/j.jpowsour.2020.228475.
- J. B. Habedank, L. Kraft, A. Rheinfeld, C. Krezdorn, A. Jossen and M. F. Zaeh, Increasing the Discharge Rate Capability of Lithium-Ion Cells with Laser-Structured Graphite Anodes: Modeling and Simulation, J. Electrochem. Soc., 2018, 165(7), A1563–A1573, DOI:10.1149/2.1181807jes.
- V. P. Nemani, S. J. Harris and K. C. Smith, Design of Bi-Tortuous, Anisotropic Graphite Anodes for Fast Ion-Transport in Li-Ion Batteries, J. Electrochem. Soc., 2015, 162(8), A1415–A1423, DOI:10.1149/2.0151508jes.
- M. F. Lagadec, R. Zahn, S. Muller and V. Wood, Topological and network analysis of lithium ion battery components: The importance of pore space connectivity for cell operation, Energy Environ. Sci., 2018, 11(11), 3194, 10.1039/c8ee00875b.
- F. Usseglio-Viretta, W. Mai, A. Colclasure, M. Doeff, E. Yi and K. Smith, Enabling fast charging of lithium-ion batteries through secondary-/dual-pore network: Part I-Analytical diffusion model, Electrochim. Acta, 2020, 342, 136034, DOI:10.1016/j.electacta.2020.136034.
- Y. Kim, A. Drews, R. Chandrasekaran, T. Miller and J. Sakamoto, Improving Li-ion battery charge rate acceptance through highly ordered hierarchical electrode design, Ionics, 2018, 24, 2935, DOI:10.1007/s11581-018-2502-x.
- R. Dubey, M. D. Zwahlen, Y. Shynkarenko, S. Yakunin, A. Fuerst, M. V. Kovalenko and K. V. Kravchyk, Laser patterning of high-mass-loading graphite anodes for high-performance Li-ion batteries, Batteries Supercaps, 2021, 4, 464, DOI:10.1002/batt.202000253.
- V. Goel, K. H. Chen, N. P. Dasgupta and K. Thornton, Optimization of laser-patterned electrode architectures for fast charging of Li-ion batteries using simulations parameterized by machine learning, Energy Storage Mater., 2023, 57, 44–58, DOI:10.1016/j.ensm.2023.01.050.
- T. R. Ferguson and M. Z. Bazant, Phase transformation dynamics in porous battery electrodes, Electrochim. Acta, 2014, 146, 89–97, DOI:10.1016/j.electacta.2014.08.083.
- D. P. Finegan, A. Quinn, D. S. Wragg, A. M. Colclasure, X. Lu, C. Tan, T. M. Heenan, R. Jervis, D. J. Brett, S. Das, T. Gao, D. A. Cogswell, M. Z. Bazant, M. D. Michiel, S. Checchia, P. R. Shearing and K. Smith, Spatial dynamics of lithiation and lithium plating during high-rate operation of graphite electrodes, Energy Environ. Sci., 2020, 13(8), 2570, 10.1039/d0ee01191f.
- K. P. Yao, J. S. Okasinski, K. Kalaga, I. A. Shkrob and D. P. Abraham, Quantifying lithium concentration gradients in the graphite electrode of Li-ion cells using operando energy dispersive X-ray diffraction, Energy Environ. Sci., 2019, 12, 656, 10.1039/C8EE02373E.
- S. J. Harris, A. Timmons, D. R. Baker and C. Monroe, Direct in situ measurements of Li transport in Li-ion battery negative electrodes, Chem. Phys. Lett., 2010, 485, 265, DOI:10.1016/j.cplett.2009.12.033.
- M. Ebner, D. W. Chung, R. E. Garcia and V. Wood, Tortuosity anisotropy in lithium-ion battery electrodes, Adv. Energy Mater., 2014, 4(5) DOI:10.1002/aenm.201301278.
- F. L. Usseglio-Viretta, A. Colclasure, A. N. Mistry, K. P. Y. Claver, F. Pouraghajan, D. P. Finegan, T. M. Heenan, D. Abraham, P. P. Mukherjee, D. Wheeler, P. Shearing, S. J. Cooper and K. Smith, Resolving the discrepancy in tortuosity factor estimation for Li-ion battery electrodes through micro-macro modeling and experiment, J. Electrochem. Soc., 2018, 165, A3403, DOI:10.1149/2.0731814jes.
- M. Heß and P. Novak, Shrinking annuli mechanism and stage-dependent rate capability of thinlayer graphite electrodes for lithium-ion batteries, Electrochim. Acta, 2013, 106, 149, DOI:10.1016/j.electacta.2013.05.056.
- D. Fraggedakis, N. Nadkarni, T. Gao, T. Zhou, Y. Zhang, Y. Han, R. M. Stephens, Y. Shao-Horn and M. Z. Bazant, A scaling law to determine phase morphologies during ion intercalation, Energy Environ. Sci., 2020, 13, 2142, 10.1039/D0EE00653J.
- S. Agrawal and P. Bai, Dynamic interplay between phase transformation instabilities and reaction heterogeneities in particulate intercalation electrodes, Cell Rep. Phys. Sci., 2022, 3, 100854, DOI:10.1016/j.xcrp.2022.100854.
- X. M. Liu, A. Fang, M. P. Haataja and C. B. Arnold, Size Dependence of Transport Non-Uniformities on Localized Plating in Lithium-Ion Batteries, J. Electrochem. Soc., 2018, 165(5), A1147–A1155, DOI:10.1149/2.1181805jes.
- X. M. Liu and C. B. Arnold, Effects of Current Density on Defect-Induced Capacity Fade through Localized Plating in Lithium-Ion Batteries, J. Electrochem. Soc., 2020, 167(13), 130519, DOI:10.1149/1945-7111/abb838.
- P. Arora, M. Doyle and R. E. White, Mathematical modeling of the lithium deposition overcharge reaction in lithium-Ion batteries using carbon-based negative electrodes, J. Electrochem. Soc., 1999, 146(10), 3543, DOI:10.1149/1.1392512.
- T. F. Fuller, M. Doyle and J. Newman, Simulation and optimization of the dual lithium ion insertion cell, J. Electrochem. Soc., 1994, 141, 1, DOI:10.1149/1.2054684.
- R. B. Smith and M. Z. Bazant, Multiphase porous electrode theory, J. Electrochem. Soc., 2017, 164, E3291, DOI:10.1149/2.0171711jes.
- A. Schmidt, E. Ramani, T. Carraro, J. Joos, A. Weber, M. Kamlah and E. Ivers-Tiffee, Understanding deviations between spatially resolved and homogenized cathode models of lithium-ion batteries, Energy Technol., 2021, 9, 2000881, DOI:10.1002/ente.202000881.
- M. Ecker, S. Kabitz, I. Laresgoiti and D. U. Sauer, Parameterization of a physico-chemical model of a lithium-ion battery: II. Model validation, J. Electrochem. Soc., 2015, 162, A1849, DOI:10.1149/2.0541509jes.
- A. Garcia, J. Monsalve-Serrano, A. Ponce-Mora and A. Fogue-Robles, Development of a calibration methodology for fitting the response of a lithium-ion cell P2D model using real driving cycles, Energy, 2023, 271, 126992, DOI:10.1149/1945-7111/ad1e3d.
- N. Dufour, M. Chandesris, S. Genies, M. Cugnet and Y. Bultel, Lithiation heterogeneities of graphite according to C-rate and mass-loading: A model study, Electrochim. Acta, 2018, 272, 97–107, DOI:10.1016/j.electacta.2018.03.196.
- Z. Chen, D. L. Danilov, R. A. Eichel and P. H. Notten, Li+ concentration waves in a liquid electrolyte of Li-ion batteries with porous graphite-based electrodes, Energy Storage Mater., 2022, 48, 475, DOI:10.1016/j.ensm.2022.03.037.
- C. Von Luders, J. Keil, M. Webersberger and A. Jossen, Modeling of lithium plating and lithium stripping in lithium-ion batteries, J. Power Sources, 2019, 414, 41 CrossRef.
- R. Chandrasekaran, Quantification of contributions to the cell overpotential during galvanostatic discharge of a lithium-ion cell, J. Power Sources, 2014, 262, 501, DOI:10.1016/j.jpowsour.
- Z. Chen, D. L. Danilov, L. H. Raijmakers, K. Chayambuka, M. Jiang, L. Zhou, J. Zhou, R. A. Eichel and P. H. Notten, Overpotential analysis of graphite-based Li-ion batteries seen from a porous electrode modeling perspective, J. Power Sources, 2021, 509, 230345, DOI:10.1016/j.jpowsour.
- L. Kraft, J. B. Habedank, A. Frank, A. Rheinfeld and A. Jossen, Modeling and simulation of pore morphology modifications using laser-structured graphite anodes in lithium-ion batteries, J. Electrochem. Soc., 2020, 167, 013506, DOI:10.1149/2.0062001JES.
- W. Mei, L. Zhang, J. Sun and Q. Wang, Experimental and numerical methods to investigate the overcharge caused lithium plating for lithium ion battery, Energy Storage Mater., 2020, 32, 91–104, DOI:10.1016/j.ensm.2020.06.021.
- H. Lian and M. Z. Bazant, Modeling lithium plating onset on porous graphite electrodes under fast charging with hierarchical multiphase porous electrode theory, J. Electrochem. Soc., 2024, 171, 010526, DOI:10.1149/1945-7111/ad1e3d.
- A. S. Mijailovic, G. Wang, M. Luo, W. Lu, Q. Wu and B. W. A. Sheldon, Master Curve Describing Reaction Inhomogeneity and Plating Onset during Fast-Charging of Graphite Electrodes, J. Electrochem. Soc., 2023, 170, 070508, DOI:10.1149/1945-7111/acd963.
- F. Wang and M. Tang, A Quantitative Analytical Model for Predicting and Optimizing the Rate Performance of Battery Cells, Cell Rep. Phys. Sci., 2020, 1(9) DOI:10.1016/j.xcrp.2020.100192.
- F. Wang and M. Tang, Thermodynamic Origin of Reaction Non-Uniformity in Battery Porous Electrodes and Its Mitigation, J. Electrochem. Soc., 2020, 167(12), 120543, DOI:10.1149/1945-7111/abb383.
- S. Atlung, B. Zachau-Christiansen, K. West and T. Jacobsen, The composite insertion electrode: theoretical part. Equilibrium in the insertion compound and linear potential dependence, J. Electrochem. Soc., 1984, 131, 1200, DOI:10.1149/1.2115778.
- M. Doyle and J. Newman, Modeling the performance of rechargeable lithium-based cells: design correlations for limiting cases, J. Power Sources, 1995, 54, 46–51, DOI:10.1016/0378-7753(94)02038-5.
- J. S. Newman and C. W. Tobias, Theoretical analysis of current distribution in porous electrodes, J. Electrochem. Soc., 1962, 109, 1183, DOI:10.1149/1.2425269.
- C. Heubner, M. Schneider and A. Michaelis, Diffusion-limited C-rate: a fundamental principle quantifying the intrinsic limits of Li-ion batteries, Adv. Energy Mater., 2020, 10, 1902523, DOI:10.1002/aenm.201902523.
- T. R. Tanim, P. P. Paul, V. Thampy, C. Cao, H. G. Steinruck, J. Nelson Weker, M. F. Toney, E. J. Dufek, M. C. Evans, A. N. Jansen, B. J. Polzin, A. R. Dunlop and S. E. Trask, Heterogeneous Behavior of Lithium Plating during Extreme Fast Charging, Cell Rep. Phys. Sci., 2020, 1, 100114, DOI:10.1016/j.xcrp.2020.100114.
- S. Taminato, M. Yonemura, S. Shiotani, K. Takashi, S. Torii, M. Nagao, Y. Ishikawa, K. Mori, T. Fukunaga, Y. Onodera, T. Naka, M. Morishima, Y. Ukyo, D. Adipranoto, H. Arai, Y. Uchimoto, Z. Ogumi, K. Suzuki, M. Hirayama and R. Kanno, Real-time observations of lithium battery reactions - Operando neutron diffraction analysis during practical operation, Sci. Rep., 2016, 6, 28843, DOI:10.1038/srep28843.
- P. Maire, A. Evans, H. Kaiser, W. Scheifele and P. Novak, Colorimetric Determination of Lithium Content in Electrodes of Lithium-Ion Batteries, J. Electrochem. Soc., 2008, 155, A862, DOI:10.1149/1.2979696.
- B. Shi, Y. Kang, H. Xie, H. Song and Q. Zhang, In situ measurement and experimental analysis of lithium mass transport in graphite electrodes, Electrochim. Acta, 2018, 284, 142, DOI:10.1016/j.electacta.2018.07.079.
- X. Lu, M. Lagnoni, A. Bertei, S. Das, R. E. Owen, Q. Li, K. O’Regan, A. Wade, D. P. Finegan, E. Kendrick, M. Z. Bazant, D. J. L. Brett and P. R. Shearing, Multiscale dynamics of charging and plating in graphite electrodes coupling operando microscopy and phase-field modelling, Nat. Commun., 2023, 14(1), 5127, DOI:10.1038/s41467-023-40574-6.
- T. Fang, G. Jiang, Y. Xia and P. Ying, Intra-Layer Inhomogeneity of the Anode in Commercial Li-Ion Batteries, Batteries, 2023, 9, 463, DOI:10.3390/batteries9090463.
- J. Kim, M. H. Kim, Y. Kim, M. S. Kim, A. Choi, K. M. Jeong and H. W. Lee, Unveiling the role of electrode-level heterogeneity alleviated in a silicon-graphite electrode under operando microscopy, Energy Storage Mater., 2023, 57, 269, DOI:10.1016/j.ensm.2023.02.025.
- P. Maire, H. Kaiser, W. Scheifele and P. Novak, Colorimetric determination of lithium-ion mobility in graphite composite electrodes, J. Electroanal. Chem., 2010, 644, 127, DOI:10.1016/j.jelechem.2009.09.011.
- B. Shi, B. Han, H. Xie, Y. Kang and Q. Zhang, C-rate related diffusion process of the graphite electrode by in situ experiment and analysis, Electrochim. Acta, 2021, 378, 138151, DOI:10.1016/j.electacta.2021.138151.
- Y. Chen, K. H. Chen, A. J. Sanchez, E. Kazyak, V. Goel, Y. Gorlin, J. Christensen, K. Thornton and N. P. Dasgupta, Operando video microscopy of Li plating and re-intercalation on graphite anodes during fast charging, J. Mater. Chem. A, 2021, 9, 23522, 10.1039/D1TA06023F.
- C. Uhlmann, J. Illig, M. Ender, R. Schuster and E. Ivers-Tiffee, In situ detection of lithium metal plating on graphite in experimental cells, J. Power Sources, 2015, 279, 428, DOI:10.1016/j.jpowsour.2015.01.046.
- T. Gao, Y. Han, D. Fraggedakis, S. Das, T. Zhou, C. N. Yeh, S. Xu, W. C. Chueh, J. Li and M. Z. Bazant, Interplay of Lithium Intercalation and Plating on a Single Graphite Particle, Joule, 2021, 5(2), 393–414, DOI:10.1016/j.joule.2020.12.020.
- K. E. Thomas-Alyea, C. Jung, R. B. Smith and M. Z. Bazant, In situ observation and mathematical modeling of lithium distribution within graphite, J. Electrochem. Soc., 2017, 164, E3063, DOI:10.1149/2.0061711jes.
- D. Guerard and A. Herold, Intercalation of lithium into graphite and other carbons, Carbon, 1975, 13, 337, DOI:10.1016/0008-6223(75)90040-8.
- K. C. Woo, H. Mertwoy, J. E. Fischer, W. A. Kamitakahara and D. S. Robinson, Experimental phase diagram of lithium-intercalated graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 7831, DOI:10.1103/PhysRevB.27.7831.
- J. R. Dahn, Phase diagram of LixC6, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170, DOI:10.1103/PhysRevB.44.9170.
- M. Rykner and M. Chandesris, Free Energy Model for Lithium Intercalation in Graphite: Focusing on the Coupling with Graphene Stacking Sequence, J. Phys. Chem. C, 2022, 126, 5457, DOI:10.1021/acs.jpcc.1c10800.
- T. D. Tran, X. Y. Song and K. Kinoshita, Investigation of Lithiated Carbons by Transmission Electron Microscopy and X-Ray Diffraction Analysis, MRS Proc., 1998, 548, 37, DOI:10.1557/PROC548-37.
- D. Billaud, F. X. Henry, M. Lelaurain and P. Willmann, Revisited structures of dense and dilute stage II lithium-graphite intercalation compounds, Proceeding of the 8th International Symposium on Intercalation Compounds, J. Phys. Chem. Solids, 1996, 57, 775, DOI:10.1016/0022-3697(95)00348-7.
- T. Ohzuku, Y. Iwakoshi and K. Sawai, Formation of Lithium-Graphite Intercalation Compounds in Nonaqueous Electrolytes and Their Application as a Negative Electrode for a Lithium Ion (Shuttlecock) Cell, J. Electrochem. Soc., 1993, 140, 2490, DOI:10.1149/1.2220849.
- T. R. Ferguson and M. Z. Bazant, Nonequilibrium thermodynamics of porous electrodes, J. Electrochem. Soc., 2012, 159, A1967, DOI:10.1149/2.048212jes.
- A. S. Mijailovic, S. Wagg-Swift, G. Wang, M. Luo, W. Lu, Q. Wu and B. W. Sheldon, Scaling laws in porous electrode theory: Roles of electrolyte transport, thermodynamics, and interfacial reaction kinetics in plating onset during fast charging, in preparation.
- G. Wang, A. Mijailovic, J. Yang, J. Xiong, S. E. Beasley, K. Mathew, B. Zhou, W. Lu, B. W. Sheldon and Q. Wu, Particle size effect of graphite anodes on performance of fast charging Li-ion batteries, J. Mater. Chem. A, 2023, 11, 21793, 10.1039/D3TA00608E.
- W. A. Paxton, Z. Zhong and T. Tsakalakos, Tracking inhomogeneity in high-capacity lithium iron phosphate batteries, J. Power Sources, 2015, 275, 429, DOI:10.1016/j.jpowsour.2014.11.035.
- F. Grimsmann, T. Gerbert, F. Brauchle, A. Gruhle, J. Parisi and M. Knipper, Hysteresis and current dependence of the graphite anode color in a lithium-ion cell and analysis of lithium plating at the cell edge, J. Energy Storage, 2018, 15, 17–22, DOI:10.1016/j.est.2017.10.015.
- M. Bauer, B. Rieger, S. Schindler, P. Keil, M. Wachtler, M. A. Danzer and A. Jossen, Multi-phase formation induced by kinetic limitations in graphite-based lithium-ion cells: Analyzing the effects on dilation and voltage response, J. Energy Storage, 2017, 10, 1–10, DOI:10.1016/j.est.2016.11.006.
- R. B. Smith, E. Khoo and M. Z. Bazant, Intercalation kinetics in multiphase layered materials, J. Phys. Chem. C, 2017, 121, 12505, DOI:10.1021/acs.jpcc.7b00185.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02211d |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |