 Open Access Article
Open Access ArticleImproved prediction of PFAS partitioning with PPLFERs and QSPRs†
Trevor N.
Brown
 *a,
James M.
Armitage
b,
Alessandro
Sangion
a and
Jon A.
Arnot
*a,
James M.
Armitage
b,
Alessandro
Sangion
a and
Jon A.
Arnot
 acd
acd
aARC Arnot Research & Consulting, Toronto, Ontario M4C 2B4, Canada. E-mail: trevor.n.brown@gmail.com; alessandro@arnotresearch.com; jon@arnotresearch.com
bAES Armitage Environmental Sciences, Ottawa, Ontario K1L 8C3, Canada. E-mail: aesenvsci@outlook.com
cDepartment of Physical and Environmental Sciences, University of Toronto Scarborough, Toronto, Ontario M1C 1A4, Canada
dDepartment of Pharmacology and Toxicology, University of Toronto, Toronto, Ontario M5S 1A8, Canada
First published on 26th September 2024
Abstract
Per- and polyfluoroalkyl substances (PFAS) are chemicals of high concern and are undergoing hazard and risk assessment worldwide. Reliable physicochemical property (PCP) data are fundamental to assessments. However, experimental PCP data for PFAS are limited and property prediction tools such as quantitative structure–property relationships (QSPRs) therefore have poor predictive power for PFAS. New experimental data from Endo 2023 are used to improve QSPRs for predicting poly-parameter linear free energy relationship (PPLFER) descriptors for calculating water solubility (SW), vapor pressure (VP) and the octanol–water (KOW), octanol–air (KOA) and air–water (KAW) partition ratios. The new experimental data are only for neutral PFAS, and the QSPRs are only applicable to neutral chemicals. A key PPLFER descriptor for PFAS is the molar volume and this work compares different versions and makes recommendations for obtaining the best PCP predictions. The new models are included in the freely available IFSQSAR package (version 1.1.1), and property predictions are compared to those from the previous IFSQSAR (version 1.1.0) and from QSPRs in the US EPA's EPI Suite (version 4.11) and OPERA (version 2.9) models. The results from the new IFSQSAR models show improvements for predicting PFAS PCPs. The root mean squared error (RMSE) for predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOWversus expected values from quantum chemical calculations was reduced by approximately 1 log unit whereas the RMSE for predicting log
KOWversus expected values from quantum chemical calculations was reduced by approximately 1 log unit whereas the RMSE for predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA was reduced by 0.2 log units. IFSQSAR v.1.1.1 has an RMSE one or more log units lower than predictions from OPERA and EPI Suite when compared to expected values of log
KOA was reduced by 0.2 log units. IFSQSAR v.1.1.1 has an RMSE one or more log units lower than predictions from OPERA and EPI Suite when compared to expected values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA for PFAS, except for EPI Suite predictions for log KOW which have a comparable RMSE. Recommendations for future experimental work for PPLFER descriptors for PFAS and future research to improve PCP predictions for PFAS are presented.
KOA for PFAS, except for EPI Suite predictions for log KOW which have a comparable RMSE. Recommendations for future experimental work for PPLFER descriptors for PFAS and future research to improve PCP predictions for PFAS are presented.
Environmental significanceQSPR predictions for partitioning properties of PFAS have been found to be inaccurate due to their unique properties and a lack of experimental data. Accurate values for partitioning are important for assessing the hazard and risk that PFAS pose to humans and ecosystems. This work finds that by leveraging recently published experimental data, QSPRs can be recalibrated to produce more accurate predictions for partitioning properties. The model validations and mechanistic insights from this work can be used to guide the improvement of other QSPRs, and to prioritize further experimental work. |
1. Introduction
Physicochemical property (PCP) data are essential for conducting legislated ecological and human health assessment.1–3 Commonly required properties include water solubility (SW; mol L−1), vapor pressure (VP; Pa), and the octanol–water (KOW), octanol–air (KOA), and air–water (KAW) partition ratios. Chemical assessment outcomes are sensitive to selected property values, e.g.,4–7 and thus reliable measured or predicted property data are necessary for reliable chemical assessments.8,9 Per- and polyfluoroalkyl substances (PFAS) are chemicals of high concern with extensive data gaps, including basic PCPs.10–13 The US Environmental Protection Agency (EPA) has outlined testing strategies, road maps, and action plans that seek to address data gaps for PFAS assessments for as many as 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 substances.14–17 There are technical challenges for obtaining PCP measurements for certain PFAS18–20 which contributes to the recognized data gaps and emphasizes the need for reliable predictions that ideally also convey key information for considering the use of the predicted values such as the applicability domain (AD) and the uncertainty of the prediction.21 In this work we use the definition of Gaines et al.17 to help classify chemicals in various datasets as PFAS. In this definition a chemical is classified as a PFAS if one of four substructures is present, or if fluorine makes up 30% or more of the non-hydrogen atoms.
000 substances.14–17 There are technical challenges for obtaining PCP measurements for certain PFAS18–20 which contributes to the recognized data gaps and emphasizes the need for reliable predictions that ideally also convey key information for considering the use of the predicted values such as the applicability domain (AD) and the uncertainty of the prediction.21 In this work we use the definition of Gaines et al.17 to help classify chemicals in various datasets as PFAS. In this definition a chemical is classified as a PFAS if one of four substructures is present, or if fluorine makes up 30% or more of the non-hydrogen atoms.
Two general approaches for predicting PCPs are quantitative structure–property relationships (QSPRs) and poly-parameter linear free energy relationships (PPLFERs). QSPRs are developed from experimental datasets for a property of interest in which the molecule (structure) is expressed in terms of structural fragments, topological descriptors, or whole molecular descriptors.22,23 The fragment-based QSPR approach is used in several models within the US EPA's Estimation Program Interface Suite (EPI Suite™) program24 and for predicting PCPs and solute descriptors in the Iterative Fragment Selection Quantitative Structure–Activity Relationships (IFSQSAR) system developed by Brown and colleagues.25,26 The QSPRs in the US EPA's Open (Quantitative) Structure–activity/property Relationship App (OPERA) use a nearest neighbours approach by selecting the best descriptors for each property from a pool of fragments, topological, and other descriptors.23 PPLFERs are models calibrated with experimental data for PCPs and empirically-derived or predicted solute descriptors that correlate with molecular interactions of a solute of interest, e.g., a PFAS chemical, in a system of interest, e.g., octanol–water. There are two sets of PPLFER solute descriptors for PFAS in the literature. The original set of solute descriptors was developed by Abraham and colleagues and incrementally expanded over many years,27,28 exemplified by a recent publication of values for fluorotelomer alcohols (FTOHs).29 In the database of reliable solute descriptors developed in previous work30,31 there are 385 solutes containing fluorine atoms, 180 of which meet the definition of PFAS proposed by Gaines et al..17 Another set of solute descriptors was developed by Goss and colleagues,32–34 and is exemplified by the recent publication of Endo which presents values for PFAS, including FTOHs.35 There are 47 fully calibrated solutes in the Endo set, all of which meet the Gaines et al.17 definition of PFAS. It should be noted that all the PFAS calibrated by Endo are neutrals, so the results of this work are only applicable to neutral PFAS. The two sets of solute descriptors are calibrated using the same types of data, i.e., gas chromatogram (GC) retention data and partition ratios in reference solvent-air or solvent-water systems.28,36 In the calibration some solute descriptors are fixed or directly measured while the others, primarily the hydrogen bonding and polarity descriptors, are simultaneously calibrated to fit the experimental data. Because of this simultaneous calibration differing assumptions and fixed values can result in different calibrated values. The primary difference between the two sets of solute descriptors is one solute descriptor with a fixed value, McGowan volume, to which Goss and colleagues made an alteration to bring it more in line with liquid molar volume, which improved predictive power for PFAS.32 However, this difference propagates through the calibration process causing the other solute descriptors to also be different between the two PFAS solute descriptor sets.
The goal of this work is to improve the IFSQSAR QSPRs to predict solute descriptors and subsequently parameterize PPLFER equations for common PCPs of PFAS by leveraging recently published PFAS solute descriptors and other data. To achieve this, we investigate the differences between the competing PFAS solute descriptor sets and make recommendations for selecting the most reliable values. This analysis leads to updated QSPRs for solute descriptors and refitted PPLFER equations which are implemented in IFSQSAR v.1.1.1 models for several PCPs. The new IFSQSAR property predictions are compared to predictions from the previous IFSQSAR version (v.1.1.0), predictions from QSPRs in EPI Suite and OPERA, COSMOtherm calculations, and to available measured data. Finally, recommendations to further improve the prediction of PCPs for PFAS using PPFLERs are provided.
2. Methods
2.1 PPLFER theory
The theory, application, and interpretation of PPLFER equations have been extensively reviewed28,37 and are briefly outlined here to communicate the differences between the two sets of PFAS solute descriptors. Eqn (1) and (2) show the PPLFER equations developed by Abraham for liquid–liquid and liquid–gas27,38 partitioning systems, respectively. Goss proposed eqn (3) as an alternative because, among other reasons, it better explained the partitioning of PFAS.39log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = eE + sS + aA + bB + vV + c K = eE + sS + aA + bB + vV + c | (1) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = eE + sS + aA + bB + lL + c K = eE + sS + aA + bB + lL + c | (2) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = sS + aA + bB + vV + lL + c K = sS + aA + bB + vV + lL + c | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K is a partition ratio between two phases, e.g., solvents, water, air, or other natural matrixes. Lowercase letters are the system parameters quantifying the relative propensity of the two phases to engage in molecular interactions with the solute, and uppercase letters are solute descriptors which are specific for a given solute and correlate with various molecular interactions. E is excess molar refraction which correlates with van der Waals interactions and polarizability, and S correlates with solute dipolarity and polarizability. Important to note for this work is that E and S are expected to have low values for PFAS because they correlate with polarizability, and fluorine atoms are very electronegative. A is hydrogen bond acidity, B is hydrogen bond basicity, V is McGowan volume which correlates with cavitation energy i.e., the energy required for the solute to make space for itself in the solvent,40,41 and L is the log10 partition ratio between n-hexadecane and air which correlates with van der Waals interactions. Goss et al. suggested an adjustment to V specifically for fluorine atoms, to eliminate an observed deviation between V and the molar volume (MV).32 We refer to this adjusted McGowan volume as VF in this work.
K is a partition ratio between two phases, e.g., solvents, water, air, or other natural matrixes. Lowercase letters are the system parameters quantifying the relative propensity of the two phases to engage in molecular interactions with the solute, and uppercase letters are solute descriptors which are specific for a given solute and correlate with various molecular interactions. E is excess molar refraction which correlates with van der Waals interactions and polarizability, and S correlates with solute dipolarity and polarizability. Important to note for this work is that E and S are expected to have low values for PFAS because they correlate with polarizability, and fluorine atoms are very electronegative. A is hydrogen bond acidity, B is hydrogen bond basicity, V is McGowan volume which correlates with cavitation energy i.e., the energy required for the solute to make space for itself in the solvent,40,41 and L is the log10 partition ratio between n-hexadecane and air which correlates with van der Waals interactions. Goss et al. suggested an adjustment to V specifically for fluorine atoms, to eliminate an observed deviation between V and the molar volume (MV).32 We refer to this adjusted McGowan volume as VF in this work.
2.2 Analysis of PPLFER parameters for PFAS
The only PFAS solutes from Endo35 with measured values for all three partition ratios of interest in this study, i.e., KOW, KOA, and KAW, are 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 6
2, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 8
2 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOHs. Table 1 shows two sets of solute descriptors (“Abraham” and “Endo”) with the PFAS arranged together with their corresponding fluorine-free alkane backbone for comparison. The values for V and VF are notably different between the two datasets because of the different calculation procedures. Abraham uses the V calculation as developed by McGowan,40 while Endo uses the modification by Goss32 which is the same for all atoms except for F which is increased so that VF is significantly larger than V for PFAS, this difference is discussed in more detail below and in the ESI.† The value of E is calculated from an experimental refractive index, but the calculation uses the V or VF descriptor, so the values are different between the two solute descriptor sets but are not calibrated with partitioning data. The L descriptor can be directly measured for small solutes but is calibrated by regression vs. GC retention times on non-polar stationary phases for larger solutes. The calibration of L is quite reliable and independent, so it is typically done separately and considered to be fixed in the calibration of the hydrogen bonding and polar solute descriptors. In the case of Endo35,45 the L values were calibrated with GC retention times on non-polar stationary phases. This method uses the V descriptor in the calibration, so the choice of using V or VF may influence the results, but Table 1 shows the L values are nearly identical to the values from Abraham and Acree.29 The S, A, and B descriptors are either calibrated or set to an assumed value of 0 in both sets and therefore the difference between the V and VF solute descriptors manifests in the calibrated descriptor values. The Abraham group solute descriptors have higher A and B values for the FTOHs than the Goss/Endo group, but by far the largest discrepancy is between the S values which also have different signs. This presents a problem for recalibrating QSPRs for the solute descriptors, because including data from both competing sets in a recalibration of the QSPRs would result in predictions that are consistent with neither set which will likely result in poor predictive power. No explanation for the large discrepancy between the S values is offered by either of the competing groups. A key objective of this work is to examine and resolve the discrepancies between the two sets of solute descriptors.
2 FTOHs. Table 1 shows two sets of solute descriptors (“Abraham” and “Endo”) with the PFAS arranged together with their corresponding fluorine-free alkane backbone for comparison. The values for V and VF are notably different between the two datasets because of the different calculation procedures. Abraham uses the V calculation as developed by McGowan,40 while Endo uses the modification by Goss32 which is the same for all atoms except for F which is increased so that VF is significantly larger than V for PFAS, this difference is discussed in more detail below and in the ESI.† The value of E is calculated from an experimental refractive index, but the calculation uses the V or VF descriptor, so the values are different between the two solute descriptor sets but are not calibrated with partitioning data. The L descriptor can be directly measured for small solutes but is calibrated by regression vs. GC retention times on non-polar stationary phases for larger solutes. The calibration of L is quite reliable and independent, so it is typically done separately and considered to be fixed in the calibration of the hydrogen bonding and polar solute descriptors. In the case of Endo35,45 the L values were calibrated with GC retention times on non-polar stationary phases. This method uses the V descriptor in the calibration, so the choice of using V or VF may influence the results, but Table 1 shows the L values are nearly identical to the values from Abraham and Acree.29 The S, A, and B descriptors are either calibrated or set to an assumed value of 0 in both sets and therefore the difference between the V and VF solute descriptors manifests in the calibrated descriptor values. The Abraham group solute descriptors have higher A and B values for the FTOHs than the Goss/Endo group, but by far the largest discrepancy is between the S values which also have different signs. This presents a problem for recalibrating QSPRs for the solute descriptors, because including data from both competing sets in a recalibration of the QSPRs would result in predictions that are consistent with neither set which will likely result in poor predictive power. No explanation for the large discrepancy between the S values is offered by either of the competing groups. A key objective of this work is to examine and resolve the discrepancies between the two sets of solute descriptors.
| CAS | Name | Sourcea | E | S | A | B | V or V F | L | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Competing group of solute descriptors, Abraham and colleagues,29 or Goss and colleagues,32 exemplified by the recent publication of Endo.35 b Endo did not measure the E descriptor, E values used in this work are calculated from measured refractive indexes from other sources,32 or refractive indexes predicted using ACD Labs. The calculation of E includes the V descriptor, so an adjustment is made to the value when using VF. | |||||||||
| 2043-47-2 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Abraham | −0.51 | −0.43 | 0.84 | 0.41 | 1.172 | 2.520 | 29 |
| 2043-47-2 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Endo | −0.67b | 0.35 | 0.60 | 0.31 | 1.352 | 2.421 | 35 |
| 111-27-3 | 1-hexanol | 0.21 | 0.42 | 0.37 | 0.48 | 1.013 | 3.610 | 42 | |
| 647-42-7 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Abraham | −0.83 | −0.89 | 0.79 | 0.54 | 1.525 | 2.960 | 29 |
| 647-42-7 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Endo | −1.04b | 0.35 | 0.60 | 0.31 | 1.785 | 2.997 | 35 |
| 111-87-5 | 1-octanol | 0.2 | 0.42 | 0.37 | 0.48 | 1.294 | 4.619 | 42 | |
| 678-39-7 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Abraham | −1.19 | −1.25 | 0.82 | 0.51 | 1.875 | 3.470 | 29 |
| 678-39-7 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 FTOH 2 FTOH |
Endo | −1.87b | 0.35 | 0.60 | 0.31 | 2.217 | 3.554 | 35 |
| 112-30-1 | 1-decanol | 0.191 | 0.42 | 0.37 | 0.48 | 1.576 | 5.610 | 42 | |
| 307-34-6 | Perfluorooctane | Abraham | −1.130 | −1.45 | 0 | 0.42 | 1.554 | 2.165 | 43 |
| 375-96-2 | Perfluorononane | Endo | −1.819b | −0.19 | 0 | 0 | 2.131 | 1.571 | 35 |
| 111-65-9 | n-octane | 0 | 0 | 0 | 0 | 1.236 | 3.677 | 44 | |
| 111-84-2 | n-nonane | 0 | 0 | 0 | 0 | 1.377 | 4.182 | 44 | |
Each competing set of solute descriptors can be compared to the values and trends observed for other chemicals in the database of reliable solute descriptors. This comparison shows that the competing solute descriptor sets have different merits and limitations, but this comparison does not conclusively favor one set or the other. More details about this comparison can be found in Section SI1.†
The competing solute descriptor sets can also be compared to the theoretical background and original calibration data of PPLFER solute descriptors to see which is most supported. Using gas–liquid chromatography (GLC) data for various polar stationary phases Abraham et al. recalibrated the S descriptor (then named πH2) for about 400 solutes46 from a previous version developed by Kamlet and Taft.47,48 This dataset was used to calibrate system parameters for various partitioning systems which have subsequently been used to calibrate the rest of the ca. 8000 solutes in the Abraham database. The dataset notably contains no negative values of S, and very few fluorinated chemicals. Only three solutes have a high degree of fluorination: 2,2,2-trifluoroethanol, hexafluoropropan-2-ol, and dodecafluoroheptan-1-ol. These are assigned S values of 0.60, 0.55, and 0.55 respectively, values which are more in line with the values of the Goss/Endo set. The strongly negative values of S suggested by the Abraham group are clearly outside of the calibration range of the original dataset of S values.
In early versions of the PPLFER equations Abraham used liquid molar volume (MV[l]) as a solute descriptor, but after some analysis in collaboration with McGowan it was decided to change from MV[l] to V.41 Abraham concluded that intrinsic molar volume was a better metric for the cavitation energy and found that using MV[l] instead of V while calibrating PPLFER equations would produce different system parameters s, a, and b which capture the molecular effects of dipolarity/polarizability and hydrogen bonding.41 There is more discussion on this topic in Section SI1.† When Goss et al. adjusted the V parameter for fluorine atoms they did so to make VF for fluorinated solutes fall into the general correlation between V and MV[l] for organic compounds,32 which is a major departure from the theoretical background of PPLFERs. Based on recent work26 other atoms with discrepancies between V and MV[l] have been identified, see Section SI1 and Fig. S2† for more discussion. Chlorine and bromine atoms also have a discrepancy, though smaller than fluorine, while boron and silicon have an even larger discrepancy than fluorine. The solute descriptors of organosilicon compounds have also been noted to be anomalous.34
2.3 IFSQSAR
The IFSQSAR QSPRs for PPLFER solute descriptors are described in detail in Brown 2022.31 The IFSQSAR PCP models combine these solute descriptor QSPRs with PPLFER equations that were calibrated with experimental data in IFSQSAR v.1.1.0.26,30 The models use experimental solute descriptors if available, but this behaviour can be overridden. The applicability domain (AD) and the prediction uncertainty of the models are well defined and thoroughly quantified.26 One goal of this work is to update the IFSQSAR QSPRs and the PPLFER equations with the new data from Endo,35 resulting in IFSQSAR v.1.1.1. IFSQSAR is available on GitHub (https://github.com/tnbrowncontam/ifsqsar) and is integrated in the Exposure And Safety Estimation (EAS-E) Suite online platform (https://www.eas-e-suite.com).More details of the QSPR development are available in the literature.25,26 Briefly, IFSQSAR QSPRs are group contribution models in which counts of molecular fragments are multiplied by coefficients and then summed to obtain predictions. The model development proceeds by first creating a pool of molecular fragments from the dataset to be predicted and then rational splitting into training and external validation datasets ensuring that the maximum possible number of fragments are represented in both the training and validation datasets. The training dataset is then split into internal cross-validation datasets. Model parameter selection proceeds by choosing fragments from the pool based on predictive power assessed by cross-validation, beginning with simple fragments and proceeding to more complex fragments. The model parameters are fitted by multiple linear regression (MLR) of fragment counts against the expected property values. The final steps are to define the AD and quantify the prediction uncertainty.
The existing IFSQSAR QSPRs can be updated with new data in two different ways. In the first method, the selected fragments are kept unchanged and new data are inserted into the existing training, validation and cross validation datasets, then MLR is applied to update the regression coefficients. In the second method the new data are again inserted into to the existing training, validation and cross validation datasets, but the selected fragments are reset, and new fragments are selected from the original pool to train a new QSPR. The selected fragments would then be different because of the new data.
3. Results and discussion
3.1 Recommendations for selecting PPLFER descriptors for PFAS
Based only on the analysis of PPLFER parameters for PFAS it is not evident which of the two solute descriptor sets is best for making PCP predictions with PPLFERs for PFAS. The two solute descriptor sets are calibrated on different data, the Abraham set uses eqn (1) and (2) whereas the Endo set uses eqn (3), the Abraham set uses the V solute descriptor whereas the Endo set uses VF, and other details are different as described in Section SI1.† To decide which set to use we re-created the calibrations of the two sets and compared the predictive power of the sets to experimental data. First the calibration of the two solute descriptor sets was investigated. Further details are available in Section SI1,† but in brief we took the data from each set and applied the calibration methods of the other set, to see if we could force the solute descriptors of the Abraham set to match the Endo set, or vice versa. For the Abraham set the calibrated solute descriptors could be exactly reproduced. Various adjustments were made to the calibration such as using eqn (3) instead of eqn (1) and (2) and changing V to VF. Using these and other alterations described in Section SI1† it was possible to make the Abraham set of solute descriptors approximately match the Endo set. The reverse was also attempted. The Endo set calibration was reasonably but not exactly reproduced; the data and calibration methods are much more complex than those used to calibrate the Abraham set. The same alterations were made in reverse, but it was found that the Endo solute descriptors were quite stable. It was not possible to force the Endo set solute descriptors to match the Abraham set by using V instead of VF, and by using eqn (1) and (2) instead of eqn (3). This test indicates that the Endo calibration data are sufficient to provide a unique set of solute descriptors, while the data used by Abraham leaves the calibration under-determined meaning that multiple solutions can exist.Partition ratios calculated with the solute descriptor sets and PPLFER equations were compared to the experimental data. More discussion of this comparison can be found in Section SI1,† but in brief the results are consistent with previous analyses by Endo and Goss,34 which found that the PPLFER equations make the most accurate predictions for PFAS when they have been included in the training set of the PPLFER equation, and when eqn (3) is used. Based on the stability of the calibration and the fit with experimental data the Endo set is recommended. Including PFAS in the calibration dataset of PPLFER system parameters is required for making accurate predictions for this chemical class, as demonstrated here and in previous work by Endo and Goss.34 While testing the calibration of the 47 PFAS solute descriptors from Endo it was confirmed that the accuracy of the partition ratio calculations was best when using VF instead of V. However, this was only true when using eqn (3). Using the Endo solute descriptors with eqn (1) or (2) resulted in a larger deviation between calculated and experimental values.
The 47 PFAS calibrated solute descriptors from Endo have been added to the database of reliable solute descriptors used to train the IFSQSAR QSPRs using eqn (3). The measured and curated partition ratio data in Endo35 have also been added to the system parameters training dataset. However, the IFSQSAR training and external validation datasets already contain 383 fluorinated solutes, some of which are from previous work of the Goss group,32,34,49 but most have been calibrated by the Abraham group. Removing so much data and adding only 47 solutes from Endo would likely degrade the predictive power of the QSPRs, so we only removed some of the fluorinated solutes calibrated by Abraham group based on reasonable selection criteria derived from the comparison between the two sets.
Some solutes fail both selection criteria, so the total number of PFAS solutes removed is 64. After applying the selection criteria there are 321 fluorine-containing solutes from the Abraham set remaining in the database of reliable solute descriptors, 116 of which meet the Gaines et al.17 definition for PFAS. The PFAS from the Abraham set are mostly small solutes that are likely refrigerants. The 47 Endo set solutes are added to these bringing the number of PFAS in the database of reliable solute descriptors to 163.
3.2 Model recalibration and validation
The partitioning property QSPRs in IFSQSAR are hybrid models which combine PPLFER equations (system parameters) calibrated with experimental data and QSPRs trained for the individual solute descriptors S, A, B, V/VF, and L. The system parameters for nine PPLFER equations calibrated in previous work26,30 have been recalibrated by removing experimental data for fluorinated chemicals that meet the criteria outlined in Section 3.1, and adding PFAS with calibrated solute descriptors and experimental partitioning data from Endo.35 The recalibrated equations are shown in Table 2. The b system parameters are mostly unchanged by this recalibration, the a and s system parameters have larger changes, but the v and l system parameters have the largest and most influential differences.| System | s | a | b | d | v | l | c | Total s.e. |
|---|---|---|---|---|---|---|---|---|
| a The standard error (s.e.) for each system parameter is shown in parentheses. b System parameter corresponding to the term (A·B)0.5. c System parameters calculated by thermodynamic cycle. Total s.e. and s.e. of the coefficients are estimated by propagation of uncertainty. | ||||||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW KAW |
−2.127 (0.038) | −3.69 (0.038) | −4.783 (0.037) | 2.505 (0.047) | −0.445 (0.013) | 0.504 (0.027) | 0.153 | |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA KOA |
0.475 (0.05) | 3.566 (0.052) | 0.885 (0.049) | 0.109 (0.059) | 0.892 (0.016) | −0.166 (0.028) | 0.156 | |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW KOW |
−1.219 (0.035) | −0.058 (0.028) | −3.579 (0.034) | 2.702 (0.047) | 0.341 (0.012) | 0.326 (0.025) | 0.162 | |
Dry log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOWc KOWc |
−1.652 (0.063) | −0.124 (0.064) | −3.898 (0.062) | 2.614 (0.076) | 0.447 (0.021) | 0.339 (0.039) | 0.219 | |
| log KO[w]O[d]c | 0.433 (0.072) | 0.066 (0.07) | 0.319 (0.07) | 0.087 (0.089) | −0.106 (0.024) | −0.013 (0.046) | 0.272 | |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP[l]c (Pa) VP[l]c (Pa) |
−1.309 (0.098) | −0.983 (0.217) | −0.558 (0.118) | −1.629 (0.257) | −0.779 (0.132) | −0.655 (0.035) | 7.084 (0.068) | 0.607 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SW[l] (mol L−1) SW[l] (mol L−1) |
0.831 (0.091) | 2.707 (0.213) | 4.218 (0.112) | −1.629 (0.257) | −3.316 (0.124) | −0.206 (0.033) | 0.194 (0.062) | 0.587 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SO[d][l]c (mol L−1) SO[d][l]c (mol L−1) |
−0.821 (0.11) | 2.583 (0.223) | 0.32 (0.128) | −1.629 (0.257) | −0.702 (0.145) | 0.241 (0.039) | 0.532 (0.073) | 0.627 |
| log SO[w][l]c (mol L−1) | −0.388 (0.097) | 2.649 (0.215) | 0.639 (0.117) | −1.629 (0.257) | −0.615 (0.132) | 0.136 (0.035) | 0.519 (0.067) | 0.609 |
The fragment-based QSPRs for the individual solute descriptors have also been updated, the QSPR training and validation datasets in IFSQSAR have been updated by removing and adding PFAS solutes as described in Section 3.1. The Endo solutes were split between the training and validation datasets in a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Solutes were sorted, and every third solute was assigned to the validation dataset. This was done in steps, sorting by partitioning properties where available and sorting by the L solute descriptors for PFAS with no measured partitioning, ensuring that the solutes with available partitioning data were present in both training and validation datasets. The regression coefficients of the MLR for all fragments in the QSPRs were then retrained with the new datasets, no fragments were added or removed in this process.
1. Solutes were sorted, and every third solute was assigned to the validation dataset. This was done in steps, sorting by partitioning properties where available and sorting by the L solute descriptors for PFAS with no measured partitioning, ensuring that the solutes with available partitioning data were present in both training and validation datasets. The regression coefficients of the MLR for all fragments in the QSPRs were then retrained with the new datasets, no fragments were added or removed in this process.
New PCP models have been implemented in IFSQSAR which combine the retrained solute descriptors QSPRs with the recalibrated PPLFER equations (system parameters) in the form of eqn (3). A new QSPR for VF has been implemented in IFSQSAR and is now used in these models instead of the V solute descriptor. These updates are part of IFSQSAR version 1.1.1. The previous versions of the partitioning models are still available in IFSQSAR and can be applied by users for comparison by specifying the version making calculations. These new models were validated using data from Endo,35 who applied the quantum chemistry-based software COSMOtherm to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, and log
KAW, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA for the same solutes for which solute descriptors were calibrated, as well as a diverse dataset of other PFAS. COSMOtherm is an upper tier prediction method for PCPs and Endo found the root mean squared error (RMSE) between the predictions and PPLFER calculated values was 0.33 to 0.42 log units.
KOA for the same solutes for which solute descriptors were calibrated, as well as a diverse dataset of other PFAS. COSMOtherm is an upper tier prediction method for PCPs and Endo found the root mean squared error (RMSE) between the predictions and PPLFER calculated values was 0.33 to 0.42 log units.
3.3 Comparison of IFSQSAR v.1.1.1 to other QSPRs
Predictions have been made for the PFAS partition ratios using: (1) the old version of IFSQSAR (v.1.1.0), (2) the new version of IFSQSAR (v.1.1.1) which implements the solute descriptor QSPRs and system parameters recalibrated with the new PFAS data from Endo, (3) OPERA v.2.9,23 and (4) EPI Suite v.4.11.24 These predictions are plotted against expected values and are shown in Fig. 1, 2, and 3 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, and log
KAW, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA, respectively. Note that only the green triangles in these figures are cases where the expected values are experimental partition ratios. The blue circles represent cases where the expected values are partition ratios calculated using the PPLFER equations and solute descriptors calibrated with experimental data from Endo 2023, and the orange squares represent cases where the expected values are partition ratios calculated with COSMOtherm from the ESI† of Endo 2023.35 Predictions for the three partitioning properties have also been made using solute descriptors calculated using ACD Labs 2023.1.0 (Build 3666) combined with PPLFER equations from previous work,26 these are shown in Fig. S5.† PFAS solutes with experimental partitioning data or with calibrated solute descriptors which were assigned to the validation dataset are shown in green and blue, respectively. It should be noted that all the partitioning data were used by Endo to calibrate the solute descriptors, so there is “information leakage” into the validation dataset making this not a completely independent external validation for IFSQSAR. OPERA v.2.9 and EPI Suite v.4.11 do not use the new data from Endo but do include other experimentally measured partition ratios from the literature in their training datasets. There are 172 to 175 novel PFAS solutes with no experimental or PPLFER data available but have values predicted with COSMOtherm; these are the orange points in the figures. In panels A and B of Fig. 1, 2, and 3 the results for IFSQSAR v.1.1.0 and IFSQSAR v.1.1.1 can be compared. Adding new data has improved the predictive power dramatically for log
KOA, respectively. Note that only the green triangles in these figures are cases where the expected values are experimental partition ratios. The blue circles represent cases where the expected values are partition ratios calculated using the PPLFER equations and solute descriptors calibrated with experimental data from Endo 2023, and the orange squares represent cases where the expected values are partition ratios calculated with COSMOtherm from the ESI† of Endo 2023.35 Predictions for the three partitioning properties have also been made using solute descriptors calculated using ACD Labs 2023.1.0 (Build 3666) combined with PPLFER equations from previous work,26 these are shown in Fig. S5.† PFAS solutes with experimental partitioning data or with calibrated solute descriptors which were assigned to the validation dataset are shown in green and blue, respectively. It should be noted that all the partitioning data were used by Endo to calibrate the solute descriptors, so there is “information leakage” into the validation dataset making this not a completely independent external validation for IFSQSAR. OPERA v.2.9 and EPI Suite v.4.11 do not use the new data from Endo but do include other experimentally measured partition ratios from the literature in their training datasets. There are 172 to 175 novel PFAS solutes with no experimental or PPLFER data available but have values predicted with COSMOtherm; these are the orange points in the figures. In panels A and B of Fig. 1, 2, and 3 the results for IFSQSAR v.1.1.0 and IFSQSAR v.1.1.1 can be compared. Adding new data has improved the predictive power dramatically for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW reducing the RMSE against the COSMOtherm predictions from 2.1 to 1.2 log units, log
KOW reducing the RMSE against the COSMOtherm predictions from 2.1 to 1.2 log units, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA also show modest improvement with the RMSE of both reduced from about 1.7 to 1.5 log units. The RMSE for IFSQSAR v.1.1.1 predictions against PPLFER calculated values is also reduced for all three partition ratios, though the number of solutes (11 to 13) is relatively small. Only 1 to 3 experimental partition ratios are available in the validation dataset which are too few data to draw conclusions. Outliers are identified as chemicals with deviations between predicted and expected values greater than 3 × RMSE. Only three PFAS are identified as outliers for the IFSQSAR v.1.1.1 log
KOA also show modest improvement with the RMSE of both reduced from about 1.7 to 1.5 log units. The RMSE for IFSQSAR v.1.1.1 predictions against PPLFER calculated values is also reduced for all three partition ratios, though the number of solutes (11 to 13) is relatively small. Only 1 to 3 experimental partition ratios are available in the validation dataset which are too few data to draw conclusions. Outliers are identified as chemicals with deviations between predicted and expected values greater than 3 × RMSE. Only three PFAS are identified as outliers for the IFSQSAR v.1.1.1 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW predictions: hexafluoroglutaryl chloride, 2-aminohexafluoropropan-2-ol, and 3H-perfluoro-2,2,4,4-tetrahydroxypentane; and only two PFAS are identified as outliers for the log
KAW predictions: hexafluoroglutaryl chloride, 2-aminohexafluoropropan-2-ol, and 3H-perfluoro-2,2,4,4-tetrahydroxypentane; and only two PFAS are identified as outliers for the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA predictions: 6
KOA predictions: 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 monoPAP and 8
2 monoPAP and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 monoPAP. None are identified as outliers by this criterion in the log
2 monoPAP. None are identified as outliers by this criterion in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW predictions. Applying a criterion of 1.5 × RMSE gives a longer list of outliers, common PFAS classes flagged as outliers are sulfonic acids (PFSAs), sulfonyl fluorides (PASFs), phosphinic acids (PFPiAs), and phosphates (PAPs).
KOW predictions. Applying a criterion of 1.5 × RMSE gives a longer list of outliers, common PFAS classes flagged as outliers are sulfonic acids (PFSAs), sulfonyl fluorides (PASFs), phosphinic acids (PFPiAs), and phosphates (PAPs).
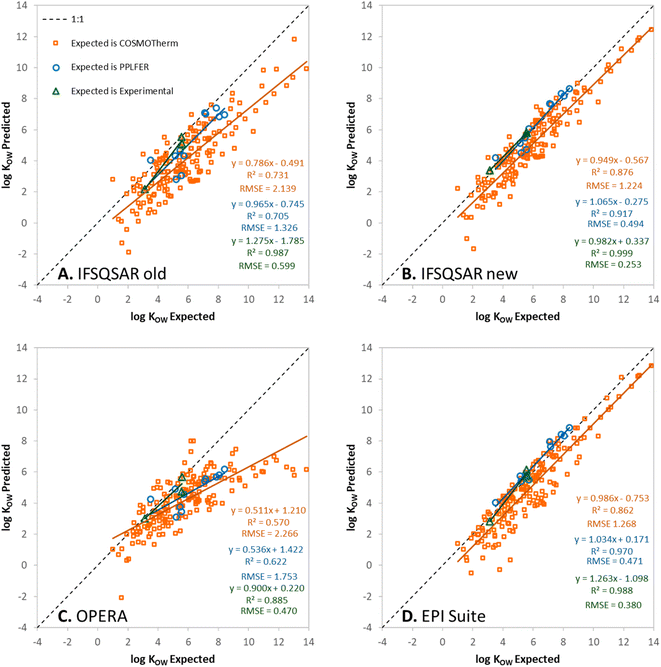 | ||
Fig. 1 Predicted vs. expected log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. KOW for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. | ||
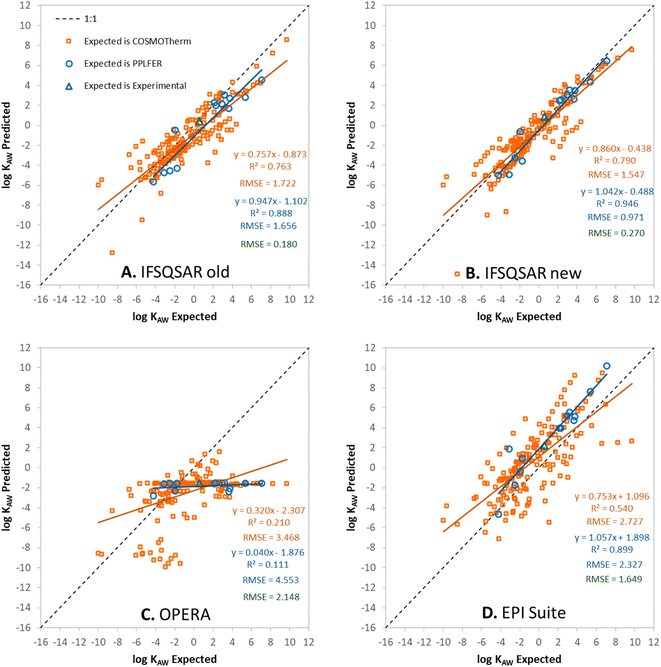 | ||
Fig. 2 Predicted vs. expected log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. KAW for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. | ||
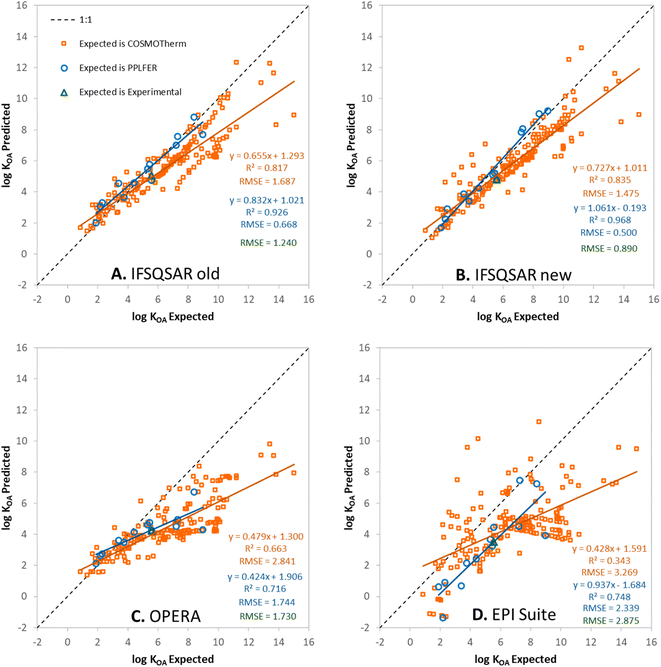 | ||
Fig. 3 Predicted vs. expected log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. KOA for (A) IFSQSAR old, (B) IFSQSAR new, (C) OPERA, and (D) EPI Suite. | ||
Fig. 1C, 2C and 3C show OPERA predictions vs. expected values for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, and log
KAW, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA of PFAS. OPERA is a nearest neighbors QSPR, where predictions are made by comparing a chemical structure to structures in the database and calculating an average value from available experimental data. These types of models have good performance when interpolating between existing data. Other researchers have found that OPERA made accurate predictions of the partitioning of PFAS when compared to experimental data.50 However, it should be noted that the PFAS used in the previous model evaluation50 were all data rich PFAS which are most likely to have neighbors with experimental partitioning data in the internal OPERA database. In fact, when OPERA identifies an exact match for the predicted chemical within its internal database, it directly provides that value from the database without averaging with the nearest neighbors. In other words, the program is selecting the experiment value, rather than making a prediction. When OPERA predictions are compared to COSMOtherm predictions for novel PFAS from Endo, and even many of the PFAS with newly fitted PPLFER solute descriptors, the OPERA predictions are not as accurate. This is expected behavior because nearest neighbor QSPRs cannot extrapolate to new chemistries, only interpolate between existing chemistries. The horizontal lines of solutes in Fig. 2C for log
KOA of PFAS. OPERA is a nearest neighbors QSPR, where predictions are made by comparing a chemical structure to structures in the database and calculating an average value from available experimental data. These types of models have good performance when interpolating between existing data. Other researchers have found that OPERA made accurate predictions of the partitioning of PFAS when compared to experimental data.50 However, it should be noted that the PFAS used in the previous model evaluation50 were all data rich PFAS which are most likely to have neighbors with experimental partitioning data in the internal OPERA database. In fact, when OPERA identifies an exact match for the predicted chemical within its internal database, it directly provides that value from the database without averaging with the nearest neighbors. In other words, the program is selecting the experiment value, rather than making a prediction. When OPERA predictions are compared to COSMOtherm predictions for novel PFAS from Endo, and even many of the PFAS with newly fitted PPLFER solute descriptors, the OPERA predictions are not as accurate. This is expected behavior because nearest neighbor QSPRs cannot extrapolate to new chemistries, only interpolate between existing chemistries. The horizontal lines of solutes in Fig. 2C for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW indicate that the OPERA predictions are using a small number of experimental PFAS data to make predictions for most novel PFAS.
KAW indicate that the OPERA predictions are using a small number of experimental PFAS data to make predictions for most novel PFAS.
Fig. 1D, 2D, and 3D show EPI Suite v.4.11 predictions against expected values for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, and log
KAW, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA of PFAS. Predictions for log
KOA of PFAS. Predictions for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW are good, comparable to IFSQSAR v.1.1.1 with high R2 (0.86–0.99) and low RMSE (0.38–1.27) values. EPI Suite predictions for log
KOW are good, comparable to IFSQSAR v.1.1.1 with high R2 (0.86–0.99) and low RMSE (0.38–1.27) values. EPI Suite predictions for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA against experimental and PPLFER-calculated values have moderate to strong correlations with R2 values of 0.90 to 0.75 but they tend to over-predict volatility, with log
KOA against experimental and PPLFER-calculated values have moderate to strong correlations with R2 values of 0.90 to 0.75 but they tend to over-predict volatility, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW values biased high and log
KAW values biased high and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values biased low, resulting in high RMSE values of about 2.3 log units for both. The predictions for log
KOA values biased low, resulting in high RMSE values of about 2.3 log units for both. The predictions for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA of novel PFAS are poor, with high RMSE values of 2.7 to 3.3 log units compared to the COSMOtherm calculated values. It should be noted that EPI Suite v.4.11 does not have an independent log
KOA of novel PFAS are poor, with high RMSE values of 2.7 to 3.3 log units compared to the COSMOtherm calculated values. It should be noted that EPI Suite v.4.11 does not have an independent log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA QSPR, the predictions are calculated by thermodynamic cycle from log
KOA QSPR, the predictions are calculated by thermodynamic cycle from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW and log
KOW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, which does not account for the discrepancy between wet and dry octanol. Clearly the fragment based QSPRs in EPI Suite can make good predictions for partitioning properties when they are calibrated with adequate data as shown by the good predictions for log
KAW, which does not account for the discrepancy between wet and dry octanol. Clearly the fragment based QSPRs in EPI Suite can make good predictions for partitioning properties when they are calibrated with adequate data as shown by the good predictions for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, but some of the QSPRs are lacking adequate calibration data for PFAS.
KOW, but some of the QSPRs are lacking adequate calibration data for PFAS.
The plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values calculated by IFSQSAR v.1.1.1 showed an under-prediction bias with a slope of 0.623 when compared to the COSMOtherm calculated values, see Fig. S4A.† The log
KOA values calculated by IFSQSAR v.1.1.1 showed an under-prediction bias with a slope of 0.623 when compared to the COSMOtherm calculated values, see Fig. S4A.† The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values did not show the same under-prediction bias when compared to the experimental and PPLFER expected values. Hammer and Endo found that COSMOtherm tends to over-predict solvent-air partitioning, which would explain some of the observed bias.45 An extensive investigation of the under-prediction bias was undertaken but the cause could not be definitively identified. There is a notable discrepancy in the difference between partitioning of PFAS in wet vs. dry octanol, i.e., octanol that is saturated with water as is the case for log
KOA values did not show the same under-prediction bias when compared to the experimental and PPLFER expected values. Hammer and Endo found that COSMOtherm tends to over-predict solvent-air partitioning, which would explain some of the observed bias.45 An extensive investigation of the under-prediction bias was undertaken but the cause could not be definitively identified. There is a notable discrepancy in the difference between partitioning of PFAS in wet vs. dry octanol, i.e., octanol that is saturated with water as is the case for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW measurements vs. octanol that contains no water as is the case for log
KOW measurements vs. octanol that contains no water as is the case for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA measurements. The new IFSQSAR v1.1.1 and the COSMOtherm predictions do not match the same trends observed for other chemical classes, see Section SI2† for details. During this investigation the A solute descriptor QSPR in IFSQSAR was re-created de novo to include the new PFAS data. This improved the statistics of the external validation but did not completely resolve the under-prediction bias, as seen in Fig. 3B the slope of the log
KOA measurements. The new IFSQSAR v1.1.1 and the COSMOtherm predictions do not match the same trends observed for other chemical classes, see Section SI2† for details. During this investigation the A solute descriptor QSPR in IFSQSAR was re-created de novo to include the new PFAS data. This improved the statistics of the external validation but did not completely resolve the under-prediction bias, as seen in Fig. 3B the slope of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA plot for IFSQSAR predictions against COSMOtherm predictions was increased to 0.727. IFSQSAR v.1.1.1 uses the A QSPR that was re-created de novo, and this is what is shown in the rest of the figures and statistics in Section 3.3.
KOA plot for IFSQSAR predictions against COSMOtherm predictions was increased to 0.727. IFSQSAR v.1.1.1 uses the A QSPR that was re-created de novo, and this is what is shown in the rest of the figures and statistics in Section 3.3.
Fig. S5† compares PPLFER calculations parameterized by solute descriptors predicted in ACD Labs. ACD Labs predicts the V solute descriptor rather than VF, and PPLFER equations from our previous work calibrated to use V were applied.26,30 The PPLFER predictions for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW made using the solute descriptors from ACD Labs show a better match with expected values than OPERA and IFSQSAR v.1.1.0, but worse than EPI Suite or IFSQSAR v.1.1.1. For log
KOW made using the solute descriptors from ACD Labs show a better match with expected values than OPERA and IFSQSAR v.1.1.0, but worse than EPI Suite or IFSQSAR v.1.1.1. For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW and log
KAW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA the PPLFER predictions using solute descriptors predicted by ACD Labs are a better match with expected values than predictions from EPI Suite or OPERA but are worse than predictions from IFSQSAR v.1.1.0 or v.1.1.1.
KOA the PPLFER predictions using solute descriptors predicted by ACD Labs are a better match with expected values than predictions from EPI Suite or OPERA but are worse than predictions from IFSQSAR v.1.1.0 or v.1.1.1.
PFAS are relatively scarce in the training datasets used to develop EPI Suite v.4.11, OPERA v.2.9, and before this work also IFSQSAR. All these models are still only able to generate predictions for the neutral form of ionizable PFAS such as perfluoroalkyl acids (PFAAs). As documented in the literature for KOW,51,52 there can be substantial discrepancies in the predicted values generated by different QSARs/software packages and also in the predicted values generated by different versions of the same QSAR/software package. For example, the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of the neutral form of PFOS (referred to as log
KOW of the neutral form of PFOS (referred to as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW,N) generated by EPI Suite KOWWIN v1.67 is 6.28 but is 4.49 if using EPI Suite KOWWIN v1.68 or later versions. This is due to the inclusion of the “–CF2(–CF2)(–CF2) (linear –CF2–core)” factor in KOWWIN v1.68 and later versions.
KOW,N) generated by EPI Suite KOWWIN v1.67 is 6.28 but is 4.49 if using EPI Suite KOWWIN v1.68 or later versions. This is due to the inclusion of the “–CF2(–CF2)(–CF2) (linear –CF2–core)” factor in KOWWIN v1.68 and later versions.
Upon inspection of some of the property data included in the US EPA CompTox dashboard for PFAAs which uses OPERA for property prediction, there are instances of pseudo-replication (same value attributed to multiple sources), mischaracterization of predicted values as “experimental”, and inclusion of anionic (i.e., charged form/salt) property values with neutral form property values. There are also instances when the OPERA v.2.9 predicted values are exactly or nearly identical to the average of “experimental” values (but which may in fact be a set of predicted values). As explained above, this is because the average “experimental” values from the US EPA CompTox database are included in OPERA and are preferentially selected when a perfect match is found. See Section S3† for additional details. While some of these issues are not uncommon when compiling large quantities of property data from numerous sources, it is important to account for them when selecting property values.
4. Conclusion
In this work we found that the best predictive power for PCP of PFAS with PPLFERs was obtained when three criteria were met: VF was used instead of V, eqn (3) was used instead of eqn (1) and (2), and the PPLFER calibration datasets included PFAS. We have recalibrated PPLFER equations, i.e.Table 2, and IFSQSAR for the most commonly used PCP so that these three criteria are met. Abraham and Acree argued that the inclusion of VF was unnecessary in their calibration of solute descriptors for FTOHs, and used eqn (1) and (2).29 However, we have determined in this work that their calibration was underdetermined due to insufficient data, meaning that the PCP data could be fit exactly but the predictive power would be poor for other systems. The large discrepancy observed between S solute descriptor values from the two competing sets also appears to have been due mainly to insufficient training data available to be used by Abraham and Acree. Only four partition ratios, SW, and VP were used in the Abraham calibration,29 whereas Endo used the same partition ratios plus multiple GC retention time measurements on columns with different polarities.35 Applying equations and fitting methods favored by the Abraham group on the data from Endo still resulted in S values which were close to the Endo set, so the results are quite stable. In contrast, applying the equations and fitting methods used by Endo to the data from Abraham dramatically changed results. The S values in the Endo set are consistent with data from the original derivation of the S.46 However, the S, A, and B values of PFAS will still have differences due to the three criteria outlined above.The introduction of VF and eqn (3) by Goss, Endo and colleagues has improved the predictive power of PPLFERs for PFAS, though we view VF an interim method because it conflicts with the underlying theory as developed by Abraham and McGowan. Additionally, because we found deviations between V and MV[l] for other atoms, see Section SI1 and Fig. S2,† further adjustments may be needed or a new volume parameter selected. Another example of an adjustment made to the calculation of V is when van Noort et al. adjusted V for PCBs by fitting it along with the other solute descriptors.53 They attributed this change to steric effects when chlorine atoms are in the ortho position, but it is interesting that this adjustment was made for another class of highly halogenated solutes which have a discrepancy between V and MV[l]. Changing the V descriptor to a different characteristic volume might resolve the observed discrepancies but would require recalibrating the entire PPLFER system and the community should agree on what to use. Abraham's original criteria for selecting V are still a good guide,41 these are as follows. (1) The descriptor should correlate with the cavitation free energy, i.e., the energy required to make space for the solute in a solvent. (2) The calculation should be trivial to make calibrating the other descriptors easier. (3) The descriptor should be largely an intrinsic solute property, independent of the partitioning system. Not explicitly stated by Abraham but also important is: (4) the descriptor should be orthogonal to the other descriptors as much as possible. Criterion 2 is not very restrictive, a QSPR based on McGowan's method for calculating V can be fitted to any volume dataset, such as was done for MV[l] in our recent work.26 Molar volume at the critical point (critical volume, VC) is used as the characteristic volume in some equation of state models, and specific molecular interactions such as hydrogen bonding do not occur in the critical state so this would meet criterion 4. Partial molar volume in a reference solvent, such as water, super critical water, or some other solvent may also be an option provided that the training data and model fitting are selected to reduce the effects of hydrogen bonding and dipole interactions. van Noort used the solvent accessible volume to justify the adjustments made to V made for PCBs,53 which can be calculated by various software.
The work of Endo35 also includes another important departure from how the solute descriptors are typically calibrated. During the fitting procedure the PFAS were also included in the training dataset of the PPLFER system parameters, and both the solute descriptors for PFAS and system parameters of the PPLFER equations were calibrated together in an iterative procedure. Similar iterative fitting was done when Abraham was originally creating the PPLFER system, but the typical procedure now is to keep the system parameters fixed and calibrate only the solute descriptors,28 or keep the solute descriptors fixed and calibrate the system parameters. Endo kept the solute descriptors for non-PFAS solutes fixed, so the calibrated PFAS solute descriptors should still be consistent with the Abraham PPLFER system. There is a competing PPLFER system constructed by Poole54 which uses the same solute descriptors and equations as the Abraham system, but it uses the iterative refitting procedure to calibrate the entire system simultaneously, and the result is that the solute descriptors and system parameters are different enough that the two systems are no longer compatible. The Abraham system would likely also benefit from a full recalibration using this iterative procedure, or some other simultaneous fitting procedure.
Another aspect of the Abraham PPLFER system relevant for PFAS is the extension for ionized solutes because some of the most problematic PFAS are ionized at environmental pH. The system requires two additional solute descriptors to account for molecular interactions of ions, but the number of solutes with calibrated descriptors is still small. This system is a simplification, because it does not account for ion pairing and other process which can affect ion partitioning. Properly accounting for these additional effects is still a research need. The easiest method to calibrate the new descriptors is using empirical regressions with the other solute descriptors.55 However, the number of ionizable groups with empirical regressions is small and these are unlikely to work for ionizable PFAS. In our previous work developing empirical regressions with solute descriptors30 PFAS were strong outliers that had to be excluded. Including the extension for the partitioning of ions in a full, iterative recalibration of the Abaraham system may allow for expanding the applicability.
The solute descriptors and PPLFER equations calibrated by Endo, and those calibrated in this work, are only applicable to neutral PFAS and to the neutral forms of ionizable PFAS, so they will generally not be applicable to PFAAs. Caution and additional scrutiny are required when compiling PCP data for PFAS in general but PFAAs in particular because of their strong tendency to dissociate (i.e., pKa values < 2).56,57 Measured property data (e.g., water solubility, octanol–water partitioning, biopartitioning) for PFAAs should be assumed to predominantly represent the behaviour of the charged form unless it is explicitly stated that experimental conditions have been established such that the presence of the neutral form is favoured. Despite the extra steps taken in this work to improve the prediction of the A solute descriptor for PFAS with sulfonic and sulfonamide functional groups these still have some of the largest discrepancies between predicted and expected values for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, log
KOW, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA, and log
KOA, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW. This may be because they are functional groups that are not well represented in the PPLFER training datasets, or it may be because they are ionizing. Sulfur-containing and ionizing PFAS are obvious candidates for future experimental work, measurements of the partitioning of neutral and ionized species would help to improve QSPRs and yield further mechanistic insights. However, for strongly ionizing PFAS such as those containing sulfonic acid functional groups measuring the partitioning of the neutral form is likely impossible, so some combination of theory, e.g., COSMOtherm calculations, and measurements will be required.
KAW. This may be because they are functional groups that are not well represented in the PPLFER training datasets, or it may be because they are ionizing. Sulfur-containing and ionizing PFAS are obvious candidates for future experimental work, measurements of the partitioning of neutral and ionized species would help to improve QSPRs and yield further mechanistic insights. However, for strongly ionizing PFAS such as those containing sulfonic acid functional groups measuring the partitioning of the neutral form is likely impossible, so some combination of theory, e.g., COSMOtherm calculations, and measurements will be required.
Data availability
Experimental and quantum chemical data for PFAS partitioning, retention times, and solute descriptors used in this work is from the following paper: Endo, S., Intermolecular interactions, solute descriptors, and partition properties of neutral Per- and Polyfluoroalkyl Substances (PFAS), Environ. Sci. Technol., 2023, 57(45): pp. 17534–17541. IFSQSAR code developed in this work is available on GitHub: https://github.com/tnbrowncontam/ifsqsar.Author contributions
Trevor N. Brown: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing. James M. Armitage: data curation, writing – review & editing. Alessandro Sangion: data curation, writing – review & editing. Jon A. Arnot: conceptualization, funding acquisition, project administration, supervision, writing – review & editing.Conflicts of interest
In addition to the acknowledged funding for this research the authors have received funding from other agencies for related research in the last ten years: European Chemical Industry Council Long-range Research Initiative (CEFIC-LRI), ExxonMobil Biomedical Sciences (EMBSI), European Fuel Manufacturers Association (Concawe), Silicones Europe, Health Canada (HC), Environment and Climate Change Canada (ECCC), and the United Kingdom Environment Agency (UKEA).Acknowledgements
We gratefully acknowledge Satoshi Endo for providing comments on an earlier draft of this work and providing us with access to some data files. The authors acknowledge funding from the American Chemistry Council Long-Range Research Initiative. As this publication has not been formally reviewed by the American Chemistry Council, views expressed in this document are solely those of the authors.References
- Government of Canada, Canadian Environmental Protection Act 1999, Canada Gazette Part III, 1999, vol. 22, p. 3 Search PubMed.
- European Commission, Regulation (EC) No 1907/2006 - Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH), Off. J. Eur. Union, 2007, L 136, 3–280 Search PubMed.
- U.S. EPA, Assessing and Managing Chemicals under TSCA; The Frank R. Lautenberg Chemical Safety for the 21st Century Act, https://www.epa.gov/assessing-and-managing-chemicals-under-tsca/frank-r-lautenberg-chemical-safety-21st-century-act.
- F. Wegmann, L. Cavin, M. MacLeod, M. Scheringer and K. Hungerbühler, The OECD software tool for screening chemicals for persistence and long-range transport potential, Environ. Model. Software, 2009, 24, 228–237 CrossRef.
- T. Meyer, F. Wania and K. Breivik, Illustrating sensitivity and uncertainty in environmental fate models using partitioning maps, Environ. Sci. Technol., 2005, 39, 3186–3196 CrossRef CAS PubMed.
- J. M. Armitage, F. Wania and J. A. Arnot, Application of mass balance models and the chemical activity concept to facilitate the use of in vitro toxicity data for risk assessment, Environ. Sci. Technol., 2014, 48, 9770–9779 CrossRef CAS PubMed.
- F. Wania, Y. D. Lei, S. Baskaran and A. Sangion, Identifying organic chemicals not subject to bioaccumulation in air-breathing organisms using predicted partitioning and biotransformation properties, Integrated Environ. Assess. Manag., 2022, 18, 1297–1312 CrossRef CAS PubMed.
- A. M. Buser, M. MacLeod, M. Scheringer, D. Mackay, M. Bonnell, M. H. Russell, J. V. DePinto and K. Hungerbühler, Good modeling practice guidelines for applying multimedia models in chemical assessments, Integrated Environ. Assess. Manag., 2012, 8, 703–708 CrossRef CAS PubMed.
- L. Li, Z. Zhang, Y. Men, S. Baskaran, A. Sangion, S. Wang, J. A. Arnot and F. Wania, Retrieval, selection, and evaluation of chemical property data for assessments of chemical emissions, fate, hazard, exposure, and risks, ACS Environ. Au, 2022, 2, 376–395 CrossRef CAS PubMed.
- E. M. Sunderland, X. C. Hu, C. Dassuncao, A. K. Tokranov, C. C. Wagner and J. G. Allen, A review of the pathways of human exposure to poly- and perfluoroalkyl substances (PFASs) and present understanding of health effects, J. Expo. Sci. Environ. Epidemiol., 2019, 29, 131–147 CrossRef CAS PubMed.
- I. S. Gkika, G. Xie, C. A. M. van Gestel, T. L. Ter Laak, J. A. Vonk, A. P. van Wezel and M. H. S. Kraak, Research priorities for the environmental risk assessment of Per- and Polyfluorinated Substances, Environ. Toxicol. Chem., 2023, 42, 2302–2316 CrossRef CAS PubMed.
- A. O. De Silva, J. M. Armitage, T. A. Bruton, C. Dassuncao, W. Heiger-Bernays, X. C. Hu, A. Kärrman, B. Kelly, C. Ng, A. Robuck, M. Sun, T. F. Webster and E. M. Sunderland, PFAS exposure pathways for humans and wildlife: a synthesis of current knowledge and key gaps in understanding, Environ. Toxicol. Chem., 2021, 40, 631–657 CrossRef CAS PubMed.
- C. Ng, I. T. Cousins, J. C. DeWitt, J. Glüge, G. Goldenman, D. Herzke, R. Lohmann, M. Miller, S. Patton, M. Scheringer, X. Trier and Z. Wang, Addressing urgent questions for PFAS in the 21st century, Environ. Sci. Technol., 2021, 55, 12755–12765 CAS.
- U.S. EPA, PFAS strategic roadmap: EPA's Commitment to action 2021–2024, 2021, https://www.epa.gov/system/files/documents/2021-10/pfas-roadmap_final-508.pdf Search PubMed.
- U.S. EPA, National PFAS testing strategy: identification of candidate Per- and Polyfluoroalkyl Substances (PFAS) for testing, 2021, https://downloads.regulations.gov/EPA-HQ-OLEM-2023-0278-0154/content.pdf Search PubMed.
- A. M. Richard, R. Lougee, M. Adams, H. Hidle, C. Yang, J. Rathman, T. Magdziarz, B. Bienfait, A. J. Williams and G. Patlewicz, A new CSRML structure-based fingerprint method for profiling and categorizing Per- and Polyfluoroalkyl Substances (PFAS), Chem. Res. Toxicol., 2023, 36, 508–534 Search PubMed.
- L. G. T. Gaines, G. Sinclair and A. J. Williams, A proposed approach to defining per- and polyfluoroalkyl substances (PFAS) based on molecular structure and formula, Integrated Environ. Assess. Manag., 2023, 19, 1333–1347 Search PubMed.
- S. Endo, J. Hammer and S. Matsuzawa, Experimental determination of air/water partition coefficients for 21 Per-and Polyfluoroalkyl Substances reveals variable performance of property prediction models, Environ. Sci. Technol., 2023, 57(22), 8406–8413 CrossRef CAS PubMed.
- U.S. Department of Health and Human Services, Toxicological profile for perfluoroalkylsls, 2021, https://www.atsdr.cdc.gov/ToxProfiles/tp200.pdf Search PubMed.
- G. Ding and W. J. G. M. Peijnenburg, Physicochemical properties and aquatic toxicity of Poly- and Perfluorinated Compounds, Crit. Rev. Environ. Sci. Technol., 2013, 43, 598–678 CrossRef CAS.
- Z. Zhang, A. Sangion, S. Wang, T. Gouin, T. Brown, J. A. Arnot and L. Li, Chemical space covered by applicability domains of quantitative structure–property relationships and semiempirical relationships in chemical assessments, Environ. Sci. Technol., 2024, 58, 3386–3398 CAS.
- P. Gramatica, On the Development and Validation of QSAR Models, in Computational Toxicology, ed. B. Reisfeld and A. N. Mayeno, Humana Press, Totowa, NJ, 2013, vol. II, pp. 499–526, DOI:10.1007/978-1-62703-059-5_21.
- K. Mansouri, C. M. Grulke, R. S. Judson and A. J. Williams, OPERA models for predicting physicochemical properties and environmental fate endpoints, J. Cheminf., 2018, 10, 1–19 Search PubMed.
- U.S. EPA, Estimation Programs Interface (EPI) Suite for Microsoft® Windows, Ver 4.11, 2017 Search PubMed.
- T. N. Brown, J. A. Arnot and F. Wania, Iterative fragment selection: a group contribution approach to predicting fish biotransformation half-lives, Environ. Sci. Technol., 2012, 46, 8253–8260 CrossRef CAS PubMed.
- T. N. Brown, A. Sangion and J. A. Arnot, Identifying uncertainty in physical-chemical property estimation with IFSQSAR, J. Cheminf., 2024, 16, 65 CAS.
- M. H. Abraham, Scales of solute hydrogen-bonding: their construction and application to physicochemical and biochemical processes, Chem. Soc. Rev., 1993, 22, 73 RSC.
- M. H. Abraham, A. Ibrahim and A. M. Zissimos, Determination of sets of solute descriptors from chromatographic measurements, J. Chromatogr. A, 2004, 1037, 29–47 CrossRef CAS PubMed.
- M. H. Abraham and W. E. Acree, Descriptors for fluorotelomere alcohols. Calculation of physicochemical properties, Phys. Chem. Liq., 2021, 59, 932–937 CrossRef CAS.
- T. N. Brown, Empirical regressions between system parameters and solute descriptors of polyparameter linear free energy relationships (PPLFERs) for predicting solvent-air partitioning, Fluid Phase Equilib., 2021, 540, 113035 CrossRef CAS.
- T. N. Brown, QSPRs for predicting equilibrium partitioning in solvent–air systems from the chemical structures of solutes and solvents, J. Solution Chem., 2022, 51, 1101–1132 CrossRef CAS.
- K.-U. Goss, G. Bronner, T. Harner, M. Hertel and T. C. Schmidt, The partition behavior of fluorotelomer alcohols and olefins, Environ. Sci. Technol., 2006, 40, 3572–3577 CrossRef CAS PubMed.
- H. P. H. Arp, C. Niederer and K.-U. Goss, Predicting the partitioning behavior of various highly fluorinated compounds, Environ. Sci. Technol., 2006, 40, 7298–7304 CrossRef CAS PubMed.
- S. Endo and K. U. Goss, Predicting partition coefficients of polyfluorinated and organosilicon compounds using polyparameter linear free energy relationships (PP-LFERs), Environ. Sci. Technol., 2014, 48, 2776–2784 CrossRef CAS PubMed.
- S. Endo, Intermolecular interactions, solute descriptors, and partition properties of neutral Per- and Polyfluoroalkyl Substances (PFAS), Environ. Sci. Technol., 2023, 57, 17534–17541 CrossRef CAS PubMed.
- C. F. Poole, S. N. Atapattu, S. K. Poole and A. K. Bell, Determination of solute descriptors by chromatographic methods, Anal. Chim. Acta, 2009, 652, 32–53 CrossRef CAS PubMed.
- S. Endo and K.-U. Goss, Applications of polyparameter linear free energy relationships in environmental chemistry, Environ. Sci. Technol., 2014, 48, 12477–12491 CrossRef CAS PubMed.
- M. H. Abraham, R. E. Smith, R. Luchtefeld, A. J. Boorem, R. Luo and W. E. Acree, Jr., Prediction of solubility of drugs and other compounds in organic solvents, J. Pharm. Sci., 2010, 99, 1500–1515 CrossRef CAS PubMed.
- K.-U. Goss, Predicting the equilibrium partitioning of organic compounds using just one linear solvation energy relationship (LSER), Fluid Phase Equilib., 2005, 233, 19–22 CrossRef CAS.
- J. C. Mcgowan, The estimation of solubility parameters and related properties of liquids, J. Chem. Technol. Biotechnol., 1984, 34, 38–42 CrossRef.
- M. H. Abraham and J. McGowan, The use of characteristic volumes to measure cavity terms in reversed phase liquid chromatography, Chromatographia, 1987, 23, 243–246 CrossRef CAS.
- M. H. Abraham, J. Andonian-Haftvan, G. S. Whiting, A. Leo and R. S. Taft, Hydrogen bonding. Part 34. The factors that influence the solubility of gases and vapours in water at 298 K, and a new method for its determination, J. Chem. Soc., Perkin Trans. 2, 1994, 1777–1791, 10.1039/p29940001777.
- M. H. Abraham, W. E. Acree and E. Matteoli, The factors that influence solubility in perfluoroalkane solvents, Fluid Phase Equilib., 2016, 421, 59–66 CrossRef CAS.
- L. Sprunger, A. Proctor, W. E. Acree and M. H. Abraham, Characterization of the sorption of gaseous and organic solutes onto polydimethyl siloxane solid-phase microextraction surfaces using the Abraham model, J. Chromatogr. A, 2007, 1175, 162–173 CrossRef CAS PubMed.
- J. Hammer and S. Endo, Volatility and nonspecific van der Waals interaction properties of Per- and Polyfluoroalkyl Substances (PFAS): evaluation using hexadecane/air partition coefficients, Environ. Sci. Technol., 2022, 56, 15737–15745 CrossRef CAS PubMed.
- M. H. Abraham, G. S. Whiting, R. M. Doherty and W. J. Shuely, Hydrogen bonding XVI. A new solute solvation parameter, S, from gas chromatographic data, J. Chromatogr. A, 1991, 587, 213–228 CrossRef CAS.
- M. J. Kamlet, M. H. Abraham, R. M. Doherty and R. W. Taft, Solubility properties in polymers and biological media. 4. Correlation of octanol/water partition coefficients with solvatochromic parameters, J. Am. Chem. Soc., 1984, 106, 464–466 CrossRef CAS.
- R. W. Taft, M. H. Abraham, G. R. Famini, R. M. Doherty, J.-L. M. Abboud and M. J. Kamlet, Solubility properties in polymers and biological media 5: an analysis of the physicochemical properties which influence octanol–water partition coefficients of aliphatic and aromatic solutes, J. Pharm. Sci., 1985, 74, 807–814 CrossRef CAS PubMed.
- A. Stenzel, K.-U. Goss and S. Endo, Experimental determination of polyparameter Linear Free Energy Relationship (pp-LFER) substance descriptors for pesticides and other contaminants: new measurements and recommendations, Environ. Sci. Technol., 2013, 47, 14204–14214 CrossRef CAS PubMed.
- A. Lampic and J. M. Parnis, Property estimation of per-and polyfluoroalkyl substances: A comparative assessment of estimation methods, Environ. Toxicol. Chem., 2020, 39, 775–786 CrossRef CAS PubMed.
- S. Rayne and K. Forest, Perfluoroalkyl sulfonic and carboxylic acids: A critical review of physicochemical properties, levels and patterns in waters and wastewaters, and treatment methods, J. Environ. Sci. Health, Part A, 2009, 44, 1145–1199 CrossRef CAS PubMed.
- J. M. Armitage, J. A. Arnot, F. Wania and D. Mackay, Development and evaluation of a mechanistic bioconcentration model for ionogenic organic chemicals in fish, Environ. Toxicol. Chem., 2013, 32, 115–128 CrossRef CAS PubMed.
- P. C. van Noort, J. J. Haftka and J. R. Parsons, Updated Abraham solvation parameters for polychlorinated biphenyls, Environ. Sci. Technol., 2010, 44, 7037–7042 CrossRef CAS PubMed.
- C. F. Poole, Wayne State University experimental descriptor database for use with the solvation parameter model, J. Chromatogr. A, 2020, 1617, 460841 CrossRef CAS PubMed.
- M. H. Abraham, The permeation of neutral molecules, ions, and ionic species through membranes: brain permeation as an example, J. Pharm. Sci., 2011, 100, 1690–1701 CrossRef CAS PubMed.
- K.-U. Goss, The pKa values of PFOA and other highly fluorinated carboxylic acids, Environ. Sci. Technol., 2008, 42, 456–458 CrossRef CAS PubMed.
- L. Vierke, U. Berger and I. T. Cousins, Estimation of the acid dissociation constant of perfluoroalkyl carboxylic acids through an experimental investigation of their water-to-air transport, Environ. Sci. Technol., 2013, 47, 11032–11039 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00485j |
| This journal is © The Royal Society of Chemistry 2024 |
