Estimating impacts of LCRR's fifth-liter sampling and find-and-fix requirements on large water systems

Abstract

The United States Environmental Protection Agency's (USEPA's) Lead and Copper Rule Revisions (LCRR) introduced many changes to the existing regulation. Two major changes are the change in sample methodology to fifth-liter (L5) sampling for homes with lead service lines and the find-and-fix (FaF) provision following any single home lead action level exceedance. This research proposes a method which estimates L5 lead levels from first-draw (L1) LCR data. Using L1 data along with paired L5–L1 difference data from other systems with similar L1 results, L5 data can be estimated accurately by bootstrapping. Using L1 data from two utilities (DC Water and Utility B) with known L5 data, this method was validated to accurately estimate L5 data. This method was then applied to a third utility (Philadelphia Water Department, PWD) with LCR data without paired L5 results to estimate what it can expect from this sample methodology. This same method was then applied to PWD to estimate the impact that FaF would have on the system by identifying how quickly new, permanent Water Quality Parameter (WQP) sites would have to be added. Under all simulations, PWD eventually would reach the maximum number of required WQP sites.

---

Water impact

There are many unknowns for utilities switching to fifth-liter sampling under the Lead and Copper Rule Revisions. This study demonstrates a method for utilities to estimate their fifth-liter lead levels from first-liter lead levels to assess the impacts of this change on their system.

Introduction

The Lead and Copper Rule (LCR) was promulgated in 1991 and its purpose was to decrease exposure to lead and copper in drinking water by establishing a treatment technique for corrosion control treatment within drinking water systems.¹ Corrosion control treatment is a water treatment process where either chemical inhibitors are added to the water (e.g., phosphate based or silicates) or the water's pH is adjusted with the goal of reducing the solubility of lead and copper in residential plumbing systems. The LCR established methods to evaluate whether or not corrosion control was required within a drinking water system, and then to continually evaluate established corrosion control treatments, through water quality parameter monitoring and collecting first-draw, one-liter samples from consumer's homes. The LCR established an action level (AL) for lead of 15 ppb for the 90th percentile of one liter first draw samples collected from consumers' homes after a minimum 6-hour stagnation. The issue of lead in drinking water became national news following the events that took place in Flint, Michigan in 2014 and 2015 where a change in source water without adequate corrosion control treatment resulted in extremely large amounts of lead to leach from plumbing materials.²

In December 2020, the U.S. Environmental Protection Agency (EPA) published the final Lead and Copper Rule Revisions (LCRR).³ On January 16, 2021, the effective date of LCRR was delayed until December 16, 2021, to allow the Agency sufficient time to review the LCRR requirements and determine whether additional regulatory changes were needed.⁴ The LCRR contains numerous new aspects such as changes to sampling methods (e.g., 5th liter samples) and sample location (e.g., all sample sites in systems with lead service lines (LSLs) must have a LSL) requirements, the inclusion of required “find-and-fix” (FaF) follow up procedures for single-home exceedances of the AL, the addition of mandatory school and child-care facility lead monitoring and education programs, development of service line inventories, and new requirements for sampling and education following lead service line replacements.³ The LCRR also established a trigger level (TL) of 10 ppb as a secondary threshold that preemptively initiates action by the utility before they exceed the AL.

5th liter sampling

One of the major aspects of the LCRR that is likely to impact utilities is the change in compliance sampling methodology from the existing first liter (L1) sample requirements to fifth liter (L5) sampling for all homes with lead service lines (LSLs). This change was based on studies that investigated profile (or sequential) sampling events measured lead levels in water throughout the premise plumbing system to identify where exactly high levels of lead are seen.^5–7 These studies indicate that LSLs contribute a large amount of the total mass of lead in water samples, with total mass of lead in water being reduced by 86% on average following the removal of a LSL.⁵ The EPA states that they used three studies “to determine the liter in any given sequential sampling profile that was most likely to contain the water that remained stagnant within a customer-owned LSL”. This resulted in the final determination that the L5 sample was most likely to result in sampling water in contact with the lead service line. Several recent studies have found that this new sampling approach is more likely to collect water in contact with the LSL and will significantly increase the number of systems that exceed the AL and TL.^8–10 However, L5 is not always associated with water in contact with a LSL since the source of lead is highly dependent on the size of the home, the complexity of the premise plumbing system, and the length of the service line.¹¹

The change in sampling methodology adds significant complexity to the LCRR compliance programs for utilities. This method requires samplers to accurately capture five consecutive samples while losing as little water as possible between samples. In the authors' experience, this change greatly increases the level of difficulty in performing the sampling. Additional complexity is added due to the fact that L5 sampling does not apply to all tiers of homes sampled during compliance. This change only applies to tier 1 and tier 2 sites (homes with a LSL). For the remainder of homes sampled, the documented water lead level is based on the L1 sample. All results collected using these different sampling methodology are included in the final calculation for the 90th percentile. Systems with LSLs will be required to collect all LCRR compliance samples from homes with LSLs. This is an increase from previous requirements that only required 50% of homes sampled to have a LSL.

LCRR find-and-fix requirements

Another major change in the LCRR is the FaF requirement for any single home exceedance of the 15 ppb AL. Whenever a home's lead level exceeds 15 ppb, the utility must take specific actions to investigate including collecting water quality parameter (WQP) samples, collecting follow up lead samples, evaluating results and making recommendations to the state. The state must review and approve the recommendations from the system and may require re-optimization of a systems corrosion control treatment (CCT).

The FaF provision also requires utilities to collect a WQP sample be collected after every single-home exceedance of the AL. This WQP sample must be collected from a tap (that is not the LCR tap itself) from a nearby site that is within half a mile, within the same pressure district, and connected to the same size main as the LCR site.³ If an existing site does not exist, then the utility must identify a new site and perform sampling within the 5-day window. This new site would then become a permanent WQP site. While utilities certainly have routine grab sampling locations spread throughout their systems, most systems are likely to have varying main diameters that will result in mismatches between LCR sites and grab sampling sites.

This study investigates the potential impacts of L5 sampling and the FaF provision of the LCRR on a large public water system (i.e., serving over 50 000 people): Philadelphia Water Department (PWD). In order to assess the potential impact of L5 sampling and the FaF requirements, a simulation method is proposed to estimate L5 results directly from L1 results. This method is validated against paired L1 and L5 data from two other large public water systems: DC Water and Utility B. The method is then applied to PWD to evaluate how L5 sampling will impact PWD's compliance with the AL and TL and how the FaF requirements will impact the system, specifically looking at the requirement to add WQP locations to match characteristics of sites with single-home exceedances. This method will allow systems to preemptively begin to assess their corrosion control programs to improve water quality for their consumers and plan for any upcoming capital costs that may be required to comply with the LCRR.

Methods

Data sources

LCR compliance data was obtained from three different utilities (DC Water, Utility B, and PWD). System details and LCR sampling information for these three systems can be found in ESI.† Briefly, there were six rounds of paired L1 and L5 results for DC Water and one round of paired L1 and L5 results for Utility B. There were three rounds of L1 results without paired L5 data from PWD. The two utilities with paired L5 data were used to validate the estimated L5 results against true paired results. For additional information about these three utilities, please see the ESI.†

Michigan LCR compliance data used as the L5–L1 difference data in this study was obtained from Masters et al.⁸ This data covered the 2019 compliance sampling from Michigan systems following Michigan's state LCR revisions, which required a paired L1 and L5 sample for all homes that had a LSL (n = 2909). No difference data points over 100 ppb were included in this analysis (see ESI† for more details).^12,13 From this overall dataset, three data subsets were defined to ensure that difference data was only used from Michigan utilities that matched the target utilities (i.e., DC Water, PWD, or Utility B) L1 data characteristics. The first subset included only results from Michigan water systems with a 90th percentile value less than 5 ppb (n = 1817) and was used for simulations for DC Water and PWD. The second subset included only results from Michigan water systems with a 90th percentile value less than 5 ppb and a standard deviation greater than 3 ppb (n = 689) and was used for simulations for PWD. The third subset included only results from Michigan water systems with a 90th percentile value between 5 ppb and 15 ppb (n = 907) and was used for comparison with Utility B. There was no information available regarding the corrosion control methods employed by the systems included in the Michigan LCR compliance dataset.

All data used for this study were from homes with LSLs.

Statistical analyses

Estimating L5 results

L5 sample results were estimated by randomly sampling 100 L1 lead results with replacement from the pool of lead results from homes with LSLs available and randomly sampling 100 values with replacement directly from the sample pool of L5–L1 differences. Results from LCR sampling rounds are assumed to be representative of lead levels from LSL within the system. Using this assumption, lead results were allowed to be sampled with replacement, as any of these representative values are equally likely to appear any number of times in a LCR sampling round. The 100 L1 random samples were then added pairwise to the 100 randomly sampled difference values to obtain 100 estimated L5 lead levels. Any L5 estimated result less than zero due to a negative difference (i.e., L1 greater than L5) was set to zero. The 90th percentile was then calculated from these values. This process was replicated (or bootstrapped) 1000 times. Each of the 1000 iterations represents one LCR sampling round for the utility it is applied to. Summary statistics (e.g., mean, 90th percentile, standard deviation) were calculated for each of iterations, as well as the number of exceedances. The workflow for this bootstrap method is illustrated in Fig. S1.† To assess whether it is better to sample the difference data from the best-fit MLE distribution or to sample directly from the difference data, the estimated L5 results for DC Water using both methods were compared to actual L5 results.

This bootstrap method makes two major assumptions: 1) the L5 sample result is dependent on the L1 sample results (i.e., if a home has a high L1 result, they are more likely to have a high L5 result) and 2) The difference between paired L5 and L1 results is independent of the L1 level within the home. To confirm these assumptions, Spearman rank correlations were performed between paired L1 and L5 results and L1 and L5–L1 differences for the DC Water, Utility B, and 2019 Michigan LCR data sets.

This method was applied to LCR compliance data for three utilities: DC Water, Utility B, and PWD. Using DC Water and Utility B paired L1 and L5 sample results from the sampling rounds included in this study (six sampling rounds for DC Water and one for Utility B), “true” summary statistics were calculated for each of the 1000 simulated sampling rounds. These true summary statistics were calculated from the paired L5 samples that were collected from the 100 randomly selected L1 results for that iteration. It is important to note that the “true” 90th percentile associated with each of the iterations does not represent the system's actual compliance 90th percentile for each LCR sampling round. Using the calculated summary statistics for the “estimated” L5 data and the “true” L5 data, the efficacy of the simulation method was assessed. 95% confidence intervals (CI) were calculated for each of the summary statistics by taking the 2.5% and 97.5% percentile values of the 1000 values. If the mean value of the summary statistic for the “estimated” L5 values fell within the 95% CI of the “true” L5 values than the distributions were not considered significantly different. In addition to comparing the summary statistics of “true” vs. “estimated” L5 results, the differences between true and estimated L5 results were compared on a (simulated) round by round basis to determine if there was a significant difference between the distribution of results. Differences between the individual sampling round data sets were assessed using the non-parametric Mann–Whitney U test. This analysis was applied to four different subsets of the DC Water LCR data set: 1) all six sampling rounds 2018–2020, 2) the two 2018 sampling rounds, 3) the two 2019 sampling rounds, and 4) the two 2020 sampling rounds. Comparisons were made between the “true” and “estimated” L5 results for each of these four subsets and the Utility B paired data to further assess the efficacy of this method on smaller data sets.

PWD did not have paired L1 and L5 data for the sampling rounds included in this study (2016, 2017, and 2019) to directly compare “estimated” vs. “true” L5 results. However, this method can be applied to give the utility an estimate of where the L5 90th percentile may likely fall when L5 sampling is implemented. The bootstrap simulation was applied to PWD using two different subsets of the Michigan L5–L1 difference data. PWD's 90th percentile was less than 5 ppb for all three sampling rounds included in this study (2016, 2017, and 2019), but its standard deviation was greater than 3 ppb for all sampling rounds. To get an idea of how L5 could vary, two subsets of the overall Michigan data set were defined to include 1) all systems with a 90th percentile less than 5 ppb (53 systems and 1817 paired lead results) and 2) all systems with a 90th percentile less than 5 ppb and a standard deviation greater than 3 ppb (15 systems and 689 paired lead results). These two subsets will be defined within as “best case” and “conservative case” for PWD's simulation results, respectively. For both “best” and “conservative” cases, estimated L5 results were assessed to determine what PWD can expect from L5 sampling and how likely they are to exceed both the TL and the AL. 95% confidence intervals were calculated for the 90th percentile statistic for each of these cases. Lead distribution tables were developed for five randomly selected iterations to assess how L5 results compare to lead distribution tables previously published for PWD's L1 data.^14,15

Estimating impact of FaF

To estimate the impact of the LCRR FaF on WQP monitoring over time a similar approach was taken to estimating L5 sample values. However, instead of simulating 1000 stand-alone sampling rounds, in this simulation 100 consecutive sampling rounds were simulated 1000 times. For each consecutive sampling round within a single iteration, all single-exceedances at LCR sampling rounds were matched with one of the following:

1. An existing WQP monitoring site that meets the FaF requirements,

2. An existing non-WQP, RTCR monitoring site that meets FaF requirements, or

3. The closest hydrant that meets FaF requirements.

If either option 2 or 3 had to be used, then that RTCR site or hydrant was added to the permanent list of WQP sites for the rest of that iteration. This means that for all the remaining consecutive sample rounds within that iteration, that RTCR site or hydrant would now be included in the first category of existing WQP monitoring sites. By simulating these 100 consecutive sampling rounds (which would cover at a minimum 50 years of biannual sampling periods), water systems can see how the change to L5 sampling and the implementation of FaF may impact their WQP over the coming years and decades. This method resulted in 1000 simulations of the increase of WQP monitoring requirements over time for a utility and 100 000 individual LCRR sampling round simulations.

Only 12 grab locations are currently monitored by PWD for OCCT on a quarterly basis, with 10 being required during reduced monitoring under the current LCR. The new LCRR will require this number to be increased to 25 as PWD will be moved back to standard monitoring. In order to perform this simulation, the initial list of 25 starting WQP sites was made by combining the 12 current WQP sites, the 11 disinfection by-product (DBP) monitoring sites that are not already WQP monitoring sites, and two easily accessible coliform sites. All of the DBP monitoring locations are also used for RTCR monitoring. These 25 sample locations are spread geographically throughout PWD's system covering all service areas.

Results and discussion

Summary of LCR data from DC Water, Utility B, and PWD

For sampling rounds in 2016, 2017, and 2019, PWD has had lead 90th percentile less than 5 ppb (Table 1). Given the similarity in treatment and distribution conditions between these three sampling rounds, all three were pooled together for this study to increase the number of representative L1 samples to be used. These sampling rounds had a total of 68, 89, and 99 homes sampled in each of the sampling rounds, respectively (Table 1). With some homes being sampled in multiple rounds, there were a total of 146 homes included in this analysis. In all three sample rounds, the L1 90th percentile was less than or equal to 3 ppb. The 2017 sample round had an increased standard deviation compared to the other two rounds that was driven by a single high lead result. It is not expected that this single elevated value would have an impact of the simulation method presented herein.

Table 1 LCR sampling round results from the Philadelphia Water Department, DC Water, and Utility B. ‘a’ and ‘b’ denotations for different sampling rounds denote January–June and July–December sampling rounds, respectively, conducted in the same year

Sampling round	First liter				Fifth liter
	N	Mean (ppb)	90% (ppb)	Std. dev. (ppb)	N	Mean (ppb)	90% (ppb)	Std. dev. (ppb)
Philadelphia Water Department
2016	68	1.8	3.0	3.5	0	—	—	—
2017	89	13.8	2.2	80.2	0	—	—	—
2019	99	2.4	3.0	7.8	0	—	—	—
DC Water
2018a	118	7.0	2.8	56.2	116	2.8	4.8	8.9
2018b	104	1.0	2.3	1.0	101	2.3	6.0	2.4
2019a	109	1.5	2.2	4.0	105	1.7	3.8	3.0
2019b	108	3.0	2.3	20.0	107	2.5	6.0	2.5
2020a	107	1.2	1.8	2.8	104	2.3	3.2	10.5
2020b	105	1.4	2.8	3.7	104	2.1	5.1	2.4
Utility B
2021a	88	4.3	9.1	10.6	88	6.6	19.3	15.7

---

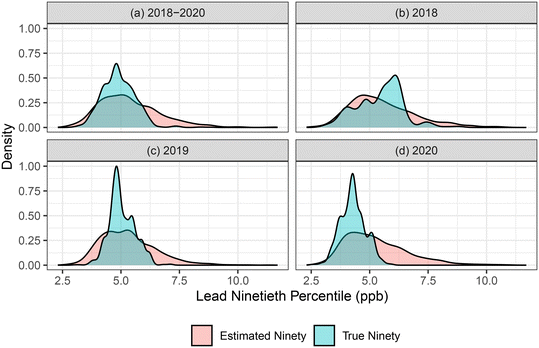
Since the first 2018 sampling round, DC Water has collected paired L1 and L5 samples during LCR compliance monitoring. In total, DC Water performed six LCR compliance sampling rounds between 2018 and 2020 with paired L1 and L5 samples collected during all of these (Table 1). The L1 90th percentile for all six sampling rounds has been below 3 ppb, with the highest 90th percentile value being 2.8 ppb. The L5 90th percentile value has been slightly higher for the six sampling rounds, although still well below the TL and AL, with a maximum value of 6 ppb. Similar to PWD, one of the sample rounds from DC Water had an increased standard deviation that was driven by a single high lead result. It is unexpected that this will impact the effectiveness of the model.

Utility B collected paired L1 and L5 samples during the January–June 2021 LCR sampling round. 88 paired samples were collected during this sample round. Unlike, DC Water and PWD, Utility B experiences slightly higher L1 levels with an L1 90th percentile value of 9.1 ppb. While this value is less than both the AL and the TL, the L5 90th percentile value from this sample round would have exceeded both limits with a value of 19.3 ppb (Table 1).

A major assumption used in this method is that the L5 result is dependent on the L1 result, however, the difference between L5 and L1 result is independent of L1 result. To verify this assumption, Spearman rank correlations were performed between L1 and L5 paired results from the Michigan 2019 LCR sampling round, DC Water, and Utility B paired L1/L5 data sets. Similarly, Spearman rank correlations were performed between L1 and paired L5–L1 difference results for the same three data sets. All three of these data sets demonstrated statistically significant, strong correlations (rho = 0.73–0.89) between L1 and L5 paired results. From these results, it is clear that L5 results increase as L1 results increase, indicating that the L5 result is dependent on the L1 result. Conversely, the correlations between L1 results and L1/L5 difference results indicate no or very weak correlations (rho = 0–0.27). This confirms the assumption that while the L5 result is dependent on the L1 result, the difference between the two is independent of the L1 lead level.

Estimating L5 results from L1 samples

In order to provide an estimation of what 5th liter samples may look like for systems, the estimated distribution of differences between L1 and L5 samples can be used to estimate its impact on utilities around the country. This approach allows for an approximation of what 5th liter samples could look like for systems based on their recent L1 compliance sampling results. This method assumes that systems with similar distributions of L1 data will have similar distributions of L5–L1 results. However, this method cannot be used for systems that have changed their treatment process or source water. Where feasible, utilities should collect paired L1 and L5 samples prior to the enforcement of the LCRR to get an accurate understanding of how this change in sampling methodology will impact a system's compliance. To validate our method, it was applied to two utilities (DC Water and Utility B) with LCR compliance data that has been collected with paired L5 data.

Applying L5 estimation method to utilities with known L5

DC Water – low L1 90th percentiles. Overall, there was a large amount of agreement between estimated L5 results and true L5 results. When comparing the distribution of 90th percentile results for true and estimated L5 lead results from 1000 simulated sample rounds using all paired data from the six sample rounds, there is a large amount of overlap between the two distributions, with 70.7% of the estimated 90th percentile results falling within the 95% confidence interval (CI) of the true 90th percentile (3.7–6.2 ppb) (Fig. 1a). The average 90th percentile value for the estimated data sets (5.37 ppb) also falls within the true 90th percentile 95% CI, indicating there is no statistically significant difference between the two distributions. The mean difference between paired estimated and true 90th percentile results was 0.47.

Fig. 1 Distribution of ‘true’ and ‘estimated’ L5 ninetieth percentile results for DC Water from 1000 simulations for each of the four datasets: (a) simulated LCR sampling rounds were generated by randomly selecting from all paired L1 and L5 samples from 2018–2020, (b) sample rounds were generated by using paired samples from the two 2018 LCR sample rounds, (c) sample rounds were generated by using paired samples from the two 2019 sample rounds, and (d) sample rounds were generated by using paired samples from the two 2020 sample rounds.

Similarly, the mean of the estimated 90th percentile distribution fell within the 95% CI for the true 90th percentile distribution when simulated sample rounds were generated only using 2018 and 2019 LCR data, respectively. In 2018, the estimated 90th percentile distribution had a mean of 5.54 ppb, which falls between the true 90th percentile distributions 95% CI of 3.61 and 7.52 ppb. In 2019, the estimated 90th percentile distribution had a mean of 5.3 ppb, which falls between the true 90th percentile distributions 95% CI of 4.11 and 6.2 ppb. Unlike the other three simulated data sets, the simulated LCR rounds using only 2020 LCR data did have a significant difference between the estimated 90th percentile distribution and the true 90th percentile distribution. In 2020, the estimated 90th percentile distribution had a mean of 5.27 ppb, which falls just outside of the 95% CI of the true 90th percentile of 3.31 and 5.23.

For all four of the bootstrap simulations, the estimated 90th percentile values tended to be slightly higher than the true 90th percentile levels. From the cumulative density plot of the true vs. estimated distributions, the estimated 90th percentile distribution is shifted to right of the true 90th percentile distribution (Fig. S3†). This indicates that while there are not significant differences between the estimated and true distributions, the estimated distribution may slightly overestimate L5 lead results. However, given that this method is designed to give utilities an understanding of how the LCRR change in sampling method may impact their compliance and the level of effort required to comply with the new rule, the authors believe that a slight overestimation is not an issue.

Non-parametric Wilcoxon-rank sum tests were performed to assess whether the distribution of true and estimated L5 results were significantly different for each simulated sampling round. Of the 1000 simulated sampling rounds, 265 had a statistically significant difference between the two distributions. Randomly sampling 10 sampling rounds from the 1000 simulations shows us that the overall spread of the data is relatively the same for both the true and estimated data sets (Fig. S4†). In general, estimated L5 results tended to have more single sample exceedances of the 15 ppb AL than true L5 results, with averages of 2.3 and 1.1 samples exceeding 15 ppb, respectively. The estimated L5 results closely matched the distribution of true L5 results from the same subset of homes. By accurately estimating the L5 distribution, this method gives utilities an understanding of where their L5 results may fall.

One of the factors that is likely to have an impact on the effectiveness of this simulation method is how many L1 data points are used to estimate the L5 90th percentiles. To assess this factors impact on the method, the method was repeated on all DC water data five different times (1000 simulations each time) using 30, 50, 70, 90, and 110 lead results in each simulation round, respectively. These simulations show that even at smaller sample sizes (n = 30) the centroid of the distribution was consistent with simulations using larger sample sizes and with the actual 90th percentiles from DC Water's sampling rounds (Fig. S9†). However, the distribution of 90th percentile results from simulations that used smaller sample sizes showed longer tails both in the estimated and true 90th percentile values calculated from the model. This indicates that the while the method can still provide utilities with an estimate of the L5 90th percentile with limited L1 data, these estimates will be less accurate then simulations performed where more L1 data is available. Based on this sensitivity analysis, utilities would want to include at least 70 L1 data points in the simulation to get a more accurate range of possible L5 90th percentiles.

Utility B – moderate L1 90th percentile. Utility B collected paired L1 and L5 samples for its 2021A sampling round. Utility B experienced a moderate 90th percentile result for the L1 samples collected during this sampling period. Utility B had 88 paired samples collected in its 2021A sample round. The L1 90th percentile was 9.1 ppb for these 88 samples (Table 1). As a result, only systems in the Michigan data set that had L1 90th percentiles between 5 ppb and 15 ppb were included in the difference data used during the simulation. Utility B provides a useful contrast to DC Water who experienced a low L1 90th for all sampling rounds included in this analysis. Simulated sample rounds were generated by randomly selecting 50 of the 88 samples and 50 L5–L1 differences from MI systems meeting the criteria described above. These values were added together pairwise. This process was repeated 1000 times to generate 1000 simulated L5 LCRR sample rounds.

The distributions of the “true” and “estimated” 90th percentile result overall shared a similar profile (Fig. S5†). The distribution of “true” 90th percentile values displayed a bimodal distribution with more results skewing higher than what is seen in the “estimated” 90th percentile distribution. However, the largest peak in the “true” 90th percentile distribution matches that of the “estimated” 90th percentile distribution with results ranging primarily from 10 ppb to 30 ppb. From the estimated distribution, Utility B would exceed the AL 62% of the time and would exceed the TL 97% of the time. The true distribution shows that Utility B would have exceeded the AL and TL 56% and 86% of the time, respectively. The results from the estimated 90th percentile simulations perform well when estimating whether a system is likely to exceed either the TL or AL.

When comparing the distribution of estimated L5 results to true L5 results, not 90th percentiles, 30% of the 1000 simulations saw significant differences (Mann–Whitney p-value < 0.05) between the two difference L5 distributions. Overall, the majority of simulated sampling rounds did not experience a significant difference between the true and estimated L5 results. This illustrates that this simulation method is effective in estimating what a utility is likely to experience when collecting L5 lead samples in their system by using only the L1 data that they have available.

While the results presented here show that the method was effective in estimating the L5 results for Utility B, it is worth noting that the agreement between true and estimated L5 results was lower for Utility B compared to DC Water. The two suspected causes for this decreased accuracy are either the increased magnitude and variability in lead levels observed at Utility B or the use of pH adjustment as a CCT. From the true L1 and L5 data for Utility B, lead levels are less controlled in this system compared to DC Water and as such, that could result in less consistent differences between L1 and L5 results. This may indicate that it is potentially harder to estimate L5 results in systems that do not have stable corrosion control and consistent lead levels. Unfortunately, it is hard to assess the impacts of the choice of corrosion control on the efficacy of the simulation method with only one utility with known L5 data investigated using each type of corrosion control. It would be of interest in future research to test this method on more systems with each type of corrosion control to evaluate its accuracy between corrosion control treatment techniques.

Applying method to utility LCR data without paired L5. PWD L1 results were randomly selected from 146 LCR locations pooled from the last three LCR compliance sampling rounds (2016, 2017, 2019). LCR locations with sample results for multiple sampling rounds had one of the results randomly sampled from their home. The randomly selected L1 results were compared to randomly selected L5–L1 difference data from Michigan's 2019 LCR compliance dataset. Bootstrap analysis showed that 90th percentile lead levels were higher than levels PWD has experienced over the last several sampling round (Fig. 2). The simulated L5 results indicate that PWD has a 100% chance of being below the 15 ppb AL for the “best case” and a 99.7% chance in the “conservative case” scenarios. The simulation results also indicate that PWD has a 4% chance of exceeding the 10 ppb TL in the “best case” scenario and a 18% percent chance of exceeding the TL in the “conservative case” scenario. While these results suggests that PWD is likely to remain under the TL in either scenario, this analysis indicates that they should be prepared to deal with the ramifications that will occur if the TL is exceeded. An exceedance of the TL will also result in annual LCRR compliance monitoring as opposed to reducing monitoring to the triennial monitoring schedule. In addition, while not decided at the time of writing, the review of the LCRR indicates that the EPA may consolidate the AL and TL to a single value again and that it may be lowered from the current AL of 15.¹⁶ This could mean that PWD will be at risk of potentially exceeding the AL if it is lowered to the 10 ppb TL. The average (95% CI) 90th percentile value from the “best” and “conservative” scenarios from the 1000 simulations was 6.6 (4–10.4) ppb and 8.2 (5.1–12.6).

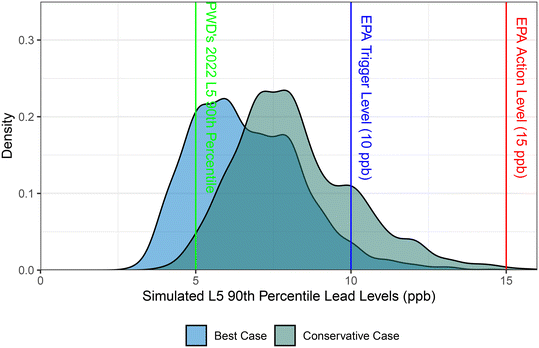Fig. 2 Distribution of estimated L5 90th percentile values for PWD calculated from 1000 simulations.

During the 2022 LCR monitoring period, PWD modified its sampling methodology to have customers collect both L1 and L5 samples. All EPA recommended sampling methods (i.e. no pre-flush, no aerator removal, etc.) were followed as they have been since 2016. A total of 104 homes were sampled during this sampling round. The L1 90th percentile remained consistent with previous years, matching the systems lowest L1 90th percentile, at 2 ppb. The L5 90th percentile value for this non-regulatory sampling was 5 ppb. While this is only a single monitoring period, this is indicative to that fact that PWD may be more closely grouped in the “best case” scenario when looking ahead at future monitoring rounds for the L5 sample results.

While investigating the impacts of L5 samples on the 90th percentile is critically important for compliance, it is also still important to investigate the overall distribution of simulated L5 sampling rounds. Fig. S6 and Table S1† illustrates the overall distribution of lead levels in ten and five randomly selected iterations, respectively. We can see from Fig. S6† that for all ten iterations that the majority of samples fall between 1 ppb and 10 ppb. However, investigating the lead distribution table (Table S1†) we can see that the percentage of samples less than 5 ppb has shifted from previously reported values for PWD in the mid-90s for L1 samples to the mid- to low-80s for L5 samples.^14,15

Impact of find-and-fix WQP on PWD

PWD's drinking water distribution system is divided into 12 pressure districts and has 75 coliform grab sampling sites throughout its distribution system. In the last three LCR sampling rounds performed by PWD, in 2016, 2017 and 2019, there were a total of 146 unique homes that were sampled, with 55 homes sampled in all three rounds. From these sampling rounds, there were 1, 3, and 2 individual lead results that were above the LCR AL, respectively.

While the EPA suggests that large utilities will likely be able to rely on coliform sites to collect WQP FaF samples, this may not be true for all systems and systems should assess the level of effort that this requirement will have on them. In the three sampling rounds included, there were only 32 LCR sampling sites that had an RTCR grab sampling site meeting the requirements of the LCRR FaF mandate, compared with 114 LCR sites without RTCR sites meeting the LCRR requirements. If these FaF requirements had been in place during the 2016, 2017, and 2019 sampling round, 0, 2, and 1 new WQP grab sampling sites would have had to have been established in each round, respectively. While one could argue that establishing only three new locations over three monitoring periods is not a large burden, it is likely still understating the level of effort that this FaF requirement may have under the new LCRR. Firstly, PWD has a stable CCT in place and experiences very few single home exceedances of the AL. However, systems that are well within the 90th percentile AL, but experience more single home exceedances could see this number increase from 1 to 2 new WQP sites per sampling round to 3 to 5. This could result in these systems hitting the maximum number of WQP sites (50) within only a few monitoring periods. Secondly, under the new LCRR, with all systems being reverted to standard monitoring, systems will have single home exceedances more frequently than if they were on reduced monitoring. Finally, with the change in sampling methods, if the L5 sample does indeed result in more single home exceedances, then the number of new WQP sites required could increase at an even faster rate.

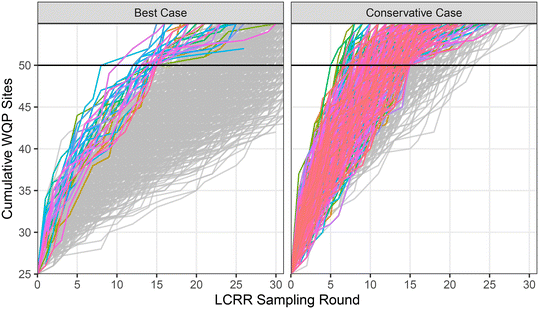
Systems must prepare for what impact this will then subsequently have on FaF and on WQP monitoring within their systems. From the 1000 FaF simulations performed, on average PWD reached 50 permanent WQP sites by round 26 in the “best case” scenario and by round 13 in the “conservative case” scenario. The fastest that 50 permanent WQP sites were reached was after 8 rounds in the “best case” scenario compared to 5 in the “conservative case”. The highest number of sampling rounds to reach 50 WQP sites could be as high as 48 and 23 rounds in the “best case” and “conservative case” scenarios, respectively. Based on this simulation, it would take between 13 and 72 (“best case”) or 6 and 34 (“conservative case”) for PWD to reach 50 WQP sites depending on if they are on standard or reduced monitoring. However, since every simulation reached 50 WQP monitoring sites at some point, unless the water system removes all LSL, they will eventually have 50 unique WQP sites (Fig. 3).

Fig. 3 1000 simulation results demonstrating the number of sampling rounds required using simulated L5 lead results to increase the number of permanent WQP sites from 25 to 50 (the max). All iterations that reached 50 permanent WQP sites within 15 rounds are highlighted.

On average, PWD would be adding new WQP sites in 41 of the first 100 sampling rounds for “best case” and 50 of the first 100 sampling rounds for “conservative case” under the LCRR. In the first 10 rounds, PWD would be adding new sites in 7 and 9 of these rounds under “best case” and “conservative case”, respectively. This is likely to be a slight underestimation because the same 146 sites are used as the sampling pool for all 100 consecutive rounds. It is likely that the sampling pool will change over time, introducing sites that do not have an existing WQP site meeting the FaF requirements. However, this analysis demonstrates that eventually they all reach 50 WQP sites that must permanently be monitored.

Conclusions

Water systems are likely to experience many changes over the coming years as they work to address the new requirements of the LCRR. This study developed a method for estimating L5 data from L1 data and how this could impact a water systems' 90th percentile compliance value and its WQP monitoring program. It is important to note that these simulations are estimates and without actual L5 data to compare them to, they should not be taken as ground truth. Rather these simulations provide water systems with an idea of what its L5 sample results may look like, allowing it to better prepare for how the LCRR may impact their operations. Although beyond the intended scope of this paper, this model could be further extended to investigate other potential impacts of L5 sampling such as impacts of sample size on compliance or lead exposure models.

The LCRR will have a major impact on water systems across the country. The change in sample methodology in the LCRR may leave water systems unsure of whether they will remain in compliance, even if they have been in compliance with the current LCR for years. It is imperative that water systems start to assess their L5 lead levels to begin effectively planning for compliance with the LCRR. This method can provide systems with a starting point for this assessment of their corrosion control programs to improve water quality for its customers and plan for any potentially required capital costs associated with this regulation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Maureen Schmelling for providing data for this study and Gary Burlingame for his review of the manuscript.

References

1. U.S. EPA, Lead and copper rule [Internet]. 40 C.F.R. 141.80, 1991, [cited 2023 Apr 27], Available from: https://www.ecfr.gov/current/title-40/chapter-I/subchapter-D/part-141/subpart-I.
2. K. J. Pieper, R. Martin, M. Tang, L. Walters, J. Parks and S. Roy, et al., Evaluating water lead levels during the flint water crisis, Environ. Sci. Technol., 2018, 52(15), 8124–8132.
3. U.S. EPA, Lead and copper rule revisions [Internet], 2020, [cited 2021 Dec 29], Available from: https://www.epa.gov/sites/default/files/2020-12/documents/lcrr prepublicationnotice frl-10019-23-ow.final.pdf.
4. U.S. EPA, Lead and copper rule revisions; delay of effective compliance dates [Internet], 2021, [cited 2021 Dec 29]. Available from: https://www.govinfo.gov/content/pkg/FR-2021-06-16/pdf/2021-12600.pdf?utm campaign=subscription+mailing+list&utm source=federalregister.gov&utm medium=email.
5. D. A. Lytle, M. R. Schock, K. Wait, K. Cahalan, V. Bosscher and A. Porter, et al., Sequential drinking water sampling as a tool for evaluating lead in flint, michigan, Water Res., 2019, 157, 40–54.
6. A. Sandvig, P. Kwan, G. Kirmeyer, B. Maynard, D. Mast and R. Trussel, et al., Contribution of service line and plumbing fixtures to lead and copper rule compliance issues, AWWA Research Foundation, 2008.
7. M. A. Del Toral, A. Porter and M. R. Schock, Detection and evaluation of elevated lead release from service lines: A field study, Environ. Sci. Technol., 2013, 47(16), 9300–9307.
8. S. V. Masters, T. C. Bradley, G. A. Burlingame, C. J. Seidel, M. Schmelling and T. A. Bartrand, What can utilities expect from new lead fifth-liter sampling based on historic first-draw data?, Environ. Sci. Technol., 2021, 55(17), 11491–11500.
9. E. Betanzo, C. Rhyan and M. Hanna-Attisha, Lessons from the first year of compliance sampling under michigan's revised lead and copper rule and national lead and copper rule implications, AWWA Water Sci., 2021, 3(6), e1261.
10. A. Mishrra, E. Johnson and D. E. Giammar, Estimating lead concentrations in drinking water after stagnation in lead service lines using water quality data from across the united states, Environ. Sci. Technol. Lett., 2021, 8(10), 878–883.
11. S. Triantafyllidou, J. Burkhardt, J. Tully, K. Cahalan, M. DeSantis and D. Lytle, et al. Variability and sampling of lead (pb) in drinking water: Assessing potential human exposure depends on the sampling protocol, Environ. Int., 2021, 146, 106259.
12. S. Masters, G. J. Welter and M. Edwards, Seasonal variations in lead release to potable water, Environ. Sci. Technol., 2016, 50(10), 5269–5277.
13. B. Clark, S. Masters and M. Edwards, Profile sampling to characterize particulate lead risks in potable water, Environ. Sci. Technol., 2014, 48(12), 6836–6843.
14. G. A. Burlingame and A. Sandvig, How to mine your lead and copper data, Opflow, 2004, 30(6), 16–19.
15. T. Bradley and N. Horscroft, Using historical LCR and water quality data to evaluate corrosion control treatment, J. - Am. Water Works Assoc., 2018, E51–66.
16. U.S. EPA, Review of national primary drinking water regulation: Lead and copper rule revisions [Internet], 2021, [cited 2021 Dec 29]. Available from: https://www.epa.gov/system/files/documents/2021-12/review-of-lcrr prepublicationnotice final.pdf.

---

Footnote

† Electronic supplementary information (ESI) available: Additional water system details, methodological details, and figures and tables supporting analysis results. See DOI: https://doi.org/10.1039/d3ew00631j

---