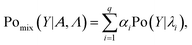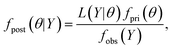Bayesian estimation to deconvolute single-particle ICP-MS data with a mixed Poisson distribution†
Yoshinari
Suzuki
 *a,
Midori
Kondo
a,
Masae
Harimoto
a,
Yusuke
Okamoto
a,
Yu-ki
Tanaka
*a,
Midori
Kondo
a,
Masae
Harimoto
a,
Yusuke
Okamoto
a,
Yu-ki
Tanaka
 b,
Yasumitsu
Ogra
b,
Yasumitsu
Ogra
 b and
Hiroshi
Akiyama
b and
Hiroshi
Akiyama
 ac
ac
aDivision of Foods, National Institute of Health Sciences, 3-25-26 Tonomachi, Kawasaki-ku, Kawasaki-shi, Kanagawa 210-9501, Japan. E-mail: szk-yoshi@nihs.go.jp
bGraduate School of Pharmaceutical Sciences, Chiba University, 1-8-1 Inohana, Chuo-ku, Chiba-shi, Chiba 260-8675, Japan
cDepartment of Analytical Chemistry, Hoshi University, 2-4-41 Ebara, Shinagawa-ku, Tokyo 142-8501, Japan
First published on 30th November 2023
Abstract
Single-particle ICP-MS (spICP-MS) is an established method for the determination of inorganic nanoparticle (NP) mass distributions and particle number concentrations. However, spICP-MS is not applicable to some cases, especially cases that require distinguishing signals from dissolved ions and signals from relatively small NPs. To deconvolute spICP-MS data, which is obtained by setting the dwell time similar to the particle event duration time, a Bayesian estimation method was developed for spICP-MS analysis using silver (Ag) and silica (SiO2) NPs. The signal distributions of the spICP-MS data were parameterised using a Bayesian estimation method on the assumption that they could be described by mixed Poisson distributions. Analytical results were then compared to results obtained with conventional criteria. When the instrument parameters were set so that the particle-event duration was within 2 readings and hence did not deviate from the assumptions of the current Bayesian model, better estimation results could be obtained with the Bayesian estimation method than with methods based on conventional criteria, especially for a sample with high particle number concentration. Furthermore, applying the specific informative prior distribution enabled us to obtain reasonable estimation results, even when the signal counts were 6 or less and the background counts were high. Because appropriate NP information was obtained for Ag-NP and SiO2-NP, the Bayesian estimation method can be universally adopted with inorganic NPs detectable by ICP-MS.
Introduction
Single-particle inductively coupled plasma mass spectrometry (spICP-MS) is a simple and useful method for analysing the properties of metal and metal-oxide nanoparticles (NPs). spICP-MS utilizes short dwell times (DTs) (typically in the low to sub-millisecond range) and time-resolved data acquisition to detect single NPs in liquid suspensions. Individual NPs can be detected as sharp, transient signals above the background signal. Because the signal intensity is proportional to the mass of the NP, spICP-MS data allow estimation of not only the particle number concentration and elemental composition information, but also NP size (assuming a spherical geometry).1,2 Currently, spICP-MS is considered to be an established method for the determination of metal and metal-oxide NP mass distributions and particle number concentrations.3 In a general spICP-MS analysis, criteria are set both for determining the particle event and for selecting the NP signals to be analysed from the obtained histogram of particle-event intensities. In analytical chemistry, it is common to select and analyse only signals above a specific threshold value. However, small NPs produce low-count signals that are below the threshold and are neither detected nor analysed. Consequently, the particle number concentration is underestimated, the average particle mass is overestimated, and therefore the particle diameter is also overestimated. Similar results have been reported when high background signals have been observed. In many reports, the presence of backgrounds for target elements in their ionic state and spectral interferences have resulted in an increase of the calculated particle size compared with particle sizes estimated in the absence of backgrounds.1,4,5An improved data acquisition system could help to mitigate this problem. If particle events are recorded as one-reading events, the use of a shorter DT makes it possible to increase the signal-to-background (S/B) ratio. In 2002, Nomizu et al.6 developed a high-speed, digital, signal-processing system that enabled analyses with a DT of 20 μs, and they subsequently used the system to analyse individual airborne particles. The performance of the ultrafast data acquisition system for analysis of NPs was first reported by Hineman and Stephan.7 They analysed Au-NPs with 60 nm diameters using DTs ranging from 10 μs to 10 ms, and they discussed the effects of varying the DT on particle integration, particle counting, particle sizing, and the background signal. Miyashita et al.8 assembled their own home-built data acquisition unit, which was capable of communicating with a manufactured ICP-MS, and they applied the unit to single-cell analysis at a DT of 50 μs or 100 μs. Several attempts have subsequently been made to improve the time resolution in spICP-MS.4,9,10 A new generation of ICP-MS spectrometers was released around 2011, allowing the minimum DT to be decreased to as low as 10 μs.11 Use of shorter DTs, as well as diluting the particle number concentration, also reduces overlapping of particle events and thus leads to valid estimation of particle number concentrations. However, using shorter DTs increases the possibility that a particle event does not completely coincide with a DT and thus broadens the particle signal distribution and lowers signal intensities.11,12
Applying advanced statistical methods could be another solution. Researchers typically distinguish NP signals from background signals by using three times the standard deviation (σ) of the background signals as a criterion,2 although different threshold values, such as the mean plus 5σ, have been applied in some cases.13,14 Bi et al.15 applied a K-means clustering algorithm to signal processing of spICP-MS raw data. Tuoriniemi et al.16 introduced an algorithm based on outlier detection for data with time resolution of 100 ms. An approach reported by Donard et al.17,18 was based on the detection of peak maxima. Bolea-Fernandez et al.5 used a Gaussian model followed by a deconvolution approach to characterize SiO2-NPs in the presence of a background signal. Gundlach-Graham et al.19 used a Monte-Carlo simulation to obtain a new detection criterion after fitting to a compound Poisson distribution. Hadioui et al.20 applied repeated signal smoothing (3–4 iterations) and then detected NPs if the associated signals were more than 3σ above the mean. Mozhayeva and Engelhard21 applied a Poisson distribution and set the criterion for detection based on a false positive probability of 5%.
Even if an optimal criterion has been determined and a distinction between particle event and background has been made, there are still other difficulties. It is necessary to confirm the particle-event shapes for all NPs. If a bimodal particle event is detected, it must be divided, and some particle event may be excluded based on their shapes. spICP-MS measurements often yield more than 1000 particle events, and confirming the identification of that many particle events can be a time-consuming task that requires perseverance. Although automated data processing software for spICP-MS has been developed by major ICP-MS suppliers,22–25 there is still room for improvement and the development of algorithms for routine analysis that enable processing of multiple samples.
We hypothesized that describing a data generation process as a statistical model would be a useful approach that would not use criteria and would not require taking the sum of intensities for particle-event. A statistical model is a probability distribution constructed to enable inferences to be drawn or decisions to be made based on data.26 This concept is quite similar to the approach reported by Cornelis and Hassellöv.27 They used a method of maximum likelihood estimation (MLE: actually, they used an algorithm that minimized negative likelihood) to deconvolute the background signals from the particle signals under the assumption of a Pólya-Gaussian distribution.27 (n.b., a Pólya distribution is a special case of a negative binomial distribution.) Their approach was to analyse only the probability distribution of the obtained signal, but it is better to assume a state-space model for the signal obtained by spICP-MS. In other words, when the particle event is observed at the ith reading, it is more natural to consider the relationship of that signal with the signals at the (i − 1)th and/or (i + 1)th readings. Furthermore, there is a drawback to using the MLE method. Because the recorded signals (counts) are positive integer numbers, the data should be described with a discrete distribution such as a Poisson distribution.21 The spICP-MS data are considered to be a mixture of a Poisson distribution associated with the background counts and another Poisson distribution due to the counts associated with the NPs. That is, the signal is considered to follow a mixed Poisson distribution. The generalization error is known to be lower for Bayesian inference versus MLE in singular models such as a mixture of distributions.28
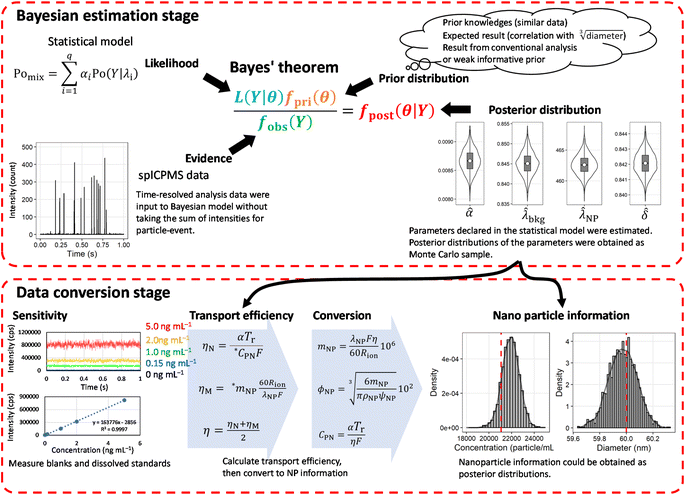
In this study, we investigated a method to extract information about NPs from spICP-MS data by describing the data generation process with Bayesian estimation (BE) based on a mixed Poisson distribution. First, a numerical simulation was performed to evaluate the validity of a Bayesian model. Then, the proposed BE method was used to interpret the actual spICP-MS results, and the performance of the BE method was compared with that of a method based on conventional criteria (CC).
Theory
Statistical model
The spICP-MS signal Y was considered to be a mixture of a Poisson distribution due to the background counts and a Poisson distribution due to the counts associated with the NPs. Because the counts associated with the NPs are also affected by the background counts, the probability mass function (PMF) of the mixed Poisson distribution for Y can be expressed as| Pomix(Y|α, λbkg, λbkg + λNP) = (1 − α)Po(Y|λbkg) + αPo(Y|λbkg + λNP), | (1) |
Eqn (1) assumes that all signals associated with NPs are detected within one reading, but normally NP signals are observed over multiple readings. Thus, extension to a mixture of q Poisson distributions leads to a generalized mixed Poisson distribution given by
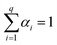 , and Λ indicates a q-dimensional vector with parameters (λ1, λ2,⋯, λq) of Poisson distributions.
, and Λ indicates a q-dimensional vector with parameters (λ1, λ2,⋯, λq) of Poisson distributions.
It was reported that a typical NP pulse lasts for 0.3–0.5 ms.29 A previous study has reported that the duration of the ion signal for one 60 nm Ag-NP is approximately 0.5 ms.30 Thus, when the DT is set to 0.5 ms and a 60 nm Ag-NP particle is measured, if the signal Yi associated with the ith reading is the peak of the particle event, then the signal is split and is expected to be observed at the (i − 1)th or (i + 1)th reading. However, when Yi is the background signal and Yi−1 and/or Yi+1 are the peaks of the particle event(s), the split signal(s) may overlap the background Yi. The probabilities of whether the split signal from Yi overlaps at Yi−1 or Yi+1 are considered to be equal. If δ (0.5 ≤ δ ≤ 1) is the dimensionless split coefficient of the particle-event intensity, then the split patterns and their PMF can be summarized as shown in Fig. 1. In the pattern 7, although the expected signal is λbkg + δλNP, we estimate λNP, which is equivalent to particle-event intensity. In the pattern 6, the tails of the particle-event overlap. In the pattern 8 and 9, the particle events are merged, and it may be difficult to divide them into individual particle-event. Although these split patterns do not satisfy the condition 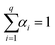 unless the probability of NP's being observed three times in a row is realistically taken into consideration, the probability of this event's occurring (α3; if α = 0.01, the probability of this event's occurring is 10−6) is very low. That case was therefore intentionally excluded to simplify the model. Briefly, this model is a method to calculate the expected particle-event intensity without calculating the intensity of each particle event.
unless the probability of NP's being observed three times in a row is realistically taken into consideration, the probability of this event's occurring (α3; if α = 0.01, the probability of this event's occurring is 10−6) is very low. That case was therefore intentionally excluded to simplify the model. Briefly, this model is a method to calculate the expected particle-event intensity without calculating the intensity of each particle event.
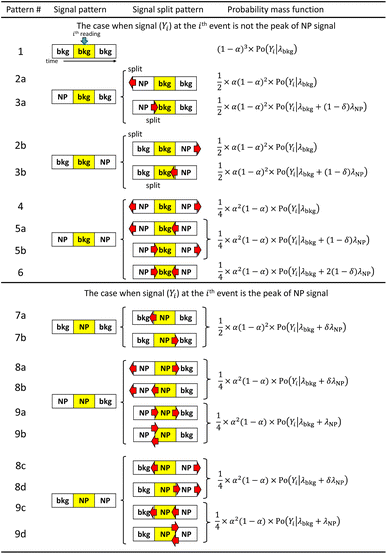 | ||
| Fig. 1 Signal split patterns and probability mass function based on mixed Poisson distribution for spICP-MS. Symbols are explained in the list of symbols and throughout the text. | ||
Bayesian estimation
Let f(Y|α, λbkg, λNP, δ) be the PMF that takes into account all the cases shown in Fig. 1. The likelihood function in this statistical model is then given by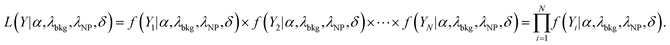 | (3) |
where θ is a q-dimensional vector (θ1, θ2,⋯, θq) of declared parameters, fpri(θ) is the prior distribution of parameter θ, and fobs(Y) is the observed distribution of Y. Because fobs(Y) does not depend on θ, the posterior distribution is often simplified by assuming that it is proportional to the product of the likelihood function by the prior distribution:
| fpost(θ|Y) ∝ L(Y|θ)fpri(θ). | (5) |
Experimental section
Simulation study
We generated 104 random numbers according to a mixed Poisson distribution, which we assumed to be the data generation process. Parameters were set as follows: α = 0.01, λblk = 1, and λNP = 100. We set δ to be a random number with an average of 0.84 and a standard deviation of 0.15 (see S1 and Fig. S1† for examples of R codes and S2 and Fig. S2† for details about the algorithm). Other simulations were performed to evaluate the analytical performance under different S/B ratios. Parameters were set as follows: α = 0.01, λblk = (0.3, 1, 3, 10, 30), and λNP = 30. The BE and CC methods were performed by using these simulation data.Sample preparation
Monodisperse spherical Ag-NPs with nominal diameters of 10, 20, 40, and 60 nm at an initial concentration of 0.02 mg mL−1 were purchased from Sigma-Aldrich (Tokyo, Japan). The certified diameter values of the Ag-NPs determined by transmission electron microscopy by the manufacturer were 10 ± 4, 20 ± 4, 40 ± 4, and 60 ± 8 nm, respectively. Monodisperse spherical SiO2-NPs with a nominal diameter of 500 and 1000 nm at initial concentrations of 10% w/v were purchased from Sigma-Aldrich. The calibrated diameter values of the SiO2-NPs determined by transmission electron microscopy by the manufacturer were 492 ± 20, 976 ± 30 nm, respectively. Basically, the dispersed NP standards were agitated with an ultrasonic bath for 10 min before dilution to the desired concentration so that 100–1000 particles could be obtained during the total scan time of 1 min. (see Table S1† for the prepared concentration.) Ag-NP and SiO2-NP were dispersed in 1% v/v Tween-20 and ultrapure water, respectively. Sample analysis was performed immediately after dilution.Dissolved ion standards for Ag (1000 mg L−1, for atomic absorption spectrometry analysis, Kanto Chemical, Tokyo, Japan) and Si (1000 mg L−1, for ICP analysis, Fujifilm-Wako Chemical, Tokyo, Japan) were used for external calibration.
ICP-MS measurements
All measurements were performed on a model ICAP Qc (Thermo Fisher Scientific, Tokyo, Japan) ICP-Q-MS instrument. The instrument was controlled with Qtegra ISDS software (2.10.3324.109, Thermo Fisher Scientific). The ICP-Q-MS was equipped with a model ASX-520 autosampler (CETAC) and a model MicroFlow PFA nebulizer (Thermo Fisher Scientific) with a flow rate of about 0.31 mL min−1.Dwell time was set to 0.5 ms, which is similar to the particle-event duration, and time resolved analysis was performed for 60 s. In this study, the particle-event duration is defined as the product of the dwell time and the number of consecutive readings of the signal above the baseline. Ag (m/z = 107) was measured under a no-gas mode, and Si (m/z = 28) was measured under an H2 reaction mode (flow rate was 5.5 mL min−1). To reduce background signal of Si, a PLUS torch (Thermo Fisher Scientific) and a sapphire injector (Thermo Fisher Scientific) were used for SiO2-NP analysis. Other main instrumental parameters of the ICP-MS are presented in Table S2.† The probe was rinsed with 2% HNO3 between sample measurements.
Data analysis
Particle event detection with conventional criteria method The particle-event intensity and duration derived from the NPs were calculated using the analytical software NanoQuant developed by Suzuki et al.31 Any particle event whose height was larger than the mean plus 3σ of the blank signal (criteria for detection) was used for further analysis. The lower and upper limits (criteria for histogram) of a signal considered to be NPs were determined from the histogram of the particle-event intensity. Only the signals within the range of criteria for the histogram were analysed as NPs.Bayesian estimation method Fig. 2 shows a schematic overview of the proposed BE method and data conversion to NP information. Because the signals were saved as counts per second, the data were converted to integers (counts) using the DT.
To obtain posterior distribution(s), the probabilistic programming language Stan, developed by Gelman et al.,32 was used in this study. A key feature of Stan is that it uses NUTS (No-U-Turn Sampler), which is an implementation of Hamiltonian Monte Carlo, one of the algorithms of the Markov chain Monte Carlo (MCMC) method. Various Bayesian modelling sources using Stan have been published, and documentation is abundantly available online (see S2†).33
Four parallel Markov chains were calculated using MCMC to check convergence. The number of iterations, warm-up, and thinning were set to 1 × 103, 0.5 × 103, and 1, respectively. After we confirmed convergence of the parameters (see S3 and Fig. S3† for more details), we used an expected a posteriori (EAP), which is the mean of the posterior distribution, as a point estimator (see S4† for more details).
Statistical analysis was performed with R (ver. 3.4.0) via RStudio (ver. 1.3.1093). The R package rstan (ver. 2.16.2) or cmdstanr (ver. 0.4.0) was used for the BE method. To eliminate agglomerated NP signals, the Bayesian analysis was performed after selecting a duration that produced stable transient signals in some cases.
Conversion to NP information As shown in Fig. 2, NP information was calculated from a posterior distribution. As described by Pace et al.,2 a mass flux curve could be obtained from measurements of dissolved ion standards and the NP standard. Thus, the mass of each NP, mNP (fg per particle), was calculated with the following equation:
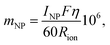 | (6) |
![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) NP was used as INP, whereas in the CC method, the particle-event intensities of the NP were used as INP.
NP was used as INP, whereas in the CC method, the particle-event intensities of the NP were used as INP.
The dimensionless transport efficiency η was calculated from the measurement results for 25 pg mL−1 Ag-NPs with 60 nm diameters. That efficiency was also applied to other Ag-NPs with different diameters. The number-based (ηN) and mass-based (ηM) transport efficiencies were calculated, and the mean of ηN and ηM was used as η. Let *CPN (particles per mL) be the prepared particle number concentration of Ag-NPs with 60 nm diameters. The dimensionless parameter ηN was then calculated from the ratio of the number of detected NPs to the number concentration of standard NPs as follows:
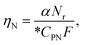 | (7) |
Let *mNP (fg per particle) be the theoretical mass per particle of Ag-NPs with diameters of 60 nm. The dimensionless parameter ηM was then calculated with following equation:
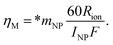 | (8) |
The transportation efficiency was calculated on a daily basis and was about 10% through the analysis.
The NP was assumed to be spherical, and its diameter ϕNP (nm) was calculated from mNP as follows:
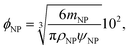 | (9) |
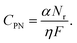 | (10) |
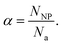 | (11) |
Results
Simulation study
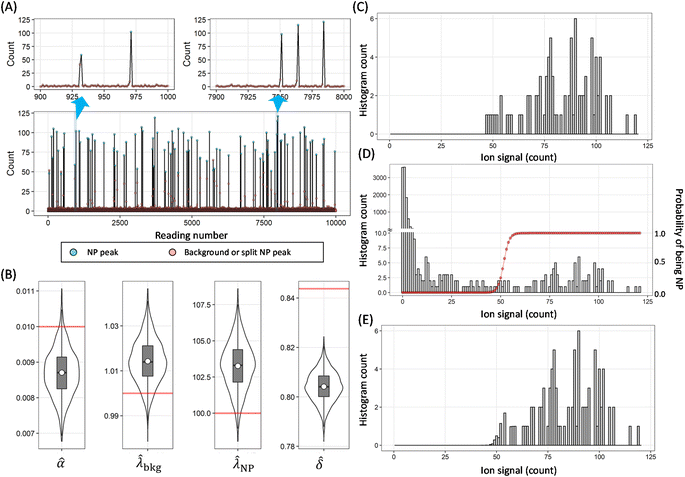
Fig. 3A shows the simulated counts for the time-resolved analysis obtained by spICP-MS, and Fig. 3B shows the estimated model parameters obtained with the BE method for those data. The true values were distributed within the 95% credible interval (CrI, see S5† for more details about CrI) of the posterior distributions for 3 parameters (α, λbkg, and λNP). Although the true value δ corresponds to the variable with a mean of 0.84 and a standard deviation of 0.15, the average value was estimated with this model. The relative bias of![[small delta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b1.gif) from the true mean value was about 4.7%, and the posterior distribution did not completely overlap the true value, but the value of δ has no effect when converting to NP information. These results indicate that a valid estimation is possible with the Bayesian model when the data obtained by spICP-MS follow the assumed data generation process.
from the true mean value was about 4.7%, and the posterior distribution did not completely overlap the true value, but the value of δ has no effect when converting to NP information. These results indicate that a valid estimation is possible with the Bayesian model when the data obtained by spICP-MS follow the assumed data generation process.
Fig. 3C shows a histogram of the particle-event intensity, and Fig. 3D shows a histogram of all the signals in Fig. 3A. Unlike the approach of subtracting background,5,27 we used the probability approach. Using the probabilistic model, it is possible to calculate the PMF that gives the signal k as the background [PMFbkg(k)] and the PMF that gives the signal k of the NPs [PMFNP(k)]. That is, the probability that Y is a NP when the value of Y is k [PNP(k)] can be calculated with the following equation:
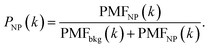 | (12) |
The red curve in Fig. 3D shows the estimated PNP(k). Let HF(k) be the histogram frequency of the signal k. The histogram frequency of the NP-derived signal can then be calculated as follows:
| HFNP(k) = HF(k) × PNP(k). | (13) |
Fig. 3E shows the histogram of the particle event intensity restored by using the BE method. The histogram was calculated by substituting the EAP of the posterior distribution into eqn (13). The similarity of the histograms in Fig. 3C and E indicates that estimation with the BE method is appropriate (see S2† for more detailed information about the simulation study).
When this simulation data was estimated using the CC method, the average value of the particle-event intensity was 104 ± 11 counts and the particle-event frequency was 0.91%. For the data generated according to the assumed model, the CC method and the BE method gave similar estimation results. Another example for small signal (λNP =10 and λbkg = 1) was shown in Fig. S4.† We could obtain reliable estimates for small signals (S6†).
Application to Ag-NPs and comparison with conventional criteria method
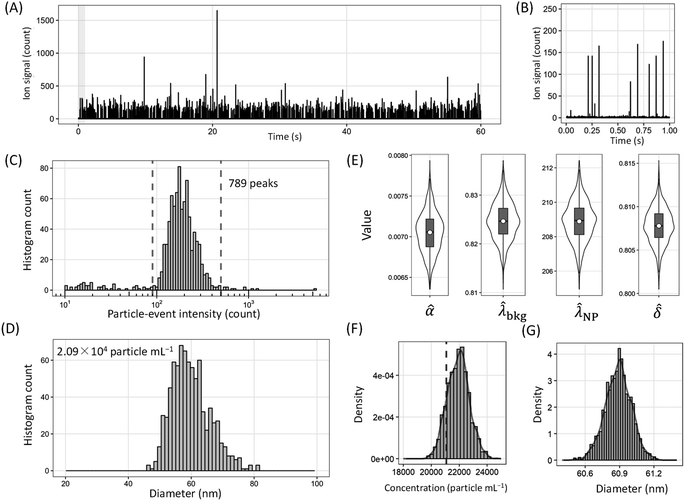
Fig. 4A and B shows the results of a time-resolved analysis of Ag-NPs with 60 nm diameters. Fig. 4C and D shows the results of estimation with the CC method, and Fig. 4E–G shows the results of estimation with the BE method. 789 particle events were obtained for 1-minute measurement within particle-event intensity of 90–500 counts, and average particle-event intensity was 199 counts. The median particle-event duration was 1.0 ms (Fig. S5A†). Using F of 0.31 mL min−1 and Rion of 1.07 × 105 cps ng−1 mL, the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CC was calculated to be 12.2% (
CC was calculated to be 12.2% (![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCN = 12.1%,
CCN = 12.1%, ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCM = 12.3%). When this data was calculated using the BE method,
CCM = 12.3%). When this data was calculated using the BE method, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) was estimated to (7.04 ± 0.24) × 10−3 and
was estimated to (7.04 ± 0.24) × 10−3 and ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) NP was estimated to 209 ± 1, consequently the
NP was estimated to 209 ± 1, consequently the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BE was estimated to be 12.2% (
BE was estimated to be 12.2% (![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEN = 12.7%,
BEN = 12.7%, ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEM = 11.8%). The both mean
BEM = 11.8%). The both mean ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCNP of 59.9 nm and mean
CCNP of 59.9 nm and mean ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP of 60.9 nm showed good agreement with the nominal particle diameter of 60 nm. The 95%CrI of
BENP of 60.9 nm showed good agreement with the nominal particle diameter of 60 nm. The 95%CrI of ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP (60.7–61.0 nm)‡ was within the uncertainty of the calibrated diameter (60 ± 8 nm).
BENP (60.7–61.0 nm)‡ was within the uncertainty of the calibrated diameter (60 ± 8 nm).
The both ĈCCPN of 2.09 × 104 particles per mL and the ĈBEPN of 2.19 × 104 particles per mL showed good agreements with the prepared concentration of 2.11 × 104 particles per mL. Moreover, the prepared concentration was within the 95% CrI of the ĈBEPN (2.04 × 104–2.34 × 104 particles per mL.
For the analytical results for Ag-NPs with diameters of 20–60 nm, both methods showed good agreement with the nominal particle size (Fig. S6†). When ideal spICP-MS data are obtained, the BE method and the CC method gave similar estimation results.
Application to data with large size particle
In the current Bayesian model, it is assumed that signals derived from single NP are observed within 2 readings. Since the longest transient time/the shortest transient time ratio correlated with aspect ratio of gold nanorods,34 it was thought that large particles might deviate from this assumption. Moreover, the use of collision/reaction cell (CRC) gas has been reported to significantly increase the particle-event duration of the NP signal.35 To examine whether the model is applicable to larger particles that deviate from this assumption, SiO2-NPs with 500 nm and 1000 nm diameters were measured under H2-gas mode and analysed using the weak informative prior distribution.
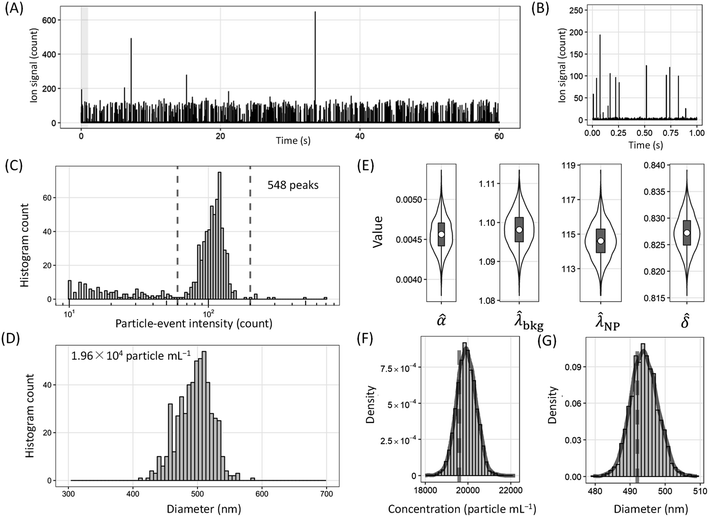
Fig. 5A and B show the results of a time-resolved analysis of SiO2-NPs with 500 nm diameters. Fig. 5C and D show the results of estimation with the CC method, and Fig. 5E–G show the results of estimation using the BE method. The median particle-event duration was 1.0 ms (Fig. S5B†). The both mean ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCNP (496 nm) and
CCNP (496 nm) and ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP (494 nm) show good agreements with the nominal diameter of 492 nm. Moreover, the both ĈCCPN (1.96 × 104 particles per mL) and ĈBEPN (1.95 × 104 particles per mL) showed similar values to the prepared concentration of 1.96 × 104 particles per mL. Similar results were obtained for 1000 nm SiO2-NP with median particle-event duration of 1.0 ms (see S7, S5C, and Fig. S7† for more detail).
BENP (494 nm) show good agreements with the nominal diameter of 492 nm. Moreover, the both ĈCCPN (1.96 × 104 particles per mL) and ĈBEPN (1.95 × 104 particles per mL) showed similar values to the prepared concentration of 1.96 × 104 particles per mL. Similar results were obtained for 1000 nm SiO2-NP with median particle-event duration of 1.0 ms (see S7, S5C, and Fig. S7† for more detail).
Application to data with high backgrounds
To examine whether high-background data can be analysed adequately, 100 ng L−1 of Ag ion standard solution (expected signal was about 10 counts per reading) was added to Ag-NPs with 20 nm diameters (expected signal was about 20 counts). The background signal was (25.1 ± 7.5) × 104 cps, which was equivalent to 12.6 ± 3.7 counts per reading. When the criterion for NP was set as the mean plus 3σ, many transient signals that appeared to be derived from NPs were excluded (Fig. S8†). Compared to the data without dissolved Ag ions, ĈCCPN was underestimated to be (0.92 ± 0.13) × 104 particle per mL, and![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCNP was overestimated to be 23.8 ± 0.2 nm. Similarly, lower ĈBEPN [(0.82 ± 0.05) × 104 particle per mL] and larger
CCNP was overestimated to be 23.8 ± 0.2 nm. Similarly, lower ĈBEPN [(0.82 ± 0.05) × 104 particle per mL] and larger ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP (33.3 ± 2.4 nm) were obtained by using the same weak informative prior distribution that was used in the previous section (Table 1).
BENP (33.3 ± 2.4 nm) were obtained by using the same weak informative prior distribution that was used in the previous section (Table 1).
| Condition | Estimation method | Concentration (×104 particle per mL) | Ion concentration (ng L−1) | Estimated diameter (nm) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Values indicate mean ± combined uncertainly. CC: conventional criteria method, BE: Bayesian estimation method, WIP: weak informative prior distribution, SIP: specific informative prior distribution. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ag-NP | CC | 2.3 ± 0.2 | — | 21.3 ± 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BE (WIP) | 2.3 ± 0.2 | — | 21.4 ± 0.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ag-NP + Ag ion (100 ng L−1) | CC | 0.92 ± 0.13 | 107 ± 3 | 23.8 ± 0.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BE (WIP) | 0.82 ± 0.05 | 104 ± 1 | 33.3 ± 2.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BE (SIP) | 2.6 ± 0.2 | 105 ± 1 | 22.5 ± 1.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To improve the estimation results, we applied the specific informative prior (SIP) distribution of α ∼ N(0.005, 0.001) and λNP ∼ N(22, 0.4) based on the BE result for Ag-NPs with 20 nm diameters without dissolved Ag ions. The designation X ∼ N(μ, σ) indicates that the variable X follows a normal distribution with a mean of μ and standard deviation of σ. We could consequently obtain similar results [ĈBEPN: (2.6 ± 0.2) × 104 particle per mL,![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP: 22.5 ± 1.2 nm] from data with high backgrounds and data obtained without dissolved Ag ions (Table 1).
BENP: 22.5 ± 1.2 nm] from data with high backgrounds and data obtained without dissolved Ag ions (Table 1).
To evaluate the estimation performance under the various S/B ratios, we executed a numerical simulation with the following parameters; α = 0.01, λblk = (0.3, 1, 3, 10, 30), and λNP = 30. Prior distributions used in this simulation were listed in Table S3 (see S8† for more detail). For the CC method, the 95% range of Po(λ = 30) (20–41) was set as the criterion for histogram.
Regarding the particle-event frequency, remarkable differences were observed between the BE and the CC method (Fig. S9A†). Although the true value was distributed within the uncertainty range using the BE method, when the S/B ratio was 3 or less, the BE method provided slightly large particle-event frequencies. On the other hand, the CC method tends to underestimate the particle-event frequencies. In the situation when the S/B ratio is 1, the error in the particle-event frequency estimated by the BE method was +3.5%, while the error in the particle-event frequency estimated by the CC method was −37%.
Regarding the particle-event intensity, both the BE and the CC methods provided estimates relatively close to the true value (Fig. S9B†). Compared to the BE method, the CC method tended to estimate a larger particle-event intensity, but even when the S/B ratio was 1, the error was only +5.2%.
In this simulation, we used the SIP for δR. δR is a parameter that does not directly relate to NP information (see S8† for more detail). By setting an almost constant-like prior distribution close to the expected value of δR (0.5), reasonable estimation results were obtained in situations where the S/B ratio is more than 3. However, when the S/B ratio is 1, it is necessary to set the SIP distribution for parameters other than δR.
Application to low-count data
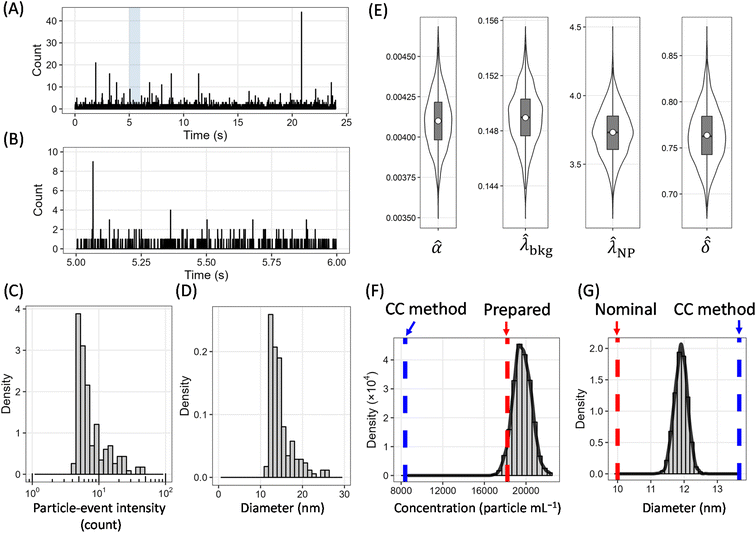
To confirm whether NP signals less than 10 counts could be estimated, we present the case of Ag-NPs with 10 nm diameters. In this case, the prior distributions for λNP were specified based on the posterior distribution for Ag-NPs with 20 nm diameters. The mean value of![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) NP for Ag-NPs with 20 nm diameters was 22.7 ± 0.5 count. Assuming a spherical geometry, the signal is proportional to the cube of the particle size. Thus, we used a prior distribution of λNP ∼ N(2.8, 2.8/20) for Ag-NPs with 10 nm diameters. We prepared the Ag-NPs with 10 nm diameters at a particle number concentration of 1.8 × 104 particles per mL (0.1 μg L−1 as Ag). Based on a transport efficiency of 8% (transport efficiency was calculated using 60 nm Ag-NP data on the same day), about 446 particle events were expected to be detected during a time interval of 1 min (1.2× 105 readings). Thus, we used a prior distribution of α ∼ N(0.0037, 0.0037/20).
NP for Ag-NPs with 20 nm diameters was 22.7 ± 0.5 count. Assuming a spherical geometry, the signal is proportional to the cube of the particle size. Thus, we used a prior distribution of λNP ∼ N(2.8, 2.8/20) for Ag-NPs with 10 nm diameters. We prepared the Ag-NPs with 10 nm diameters at a particle number concentration of 1.8 × 104 particles per mL (0.1 μg L−1 as Ag). Based on a transport efficiency of 8% (transport efficiency was calculated using 60 nm Ag-NP data on the same day), about 446 particle events were expected to be detected during a time interval of 1 min (1.2× 105 readings). Thus, we used a prior distribution of α ∼ N(0.0037, 0.0037/20).
By using the specific informative prior distribution, we estimated the ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) NP to be 3.7 ± 0.2 counts (Fig. 6). Although the nominal diameter (10 nm) was not distributed within the 95%CrI of
NP to be 3.7 ± 0.2 counts (Fig. 6). Although the nominal diameter (10 nm) was not distributed within the 95%CrI of ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP (11.5–12.3 nm), the analytical results of
BENP (11.5–12.3 nm), the analytical results of ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP (12.2 ± 0.4 nm) for triplicate measurements were closer to the nominal diameter compared to the
BENP (12.2 ± 0.4 nm) for triplicate measurements were closer to the nominal diameter compared to the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCNP (13.7 ± 0.3 nm) (Table 2). Whatever the case, both methods provided estimates within the uncertainty range (10 ± 4 nm). The prepared CPN (1.8 × 104) was distributed within the 95% CrI of ĈBEPN [(1.8–2.1) × 104 particle per mL]. The ĈCCPN (0.81 × 104 particle per mL) was less than the half of the prepared CPN. The analytical results of ĈBEPN [(1.9 ± 0.1) × 104 particle per mL] for triplicate measurements were closer to the prepared CPN compared to the ĈCCPN [(0.84 ± 0.05) × 104 particle per mL] (Table 2). These results indicate that the BE method can provide a more valid estimate for low-count NP-delivered signals compared to the CC method.
CCNP (13.7 ± 0.3 nm) (Table 2). Whatever the case, both methods provided estimates within the uncertainty range (10 ± 4 nm). The prepared CPN (1.8 × 104) was distributed within the 95% CrI of ĈBEPN [(1.8–2.1) × 104 particle per mL]. The ĈCCPN (0.81 × 104 particle per mL) was less than the half of the prepared CPN. The analytical results of ĈBEPN [(1.9 ± 0.1) × 104 particle per mL] for triplicate measurements were closer to the prepared CPN compared to the ĈCCPN [(0.84 ± 0.05) × 104 particle per mL] (Table 2). These results indicate that the BE method can provide a more valid estimate for low-count NP-delivered signals compared to the CC method.
| Estimation method | Concentration (×104 particle per mL) | Estimated diameter (nm) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Values indicate mean ± combined uncertainly. CC: conventional criteria method, BE: Bayesian estimation method. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CC | 0.84 ± 0.05 | 13.7 ± 0.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BE | 1.9 ± 0.1 | 12.2 ± 0.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
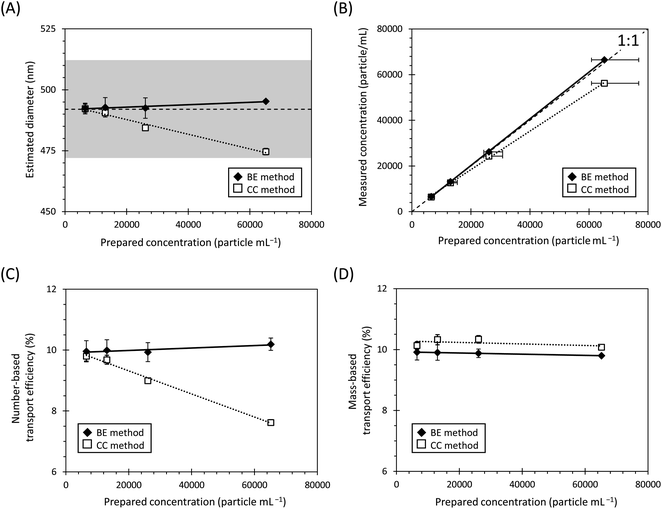
Application to data with increasing particle number concentration
The higher CPN of sample, the higher the probability that the multiple particle event will coalesce. Thus, the number of particle events may be underestimated and the particle-event intensity may be overestimated. To examine whether NP information with increasing CPN could be estimated, 500 nm diameter SiO2-NP with different CPN were measured and analysed (Fig. 7). Here, in order to evaluate whether the particle-event overlap phenomenon considered by this model can be calculated well even when the CPN is high, no informative prior distributions were used for α and λNP.Using the CC method, although the estimated particle sizes were within the uncertainty of the nominal diameter, the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCNP tend to decrease as the prepared CPN increase. Although the ĈCCPN distributed within the uncertainly of the prepared CPN derived from the uncertainly of diameter by the manufacture, except for the prepared CPN of 2.5 × 104 particle per mL, the ĈCCPN tend to decrease as the prepared CPN increase. Moreover, the influence of the prepared CPN on the ĈCCPN was more pronounced than that on
CCNP tend to decrease as the prepared CPN increase. Although the ĈCCPN distributed within the uncertainly of the prepared CPN derived from the uncertainly of diameter by the manufacture, except for the prepared CPN of 2.5 × 104 particle per mL, the ĈCCPN tend to decrease as the prepared CPN increase. Moreover, the influence of the prepared CPN on the ĈCCPN was more pronounced than that on ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) CCPN. Contrary to the CC method, using the BE method, the
CCPN. Contrary to the CC method, using the BE method, the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) BENP and the ĈBEPN are estimated appropriately regardless of the high concentrations of the prepared CPN.
BENP and the ĈBEPN are estimated appropriately regardless of the high concentrations of the prepared CPN.
Since TE is critical factor to calculate NP parameters, we evaluated the estimation results of TE with increasing the prepared CPN. The difference between ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEN and
BEN and ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCN tended to increase with increasing the prepared CPN. In contrast,
CCN tended to increase with increasing the prepared CPN. In contrast, ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEM and
BEM and ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCM showed almost constant values with increasing number concentration. In o ther words, the difference between
CCM showed almost constant values with increasing number concentration. In o ther words, the difference between ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/char_e108.gif) CCN and
CCN and ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/char_e108.gif) CCM increased with increasing the prepared CPN in the CC method, but no such difference occurred in the BE method.
CCM increased with increasing the prepared CPN in the CC method, but no such difference occurred in the BE method.
Discussion
Validity of the Bayesian model
Application of the BE method to Ag-NPs with 20–60 nm diameters resulted in good estimates for the nominal diameter, as well as the CC method. Application of the BE method to SiO2-NPs with 500- and 1000 nm diameters, which was measured under H2 gas mode, resulted in adequate estimates with respect to particle size and number concentration.Although the use of CRC gas was reported to broaden the particle-event duration,35 which may cause the measured data to deviate from the assumed model, the particle-event duration of SiO2-NP with 500 nm diameter (median: 1.0 ms) showed equivalent value to that of Ag-NP with 60 nm diameter (median: 1.0 ms). However, there is a possibility that the broadening of particle-event duration due to the use of H2 gas was not observed under the current conditions. Since the obtained particle-event durations were within 2 readings (1.0 ms), our data did not deviate significantly from the model assumed in this study.
From these results, it was shown that particles up to about 1000 nm can be analysed by the BE method without deviating greatly from the assumptions of the model. The influence of the use of H2 gas could be ignored under the conditions of this study. Although a potential problem in analysis of the large particles with high-boiling points is incomplete vaporization, the influence of incomplete vaporization was not observed in this study. If the ionization efficiency of the particles is different from that of non-particulate chemicals due to the high boiling point and large particle size, it is expected that the BE and the CC methods will not be able to estimate the particle size equally well.
Advantages of the BE method
The BE method has some advantages over the CC method. As for high-background data, by setting SIP distribution, more reliable information could be obtained using the BE method compared to the CC method. Similar results were obtained in numerical simulation study under the various S/B ratios. However, using the BE method provided slightly large particle-event frequencies when the S/B ratio was 3 or less. This is considered to be due to an increased probability of misrecognizing background noise as a particle event. In the CC method, the particle-event intensity could be evaluated more appropriately than the particle-event frequency. Depending on the settings of the criteria for histogram, excluding outlier particle-event intensities will lead to a decrease in the frequency of particle events, and including outlier particle-event intensities will lead to an increase in particle-event intensities.As a low-count signal, using the BE method with setting SIP distributions provided better estimation results for 10 nm Ag-NP with particle number concentration of 1.8 × 104 particles per mL compared to the CC method. The particle-event intensity estimated using the BE method at this time was 3.7 ± 0.4 counts. This result indicates that by setting SIP, the BE method could provide a smaller estimate of particle-event intensities than the CC method.
Furthermore, application of the BE method to 500 nm SiO2-NPs with particle number concentration of 0.65–6.5 × 104 particles per mL resulted in higher linearity than those obtained using the CC method even when NIP distribution was set. This result indicates that the BE method may be more robust than the CC method against increases in particle number concentration.
From the above results, it was considered that the BE method is a versatile calculation method that can be used for various spICP-MS data. Data with high background or various PNC can be dealt with by using short-DT and/or diluting the sample. However, if the sample is no longer available, the BE method can be used to re-analyse past measurement data. Although the BE method is useful in limited situations, it is a valuable alternative tool for analysing spICP-MS data.
Sources of error in the determination of the number-based transport efficiency
In this section, we discuss the sources of error in the determination of transport efficiency. It has been reported that the error in transport efficiency estimation theoretically affects the accuracy of CPN greater than particle size.20,36 While the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCN tends to decrease as the prepared CPN increased, the
CCN tends to decrease as the prepared CPN increased, the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) CCM showed almost constant values. Using the BE method, both the
CCM showed almost constant values. Using the BE method, both the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEN and the
BEN and the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) BEM showed almost same values and did not change with increase in the prepared CPN. It is considered that such a difference occurred for the following reasons. The CC method underestimates the number of particle events when the particle events are completely coalescent and cannot be divided into individual particle events. On the other hand, the BE method uses a model in which two particle events are stochastically merged, thus the
BEM showed almost same values and did not change with increase in the prepared CPN. It is considered that such a difference occurred for the following reasons. The CC method underestimates the number of particle events when the particle events are completely coalescent and cannot be divided into individual particle events. On the other hand, the BE method uses a model in which two particle events are stochastically merged, thus the ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/char_e101.gif) , which is the particle-event frequency, tends to be larger than the actual number of particle events.
, which is the particle-event frequency, tends to be larger than the actual number of particle events.
Contrary, the ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) M was not affected by the number concentration even with the CC method. Theoretically, if the number of particle events decreases by x%, the mean particle-event intensity increases by a factor of 1/(1 − x/100). However, the obtained results were not the case. The reason for this may be to eliminate outliers from the distribution in the process of selecting particle events to be used for the converting process to NP information. From the histogram of the signal intensities derived from SiO2-NP (Fig. 5), the 95% range was 76–141 counts. Since the expected particle-event intensity of the coalescent particle-event was 219 counts, the coalescent particle-event was removed as outlier. In the CC method, in addition to the particle-event detection criteria, the influence of the criteria for histogram cannot be ignored for the case of high CPN as well as high backgrounds.
M was not affected by the number concentration even with the CC method. Theoretically, if the number of particle events decreases by x%, the mean particle-event intensity increases by a factor of 1/(1 − x/100). However, the obtained results were not the case. The reason for this may be to eliminate outliers from the distribution in the process of selecting particle events to be used for the converting process to NP information. From the histogram of the signal intensities derived from SiO2-NP (Fig. 5), the 95% range was 76–141 counts. Since the expected particle-event intensity of the coalescent particle-event was 219 counts, the coalescent particle-event was removed as outlier. In the CC method, in addition to the particle-event detection criteria, the influence of the criteria for histogram cannot be ignored for the case of high CPN as well as high backgrounds.
The smaller difference between ηN and ηM is probably the reason why the accuracy of NP information is improved by use of the BE method. An approach that minimizes the difference between ηM and ηN may be more useful than an approach that calculates log-likelihood. In addition, in terms of reducing the discrepancy between ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) N and
N and ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) M, using an introduction system that achieves 100% transport efficiency, such as a total-consumption nebulizer37 or droplet nebulizer,38 is useful method to solve the problem of TE calculation. Relative estimation errors in transport efficiency may be suppressed because conventional nebulizers are more sensitive to a 1% difference in transport efficiency compared to high-efficiency nebulizers.
M, using an introduction system that achieves 100% transport efficiency, such as a total-consumption nebulizer37 or droplet nebulizer,38 is useful method to solve the problem of TE calculation. Relative estimation errors in transport efficiency may be suppressed because conventional nebulizers are more sensitive to a 1% difference in transport efficiency compared to high-efficiency nebulizers.
How to determine appropriate informative prior distributions
The adoption of Bayesian estimation was effective for analysing data with increasing particle number concentration, high backgrounds, and low-count particle events. Such data are difficult to analyse with CC methods. However, to obtain accurate estimates, specific informative prior distributions are required. Careful analysis of the raw data may give a reasonable prior distribution for λbkg. In addition, because similar posterior distributions of![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) bkg were obtained using weak informative prior distributions, there seem to be a few problems to estimating λbkg. In the cases of α and λNP, however, if information on particle size and number concentration is available in advance, it is possible to apply specific informative prior distributions.
bkg were obtained using weak informative prior distributions, there seem to be a few problems to estimating λbkg. In the cases of α and λNP, however, if information on particle size and number concentration is available in advance, it is possible to apply specific informative prior distributions.
Because there is no information about α and λNP for unknown samples, it is difficult to identify a logical, specific informative prior distribution. In the data with many NP signals associated with smaller particle sizes, an appropriate estimate might be obtained with use of a prior distribution with a large α and small λNP that reflected the analytical result with the CC method. In any case, it will be necessary to go through a process of trial and error using models with different prior distributions. It is then appropriate to select an optimum model based on objective indicators such as the widely applicable information criterion.28
On the other hand, in numerical simulations of various S/B ratios, there were cases in which reasonable estimation results were obtained simply by setting the SIP to δR. The random number generation model assumes that δR is a variable that follows a uniform distribution between 0 and 1. In this case, the SIP is intended to be the expected value of 0.5. Since δR is not directly involved in the information of NP, there is a possibility that it can be applied to unknown samples.
Because the selection of a prior distribution in Bayesian estimation depends on the analyst, Bayesian estimation has been criticized on the grounds that it is not objective. However, because the criteria that are used depend on the researcher (for example, whether the requirement for NPs is mean plus 3σ or 5σ), the CC method is also subjective. Prior distributions can be used as tools to allow for data-informed shrinkage, to enact regularization, or to nudge algorithms towards a likely high-density region and thereby improve estimation efficiency.39,40 These considerations suggest that it is possible to select the appropriate operation using the BE method complemented with the CC method or other published methods.
Limitation of current Bayesian model
In the current model, we intentionally excluded two cases: one was the case of NP coincidence at one reading; and the other was a case where the peak tops of the particle events were measured continuously for three readings. These possibilities are considered to have little effect on the analysis if the sample is diluted until![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) is less than 0.007. Alternatively, it is possible to deal with these cases by extending the model, and the correspondence is relatively easy.
is less than 0.007. Alternatively, it is possible to deal with these cases by extending the model, and the correspondence is relatively easy.
The case of NPs with multiple diameters is very different from the current model. It would be ideal if we could obtain a bimodal posterior distribution as an estimate of the result for NPs with multiple diameters. However, a numerical simulation showed that the posterior distribution was close to the average value of the counts of the two NPs (data not shown). It is therefore necessary to extend the model. Another scenario that is not assumed in the current study is a particle event that spans three or more readings. As a compromise between signal-to-noise ratio and possibilities for transient time measurement, a value of 50–100 μs is often preferred.29 The conventional goal of spICP-MS analysis is to measure with a shorter DT (∼100 μs) and detect the particle event at multiple readings. Bayesian algorithms that can detect particle events that span more readings will be needed to achieve that goal.
In this study, a Poisson distribution with one parameter was used to facilitate making estimates. Because the variance of the Poisson distribution is equivalent to the expectation value, it is likely to be unreliable for under- and over-dispersed data. For such data, consideration should be given to models that use other probability density functions, such as a hypergeometric distribution, negative binomial distribution, or double Poisson distribution. In such distributions, more than 2 parameters take on non-negative integer values.
Many studies that have used spICP-MS to obtain information about NPs have treated the distribution of the NP signal as if it represented the distribution of the NP mass. Laborda et al.41 have reported that the particle size distributions analysed using spICP-MS are broadened relative to distributions analysed with other techniques. In general, spICP-MS analyses evaluate NP information without classifying the variance of the ICP-MS signals or the variance of the NP masses. We consider that this characteristic of spICP-MS analyses is the main cause of the broadened size distribution. In the Bayesian framework, it may be possible to separately analyse the variation of the ICP-MS signal itself and the variation of the signal caused by NPs by extension to a hierarchical Bayesian model that considers random effects. In general, hierarchical Bayesian models take longer to calculate than non-hierarchical Bayesian models. It is therefore presently difficult to analyse large datasets such as spICP-MS data in a realistic amount of time. We expect that it will be possible to implement more realistic algorithms by improving the analysis environment as well as improving the system of detection by ICP-MS.
Conclusions
To date, although spICP-MS is an established method for the determination of metal and metal-oxide NP mass distributions and particle number concentrations, it is difficult to detect low-count signals, especially signals of particles overlapped by signals of dissolved ions. To deconvolute spICP-MS data, which is obtained by setting the dwell time similar to the particle event duration time, we applied Bayesian estimation with a mixed Poisson distribution based on an assumed process of data generation. When the instrument parameter was set so as not to deviate from the assumption of the current model (in other words, the DT was set so that the particle-event durations were equivalent to 2 readings), adequate estimation results could be obtained using the BE method, as well as the CC method. Because appropriate NP information was obtained for both Ag-NPs and SiO2-NPs, the Bayesian estimation method can always be used with NPs that contain elements detectable by ICP-MS. Furthermore, compared to the CC method, using a specific informative prior distribution to the BE method enabled us to obtain reasonable estimates even when the count signal was as low as 4 counts or less and the background counts were high. Because there have been few applications of the current Bayesian model, we expect that the scope of application of Bayesian estimation will be expanded in the future.Symbols and abbreviations
| BE | Bayesian estimation |
| bkg | Background |
| CC | Conventional criteria (method) |
| C PN | Particle number concentration |
| CrI | Credible interval |
| DT | Dwell time |
| IBE | Indirect Bayesian estimation |
| L | Likelihood function |
| MCMC | Markov chain Monte Carlo |
| MLE | Maximum likelihood estimation |
| N a | Number of readings per measurement |
| N r | Number of readings per minute |
| NP | Nanoparticle |
| N(μ,σ) | Normal distribution with μ and σ |
| PMF | probability mass function |
| Po(Y|λ) | Variable Y follows Poisson distribution with parameter λ |
| R ion | Sensitivity of the ionic standard solution (cps ng−1 mL) |
| α | Frequency parameter of particle event |
| δ | Signal split coefficient for particle volume |
| δ R | Signal split coefficient for particle diameter |
| η | Transport efficiency |
| η M | Mass-based transport efficiency |
| η N | Number-based transport efficiency |
| λ bkg | Parameter for background signal (count) |
| λ NP | Parameter for particle-event intensity (count) |
| μ | Mean |
| ρ NP | Density of the NP (g cm−3) |
| ϕ NP | NP diameter |
| σ | Standard deviation |
| ψ NP | Mass fraction of analytical elements in the NP Hat notation indicates an estimate. Upper-right letters in variable indicate estimation methods. Lower-right letters in variable indicate simple description for variables |
Code availability
The codes included in this paper is available via GitHub (https://github.com/Yoshinari-Suzuki/Bayesian-spICP-MS-analysis.git). See S1† for more detail.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Prof. Takahumi Hirata of The University of Tokyo, who kindly provided NanoQuant software. This work was supported by a Grant-in-Aid from the Ministry of Education, Culture, Sports, Science and Technology of Japan (no. 19K05924 and no. 22K05486) and a grant from the Food Safety Commission, Cabinet Office, Government of Japan (Research Program for Risk Assessment Study on Food Safety, No. 1905).References
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2011, 26, 1362 RSC.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2020, 35, 1740–1783 RSC.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- E. Bolea-Fernandez, D. Leite, A. Rua-Ibarz, L. Balcaen, M. Aramendía, M. Resano and F. Vanhaecke, J. Anal. At. Spectrom., 2017, 32, 2140–2152 RSC.
- T. Nomizu, H. Hayashi, N. Hoshino, T. Tanaka, H. Kawaguchi, K. Kitagawa and S. Kaneco, J. Anal. At. Spectrom., 2002, 17, 592–595 RSC.
- A. Hineman and C. Stephan, J. Anal. At. Spectrom., 2014, 29, 1252–1257 RSC.
- S.-i. Miyashita, A. S. Groombridge, S.-i. Fujii, A. Minoda, A. Takatsu, A. Hioki, K. Chiba and K. Inagaki, J. Anal. At. Spectrom., 2014, 29, 1598–1606 RSC.
- J. Liu, K. E. Murphy, R. I. MacCuspie and M. R. Winchester, Anal. Chem., 2014, 86, 3405–3414 CrossRef CAS PubMed.
- I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016, 31, 135–144 RSC.
- A. Kaňa, M. Loula, R. Koplík, M. Vosmanská and O. Mestek, Talanta, 2019, 197, 189–198 CrossRef PubMed.
- J. Tuoriniemi, G. Cornelis and M. Hassellov, Anal. Chem., 2012, 84, 3965–3972 CrossRef CAS PubMed.
- R. B. Reed, D. G. Goodwin, K. L. Marsh, S. S. Capracotta, C. P. Higgins, D. H. Fairbrother and J. F. Ranville, Environ. Sci.: Processes Impacts, 2013, 15, 204–213 RSC.
- V. Geertsen, E. Barruet, F. Gobeaux, J.-L. Lacour and O. Taché, Anal. Chem., 2018, 90, 9742–9750 CrossRef CAS PubMed.
- X. Bi, S. Lee, J. F. Ranville, P. Sattigeri, A. Spanias, P. Herckes and P. Westerhoff, J. Anal. At. Spectrom., 2014, 29, 1630–1639 RSC.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2015, 30, 1723–1729 RSC.
- P. Shaw and A. Donard, J. Anal. At. Spectrom., 2016, 31, 1234–1242 RSC.
- K. Newman, C. Metcalfe, J. Martin, H. Hintelmann, P. Shaw and A. Donard, J. Anal. At. Spectrom., 2016, 31, 2069–2077 RSC.
- A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855 CrossRef CAS PubMed.
- M. Hadioui, G. Knapp, A. Azimzada, I. Jreije, L. Frechette-Viens and K. J. Wilkinson, Anal. Chem., 2019, 91, 13275–13284 CrossRef CAS PubMed.
- D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2019, 34, 1571–1580 RSC.
- C. Stephan and A. Hineman, Analysis of NIST Gold Nanoparticles Reference Materials Using the NexION 350 ICP-MS in Single Particle Mode, 2012 Search PubMed.
- M. Hadiou, K. Wilkinson and C. Stephan, Assessing the Fate of Silver Nanoparticles in Surface Water Using Single Particle ICP-MS, 2014 Search PubMed.
- S. Sannac, Single Particle Analysis of Nanomaterials Using the Agilent 7900, ICP-MS, 2015 Search PubMed.
- D. Kutscher, J. D. Wills and S. M. Duco, Nanoparticle Characterization via Single Particle Inductively Coupled Plasma – Mass Spectrometry (spICP-MS) Using a Dedicated Plug-In for Qtegra ISDS Software, 2015 Search PubMed.
- A. C. Davison, Statistical Models, Cambridge university press, 2003 Search PubMed.
- G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 134–144 RSC.
- S. Watanabe, J. Mach. Learn. Res., 2010, 11, 3571–3594 Search PubMed.
- M. Resano, M. Aramendía, E. García-Ruiz, A. Bazo, E. Bolea-Fernandez and F. Vanhaecke, Chem. Sci., 2022, 13, 4436–4473 RSC.
- D. Mozhayeva, I. Strenge and C. Engelhard, Anal. Chem., 2017, 89, 7152–7159 CrossRef CAS PubMed.
- T. Suzuki, S. Yamashita, Y. Yoshikuni and T. Hirata, J. Mass Spectrom. Soc. Jpn., 2019, 67, 147–153 CrossRef CAS.
- A. Gelman, D. Lee and J. Q. Guo, J Educ Behav Stat, 2015, 40, 530–543 CrossRef.
- B. Carpenter, A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. Brubaker, J. Guo, P. Li and A. Riddell, J. Stat. Softw., 2017, 76, 1–32 Search PubMed.
- I. Kálomista, A. Kéri, D. Ungor, E. Csapó, I. Dékány, T. Prohaska and G. Galbács, J. Anal. At. Spectrom., 2017, 32, 2455–2462 RSC.
- E. Bolea-Fernandez, D. Leite, A. Rua-Ibarz, T. Liu, G. Woods, M. Aramendia, M. Resano and F. Vanhaecke, Anal. Chim. Acta, 2019, 1077, 95–106 CrossRef CAS PubMed.
- J. Liu, K. E. Murphy, M. R. Winchester and V. A. Hackley, Anal. Bioanal. Chem., 2017, 409, 6027–6039 CrossRef CAS PubMed.
- S.-i. Miyashita, H. Mitsuhashi, S.-i. Fujii, A. Takatsu, K. Inagaki and T. Fujimoto, Anal. Bioanal. Chem., 2017, 409, 1531–1545 CrossRef CAS PubMed.
- A. Gundlach-Graham and K. Mehrabi, J. Anal. At. Spectrom., 2020, 35, 1727–1739 RSC.
- A. Gelman, D. Simpson and M. Betancourt, Entropy, 2017, 19, 555 CrossRef.
- R. van de Schoot, S. Depaoli, R. King, B. Kramer, K. Märtens, M. G. Tadesse, M. Vannucci, A. Gelman, D. Veen, J. Willemsen and C. Yau, Nat. Rev. Methods Primers, 2021, 1, 1 CrossRef CAS.
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2013, 28, 1220–1232 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: The detail description of Stan codes and other examples were shown. See DOI: https://doi.org/10.1039/d3ja00220a |
| ‡ Although Fig. 4G, 5G, and 6G show histograms of diameters, it does not show the particle size distribution, which has frequently been shown in other papers discussing spICP-MS. The mean value of the sample particle size and its uncertainty are expressed as a posterior distribution. |
| This journal is © The Royal Society of Chemistry 2024 |