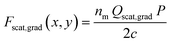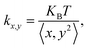Open Access Article
Open Access ArticleOpto-hydrodynamic tweezers†
Shreyas
Vasantham‡
 a,
Abhay
Kotnala‡
*ab,
Yurii
Promovych
a,
Piotr
Garstecki
a,
Abhay
Kotnala‡
*ab,
Yurii
Promovych
a,
Piotr
Garstecki
 a and
Ladislav
Derzsi
a and
Ladislav
Derzsi
 *a
*a
aInstitute of Physical Chemistry, Polish Academy of Sciences, ul. Kasprzaka 44/52, 01-224, Warsaw, Poland. E-mail: akotnala@central.uh.edu; lderzsi@ichf.edu.pl
bDepartment of Electrical and Computer Engineering, University of Houston, Houston, Texas 77204, USA
First published on 21st December 2023
Abstract
Optical fiber tweezers offer a simple, low-cost and portable solution for non-invasive trapping and manipulation of particles. However, single-fiber tweezers require fiber tip modification (tapering, lensing, etc.) and the dual-fiber approach demands strict alignment and positioning of fibers for robust trapping of particles. In addition, both tweezing techniques offer a limited range of particle manipulation and operate in low flow velocity regimes (a few 100 μm s−1) when integrated with microfluidic devices. In this paper, we report a novel opto-hydrodynamic fiber tweezers (OHT) platform that exploits the balance between the hydrodynamic drag force and optical scattering forces to trap and manipulate single or multiple particles of various shapes, sizes, and material compositions in a microfluidic channel. 3D hydrodynamic flow focusing offers an easy and dynamic alignment of the particle trajectories with the optical axis of the fiber, which enables robust trapping of particles with high efficiency of >70% and throughput of 14 particles per minute (operating flow velocity: 1000 μm s−1) without the need for precision stages or complex fabrication. By regulating the optical power and flow rates, we were able to trap single particles at desired positions in the channel with a precision of ±10 μm as well as manipulate them over a long range upstream or downstream with a maximum distance of 500 μm. Our opto-hydrodynamic tweezers offer an alternative to conventional optical fiber tweezers for several applications in physics, biology, medicine, etc.
Introduction
Optical tweezers, which were first demonstrated by Arthur Ashkin in the 1970s, continue to be the preferred approach for contactless and non-invasive manipulation of single particles ranging from colloids, hard spheres, polymers, gels, cells, bacteria, and viruses to biological macromolecules.1–6 Based on strong optical gradient forces, conventional tweezers use high numerical aperture (NA) microscope objective lenses to trap particles at the focus of the laser. The integration of tweezers with other investigative techniques such as microscopy and spectroscopy has advanced our understanding of single particles particularly within the fields of biology and medicine. For example, a single E. coli bacterium has been trapped by optical tweezers to characterize its “run and tumble” swimming behaviour.1 In another study, a single DNA strand was trapped and manipulated to measure its spring constant.7 It was also possible to resolve the angstrom-level stepwise motion of motor proteins on microtubules by manipulating a protein-tethered bead with optical tweezers. Although optical tweezers presented an elegant way to probe single particles, certain constraints, such as the need for high NA lenses, small working distances, complex instrumentation and operation, and lack of portability, have limited its widespread applicability.Optical fiber tweezers overcome the limitations imposed by traditional optical tweezers and provide a simple, cost-effective, and portable solution to trap particles. Among several fiber-based tweezer designs, dual-beam fiber tweezers that use two opposing diverging beams for trapping a particle are most popular and have been used for several applications such as rotation of particles, Raman spectroscopy of single cells, and, most importantly, as optical stretchers to study single-cell deformability.8–12 Nonetheless, robust trapping of particles requires strict positioning and axial alignment of the two fibers with a precision down to one micron, otherwise the particles tend to oscillate within the trapping region.13 To achieve precise alignment and positioning of the fibers, high-precision motion stages or fabrication of fiber-guiding structures on the chip are necessary.14,15 The use of high-precision stages increases the cost and form factor of the dual-fiber tweezers while fiber-guiding structures increase the device complexity and rigidity, offering no flexibility to the alignment process in case of fabrication errors etc. Although with excellent alignment, the dual-beam fiber tweezers can efficiently trap particles; their ability to manipulate the trapped particle is limited along their optical axis—i.e., over the width of the channel (typically <100 μm)—if the fibers are positioned perpendicular to the flow direction.10 Furthermore, their operation is restricted to slow flow rates in the channel. Since gradient forces are mainly responsible for trapping of particles in the flow direction, at high flow rates, the drag force acting on the particle/cell overcomes the optical gradient force, yielding poor trapping efficiencies and limiting application throughput.
Because single-fiber tweezers do not need any fiber alignment, they are preferred over dual-beam fiber tweezers. They can provide a significant gradient force to capture particles but require fiber tip modification in the form of a taper or machining to create a lens.16 Furthermore, particle manipulation necessitates physical movement of the fiber and hence cannot be employed for on-chip particle manipulation. Because of the increased fabrication complexity, high optical intensity operation, and limited particle manipulation capability, single-fiber tweezers are a less appealing solution for many applications.17–22
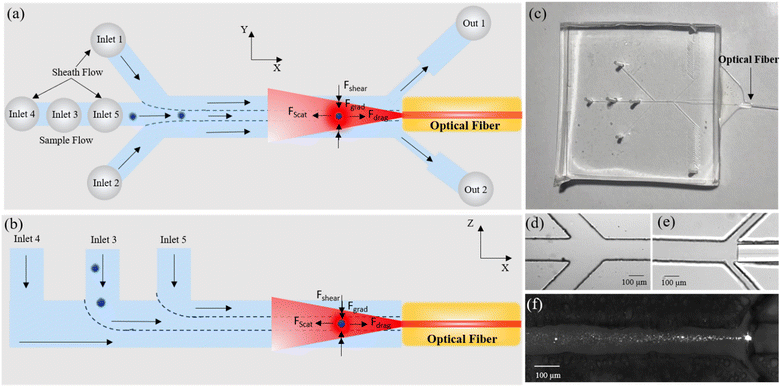
In this paper, we present a novel optofluidic platform for trapping and manipulation of single as well as multiple particles and cells. The device utilizes laminar flow in microchannels to hydrodynamically focus and deliver particles or cells to the trapping zone. In contrast to the standard orthogonal alignment of the fibers with the flow direction, in our device a single optical fiber embedded in the microchannel is oriented parallel to the flow direction (see Fig. 1(a) and (b)). As a result, particles can be trapped at specific locations in the channel, where there is a balance between the optical and hydrodynamic (shear and drag) forces acting on the particle as shown in Fig. 1a and b.
The synergy of laminar flow in microfluidic channels along with the compactness of optical fibers creates opto-hydrodynamic tweezers (OHT). The trajectory of particles in the channel can be altered by adjusting the sheath flow rates, which allows for easy and dynamic alignment of particles with the optical fiber resulting in efficient trapping of particles.
Moreover, since the drag force is balanced by the optical scattering force rather than by the gradient force as in the case of conventional optical fiber tweezers, OHT can work at significantly higher flow velocities (up to 4300 μm s−1), which is more than ten times the operating flow velocities of conventional optical fiber tweezers.10 By regulating the optical power and flow rates in the channel, the trapped particle can be manipulated/translated over a long range along the length of the channel up to a maximum distance of 500 μm.
The ability to dynamically control and align the trajectory of particles with the optical axis of the fiber by simply modulating the sheath flow rates is one of the distinguishing features of OHT. It enables robust trapping of particles with high efficiency (given by the number of trapped particles/total number of particles flowed in the channel). Moreover, OHT offers long-range manipulation of particles along the length of the channel by varying either the optical power or flow rates. This is in direct contrast to dual-fiber-based trapping approaches, where the fiber–particle alignment is static, prone to misalignment, and has a small particle manipulation range. OHT also offers several additional benefits over conventional optical fiber tweezers: the use of a single optical fiber as compared to two used in dual-beam fiber tweezers minimizes the overall optical radiation intensity on the particle, hence limiting damage to the trapped particle.
The unique design of OHT, which places the fiber directly in the flow channel, eliminates material interfaces between the fiber and the particle, which are common in dual-beam fiber tweezers. This prevents unwanted scattering of the output laser beam, which can degrade trapping performance owing to changes in the laser beam profile or a drop in absolute trapping power.
OHT can be empowered further by incorporating more fiber sources and detectors along the length of the channel to integrate optical investigation schemes such as Raman spectroscopy, fluorescence imaging, etc. With a facile design and easy alignment process, OHT offers a portable, robust, and cost-effective lab-on-chip platform for particle trapping and manipulation (Table 1).
| Objective-based optical tweezers | Dual-beam fiber tweezers | Single-beam fiber tweezers | Evanescent wave trapping | Opto-hydrodynamic tweezers | |
|---|---|---|---|---|---|
| Trapping force (dominant) | Optical gradient | Optical gradient and scattering | Optical gradient | Optical near-field gradient | Optical scattering and hydrodynamic drag |
| Direction of flow (with respect to trapping laser direction) | Orthogonal | Orthogonal | Orthogonal | Orthogonal | Parallel |
| Trapping particle size | 0.2 nm–5 μm | 50 nm–100 μm | 100 nm–15 μm | 10 nm–5 μm | 3–50 μm |
| Numerical aperture | 1.2–1.4 | 0.1–0.2 | 0.1–0.2 | 0.17–0.19 | 0.12 |
| Operational flow velocities | Up to 1400 μm s−1 | Up to 100 μm s−1 | Up to 100 μm s−1 | NA | 190–4500 μm s−1 |
| References | 23 | 14, 24, 25 | 16, 18, 26–29 | 30–32 | Present work |
Experimental
Design and fabrication of microfluidic device
A polydimethylsiloxane (PDMS)-based microfluidic device (Fig. 1c) was fabricated using soft lithography according to standard procedure.33 Briefly, photomasks were designed in AutoCAD (AutoCAD 2020, Version 1.4) and printed at 3200 dpi to a flexible plastic film. SU-8 2100 negative photoresist (Kayaku Advanced Materials, USA) was used to fabricate the channel mould on a 4 inch silicon wafer using a standard UV lithography process. To achieve a channel thickness of 125 μm, similar to the cladding diameter of the optical fiber, the resist was spin-coated at a speed specified by the manufacturer. The master mould was obtained after UV exposure over the photomask and subsequent development. PDMS (Sylgard 184, Dow Corning, USA) was poured onto the master mould after mixing it in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with the curing agent. After removing the bubbles and curing for 2 hours at 75 °C, the solidified clear PDMS was peeled off from the master mould and a 0.5 mm biopsy puncher (inner diameter: 0.5 mm, Electron Microscopy Sciences, USA) was used to punch inlet/outlet ports. In the next step, the PDMS block was bonded to a cover glass (48 mm × 60 mm, No. 1 thickness, Brain Research Lab, USA) after plasma treatment for 60 seconds (Harrick plasma, PDC-002-CE, USA). After bonding, a single-mode optical fiber (Thorlabs, USA; NA: 0.1, core diameter: 6.2 μm, cladding: 125 μm) was inserted by slipping it from the side through an open end into the dedicated channel (as shown in Fig. 1e) and glued with the help of a UV-curable, epoxy-based resin (Drei Bond 6020, Germany).
1 ratio with the curing agent. After removing the bubbles and curing for 2 hours at 75 °C, the solidified clear PDMS was peeled off from the master mould and a 0.5 mm biopsy puncher (inner diameter: 0.5 mm, Electron Microscopy Sciences, USA) was used to punch inlet/outlet ports. In the next step, the PDMS block was bonded to a cover glass (48 mm × 60 mm, No. 1 thickness, Brain Research Lab, USA) after plasma treatment for 60 seconds (Harrick plasma, PDC-002-CE, USA). After bonding, a single-mode optical fiber (Thorlabs, USA; NA: 0.1, core diameter: 6.2 μm, cladding: 125 μm) was inserted by slipping it from the side through an open end into the dedicated channel (as shown in Fig. 1e) and glued with the help of a UV-curable, epoxy-based resin (Drei Bond 6020, Germany).
Opto-hydrodynamic tweezers set-up and working principle
After bonding the PDMS mould to glass, an end of the optical fiber was stripped, cleaved and inserted from the side into the dedicated fiber-guide channel as shown in Fig. 1e and S1b.† The fiber is inserted flat up until the main channel of the device without blocking the adjacent outlets and the face of the fiber must be cleaved to obtain a flat uniform cut. A drop of UV epoxy (Drei Bond 6020, viscosity 2200–2900 cP @ 25 °C) was used to fix the position of the optical fiber and simultaneously block the channel to avoid leakage. The glue flows into the channel via capillary action and the process is monitored under a microscope. When the glue covers most of the fiber uniformly and is just a few microns away from the main channel, it is cured with the help of a spot cure UV gun for 30 s. The fiber insertion process might result in an offset of the core position, especially during insertion and gluing. We note, however, that utilizing all 5 inlets enables precise control of beads/cell positioning along three axes and allows one to offset any error in the position of the fiber (±10 μm deviation) during insertion or fixation into the waveguide. For more details on the process please see the ESI† (S8). Sample and sheath liquid solutions were injected from 1 mL glass syringes (Hamilton, USA) via PTFE tubes (0.46 mm inner diameter, Adtech, UK) individually into each of the 5 inlet ports of the microfluidic device to perform 3D hydrodynamic flow focusing. The flow was controlled by high-precision, low-pressure syringe pumps (NemeSYS, Cetoni, Germany). The microfluidic chip was placed on the stage of an inverted microscope (Nikon Ti2 Eclipse) and imaged using a 10× microscope objective (Nikon, Plan Fluor 10× NA 0.3, WD 16 mm) connected to a CMOS detector (Andor Zyla, UK). A short pass filter (Thorlabs, FES0750, cut-off wavelength 750 nm) was inserted between the objective lens and CMOS camera to block the scattered laser beam from the trapped particle.
Similarly, the top and bottom sheath flows from inlets 4 and 5 were employed to compress the sample flow in the vertical direction (Z-axis, along the height of the channel). The flow rates of the sheathing liquids (via inlets 1, 2, 4, 5) can be independently controlled to change the flow trajectories of particles within the microfluidic channel and dynamically align them with the optical axis of the fiber by varying the ratio of sheath flow rates, thus enabling the trapping of particles with high efficiency and throughput.
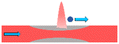
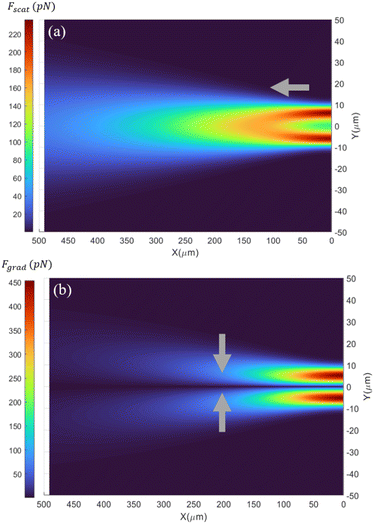
where nm is the refractive index of the medium, c is the speed of light, Qscat and Qgrad are the dimensionless coefficients of the scattering and gradient force similar to that found in Ashkin's work37 and P is the incident optical power on the particle (for a more detailed description, see ESI† S2). Fig. 2a shows the spatial distribution of the optical scattering force that would be exerted on a 15 μm polystyrene particle flowing in the microfluidic channel, by the laser output from the optical fiber (λlaser = 973 nm; P = 550 mW, MFD = 6.6 μm) (ESI† Fig. S2). For locations less than ∼100 μm from the optical fiber's tip, the beam diameter is smaller than the size of the particle (15 μm), due to which the scattering force is maximum at transverse positions comparable to the radius of the particle from the beam axis. This is because of the larger overlap between the diverging beam and the particle, resulting in strong momentum transfer and hence a large optical scattering force. However, at a distance beyond 100 μm from the tip of the fiber, the diameter of the beam is larger than the size of the particles and therefore the scattering force is maximum at the laser beam axis and decreases as one moves away from it in the direction perpendicular to the optical axis. This is due to the Gaussian intensity distribution of the laser beam output from the fiber. Along the beam axis (Y = 0), the scattering forces decrease as one moves away from the optical fiber. This is due to the divergence of the laser beam that results in radially weakening intensity and consequently lower scattering forces.
In addition to the scattering force, the optical gradient force also acts on particles flowing in the channel. The gradient forces pull the particle towards the region of maximum intensity (i.e. towards the laser beam's optical axis) and are calculated using eqn (1) (see ESI† S2). The optical gradient forces are zero in the transverse direction for particles perfectly aligned with the laser beam axis. With increasing displacement from the beam axis, the gradient forces initially increase and then decrease, reaching a maximum at displacements nearly equal to the radius of the particle. The optical gradient forces contribute to the particle trapping in the transverse direction, i.e. perpendicular to the laser beam's axis. Particles that flow slightly off-track from the beam axis can get pulled into the beam and ultimately get trapped by OHT. Once aligned, gradient force confines the particle in the transverse plane. However, along the axial direction, the gradient force acting on the particle is smaller compared to the scattering force due to the low numerical aperture of the optical fiber (NA ∼0.1) and therefore does not play a major role in the trapping process.
The trapping location depends on the magnitude of the hydrodynamic drag force acting on the particle, which is calculated using Stokes' law. At low Reynolds numbers, (negligible) inertial forces in homogenous viscous media and for a rigid non-rotating spherical particle Stokes drag is given by:
| Fdrag = 6πηaν |
Particles can be trapped at different positions along the laser beam axis depending on the flow velocity in the channel, where the scattering force equals the drag force. According to the scattering map shown in Fig. 2a, if a 15 μm polystyrene particle moving in the channel at a velocity of 1000 μm s−1 with its trajectory exactly aligned with the optical axis of the optical fiber and the fiber emits a Gaussian laser beam at an output power of 550 mW, then the particle would be trapped 123 μm from the fiber's tip, where the scattering force is equal to the anticipated drag force (125 pN).
Fig. 2a also highlights the importance of the alignment of the trajectory of particles with the optical axis of the fiber for enabling the trapping process. As the particle trajectory deviates from the laser beam axis, it experiences weaker or almost negligible optical scattering force, depending on the extent of the deviation. For example, a 15 μm polystyrene particle at the distance of 100 μm from the fiber's tip experiences 55% and 99% lower scattering force for a deviation of 10 and 20 μm, respectively, from the beam's axis (Fig. 2a). Consequently, a particle flowing at a speed of 1000 μm s−1 would not be trapped if its trajectory deviates by more than 5 μm from the beam axis as opposed to when perfectly aligned with the beam axis.
The necessity for exact alignment of particle trajectories with the beam axis is relaxed to some extent by the strong optical gradient forces acting on the particle near the beam axis. For example, a 15 μm polystyrene particle travelling at a speed of 1000 μm s−1 in the channel experiences larger gradient forces than the drag force at distances less than 130 μm from the fiber (Fig. 2b). Particles whose paths deviate by less than 9 μm from the optical axis will be pulled to the centre of the beam, where they spontaneously align with the beam and get trapped.
In addition to the optical gradient forces, in the transverse directions, the particle also experiences shear gradient- and wall-lift forces, but the forces are almost three orders of magnitude smaller than the optical forces for particles flowing at the centre of the channel. While the shear gradient lift force tries to move the particles toward the walls of the channel, the wall-induced lift force acts oppositely and moves the particles away from the wall.38 For our channel geometry (125 μm × 125 μm) and the trapping position at the centre of the channel, both the shear stress and the net lift forces acting on the particle are negligible compared to the optical gradient forces. The density of the particle and the surrounding liquid is nearly equal; thus gravitational and buoyancy forces can be neglected (see ESI† S3).
Results and discussion
3D hydrodynamic flow focusing and trapping of microparticles
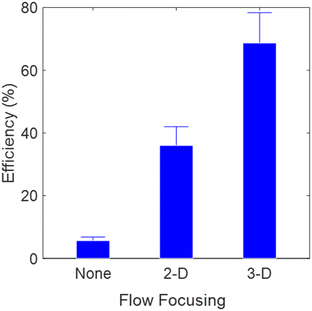
Trapping of particles in OHT is initiated by aligning the trajectories of particles flowing in the channel with the optical axis of the fiber. First, the sample solution of 0.02% (w/v) of polystyrene particles (diameter: 15 μm) was flowed from inlet 3, without the sheath flows. During this time, the polystyrene particles flowed across the whole cross section of the channel, resulting in poor trapping efficiency of 5% as shown in Fig. 3 (we define trapping efficiency as the percentage of particles trapped by the OHT with respect to the total number of particles flowed through the entire cross section of the channel at the trapping location). The poor efficiency, in this case, is because particles flow arbitrarily across the channel cross section and only a few particles which are aligned with the optical axis of the fiber are trapped. In the next step the trajectories of particles were spatially confined in the Y-direction, i.e. along the width of the channel, by slowly increasing the side sheath flow rates (inlets 1 and 2). The sheath-to-sample flow rates were adjusted to a ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, for which the trajectories of particles coincided with the optical axis of the fiber in the Y-direction. This is referred to as 2D focusing. We now observed a trapping efficiency of 35% as almost all the particles were aligned with the core of the fiber in the Y-direction, but only a fraction of them were at the correct position along the Z-direction, i.e., along the height of the channel. To further increase the trapping efficiency, both the top and bottom sheath flows (inlets 4 and 5) were steadily increased such that the particles were also confined in the Z-direction and aligned completely with the fiber axis, resulting in continuous trapping of particles with an efficiency of >70% (see ESI† Video S2). A detailed description of the process of alignment of the trajectory of particles with the optical axis of the fiber is given in ESI† S4. To achieve 100% trapping efficiency, all the particles flowing in the channel need to be aligned with the optical axis with high precision. This requires extremely high sheath flow rates, which results in strong drag forces that cannot be balanced by the optical scattering forces in our system. In addition to enabling robust and highly efficient particle trapping, 3D flow focusing in OHT also provides the flexibility to correct for positional inaccuracy in fiber placement within the channel by altering the ratio of sheath flow rates to help particles align with the optical fiber's axis.
1, for which the trajectories of particles coincided with the optical axis of the fiber in the Y-direction. This is referred to as 2D focusing. We now observed a trapping efficiency of 35% as almost all the particles were aligned with the core of the fiber in the Y-direction, but only a fraction of them were at the correct position along the Z-direction, i.e., along the height of the channel. To further increase the trapping efficiency, both the top and bottom sheath flows (inlets 4 and 5) were steadily increased such that the particles were also confined in the Z-direction and aligned completely with the fiber axis, resulting in continuous trapping of particles with an efficiency of >70% (see ESI† Video S2). A detailed description of the process of alignment of the trajectory of particles with the optical axis of the fiber is given in ESI† S4. To achieve 100% trapping efficiency, all the particles flowing in the channel need to be aligned with the optical axis with high precision. This requires extremely high sheath flow rates, which results in strong drag forces that cannot be balanced by the optical scattering forces in our system. In addition to enabling robust and highly efficient particle trapping, 3D flow focusing in OHT also provides the flexibility to correct for positional inaccuracy in fiber placement within the channel by altering the ratio of sheath flow rates to help particles align with the optical fiber's axis.
Depending on the applications, particles either can be trapped and released continuously to collect information about the specimen in a high-throughput manner or a single particle can be analysed for a long duration by stopping the sample flow (inlet 3) while maintaining all the sheath flows. We note that the concentration of the particles can be adjusted to maintain a specific average frequency of incoming particles in the trap such that the particle can be released after collecting the required information before the arrival of another. In our case for a particle concentration of 0.02% (w/v) flowing at a speed of 1000 μm s−1, we obtained a high trapping efficiency of 14 particles per min. We also observed the trapping of multiple particles simultaneously in the OHT, interestingly in a chain format (see ESI† Video S3). At a laser power of 860 mW, the OHT were capable of trapping up to 12 beads. Beyond 12 beads, the optical scattering and gradient forces acting on the incoming particles become weak and no further trapping of beads was observed. The length of the chain of trapped particles is dependent on the optical power and flow velocity in the channel. Trapping of particles in the form of linear chains might be advantageous for cell–cell interaction studies.39,40
Manipulation of trapped microparticles in OHT
A particle is trapped once it is at the location of the microchannel where the optical and hydrodynamic forces acting on it are equal in magnitude (and opposite in direction). The trap is located along the optical axis of the fiber (along the x-axis), but its exact position depends on the laser's power and the flow velocity in the channel. Fig. 4a shows the optical image of a single 15 μm polystyrene bead trapped at a distance of 150 μm from the tip of the fiber by OHT (see ESI† Video S4). The particle flowed at an average velocity of ∼1400 μm s−1 inside the microfluidic channel. Fig. 4b shows the optical scattering and drag forces acting on the bead, flowing along the optical axis of the fiber in the microfluidic channel. The scattering force is maximum at a distance of ∼100 μm from the tip of the fiber (X = 0) and decreases as one moves away from it due to lower laser intensities. Since the flow velocity is almost constant along the channel, the hydrodynamic drag force acting on the particle remains constant. For an output laser power of 860 mW, the magnitude of the optical scattering forces equals the drag force at the furthest distance of 134 μm from the fiber tip, which is the position where we expected the particle to be trapped as shown in Fig. 4b. The theoretically estimated trap position is comparable to that observed experimentally, ∼150 μm from the fiber tip as shown in Fig. 4a. In the lateral direction, i.e., the Y- and Z-directions, the particle is confined due to the optical gradient force and equal and opposing shear lift force.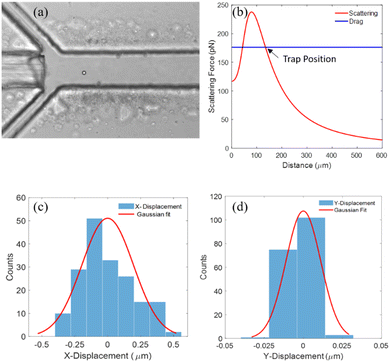 | ||
| Fig. 4 (a) Optical image of a single 15 μm polystyrene particle trapped in the microfluidic channel using OHT. (b) Theoretically calculated optical scattering force and drag force acting on a 15 μm polystyrene particle as a function of the particle's position along the length of the channel. The fiber tip is positioned at X = 0. The flow velocity used to calculate the drag force on the particle within the channel was extracted from the time trajectory of the trapped particle once it was released from the trap (see ESI† S6). (c) and (d) Histogram of the positional fluctuations of the trapped particle (15 μm PS) in the X- and Y-direction, respectively. | ||
We also experimentally observed the role of optical gradient forces in the auto-alignment of particles flowing off the optical axis in OHT and thus aiding the trapping process. In our experiments, we observed that particles flowing at a velocity of 800 μm s−1 that deviated slightly (∼10 μm from the beam axis) from the main trajectory at the center of the channel were seen to be pulled to the beam axis at a distance of approximately 143 μm from the tip of the optical fiber (at an applied laser power of 850 mW). This is because the optical gradient forces dominated the drag forces, resulting in the pulling of particles towards the beam axis. This led to “auto-alignment” of the particles with the beam axis and ultimately trapping of these particles (see ESI† Video S5). For particles whose trajectories deviated from the beam axis by more than 20 μm or flowed at higher flow velocities (>4000 μm s−1), the gradient forces were not sufficient to overcome the drag forces. As a result, no particles were pulled towards the beam axis and no trapping was observed. Trapping of particles using OHT is robust and stable.
To assess the trapping stability, we measured the trap stiffness of the trapped particle. The variance in position fluctuations was used to calculate the trap stiffness based on the equipartition method.41 The trap stiffness in the X- and Y-directions is given by
Trapping versatility
OHTs show high versatility in trapping particles of different sizes, shapes, and material compositions. As long as sufficient scattering forces larger than the hydrodynamic drag force can be exerted on particles, it is possible to trap particles with OHT. As a demonstration, we show the trapping of polystyrene particles of diameters 5 μm and 15 μm as shown in Fig. 5a and b, respectively. Single mammalian cells like leukaemia cells (THP-1; received from the Institute of Hematology and Transfusion Medicine, Warsaw, Poland) of size ranging from 10 to 30 μm (Fig. 5d) as well as microorganisms such as yeast (3–5 μm) were also trapped to demonstrate trapping of particles with lower refractive index, almost identical to that of the medium (see ESI† Video S6). However, smaller-sized particles, such as polystyrene beads smaller than 1 μm and bacterial E. coli cells (1–2 μm), could not be stably trapped in OHT due to relatively small optical scattering and gradient forces acting on them compared to the drag force, even when operating OHT at the minimum flow velocity. Our demonstrations clearly show the wide applicability of OHT including for single-cell studies in a fully lab-on-chip format. | ||
| Fig. 5 Trapping versatility of OHT. Optical image of a single (a) 5 μm polystyrene particle, (b) 15 μm polystyrene particle, (c) 5 μm yeast cell, and (d) 30 μm THP cell trapped in the OHT. | ||
Long-range manipulation of particles in OHT
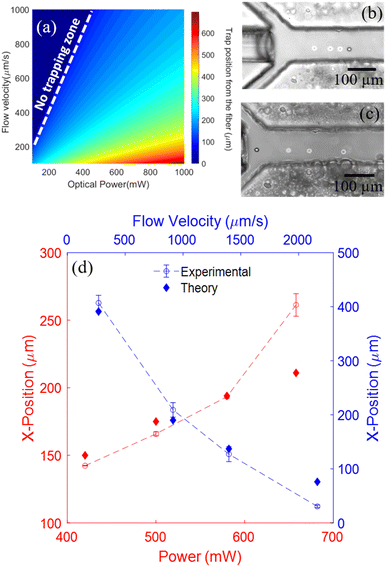
The position of a trapped particle in the OHT is dependent on both the magnitude of the optical scattering force and the drag force acting on it. One can control either the flow velocity or the output optical power from the fiber to trap particles at the desired locations and also manipulate them over long distances along the length of the channel. The ability to precisely position and manipulate particles by simply regulating the optical power or flow rates makes the OHT particularly attractive over conventional fiber-tweezer approaches with limited manipulation capability. The functionality of OHT can be expanded through precise and well-controlled single-particle manipulation. For instance, by integrating multiple fiber sources and detectors along the length of the channel and moving the trapped particle into different detection zones within the channel, multimodal analysis of trapped particles based on optical scattering, fluorescence, or Raman spectroscopy can be performed within a single platform.Fig. 6a shows the heat map distribution of the trapping positions of 15 μm polystyrene particles with respect to the tip of the optical fiber for different optical power and flow rate combinations in OHT. For fiber output powers and flow velocities, where the drag forces dominate over the optical scattering force, no particle can be trapped as indicated by the non-trapping zone. For other combinations of fiber power and flow velocities, there always exists a position within the channel along the beam axis where the two opposing forces balance each other, resulting in the trapping of particles at those specific locations.
As a demonstration, we trapped and manipulated a single polystyrene particle of diameter 15 μm in the channel by modulating the output optical power and flow velocity. The range and precision of particle manipulation by OHT were subsequently evaluated. First, we trapped a single polystyrene particle flowing at a velocity of 600 μm s−1. Subsequently, by varying the fiber laser's optical power from 420 mW to 660 mW in steps of ∼80 mW, the particle was moved along the length of the channel from ∼140 to 260 μm from the tip of the fiber as shown in Fig. 6b. As we increase the laser power, the optical scattering forces acting on the particle are increased, shifting the balance position of the two forces, i.e. the trapping location further away from the fiber tip. The trapping positions observed in the experiments were found to be close to the expected trap locations calculated theoretically (Fig. 6d). It should be noted that the laser power can be increased beyond the maximum power used in our demonstrations to further increase the range of manipulation. The maximal power is limited to values beyond which the localized heating of the surrounding medium causes bubble formation or damage to the trapped particle. The lowest power is set to the minimum value at which the scattering forces are just enough to overcome the drag forces in OHT. To test the precision of particle manipulation by OHT via optical power modulation a single trapped particle was moved multiple times between two positions in the channel by switching between two optical powers (P1: 182 mW; P2: 500 mW). The position of the bead (centroid) was measured for each iteration to determine the precision of particle manipulation using OHT (see ESI† S7). OHTs were able to manipulate particles with a positional precision of less than ±10 μm by varying the output optical power.
Another parameter that can be exploited to manipulate particles in the OHT is the flow velocity in the channel. By varying the flow velocity in the microfluidic channel, the drag force acting on the particle can be modulated due to which the position at which two forces balance each other, i.e. the trap location, can be shifted, resulting in the manipulation of the trapped particle. We trapped a 15 μm polystyrene particle and then moved it along the length of the channel by slowly increasing the flow velocity as shown in Fig. 6c. Once the particle was trapped, only the side sheath flow rates (inlets 1 and 2) were changed proportionally to increase the average flow velocity in the channel, while flow rates via other inlets were maintained at a minimum value (the lowest pulsation-free flow rate supported by the syringe pump for a 1000 μL glass syringe was 2 μL h−1). The optical output power from the fiber was kept constant at 860 mW. This way we were able to manipulate particles by the OHT over a long range of 370 μm ranging from 30 to 407 μm from the tip of the fiber by modulating the average flow velocity in the channel (270–2100 μm s−1) as shown in Fig. 6d. The higher the flow velocity in the channel, the closer the particles are trapped to the fiber's tip, where large optical scattering forces compensate for the particle's high drag force. To trap or move particles away from the fiber, the overall flow velocity in the channel can be reduced by decreasing sheath flow rates proportionally. The minimum operational flow velocities required in the OHT are those at which inertial forces (drag and lift) are sufficient to overcome diffusion and gravitational forces. At these flow velocities, the particle can be trapped furthest from the optical fiber for a given power without leaving the trap. The maximum drag force that can be balanced by the optical scattering force at the given output optical power determines the flow velocity's upper limit. The precision of particle manipulation by OHT via regulation of flow velocity in the channel was measured by moving a single trapped particle multiple times between two positions in the channel by switching between two flow velocities. The position of the bead (centroid) was measured for each iteration to determine the precision of particle manipulation. OHTs were able to manipulate particles with a positional precision of ±10 μm by varying the average flow velocity in the microfluidic channel. We note that the precision of particle manipulation by modulation of flow velocities is susceptible to flow fluctuations caused by mechanical syringe pumps, particularly when operating at low flow rates.
The maximum range of particle manipulation in OHT for a 15 μm polystyrene particle was ∼500 μm, which was achieved by operating it at a maximum laser power of 880 mW and the lowest average flow velocity of 190 μm s−1. The maximum fiber power was limited to the magnitude beyond which there was bubble formation due to the heating of the surrounding medium. The flow velocity, on the other hand, was kept to the minimum below which syringe pump induced flow fluctuation becomes significant and the particle moves out of the trap. In summary, OHT allow long-range manipulation of the trapped particle along the length of the channel by regulating either the optical power or flow velocity, thus offering superior manipulation capabilities over conventional fiber tweezers which have limited manipulation range or require physical movement of the optical fiber (Table 2).
| Manipulation approach | Trap translation range (μm) | Precision (μm) |
|---|---|---|
| Fiber optical power (flow velocity = 600 μm s−1) | 140–260 | ±10 |
| Flow velocity (optical power = 860 mW) | 30–407 | ±10 |
Conclusions
We demonstrated novel opto-hydrodynamic tweezers (OHT) for trapping and manipulating single particles and cells of varying sizes, shapes, and compositions. OHT combines 3D flow focusing and optical forces via fiber optics in microfluidic channels, where flow focusing allows for simple and dynamic alignment of particle trajectories with the fiber axis, resulting in efficient and high-throughput particle trapping. By regulating the optical power and flow velocity in the channels individual particles can be trapped at specific spots and manipulated over a wide range, extending up to several hundred microns along the channel length with a precision of ±10 μm. With a simple design, small form factor, dynamic alignment of a particle with fiber optical axis, versatile manipulation, and the possibility of integrating various optical investigation schemes, this optofluidic tweezers platform offers a multipurpose solution for single-particle analysis—all in a fully lab-on-chip device.Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.Author contributions
Abhay Kotnala and Shreyas Vasantham: conceptualization, formal analysis, methodology, validation, writing – original draft. Yurii Promovych: methodology, validation. Piotr Garstecki: funding acquisition, resources, supervision, writing – review & editing. Ladislav Derzsi: funding acquisition, project administration, resources, methodology, supervision, writing – review & editing. All authors have approved the final version of the manuscript.Conflicts of interest
Patent applications for the demonstrated approaches and designs are pending.Acknowledgements
This project was supported by the Foundation for Polish Science TEAM NET project POIR.04.04.00-00-16ED/18-00. Authors gratefully acknowledge Dr. Piotr Mrówka from the Institute of Hematology and Transfusion Medicine, Warsaw for providing the THP-1 leukaemic cell lines. S. V. is also grateful for the scholarship from the Institute of Physical Chemistry, Polish Academy of Sciences, as part of the Warsaw4PhD initiative.Notes and references
- D. J. Armstrong, T. A. Nieminen, A. B. Stilgoe, A. V. Kashchuk, I. C. D. Lenton and H. Rubinsztein-Dunlop, Swimming force and behavior of optically trapped micro-organisms, Optica, 2020, 7(8), 989 CrossRef CAS.
- A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Observation of a single-beam gradient force optical trap for dielectric particles, Opt. Lett., 1986, 11(5), 288 CrossRef CAS PubMed.
- A. Ashkin and J. M. Dziedzic, Optical Trapping and Manipulation of Viruses and Bacteria, Science, 1987, 235(4795), 1517–1520 CrossRef CAS PubMed.
- S. M. Block, D. F. Blair and H. C. Berg, Compliance of bacterial flagella measured with optical tweezers, Nature, 1989, 338(6215), 514–518 CrossRef CAS PubMed.
- A. D. Mehta, M. Rief, J. A. Spudich, D. A. Smith and R. M. Simmons, Single-Molecule Biomechanics with Optical Methods, Science, 1999, 283(5408), 1689–1695 CrossRef CAS PubMed.
- Y. Pang, H. Song, J. H. Kim, X. Hou and W. Cheng, Optical trapping of individual human immunodeficiency viruses in culture fluid reveals heterogeneity with single-molecule resolution, Nat. Nanotechnol., 2014, 9(8), 624–630 CrossRef CAS PubMed.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Stretching DNA with optical tweezers, Biophys. J., 1997, 72(3), 1335–1346 CrossRef CAS PubMed.
- B. J. Black and S. K. Mohanty, Fiber-optic spanner, Opt. Lett., 2012, 37(24), 5030 CrossRef CAS PubMed.
- J. Guck, R. Ananthakrishnan, H. Mahmood, T. J. Moon, C. C. Cunningham and J. Käs, The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells, Biophys. J., 2001, 81(2), 767–784 CrossRef CAS PubMed.
- P. R. T. Jess, V. Garcés-Chávez, D. Smith, M. Mazilu, L. Paterson and A. Riches, et al., Dual beam fibre trap for Raman micro-spectroscopy of single cells, Opt. Express, 2006, 14(12), 5779 CrossRef CAS PubMed.
- S. Rancourt-Grenier, M. T. Wei, J. J. Bai, A. Chiou, P. P. Bareil and P. L. Duval, et al., Dynamic deformation of red blood cell in Dual-trap Optical Tweezers, Opt. Express, 2010, 18(10), 10462 CrossRef CAS PubMed.
- S. Sil, T. K. Saha, A. Kumar, S. K. Bera and A. Banerjee, Dual-mode optical fiber-based tweezers for robust trapping and manipulation of absorbing particles in air, J. Opt., 2017, 19(12), 12LT02 CrossRef.
- Y. Liu and M. Yu, Investigation of inclined dual-fiber optical tweezers for 3D manipulation and force sensing, Opt. Express, 2009, 17(16), 13624 CrossRef CAS PubMed.
- B. Lincoln, S. Schinkinger, K. Travis, F. Wottawah, S. Ebert and F. Sauer, et al., Reconfigurable microfluidic integration of a dual-beam laser trap with biomedical applications, Biomed. Microdevices, 2007, 9(5), 703–710 CrossRef PubMed.
- L. Huang, Y. Feng, F. Liang, P. Zhao and W. Wang, Dual-fiber microfluidic chip for multimodal manipulation of single cells, Biomicrofluidics, 2021, 15(1), 014106 CrossRef CAS PubMed.
- Z. Liu, C. Guo, J. Yang and L. Yuan, Tapered fiber optical tweezers for microscopic particle trapping: fabrication and application, Opt. Express, 2006, 14(25), 12510 CrossRef PubMed.
- A. Asadollahbaik, S. Thiele, K. Weber, A. Kumar, J. Drozella and F. Sterl, et al., Highly Efficient Dual-Fiber Optical Trapping with 3D Printed Diffractive Fresnel Lenses, ACS Photonics, 2020, 7(1), 88–97 CrossRef CAS.
- A. Asadollahbaik, A. Kumar, M. Heymann, H. Giessen and J. Fick, Fresnel lens optical fiber tweezers to evaluate the vitality of single algae cells, Opt. Lett., 2022, 47(1), 170 CrossRef CAS PubMed.
- J. B. Decombe, S. Huant and J. Fick, Single and dual fiber nano-tip optical tweezers: trapping and analysis, Opt. Express, 2013, 21(25), 30521 CrossRef PubMed.
- M. Plidschun, H. Ren, J. Kim, R. Förster, S. A. Maier and M. A. Schmidt, Ultrahigh numerical aperture meta-fibre for flexible optical trapping, Light: Sci. Appl., 2021, 10(1), 57 CrossRef CAS PubMed.
- H. Xin, R. Xu and B. Li, Optical trapping, driving and arrangement of particles using a tapered fibre probe, Sci. Rep., 2012, 2(1), 818 CrossRef PubMed.
- H. Xin, Y. Li, L. Li, R. Xu and B. Li, Optofluidic manipulation of Escherichia coli in a microfluidic channel using an abruptly tapered optical fiber, Appl. Phys. Lett., 2013, 103(3), 033703 CrossRef.
- A. Kotnala, Y. Zheng, J. Fu and W. Cheng, Microfluidic-based high-throughput optical trapping of nanoparticles, Lab Chip, 2017, 17(12), 2125–2134 RSC.
- X. Xu, C. Cheng, Y. Zhang, H. Lei and B. Li, Dual focused coherent beams for three-dimensional optical trapping and continuous rotation of metallic nanostructures, Sci. Rep., 2016, 6(1), 29449 CrossRef CAS PubMed.
- P. R. T. Jess, V. Garcés-Chávez, D. Smith, M. Mazilu, L. Paterson and A. Riches, et al., Dual beam fibre trap for Raman micro-spectroscopy of single cells, Opt. Express, 2006, 14(12), 5779 CrossRef CAS PubMed.
- S. K. Mohanty, K. Mohanty and M. W. Berns, Manipulation of mammalian cells using a single-fiber optical microbeam, J. Biomed. Opt., 2008, 13(05), 1 Search PubMed.
- H. Wu, C. Jiang, A. Ren, T. Dong and X. Cui, Single-fiber optical tweezers for particle trapping and axial reciprocating motion using dual wavelength and dual mode, Opt. Commun., 2022, 517, 128333 CrossRef CAS.
- H. Xin, R. Xu and B. Li, Optical trapping, driving and arrangement of particles using a tapered fibre probe, Sci. Rep., 2012, 2(1), 818 CrossRef PubMed.
- H. Xin, Y. Li, D. Xu, Y. Zhang, C. Chen and B. Li, Single Upconversion Nanoparticle–Bacterium Cotrapping for Single-Bacterium Labeling and Analysis, Small, 2017, 13(14), 1603418 CrossRef PubMed.
- M. Daly, V. G. Truong and S. N. Chormaic, Evanescent field trapping of nanoparticles using nanostructured ultrathin optical fibers, Opt. Express, 2016, 24(13), 14470 CrossRef CAS PubMed.
- S. E. Skelton, M. Sergides, R. Patel, E. Karczewska, O. M. Maragó and P. H. Jones, Evanescent wave optical trapping and transport of micro- and nanoparticles on tapered optical fibers, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113(18), 2512–2520 CrossRef CAS.
- G. Tkachenko, V. G. Truong, C. L. Esporlas, I. Sanskriti and S. Nic Chormaic, Evanescent field trapping and propulsion of Janus particles along optical nanofibers, Nat. Commun., 2023, 14(1), 1691 CrossRef CAS PubMed.
- Y. Xia and G. M. Whitesides, Soft Lithography, Angew. Chem., Int. Ed., 1998, 37(5), 550–575 CrossRef CAS PubMed.
- K. C. Neuman, E. H. Chadd, G. F. Liou, K. Bergman and S. M. Block, Characterization of Photodamage to Escherichia coli in Optical Traps, Biophys. J., 1999, 77(5), 2856–2863 CrossRef CAS PubMed.
- D. Huber, A. Oskooei, X. Casadevall i Solvas, A. deMello and G. V. Kaigala, Hydrodynamics in Cell Studies, Chem. Rev., 2018, 118(4), 2042–2079 CrossRef CAS PubMed.
- Y. Zhao, Q. Li and X. Hu, Universally applicable three-dimensional hydrodynamic focusing in a single-layer channel for single cell analysis, Anal. Methods, 2018, 10(28), 3489–3497 RSC.
- A. Ashkin, Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime, Biophys. J., 1992, 61(2), 569–582 CrossRef CAS PubMed.
- D. Di Carlo, Inertial microfluidics, Lab Chip, 2009, 9(21), 3038 RSC.
- M. Rothbauer, H. Zirath and P. Ertl, Recent advances in microfluidic technologies for cell-to-cell interaction studies, Lab Chip, 2018, 18(2), 249–270 RSC.
- B. Prabhakarpandian, M. C. Shen, K. Pant and M. F. Kiani, Microfluidic devices for modeling cell–cell and particle–cell interactions in the microvasculature, Microvasc. Res., 2011, 82(3), 210–220 CrossRef PubMed.
- A. A. M. Bui, A. V. Kashchuk, M. A. Balanant, T. A. Nieminen, H. Rubinsztein-Dunlop and A. B. Stilgoe, Calibration of force detection for arbitrarily shaped particles in optical tweezers, Sci. Rep., 2018, 8(1), 10798 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary Video S1: 3D hydrodynamic flow focusing in a microfluidic channel. Supplementary Video S2: continuous trapping of single polystyrene particles with high efficiency and throughput in an OHT. Supplementary Video S3: simultaneous trapping of multiple polystyrene particles forming linear chains in an OHT. Supplementary Video S4: trapping of a single 15 μm polystyrene particle in an OHT. Supplementary Video S5: auto-alignment of particle trajectory by optical gradient force in OHT. Supplementary Video S6: trapping of particles of different sizes, shapes, and refractive indices, including mammalian cells, with OHT. See DOI: https://doi.org/10.1039/d3lc00733b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |