Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Zeta potential characterization using commercial microfluidic chips†
Jonathan
Cottet
 a,
Josephine O.
Oshodi
a,
Josephine O.
Oshodi
 ab,
Jesse
Yebouet
ab,
Jesse
Yebouet
 a,
Andrea
Leang
a,
Andrea
Leang
 a,
Ariel L.
Furst
a,
Ariel L.
Furst
 bc and
Cullen R.
Buie
bc and
Cullen R.
Buie
 *a
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: crb@mit.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA
cCenter for Environmental Health Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA
First published on 29th November 2023
Abstract
Surface charge is a critical feature of microbes that affects their interactions with other cells and their environment. Because bacterial surface charge is difficult to measure directly, it is typically indirectly inferred through zeta potential measurements. Existing tools to perform such characterization are either costly and ill-suited for non-spherical samples or rely on microfluidic techniques requiring expensive fabrication equipment or specialized facilities. Here, we report the application of commercially available PMMA microfluidic chips and open-source data analysis workflows for facile electrokinetic characterization of particles and cells after prior zeta potential measurement with a Zetasizer for calibration. Our workflows eliminate the need for microchannel fabrication, increase measurement reproducibility, and make zeta potential measurements more accessible. This novel methodology was tested with functionalized 1 μm and 2 μm polystyrene beads as well as Escherichia coli MG1655 strain. Measured zeta potentials for these samples were in agreement with literature values obtained by conventional measurement methods. Taken together, our data demonstrate the power of this workflow to broadly enable critical measurements of particle and bacterial zeta potential for numerous applications.
Introduction
Microbial surface charge impacts a cell's interaction with its local environment, including other cells, ions and particles. The exposed carboxyl and amine groups from bacterial peptidoglycans renders most negatively charged. This negative charge is crucial for nutrient, metabolite, and ionic interactions within the bacteria as well as their transport into the cell.1–4 Moreover, surface charge and hydrophobicity are predictive of bacterial adhesion, which is critical for host invasion by pathogens and biofilm formation.5 Importantly, surface charge has also been linked to the virulence of different bacterial strains; as an example, Mycobacterium tuberculosis strains, with differential virulence have divergent surface charges.1 Finally, this physical property can be used to separate microbes using capillary electrokinetics.6 Therefore, quantifying microbial surface charge provides critical phenotypic information.7Unfortunately, bacterial surface charge typically cannot be directly measured but must instead be inferred through zeta potential, ζ. When charged particles are suspended in an electrolyte solution, counter ions from the bulk form a thin electrical double layer (EDL) at the solid–liquid interface.8,9 The ζ is the electric potential at this interface between the inner and outer layers of the EDL.10,11 The inner layer contains the fixed Stern layer and an almost immobile shear layer, while the outer layer (the diffusive layer) is comprised of mobile ions in proximity to the surface due to electrostatic forces. The ζ of a particle in solution is therefore defined by both its surface characteristics as well as the composition of the solution it is in (e.g. pH, ionic strength and electrical conductivity7,12). This influence of the environment can make measuring the ζ challenging and can lead to irreproducibility.7,12
Since ζ is an important method for inferring surface charge, significant effort has been devoted to measuring it. Typically, a capillary cell is used with electrodes at both ends where a potential is applied.7,12 Particles move towards the electrode with opposite charge while their velocity is recorded. Such commercial instruments typically use dynamic light scattering (DLS) to extrapolate ζ and has enabled researchers to rapidly measure this parameter. However, these systems also have significant limitations; they are very costly, utilize DLS and must assume spherical particles for its calculations, and are therefore not suited for non-spherical particles (such as many bacteria).13–16
To enable consistent, reproducible ζ measurements with a broader range of samples and at lower cost, many research groups have leveraged microfluidics. Lapizco-Encinas and co-workers have specialized in using polydimethylsiloxane (PDMS) microchannels for electrokinetic characterization of particles and cells.17 These chips have been used to measure the non-linear electrophoretic mobility of cells and particles using particle tracking velocimetry (PTV).18–21 However, the application of in-house fabricated PDMS molds requires specialized expertise and cleanroom access, limiting the technique to labs with such capabilities. Additionally, the ζ of the microchannel must be measured in the media used prior to experiments through current monitoring, a method limited to solutions with low electrical conductivities.22 More recently, some have moved to polymethyl methacrylate (PMMA) microchannels, but this method still requires expensive computer numerical control (CNC) machines and fabrication expertise.23,24 Further, all current methods lack precise electrode positioning and require tedious microchannel conditioning. Thus, the field will benefit from new solutions that circumvent these costly fabrication and measurement limitations.
Here we report the use of commercial PMMA microfluidic chips to perform electrokinetic characterization of particles and bacteria, negating the need for microchannel microfabrication. The method employed herein results in increased measurement reproducibility and is more accessible (in terms of both cost and expertise required) than previous techniques. All components were developed to enable broad adoption, combining commercial platforms with open-source software. This methodology was tested with functionalized 1 μm and 2 μm polystyrene beads as well as a prevalent strain of Escherichia coli, MG1655, yielding values in agreement with the literature.17
Theory
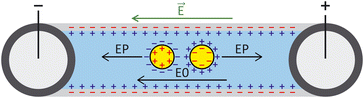
ζ measurements rely on particle velocity estimation. Under an electric field E in a microchannel, the electrokinetic velocity vEK of particles in a fluid of viscosity η and permittivity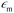 is linked to two phenomena: electrophoresis (EP) due to the zeta potential of the particle ζp and electroosmosis (EO) due to the zeta potential of the channel wall ζw (Fig. 1).
is linked to two phenomena: electrophoresis (EP) due to the zeta potential of the particle ζp and electroosmosis (EO) due to the zeta potential of the channel wall ζw (Fig. 1).
The electrophoretic component of the velocity has a linear component (proportional to E) and non-linear component (proportional to E3 or E3/2).25–27 The nonlinear component can be ignored if the Peclet number is smaller or equal to 1 and the Dukhin number is much smaller than 0.1.28,29 The Peclet number corresponds to the ratio of the convective to the diffusive movement of the ions located close to the surface of the particle, while the Dukhin number refers to the ratio of the surface conductivity to the bulk conductivity of the medium. Additionally, the Helmholtz–Smoluchowski model can be applied for particles that are large compared to their EDL (more than a factor 10), which is valid for moderate- to high-ionic strength solutions.16 For low electric fields, particles are in the linear regime and the total vEK can therefore be expressed as eqn (1):
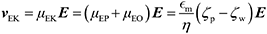 | (1) |
The first step in characterization is typically to evaluate ζw, generally through various techniques: through the difference of time scale between EO flow and EP,30,31 the use of open-end and closed-end microchannels32 or current monitoring and/or particle image velocimetry (PIV) or PTV.33,34 In classical electrokinetic PTV experiments, vEK is measured at different electric fields E. Such PTV measurements typically correspond to several experiments performed consecutively for each value E. vEK is plotted as a function of E and the associated slope corresponds to μEK. In the linear regime, μEK can be linearly correlated to ζp − ζw as expressed in eqn (1).
However, most of these techniques rely on customized equipment, high speed imaging or precise current quantification, making ζw measurement challenging.
Materials and methods
Chips
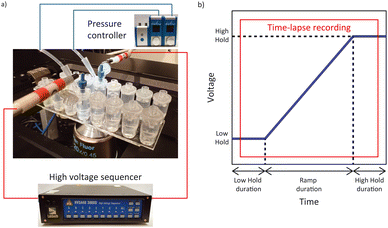
PMMA microchannels with a Luer interface from Microfluidic ChipShop (Jena, Germany) were used in this study. The microchannels have a consistent size: length of 18 mm, height of 100 μm and width of 100 μm (Fluidic 157, PMMA, Microfluidic ChipShop, Jena, Germany). 200 μl polypropylene (PP) reservoirs with Mini Luer interface (Fluidic 934, Microfluidic ChipShop, Jena, Germany) were added on each Luer interface (Fig. 2).Suspending solution
10 mM N-(2-hydroxyethyl)piperazine-N′-(2-ethanesulfonic acid) (HEPES) was prepared with HEPES powder Millipore-Sigma (CAS 7365-45-9) in Milli-Q® water. The pH was then adjusted to 7.2 by adding NaOH. The final suspending medium had a conductivity of 172.3 μS cm−1 and a corresponding Debye length of 7 nm ± 2 nm.35Particles
1 μm and 2 μm yellow-green fluorescent polystyrene beads with different surface functionalizations (nonfunctionalized polystyrene (PS), sulfate-modified (SU-modified), carboxylate-modified (CO-modified) and amine-modified (AM-modified)) from Invitrogen (Waltham, MA, USA) and Magsphere (Pasadena, CA, USA) were used in this study (Tables S1 and S2†). Stock solutions were diluted in the 10 mM HEPES solution to final concentrations of 108 particles per ml (except the 1 μm AM-modified particles from Magsphere, which were suspended to a concentration of 3 × 109 particles per ml due to their low ζ). All suspensions were prepared 48 h prior to experiments to allow ζ to stabilize. Solutions were vortexed just prior to their addition to the microfluidic chip.Bacteria samples
E. coli MG1655 (ATCC700926, Manassas, VA, USA) were cultured overnight from individual colonies in Luria–Bertani (LB) broth to stationary phase. Cells were centrifuged at 5000 r.p.m. for 4 min and the supernatant removed. Fresh LB was added, and cells were again centrifuged, constituting a “wash”. A total of three LB washes were performed, followed by DAPI staining through the addition of a stock solution of DAPI (4′,6-diamidino-2-phenylindole) (CAS 28718-90-3) to a final concentration of 1 μg ml−1. Samples were covered in foil and allowed to incubate for 10 min. The stained bacteria were then “washed” three times in the 10 mM HEPES suspending solution and resuspended at an optical density at 600 nm (OD600) of 0.2 prior to experiments.Equipment and software
Conductivity and pH were measured respectively using the InLab 741-ISM and InLab Expert Pro ISM with the SevenCompact™ Duo S213 Benchtop (Mettler Toledo, Columbus, OH, USA). Time-lapse fluorescent image sequences were recorded using a Ti-Eclipse inverted fluorescent microscope (Nikon, Minato City, Tokyo, Japan) with the Zyla 4.2 sCMOS camera (Andor – Oxford Instruments, Abingdon, United Kingdom). The Sequencer software was used to calibrate the high voltage sequencer (Model HVS3000D, LabSmith, Livermore, CA, USA) and a custom LabVIEW™ program (National Instruments, Austin, TX, USA) was used to apply voltage sequences to the microchannels via platinum electrodes (diameter 584 μm, Pure Platinum Wire, Surepure Chemetals Inc, Florham Park, NJ, USA). Two 25 mbar Flow EZ pressure controllers (Fluigent, Le Kremlin-Bicêtre, France) were used to eliminate flow in the channel by pressurizing the inlet and outlet reservoirs. Control ζ measurements were performed with the Zetasizer Ultra (Malvern Panalytical, Malvern, United Kingdom) (Fig. 3).Reservoir cap modification
To enable reproducible electrode placement in the reservoirs, the caps of the 200 μl reservoirs with Mini Luer interface were modified to accommodate a pipette tip to pressurize both the inlet and outlet reservoirs (see ESI† for more details). The caps were connected to the pressure controllers through the pressurized 2 ml reservoirs and connection kit (PCAP, Fluigent, Le Kremlin-Bicêtre, France). Tubing was inserted in the modified caps' pipette tips with pressure. Electrodes were inserted on the Mini Luer interface via a Male Mini Luer fluid connector single (Fluidic 331, PP, Microfluidic ChipShop). Electrodes were bent 90° in an L shape of 18 mm × 10 mm where the tip of the longer side would be in contact with the liquid and the shorter side connected directly to the high voltage sequencer. Precaution in the placement of the electrodes (top of the reservoirs and relatively low electric conductivity suspending medium) were taken to avoid changes (pH and conductivity) in the channel associated with Joule heating and electrochemistry. The full experimental setup is presented in Fig. 2.Fluid insertion in PMMA chip
The reservoir caps are not air or liquid tight, therefore, a 1 cm × 1 cm parafilm square (composed of 2 layers of parafilm) with a hole in the center obtained using a 3.5 mm diameter sampling tool (Electron Microscopy Sciences, Hatfield, PA, USA) was used to seal the reservoir when pumping liquid. In total, 400 μl of solution was added to the channel and reservoirs. The channel was viewed under the microscope, and any bubbles in the inlet and outlet reservoirs were removed with a 200 μl pipette tip.Chip conditioning and applied potentials
A potential difference of 600 V was applied between the inlet and outlet electrodes for 10 min to electrically condition the microchannel containing the 10 mM HEPES, as proposed by Shao and Devoe.36 The voltage difference was applied between 500 V and 1100 V to avoid inaccuracy of the high voltage sequencer at voltages below 100 V (LabSmith). The solution was subsequently removed and replaced with fresh 10 mM HEPES. The voltage sequence employed during the experiment consisted of a voltage ramp between a low hold and a high hold. The voltage sequence applied involved a low voltage hold (25 V) for 25 s followed by a 40 s voltage ramp with a 1 V s−1 increase and a high voltage hold (65 V) for 25 s (Fig. 2b).Sample insertion in the chip
After conditioning, the fresh 10 mM HEPES was replaced by 400 μl of the sample suspension with approximately the same volume in both the inlet and outlet reservoirs. The channel was viewed under the microscope, and bubbles in the inlet and outlet reservoirs were removed with a 200 μl pipette. Both reservoirs were closed with the modified caps, electrodes were placed, and both the inlet and outlet reservoirs were connected to the 25 mbar pressure controllers. The pressure on each reservoir was set to 1 mbar and then adjusted until the beads were no longer moving (zero flow condition). The focusing plane of interest was selected at the channel midplane where beads are moving the fastest. The 90 s voltage sequence employed during the experiment consisted in a voltage ramp between a low hold and a high hold and is listed above. After 5 s, time-lapse fluorescent images were recorded every 100 ms for 80 s with a 10 ms exposure time. Each channel was used for a single type of particle, and the experiment was repeated eight times. Flow was brought to zero between each experiment.Data analysis workflow
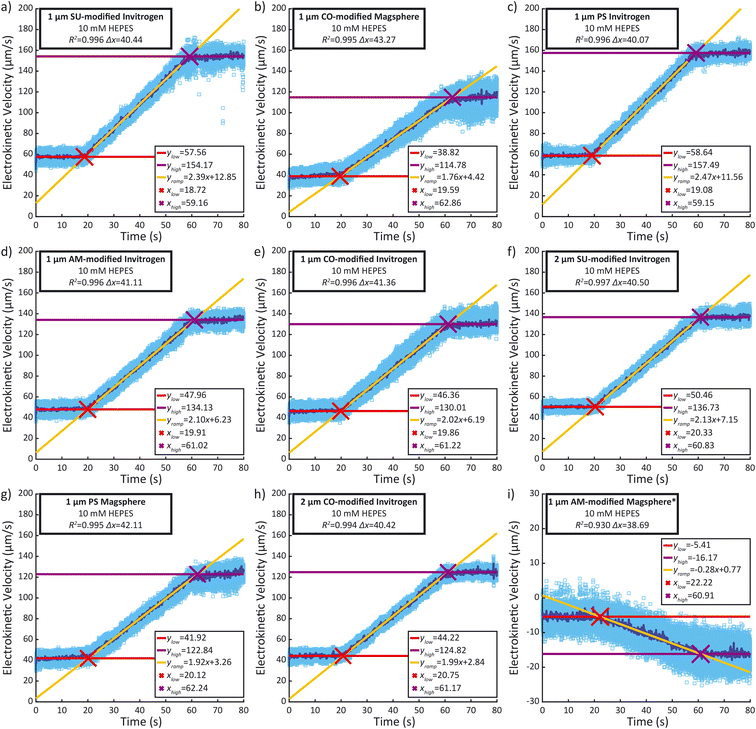
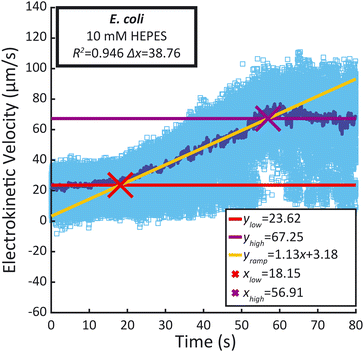
Recorded time-lapse fluorescent image sequences were automatically analyzed using Matlab, Fiji and the TrackMate plugin.37,38 The contrast of each video was adjusted to facilitate particle discrimination. All parameters for tracking individual particles using PTV were determined by examining the first repeat of each sample type with Fiji and TrackMate. Video analysis was performed using Matlab and ImageJ (ImageJ-MATLAB) to extract the velocity of each particle between each frame. In order to mitigate the effects of incorrectly labelled velocities identified in the PTV data, velocity outliers observed between sequential frames were systematically excluded from the analysis, as detailed in the ESI.† The remaining individual particle velocities were then plotted against time (light blue dots), as well as the median velocity per frame (dark blue line) (Fig. 4). A linear regression was performed during the ramp (between 25 s and 55 s) as well as during the low voltage hold (0 s to 15 s) and the high voltage hold (65 s to 80 s). xlow, the abscissa of the intersection between the regressions of the low voltage hold (ylow) and the voltage ramp (yramp) as well as xhigh, the abscissa of the intersection between the regressions of the high voltage hold (yhigh) and the voltage ramp (xhigh) were calculated along with the difference between both (Δx). They were compared to the theoretical 40 s duration of the ramp. Additionally, the coefficient of determination (R2) of the voltage ramp fit yramp is displayed. Both the R2 of the voltage ramp fit and the Δx were used to select five repeats among the eight performed, excluding the first repeat performed. The average electrokinetic ramp slope was then calculated as well as the standard deviation and plotted against the ζ obtained with Zetasizer Ultra for a sample of the same batch (Fig. 5). The full experimental flow chart is available in Fig. S3.†Results and discussion
Control measurements with the Zetasizer
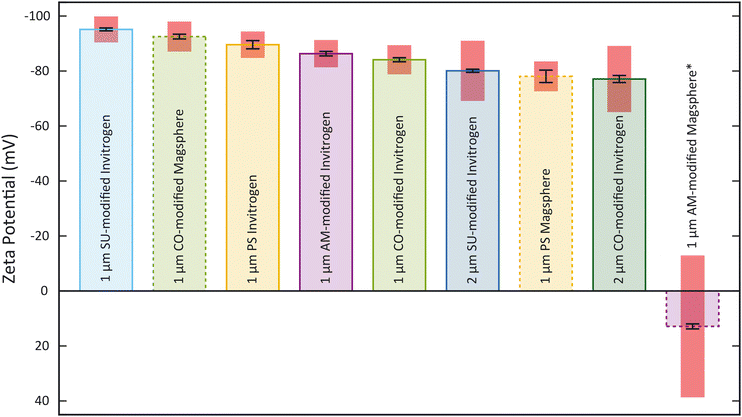
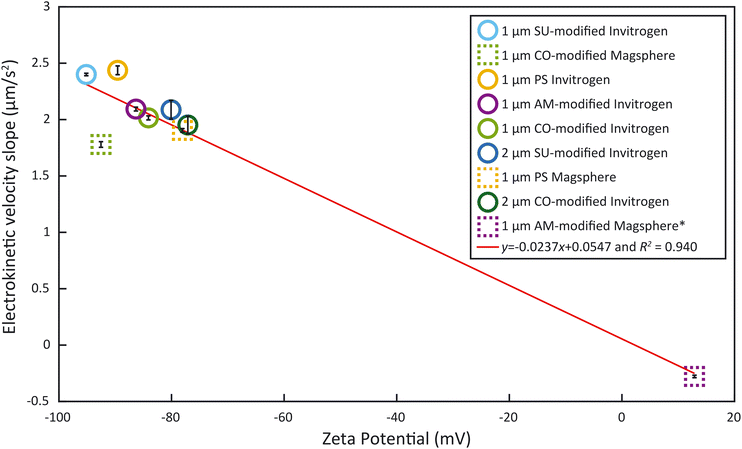
To obtain ζp from an electrokinetic measurement, ζw is needed as well as the value of the electric field E, which depends on the electrode positioning, as expressed in eqn (1). Since both values are unknown, this requires a characterization step to be able to correlate ζp and vEK. Such reference was obtained measuring ζ of each type of particle with the Zetasizer Ultra first (Fig. 3, Tables S1 and S2†). Both the surface chemistry and the manufacturing process impact ζ and all measured values fall within two regimes: between −96 mV and −75 mV and ≈13 mV. These results were acquired through five measurements of each sample. For each measurement, a ζ distribution is given.The zeta potential mean (Fig. 3) corresponds to the mean of the mean of each measurement. The standard deviation of the distribution (zeta deviation) shows how broad this deviation is around the mean and corresponds to the half-width at half the maximum amplitude of the distribution (ESI†). The zeta deviation was greater than 10 mV for the 2 μm particles from Invitrogen (SU-modified and CO-modified) as well as the 1 μm Magsphere AM-modified particles which is more than the double than for the other samples tested. For the 2 μm particles, the distribution is not Gaussian (ESI†), which is likely a result of the manufacturing process. The 1 μm Magsphere AM-modified particles have low absolute ζ, indicating that the suspension is less stable.
Determination of individual velocities
All particle velocities were determined through PTV measurement in the microfluidic electrokinetic experimental setup. Fig. 4 presents a representative PTV measurement for each of the different particles, and the mean electrokinetic velocity slopes and corresponding standard deviation of five measurements are presented in Table S1.† All particles except the 1 μm Magsphere AM-modified particles show a strong correlation coefficient (above 0.99) between the median electrokinetic velocity during the ramp (between 25 s and 55 s) and the fitted results. At high velocities (high voltage hold), the number of particles per frame increases, decreasing robustness for particle tracking. Assessing the particle velocity at high voltage hold is therefore more subject to errors, impacting the assessment of yhigh and xhigh (and therefore Δx). The electrokinetic velocity slope for the 1 μm Magsphere AM-modified particles has a lower coefficient of determination than for other particles which is explained by the intrinsic ζ variability of this sample (ESI†).Correlation between ζ and electrokinetic velocity slope
As the electrokinetic velocity is proportional to ζ (eqn (1)), we sought to determine the proportionality coefficient between the electrokinetic velocity slope during the ramp, acquired with our method, and the ζ, obtained with the Zetasizer Ultra. Given that we linearly modulate E during the ramp by adjusting the voltage within the linear regime, the resultant slope of electrokinetic velocity provides a direct representation of the electrokinetic mobility μEK and ζp − ζw, as formulated in eqn (1). Fig. 5 presents the particle electrokinetic velocity slopes, measured with the microfluidic electrokinetic characterization method, as a function of ζ, measured with the Zetasizer. The two measurements are highly correlated (R2 = 0.940). The resultant equation for the fitting is y = −0.0237x + 0.0547, with y being the EK velocity slope and x the ζ. This equation could also be used to assess ζw, which would be 2.3 mV at a zero electrokinetic velocity (y = 0). With such a low value, ζw can therefore be considered small and the influence of electroosmosis negligible. This method therefore allows us to estimate the wall zeta potential without using current monitoring, which is not feasible here due to the high solution conductivity.22As can be seen in Fig. 5, the majority of particles examined cluster is in the ζ region below −75 mV. Yet, studies have shown that bacteria have a ζ between −75 mV and 0 mV around pH 7.39,40 Unfortunately, none of the surface-functionalized particles exhibited a ζ in this range. This emphasizes the importance of having samples outside of the lower end of ζ measured (−75 mV) such as the Magsphere 1 μm AM-modified particles. These exhibit a slightly positive ζ (12.89 mV), which is typically characteristic of an incipient solution instability.41 Furthermore, these samples are critical to obtain the correlation between the particle electrokinetic velocity slopes, measured by microfluidic electrokinetic characterization, and ζ, obtained with the Zetasizer Ultra. This fitting curve in Fig. 5 can also serve as a calibration curve to extrapolate ζ of samples, such as bacteria, which can be measured with the microfluidic electrokinetic characterization presented but not with the Zetasizer, due to their non-spherical shape.
Assessing the zeta potential of E. coli
The overall goal of this work is to develop an easy-to-use platform to broadly enable ζ measurements. Thus, to expand applications beyond abiotic particles, we applied the workflow to determine the ζ of bacteria. We applied our microfluidic electrokinetic characterization to E. coli MG1655 suspended in 10 mM HEPES. Fig. 6 presents a representative PTV measurement for E. coli MG1655. The mean and standard deviation of the electrokinetic velocity slopes obtained from five measurements are 1.097 μm s−2 and 0.062 μm s−2, respectively. Using the obtained fitting curve, these slopes correspond to ζ of −44 ± 3 mV. This value is similar to what was previously reported for a similar E. coli strain (FDA strain Seattle 1946, ATCC 25922) by Antunez-Vela et al.17 They determined ζ as −49 ± 4 mV with a microfluidic electrokinetic characterization performed in a PDMS chip, and 0.2 mM K2HPO4 media (41 μS cm−1) with a pH of 7.3. The similar ζ values across methods validate our workflow and provide further confidence in the platform.Discussion
The method developed in this study leverages a combination of electrokinetic measurements and correlation with ζ, obtained with a Zetasizer, for different spherical particles to evaluate the zeta potential of E. coli that couldn't be assessed previously due to their non-spherical shape. Most of the deviation from the trend observed in the fitting curve in Fig. 5 is caused by the 1 μm Magsphere CO-modified particles. Those CO-modified particles have been characterized by the manufacturer Magsphere to have a charge density of 0.017 meq g−1 while the charge density isn't provided for PS and AM-modified particles. Such particles appear as an outlier and the discrepancy likely comes from the surface functionalization or Zetasizer measurements, but the explanation is beyond the scope of this study. Excluding that particle type results in an R2 = 0.989 with a linear equation of y = −0.0248x + 0.0325, making ζw an estimated 1.3 mV. With such calibration curve the slopes obtained for the E. coli samples would correspond to ζ of −43 ± 2 mV which, despite the significant improvement in R2, would minimally change the previously estimated ζ of −44 ± 3 mV. Low values of ζw for PMMA have been reported for high conductivity solutions.42 In any case, the low value estimated for ζw may also indicate that the channel dimensions used in this study hinder electroosmosis.43This work still relies on a prior zeta potential measurement with a Zetasizer for calibration, measurement that is dependent upon the suspension media used. In the future, reproducible electrode positioning could be corelated to electric field values E in the channel, enabling a direct assessment of the electrokinetic mobility μEK from the measurement of the electrokinetic velocity vEK. Translation into a value of ζp would still require a separate assessment of ζw. An alternative could be to completely suppress electroosmosis using an EOF suppressor.44
All the data analysis presented is adjusted for the analysis of monodispersed zeta potential distributions. Future improvement of the algorithm could provide the ability to automatically analyze samples containing multiple distributions. The microchannels used in this study are relatively wide (100 μm × 100 μm) which could be a limitation to analyze particles smaller than 1 μm. In that case smaller microchannels could be used to perform such characterization at a higher magnification (×40 vs. ×20 in this study).
Conclusions
We have developed and validated an experimental setup and data analysis workflow for electrokinetic characterization of particles and cells using commercial chips and open-source software. This commercial platform removes the need for complicated and expensive microfabrication, which involves costly tools that are most often found in cleanrooms. The ability to use off-the-shelf chips while obtaining reproducible results will allow broader access to ζ analysis for the scientific community that may not otherwise have access to necessary resources.This work is further enabled by particle tracking velocimetry (PTV) using open-source software (Fiji and the TrackMate plugin), which enables the user to tune parameters depending on the sample. Such flexibility also allows characterization of non-spherical particles (such as most cells), which are not compatible with the classical dynamic light scattering (DLS) method used by commercial systems.
Taken together, the novel experimental setup and analysis workflow represent a unique enabling technology for the scientific community. The ability to measure the ζ of a sample of non-spherical particles will have applications well beyond those described here. Nanoparticle research, which currently relies on inaccurate, bulk ζ measurements, will benefit from this workflow, as will the microbiological community, which does not employ ζ as a standard measurement despite its potential utility. When combined with innovations in microscopy, we anticipate this technology being transformative for researchers in reduced resource settings.
Author contributions
Conceptualization J. C., A. L. F. and C. R. B. – data curation J. C. – formal analysis J. C., J. O. O. and A. F. L. – funding acquisition A. L. F. and C. R. B. – investigation J. C., J. O. O. and J. Y. – methodology J. C., A. L. F. and C. R. B. – project administration J. C., A. L. F. and C. R. B. – resources A. L. F. and C. R. B. – software J. C., J. O. O. and A. L. – supervision J. C., A. L. F. and C. R. B. – visualization J. C., J. O. O. – writing – original draft J. C. – writing – review & editing J. C., A. L. F. and C. R. B.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the Office of Naval Research (N00014-18-1-2632). J. O. O. and A. L.'s work were funded through the Undergraduate Research Opportunities Program (UROP) at MIT. J. Y.'s work was funded through the MIT Summer Research Program (MSRP). The authors would like to thank Professor Giovanni Traverso and Dr. Ming Zhao for the access to and help with the Zetasizer Ultra. The authors would also like to thank Gabriel Safar for his help developing the custom LabVIEW™ program.References
- C. Ayala-Torres, N. Hernández, A. Galeano, L. Novoa-Aponte and C.-Y. Soto, Zeta potential as a measure of the surface charge of mycobacterial cells, Ann. Microbiol., 2013, 64, 1189–1195, DOI:10.1007/s13213-013-0758-y.
- R. M. Goulter, I. R. Gentle and G. A. Dykes, Issues in determining factors influencing bacterial attachment: a review using the attachment of Escherichia coli to abiotic surfaces as an example, Lett. Appl. Microbiol., 2009, 49, 1–7, DOI:10.1111/j.1472-765X.2009.02591.x.
- D. O. Ukuku and W. F. Fett, Relationship of cell surface charge and hydrophobicity to strength of attachment of bacteria to cantaloupe rind, J. Food Prot., 2002, 65, 1093–1099, DOI:10.4315/0362-028x-65.7.1093.
- L. Rivas, N. Fegan and G. A. Dykes, Physicochemical properties of Shiga toxigenic Escherichia coli, J. Appl. Microbiol., 2005, 99, 716–727, DOI:10.1111/j.1365-2672.2005.02688.x.
- M. C. van Loosdrecht, J. Lyklema, W. Norde, G. Schraa and A. J. Zehnder, Electrophoretic mobility and hydrophobicity as a measured to predict the initial steps of bacterial adhesion, Appl. Environ. Microbiol., 1987, 53, 1898–1901, DOI:10.1128/aem.53.8.1898-1901.1987.
- D. W. Armstrong, G. Schulte, J. M. Schneiderheinze and D. J. Westenberg, Separating microbes in the manner of molecules. 1. Capillary electrokinetic approaches, Anal. Chem., 1999, 71, 5465–5469, DOI:10.1021/ac990779z.
- A. P. V. Ferreya Maillard, J. C. Espeche, P. Maturana, A. C. Cutro and A. Hollmann, Zeta potential beyond materials science: Applications to bacterial systems and to the development of novel antimicrobials, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183597, DOI:10.1016/j.bbamem.2021.183597.
- R. J. Hunter, Zeta Potential in Colloid Science, Academic press, 1981, DOI:10.1016/c2013-0-07389-6.
- P. C. Hiemenz and R. Rajagopalan, Principles of Colloid and Surface Chemistry, Revised and Expanded, CRC press, 2016, DOI:10.1201/9781315274287.
- D. P. Barz and P. Ehrhard, Model and verification of electrokinetic flow and transport in a micro-electrophoresis device, Lab Chip, 2005, 5, 949–958, 10.1039/b503696h.
- J. Cottet and P. Renaud, Introduction to microfluidics, in Drug Delivery Devices and Therapeutic Systems, ed. E. Chappel, Academic Press, 2021, ch. 1, pp. 3–17, DOI:10.1016/b978-0-12-819838-4.00014-6.
- W. W. Wilson, M. M. Wade, S. C. Holman and F. R. Champlin, Status of methods for assessing bacterial cell surface charge properties based on zeta potential measurements, J. Microbiol. Methods, 2001, 43, 153–164, DOI:10.1016/s0167-7012(00)00224-4.
- R. F. Domingos, M. A. Baalousha, Y. Ju-Nam, M. M. Reid, N. Tufenkji, J. R. Lead, G. G. Leppard and K. J. Wilkinson, Characterizing manufactured nanoparticles in the environment: multimethod determination of particle sizes, Environ. Sci. Technol., 2009, 43, 7277–7284, DOI:10.1021/es900249m.
- S. Bhattacharjee, DLS and zeta potential – What they are and what they are not?, J. Controlled Release, 2016, 235, 337–351, DOI:10.1016/j.jconrel.2016.06.017.
- S. Skoglund, J. Hedberg, E. Yunda, A. Godymchuk, E. Blomberg and I. O. Wallinder, Difficulties and flaws in performing accurate determinations of zeta potentials of metal nanoparticles in complex solutions-Four case studies, PLoS One, 2017, 12, e0181735, DOI:10.1371/journal.pone.0181735.
- A. L. Polaczyk, J. E. Amburgey, A. Alansari, J. C. Poler, M. Propato and V. R. Hill, Calculation and uncertainty of zeta potentials of microorganisms in a 1:1 electrolyte with a conductivity similar to surface water, Colloids Surf., A, 2020, 586, 124097, DOI:10.1016/j.colsurfa.2019.124097.
- S. Antunez-Vela, V. H. Perez-Gonzalez, A. C. De Pena, C. J. Lentz and B. H. Lapizco-Encinas, Simultaneous Determination of Linear and Nonlinear Electrophoretic Mobilities of Cells and Microparticles, Anal. Chem., 2020, 92, 14885–14891, DOI:10.1021/acs.analchem.0c03525.
- A. Coll De Pena, A. Miller, C. J. Lentz, N. Hill, A. Parthasarathy, A. O. Hudson and B. H. Lapizco-Encinas, Creation of an electrokinetic characterization library for the detection and identification of biological cells, Anal. Bioanal. Chem., 2020, 412, 3935–3945, DOI:10.1007/s00216-020-02621-9.
- A. Coll De Pena, N. Hill and B. H. Lapizco-Encinas, Determination of the Empirical Electrokinetic Equilibrium Condition of Microorganisms in Microfluidic Devices, Biosensors, 2020, 10, 10, DOI:10.3390/bios10100148.
- B. Cardenas-Benitez, B. Jind, R. C. Gallo-Villanueva, S. O. Martinez-Chapa, B. H. Lapizco-Encinas and V. H. Perez-Gonzalez, Direct Current Electrokinetic Particle Trapping in Insulator-Based Microfluidics: Theory and Experiments, Anal. Chem., 2020, 92, 12871–12879, DOI:10.1021/acs.analchem.0c01303.
- S. Hidalgo-Caballero, C. J. Lentz and B. H. Lapizco-Encinas, Assessment of submicron particle zeta potential in simple electrokinetic microdevices, Electrophoresis, 2019, 40, 1395–1399, DOI:10.1002/elps.201800425.
- M. A. Saucedo-Espinosa and B. H. Lapizco-Encinas, Refinement of current monitoring methodology for electroosmotic flow assessment under low ionic strength conditions, Biomicrofluidics, 2016, 10(3), 033104, DOI:10.1063/1.4953183.
- W. A. Braff, D. Willner, P. Hugenholtz, K. Rabaey and C. R. Buie, Dielectrophoresis-Based Discrimination of Bacteria at the Strain Level Based on Their Surface Properties, PLoS One, 2013, 8(10) DOI:10.1371/journal.pone.0076751.
- Q. Wang, A. A. D. Jones, J. A. Gralnick, L. W. Lin and C. R. Buie, Microfluidic dielectrophoresis illuminates the relationship between microbial cell envelope polarizability and electrochemical activity, Sci. Adv., 2019, 5(1) DOI:10.1126/sciadv.aat5664.
- O. D. Ernst, A. Vaghef-Koodehi, C. Dillis, A. Lomeli-Martin and B. H. Lapizco-Encinas, Dependence of Nonlinear Electrophoresis on Particle Size and Electrical Charge, Anal. Chem., 2023, 95(16), 6595–6602, DOI:10.1021/acs.analchem.2c05595.
- A. Lomeli-Martin, O. D. Ernst, B. Cardenas-Benitez, R. Cobos, A. S. Khair and B. H. Lapizco-Encinas, Characterization of the Nonlinear Electrophoretic Behavior of Colloidal Particles in a Microfluidic Channel, Anal. Chem., 2023, 95, 6740–6747, DOI:10.1021/acs.analchem.3c00782.
- J. Bentor, H. Dort, R. A. Chitrao, Y. Zhang and X. Xuan, Nonlinear electrophoresis of dielectric particles in Newtonian fluids, Electrophoresis, 2023, 44, 938–946, DOI:10.1002/elps.202200213.
- A. S. Khair, Nonlinear electrophoresis of colloidal particles, Curr. Opin. Colloid Interface Sci., 2022, 59, 101587, DOI:10.1016/j.cocis.2022.101587.
- M. Rouhi Youssefi and F. J. Diez, Ultrafast electrokinetics, Electrophoresis, 2016, 37, 692–698, DOI:10.1002/elps.201500392.
- D. Yan, N. T. Nguyen, C. Yang and X. Huang, Visualizing the transient electroosmotic flow and measuring the zeta potential of microchannels with a micro-PIV technique, J. Chem. Phys., 2006, 124, 021103, DOI:10.1063/1.2162533.
- M. Sureda, A. Miller and F. J. Diez, In situ particle zeta potential evaluation in electroosmotic flows from time-resolved microPIV measurements, Electrophoresis, 2012, 33, 2759–2768, DOI:10.1002/elps.201200202.
- D. Yan, C. Yang, N. T. Nguyen and X. Huang, A method for simultaneously determining the zeta potentials of the channel surface and the tracer particles using microparticle image velocimetry technique, Electrophoresis, 2006, 27, 620–627, DOI:10.1002/elps.200500713.
- S. Devasenathipathy, J. G. Santiago and K. Takehara, Particle tracking techniques for electrokinetic microchannel flows, Anal. Chem., 2002, 74, 3704–3713, DOI:10.1021/ac011243s.
- S. Devasenathipathy and J. G. Santiago, Electrokinetic Flow Diagnostics, in Microscale Diagnostic Techniques, ed. K. S. Breuer, Springer, Berlin, Heidelberg, 2005, ch. 3, pp. 113–154, DOI:10.1007/3-540-26449-3_3.
- A. S. Dukhin and P. J. Goetz, Fundamentals of Interface and Colloid Science, in Characterization of Liquids, Dispersions, Emulsions, and Porous Materials Using Ultrasound, ed. A. S. Dukhin and P. J. Goetz, Elsevier, 2017, ch. 2, pp. 19–83, DOI:10.1016/b978-0-444-63908-0.00002-8.
- C. Shao and D. L. Devoe, Measuring microchannel electroosmotic mobility and zeta potential by the current monitoring method, Methods Mol. Biol., 2013, 949, 55–63, DOI:10.1007/978-1-62703-134-9_4.
- J. Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, TrackMate: An open and extensible platform for single-particle tracking, Methods, 2017, 115, 80–90, DOI:10.1016/j.ymeth.2016.09.016.
- D. Ershov, M.-S. Phan, J. W. Pylvänäinen, S. U. Rigaud, L. Le Blanc, A. Charles-Orszag, J. R. W. Conway, R. F. Laine, N. H. Roy, D. Bonazzi, G. Duménil, G. Jacquemet and J.-Y. Tinevez, Bringing TrackMate into the era of machine-learning and deep-learning, bioRxiv, 2021, preprint, DOI:10.1101/2021.09.03.458852.
- E. Klodzinska, M. Szumski, E. Dziubakiewicz, K. Hrynkiewicz, E. Skwarek, W. Janusz and B. Buszewski, Effect of zeta potential value on bacterial behavior during electrophoretic separation, Electrophoresis, 2010, 31, 1590–1596, DOI:10.1002/elps.200900559.
- E. Dziubakiewicz and B. Buszewski, Capillary electrophoresis of microbial aggregates, Electrophoresis, 2014, 35, 1160–1164, DOI:10.1002/elps.201300588.
- A. Kumar and C. K. Dixit, Methods for characterization of nanoparticles, in Advances in Nanomedicine for the Delivery of Therapeutic Nucleic Acids, ed. S. Nimesh, R. Chandra and N. Gupta, Woodhead Publishing, 2017, ch. 3, pp. 43–58, DOI:10.1016/b978-0-08-100557-6.00003-1.
- H. Falahati, L. Wong, L. Davarpanah, A. Garg, P. Schmitz and D. P. Barz, The zeta potential of PMMA in contact with electrolytes of various conditions: theoretical and experimental investigation, Electrophoresis, 2014, 35, 870–882, DOI:10.1002/elps.201300436.
- B. J. Kirby, Micro-and nanoscale fluid mechanics: transport in microfluidic devices, Cambridge University Press, 2010, DOI:10.1017/CBO9780511760723.
- T. Kaneta, T. Ueda, K. Hata and T. Imasaka, Suppression of electroosmotic flow and its application to determination of electrophoretic mobilities in a poly(vinylpyrrolidone)-coated capillary, J. Chromatogr. A, 2006, 1106, 52–55, DOI:10.1016/j.chroma.2005.08.062.
Footnote |
| † Electronic supplementary information (ESI) available: Microparticle information determined in this study with the Zetasizer Ultra and with electrokinetics results as well as reservoir caps modification procedure, outlier removal discussion and experimental flow chart. See DOI: https://doi.org/10.1039/d3lc00825h |
| This journal is © The Royal Society of Chemistry 2024 |