Open Access Article
Open Access ArticleProgrammable metachronal motion of closely packed magnetic artificial cilia†
Tongsheng
Wang
 ab,
Tanveer
ul Islam
ab,
Tanveer
ul Islam
 ab,
Erik
Steur
ab,
Tess
Homan
a,
Ishu
Aggarwal
c,
Patrick R.
Onck
ab,
Erik
Steur
ab,
Tess
Homan
a,
Ishu
Aggarwal
c,
Patrick R.
Onck
 c,
Jaap M. J.
den Toonder
c,
Jaap M. J.
den Toonder
 ab and
Ye
Wang
ab and
Ye
Wang
 *ab
*ab
aDepartment of Mechanical Engineering, Eindhoven University of Technology, 5600 MB, Eindhoven, The Netherlands. E-mail: y.wang2@tue.nl
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, 5600 MB, Eindhoven, The Netherlands
cZernike Institute for Advanced Materials, University of Groningen, 9747 AG, Groningen, The Netherlands
First published on 24th January 2024
Abstract
Despite recent advances in artificial cilia technologies, the application of metachrony, which is the collective wavelike motion by cilia moving out-of-phase, has been severely hampered by difficulties in controlling closely packed artificial cilia at micrometer length scales. Moreover, there has been no direct experimental proof yet that a metachronal wave in combination with fully reciprocal ciliary motion can generate significant microfluidic flow on a micrometer scale as theoretically predicted. In this study, using an in-house developed precise micro-molding technique, we have fabricated closely packed magnetic artificial cilia that can generate well-controlled metachronal waves. We studied the effect of pure metachrony on fluid flow by excluding all symmetry-breaking ciliary features. Experimental and simulation results prove that net fluid transport can be generated by metachronal motion alone, and the effectiveness is strongly dependent on cilia spacing. This technique not only offers a biomimetic experimental platform to better understand the mechanisms underlying metachrony, it also opens new pathways towards advanced industrial applications.
Introduction
Cilia exist ubiquitously in nature and play key roles in many biological functions, such as locomotion, hearing, feeding, immune responses and reproduction.1 Inspired by nature, various types of artificial cilia have been developed2 in the past two decades as sensors or actuators that can respond to or be driven by external stimuli, such as electrostatic fields,3 magnetic fields,4–15 light,16 pneumatic pressure,17–20 sound21 and pH.22 Most of them are used as in situ pumps and mixers within microfluidic devices, and they most commonly use magnetic actuation due to the advantage of untethered power transfer and the compatibility with biological materials. The study of magnetic artificial cilia started with synchronous, non-reciprocal motion, which has been shown to be effective in producing fluid flow in a microfluidic environment.7,9,11,12,20,23–27In recent years, there has been an increased focus in studying metachronal motion, i.e. the collective wavelike motion resulting from neighboring cilia moving slightly out-of-phase. Researchers have studied the origin and the functional effects of metachronal motion25,28–30 by modeling or mimicking this signature behavior using artificial cilia, with the intention of eventually leveraging the insights towards practical applications. For magnetic artificial cilia, metachronal motion can be generated either by applying a spatially non-uniform magnetic field to an array of identical cilia,28 or by engineering different responses of each individual cilium to the same uniform magnetic field.26,29,31–33 For the first approach, the challenge lies in the generation of sufficiently large local variations in the magnetic field. Such fields can be generated only with an array of carefully arranged small magnets,28 but the field strength quickly diminishes with increasing distance to the array, making it impractical for real applications. The second approach, on the other hand, puts a challenge on the fabrication process, as the neighboring cilia need to have sufficiently different properties in order to generate regular and tunable phase differences. As a result, those artificial cilia are mostly fabricated at length scales of millimeters or larger,33–35 restraining these technologies to down-scale the dimensions as is more and more required in the miniaturization of microfluidic devices.2 Another, perhaps more fundamental issue with the current approaches, is that the spacing between the artificial cilia are about the same as their length,28,29 while natural cilia are much more closely packed.30,36 This is not coincidental: when the magnetic cilia are too close to each other, the dipole–dipole interactions between them will interfere with their motion, causing the formation of ciliary pairs or bundles, after which their motion can no longer be controlled.4,26 This is not a trivial problem because interciliary spacing is critical to the mechanism of metachronal motion and reducing spacing can strongly increase fluid transport, as shown earlier by theoretical and numerical studies.37–43 To overcome these drawbacks, we developed a well-controlled experimental set-up consisting of mm-scale magnetic artificial cilia at small interciliary distances.
In this work, we have fabricated closely packed magnetic artificial cilia with programmable metachronal motion, using a precise micro molding method. The magnetic dipole interaction between cilia was minimized by making only the base part magnetic, allowing us to fully control their motion while having them closely spaced. The base of every cilium follows the shape of the mold with specifically designed inclination angles, which determine the phases of their motion during the actuation. The molds were made from fused silica with a femtosecond laser-assisted etching (FLAE) process, enabling precise control over the geometries. Then, artificial cilia were made by transfer molding two layers of precursor materials with controlled thicknesses into the glass mold: a magnetic layer forms the base part of the cilia, and a nonmagnetic layer forms the top part. The cilia were actuated by an in-house magnetic actuator set-up and the motion and flow generated by various cilia arrays were analyzed using high-speed imaging and particle tracking, and the results were compared with and supported by numerical simulations that fully couple the effects of elasticity, magnetism and fluid dynamics.
Results
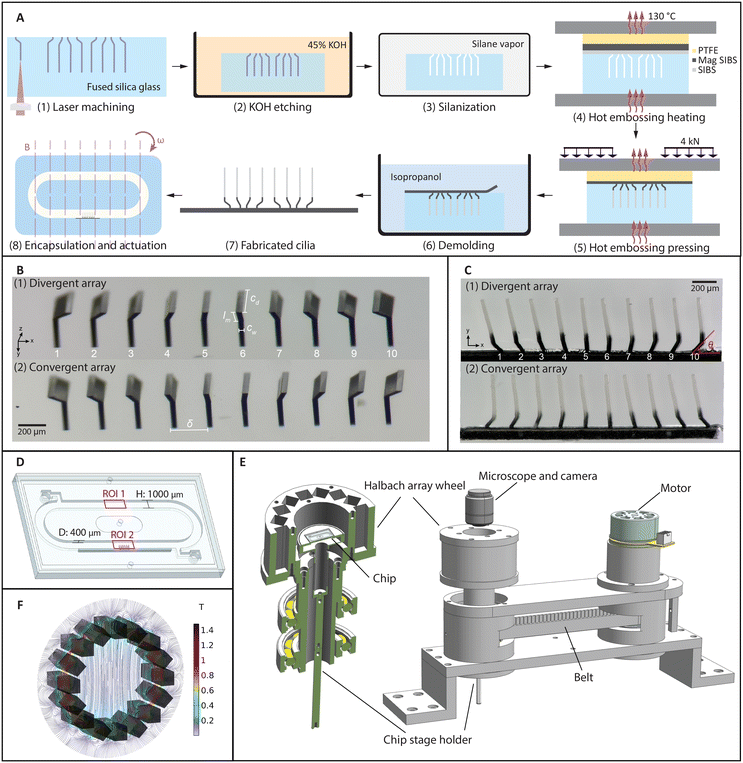
Fabrication and actuation of the closely packed artificial cilia
The cilia fabrication process involves a femtosecond laser-assisted etching step44,45 and a subsequent two-layer molding step. As shown schematically in Fig. 1A (1–3), after laser machining a pre-designed path into a fused silica slide using a focused femtosecond laser (FEMTOprint f200), the slide was put in an 85 °C ultrasonic bath of a 45 wt% potassium hydroxide solution to remove the modified part. Using this method, all the geometrical parameters can be adjusted and realized with micrometer accuracy, as shown in Fig. 1(B). Two molds are shown here, which were used to fabricate cilia that can generate opposite metachronal motion. For the so-called divergent array shown in Fig. 1B (1), the base inclination angles θ change from 135° to 45° in steps of 10°. Similarly, in Fig. 1B (2), the inclination angles change in the opposite way, forming a so-called convergent array.A two-layer transfer molding technique was developed to fabricate partially magnetized cilia. Fig. 1A (4–6) shows the schematics of the molding and demolding process. Fig. 1C shows two different arrays of cilia that contain the same individual cilium but in different arrangements, corresponding to the molds shown in Fig. 1B. The black part of the cilia is magnetic and the transparent part is nonmagnetic. These cilia have a width cw = 24 μm, length from tip to substrate cl = 500 μm, depth cd = 200 μm, and tip-to-tip pitch δ = 200 μm; the length of the inclined part lm is 100 μm for all the cilia. They are arranged in a 1D array to create a more homogeneous flow field in the direction of observation so that the effect of metachrony can be properly analyzed without being significantly obscured by out-of-plane influences such as small cilia widths and the possible variations between cilia in the out-of-plane direction. Note that both the laser fabrication and the molding steps are different from the method we recently reported,45 in which the cilia were simple all-magnetic cylindrical micropillars. For example, the height of the nonmagnetic and magnetic parts are greatly influenced by the processing conditions and the thicknesses of the precursor layers, and extra molds were used to fabricate the precursor layers with desired thicknesses. The ellipsoidal shape of the laser focal voxel needs to be considered when designing the laser path for the bending at the base of the cilia, and extra care needs to be taken while demolding due to the curvature of the cilia base. Details of the fabrication process can be found in the ESI.†
The demolded cilia patch was then integrated into a microfluidic chip containing a recirculation channel, as illustrated in Fig. 1D. The channel was also made with FLAE using a 1 mm thick fused silica glass slide. After integrating the cilia patch on one of the sidewalls of the channel by gluing, the channel slide was capped off with a flat glass slide. On the back of the channel slide, there are two openings for filling liquid with tracer particles, which can be sealed with tape afterwards (see the ESI,† Fig. S9). The assembled chip was then placed on the chip holder, where the cilia patch was in the central area of a Halbach array (Fig. 1E). The Halbach array consists of 16 neodymium magnets of 10 mm × 10 mm × 40 mm, arranged in a specific way to generate a uniform and unidirectional magnetic field.46Fig. 1F shows a simulation result of the magnetic field, where the field strength in the central area is 0.22 T, which is validated by measurement using a gaussmeter. Note that although a stronger magnetic field can increase the movement amplitude of the cilia, and hence improve the flow generation, the current Halbach array is chosen for practicality and measurement accuracy. A larger field can also be generated by fewer magnets (for example two), but with a much larger field gradient. A field with a strong gradient will cause other types of asymmetries, which interferes with the purpose of this study. With electromagnets, generating a field with the magnitude, homogeneity, and frequencies as we reported requires much more sophisticated hardware and is in general less practical. The Halbach array is rotated using a DC motor with a timing belt, as shown in Fig. 1E, with the speed up to 6000 rpm, allowing us to apply a highly controlled rotating uniform field to the cilia at different frequencies.
Individual and collective motion
There are two main mechanisms for flow generation by artificial cilia when they are moving synchronously (no metachrony), namely the spatial asymmetry of the cilia motion and the effect of inertia in the case of temporal asymmetrical motion. In both cases, the motion can be divided into an effective stroke, where more fluid is driven in one direction, and a recovery stroke, where less fluid is driven back. For fully magnetic cilia in previous studies,9,11,18,23,28,29,33,47 spatial asymmetry was the main mechanism in net flow generation, while inertia has also been found to induce or enhance the net flow in some cases, when during the effective stroke the local Reynolds number (Re) at the cilia tip reaches a value much larger than 1.3,29Interestingly, in all the experimental studies on flow generation by cilia undergoing metachronal waves, these asymmetries are always present when a substantial net flow is observed. This is partially by design, aimed at further enhancing the net flow generation, especially for millimeter-sized cilia.18 However, in the case of smaller cilia with dimensions of hundreds of micrometers or smaller, these effects are intrinsic to their dynamics and cannot be turned off. This is because the motion is always slower when the cilia are following the magnetic field, and faster when they bounce back elastically, inducing temporal asymmetry as well as spatial asymmetry due to different levels of drag-induced bending between the two strokes.
In this work, the motion of cilia is both spatially and temporally symmetrical and there is no effective or recovery stroke, allowing us to study the effect of pure metachrony. This is achieved by the two-segment design, in which the magnetic root controls the phase of the motion, and the nonmagnetic part provides enough damping to eliminate both asymmetries.
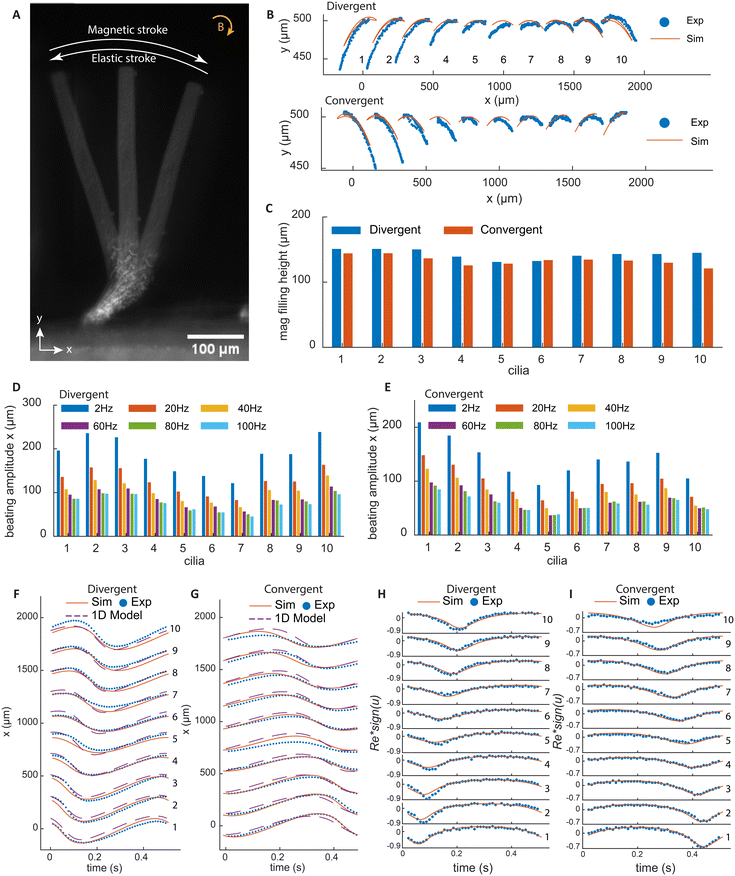
Fig. 2A shows a superimposed image of a cilium at three time points in one beating cycle under a clockwise rotating magnetic field. During the magnetic stroke, the torque bends the cilia root to the right and the rest of the non-magnetic cilia body follows this motion. As the magnetic field rotates, the elastic torque builds up until it exceeds the magnetic torque, and the cilium bends back, performing the elastic stroke. Fig. 2B shows the tip trajectories of all cilia, with both experimental and simulation results. It can be seen that for each cilium, the tip trajectories during the magnetic and elastic strokes collapse onto the same line, without an enclosed area, so there is no spatial asymmetry in motion.
Fig. 2F and G show the x-position of the cilia for the two types of arrays with results from both experiments and simulations. It can be clearly seen that the two arrays generate metachronal waves in opposite directions, in which the movement profiles are similar but shift incrementally with regular intervals. Moreover, the profiles are roughly sinusoidal without sudden movement as a result of the damping of the elastic stroke by the non-magnetic part. In addition to the experimental and numerical results, we also show the results from a 1DOF analytical model, which is capable of capturing the dynamics of the cilia motion and giving an estimate of the relevant forces. The details of the 1DOF model can be found in ESI† 7. Fig. 2H and I show the local Re at the cilia tip, which is defined as Re = ρucl/μ, where ρ is the density of fluid, u is the cilia tip speed, cl is the cilia length, and μ is the dynamic viscosity. Re is always small, meaning that the inertial effects are thus negligible. In this way, the effect of temporal asymmetry and inertia are also eliminated.
Note that the beating amplitude is sensitive to the magnetic filling height, which is defined by the distance from the top of the magnetic part to the substrate. The variation in the height of the magnetic part for each cilium in the arrays is very small, about ±10 μm, as shown in Fig. 2C. However, due to the difference in the inclination angles, the cilia on the far ends of the arrays have longer magnetic parts, which results in higher beating amplitudes for these cilia, as shown in Fig. 2D and E. Note that these variations do not induce notable shape anisotropy or affect phase differences of the metachronal motion. As the actuation frequency increases, the increased hydrodynamic drag reduces the amplitude of the motion, as shown also in Fig. 2D and E.
Characterization of local vortices and global net flow
By eliminating motion asymmetry and inertial effects, any net flow generation in our system can only be attributed to metachronal waves. We performed a detailed analysis of both local and global flow. Fig. 3A and B show the time-dependent flow fields containing what can be described as walking vortices, for the divergent and the convergent array, respectively. As shown by both the experimental results (left column) and the simulation results (right column) at an actuation frequency of 2 Hz, the streamlines form two counterrotating vortices above the cilia arrays, and these vortices travel in the same direction as the metachronal wave. Note that for both the divergent and the convergent cilia arrays, the magnetic strokes are all toward the right and the elastic strokes are toward the left because in both cases the cilia are subjected to a clockwise magnetic field. However, the propagation direction of the metachronal wave follows the magnetic stroke for the divergent array but the elastic stroke for the convergent array, which means that the vortex travel direction is determined by the wave propagation direction rather than the individual cilia motion. This is important because this means that if a global net flow is generated purely by metachrony, one would expect that these two arrays will generate opposite net flow with the same amplitude, which is indeed the case as shown below.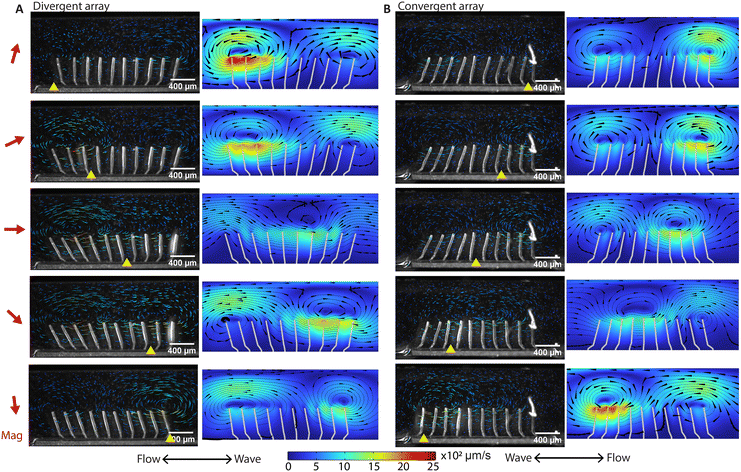 | ||
| Fig. 3 High-speed imaging of metachronal motion and the resulting velocity field showing the ‘walking vortices’. (A and B) The results of the experiment (left column) and simulation (right column) of the metachronal motion and the resulting vortices for the divergent array (A) and the convergent array (B), actuated at 2 Hz. The images are captured at a frame rate of 180 fps. The red arrow on the left side of the figure is the magnetic field direction at the corresponding moments. The yellow triangle on the bottom of the image is the position where the cilia engage in the elastic stroke, when they can no longer follow the magnetic field and start moving in the opposite direction. In the experiments, tracer particles with a diameter of 5 μm are used to visualize the velocity field. The tail-like lines in the experimental images are the trajectories of the tracer particles during the past 30 frames or 0.17 seconds, and the color indicates the magnitude of velocity. In the simulation results, the streamlines show the instantaneous velocity field. The arrows are the velocity direction and the color is the magnitude. The corresponding videos can be found in the ESI.† These results show that divergent and convergent arrays generate opposite metachronal waves with the same magnetic field, and they generate similar patterned walking vortices in opposite directions. The double-ended arrows on the bottom indicate the net flow direction and the wave propagation direction, with the net flow determined from the measurement in the recirculation channel (Fig. 4). | ||
Fig. 4B shows the tracer particle trajectories in the recirculation channel (ROI 1 in Fig. 4A) for the divergent cilia array actuated at 100 Hz. Fig. 4C shows the velocities derived from Fig. 4B, which fits well to the theoretically derived flow profile.48 Note that the direction of the net flow generated is opposite to the propagation direction of the metachronal wave for both divergent and convergent arrays. Fig. 4D and E show particle trajectories above the two arrays. In each of the panels, four cycles of particle movement at different y-levels are shown. It can be seen that the traces of particles are non-reciprocal, and they show different net displacement on different height levels. The time averaged particle velocities in the x-direction with respect to the vertical distance above cilia tips are shown in Fig. 4F, where the largest velocity appears near the cilia tips with the same direction as the overall net flow, and the velocities decrease and reverse as the distance increases. Note that the flow profiles are mirrored for the two different arrays, even though all cilia in both cases have the same magnetic and elastic stroke directions, confirming that the flow is entirely due to metachrony.
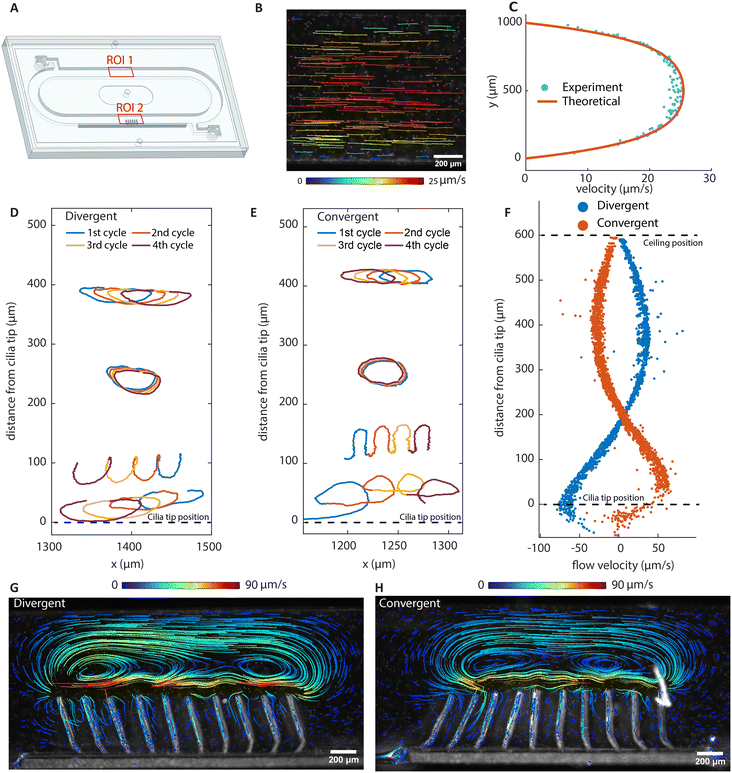 | ||
| Fig. 4 Net flow generation and particle tracing. (A) Schematic of the assembled chip containing a recirculating channel and a cilia patch. ROI 1 corresponds to (B) and (C), and ROI 2 corresponds to (D)–(H). (B) Particle trajectories of the fully developed flow with the divergent cilia array actuating at 100 Hz, showing the net effect of metachronal pumping. (C) The velocity profile along the channel height using the divergent array at an actuation frequency of 100 Hz. (D and E) Tracer particle trajectories imaged at 2 Hz of beating frequency above cilia tips. The trajectories of four cycles represent typical trajectories at different distances above the cilia tip. (F) The net local flow velocities in the x direction above the cilia tip derived from particle tracing. (G and H) The stable vortical streamlines obtained with stroboscopic imaging at a beating frequency of 2 Hz. They show opposite, almost mirrored vortex structures. Note that although the instantaneous velocity fields show repetitive moving vortices, as shown in Fig. 3, long-term tracing of particles show static and stable streamlines, as shown here using stroboscopic imaging. The flow direction close to the cilia tip is the same as the overall net flow direction, which is to the left for the divergent array and to the right for the convergent array. | ||
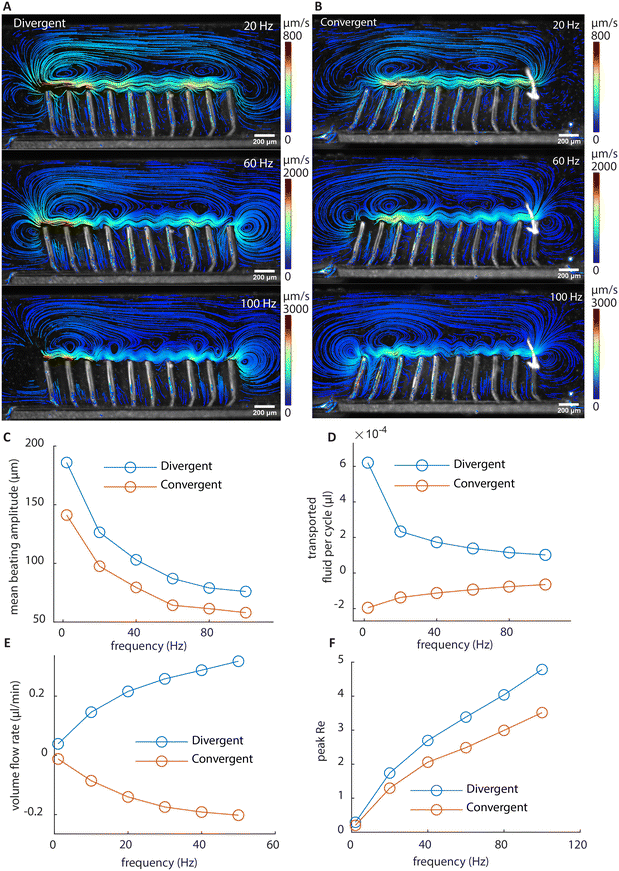
To study the time-integrated flow profile, we performed longer duration particle tracking using stroboscopic imaging with the frame rate matching the cilia beating frequency. The results are shown in Fig. 4G and H; the corresponding movies and recording parameters can be found in the ESI.† Different from the dynamic walking vortices from the time-dependent instantaneous flow fields, stroboscopic imaging reveals stable, larger scale flow patterns, which are similar for the two arrays, but in opposite directions. Note that the flow rate achieved by these cilia are comparable to that achieved in the literature with asymmetrical cilia motions. These nearly mirrored flow patterns and the substantial net flows generated by reversing the wave direction prove that metachronal wave alone can generate effective fluid pumping without the need for individual cilium performing any asymmetrical motion.
Effect of actuation frequency and cilia pitch on flow generation
The flow structures at higher frequencies visualized using stroboscopic imaging are shown in Fig. 5A and B. The particle trajectories show the local net movement over 3 seconds. Due to the increased fluid drag reducing the amplitude of cilia motion as shown in Fig. 5C, the amount of fluid transported per beating cycle is reduced with increasing beating frequency as shown in Fig. 5D. However, the increase in the beating frequency compensates for the loss, resulting in a nonlinear increase of the volume flow rate at higher frequencies measured in the recirculation channel, as shown in Fig. 5E. Fig. 5F shows the peak Re at different frequencies. The Re exceeds 1 at higher frequencies, reaching about 5 at 100 Hz, which is still relatively low. Indeed, if inertia is substantial, the flow generated by the two arrays would not be mirrored anymore at high frequencies, since they share the same individual cilia motions. As shown in Fig. 5E, with the two arrays showing mirrored flow rates, it can be concluded that inertia can be ignored for net flow generation even at high frequencies. Note that there is a larger deviation from perfect mirroring at 2 Hz for the divergent cilia array. We believe the reason lies in the slight difference in the beating amplitudes between the two arrays (shown in Fig. 5C), with the divergent array having a slightly higher amplitude, thus generating a slightly larger flow overall. The difference comes from the difference in the filling height of the magnetic base part, as shown in Fig. 2C, where the cilia in the divergent array have a slightly longer magnetic part than the ones in the convergent array. It is an intrinsic variation for the current fabrication process, and reducing it requires further experimental optimization.To investigate the effect of cilia spacing, we performed 2D numerical simulations using COMSOL Multiphysics®. The results are shown in Fig. 6. A 2D model is chosen for computational efficiency and it can sufficiently represent the flap-like shaped cilia, which perform 2D motion, and generate mostly 2D flow patterns. In the model, the cross-sectional geometries of the cilia and the magnetic filling height are the same as in the experiments shown in Fig. 2E. Validation was first performed using experimental results from both convergent and divergent arrays with a cilia pitch of 200 μm to ensure the reliability of the simulation results. These comparisons between simulation and experiments have already been shown in Fig. 2 and 3.
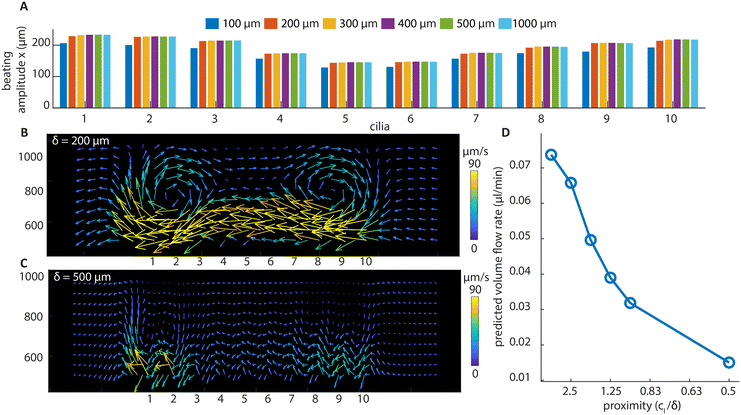 | ||
| Fig. 6 Simulation results of divergent cilia arrays with different cilia spacings at 2 Hz beating frequency. (A) The beating amplitude in the x direction for every cilium. It can be seen that the amplitude is stable above 200 μm cilia spacing. (B) The flow structure with 200 μm cilia spacing, generated by the particle tracking postprocessing of the flow, and it shows a similar vortex structure as in the experiment (Fig. 4(G)). (C) The flow structure with 500 μm cilia spacing. No vortex structure is observed, and the velocities are smaller than with 200 μm spacing. (D) The predicted volume flow rate for different cilia proximity values based on simulation results; the calculation can be found in ESI† 5. | ||
It can be seen from Fig. 6A that only when below 200 μm, the spacing of the cilia starts to substantially affect their beating amplitude. This means that the hydrodynamic interaction forces between cilia are relatively small compared to the magnetic and elastic forces, and a substantial change in the generated net flow with respect to the spacing, which will be shown below, cannot be attributed to the changes in the individual cilium motion. Using numerical simulation, we have also shown that the base angle pitch between cilia will also affect the flow generated, but to a lesser extent than the effect of spacing. The results are shown in ESI† 5 and Movie S7.
Fig. 6B and C show the particle tracking results from the simulation of divergent cilia arrays with 200 and 500 μm spacings, respectively. Fig. 6B matches the experimental result shown in Fig. 4G, indicating the validity of the simulation. Comparing Fig. 6B and C, the vortex structure diminishes when the spacing increases, and the predicted volume flow rate decreases as a result, as shown in Fig. 6D. We use the proximity value cl/δ to represent cilia spacing for better comparison with the literature.36 Note that in earlier simulation studies, similar effects of cilia spacing on flow generation have been found using a different numerical framework.41 Our current results experimentally demonstrate and numerically confirm these earlier studies that fluid flow can indeed be generated by reciprocal cilia subjected to metachronal waves. These results further highlight not only the exciting opportunity of creating closely packed cilia for enhanced fluid flow, they can also be used as an experimental biomimetic platform for studying the fundamental mechanisms underlying metachronal motion.
Conclusions
In this study, we have created closely packed magnetic artificial cilia using a femtosecond laser-assisted etching process combined with a double-layer micro molding technique. To study the effect of pure metachronal waves on flow generation, we have engineered our system to eliminate the effects of spatial and temporal asymmetry in individual cilia motion. This has been achieved by designing the cilia with a magnetic base, which controls the phase of their motion, and a nonmagnetic body, which introduces high hydrodynamic damping, resulting in reciprocal individual cilia motion. We have performed detailed studies of the cilia motion, flow patterns and net flow generation for opposite metachronal waves under different actuation frequencies, using both experiments and simulations. We also performed further analysis of the effect of cilia spacing on flow generation with experimentally validated numerical simulation.We developed a method to understand the effect of metachrony on flow generation, complementary to what has been published before, and with the unique feature that it decouples metachronal effects from any other asymmetries in the system. As mentioned in the introduction, some form of cilia motion asymmetry is always present when net fluid pumping is observed in previous experimental studies of artificial cilia. However, no experimental study has directly proven the flow pumping capability of metachrony alone, while the possibility has been predicted from numerical studies.41 Since these asymmetries are indeed very difficult to eliminate in experiments at small scales, innovative designs and fabrication techniques need to be developed, as reported in this study. Some studies49 show that both symplectic and antiplectic waves can enhance flow when special asymmetric cilia motion is present. Hence it is very difficult to link the flow generated directly to metachrony when other effects are present at the same time.
In this study, a strong influence of the spacing between cilia on the flow generation is found, where the flow becomes notable only when the cilia are close together. Although similar effects were found by theoretical and numerical study,41 experimental proof was not shown in the literature so far, because almost all metachronal ciliary systems created in the past were sparsely distributed, with the gaps between the cilia similar to or larger than their lengths, or otherwise having their motion severely hindered by magnetic interactions between cilia. It shows the importance of using such a closely packed cilia system as an experimental platform for studying important physiological functions of metachronal waves, such as particle and viscoelastic fluid transportation. In addition, the magnitude of the flow generated in this work is comparable to other artificial cilia that rely on nonreciprocal motions.2 Our findings can provide guidelines for designing artificial cilia arrays and actuation strategies for flow generation and pumping in microfluidic devices, which is relevant for applications such as lab-on-a-chip or organ-on-a-chip. Besides fluid pumping, mixing is another very interesting application for artificial cilia.3,50 Although it is not the aim of the current study, it is interesting to use a similar system to study the effect on mixing of metachronal motion.
Our findings also suggest that the close spacing of the cilia found in nature, for example on the surface of the trachea epithelium, results in a substantial contribution from metachrony to the flow generation, in addition to the non-reciprocal motion of the cilia. A one-on-one comparison between the flow generated by asymmetric motion alone and that induced by pure metachrony can be difficult, since both mechanisms depend on the shapes and paths of motion of the cilia themselves, which are different for cases in which either one or the other is induced separately. Nevertheless, it is interesting to further investigate the combination of the two effects by constructing and comparing artificial cilia arrays with and without asymmetrical motion but having the same amplitude, pitch and phase differences. The combination of these flow generating mechanisms can quite possibly lead to further optimization of the artificial cilia flow generation. On the other hand, there can be scenarios in which using pure 2D metachrony for flow generation is preferable. For example, using a 3D tilted conical motion to generate flow, although effective, is very sensitive to the actuator positioning and field direction, and a slight deviation can result in a drastically different flow rate.51,52 Moreover, a 2D non-reciprocal motion is difficult to achieve and control at micrometer scales. With the method in this study, since the Halbach array generates a uniform field in a relatively big volume, we can create a well-controlled flow with large tolerance in the relative positioning of the cilia array with respect to the actuator.
Moreover, the fabrication method developed in this work enables an unprecedented level of control over a combination of geometry and distribution of materials of different properties in 3D on a micrometer scale, which opens the possibilities for creating micro-actuators and sensors with hitherto unrealizable degrees of freedom in designing and controlling their motion. This method can also be applied for fabrication of devices made from other types of polymeric materials, such as light- and temperature-responsive ones. As a replica molding technique, which is beneficial for production scale-up, this approach has the potential to bring profound impact to microfluidic applications as well as other fields of application, such as dynamic surface topographies53–56 and microrobotics.57,58
Materials and methods
The fabrication process of cilia mold and channel
A femtosecond laser with a wavelength of 1030 nm, repetition rate of 1000 kHz, and 230 nJ pulse energy was used to induce local microstructure changes in a 76 mm × 26 mm × 1 mm fused silica glass slide along the designed paths. The laser system is integrated into FEMTOprint f200 aHead. The laser is focused through a Thorlabs 20× lens, resulting in an effective voxel with an ellipsoidal shape, which has a 3 μm short axis in the x–y plane and a 24 μm long axis in the z direction.The laser tool path is generated in Alphacam Ultimate Mill software. Using rough/finish, pocketing and 3D machining tools in the software and a well-designed tool path strategy, the laser writing of 3D structures is possible. After laser machining, the glass slides are put in a 45 wt% KOH bath for the etching process. The machined part has a faster etching speed, roughly 130 μm h−1, than the unmachined part which is 0.7 μm h−1, resulting in removal of the laser written structures.
Both the cilia mold and the microfluidic channels were made using FLAE. After etching, the channel was ready for integration and no further processing was performed. The mold was cleaned in an ultrasonic bath with DI water and dried for surface silanization with a drop of trichloro(1H,1H,2H,2H-perfluorooctyl)silane in a vacuum desiccator overnight in order to reduce the adhesion between the mold and the artificial cilia for easier demolding.
Transfer molding process
The molding was performed using a Specac hydraulic press with a heating unit, as shown in ESI† 2. A premade thin layer of poly(styrene-block-isobutylene-block-styrene) or SIBS (Kaneka Corporation) was first placed on the mold, which was then covered by another premade thin layer of magnetic SIBS containing 70 wt% superparamagnetic carbonyl-iron powder from Sigma-Aldrich. The mixing was performed using a twin screw extruder mixer, shown in ESI† 2. A PTFE sheet was placed to separate the top layer and the compression plate to prevent adhesion. The thicknesses of the pure and magnetic SIBS layers were fine-tuned to achieve a desirable magnetic filling height (ESI† 2). In this particular case, they were 70 μm and 280 μm, respectively. The mold and the two layers of SIBS were first heated to 130 °C, then a force of 4 kN was applied to press the layers into the mold. After 15 min, the temperature was decreased to 90 °C, at a rate of 2.5–3 °C min−1. After that, the pressure was released and the cilia patch was manually demolded while the mold was submerged in isopropanol.Visualization of the flow field
The flow field was observed through an Olympus microscope, and the videos were captured by a camera connected to it. The cilia motion and the vortex structures were measured at ROI 2, as indicated in Fig. 1D, and the fully developed flow was measured at ROI 1. ESI† 4 shows the information on lens, cameras, and capture fps. We used a high frame rate to record the beating of cilia and walking vortices, and a low frame rate for the stroboscopic view of the vortex. Tracing particles (5 μm carboxyl-functionalized polystyrene particles, microParticles GmbH) were used to visualize the flow field. The recorded videos were analyzed in Fiji software with the TrackMate59,60 plugin. The tracking results were then transferred to MATLAB for further analysis.COMSOL® simulation model
To help the analysis of cilia motion and the flow structures, we developed a 2D COMSOL® simulation model, fully coupling magnetism, solid mechanics and fluid mechanics. The governing equations are as follows:| ∇·B = 0 | (1) |
| H = −∇Vm + Hb | (2) |
| B = μ0μrH | (3) |
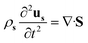 | (4) |
| ∇·vf = 0 | (5) |
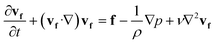 | (6) |
| σ·n = f·n | (7) |
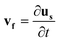 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft), Hby = Hb
sin(2πft), Hby = Hb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πft), where f is the actuation frequency and t is the time. A zero scalar potential is assigned to an arbitrary boundary. The magnetic flux density, B, is measured in Tesla and is related to H by eqn (3), where μ0 = 4π × 107 H m−1. For magnetic SIBS, μr = 1.32, which is fitted from comparing simulation to the experimental results, whereas it is 1 for pure SIBS and water. Eqn (4) represents the solid mechanics equation, where the solid density ρs = 970 kg m−3, us is the solid displacement field, and S represents the Cauchy stress tensor. Young's modulus E = 0.7 MPa, and the Poisson ratio γ = 0.49 are given by the product company (Kaneka Corporation). In the simulation, eqn (5) and (6) describe the fluid continuity and momentum, where vf is the fluid velocity, ρ is the fluid density, p is the fluid pressure and ν is the fluid kinematic viscosity. Eqn (7) and (8) are the arbitrary Lagrangian–Eulerian (ALE) method, where σ is the solid stress and f is the fluid force on the boundary of the solid. The no-slip boundary condition is set on the cilia surfaces and on the wall of the channel, whereas an open boundary condition is applied at the inlet and outlet. The magnetic force acting on the cilia is determined using the Maxwell surface stress tensor. The equations are fully coupled, and the MUMPS solver is used. The time discretization is backward differentiation formula (BDF) with maximum order of 5.
cos(2πft), where f is the actuation frequency and t is the time. A zero scalar potential is assigned to an arbitrary boundary. The magnetic flux density, B, is measured in Tesla and is related to H by eqn (3), where μ0 = 4π × 107 H m−1. For magnetic SIBS, μr = 1.32, which is fitted from comparing simulation to the experimental results, whereas it is 1 for pure SIBS and water. Eqn (4) represents the solid mechanics equation, where the solid density ρs = 970 kg m−3, us is the solid displacement field, and S represents the Cauchy stress tensor. Young's modulus E = 0.7 MPa, and the Poisson ratio γ = 0.49 are given by the product company (Kaneka Corporation). In the simulation, eqn (5) and (6) describe the fluid continuity and momentum, where vf is the fluid velocity, ρ is the fluid density, p is the fluid pressure and ν is the fluid kinematic viscosity. Eqn (7) and (8) are the arbitrary Lagrangian–Eulerian (ALE) method, where σ is the solid stress and f is the fluid force on the boundary of the solid. The no-slip boundary condition is set on the cilia surfaces and on the wall of the channel, whereas an open boundary condition is applied at the inlet and outlet. The magnetic force acting on the cilia is determined using the Maxwell surface stress tensor. The equations are fully coupled, and the MUMPS solver is used. The time discretization is backward differentiation formula (BDF) with maximum order of 5.
Author contributions
Conceptualization: TW, ES, TH, YW. Conducting experiments and simulations: TW. Designing the experiment setup: TuI. Collecting data and analyzing: TW. Writing – editing: TW, YW, TuI, ES, TH, IA, PRO, JdT. Supervision and financial support: JdT, YW, ES, TH.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
The authors acknowledge the European Union's Horizon 2020 Framework Programme no. 833214 and no. 953234, ACD project, Department of Mechanical Engineering, Eindhoven University of Technology. The authors would like to thank Martijn Kuijpers for helping with the development of the 1DOF analytical model and the Equipment and Prototyping Center of TU/e for fabrication of the actuation setup.References
- I. Ibañez-Tallon, N. Heintz and H. Omran, Hum. Mol. Genet., 2003, 12, R27–R35 CrossRef PubMed.
- T. ul Islam, Y. Wang, I. Aggarwal, Z. Cui, H. E. Amirabadi, H. Garg, R. Kooi, B. B. Venkataramanachar, T. Wang, S. Zhang, P. R. Onck and J. M. J. den Toonder, Lab Chip, 2022, 22, 1650–1679 RSC.
- J. den Toonder, F. Bos, D. Broer, L. Filippini, M. Gillies, J. de Goede, T. Mol, M. Reijme, W. Talen and H. Wilderbeek, Lab Chip, 2008, 8, 533–541 RSC.
- A. Shields, B. Fiser, B. Evans, M. Falvo, S. Washburn and R. Superfine, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15670–15675 CrossRef CAS PubMed.
- F. Fahrni, M. W. Prins and L. J. van IJzendoorn, Lab Chip, 2009, 9, 3413–3421 RSC.
- M. Vilfan, A. Potočnik, B. Kavčič, N. Osterman, I. Poberaj, A. Vilfan and D. Babič, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1844–1847 CrossRef CAS PubMed.
- J. Hussong, N. Schorr, J. Belardi, O. Prucker, J. Rühe and J. Westerweel, Lab Chip, 2011, 11, 2017–2022 RSC.
- Y. Wang, Y. Gao, H. Wyss, P. Anderson and J. den Toonder, Lab Chip, 2013, 13, 3360–3366 RSC.
- S. Zhang, Y. Wang, R. Lavrijsen, P. R. Onck and J. M. den Toonder, Sens. Actuators, B, 2018, 263, 614–624 CrossRef CAS.
- S. Broeren, I. F. Pereira, T. Wang, J. den Toonder and Y. Wang, Lab Chip, 2023, 23, 1524–1530 RSC.
- S. Zhang, P. Zuo, Y. Wang, P. Onck and J. M. d. Toonder, ACS Appl. Mater. Interfaces, 2020, 12, 27726–27736 CrossRef CAS PubMed.
- S. Zhang, Y. Wang, P. Onck and J. den Toonder, Microfluid. Nanofluid., 2020, 24, 24 CrossRef.
- A. Babataheri, M. Roper, M. Fermigier and O. Du Roure, J. Fluid Mech., 2011, 678, 5–13 CrossRef.
- N. Coq, A. Bricard, F.-D. Delapierre, L. Malaquin, O. Du Roure, M. Fermigier and D. Bartolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 107, 014501 Search PubMed.
- N. Coq, S. Ngo, O. Du Roure, M. Fermigier and D. Bartolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041503 CrossRef PubMed.
- K. Oh, J.-H. Chung, S. Devasia and J. J. Riley, Lab Chip, 2009, 9, 1561–1566 RSC.
- B. Gorissen, M. De Volder and D. Reynaerts, Lab Chip, 2015, 15, 4348–4355 RSC.
- R. Zhang, J. den Toonder and P. R. Onck, Phys. Fluids, 2021, 33, 092009 CrossRef CAS.
- E. Milana, R. Zhang, M. R. Vetrano, S. Peerlinck, M. De Volder, P. R. Onck, D. Reynaerts and B. Gorissen, Sci. Adv., 2020, 6, eabd2508 CrossRef CAS PubMed.
- E. Milana, B. Gorissen, S. Peerlinck, M. De Volder and D. Reynaerts, Adv. Funct. Mater., 2019, 29, 1900462 CrossRef.
- S. Orbay, A. Ozcelik, H. Bachman and T. J. Huang, J. Micromech. Microeng., 2018, 28, 025012 CrossRef PubMed.
- L. D. Zarzar, P. Kim and J. Aizenberg, Adv. Mater., 2011, 23, 1442–1446 CrossRef CAS PubMed.
- S. Zhang, Y. Wang, P. R. Onck and J. M. den Toonder, Adv. Funct. Mater., 2019, 29, 1806434 CrossRef.
- T. u. Islam, Y. Bellouard and J. M. den Toonder, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104930118 CrossRef CAS PubMed.
- N. Osterman and A. Vilfan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15727–15732 CrossRef CAS PubMed.
- H. Gu, Q. Boehler, H. Cui, E. Secchi, G. Savorana, C. De Marco, S. Gervasoni, Q. Peyron, T.-Y. Huang and S. Pane, Nat. Commun., 2020, 11, 2637 CrossRef CAS PubMed.
- B. Panigrahi, V. Sahadevan and C.-Y. Chen, iScience, 2021, 24, 103367 CrossRef CAS PubMed.
- S. Zhang, Z. Cui, Y. Wang and J. M. den Toonder, Lab Chip, 2020, 20, 3569–3581 RSC.
- S. Zhang, Z. Cui, Y. Wang and J. den Toonder, ACS Appl. Mater. Interfaces, 2021, 13, 20845–20857 CrossRef CAS PubMed.
- W. Gilpin, V. N. Prakash and M. Prakash, Nat. Phys., 2017, 13, 380–386 Search PubMed.
- S. Hanasoge, P. J. Hesketh and A. Alexeev, Soft Matter, 2018, 14, 3689–3693 RSC.
- S. Hanasoge, P. J. Hesketh and A. Alexeev, ACS Appl. Mater. Interfaces, 2020, 12, 46963–46971 CrossRef CAS PubMed.
- X. Dong, G. Z. Lum, W. Hu, R. Zhang, Z. Ren, P. R. Onck and M. Sitti, Sci. Adv., 2020, 6, eabc9323 CrossRef CAS PubMed.
- L. Zhang, J. J. Abbott, L. Dong, B. E. Kratochvil, D. Bell and B. J. Nelson, Appl. Phys. Lett., 2009, 94, 064107 CrossRef.
- S. Tottori, L. Zhang, F. Qiu, K. K. Krawczyk, A. Franco-Obregón and B. J. Nelson, Adv. Mater., 2012, 24, 811–816 CrossRef CAS PubMed.
- S. Peerlinck, E. Milana, E. De Smet, M. De Volder, D. Reynaerts and B. Gorissen, Adv. Funct. Mater., 2023, 2300856 CrossRef CAS.
- S. N. Khaderi, C. Craus, J. Hussong, N. Schorr, J. Belardi, J. Westerweel, O. Prucker, J. Rühe, J. Den Toonder and P. Onck, Lab Chip, 2011, 11, 2002–2010 RSC.
- S. Khaderi, J. Den Toonder and P. Onck, Langmuir, 2012, 28, 7921–7937 CrossRef CAS PubMed.
- S. Khaderi, J. Hussong, J. Westerweel, J. den Toonder and P. Onck, RSC Adv., 2013, 3, 12735–12742 RSC.
- S. Khaderi, M. Baltussen, P. Anderson, D. Ioan, J. Den Toonder and P. Onck, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 046304 CrossRef CAS PubMed.
- S. Khaderi, J. Den Toonder and P. Onck, Biomicrofluidics, 2012, 6, 014106 CrossRef CAS PubMed.
- S. Khaderi and P. Onck, J. Fluid Mech., 2012, 708, 303–328 CrossRef.
- S. Khaderi, J. M. den Toonder and P. Onck, in Atlas of cilia bioengineering and biocomputing, River Publishers, 2022, pp. 137–148 Search PubMed.
- Y. Bellouard, A. Said, M. Dugan and P. Bado, Opt. Express, 2004, 12, 2120–2129 CrossRef CAS PubMed.
- Z. Cui, Y. Wang, S. Zhang, T. Wang and J. M. den Toonder, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2304519120 CrossRef CAS PubMed.
- H. Raich and P. Blümler, Concepts Magn. Reson., Part B, 2004, 23, 16–25 CrossRef.
- S. Zhang, R. Zhang, Y. Wang, P. R. Onck and J. M. den Toonder, ACS Nano, 2020, 14, 10313–10323 CrossRef CAS PubMed.
- F. M. White and J. Majdalani, Viscous fluid flow, McGraw-Hill New York, 2006 Search PubMed.
- S. Khaderi, J. Den Toonder and P. Onck, J. Fluid Mech., 2011, 688, 44–65 CrossRef.
- Y. Ding, J. C. Nawroth, M. J. McFall-Ngai and E. Kanso, J. Fluid Mech., 2014, 743, 124–140 CrossRef.
- Y. Wang, Y. Gao, H. M. Wyss, P. D. Anderson and J. M. den Toonder, Microfluid. Nanofluid., 2015, 18, 167–174 CrossRef CAS.
- M. Downton and H. J. E. L. Stark, EPL, 2009, 85, 44002 CrossRef.
- P. Shivapooja, Q. Wang, B. Orihuela, D. Rittschof, G. P. López and X. Zhao, Adv. Mater., 2013, 25, 1430–1434 CrossRef CAS PubMed.
- X. Yao, Y. Hu, A. Grinthal, T.-S. Wong, L. Mahadevan and J. Aizenberg, Nat. Mater., 2013, 12, 529–534 CrossRef CAS PubMed.
- J. Kim, J. Yoon and R. C. Hayward, Nat. Mater., 2010, 9, 159–164 CrossRef CAS PubMed.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed.
- S. Palagi and P. Fischer, Nat. Rev. Mater., 2018, 3, 113–124 CrossRef CAS.
- S. R. Dabbagh, M. R. Sarabi, M. T. Birtek, S. Seyfi, M. Sitti and S. Tasoglu, Nat. Commun., 2022, 13, 5875 CrossRef CAS PubMed.
- D. Ershov, M.-S. Phan, J. W. Pylvänäinen, S. U. Rigaud, L. Le Blanc, A. Charles-Orszag, J. R. Conway, R. F. Laine, N. H. Roy and D. Bonazzi, Nat. Methods, 2022, 19, 829–832 CrossRef CAS PubMed.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00956d |
| This journal is © The Royal Society of Chemistry 2024 |