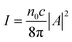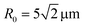Open Access Article
Open Access ArticleDeveloping 3D computational models to capture the spatial, temporal and thermal behavior as laser beams propagate through photo-thermally responsive gels†
Victor V.
Yashin
 a,
Fariha
Mahmood
a,
Fariha
Mahmood
 b,
Kalaichelvi
Saravanamuttu
b,
Kalaichelvi
Saravanamuttu
 b and
Anna C.
Balazs
b and
Anna C.
Balazs
 *a
*a
aDepartment of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: balazs@pitt.edu
bDepartment of Chemistry and Chemical Biology, McMaster University, ON L8S 4M1, Canada
First published on 16th November 2023
Abstract
By developing a new 3D computational model for laser beams propagating through photo-thermally responsive hydrogels, we investigate the complex feedback that occurs as the propagating beam forms a waveguide, which in turn affects the passage of light through the sample. As the beam passes through a poly-(N-isopropylacrylamide) (pNIPAAm) hydrogel, the pendent spiropyran (SP) chromophores isomerize to a hydrophobic state. In water, the resultant localized collapse of the hydrogel leads to a local increase the refractive index, which alters the spatial distribution of light in the sample and leads to the formation of the waveguide. The system displays self-trapping as the light is confined to propagate within the generated waveguide. Our 3D model captures the cooperative interactions among the light propagation, photochemical reaction, hydrogel dynamics, and local heating due to the absorption of light and thereby allows us to characterize the spatial, temporal and thermal variations in the system as the beam traverses the gels. Consequently, the simulations reveal the spatiotemporal behavior as heating due to absorption of light promotes the waveguide formation and leads to a strong attractive interaction between two beams. The strength of interaction between two beams can be tuned by varying the beam intensity, ambient temperature and inter-beam distance. Our results show that two Gaussian beams can cross each other if the interaction is sufficiently strong. The simulations also reveal the long-time dynamics and further elucidate the evolution of the cooperative behavior that leads to this non-linear optical phenomenon.
Introduction
Feedback in biology enables self-regulating processes that bridge not only length and time scales, but also different forms of energy expenditure (e.g., chemical, optical, mechanical) needed to maintain homeostatic conditions. For example, feedback drives ocular pupils to mechanically contract with increased exposure to light and thereby let less light to penetrate the eye. Few synthetic materials display feedback controlled, closed loop behavior1–4 that does not require human intervention to maintain the proper functioning of the material. Recently, researchers found that the behavior of certain photo-responsive hydrogels grossly mimics the above mentioned ocular self-regulation: an incoming thin laser beam was self-trapped and confined in the photo-responsive gel.5 The photo-responsive hydrogel in these systems was composed of cross-linked poly(acrylamide-co-acrylic acid) (p(AAm-co-AAc)) that encompasses spiro-benzopyran (SP) chromophores grafted to the polymer chains. Photo-isomerization of the chromophores changes the interactions between the polymer and water, causing the laser beam to become trapped within a waveguide, which corresponds to an area with increased polymer content (the mechanism is discussed in detail below). In contrast to other photo-reactive soft matter systems where self-trapping is observed,6,7 waveguides formed in the SP-modified hydrogels are transient and rapidly dissipate after the laser beams are removed.5 The latter reversibility of the self-trapping could facilitate novel photonics applications where structures could be repeatedly formed and erased.5Theoretical and 2D computational models were developed to simulate the self-trapping of laser beams in p(AAm-co-AAc) gels containing grafted SP units.5 The simulation results captured the peak intensity as a function time and showed qualitative agreement with corresponding experiments.5 To obtain a more complete description of these photo-responsive gels, we herein perform new 3D modeling studies. The 3D studies are important since they allow us to correlate the simultaneous changes in space, time and temperature as a laser beam propagates through the gel. For example, we construct contour plots that reveal how the lateral spread in temperature contributes to the spatial gradients in the polymer volume fraction, and the width of the self-trapped beam. Hence, the 3D simulations allow us to analyze how the interconnected spatial, temporal and thermal evolution in the system enables the generation of a waveguide, which in turn directs the transmission of light through the rest of the sample.
The photo-responsive hydrogel in our computational study is composed of poly(N-isopropylacrylamide) (pNIPAAm) with grafted SP units. This gel exhibits a lower critical solubility temperature (LCST) and thus shrinks with increases in temperature. For a sample immersed in water, the application of light triggers a cascade of interconnected events. In the illuminated materials, the once hydrophilic ring-open merocyanine form of spiro-benzopyran isomerizes into the hydrophobic SP state.8,9 The induced incompatibility between the solvent and gel causes the sample to shrink and thereby increase the local polymer volume fraction, ϕ. Concurrently, the light absorbed by the gel increases the local temperature and provides another stimulus for gel contraction. The resulting increases in ϕ lead to an increase in the index of refraction, n, in the material. The local increase in n in turn causes a redistribution of the local intensity of light, I, along the propagation direction due to the self-focusing effect.10,11 The changes in the partial distribution of I affect the local extent of SP isomerization. The latter changes in the degree of isomerization then trigger the further evolution of the local volume fraction of the polymer and hence, drives the continuation of the above feedback within the system. In this manner, the cycle of interactions throughout the sample and the expenditure of different forms of energy enable the material itself to regulate the global shrinkage of the gel and trap light in the collapsed polymer domains. When the light is removed, the system returns to the initial conditions, making the process reversible.
The computational model (detailed in the next section) takes into account the propagation of light, photochemical reactions, hydrogel dynamics, and local heating in the material. Hence, we can analyze the cooperative spatiotemporal behavior that emerges with the entrance of the light beam into the sample, the concurrent formation of the waveguide and the subsequent passage of the beam through the material. Consequently, we can characterize how the observed non-linear optical effects develop in both space and time. Our 3D simulations also provide a more accurate description of photo-responsive gels relative to the description obtained from the previous 2D simulations. The latter simulations were based on the linearized equations of gel dynamics and did not account for local heating due to the absorption of light.5 In general, 2D models overestimate the magnitude of the interaction strength between beams and the thermal effects in the system. Namely, the extent of overlap between beams is enhanced as the system is constricted to a lower dimensionality. Moreover, the dissipation of heat through thermal diffusion is less effective in 2D than in 3D. These 3D simulations were now run for sufficiently long times to reveal the system's late-stage behavior. Additionally, we characterize the fading of the waveguide when the incident laser beam is blocked.
In addition to analyzing the spatiotemporal behavior of a single propagating beam, we examine a two-beam system, pinpointing factors that influence the shape of the waveguides formed as the beams interact within the body of the gel. The intensity of the beams at the exit from the sample produces a distinct signature, indicating that the gels' inherent photo- and thermo-responsive behavior enabled the confinement of two diverging beams into distinct rays. In turn, the existing rays of light can be used to analyze and characterize the unknown properties of the sample. Overall, the computer simulations provide information valuable for interpreting future experimental results. The findings from our study can facilitate the development of hydrogel-based devices for storing and processing information. The inherent beaming merging is useful for a variety of photonic applications.
Methodology
A. Theoretical model
Below, we provide a brief description of the theoretical model used in these studies.5,12,13 We consider a hydrogel swollen at temperature T and composed of cross-linked pNIPAAm polymer chains encompassing grafted spiropyran (SP) units. The hydrogel is characterized by the crosslink density c0, volume fraction of the polymer in the as prepared (un-deformed) gel ϕ0, actual volume fraction of the polymer in gel ϕ, and fraction of SP-containing monomeric units, fsp. When illuminated by light of a specific wavelength and intensity I, the grafted SP units undergo a reversible transition from the ring-open to ring-closed isomeric state. The degree of isomerization is characterized by the fraction of ring-closed SP isomers, psp. The ring-closed SP isomer is hydrophobic and hence, the illumination induces a shrinking of the hydrogel through the expulsion of the excessive solvent. We assume for simplicity that the polymer–solvent interdiffusion is the only transport process in the gel, so that ϕvp + (1 − ϕ)vs = 0, where vs is the velocity of the solvent and vp is the velocity of the polymer.The system is described by the following list of equations:
| ∂ϕ/∂t = −∇·(ϕvp) | (1) |
| ∂psp/∂t + vp·∇psp = K+I(1 − psp) − K−psp | (2) |
The velocity of the polymer in the swollen gel is taken to be proportional to the forces acting on the network (relaxational dynamics). Under the above assumptions, the velocity of the polymer is calculated as
vp = Λ(ϕ)∇·![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) | (3) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) is the stress tensor and Λ(ϕ) is the kinetic coefficient
is the stress tensor and Λ(ϕ) is the kinetic coefficient| Λ(ϕ) = Λ0(1 − ϕ)(ϕ/ϕ0)−3/2 | (4) |
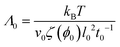 | (5) |
The stress tensor ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) in eqn (3) includes contributions from the osmotic and elastic forces:
in eqn (3) includes contributions from the osmotic and elastic forces:
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) = −πosm(ϕ, psp, T)Î + = −πosm(ϕ, psp, T)Î + ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) el el | (6) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) el is the stress tensor describing the elasticity of the polymer network. The elastic contribution is described by the neo-Hookean model
el is the stress tensor describing the elasticity of the polymer network. The elastic contribution is described by the neo-Hookean model![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) el = −c0(2ϕ0)−1ϕÎ + c0ϕ0−1ϕ el = −c0(2ϕ0)−1ϕÎ + c0ϕ0−1ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[B with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0042_0302.gif) | (7) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0042_0302.gif) are the respective unit and finger strain tensors. The osmotic pressure in eqn (6) is calculated as
are the respective unit and finger strain tensors. The osmotic pressure in eqn (6) is calculated as| πosm(ϕ, psp, T) = πFH(ϕ, T) − χsp(T)fsppspϕ2 | (8) |
| c0ϕ0−1ϕ[(ϕ0/ϕ)2/3 − 1/2] = πFH(ϕ, T) | (9) |
The problem of self-focusing (self-trapping) concerns the propagation of a beam of light in a medium where the interaction between light and matter results in an increase in the refractive index of the medium. In the SP-modified hydrogels in the dark, the refractive index of a uniform SP-modified hydrogel under swelling equilibrium is n0 = ϕeqnp + (1 − ϕeq)ns, where np and ns are the respective refractive indices of the polymer and solvent. Propagation of a beam of light causes a local increase in the volume fraction of the polymer due to hydrophobicity of the ring-closed SP unit, δϕ = ϕ − ϕeq > 0, and that, in turn, leads to a change in the refractive index
| δn = n − n0 = (np − ns)δϕ | (10) |
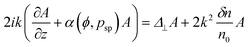 | (11) |
where c is the velocity of light under vacuum. Eqn (11) is applicable only if δn/n0 is small, and δn varies on a length scale much larger than the wavelength of light.10,11
Finally, the theoretical model takes into account the conversion of absorbed light to heat that leads to an increase in local temperature, δT. The experimental study demonstrated that the thermal effects cannot be neglected, and that they have a strong effect on interaction between propagating laser beams.13 The local heating is described by the equation of thermal conductivity with a source
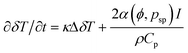 | (12) |
B. Model parameters and characteristic scales
In this study, we consider a pNIPAAm-based polymer network having a crosslink density of c0 = 1.08 × 10−3 and the volume fraction of the polymer in the as prepared gel of ϕ0 = 0.129. Such a material could be fabricated through simultaneous polymerization and crosslinking in a solution of monomers and cross-linkers of concentration 1.2 M and 0.03 M, respectively. We assume that the fraction of the monomeric units containing grafted SP chromophore is fsp = 2.5 × 10−3 as in the experimental studies in ref. 5 and 13. The experimental data reported in ref. 5 is used for modeling kinetics of the light-induced SP isomerization. The rate constants of forward and backward isomerization reactions are taken K+ = 1.53 × 105 μm2 W−1 s−1 and K− = 0.015 s−1, respectively.Interactions between the pNIPAAm polymer network and water are introduced through the Flory–Huggins parameter χ(ϕ, T) = χ0(T) + χ1ϕ, where T is the absolute temperature, χ0(T) = 3.416 − 902.441/T, and χ1 = 0.518.14 The temperature-dependent contribution to χ is instructive to present in the form characteristic for the virial expansion of the Flory–Huggins osmotic pressure πFH, namely, χ0(T) = 1/2 + b(1 − Tc/T). Here, b = 2.92, and Tc = 309.4 K is the critical temperature, above which χ0(T) > 1/2 and a pNIPAAm gel is in the collapsed state according to the Flory–Huggins theory. To introduce the hydrophobic effect of the isomerized SP units, we assume that it has the form χsp(T) = −aspb(1 − Tc/T) so that the temperature dependent contribution to the polymer–solvent interactions is
| χ0(T) + pspfspχsp(T) = 1/2 + b(1 − pspfspasp)(1 − Tc/T) |
The dimensionless mobility is determined in the simulations as
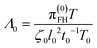 | (13) |
Simulations of light propagation are performed at the wavelength of light λ = 532 nm, and the refractive indices of the solvent and polymer of ns = 1.334 and np = 1.49, respectively.5 The wave number is calculated as 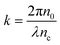 , where nc = 1.4 is the correction factor.5 Absorption of light depends on the degree of isomerization of grafted SP units psp as reported in ref. 5. We use the following equation to determine the value of α(ϕ, psp)
, where nc = 1.4 is the correction factor.5 Absorption of light depends on the degree of isomerization of grafted SP units psp as reported in ref. 5. We use the following equation to determine the value of α(ϕ, psp)
| α(ϕ, psp) = αw + ϕref−1ϕ[α0(1 − psp) + α1psp] |
We study the propagation of Gaussian beams in the SP-modified gel. The gel layer is assumed to be oriented parallel to the XY plane, and incident beams propagate along the Z axis in the positive direction. An incident beam is focused at the bottom gel surface at z = 0, so the 2D distribution of the amplitude A is
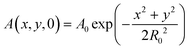 | (14) |
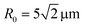 , which corresponds to wb = 10 μm used in the experimental studies.
, which corresponds to wb = 10 μm used in the experimental studies.
The radius of the beam provides the natural length scale in the XY plane normal to the incident beam. In the direction of beam propagation, along the Z axis, the characteristic length scale of the problem is provided by the diffraction length of the beam zd = kR02.11 The latter two length scales are numerically quite different since zd ≈ 0.57 mm so that zd/R0 ≈ 80 for our model parameters. In our simulations, the thickness of the gel layer is H = 3 mm for which H/zd ≈ 5.3. The third characteristic length scale is given by the attenuation of propagating light described by the absorbance coefficient α(ϕ,psp). It worth noting that α−1 > H for our model parameters. Specifically, in a gel at equilibrium swelling at psp = 0 (no illumination), α−1 ≈ 4.01 mm at the ambient temperature of T = 15 °C and α−1 ≈ 3.1 mm at T = 25 °C.
For the characteristic intensity in the center of a focused Gaussian beam, I0 ∼ |A0|2, we use Iref = 1 × 10−5 W μm−2. This value corresponds to the power of the beam Pref = π/2 mW since the power of the Gaussian beam and intensity I0 are related to each other as P = πR02I0.11 Finally, l0 = R0/4 and t0 = (K+Iref)−1 ≈ 0.65 s are chosen for the respective length and time scales in the simulations.
C. Numerical simulations
The simulations proceed through the following steps. At t = 0, the gel is taken to display the equilibrium degree of swelling for psp = 0 and temperature T. This state constitutes the initial condition for a gel sample that is then irradiated with light at a given ambient temperature T. For this initial condition, we specify the volume fraction of the polymer in the gel, ϕ, and the fraction of SP-containing monomeric units, fsp. At each time step in the simulation, we first solve eqn (11) for the complex amplitude A at the conditions given by eqn (14) at z = 0 and the current local values of the volume fraction of the polymer ϕ and the degree of SP isomerization, psp. Then, we update the local values of psp in the gel according to eqn (2) for the obtained distribution of light intensity I ∼ |A|2. Next, we update the local temperature increase δT, eqn (12), at the current spatial distributions of psp, I and ϕ. Finally, the time step in gel dynamics is performed according to the gLSM equations (see eqn (15) below), where the osmotic contribution for the nodal force FN is calculated for the current values of psp and temperature T + δT.The equations for the model are solved numerically using two grids, one static and one moving. Information between the static and moving grids is transferred through the local interpolation. The equations for beam propagation, eqn (11), and thermal conductivity, eqn (12), are solved using the fast Fourier transform (FFT) method15 within the simulation box on the static grid of lattice sizes hx = hy = l0, where l0 = R0/4 is the length scale in simulations, and hz = zd/6. See the ESI† for further details.
The equations for the gel dynamics and the kinetics of the SP isomerization, eqn (1)–(3), are solved on a moving grid using the gel lattice-spring model (gLSM) approach that we developed previously. The latter approach is discussed in detail elsewhere16,17 (the previous 2D simulations were based on the linearized equations of gel dynamics and were performed using the commercial Mathematica™ software5). Within the gLSM approach, the gel is represented by elements, and the nodal points move under the action of the elastic and osmotic forces exerted on the nodes from within the adjacent elements (in the present study, the gel elements are not cubic as in the original 3D gLSM formulation17). The necessary modifications of the gLSM formulation were made to take the non-cubic element shape into account. The equation of motion of node number N has the following simple form:
| drN/dt = MNFN | (15) |
The element sizes of gel in the un-deformed state are taken Δi = 1.01λeq−1hi, i = x, y, z, where λeq is the equilibrium degree of swelling of the gel at a given temperature at psp = 0 (in the dark). Hence, the swelling of the gel sample at equilibrium has the same size at any temperature.
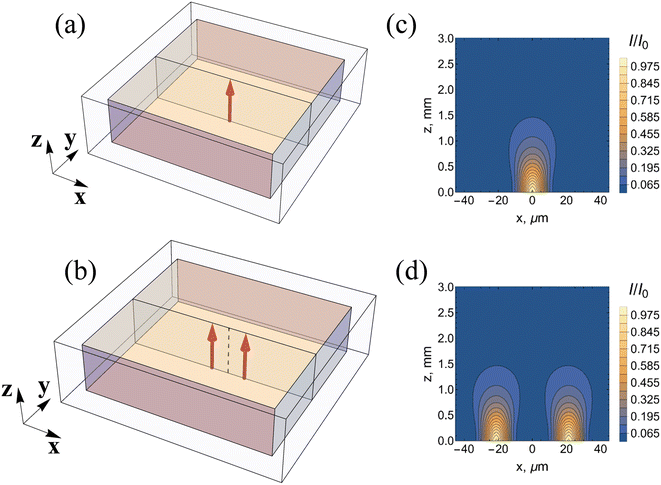
Using this protocol, we model the self-trapping (self-focusing) of one beam or two incoherent beams propagating through a layer of a swollen SP-modified pNIPAAm gel. Fig. 1a and b show the schematics of the two model systems. In the single beam system, the beam propagates along Z in the positive direction, and the beam axis goes through the center of the gel sample, as shown in Fig. 1a. The sample of gel under swelling equilibrium at ambient temperature T = 15 °C or 25 °C is of size 25R0 × 25R0 × 3 mm in the respective X, Y, Z directions. The sample is placed in the center of a box filled with water of size 40R0 × 40R0 × 3.75 mm. In the case of two beams, the incident beams propagate normal to the gel layer (Fig. 1b); their axes are separated by the distance of Δx = 3R0 or 6R0 and located at the coordinates (x, y) = (±Δx/2, 0). The sizes of the gel and box in the X direction are increased to the respective 25R0 + Δx and 40R0 + Δx in a two-beam system.
Results and discussion
A. The effect of uniform illumination on the equilibrium swelling of the gel
We begin by describing the equilibrium properties of SP-containing pNIPAAm gels under uniform illumination and unconstrained swelling. As we show below, the swelling of a small pNIPAAm gel sample does not lead to dramatic changes under uniform illumination (Fig. 2); however, the scenario is very different when a thin beam of incident light is focused on one side of a thicker sample (Fig. 3).The gel sample is assumed to be sufficiently small that the effects of heating due to light absorption can be neglected. In this case, the equation for the equilibrium degree of isomerization of the SP-units is given as
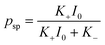 | (16) |
| c0λ−3(λ2 − 1/2) = πFH(ϕ, T) − χsp(T)fsppspϕ2 | (17) |
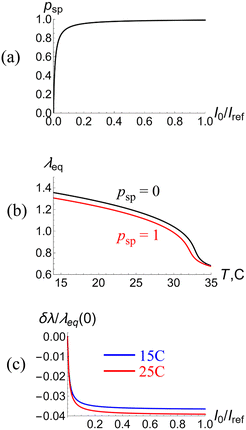
Isomerization of the SP units results in an increase in the hydrophobicity of the polymer network, eqn (17), causing a decrease in the degree of gel swelling. Fig. 2a shows the effect of SP isomerization on the equilibrium degree of swelling as a function of temperature for the non-illuminated (psp = 0, black line) and well illuminated (psp = 1, red line) gels. Notably, the illuminated gel is smaller in size than the non-illuminated sample.
The value of psp depends on the intensity of light I0 (see eqn (17)); this dependence is shown in Fig. 2b. The intensity is normalized to the reference intensity Iref, which corresponds to the maximal intensity in a Gaussian beam of radius 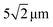 and power π/2 mW. For the chosen values of the model parameters, all the SP units are isomerized at intensities greater than 0.2Iref (see Fig. 2b).
and power π/2 mW. For the chosen values of the model parameters, all the SP units are isomerized at intensities greater than 0.2Iref (see Fig. 2b).
To quantify the effect of illumination on gel swelling, we plot (Fig. 2c) the relative change in gel size, δλ(I0)/λeq(0), as a function of I0/Iref at temperatures of 15 °C (blue line) and 25 °C (red line). As an LCST system, the gel size decreases with an increase in temperature and exhibits a swelling–deswelling transition at about 33 °C. For the chosen model parameters, the uniform illumination of a small gel results in a decrease in sample size of about 3.5% at 15 °C and 4% at 25 °C (Fig. 2c).
In the next section, we analyze the phenomena that occur when the uniform illumination is replaced by a Gaussian beam that propagates through the sample. As shown below, the subtle changes displayed in Fig. 2 are distinct from the pronounced perturbations shown in Fig. 3.
B. Self-focusing of single Gaussian beam
The major difference between propagation of a plane wave of light and that of a thin Gaussian beam arises from the divergence of the Gaussian beam due to diffraction.11 When propagating through a responsive medium, the Gaussian beam increases the local index of refraction n, which decreases the diffraction divergence of the beam.10,11Recently, experiments were conducted to determine the effect of Gaussian beams propagating through SP-containing PAAm-5,13 and pNIPPAm-based13 hydrogels. The results showed that for sufficiently high light intensities, the propagating beam undergoes a self-focusing behavior, where the light is trapped and travels within just a narrow region of the sample. In the studies below, we undertake comprehensive numerical calculations to characterize the spatial and temporal features of this self-trapping in SP-containing pNIPPAm-based hydrogels at different temperatures and light intensities.
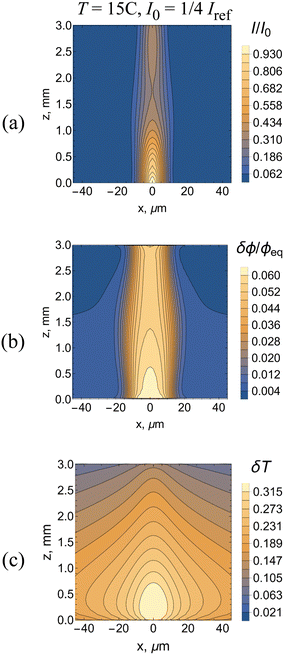
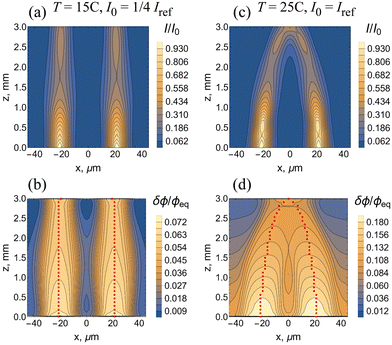
The images in Fig. 3a–c from our 3D computer simulations show the self-trapping of the light at late times, where all the images correspond to the same instant. The incoming Gaussian beam has a radius 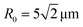 (Fig. 1c) at T = 15 °C and the beam intensity is equal to I0 = 1/4Iref. The image in Fig. 3a presents the spatial distribution of the light intensity taken from the middle cross section of a 3 mm thick sample. At this late time, the radius of the self-trapped beam is comparable to the radius of the incident beam (the same value as that used to illuminate one unperturbed Gaussian beam in Fig. 1a). The initial stage of self-focusing is presented in movies M1 and M2 (see the ESI†). Movie M1 shows the evolution of the spatial distribution of the light intensity in the middle cross-section and M2 shows the behavior of the light intensity of the exiting beam at z = 3 mm. The self-trapping process occurs due to the formation of a waveguide (Fig. 3b), which occupies the area around the beam axis where the polymer volume fraction, ϕ, is greater than the equilibrium value. In this millimeter sized sample, the local heating due to the absorption of light leads to an increase in temperature around the beam axis (Fig. 3c). The temperature increase in turn promotes the formation of the waveguide since the pNIPAAm gel shrinks upon heating.
(Fig. 1c) at T = 15 °C and the beam intensity is equal to I0 = 1/4Iref. The image in Fig. 3a presents the spatial distribution of the light intensity taken from the middle cross section of a 3 mm thick sample. At this late time, the radius of the self-trapped beam is comparable to the radius of the incident beam (the same value as that used to illuminate one unperturbed Gaussian beam in Fig. 1a). The initial stage of self-focusing is presented in movies M1 and M2 (see the ESI†). Movie M1 shows the evolution of the spatial distribution of the light intensity in the middle cross-section and M2 shows the behavior of the light intensity of the exiting beam at z = 3 mm. The self-trapping process occurs due to the formation of a waveguide (Fig. 3b), which occupies the area around the beam axis where the polymer volume fraction, ϕ, is greater than the equilibrium value. In this millimeter sized sample, the local heating due to the absorption of light leads to an increase in temperature around the beam axis (Fig. 3c). The temperature increase in turn promotes the formation of the waveguide since the pNIPAAm gel shrinks upon heating.
Notably, the values of I/I0 (Fig. 3a) and δϕ/ϕeq (Fig. 3b) are greatest at the highest temperatures (Fig. 3c) Additionally, the rapid, spatially broad diffusion of heat (Fig. 3c) leads to a spatially more confined region of collapsed gel (Fig. 3b), which confines the propagating beam to an even narrower “column” in the material (Fig. 3c).
The images are useful in illustrating the full extent of feedback evident in the system. The shrinkage of the gel due to both the isomerization reaction and propagation of heat leads to an increase in the value of ϕ, which in turn leads to an increase (δn) in the refractive index in the material, The increase in δn alters the spatial distribution of the intensity I of the propagating beam (see eqn (10) and (11)). If δn is zero, then the light diverges. In effect, the increase in n causes the self-focusing and results in an increase of light intensity along the beam axis and a decrease in I away from the axis. In turn, the decrease in I away from the beam leads to a decrease in the extent of isomerization in this area (see Fig. 2b and c for the number fraction of SP units in the hydrophobic state as a function of I), maintaining the confinement of light along the beam axis. In this manner, the cycle of interactions enables the material itself to control this self-focusing behavior (Fig. 3a–c).
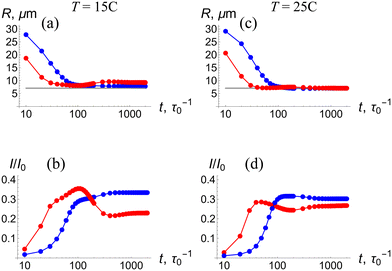
To characterize the kinetics of this process, we plot the radius R and the relative intensity I/I0 of an exiting beam as functions of time t at ambient temperatures of T = 15 °C (Fig. 4a and b) and 25 °C (Fig. 4c and d) and intensities of the incoming laser beam of I0 = 1/4Iref (blue) and Iref (red). The log-linear plots display the kinetics within a wide interval of time of 10 ≤ t ≤ 2000τ0, permitting a comparison of the early and late time behavior (the simulation time of t = 2000τ0, corresponds to about 22 min). Hereafter, the solid disks represent the results of simulations, and the straight lines connecting the symbols serve as a guide to the eye.
The temporal evolution displayed in Fig. 4 reveals that self-trapping occurs in two stages. The first stage corresponds to the formation of a waveguide around the axis of the beam propagation. Namely, at early times, the radius of the exiting beam monotonically decreases to 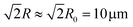 and the intensity of the beam monotonically increases. At both T = 15 °C and T = 25 °C, this first stage is shorter for the higher beam intensity of Iref (red) (see a blowup of this region in Fig. S2†) because the higher light intensity produces greater local heating in the LCST gel (see Fig. 2b). The shrinkage occurs normal to the propagation direction, yielding a value of the radius R that is comparable to the value of R0 for the incident beam.
and the intensity of the beam monotonically increases. At both T = 15 °C and T = 25 °C, this first stage is shorter for the higher beam intensity of Iref (red) (see a blowup of this region in Fig. S2†) because the higher light intensity produces greater local heating in the LCST gel (see Fig. 2b). The shrinkage occurs normal to the propagation direction, yielding a value of the radius R that is comparable to the value of R0 for the incident beam.
After this first stage of self-trapping, the radius of beam, R, remains essentially constant (Fig. 4a and c) whereas the intensity I/I0 continues to evolve for long times (Fig. 4b and d). Moreover, at I0 = Iref, the intensity of the exiting beam reaches a maximum before attaining a steady value at later times (see red lines in Fig. 4b and d). Notably, the maxima occur at approximately the same times that values of R attain minima, indicating that the maximal intensity is restricted by the decrease in the radius (similarly, for I0 = 1/4Iref, the curves begin to plateau at the corresponding minima in R). During this second stage, the waveguide evolves in the direction of beam propagation for a relatively long time. Hence, the second stage of self-trapping lasts longer than the first.
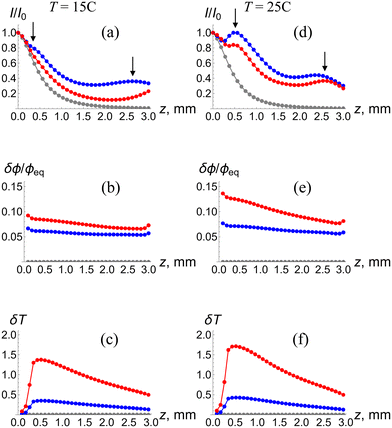
The spatial characteristics of the waveguide along the beam axis after the second stage of self-trapping are shown in Fig. 5, which displays the intensity of light I/I0, relative variation of volume fraction of the polymer in the gel δϕ/ϕeq, and local increase in temperature δT due to heating. The latter characteristics are plotted for the same moment of time as functions of Z (marked in Fig. 1) at ambient temperatures of T = 15 °C (Fig. 5a–c) and 25 °C (Fig. 5d–f) and the intensities of the incoming laser beam of I0 = 1/4Iref (blue lines) and Iref (red lines). The grey lines in Fig. 5a and d indicate the intensity of a Gaussian beam at the initial moment of time t = 0. The general decrease of I (Fig. 5) with increasing z is attributed to both the eventual beam divergence due to diffraction and the absorption of light in the medium.
At this late time (t = 2000τ0), the intensity of light as a function of z exhibits local maxima, indicated by the arrows in Fig. 5a and d. The observed maxima can be attributed to the modulation of the phase of the complex amplitude A known for self-trapped beams.6 The maxima are especially pronounced at a higher temperature T = 25 °C (Fig. 5d), where the gel is more compact and the interaction between the laser beam and SP-modified pNIPAAm gel is stronger. The observed non-monotonic temporal behavior of the intensity of the exiting beam in Fig. 4b and d is associated with the evolution of the magnitudes of the maxima and their locations along the beam axis.
The structural evolution of the waveguide is characterized by the values of δϕ/ϕeq as a function of z (Fig. 5b and e). The volume fraction of the polymer in the center of the waveguide exhibits an essentially linear decrease with increasing z (Fig. 5b and e) since the temperature increase δT is maximal where a laser beam enters the gel and then decreases almost linearly (Fig. 5c and f). The local heating and density of the waveguide are seen to increase with an increase in the intensity of the incoming beam and equilibrium density of the gel, i.e., when the interaction between light and the SP-modified pNIPAAm gel is especially strong. Specifically, at I0 = Iref and T = 25 °C, the volume fraction of the polymer in the gel exhibits an increase up to δϕ/ϕeq = 0.14 (red line in Fig. 5e) and the local temperature increases up to δT ≈ 1.75 °C (red line in Fig. 5f).
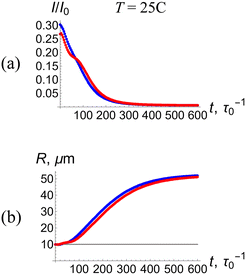
Self-trapping is a reversible phenomenon: the area of elevated polymer volume fraction forming the waveguide gradually relaxes due to the dynamic behavior of the gel when the incident laser beam is blocked and the isomerized hydrophobic SP units return to the hydrophilic state. The kinetics associated with the relaxation of the waveguide can be determined by exposing the sample to the incident Gaussian beam for short times so that no light-induced isomerization and heating take place. Fig. 6 shows the relaxation kinetics for waveguides formed by Gaussian beams of intensity I0 = 1/4Iref (blue lines) and Iref (red lines) at the ambient temperature of T = 25 °C. The intensity I/I0 of the exiting beam decreases (Fig. 6a) and its radius R increases (Fig. 6b) in the course of relaxation of the waveguide. The computer simulations show that relaxation is complete after about 600τ0 ≈ 6.5 min (Fig. 6).
In summary, a thin Gaussian beam propagating through in a SP-containing pNIPAAm gel exhibits self-focusing (self-trapping) due to the contraction of the gel and local heating, which results in the formation of a waveguide. These results allow us to analyze the interaction between two incoherent Gaussian beams propagating through such gels.
C. Interaction between two incoherent self-trapped Gaussian beams
We consider the system shown schematically in Fig. 1b. We assume that the two incoming beams are parallel to each other, have the same radius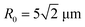 and the same intensity I0. In addition, we assume that the beams are incoherent, so that no optical interference takes place between these beams. The intensity of light in the system is I ∼ |A1|2 + |A2|2, where A1 and A2 are the complex amplitudes of the two propagating Gaussian beams. Experimentally, such a system is realized when polarizations of the two beams are orthogonal to each other.5,13 Although there is no optical interference between the beams, the self-trapped beams interact through the waveguides formed by the deformations in the polymer network due, in part, to increases in temperature with the absorption of light.13 In the case of the pNIPAAm-based hydrogel encompassing grafted SP units, the interaction between two propagating beams results in an attraction between these beams.13 We use the 3D computer simulations to uncover the effects of the beam intensity I0, ambient temperature T, and distance between beams Δx on the interaction between the two Gaussian beams.
and the same intensity I0. In addition, we assume that the beams are incoherent, so that no optical interference takes place between these beams. The intensity of light in the system is I ∼ |A1|2 + |A2|2, where A1 and A2 are the complex amplitudes of the two propagating Gaussian beams. Experimentally, such a system is realized when polarizations of the two beams are orthogonal to each other.5,13 Although there is no optical interference between the beams, the self-trapped beams interact through the waveguides formed by the deformations in the polymer network due, in part, to increases in temperature with the absorption of light.13 In the case of the pNIPAAm-based hydrogel encompassing grafted SP units, the interaction between two propagating beams results in an attraction between these beams.13 We use the 3D computer simulations to uncover the effects of the beam intensity I0, ambient temperature T, and distance between beams Δx on the interaction between the two Gaussian beams.
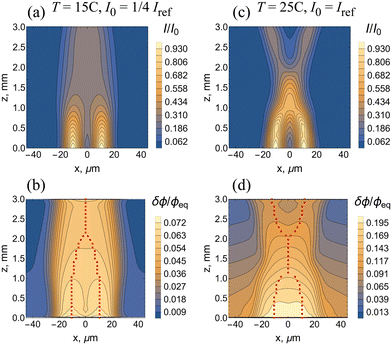
We begin by considering the case of a larger spatial separation of Δx = 6R0 between the beams; Fig. 7 shows the results of the 3D computer simulations for the weaker interaction between the beam and SP-modified gel at T = 15 °C and I0 = 1/4Iref (Fig. 7a and b), and for the stronger beam–gel interaction at T = 25 °C and I0 = Iref (Fig. 7c and d). As discussed above, the strength of interaction increases with an increase in the intensity of the beam and in the density of the gel. For the case of weaker interaction, Fig. 7a shows the two self-trapped beams, which hardly affect each other, as the spatial distribution of intensity of light I/I0 in each beam is very similar to that shown in Fig. 3a. Fig. 7b for the relative variation of the volume fraction of the polymer in the gel δϕ/ϕeq reveals that the two waveguides do not overlap. The red dots in Fig. 7b indicate the positions of local maxima of the intensity of light in the system, i.e., can be interpreted as rays in geometrical optics. As seen in Fig. 7b, the two “rays” are parallel to each other.
For the stronger interaction between the beam and gel at T = 25 °C and I0 = Iref, Fig. 7c shows that the two beams approach each other; this can be interpreted as an effective attraction between the beams. The waveguides overlap as seen in Fig. 7d and the “rays” propagating within these waveguides are curved. Note that the maximal value of δϕ/ϕeq is about 0.18 in Fig. 7d whereas it is about 0.14 in the single beam system (see Fig. 5c). The observed increase in δϕ/ϕeq is due to the greater heating in the system containing two beams, leading to a greater local shrinking of the NIPAAm network (Fig. 2b). The effective attraction between the two beams seen in Fig. 7c is the result of thermal effects (see also ref. 13).
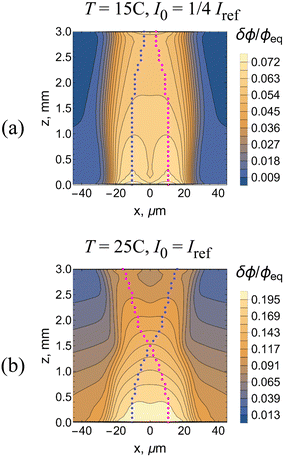
The interaction between two beams becomes stronger at a shorter separation distance as shown in Fig. 8, which presents the results of the 3D computer simulations at Δx = 3R0. At the weaker beam–gel interaction, the two beams and waveguides merge as seen in Fig. 8a and b, respectively. The system at T = 25 °C and I0 = Iref exhibits an even more drastic change in behavior. Fig. 8c shows that the spatial distribution of intensity of light I/I0 in the system has the shape of character “X”. The two beams propagate within a single waveguide of a complicated structure as evident from Fig. 8d for the variation of polymer density δϕ/ϕeq. The two “rays” merge and then separate within the waveguide (Fig. 8d).
Note that the two beams are incoherent, so the total intensity of light is a sum of two intensities, I = I1 + I2. By plotting the positions of local maxima of I1 and I2 separately, it is possible to visualize propagation of each individual beam. Fig. 9a and b are obtained by replotting Fig. 8b and d, respectively, with the magenta- and blue-colored dots presenting the “rays” associated with the two individual beams. At the weaker strength of beam–gel interaction, the individual beams merely approach each other due to the effective attraction (Fig. 9a). An increase in the strength of interaction makes the individual beams cross each other (Fig. 9b). Note that the numerical simulation for the propagation of three incoherent beams at Δx = 3R0, T = 25 °C and I0 = Iref also gives the pattern with crossing beams (see Fig. S3 in the ESI†).
Conclusions
We developed 3D computer simulations to detail how interactions between Gaussian laser beams and SP-modified responsive pNIPAAm hydrogels result in the nonlinear optical phenomena of self-trapping (self-focusing) for a single beam. Using this model, we then examined the hydrogel-mediated attraction between two propagating incoherent beams. This system displays multipart feedback: the propagation of light through the material triggers the chemo-thermal interactions that induce a mechanical shrinking of the gel. The latter shrinking in turn modifies the material properties, increasing both the local polymer volume fraction and index of refraction. The changes in material properties then affect the continued propagation of light in the gel. Hence the system encompasses changes in chemical, thermal and mechanical energies in the material. Moreover, the responsive behavior acts across length scales as a molecular conformational change (from ring open to ring closed) in the gel network which ultimately leads to the formation of a macroscopic waveguide.Our simulations revealed that the self-trapping of a single Gaussian beam proceeds in two stages characterized by quite different time scales. During the first, shorter stage the formation of a waveguide results in self-focusing manifested as a decrease of the beam radius at the exit. The simulations show that the intensity of light is not monotonic along the axis of a propagating self-trapped Gaussian beam. The intensity of light exhibits local maxima, which have been experimentally observed for self-trapped beams in other systems.6 The maxima become more pronounced with an increase in the intensity of light and ambient temperature. During the second, longer stage of the self-trapping, the light intensity displays non-monotonic behavior at the exit that is attributed to the maxima observed during the first stage.
The self-trapping of a laser beam is a reversible process. We demonstrated that after switching “off” the laser beam, the self-focusing disappears due to the relaxation of local non-uniformities of gel structure in the course of gel dynamics.
In the case of two incoherent parallel beams, the local heating leads to an effective attraction of the propagating beams. The simulations demonstrate that at a greater spatial separation between the two incident beams, an increase in the beam intensity and ambient temperature leads to partial overlap of the waveguides, which curve toward each other. In other words, the beams seem to experience an attractive interaction. As a result, the distance between the light beams at the exit is shorter than the separation between the incident beams. At a smaller separation between the incident beams, the simulations show the formation of a single waveguide that displays a complex structure at higher values of the beam intensity and ambient temperature. The spatial distribution of light intensity exhibits the shape of the letter “X”. We demonstrated that such strong effective attraction between the beams causes the beams to cross each other.
The simulations provide valuable information correlating the physicochemical changes in the gel to the behavior of the light intensity at the exit and can be valuable for interpreting experimental findings. The results of our study can be utilized for developing hydrogel-based devices for storing and processing information.7
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. B. gratefully acknowledges funding US Army Research Office under Award W911NF-17-1-0351. This research was supported in part by the University of Pittsburgh Center for Research Computing, RRID:SCR_022735, through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681. The authors thank Dr. Amos Meeks and Prof. Joanna Aizenberg for fruitful discussions.References
- M. M. Lerch, A. Grinthal and J. Aizenberg, Adv. Mater., 2020, 32, 1905554 CrossRef CAS PubMed.
- X. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Nature, 2012, 487, 214–218 CrossRef CAS PubMed.
- J. Y. Kim, Y. J. Yun, J. Jeong, C. Y. Kim, K. R. Müller and S. W. Lee, Sci. Adv., 2021, 7, eabe7432 CrossRef CAS PubMed.
- H. Zhang, H. Zeng, A. Eklund, H. Guo, A. Priimagi and O. Ikkala, Nat. Nanotechnol., 2022, 17, 1303–1310 CrossRef CAS PubMed.
- D. R. Morim, A. Meeks, A. Shastri, A. Tran, A. V. Shneidman, V. V. Yashin, F. Mahmood, A. C. Balazs, J. Aizenberg and K. Saravanamuttu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 3953–3959 CrossRef CAS PubMed.
- S. Biria, D. R. Morim, F. An Tsao, K. Saravanamuttu and I. D. Hosein, Chaos, 2017, 27, 104611 CrossRef PubMed.
- A. D. Hudson, M. R. Ponte, F. Mahmood, T. P. Ventura and K. Saravanamuttu, Nat. Commun., 2019, 10, 2310 CrossRef PubMed.
- A. Szilagyi, K. Sumaru, S. Sugiura, T. Takagi, T. Shinbo, M. Zrinyi and T. Kanamori, Chem. Mater., 2007, 19, 2730–2732 CrossRef CAS.
- R. Klajn, Chem. Soc. Rev., 2014, 43, 148–184 RSC.
- Y. R. Shen, The principles of non-linear optics, Wiley, 1984 Search PubMed.
- S. A. Akhmanov and S. Y. Nikitin, Physical optics, Clarendon Press, 1997 Search PubMed.
- O. Kuksenok and A. C. Balazs, Adv. Funct. Mater., 2013, 23, 4601–4610 CrossRef CAS.
- A. Meeks, R. Mac, S. Chathanat and J. Aizenberg, Chem. Mater., 2020, 32, 10594–10600 CrossRef CAS.
- S. Hirotsu, J. Chem. Phys., 1991, 94, 3949–3957 CrossRef CAS.
- W. L. Briggs and V. E. Henson, The DFT: An owners' manual for the discrete Fourier transform, SIAM, 1995 Search PubMed.
- V. V. Yashin and A. C. Balazs, J. Chem. Phys., 2007, 126, 124707 CrossRef PubMed.
- O. Kuksenok, V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041406 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lf00156c |
| This journal is © The Royal Society of Chemistry 2024 |