Engineering Maxwell–Wagner relaxation and interface carrier confinement in Al₂O₃/TiO₂ subnanometric laminates for high-density energy storage applications

Abstract

The Al₂O₃/TiO₂ nanolaminates (ATA NLs), with the dominant Maxwell–Wagner interfacial polarization, have been extensively explored in last decade due to their potential for new-generation energy storage applications. Here, we report the fabrication of device-grade sub-nanometric (<1 nm) ATA NLs using an optimized pulsed laser deposition technique, where the interface-confined carrier relaxation and sublayer conductivity contrast-induced Maxwell–Wagner interfacial polarization mechanism was engineered by precisely tailoring the individual Al₂O₃ and TiO₂ sublayer thickness along with the top-bottom capping layer thickness. The formation of oxygen vacancy-generated carriers in reduced titania sublayers across Al₂O₃/TiO₂ heterointerfaces and their relative response towards the applied field were responsible for both charge storage and leakage. An NL with a TiO₂ and Al₂O₃ sublayer thickness of ∼1 and 0.6 nm, respectively, sandwiched between ∼3 nm Al₂O₃ barrier layers, has demonstrated an improved capacitance density of ∼33.1 fF μm⁻² and a high cut-off frequency up to ∼0.5 MHz, along with a low dielectric loss of ∼0.032 and a reduced leakage current density of ∼3.08 × 10⁻⁷ A cm⁻² at 1 V. The calculated energy density value of ∼4.6 J cm⁻³ achieved with this optimized subnanometric Al₂O₃/TiO₂ laminate is comparable to those of state-of-the-art capacitive devices. These superior electrical properties and controllable dielectric relaxation make this laminate a promising high-k and low-loss dielectric material for next-generation nano-electronics and high-density energy storage capacitors.

---

1. Introduction

Rechargeable energy storage capacitors are vital components of electric vehicles, portable electronics and computing systems, for which a dielectric material with high dielectric constant (k) and breakdown strength (E_b) values is necessary.^1,2 In the last decade, the pursuit of an alternative high-k and low loss (tan δ) material for such storage devices, using a simple fabrication process, and cost reduction remained as main objectives of the scientific community. Recently, polymer-based composites like PVDF with BaTiO₃ and TiO₂ nanofibers displayed a high energy storage density (U) of ∼20 J cm⁻³, however with a limited working temperature regime.^3,4 On the other hand, although inorganic ceramics are capable of tolerating high working temperature, the U is <3 J cm⁻³, owing to their very low E_b.^5,6 Since dielectric thin films possess much higher E_b and display a good temperature stability relative to bulk ceramics, these are considered as the most suitable materials for energy storage applications.⁷ Although several binary oxide thin film laminates of Al₂O₃, ZrO₂, ZnO and HfO₂ have been investigated, as alternative high-k dielectric materials,^8–10 the Maxwell–Wagner (M–W) relaxation-driven high-k values in Al₂O₃/TiO₂ nanolaminates (ATA NLs) have recently opened up a channel for new generation energy storage applications.^8,9 Typically, this M–W relaxation process in interface polarization-dominated multilayer dielectric materials solely depends on the charge carrier concentration and their mobility.^8,11,12 Meanwhile, the dielectric permittivity and the interface confined carrier relaxation time (τ) are mainly decided by the relative thickness/size of conducting and resistive elements as well as the interface density.^8,9,13,14

In our previous report, we demonstrated the scope of engineering the interfacial polarization effect in pulsed laser deposited (PLD) ATA NLs by tailoring the sublayer conductivity contrast.⁹ The best dielectric performance was obtained from the NL with a total stack thickness (d) of ∼60 nm and a bilayer thickness (t_bl) of ∼1.6 nm (i.e. ∼0.8 nm sublayer thickness (t_s) for both Al₂O₃ and TiO₂ sublayers). However, further scaling down to the subnanometric level, the NLs suffered from degradation of dielectric constant, cut-off frequency (f_c) and E_b values along with a high dielectric loss (tan δ) and high leakage current density (J_leak) issues.⁹ This scaling down-assisted dielectric and electric property degradation in the subnanometric regime is also observed in laminates of different material combinations, which hinders the processing of these NLs in commercial device applications.^9,15,16 Recently, a few approaches have been made to reduce the carrier loss in NLs by inserting an insulating interfacial layer across the NL/electrode interface; however, most of them lack an explicit investigation regarding their influence on carrier dynamics and dielectric properties.^16–19 Furthermore, the role of interface defect states and their interdiffusion in the carrier relaxation and an analytical testing or evaluation of the energy storage properties have not yet been addressed. Since most of the storage applications demand a simultaneous requirement of high-k, low tan δ and reduced I_leak values,^8,9 a detailed investigation towards further improvement in areal capacitance density (capacitance (C)/area (A)) and reduction in charge carrier loss in these ATA NL superlattice structures will be highly beneficial.

In relation to this scientific goal, here we report the deposition and characterization of device grade ATA NLs using optimized PLD growth conditions, wherein the interface confined carrier relaxation and M–W interfacial polarization process in subnanometric layers have been tailored by precisely controlling the sublayer and capping layer thicknesses. The experimental protocol reported here is designed to tailor the M–W relaxation assisted dielectric properties and subsequently to improve the storage performance of ATA NL-based nanocapacitors, by tailoring the interface confined carrier relaxation time (τ) and sublayer conductivity contrast. As an important part of the research, we have investigated the effect of Al₂O₃ top-bottom barrier layer thickness on carrier loss and leakage properties. In this work, Al₂O₃ layers of different thicknesses varying between 1 and 5 nm were inserted across both top and bottom electrode/ATA-NL interfaces, to minimize carrier losses and leakage while maintaining a high-k value up to a higher f_c limit. The optimized ATA NL-based capacitors with a 3 nm Al₂O₃ capping layer have displayed a superior C/A of ∼33.2 fF μm⁻², low loss and reduced J_leak of ∼3.08 × 10⁻⁷ A cm⁻² at 1 V along with a higher breakdown voltage of ∼0.65 MV cm⁻¹. The investigation protocols, in this work, adopted for engineering the carrier relaxation and transport properties across Al₂O₃/TiO₂ interfaces can be implemented for other binary metal oxide combinations in NL structures and the obtained results may open up new avenues for next-generation nanoelectronics and energy storage capacitors.

2. Experimental details

2.1 Synthesis of ATA NLs and device fabrication

A KrF excimer laser-based optimized PLD system was implemented to fabricate Al₂O₃/TiO₂ nanolaminates (ATA NLs) with an alternating sublayer thickness (t_s) varying between 0.4 to 1.2 nm, while maintaining a fixed NL stack (d) and bilayer thickness (t_bl) of 60 nm and ∼1.6 nm, respectively. The substrate temperature, oxygen partial pressure, substrate–target separation and pulse repetition rate were maintained at ∼300 °C, 0.01 mbar, 4.5 cm and 5 Hz, respectively, during the growth of these NLs. Specifically, the laser fluence was maintained close to the ablation threshold (i.e. ∼0.5 J cm⁻²) to reduce the interface intermixing effcet in NLs, which may likely arise from the bombardment of incoming energetic ablated particles. The inference of these optimized growth parameters for these NLs was taken from our previous work.⁹ The NLs were deposited on sapphire, n-Si (100), and TiN film coated Si substrates with surface r.m.s roughness values of ∼0.5 nm and ∼1.1 nm, respectively.

For convenience, the NL with an Al₂O₃ sublayer thickness (t_A) and TiO₂ sublayer thickness (t_T) of ∼0.6 nm and 1 nm, respectively, is labelled 0.6A-1T-0.6A NL and the NLs capped with Al₂O₃ top and bottom barrier layers of 1, 3, and 5 nm thicknesses are denoted as 1A/(0.6A-1T-0.6A)/1A, 3A/(0.6A-1T-0.6A)/3A and 5A/(0.6A-1T-0.6A)/5A NL, respectively. The dielectric and electrical characterization of the as-grown NLs was carried out in a metal–insulator–metal (MIM)-based capacitor (MIMCAP) configuration, where the RF-magnetron sputtered top-bottom conducting TiN (∼300 μΩ cm) circular electrodes of ∼50 nm thickness and ∼200 μm diameter were defined using a stainless-steel shadow mask. For ∼60 nm thick NL-based MIMCAPs, the empty cell (air) capacitance (C₀ = ε₀A/d) becomes ∼5.6 pF.

2.2 Characterization methods

The interface quality of these NLs was examined using Cu-Kα (8.05 keV) radiation-based X-ray reflectivity (XRR) measurements. To obtain the thickness (d), electron density (ρ_el) and interfacial roughness (σ) of different sublayers in ATA NLs, the measured XRR curves are successfully modelled and fitted using MATLAB program-based “REFLEX” software.⁸ The long-range thickness uniformity of individual sublayers in the NL was revealed by using a cross-sectional transmission electron microscopy (TEM) system (Philips CM 200 TEM) operated at 200 keV. To investigate the change in the band gap and any quantum confinement effect in the as-grown NLs, the UV-visible transmission spectroscopy measurements of the NLs were carried out using a spectrophotometer (make: Lab-India) in the wavelength range of 600 nm to 190 nm.

To find out the type of defect states and their concentration in these NLs, X-ray photoemission spectroscopy (XPS) measurements were performed using an Al Kα source with ∼1486 eV photon energy and 0.5 eV energy resolution. In order to verify the results from XPS measurements, the valence band resonant photoemission spectroscopy (VB-RPES) measurements of a representative 0.8A-0.8T NL were performed at the Beamline-10 (BL-10) of Indus-2, RRCAT, India. The beamline (BL-10) details can be found elsewhere.²⁰ Prior to measurements, the samples were electrically grounded using silver contacts and Ar⁺ ion sputtering at 1.5 kV and 6.0 mA for ∼1 min was performed to clean the sample surface. A hemispherical electron energy analyser SPECS Phoibos 150, with a typical energy resolution of 40 meV at 90 eV photon energy, was used to record the high-resolution photoemission spectra. The VB spectra were collected in the angle integrated mode and normalized to the mirror current recorded during the measurement. The binding energy calibration was performed with the Ag 3d lines and Fermi edge using the standard procedure.^20,21 The VB-RPES spectra were recorded across the Ti 2p-3d and Al 2p-3s transition i.e. at ∼458.5 eV and 74.3 eV photon excitation energies, respectively. The typical energy resolution around the Ti 2p-3d resonance is 200 meV and around the Al 2p-3s resonance is 35 meV. All the measurements were performed at room temperature and in an ultrahigh vacuum of 7 × 10⁻¹¹ mbar. The measured XPS spectra were deconvoluted using XPS PeakFit 4.11 software, whereas the inelastic background of the core levels was subtracted using the Shirley method.²²

The frequency-dependent dielectric measurements of NL-based MIMCAPs were performed in the range from 10 to 10⁶ Hz using an impedance analyzer (Solartron make: SI-1206) with 100 mV applied AC bias. To understand the influence of t_s on the M–W interfacial polarization mechanism and the carrier relaxation time, temperature dependent dielectric measurements were carried out in the range of 303–363 K, at an interval of 10 K and with an accuracy of ±1 K. The temperature was controlled using an Angstrom Sun PID controlled heater (Ang-A1205) combined with a chiller. The current–voltage measurements of these MIMCAPs were carried out using a source measurement unit (Keithley 2636B).

3. Results and discussion

3.1 Role of Al₂O₃ and TiO₂ sublayer thickness

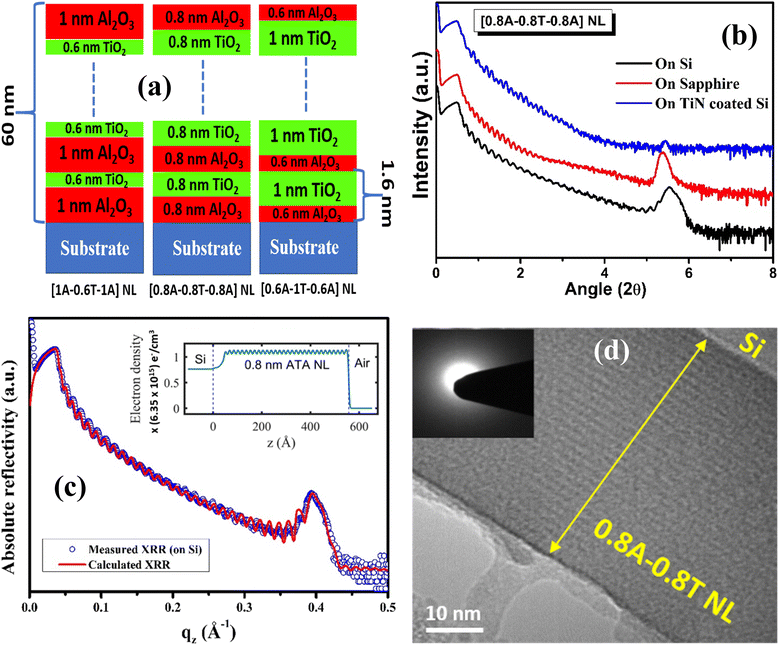
We have fabricated five different ATA NLs with the TiO₂ and Al₂O₃ sublayer thicknesses varying between ∼1.2 and 0.4 nm, whereas the ‘d’ and ‘t_bl’ are kept fixed at ∼60 nm and 1.6 nm, respectively. These 5 ATA NLs are labelled [1.2A-0.4T-1.2A] NL, [1A-0.6T-1A] NL, [0.8A-0.8T-0.8A] NL, [0.6A-1T-0.6A] NL, and [0.4A-1.2T-0.4A] NL, wherein the denotations, e.g. [1A-0.6T-1A] NL, represent an ATA NL with a t_A of ∼1 nm and t_T of ∼0.6 nm, respectively. The schematic in Fig. 1(a) illustrates three representative NLs with an increasing order of TiO₂ content (from left to right), i.e. [1A-0.6T-1A] NL, [0.8A-0.8T-0.8A] NL, and [0.6A-1T-0.6A] NL.

Fig. 1 a) Schematic of three representative NLs labelled 1A-0.6T-1A NL, 0.8A-0.8T-0.8A NL, and 0.6A-1T-0.6A NL, where the number of interfaces, total stack thickness, and bilayer thicknesses were kept constant at 38, 60 nm, and 1.6 nm, respectively. (b) Measured XRR profiles, with Y-offsets, of a representative ATA NL with 0.8 nm sublayer thickness deposited on TiN coated Si, sapphire, and Si substrates. (c) Fitted XRR spectra of the representative 0.8T-0.8A NL deposited on TiN coated Si and the inset displays the corresponding EDP. (d) Cross-sectional TEM image of [0.8A-0.8T-0.8A] NL deposited on Si. The selected area electron diffraction pattern is depicted in the inset.

To verify the artificial periodic structure in the as-grown ATA NLs, XRR measurements of a representative ATA NL with 0.8 nm sublayer thickness grown on TiN coated Si, sapphire and Si substrates are carried out and the measured XRR profiles are depicted in Fig. 1(b) with Y-offsets. The main purpose of growing NLs on Si and sapphire was to investigate their interfacial and optical properties, whereas the growth of NLs on the TiN coated Si substrate was intended to construct the MIM capacitor structure for dielectric and electrical characterization. The presence of Bragg peaks in the XRR profiles is clearly indicating the maintained distinct layer feature in [0.8A-0.8T-0.8A] NL grown on all three substrates. The relative reduction in Bragg peak intensity observed for the NL grown on TiN coated Si, as compared to the bare Si and sapphire substrate, indicates slightly higher interface intermixing, which is likely due to the propagation of TiN layer roughness into the subsequent sublayers of the NL.⁸ Furthermore, the Bragg peak intensity drastically reduced for lower t_s values, which indicates higher interface roughness and enhanced interface intermixing. The observed Bragg peak broadness indicates a slight aperiodicity in the bottom and topmost bilayer thickness of the NL, likely due to slight non uniformities across these substrates arising from the narrow angular distribution profile of the PLD plasma plume. To calculate the measured XRR profiles, a small aperiodicity in t_s values and a Si-SiO₂-(Al₂O₃-TiO₂)₃₀-Al₂O₃ based multilayer model, mimicking the NL structure, are implemented. An excellent match between the measured and calculated XRR profiles for [0.8A-0.8T-0.8A] NL can be observed in Fig. 1(c). The alternating alumina and titania sublayer growth in the NL structure can be confirmed from the electron density profile (EDP), illustrated in the inset of Fig. 1(c). The best fit results including the calculated aperiodicity, layer thickness, densities and interface width for 0.8A-0.8T NL grown on Si and TiN coated Si obtained from XRR curve fitting are summarized in Table S1 of the ESI.†

Cross-sectional transmission electron microscopy (TEM) measurement of a representative 0.8A-0.8T NL, grown on Si substrates, is carried out to demonstrate the controllability of optimized PLD parameters in growing subnanometric layers and to validate the multilayer periodicity in the as-grown NLs. The distinctive layer structure, shown in Fig. 1(d), confirms the long-range sublayer thickness uniformity and distinct interfaces even in the subnanometric regime. From the intensity distribution profiles, as depicted in Fig. S1(b) of the ESI,† the measured t_s values for Al₂O₃ and TiO₂ sublayers are measured to be ∼0.79 and 0.81 nm, respectively, which indicate the control in the deposition of subnanometric layers using the optimized PLD technique. The absence of any discernable crystalline phases in the selected area electron diffraction (SAED) pattern of the 0.8A-0.8T NL, shown in the inset of Fig. 1(d), confirms the amorphous nature of the deposited subnanometric layers. The finite interface interdiffusion observed from the TEM images also corroborates with the XRR results.

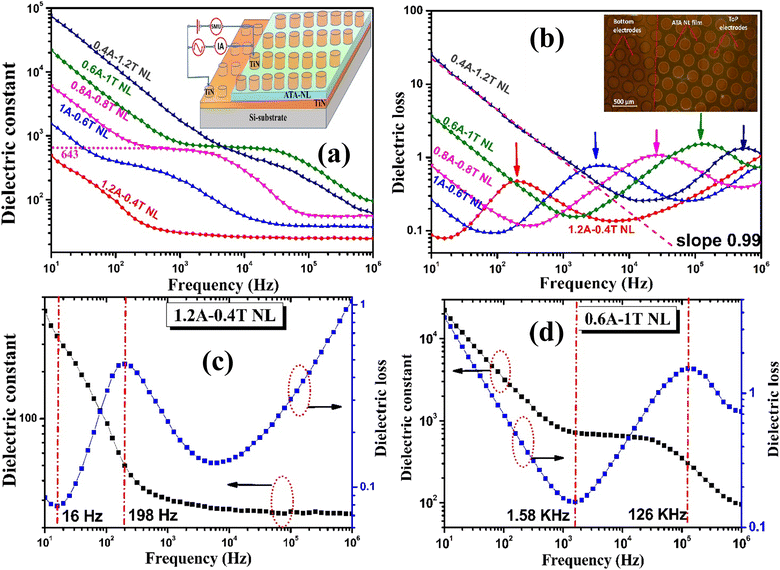
The impedance spectroscopy measurements of the five as-grown TiN/ATA-NL/TiN-based MIMCAPs are carried out to examine the effect of variation in t_T and t_A on the interfacial and dielectric properties. The schematic of one of the MIMCAPs is depicted in the inset of Fig. 2(a), and the top view of an actual device structure is shown in the inset of Fig. 2(b). It is relevant to discuss a few key observations from the frequency dispersed ε_r and tan δ spectra, as depicted in Fig. 2(a) and (b), respectively. From a cursory overview of frequency dispersed ε_r and tan δ spectra, as depicted in Fig. 2(a) and (b), respectively, the ε_r plateau, tan δ valley, and the f_c values are found to be directly proportional to t_T and inversely proportional to t_A values up to a certain sublayer thickness limit. The ε_r plateau and tan δ values demonstrate a monotonous increment from ∼260 to 720 and ∼0.31 to 0.7 with an increase in t_T from 0.4 to 1 nm and a simultaneous decrease in t_A from 1 to 0.4 nm, respectively. Since the total number of interfaces of these ATA NLs is kept constant at ∼76, the variation in dielectric contributions is independent of interface density and is solely decided by the change in sublayer conductivity contrast.

Fig. 2 (a) and (b) The measured frequency dispersed ε_r and tan δ profiles for different ATA NLs with t_T/t_A varying between 0.33 and 3. The corresponding insets show the schematic of the TiN/ATA NL/TiN based MIM capacitor configuration and the actual device image with TiN top-bottom electrodes. (c) and (d) The combined ε_r and tan δ profiles for [1.2A-0.4T-1.2A] NL and [0.6A-1T-0.6A] NL, respectively. The area confined by vertical red dashed lines, where the ε_r is increasing and tan δ is decreasing, indicates the working frequency regime for ATA NL-based energy storage capacitors.

Furthermore, with the increase in TiO₂ content, the M–W interfacial carrier relaxation frequency peak positions in frequency dispersed tan δ plots are found to shift towards the high frequency side, as shown by arrow marks in Fig. 2(b). This clearly indicates an improvement in the semiconducting nature of titania sublayers with the increase in TiO₂ content up to ∼63% in a given bilayer, which is possibly due to the increase in the Ti³⁺ and O_v defect generated carrier concentration.^8,13 This observation concludes that the concentration of charge carriers in the ATA NLs is increasing with t_T, which is increasing the sublayer conductivity contrast assisted M–W interfacial polarization and resulting monotonous increment in ε_r values. On the other hand, due to a fixed t_bl of ∼1.6 nm, the Al₂O₃ barrier layers are simultaneously getting thinner with an increase in TiO₂ content, hence resulting in an increase in the tan δ values. We can also observe that with an increase in t_T up to 1 nm, the cut-off frequency (f_c) for high k values of 0.6A-1T-0.6A NL extends up to ∼3 × 10⁵ Hz. With an increase in TiO₂/Al₂O₃ content up to ∼66.3%, the increase and decrease in f_c and τ values, respectively, can be attributed to the increase in carrier concentration of TiO₂ layers. Meanwhile, further reduction in t_T down to ∼0.4 nm leads to trend reversal in f_c values, possibly due to the enhanced interface intermixing of sublayers. With an increase in t_T from ∼0.4 to 1 nm, there is an improvement in the working frequency domain from 16 Hz to 198 Hz in 1.2A-0.4 T NL and 1.58 KHz to 126 KHz in 0.6A-1T NL, as depicted in Fig. 2(c) and (d). The above observations strongly support that the ε_r and f_c values of these ATA NLs are mainly dependent on the amount of charge carriers in the oxygen deficient TiO₂ (TiO_2−δ) sublayers. Meanwhile, the tan δ and J_leak values rely on the insulating nature of the Al₂O₃ barrier layers. Furthermore, at room temperature, the M–W relaxation process and hence the dielectric properties of these PLD-grown ATA NLs can be tailored by only varying individual sublayer thicknesses. Since the dielectric measurements for all the NL samples were carried out at room temperature, the change in τ and f_c is definitely not a thermally induced effect.

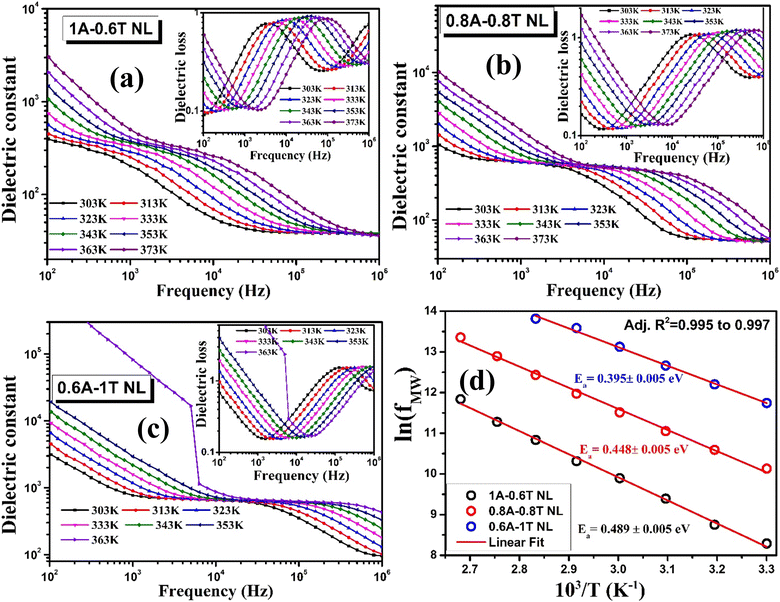
To investigate the effect of the relative variation in t_A and t_T on the carrier relaxation and transport mechanism in the aforesaid NLs, the temperature dependent dielectric measurements are carried out in a temperature range from ∼303 to 373 K. The frequency dispersed ε_r and tan δ profiles of a few representative NLs, labelled 1A-0.6T NL, 0.8A-0.8T NL, 0.6A-1T NL, are depicted in Fig. 3(a)–(c) and in their corresponding insets, respectively. With an increase in temperature, the shift in the ε_r profile and the relaxation peaks towards the high frequency side indicates the thermally activated nature of this M–W relaxation process. The two sets of relaxation peaks observed in the tan δ vs. f plots support the M–W relaxation in these NLs and the decrease in τ for interface confined carriers at elevated temperature is owing to the increase in charge carrier mobility. With an increase in temperature, the tan δ values of 1A-0.6T NL initially increased and saturated at ∼353 K, whereas the trend reversed with further increase in temperature to 373 K. A higher Al interdiffusion into the TiO₂ sublayer is expected, with an increase in temperature, owing to the smaller Al cation size as compared to Ti.^3,4,9 Additionally, an abrupt increase in the measured ε_r and tan δ values for 0.6A-1T NL is observed around 363 K, as shown in Fig. 3(c), and is likely owing to the thermal soft breakdown of thinner Al₂O₃ barrier layers (∼0.6 nm).⁹ This observation further indicates that decreasing the t_A below 0.6 nm severely degrades the charge holding capability, which subsequently deteriorates the M–W relaxation assisted dielectric properties. The reciprocal temperature variation of the M–W relaxation peak positions is linearly fitted using the Arrhenius equation, f(T) = f₀ exp(−E_a/K_βT), as shown in Fig. 3(d), and the activation energies (E_a) for interfacial carrier relaxation is calculated to be in the range from ∼0.395 to 0.489 eV. This E_a values are closely matching with the literature reported activation energy values of oxygen vacancy (OV) defect states in TiO₂, and it can be assigned responsible for M–W relaxation mechanism in ATA NLs.⁸

Fig. 3 Frequency dispersed ε_r and tan δ spectra for (a) 1A-0.6T NL, (b) 0.8A-0.8T NL and (c) 0.6A-1T NL measured in a temperature range from 303 K to 373 K are depicted in the main figure and inset, respectively. (d) Arrhenius linear curve fitting for M–W relaxation peak position variation with experimental temperature with adj. R² values close to unity.

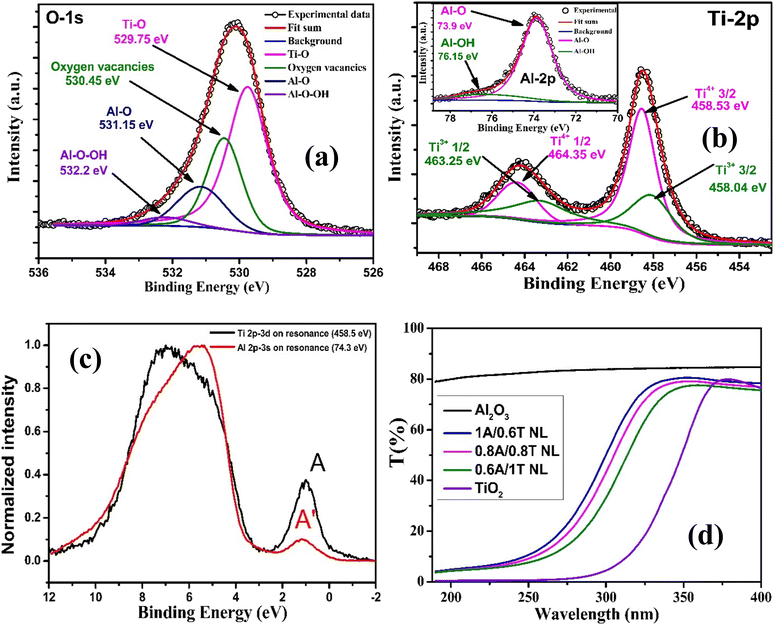
The X-ray photoelectron spectroscopy (XPS) measurement of a representative 0.8A-0.8T NL was carried out using Al k_α (∼1486 eV) photon energy, to verify the role of OV related defect states in the origin of M–W relaxation induced enhanced dielectric properties in these ATA NLs. O 1s core level spectra are deconvoluted into four peaks, as depicted in Fig. 4(a), where the 1st and 3rd peaks around 529.7 ± 0.1 eV and 531.15 ± 0.1 are assigned to the lattice oxygens in Ti–O and Al–O bonds, respectively. The shoulder peaks observed around 530.45 ± 0.1 and 532.2 ± 0.1 eV are assigned to OV related defect states in TiO₂ sublayers and surface adsorbed oxygen in the form of C–O & O–H bonds on the top Al₂O₃ sublayer (labelled as Al–O–OH), respectively.⁸ The recorded Ti 2p and Al 2p core level scans and their deconvoluted spectra are depicted in Fig. 4(b) and the inset, respectively. The Ti core level peak is deconvoluted into two sets of spin orbit splitting Ti 2p_3/2 and Ti 2p_1/2 peaks, corresponding to Ti⁴⁺ and Ti³⁺ states, with a peak separation of ∼5.9 and ∼5.78 eV, respectively. The presence of both Ti⁴⁺ and Ti³⁺ states in the Ti 2p core level deconvoluted spectra confirms the OV induced reduced titania (Ti₂O₃) phase, in the TiO₂ sublayers of 0.8A-0.8T NL.¹³ These defect states, as a source of high concentration unpaired electrons, are known to improve the conductivity of thin TiO₂ sublayers making them n-type semiconducting in nature. The deconvoluted spectra of high-resolution Al 2p core levels and the corresponding binding energy (BE) positions, shown in the inset of Fig. 4(b), clearly indicate the absence of any Al related defect states except an Al–O bonding and Al–OH related surface contamination contribution.⁸

Fig. 4 The measured and deconvoluted (a) O 1s, (b) Ti 2p, (inset) Al 2p core levels XPS spectra of 0.8A-0.8T NL, (c) the recorded Al 2p-3s and Ti 2p-3d VB-RPES spectra of 0.8A-0.8T NL at the resonance photon excitation energy of ∼458.5 eV and 74.3 eV respectively. (d) Transmission vs. wavelength spectra of ∼60 nm TiO₂, Al₂O₃ film and for three ∼60 nm thick representative NLs, i.e. 1A/0.6T, 0.8A/0.8T and 0.6A/1T NL.

Furthermore, VB-RPES measurements of a representative 0.8A-0.8T NL are performed to identify the source of defect states through a detailed understanding of the sublayer electronic structure and the recorded spectra are shown in Fig. 4(c). In the Ti 2p to 3d VB-RPES spectra, ∼1 eV below the Fermi level, the appearance of the in-gap-state (IGS) feature ‘A’ clearly signifies the presence of OV defect states as trap centers for available charge carriers.^23–25 The appearance of IGS A′ in the Al 2p-3s RPES spectra and its close matching of the BE positions with those of feature A indicate the Al 3s and Ti 3d states' hybridization effect due to finite sublayer interface intermixing in the 0.8A-0.8T NL, as verified from XRR and cross-sectional TEM measurements.²⁶

Additionally, one more important aspect can be observed from Fig. 3(d), i.e. the increment in E_a values from ∼0.395 to 0.489 eV with an increase in Al₂O₃ barrier layer thickness from 0.6 to 1 nm and decrease in TiO₂ quantum well (QW) thickness from 1 to 0.6 nm. This increasing trend in E_a with an increase in t_A can be explained by considering NLs as multiple QW structures and a strong quantum confinement effect in this 1A-0.6T NL.²⁷ To verify this effect, UV-VIS transmission spectroscopy measurements of the aforesaid three representative NLs, grown on sapphire substrates, were carried out and are depicted in Fig. 4(b). With an increase in t_A from 0.6 to 1 nm and a simultaneous decrement in the t_T value from 1 to 0.6 nm, a blue shift in the measured T% vs. wavelength spectra can be observed. This confirms an improvement in the carrier confinement effect with an increase in t_A and decrease in t_T, which further supports the decrement in carrier loss observed from frequency dispersed tan δ profiles, shown in Fig. 2(b).

3.2 Role of top-bottom Al₂O₃ barrier layer thickness

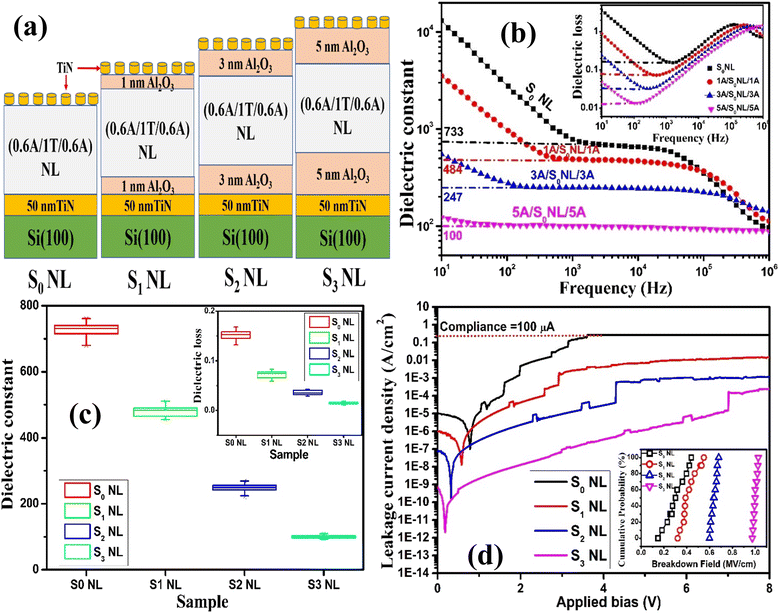
Albeit, the observed ε_r (∼732) and f_c (∼126 KHz) values for the 0.6A-1T NL (S₀ NL) are quite significant in magnitude; high tan δ and J_leak values are observed owing to the enhanced semiconducting nature of titania layers and thinner Al₂O₃ insulating layers. However, the improvement in charge carrier loss and leakage current, without much interference with the M–W relaxation and cut-off frequency, can be achieved by introducing high band gap barrier layers across the NL/electrode interfaces and high work function electrodes.^13,28 By taking inference from this work, the S₀ NL is sandwiched between 1, 3, and 5 nm top-bottom Al₂O₃ barrier layers and the resulting NLs are labelled S₁ NL, S₂ NL and S₃ NL, respectively. The schematic of these NLs is depicted in Fig. 5(a). The influence of top-bottom Al₂O₃ interfacial barrier layer thickness (t_Al2O3) on the frequency dispersed ε_r and tan δ spectra of the S₀, S₁, S₂ and S₃ NLs is depicted in Fig. 5(b) and its inset, respectively. It is important to note that with the increase in t_Al2O3 from 1 to 5 nm, the low frequency ε_r and tan δ values decreased from ∼733 to ∼100 and ∼0.17 to 0.015, respectively. Introducing these thicker low permittivity (ε_r ∼ 11) Al₂O₃ barrier layers in series with the NL decreases the apparent stack permittivity and limits the total stack capacitance. Meanwhile, the high band gap (E_g > 7 eV) and insulating nature of alumina are significantly reducing the dc conductivity of charge carriers from the NLs to electrodes, hence reducing the tan δ values. Additionally, by increasing t_Al2O3 from 1 to 5 nm, there was a finite increment in the f_c values from ∼126 KHz to 1 MHz is observed. This is possibly owing to the improvement in titania sublayer conductivity from the controlled elemental interface interdiffusion and also due to the smooth interface geometry of the NL matrix provided by the sufficiently thick smooth bottom amorphous alumina platform.

Fig. 5 (a) Schematic of the ATA NL with the Al₂O₃ capping layer thickness varying between 1 and 5 nm. The NLs are denoted as S₀ NL, S₁ NL, S₂ NL, and S₃ NL. (b) The measured frequency dispersed dielectric constant and (in the inset) the tan δ spectra for the curves of S₀, S₁, S₂, and S₃ NLs. (c) Box chart representation of the low frequency dielectric constant and tan δ distribution of 10 random devices from each of the aforementioned NL stack. (d) The J_leakvs. applied bias characteristic curves for 0.8A-0.8T NL; the inset shows the cumulative probability of the electrical breakdown field of the S₀, S₁, S₂, S₃ NL-based MIM structures.

To demonstrate the reliability of the measured dielectric properties, the ε_r and tan δ values of 12 MIM devices from each of the S₀, S₁, S₂, S₃ NLs are depicted in the form of box chart representation, in Fig. 5(c) and the inset. A relatively broad distribution of ε_r and tan δ values for the S₀ NL was found with the median value of ∼730; however, a decrease in this distribution profile with an increase in t_Al2O3 indicates an improvement in the device stability. Furthermore, the distributions in the ε_r and tan δ values of ∼68%, 75%, 86%, and 95% of the tested devices of the S₀, S₁, S₂, and S₃ NLs, respectively, are found within the upper and lower quartile profiles of the box chart, which clearly suggests a consistent improvement in the stability of the device performance parameters with the increase in t_Al2O3. This might be owing to the better flat and amorphous platform provided by thicker alumina layers across top-bottom electrodes, which restricts the propagation of bottom electrode roughness into the subsequent interfaces of the NL.

To investigate the role of t_Al2O3 in the conduction mechanism as well as to calculate the bias dependent J_leak values, current–voltage (I–V) measurements were performed on the S₀, S₁, S₂ and S₃ NL-based MIMCAPs in the voltage range from 0 to 8 V. From the I–V profiles, as depicted in Fig. 5(d), the J_leak values for all the NLs at a low applied bias (V_app) decreased with the increase in V_app, reaching a minimum. Non-zero crossing current features appeared due to the M–W interfacial polarization induced built-in potential or induced back emf in these NL structures, which opposed the applied field and resulted in a reduction in charge carrier leakage across the interfaces.^8,29 The electrons can quantum mechanically tunnel through ultrathin alumina barrier layers in these NLs and strongly couple with the neighboring quantum wells to form delocalized minibands, which help in vertical carrier transport and increase the tunneling current through the NLs.³⁰ With the increase in V_app, the J_leak values increased exponentially passing through current kinks/spikes, which are assigned to negative differential resistance (NDR) features in these ATA NL-based multiple QW structures.^8,31 Further increase in V_app promotes electron tunneling through the triangular potential barriers, resulting in an exponential increase in J_leak, as shown in Fig. 5(d),³² which supports the Fowler–Nordheim tunneling (FNT) transport in these NLs.³³ Hence, the dominant leakage current mechanism and the observed NDR feature can be explained by considering the low bias trap-assisted and higher bias triangle barrier quantum mechanical tunneling mechanism through these subnanometric Al₂O₃ barrier layers.^28,30

For the S₀ NL, the higher J_leak and higher number of increasing current steps along with the diminished NDR feature were possibly owing to the soft breakdown of ultrathin (∼0.6 nm) barrier layers at low V_app.²⁷ By introducing 1 to 5 nm thick Al₂O₃ barrier layers across the NL/electrode interface, the J_leak reduced drastically from 1.18 × 10⁻⁵ to 2.11 × 10⁻⁹ @ 1 V. Considering the rapid current surge steps in each NL as the soft breakdown of Al₂O₃ barrier layers, the cumulative probability distributions of the electrical soft breakdown field strengths (E_break) of the 12 MIM devices from the S₀, S₁, S₂ and S₃ NL stacks are calculated and are displayed in the inset of Fig. 5(d). Although the distribution in E_break is relatively broad for the S₀ NL, an improvement in the average distribution of the E_break values and also in the median values (from ∼0.3 MV cm⁻¹ to 1.01 MV cm⁻¹) can be observed with the increase in t_Al2O3 from 1 to 5 nm. This improvement in the magnitude and distribution of E_break indicates an increase in the insulating properties and stability of the performance parameters of NLs.¹³ The overall fluctuation in the measured dielectric and electrical parameters observed from device to device in a given NL can be attributed to the thickness non-uniformity issues in PLD-grown thin films and/or the randomness in manually applied probe tip pressure.

In Table S1 of the ESI,† the important fundamental and derived dielectric performance parameters of our S₀, S₁, S₂ and S₃ NL stack-based MIM capacitors are compared with the literature reports on other metal oxide NL-based devices produced through different fabrication technologies and having different electrodes, device areas, layer thicknesses, etc. The device performance parameters for our optimised NL stacks seem to be comparable and/or superior, among previous reports, even with a relatively larger electrode area of ∼3.9 × 10⁴ μm². Although the series capacitances of the low dielectric constant Al₂O₃ barrier layers impose an adverse effect on the overall high dielectric constant, it is highly beneficial for the reduction in carrier loss and leakage current in these NLs. Hence, to maintain a sizeable M–W effect along with a simultaneous reduction of the tan δ and J_leak values in ATA NLs, an optimized t_Al2O3 is needed before integrating these NLs into the final electronic circuits. The International Technology Roadmap of Semiconductors (ITRS)-2023 has set required device performance parameters for energy storage applications of MIM capacitors, such as a C/A > 13 fF um⁻², J_leak < 1 × 10⁻⁸ A cm⁻², equivalent oxide thickness (EOT) <2 nm, etc.^8,34 Considering these requirements, the observed high C/A (∼33.2 fF μm⁻²), low tan δ (∼0.032), low EOT (∼1.04 nm), and reduced J_leak (∼3.08 × 10⁻⁷ A cm⁻² at 1 V bias) values for the S₂ NL capacitor make it highly suitable for high-density energy storage and advanced MIM capacitor applications. The volumetric energy density [U = (1/2) (C/(Ad)) (E_b)²] of this optimized NL structure (S₂ NL) is computed to compare with the other dielectric thin film capacitors, documented in the literature. Using the values of C/A = ∼33.2 fF μm⁻², d = 60 nm, and E_b = 0.65 MV cm⁻¹, the energy density (U) value is calculated to be ∼4.6 J cm⁻³, which is on par with those reported for commercial dielectric thin film capacitors (1–2 J cm⁻³),³⁵ lead lanthanum zirconated titanate (PLZT) dielectrics (<3 J cm⁻³),³⁶ and nanocomposite multilayer capacitors (<2.5 J cm⁻³).³⁷ The calculated U for our optimized ATA NL is not only superior to pure TiO₂ (0.76 J cm⁻³) and Al₂O₃/TiO₂ nanocomposites, (1.05 J cm⁻³),³⁸ but also comparable to the volume energy density values reported for atomic layer deposited Al₂O₃/TiO₂ NLs.³⁹ The further increment in the calculated energy density values of our optimized NL structure can be achieved through improving the C/A and the E_b values, by increasing the NL interface density and employing high-work function electrodes like Au or Pt, respectively. Device performance optimization in this direction is ongoing.

Conclusions

In conclusion, the device grade Al₂O₃/TiO₂ subnanometric laminates are fabricated using an optimized pulsed laser deposition technique, where the interface confined carrier relaxation and M–W interface polarization mechanism was engineered by precisely controlling the sublayer and capping barrier layer thickness. X-ray reflectivity and transmission electron microscopy measurements revealed the NL growth in an artificial periodic geometry with well-defined sublayers and distinct interfaces, even in the subnanometric regime. The carrier relaxation time and the sublayer conductivity contrast were tailored by varying the individual Al₂O₃ and TiO₂ sublayer thickness between ∼1.2 and 0.4 nm, while maintaining a fixed number of interfaces (∼76) and bilayer thickness (∼1.6 nm). The formation of oxygen vacancy generated carriers in reduced titania sublayers and their relative response towards applied AC and DC bias fields were responsible for the charge storage and leakage probability in these NL structures. The NL with a TiO₂ and Al₂O₃ sublayer thickness of ∼1 and 0.6 nm, respectively, has demonstrated a high dielectric constant of ∼770 up to ∼2 × 10⁵ Hz cut-off frequency, although with a relatively higher dielectric loss and leakage current density. By introducing Al₂O₃ barrier layers with thicknesses from 1 to 5 nm, across the NL/electrode interfaces, the leakage paths are substantially reduced, resulting in significant improvement in the dielectric loss (reduced from 0.1 to 0.01), leakage current density (reduced from ∼1.1×10⁻⁵ to 2.1 × 10⁻⁹ A cm⁻² at 1 V applied bias), and breakdown field (increase from 0.26 to 1.01 MV cm⁻¹), albeit with an adverse effect on the dielectric constant. Notably, the optimized ATA NL with a ∼3 nm Al₂O₃ interfacial barrier layer has demonstrated a high dielectric constant (∼250 up to 0.5 MHz) resulting in a high capacitance density of 33.13 fF μm⁻² and a low equivalent oxide thickness of ∼1.04 nm, along with a low dielectric loss (∼0.032), a reduced leakage current density of ∼3.08 × 10⁻⁷ A cm⁻² at 1 V and a higher breakdown field of ∼0.65 MV cm⁻¹. The calculated energy density value of ∼4.6 J cm⁻³ achieved with this optimized pulsed laser deposition-processed Al₂O₃/TiO₂ subnanometric laminate is akin to those of state-of-the-art capacitive devices. These superior electrical properties and controllable dielectric relaxation make this ATA NL a promising dielectric material for next generation energy storage applications.

Data availability

The data supporting this article have been included in the ESI.†

Author contributions

All authors have contributed equally in writing the manuscript and have given approval to the final version of the manuscript. Partha Sarathi Padhi: conceptualization, methodology, formal analysis, data curation, investigation, and writing – original draft. Sanjay Kumar Rai: methodology, formal analysis, and writing—review and editing. R. S. Ajimsha: methodology and writing—review and editing. Pankaj Misra: visualization, supervision, project administration, resources, and writing—review and editing.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

One of the authors (PSP) acknowledges the Homi Bhabha National Institute, Mumbai and the Raja Ramanna Centre for Advanced Technology, Indore for financial support. The authors wish to thank Tapas Ganguli, A. K. Srivastava and H. Srivastava from the Accelerator Physics Synchrotron Utilization Division, RRCAT, and A. K Das and V. K. Sahu of the Oxide Nano Electronics Laboratory, Laser Materials Processing Division, RRCAT, for extending the experimental facilities. Dr. Soma Banik, Ms. Kritika Vijay and Mr. S. Paul of Beamline-10, Indus-2, RRCAT are thanked for their assistance in RPES measurements. The authors are also thankful to Mr. Rakesh Kaul, Head, Laser Materials Processing Division and Associate Director, Materials Science and Advanced Technology Group, RRCAT, Indore for his constant support and encouragement during this work.

References

1. B. Kang and G. Ceder, Battery materials for ultrafast charging and discharging, Nature, 2009, 458(7235), 190–193.
2. J. Li, M. Liu and X. Bi, Interface electron polarization based high-k Al₂O₃/ZnO nanolaminates with excellent temperature stability and ultrahigh energy-storage density by atomic layer deposition, J. Mater. Chem. A, 2019, 7(17), 10303–10318.
3. Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, H. Li, A. Haque, L. Q. Chen, T. Jackson and Q. Wang, Flexible High-Temperature Dielectric Materials from Polymer Nanocomposites, Nature, 2015, 523(7562), 576–579.
4. X. Zhang, Y. Shen, Q. Zhang, L. Gu, Y. Hu, J. Du, Y. Lin and C. W. Nan, Ultrahigh Energy Density of Polymer Nanocomposites Containing BaTiO₃@TiO₂ Nanofibers by Atomic-Scale Interface Engineering, Adv. Mater., 2015, 27(5), 819–824.
5. G. F. Zhang, H. Liu, Z. Yao, M. Cao and H. Hao, Effects of Ca Doping on the Energy Storage Properties of (Sr, Ca)TiO₃ Paraelectric Ceramics, J. Mater. Sci.: Mater. Electron., 2015, 26, 2726–2732.
6. C. Hou, W. Huang, W. Zhao, D. Zhang, Y. Yin and X. Li, Ultrahigh Energy Density in SrTiO₃ Film Capacitors, ACS Appl. Mater. Interfaces, 2017, 9(24), 20484–20490.
7. B. Peng, Q. Zhang, X. Li, T. Sun, H. Fan, S. Ke, M. Ye, Y. Wang, W. Lu, H. Niu, J. F. Scott, X. Zeng and H. Huang, Giant Electric Energy Density in Epitaxial Lead-Free Thin Films with Coexistence of Ferroelectrics and Antiferroelectrics, Adv. Electron. Mater., 2015, 1(5), 1500052–1500058.
8. P. S. Padhi, R. S. Ajimsha, S. K. Rai, U. K. Goutam, A. Bose, S. Bhartiya and P. Misra, Process Temperature dependent Interface Quality and Maxwell-Wagner Interfacial Polarization in Atomic Layer Deposited Al₂O₃/TiO₂ Nanolaminates for Energy Storage Application, Nanoscale, 2023, 15, 8337–8355.
9. P. S. Padhi, S. K. Rai, H. Srivastava, R. S. Ajimsha, A. K. Srivastava and P. Misra, Maxwell–Wagner Relaxation-Driven High Dielectric Constant in Al₂O₃/TiO₂ Nanolaminates Grown by Pulsed Laser Deposition, ACS Appl. Mater. Interfaces, 2022, 14(10), 12873–12882.
10. J. Azadmanjiri, C. C. Berndt, J. Wang, A. Kapoor, V. K. Srivastava and C. Wen, A review on hybrid nanolaminate materials synthesized by deposition techniques for energy storage applications, J. Mater. Chem. A, 2014, 2(11), 3695–3708.
11. U. Passlack, N. Simon, V. Bucher, C. Harendt, T. Stieglitz and J. N. Burghartz, Flexible Ultrathin Chip-Film Patch for Electronic Component Integration and Encapsulation using Atomic Layer-Deposited Al₂O₃–TiO₂ Nanolaminates, ACS Appl. Mater. Interfaces, 2023, 15(12), 16221–16231.
12. M. Iwamoto, Maxwell–Wagner Effect, Encyclopedia of Nanotechnology, 2015, pp. 1–13.
13. P. S. Padhi, R. S. Ajimsha, S. K. Rai, A. Bose and P. Misra, Effect of Al₂O₃ layer thickness on leakage current and dielectric properties of atomic layer deposited Al₂O₃/TiO₂/Al₂O₃ nano-stack, J. Mater. Sci.: Mater. Electron., 2023, 34(14), 1160.
14. G. Lee, B. K. Lai, C. Pathak, R. S. Katiyar and O. Auciello, Tailoring dielectric relaxation in ultra-thin high-dielectric constant nanolaminates for nanoelectronics, Appl. Phys. Lett., 2013, 102, 142901.
15. M. B. Elbahri, A. Kahouli, B. Mercey, O. Lebedev, W. Donner and U. Lüders, Study on the dielectric properties of Al₂O₃/TiO₂ sub-nanometric laminates: effect of the bottom electrode and the total thickness, J. Phys. D: Appl. Phys., 2018, 51(6), 065101.
16. M. Upadhyay, M. B. Elbahri, M. Mezhoud, R. C. Germanicus and U. Lüders, Thickness dependence of dielectric properties in sub-nanometric Al₂O₃/ZnO laminates, Solid-State Electron., 2021, 186, 108070.
17. Y. Chen, C. Wu, D. Riley, I. Mejia, J. Alcantar-Peña and O. Auciello, “Reliable High-K Dielectric Oxide-Based Nanolaminates for Next-Generation Logic Analog and Memory Semiconductor Devices,” presented at the materials Research Society Spring Meeting, Symposium on Devices and Materials to Extend the CMOS Roadmap for Logic and Memory Applications, Session EP09-08, ALD, High K, Ge, 2D and Others, Phoenix, 2019, p. 273.
18. W. Li, O. Auciello, R. N. Premnath and B. Kabius, Giant dielectric constant dominated by Maxwell–Wagner relaxation in Al₂O₃/TiO₂ nanolaminates synthesized by atomic layer deposition, Appl. Phys. Lett., 2010, 96, 162907.
19. W. Li, Z. Chen, R. N. Premnath, B. Kabius and O. Auciello, Controllable giant dielectric constant in AlOx/TiOy nanolaminates, J. Appl. Phys., 2011, 110(2), 024106.
20. S. Banik, M. K. Chattopadhyay, S. Tripathi, R. Rawat and S. N. Jha, Large positive magnetoresistance and Dzyaloshinskii–Moriya interaction in CrSi driven by Cr3d localization, Sci. Rep., 2020, 10(1), 12030.
21. S. Banik, P. I. Samina, P. N. Rao, H. Srivastava and A. Sagdeo, Probing interband and intraband transitions in magneto-optical FeT (T= Cr, Co, Ni) alloys from electronic structure studies, Appl. Surf. Sci., 2021, 546, 148896.
22. S. Banik, K. Vijay, S. Paul, N. Mansuri, D. K. Shukla, S. K. Srivastava, A. Sagdeo, K. Kumar, S. Tripathi and S. N. Jha, Spin reorientation transition driven by polaronic states in Nd₂CuO₄, Mater. Adv., 2022, 3(20), 7559–7568.
23. M. H. Richter, W. H. Cheng, E. J. Crumlin, W. S. Drisdell, H. A. Atwater, D. Schmeißer, N. S. Lewis and B. S. Brunschwig, X-ray photoelectron spectroscopy and resonant X-ray spectroscopy investigations of interactions between thin metal catalyst films and amorphous titanium dioxide photoelectrode protection layers, Chem. Mater., 2021, 33(4), 1265–1275.
24. A. Sharma, P. Yadav, R. Bhatt, S. Banik, G. Singh and I. Bhaumik, Effect of Nb substitution on the electronic property of lead-free piezoelectric (Na_0.41K_0.09Bi_0.50)TiO₃ single crystal: Optical absorption and photoelectron study, J. Appl. Phys., 2022, 132(20), 205103.
25. C. Di Valentin, G. Pacchioni and A. Selloni, Electronic structure of defect states in hydroxylated and reduced rutile TiO₂ (110) surfaces, Phys. Rev. Lett., 2006, 97(16), 166803.
26. D. Mondal, S. Banik, C. Kamal, M. Nand, S. N. Jha, D. M. Phase and T. Ganguli, Electronic structure of FeAl alloy studied by resonant photoemission spectroscopy and Ab initio calculations, J. Alloys Compd., 2016, 688, 187–194.
27. P. S. Padhi, S. K. Rai, K. Vijay, H. Srivastava, S. Banik, R. S. Ajimsha, A. Srivastava and P. Misra, Tuneable nanobattery effect and negative differential resistance characteristic in Maxwell–Wagner interfacial polarization dominated Al2O3/TiO2 Nanolaminates, ACS Appl. Nano Mater., 2024, 7, 13928–13935.
28. P. S. Padhi, R. S. Ajimsha, S. K. Chetia, A. K. Das, V. K. Sahu and P. Misra, Reduced leakage current in Al₂O₃/TiO₂/Al₂O₃ dielectric stacks grown by pulsed laser deposition, AIP Conf. Proc., 2020, 2265(1), 030190.
29. T. A. Growden, W. Zhang, E. R. Brown, D. F. Storm, K. Hansen, P. Fakhimi and P. R. Berger, 431 kA/cm² peak tunneling current density in GaN/AlN resonant tunneling diodes, Appl. Phys. Lett., 2018, 112(3), 033508.
30. W. Maryam, A. V. Akimov, R. P. Campion and A. J. Kent, Dynamics of a vertical cavity quantum cascade phonon laser structure, Nat. Commun., 2013, 4(1), 2184.
31. P. S. Padhi, S. K. Rai, K. Vijay, H. Srivastava, S. Banik, R. S. Ajimsha, A. K. Srivastava and P. Misra, Small-polaron hopping and tunneling transport in Maxwell-Wagner relaxation dominated Al₂O₃/TiO₂ subnanometric laminates, Appl. Phys. Lett., 2024, 124(23), 233504.
32. L. Shen, X. Cheng, Z. Wang, D. Cao, Q. Li Zheng and Y. Yu Wang, Negative differential resistance in the I–V curves of Al₂O₃/AlGaN/GaN MIS structures, RSC Adv., 2016, 6(7), 5671–5676.
33. A. Kahouli, O. Lebedev, V. H. Dao, M. B. Elbahri, W. Prellier and U. Lüders, Electrical characteristics and conduction mechanisms of amorphous subnanometric Al₂O₃–TiO₂ laminate dielectrics deposited by atomic layer deposition, Appl. Phys. Lett., 2016, 109(20), 202901.
34. P. S. Padhi, R. S. Ajimsha, S. K. Rai, S. Bhartiya, A. Bose, B. Das, M. K. Tiwari and P. Misra, Correlation of interfacial and dielectric characteristics in atomic layer deposited Al₂O₃/TiO₂ nanolaminates grown with different precursor purge times, J. Vac. Sci. Technol., A, 2023, 41(6), 063201.
35. L. Zhen, B. Yang, W. Cao, E. Fohtung and T. Lookman, Enhanced energy storage with polar vortices in ferroelectric nanocomposites, Phys. Rev. Appl., 2017, 8(3), 034014.
36. B. Ma, D. K. Kwon, M. Narayanan and U. Balachandran, Dielectric properties and energy storage capability of antiferroelectric Pb_{0. 92}La_{0. 08}Zr_{0. 95}Ti_{0. 05}O₃ film-on-foil capacitors, J. Mater. Res., 2009, 24(9), 2993–2996.
37. M. Rahimabady, L. Lu and K. Yao, Nanocomposite multilayer capacitors comprising BaTiO₃-TiO₂ and poly (vinylidene fluoride-hexafluoropropylene) for dielectric-based energy storage, J. Adv. Dielectr., 2014, 4(02), 1450009.
38. M. Wei, J. Zhang, J. Huang, H. Chen and C. Yang, Microstructure and electrical properties of TiO₂–CaO–MgO–Al₂O₃–SiO₂ glass-ceramic with sol–gel method, J. Mater. Sci.: Mater. Electron., 2016, 27(11), 11623–11627.
39. H. Spahr, C. Nowak, F. Hirschberg, J. Reinker, W. Kowalsky, D. Hente and H.-H. Johannes, Enhancement of the maximum energy density in atomic layer deposited oxide based thin film capacitors, Appl. Phys. Lett., 2013, 103(4), 042907.

---

Footnote

† Electronic supplementary information (ESI) available: The interfacial analysis of representative ATA NLs is presented. Comparison of performance parameters of our optimised TiN/ATA NL/TiN capacitors with the previously reported NLs in the literature is also illustrated (PDF). Fig. S1. (a) Measured XRR curves for three representative ATA NLs deposited on a TiN coated Si substrate with Y-offsets. (b) Measured and fitted XRR profiles of [1A-1T-1A] NL grown on a TiN coated Si substrate and the depth variation of the electron density profile is displayed. (c) High-resolution transmission electron microscopy image and (d) the intensity variation profile of a representative [0.8A-0.8T-0.8T] NL. Table S1 Structural parameters of [0.8A-0.8T-0.8T] NL deposited on Si and TiN coated Si substrates extracted from best fit results of XRR data. Table S2: Comparison of the performance parameters of our PLD grown TiN/ATA NL/TiN capacitors with previously reported NLs in the literature. See DOI: https://doi.org/10.1039/d4lf00125g

---