Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles modelling of the thermoelectric properties of n-type CaTiO3, SrTiO3 and BaTiO3†
Alveena Z.
Khan
 ,
Joseph M.
Flitcroft
,
Joseph M.
Flitcroft
 and
Jonathan M.
Skelton
and
Jonathan M.
Skelton
 *
*
Department of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: jonathan.skelton@manchester.ac.uk
First published on 6th December 2023
Abstract
Mitigating anthropogenic climate change requires a package of technologies including methods to improve the efficiency of energy-intensive transportation and industry. Thermoelectric (TE) power, which harnesses the Seebeck effect in a TE material to extract electrical energy from a temperature gradient, is a proven technology with the potential to meet this need. Oxide-based TEs are desirable for their low cost, high chemical stability and low toxicity, but are generally limited by a low electrical conductivity and high thermal conductivity. In this study, we employ a fully ab initio approach to predict the electrical and thermal transport and thermoelectric figure of merit ZT of the oxide perovskites CaTiO3, SrTiO3 and BaTiO3 as a function of carrier concentration and temperature. We predict that carrier concentrations of n ≈ 1021 cm−3 are required to optimise the thermoelectric power factor, and that the piezoelectric scattering in rhombohedral BaTiO3 limits the electrical conductivity compared to the other two systems. We find that the lattice thermal conductivity κlatt is primarily determined by the structure type and chemical bonding through the phonon group velocities. We predict that CaTiO3 and SrTiO3 can achieve ZT > 1 at high temperature, and that the ZT of SrTiO3 could be further enhanced by the impact of doping or alloying to obtain the required n on the κlatt. The favourable comparison to experimental measurements suggests that this modelling approach has considerable predictive power, and could therefore serve as a valuable complement to experiments to identify new high-performance oxide TEs.
1 Introduction
With continued growth in the global demand for energy and the urgent need to reduce greenhouse gas (GHG) emissions to limit anthropogenic climate change, the importance of technologies to provide clean energy and enhance the efficiency of energy use cannot be understated. A substantial proportion of the industry and technology that underpin modern life generates waste heat, with an estimated 60% of global energy lost through this route.1 In particular, the difficult-to-decarbonise industry and transport sectors were estimated to be responsible for ∼24 and 16% of GHG emissions in 2016,2,3 highlighting the significant potential for reductions from improving efficiency.Thermoelectric generators (TEGs) are solid-state devices that convert thermal energy directly to electricity via the Seebeck effect in a thermoelectric material. TEGs have no moving parts and are thus easy to maintain, have proven reliability in the aerospace industry, and are potentially scaleable to a wide range of applications.3 The performance of a TE material is measured using the dimensionless figure of merit ZT defined by:1,3
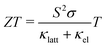 | (1) |
To optimise the ZT, the power factor should be maximised and the thermal conductivity minimised. S, σ, and κel depend on the electronic structure and are typically related through the carrier concentration n such that increasing n increases the σ and κel but reduces the S.1 Materials-engineering strategies such as “band convergence” can in some case enhance the S without degrading the conductivity, but aside from these optimising the electrical properties entails balancing the σ, S and κel by optimising n, and the best balance is typically found in heavily-doped semiconductors. On the other hand, the lattice thermal conductivity is independent of the electrical properties and depends on the material structure and chemical bonding. The links between structure/composition and κlatt are at present not well understood, but low κlatt is often associated with materials composed of heavy elements, with weak chemical bonding, and/or with strongly-anharmonic lattice dynamics arising from e.g. displacive phase transitions and active lone pairs.4–8
The current industry standard TEs are Bi2Te3 for applications around room temperature (ZT ≈ 1 from 350–450 K)3 and PbTe for high-temperature applications (ZT = 2.2 at 915 K),9 due to their favourable electronic structure and intrinsically low thermal conductivity.10,11 However, the low elemental abundance of Te and the environmental toxicity of Pb all but rule out widespread deployment, restricting Bi2Te3- and PbTe-based TEGs to niche applications.12 Mass production of TEGs thus requires alternative candidate materials to be found that balance high performance against sustainability and cost requirements.
Oxide materials are attractive for their low toxicity, low cost, and high chemical robustness, which make them particularly suitable for high-temperature automotive and industrial applications. However, while oxides often show large Seebeck coefficients, they also tend to have low electrical conductivity, high lattice thermal conductivity, and hence low ZT. There has therefore been substantial research into enhancing the σ and minimising the κlatt of oxides, for example by doping and alloying. Reports of large theromelectric power factors in cobaltites in the 1990s initiated research into several families of materials,13 leading to promising candidates including the p-type layered cobaltites NaxCoO2,13–16 Ca3Co4O917–19 and Bi2Sr2Co2Oy,20–22 and n-type ZnO23, SrTiO324–26 and CaMnO3.27,28 Of these, SrTiO3 is among the most promising and widely studied thermoelectric oxide perovskite due to its chemical flexibility and high thermal stability.29 However, there have been relatively few studies of the thermoelectric properties of CaTiO3 and BaTiO3,30–32 particularly in the non-cubic space groups adopted by these systems at low-to-mid temperature.
The major challenge to designing high-performance TEs is navigating the space of interlinked physical properties that need to be optimised. In this context, all four of the quantities in the ZT equation are amenable to first-principles calculations, allowing, in principle, the ZT to be estimated as a function of the extrinsic carrier concentration (“doping level”) and temperature through a fully ab initio approach. In particular, a recent approach to calculating electronic transport properties, including a model for the electron relaxation times,33 when paired with established approaches to predicting the κlatt,34 has been shown to yield very good predictions for the well-characterised tin chalcogenides SnS and SnSe35 and has been applied to novel candidate TEs including the ternary oxide Bi2Sn2O736 and the quaternary oxysulphide Y2Ti2O5S2.37 This type of calculation can provide valuable guidance to experiments as to the conditions where the maximum ZT is likely to be obtained and thus define potential application areas for a material.
In this work, we apply this approach to the Group II titanate perovskites CaTiO3 (CTO), SrTiO3 (STO) and BaTiO3 (BTO), in the orthorhombic Pnma, tetragonal I4/mcm and rhombohedral R3m phases, respectively, allowing us to investigate the impact of the A-site cation and structure type on the thermoelectric performance. We find that STO has the best electrical transport properties, whereas the lower-symmetry structure of CTO lends itself to a low κlatt. On the other hand, BTO is predicted to have a relatively high κlatt and limited σ due to piezoelectric scattering leading to short electron lifetimes. We predict maximal ZTmax ≈ 0.2 and 0.5 at mid and high temperatures of 600 and 1000 K and doping levels on the order of 1021 cm−3. Industrially viable ZTmax > 1 are only obtained at temperatures above ∼1500 K. The low-temperature ZT is limited by the large κlatt, arising from the strong chemical bonding and resultant large phonon group velocities, and could be mitigated as a positive side effect of the chemical modifications required to optimise the electrical properties. Our findings provide valuable insight to ongoing efforts to optimise these systems, and, importantly, demonstrate that this ab initio workflow can provide useful predictions to support ongoing efforts to obtain high-performance oxide TEs.
2 Methodology
Calculations were performed using pseudopotential plane wave density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) code.42Initial structures of CaTiO3, SrTiO3 and BaTiO3 in the Pnma, I4/mcm and R3m spacegroups, respectively, were taken from the Materials Project (MP) database43 (mp-4019, mp-4651, mp-5020) and optimised to tight tolerances of 10−8 eV on the total energy and 10−3 eV Å−1 on the forces.
Electron exchange and correlation were described using the PBEsol generalised-gradient approximation (GGA) functional.44 The ion cores were modelled using projector-augmented wave (PAW) pseudopotentials45,46 with valence configurations of: Ti – 3d2 4s2; O – 2s2 2p4; Ca – 3p6 4s2; Sr – 4s2 4p6 5s2; and Ba – 5s2 5p6 6s2. The valence wavefunctions were described using a plane-wave basis with an 800 eV kinetic-energy cutoff, and the electronic Brillouin zones were sampled using Γ-centred Monkhorst–Pack k-point meshes47 with 4 × 4 × 2, 5 × 5 × 3 and 4 × 4 × 4 subdivisions for the CTO, STO and BTO primitive cells, respectively. These parameters were chosen based on explicit testing to converge the absolute total energies to <1 meV atom−1 and the external pressure to <1 kbar (0.1 GPa).
Lattice-dynamics and thermal-conductivity calculations were performed using the supercell finite-differences approach implemented in the Phonopy and Phono3py packages.34,48
The second-order (harmonic) force constants were computed in a 4 × 2 × 4 expansion of the CTO unit cell (640 atoms), and 4 × 4 × 4 expansions of the STO and BTO primitive unit cells (640/320 atoms). Atom-projected phonon density of states (PDoS) curves were computed by interpolating the phonon frequencies onto regular Γ-centred q-point grids with 12 × 12 × 12 subdivisions using the linear tetrahedron method for Brillouin-zone integration. Phonon dispersions were obtained by evaluating the frequencies at strings of q-points passing through the high-symmetry points in the respective Brillouin zones. Non-analytical corrections to the dynamical matrices at q → Γ were included using the approach in ref. 49 using Born effective-charge tensors Z* and high-frequency dielectric constants ε∞ computed using the density-functional perturbation theory (DFPT) routines in VASP.50
The third-order (anharmonic) force constants were computed in a 2 × 1 × 2 expansion of the CTO unit cell (80 atoms) and 2 × 2 × 2 expansions of the STO and BTO primitive cells (80/135 atoms). The lattice thermal conductivities were then calculated within the single-mode relaxation-time approximation (SM-RTA) by combining the second- and third-order force constants to obtain modal heat capacities Cλ, group velocities νλ and lifetimes τλ on uniform Γ-centered 8 × 8 × 8 q-point sampling meshes. This mesh was chosen based on explicit testing to converge the average of the three diagonal components of the κlatt tensors, κave = (κxx + κyy + κzz)/3, to within 5% of the values obtained with larger sampling meshes.
Electronic transport calculations were performed using the AMSET code.33
Accurate band gaps Eg were obtained using non self-consistent calculations with the HSE06 hybrid functional,51,52 where a single-point calculation with PBE53 is performed to obtain a set of Kohn–Sham orbitals and the band energies recalculated with HSE06 using the PBE orbitals. Uniform band-structure calculations were then performed with PBEsol and denser 8 × 8 × 4, 10 × 10 × 6 and 8 × 8 × 8 k-point meshes for CTO, STO and BTO, respectively, and the bandgaps increased to the HSE06 values using scissors operators. These meshes were further interpolated to a ∼30× higher density when calculating the transport properties.
AMSET estimates the electronic relaxation times by summing scattering rates from four different processes, viz. acoustic deformation potential (ADP), polar optic phonon (POP), piezoelectric (PIE), and ionised impurity (IMP) scattering, requiring a range of material properties to be calculated. Deformation potentials were computed by performing a series of single-point energy calculations on deformed structures, generated using AMSET, with PBEsol. High-frequency dielectric constants ε∞, Born effective charges Z* and piezoelectric moduli were determined using DFPT.50 For these calculations, convergence tests indicated that 3× denser k-point sampling along each reciprocal-lattice vector compared to the “base” meshes used for geometry optimisation were required to converge the ε∞. The Z* were used to determine the infrared (IR) activities of the phonon modes at q = Γ,54,55 evaluated with Phonopy, and to calculate the polar optic phonon (POP) frequencies. The elastic constants Cij and ionic contributions to the dielectric constant, εionic, were computed using PBEsol and the finite-differences routines in VASP, the latter of which was used to obtain the static dielectric constant εs = ε∞ + εionic.
3 Results and discussion
3.1 Optimised structures
The optimised structures of CTO, STO and BTO, converted to the conventional crystallographic unit cells, are shown in Fig. 1. The ABX3 structure comprises a network of corner-sharing BX6 octahedra surrounding cuboctahedral cavities filled by the A-site cations. The ideal perovskite structure is cubic with the Pm3m spacegroup, but this is often not the lowest-energy configuration. Instead, many perovskites adopt one of a rich variety of structures obtained by rigid tilting of the octahedra and/or by displacements of the A- or B-site cations from their ideal positions in the cubic phase.56,57 In this case, the higher-symmetry rhombohedral R3m structure of BTO is derived from the cubic aristotype by a displacement of the B-site cation along the [111] direction,57 while the lower-symmetry tetragonal I4/mcm structure of STO is derived by a single octahedral tilt and the orthorhombic Pnma structure of CTO is derived by three independent tilts.56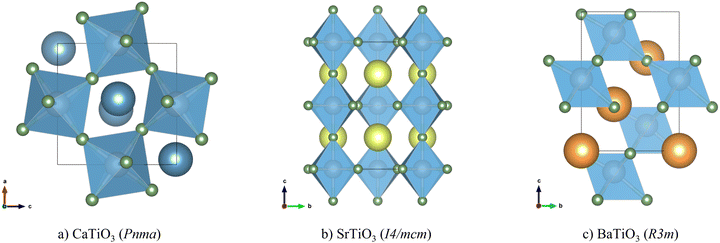 | ||
| Fig. 1 Conventional cells of CaTiO3 in the Pnma space group (a), SrTiO3 in the I4/mcm space group (b) and BaTiO3 in the R3m space group (c). Atom colours: Ca – blue; Sr – yellow; Ba – orange; Ti – grey; O – green. These images were prepared using the VESTA software.38 | ||
The optimised lattice parameters are collected in Table 1 and compared to experimental measurements from the literature. The lattice parameters of CTO, STO and BTO are within 2%, 1% and 0.5%, respectively, of the experimental measurements. We note that our “athermal” optimised structures are those at 0 K without corrections for the vibrational zero-point energy, whereas the experimental measurements are performed at finite temperature and may include changes to the lattice constants due to thermal expansion or contraction, so we therefore consider these small differences acceptable. Our optimised lattice parameters are also within 5% of those of the initial MP structures, although these are optimised with the PBE functional, which typically overestimates lattice parameters and unit-cell volumes relative to experiments.
3.2 Lattice dynamics and lattice thermal conductivity
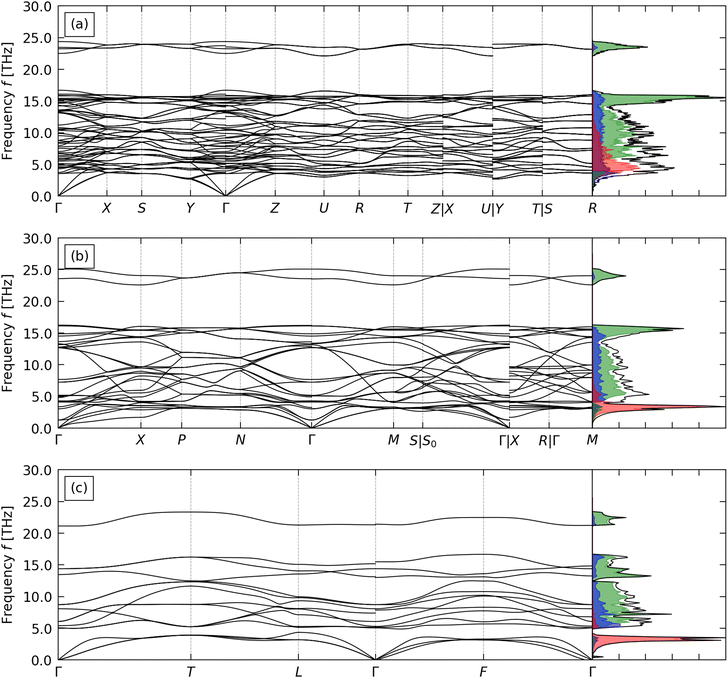
The calculated phonon dispersion and density of states (DoS) curves for CTO, STO and BTO are shown in Fig. 2.BTO has na = 5 atoms in the primitive cell, resulting in 3na = 15 branches at each phonon wavevector q. CTO and STO have na = 10 and 20, respectively, and thus considerably more complex phonon spectra with 30 and 60 bands at each q. This increase in complexity due to the larger primitive unit cells is compounded by the reduction in symmetry resulting in fewer degenerate bands. The absence of imaginary harmonic modes in all three phonon dispersion curves indicates that the three structures are dynamically stable.
In all three systems the A-site cations make the largest contributions to the low-frequency acoustic modes. Heavier cations produce lower-frequency, sharper peaks in the PDoS consistent with “rattling” behaviour, indicating weaker interactions between the A-site cations and the TiO6 octahedral framework. The higher-frequency optic modes are predominantly due to the motion of the Ti and O atoms and correspond to deformations of the TiO6 octahedra. In all three systems the optic modes are separated into a broad band of mid-frequency modes involving motion of the Ti and O atoms and an isolated group of high-frequency modes associated primarily with O. The calculated phonon spectra of STO and CTO agree well with previous calculations.59,60 While we were not able to find reference phonon spectra for R3m BTO to compare to, the good agreement for STO and CTO gives us confidence in our calculation on BTO.
To predict the lattice thermal conductivity κlatt, we used the single-mode relaxation time approximation (SM-RTA) model.34 The κlatt are 3 × 3 tensors, where the diagonal elements correspond to transport along the three Cartesian directions. Since practical thermoelectric devices tend to be based around thin films or pressed pellets composed of randomly-oriented crystal grains, we focus mainly on the scalar average κave = (κxx + κyy + κzz)/3, which we also denote κlatt. Fig. 3(a) shows the predicted κlatt of the three perovskites as a function of temperature, and values at T = 1000 K are collected in Table 2.
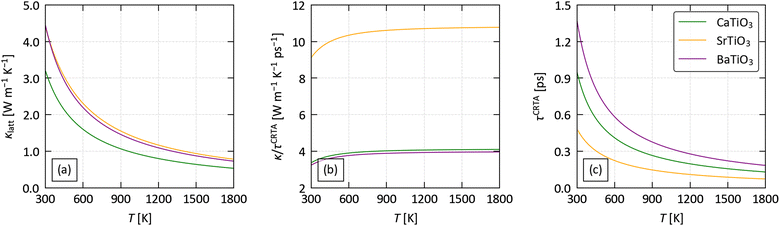 | ||
| Fig. 3 Analysis of the predicted lattice thermal conductivity of CaTiO3, SrTiO3 and BaTiO3 using the constant relaxation-time approximation defined in eqn (2): averaged thermal conductivity κlatt (a), harmonic term κ/τCTRA (b) and averaged lifetime τCTRA (c) as a function of temperature. | ||
| m A [amu] | r A [pm] | κ latt [W m−1 K−1] | (κ/τCRTA)ave [W m−1 K−1 p−1] | τ CRTA [ps] | ||||
|---|---|---|---|---|---|---|---|---|
| κ xx | κ yy | κ zz | κ ave | |||||
| CaTiO3 | 40.1 | 180 | 0.984 | 0.980 | 0.916 | 0.960 | 4.04 | 0.237 |
| SrTiO3 | 87.6 | 200 | 1.293 | — | 1.614 | 1.400 | 10.65 | 0.131 |
| BaTiO3 | 137 | 215 | 1.286 | — | 1.366 | 1.313 | 3.91 | 0.336 |
The predicted averaged thermal conductivities fall in the order of CTO < STO ≈ BTO. The κlatt of CTO, STO and BTO are 3.2, 4.4 and 4.5 W m−1 K−1 at 300 K, and decrease sharply with temperature to 0.96, 1.4 and 1.3 W m−1 K−1 at 1000 K.
Ref. 61 reports total thermal conductivities of 4 and 3 W m−1 K−1 for STO at 300 and 1000 K, respectively, while ref. 62 reports a larger 6.5 W m−1 K−1 at 400 K and a comparable κ = 3.25 W m−1 K−1 at 1000 K. The measurements in ref. 63 on La- and Nb-doped single crystals cite even higher κlatt of ∼8–10 W m−1 K−1 at 300 K, but similar values around 3 W m−1 K−1 at 1000 K. The factor of three variation in the low-temperature κlatt highlights the sensitivity of these measurements to the sample preparation and morphology. In principle, the single-crystal measurements should be most comparable to our calculations, but we find we consistently underestimate the experiments by a factor of ∼2× (see Section 1 of the ESI†). Given that the tetragonal-to-cubic phase transition in STO occurs around 100 K,64 we would expect the crystals to be in the higher-symmetry cubic phase, so we tentatively put this discrepancy down to us modelling the tetragonal structure.
On the other hand, comparison to the measurements on CaTiO3 in ref. 30, which obtained κlatt ≈ 2–4.5 and 2–3 W m−1 K−1 at 300 and 1000 K, suggest that our calculations on this system also underestimate the κlatt at high temperature. Given that the orthorhombic-to-cubic transition in CTO occurs well above 1000 K,65 the experiments and calculations for this system should be on the same crystal phase.
Both our predictions and the experimental measurements are nevertheless considerably larger than the κlatt of flagship materials such as Bi2Te3 and SnSe, for which we calculated lattice thermal conductivities of 0.88 and 1.58 W m−1 K−1 in previous studies using similar methodology (the experimental values are 1.28/1.3766,67 and 0.5–1.4 W m−1 K−1).68 However, the measurements in ref. 30, and experiments on high-entropy perovskite oxides,69 demonstrate that the κlatt can be significantly reduced by controlling the chemical composition, providing a means to mitigate this.
Given that the anisotropy in the thermal transport of the flagship thermoelectric SnSe plays an important role in its large high-temperature figure of merit,5,70 we also investigated the anisotropy in the κlatt of CTO, STO and BTO (Table 2 and Fig. S4–S6, ESI†). For the tetragonal I4/mcm and rhombohedral R3m spacegroups of STO and BTO, respectively, symmetry dictates that κxx = κyy ≠ κzz, whereas in the lower-symmetry orthorhombic Pnma spacegroup of CTO κxx ≠ κyy ≠ κzz. For STO and BTO, we predict κxx = κyy < κzz, while for CTO we predict κxx ≈ κyy > κzz. The anisotropy in CTO and BTO is relatively small, with a maximum variation of 4–5% in the directional components relative to the average, whereas STO shows a larger variation of around 15%.
Low κlatt is often associated with materials composed of heavy elements with weak chemical bonds,4 and it is therefore interesting that, given CTO is the lightest of the three materials (cf.Table 2), it also has the lowest κlatt. This indicates that differences in structure and bonding, rather than the mass of the A-site cation, play a significant role in determining the lattice thermal conductivity. To investigate this further, we applied the constant relaxation-time approximation (CRTA) analysis developed in previous work71,72 to the κave. In this model, the κlatt is written as:
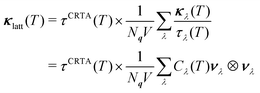 | (2) |
The averaged (κ/τCRTA) and τCRTA of the three systems are shown in Fig. 3(b) and (c), and the values at 1000 K are included in Table 2.
In our previous work on Si clathrates we found a strong correlation between the group velocities and the number of atoms na in the primitive cell, and a secondary correlation with crystal symmetry (spacegroup).73 Based on this, we would expect the κ/τCRTA to vary in the order BTO (rhombohedral, na = 5) > STO (tetragonal, na = 10) > CTO (orthorhombic, na = 20). CTO and STO follow this trend, with κ/τCRTA = 4 and 10.7 at 1000 K, whereas for BTO κ/τCRTA = 3.9 which is comparable to but slightly lower than CTO. This is consistent with the phonon dispersions in Fig. 2, which show a notably shallower dispersion for BTO, particularly in the low-frequency acoustic modes. The much larger κ/τCRTA of STO compared to CTO, despite the larger mass mA of the A-site cation, suggests that this cannot be attributed to Ba having the largest mA. One explanation is that accommodating the larger Ba cation places a strain on the TiO6 octahedral framework, which may be reflected in the larger volume per formula unit of BTO compared to the similar volumes of CTO and STO (cf.Table 1). Another is that the off-centering of the B-site Ti4+ cation in the R3m structure has a larger impact on the chemical bonding in the TiO6 octahedral framework than the rigid tilting in the I4/mcm and Pnma structures.
All three compounds show sub-picosecond averaged lifetimes τCRTA at 1000 K. The τCRTA vary by ∼2.6× and show the opposite trend to the harmonic terms, i.e. are shortest for STO and longest for BTO. The combination of the 2.7× larger κ/τCRTA and shorter averaged lifetimes of STO compared to BTO result in the two systems having similar κlatt, while the low group velocities and intermediate τCRTA of CTO lead to the lowest κlatt of the three systems. The long τCRTA of BTO are perhaps also unexpected given the localised A-site feature in the phonon DoS (cf.Fig. 2). However, following a similar thought process to the analysis of the κ/τCRTA, the larger radius rA of the Ba cation (cf.Table 2) may limit its ability to rattle and produce the expected phonon scattering.
Compared to the flagship thermoelectrics SnSe and Bi2Te3, the κ/τCRTA at 300 K are much larger (3.24–9.12 W m−1 K−1 ps−1 compared to 0.37 and 0.2 W m−1 K−1 ps−1 for SnSe72 and Bi2Te374), whereas the τCRTA are shorter (0.48–1.37 ps compared to 4.23/4.41 ps for SnSe/Bi2Te372,74). This is consistent with the stronger bonding in oxides, which would both produce larger group velocities but also stronger phonon interactions, and suggests that the common strategies for optimising the electrical properties (e.g. introducing oxygen vacancies and heavy doping72) would likely have a synergistic effect of reducing the lattice thermal conductivity. We defer further exploration of this to a future study.
3.3 Electronic structure and transport properties
The calculated electronic band structures of the three perovskites are provided in Fig. S7–S9 (ESI†), and the calculated electronic band gaps Eg are compared to previous experimental and theoretical studies in Table 3. The calculated Eg = 4.5 eV for CTO agrees well with the upper range of the experimental values reported in ref. 75. We were not able to find an experimental bandgap for R3m BTO, but our predicted Eg = 4.42 eV is consistent with the values of 4.9 and 5.18 eV obtained in previous theoretical studies.76,77 (We attribute our smaller predicted value to our use of the screened HSE06 hybrid functional rather than the unscreened PBE078 used in ref. 76 and 77.) On the other hand, our predicted Eg = 4.15 eV for STO is considerably larger than the 3.4 eV predicted in previous calculations79 and is also larger than the measured Eg = 3.25 eV of cubic STO.80 Despite these discrepancies, all three perovskites are predicted to be insulators, and we would not expect the possible overestimation of the bandgap of STO to significantly impact the calculated electrical properties.We therefore proceeded to use the semi-classical Boltzmann transport theory and approximate electron scattering models implemented in the AMSET code33 to estimate the three electrical transport properties in eqn (1), viz. the Seebeck coefficient S, electrical conductivity σ and electronic thermal conductivity κel.
In these calculations, the properties are determined for a series of extrinsic carrier concentrations (“doping levels”) n and temperatures. The doping level is set by adjusting the Fermi level EF in the electronic-structure calculation, and do not take into account the practicalities or potential impacts81 of doping to obtain a given n. The electron relaxation times are determined approximately by summing the rates from four scattering mechanisms, viz. acoustic deformation potential (ADP), piezoelectric (PIE), polar optical phonon (POP) and ionised impurity (IMP) scattering. Full details of these calculations are provided in ref. 33.
As for the κlatt, the σ, S and κel are 3 × 3 tensors, and we again focus mainly on the scalar averages (xx + yy + zz)/3, which we denote σ, S and κel to distinguish them from the tensor quantities.
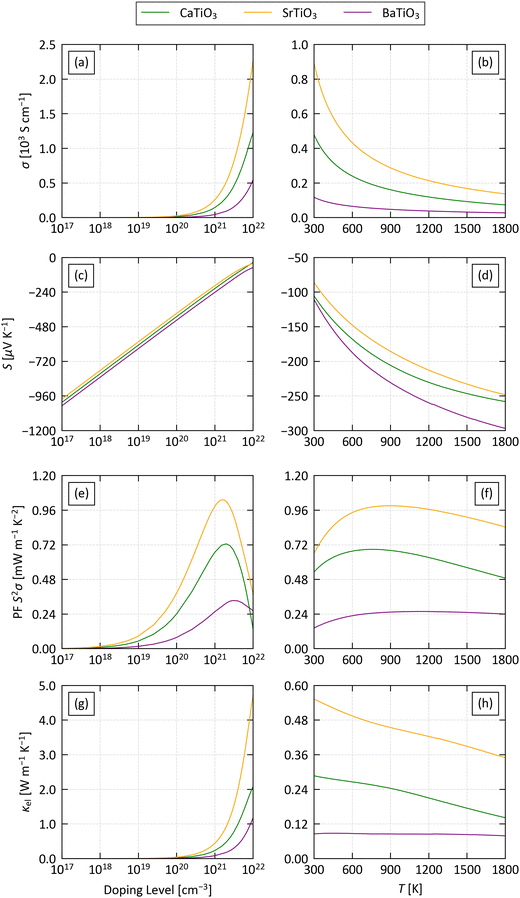
Fig. 4 shows the calculated electrical properties as a function of electron carrier concentration n between 1016 and 1022 cm−3 at a fixed T = 1000 K, and as a function of temperature between 300–1800 K at a fixed n = 1021 cm−3. Pristine STO has a relatively low n on the order of 1015 cm−3, as expected for an insulator.82 However, depending on the preparation conditions, experimental samples can have a high concentration of oxygen vacancies that act as electron donors and produce a much higher n, and carrier concentrations as high as 3.5 × 1020 cm−3 have been reported in undoped SrTiO3 thin films.83 The chemical flexibility of the perovskite structure also allows it to accommodate a wide range of dopants that can enhance the n, yielding concentrations well in excess of 1021 cm−3 in experiments.82–85 The fixed n = 1021 cm−3 is therefore a conservative estimate of what should be possible in experiments. While perovskites are stable to high temperatures, we took T = 1000 K as a reference point to match the high-temperature heat-recovery scenario outlined in ref. 86.
At T = 1000 K and the lowest n = 1016 cm−3 we studied, the S are on the order of −1200 μV K−1 and decrease monotonically with n to around −50 μV K−1 at n = 1022 cm−3. On the other hand, the σ are negligible up to n ≈ 1019 cm−3 and increase sharply at higher carrier concentrations. The increase in the conductivity dominates the PF S2σ up to n ≃ 1021− 5 × 1022 cm−3 cm−3, while at larger n the decrease in S becomes dominant, producing a maximum in the PF around 1021 cm−3. We therefore conclude that carrier concentrations above ∼1019 cm−3 are necessary to obtain a reasonable PF, but very high n are detrimental. On the other hand, the κel increases with σ following the Wiedemann–Franz law:
| κel(T) = Lσ(T)T | (3) |
At a fixed n = 1021 cm−3 the σ decrease with temperature in all three systems, indicative of degenerate semiconductors with metallic-like conductivity. On the other hand, the absolute values of the S increase with temperature from 100 μV K−1 at 200 K to around 200–250 μV K−1 at 1200 K. This balance results in a rise in the PF from 300 K and a subsequent levelling off from ∼750 K. The temperature dependence of the κel mirrors the behaviour of the electrical conductivity, in keeping with the Wiedemann–Franz law, but at this modest n the values are a relatively small 0.1–0.6 W m−1 K−1.
The three systems are predicted to have very similar Seebeck coefficients, but the conductivities, power factors and electrical thermal conductivities fall in the order of STO > CTO > BTO. Our calculations predict a maximum PF around 1 mW m−1 K−1 for STO at n = 2 × 1021 cm−3 and T = 1360 K, and under these conditions the κel is on the order of 0.8 W m−1 K−1. Conversely, the low σ of BTO results in a maximum PF of 0.4 mW m−1 K−1 at n = 5 × 1021 cm−3 and T = 1640 K. Comparing the scattering rates of the three materials at n = 1021 cm−3 and T = 1000 K (Fig. S10–S12, ESI†) indicates that the low σ of BTO is due to the impact of piezoelectric (PIE) scattering on the electron relaxation times – this mechanism is only active in the non-centrosymmetric R3m spacegroup, and indicates that the B-site cation off-centering may be detrimental to the electrical transport.
Finally, a comparison of the xx, yy anad zz components of the electrical transport tensors to the average values discussed here shows relatively minimal anisotropy (Fig. S13–S15, ESI†). The Seebeck coefficients of all three systems are essentially isotropic. The conductivity in STO and BTO is also largely isotropic, resulting in minimal variability in the PFs and κel. On the other hand, the σ of CTO shows modest anisotropy such that the a and b directions represent “easy” and “hard” axes for transport, respectively, and the PFs are ∼0.1 mW m−1 K−2 (15%) larger/smaller than the average.
We previously employed this procedure to calculate the electrical properties of SnS and SnSe and obtained very good agreement with experimental measurements.35
Measurements on 20% La-doped cubic STO obtained a σ, S and PF on the order of 150 S cm−1, −250 μV K−1 and 0.9 mW m−1 K−2 at 1000 K.61 With a comparable n = 3 × 1021 cm−3 we predict a larger σ = 775 S cm−1, a smaller absolute S = −109 μV K−1, and a similar PF of 0.93 mW m−1 K−2. Measurements on (La0.12Sr0.88)0.95TiO3 yielded σ ≈ 100 S cm−1, S ≈ − 200 μV K−1 and S2σ ≈ 0.3–0.4 mW m−1 K−2 at 900 K,62 and using a (estimated) comparable n = 2.5 × 1020 cm−3 we predict values of σ = 71 S cm−1, S = −299 μV K−1 and S2σ = 0.63 mW m−1 K−2. Finally, measurements on Nb-doped SrTiO3 films, with n ≈ 1.5–2 × 1021 in the thickest samples, obtained a maximum σ and S around 600 S cm−1 and −120 μV K−1 at room temperature,87 and we predict σ = 238 S cm−1 and S = −44 μV K−1 with n = 2.5 × 1021 cm−3.
We also performed a more quantitative comparison of our predicted σ and S to measurements on the four doped single-crystal STO samples reported in ref. 63 (Section 1 of the ESI†). This shows that the calculations tend to over- and underestimate the carrier concentration required to achieve a given σ at low and high T, respectively. On the other hand, the calculations appear to consistently underestimate the n required to obtain a given S. Equivalently, for a given n the comparison suggests the calculations are likely to under- or overestimate the σ compared to experiments at low and high temperature, and, given the monotonic reduction in the absolute value of S with carrier concentration, to underestimate the S.
The vacancy/dopant concentrations in these studies are up to several tens of at%, which means that the assumption of the rigid-band approximation, i.e. that the defects do not change the host electronic structure beyond simply increasing the n, may not be valid.81 Also, the grain boundaries in “granular” bulk materials composed of randomly-oriented crystal grains, such as pressed pellets or consolidated powders, can result in energy filtering and carrier trapping, which can impact upon the S and σ.88 This may be applicable to some of the experimental samples, and similar phenomena could arise from the point defects in the heavily-doped single-crystal STO samples in ref. 63. Finally, as for the κlatt, some of the discrepancies could also be due to the measurements being carried out on the cubic rather than the tetragonal phase.
STO is the most widely-studied of the three perovskites, but we were able to find measurements on a variety of (Ca1−xLax)TiO3−δ materials to compare our predictions for CTO against.30 The pristine material was reported to have a negligible σ = 10−5 S cm−1 at 1000 K, but introducing O vacancies produced a much larger n ≈ 2 × 1020 cm−3 and σ ≈ 100 S cm−1 with S = − 375 μV K−1. With n = 2.5 × 1020, our calculations predict σ = 36 S cm−1 and S = −331 μV K−1, which we again consider to be reasonable agreement. For a variety of La-doped samples, for which we estimate that n > 1021 cm−3, maximum σ and S around 250 S cm−1 and −175 μV K−1 were measured at 1000 K, and using n = 1021 cm−3 we predict values of 144 S cm−1 and −215 μV K−1 respectively. Our predictions for CTO are generally closer to measurements than those for STO, which, given that we would expect the measurements on CTO to be on the orthorhombic phase modelled in the calculations,65 supports the suggestion that some of the discrepancies in our predictions for STO can indeed be put down to the calculations being performed on the tetragonal rather than the cubic phase.
Qualitatively, all three sets of experiments indicate a decrease in σ and an increase in the absolute value of S with temperature, consistent with our predictions. Unfortunately, the majority of these papers do not separate the thermal conductivity into electronic and lattice contributions, but the measurements in ref. 30 suggest values of <1 W m−1 K−1 at 1000 K and n on the order of 1020 cm−3, which is again consistent with our predictions.
3.4 Thermoelectric figure of merit
We now combine the calculated electrical-transport and κlatt to predict the thermoelectric figure of merit ZT as a function of doping level and temperature using eqn (1) (Fig. 5). We summarise the minimal temperatures and n for which ZT > 1, and the corresponding transport properties, in Table 4, together with the predicted ZTmax at T = 400, 600 and 1000 K corresponding roughly to the low- mid- and high-temperature heat-recovery scenarios in ref. 86.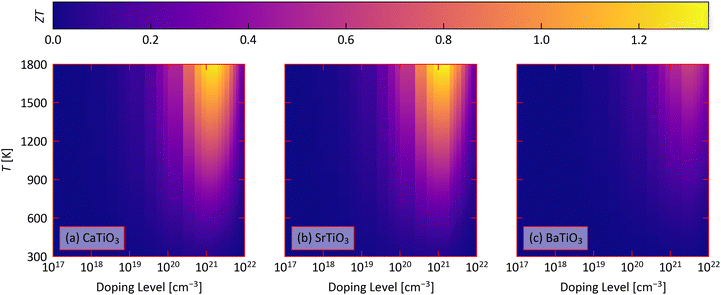 | ||
| Fig. 5 Predicted thermoelectric figure of merit ZT of CaTiO3 (a), SrTiO3 (b) and BaTiO3 (c) as a function of doping level n and temperature obtained using eqn (1). | ||
| T [K] | n [cm−3] | ZT | S [μV K−1] | σ [S cm−1] | S 2 σ (PF) [mW m−1 K−2] | κ [W m−1 K−1] | |||
|---|---|---|---|---|---|---|---|---|---|
| κ el | κ latt | κ tot | |||||||
| CaTiO3 | 400 | 7.5 × 1020 | 0.09 | −150 | 265 | 0.60 | 0.21 | 2.40 | 2.61 |
| 600 | 1 × 1021 | 0.22 | −168 | 240 | 0.68 | 0.27 | 1.60 | 1.87 | |
| 1000 | 1 × 1021 | 0.56 | −215 | 144 | 0.67 | 0.23 | 0.96 | 1.19 | |
| 1640 | 5 × 1020 | 1 | −312 | 41.6 | 0.41 | 0.08 | 0.65 | 0.73 | |
| SrTiO3 | 400 | 7.5 × 1020 | 0.08 | −128 | 484 | 0.79 | 0.40 | 3.39 | 3.79 |
| 600 | 7.5 × 1020 | 0.21 | −169 | 322 | 0.91 | 0.37 | 2.31 | 2.68 | |
| 1000 | 7.5 × 1020 | 0.54 | −219 | 193 | 0.93 | 0.33 | 1.40 | 1.73 | |
| 1480 | 7.5 × 1020 | 1 | −256 | 128 | 0.84 | 0.29 | 0.95 | 1.24 | |
| BaTiO3 | 400 | 2.5 × 1021 | 0.03 | −93.6 | 265 | 0.23 | 0.24 | 3.31 | 3.54 |
| 600 | 2.5 × 1021 | 0.07 | −124 | 185 | 0.29 | 0.23 | 2.19 | 2.42 | |
| 1000 | 2.5 × 1021 | 0.21 | −166 | 119 | 0.33 | 0.23 | 1.31 | 1.54 | |
| 1800 | 2.5 × 1021 | 0.64 | −218 | 70.3 | 0.33 | 0.21 | 0.73 | 0.93 | |
We predict that the industry-standard ZT = 1 can be achieved for STO at 1480 K with n = 1021, and for CTO at 1640 K with n = 5 × 1020 cm−3. On the other hand, we predict BTO can achieve a ZTmax of just 0.64 with n = 2.5 × 1021 cm−3 and at T = 1800 K.
At 1000 K, we predict ZTmax of 0.560 for CTO, 0.535 for STO, and 0.214 for BTO, all of which require n on the order of 1021 cm−3. At lower temperatures of 400 and 600 K, we predict much smaller ZTmax of 0.07–0.22 at 600 K and 0.03–0.09 at 400 K, which also require similarly large n. While the combination of a higher Seebeck coefficient but lower electrical conductivity results in ∼10–40% larger PFs at higher temperatures, the increase in ZT with temperature is largely dominated by a ∼60% fall in the lattice thermal conductivity.
CTO and STO are predicted to have similar ZT due to a balance of a ∼30–40% larger PF in STO and a ∼30% smaller κlatt in CTO. On the other hand, BTO is predicted to have a lower Seebeck coefficient, conductivity and power factor than the other two perovskites and a comparable κlatt to CTO, resulting in lower ZT. This comparison suggests the ZT of CTO a could potentially be enhanced by improving the electrical properties, specifically the conductivity, and the ZT of STO could be improved by reducing the κlatt.
Given the relatively small anisotropy in the predicted electrical properties and κlatt, we predict that the ZT are relatively isotropic (Fig. S16–S18, ESI†). In CTO, the ZT is largest along the a direction and smallest along the b direction, at ∼5–10% larger and 10–15% smaller than the average value, respectively, depending on the temperature. This is due to the anisotropy in the electrical conductivity and power factor. In STO, the ZT is 6–8% larger than the average along the equivalent a and b directions and ∼10–15% smaller along the c direction, due largely to the anisotropy in the lattice thermal conductivity. In BTO, on the other hand, the ZT varies by a more modest ∼1–5% and is largest along the equivalent a and b directions.
Despite the disagreement in some of the predicted electrical- and thermal-transport properties to experiments, comparison with the literature suggests the predicted ZT are very reasonable. Ref. 30 investigated 20% La-doped CaTiO3 with n ≈ 2.0 × 1020 cm−3 and obtained ZT ≈ 0.1 at T = 300 K and 0.4 at T = 1100 K. With n = 2.5 × 1020 cm−3 and T = 300 K, we predict a smaller ZT = 0.04, while at the higher T = 1100 K we predict a similar ZT = 0.45. We ascribe the discrepancy at low temperature to the likely impact of the doping on reducing the κlatt. Ref. 89 investigated 8% Pm-doped STO and obtained a ZT of 0.64 at 1200 K. While the authors do not quote a carrier concentration, we obtain and a similar ZT = 0.68 with n = 5 × 1020 cm−3. We were unfortunately not able to find ZT values for n-type BaTiO3 for comparison.
As noted above, comparison of the predicted electrical and thermal transport properties to experiments suggests a tendency for the calculations to overestimate the power factors and underestimate the lattice thermal conductivities. This should in principle lead to an overestimate of the ZT. The fact that the predicted ZT are close to the experimental values therefore suggests these discrepancies have a small impact on the calculated figure of merit, at least at the higher temperatures and n for which the largest ZTmax are obtained.
4 Conclusions
In this work we have applied a fully ab initio approach to model the electrical- and thermal-transport properties and thermoelectric figure of merit of orthorhombic CaTiO3, tetragonal SrTiO3, and rhombohedral BaTiO3. The differences in the electrical properties are dominated by the electrical conductivity, and the piezoelectric scattering enabled by the non-centrosymmetric R3m spacegroup of BTO results in a significant suppression of the σ. We predict that doping levels on the order of 1021 cm−3 are required to obtain reasonable power factors, while larger n have a detrimental impact on the Seebeck coefficients. The lattice thermal conductivity plays an important role in determining the ZT, with a steep temperature dependence resulting in the benchmark ZT > 1 only being attained at high temperatures. Analysis of the κlatt demonstrates that differences in structure and chemical bonding, rather than the mass of the A-site cation, is the key descriptor, and that the relatively high thermal conductivity of STO is due to large phonon group velocities.The relatively good agreement between our calculations and experimental measurements, in particular for the predicted ZT, demonstrates considerable promise for the application of our workflow to other perovskites and oxides more generally. In particular, our calculations suggest it is possible to make a good estimate of the ZTmax and the carrier concentration and temperature required to achieve it, which could provide an indication of potential applications and whether the required doping level is feasible. These calculations could therefore serve as a valuable complement to experiments in the ongoing search for high-performance oxide thermoelectrics. However, for improved quantitative predictions it is likely to be necessary to investigate the impact of the crystal structure in more detail, and to establish the impact of dopants and vacancies present at high concentrations (few at%) on the electrical and thermal properties. We aim to explore both of these topics in future studies.
Author contributions
Conceptualisation – JMS; methodology – all authors; data curation – all authors; formal analysis and investigation – all authors; writing (original draft) – AZK and JMF; writing (review and editing) – all authors; funding acquisition – JMS. All authors have read and agreed to the published version of the paper.Data-access statement
Raw data from the calculations performed in this study will be made available to download free of charge from an online repository at https://doi.org/10.17632/mzwcgry9dd.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge helpful comments from Prof. Nikolas Kaltsoyannis at the University of Manchester (UoM) on a draft version of this manuscript. AZK is supported by a UoM PhD studentship. JMS and JMF are supported by a UKRI Future Leaders Fellowship (MR/T043121/1), and JMS previously held a UoM Presidential Fellowship. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431 and EP/X035859), this work used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk). A subset of our calculations also made use of the UoM Computational Shared Facility (CSF) computing cluster, which is maintained by UoM Research IT.Notes and references
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- H. Ritchie, M. Roser and P. Rosado, CO2 and Greenhouse Gas Emissions, 2020, https://ourworldindata.org/co2-and-greenhouse-gas-emissions.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS PubMed.
- C. Li, J. Hong, A. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef CAS PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. B, 2019, 100, 214307 CrossRef CAS.
- M. D. Nielsen, V. Ozolins and J. P. Heremans, Energy Environ. Sci., 2013, 6, 570–578 RSC.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- Z. M. Gibbs, H. Kim, H. Wang, R. L. White, F. Drymiotis, M. Kaviany and G. Jeffrey Snyder, Appl. Phys. Lett., 2013, 103, 262109 CrossRef.
- O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M.-H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden and B. C. Sales, Nat. Mater., 2011, 10, 614–619 CrossRef CAS PubMed.
- D. Champier, Energy Convers. Manage., 2017, 140, 167–181 CrossRef.
- I. Terasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 685–687 CrossRef.
- H. Yakabe, K. Kikuchi, I. Terasaki, Y. Sasago and K. Uchinokura, Proceedings of the 1997 16th International Conference on Thermoelectrics, 1997, pp. 523–527 Search PubMed.
- W. Koshibae, K. Tsutsui and S. Maekawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6869–6872 CrossRef CAS.
- Y. Miyazaki, Solid State Ionics, 2004, 172, 463–467 CrossRef CAS.
- M. Shikano and R. Funahashi, Appl. Phys. Lett., 2003, 82, 1851–1853 CrossRef CAS.
- H. Fukutomi, Y. Konno, K. Okayasu, M. Hasegawa and H. Nakatsugawa, Mater. Sci. Eng., A, 2009, 527, 61–64 CrossRef.
- J. D. Baran, M. Molinari, N. Kulwongwit, F. Azough, R. Freer, D. Kepaptsoglou, Q. M. Ramasse and S. C. Parker, J. Phys. Chem. C, 2015, 119, 21818–21827 CrossRef CAS.
- R. Funahashi, I. Matsubara and S. Sodeoka, Appl. Phys. Lett., 2000, 76, 2385–2387 CrossRef CAS.
- J. Diez, E. Guilmeau, M. Madre, S. Marinel, S. Lemonnier and A. Sotelo, Solid State Ionics, 2009, 180, 827–830 CrossRef CAS.
- E. Combe, R. Funahashi, T. Barbier, F. Azough and R. Freer, J. Mater. Res., 2016, 31, 1296–1305 CrossRef CAS.
- T. Tsubota, M. Ohtaki, K. Eguchi and H. Arai, J. Mater. Chem., 1997, 7, 85–90 RSC.
- T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104 CrossRef.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2003, 350, 292–295 CrossRef CAS.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2005, 392, 306–309 CrossRef CAS.
- T. Kobayashi, H. Takizawa, T. Endo, T. Sato, M. Shimada, H. Taguchi and M. Nagao, J. Solid State Chem., 1991, 92, 116–129 CrossRef CAS.
- D. Flahaut, T. Mihara, R. Funahashi, N. Nabeshima, K. Lee, H. Ohta and K. Koumoto, J. Appl. Phys., 2006, 100, 084911 CrossRef.
- D. A. Muller, N. Nakagawa, A. Ohtomo, J. L. Grazul and H. Y. Hwang, Nature, 2004, 430, 657–661 CrossRef CAS PubMed.
- J. Li, Y. Wang, X. Yang, H. Kang, Z. Cao, X. Jiang, Z. Chen, E. Guo and T. Wang, Chem. Eng. J., 2022, 428, 131121 CrossRef CAS.
- R. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5828–5844 CrossRef CAS PubMed.
- S. Dahbi, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, Chem. Phys., 2021, 544, 111105 CrossRef CAS.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS PubMed.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- J. M. Flitcroft, I. Pallikara and J. M. Skelton, Solids, 2022, 3, 155–176 CrossRef CAS.
- W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 16405–16420 RSC.
- K. Brlec, K. B. Spooner, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2022, 10, 16813–16824 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. Ali and M. Yashima, J. Solid State Chem., 2005, 178, 2867–2872 CrossRef CAS.
- J. M. Kiat and T. Roisnel, J. Phys.: Condens. Matter, 1996, 8, 3471 CrossRef CAS.
- A. W. Hewat, Ferroelectrics, 1973, 6, 215–218 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- J. M. Skelton, D. S. D. Gunn, S. Metz and S. C. Parker, J. Chem. Theory Comput., 2020, 16, 3543–3557 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Porezag and M. R. Pederson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7830–7836 CrossRef CAS PubMed.
- J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452–12465 RSC.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- M. Morana, J. Wiktor, M. Coduri, R. Chiara, C. Giacobbe, E. L. Bright, F. Ambrosio, F. De Angelis and L. Malavasi, J. Phys. Chem. Lett., 2023, 14, 2178–2186 CrossRef CAS PubMed.
- J. C. Slater, J. Chem. Phys., 2004, 41, 3199–3204 CrossRef.
- Z. Zhang, K. Yuan, J. Zhu, X. Fan, J. Zhou and D. Tang, Appl. Phys. Lett., 2022, 120, 262201 CrossRef CAS.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- A. J. Ahmed, S. M. K. Nazrul Islam, R. Hossain, J. Kim, M. Kim, M. Billah, M. S. A. Hossain, Y. Yamauchi and X. Wang, R. Soc. Open Sci., 2019, 6, 190870 CrossRef CAS PubMed.
- S. P. Singh, N. Kanas, T. D. Desissa, M. Johnsson, M.-A. Einarsrud, T. Norby and K. Wiik, J. Eur. Ceram. Soc., 2020, 40, 401–407 CrossRef CAS.
- S. Ohta, T. Nomura, H. Ohta and K. Koumoto, J. Appl. Phys., 2005, 97, 034106 CrossRef.
- R. He, H. Wu, L. Zhang, X. Wang, F. Fu, S. Liu and Z. Zhong, Phys. Rev. B, 2022, 105, 064104 CrossRef CAS.
- F. Guyot, P. Richet, P. Courtial and P. Gillet, Phys. Chem. Miner., 1993, 20, 141–146 CrossRef CAS.
- H. J. Goldsmid, Proc. Phys. Soc., London, Sect. B, 1956, 69, 203 CrossRef.
- I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904 CrossRef.
- P.-C. Wei, S. Bhattacharya, J. He, S. Neeleshwar, R. Podila, Y. Y. Chen and A. M. Rao, Nature, 2016, 539, E1–E2 CrossRef CAS PubMed.
- R. Banerjee, S. Chatterjee, M. Ranjan, T. Bhattacharya, S. Mukherjee, S. S. Jana, A. Dwivedi and T. Maiti, ACS Sustainable Chem. Eng., 2020, 8, 17022–17032 CrossRef CAS.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- J. Tang and J. M. Skelton, J. Phys.: Condens. Matter, 2021, 33, 164002 CrossRef CAS PubMed.
- J. M. Skelton, J. Mater. Chem. C, 2021, 9, 11772–11787 RSC.
- B. Wei, J. M. Flitcroft and J. M. Skelton, Molecules, 2022, 27, 6431 CrossRef CAS PubMed.
- J. Cen, I. Pallikara and J. M. Skelton, Chem. Mater., 2021, 33, 8404–8417 CrossRef CAS.
- A. Krause, W. M. Weber, D. Pohl, B. Rellinghaus, A. Kersch and T. Mikolajick, J. Phys. D: Appl. Phys., 2015, 48, 415304 CrossRef.
- M. C. Oliveira, R. A. P. Ribeiro, E. Longo, M. R. D. Bomio, F. V. Motta and S. R. de Lazaro, Int. J. Quantum Chem., 2020, 120, e26054 CrossRef CAS.
- R. A. Evarestov and A. V. Bandura, J. Comput. Chem., 2012, 33, 1123–1130 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Kar, Electronic and optical properties of SrTiO3 perovskite using semi-local and hybrid first principles density functional theory, 2021 Search PubMed.
- M. Cardona, Phys. Rev., 1965, 140, A651–A655 CrossRef.
- M.-S. Lee and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165149 CrossRef.
- X.-L. Shi, H. Wu, Q. Liu, W. Zhou, S. Lu, Z. Shao, M. Dargusch and Z.-G. Chen, Nano Energy, 2020, 78, 105195 CrossRef CAS.
- J. Ravichandran, W. Siemons, D.-W. Oh, J. T. Kardel, A. Chari, H. Heijmerikx, M. L. Scullin, A. Majumdar, R. Ramesh and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165126 CrossRef.
- J. Wang, B.-Y. Zhang, H.-J. Kang, Y. Li, X. Yaer, J.-F. Li, Q. Tan, S. Zhang, G.-H. Fan, C.-Y. Liu, L. Miao, D. Nan, T.-M. Wang and L.-D. Zhao, Nano Energy, 2017, 35, 387–395 CrossRef CAS.
- S. Ohta, T. Nomura, H. Ohta, M. Hirano, H. Hosono and K. Koumoto, Appl. Phys. Lett., 2005, 87, 092108 CrossRef.
- S. LeBlanc, S. K. Yee, M. L. Scullin, C. Dames and K. E. Goodson, Renewable Sustainable Energy Rev., 2014, 32, 313–327 CrossRef CAS.
- A. Chatterjee, Z. Lan, D. V. Christensen, F. Bauitti, A. Morata, E. Chavez-Angel, S. Sanna, I. E. Castelli, Y. Chen, A. Tarancon and N. Pryds, Phys. Chem. Chem. Phys., 2022, 24, 3741–3748 RSC.
- D. Narducci, E. Selezneva, G. Cerofolini, S. Frabboni and G. Ottaviani, J. Solid State Chem., 2012, 193, 19–25 CrossRef CAS.
- A. A. Adewale, A. Chik, R. M. Zaki, F. C. Pa, Y. C. Keat and N. H. Jamil, Sustainable Mater., 2018, 3–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison of calculations on SrTiO3 to measurements on doped single crystals, calculated electronic band structures and density of states curves, calculated electron scattering rates, and plots showing the anisotropy in the calculated electrical transport properties, lattice thermal conductivity and thermoelectric figure of merit. See DOI: https://doi.org/10.1039/d3ma00624g |
| This journal is © The Royal Society of Chemistry 2024 |