Paving the way for future Ca metal batteries through comprehensive electrochemical testing of organic polymer cathodes

Abstract

The quest for new and more sustainable battery systems is leading us to frontiers of less visited and less understood battery chemistries. While many of these systems offer high theoretical energy densities, actual electrochemical performance is often quite poor, as well as plagued by high overpotential and side reactions, resulting in a limited understanding of their practical significance. In this work, we start from evaluating the Ca storage potential of three commercially available aromatic anhydrides. The best-performing building blocks were selected for polymerization. Practical performance of obtained polymers was investigated through a combination of 3-electrode and symmetric cell electrochemical testing. These tests revealed the intrinsic performance of polyimides and significant differences among perylene and naphthalene building blocks. The electrochemical mechanism was investigated through a combination of ex situ IR and SEM-EDS and revealed good reversibility as well as the presence of calcium cation–anion pairs. Experimental results are supported by density functional theory (DFT) calculations. The study demonstrates the importance of comprehensive testing of organic materials in multivalent batteries, reveals their potential for high energy density Ca metal–anode organic batteries, and outlines further necessary steps for their practical development and improved understanding.

---

Introduction

Energy storage is the biggest technological challenge of our current energy transition from fossil energy resources to renewables. Batteries are the best solution for short- to mid-term energy storage because they are compact, can be deployed in dispersed locations, and have good energy efficiency. However, the huge and rapidly growing market demand mainly driven by electromobility raises important concerns about the future availability and price of the materials used in contemporary Li-ion batteries. Many of them are already listed as critical raw materials (CRMs) by the European Union (Co, Li, Si, graphite).¹ List of CRMs was further expanded by the addition of Ni in 2022 by the United States Geological Survey due to increased demand and geopolitical instabilities connected with the war in Ukraine and resulting economic sanctions. This has incited researchers to search for alternative battery technologies that would be based on more abundant and geographically evenly distributed materials.

Multivalent batteries (Ca, Mg, Al) have elicited significant attention in recent years owing to the abundance of these elements and the high gravimetric and volumetric capacity of corresponding metal anodes.² Their downside is the higher standard redox potential compared to Li metal, 0.17 V for Ca metal, 0.67 V for Mg metal, and 1.38 V for Al metal, which would result in a lower potential of battery cells. In practice, the actual application of multivalent battery systems is still in the distant future due to the lack of both multivalent electrolytes and cathodes. In recent years, significant advances have been made in the field of multivalent electrolytes, but the insertion of multivalent cations into inorganic hosts still remains a significant challenge.³ This fact is mainly connected to the high charge density of multivalent cations, which leads to difficult desolvation, slow solid-state diffusion, and promotes irreversible conversion reactions instead of multivalent cation insertion.⁴ Thus far, a handful of inorganic cathodes has been reported, including Prussian blue analogues and metal sulfides, with significant drawbacks such as low redox potentials or poor cycling stability.^5,6 On the other hand, organic cathodes and sulfur have shown good electrochemical reversibility in multivalent electrolytes, opening an alternative path for multivalent battery development.⁷ Given the small difference in redox potential between Ca metal and Li metal, Ca metal-based batteries could offer a high-voltage alternative to Li-ion batteries while being based on abundant materials.

The main challenge on the metal anode side is the reductive decomposition of electrolytes promoted by the low redox potential of Ca metal.⁸ At the same time, calcium ions are unable to easily migrate through the passive metal anode layer that is formed. A major breakthrough in Ca electrolyte development was made by using Ca(BF₄)₂ in carbonates, which enabled Ca plating/stripping at elevated temperatures.⁹ Room temperature Ca plating and stripping was achieved by the use of Ca(BH₄)₂ in THF, which displayed good cycling efficiency, but limited oxidative stability and high chemical reactivity. Not too long ago, a calcium tetrakis(hexafluoroisopropyloxy)borate (Ca[B(hfip)₄]₂) salt was reported. The Ca[B(hfip)₄]₂ salt dissolved in 1,2-dimethoxyethane (DME) exhibits good oxidative stability while at the same time enabling reversible Ca metal plating/stripping. Additionally, Ca[B(hfip)₄]₂ is a non-nucleophilic salt, which allows the use of electrophilic cathodes such as sulfur and organic carbonyl compounds, thus bypassing poorly reversible insertion reactions.^10,11

The problems associated with the high charge density of calcium cations, which translate into problems with insertion into inorganic hosts, can be mitigated by the use of organic materials as cathodes. Organic compounds are a very diverse group of materials spanning various functional groups (conjugated carbonyls, disulfides, azo groups, nitriles, amines, ether oxides, thioethers, and nitroxide radicals).¹² They can undergo either an n-type or p-type electrochemical mechanism or even both (bipolar, e.g., nitroxide radicals). While p-type organics involve anion uptake to counterbalance the positive charge created in the process of oxidation, n-type organics undergo reduction followed by cation uptake. This implies that n-type compounds can be combined with metal anodes to yield high energy density batteries in which electrolyte concentration remains constant throughout cycling (i.e. lean electrolyte conditions). Moreover, some organic compounds can also be produced from abundant resources without the energy-intensive ceramic synthesis normally used to produce inorganic materials which could greatly decrease battery production footprint.¹³ On top of that, their structural tunability enables modification of both stability and redox potential through molecular engineering.¹⁴ An inherent drawback of organic materials is their low density and poor conductivity. The poor conductivity can be mitigated by the addition of conductive carbon, which results in a decrease in the gravimetric energy density and a further decrease in volumetric energy density of the final cell. However, the low volumetric capacity of the organic cathodes can be effectively compensated by the high volumetric capacity of the Ca metal anode, which is on par with Li metal.

Among the various n-type compounds, polyimides are highly perspective materials due to their high mechanical strength and excellent thermal stability.¹⁵ In this work, we take a detailed look at the electrochemical performance of different aromatic dianhydrides that can be readily used for the preparation of polyimide polymers. Dianhydrides and polyimides derived from them have been extensively studied in metal–organic Li batteries.^15–17 Dianhydrides can be polymerized with various linkers, allowing the preparation of highly variable polymers. In some cases, even electroactive compounds have been used, which prevents a decrease of the specific capacity due to the presence of non-active linkers.¹⁷ However, the application of imide-based polymers in divalent batteries has been mostly limited to Mg batteries. In Mg batteries, polyimides have displayed good reversibility with long-term capacity retention.^15,18 Both dianhydride and polyimide groups have been used as potential storage material for aqueous Mg and Ca batteries.^19,20 Due to the low redox potential of Ca and Mg metals, aqueous electrolytes cannot be considered a realistic approach for metal anode cells. Hence, the focus of battery research is on the development and application of non-aqueous electrolytes. However, practical research in non-aqueous setups is often plagued by the high overpotential of metal anode leading to poor cycling half-cell setups. The use of reference electrode can circumvent this limitation, but Ca metal reference electrode can easily get passivated leading to limited reliability.²¹ Recently, we have shown that the symmetric cell approach allows us to measure intrinsic organic electrode performance.²² In this work, we showcase the organic electrode development approach with detailed electrochemical and material characterization on a case study of different conjugated dianhydrides and derived polyimides in a state-of-the-art Ca battery setup employing a Ca[B(hfip)₄]₂-based electrolyte in glyme solvent. DFT modelling is used to correctly assign infrared (IR) bands and obtain deeper insight of the IR characterization of organic electrodes and improved understanding of electrochemical mechanism. By combining variable experiment setups and modelling, we illustrate the multi-step approach for direct comparison of different compounds in multivalent battery system.

Results and discussion

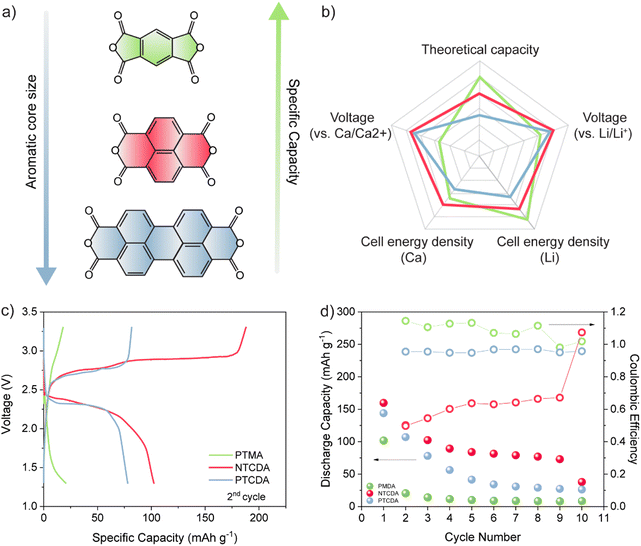
All selected dianhydrides (pyromellitic dianhydride (PMDA), 1,4,5,8-naphthalenetetracarboxylic dianhydride (NTCDA), and 3,4,9,10-perylenetetracarboxylic dianhydride (PTCDA)) have two electroactive carbonyl groups, but they differ in the number of conjugated aromatic rings and thus in their theoretical capacities. From the standpoint of theoretical values, PMDA has the highest capacity due to the smallest structure, followed by NTCDA and PTCDA. However, PMDA has the lowest redox potential, which means that the theoretical energy density differences are somewhat smaller than differences in dianhydride capacities. The difference in the energy density between PMDA and NTCDA is relatively small, while the PTCDA structure has a significantly lower theoretical value owing to the bulky inactive aromatic core (Fig. 1(a)). To assess the practical utilization, the electrochemical performance of the selected dianhydrides in Ca[B(hfip)₄]₂ (Fig. S1, ESI†) in DME was studied at a specific current of 50 mA g⁻¹. In the first discharge, capacities of 102, 160, and 145 mA h g⁻¹ were obtained for PMDA, NTCDA, and PTCDA, respectively. Although PMDA has the highest theoretical value of the specific capacity, the lowest molecular weight results in high solubility of this compound in the electrolyte, leading to an extremely rapid capacity decay, with less than 20% of the initial capacity retained in the second discharge. Low initial capacity observed in the case of this dianhydride could also be explained through high dissolution of the compound, but also relatively poor electrochemical utilization. Additionally, Coulombic efficiency higher than 100% indicates utilization of residual charged active material or possibility of side reactions. The bulkier NTCDA shows more stable cycling with a less severe capacity fade. A sudden drop in capacity in the first two cycles is followed by stabilization of value at about 80 mA h g⁻¹ in subsequent cycles. NTCDA demonstrated very poor Coulombic efficiency, with overcharging present throughout the cycling. Due to the repeatability of the observed phenomena, we believe this is associated with shuttling of dissolved species.²³ To confirm this hypothesis, we have cycled electrode consisting of carbon black and PTFE in Ca half-cell with electrolyte containing dissolved NTCDA species (Fig. S2, ESI†) and observed significant overcharging. The anhydride with low solubility in most organic solvents, PTCDA, shows a gradual decrease in capacity over 6 cycles, retaining about 25% of the original value in the 6th cycle.

Fig. 1 Graphical representation of PMDA, NTCDA and PTCDA electroactive groups (a). Spider chart comparison of theoretical capacity, voltage and energy density of all three anhydrides in Li and Ca setups (b). Comparison of galvanostatic cycles of PMDA, NTCDA and PTCDA in Ca half-cells at 50 mA g⁻¹ (c). Cycling stability and Coulombic efficiency of all three anhydrides in the first 10 cycles (d).

Another important difference between selected anhydrides in Ca cells is their voltage profile. In order to gain a comprehensive understanding of changes happening in the transition from monovalent to multivalent chemistry, all three materials were tested in LiTFSI DOL/DME electrolyte (Fig. S3, ESI†). NTCDA and PTCDA both show two well-defined plateaus with respect to Li/Li⁺ at about 2.6/2.4 V and 2.5/2.4 V, while in the case of calcium, only one plateau is observed at around 2.4 V for NTCDA and 2.3 V for PTCDA. This is a consequence of the divalence of the charge carriers in combination with a different type of electrolyte that was already observed for conjugated carbonyl compounds in the presence of multivalent cations.²⁴ PMDA, on the other hand, exhibits a single plateau in both systems, with an average discharge voltage of 2.2 V versus Li/Li⁺ and a significantly lower value of 1.7 V versus Ca/Ca²⁺.

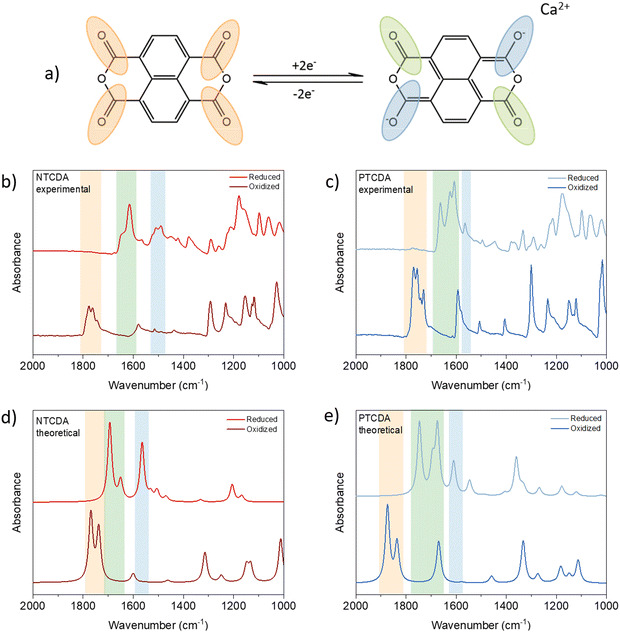
The reversibility of the electrochemical mechanism of anhydrides in Ca electrolytes can be investigated by IR spectroscopy.²⁵ The postulated mechanism assumes a reversible reduction of two of the four carbonyl groups, as Fig. 2(a) shows. In the infrared spectra, this can be followed by changes in the intensity of the band associated with carbonyl stretching. Upon reduction of active carbonyl groups, the formation of enolates can be identified by a new band appearing somewhere between 1300 and 1500 cm⁻¹ in the spectrum of reduced anhydrides. These changes can be followed either by ex situ or operando IR spectroscopy. Although operando tracking is more informative due to continuous monitoring, used setups can lead to the observation of artifacts when the electrode materials are highly soluble, as in the case of anhydrides.²⁶ Therefore, we decided to perform an ex situ analysis of anhydride-based cathodes.

Fig. 2 Schematics of the electrochemical mechanism of NTCDA (a). Experimental IR spectra of oxidized and reduced NTCDA (b) and PTCDA (c) cathodes in the range from 2000 to 1000 cm⁻¹. DFT calculated infrared spectra of oxidized and reduced NTCDA (d) and PTCDA (e).

A total of four sets of electrodes were prepared for each anhydride. To see the effects of soaking and washing, the pristine and soaked electrodes were compared. No significant differences between pristine and soaked electrodes were found in the spectra, confirming that soaking and washing did not affect the final spectra (Fig. S4, ESI†). The reduced (discharged) and oxidized (charged) electrodes were washed rapidly in 2 ml DME due to the solubility of the materials. As a result of the rapid washing, salt residues are present in both the oxidized and reduced cathodes and the peaks that appear in 1300 to 600 cm⁻¹ range partially originate from the salt anion and additionally complicate the analysis of the fingerprint region of the anhydrides. Accordingly, in this study, we focus on the changes in the carbonyl-related bands. (For full IR spectra see Fig. S5, ESI†).

As expected, all pristine anhydride electrodes show strong carbonyl peaks in the 1800–1700 cm⁻¹ region. In both NTCDA and PTCDA spectra, peaks corresponding to symmetric and asymmetric carbonyl stretching disappear upon reduction and reappear in subsequent charge, indicating the reversibility of electrochemical mechanism. In infrared spectra of reduced electrodes, new peaks can be observed at 1614 and 1505 cm⁻¹ in the case of NTCDA, which can be assigned to stretching of inactive carbonyl groups and newly formed C–O⁻ band.^27,28 PTCDA follows a similar pattern with stretching of unreacted C=O moving to lower frequencies at around 1664 and 1623 cm⁻¹ with C–O⁻ stretching appearing at 1563 cm⁻¹.¹⁹ When compared to DFT derived spectra, experimental data are in good agreement with minor differences in fingerprint region, where salt residue is still present and contributes to the final experimental spectra. As a consequence of poor electrochemical performance and severe solubility of discharged product, resulting in poor quality of infrared spectra, PMDA is omitted from detailed analysis (for infrared data of PMDA, see Fig. S5b, ESI†).

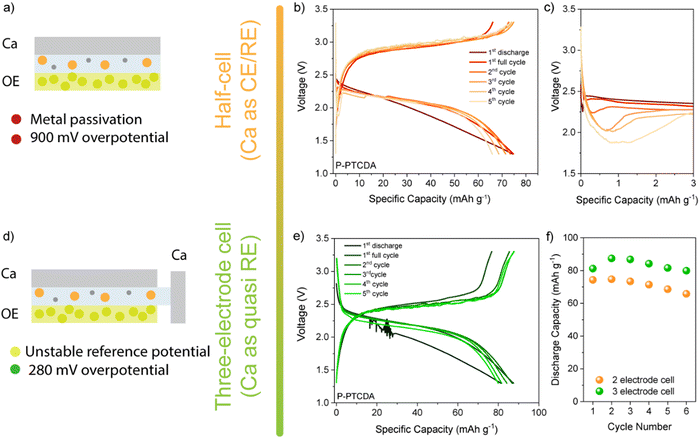
Despite high theoretical capacities, the high solubility of aromatic dianhydrides severely limits any practical applications. To improve cycling stability more stable polyimide polymers based on NTCDA- and PTCDA-based precursors (denoted as P-NTCDA and P-PTCDA), were synthesized. Polymerization is known to suppress solubility and lead to more stable galvanostatic cycling.^29,30 PMDA was excluded from the further investigation as it has shown very limited electrochemical reversibility and poor capacity utilization. A recent study compared the stability of different diimide linkers in Li, Na, and K batteries.³¹ Flexible aliphatic linker allowed for the highest capacity utilization and stability in these monovalent systems, which is why ethylenediamine was chosen as a linker in this study (for details of synthetic procedure and characterization, see Experimental and Fig. S6, ESI†). Polyimides were first cycled in a two-electrode setup (Fig. 3(a)). In the interest of simplicity, the results for P-NTCDA can be found in ESI† (Fig. S7); both polymers exhibit similar electrochemical behaviour. The sloping voltage curves are accompanied by a voltage dip at the beginning of the discharge half-cycle, which becomes more pronounced in each subsequent cycle. No capacity is observed in the sixth cycle, indicating blocking passivation of the metal anode surface, resulting in the cell failure.

Fig. 3 Illustration of the two-electrode setup (a), P-PTCDA performance in two-electrode setup (b) and zoomed-in discharge curves to show voltage dip (c). Illustration of three-electrode setup (d) and P-PTCDA performance in three electrode setup (e). Comparison between capacities of P-PTCDA obtained in two- and three-electrode setups (f).

The cycling of selected diimides and cycling of any other cathode against metallic calcium is severely limited by the anode. The gradual increase in the overpotential observed in galvanostatic cycling is accompanied by the appearance of the voltage dip at the beginning of the discharge curve. This phenomenon has been observed in the poly(anthraquinonyl)sulfide calcium (PAQS/Ca) battery and is attributed to the increase in the overpotential for Ca stripping.¹⁰ Although less severe than in the PAQS/Ca system, the gradual increase in the overpotential and voltage dip in diimide/Ca cells leads to eventual cell failure. These limitations imposed by the calcium metal anode prevent the assessment of the long-term cycling performance of Ca batteries. To circumvent the Ca metal anode passivation issue, we tested the polyimides in a three-electrode setup, using calcium metal as both the working and reference electrode (Fig. 3 bottom and Fig. S7c, ESI†). First, the transition to the three-electrode setup does not affect the shape of the galvanostatic curves, although a significant decrease in overpotential is observed (from 900 mV to 280 mV). The pronounced voltage drop that occurs in the two-electrode cells cannot be observed in the three-electrode cells, allowing longer galvanostatic cycling. The highest capacities obtained at 50 mA g⁻¹ were 88 mA h g⁻¹ for P-PTCDA and 83 mAh g⁻¹ for P-NTCDA, which is about 73% and 53% of the values obtained in Li, respectively (Fig. S8, ESI†). Note that low utilization of active sites in polymers is a critical problem that occurs in both magnesium and calcium batteries and is not unique to these polymers.³² It was suggested that low utilization is connected with poor redox active site availability and limited swelling of linear polymers.³³ Regardless of the incomplete utilization, the stability of cycling is significantly improved in polyimides compared to the monomers (NTCDA and PTCDA). Further optimization of the polymer structures by molecular engineering or hybridization with conductive carbons could help in the utilization of the active sites.^10,34

As the result above show, using Ca metal as both reference and counter electrode brings plethora of issues in electrochemical characterization of positive electrode materials. Use of three-electrode setup does solve some of the limitations imposed by the metal anode, but the problem of reliable reference electrode for multivalent systems still remains an issue. This is mostly due to poor stability of Ca metal reference and difficulty in obtaining adequate cell geometry. In order to avoid complicated cell assemblies, artefacts, and problems with reproducibility, we have tested both polymers in two-electrode symmetric cell setup. As described in our previous publication, these cells allow for fair comparison of electrode materials while not being constrained by metal anode performance or reference electrode artefacts.²² For detailed cell assembly procedure, see ESI† (Fig. S9). If we compare stability over 100 cycles of P-NTCDA and P-PTCDA in a symmetric cell setup (Fig. 4(a)), we observe much worse capacity retention compared to the result obtained in Li half-cells. Both polymers show great stability in Li-half cells, but, capacity fade of active material seems to be more severe in calcium electrolyte. If we compare observed performance of P-NTCDA with previously reported cycling in 2.5 M Ca(NO₃)₂ water-based electrolyte, both higher capacity and better stability are observed in aqueous electrolyte.²⁰ Inferior performance in ether-based electrolyte may be a consequence of the effect of poorer dissociation of Ca²⁺ in ether solvent, different complexation species leading to decreased stability, increased solubility of discharged species in non-aqueous Ca electrolyte, or some other phenomena.

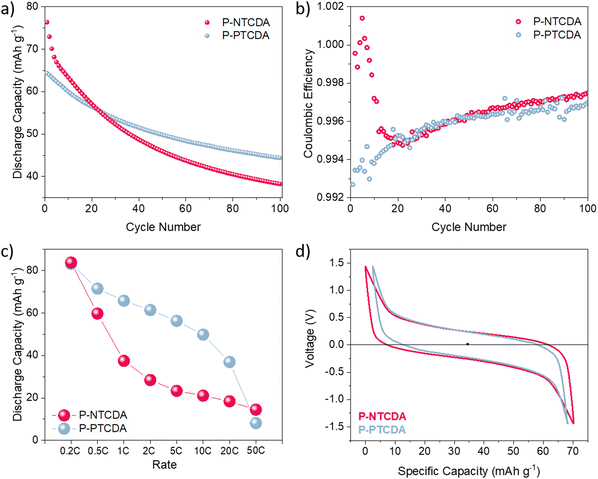Fig. 4 P-NTCDA (red) and P-PTCDA (blue) performance in symmetric cell setup. Stability over 100 cycles at 0.5C (a) and corresponding coulombic efficiency (b). Rate performance of symmetric cells (c). Comparison of voltage hysteresis obtained at 0.5C (5th cycle) (d). For non-shifted galvanostatic curves, see Fig. S10 (ESI†).

Elimination of Ca metal overpotential contribution allows for the assessment of overpotentials of P-NTCDA and P-PTCDA electrodes. In symmetric cell setup, measured hysteresis contains double contribution from the organic cathode of choice, as two electrodes of same composition are present in a cell. By dividing the hysteresis value to compensate for doubled contribution of organic electrode, we get the overpotential value for P-NTCDA to be 126 mV, and for P-PTCDA 116 mV. Flexible structures of organic polymers should allow for fast charging/discharging, giving them potential to find place in high-power density applications.³⁵ For this reason, rate performance of symmetric cells was compared at current ranging from 0.2C to 50C, and as Fig. 4(c) shows, P-PTCDA performs significantly better at higher rates, retaining 60% of the initial capacity at 10C. Overall, we can conclude that while P-PTCDA initially seems to be less favorable compound due to smaller theoretical capacity and lower initial capacity, it outperforms P-NTCDA in terms of capacity utilization and retention, as well as high-rate performance.

To further examine the electrochemical mechanism, polyimides were also subjected to ex situ IR analysis. The electrode preparation was the same as for the simple dianhydrides (for the effect of soaking and inactive component contribution to the spectra, see Fig. S10 and S11, ESI†). DFT calculations were performed to aid the peak assignation and allow for the comparison of experimentally obtained spectra with possible scenarios of one and two electron reduction. In pristine electrodes, peaks corresponding to symmetric and asymmetric C=O stretching that we will be focusing on in this analysis lie at 1700 and 1665 cm⁻¹ in the case of P-NTCDA or 1694 and 1663 cm⁻¹ in case of P-PTCDA. Note that in experimental spectra, the electrode that has not been subjected to any electrochemical cycling is referred to as “pristine” although it is fully oxidized, in order to distinguish between spectrum of the electrode that has not gone through any cycling and electrode that has been reduced and then re-oxidized.

As was the case with anhydrides, both polymers contain four carbonyl groups per repeating unit, but only two are reversibly participating in the electrochemical reaction. In complete two electron reduction, we would expect symmetric and asymmetric stretching of unreacted C=O to move to lower frequencies, with the appearance of new band corresponding to enolate formation C–O⁻ somewhere around 1500 cm⁻¹, similar to what is observed in anhydride building blocks. The position of C–O⁻ stretching can be affected by charge delocalization, so the peak can appear at higher wavenumbers, depending on the core structure. In the case of reduced polymers, C–O⁻ stretching band lies at 1514 for P-NTCDA (Fig. S13, ESI†) and 1520 cm⁻¹ for P-PTCDA (Fig. 5). The peak disappears upon subsequent oxidation, which points to the reversibility of the electrochemical mechanism in case of both polymers. Taking into the account the low capacity utilization, we have explored the possibility of one electron reduction in these materials with the help of DFT calculations. This allowed us to compare experimental spectra with theoretically derived ones and asses one and two electron reduction contributions. Experimental IR spectra of P-PTCDA reveals that there is still a small residue of non-reacted polymer in the discharge. The main contributions seem to be from both reduced electroactive groups that underwent two and one electron exchange, with a significantly larger contribution of the former as can be seen from comparison with theoretical spectra. In the case of P-NTCDA, there is significantly larger contribution of non-reacted polymer, which points to poor active material utilization of the active groups connected with limited electrochemical accessibility. This is in accordance with the observed electrochemical performance, where active material utilization in P-NTCDA reaches only 34% at 0.5C while this value goes up to almost 55% in the case of P-PTCDA. Differences in complexity of the real system and simplified theoretical model consisting of only single monomeric unit, neglecting intra and inter polymer chain interaction, (see Computational details) results in greater number of peaks being present in experimental spectra, with some peaks superimposing. Furthermore, due to omitting the usage of scaling factor for DFT results, a mismatch between theoretical and experimental frequencies is observed. We emphasize that this does not influence the reliability of peak assignation of experimentally observed spectra.

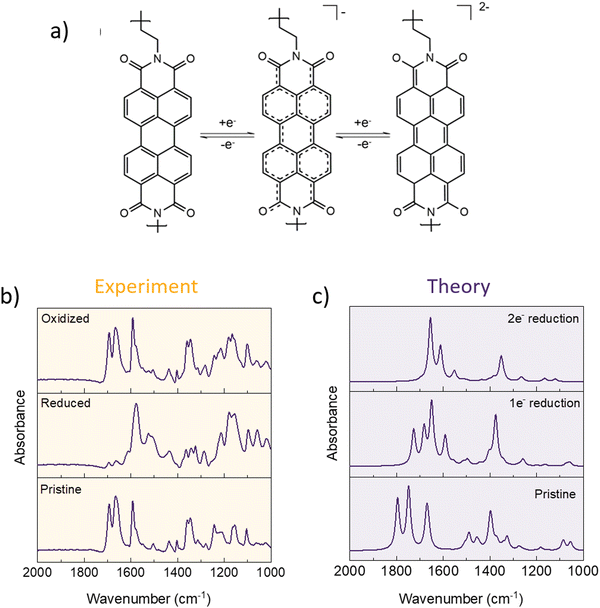Fig. 5 One and two electron reduction mechanism for P-PTCDA (a). Pristine, reduced, and oxidized spectra of P-PTCDA obtained experimentally (b). DFT derived IR spectra for fully oxidized, one electron reduction, and two electron reduction for P-PTCDA (c). For P-NTCDA spectra, see Fig. S13 (ESI†).

The energy density of multivalent metal–organic batteries depends strongly on the species that compensate the negative charge accumulated in organic active compounds during discharge.³⁶ To enable lean electrolyte conditions and maximize the energy density of the system, polymers derived from aromatic dianhydrides should store Ca²⁺ ions exclusively. To assess the coordination in polyimide polymers, we performed SEM/EDS and mass analysis of ex situ electrodes (Table 1 and Fig. S14, ESI†). Considering that the electrodes contain 60 wt% active material, we can estimate what the mass increase of the reduced electrodes would be in the two limiting cases, storage of Ca²⁺ or [CaB(hfip)₄]⁺ (CaA⁺) in the reduced polymer. If the coordination is done with Ca²⁺ ions only, and we assume complete capacity utilization, the expected mass increase would be about 8% for P-NTCDA or 6% for P-PTCDA. In the case of exclusive ion-complex coordination, the expected mass increase would be 255% for P-NTCDA or 207% for P-PTCDA because the two bulky monovalent Ca cation–anion pairs are needed for charge balance of fully reduced electroactive group. Based on mass increases observed in soaked electrodes, we can conclude that certain amount of salt cannot be washed out and it adds to the mass increase measured in case of ex situ electrodes. Taking into the account the capacity utilization, we can calculate expected increases in both borderline cases. In case of P-NTCDA utilization was 34% and exclusive Ca coordination would lead to the mass increase of 3% while exclusive monovalent coordination leads to the mass increase of 100%. In the case of P-PTCDA, utilization of 54% implies that the expected increase in the case of Ca²⁺ coordination would be around 3% while cation–anion pair coordination would yield 110% mass increase. Mass increases of 36% for P-NTCDA or 40% for P-PTCDA indicate presence of both divalent Ca cations and some monovalent ionic complexes, which is in accordance with previous estimation reported for PAQS cathode in the same electrolyte. Due to lack of standards and incomplete electrolyte removal during washing, exact ratios between Ca²⁺ and CaA⁺ ion pairs cannot be obtained. However, it is quite clear that the major coordinating species are Ca²⁺ ions with a substantial contribution of CaA⁺ ions.

Table 1 Atomic percentage of elements present in pristine, soaked, reduced, and oxidized P-NTCDA (in bold) and p-PTCDA (in italics) electrodes, measured by EDS; relative mass increase of electrodes

	C	N^a	O	F total	F active	Ca	Mass increase
a As N line lies between carbon and oxygen and overlaps with calcium, nitrogen cannot be detected with the high degree of certainty.
Pristine	85.5		8.6	4.9	—	—	—
Soaked	84.2	—	10.2	5.6	0.7	0.14	4%
Reduced	78.2	—	7.9	9.8	4.9	1.03	36%
Oxidized	85.3	—	9.1	5.4	0.5	0.12	4%
Pristine	86.8	—	7.6	5.6	—	—	—
Soaked	85.2	—	7.1	7.5	1.9	0.2	4%
Reduced	76.2	—	8.3	14.0	8.6	1.4	40%
Oxidized	86.0	—	6.4	6.1	0.5	0.2	4%

---

Conclusion

At the moment path towards practical Ca metal rechargeable batteries seems far from being straightforward due to the limited performance of Ca electrolytes as well as the insufficient performance of cathode materials. To advance practical research in this area, enhanced material characterization methodologies are essential. Herein, we have employed such methodology to investigate aromatic dianhydrides and their performance in calcium metal batteries. These organic compounds were tested in state-of-the-art chloride-free non-nucleophilic electrolyte with weakly coordinating anions. The reversibility of the electrochemical reaction was assessed by ex situ infrared spectroscopy aided by computationally modelled infrared spectra to gain deeper insights into the electrochemical mechanism of electroactive groups. The synthesis of polyimides derived from NTCDA and PTCDA mitigated the solubility of anhydrides. The performance of the two-electrode cell was greatly affected by the passivation of the calcium metal anode. When the organic polymers were used in a three-electrode cell, higher stability was observed with significantly reduced overpotential. In order to enable direct comparison between the two polymers and extract organic material performance, we tested them in two electrode symmetric cell setup. Symmetric cell investigation enabled both high-rate and long-term testing, which revealed that P-PTCDA shows better stability, better rate performance, and better capacity utilization. Additionally, the overpotential of P-PTCDA is smaller than P-NTCDA. Finally, the coordinating species assessed through ex situ EDS analysis revealed that the coordination predominantly occurred with Ca²⁺ ions, indicating the potential for future high energy density Ca-organic batteries. The results demonstrate the feasibility of using aromatic anhydrides as the basis for new organic-based cathode materials. However, significant advancements are needed to increase their practical capacity utilization as well as long-term capacity retention. Together with the simultaneous development of new electrolytes that allow reversible plating and stripping at room temperature and improved cation dissociation, calcium metal batteries should be able to reach their full potential. This remains a far stretch, but with the combination of complementary electrochemical and material characterization tools as well as computation modelling, researchers should be better equipped to address these challenges.

Experimental

Materials

Pyromellitic dianhydride (PMDA, Alfa Aesar, 97%), 1,4,5,8-naphthalenetetracarboxylic dianhydride (NTCDA, abcr, 96%), 3,4,9,10-perylenetetracarboxylic dianhydride (PTCDA, Sigma-Aldrich, 97%), ethylenediamine (Sigma-Aldrich, synthesis grade), Printex XE2 carbon black, polytetrafluoroethylene (PTFE) water dispersion (60% in water, Sigma-Aldrich), and calcium borohydride bis(tetrahydrofuran) (Sigma-Aldrich) were used as received. 1,2-Dimethoxyethane (DME) (Sigma-Aldrich, HPLC grade, 99.9%) was dried with 4 Å molecular sieves for several days, refluxed with Na/K alloy (ca. 1 ml l⁻¹) overnight and afterwards subjected to fractional distillation. 1,1,1,3,3,3-Hexafluoropropan-2-ol (HFIP) (Apollo Scientific, 99.9%) and hexane (Carlo Erba) were dried with 4 Å molecular sieves inside an Ar-filled glovebox for several days. Final water content was determined by Karl–Fischer titration (<1 ppm).

Salt and polymer synthesis

Salt¹⁰ and polymers³¹ we synthesized through previously reported procedure. For details of the procedure with chemical characterization, see ESI† (Fig. S1 and S5).

Electrochemical characterization

The cathodes were prepared by mixing the active materials with Printex XE2 and PTFE in a weight ratio of 6 : 3 : 1. The components were dispersed in isopropanol and ball milled on a Retsch PM100 at 300 rpm for 30 minutes. The resulting rubbery slurry was then rolled between a glass plate and a sheet of parchment paper. Self-standing electrodes (12 mm) were cut, dried overnight, and placed in an Ar-filled glovebox. Active material loading ranged between 2.5–3.0 mg cm⁻². Two- and three-electrode Swagelok-type cells were used for all electrochemical tests. In three electrode setup, Ca metal was used as the counter electrode. Ca shots (Alfa Aesar, 1 cm and down, 99%) were punched into 12 mm discs and scratched with a spatula until a shiny surface was formed. Glassy fibers GF/A were used as separators. Each cell contained 130 μl of 0.2 M Ca[B(hfip)₄]₂/DME. Electrochemical tests were performed in galvanostatic mode using the VMP3 potentiostat from Bio Logic S. A. The largest uncertainty in measuring specific capacity originates from the weighing error of the active material electrode, which is ±0.1 mg, which translates to a mistake of around 5% in the capacity estimation of our electrodes.

Symmetric cell assembly

Before symmetric cells were assembled, one electrode was discharged versus metal calcium with C/10 down to 1.3 V, and the voltage was held for 12 h (until the current dropped to the value corresponding to C/100). Discharged cell was transferred inside an Ar-filled glovebox where it was disassembled. Discharged electrode was then paired with pristine, fully charged, electrode. Mass deviation between electrodes was no more than 5%. Fresh glassy fiber separator and additional 90 μl of Ca[B(hfip)₄]₂/DME were added. Voltage window for symmetric cell cycling was calculated according to the average discharge voltage of organic electrodes, and in this case was between −1.4 and 1.4 V.

Ex situ IR spectroscopy

IR characterization was carried out in an Ar-filled glovebox using ATR-IR Alpha II (Bruker) with Ge crystal. Measurements were performed in the range 4000 to 600 cm⁻¹ with a resolution of 4 cm⁻¹. The cathodes for the ex situ measurements were discharged and charged at 0.5C to achieve high capacity utilization. The cathodes were then removed from the stainless-steel plunger and washed three times for 2 minutes in 2 ml of fresh DME. Because of the high solubility of anhydrides in the discharged state, the washing was performed quickly, and some salt residue is still present in the recorded IR spectra.

SEM/EDS analysis

SEM/EDS analysis was conducted on FE-SEM Supra 35 VP Carl Zeiss, at accelerating voltage of 20 kV using Oxford Instrument Ultim Max 100 EDS detector. Electrodes were discharged and charged at 0.5C to the cut-off voltage of 1.3 and 3.3 V, respectively, and washed two times in 2 ml DME, dried inside the glovebox, and transferred to the microscope using the vacuum stage sample holder.

Computational details

Density functional theory calculations were performed by Gaussian 16 software.³⁷ Full geometry optimization was done, followed by computation of harmonic vibrational frequencies and IR intensities. M06-2X hybrid functional³⁸ was used for both PTCDA and NTCDA. In the case of PTCDA, 6-31+G(d,p) basis set was used, whereas in the case of NTCDA a more accurate AUG-cc-pVTZ basis set was used. The choice for different basis sets stems from the much larger number of atoms in the case of PTCDA, calling for reduced accuracy. However, it has been shown before that 6-31+G(d,p) basis set is accurate enough to get reliable computed vibrational IR spectra.²⁵ To describe the surrounding environment, a dielectric continuum with dielectric constant of 7.4 was used, as implemented in polarizable continuum model.

All polymeric structures were modelled with a monomeric unit ending with methyl groups. This introduces two approximations that can influence theoretical IR spectra:

(1) The polymeric structure is not taken into the account, thus the environment of the molecule is idealized, and described only by polarizable continuum model, as discussed above. Additionally, we expect that the molecule itself, modelled with one unit instead of a larger number of units, demonstrates a slightly different electronic structure. Increasing the number of monomeric units in the theoretical model would presumably slightly improve the accuracy of the obtained IR spectra, but the computational cost would increase drastically. As we are interested only in the trend of IR vibrational frequencies that allows peak assignation, the influence that this approximation has on the reliability of theoretical spectra is insignificant.

(2) The methyl groups introduce additional vibrational frequencies into the IR spectra. However, these vibrations are in the fingerprint region and their intensity is not high. Thus, this approach has no actual effect on the peak assignation presented in this work.

It is commonly observed that theoretical DFT models used to calculate IR spectra overestimate the frequencies by 5–10%. The discrepancies between theoretical and experimental results are attributed to approximations, such as harmonic approximation and implicit treatment of surroundings, that are done in DFT calculations. To minimize these discrepancies and obtain better visual agreement of theoretical and experimental IR spectra, often a scaling factor is used. We emphasize that no scaling factor was used in this manuscript. The qualitative trend of theoretical data is in the agreement with experimentally obtained spectra, thus supporting experimentally based result analysis and allowing reliable vibrational assignations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 860403 and Slovenian Research Agency through research programs P2-0423 and research projects J2-4462 and N2-0279.

References

1. S. Bobba, S. Carrara, J. Huisman, F. Mathieux and C. Pavel, Critical Raw Materials for Strategic Technologies and Sectors in the EU – a Foresight Study, 2020.
2. A. Ponrouch, J. Bitenc, R. Dominko, N. Lindahl, P. Johansson and M. R. Palacin, Energy Storage Mater., 2019, 20, 253–262.
3. L. Stievano, I. de Meatza, J. Bitenc, C. Cavallo, S. Brutti and M. A. Navarra, J. Power Sources, 2021, 482, 228875.
4. P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341.
5. T. N. Vo, J. Hur and I. T. Kim, ACS Sustainable Chem. Eng., 2020, 8, 2596–2601.
6. Z. Li, B. P. Vinayan, P. Jankowski, C. Njel, A. Roy, T. Vegge, J. Maibach, J. M. G. Lastra, M. Fichtner and Z. Zhao-Karger, Angew. Chem., Int. Ed., 2020, 59, 11483–11490.
7. J. Bitenc and R. Dominko, Front. Chem., 2018, 6, 634.
8. Q. Wei, L. Zhang, X. Sun and T. L. Liu, Chem. Sci., 2022, 13, 5797–5812.
9. A. Ponrouch, C. Frontera, F. Bardé and M. R. Palacín, Nat. Mater., 2016, 15, 169–172.
10. J. Bitenc, A. Scafuri, K. Pirnat, M. Lozinšek, I. Jerman, J. Grdadolnik, B. Fraisse, R. Berthelot, L. Stievano and R. Dominko, Batteries Supercaps, 2021, 4, 214–220.
11. A. Scafuri, R. Berthelot, K. Pirnat, A. Vizintin, J. Bitenc, G. Aquilanti, D. Foix, R. Dedryvère, I. Arčon, R. Dominko and L. Stievano, Chem. Mater., 2020, 32, 8266–8275.
12. P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120, 6490–6557.
13. T. B. Schon, B. T. McAllister, P.-F. Li and D. S. Seferos, Chem. Soc. Rev., 2016, 45, 6345–6404.
14. R. B. Araujo, A. Banerjee, P. Panigrahi, L. Yang, M. Strømme, M. Sjödin, C. M. Araujo and R. Ahuja, J. Mater. Chem. A, 2017, 5, 4430–4454.
15. P. Sharma, D. Damien, K. Nagarajan, M. M. Shaijumon and M. Hariharan, J. Phys. Chem. Lett., 2013, 4, 3192–3197.
16. Z. Song, H. Zhan and Y. Zhou, Angew. Chem., Int. Ed., 2010, 49, 8444–8448.
17. B. Tian, G.-H. Ning, W. Tang, C. Peng, D. Yu, Z. Chen, Y. Xiao, C. Su and K. P. Loh, Mater. Horiz., 2016, 3, 429–433.
18. T. Bančič, J. Bitenc, K. Pirnat, A. Kopač Lautar, J. Grdadolnik, A. Randon Vitanova and R. Dominko, J. Power Sources, 2018, 395, 25–30.
19. I. A. Rodríguez-Pérez, Y. Yuan, C. Bommier, X. Wang, L. Ma, D. P. Leonard, M. M. Lerner, R. G. Carter, T. Wu, P. A. Greaney, J. Lu and X. Ji, J. Am. Chem. Soc., 2017, 139, 13031–13037.
20. S. Gheytani, Y. Liang, F. Wu, Y. Jing, H. Dong, K. K. Rao, X. Chi, F. Fang and Y. Yao, Adv. Sci., 2017, 4, 1700465.
21. D. S. Tchitchekova, D. Monti, P. Johansson, F. Bardé, A. Randon-Vitanova, M. R. Palacín and A. Ponrouch, J. Electrochem. Soc., 2017, 164, A1384–A1392.
22. O. Lužanin, J. Moškon, T. Pavčnik, R. Dominko and J. Bitenc, Batteries Supercaps, 2023, 6, e202200437.
23. V. W. Hei Lau, I. Moudrakovski, J. Yang, J. Zhang and Y. M. Kang, Angew. Chem., Int. Ed., 2020, 59, 4023–4034.
24. K. Hernandez-Burgos, G. Rodriguez-Calero, W. Zhou, S. E. Burkhardt and H. D. Abruña, J. Am. Chem. Soc., 2013, 135, 14532–14535.
25. A. Vizintin, J. Bitenc, A. Kopač Lautar, K. Pirnat, J. Grdadolnik, J. Stare, A. Randon-Vitanova and R. Dominko, Nat. Commun., 2018, 9, 661.
26. J. Bitenc, A. Vizintin, J. Grdadolnik and R. Dominko, Energy Storage Mater., 2019, 21, 347–353.
27. M. Ghosh, V. Vijayakumar, M. Kurian, S. Dilwale and S. Kurungot, Dalton Trans., 2021, 50, 4237–4243.
28. L. Tao, J. Zhao, J. Chen, C. Ou, W. Lv and S. Zhong, Nanoscale Adv., 2021, 3, 3199–3215.
29. Y. Lu and J. Chen, Nat. Rev. Chem., 2020, 4, 127–142.
30. A. Banerjee, N. Khossossi, W. Luo and R. Ahuja, J. Mater. Chem. A, 2022, 10, 15215–15234.
31. C. N. Gannett, J. Kim, D. Tirtariyadi, P. J. Milner and H. D. Abruña, Chem. Sci., 2022, 13, 9191–9201.
32. H. Wang, M. Mao and C. Wang, Macromol. Rapid Commun., 2022, 43, 2200198.
33. X. Wang, H. Dong, A. Eddine Lakraychi, Y. Zhang, X. Yang, H. Zheng, X. Han, X. Shan, C. He and Y. Yao, Mater. Today, 2022, 55, 29–36.
34. J. Bitenc, N. Lindahl, A. Vizintin, M. E. Abdelhamid, R. Dominko and P. Johansson, Energy Storage Mater., 2020, 24, 379–383.
35. C. N. Gannett, L. Melecio-Zambrano, M. J. Theibault, B. M. Peterson, B. P. Fors and H. D. Abruña, Mater. Rep.: Energy, 2021, 1, 100008.
36. H. Dong, Y. Liang, O. Tutusaus, R. Mohtadi, Y. Zhang, F. Hao and Y. Yao, Joule, 2019, 3, 782–793.
37. M. J. Frisch et al. , Gaussian 16 (Revision C.02), Gaussian Inc., Wallingford CT, 2019.
38. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00805c

---