Open Access Article
Open Access ArticleCharacterization of FeS2 pyrite microcrystals synthesized in different flux media†
Katriin
Kristmann
 *a,
Taavi
Raadik
a,
Mare
Altosaar
a,
Mati
Danilson
*a,
Taavi
Raadik
a,
Mare
Altosaar
a,
Mati
Danilson
 a,
Jüri
Krustok
a,
Peeter
Paaver
b and
Yuriy
Butenko
c
a,
Jüri
Krustok
a,
Peeter
Paaver
b and
Yuriy
Butenko
c
aDepartment of Materials and Environmental Technology, Tallinn University of Technology, Ehitajate Tee 5, 19086, Tallinn, Estonia. E-mail: katriin.kristmann@taltech.ee
bInstitute of Ecology and Earth Sciences, Tartu University, Ülikooli 18, 50090, Tartu, Estonia
cEuropean Space Research and Technology Centre (ESTEC), Keplerlaan 1, 2201 AZ, Noordwijk, The Netherlands
First published on 22nd December 2023
Abstract
Pyrite FeS2 has significant promise as a low-cost, earth-abundant photovoltaic material and has thus been the focus of solar energy researchers for years. Despite the effort, its efficiency has remained at around 3%, much lower than what is expected from the material properties. The inability to understand and control the effects of impurities in pyrite has increased difficulties in fabricating successful pyrite solar cells. Recent reports have shown evidence of phosphorus and cobalt as prospective dopants for improved optoelectronic properties and charge separation. Here, we demonstrate the optoelectric effects of alkali metal impurities in pyrite by synthesizing highly crystalline n-type pyrite microcrystals in different growth media. We find that the synthesis medium affects the impurity content of the final material. Alkali metals such as lithium, sodium, potassium, and cesium in pyrite are shown to create defect levels that cause the Fermi level to increase from −5.15 to −4.56 eV, depending on the amount of the impurity. Creation of solid solutions is suggested by the increased energy of the valence band maximum (EVBM) from −6.17 to −5.52 eV. We show how much the concentration of these impurities can be reduced via recrystallization of FeS2 crystals in molten salt to lower the energies of the EVBM and Fermi levels. The effect of impurities on the photoluminescence emission of pyrite is well linked to the changes in the energy band diagram.
Introduction
Iron pyrite is the most abundant sulfide mineral. Synthetic single-crystalline and high-purity FeS2 (iron disulfide of pyrite structure) is an n-type (S-vacancy-doped) semiconductor. Pyrite has many physical properties that are attractive for an absorber material in photovoltaic solar energy converters. Pyrite has a bandgap of 0.95 eV, a high light absorption coefficient (>105 cm−1), and high carrier mobility.1–3 These properties and the abundance of inexpensive, nontoxic constituent elements make pyrite a desirable solar energy absorber material for large-scale energy production.4,5 It has been compared that a pyrite solar cell with only 4% efficiency could produce electricity for the same price as a 19% efficient silicon solar cell.6 Pyrite absorbers have also been considered for extraterrestrial solar applications because of their low energy input for extraction and production, making them a great candidate for power production in the lunar base concept7 and for the approach of space-based solar power satellites manufactured on the Moon.8However, the solar energy conversion efficiencies of FeS2-based devices have never exceeded 3%.4,9 These low efficiencies are caused by low VOC values in pyrite devices, attributed to the formation of a very thin p-type surface inversion layer on n-type pyrite crystals, which forms a leaky internal junction.10,11 This phenomenon is more noticeable in thin films where the surface-to-bulk ratio is higher than in single crystals. There are a lot of studies in the literature that are focused on the reasons and mechanisms of this surface layer formation11–13 and on the removal of the surface layer by chemical or electrochemical etchings.14
Recently, Voigt et al.15 demonstrated a possibility to mitigate the internal p–n junction by fabricating metallic CoS2 contacts via a process that simultaneously diffuses Co (a shallow donor) into the FeS2 crystal, yielding direct Ohmic contact to the interior. A more recent study of the same research group9 presents a perfect detailed overview of the research history of pyrite FeS2 over more than 30 years and proposes to form homojunctions via p-type doping of single-crystalline FeS2 with phosphorus (P). They found experimentally that the P-acceptor turns FeS2 from n-type to p-type and allows it to form a homojunction. They determined the acceptor level at 175 ± 10 meV above the valence band maximum. This study opened the door to overcome the historical inability to understand and control the p-type doping in pyrite FeS2 and provided new opportunities for solar cells based on this extraordinary semiconductor.9
In the present work, the synthesis-growth method in molten salts is used to produce FeS2 monograin powder crystals. The individual powder particles formed in this process are mainly single crystals, as found in our previous study.16 FeS2 monograin powder crystals, grown in molten potassium iodide (KI), exhibited n-type conductivity, and had charge carrier concentrations around 1017 cm−3, as found from capacitance–voltage measurements of n-type FeS2/p-type NiO heterostructures and FeS2/Pt Schottky diodes.
For making the above-mentioned heterostructures, FeS2 powder crystals of uniform size were fixed in a thin layer of epoxy, thus forming a monograin membrane (used also as the absorber layer in monograin membrane solar cells).17,18 In the present study, we study the effect of different flux salts on the properties of pyrite FeS2 crystals as the constituent elements of salts are incorporated into the FeS2 crystals during the synthesis-growth process. The obtained different FeS2 microcrystals fixed in the form of monograin membranes can be used as absorber layers in monograin layer (MGL) solar cells. MGL technology has not been used for pyrite solar cells before, and it has some unique advantages, such as the possibility to separate the production of absorber crystals from the preparation of the solar cell stack. The synthesis conditions (temperature and sulfur vapor pressure) of the absorber material can be accurately controlled and the process may proceed at higher temperatures than those possible in thin film technologies, thanks to monograin powder synthesis-growth in sealed quartz ampoules.17–19
During the synthesis of pyrite crystals in the liquid salt medium, the precursors (and their residual impurities) and the formed FeS2 dissolve in the liquid phase up to their solubility limit at the synthesis temperature. After the formation reaction, the FeS2 solid particles start to recrystallize and grow at the expense of the dissolved material, following the Ostwald ripening mechanism.20 In the present study, we use different alkali metal salts in the synthesis process, and therefore there is a question about the doping of pyrite crystals with constituent elements of the used salts.
It is known that halogens in pyrite behave as donors.21 The effects of doping with transition metals (originating in this work from FeS precursors of different purities) have also been studied previously. It was found that transition metals cause changes in the band gap energies at different doping levels.22 Cobalt was found to increase the free electron concentration and therefore was termed as a n-type dopant,23,24 while nickel and chrome did not affect the free electron concentration in pyrite so extensively. 23,24 It has been suggested that cobalt on an iron site (CoFe) is a very shallow donor and nickel on the iron site (NiFe) is a very deep donor at a level around the middle of the band gap. Other metals are expected to incorporate into the pyrite lattice via a substitution process.25,26 At greater doping densities, CrFe is a deep but extremely poor donor that becomes increasingly compensated.24 Since CrS2 does not crystallize in the pyrite structure, it is also not beneficial to use it as a dopant. All the transition metal impurities were thought to increase the pyrite lattice constant.22,26,27
Group 5 and 6 nonmetal impurities have been found to occupy a vacant sulfur site. The arsenic impurity mainly affects the electronic structure at shallow and deep valence bands, while selenium and tellurium impurities were found to affect the electronic structures at deep valence bands of pyrite.26 Based on the calculations, it was suggested that As-, Se-, and Te-substituted pyrites exhibit p-type conductivity. This agrees quite well with the experimental findings of Voigt et al.9 Pyrite also has native defects and strong evidence shows that S-vacancy (VS)-based native defects are present and are responsible for the unintentional bulk n-doping in pyrite crystals.15,28 Experiments have identified an ∼225 meV deep donor and linked it to VS. The doping effect of alkali metals (lithium, sodium, potassium, and cesium) in pyrite has not been sufficiently studied. However, the influence of doping with alkali metals in other semiconductor compounds has been intensively investigated. It was found that alkali doping is crucial for a wide range of chalcogenide materials used for photovoltaics (CdTe, Cu(In,Ga)Se2, Cu2ZnSn(S,Se)4) and thermoelectricity (Pb(S,Se,Te)) up to superconductivity (KFeSe2) and for two-dimensional materials (MoS2 and WSe2).29 Alkali doping helped to increase the efficiency of Cu(In,Ga)Se2 (CIGS)-based solar cells. It has been commonly agreed that doping with alkali elements passivates the defects at the p-type CIGS absorber surface or at grain boundaries. It does not change the acceptor concentration but decreases the compensating donors’ concentration.30 As the free carrier density is determined by the difference in acceptor and donor concentrations, the p-type carrier concentration increases, and as a result, the Fermi level (EF) is lowered. Thus, an enlarged EF difference will produce higher VOC and FF values.31
In our previous work, we found the synthesis-growth conditions for pyrite monograin powders in molten potassium iodide (KI).7,16 In the present work, using different flux salts, we study the effects of different alkali metal iodides on the morphology and physical properties of pyrite crystals. We determine the concentrations of flux salts’ constituent elements grown into the formed pyrite crystals. We report the photoluminescence (PL) spectra of the materials and determine the Fermi levels and valence band maxima positions of FeS2 grown in different molten alkali metal salts. We also discover a method to significantly decrease the content of Cu-impurity in the pyrite crystals, opening a discussion for the possibility to control the level of different impurities in pyrite by recrystallizing it in large amounts of a flux salt.
Experimental
Pyrite microcrystals in the monograin powder form were produced by the molten flux synthesis-growth method, and for comparison, as a polycrystalline powder (without any added flux salt). FeS powder (3N) acquired from Thermo Scientific and S powder (5N) acquired from Alfa Aesar were used as precursors for FeS2 synthesis. The precursors, FeS and S, were weighted in amounts necessary for the synthesis of stoichiometric FeS2. Quartz ampoules were filled with these precursors and the respective flux materials. Different flux materials (KI, LiI, CsI and Na2Sx, where x > 2) were added into individual separate ampoules to ensure the formation of liquid phase of flux during the high temperature synthesis-growth process. Flux salts were taken in amounts providing the volume of the formed liquid phase approximately equal to the volume of solid FeS2. With this volume ratio, it is guaranteed that the solid FeS2 powder particles, formed in the synthesis reaction, start to grow separately, which are pushed apart from each other by repulsive capillary forces.20 For comparison, the synthesis of FeS2 was performed without the presence of any flux material with the aim to produce FeS2 polycrystalline powder. Later, the FeS2 monograin powder material, originally synthesized in KI with equal volumes of liquid and solid phases (Vliquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KI = Vsolid
KI = Vsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeS2), was recrystallized in four- and ten-times higher amounts of KI with the purpose of removing some impurities from pyrite by the effect of distribution of impurities between liquid and solid phases. For recrystallization, the portions of pyrite powder were loaded into quartz ampoules with 4 times (Vliquid
FeS2), was recrystallized in four- and ten-times higher amounts of KI with the purpose of removing some impurities from pyrite by the effect of distribution of impurities between liquid and solid phases. For recrystallization, the portions of pyrite powder were loaded into quartz ampoules with 4 times (Vliquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KI = 4 Vsolid
KI = 4 Vsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeS2) and 10 times bigger (Vliquid
FeS2) and 10 times bigger (Vliquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KI = 10 Vsolid
KI = 10 Vsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeS2) amount of KI as the flux material. The ampoules were heated in the furnace for 10 days at 690 °C (see Table 1). To obtain even higher purity pyrite, a FeS precursor of 4N purity (instead of the previous 3N) was purchased from Apollo Scientific and used to synthesize pyrite in the KI flux (Vliquid
FeS2) amount of KI as the flux material. The ampoules were heated in the furnace for 10 days at 690 °C (see Table 1). To obtain even higher purity pyrite, a FeS precursor of 4N purity (instead of the previous 3N) was purchased from Apollo Scientific and used to synthesize pyrite in the KI flux (Vliquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KI = Vsolid
KI = Vsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeS2). Synthesis temperatures were chosen so that the synthesis would proceed at a temperature higher than the melting point of the used flux material. The melting temperatures of KI, LiI, CsI, and Na2Sx are 681 °C, 469 °C, 621 °C, and 400 °C, respectively.32,33 Thus, the synthesis temperatures were set as 690 °C for the iodide salts and 475 °C for Na2Sx flux (see Table 1, Results and discussion). All the ampoules were heated for 10 days. Fig. 1 shows the FeS2 powder production steps and Table 1 shows the used flux salts, precursors, synthesis temperatures, and the compositions of obtained FeS2 materials.
FeS2). Synthesis temperatures were chosen so that the synthesis would proceed at a temperature higher than the melting point of the used flux material. The melting temperatures of KI, LiI, CsI, and Na2Sx are 681 °C, 469 °C, 621 °C, and 400 °C, respectively.32,33 Thus, the synthesis temperatures were set as 690 °C for the iodide salts and 475 °C for Na2Sx flux (see Table 1, Results and discussion). All the ampoules were heated for 10 days. Fig. 1 shows the FeS2 powder production steps and Table 1 shows the used flux salts, precursors, synthesis temperatures, and the compositions of obtained FeS2 materials.
| Fe/at% | S/at% | Material | Flux | Synth. T (°C) |
|---|---|---|---|---|
| 33.5 | 66.5 | FeS2 | KI | 690 |
| 33.0 | 67.0 | FeS2 | LiI | 690 |
| 33.7 | 66.3 | FeS2 | CsI | 690 |
| 33.3 | 66.7 | FeS2 | Na2Sx | 475 |
| 34.0 | 66.0 | FeS2 | — | 500 |
| 33.8 | 66.2 | FeS2 | KI (4× volume) | 690 |
| 33.9 | 66.1 | FeS2 | KI (10× volume) | 690 |
| 33.9 | 66.1 | FeS2, 4N FeS precursor | KI | 690 |
The materials’ properties were studied using different analytical methods with the goal to use them as absorber layers in monograin layer solar cells. The chemical composition of FeS2 powder crystals was determined via energy dispersive X-ray spectroscopy (EDX) using a Bruker Esprit 1.8 system. The morphology of crystals was studied using the high-resolution scanning electron microscope (HR-SEM), Zeiss ULTRA 55. The phase composition of the synthesized FeS2 powders was confirmed using X-ray diffraction (XRD) and Raman spectroscopy methods. Raman spectra were recorded using the Horiba LabRam HR800 spectrometer equipped with a multichannel CCD detection system in the backscattering configuration. The 532 nm laser line with a spot size of 5 μm was applied for excitation. XRD patterns were recorded on a Rigaku Ultima IV diffractometer undergoing Cu Kα radiation (λ = 1.5406 Å). PDXL 2 software was used for the derivation of crystal structure information from the recorded XRD data. Impurities in powder materials were determined by TOF-SIMS 5 using IONTOF. Oxygen etching at 2 keV was used for the negative mode measurement, while cesium etching at 0.5–1 keV was used for the positive mode. The measurements were carried out using vanadium primary ions with the ion gun working at 25 keV. Impurities’ concentrations in the pyrite crystals were quantified via inductively coupled plasma mass spectroscopy (ICPMS). 0.1 g of sample material was dissolved using the Anton Paar Multiwave PRO microwave digestion system in NXF100 vessels (PTFE/TFM liner) using an acid mixture of 8 mL of HNO3 (65%; Carl Roth, ROTIPURAN® Supra) and 2 mL of H2O2 (30%; Carl Roth, ROTIPURAN®). Samples were digested at 230 °C and at pressures between 45 and 50 bar. After dissolution, the samples were diluted with 2% HNO3 solution. Elemental impurities were measured using Agilent 8800 ICPMS/MS. 7Li, 127I and 133Cs were measured in NoGas mode and 23Na, 39K, 40Ca, 59Co using He collision gas on mass. 52Cr, 60Ni, and 63Cu were measured in O2 mode as M16O+ reaction products. Indium was used as an internal standard element added online by mixing T and NIST 1643f, which were used as references for quality control. The Fermi levels’ and valence band maxima energies of materials were determined via ultraviolet photoelectron spectroscopy (UPS) using an Axis Ultra DLD photoelectron spectrometer (Kratos Analytical) fitted with a helium discharge lamp. The He discharge lamp with resonance line He(I) (hν = 21.21 eV) was used to obtain UPS spectra. For photoluminescence (PL) measurements, the FeS2 crystals were fixed into an indium pad, placed in a closed cycle helium cryostat (Janis CCS-150) and cooled down to 8 K. The temperature was adjusted up to RT using a temperature controller (LakeShore Model 335). The beam of a semiconductor laser (532 nm) was used for PL excitation. The PL signal was focused into the computer controlled single grating monochromator Horiba Jobin Yvon FHR640 and detected using the Hamamatsu InGaAs photomultiplier tube. To prevent the pyrite surface from oxidation and thus to obtain the PL signal from pure FeS2, the surface of FeS2 crystals was covered with an ultrathin protective layer of ZnS34 just after the removal of flux salt and before PL measurements. ZnS was deposited by the chemical solution deposition method. The solution for ZnS deposition contained Zn sulfate (0.1 M in solution) and thiourea (0.75 M) as precursors and sodium citrate (0.8 M) and ammonia (0.7 M) as complexing agents.35
Results and discussion
Morphology and composition
The morphology of powder crystals was studied via scanning electron microscopy (SEM). SEM images are shown in Fig. 2. FeS2 crystals synthesized in KI, LiI and CsI have mostly round shape and smooth surfaces. All the materials that were synthesized or recrystallized in KI flux, regardless of the flux amount, were morphologically very similar to each other, and therefore not duplicated in Fig. 2. The crystal growth process can be described by the thermodynamic equilibrium formed in sealed synthesis ampoules corresponding to the synthesis conditions. In the monograin powder technology, the growth of crystals is affected not only by synthesis temperature and time but also by other different parameters such as the solubility of materials in flux and the transport properties of components in the molten phase of the selected flux material.When the FeS2 formation reaction between S and FeS is finished, the preliminary crystallites of FeS2 start to grow via diffusion at the expense of the dissolved material. The difference in surface energies of crystals of different sizes and at different areas of individual crystals is the only factor that drives the growth of crystals under the formed isothermal equilibrium conditions in closed ampoules; the surface energy of smaller crystals is greater than that of larger crystals, and the surface energy at grain edges and tips is higher than at plain surfaces. During the synthesis-growth process, the precursors and the formed compound dissolve in the molten liquid flux salt up to their solubility at the process temperature. If the solubility of the material in the liquid phase is high and the liquid phase is more saturated with dissolved materials, then crystal growth is faster, and crystals can grow larger during the same time period. Similarly, more roundly shaped crystals will grow if the solubility of components in the liquid phase is high.19,20 The forming equilibrium between liquid and solid phases in the FeS2 synthesis-growth process is not studied yet.
Some irregularly shaped agglomerates, which were sintered to each other, were also detected among the individual crystals. Before the melting of the flux salt, the sintering of precursors’ particles can occur if some substances with melting temperatures lower than that of flux exist in the initial mixture. Sintering is caused by contracting capillary forces that arise in the solid–liquid phase boundaries due to the insufficient amount of the liquid phase.36 Sintering of precursor particles can also occur because the liquid phase of sulfur forms already at TM,sulfur = 112.8 °C.37 The FeS2 formation reaction consumes liquid S, its volume diminishes and allows sintering.
FeS2 crystals synthesized in the presence of Na2Sx have an appearance similar to the polycrystalline powder particles synthesized without any flux. Both materials have tiny crystallites without any geometrical shape. The synthesis temperature (475 °C), used to synthesize pyrite in the liquid phase of Na2Sx flux, was lower compared to the other materials. The lower synthesis temperature might be one of the reasons why the pyrite crystals obtained from this synthesis batch were quite small, as low synthesis temperature is linked to a slower crystal growth rate. Sintering was likely the main factor that drove the growth process in the two latter materials (synthesized in Na2Sx and without flux).
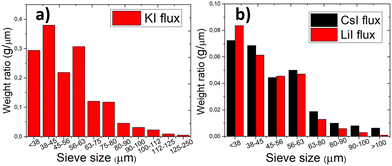
The particle size distribution of powders was characterized by sieving analysis. Only the materials that were obtained as monograin crystals (the ones that were synthesized in iodide salts) were analyzed and compared because the irregular shape and high agglomeration rate of materials synthesized in Na2Sx or without flux ruled out the possibility to characterize them by sieving analysis. The materials synthesized in KI, LiI and CsI were sieved into narrow granulometric fractions between 38 μm and 250 μm. When only one growth mechanism (Ostwald ripening) prevails, the Gaussian size distribution is predicted.38–40 The results of sieving analysis show no significant differences in the crystals’ size distribution (Fig. 3).
The elemental composition of microcrystals’ bulk was determined via EDX from polished flat surfaces of powder particles fixed in epoxy because geometrical factors can interfere with the EDX results. The average atomic percentages of eight different individual crystals for each material are shown in Table 1. All materials have compositions close to the stoichiometric composition of FeS2 with the Fe/S ratio of ∼0.5.
EDX spectra of all the FeS2 materials are shown in the ESI.†
Phase composition and lattice parameters
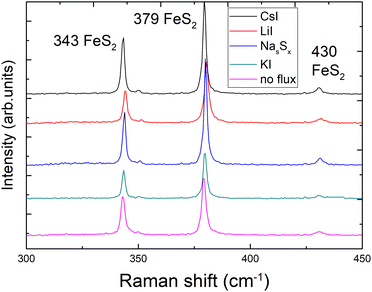
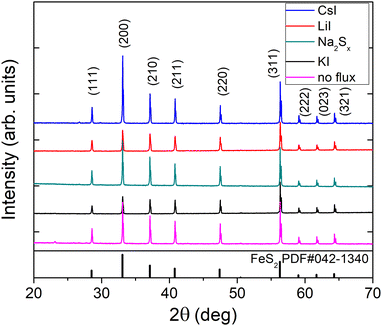
X-ray diffraction (XRD) and Raman spectroscopy were used to study the phase composition of the synthesized powder crystals to evaluate the effect of different flux media. Raman spectra are presented in Fig. 4. All samples show Raman spectra with peaks belonging to the pyrite crystalline phase. Sharp peaks with narrow halfwidths indicate high crystalline quality, regardless of the used synthesis temperatures or flux salts. The Raman mode at 343 cm−1 belongs to the Eg symmetry with the S–S pair in liberational mode.41 The signal at 380 cm−1 is the most significant Raman peak of pyrite and belongs to the Ag symmetry in-phase stretching mode of the S–S pair. A smaller peak at 430 cm−1 belongs to the Tg liberational and stretching mode, as does the very small peak at 350 cm−1.41,42The XRD diffractograms are presented in Fig. 5. Lattice parameters of the synthesized powder materials were calculated from the XRD measurements as a = b = c = 5.4154 Å, confirming the cubic crystal structure of all pyrite samples. As the lattice constants of all the materials (including polycrystalline FeS2) fully coincide, we can conclude that the incorporation of constituent elements of the used flux salts into pyrite FeS2 crystals is too low to affect the lattice parameter. These results indicate that it is possible to rely on the flux growth process and to use different fluxes for the synthesis of highly crystalline pyrite materials.
Concentration of impurities
In the monograin synthesis-growth process, the liquid phase of flux salt is an inexhaustible source of its constituent elements. Therefore, the concentration of a flux salt element grown into pyrite crystals as impurities is affected by the process conditions (temperature and mainly the sulfur vapor pressure in the ampoule) and is limited by the solubility of the incorporated element. On the other side, the impurities introduced by precursor materials distribute between solid and liquid phases according to their distribution coefficient. This effect is widely used in purification processes like recrystallization of chemicals and molten zone refining of metals. Thus, iodine from iodide salts and different alkali metals (K, Na, Li and Cs) may be present in the FeS2 crystals as doping impurities. By using the same precursors (FeS and S) in different syntheses, we can compare the concentrations of impurities originating from the different alkali metal salts. It is important to study the impact of impurities on the FeS2 properties because the elements incorporated in the pyrite lattice affect its optoelectronic properties by introducing new energy levels for recombination.43,44 For instance, it has been shown that chemical vapor growth in different halogens can affect even the conductivity type of pyrite crystals,21 when they occupy the sulfur lattice sites. Metals, however, may increase carrier concentration or even induce metallic behavior.24 The inductively coupled plasma mass spectrometry (ICPMS) analysis was used to determine the concentrations of nine different elements present in the synthesized FeS2 materials. It was found that all materials contained transition metals, such as Cr, Co and Ni, at the level of ∼1018 at cm−3. These concentrations are significant considering that there are 2.5 × 1022 lattice sites in 1 cm3 of FeS2. The contents of transition metal impurities are close to each other, indicating that they originate from the same source – the FeS precursor. The ICPMS analysis of the FeS precursors indicated that the iron mono-sulfides used in the syntheses indeed contained transition metal impurities in the range of 1018 at cm−3, along with lithium and iodine impurities as well (the full analysis of impurities in the used precursors and flux salts is described in the ESI†). Our own experience (unpublished results) with increased Cu content in pyrite showed that a weak PL signal disappeared completely after a series of doping with Cu. Thus, copper must be a strong suppressor (killer) of photoluminescence in pyrite, which is highly undesirably.The most significant data from the ICPMS measurements are presented in Fig. 6, while complete data are provided in the ESI.† Potassium and sodium concentrations were below their detection limit and therefore not determined, however KI and Na2Sx salts, as K and Na sources respectively, were used in syntheses. The iodine concentration in the materials that were synthesized in metal iodide salts was quite high at around 1–4 × 1019 cm−3. The highest Li content 4 × 1019 cm−3 was determined in the FeS2 material grown in LiI. Such concentration may suggest the formation of a solid solution, although the FeS2 crystal lattice parameter was not affected, as found by the XRD analysis of pyrite crystals. Li may also be present as a separate phase, such as LiI or Li2S but cannot be confirmed at this point. As expected, the highest Cs concentration was determined in the material synthesized in CsI, but Cs concentration was relatively high also for another material synthesized in LiI. To understand the origin of the Cs impurity, we studied the flux salts used by ICPMS. It was found that the LiI salt contained 4.4 × 1016 cm−3 of Cs. This concentration is two orders of magnitude higher than it was in KI and in Na2Sx (exact concentrations in ESI†).
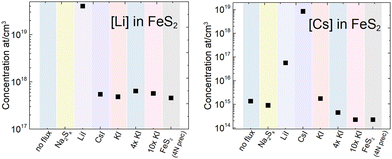 | ||
| Fig. 6 Comparison of lithium and cesium concentrations found in the pyrite crystals synthesized in different alkali metal salts. | ||
It is remarkable that we could not synthesize a higher purity pyrite from a higher purity FeS (4N) precursor than from 3N purity FeS. However, we recognized that the concentrations of transition metals in the synthesized FeS2 powder crystals were decreased, if compared with their concentrations in the precursors. Copper is one of the most problematic impurities in pyrite, and it was found that the copper content can be significantly lowered by recrystallizing pyrite in higher amounts of KI flux salt. To demonstrate the purification effect, we recrystallized the FeS2 monograin powder (synthesized from 3N FeS in KI with volume ratio (Vliquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KI = Vsolid
KI = Vsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeS2)) in 4 times and 10 times the amounts of KI flux. The concentration of different impurities was compared by ICPMS analysis and is presented in Table 2. The purification effect is strongest in the case of the Cu impurity – copper concentration decreased from 7.3 × 1017 to 3.2 × 1016 at cm−3 by recrystallization in KI. Chromium and lithium concentrations were somewhat lowered during the recrystallizations in higher amounts of flux, while cobalt and nickel concentrations were not decreased at all. The amount of impurity that remains in the material after recrystallization depends on the solubility of that element in the given environment. Thus, it may be easy to remove copper from pyrite using this method, but it may not be possible to remove cobalt.
FeS2)) in 4 times and 10 times the amounts of KI flux. The concentration of different impurities was compared by ICPMS analysis and is presented in Table 2. The purification effect is strongest in the case of the Cu impurity – copper concentration decreased from 7.3 × 1017 to 3.2 × 1016 at cm−3 by recrystallization in KI. Chromium and lithium concentrations were somewhat lowered during the recrystallizations in higher amounts of flux, while cobalt and nickel concentrations were not decreased at all. The amount of impurity that remains in the material after recrystallization depends on the solubility of that element in the given environment. Thus, it may be easy to remove copper from pyrite using this method, but it may not be possible to remove cobalt.
| Material | Li, at cm−3 | Cr, at cm−3 | Cu, at cm−3 | Co, at cm−3 | Ni, at cm−3 |
|---|---|---|---|---|---|
| FeS2 synthesized from the 3N FeS precursor | 4.9 × 1017 | 4.8 × 1018 | 7.3 × 1017 | 3.1 × 1018 | 6.6 × 1018 |
| Same material recrystallized with 4× bigger amount of KI as flux | 5.7 × 1017 | 1.8 × 1018 | 2.3 × 1017 | 4.8 × 1018 | 9.3 × 1018 |
| Same material recrystallized with 10× bigger amount of KI as flux | 4.6 × 1017 | 4 × 1018 | 3.2 × 1016 | 4.7 × 1018 | 8.3 × 1018 |
The ICPMS results were confirmed qualitatively by the time-of-flight secondary ion mass spectroscopy (ToF-SIMS) measurements, shown in Fig. 7. Although the ToF-SIMS results do not provide the exact concentrations of impurities, it is still valuable to confirm the presence of the impurities detected by the ICPMS measurements.
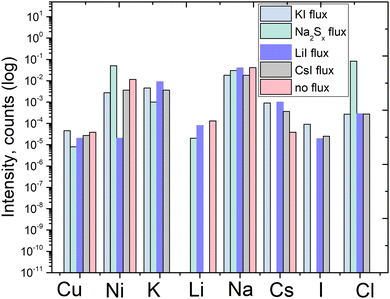 | ||
| Fig. 7 ToF-SIMS qualitative results of pyrite synthesized in different fluxes, and qualitative comparison of elemental impurities’ concentration. | ||
It can be seen that Cu content is at a similar level in all the measured materials. Potassium and sodium as impurities were both detected by ToF-SIMS. However, due to the sensitivity of the ToF-SIMS technique, and as the detection limit depends on the matrix as well, we expect the Na and K concentrations to be very low. Lithium as an impurity was detected in the material synthesized in LiI, as could be expected. Cesium was detected in all the materials synthesized in iodide salts, likely because all the salts included low amounts of cesium as an impurity, as confirmed by the ICPMS analysis of the flux salts.
The analysis data confirm that the constituent elements of the flux salts are incorporated into the formed pyrite crystals. Moreover, the purity of the used precursors and the flux materials affects the purity of FeS2 crystals as well. In the next chapters, we compare the optoelectronic properties of pyrite materials synthesized in different alkali metal salts.
Photoelectron spectroscopy results
It is known that the Fermi level position and electronic structure of various semiconductors can be controlled by doping.24,43,45–48 In pyrite, Co and Ni impurities substitute for Fe and introduce bulk defect states that are deep and/or induced near the band gap edge, generated by the 2d and 3d orbitals of the metals.47,48 In addition, halogens (F, Cl, and Br at the position of S) in the pyrite lattice cause very localized gap states close to the Fermi level in the minority spin channel, modifying pyrite electrochemical performance.47 On the other hand, Se as an impurity in pyrite does not introduce changes in the electronic structure.48 The results of ICPMS and ToF-SIMS measurements of pyrite samples show that all materials contain halogens, alkali metals and transition metals as impurities. The electronic structure of FeS2 materials was studied by ultraviolet photoelectron spectroscopy (UPS) to determine the valence band maxima and to see the impact of impurities to our materials, also to find out if iodine has the same effect as reported for other halogens, because it is one of the primary impurities in our materials.Surface valence band energies were obtained from the UPS measurements. A bias of −9.124 V was used to separate the analyser and the secondary edges of the sample. The bias was optimized to shift the Ag spectrum into the linear region of the analyser (kinetic energy of 0–10 eV). A spectrometer with a pass energy of 5 eV and a large area aperture of 300 μm × 700 μm was used. Under these conditions, the energy resolution of the spectra was measured at the Fermi edge of the clean Ag foil at room temperature.49 The FeS2 work function (Φ) was determined using eqn (1).49,50
| Φ = hν – Ecutoff | (1) |
Fig. 8 shows the full He(I) UPS spectra of the pyrite microcrystals synthesized in different salt media. The UPS spectrum of the material synthesized without flux shows a low-intensity peak below the Fermi level (EF) which is used to determine the position of the valence band maximum or EVBM. The photoelectron counts (intensity on the y-axis) are proportional to the density of states at this region,51 so the small peak may represent a very low but noteworthy density of states above the EVBM. The other materials measured in this study (see Fig. 8b) show a much smaller but still visible peak near the EF. This phenomenon in UPS measurements of pyrite was reported by Cabán-Acevedo et al.52 but not thoroughly explained. UPS measurements of semiconductors can exhibit some ambiguity in assigning values near the EF and at the Ecutoff.51 The small peak near the 0 eV binding energy in Fig. 8b (0 eV represents the EF) can be due to a lack of sulfur on the pyrite surface. Lack of sulfur at the outermost surface may lead to the pyrite surface turning metallic and closer to a FeS chemistry, which is too thin or “patchy” of a layer to be detected by EDX. FeS has a very narrow band gap and p-type conductivity53 and therefore could explain the density of states above pyrite's EVBM. The material with the most visible low binding energy peak was synthesized without any flux salt, showing at the same time the lowest EVBM position (see Fig. 9). Variations near the Ecutoff which are seen at the left-hand side in Fig. 8 can be due to inhomogeneities and position of the sample surface.51 Helander et al.54 have proposed an origin for such effect, as arising due to electric field artifacts that can be increased when the sample plane is not perpendicular to the entrance of the energy analyzer. Our materials are in the form of microcrystalline powder, so the sample surface can be at an unpredictable angle compared to the energy analyzer. Another reason for multiple apparent Ecutoff values is inhomogeneities and defects in the sample surface, which are formed due to surface roughness or a different surface chemistry.54
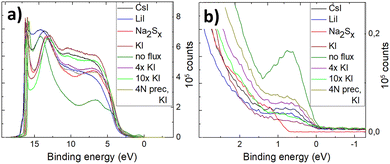 | ||
| Fig. 8 (a) Full He(I) UPS spectra of FeS2 synthesized in different fluxes, (b) all spectra zoomed in near 0 eV binding energy. | ||
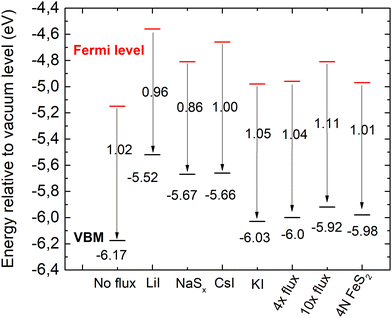 | ||
| Fig. 9 Energy band diagrams of pyrite FeS2 synthesized in different fluxes. EVBM is marked in black and Fermi level energies in red. | ||
The valence band maxima were determined from pyrite spectra, leaving out the low-energy peak because it extended into the negative binding energies and did not represent the properties of pyrite. The values of EVBM from the vacuum level were determined between 5.52 and 6.17 eV and are plotted in Fig. 9.
It is clearly seen that all pyrite crystals either synthesized in KI or recrystallized in the KI flux, have similar energy band structures with valence band maxima around −6.0 eV from the vacuum level, and the Fermi level energy values are also quite close to each other. The energy band diagrams are different if LiI, CsI and Na2Sx fluxes were used in FeS2 syntheses. The higher values of EVBM in the latter cases indicate the possible formation of solid solutions at the surface with changes in the bandgap energies. The ICPMS analysis revealed the Li impurity level at 4 × 1019 and Cs at 8 × 1018 cm−3 in the pyrite crystals grown in LiI and CsI flux, respectively. These levels are nearly high enough to form solid solutions, however not detected yet by a change in the lattice parameters in the XRD analysis. Therefore, we suppose that solid solutions could be formed on the very top of the pyrite crystals’ surfaces, detectable only by using a very surface sensitive technique like UPS, while XRD measurements reveal the bulk of the material.
The work function (Φ) values of our materials were derived from the Ecutoff values as shown in Fig. 8b by applying eqn (1). The Φ values varied between 4.58 and 5.11 eV for different materials. These values correlate well with the literature data, reporting pyrite work function values between 3.9 eV and 4.8–5.4 eV.52,55–57 The energy band diagrams of the materials derived from the UPS data are plotted in Fig. 9.
According to different reports,1,3,58 the band gap energy of pyrite is around 1 eV. Thus, there is strong indication that the measured crystals have n-type conductivity. As seen from the diagrams in Fig. 9, the measured Fermi levels are very close to the expected energy of the conduction band minimum. Pyrite crystals are well known to have n-type conductivity, while pyrite thin films often have p-type conductivity – a phenomenon known as the surface inversion of pyrite.11,12 The energy band diagram of the polycrystalline material synthesized without flux should be closest to pure pyrite, because this material has the lowest content of impurities. The band diagram of the material recrystallized and purified in the liquid phase of potassium iodide is closest to the polycrystalline material's band diagram. This may be due to a similarly low level of Cs doping in the latter material. However, the effects of Cs doping in pyrite have not been thoroughly studied. The analysis reveals that copper impurities do not affect the band gap or EVBM of pyrite, as the electronic structure is very similar for a material with a significant amount of Cu impurities (no-flux material) and a purified material that was recrystallized in 10× the amount of KI flux.
Photoluminescence results
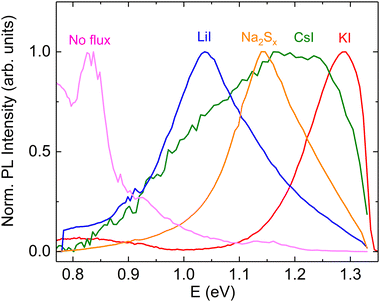
Photoluminescence spectroscopy is a proven tool to study the recombination processes in semiconductors and changes in the optoelectronic properties. The available literature offers limited insights into the photoluminescence emission characteristics and dominant recombination mechanisms of pyrite FeS2. It is known from the literature that the pyrite surface tends to oxidize very quickly in an atmosphere that contains oxygen.59 Our group has experienced that oxidation could diminish or even quench the PL signal of FeS2. Therefore, we encapsulated the pyrite crystals’ surfaces from the external influences by covering the synthesized crystals with a ZnS protective layer.60 A chemical solution deposition of ZnS resulted in a layer thickness of approximately 10 nm. ZnS does not have PL emission bands between 0.8 and 1.3 eV61 so it should not affect the pyrite PL spectra. The results of low temperature photoluminescence measurements can be seen in Fig. 10. It is seen that the PL spectra of pyrite crystals grown in different molten fluxes show very different shapes and positions for each peak, which indicates the different recombination mechanisms and the possible change in the bandgap energy. A similar effect has been shown by Ghisani et al.40 where they studied tetrahedrite microcrystals grown in different fluxes. All the measured pyrite samples have a broad asymmetric PL peak shape that is typical for semiconductors with high defect concentrations.62 The PL spectra were fitted using the empirical asymmetric double sigmoid function63 to find the position of each peak. The pyrite polycrystals, synthesized without any flux, had a main peak at the lowest energy with the center at 0.83 eV. The microcrystals synthesized in KI also have a weak peak close to the polycrystalline material with an energy value of 0.85 eV. These peaks are likely to have the same origin, probably related to some deep defects. As we have already seen from the UPS measurements, the formation of a solid solution is likely in the case of Li and Cs containing pyrite crystals. The shift in the PL peak position indicates the change in the bandgap energy, while some PL bands, for example near 1.3 eV, are at notably higher energies compared to the pyrite band gap. This could be due to a quantum confinement effect64,65 where there are some nanocrystals on the pyrite surface, which have a larger band gap compared to the bulk material. The nanocrystals on the pyrite surface might also have a different chemistry than FeS2. The solubility of copper impurity compounds in KI is quite high.66 Thus, there is a possibility that copper that is dissolved at synthesis temperature may precipitate onto the pyrite crystals during cooling and form chalcopyrite (CuFeS2) which has a band gap larger than the pyrite bulk material.46 The fact that we did not observe a photoluminescence signal from the materials with lowered Cu concentration may be a proof to that effect. This intriguing question will be investigated further in our future studies. In conclusion, we can say that the shift in peak positions and the change of the PL peak shape suggest an important role of the different flux materials and impurities that are introduced using the flux growth method. A thorough analysis of the origin of the PL emission in pyrite is underway by our group.Conclusions
FeS2 pyrite microcrystals were successfully synthesized in the molten phase of different alkali metal salts (KI, LiI, CsI, and Na2Sx) and without the presence of any molten flux. All the materials had a highly crystalline pyrite structure with no change in the lattice parameter, as determined by XRD and Raman analyses. The synthesized materials were analyzed by ICPMS to compare the concentrations of different alkali metal impurities and iodine incorporated during the growth process. The lithium and cesium concentrations varied the most, while sodium and potassium contents were below the determination limit. The highest Li content of 4 × 1019 cm−3 and Cs content around 1019 cm−3 were determined in the FeS2 materials grown in LiI and CsI, respectively. The other used alkali metal salts contained Li and Cs as residual impurities. These residual impurities also incorporated into the formed FeS2 but at much lower levels than from LiI and CsI. Iodine concentrations in the FeS2 materials obtained from the used iodide salts were determined to be 1–4 × 1019 cm−3. It was found that transition metal impurities at high levels originated from the FeS precursor. The different alkali metals from the used flux salts affected the energy band diagrams of pyrite FeS2, as the materials synthesized in KI had significantly lower EVBM values, while pyrite that was synthesized in LiI, CsI or Na2Sx had all higher energies of valence band maxima. It was suggested that solid solutions might have been formed on the pyrite crystals’ surfaces, which are detectable only by using the very surface sensitive UPS method.The present study revealed a method to remove copper and lower the concentrations of other impurities from pyrite by recrystallization or its synthesis in increased amounts of flux salts by the different distribution of impurity elements between liquid and solid phases. Copper is one of the most harmful impurities in pyrite, and decreasing the contamination of copper was confirmed using the ICPMS technique.
The results of low-temperature photoluminescence measurements show a strong shift in peak positions and peak shapes of the PL spectra of materials synthesized in different fluxes, likely due to a change in the band gap values of the different materials.
Author contributions
Katriin Kristmann: conceptualization, data curation, formal analysis, investigation, visualization, writing – original draft, and writing – review & editing. Taavi Raadik: formal analysis, funding acquisition, investigation, project administration, resources, supervision, and writing – review & editing. Mare Altosaar: methodology, supervision, validation, and writing – review & editing. Mati Danilson: investigation, validation, and writing – review & editing. Jüri Krustok: methodology, validation, and writing – review & editing. Peeter Paaver: investigation. Yuriy Butenko: investigation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Estonian Ministry of Education and Research, Estonian Research Council projects PRG1815, PRG1023, RVTT7 and the ESA Discovery programme under Contract no. 4000134676.Notes and references
- A. Ennaoui and H. Tributsch, Sol. Cells, 1984, 13, 197–200 CrossRef CAS
.
-
M. Law, Pyrite Iron Sulfide Solar Cells Made from Solution, Irvine, 2017 Search PubMed
.
- C. Steinhagen, T. B. Harvey, C. J. Stolle, J. Harris and B. A. Korgel, J. Phys. Chem. Lett., 2012, 3(17), 2352–2356 CrossRef CAS PubMed
.
- S. Gohri, J. Madan, M. K. A. Mohammed and R. Pandey, Mater. Res. Express, 2023, 10, 024001 CrossRef
.
- M. Limpinsel, PhD thesis, University of California, 2015.
- C. Wadia, A. P. Alivisatos and D. M. Kammen, Environ. Sci. Technol., 2009, 43(6), 2072–2077 CrossRef CAS PubMed
.
- K. Kristmann, T. Raadik, M. Altosaar, M. Grossberg-Kuusk, J. Krustok, M. Pilvet, V. Mikli, M. Kauk-Kuusik and A. Makaya, Acta Astronaut., 2022, 199, 420–424 CrossRef CAS
.
- T. Raadik, K. Kristmann, J. Ciazela, M. Jozefowicz, M. Kowalinski, A. Sniadkowski, J. Bakala, M. Steslicki, N. Zalewska, B. Pieterek, M. Ciazela, D. Marciniak, G. Paslawski, Z. Szaforz, A. Woods and A. Makaya, Proceedings of the International Astronautical Congress in Baku.
- B. Voigt, L. S. Valor, W. Moore, J. Jeremiason, J. Kakalios, E. S. Aydil and C. Leighton, ACS Appl. Mater. Interfaces, 2023, 15, 28258–28266 CrossRef CAS PubMed
.
- B. Voigt, W. Moore, M. Maiti, J. Walter, B. Das, M. Manno, C. Leighton and E. S. Aydil, ACS Mater. Lett., 2020, 2, 861–868 CrossRef CAS
.
- M. Limpinsel, N. Farhi, N. Berry, J. Lindemuth, C. L. Perkins, Q. Lin and M. Law, Energy Environ. Sci., 2014, 7, 1974–1989 RSC
.
- S. Uchiyama, Y. Ishikawa and Y. Uraoka, Jpn. J. Appl. Phys., 2018, 57, 032301 CrossRef
.
- D. Ray, B. Voigt, M. Manno, C. Leighton, E. S. Aydil and L. Gagliardi, Chem. Mater., 2020, 32, 4820–4831 CrossRef CAS
.
- K. Büker, N. Alonso-Vante, R. Scheer and H. Tributsch, Ber. Bunsen-Ges., 1994, 98, 674–682 CrossRef
.
- B. Voigt, B. Das, D. M. Carr, D. Ray, M. Maiti, W. Moore, M. Manno, J. Walter, E. S. Aydil and C. Leighton, Phys. Rev. Mater., 2021, 5, 025405 CrossRef CAS
.
- K. Kristmann, M. Altosaar, J. Raudoja, J. Krustok, M. Pilvet, V. Mikli, M. Grossberg, M. Danilson and T. Raadik, Thin Solid Films, 2022, 743, 139068 CrossRef CAS
.
- M. Kauk-Kuusik, X. Li, M. Pilvet, K. Timmo, M. Grossberg, T. Raadik, M. Danilson, V. Mikli, M. Altosaar, J. Krustok and J. Raudoja, Thin Solid Films, 2018, 666, 15–19 CrossRef CAS
.
- F. Ghisani, K. Timmo, M. Altosaar, J. Raudoja, V. Mikli, M. Pilvet, M. Kauk-Kuusik and M. Grossberg, Mater. Sci. Semicond. Process., 2020, 110, 104973 CrossRef CAS
.
- E. Mellikov, J. Hiie and M. Altosaar, Int. J. Mater. Prod. Technol., 2007, 28, 291–311 CrossRef CAS
.
- P. W. Voorhees, Ostwald ripening of two-phase mixtures, Annu. Rev. Mater. Sci., 1992, 22, 197–215 CrossRef CAS
.
- S. Fiechter, J. Mai, A. Ennaoui and W. Szacki, J. Cryst. Growth, 1986, 78, 438–444 CrossRef CAS
.
- S. Khalid, M. A. Malik, D. J. Lewis, P. Kevin, E. Ahmed, Y. Khan and P. O’Brien, J. Mater. Chem. C, 2015, 3, 12068–12076 RSC
.
- S. W. Lehner, K. S. Savage and J. C. Ayers, J. Cryst. Growth, 2006, 286, 306–317 CrossRef CAS
.
-
T. Salk, Master's thesis, University of California, 2019 Search PubMed
.
- R. N. Chandler and R. W. Bené, Phys. Rev. B: Solid State, 1973, 8, 4979–4988 CrossRef CAS
.
- Y. Li, J. Chen, Y. Chen and J. Guo, Trans. Nonferrous Met. Soc. China, 2011, 21, 1887–1895 CrossRef CAS
.
- I. J. Ferrer, C. de la Heras and C. Sanchez, J. Phys.: Condens. Matter, 1995, 7, 2115–2121 CrossRef CAS
.
- X. Zhang, M. Li, J. Walter, L. O’Brien, M. A. Manno, B. Voigt, F. Mork, S. V. Baryshev, J. Kakalios, E. S. Aydil and C. Leighton, Phys. Rev. Mater., 2017, 1, 015402 CrossRef
.
- D. Colombara, U. Berner, A. Ciccioli, J. C. Malaquias, T. Bertram, A. Crossay, M. Schöneich, H. J. Meadows, D. Regesch, S. Delsante, G. Gigli, N. Valle, J. Guillot, B. El Adib, P. Grysan and P. J. Dale, Sci. Rep., 2017, 7, 43266 CrossRef PubMed
.
- F. Pianezzi, P. Reinhard, A. Chirilă, B. Bissig, S. Nishiwaki, S. Buecheler and A. N. Tiwari, Phys. Chem. Chem. Phys., 2014, 16, 8843 RSC
.
- Y. Sun, S. Lin, W. Li, S. Cheng, Y. Zhang, Y. Liu and W. Liu, Engineering, 2017, 3, 452–459 CrossRef CAS
.
- Y. Iwadate and T. Ohkubo, J. Chem. Eng. Data, 2020, 65, 5240–5248 CrossRef CAS
.
-
J. Sangster and A. D. Pelton, The Na-S (Sodium-Sulfur) System Equilibrium Diagram, 1997, vol. 18 Search PubMed
.
- J. D. Myers, J. A. Frantz, C. C. Baker, S. C. Erwin, S. N. Qadri, N. Bassim, S. B. Qadri, R. Y. Bekele and J. S. Sanghera, Opt. Mater. Express, 2018, 8, 3835 CrossRef CAS
.
- J. Liu, A. Wei and Y. Zhao, J. Alloys Compd., 2014, 588, 228–234 CrossRef CAS
.
- E. Mellikov, D. Meissner, T. Varema, M. Altosaar, M. Kauk, O. Volobujeva, J. Raudoja, K. Timmo and M. Danilson, Sol. Energy Mater. Sol. Cells, 2009, 93(1), 65–68 CrossRef CAS
.
- R. Steudel, Top. Curr. Chem., 2003, 230, 81–116 CrossRef CAS
.
- M. Kauk-Kuusik, X. Li, M. Pilvet, K. Timmo, M. Grossberg, T. Raadik, M. Danilson, V. Mikli, M. Altosaar, J. Krustok and J. Raudoja, Thin Solid Films, 2018, 666, 15–19 CrossRef CAS
.
- T. Bergfors, J. Struct. Biol., 2003, 142, 66–76 CrossRef CAS PubMed
.
- F. Ghisani, K. Timmo, M. Altosaar, V. Mikli, M. Pilvet, R. Kaupmees, J. Krustok, M. Grossberg and M. Kauk-Kuusik, Thin Solid Films, 2021, 739, 138980 CrossRef CAS
.
- A. N. Utyuzh, Phys. Solid State, 2014, 56, 2050–2055 CrossRef CAS
.
- Z. Mutlu, B. Debnath, S. Su, C. Li, M. Ozkan, K. N. Bozhilov, R. K. Lake and C. S. Ozkan, J. Mater. Chem. C, 2018, 6, 4753–4759 RSC
.
- Y. Li, J. Chen, Y. Chen and J. Guo, Trans. Nonferrous Met. Soc. China, 2011, 21, 1887–1895 CrossRef CAS
.
- S. W. Lehner, N. Newman, M. van Schilfgaarde, S. Bandyopadhyay, K. Savage and P. R. Buseck, J. Appl. Phys., 2012, 111(8), 083717 CrossRef
.
- J. Jia, A. Takasaki, N. Oka and Y. Shigesato, J. Appl. Phys., 2012, 112(1), 013718 CrossRef
.
- S. Ghosh, T. Avellini, A. Petrelli, I. Kriegel, R. Gaspari, G. Almeida, G. Bertoni, A. Cavalli, F. Scotognella, T. Pellegrino and L. Manna, Chem. Mater., 2016, 28, 4848–4858 CrossRef CAS PubMed
.
- S. Li, Y. Zhang and X. Niu, Phys. Chem. Chem. Phys., 2018, 20, 11649–11655 RSC
.
- K. S. Savage, D. Stefan and S. W. Lehner, Appl. Geochem., 2008, 23, 103–120 CrossRef CAS
.
- C. Maheu, L. Cardenas, E. Puzenat, P. Afanasiev and C. Geantet, Phys. Chem. Chem. Phys., 2018, 20, 25629–25637 RSC
.
- V. R. Koppolu, M. C. Gupta and L. Scudiero, Sol. Energy Mater. Sol. Cells, 2011, 95, 1111–1118 CrossRef CAS
.
- J. E. Whitten, Appl. Surf. Sci. Adv., 2023, 13, 100384 CrossRef
.
- M. Cabán-Acevedo, N. S. Kaiser, C. R. English, D. Liang, B. J. Thompson, H.-E. Chen, K. J. Czech, J. C. Wright, R. J. Hamers and S. Jin, J. Am. Chem. Soc., 2014, 136, 17163–17179 CrossRef PubMed
.
- C. Tresca, G. Giovannetti, M. Capone and G. Profeta, Phys. Rev. B, 2017, 95, 205117 CrossRef
.
- M. G. Helander, M. T. Greiner, Z. B. Wang and Z. H. Lu, Appl. Surf. Sci., 2010, 256, 2602–2605 CrossRef CAS
.
- H. Xian, R. Du, J. Zhu, M. Chen, W. Tan, R. Zhu, J. Wei and H. He, Appl. Phys. Lett., 2018, 113, 123901 CrossRef
.
- L. Wu, N. Y. Dzade, L. Gao, D. O. Scanlon, Z. Öztürk, N. Hollingsworth, B. M. Weckhuysen, E. J. M. Hensen, N. H. de Leeuw and J. P. Hofmann, Adv. Mater., 2016, 28(43), 9602–9607 CrossRef CAS PubMed
.
- K. P. Bhandari, P. Koirala, N. R. Paudel, R. R. Khanal, A. B. Phillips, Y. Yan, R. W. Collins, M. J. Heben and R. J. Ellingson, Sol. Energy Mater. Sol. Cells, 2015, 140, 108–114 CrossRef CAS
.
- M. Rahman, G. Boschloo, A. Hagfeldt and T. Edvinsson, Adv. Mater., 2020, 32(26), 1905653 CrossRef CAS PubMed
.
- H. W. Nesbitt, G. M. Bancroft, A. R. Pratt and M. J. Scaini, Am. Mineral., 1998, 83, 1067–1076 CrossRef CAS
.
- J. D. Myers, J. A. Frantz, C. C. Baker, S. C. Erwin, S. N. Qadri, N. Bassim, S. B. Qadri, R. Y. Bekele and J. S. Sanghera, Opt. Mater. Express, 2018, 8, 3835 CrossRef CAS
.
- A. I. Inamdar, S. Cho, Y. Jo, J. Kim, J. Han, S. M. Pawar, H. Woo, R. S. Kalubarme, C. Park, H. Kim and H. Im, Mater. Lett., 2016, 163, 126–129 CrossRef CAS
.
- M. Grossberg, T. Raadik, J. Raudoja and J. Krustok, Curr. Appl. Phys., 2014, 14, 447–450 CrossRef
.
- J. Krustok, H. Collan, M. Yakushev and K. Hjelt, Phys. Scr., 1999, T79, 179 CrossRef CAS
.
-
G. Ramalingam, P. Kathirgamanathan, G. Ravi, T. Elangovan, B. Arjun Kumar, N. Manivannan and K. Kaviyarasu, Quantum Confinement, 2020 Search PubMed
.
- M. K. Sahoo and P. Kale, Superlattices Microstruct., 2021, 156, 106949 CrossRef CAS
.
- I. Leinemann, K. Timmo, M. Grossberg, T. Kaljuvee, K. Tõnsuaadu, R. Traksmaa, M. Altosaar and D. Meissner, J. Therm. Anal. Calorim., 2015, 119, 1555–1564 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00697b |
| This journal is © The Royal Society of Chemistry 2024 |