Open Access Article
Open Access ArticleNew findings on a Zintl phased K3Ag3As2 ternary semiconductor compound for photovoltaic applications by first-principles methods
Magdalene Mutheu
Kimuyu
,
Robinson
Musembi
 *,
Julius
Mwabora
and
Francis
Nyongesa
*,
Julius
Mwabora
and
Francis
Nyongesa
Monolith Research Group, Department of Physics, University of Nairobi, Kenya. E-mail: musembirj@uonbi.ac.ke
First published on 28th December 2023
Abstract
A Zintl-phased K3Ag3As2 ternary compound previously not studied using ab initio techniques was analysed for its structural, electronic, mechanical, elastic, and optical properties using LDA-PZ, GGA-EV, GGA-PBE, GGA-PBESol, GGA-revPBE, and SO-GGA as the exchange correlation functionals. The structural property calculations showed that the material adopts a rhombohedral crystal structure with a mean lattice parameter of 15.1808 a.u. The material has been found to have a direct bandgap where the lowest value has been found to be 1.07 eV while the highest value was 1.74 eV when using PZ-LDA and EV-GGA, respectively. The density of states calculations have shown that the valence band formation is dominated by orbitals As 2p and Ag 3d, whereas the conduction band is mainly formed through the hybridisation of Ag 2p and As 2p orbitals. This material has been found to be mechanically stable and ductile and has ionic bonding. The optical property calculations have shown that it is suitable for optoelectronic applications. The obtained values have been found to be consistent with the experimental values obtained previously.
Introduction
For many years, materials science has been at the forefront of fostering the development of new materials for technological advancement that could potentially address ecological and economic sustainability.1 In the recent past, there has been a plethora of compound materials reported including binary, ternary, and even quaternary materials with very interesting properties, such as ternary Zintl compounds which have attracted significant attention among materials scientists because of their potential applications in electronic, spintronic, thermoelectric, health, space science, and optoelectronic industries.2–4 The classical Zintl concept materials are mainly binary compounds, and as more compounds were discovered, including ternary and quaternary structures, the definition describing them became limiting.5 Therefore, Schafer et al.6 proposed a more generalised definition that accommodates many elements. Ternary Zintl compounds are formed from the combination of elements from electropositive group IA (Na, K, Rb, and Cs) or group IIA (Mg, Ca, Sr, and Ba) with group VA (P, As, Sb, and Bi) and group IB (Cu, Ag, and Au).7 Different ternary compounds adopting varied stoichiometric structures have been investigated in the past for different applications; nonetheless, semiconductors for optoelectronic applications are less studied,8–10 and therefore, the basis and the motivation for this work, furthermore, A3B3X2 stoichiometric ternary compounds remain widely unexplored. An experimental and theoretical analysis of the crystal structure of rubidium copper arsenide Rb3Cu3As2 was reported by Ovchinnikov et al.,11 in which the material was observed to exhibit semiconducting properties following the electron counting scheme,5 and the chemical bonding was covalent for the Cu-As bond and ionic for the Rb–As bond. Similar 3–3–2 structures have been previously studied experimentally, as well as using ab initio methods for K3Cu3P2, K3Cu3As2, K3Cu3Ag2, K3Au3Sb2, and Rb3Au3Sb2. All the compounds reported here can be rationalised using the Zintl concept scheme, such that (A+)3(B+)3(X3−)2, where A is group IA or IIA, B is a group IB, and X is a group VA element. In this work, for the first time, previously existing experimental data12 have been utilised for Zintl phased K3Ag3As2 ternary semiconductor materials to computationally investigate their structural, electronic, mechanical, elastic, and optical properties using first-principles methods for optoelectronic applications.Computational methods
All calculations for the structural, electronic, mechanical, elastic, and optical properties of the K3Ag3As2 ternary compound were performed using the plane wave self-consistent field PWscf method based on density functional theory, as implemented in the Quantum ESPRESSO computational code.13,14 The interactions between the ionic core electrons and the valence electrons were described using the scalar relativistic core correction pseudopotential method, mainly ultrasoft, for most of the calculations, except for the optical properties which are best performed using the norm-conserving pseudopotentials, in which the valence electron configurations for the K3Ag3As2 ternary compound are K [Ar] 4s, Ag [Kr] 4d105s, and As [Ar] 3d104s24p3, respectively. The exchange–correction functional was described using different functionals depending on the exchange–correction potential being calculated. In this work, for the local density approximation, LDA-PZ (Perdew–Zunger)15 was used; on the other hand, for the generalised gradient approximation, GGA-EV (Engel–Vosko),16 SO-GGA (second order GGA),17 GGA-PBE (Perdew–Burke–Ernzerhof), GGA-PBESol (Perdew–Burke–Ernzerhof for solids),18 and GGA-revPBE (revised Perdew–Burke–Ernzerhof)19 were used to triangulate and obtain the best approximation for the compound. The choice of the exchange correlation potential depends on the specific problem being studied and the level of accuracy required. Each functional has strengths and weaknesses, and there is no one-size-fits-all solution in computational materials science. Researchers often use a combination of different functionals to obtain a more accurate description of a system under investigation. The local density approximation, LDA, and the generalised gradient approximation, PBE and PBESol, have been widely used to describe the properties of periodic material systems since their respective pseudopotentials have been optimised and are readily available in most databases. The first irreducible Brillouin zone (BZ) sampling was performed using the Monkhorst–Pack scheme,20 and the first BZ k-points used during optimisation were 8 × 8 × 8 with an offset of 0. Other optimizations done were for the kinetic energy and charge density cut-off which were set to be 60.0 and 480.0 Rydberg, respectively, and the lattice parameter ao as a function of total energy, and the variable cell relaxation, was calculated at 0.0 applied pressure following the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, thereafter it was set as the default value for any subsequent calculation. In all the calculations the convergence tolerance was set at 2.0 × 10−9. After optimisation, the kinetic energy and charge density cut-off were set at 140.0 and 1120.0, respectively, and the BZ k-points were set at 9 × 9 × 9 at offset 0 for most of the calculations, except during the non-self-consistent field calculations for which they were set at 14 × 14 × 14 at offset 0.21,22 After obtaining the optimised values, subsequent calculations were performed using a self-consistent field calculation for the electronic, mechanical, elastic, and optical properties. The obtained results were subjected to post-processing procedures using various tools to extract and visualise the results.Results and discussion
A. Structural properties
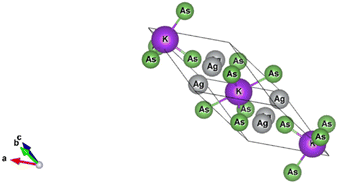
The K3Ag3As2 compound crystallises into a trigonal crystal system while the lattice adopts a rhombohedral structure with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m number 166, the lattice parameters for the conventional system are a = b = 5.99 Å, c = 21.42 Å; α = β = 90°, γ = 120°, and the crystal structure is shown in Fig. (1).
m number 166, the lattice parameters for the conventional system are a = b = 5.99 Å, c = 21.42 Å; α = β = 90°, γ = 120°, and the crystal structure is shown in Fig. (1).
In the K3Ag3As2 crystal system, the K+ atoms are positioned at two inequivalent locations. In the first instance, K+ is bonded to four equidistant As3− atoms to form a K–As4 trigonal pyramid. The K–As bond lengths are inequivalent, there are one shorter (3.31 Å) and three longer (3.46 Å) bond lengths. In the second instance, the K+ atom is bonded to six equivalent As3− atoms. All K–As bond lengths are 3.85 Å. Ag+ is bonded collinearly to two equidistant As3− atoms. The Ag–As bond length is 2.56 Å. The lattice parameters of the material were analysed by fitting total energy against the lattice parameter, ao, data to the Birch–Murnaghan equation23 of state as given in eqn (1), where E(V) is the total energy of a unit cell of volume V, Eo is the ground state energy corresponding to the equilibrium unit cell volume, Vo is the volume of the unit cell at the ground state, and Bo is the first pressure derivative of the bulk modulus B.
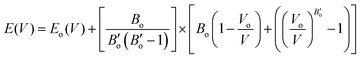 | (1) |
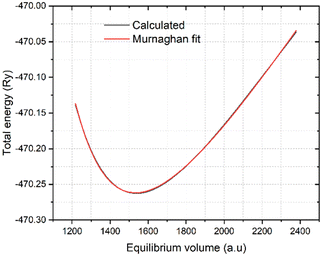 | ||
| Fig. 2 Calculated and Murnaghan fitted equilibrium cell volume of K3Ag3As2 ternary compound using PBE functional. | ||
| Lattice parameter ao (a.u.) | Bulk modulus Bo GPa | Equilibrium volume (a.u.)3 | Enthalpy of formation ΔHf (Ry) | |
|---|---|---|---|---|
| LDA | 14.5735 | 52.1 | 1373.3 | −465.7 |
| EV | 17.0635 | 13.1 | 2205.0 | −474.9 |
| SOGGA | 14.2105 | 91.1 | 1273.6 | −468.1 |
| PBE | 15.1151 | 33.4 | 1532.6 | −470.3 |
| PBESol | 14.8015 | 41.7 | 1439.2 | −464.3 |
| revPBE | 15.3209 | 28.8 | 1596.1 | −470.5 |
| Experimental work | 15.159012 |
B. Electronic properties
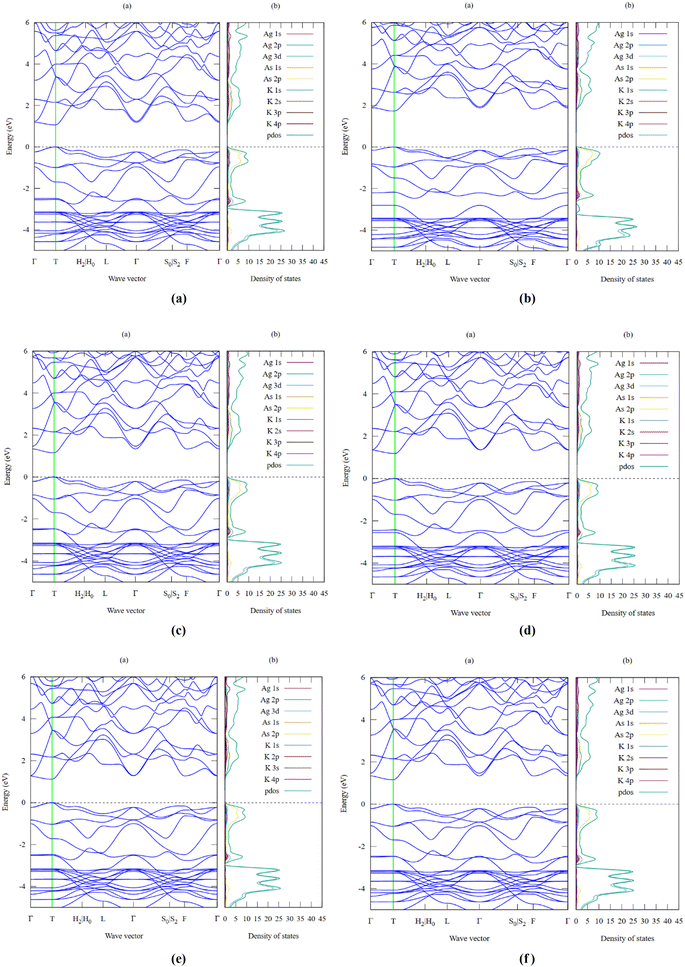
One of the key criteria for understanding the properties of a material is to study its electronic properties, which are a function of the electronic states and their intrinsic behaviour. The analysis of the electronic properties, including the band structure and projected density of states for the K3Ag3As2 ternary compound, was performed using all the 6-exchange correlation functionals to triangulate the best prediction for the band gap which is a useful characteristic, especially for photovoltaic applications, as well as other optoelectronic applications. The calculations were performed in the first Brillouin zone using the following 10 high-symmetry points: Γ–T–H2|H0–L–Γ–S0|S2–F–Γ. The results obtained are illustrated for each of the respective functional in Fig. 3(a–f), with the Fermi level at 0 and the energy band plot ranging between −5.0 eV and 6.0 eV for minima and maxima, respectively. The smallest band gap was predicted to be 1.07 eV using LDA-PZ, Fig. 3(a), which is lower than that listed in the database from which the crystallographic information file was obtained.24 This is attributed to the fact that the local density approximation method based on the Perdew–Zunger exchange correlation functional underestimates the size of the band gap, as has been reported previously in the literature.25,26 In contrast, the largest band gap was predicted to be 1.74 eV using the Engel-Vosko exchange correlation functional, as shown in Fig. 3(b), a value that is higher than that provided in the database. This is attributed to the fact that, in most cases, the Engel–Vosko exchange correlation functional gives an overestimated value higher than the experimental value and those obtained using other functionals such as metaGGA and hybrid functionals.27 The band gaps obtained from the other functionals were 1.16 eV using second-order SO-GGA, 1.19 eV using GGA-PBE, 1.13 eV using GGA-PBESol, and 1.23 eV using GGA-revPBE. The bandgaps predicted using the six functionals suggest that K3Ag3As2 is a semiconductor material with a direct band gap which is located at symmetry point T where both the valence band maxima and conduction band minima are located, and it is clearly seen that the band gap lies within the visible and near-infrared region of the electromagnetic spectra, indicating that K3Ag3As2 may be suitable for photovoltaic applications, especially in solar cells. The projected density of states predicted using the six functionals showed a closer relationship, and the major difference was only seen in the total projected density of states. The results for the projected density of states are shown together with the electronic band structures for the six functionals. The valence band formation was observed to be mainly due to the As 2p and Ag 3d orbitals while the rest of the orbitals made minimal contributions. On the other hand, the conduction band formation was majorly due to contributions from the Ag 2p and As 2p orbitals, and similarly, the rest of the orbitals made minor contributions. The results obtained from the projected density of states seem to corroborate those obtained from the electronic band structure, especially the size of bandgap formation and the Fermi level position.C. Elastic and mechanical properties
To describe the mechanical properties of a material, the elastic constants are crucial and fundamental parameters of study. The elastic constants help in understanding how a material behaves under deformation and its resilience to plasticity. The elastic constants also serve as a connection between the mechanical and dynamical behaviour of a crystal structure of a material.28,29The K3Ag3As2 ternary compound adopts a rhombohedral class I structure, in this class, it features 6 independent elastic constants namely C11, C12, C13, C14, C33, C44 and one dependent elastic constant, that is C66 = (C11 − C12)/2.30 For the mechanical stability of this material, it should fulfil the following necessary and sufficient conditions:
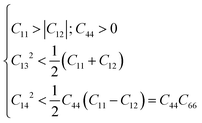 | (2) |
| B (GPa) | E (GPa) | G (GPa) | B/G | σ | θ D (K) | |
|---|---|---|---|---|---|---|
| LDA | 19.97 | 23.19 | 8.94 | 2.23 | 0.297 | 149.1 |
| EV | 37.68 | 28.28 | 10.33 | 3.65 | 0.370 | 166.3 |
| SOGGA | 33.10 | 47.84 | 19.05 | 1.74 | 0.256 | 217.8 |
| PBE | 23.17 | 24.34 | 9.24 | 2.51 | 0.318 | 154.4 |
| PBESol | 23.45 | 26.35 | 10.09 | 2.32 | 0.306 | 159.9 |
| revPBE | 20.98 | 21.48 | 8.14 | 2.58 | 0.320 | 144.5 |
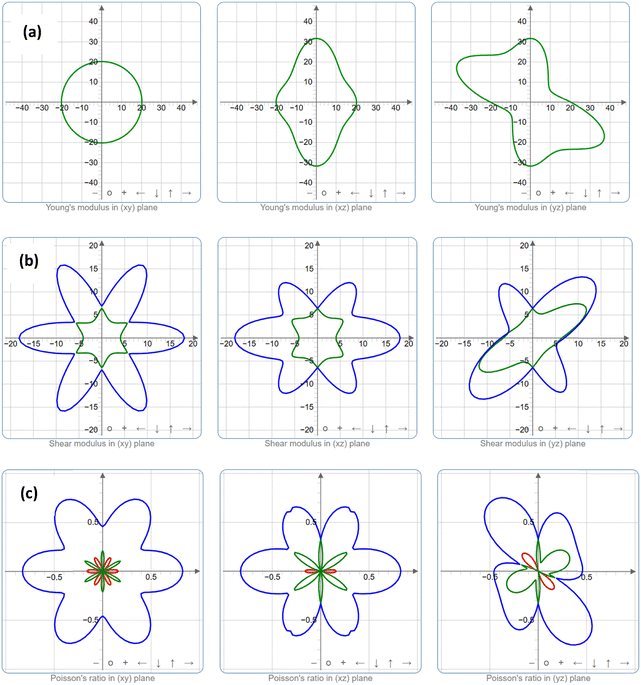
The crystal structure orientation and the anisotropy characteristics are closely interrelated. In this work, two-dimensional (2D) analysis was performed on the anisotropy relationship for Youngs's modulus, shear modulus, and Poisson ratio.34 The anisotropy of a crystal structure is represented by a deviation from a perfect circle under applied pressure. A perfect circle represents the isotropy of the crystal structure plane. In Fig. 4, the blue colour represents anisotropy/isotropy, while linear compressibility is represented in the green colour for positive values and the red colour for negative values. Fig. 4a shows the spatial dependence of Young's modulus plotted for xy, xz, and yz in the 2D scheme.35 In the first instance, the xy spatial dependence of the Young's modulus shows that it is a perfect circle indicating that in this orientation the crystal plane is isotropic otherwise in the xz and yz planes which predicts anisotropic behaviour. In the case of spatial dependence of shear modulus, the crystal plane shows that it is anisotropic for all planes considered.35 The same is true for the consideration of spatial dependence of Poisson's ratio, nonetheless, it shows some degree of symmetry in all sides of the quadrant.34
D. Optical properties
For materials meant for application in optoelectronics, it is necessary to analyse their optical response behaviour in various electromagnetic spectral ranges.The band structure of a semiconductor material influences the optical properties of the material and affects the optical permittivity as well as the optical absorption behaviour. The complex dielectric function is a frequency-dependent parameter used in analysing the optical response, and it is composed of two parts related to each other by the eqn (3).28,29,36–38
| ε(ω) = ε1(ω) + jε2(ω) | (3) |
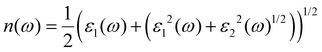 | (4) |
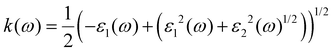 | (5) |
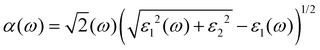 | (6) |
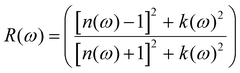 | (7) |
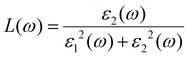 | (8) |
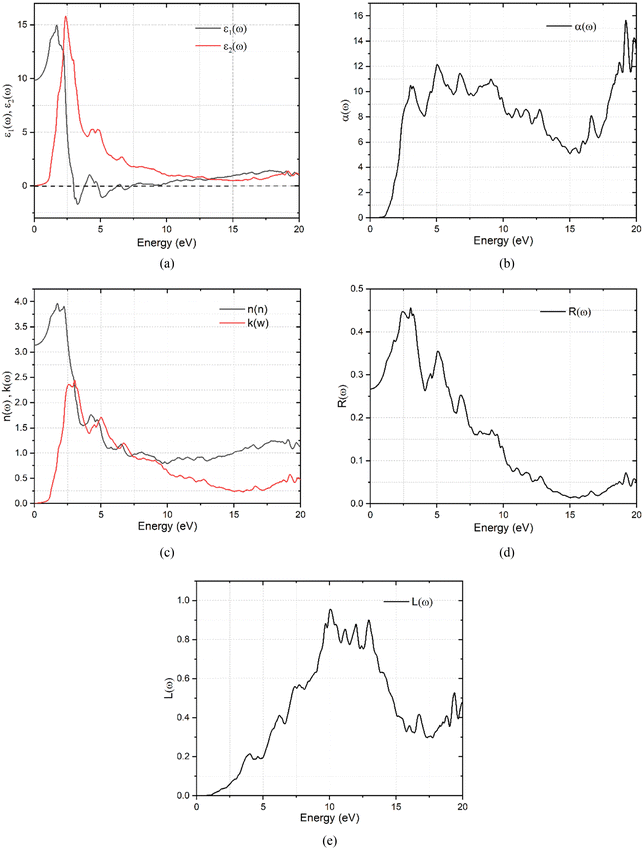
It can be observed in Fig. 5(a) that the real part of the dielectric function ε1(ω) has a higher signal between 0 and 2.53 eV, from there it assumes a negative signal from 2.53 eV to 3.87 eV followed by a brief positive signal before assuming another section of negative signal between 4.35 eV and 8.02 eV. In the sections where it has a negative signal, the photons of the electromagnetic waves in those regions are completely attenuated and the material exhibits a metallic behaviour. In the case of the imaginary dielectric function ε2(ω), it shows a large absorption peak between 0.6–3.78 eV, this section lies the visible region to the near-infrared region of the spectrum and reveals that this material may be suitable for application in photovoltaics. The imaginary dielectric function is closely related to the absorption coefficient shown in Fig. 5(b).41 The absorption coefficient reveals the skin depth of a material by determining how far light photons of a particular wavelength penetrate and their penetration depth before they get completely attenuated, and it is noteworthy that absorption is dependent on the material and the incident wavelength.
The material shows that it had strong absorption from 0.6 eV to 20.0 eV, with dispersion shoulders shown by peaks at 1.21 eV and another peak at 1.67 eV, these shoulders lie at points where some functional predicted the band gap of the semiconductor material. The dispersion of the incidence electromagnetic waves is described by the refractive index of a material. The refractive index tells how much the incident rays are refracted by a material while the extinction coefficient describes its absorption or attenuation by a material, and it is related to the absorption coefficient by α = 4πk/λ where λ is the wavelength of incidence light in free space. The refractive index and the extinction coefficient of the K3Ag3As2 ternary compound are shown in Fig. 5(c). In Fig. 5(c), it can be seen that the refractive index dispersion is closely related to the real part of the dielectric constant ε1(ω). The material shows that both the refractive index and the extinction coefficient had higher dispersion in the lower energy region from 0.0 to 10.0 eV, while from 10.0 to 20.0 eV, their dispersion was very low. Another optical parameter essential for the study of optoelectronics is the reflectivity. The reflectivity properties of K3Ag3As2 are shown in Fig. 5(d).
When the incident electromagnetic waves interact with a material, depending on the nature of the material whether a good conductor, lossy dielectric or lossless dielectric, the incident wave part of it is either gets reflected and the other part is transmitted or absorbed by the material. The material shows strong reflectivity characteristics in the lower energy region than in the higher energy region. To understand further what happens during the interaction of the photons with the material, there is a need to look at the energy loss spectra shown in Fig. 5(e).
The energy loss spectra describe the relation between the amount of energy lost by the incidence photons when they interact with a material. K3Ag3As2 shows strong energy loss between the 5.0 eV to 17.0 eV part of the spectrum.
The information gathered on optical properties is useful in determining application suitability in various optoelectronic devices such as photovoltaic solar cells, photodetectors, light-emitting diodes, lasers, etc. From the analysis carried out on K3Ag3As2, it was found that it is suitable for application in optoelectronics especially in photovoltaics.
Conclusions
First principles methods have been used to study the structural, electronic, mechanical, elastic and optical properties of a K3Ag3As2 Zintl phased ternary semiconductor compound using six different exchange correlation functionals including LDA-PZ, GGA-EV, SO-GGA, GGA-PBE, GGA-PBESol, and GGA-revPBE. These functionals have played a role in complementing each other since each has different strengths in different calculations. The structural property calculations have shown that the material adopts a rhombohedral crystal structure and the mean lattice parameter was 15.1808 a.u., and this value has been found to agree closely with the previously calculated experimental value of 15.1590 a.u. The electronic band structure has been found to range between 1.07 eV and 1.74 eV. The study of the orbital contribution to the formation of bands has shown that valence band formation is mainly due to As 2p and Ag 3d orbitals with minimal contributions from other orbitals, while the conduction band formation is majorly due to contributions from the Ag 2p and As 2p orbitals with minor contributions from other orbitals. The material has been found to be soft, ductile and possess ionic bonds. The optical properties have shown that the material is suitable for optoelectronic applications.Author contributions
M. M. K. contributed during conceptualization, data curation, analysis, investigation, methodology, and draft writing – review and editing. R. M., F. N. and J. M. made equal contributions during conceptualization, data curation, analysis, investigation, methodology, and draft writing – review and editing, and they were involved in the supervision and mobilization of resources.Conflicts of interest
All authors have no conflict of interest to declare.Acknowledgements
The authors acknowledge the RSIF grant number RSIF_RA_015 for support in some of the resources used in this work, the International Science Program for computational seed grant through KEN02 grant, and the Centre for High Performance Computing CHPC-RSA for computing resources.References
- S. H. Ali, Nat. Mater., 2018, 17, 1052–1053 CrossRef CAS PubMed.
- T. Seddik, B. Rezini, K. Djelid, B. U. Haq, S. H. Kim, M. Batouche, S. Fahad, A. Djelloul and G. Yumnam, Phys. B, 2023, 668, 415209 CrossRef CAS.
- M. Manzoor, D. Behera, R. Sharma, M. W. Iqbal, S. K. Mukherjee, R. Khenata, S. Bin-Omran, T. Alshahrani, E. El Shiekh and T. Ouahrani, J. Solid State Chem., 2023, 124188 CrossRef CAS.
- D. Behera, R. Sharma, H. Ullah, H. S. Waheed and S. K. Mukherjee, J. Solid State Chem., 2022, 312, 123259 CrossRef CAS.
- O. Janka and S. M. Kauzlarich, Encyclopedia of Inorganic and Bioinorganic Chemistry, Wiley, 2021, pp. 1–19 Search PubMed.
- H. Schäfer, B. Eisenmann and W. Müller, Angew. Chem., Int. Ed. Engl., 1973, 12, 694–712 CrossRef.
- S. Maabed, M. Halit, A. Bouhemadou, A. Benmakhlouf and M. Bouchenafa, J. Alloys Compd., 2019, 804, 128–138 CrossRef CAS.
- P. Larson, S. D. Mahanti, J. Salvador and M. G. Kanatzidis, Phys. Rev. B, 2006, 74, 035111 CrossRef.
- J. Wang, B. Owens-Baird and K. Kovnir, Inorg. Chem., 2022, 61, 533–541 CrossRef CAS PubMed.
- Y. Wang and S. Bobev, Materials, 2023, 16, 1428 CrossRef CAS PubMed.
- A. Ovchinnikov and S. Bobev, J. Solid State Chem., 2019, 270, 346–359 CrossRef CAS.
- G. Savelsberg and H. Schäfer, Z. Naturforsch. B, 1979, 34, 1033–1034 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Ziesche, S. Kurth and J. P. Perdew, Comput. Mater. Sci., 1998, 11, 122–127 CrossRef.
- E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164–13174 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2008, 128, 184109 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. Musembi and M. Mbilo, MRS Adv., 2023, 8, 640–644 CrossRef CAS.
- M. Mbilo and R. Musembi, AIP Adv., 2022, 12, 105018 CrossRef CAS.
- V. G. Tyuterev and N. Vast, Comput. Mater. Sci., 2006, 38, 350–353 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. Seidl, A. Görling, P. Vogl, J. Majewski and M. Levy, Phys. Rev. B, 1996, 53, 3764–3774 CrossRef CAS PubMed.
- J. P. Perdew, Int. J. Quantum Chem., 2009, 28, 497–523 CrossRef.
- N. Muhammad, A. Khan, S. Haidar Khan, M. Sajjaj Siraj, S. S. A. Shah and G. Murtaza, Phys. B, 2017, 521, 62–68 CrossRef CAS.
- M. Yusuf, F. O. Saouma, G. S. Manyali, J. W. Wafula and O. Huxley, Solid State Commun., 2023, 370, 115219 CrossRef CAS.
- J. Yu, S. Chen, Y. Chen, J. Hou, S. Li and Z. Shi, Mater. Today Commun., 2023, 34, 105258 CrossRef CAS.
- H. Yao, L. Ouyang and W. Y. Ching, J. Am. Ceram. Soc., 2007, 90, 3194–3204 CrossRef CAS.
- R. Anbarasan, V. Balasubramani, M. Srinivasan, J. K. Sundar, P. Ramasamy, A. A. Al-Kahtani, M. Ubaidullah, I. A. Setiawan, W. K. Kim and S. Gedi, J. Solid State Chem., 2022, 316, 123590 CrossRef CAS.
- Z. Chen, U. Gandhi, J. Lee and R. H. Wagoner, J. Mater. Process. Technol., 2016, 227, 227–243 CrossRef CAS.
- J. K. Luo, Y. Q. Fu, H. R. Le, J. A. Williams, S. M. Spearing and W. I. Milne, J. Micromech. Microeng., 2007, 17, S147–S163 CrossRef CAS.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef PubMed.
- J. Wang, H. Qin, J. Chen, D. Yang and G. Zhang, Metals, 2022, 12, 959 CrossRef CAS.
- H. A. Mezher, K. Al-Attafi, A. Obies Muhsen Almayyali, S. Hamzawy and J. Ho Kim, ChemistrySelect, 2023, 8, 1–9 CrossRef.
- H. J. Wu, Q. Yang, C. E. Hu, Y. Cheng and G. F. Ji, Mater. Sci. Semicond. Process., 2023, 153, 107165 CrossRef CAS.
- A. K. Mondal, M. A. Mohamed, L. K. Ping, M. F. M. Taib, M. H. Samat, M. A. S. M. Haniff and R. Bahru, Materials, 2021, 14, 604 CrossRef CAS PubMed.
- A. Es-Smairi, N. Fazouan, H. Joshi and E. H. Atmani, J. Phys. Chem. Solids, 2022, 160, 110305 CrossRef CAS.
- M. S. Yaseen, G. Murtaza and R. M. Arif Khalil, Opt. Quantum Electron., 2019, 51, 367 CrossRef.
- M. Fox and G. F. Bertsch, Am. J. Phys., 2002, 70, 1269–1270 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |