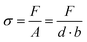Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling parameter interactions in calcium alginate/polyacrylamide double network hydrogels using a design of experiments approach for the optimization of mechanical properties†
Oliver
Gorke
a,
Marc
Stuhlmüller
a,
Günter E. M.
Tovar
 ab and
Alexander
Southan
ab and
Alexander
Southan
 *ac
*ac
aInstitute of Interfacial Process Engineering and Plasma Technology IGVP, University of Stuttgart, Nobelstr. 12, 70569 Stuttgart, Germany
bFraunhofer Institute for Interfacial Engineering and Biotechnology IGB, Nobelstr. 12, 70569 Stuttgart, Germany
cMax Planck Institute for Intelligent Systems, Heisenbergstr. 3, 70569 Stuttgart, Germany. E-mail: southan@is.mpg.de
First published on 16th February 2024
Abstract
Calcium alginate/polyacrylamide double network hydrogels were reported to be exceptionally tough. However, literature reports so far varied the sample compositions mainly by one parameter at a time approaches, thus only drawing an incomplete picture of achievable material properties. In this contribution, sample compositions are varied according to a face-centered central composite experimental design taking into account the four parameters of alginate concentration cAlg, high/low molar mass alginate mixing ratio RP, acrylamide concentration cAAm, and N,N′-methylenebisacrylamide concentration cMBA. Each sample composition is investigated in triplicate. Thus, 75 samples were investigated by tensile testing, and a detailed analysis of the significant parameters and parameter interactions influencing the mechanical properties is conducted. The data shows that two parameter interactions, involving all four tested parameters, have a large effect on the Young's modulus, the strength, the toughness and the strain at material failure. As a consequence, it becomes evident that the experimental procedure from previous studies did not always result in optimum sample compositions. The results allow optimization of the mechanical properties within the studied parameter space, and a new maximum value of the strength of 710 kPa is reported. The data also give rise to the assumption that other parameters and parameter interactions ignored also in this study may allow further tailoring of mechanical properties.
Introduction
Hydrogels are highly attractive materials in such diverse fields such as tissue engineering,1–3 soft robotics,4–7 drug delivery,8–10 or sensing.11 This is facilitated by the many advantageous properties of hydrogels like biocompatibility,12,13 responsiveness,14,15 or permeability for solutes.16,17 However, one of the outstanding weaknesses of many hydrogel materials is their poor mechanical stability. Hydrogels typically have rather low Young's moduli in the order of 10 kPa and rarely above 100 kPa,18,19 and fracture energies often below 10 J m−2,20,21 limiting their application in load-bearing environments. One approach to overcome these shortcomings are the so-called double network (DN) hydrogels, consisting of two intertwined, independent, swollen polymer networks.22,23One popular DN hydrogel class is composed of chemically cross-linked polyacrylamide (PAAm) as the first network and physically cross-linked alginate (Alg) as the second network, first described by Sun et al.24 The Alg is most frequently cross-linked with Ca2+ ions and the resulting materials are called Ca-Alg/PAAm DN hydrogels. When deforming these materials, crack bridging occurs by the PAAm network simultaneous to energy dissipation by unzipping ionic cross-links in the alginate network.25 As a result, Ca-Alg/PAAm DN hydrogels were shown to have outstanding properties, such as tunable Young's moduli E between just a few kPa up to approx. 1 MPa, and fracture energies of up to approx. 16 kJ m−2.24,25 Among others, these remarkable characteristics have led to applications of Ca-Alg/PAAm DN hydrogels in 3D printing,26,27 tissue engineering,28–30 stretchable optical fibers31 and electronics,32,33 wet adhesives,34 hydrogel folding,35,36 sensors,37 and actuators.38
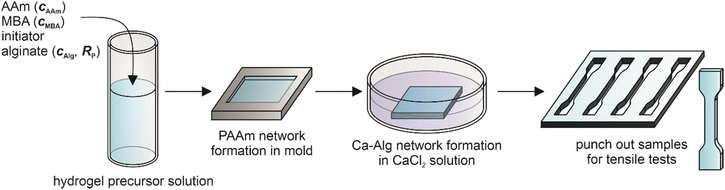
The exact material properties depend on the preparation conditions and the sample composition. Ca-Alg/PAAm DN hydrogel preparation is usually achieved by first forming the PAAm network by free radical polymerization in the presence of sodium alginate (Na-Alg), followed by cross-linking of the Alg with Ca2+ ions (Scheme 1). In this context, especially the method to introduce the Ca2+ ions into the hydrogels was studied. Initial reports used CaSO4 particles dispersed in the precursor solution which slowly released Ca2+ ions into the formulation.24,39 However, due to limited solubility of CaSO4 the achieved cross-link density of Alg was low, so not the entire possible spectrum of mechanical properties was harnessed, and for examples the achieved Young's moduli were relatively low up to approx. 300 kPa.24 Later, instead of using CaSO4 particles, the pre-formed PAAm hydrogel containing Na-Alg was submerged in rather concentrated CaCl2 solutions, allowing the Ca2+ ions to diffuse into the gel.25,26,29,40–42 The resulting high cross-link density of Alg allows the above mentioned high Young's moduli up to 1000 kPa and fracture energies of up to 16 kJ m−2, albeit not for the same sample composition, if simultaneously the Alg concentration is adjusted accordingly.25 Another method involves a mixture of CaCO3 particles and D-glucono-δ-lactone (GDL).43–45 GDL hydrolyzes slowly, thus lowering the pH and decomposing the CaCO3 to make the Ca2+ ions accessible in solution.
The description of the sample preparation process demonstrates that a multitude of parameters influence the final properties of the materials. Within the precursor solution, various components are present: The monomer acrylamide (AAm), the cross-linker N,N′-methylenebisacrylamide (MBA), a radical initiator (typically ammonium persulfate, APS), N,N,N′,N′-tetramethyl ethylenediamine as a catalyst, and Na-Alg. The Na-Alg can come from different sources with varying molar mass or molecular structure.46 Finally, the concentration and application method of the calcium ion cross-linker is crucial. The sample composition is governed by the concentrations of all components in the precursor solution. It becomes evident that it is difficult to study the whole parameter space for sample preparation, and thus it is difficult to access the optimum conditions, e.g., to maximize the Young's modulus.
As a result, the pioneering studies published so far put forward mainly variations of one parameter at a time and thus provided a starting point to understand the Ca-Alg/PAAm DN hydrogel behavior. Sun et al. varied the AAm fraction in the total monomer content (cAAm + cAlg) as well as changed the CaSO4 and MBA concentrations.24 Others studied different total Alg concentrations in the precursor solutions,25,26,41 or varied the APS concentration,43 MBA concentration,39 or used different metal ions to cross-link the Alg.35,40,47 Naficy et al. and Fitzgerald et al. in principle varied two parameters simultaneously (Alg/MBA concentrations and MBA/Ca2+ cross-linker concentrations, respectively), however did not go into detail concerning possible parameter interactions.41,43 In order to illustrate what a two-factor interaction is, the data reported by Li et al. is helpful.25 They showed an increase of E with increasing Alg concentration while keeping the AAm concentration constant. A change of the AAm concentration could of course have an effect on E, but this is not the important point for a two-factor interaction. A two-factor interaction would mean that the change of AAm concentration, on top of its own effect, induces an additional change of the dependence of E with the Alg concentration, possibly causing a large leveraging effect on E. Thus, such two-factor interactions can be expected to be extremely important for optimization of mechanical properties of Ca-Alg/PAAm hydrogels.
However, up to now no studies exist which cover a larger part of the parameter space concerning the sample composition, and as a consequence it is completely unknown in how far parameter interactions influence the outcome of the experiments and induce leveraging effects on the material properties. Therefore, we hypothesize that the ideal preparation conditions for Ca-Alg/PAAm DN hydrogels have not been found yet. In this contribution, we aim to systematically vary the following four important parameters dealing with the composition of the hydrogel precursor solution (Scheme 1) in a design of experiments (DoE) approach,48 and investigate their impact on the mechanical properties: (1) Alg concentration cAlg, (2) fraction RP of high molar mass Alg in total Alg concentration, (3) AAm concentration cAAm, and (4) MBA concentration cMBA. We especially will study two parameter interactions in detail for the first time. We thus hope to contribute to a more comprehensive understanding of the principles that govern the Ca-Alg/PAAm DN hydrogel properties.
Experimental
Materials
The following materials were purchased from Sigma-Aldrich (Germany): Acrylamide (AAm, ≥99%), ammonium peroxodisulfate (APS, ≥98%), calcium chloride dihydrate (CaCl2·2H2O, ≥99%), disodium hydrogen phosphate (Na2HPO4, ≥99%), N,N′-methylenebisacrylamide (MBA, 99%), N,N,N′,N′-tetramethyl ethylenediamine (TEMED, 99%). The sodium alginates Protanal LF 10/60 and Manucol LD were obtained from FMC BioPolymer (USA). Poly(methacrylic acid) (PMAA) standards for size exclusion chromatography were purchased from PSS Polymer Standards Service (Germany).Size exclusion chromatography
The molar mass distribution of the two alginates Protanal LF 10/60 and Manucol LD were investigated at 40 °C by size exclusion chromatography using a 1260 infinity GPC-SEC analysis system (Agilent Technologies, USA) equipped with a Suprema Linear M column (PSS Polymer Standards Service, Germany) in the range of 1 kDa to 1000 kDa. A 0.07 M solution of Na2HPO4 in ultrapure water was used as the eluent and to dissolve the respective alginates (1 mg mL−1). The flow rate was set to 1 mL min−1, the injection volume was 50 µL. For universal calibration of the measuring system polymethacrylic acid standards were dissolved and measured with a concentration of 1 mg mL−1 in Na2HPO4 (0.07 M) combining refractive index (RI) and viscometer detectors.General procedure for preparation of hydrogel samples for tensile tests
Ca-Alg/PAAm DN hydrogels were prepared according to the experimental plan described below using a two-step method in which first the PAAm network is produced in the presence of sodium alginate (Scheme 1).40,49 For this purpose, the sodium alginates Protanal LF 10/60 and Manucol LD were mixed at the required concentrations with ultrapure water (30 mL) and stirred at 40 °C for 30 min. Subsequently, the mixture was agitated on a roller mixer at room temperature until the alginates were fully dissolved (typically approx. 1 h). Then AAm, MBA as well as APS were added in the required amounts and dissolved on the roller mixer for 15 min at room temperature. The solution was degassed in an ultrasonic bath at 40 °C for 15 min. This was followed by the addition of TEMED, which was dissolved using a roller mixer for one minute. The entire solution was pipetted into a mold consisting of two quartz glass panes separated by a silicone spacer (2 mm height) greased with polytetrafluoroethylene (PTFE) paste for better adhesion. Cross-linking of the PAAm network was carried out for 48 h at room temperature. After that, the gel was transferred into a Petri dish and covered entirely with 100 mL of a 0.5 M CaCl2 solution. The sample was swollen for 48 h at room temperature, replacing the entire volume of the CaCl2 solution after 24 h. After the swelling process, specimens for tensile tests in the shape of the S3A sample (DIN 53504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2017-03) (Fig. S1, ESI†) were punched out of the DN hydrogels and examined.
2017-03) (Fig. S1, ESI†) were punched out of the DN hydrogels and examined.
Experimental plan for the variation of the hydrogel composition
Preparation parameters varied according to a DoE were the total alginate concentration cAlg, the fraction RP of the Protanal LF 10/60 concentration of the total alginate concentration, the concentration cAAm of AAm, and the concentration cMBA of MBA. The concentrations of the initiator APS and the catalyst TEMED were fixed relative to cAAm and were 0.42% and 0.25% of cAAm, respectively. The ranges of the parameter values are given in Table 1.| Min | Center | Max | |
|---|---|---|---|
| c Alg [wt%] | 1 | 3 | 5 |
| R P | 0.17 | 0.5 | 0.83 |
| c AAm [wt%] | 6 | 12.5 | 19 |
| cMBA [wt%] | 0.01 | 0.02 | 0.03 |
| Coded values | −1 | 0 | 1 |
In this study, parameter values were varied according to a face-centered central composite design, resulting in 25 different sample compositions (Table S2, ESI†).48 Each sample composition was prepared in triplicate, so that in total 75 independently prepared samples were investigated for their mechanical properties in a randomized order (Table S3, ESI†). For the mechanical tests, five samples were punched from each of the 75 samples and characterized in a tensile test.
Uniaxial tensile tests
The mechanical characterization of the Ca-Alg/PAAm DN hydrogels was carried out by uniaxial tensile tests using the Allround-Line table-top testing machine (Zwick Roell, Germany). Sample clamping without damage was achieved with a custom-made clamping tool (Fig. S2, ESI†). Tests were prepared by pre-loading the samples with a strain rate of 5 mm min−1 until a force of 0.1 N was reached. Subsequently, samples were stretched with a strain rate of 200 mm min−1 until rupture. For the calculation of the tensile stress σ, the measured normal force F was divided by the cross sectional area A of the unstrained sample:Here, b is the sample width (4 mm) as defined by the sample geometry (Fig. S1, ESI†) and d is the sample thickness. Because d depends on sample swelling during preparation it was measured for each sample composition with a light microscope. From the resulting stress–strain curves, the mechanical properties of Young's modulus E, strength σmax, toughness UT, and strain at break εmax were determined. E was taken as the slope of the initial linear region of the stress–strain curve and was calculated by linear regression. For the regression, the data was first smoothed with a Savitzky–Golay filter50 and as many data points were included until the coefficient of determination R2 dropped to 0.995. The strength σmax was found as the highest occurring stress, while UT describes the energy absorption of a material during plastic deformation until it fails and was determined by the area underneath the stress–strain curve. The strain at break εmax was the maximum reached strain.
Statistical analysis and model fitting
A full linear model was used to describe each of the experimental responses, for the corresponding expression see eqn (S2) (ESI†). The model contained 11 regression coefficients, i.e. four front factors of the terms proportional to only one parameter (aAlg, aR, aAAm, aMBA), six front factors of two parameter interaction terms (bAlg,R, bAlg,AAm, bAlg,MBA, bR,AAm, bR,MBA, bAAm,MBA), and one intercept (r0). The statistical evaluation was carried out by analysis of variance (ANOVA) taking into account all 75 independently prepared samples with their coded parameter values. Non-significant model terms with p > 0.05 were excluded, except if they were needed to keep the model hierarchical. Experimental data in figures are generally given as mean of the measured values ± standard deviation.Results and discussion
Experimental plan
Due to the complex composition, a multitude of parameters is relevant for sample preparation and consequently for the properties of Ca-Alg/PAAm DN hydrogels. In order to end up with a manageable experimental plan, we had to select a limited number of parameters which likely influence the results significantly and which could be well controlled (Scheme 1). For this purpose, we compiled an overview of some preparation conditions used in the literature (Table S1, ESI†). From these conditions, together with the mechanical characterization data from the corresponding publications, we concluded that the four parameters Alg concentraton cAlg, fraction RP of high molar mass Alg in total Alg concentration, AAm concentration cAAm, and MBA concentration cMBA were important parameters for which also no data on two parameter interactions were collected so far.In order to vary RP, two Alg variants with different molar masses were needed. Therefore, the molar masses of the two Alg variants Protanal LF 10/60 and Manucol LD were investigated by size exclusion chromatography (SEC) (Table 2). Indeed, Protanal LF 10/60 exhibited much larger molar masses than Manucol LD, thus making the two polymers suitable to investigate the effect of the fraction of higher molar mass Alg in the Alg mixture.
| Protanal LF 10/60 | Manucol LD | |
|---|---|---|
| M n [g mol−1] | 1.70 × 105 | 2.04 × 104 |
| M w [g mol−1] | 3.10 × 105 | 1.00 × 105 |
| Đ | 1.83 | 4.93 |
Apart from the four varied parameters, all other parameters were fixed. It is conceivable that the unaltered parameters like radical initiator concentration, TEMED concentration, Ca2+ ion concentration and application method, the kind of cross-linking ion (Ca2+ or other metal ions), or sample preparation methodology also have significant effects and are also heavily involved in parameter interactions. However, the envisioned experimental plan with four parameters results in 25 different parameter settings. Due to the general variance observed in tensile tests of hydrogels, we decided to prepare three independent samples for each composition, so that in total 75 samples were investigated. A further increase of investigated parameters would rapidly increase the number of samples, making a realization impractical.
The tested value ranges of the parameters (Table 1) were derived from the values listed in Table S1 (ESI†), and to support these we conducted preliminary experiments. The goal was to make sure that it is possible to prepare defect-free Ca-Alg/PAAm DN hydrogel samples under all parameter settings that could also be submitted to mechanical tests, so that a detailed analysis of the parameter effects and, more importantly, parameter interactions was possible. The tensile tests described in the following section rely on defect-free samples. The main cause for defects were air bubbles entrapped in hydrogel precursor solutions of high viscosity, most relevant for the combination of a high cAlg and a high RP and therefore limiting the maximum cAlg to 5 wt%.
Tensile tests and resulting stress strain curves
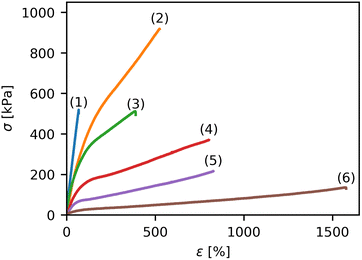
Representative stress strain curves measured for some individual Ca-Alg/PAAm DN hydrogels prepared in this study are shown in Fig. 1. Different shapes of the stress strain curves were observed. Some samples showed a very steep increase of the stress σ and subsequent failure at rather low strains ε (curve 1 in Fig. 1). In other cases, samples could be stretched to very high strains before failure while still at rather low stresses (curve 6 in Fig. 1). Within the entire dataset, various stress strain curves between these two extremes were measured (curves 3, 4 and 5), with the maximum stress observed in curve 2 (Fig. 1). The stress strain curves could generally be tuned well by adjusting the sample composition, and their general appearance was similar to previous literature reports.24,25,40 In order to further analyze the data, the Young's modulus E, the strength σmax, the toughness UT, and the strain at break εmax were extracted for all samples and will be discussed in the following section.It has to be noted that for the tensile tests, a secure clamping of the specimens in the testing machine must be achieved. In contrast to previous reports,24,25 we avoided gluing of the hydrogels because we observed optical changes on the glued sample surface and increased brittleness of the sample. Instead, we used a specially designed clamping tool (Fig. S2, ESI†). With the help of a spring, a sufficient and reproducible clamping force is achieved even with changes in the thickness of the specimen during testing.
Analysis of mechanical properties
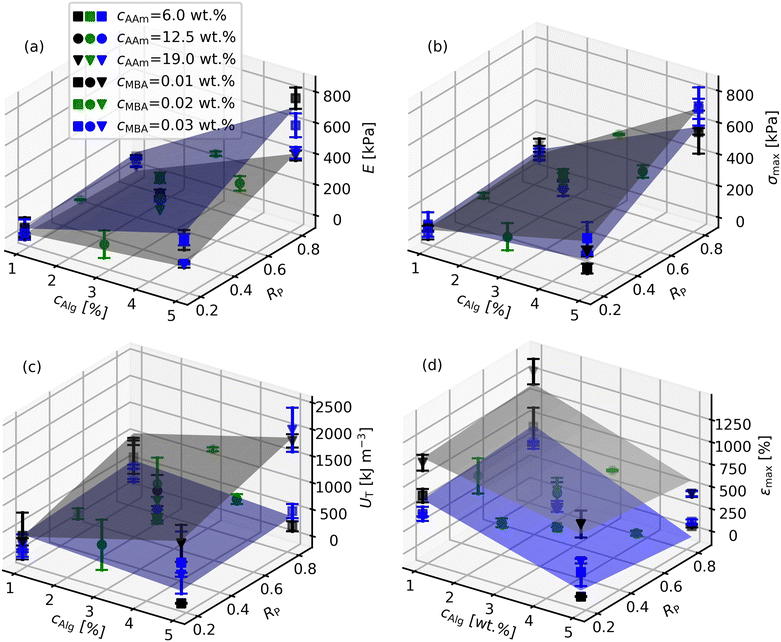
The results for the mechanical properties E, σmax, UT and εmax are shown in Fig. 2. Additionally, all individual results for the 75 investigated samples as collected chronologically are listed in Table S3, the order a result of randomization of parameter settings (ESI†). The data was assessed by analysis of variance, the corresponding p-values of the various model coefficients are listed in Table 3. Additionally, the regression coefficients after fitting the data with eqn (S2) (ESI†) are collected in Table 4. Model diagnosis graphs are shown in the ESI† (Figures S5 to S8).| a Alg | a R | a AAm | a MBA | b Alg,R | b Alg,AAm | b Alg,MBA | b R,AAm | b R,MBA | b AAm,MBA | |
|---|---|---|---|---|---|---|---|---|---|---|
| E | <10−4 | <10−4 | <10−4 | 0.13 | <10−4 | <10−4 | n.s. | 0.002 | n.s. | 0.015 |
| σ max | <10−4 | <10−4 | n.s. | 0.02 | <10−4 | n.s. | 2 × 10−4 | n.s. | n.s. | n.s. |
| U T | <10−4 | <10−4 | <10−4 | 0.29 | n.s. | <10−4 | 0.017 | 0.010 | n.s. | 0.027 |
| ε max | <10−4 | 0.42 | <10−4 | <10−4 | 0.002 | 0.023 | <10−4 | n.s. | n.s. | <10−4 |
| r 0 | a Alg | a R | a AAm | a MBA | b Alg,R | b Alg,AAm | b Alg,MBA | b R,AAm | b R,MBA | b AAm,MBA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 207.3 | 172.2 | 88.6 | −67.2 | −10.1 | 81.3 | −45.9 | — | −21.5 | — | 16.7 |
| σ max | 265.5 | 166.6 | 117.3 | — | 21.7 | 90.6 | — | 36.8 | — | — | — |
| U T | 726.4 | 281.0 | 204.8 | 242.4 | −46.3 | — | 243.7 | 126.2 | 135.8 | — | −116.5 |
| ε max | 494.8 | −156.5 | −15.1 | 162.8 | −112.9 | −58.5 | 41.9 | 108.4 | — | — | −112.8 |
Concerning the Young's modulus E, it is evident from Fig. 2(a) that the reported range is similar to previous literature reports and that varying the three parameters cAlg, RP and cAAm univariately around the center point (all coded parameter values are 0, E = 207.3 kPa) had a substantial effect, while cMBA only had a minor influence. It was observed that E generally increased with increasing cAlg and RP and with decreasing cAAm. This is also reflected by the p-values (Table 3) and regression coefficients (Table 4) of aAlg, aR, aAAm and aMBA. This univariate dependence of E was studied before. For example, Nafici et al. and Li et al. showed an increase of E with cAlg.25,41 The importance of the Alg network for E is also evident from the dramatic increase of E when exchanging Ca2+ with Fe3+.40 Fitzgerald reported an increase of E with increasing total monomer concentration (cAlg + cAAm), but a fixed ratio of cAlg and cAAm,43 thus mixing two of the parameters in this study with opposing influences. However, the absolute value of aAlg is greater than of aAAm, so their finding is also in line with our study. Similarly, Sun et al. found a decrease of E with increasing fraction of AAm in the total monomer content.24 Interestingly, the two parameters cAlg and cAAm are frequently coupled in studies so far.24,43 The results here clearly show that it is more reasonable to vary cAlg and cAAm independently for maximizing or fine-tuning E due to their opposing effects. Concerning cMBA, Nafici et al. also found it is of minor importance41 while Fitzgerald et al. reported an increase of E with cMBA.43 The reason for these seemingly conflicting findings probably is in the range of concentrations investigated: The former study was rather close to the range in this study while the latter study chose much smaller values (see Table S1, ESI†).
The major advantage of the DoE approach in this study compared to a one parameter at a time approach becomes evident when analysing the effect of RP on E. In this context, it is important to note that Li et al. already varied the ratio of a short chain alginate in the alginate mixture, similar to the variation of RP in this study.25 However, they found that there is no big variation of E with the alginate ratio in their experiments, quite in contrast to our findings here where aR was 88.6, indicative of an increase of E with RP. In order to resolve this contradiction, it is useful to look at the significant two parameter interaction terms in Table 3 and 4. Indeed, four of the two parameter interactions were significant, including bAlg,R and bAlg,AAm. This is also reflected by the different slopes of E with cAlg depending on the values of cAAm and RP (Fig. 2(a)). Expressing the experimental parameters from Li et al. in terms of the parameters used in this study, they varied RP from 0 to 1 with cAlg = 2.3 wt%, cAAm = 16.8 wt% and cMBA = 0.01 wt%,25 which is rather close to the grey surface plotted in Fig. 2(a). Indeed, at cAlg = 2.3 wt%, the slope for E with RP is quite low, in line with Li et al., thus resolving the contradiction above. It becomes evident that a high cAlg leverages up the effect of RP on E which has not been recognized in the previous literature studies. Another finding by Li et al. was an E of approx. 1000 kPa by increasing cAlg up to 6.4 wt% while fixing all other parameters. However, our data show that their choice of a rather high cAAm = 16.8 wt% was not ideal to maximize E: A simultaneous reduction of cAAm when increasing cAlg leads to further increase of E due to the two parameter interaction, especially when at the same time a high RP is adjusted, which Li et al. also did not do. These results clearly demonstrate that the experimental plan in this study allows one to navigate the entire parameter space more efficiently in order to optimize the responses such as E, compared to the univariate approaches followed in the literature so far. Thus, E values between 3.8 kPa and 766.9 kPa were reached.
Looking at the next response, the strength σmax, generally the trends were similar to the trends observed for E (Fig. 2(b)). Indeed, samples with a high E also had a high σmax, and vice versa (Figure S3, ESI†). The increase of σmax with cAlg is again in line with literature reports.26,41 Also the increase of σmax with RP was reported before.25 Nafici et al. also in principle investigated the effect of cMBA on σmax, however did not discuss their results accordingly, probably because the effect was very small, if significant at all.41 The main differences found between σmax and E in this study were that for σmax, cMBA was significant, like also the two parameter interaction of cMBA and cAlg (Table 3). However, the effect of cMBA, although significant, is not dominating due to the rather small regression coefficients aMBA and bAlg,MBA. Additionally, cAAm was not significant, and also did not participate in any parameter interaction. By contrast, like for E, the two parameter interaction term bAlg,R is of great importance due to its relatively large value. Generally, the knowledge about the significant parameters and parameter interactions and the values of the corresponding regression coefficients (Table 4) again allow to fine-tune σmax according to the needs of a specific application in the range between 46.2 kPa and 709.8 kPa. To the best of the authors’ knowledge, this is the highest value reported for the tensile strength of Ca-Alg/PAAm DN hydrogels so far, and a direct result of the systematic parameter variation in this study. For example, Li et al. were limited to strengths of approx. 470 kPa although they increased cAlg up to 6.4 wt% because they missed using high cAlg and RP simultaneously.25 Interestingly, the highest strength so far of approx. 550 kPa from Yang et al. was found at rather low cAlg = 1.56 wt% and also low cMBA = 0.0076 wt% (Table S1, ESI†) which is in contrast to the findings from the present study and other literature.
The third response, the toughness UT, is shown in Fig. 2(c). We report UT as the area under the stress strain curve, like for example also Bakarich et al.26,27 or Du et al.,45 while other literature reports focus on the fracture energy of notched samples.24,25,35,41 Therefore, only few values are available for direct comparison. Additionally, Bakarich et al. used samples prepared by extrusion-based 3D printing in their tests which usually contain defects, so that generally no consistent trend in UT was observed.26 For the analysis of our data, we start again at the experimental center point (all coded parameter values are 0, UT = 726.4 kJ m−3) and think first about univariately changing the parameter values. In this case, only the parameters cAlg, RP, and cAAm had a significant effect on UT while cMBA was found to be insignificant (Table 3). The corresponding regression coefficients of the three significant parameters are similar (Table 4), showing a similar effect of the three parameters within the studied parameter space. The toughness range achieved by univariate variation of cAlg, RP, and cAAm around the center point thus was between 191.5 kJ m−3 and 1346.1 kJ m−3, already covered solely by changing the cAlg value. However, like E and σmax above, also UT is heavily influenced by two parameter interactions with rather high values of the corresponding regression coefficients (Table 3 and 4). Therefore, by multivariate variation of all parameters, a UT range between 21.5 kJ m−3 and 2018.0 kJ m−3 is accessible, again demonstrating the advantages of a DoE approach. The reported values are somewhat smaller than the maximum value of 5100 kJ m−3 given by Du et al.45 This can be explained by their very high value of cAAm = 28% (w/v) and also rather high cAlg = 4% (w/v). The importance of the two parameter interactions for UT becomes evident when focusing on bAlg,AAm. At the lowest cAAm of 6 wt%, UT decreases with increasing cAlg (fixing RP = 0.5 and cMBA = 0.01 wt%) with a slope of −88.8 kJ m−3 in the coded parameter space, see also the blue surface in Fig. 2(c). Such a trend was also observed by Li et al. for the fracture energy.25 By contrast, at the highest cAAm of 19 wt% and again fixing RP = 0.5 and cMBA = 0.01 wt%, UT increases with increasing cAlg with a slope of 398.5 kJ m−3.
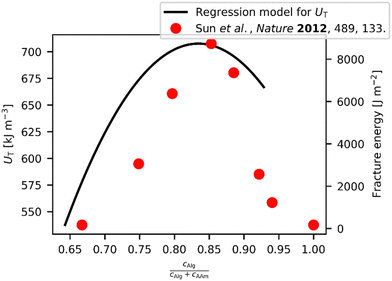
Interestingly, Sun et al. reported an optimum in fracture energy of approx. 8000 J m−2 for their Ca-Alg/PAAm DN hydrogels.24 This was found by varying the ratio of cAAm and total monomer content (cAAm + cAlg). Assuming a correlation between UT and the fracture energy, as it is sometimes observed for hydrogels,51 we should also be able to find such an optimum in our data for UT, which is apparently not present in the data shown in Fig. 2(c). However, when fixing the sum of cAlg and cAAm to 14 wt%, like done by Sun et al. in their experiments,24 and further using their other parameter settings, we can use our model to calculate a dependency of UT against the ratio of cAAm and total monomer content (Fig. 3). The result is very similar to the observation from Sun et al., including the apparent optimum in UT of 707.6 kJ m−3. However, for our data we can safely say that the thus obtained, apparently optimized result is rather far from the real optimum, and it is conceivable that this is also the case for the parameter settings used to maximize the fracture energy reported by Sun et al. Furthermore, the unnecessary coupling of the two parameters cAlg and cAAm results in an awkward path through the parameter space, while pretending a univariate parameter variation, thus concealing the individual parameter influences on UT.
Finally, the fourth response, the strain at break εmax, is plotted in Fig. 2(d). Within the tested sample compositions, a range of εmax between 32% and 1283% was observed. When varying multiple parameter values simultaneously, also for εmax two parameter interactions are highly relevant, similar to the other responses. The highest εmax was a result of the combination of low cAlg, a high cAAm and also a low cMBA. Obviously, a relatively loosely cross-linked PAAm network at a rather high concentration in combination with a low concentration of the Ca-Alg network facilitates a high extensibility of the Ca-Alg/PAAm DN hydrogels. This is also expressed by the corresponding regression coefficients (aAlg, aAAm, aMBA, bAlg,AAm, bAlg,MBA, bAAm,MBA), all pointing to a larger εmax for the mentioned combination. As a result, the samples with a very high εmax had a very low E and vice versa (Figure S4, ESI†). The results are in agreement with previous reports although the maximum strain observed is lower than the highest value of 2300% reported before.24 This can be explained by the differences in the sample preparation procedure. On the one hand, the cMBA in the previous report was lower than the minimum value in the present study, on the other hand also the cross-linking density of the Ca-Alg network was presumably lower due to the Alg cross-linking method with CaSO4 particles.24 Interestingly, our results show only a minor effect of RP on εmax, quite in contrast to its effect on E, σmax and UT. This would generally allow moderate increases in E, σmax and UT by increasing RP without much affecting εmax.
Conclusions
Previously the composition of calcium alginate/polyacrylamide double network hydrogels was varied by one parameter at a time approaches. We could show by a design of experiments approach that as a consequence the achieved, already outstanding mechanical properties were most likely not a result of a fully optimized material composition. The regression models presented here agree with literature findings so far, and additionally dramatically extend the knowledge about the Ca-Alg/PAAm DN hydrogel system by analysis of two-factor interactions. The data analysis shows the way to further improve the optimization efforts to reach well-defined mechanical properties. The investigation took into account four important parameters relevant for the sample composition, and their parameter values varied within limits which guaranteed successful sample preparation. Thus, the highest value for the tensile strength of Ca-ALg/PAAm DN hydrogels reported so far was found. However, the present study only covers a part of the entire parameter space. It is highly probable that as a consequence, still not the full potential of the calcium alginate/polyacrylamide double network hydrogels is uncovered so far. It is for example conceivable that a higher E modulus than reported so far is achievable by increasing cAlg above the maximum level used in the present investigation while keeping a low cAAm and a high RP – a parameter combination that has not been tested in any study. This hypothesis is now possible due to the model described here for the first time by extrapolating out of the investigated parameter space, therefore is speculative presently and subject to future experimental investigation. Future studies should additionally deal with the other parameters which were also ignored in this study, and further optimize the parameter settings to reach even more outstanding properties for Ca-Alg/PAAm DN hydrogels. We would also like to encourage future studies on inherently complex hydrogel systems to follow experimental plans like a design of experiments approach in order to be able to identify parameter interaction effects.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors kindly thank the German Research Foundation (DFG) for financial support of this work (grant ID SO 1387/2-1).Notes and references
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 CrossRef CAS PubMed.
- C. D. Spicer, Polym. Chem., 2020, 11, 184–219 RSC.
- V. Vassallo, A. Tsianaka, N. Alessio, J. Grübel, M. Cammarota, G. E. M. Tovar, A. Southan and C. Schiraldi, J. Biomed. Mater. Res., Part A, 2022, 110, 1210–1223 CrossRef CAS PubMed.
- S. R. Shin, B. Migliori, B. Miccoli, Y.-C. Li, P. Mostafalu, J. Seo, S. Mandla, A. Enrico, S. Antona, R. Sabarish, T. Zheng, L. Pirrami, K. Zhang, Y. S. Zhang, K.-T. Wan, D. Demarchi, M. R. Dokmeci and A. Khademhosseini, Adv. Mater., 2018, 30, 1704189 CrossRef PubMed.
- A. Heiden, D. Preninger, L. Lehner, M. Baumgartner, M. Drack, E. Woritzka, D. Schiller, R. Gerstmayr, F. Hartmann and M. Kaltenbrunner, Sci. Robot., 2022, 7, eabk2119 CrossRef CAS PubMed.
- Y. Lee, W. J. Song and J. Y. Sun, Mater. Today Phys., 2020, 15, 100258 CrossRef.
- E. H. Rumley, D. Preninger, A. Shagan Shomron, P. Rothemund, F. Hartmann, M. Baumgartner, N. Kellaris, A. Stojanovic, Z. Yoder, B. Karrer, C. Keplinger and M. Kaltenbrunner, Sci. Adv., 2023, 9, eadf5551 CrossRef CAS PubMed.
- T. R. Hoare and D. S. Kohane, Polymer, 2008, 49, 1993–2007 CrossRef CAS.
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 16071 CrossRef CAS PubMed.
- F. Dehli, H. Poole, C. Stubenrauch and A. Southan, ACS Appl. Polym. Mater., 2021, 3, 5674–5682 CrossRef CAS.
- D. Buenger, F. Topuz and J. Groll, Prog. Polym. Sci., 2012, 37, 1678–1719 CrossRef CAS.
- C. G. Williams, A. N. Malik, T. K. Kim, P. N. Manson and J. H. Elisseeff, Biomaterials, 2005, 26, 1211–1218 CrossRef CAS PubMed.
- B. Grigoryan, S. J. Paulsen, D. C. Corbett, D. W. Sazer, C. L. Fortin, A. J. Zaita, P. T. Greenfield, N. J. Calafat, J. P. Gounley, A. H. Ta, F. Johansson, A. Randles, J. E. Rosenkrantz, J. D. Louis-Rosenberg, P. A. Galie, K. R. Stevens and J. S. Miller, Science, 2019, 364, 458 CrossRef CAS PubMed.
- I. Tokarev and S. Minko, Adv. Mater., 2010, 22, 3446–3462 CrossRef CAS PubMed.
- F. Markus, F. Dreher, S. Laschat, S. Baudis, G. E. M. Tovar and A. Southan, Polymer, 2017, 108, 21–28 CrossRef CAS.
- G. Majer and A. Southan, J. Chem. Phys., 2017, 146, 225101 CrossRef PubMed.
- V. Hagel, T. Haraszti and H. Boehm, Biointerphases, 2013, 8, 36 CrossRef PubMed.
- D. Caccavo, S. Cascone, G. Lamberti and A. A. Barba, Chem. Soc. Rev., 2018, 47, 2357–2373 RSC.
- M. L. Oyen, Int. Mater. Rev., 2014, 59, 44–59 CrossRef CAS.
- Y. Tanaka, K. Fukao and Y. Miyamoto, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 395–401 CrossRef CAS.
- D. Bonn, H. Kellay, M. Prochnow, K. Ben-Djemiaa and J. Meunier, Science, 1998, 280, 265–267 CrossRef PubMed.
- Q. Chen, H. Chen, L. Zhu and J. Zheng, J. Mater. Chem. B, 2015, 3, 3654–3676 RSC.
- H. Huang, Z. Dong, X. Ren, B. Jia, G. Li, S. Zhou, X. Zhao and W. Wang, Nano Res., 2023, 16, 3475–3515 CrossRef.
- J.-Y. Sun, X. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133 CrossRef CAS PubMed.
- J. Li, W. R. K. Illeperuma, Z. Suo and J. J. Vlassak, ACS Macro Lett., 2014, 3, 520–523 CrossRef CAS PubMed.
- S. E. Bakarich, M. I. H. Panhuis, S. Beirne, G. G. Wallace and G. M. Spinks, J. Mater. Chem. B, 2013, 1, 4939–4946 RSC.
- S. E. Bakarich, R. Gorkin Iii, R. Gately, S. Naficy, M. Panhuis and G. M. Spinks, Addit. Manuf., 2017, 14, 24–30 CAS.
- P. Guo, Y. Yuan and F. Chi, Mater. Sci. Eng., C, 2014, 42, 622–628 CrossRef CAS PubMed.
- I. C. Liao, F. T. Moutos, B. T. Estes, X. Zhao and F. Guilak, Adv. Funct. Mater., 2013, 23, 5833–5839 CrossRef CAS PubMed.
- J. Wang, J. Wei, S. Su, J. Qiu and S. Wang, J. Mater. Sci., 2015, 50, 5458–5465 CrossRef CAS.
- J. Guo, X. Liu, N. Jiang, A. K. Yetisen, H. Yuk, C. Yang, A. Khademhosseini, X. Zhao and S.-H. Yun, Adv. Mater., 2016, 28, 10244–10249 CrossRef CAS PubMed.
- S. Lin, H. Yuk, T. Zhang, G. A. Parada, H. Koo, C. Yu and X. Zhao, Adv. Mater., 2016, 28, 4497–4505 CrossRef CAS PubMed.
- H. Yuk, T. Zhang, G. A. Parada, X. Liu and X. Zhao, Nat. Commun., 2016, 7, 12028 CrossRef PubMed.
- J. Li, A. D. Celiz, J. Yang, Q. Yang, I. Wamala, W. Whyte, B. R. Seo, N. V. Vasilyev, J. J. Vlassak, Z. Suo and D. J. Mooney, Science, 2017, 357, 378–381 CrossRef CAS PubMed.
- T. Li, J. Wang, L. Zhang, J. Yang, M. Yang, D. Zhu, X. Zhou, S. Handschuh-Wang, Y. Liu and X. Zhou, J. Mater. Chem. B, 2017, 5, 5726–5732 RSC.
- X. Zhou, T. Li, J. Wang, F. Chen, D. Zhou, Q. Liu, B. Li, J. Cheng, X. Zhou and B. Zheng, ACS Appl. Mater. Interfaces, 2018, 10, 9077–9084 CrossRef CAS PubMed.
- X. Liu, T.-C. Tang, E. Tham, H. Yuk, S. Lin, T. K. Lu and X. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2200–2205 CrossRef CAS PubMed.
- H. Yuk, S. Lin, C. Ma, M. Takaffoli, N. X. Fang and X. Zhao, Nat. Commun., 2017, 8, 14230 CrossRef CAS PubMed.
- M. C. Darnell, J.-Y. Sun, M. Mehta, C. Johnson, P. R. Arany, Z. Suo and D. J. Mooney, Biomaterials, 2013, 34, 8042–8048 CrossRef CAS PubMed.
- C. H. Yang, M. X. Wang, H. Haider, J. H. Yang, J.-Y. Sun, Y. M. Chen, J. Zhou and Z. Suo, ACS Appl. Mater. Interfaces, 2013, 5, 10418–10422 CrossRef CAS PubMed.
- S. Naficy, S. Kawakami, S. Sadegholvaad, M. Wakisaka and G. M. Spinks, J. Appl. Polym. Sci., 2013, 130, 2504–2513 CrossRef CAS.
- X. P. Morelle, W. R. Illeperuma, K. Tian, R. Bai, Z. Suo and J. J. Vlassak, Adv. Mater., 2018, 30, 1801541 CrossRef PubMed.
- M. M. Fitzgerald, K. Bootsma, J. A. Berberich and J. L. Sparks, Biomacromolecules, 2015, 16, 1497–1505 CrossRef CAS PubMed.
- C. Li, X. Zhou, D. Zhou, F. Chen, J. Shen, H. Li, J. Zhang and X. Zhou, ACS Appl. Polym. Mater., 2019, 1, 3222–3226 CrossRef CAS.
- G. Du, F. Wu, Y. Cong, L. Nie, S. Liu, G. Gao and J. Fu, Chem. Commun., 2015, 51, 15534–15537 RSC.
- K. Y. Lee and D. J. Mooney, Prog. Polym. Sci., 2012, 37, 106–126 CrossRef CAS PubMed.
- Z. Zhang, T. Lin, S. Li, X. Chen, X. Que, L. Sheng, Y. Hu, J. Peng, H. Ma, J. Li, W. Zhang and M. Zhai, Macromol. Biosci., 2022, 22, 2100361 CrossRef CAS PubMed.
- N. R. Draper and F. Pukelsheim, Stat. Pap., 1996, 37, 1–32 CrossRef.
- R. Bai, Q. Yang, J. Tang, X. P. Morelle, J. Vlassak and Z. Suo, Extreme Mech. Lett., 2017, 15, 91–96 CrossRef.
- A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- W. Li, S. Zheng, X. Zou, Y. Ren, Z. Liu, W. Peng, X. Wang, D. Liu, Z. Shen, Y. Hu, J. Guo, Z. Sun and F. Yan, Adv. Funct. Mater., 2022, 32, 2207348 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Literature review about synthesis parameters, details about the experimental plan, all experimental results, details about the tensile test setup, model diagnosis graphs. See DOI: https://doi.org/10.1039/d3ma00740e |
| This journal is © The Royal Society of Chemistry 2024 |