Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advancing very high temperature thermoelectric performance of Yb4Sb3 through dual-substitutions: a combined experimental and theoretical study
Hugo
Bouteiller
 *ab,
Vincent
Pelletier
*ab,
Vincent
Pelletier
 c,
Sylvain
Le Tonquesse
c,
Sylvain
Le Tonquesse
 ab,
Bruno
Fontaine
cd,
Takao
Mori
ab,
Bruno
Fontaine
cd,
Takao
Mori
 ef,
Jean-François
Halet
ef,
Jean-François
Halet
 bc,
Régis
Gautier
bc,
Régis
Gautier
 *c,
David
Berthebaud
*c,
David
Berthebaud
 *bg and
Franck
Gascoin
*bg and
Franck
Gascoin
 a
a
aLaboratoire CRISMAT, ENSICAEN, UNICAEN, CNRS Normandie Univ. (UMR 6508), Caen, France
bCNRS–Saint-Gobain–NIMS, IRL 3629, Laboratory for Innovative Key Materials and Structures (LINK), National Institute for Materials Science (NIMS), 305–0044, Tsukuba, Japan
cUniv Rennes, CNRS, Ecole Nationale Supérieure de Chimie de Rennes, ISCR-UMR6226, F–35000, Rennes, France
dSaint-Cyr Coëtquidan Military Academy, CReC, F–56380, Guer, France
eGraduate School of Pure and Applied Sciences, University of Tsukuba, 305–8671, Tsukuba, Japan
fNational Institute for Materials Science (NIMS), WPI-MANA, University of Tsukuba, 305–0044, Tsukuba, Japan
gNantes Université, CNRS, Institut des Matériaux de Nantes Jean Rouxel, IMN, Nantes F–44000, France
First published on 21st December 2023
Abstract
This article reports and discusses the synthesis and the transport properties of the binary rare-earth antimonide Yb4Sb3 and some of its substituted derivatives. Specifically, co-substitution of La on the Yb site and Bi on the Sb site was attempted to further improve its thermoelectric properties. The solubility limit of the LaxYb4−xSb2.8Bi0.2 solid solution was established to be x = 0.3. Subsequent synthesis of x = 0.1, 0.2, and 0.3 compositions at a larger scale enabled their transport property evaluation and the comparison with Yb4Sb3. The Seebeck coefficient of the substituted compounds was found to be similar to the pristine material from 373 to 1273 K, while an increase in resistivity was observed. Detailed DFT calculations confirmed that the Seebeck coefficient may not be significantly improved by La substitutions and explained the p-type conducting behavior at high temperatures of the title compounds. The thermal conductivity of La0.2Yb3.8Sb2.8Bi0.2 was found to be reduced by about 30% compared to that of the binary Yb4Sb3. The figure of merit zT of the parent Yb4Sb3 compound reaches 0.5 at 1273 K. While dual substitutions have not permitted a significant improvement in the figure of merit mostly due to a resistivity increase, this study provides a stepping stone for further optimization.
Introduction
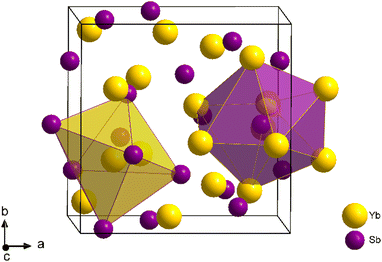
In response to the escalating global demand for energy, effective utilization of waste heat through thermoelectric energy conversion has garnered substantial attention.1–3 Industries such as steel mills or power plants operating at very high temperatures, typically above 800 K, dissipate significant amounts of heat that could be converted into electricity by thermoelectric generators.4,5 The conversion efficiency of such modules mostly depends on the performance of the integrated thermoelectric components, which is evaluated by the adimensional figure of merit zT = S2T/(ρκ), S being the Seebeck coefficient, T the absolute temperature, ρ the resistivity and κ the thermal conductivity of the material, respectively. Currently, viable solutions within the realm of very high temperatures remain rather constrained, owing to the scarcity of materials presenting suitable transport properties above 800 K.6–9 Both n- and p-type SiGe have been used for decades as the main solution by NASA,10 especially for radio-isotope thermoelectric generators (RTGs),11 complemented by the Zintl phase Yb14MnSb11 which serves as a p-type alternative.12 Recent investigations have highlighted the potential candidacy of Yb21Mn4Sb18 as well within this temperature range, exhibiting a zT value of 0.8 at 800 K.13 Furthermore, Half-Heusler compounds have also emerged as promising candidates for the development of high temperature thermoelectric modules up to 1100 K.14 While the fabrication of thermoelectric devices for power generation necessitates meticulous considerations encompassing low contact resistances and harmonious thermal expansion,15 the paramount factor governing net power generation indisputably remains the figure of merit exhibited by both n-type and p-type constituents.16 Therefore, the pursue of novel materials showcasing optimal transport properties in the very high temperature range (800–1300 K) is much needed and stand as the focus of this work.La3−xTe4 is a promising n-type material that exhibits a zT above unity around 1300 K.17 This compound crystallizes in the Th3P4 structure type, wherein vacancies are accommodated on the rare-earth sites. Rare-earth antimonides of typical formula RE4Sb3 (RE = Yb, La, Sm, Ce) are presenting the anti-Th3P4 crystal structure.18 In this cubic structural arrangement (space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d), rare-earth atoms occupy P sites (Wyckoff position 16c) at the center of a distorted octahedron, while antimony atoms occupy Th sites (12a), forming a bis-disphenoid environment shaped by two interpenetrated Yb tetrahedra (Fig. 1). As it turns out, La4Sb3, Sm4Sb3 and Ce4Sb3 all exhibit n-type metallic conductive behavior with low Seebeck values in the 300–1300 K temperature range.19 Yb4Sb3, on the other hand, present a quite different behavior: while the Seebeck coefficient is negative at room temperature (around −20 μV K−1), it then increases linearly with temperature, reaching 70 μV K−1 at 1300 K according to previous studies.19,20 Meanwhile, the resistivity remain consistently low, as expected for metallic conductive behavior, with values of about 1.2 mΩ cm at 1300 K,20 leading to a decent power factor around 4 μW cm−1 K−2 at this temperature.21 For this reason, Yb4Sb3 was investigated for possible thermoelectric applications at very high temperature as a p-type counterpart of n-type La3−xTe4. An intriguing aspect of Yb4Sb3 is its p-type conduction, dominated by hole carriers above 600 K. This is notable since other rare-earth antimonides consistently exhibit n-type behavior across all temperatures. This peculiarity arises from Yb's mixed valency, switching between 2+ and 3+ oxidation states. However, magnetic studies have shown that the oxidation state of Yb atoms was predominantly 2+, not 3+.19 This suggests, based on the Zintl formalism, that Yb atoms donate only 8 electrons per formula unit to the anionic framework, which is comprised of Sb atoms able to accept 9 electrons overall per formula unit. This electron deficiency might explain the p-type conductive behavior in Yb4Sb3 above 600 K, but this needs to be confirmed by further theoretical investigations.
3d), rare-earth atoms occupy P sites (Wyckoff position 16c) at the center of a distorted octahedron, while antimony atoms occupy Th sites (12a), forming a bis-disphenoid environment shaped by two interpenetrated Yb tetrahedra (Fig. 1). As it turns out, La4Sb3, Sm4Sb3 and Ce4Sb3 all exhibit n-type metallic conductive behavior with low Seebeck values in the 300–1300 K temperature range.19 Yb4Sb3, on the other hand, present a quite different behavior: while the Seebeck coefficient is negative at room temperature (around −20 μV K−1), it then increases linearly with temperature, reaching 70 μV K−1 at 1300 K according to previous studies.19,20 Meanwhile, the resistivity remain consistently low, as expected for metallic conductive behavior, with values of about 1.2 mΩ cm at 1300 K,20 leading to a decent power factor around 4 μW cm−1 K−2 at this temperature.21 For this reason, Yb4Sb3 was investigated for possible thermoelectric applications at very high temperature as a p-type counterpart of n-type La3−xTe4. An intriguing aspect of Yb4Sb3 is its p-type conduction, dominated by hole carriers above 600 K. This is notable since other rare-earth antimonides consistently exhibit n-type behavior across all temperatures. This peculiarity arises from Yb's mixed valency, switching between 2+ and 3+ oxidation states. However, magnetic studies have shown that the oxidation state of Yb atoms was predominantly 2+, not 3+.19 This suggests, based on the Zintl formalism, that Yb atoms donate only 8 electrons per formula unit to the anionic framework, which is comprised of Sb atoms able to accept 9 electrons overall per formula unit. This electron deficiency might explain the p-type conductive behavior in Yb4Sb3 above 600 K, but this needs to be confirmed by further theoretical investigations.
Efforts to enhance transport properties have been pursued through various strategies. Initially, substituting La for Yb was explored to lower the concentration of charge carriers, specifically holes, present in Yb4Sb3 at high temperatures. This exchange of Yb2+/3+ atoms with La3+ atoms aimed to enhance the Seebeck coefficient through the reduction of available holes. Several compositions were investigated and it was shown that La0.5Yb3.5Sb3 exhibited the best performance with an improvement of the power factor up to 10 μW cm−1 K−2 at 1300 K.19 Associated to a significantly reduced thermal conductivity of 1.7 W m−1 K−1 at 1300 K, La0.5Yb3.5Sb3 displayed a promising zT value of 0.75.19 Furthermore, substituting a small amount of Sb by Bi also yield positive results. The Yb4Sb2.8Bi0.2 composition, for instance, shows an enhanced power factor of approximately 8 μW cm−1 K−2 at 1300 K.20
Building upon prior research efforts, the main objective of this study was to investigate the outcomes of a dual substitution, involving the replacement of both La on Yb sites and Bi on Sb sites. The aim was to potentially harness synergetic effects in order to further enhance the thermoelectric properties of the parent material. The Bi substitution level was set at y = 0.2, guided by the promising outcomes observed for the Yb4Sb2.8Bi0.2 composition's transport properties. Very recently, we used a similar strategy with partial Bi substitution on Sb sites while a partial amount of Yb atoms were replaced by Ce atoms.22 Findings from this study demonstrated a significant enhancement in the thermoelectric properties of the Ce-substituted solid solution, motivating further exploration into the transport properties of the La-substituted solid solution.
To explore the limits of solubility within the LaxYb4−xSb2.8Bi0.2 solid solution, the La substitution level was progressively increased from x = 0.1 to 1. Notably, the replacement of Sb with the larger-radius Bi may allow a broader solubility range in regard to the substitution of La for Yb, eventually leading to a reduction in charge carrier concentration by introducing a greater amount of La into the structure. Upon establishing the solubility limit, the synthesis and preparation of homogeneous LaxYb4−xSb2.8Bi0.2 compositions were undertaken to characterize their transport properties. Additionally, a theoretical analysis was conducted to explore the influence of both La and Bi substitution on the electronic structure of Yb4Sb3 and better understand the transport properties of the solid solution. We thus report in this article an unprecedented combined experimental and theoretical investigation on this chemical system which shows great promise for thermoelectric applications in the very high temperature range.
Experimental and theoretical procedures
Synthesis and preparation
Yb4Sb3 and substituted LaxYb4−xSb3−yBiy compounds were synthesized in niobium tubes by mixing appropriate amounts of La (ingot, 99.8%), Yb (ingot, 99.8%), Sb (shots, 99.99%) and Bi (shots, 99.999%) within an Ar-filled glovebox. To ensure an inert reaction environment, the niobium tubes were hermetically sealed under high-purity argon, using a custom arc furnace setup, before being enclosed in fused silica tubes and further sealed to prevent oxidation of the niobium containers. The solid solution study was carried out using low quantities of reactants (500 mg). These samples were heated at 1000 °C during 96 h with heating and cooling ramps of 16 h. Subsequently, Nb containers were opened under argon atmosphere, powders were finely ground, sealed back in new Nb capsules and annealed at 1000 °C for three weeks. Samples aimed at the measurement of the transport properties were shaped from a higher quantity of powder (5 g), heated at 1050 °C, over an 8-day dwell period featuring 10-hour ramps, followed by an annealing at 1000 °C for another 8 days. X-ray diffraction measurements were carried out using an X’Pert Pro MRD (Panalytical) (Cu-Kα1 and Cu-Kα2 radiations) and a D8 Advance Vario1 (Bruker) apparatus (Cu-Kα1 radiation λ = 1.540598 Å). Structure refinements were performed using the Fullprof suite.23 Samples were densified by Spark Plasma Sintering using Dr Sinter Lab Jr's SPS-322Lx with ∅10 mm graphite dies. Uniaxial pressure of 50 MPa was applied with a temperature dwell of 1200 °C kept for 10 minutes during a one-hour run, yielding pellets of relative densities beyond 95%. Densified samples were annealed in either Ta or Mo foils at 1000 °C for 24 hours to ensure chemical stability and homogeneity. Composition and microstructure were assessed by scanning electron microscopy coupled with energy-dispersive X-ray spectroscopy. Seebeck coefficient and resistivity were measured from 373 to 1273 K on 3 × 3 × 10 mm samples by a ZEM5 apparatus (ULVAC) and thermal conductivity measurements were performed with a LFA467 HT HyperFlash (Netzsch) under N2 flux, employing Ø10 mm graphite-coated cylinders of up to 2 mm thickness.Calculations
All density functional theory (DFT) calculations were performed using the VASP software version 6.2.0.24–26 and the Perdew, Burke and Ernzerhof (PBE) exchange–correlation functional.27 Structural optimizations and average properties were performed with a cut-off energy of 350 eV and a 7 × 7 × 7 k-points grid sampled by the Monkhorst–Pack method.28 The band structure was computed with the same cut-off energy using 15 k-points per symmetry line.Electronic transport coefficients were calculated within the Boltzmann Transport Equation. A constant relaxation time τ for the electrons was assumed as well as a rigid band structure,29,30 as implemented in the BoltzTrap2 code.31 A 11 × 11 × 11 k-point grid was used to compute the band derivatives for transport calculations.
Results and discussion
Synthesis of the binary Yb4Sb3 compound
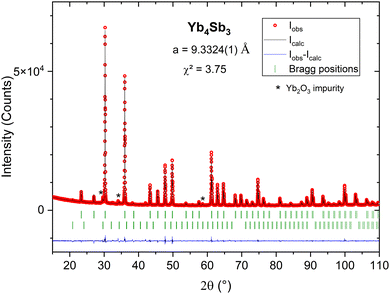
The pristine compound Yb4Sb3 was first synthesized. The obtained powder X-ray diffraction pattern was refined by the Le Bail method (Rp = 2.78; Rwp = 3.88), yielding a cell parameter a = 9.3324(1) Å (Fig. 2), which closely aligns with other previously reported values.18 Very low intensity reflections of Yb2O3 were also indexed and attributed to the slightly oxidized Yb starting reagent. Subsequently, partial substitutions of La for Yb and Bi for Sb were carried out.Study of the LaxYb4−xSb2.8Bi0.2 solid solution
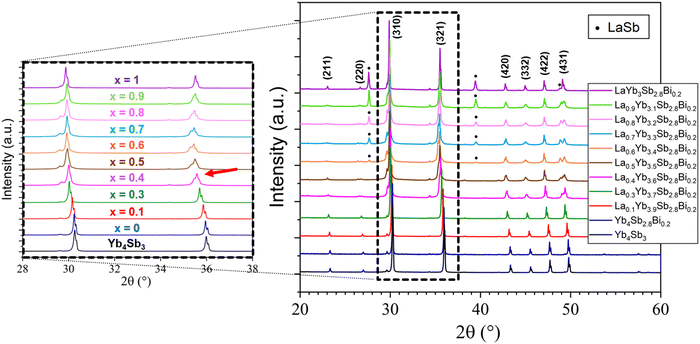
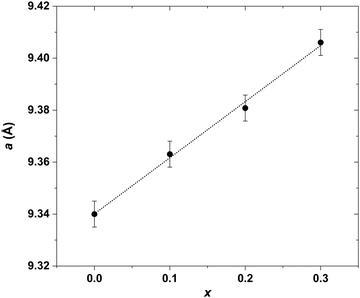
Investigation of the LaxYb4−xSb2.8Bi0.2 solid solution was initiated primarily to identify single-phase compounds for subsequent transport property measurements. Based on the findings from the previously explored LaxYb4−xSb3 solid solution, where the solubility limit was determined to be x = 0.5,19 it was of interest to investigate the potential influence of partial Sb substitution with the larger-radius Bi atoms. Given the larger atomic radius of Bi (1.60 Å) compared with that of Sb (1.45 Å), the conjecture was that this substitution could open up greater possibilities for La atom substitution on the Yb site. To test this hypothesis, the quantity of La was varied from x = 0 to 1, while maintaining a Bi stoichiometry of 0.2 on the Sb site, in line with prior studies.20,21The results sketched in Fig. 3 indicate that starting from the nominal composition La0.6Yb3.4Sb2.8Bi0.2, the presence of LaSb is detected in the bulk. This is due to the pronounced incorporation of La, resulting in a biphasic domain under the specific synthesis temperature and pressure conditions. This assumption is supported by the correlation which is observed: higher La amount corresponds to an elevated intensity of LaSb reflections (Fig. 3). In the case of La0.4Yb3.6Sb2.8Bi0.2, despite the absence of the LaSb phase, some reflections exhibit distortion, implying that the substitution level is still somewhat excessive, hindering complete integration of La and Bi atoms within the parent structure. However, compositions with x ≤ 0.3 display no LaSb impurities and exhibit undistorted peaks, signifying successful substitution of La and Bi for Yb and Sb, respectively, in the structure. This solubility limit is slightly lower than that observed in the Ce-inserted CexYb4−xSb2.8Bi0.2 solid solution (x = 0.5),22 mainly owing to the higher atomic radius of La atoms (1.95 Å) compared with Ce atoms (1.85 Å). The refined cell parameters are displayed in Fig. 4. Based on this investigation, compositions with x = 0.1, 0.2, and 0.3 have been selected for further synthesis at larger scales, targeting subsequent transport property measurements.
Scanning electron microscopy
Samples of Yb4Sb3 and LaxYb4−xSb2.8Bi0.2 (x = 0.1, 0.2 and 0.3) were characterized by SEM on densified samples. Homogeneous densified materials were observed, the illustrative case for x = 0.3 composition being displayed in Fig. 5. The examination of sample surfaces in secondary electrons mode revealed minimal porosity, the slight contrast observed being attributed to the polishing step of the assessed sample. Energy-dispersive spectroscopy analyses confirmed these findings and show great compositional homogeneity, consistent with the expected compositions. | ||
| Fig. 5 Electron Dispersive X-ray Spectroscopy characterization of the La0.3Yb3.7Sb2.8Bi0.2 compound. The presence of all elements was confirmed with a good homogeneity. | ||
Transport properties
The transport properties of the investigated compounds are shown in Fig. 6. Diligent efforts were directed toward achieving clear and reproducible results. Nonetheless, several difficulties were encountered during the measurements of the electrical transport properties. In addition to the inherent complexities associated with maintaining robust electrical contacts with the elevated temperature range, a substantial tendency of the samples to oxidize was observed. Despite the utilization of a high-purity helium partial pressure atmosphere during measurements, it is plausible that a thin oxide layer may have formed between the measurement probes and the sample surface as temperatures escalated. This occurrence is in line with a recent research work demonstrating the rapid surface oxidation of the related Yb14MnSb11 compound around 700 K,32 and was also pointed out in our recent study on the CexYb4−xSb2.8Bi0.2 solid solution.22 Although these factors contributed to certain limitations in achieving precise measurements, in particular for the La0.3Yb3.7Sb2.8Bi0.2 composition which will not be presented here, the measurements of the binary Yb4Sb3 and LaxYb4−xSb2.8Bi0.2 (x = 0.1 and 0.2) compounds were reasonably successful and allowed us to gain valuable insights into the influence of the present dual substitution on the transport properties.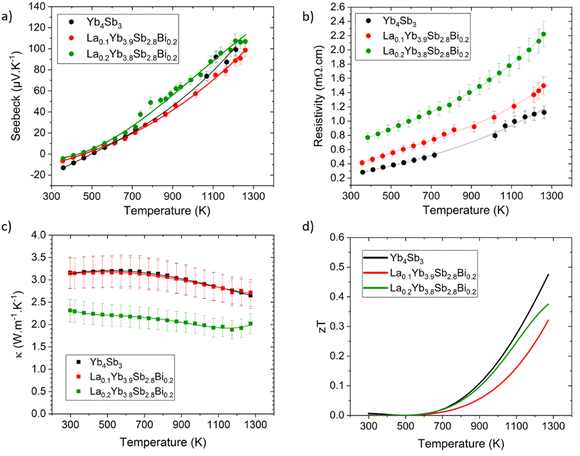 | ||
| Fig. 6 Thermoelectric properties of Yb4Sb3 and LaxYb4−xSb2.8Bi0.2 (x = 0.1 and 0.2) solid solution. (a) Seebeck coefficient, (b) resistivity, (c) thermal conductivity, and (d) figure of merit zT. | ||
The Seebeck coefficient of all compositions maintains its positive trend above 500 K, consistent with previous studies, indicating a conductive behavior dominated by holes at elevated temperatures. It can be noted that Yb4Sb3 presents a higher Seebeck coefficient at 1273 K compared to previous reports (100 μV K−1versus 65 μV K−1),19,20 leading to improved thermoelectric performance. This difference is probably due to the distinct synthesis and shaping routes that might significantly influence the transport properties. Indeed, the co-substitution of Yb by La and Sb by Bi have a relatively modest effect on the Seebeck values. However, a noteworthy enhancement was observed in the case of La0.2Yb3.8Sb2.8Bi0.2 with values around 110 μV K−1 at 1273 K, possibly stemming from a reduction in hole concentration due to the substantial Yb substitution amount with La atoms (see theoretical section below).
The resistivity trends confirm the characteristic metallic conductive behavior, with values increasing as temperature rises, ranging from 0.3 to 1.1 mΩ cm between 373 and 1273 K for the binary compound Yb4Sb3. Substituted compounds exhibit analogous conductive behavior, yet with higher resistivity values compared to the parent Yb4Sb3 compound, spanning from 0.8 to 2.2 mΩ cm between 373 and 1273 K for the x = 0.2 composition. This observation is consistent with the anticipated reduction in hole concentration due to La substitution at the Yb site. As the charge carrier concentration could not be measured in this temperature range, this point was assessed via theoretical calculations (vide infra). That being said, the evolution of the electronic transport properties is similar to that encountered in comparable systems such as Yb21Mn4Sb18 where the substitution of Yb for Na did not change much the Seebeck coefficient while the resistivity was significantly modified.13
Thermal conductivities measurements are displayed in Fig. 6c. Yb4Sb3 and La0.1Yb3.9Sb2.8Bi0.2 exhibit analogous behavior, maintaining a relatively constant value of 3.20 W m−1 K−1 up to 600 K, followed by a gradual decrease with temperature to 2.65 W m−1 K−1 at 1273 K for both compounds. The substituted La0.2Yb3.8Sb2.8Bi0.2 compound shows lower values, ranging from 2.3 W m−1 K−1 at lower temperatures down to about 1.9 W m−1 K−1 at 1173 K. This is in agreement with values already reported for LaxYb4−xSb3 where thermal conductivities of substituted compounds were decreased by the local mass fluctuation on the Yb site, contributing to enhanced phonon scattering in substituted compounds.33 While not being pronounced for the La0.1Yb3.9Sb2.8Bi0.2 composition, the phenomenon seems accentuated in the La0.2Yb3.8Sb2.8Bi0.2 compound, although it doesn't entirely account for the significant reduction in thermal conductivity observed in this particular case. The substantial increase in resistivity also plays an important role according to the Wiedemann–Franz law in diminishing the electronic contribution to thermal conductivity. This might thus explain why the thermal conductivity experiences a notable reduction (about 30%) in the case of the x = 0.2 composition, although this effect seems limited for La0.1Yb3.9Sb2.8Bi0.2 as its thermal conductivity was measured to be similar to that of the parent material within a relatively large uncertainty range.
The thermoelectric figure of merit zT of the investigated compounds demonstrates a reasonable performance at elevated temperatures (Fig. 6d). Yb4Sb3 achieves a zT value of approximately 0.5 at 1273 K, representing a notable outcome for the pristine compound. The substituted La0.1Yb3.9Sb2.8Bi0.2 and La0.2Yb3.8Sb2.8Bi0.2 compounds exhibit zT values of 0.32 and 0.38 at 1273 K, respectively, although slightly lower than that of the pure Yb4Sb3 compound. The difference can be attributed primarily to higher resistivities associated with weakly affected Seebeck coefficients in the substituted compounds. The relatively lower thermal conductivity measured for the x = 0.2 composition, while not fully compensated with the rise in resistivity, leaves room for further optimization within this family of compounds.
Theoretical insight
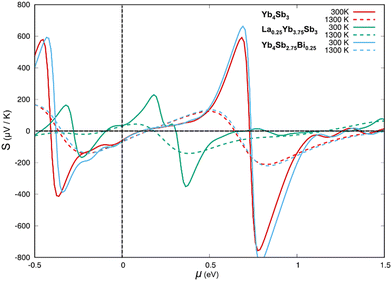
The electronic properties of Yb4Sb3 were previously theoretically studied using first-principles calculations. V. N. Antonov et al. carried out local spin density approximation (LSD) + U DFT calculations to study the heavy fermion Yb4As3 compound as well as several isostructural ytterbium pnictides including Yb4Sb3.34 They demonstrated that the width and position of the pnictide p band when going through the pnictogen group of the Periodic Table leads to a transition into a semiconducting behavior towards the light pnictogen element with a charge-transfer gap between the Yb 4f states and the pnictide p band. They also showed that this leads to an increasing carrier concentration and hence an increasing metallic character towards the heavy pnictogen element. M. Shirakawa et al. compared their de Haas-van Alphen (dHvA) measurements with local density approximation (LDA) band structure calculations.35 Further combined experimental and theoretical studies were conducted in order to better understand the dHvA effect in this compound.36 These studies showed that six bands are involved in the Fermi surfaces. They also computed total and atom-projected density of states (DOS) and showed that the top of the valence band is mainly centered on Yb-4f and Sb-5p levels whereas the bottom of the conduction band is dominated by Yb-5d levels.We ourselves first performed DFT geometry optimization of the cell parameters and atomic positions of the binary compound Yb4Sb3. As often observed in the literature, the volume of the PBE-DFT optimized unit cell is slightly larger (less than 2%) than the one obtained from X-ray diffraction studies (824.8 Å3vs. 810.1 Å3). Optimized Yb–Sb bond distances compare very well with the X-ray measured ones: 3.14 Å vs. 3.12 Å and 3.36 Å vs. 3.32 Å. The spin-polarized band structure of Yb4Sb3 is sketched in Fig. 7. It compares quite well with the LDA ones previously reported in the literature. Small differences between up and down band structures suggest weak spin-polarization. This band structure strongly differs from the one reported for the isostructural La4Sb3 compound: while the Fermi level crosses the top of the valence band in Yb4Sb3, it is located in the bottom of the conduction band in La4Sb3.37 This agrees with the lowest electronic transfer from the metal atoms towards the antimonide network in the case of the ytterbium compound, resulting in a formal Yb(II) oxidation state and p-type character of the compound. This is at the origin of the difference in the transport behavior of Yb4Sb3 with regard to other RE4Sb3 compounds where RE is a trivalent rare-earth atom.19 A full theoretical analysis of the electronic structure of both compounds will be further discussed in an upcoming study. The band structure of Yb4Sb3 shows that the bands located in the vicinity of the Fermi level are rather flat in the N → P and H → N directions and more dispersive along the Γ → N and P → Γ → H symmetry lines. Such a situation encourages higher Seebeck coefficient as well as good electronic conductivity. Electronic transport properties of the binary were simulated using a semi-classical approach assuming the constant relaxation time approximation. Fig. 8 displays the computed thermopower of Yb4Sb3 at 300 and 1300 K as a function of the chemical potential μ. It is noteworthy to mention that the Seebeck coefficient is computed to be negative for μ ∼ 0 eV. Even if the band structure suggests that several bands are involved in the conduction, this shows that electrons dominate the conduction at low temperature as observed experimentally. At higher temperature, holes dominate the conduction as expected from the previously published DOS34 and the band structure sketched in Fig. 7.
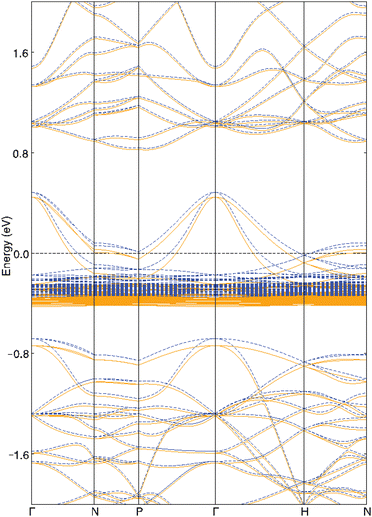 | ||
| Fig. 7 PBE-DFT spin-up (blue dotted lines) and spin-down (orange solid lines) band structures of Yb4Sb3. | ||
As massively exemplified in the literature, the thermopower can be tuned with the variation of the carrier concentration. This can be achieved in particular via doping. In order to assess the effect of doping Yb4Sb3 with La and Bi, two model compounds were computed: La0.25Yb3.75Sb3 and Yb4Sb2.75Bi0.25. Since Z equals 4 in the crystal structure of the binary compound, the computed models were obtained from the substitution of one Yb atom out of 16 by one La in the case of La0.25Yb3.75Sb3, and of one Sb atom out of 12 by one Bi for Yb4Sb2.75Bi0.25. Cell parameters and atomic positions were relaxed without any symmetry constraints. The DFT-optimized volumes of La0.25Yb3.75Sb3 and Yb4Sb2.75Bi0.25 are larger than the optimized one of Yb4Sb3 by ca. 4%. Such an increase is consistent with the larger size of La and Bi compared to Yb and Sb, respectively.
Total and atom-projected DOS are sketched in Fig. 9. It is obvious that La and Bi substitutions have different impacts on the electronic structure. Bi substitution hardly modifies the electronic structure of Yb4Sb3; this is consistent with the isovalent character of both pnictogens. Therefore, assuming similar carrier concentrations, the electronic transport properties of Bi-doped Yb4Sb3 are not expected to change significantly as shown in Fig. 8 for the Seebeck coefficient. Indeed, as previously observed experimentally,21 the Bi-doped Yb4Sb3 compound only exhibits a slightly enhanced thermopower irrespective of the chemical potential. On the other hand, the substitution of one Yb(II) atom by one La(III) atom alters much more the electronic structure and the computed electronic transport properties. One can note that spin polarization decreases in the La-doped model compound whereas it hardly changes in the Bi-doped model compound. The additional electrons brought by the lanthanum atoms contribute to fill the valence band in La0.25Yb3.75Sb3, making the compound less electron conductive. This also favours a p-type conduction and explains why the Seebeck coefficient turns positive at the Fermi level at both simulated temperatures. The thermopower is computed lower than that of the parent compound, regardless of the chemical potential. Assuming a rigid band model, the extra electron provided by La implies an increase in the Fermi level that crosses mainly dispersive bands in the Γ → N and P → Γ → H directions (see Fig. 7), which is consistent with a Seebeck coefficient reduction.
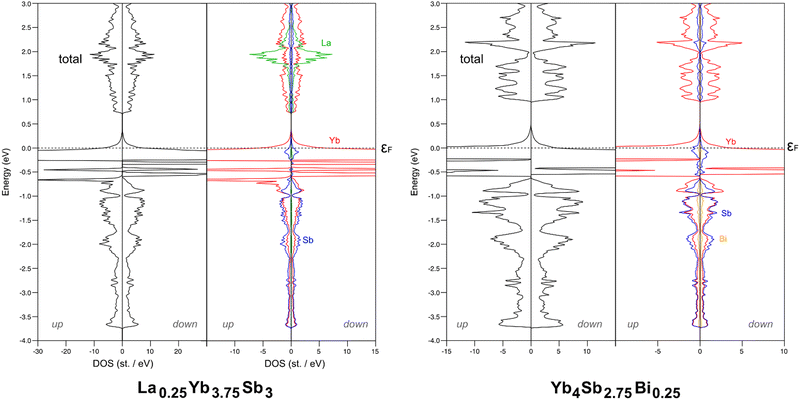 | ||
| Fig. 9 PBE-DFT total and atom projected DOS computed for La0.25Yb3.75Sb3 (left) and Yb4Sb2.75Bi0.25 (right). | ||
Conclusions
This study delved into and discussed the potential thermoelectric applications of Yb4Sb3 and related substituted compounds up to 1300 K. By simultaneously substituting Yb with La and Sb with Bi, we aimed to enhance their performance through the optimization of their figure of merit zT. Exploration of the solubility limit of the LaxYb4−xSb2.8Bi0.2 solid solution revealed a maximum value of x = 0.3, beyond which complete substitutions were not obtained. Subsequent syntheses of Yb4Sb3 and LaxYb4−xSb2.8Bi0.2 (x = 0.1, 0.2 and 0.3) on a larger scale followed by high-temperature transport properties measurements brought substantial new insights. As expected for materials exhibiting metallic conductive behavior, resistivity showcases a temperature-dependent increase while remaining in a desirable range. The Seebeck coefficients were hardly affected by the co-substitution with values reaching 110 μV K−1 at 1273 K for x = 0.2. First-principles calculations helped in understanding the electronic transport properties of Yb4Sb3, especially the n-type to p-type transition at high temperature. These calculations also confirmed that Bi-substitution left electronic transport properties unaffected, while La substitution did not enhance the Seebeck coefficient but rather increased resistivity. Furthermore, this investigation unveiled a promising zT of 0.5 for Yb4Sb3 at 1300 K, which is the highest maximum zT value reported so far for the parent compound, confirming its thermoelectric potential in high-temperature scenarios. While both experimental and theoretical results have shown that the dual substitutions did not yield a substantial enhancement of zT for the LaxYb4−xSb2.8Bi0.2 (x = 0.1 and 0.2) solid solution, the study lays a foundation for further optimization. Future directions should involve the exploration of alternative substitutions, innovative nano-structuring, or defect engineering to potentially achieve elevated zT values.Author contributions
H. Bouteiller: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. V. Pelletier: software, data curation, formal analysis, investigation, validation, visualization, writing – review & editing. S. Le Tonquesse: conceptualization, data curation, formal analysis, investigation, validation, visualization, writing – review & editing. B. Fontaine: software, data curation, formal analysis, investigation, supervision. T. Mori: funding acquisition, resources, supervision, writing – review & editing. J.-F. Halet: formal analysis, investigation, software, supervision, project administration, writing – review & editing. R. Gautier: conceptualization, data curation, formal analysis, investigation, methodology, software, supervision, validation, visualization, project administration, writing – review & editing. D. Berthebaud: conceptualization, formal analysis, investigation, methodology, project administration, resources, supervision, writing – review & editing. F. Gascoin: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the Agence Nationale de la Recherche (ANR – Project HIGHTHERM – Ref ANR-18-CE05-0037) and the Japan Society for the Promotion of Science (JSPS – PE21708) for financial support. Support from JST Mirai Program JPMJMI19A1 is also acknowledged.Notes and references
- D. Beretta, N. Neophytou, J. M. Hodges, M. G. Kanatzidis, D. Narducci, M. Martin- Gonzalez, M. Beekman, B. Balke, G. Cerretti, W. Tremel, A. Zevalkink, A. I. Hofmann, C. Müller, B. Dörling, M. Campoy-Quiles and M. Caironi, Mater. Sci. Eng. R Rep., 2019, 138, 100501 CrossRef.
- J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Adv. Phys., 2018, 67, 69–147 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- T. Mori, JOM, 2016, 68, 2673–2679 CrossRef CAS.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441 RSC.
- A. P. Gonçalves and C. Godart, Eur. Phys. J. B, 2014, 87, 1–29 CrossRef.
- S. Hébert, D. Berthebaud, R. Daou, Y. Bréard, D. Pelloquin, E. Guilmeau, F. Gascoin, O. Lebedev and A. Maignan, J. Phys.: Condens. Matter, 2015, 28, 013001 CrossRef PubMed.
- M. Wolf, R. Hinterding and A. Feldhoff, Entropy, 2019, 21, 1058 CrossRef CAS.
- T. Mori, J. Solid State Chem., 2019, 275, 70–82 CrossRef CAS.
- B. Cook, Energies, 2022, 15, 2957 CrossRef CAS.
- V. Ravi, S. Firdosy, T. Caillat, E. Brandon, K. Van Der Walde, L. Maricic and A. Sayir, J. Electron. Mater., 2009, 38, 1433–1442 CrossRef CAS.
- S. R. Brown, S. M. Kauzlarich, F. Gascoin and G. Jeffrey Snyder, Chem. Mater., 2006, 18, 1873–1877 CrossRef CAS.
- A. He, S. K. Bux, Y. Hu, D. Uhl, L. Li, D. Donadio and S. M. Kauzlarich, Chem. Mater., 2019, 31, 8076–8086 CrossRef CAS.
- J. W. G. Bos, in Thermoelectric Energy Conversion, ed. R. Funahashi, Woodhead Publishing, 2021, pp. 125–142 Search PubMed.
- Z. Ren, Y. Lan and Q. Zhang, Advanced thermoelectrics: materials, contacts, devices, and systems, 2018 Search PubMed.
- G. J. Snyder and A. H. Snyder, Energy Environ. Sci., 2017, 10, 2280–2283 RSC.
- A. F. May, J. P. Fleurial and G. J. Snyder, Chem. Mater., 2010, 22, 2995–2999 CrossRef CAS.
- D. Hohnke and E. Parthé, Acta Crystallogr., 1966, 21, 435–437 CrossRef CAS.
- A. Chamoire, F. Gascoin, C. Estournès, T. Caillat and J. C. Tédenac, Dalton Trans., 2010, 39, 1118–1123 RSC.
- A. Chamoire, R. Viennois, J. C. Tedenac, M. M. Koza and F. Gascoin, J. Electron. Mater., 2011, 40, 1171–1175 CrossRef CAS.
- A. Chamoire, PhD thesis, Université de Montpellier, 2009.
- S. Le Tonquesse, H. Bouteiller, Y. Matsushita, A. Cortez, S. K. Bux, K. Imasato, M. Ohta, J.-F. Halet, T. Mori, F. Gascoin and D. Berthebaud, ACS Appl. Energy Mater., 2023, 6(19), 10088–10097 CrossRef CAS.
- J. Rodriguez-Carvajal, Abstr. Satell. Meet. Powder Diffr. XV Congr. IUCr, 1990, 127.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210 CrossRef.
- G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146 CrossRef CAS PubMed.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- A. P. Justl and S. M. Kauzlarich, ACS Appl. Mater. Interfaces, 2022, 14, 47246–47254 CrossRef CAS PubMed.
- E. S. Toberer, L. L. Baranowski and C. Dames, Annu. Rev. Mater. Res., 2012, 42, 179–209 CrossRef CAS.
- V. N. Antonov, A. N. Yaresko, A. Y. Perlov, P. Thalmeier, P. Fulde, P. M. Oppeneer and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 9752–9762 CrossRef CAS.
- M. Shirakawa, M. Ona, H. Aoki and A. Ochiai, Acta Phys. Pol., B, 2003, 34, 1157 Search PubMed.
- M. Kakihana, K. Nishimura, Y. Ashitomi, T. Yara, D. Aoki, A. Nakamura, F. Honda, M. Nakashima, Y. Amako, Y. Uwatoko, T. Sakakibara, S. Nakamura, T. Takeuchi, Y. Haga, E. Yamamoto, M. Hedo, T. Nakama and Y. Ōnuki, J. Electron. Mater., 2017, 46, 3572–3584 CrossRef CAS.
- K. Takegahara, H. Harima and T. Kasuya, J. Magn. Magn. Mater., 1985, 52, 307–309 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |