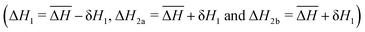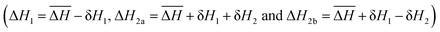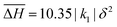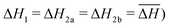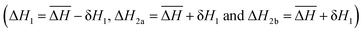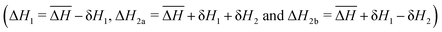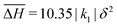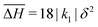Open Access Article
Open Access ArticleMultistep transitions in spin crossover materials without long-range spin state order from dimensional reduction
Gian
Ruzzi
 a,
Jace
Cruddas
a,
Jace
Cruddas
 b and
Benjamin J.
Powell
b and
Benjamin J.
Powell
 *a
*a
aSchool of Mathematics and Physics, The University of Queensland, QLD 4072, Australia. E-mail: powell@physics.uq.edu.au
bSchool of Psychological Sciences, Monash University, 770 Blackburn Road, Clayton VIC 3168, Australia
First published on 17th January 2024
Abstract
Most theories of multistep spin crossover (SCO) have focused on intermediate phases with long-range spin state order. However, disordered intermediate phases have also been observed experimentally. Here we show that the interplay of crystallographically inequivalent SCO centres with elastic interactions between SCO centres can lead to an effective reduction in the dimensionality of the system. This is highly analogous to dimensional reduction in quantum magnetism. The resulting quasi-one-dimensional and quasi-zero-dimensional models naturally result in disorder at non-zero temperatures, explaining the absence of long-range spin state order in our calculations. Furthermore, the low effective dimensionality can strongly suppress short-range correlations and hence diffuse scattering should not necessarily be expected to be observed experimentally in these disordered phases. Our model contains parameter regimes where disordered intermediate phases give rise to diffuse scattering and other regimes where disordered intermediate phases do not. Our results are in good agreement with experiments on [FeII3(saltrz)6(MII(CN)4)3]·8(H2O) [Sciortino et al., Chem. Sci., 2017, 8, 701].
1 Introduction
Disorder is crucial for the (potential) uses of many materials including photovoltaics (hybrid organic–inorganic perovskites), ferroelectrics (e.g., BaTiO3), and magnets (spinels).1 Further applications are being actively investigated,1 therefore a key goal is to identify new routes to disordered materials that provide resources for future potential applications.Disorder does not imply that the system is completely random. Typically, short-range correlations remain between the low-energy degrees of freedom in disordered materials.1 A classic example is the ice rules in water ice, which dictate the local properties of oxygen–hydrogen bonds. As an extremely large (macroscopic) number of micro-states are consistent with the ice rules, the instantaneous configurations are random on large length-scales. Nevertheless the ice-rules enforce strong short-range correlations. This results in diffuse scattering in diffraction experiments on water ice.2 Analogous ice rules give rise to a distinctive pattern of diffuse scattering, known as ‘pinch points’, in spin ices (magnetic analogues of water ice).3–5 In general, diffuse scattering is a powerful experimental signature of the short-range correlations expected in disordered phases.
Recently, several possible disordered phases of spin crossover (SCO) materials have been discussed theoretically, including spin state ice,6 Coulomb phases,7 spin state glasses,8 and spin state smectics.9 Distinctive diffuse scattering signatures are predicted for these phases. Contemporaneously, several SCO materials with significant disorder have been identified experimentally.10–17 However, to date connections between theories of and experiments on disordered SCO phases remain weak, leaving a far from complete understanding of disordered phases in SCO materials.
SCO materials contain metal centres that can take two different electronic configurations: high spin (HS) and low spin (LS). For a solution of equivalent molecules, this results in a crossover from majority HS at high temperatures to majority LS at low temperatures. This is driven by the free energy difference between HS and LS molecules, ΔG = GH − GL = ΔH − TΔS, where ΔH = HH − HL is the enthalpy difference, and ΔS = SH − SL is the entropy difference, and the subscripts H and L label the properties of HS and LS SCO centres respectively. Thus, we expect equal numbers of HS and LS SCO centres at the temperature T1/2 = ΔH/ΔS.
However, in the solid state the behaviour of SCO materials can be significantly richer. Firstly, elastic interactions between SCO centres can drive the spin crossover into a true thermodynamic phase transition between HS and LS phases. This phase transition is typically first order and therefore hysteretic. Secondly, intermediate phases are found in many SCO materials. Typically, these correspond to ordered states with repeating patterns of HS and LS molecules, that are highly analogous to antiferromagnetism.18,19
The two most discussed causes of intermediate phases are: (i) elastic interactions;19,20 and (ii) crystallographic inequivalency of SCO centres.21 Elastic interactions tend to favour near neighbours with opposite spin states.6,20 Thus, when ΔG is small, i.e., for temperatures near T1/2, elastic interactions can stabilise a phase with an alternating pattern of HS and LS molecules, for example, a chequerboard or stripe pattern.16,19,20,22–50 This leads to a two-step transition, with three plateaus observed in χT corresponding to HS fractions, γHS, of 0, 1/2, and 1, where χ is the magnetic susceptibility. Complicated interactions can lead to more complex intermediate spin state orders and hence more intermediate steps.11,16,19,24–28,31,33,39,50–55 Crystallographically inequivalent SCO centres can also lead to multi-step crossovers, with the inequivalent sets of sites changing spin states at different temperatures.21 For example, a simple model of this is to assign different ΔG to inequivalent sites.
Both of these mechanisms lead to intermediate states with an ordered pattern of HS and LS SCO centres. If all SCO centres are equivalent and interactions drive long-range spin state order, then this spontaneously breaks a crystallographic symmetry. However, if the pattern of crystallographically inequivalent centres pre-exists at high temperatures, then long range spin state ordering does not require any symmetry breaking (as the relevant symmetry is absent at high temperatures).
Many materials have both significant elastic interactions and crystallographically inequivalent SCO centres. However, this has been less well explored theoretically.21
Recently, [FeII3(saltrz)6(MII(CN)4)3]·8(H2O), where MII = Pd or Pt, and saltrz = (E)-2-((((4H-1,2,4-triazol-4-yl)imino)methyl)phenol), have been shown to undergo four-step SCO transitions with hysteresis loops around the intermediate plateaus.16 The plateaus are not very flat suggesting significant disorder in the arrangements of spin states. More direct evidence for disordered spin states comes from X-ray crystallography.16 However, puzzlingly, no diffuse scattering was observed.56
Here we demonstrate that competition between elastic interactions and variations in the local physics of the SCO centres due to crystallographic inequivalency can lead to an effective theory with lower dimensionality than the full crystal. This has important experimental consequences, particularly for understanding X-ray scattering experiments. We find that the quasi-two-dimensional model we study can be reduced to either an effective quasi-one-dimensional (q1d) model or an effective quasi-zero-dimensional (q0d) model in different intermediate plateaus. This reduced dimensionality leads to disordered phases and hence intermediate plateaus in γHS without long-range spin state order. Furthermore, the reduced dimensionality also suppresses short-range spin state order, and therefore diffuse scatter. We show that this scenario explains the observed16 SCO transitions in [FeII3(saltrz)6(MII(CN)4)3]·8(H2O) and that the absence of diffuse scatter is because the short-range correlations are extremely weak.
Finally, we discuss how stronger short range correlations can emerge from effective q1d theories and predict the diffuse scattering pattern that would be expected in this case. We show that short-range spin state correlations without long-range spin state order could explain the observed17 diffuse scattering from three analogous 1D polymeric Fe(II) SCO materials that contain the ligand 4,6-bis(2′,2′′-pyridyl)pyrazine.
2 Elastic and Ising-like models of [FeII3(saltrz)6(MII(CN)4)3]·8(H2O)
The SCO active Fe sites in [FeII3(saltrz)6(MII(CN)4)3]·8(H2O) form quasi-two-dimensional square lattices with covalently bonded networks connecting the Fe ions along the diagonal of the squares (illustrated by the grey lines in Fig. 1). Weaker interlayer elastic interactions arise from the interdigitated saltrz ligands.16 At high and low temperatures, the unit cell is composed of two unique Fe(II) sites, labelled Fe1 and Fe2. At intermediate (ca. 150–195 K) temperatures two distinct species of Fe1 and Fe2 sites are observed (labelled Fe1a, Fe1b, Fe2a and Fe2b). The distribution of crystallographically distinct Fe sites is illustrated in Fig. 1.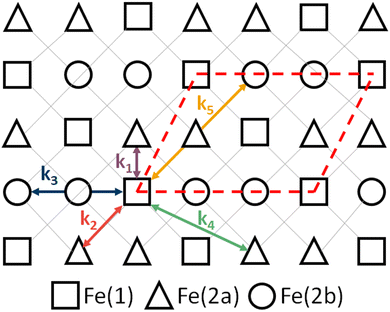 | ||
| Fig. 1 Sketch of the model studied here (eqn (1)). The nth nearest neighbours interactions, kn, are marked. The pattern of Fe1, Fe2a and Fe2b sites is that found in a single layer of [FeII3(saltrz)6(MII(CN)4)3]·8(H2O). The dashed red parallelogram indicates the primitive unit cell. | ||
Therefore, we consider a square lattice of SCO centres coupled by springs, sketched in Fig. 1, and described by the Hamiltonian6,19
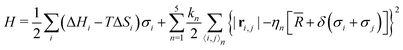 | (1) |
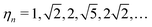 is the ratio of distances between the nth and 1st nearest-neighbour distance on the undistorted square lattice,
is the ratio of distances between the nth and 1st nearest-neighbour distance on the undistorted square lattice, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) = (RHS + RLS)/2, and δ = (RHS − RLS)/4, RHS (RLS) is the average distance between the centres of nearest neighbour SCO centres in the HS (LS) phase.
= (RHS + RLS)/2, and δ = (RHS − RLS)/4, RHS (RLS) is the average distance between the centres of nearest neighbour SCO centres in the HS (LS) phase.
Motivated by the pattern of Fe1, Fe2a and Fe2b sites observed in [FeII3(saltrz)6(MII(CN)4)3]·8(H2O),16 we consider three crystallographically distinct metal centres in the pattern shown in Fig. 1. For simplicity we neglect the differences between Fe1a and Fe1b sites found at intermediate temperatures,16 as the spin state is always the same for these two types of metal centre; and set ΔSi = ΔS on all sites, encapsulating the differences between sites solely via ΔHi.
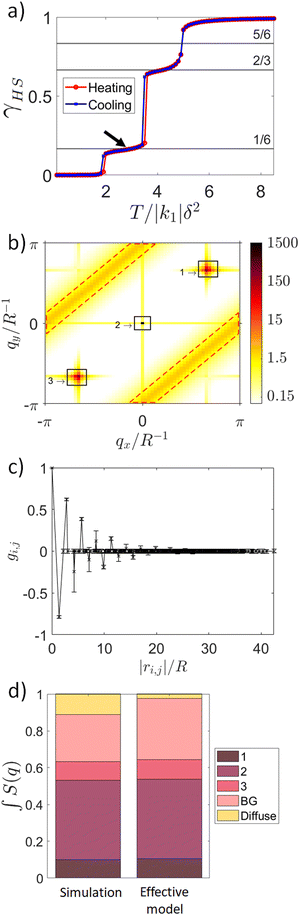
We only consider up to fifth nearest neighbor interactions. Therefore, we do not seek to fit every detail of the experiments on [FeII3(saltrz)6(MII(CN)4)3]·8(H2O), and limit ourselves to reproducing the key qualitative features. For metal centres joined by networks of covalent bonds one expects k to be large and positive, as the metal–metal separation should be close to the minimum of the potential,6,19 for our model these interactions are k2 and k5, see Fig. 1. For weak through space interactions, as is the case for k1, k3, and k4 (Fig. 1), one typically expects metal–metal separations that are larger than the distance for the minimum of the interaction potential. This leads to negative spring constants.6,19 Therefore, one expects k < 0 for many materials.19 This has profound consequences for the long range spin state order observed in different materials. In Section 3.1 we set k1 > 0, k2 = 0.48|k1|, k3 = −0.23|k1|/2, k4 = 0, and k5 = 0.09|k1| to model [FeII3(saltrz)6(MII(CN)4)3]·8(H2O). In Section 3.2 we briefly discuss the effects of varying these parameters, particularly setting k1 < 0.
We make the symmetric breathing mode approximation (SBMA).6,19 That is, we assume that the topology of the lattice is not altered by the changes in the spin states, and that the distance between any pair of nearest neighbors is ri,j = R; we variationally minimize R. In this approximation Hamiltonian (1) becomes an Ising–Husimi–Temperley model in a longitudinal field:6
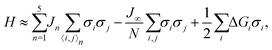 | (2) |
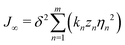 is the strain, ΔGi = ΔHi − TΔSi is the free energy difference between the HS and LS states of the ith SCO centre, zn is the coordination number for nth nearest neighbors and N is the number of metal sites.
is the strain, ΔGi = ΔHi − TΔSi is the free energy difference between the HS and LS states of the ith SCO centre, zn is the coordination number for nth nearest neighbors and N is the number of metal sites.
Although, the spring constants will often be negative for through space interactions,19 the possible range of spring constants is constrained by the fact that the lattice described by Hamiltonian (1) must be stable. Thus, we must have ∂2H/∂R2 = J∞/δ2 > 0.
We solve the Ising-Husimi-Temperley model (eqn (2)) via Metropolis Monte Carlo simulations on a N = 60 × 60 site lattice. Cooling (heating) runs are initiated with all metals in the HS (LS) state at the highest (lowest) temperature studied and the temperature is lowered (raised) in steps of 0.025|k1|δ2/kB. In each case the system is equilibrated for 4000N Monte Carlo steps and measurements are taken for 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000N steps.
000N steps.
2.1 Sum rule for the structure factor
The pseudospin structure factor,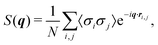 | (3) |
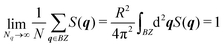 | (4) |
3 Results
3.1 Reduced dimensionality and disordered intermediate plateaus
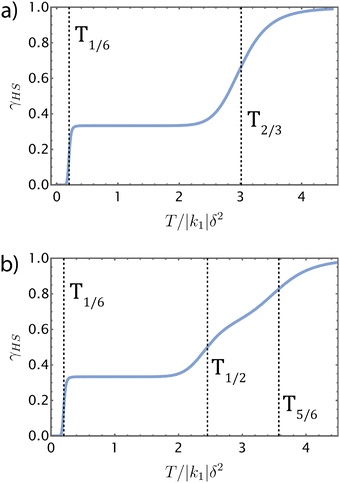
To understand the interplay between elastic interactions and multiple Fe species it is helpful to first consider what we would expect if there were no interactions between SCO centres (i.e., for all kN = 0). First let us consider ΔH1 ≪ ΔH2a = ΔH2b ≡ ΔH2, which means Fe2a and Fe2b sites are equivalent to one another but distinct from the Fe1 sites. This, gives a two step crossover, Fig. 2a. On heating from low temperatures, the first step occurs at T1/6 = ΔH1/ΔS, where the Fe1 sites have a 50% probability of being HS and the Fe2a and Fe2b are almost all LS.† As there are twice as many Fe2 sites as Fe1 sites (see Fig. 2) the total fraction of HS metals is γHS ≃ 1/6 at T = T1/6. The second step occurs at T2/3 = ΔH2/ΔS, where the Fe2 sites to have a 50% probability of being HS and almost all of the Fe1 sites are HS. Thus, γHS ≃ 2/3 at T = T2/3.For ΔH1 ≪ ΔH2b ≪ ΔH2a we expect a three step crossover, Fig. 1b. Again, the first step occurs at T1/6 = ΔH1/ΔS where γHS = 1/6. But now, the second step occurs at T1/2 = ΔH2b/ΔS, where one expects the Fe2b sites to have a 50% probability of being HS, almost all of the Fe1 sites are HS, and almost all of the Fe2a are LS, as such γHS = 1/2. The third step occurs at T5/6 = ΔH2a/ΔS, where one expects the Fe2a sites to have a 50% probability of being HS, whereas almost all of the Fe1 and Fe2b sites are HS, therefore γHS = 5/6.
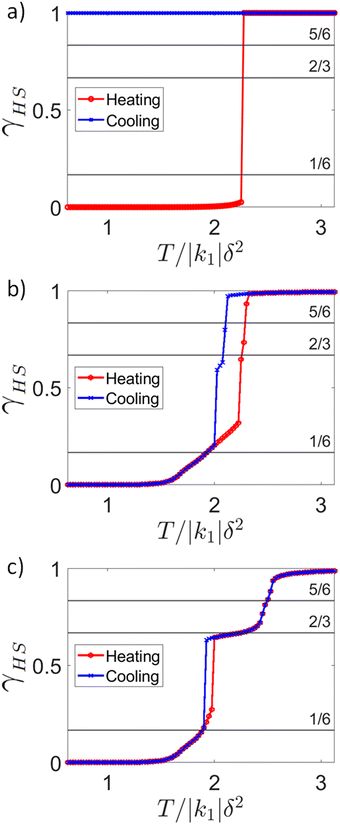
Elastic interactions significantly change the temperature dependence of the HS fraction. We show calculations for three different patterns of inequivalent Fe ions with the same elastic interactions and ΔS in Fig. 3. It is immediately clear that the inequivalent sites cause dramatic changes in the behaviour of the model and that the elastic interactions cause dramatic differences from the non-interacting model. Thus, the interplay of the pattern of inequivalent sites and elastic interactions is crucial for understanding this behaviour – neither can explain the physics alone.
When all Fe sites are equivalent (ΔH1 = ΔH2b = ΔH2a; Fig. 3a) we see a one step transition for the heating run (all sites were initialized in the LS state), and no transition for the cooling run, i.e., hidden SCO. Thus, interactions have driven the crossover (found without interactions) into a first order phase transition with a very wide hysteresis loop.
When Fe2a and Fe2b sites are equivalent to one another but distinct from Fe1 sites, (ΔH1 < ΔH2b = ΔH2a; Fig. 3b) there is a three step transition with poorly defined intermediate plateaus at γHS = 1/6 and 2/3. Thus, these plateaus occur around the crossovers expected in the non-interacting model, Fig. 2. This is what one would expect if the interactions stabilised long-range spin state order within one sublattice near the crossovers, i.e., when ΔHi/ΔS is small on the ith sublattice; analogous to chequerboard or stripe order around T1/2 when all Fe's are equivalent. However, we will show below that this is not that case and both of these plateaus are strongly disordered.
When all three Fe sublattices are inequivalent (ΔH1 < ΔH2b < ΔH2a; Fig. 3c) we observe a four step transition with intermediate plateaus at γHS = 1/6, 2/3, and 5/6. Recall that in the non-interacting model the steps are at γHS = 1/6, 1/2, and 5/6. Thus, the plateau at γHS = 1/2 is missing and the γHS = 2/3 plateau must have a different origin from the other plateaus. Furthermore, the calculated variation of γHS(T) closely resembles the variation of χT with temperature observed in [FeII3(saltrz)6(MII(CN)4)3]·8(H2O).
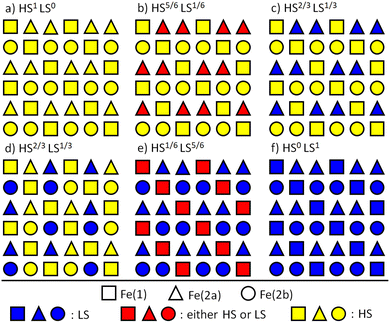
In the 1/6 plateaus shown in Fig. 3b and c the Fe2a and Fe2b sites are almost all in the LS state whereas about half of the Fe1 sites are HS (see Fig. 4a for a snapshot). T1/6 ≡ ΔH1/ΔS ≃ 0.202|k1|δ2/kB for the parameters used in Fig. 3. Notice that this temperature is significantly lower than the ranges where the γHS ≃ 1/6 plateau is observed (kBT/|k1|δ2 ≃ 1.5–2.25 in Fig. 3b, and kBT/|k1|δ2 ≃ 1.5–2.0 in Fig. 3c).
 | ||
Fig. 4 Snapshots at the three intermediate plateaus in the simulation with Fe1, Fe2a and Fe2b sites all inequivalent (from the simulations shown in Fig. 3c) taken at (a) T = 1.9|k1|δ2, (b) T = 2.25|k1|δ2, and (c) T = 2.5|k1|δ2; corresponding to the plateaus at γHS = 1/6, 2/3 and 5/6. (a) In the γHS = 1/6 plateau the Fe2a and Fe2b sites are all LS whereas the Fe1 are disordered and weakly correlated. (b) In the γHS = 2/3 plateau the Fe1 and Fe2b sites are almost all HS whereas the Fe2a are almost all LS. (c) In the γHS = 5/6 plateau the Fe1 and Fe2b sites are almost all HS whereas the Fe2a are disordered and weakly correlated. In this figure ΔS = 4ln(5)kB, 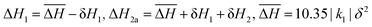 , δH1 = 9.05|k1|δ2, δH2 = 3.6|k1|δ2k1 > 0, k2 = 0.48|k1|, k3 = −0.23|k1|, k4 = 0|k1|, and k5 = 0.09|k1|. , δH1 = 9.05|k1|δ2, δH2 = 3.6|k1|δ2k1 > 0, k2 = 0.48|k1|, k3 = −0.23|k1|, k4 = 0|k1|, and k5 = 0.09|k1|. | ||
To understand this discrepancy we introduce an effective model where all of the Fe2a and Fe2b are constrained to be LS, i.e., we start from the full Hamiltonian (eqn (2)) and set σi = −1 if i is an Fe2a or Fe2b site. This leaves an effective Hamiltonian for the Fe1 sites:
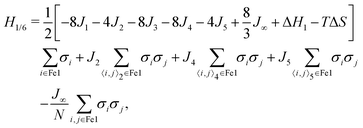 | (5) |
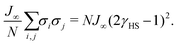 | (6) |
The effective q1D model (eqn (5)) predicts that the temperature where we expect half of the Fe1 to be HS is renormalized by the elastic interactions with the LS Fe2a and Fe2b sites to
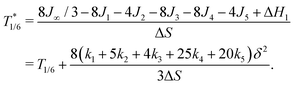 | (7) |
For the parameters in Fig. 3, 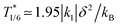 , in excellent agreement with the location of the γHS = 1/6 plateau in our Monte Carlo simulations. This strongly suggests that in the 1/6-plateau the model has become q1D.
, in excellent agreement with the location of the γHS = 1/6 plateau in our Monte Carlo simulations. This strongly suggests that in the 1/6-plateau the model has become q1D.
It is well known that there is no long-range order at finite temperature in the one-dimensional Ising model.59 Therefore, we can test our claim that the q1d model [eqn (5)] describes the 1/6 plateau by more closely examining our Monte Carlo calculations. A typical snapshot is shown in Fig. 4a. It can be clearly seen that nearly all of the Fe2a and Fe2b sites are LS and approximately half of the Fe1 sites are HS, with no apparent spin state order in the spin states of the Fe1s.
This can be made quantitative by calculating the structure factor at 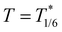 from our Monte Carlo simulations of the full model (eqn (2)). In an X-ray scatering experiment there is genuine background scatter (from sources unrelated to the spin states of the SCO centres). Therefore, when we discuss diffuse scattering below we will only be interested in clearly defined patterns that could be detected experimentally over the background noise. This, distinction between diffuse scattering and background is, unavoidably, qualitative and somewhat arbitrary. Nevertheless, it is surprising to see that the structure factor, Fig. 6a, shows little sign of structure in the diffuse scattering, even on a logarithmic scale.
from our Monte Carlo simulations of the full model (eqn (2)). In an X-ray scatering experiment there is genuine background scatter (from sources unrelated to the spin states of the SCO centres). Therefore, when we discuss diffuse scattering below we will only be interested in clearly defined patterns that could be detected experimentally over the background noise. This, distinction between diffuse scattering and background is, unavoidably, qualitative and somewhat arbitrary. Nevertheless, it is surprising to see that the structure factor, Fig. 6a, shows little sign of structure in the diffuse scattering, even on a logarithmic scale.
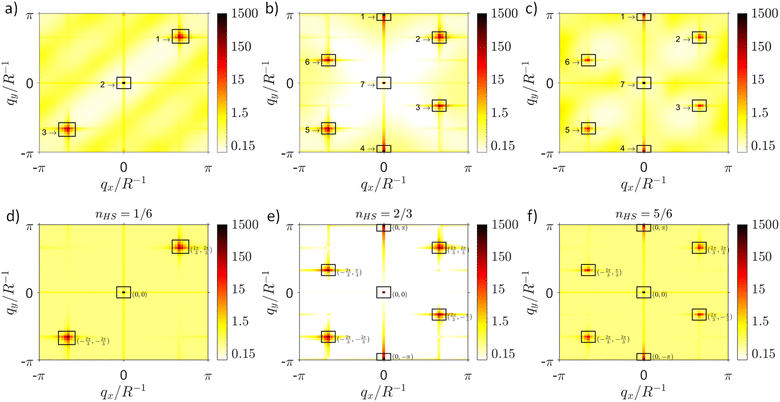 | ||
| Fig. 6 (top) Structure factors, S(q), on a logarithmic scale from the numerical simulations of the 2D model (eqn (2)) shown in Fig. 3c, taken at (a) T = 1.9|k1|δ2 (γHS = 1/6 plateau), (b) T = 2.25|k1|δ2 (γHS = 2/3 plateau), and (c) T = 2.5|k1|δ2 (γHS = 5/6 plateau). The main diffraction peaks are enclosed by black rectangles. (bottom) Normalized structure factors from (d) the effective q1d model (eqn (5)) of the γHS = 1/6 plateau, (e) the effective q1d zigzag chain model (eqn (9)) of the γHS = 2/3 plateau, and (f) the effective q0d dimer model (eqn (11)) of the γHS = 5/6 plateau. | ||
To better understand this we analytically calculated the structure factor from the effective q1d model (eqn (5)), Fig. 6d. This closely resembles our Monte Carlo simulation.
To quantify and compare the amount of scattering contributing to the observed peaks in the Monte Carlo and analytical calculations we compute the contributions to the integral 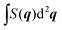 over the first Brillouin zone, of the Bragg peaks enclosed by the black squares in Fig. 6 and the background; the results are shown in Fig. 7a. We find good agreement between both calculations, the only significant difference is that slightly more scattering is present in the background of the Monte Carlo simulation; this is expected as these calculations are performed at a finite temperature, whereas the analytical calculations are effectively at zero temperature.
over the first Brillouin zone, of the Bragg peaks enclosed by the black squares in Fig. 6 and the background; the results are shown in Fig. 7a. We find good agreement between both calculations, the only significant difference is that slightly more scattering is present in the background of the Monte Carlo simulation; this is expected as these calculations are performed at a finite temperature, whereas the analytical calculations are effectively at zero temperature.
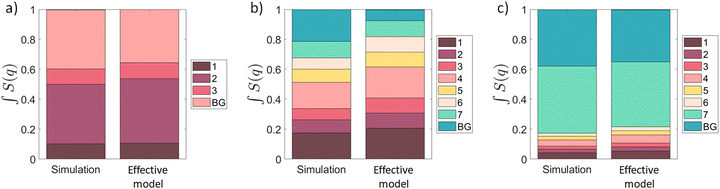 | ||
Fig. 7 Bar plots representing the integral over the first Brillouin zone of the structure factors, 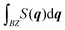 , corresponding to the numerical simulation of the 2D model (eqn (2); see Fig. 6a–c) and for the effective models (eqn (5), (9) and (11); see Fig. 6d–f). The plots indicate the portions of the integral corresponding to the Bragg peaks enclosed by rectangles in Fig. 6 and the background (BG). (a) T = 1.9|k1|δ2 in the γHS = 1/6 plateau, (b) T = 2.25|k1|δ2 in the γHS = 2/3 plateau, and (c) T = 2.5|k1|δ2 in the γHS = 5/6 plateau. , corresponding to the numerical simulation of the 2D model (eqn (2); see Fig. 6a–c) and for the effective models (eqn (5), (9) and (11); see Fig. 6d–f). The plots indicate the portions of the integral corresponding to the Bragg peaks enclosed by rectangles in Fig. 6 and the background (BG). (a) T = 1.9|k1|δ2 in the γHS = 1/6 plateau, (b) T = 2.25|k1|δ2 in the γHS = 2/3 plateau, and (c) T = 2.5|k1|δ2 in the γHS = 5/6 plateau. | ||
Further insight into the lack of diffuse scatter can be gained from the truncated two point spin state correlation function
| gi,j = 〈σiσj〉 − 〈σi〉 〈σj〉. | (8) |
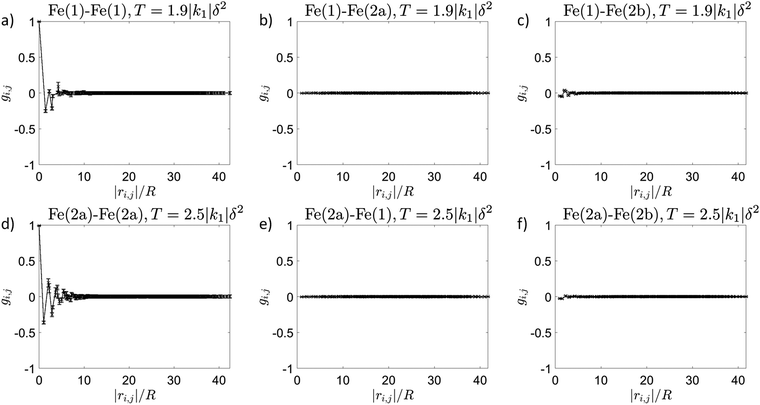 | ||
Fig. 8 Two-point spin state correlation function as a function of separation |ri,j| calculated for the simulation depicted in Fig. 3c. (a)–(c) At T = 1.9|k1|δ2 in the γHS = 1/6 plateau. (d)–(f) At T = 2.5|k1|δ2 in the γHS = 5/6 plateau. Correlations between (a) Fe1 sites, (b) Fe1 and Fe2a sites, (c) Fe1 and Fe2b sites, (d) Fe2a sites, (e) Fe2a and Fe1 sites, (f) Fe2a and Fe2b sites. For short distances the correlation between Fe1 sites at T = 1.9|k1|δ2 are weak, and decay rapidly to zero as the distance increases. Similarly, the correlations between Fe2a at T = 2.5|k1|δ2 are weak and decay rapidly to zero as the distance increases. All other correlations are essentially zero. In this figure 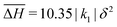 , δH1 = 9.05|k1|δ2, δH2 = 3.6|k1|δ2, k1 > 0, k2 = 0.48|k1|, k3 = −0.23|k1|, k4 = 0|k1|, k5 = 0.09|k1|, and ΔS = 4ln(5)kB. , δH1 = 9.05|k1|δ2, δH2 = 3.6|k1|δ2, k1 > 0, k2 = 0.48|k1|, k3 = −0.23|k1|, k4 = 0|k1|, k5 = 0.09|k1|, and ΔS = 4ln(5)kB. | ||
The spin state correlation function cannot be directly measured. However, as spin state and atomic position are highly entangled, we expect that the two point spin state correlation function is roughly proportional to the pair-distribution-function (PDF; the equivalent correlation function to that defined in eqn (8) for atomic position instead of spin state). The PDF is directly accessible via X-ray scattering and is a standard probe of liquids, glasses, polymers, and other structurally disordered materials.60 Thus, measurements of the PDF are vital for a deeper understanding of disorder SCO materials.
The almost complete absence of correlations between the Fe1 chains and weak short range correlations with chains explain why we find no structured diffuse scatter in the structure factor, Fig. 6a. Experimentally, in the 1/6 plateau we would expect to see a crystal structure showing mixed spin state in the Fe1 sites and no diffuse scattering, which is exactly what was reported for [FeII3(saltrz)6(MII(CN)4)3]·8(H2O).16,56
In the 2/3 plateau with only one type of Fe2 site (ΔH2a = ΔH2b = ΔH2; Fig. 3b) the Fe1 sites are almost all HS. In our Monte Carlo simulations we observe a mixture of the phases depicted in Fig. 5c and d (and states related by symmetry).
To understand the physics of the Fe2 sites it is helpful to consider the case where all of the Fe1 are HS. We can then derive an effective Hamiltonian for the Fe2 sites from the full Hamiltonian (eqn (2)) by setting σi = 1 for all Fe1. This yields
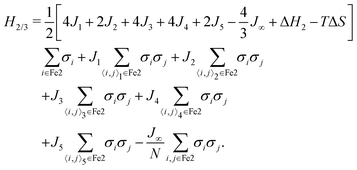 | (9) |
This model describes zigzag ladders with J2 along the legs and J1 along the rungs (plus longer range intra-ladder interactions). However, unlike the effective model of the 1/6 plateau the ladders are coupled standard Ising interactions proportional to (k3, k4 and k5).
The effective model of the 2/3 plateau (eqn (9)) predicts that T2/3 is strongly renormalized by the elastic interactions with the HS Fe1 sites, yielding
 | (10) |
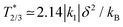 , in good agreement with our Monte Carlo results, Fig. 3b.
, in good agreement with our Monte Carlo results, Fig. 3b.
As the ladders in the effective model of the γHS = 2/3 plateau are coupled by conventional Ising interactions, and not just the long-range strain, which only couples the HS fraction (eqn (6)), the short range correlations between Fe2 sites on different ladders are stronger than those between the Fe1 sites on different chains in the γHS = 1/6 plateau. These transverse correlations result in four new Bragg peaks in the structure factor, Fig. 6b and 7b, which are accurately reproduced by the effective model (eqn (9)), Fig. 6e and 7b.
In the 2/3 plateau with two types of Fe2 site (ΔH2a > ΔH2b > ΔH1; Fig. 3c) the Fe1 and Fe2b sites are almost all HS, and the Fe2a are almost all LS, Fig. 4b. This corresponds to the phase depicted in Fig. 5c. This can be understood straightforwardly as driven by the crystallographically distinct Fe sites without needing the elastic interactions to drive the long-range spin state order. However, the elastic interactions are necessary to drive the change of spin state into a true thermodynamic phase transition rather than a crossover. Furthermore, the elastic interactions still renormalise  in a similar fashion to that described above of three inequivalent Fe sites.
in a similar fashion to that described above of three inequivalent Fe sites.
In the 5/6 plateau, Fig. 4c, the Fe1 and Fe2b sites are almost all HS. Thus, we can understand the behaviour of the Fe2a sites by considering the case where all of the Fe1 and Fe2b sites are HS. This allows us to derive an effective Hamiltonian for the Fe2a sites from the full Hamiltonian (eqn (2)) by setting σi = 1 for all Fe1 and Fe2b sites, yielding
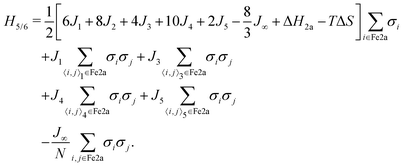 | (11) |
As we now expect, the effective q0d model of the 5/6 plateau (eqn (11)) predicts significant renormalisation of T5/6:
 | (12) |
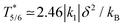 . Again, this simple theory is in good agreement with our Monte Carlo results, Fig. 3c.
. Again, this simple theory is in good agreement with our Monte Carlo results, Fig. 3c.
The truncated two point spin state correlation function reveals short range correlations between Fe2a sites, Fig. 8d, but no significant correlations between Fe2a sites and either Fe1 or Fe2b sites, Fig. 8e and f. Again, the presence of only weak short range correlations means that there is no well defined diffuse scattering pattern in the structure factor, Fig. 6c. Indeed, the structure factor calculated analytically assuming no correlations between Fe2a sites and the rest of the lattice, Fig. 6f, is in good agreement with the Monte Carlo simulation, Fig. 7c.
Thus three phases described above, namely the 1/6, 2/3 and 5/6 plateau, show disordered phases without long range spin state order and with extremely weak short range correlations. In each phase the structure factors are similar to those of long range spin state ordered phases. In particular none of the phases show well defined patterns of diffuse scattering.
3.2 Diffuse scattering from quasi-one-dimensional spin crossover chains
We do not observe well defined diffuse scattering in the previous section because in all cases the short-range correlations are extremely weak. This is in large part due to the emergent q1d and q0d descriptions and the weak interchain/interdimer interaction. However, sufficiently strong short-range correlations can give rise to diffuse scattering when there is reduced dimensionality. To show this we now report the results of Monte Carlo simulations for a different set of parameters: k1 < 0, k2 = 1.6|k1|, k3 = k4 = k5 = 0,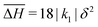 , δH1 = 17|k1|δ2, δH2 = 0|k1|δ2, ΔS = 4ln(5)kB; Fig. 9.
, δH1 = 17|k1|δ2, δH2 = 0|k1|δ2, ΔS = 4ln(5)kB; Fig. 9.
The Monte Carlo simulation shows two intermediate plateaus, one at γHS = 1/6 and the other at γHS = 2/3, Fig. 9a. The spin state ordering at γHS = 1/6 is the same as in the previous simulation (Fig. 5e), while at γHS = 2/3 we observe a mixture of the two spin state orderings depicted in Fig. 5c and d (and states related by symmetry).
The large value of k2 in this simulation causes strong intrachain correlations in the γHS = 1/6 plateau. The two-point spin state correlation function between Fe1 sites, Fig. 9c, shows much stronger and longer-ranged correlations than in the simulation described above, Fig. 8a. This leads to a clear pattern of diffuse scattering in structure factor, Fig. 9b. The integral over the first Brillouin zone of this structure factor is in reasonable agreement with the predictions of the effective q1d model (eqn (5)), Fig. 9d, although the latter slightly underestimates the diffuse scatter. This underlines that in order to get experimentally detectable diffuse scattering it is necessary to have strong short-range correlations in the disordered state, and in particular, that the range of the correlations should be significantly longer than a lattice constant.
It is interesting to compare these results to the behaviour observed by Neville, et al. for three analogous 1D polymeric iron(II) SCO materials that contain the ligand 4,6-bis(2′,2′′-pyridyl)pyrazine.17 They observed diffuse scattering planes between Bragg peaks in X-ray diffraction measurements. Neville, et al. interpreted this as HS–LS–HS–LS ordering along 1D chains, and random spin state ordering between adjacent chains.
In our simulations the Fe1 sites along the chains have a 50% chance of either being HS or LS, but display strong short-range correlations with adjacent sites tending to have opposite pseudo-spins (HS–LS), as indicated by the two-point correlation: gij ≃ −1 for nearest neighbours (Fig. 9c). However, we find much weaker correlations between chains, resulting in planes of diffuse scatter between Bragg peaks in the structure factor 9b. Thus, while the current model is clearly not appropriate for these materials, our results show that strong short-range correlations, rather than long-range spin state order, could also explain Neville et al.'s experiments.17
4 Conclusions
We have identified a route by which multistep transitions can emerge in spin crossover materials without long-range spin state order of the spin states, as observed experimentally in the SCO compound [FeII3(saltrz)6(MII(CN)4)3]·8(H2O), where MII = Pd, Pt, and saltrz = (E)-2-((((4H-1,2,4-triazol-4-yl)imino)methyl)phenol).16 We demonstrated that intermediate plateaus can emerge from the interplay between the local physics of the SCO centres (ΔHn) and the elastic interactions (ki). This interplay can reduce the effective dimensionality of the model to q0d or q1d. Reduced dimensionality leads naturally to highly disordered states at non-zero temperatures. It is interesting to note that similar mechanisms have also been proposed for the origin of quantum disorder in spin liquids.61–80We found that disordered phases with weak short-range correlations produce structure factors that are similar to those of long range spin state ordered phases, which can complicate their experimental identification. Diffuse scattering is only observed when strong short-range correlations are present. In other parameter regimes of our model we find diffuse scattering, and we used this to propose an alternative explanation of the diffuse scattering observed by Neville, et al. in three 4,6-bis(2′,2′′-pyridyl)pyrazine based SCO polymers that does not require long-range spin state order. Measurement of the PDF would provide a powerful tool to further analyse and distinguish disordered phases, as it provides the same information as the spin state correlation functions calculated above.
Author contributions
GR: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft. JC: conceptualization, methodology, supervision. BJP: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Oliver Bellwood, Cameron Kepert, Ross McKenzie, and Suzanne Neville for helpful conversations. This work was supported by the Australian Research Council through project DP200100305.References
- A. Simonov and A. L. Goodwin, Nat. Rev. Chem., 2020, 4, 657–673 CrossRef CAS PubMed
.
- B. Wehinger, D. Chernyshov, M. Krisch, S. Bulat, V. Ezhov and A. Bosak, J. Phys.: Condens. Matter, 2014, 26, 265401 CrossRef PubMed
.
- C. L. Henley, Annu. Rev. Condens. Matter Phys., 2010, 1, 179–210 CrossRef CAS
.
- T. Fennell, P. P. Deen, A. R. Wildes, K. Schmalzl, D. Prabhakaran, A. T. Boothroyd, R. J. Aldus, D. F. McMorrow and S. T. Bramwell, Science, 2009, 326, 415–417 CrossRef CAS PubMed
.
- D. J. P. Morris, D. A. Tennant, S. A. Grigera, B. Klemke, C. Castelnovo, R. Moessner, C. Czternasty, M. Meissner, K. C. Rule, J.-U. Hoffmann, K. Kiefer, S. Gerischer, D. Slobinsky and R. S. Perry, Science, 2009, 326, 411–414 CrossRef CAS PubMed
.
- J. Cruddas and B. J. Powell, J. Am. Chem. Soc., 2019, 141, 19790–19799 CrossRef CAS PubMed
.
- J. Cruddas and B. J. Powell, Phys. Rev. B, 2021, 104, 024433 CrossRef CAS
.
- I. Gudyma and V. Yarema, Appl. Nanosci., 2023, 13, 6719–6726 CrossRef CAS
.
- J. Cruddas, G. Ruzzi and B. J. Powell, J. Appl. Phys., 2021, 129, 185102 CrossRef CAS
.
- S. Pillet, J. Appl. Phys., 2021, 129, 181101 CrossRef CAS
.
- H. Watanabe, K. Tanaka, N. Bréfuel, H. Cailleau, J.-F. Létard, S. Ravy, P. Fertey, M. Nishino, S. Miyashita and E. Collet, Phys. Rev. B, 2016, 93, 014419 CrossRef
.
- E. Collet, H. Watanabe, N. Bréfuel, L. Palatinus, L. Roudaut, L. Toupet, K. Tanaka, J.-P. Tuchagues, P. Fertey, S. Ravy, B. Toudic and H. Cailleau, Phys. Rev. Lett., 2012, 109, 257206 CrossRef CAS PubMed
.
- C. Mariette, E. Trzop, S. Zerdane, P. Fertey, D. Zhang, F. J. Valverde-Muñoz, J.-A. Real and E. Collet, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 660–668 CrossRef CAS PubMed
.
- E. Collet and P. Guionneau, C. R. Chim., 2018, 21, 1133–1151 CrossRef CAS
.
- C. Bressler, W. Gawelda, A. Galler, M. M. Nielsen, V. Sundström, G. Doumy, A. M. March, S. H. Southworth, L. Young and G. Vankó, Faraday Discuss., 2014, 171, 169–178 RSC
.
- N. F. Sciortino, K. A. Zenere, M. E. Corrigan, G. J. Halder, G. Chastanet, J.-F. Létard, C. J. Kepert and S. M. Neville, Chem. Sci., 2017, 8, 701–707 RSC
.
- S. M. Neville, B. A. Leita, G. J. Halder, C. J. Kepert, B. Moubaraki, J.-F. Létard and K. S. Murray, Chem. – Eur. J., 2008, 14, 10123–10133 CrossRef CAS PubMed
.
- A. Bousseksou, F. Varret and J. Nasser, J. Phys. I, 1993, 3, 1463–1473 CrossRef CAS
.
- J. Cruddas and B. J. Powell, Inorg. Chem. Front., 2020, 7, 4424–4437 RSC
.
- M. Paez-Espejo, M. Sy and K. Boukheddaden, J. Am. Chem. Soc., 2016, 138, 3202–3210 CrossRef CAS PubMed
.
- G. Azzolina, R. Bertoni and E. Collet, J. Appl. Phys., 2021, 129, 085106 CrossRef CAS
.
- N. F. Sciortino, F. Ragon, Y. M. Klein, C. E. Housecroft, C. G. Davies, G. N. L. Jameson, G. Chastanet and S. M. Neville, Inorg. Chem., 2018, 57, 11068–11076 CrossRef CAS PubMed
.
- N. Ortega-Villar, M. Muñoz and J. Real, Magnetochemistry, 2016, 2, 16 CrossRef
.
- C.-J. Zhang, K.-T. Lian, S.-G. Wu, G.-Z. Huang, Z.-P. Ni and M.-L. Tong, Inorg. Chem. Front., 2020, 4, 911 RSC
.
- C.-J. Zhang, K.-T. Lian, G.-Z. Huang, S. Bala, Z.-P. Ni and M.-L. Tong, Chem. Commun., 2019, 55, 11033 RSC
.
- Y. Meng, Q. Sheng, M. N. Hoque, Y. Chen, S. Wu, J. Tucek, R. Zboril, T. Liu, Z. Ni and M. Tong, Chem. – Eur. J., 2017, 23, 10034 CrossRef CAS PubMed
.
- J. E. Clements, J. R. Price, S. M. Neville and C. J. Kepert, Angew. Chem., Int. Ed., 2016, 55, 15105–15109 CrossRef CAS PubMed
.
- G. Agustí, A. B. Gaspar, M. C. Muñoz, P. G. Lacroix and J. A. Real, Aust. J. Chem., 2009, 62, 1155 CrossRef
.
- K. Takashi, K.-T. Chihiro, K. Chikahide, S. Toshiaki and K. Takafumi, Chem. Lett., 2008, 37, 422 CrossRef
.
- G. Agustí, M. C. Muñoz, A. B. Gaspar and J. A. Real, Inorg. Chem., 2008, 47, 2552 CrossRef PubMed
.
- N. F. Sciortino, K. R. Scherl-Gruenwald, G. Chastanet, G. J. Halder, K. W. Chapman, J.-F. Létard and C. J. Kepert, Angew. Chem., Int. Ed., 2012, 51, 10154–10158 CrossRef CAS PubMed
.
- F.-L. Liu, D. Li, L.-J. Su and J. Tao, Dalton Trans., 2018, 47, 1407–1411 RSC
.
- M. J. Murphy, K. A. Zenere, F. Ragon, P. D. Southon, C. J. Kepert and S. M. Neville, J. Am. Chem. Soc., 2017, 139, 1330–1335 CrossRef CAS PubMed
.
- K. A. Zenere, S. G. Duyker, E. Trzop, E. Collet, B. Chan, P. W. Doheny, C. J. Kepert and S. M. Neville, Chem. Sci., 2018, 9, 5623–5629 RSC
.
- E. Milin, V. Patinec, S. Triki, E.-E. Bendeif, S. Pillet, M. Marchivie, G. Chastanet and K. Boukheddaden, Inorg. Chem., 2016, 55, 11652–11661 CrossRef CAS PubMed
.
- L. Piñeiro-López, M. Seredyuk, M. C. Muñoz and J. A. Real, Chem. Commun., 2014, 50, 1833–1835 RSC
.
- F.-L. Liu and J. Tao, Chem. – Eur. J., 2017, 23, 18252–18257 CrossRef CAS PubMed
.
- Y. M. Klein, N. F. Sciortino, F. Ragon, C. E. Housecroft, C. J. Kepert and S. M. Neville, Chem. Commun., 2014, 50, 3838–3840 RSC
.
- V. A. Money, C. Carbonera, J. Elhaïk, M. A. Halcrow, J.
A. K. Howard and J.-F. Létard, Chem. – Eur. J., 2007, 13, 5503–5514 CrossRef CAS PubMed
.
- A. J. Fitzpatrick, E. Trzop, H. Müller-Bunz, M. M. Dîrtu, Y. Garcia, E. Collet and G. G. Morgan, Chem. Commun., 2015, 51, 17540–17543 RSC
.
- J. Klingele, D. Kaase, M. H. Klingele, J. Lach and S. Demeshko, Dalton Trans., 2010, 39, 1689–1691 RSC
.
- D. Chernyshov, M. Hostettler, K. W. Törnroos and H.-B. Bürgi, Angew. Chem., Int. Ed., 2003, 42, 3825–3830 CrossRef CAS PubMed
.
- B. J. C. Vieira, J. T. Coutinho, I. C. Santos, L. C. J. Pereira, J. C. Waerenborgh and V. da Gama, Inorg. Chem., 2013, 52, 3845–3850 CrossRef CAS PubMed
.
- H. Hang, B. Fei, X. Q. Chen, M. L. Tong, V. Ksenofontov, I. A. Gural'skiy and X. Bao, J. Mater. Chem. C, 2018, 6, 3352–3361 RSC
.
- J.-B. Lin, W. Xue, B.-Y. Wang, J. Tao, W.-X. Zhang, J.-P. Zhang and X.-M. Chen, Inorg. Chem., 2012, 51, 9423 CrossRef CAS PubMed
.
- G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and J. D. Cashion, Science, 2002, 298, 1762–1765 CrossRef CAS PubMed
.
- G. J. Halder, K. W. Chapman, S. M. Neville, B. Moubaraki, K. S. Murray, J.-F. Létard and C. J. Kepert, J. Am. Chem. Soc., 2008, 130, 17552 CrossRef CAS PubMed
.
- X. Bao, P.-H. Guo, W. Liu, J. Tucek, W.-X. Zhang, J.-D. Leng, X.-M. Chen, I. A. Gural'skiy, L. Salmon, A. Bousseksou and M.-L. Tong, Chem. Sci., 2012, 3, 1629 RSC
.
- C. J. Adams, M. C. Muñoz, R. E. Waddington and J. A. Real, Inorg. Chem., 2011, 50, 10633 CrossRef CAS PubMed
.
- W. Liu, Y.-Y. Peng, S.-G. Wu, Y.-C. Chen, M. N. Hoque, Z.-P. Ni, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 14982 CrossRef CAS PubMed
.
- N. Ortega-Villar, M. C. Muñoz and J. A. Real, Magnetochemistry, 2016, 2, 16 CrossRef
.
- K. D. Murnaghan, C. Carbonera, L. Toupet, M. Griffin, M. M. Dîrtu, C. Desplanches, Y. Garcia, E. Collet, J.-F. Létard and G. G. Morgan, Chem. – Eur. J., 2014, 20, 5613–5618 CrossRef CAS PubMed
.
- J. Luan, J. Zhou, Z. Liu, B. Zhu, H. Wang, X. Bao, W. Liu, M.-L. Tong, G. Peng, H. Peng, L. Salmon and A. Bousseksou, Inorg. Chem., 2015, 54, 5145–5147 CrossRef CAS PubMed
.
- Z.-Y. Li, H. Ohtsu, T. Kojima, J.-W. Dai, T. Yoshida, B. K. Breedlove, W.-X. Zhang, H. Iguchi, O. Sato, M. Kawano and M. Yamashita, Angew. Chem., Int. Ed., 2016, 55, 5184–5189 CrossRef CAS PubMed
.
- N. Bréfuel, H. Watanabe, L. Toupet, J. Come, N. Matsumoto, E. Collet, K. Tanaka and J.-P. Tuchagues, Angew. Chem., Int. Ed., 2009, 48, 9304–9307 CrossRef PubMed
.
- S. M. Neville, private communication.
- A. Bunde, Phys. Lett. A, 1974, 47, 483–484 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
-
M. Plischke and B. Bergersen, Equilibrium Statistical Physics, World Scientific, 2006 Search PubMed
.
- M. W. Terban and S. J. L. Billinge, Chem. Rev., 2022, 122, 1208–1272 CrossRef CAS PubMed
.
- B. J. Powell and R. H. McKenzie, Phys. Rev. Lett., 2007, 98, 027005 CrossRef CAS PubMed
.
- Y. Hayashi and M. Ogata, J. Phys. Soc. Jpn., 2007, 76, 053705 CrossRef
.
- M. Kohno, O. A. Starykh and L. Balents, Nat. Phys., 2007, 3, 790–795 Search PubMed
.
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed
.
- B. J. Powell, E. P. Kenny and J. Merino, Phys. Rev. Lett., 2017, 119, 087204 CrossRef CAS PubMed
.
- E. P. Kenny, A. C. Jacko and B. J. Powell, Angew. Chem., Int. Ed., 2019, 58, 15082–15088 CrossRef CAS PubMed
.
- E. P. Kenny, G. David, N. Ferré, A. C. Jacko and B. J. Powell, Phys. Rev. Mater., 2020, 4, 044403 CrossRef CAS
.
- A. C. Jacko and B. J. Powell, Phys. Chem. Chem. Phys., 2021, 23, 5012–5019 RSC
.
- C. Dissanayake, A. C. Jacko, K. Kumarasinghe, R. Munir, H. Siddiquee, W. J. Newsome, F. J. Uribe-Romo, E. S. Choi, S. Yadav, X.-Z. Hu, Y. Takano, S. Pakhira, D. C. Johnston, Q.-P. Ding, Y. Furukawa, B. J. Powell and Y. Nakajima, Phys. Rev. B, 2023, 108, 134418 CrossRef CAS
.
- Y. Choi, S. Lee, J.-H. Lee, S. Lee, M.-J. Seong and K.-Y. Choi, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed
.
- S. A. Zvyagin, A. N. Ponomaryov, J. Wosnitza, D. Hirai, Z. Hiroi, M. Gen, Y. Kohama, A. Matsuo, Y. H. Matsuda and K. Kindo, Nat. Commun., 2022, 13, 6310 CrossRef CAS PubMed
.
- G. Cao, H. Zheng, H. Zhao, Y. Ni, C. A. Pocs, Y. Zhang, F. Ye, C. Hoffmann, X. Wang, M. Lee, M. Hermele and I. Kimchi, npj Quant. Mater., 2020, 5, 26 CrossRef
.
- S. E. Sebastian, N. Harrison, C. D. Batista, L. Balicas, M. Jaime, P. A. Sharma, N. Kawashima and I. R. Fisher, Nature, 2006, 441, 617–620 CrossRef CAS PubMed
.
- S.-H. Lee, D. Louca, H. Ueda, S. Park, T. J. Sato, M. Isobe, Y. Ueda, S. Rosenkranz, P. Zschack, J. Íñiguez, Y. Qiu and R. Osborn, Phys. Rev. Lett., 2004, 93, 156407 CrossRef PubMed
.
- R. Okuma, M. Kofu, S. Asai, M. Avdeev, A. Koda, H. Okabe, M. Hiraishi, S. Takeshita, K. M. Kojima, R. Kadono, T. Masuda, K. Nakajima and Z. Hiroi, Nat. Commun., 2021, 12, 4382 CrossRef CAS PubMed
.
- K. Ido, K. Yoshimi, T. Misawa and M. Imada, npj Quant. Mater., 2022, 7, 48 CrossRef CAS
.
- B. Zhang, Y. Zhang, Z. Wang, D. Wang, P. J. Baker, F. L. Pratt and D. Zhu, Sci. Rep., 2014, 4, 6451 CrossRef CAS PubMed
.
- R. Pohle, N. Shannon and Y. Motome, Phys. Rev. B, 2023, 107, L140403 CrossRef CAS
.
- S. Feng, A. Agarwala and N. Trivedi, arXiv, 2023, preprint, arXiv:2308.08116, DOI:10.48550/arXiv.2308.08116.
- O. R. Bellwood, H. L. Nourse and B. J. Powell, Raman scattering signatures of spinons and triplons in frustrated antiferromagnets, arXiv, 2024, preprint, arXiv:2401.10452, DOI:10.48550/arXiv.2401.10452.
Footnote |
| † They are strictly all LS in the limit ΔH2 → ∞. |
| This journal is © The Royal Society of Chemistry 2024 |