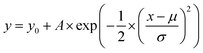Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect energetics in an high-entropy alloy fcc CoCrFeMnNi†
Chan
Gao
 *a,
Shuyu
Wang
a,
Xiao
Liu
a and
Chandra Veer
Singh
*a,
Shuyu
Wang
a,
Xiao
Liu
a and
Chandra Veer
Singh
 *bc
*bc
aInstitute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China. E-mail: gaochan@caep.cn
bDepartment of Materials Science and Engineering, University of Toronto, Toronto, ON M5S 3E4, Canada. E-mail: chandraveer.singh@utoronto.ca
cDepartment of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON M5S 3G8, Canada
First published on 1st April 2024
Abstract
High-entropy alloys (HEAs) are promising candidate materials in nuclear applications owing to their excellent mechanical properties and improved resistance to radiation damage. Defect formation energy in HEAs is directly dependent on the choice of chemical potential, and different chemical potentials can contribute to the discrepancies in the statistical spread. Herein, first-principles calculations were performed to investigate the defect energetics in a fcc CoCrFeMnNi HEA based on chemical potentials, which are back-derived in a self-consistent manner. Chemical potentials are more accurate and precise without additional computational cost and associated uncertainty. The computational results show that defect formation energy is strongly dependent on the local atomic environment and weakly dependent on the chemical composition. Moreover, vacancies prefer the Cr- and Mn-deficient as well as Ni-rich local atomic environment. There is a distinct relationship between the interstitial-specific formation energy and the number of X atoms in 1-NN, while, irrespective of interstitial species, there is no obvious trend in the dependence of the interstitial formation energy and the local atomic environment. The average vacancy migration energies follow the order: Cr < Fe < Mn < Ni < Co, which is lower than that in pure Ni, and the Fe and Cr atoms in 1-NN around vacancies prefer to exchange with vacancies to help vacancy migration. Furthermore, the local atomic environment of the Mn and Ni atoms of the chemical species that exchanges with vacancies suppresses vacancy migration and that of the Co and Fe atoms facilitates vacancy migration. The results of this work can contribute to understanding the enhanced irradiation resistance of HEAs and may provide a new paradigm for the design of advanced radiation-tolerant HEAs.
1. Introduction
The development and deployment of new-generation fission and fusion reactors is directly dependent on the evolution of advanced high-performance structural materials that can tolerate the extreme environments produced by intense radiation fields, elevated temperatures, and chemical reactive conditions.1–3 As we all know, in these environments, high-dose, high-energy neutrons collide with lattice atoms, creating numerous point defects in the material, such as interstitials and vacancies. Further evolution of these irradiation-induced defects leads to the formation of extended defect structures such as dislocation loops, stacking fault tetrahedra, and voids during continuous irradiation.2,4 These defects can degrade the physical and mechanical properties of the material, thus shortening the lifetime of nuclear reactor components and affecting the safe operation of nuclear reactors.1,2 Therefore, the development of high-performance materials that are radiation-resistant is critical for advanced nuclear reactor systems.High-entropy alloys (HEAs),5–8 usually a single phase solid solution with multiple principal elements in equiatomic or near equiatomic composition, make them promising candidate materials in nuclear applications9 owing to their excellent mechanical properties10–12 and improved resistance to radiation damage.13,14 It is well established that the production and migration of point defects under irradiation directly affect the number, distribution and agglomeration of surviving defects, and consequently, the microstructure and properties of the materials.4 Therefore, it is important to develop a quantitative understanding of the properties of point defects in HEAs. Moreover, reliable data for defect energetics from comprehensive density functional theory (DFT) calculations can provide insights into the key factors on the early stage of irradiation-induced defect production and also provide fundamental parameters in multi-scale simulations for defect evolution, which is highly crucial in understanding and even predicting the microstructural evolution of materials under irradiation environments. In addition, the formation and migration energies of point defects are important for the development and testing of semi-empirical interatomic potentials for studying radiation damage behaviors by molecular dynamics (MD) simulation in HEAs.
Theoretical calculations have been made recently to unveil the defect energies in a series of CoCrFeMnNi HEA sub-systems, including CoNi,15 FeNi,15–17 CrNi,15 CoCrNi,18 CrFeNi,17 NiFeMnCr19 and CoCrFeNi.18,20–22 However, in HEAs, the extreme chemical disorder induced by the random arrangement of different elements can lead to complex energy landscapes. Consequently, the formation and migration energies of vacancies and interstitials exhibit a distribution of values, which can significantly affect the defect production and evolution. Therefore, the theoretical determination of the defect energetics of various point defects is rather challenging. Due to the computational demands and complexity, few studies on the defect energetics of the high-entropy alloys have been performed. The vacancy formation and migration energies in CrMnFeCoNi have been investigated,23 and the average vacancy formation energy of each element is almost the same at approximately 2.0 eV, while the average vacancy migration energy of each element increases with increasing atomic number. The effects of the chemical environment and magnetic moment on point defect formations in CoCrNi, CoCrNiFe, and CoCrNiFeMn have been systemically characterized.21 It was found that vacancies prefer Ni-rich and Cr-deficient environments, and interstitial defects are primarily dominated by Co and Mn. Furthermore, the point defect formation energies are found to be negatively correlated with the anti-magnetic moment changes in 1-NN atoms.
Different studies on defect energetics in the same HEAs can produce different results. There are two key factors in the first-principles calculations: (1) supercell size; and (2) chemical potential. In general, studies based on smaller supercells produce a wider statistical spread of defect energies than those based on large supercells. Moreover, the defect formation energy is directly dependent upon the choice of chemical potential in HEAs, and different chemical potentials used in these studies can also contribute to the discrepancies in the statistical spread. In the studies on the defect energetics in HEAs, there are different methods to compute the chemical potentials of constituent elements in HEAs. For example, the chemical potential of the defect species was approximated by the total energy of their bulk counterpart with the most stable phase,20,22 but it was not precise and suitable for the defect formation energy in the HEAs. Furthermore, the chemical potentials of all chemical components can be calculated using the Widom-type substitution technique.15,19,21 Usually, sufficient separate calculations with extra computational costs are needed to obtain an accurate average value and a level of uncertainty. Therefore, a new computational method of chemical potentials of constituent elements in HEA will be proposed without extra computational costs and uncertainty.
As an application, we have chosen the well-studied prototype equiatomic fcc CoCrFeMnNi HEA, which was the first proposed HEA, also known as the Cantor alloy.8 In addition, most work has focused on the fcc CoCrFeMnNi HEA as a model system to study the irradiation resistance of HEAs.14 Herein, first-principles calculations have been performed to study the defect energetics in fcc CoCrFeMnNi HEA to obtain the formation energies of vacancies and interstitials, as well as the migration energies of the vacancies based on the special quasi-random structures (SQS) approach. First, the chemical potentials of constituent elements were calculated based on a statistical approach to give the distribution of vacancies and interstitial formation energy. Then, the defect formation energies of vacancies and interstitial were calculated, and the effect of local atomic environment on the defect formation energy was also analyzed. Finally, the migration energies of the representative vacancies were also presented. Exploiting the defect energetics in high-entropy alloys can contribute to understanding the enhanced irradiation resistance of HEAs, and may provide a new paradigm for designing structural materials with more improved radiation resistance for the future nuclear applications.
2. Computational methods
The first-principles calculations were performed in the framework of density functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP) code.24,25 The interaction between ions and electrons was treated by the projector augmented wave (PAW) method,26,27 and the exchange–correlation functional was described by the generalized gradient approximations (GGA) with the Perdew–Burke–Ernzerhof formalism.28 The cut-off energy for the plane-wave basis set was set to 350 eV for all calculations. The Brillouin zone was sampled with a 3 × 3 × 3 Γ-centered k-point mesh for the supercell. The first-order Methfessel–Paxton smearing method of the Fermi surface was used with a smearing width of 0.1 eV to account for orbital partial occupancies of the HEA systems. Furthermore, all calculations were carried out with spin polarization to take into account the magnetic properties, and according to previous ref. 29 and 30 a ferrimagnetic structure was initialized with Cr and Mn spins being aligned anti-parallel to the Fe, Co and Ni atomic spins.To model the full disorder with the best possible small periodic supercell for the fcc CoCrFeMnNi HEA, a 125-atom supercell (5 × 5 × 5 primitive cell) of special quasi-random structures (SQS)31 was generated by mcsqs code in the alloy theoretic automated toolkit (ATAT) package.32 The equilibrium volume was determined by computing the total energies for at least nine volumes around the equilibrium volume. For each structure, the internal coordinates of all atoms were first relaxed at a given volume by conjugate gradient method with a convergence criterion of 10−4 eV and 10−2 eV Å−1 for the energy and force, respectively. The optimal lattice parameter was obtained by fitting the calculated energy-volume relation to the Birch–Murnaghan equation of state. Afterwards, all of the defect properties calculations were carried out under this optimal lattice by relaxing only the atomic coordinates with the same convergence criteria.
The defect migration energies were calculated using the climbing-image nudged elastic band (CI-NEB) method,33 as implemented in VASP. A number of intermediate images are optimized along the migration path with the same convergence criteria as the defect properties calculations. To acquire the minimum energy paths (MEPs) of defects, twelve migration energies for each defect towards its first nearest neighbors (1-NN) were all calculated.
3. Results and discussion
3.1. Chemical potentials
In the HEAs, vacancies and self-interstitials were introduced by removing atoms from their regular lattice positions and placing atoms into their interstitial sites, respectively. Consequently, the defect formation energy can be calculated by comparing the difference between the energy of the relaxed defective supercell and that of the reference state, as follows:15,21| Ef = Ed − E0 ± μx | (1) |
In this study, the chemical potentials of each component were calculated based on a statistical approach to give the distribution of defect formation energy. During the calculation of vacancy formation energy, the chemical potential of the defect species X can be calculated from:34
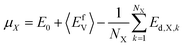 | (2) |
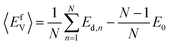 | (3) |
Following the same idea,34 in the course of the calculation of the X-interstitial formation energy with the X–X′ dumbbell, the chemical potential of type X with the X–X′ dumbbell can be calculated from,
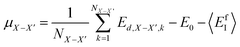 | (4) |
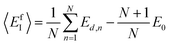 | (5) |
For the calculations of the defect formation energies, the chemical potentials of constituent elements for vacancies and interstitials with the X–X′ dumbbell are presented in Table 1, in comparison with those of pure metals and the results of references in the HEA. For the same constituent element, the chemical potentials for the vacancy and interstitials with different X–X′ dumbbells are different, while those of pure metals and the references’ results21,23 in the HEA are all the same single values. The chemical potentials depend on the vacancy and dumbbell composition. In this sense, our result should be more accurate and precise. Interestingly, the chemical potentials of Co, Fe and Ni in HEA fluctuate around those of the pure metals, while the chemical potential of Cr in the HEA is larger than that of pure Cr and the chemical potential of Mn in the HEA is smaller than that of pure Mn, which can be attributed to the ferromagnetism of Co, Fe and Ni and the anti-ferromagnetism of Cr and Mn. Moreover, our chemical potentials are comparable with the results of references21,23 in the HEA, demonstrating that our result is reasonable without additional computational cost and the associated uncertainty.
| Vacancy | μ Co | μ Cr | μ Fe | μ Mn | μ Ni | |
|---|---|---|---|---|---|---|
| −7.00 | −9.27 | −8.15 | −8.98 | −5.51 | ||
| Interstitials | Co–X | −6.98 | −9.41 | −8.26 | −9.01 | −5.26 |
| Cr–X | −7.09 | −9.13 | −8.36 | −8.91 | −5.43 | |
| Fe–X | −6.98 | −9.29 | −8.24 | −9.03 | −5.37 | |
| Mn–X | −7.14 | −9.09 | −8.31 | −8.95 | −5.42 | |
| Ni–X | −7.01 | −9.43 | −8.21 | −8.98 | −5.29 | |
| Ref. 23 | −7.03 | −9.35 | −8.21 | −9.00 | −5.54 | |
| Ref. 21 | −7.10 | −9.76 | −8.39 | −8.96 | −5.56 | |
| Pure metals | −7.04 | −9.53 | −8.25 | −8.86 | −5.48 |
3.2. Vacancy formation energy
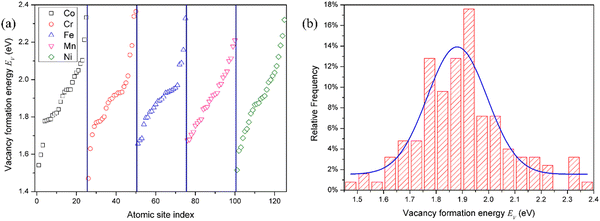
Due to the chemical disorder caused by the random arrangement of various elements, the defect formation energy is dependent on the local atomic environment in HEAs. As a result, there are large variations in defect energies. The defect formation energies take on a distribution, rather than a single value as the pure metal and dilute alloy.35 Moreover, in HEAs, the defect formation energy is usually element-specific.22 In other words, the defect formation energies are also dependent on the type of element or composition,22i.e., vacancies produced by removing the atoms of different elements or interstitials formed by adding the atoms of different compositions. In this study, the defect formation energies of all atomic sites in the SQS supercell were calculated to analyze their statistical distribution.For the convenience of description, the vacancies are denoted by the element that is removed for vacancy production. The distribution of the vacancy formation energy is plotted in Fig. 1. The vacancy formation energy for each component in HEAs varies in a relatively wide range. Due to the different local chemical atomic environment, the vacancy formation energy varies from 1.54 eV to 2.33 eV for Co, 1.47 eV to 2.36 eV for Cr, 1.66 eV to 2.33 eV for Fe, 1.68 eV to 2.21 eV for Mn, and 1.52 eV to 2.32 eV, as shown in Fig. 1 and Table 2. Interestingly, the range of vacancy formation energy for Mn is very small in comparison with those for other components, which can be attributed to the complicated magnetism of Mn. In fact, Mn exhibits a very complex magnetic structure in its stable elemental phase,19,36 and cannot be simply described as either ferromagnetic or anti-ferromagnetic. As a result, the magnetic behavior of Mn is very different from that of the other elemental constituents in CoCrFeMnNi HEA. The complex magnetic structure of Mn reduces the fluctuation of the vacancy formation energy of Mn in CoCrFeMnNi HEA, and hence the smaller spread of the vacancy formation energy of Mn. The distribution of the vacancy formation energy is different for each chemical species of the vacancy (i.e., Co, Cr, Fe, Mn or Ni), indicating that the vacancy formation energy is dependent on not only the local atomic environment, but also the chemical composition.
| Species | μ | σ | Range |
|---|---|---|---|
| V | 1.88 | 0.11 | 1.47–2.36 |
| V Co | 1.88 | 0.11 | 1.54–2.33 |
| V Cr | 1.87 | 0.10 | 1.47–2.36 |
| V Fe | 1.90 | 0.04 | 1.66–2.33 |
| V Mn | 1.77 | 0.02 | 1.68–2.21 |
| V Ni | 1.89 | 0.06 | 1.52–2.32 |
| V in Ni | 1.43 | — |
In order to quantify the mean and fluctuations (standard deviations) effect, all the data and the element-specific data can be fitted to the Gaussian function, as follows,
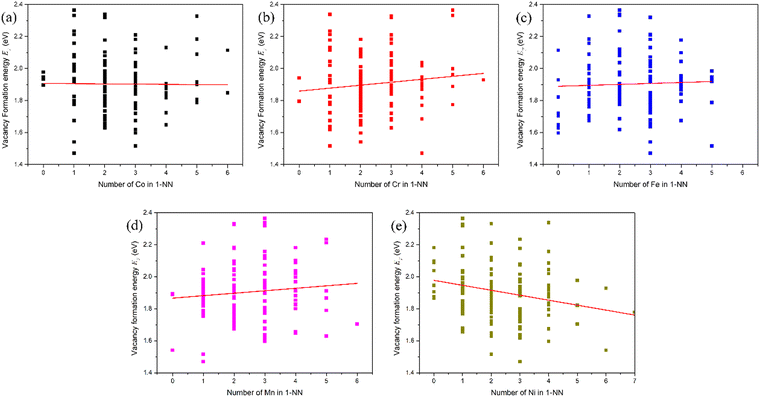
To investigate the effect of the local atomic environment on the vacancy formation energy in the HEA, the dependence of the vacancy formation energy on the number of atoms in the first nearest neighbor (1-NN) around the defect site was systematically analyzed, as shown in Fig. 2. It can be found that there is no obvious dependence of the vacancy formation energy on the number of Co and Fe atoms in the 1-NN around the vacancy, in agreement with the reference results.21 On the other hand, the vacancy formation energy increases with the number of Cr and Mn atoms in the 1-NN, while the vacancy formation energy decreases with the number of Ni atoms in the 1-NN, consistent with the trend from ref. 21 and 23. Thus, the number of Cr, Mn and Ni atoms in the 1-NN is the key factor affecting the vacancy formation energy, and vacancies will more easily form in a Cr- and Mn-deficient, as well as Ni-rich environment in fcc CoCrFeMnNi HEA.
It should be noted that the tendency of the vacancy formation energy with the number of Mn atoms is opposite with the previous results,21 which can be attributed to the complicated magnetism of the Mn element. Mn exhibits a very complicated magnetic behavior in its stable ground state.19,36 Hence, it cannot be simply described as either a ferromagnetic or anti-ferromagnetic alignment in the fcc CoCrFeMnNi HEA. Importantly, for ferromagnetic elements, there is no significant dependence between the vacancy formation energy and the numbers of Co or Fe atoms in the 1-NN, while the vacancy formation energy is seen to be negatively correlated with the number of Ni atoms in the 1-NN, which can be attributed to the Ni atoms having the smallest radius among all the elements in the fcc CoCrFeMnNi HEA. During vacancy formation, an increase in the number of Ni atoms in the 1-NN results in a decrease in the atomic perturbation induced by the smallest radius. Moreover, as the radius of the Cr atom is the largest among the constituent elements, the interaction between Cr atoms in the 1-NN is stronger than that for other elements, and increasing the number of Cr atoms in the 1-NN can help suppress the vacancy formation. It can be speculated that the atomic radius of elements can affect the vacancy formation energy in the HEA. Furthermore, the 3d orbitals of the Cr atoms are more delocalized than those of the other elements in the HEA.18,23 Thus, the degree of orbital overlap with neighboring atoms increases with the increase of Cr atoms. On contrary, the shrinking of the 3d orbitals is most significant for Ni atoms,18,23 and leads to the decrease in the vacancy formation energy with the number of Ni atoms in the 1-NN. Statically, vacancies occur more easily for those with lower formation energy, and the vacancies with mean formation energy occurs more frequently. In fact, the mean vacancy formation energy is only an artificial value, which is generated by removing the atom from the constructed supercells in the HEA. It should be noted that thermodynamically, vacancies occur more easily and frequently for those with the lowest vacancy formation energies.
3.3. Interstitial formation energy
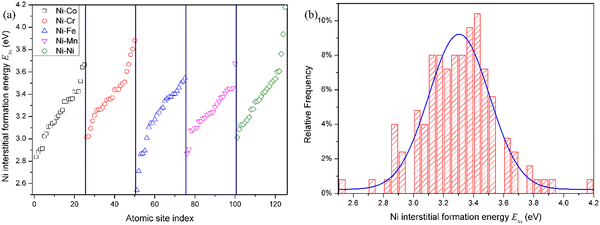
In pure fcc Ni, among six possible interstitial configurations: octahedral, tetrahedral, and crowdion, as well as [100], [110] and [111] dumbbells, it can be found that the [100] dumbbell has the lowest formation energy. Thus, the [100] dumbbell is the most stable interstitial defect configuration.15 Therefore, the interstitial formation energy in the fcc CoCrFeMnNi HEA was also calculated in the form of the [100] dumbbell. All the possible configurations in the form of the [100] dumbbell for the Co, Cr, Fe, Mn and Ni interstitials were considered, i.e., Co–Co, Co–Cr, Co–Fe, Co–Mn and Co–Ni [100] dumbbells for the Co interstitial, Cr–Co, Cr–Cr, Cr–Fe, Cr–Mn and Cr–Ni [100] dumbbells for the Cr interstitial, Fe–Co, Fe–Cr, Fe–Fe, Fe–Mn and Fe–Ni [100] dumbbells for the Fe interstitial, Mn–Co, Mn–Cr, Mn–Fe, Mn–Mn and Mn–Ni [100] dumbbells for the Mn interstitial, as well as Ni–Co, Ni–Cr, Ni–Fe, Ni–Mn and Ni–Ni [100] dumbbells for the Ni interstitial, respectively, in fcc CoCrFeMnNi HEA.For clarity, the Ni interstitial formation energy for the Ni–Co, Ni–Cr, Ni–Fe, Ni–Mn and Ni–Ni [100] dumbbells is presented in Fig. 3, while the other X (Co, Cr, Fe and Mn) interstitial formation energies for the X–Co, X–Cr, X–Fe, X–Mn and X–Ni [100] dumbbells in fcc CoCrFeMnNi HEA are presented in Fig. S1–S4 in the (ESI†). The range of Ni interstitial formation energies for the Ni–Co, Ni–Cr, Ni–Fe, Ni–Mn and Ni–Ni [100] dumbbells is from 2.84 to 3.66 eV, 3.01 to 3.88 eV, 2.54 to 3.54 eV, 2.87 to 3.68 eV and 3.01 to 4.18 eV, respectively, as shown in Table 3, and those of other X interstitial formations are also presented in Table 3. It can be seen that different [100] dumbbells produce different ranges of interstitial formation energy for different X (Co, Cr, Fe, Mn and Ni) interstitials. The distribution of interstitial formation energy mainly originates from the local atomic environment around the interstitial defect. Moreover, the range of interstitial formation energy is larger than that of the vacancy formation energy. This is due to the fact that the variation of distortion induced by the interstitial is larger than that induced by vacancy.
| Interstitial | X–Co | X–Cr | X–Fe | X–Mn | X–Ni |
|---|---|---|---|---|---|
| Co | 2.87–3.79 | 2.95–3.79 | 2.62–3.62 | 2.83–3.52 | 2.99–3.81 |
| Cr | 2.73–3.66 | 2.68–3.82 | 2.48–3.99 | 2.69–3.94 | 2.74–4.05 |
| Fe | 2.86–3.79 | 2.95–3.81 | 2.65–3.83 | 2.76–3.84 | 2.99–3.72 |
| Mn | 2.78–3.84 | 2.81–4.14 | 2.70–3.78 | 2.82–3.88 | 2.92–3.85 |
| Ni | 2.84–3.66 | 3.01–3.88 | 2.54–3.54 | 2.87–3.68 | 3.01–4.18 |
From Gaussian fit, irrespective of the [100] dumbbell type, the mean interstitial formation energies are 3.31 eV, 3.30 eV, 3.26 eV, 3.26 eV and 3.30 eV for the Co, Cr, Fe, Mn and Ni interstitials, respectively, as shown in Table 4, which are smaller than that in pure Ni of 4.38 eV. That the difference in the mean interstitial formation energy is very small shows that there is no obvious relation between the interstitial formation energy and interstitial species added by different elements. Moreover, the interstitial formation energies for many dumbbell-specific species do not follow a Gaussian distribution. In summary, the interstitial formation energy in fcc CoCrFeMnNi HEA is smaller than its counterpart in pure Ni, while the vacancy formation energy in fcc CoCrFeMnNi HEA is larger than that in pure Ni. Accordingly, it is easier for interstitial formation in fcc CoCrFeMnNi HEA than that in pure Ni, while it is the opposite for vacancy formation. Since the production of a vacancy is easier than that of an interstitial in the same material, it is more difficult to produce point defects in fcc CoCrFeMnNi HEA than pure Ni. Hence, fcc CoCrFeMnNi is more resistant to radiation damage.
| Interstitial | X-interstitial | X–Co | X–Cr | X–Fe | X–Mn | X–Ni |
|---|---|---|---|---|---|---|
| Co | 3.31 ± 0.21 | — | 3.44 ± 0.20 | — | — | 3.41 ± 0.14 |
| Cr | 3.30 ± 0.31 | 3.26 ± 0.18 | — | 3.22 ± 0.20 | — | 3.41 ± 0.33 |
| Fe | 3.26 ± 0.23 | 3.25 ± 0.12 | — | 3.12 ± 0.03 | 3.20 ± 0.09 | — |
| Mn | 3.26 ± 0.32 | — | — | 3.18 ± 0.08 | — | 3.42 ± 0.08 |
| Ni | 3.30 ± 0.20 | — | 3.35 ± 0.09 | — | — | — |
| Int in Ni | 4.38 |
The influence of the local atomic environment on the interstitial formation energy in fcc CoCrFeMnNi HEA was also analyzed following the analytic method for the vacancy formation energy. The evolution of the Ni interstitial formation energy with the number of X (Co, Cr, Fe, Mn and Ni) atoms in the 1-NN in fcc CoCrFeMnNi HEA is presented in Fig. 4. It can be found that there is no distinct relation between the Ni interstitial formation energy and the number of Co, Fe and Ni atoms in the 1-NN, while the Ni interstitial formation energy increases with the number of Cr atoms in the 1-NN and decreases with the number of Mn atoms in the 1-NN. For the Co, Cr, Fe and Mn interstitial, the dependence of the interstitial formation energy on the number of X (Co, Cr, Fe, Mn and Ni) atoms in the 1-NN was also studied, as shown in Fig. S5–S8 (ESI†). The dependence of the Co, Cr, Fe, Mn and Ni interstitial formation energy on the number of X (Co, Cr, Fe, Mn and Ni) atoms in the 1-NN is summarized in Table 5. It can be found there is a distinct relationship between the interstitial-specific formation energy and the number of X atoms in the 1-NN. Meanwhile, irrespective of the interstitial species, there is no obvious trend of the dependence of the interstitial formation energy on the local atomic environment due to the different pronounced lattice relaxations induced by the introduction of different X interstitials compared with the vacancy. The interstitial formation energy is also weakly dependent on the composition, and strongly dependent on the local atomic environment as vacancy formation energy.
| Interstitial | Co in 1-NN | Cr in 1-NN | Fe in 1-NN | Mn in 1-NN | Ni in 1-NN |
|---|---|---|---|---|---|
| Note: +: X-interstitial formation energy increases with the number of X′ atoms in 1-NN; −: X-interstitial formation energy decreases with the number of X′ atoms in 1-NN; NA: there is no obvious dependence of the X-interstitial formation energy on the number of X′ atoms in 1-NN. | |||||
| Co | + | − | − | − | + |
| Cr | − | + | − | NA | − |
| Fe | + | + | + | − | NA |
| Mn | NA | + | NA | − | + |
| Ni | NA | + | NA | − | NA |
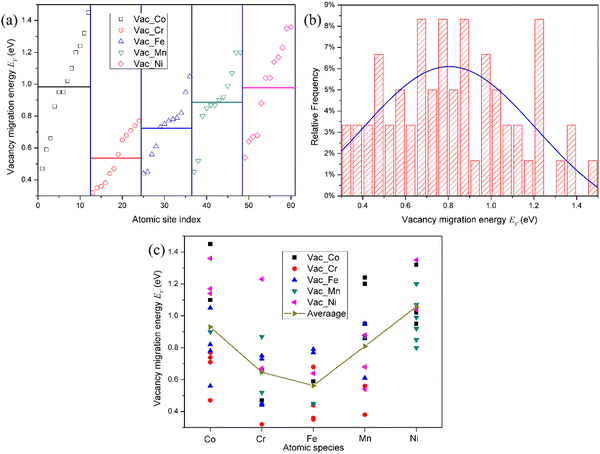
3.4. Vacancy migration energy
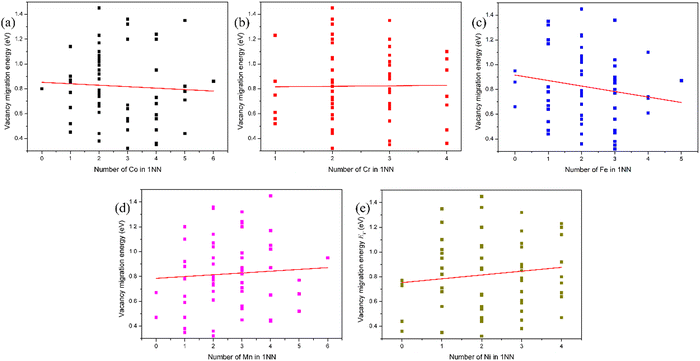
The migration barrier is an important parameter in atomic transport properties. Due to the complexity of the interstitial migration mechanism in the HEAs, it is difficult to calculate the interstitial migration energy in the fcc CoCrFeMnNi HEA. Accordingly, only the vacancy migration energy in the fcc CoCrFeMnNi HEA was studied in this work. The diffusion of vacancies is considered by directly exchanging a lattice atom between two first nearest neighbor sites. In the ref. 18 and 35, the vacancy migration barriers were calculated by directly optimizing the saddle-point structures located at the midpoints of the corresponding diffusion paths. However, due to the complicated local atomic environments around the vacancy site and the lattice atom exchange with vacancy, the saddle-point is not always located at the middle point of the diffusion path. Consequently, the vacancy migration energies were calculated using the CI-NEB method with one image, which was tested enough to get an accurate vacancy migration energy in pure Ni, as shown in Fig. S9 (ESI†). In addition, in the fcc NiFeMnCr HEA,19 the single-image NEB method provides the most efficient method to calculate the vacancy migration energy.Due to the limitation of computational resources, the migration energy of vacancy near the mean vacancy formation energy for the element-specific vacancy was calculated. The vacancy migration energy for the representative of each chemical species in fcc CoCrFeMnNi HEA is presented in Fig. 5. It can be found that due to chemical disorder, the vacancy migration barriers also exhibit distributions in the HEA. It can be seen that the average values of the vacancy migration energies in the HEA follow the order: Cr < Fe < Mn < Ni < Co, which are lower than that in pure Ni of 1.09 eV. This order corresponds to the experimentally observed order of atoms for individual constituent elements: Ni < Co < Fe < Cr < Mn,38i.e., the lower the diffusivity, the larger the value of the migration energy. It should be noted that there is no obvious dependence of the average vacancy migration energy on the atomic number for each element, i.e., it does not follow that the vacancy migration energy increases with the atomic number, as shown in the ref. 23. Actually, the vacancy migration energy decreases with the atomic radius. Furthermore, irrespective of the vacancy species, from the Gaussian fit, the mean vacancy migration energy is about 0.8 eV, which is also lower than that in pure Ni. Accordingly, the migration energy of the vacancy and interstitial will overlap with each other, which can enhance the recombination of defects in the HEA, thereby improving the irradiation resistance. It can be reasonably speculated that the lattice distortion from the chemical disorder facilitates the vacancy migration. Moreover, the order of chemical species which exchanges with the vacancy is as follows: Co < Ni < Mn < Cr < Fe, as seen from Fig. 5(c), in excellent agreement with the atomic radius of Ni < Co < Mn < Fe < Cr. Therefore, Fe and Cr atoms prefer to exchange with the vacancy to help the vacancy migration. It is worth noting that the order of the chemical species for the vacancy exchange seems to not strictly correspond with the average values of the vacancy migration energies. However, from Fig. 5(c), the difference in the migration energy that the vacancy exchanges with Cr and Fe is very small. Therefore, we can consider that the order of the chemical species for the vacancy to exchange and the average values of the vacancy migration energies remain consistent.
The lattice distortion induced by the random arrangement of different species in the HEAs significantly modifies the diffusion kinetics due to different displacements at different atomic species sites. As a result, the diffusion barrier is dependent on the local atomic environment around the vacancy site and that around the chemical species which exchanges with vacancy. The evolution of the vacancy migration energy with the number of X atoms in the first nearest neighbor (1-NN) of the chemical species that exchanges with the vacancy in fcc CoCrFeMnNi HEA is presented in Fig. 6. It can be found that the vacancy migration energy increases with the number of Mn and Ni atoms, and decreases with the number of Co and Fe atoms in the 1-NN of the chemical species which exchanges with vacancy in fcc CoCrFeMnNi HEA. In other words, the local atomic environment of Mn and Ni atoms of the chemical species that exchanges with the vacancy suppresses the vacancy migration, and that of Co and Fe atoms facilitates vacancy migration. The vacancy migration energy is dependent on not only the vacancy species and its local atomic environment, but also on the chemical species which exchanges with the vacancy and its local atomic environment. The decrease of the vacancy migration energy will significantly enhance the recombination of vacancies and interstitials, and contribute to the defect annihilation, making the HEAs more irradiation-resistant. Due to the limitation of the local atomic environment, the number of data points is very small in the calculation. As a result, it seems that the fitted lines in Fig. 2, 4 and 6 do not align well with the data points. It should be noted that in fact, the lines in Fig. 2, 4 and 6 are fitted in the term of the least squares method.
4. Conclusion
First-principles calculations have been performed to investigate the defect energetics in fcc CoCrFeMnNi HEA to obtain the formation energies of vacancies and interstitials, as well as the migration energies of the vacancies based on the SQS approach. The chemical potentials of constituent elements in HEAs are back-derived in a self-consistent manner based on a statistical approach, and the chemical potentials are more accurate and precise without additional computational cost and the associated uncertainty.The defect formation energy takes on a wide distribution due to chemical disorder induced by the random arrangement of constituent elements in fcc CoCrFeMnNi HEA. The defect formation energy is strongly dependent on the local atomic environment, and weakly dependent on the chemical composition. Moreover, vacancies prefer the Cr- and Mn-deficient, as well as Ni-rich local atomic environment. There is a distinct relationship between the interstitial-specific formation energy and the number of X atoms in the 1-NN, while irrespective of interstitial species, there is no obvious dependence of the interstitial formation energy and local atomic environment. The interstitial formation energy in fcc CoCrFeMnNi HEA is smaller than that of its counterpart in pure Ni, while the vacancy formation energy in fcc CoCrFeMnNi HEA is larger than that in pure Ni. This demonstrates that it is more difficult to produce point defects in fcc CoCrFeMnNi HEA than pure Ni. Hence, fcc CoCrFeMnNi is more resistant to radiation damage. The vacancy migration energy also exhibits distributions in fcc CoCrFeMnNi HEA, and its average values follow the order: Cr < Fe < Mn < Ni < Co, which is lower than that in pure Ni. Moreover, Fe and Cr atoms in the 1-NN around vacancy prefer to exchange with the vacancy to help the vacancy migration. The local atomic environment of Mn and Ni atoms of the chemical species that exchanges with the vacancy suppresses the vacancy migration, and that of Co and Fe atom facilitates vacancy migration.
The results of this work can certainly improve our understanding of their enhanced irradiation resistance of HEAs, and provide guidance for the design of advanced radiation-tolerant HEAs. Recently, some ref. 39 and 40 pointed out that the defect formation energy is dependent on not only the 1-NN composition, but also equally the arrangement of 1-NN atoms around the defect in concentrated solid solution alloys. In the future, the effect of the arrangement of 1-NN atoms around the defect on the defect formation energy in fcc CoCrFeMnNi HEA will be studied using machine learning based on the dataset of the first-principles results of the defect formation energy.
Author contributions
Chan Gao – conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review & editing. Shuyu Wang & Xiao Liu – validation, formal analysis, writing – review & editing. Chandra Veer Singh – software, resources, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Chan Gao and Xiao Liu thank the National Natural Science Foundation of China (No. U20B2010, 11675154), National Key Research and Development Program of China (No. 2022YFB1902504) and the Chinese Scholarship Council (CSC) for supporting this work. Chandra Veer Singh acknowledges financial support from the Nature Science and Engineer Research Council of Canada (NSERC), Hart Professorship and the University of Toronto. We also acknowledge Compute Canada for providing computing resources at the SciNet.References
- S. J. Zinkle and L. L. Snead, Designing Radiation Resistance in Materials for Fusion Energy, Annu. Rev. Mater. Res., 2014, 44, 241–267 CrossRef CAS.
- G. S. Was, D. Petti, S. Ukai and S. Zinkle, Materials for future nuclear energy systems, J. Nucl. Mater., 2019, 527, 151837 CrossRef CAS.
- M. R. Gilbert, K. Arakawa, Z. Bergstrom, M. J. Caturla, S. L. Dudarev, F. Gao, A. M. Goryaeva, S. Y. Hu, X. Hu, R. J. Kurtz, A. Litnovsky, J. Marian, M. C. Marinica, E. Martinez, E. A. Marquis, D. R. Mason, B. N. Nguyen, P. Olsson, Y. Osetskiy, D. Senor, W. Setyawan, M. P. Short, T. Suzudo, J. R. Trelewicz, T. Tsuru, G. S. Was, B. D. Wirth, L. Yang, Y. Zhang and S. J. Zinkle, Perspectives on multiscale modelling and experiments to accelerate materials development for fusion, J. Nucl. Mater., 2021, 554, 153113 CrossRef CAS.
- K. Nordlund, Historical review of computer simulation of radiation effects in materials, J. Nucl. Mater., 2019, 520, 273–295 CrossRef CAS.
- Y. F. Ye, Q. Wang, J. Lu, C. T. Liu and Y. Yang, High-entropy alloy: challenges and prospects, Mater. Today, 2016, 19, 349–362 CrossRef CAS.
- M. C. Gao and J. Qiao, High-Entropy Alloys (HEAs), Metals, 2018, 8, 108 CrossRef.
- E. P. George, D. Raabe and R. O. Ritchie, High-entropy alloys, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- B. Cantor, Multicomponent high-entropy Cantor alloys, Prog. Mater. Sci., 2021, 120, 100754 CrossRef CAS.
- E. J. Pickering, A. W. Carruthers, P. J. Barron, S. C. Middleburgh, D. E. J. Armstrong and A. S. Gandy, High-Entropy Alloys for Advanced Nuclear Applications, Entropy, 2021, 23, 98 CrossRef CAS PubMed.
- Z. Li, S. Zhao, R. O. Ritchie and M. A. Meyers, Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys, Prog. Mater. Sci., 2019, 102, 296–345 CrossRef CAS.
- E. P. George, W. A. Curtin and C. C. Tasan, High entropy alloys: A focused review of mechanical properties and deformation mechanisms, Acta Mater., 2020, 188, 435–474 CrossRef CAS.
- W. Li, D. Xie, D. Li, Y. Zhang, Y. Gao and P. K. Liaw, Mechanical behavior of high-entropy alloys, Prog. Mater. Sci., 2021, 118, 100777 CrossRef CAS.
- F. Granberg, K. Nordlund, M. W. Ullah, K. Jin, C. Lu, H. Bei, L. M. Wang, F. Djurabekova, W. J. Weber and Y. Zhang, Mechanism of Radiation Damage Reduction in Equiatomic Multicomponent Single Phase Alloys, Phys. Rev. Lett., 2016, 116, 135504 CrossRef CAS PubMed.
- Z. Zhang, D. E. J. Armstrong and P. S. Grant, The effects of irradiation on CrMnFeCoNi high-entropy alloy and its derivatives, Prog. Mater. Sci., 2022, 123, 100807 CrossRef CAS.
- S. Zhao, G. M. Stocks and Y. Zhang, Defect energetics of concentrated solid-solution alloys from ab initio calculations: Ni0.5Co0.5, Ni0.5Fe0.5, Ni0.8Fe0.2 and Ni0.8Cr0.2, Phys. Chem. Chem. Phys., 2016, 18, 24043–24056 RSC.
- S. Zhao, Y. Osetsky and Y. Zhang, Diffusion of point defects in ordered and disordered Ni–Fe alloys, J. Alloys Compd., 2019, 805, 1175–1183 CrossRef CAS.
- S. Zhao, Y. Osetsky, A. V. Barashev and Y. Zhang, Frenkel defect recombination in Ni and Ni-containing concentrated solid–solution alloys, Acta Mater., 2019, 173, 184–194 CrossRef CAS.
- S. Zhao, T. Egami, G. M. Stocks and Y. Zhang, Effect of d electrons on defect properties in equiatomic NiCoCr and NiCoFeCr concentrated solid solution alloys, Phys. Rev. Mater., 2018, 2, 013602 CrossRef CAS.
- C. Li, J. Yin, K. Odbadrakh, B. C. Sales, S. J. Zinkle, G. M. Stocks and B. D. Wirth, First principle study of magnetism and vacancy energetics in a near equimolar NiFeMnCr high entropy alloy, J. Appl. Phys., 2019, 125, 155103 CrossRef.
- W. Chen, X. Ding, Y. Feng, X. Liu, K. Liu, Z. P. Lu, D. Li, Y. Li, C. T. Liu and X.-Q. Chen, Vacancy formation enthalpies of high-entropy FeCoCrNi alloy via first-principles calculations and possible implications to its superior radiation tolerance, J. Mater. Sci. Technol., 2018, 34, 355–364 CrossRef CAS.
- H. Guan, S. Huang, J. Ding, F. Tian, Q. Xu and J. Zhao, Chemical environment and magnetic moment effects on point defect formations in CoCrNi-based concentrated solid-solution alloys, Acta Mater., 2020, 187, 122–134 CrossRef CAS.
- S. C. Middleburgh, D. M. King, G. R. Lumpkin, M. Cortie and L. Edwards, Segregation and migration of species in the CrCoFeNi high entropy alloy, J. Alloys Compd., 2014, 599, 179–182 CrossRef CAS.
- M. Mizuno, K. Sugita and H. Araki, Defect energetics for diffusion in CrMnFeCoNi high-entropy alloy from first-principles calculations, Comput. Mater. Sci., 2019, 170, 109163 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. S. Oh, D. Ma, G. P. Leyson, B. Grabowski, E. S. Park, F. Körmann and D. Raabe, Lattice Distortions in the FeCoNiCrMn High Entropy Alloy Studied by Theory and Experiment, Entropy, 2016, 18, 321 CrossRef.
- Y. Ikeda, B. Grabowski and F. Körmann, Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys, Mater. Charact., 2019, 147, 464–511 CrossRef CAS.
- A. van de Walle, P. Tiwary, M. de Jong, D. L. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L. Q. Chen and Z. K. Liu, Efficient stochastic generation of special quasirandom structures, Calphad, 2013, 42, 13–18 CrossRef CAS.
- A. van de Walle, M. Asta and G. Ceder, The alloy theoretic automated toolkit: A user guide, Calphad, 2002, 26, 539–553 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- Y. Zhang, A. Manzoor, C. Jiang, D. Aidhy and D. Schwen, A statistical approach for atomistic calculations of vacancy formation energy and chemical potentials in concentrated solid-solution alloys, Comput. Mater. Sci., 2021, 190, 110308 CrossRef CAS.
- Z. H. Aitken, V. Sorkin and Y.-W. Zhang, Atomistic modeling of nanoscale plasticity in high-entropy alloys, J. Mater. Res., 2019, 34, 1509–1532 CrossRef CAS.
- D. Hobbs, J. Hafner and D. Spišák, Understanding the complex metallic element Mn. I. Crystalline and noncollinear magnetic structure of α-Mn, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 014407 CrossRef.
- K. Sugita, N. Matsuoka, M. Mizuno and H. Araki, Vacancy formation enthalpy in CoCrFeMnNi high-entropy alloy, Scr. Mater., 2020, 176, 32–35 CrossRef CAS.
- K. Y. Tsai, M. H. Tsai and J. W. Yeh, Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys, Acta Mater., 2013, 61, 4887–4897 CrossRef CAS.
- A. Manzoor, Y. Zhang and D. S. Aidhy, Factors affecting the vacancy formation energy in Fe70Ni10Cr20 random concentrated alloy, Comput. Mater. Sci., 2021, 198, 110669 CrossRef CAS.
- A. Manzoor, G. Arora, B. Jerome, N. Linton, B. Norman and D. S. Aidhy, Machine Learning Based Methodology to Predict Point Defect Energies in Multi-Principal Element Alloys, Frontiers in, Materials, 2021, 8, 673574 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma01148h |
| This journal is © The Royal Society of Chemistry 2024 |