Open Access Article
Open Access ArticleInfluence of Cr3+ cluster defects on crystal structure and optical properties of KDP crystals studied by DFT and UV-Vis
Yang
Li
 ab,
Lisong
Zhang
*ab,
Xun
Sun
*ab,
Mingxia
Xu
ab,
Baoan
Liu
ab,
Xian
Zhao
a,
Guokai
Hao
ab,
Lisong
Zhang
*ab,
Xun
Sun
*ab,
Mingxia
Xu
ab,
Baoan
Liu
ab,
Xian
Zhao
a,
Guokai
Hao
 ab,
Jianyu
Bai
ab,
Jianyu
Bai
 ab and
Xiaojing
Lin
ab
ab and
Xiaojing
Lin
ab
aState Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China. E-mail: zhls@sdu.edu.cn; sunxun@sdu.edu.cn
bKey Laboratory of Functional Crystal Materials and Device, Ministry of Education, Shandong University, Jinan 250100, China
First published on 25th May 2024
Abstract
Cr3+ ions are impurity cations that lower the laser-induced damage threshold of crystals. Herein, the stability of Cr3+ cluster defects and their effects on crystal structure, electronic structure and optical properties were examined by DFT and UV-Vis spectroscopy. Two stabilizing CrK2+ + 2VH− cluster configurations were constructed using first-principles calculations for the point defect where Cr3+ ions are substituted for K+ ions. Cluster defects lead to large deformations in the O–H bonds of KDP crystals and introduce multiple defect states in the crystal band gap. Due to the absorption between impurity energy levels and the entire energy band, Cr3+ ions cause optical absorption in the crystal at 285 nm, 451 nm and 650 nm. Cr3+ ions cause additional energy to be absorbed during laser irradiation of the KDP crystals, which in turn adversely affects the laser-induced damage threshold of the crystal. Our data indicate that the laser-induced damage threshold of the KDP crystals can be increased by decreasing the concentration of the cluster defects in the KDP crystals.
1. Introduction
Potassium dihydrogen phosphate (KDP) crystals are in tetragonal form at room temperature. The point group of the KDP crystals is D2d-![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m, and the space group is D122d-I
2m, and the space group is D122d-I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d.1 Due to the high laser-induced damage threshold and ease with which they are grown into large-aperture single crystals, KDP and its isomorphs are the only nonlinear optical crystals that can be used in inertial confinement fusion (ICF) laser systems.2–5 In practical applications, the laser-induced damage threshold of a KDP crystal is far below its theoretical value by an order of magnitude, and the damage is severe during UV laser irradiation, which reduces the energy of the output laser and lifetime of upstream and downstream components.6,7
2d.1 Due to the high laser-induced damage threshold and ease with which they are grown into large-aperture single crystals, KDP and its isomorphs are the only nonlinear optical crystals that can be used in inertial confinement fusion (ICF) laser systems.2–5 In practical applications, the laser-induced damage threshold of a KDP crystal is far below its theoretical value by an order of magnitude, and the damage is severe during UV laser irradiation, which reduces the energy of the output laser and lifetime of upstream and downstream components.6,7
Experimental and theoretical studies have shown that impurity ions are one of the main reasons for the decrease in the laser-induced damage threshold of the KDP crystals.8–10 Cr3+ ions are common high-valence cations in crystals. It was previously shown that 30 ppm and 50 ppm Cr3+ doping resulted in no significant effect on the transmittance of KDP in the infrared band, but the transmittance in ultraviolet and visible ranges was reduced to a certain extent.11 Cr3+ ions are tentatively characterized by electron resonance spectroscopy to substitute for K+ ions in KDP crystals.12,13 However, the charge state of point defects and compounding of point defects with intrinsic defects have not been explicitly studied. It is experimentally difficult to further develop this type of study at the atomic level.
First-principles calculations are an effective means of studying defects at the atomic level in the KDP crystals. It was found that the [010] screw dislocation increases the total system energy and narrows the band gap of the KDP crystals.14 Single water molecule adsorption on the (100) and (101) surfaces of the KDP crystals was also studied by density functional theory (DFT).15 It was found that Fe3+ ions increase the linear optical absorption of the KDP crystals, which in turn adversely affects the laser-induced damage threshold of the KDP crystals.16,17 It is found that for KDP crystals containing Mg ions, DFT indicated that the absorption peak locates at 4.37 eV (284 nm) in PE-KDP, and the absorption peak locates at 4.66 eV (266 nm) in FE-KDP, by DFT.18 A large lattice distortion (9.26–22.33%) in H–O bonds induced by BaK defects was found in paraelectric phase KDP crystals.19 The linear absorption spectra indicate that the presence of Al3+ ions minimally impacts the linear absorption of the KDP crystals.20 The influence of the Zn2+ ion and its cluster defects on the KDP crystals was also studied by DFT, and it is found that with increasing Zn2+ concentration, the crystal structure becomes unstable, which will affect the optical properties.21
To understand the mechanism of action of Cr3+ ions, in this study, the cluster defects composed of Cr3+ ions and hydrogen vacancies were introduced by DFT. The influence of the cluster defects on the structural and electronic properties was also determined. In addition, Cr3+ ion-doped KDP crystals were characterized by UV-Vis spectroscopy, and absorption peaks in the spectra were analyzed. It is beneficial to understand the mechanism of the cluster defects consisting of Cr3+ ions and intrinsic hydrogen vacancies affecting the laser-induced damage threshold of the KDP crystals.
2. Computational details
The Vienna ab initio simulation package (VASP)22,23 based on first-principles calculations was applied in this manuscript. The electron exchange and correlation (XC) functional of the general gradient approximation (GGA)24–27 of the Perdew–Burke–Ernzerhof (PBE) function28,29 was adopted for the exchange–correlation potential to optimize the crystal structure. Monkhorst–Pack k-point meshes of 1 × 1 × 117,21,30 were used for the calculations. The force convergence criterion for structural relaxation was set to 0.01 eV Å−1.17,31 The electronic wave functions were expanded as plane waves using an energy cutoff of 680 eV.32–35In our previous study, the Heyd–Scuseria–Ernzerhof (HSE06)36–38 hybrid functional method was more suitable for calculating the electronic properties of the KDP crystals because the band gap obtained using this calculation method (7.2 eV17,21) was similar to the experimental value (∼7.6 eV39).31,40 Therefore, the energetic, electronic and optical properties were analyzed using the HSE06 method. The H 1s1, P 3s23p3, O 2s22p4, K 4s1 and Cr 3d5 4s1 states were treated as valence electrons.
The lattice constants of the unit cell are a = b = 7.50 Å and c = 6.96 Å, and experimental values are a = b = 7.45 Å and c = 6.79 Å.41–43 Calculated values are in satisfactory agreement with the experimental values. Tetragonal supercells with 256 atoms (32 KDP molecules) were used to model defect structures. The Cr3+ ion defect model was constructed by replacing a K atom with a Cr atom in the KDP supercell. The concentration of the point defect was 0.39%, and charge state point defects were obtained by removing one or two electrons in the system. All parameters used in this study were obtained by performing convergence tests.
The formation energies of the defects with the charge state q dependent on the Fermi level position are defined as:44–46
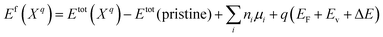 | (1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and K2O with Fm
c and K2O with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space groups through:
m space groups through: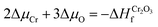 | (2) |
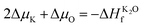 | (3) |
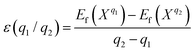 | (4) |
3. Results and discussion
3.1. Stability of the cluster defects in the KDP crystal
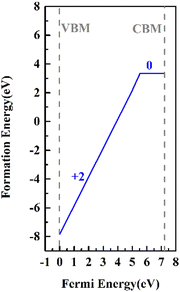
In our previous studies, it was clarified by electron paramagnetic resonance spectroscopy and DFT that Cr3+ ions mainly replace K+ ions in the KDP crystals (the defect formation energy of Cr3+ that replaces K+ is 3.31 eV).12 In electron paramagnetic resonance spectra, there were two sets of resonance peaks for Cr3+, which were caused by the different relative positions of hydrogen vacancies near Cr3+. To further clarify the charge state of the point defects and build a reasonable cluster defect model, the defect formation energies of the point defects with different charge states were calculated. The formation energies of the defects in charged states are a function of the Fermi energy level and were calculated by eqn (1). The results are shown in Fig. 1.The thermodynamic transition level was calculated by eqn (4) (due to the instability of the +1 state, it is not shown in Fig. 1). As the Fermi level at the VBM, the point defect stabilizes as CrK2+. When the Fermi level moves up to the position of about 5.6 eV, the defect traps two electrons and stabilizes as CrK0. From the VBM to the CBM range of the KDP crystals, CrK+ is unstable. At low defect concentrations, the Fermi level of the KDP crystals is located at the center of the bandgap, and therefore, in the KDP crystals with low concentrations of defects, Cr3+ ions stably exist in the crystals as CrK2+ point defects.
Considering charge compensation to maintain the electric neutrality of the crystal, the generation of CrK2+ was accompanied by hydrogen vacancies or potassium vacancies. By studying the EPR spectra of Cr3+-doped KDP crystals, the CrK2+ point defects mainly complex with H vacancies.13,47 There are two sets of electronic paramagnetic resonance peaks of Cr3+ in the EPR spectra of the Cr3+-doped KDP crystals. This is mainly due to the different relative positions of the hydrogen vacancies complexed with Cr3+.12,13 By analyzing the stability of the cluster defects in the KDP crystals, the most stable defect clusters are formed by complexing with the nearest neighboring hydrogen vacancies.17,31 Therefore, neighboring hydrogen atoms are removed to form the CrK2+ + 2VH− cluster defect.
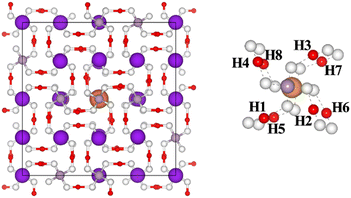
There are eight nearest neighbor H atoms around the CrK2+ point defect. Fig. 2 shows the top view of the CrK2+ point defect system (after performing structural optimization) along the z-axis. Purple, gray, white, red, and orange balls in the figure represent potassium, phosphorus, oxygen, hydrogen, and chromium atoms, respectively. To build two stable cluster defect models for Cr3+ in the KDP crystals, defect formation energies of the clusters formed by CrK2+ with the hydrogen vacancies at H1H2, H1H3, H1H4…H1H8 positions were separately calculated, as shown in Fig. 2. The formation energies of the cluster defects were calculated using eqn (1). It should be noted that the defect clusters with low formation energies are thermodynamically more stable.
Table 1 shows the formation energies of CrK2+ + 2VH− cluster defects. Different combinatorial configurations of CrK2+ with the nearest eight neighboring hydrogen vacancies were calculated, and it was determined that the change in the positions of the eight hydrogen vacancies had a minor effect on the stability of the CrK2+ + 2VH− cluster defects. The lowest defect formation energy (5.34 eV) was measured for the cluster defects consisting of the hydrogen vacancies at H1 and H8 (H1 (0.35968 0.41425 0.90441), H8 (0.41425 0.64032 0.59559)) sites, and the CrK2+ point defects, and therefore, this defect configuration was the most thermodynamically stable. The notation CrK2+ + 2VH− (1) is used in the section following the manuscript to notate the defect configuration consisting of the hydrogen vacancies at the H1 and H8 sites and CrK2+ point defect. The defect formation energy of CrK2+ + 2VH− (2) is 5.40 eV, and therefore, it is thermodynamically second only to CrK2+ + 2VH− (1) in stability.
| Position of hydrogen vacancies | Formation energies (eV) |
|---|---|
| H1H2 | 5.76 |
| H1H3 | 5.58 |
| H1H4 | 5.64 |
| H1H5 | 5.77 |
| H1H6 | 5.44 |
| H1H7 | 5.40 |
| H1H8 | 5.34 |
3.2. Structure of cluster defects in the KDP crystals
The cluster defects composed of Cr3+ complexed with the hydrogen vacancies are large in size, and therefore, their influence on the chemical bonding in the crystal should not be neglected. The deformation of O–H and P–O bonds are calculated as follows: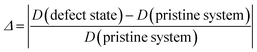 | (5) |
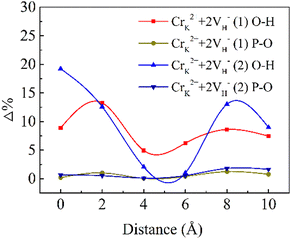
The D (defect state) represents the bond lengths in defective systems, and D (pristine system) represents the bond lengths in the pristine system. Δ denotes the absolute value of the deformation. Fig. 3 shows the deformation of the P–O bonds and O–H bonds.
For the CrK2+ + 2VH− (1) cluster, the O–H bonds around the defect center are extended by 8.9%, and the P–O bonds are shortened by 0.2%. For the CrK2+ + 2VH− (2) cluster, the deformation of the O–H bonds is 19.2% and that of the P–O bonds are 0.7%. At the defect center, the deformation induced by the CrK2+ + 2VH− (2) cluster is larger than that induced by CrK2+ + 2VH− (1). The CrK2+ + 2VH− (2) cluster leads to greater lattice relaxation of surrounding atoms compared to CrK2+ + 2VH− (1), which may lead to decreased stability of the CrK2+ + 2VH− (2) cluster. After relaxation in the crystal, at 10 Å from the defect center, the deformation induced by CrK2+ + 2VH− (2) is larger than that induced by CrK2+ + 2VH− (1).
Compared with the O–H bonds, the deformation of the P–O bonds is small. Cr3+ ion cluster defects mainly lead to large deformations of the O–H bonds in the KDP crystals. In the KDP crystals, the O–H bond serves to connect the nonlinear primitive phosphorus-oxygen tetrahedral skeleton of the crystal. As the concentration of Cr3+ ions increases, additional defect clusters will be formed, which can lead to the deformation of additional O–H bonds linked to PO4 in the KDP crystals. The accumulation of distortions at this connection with increasing defect concentration leads to a decrease in the stability of the crystal structure, and the structural instability could be rapidly enhanced by increasing the defect concentration. The Cr3+ cluster defects adversely affect the structural stability of the KDP crystals. When the concentration of Cr3+ ions in the crystal is high, the concentration of cluster defects may be subsequently increased, and the structural stability of the crystal decreases, which will adversely affect the laser-induced damage threshold of the KDP crystals.
3.3. Electronic and optical properties of the cluster defects in the KDP crystals
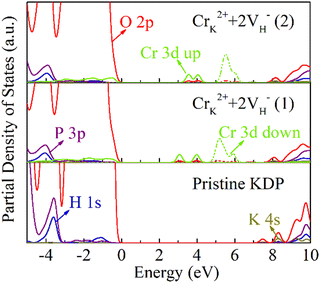
Hydrogen vacancies affect the electronic structure of the crystals.30 A hydrogen vacancy could introduce a defect state at 0.8 eV, and the defect state is composed of the electronic states of adjacent O atoms. The position of the defect state shifts to the CBM at 1.8 eV, as the concentration of the hydrogen vacancies increases to 0.78% (2VH).28 Cr3+ ions are high-valent impurities whose 3d orbital electrons are active. The cluster defects consisting of CrK2+ and the hydrogen vacancies may induce large effects on the electronic structure of the crystal, and thus affect the optical properties of the crystal.To clarify the effect of the Cr3+ cluster defects on the electronic structure of the KDP crystals, the partial density of states (PDOS) were calculated, as shown in Fig. 4. The band gap of pristine KDP is 7.2 eV. The impurity states at 2.8 eV, 3.6 eV and 4.7 eV were induced by the CrK2+ + 2VH− (1) cluster. The impurity states at 2.8 eV and 3.6 eV are mainly composed of Cr 3d spin-up states and O 2p states, and the impurity states at 4.7 eV are mainly composed of the Cr 3d spin-down states and O 2p states. For the CrK2+ + 2VH− (2) cluster, there are impurity states at 3.1 eV and 4.9 eV. The impurity states at 3.1 eV are mainly composed of the Cr 3d spin-up states and O 2p states. The impurity states at 4.9 eV are mainly composed of the Cr 3d spin-down states and O 2p states.
In the band gap of the KDP crystals, the impurity states induced by the CrK2+ + 2VH− (1) cluster and CrK2+ + 2VH− (2) cluster are slightly different. This is due to the slightly different charge transfer between the different hydrogen vacancies and oxygen atom, which in turn leads to different interactions between the O 2p states and the Cr 3d states, as shown in Fig. 5. Through the calculation of the electronic structure of the KDP crystals, it was determined that the Cr3+ cluster defects induce impurity states in the crystal band gap. These impurity states may cause multiphoton absorption in the KDP crystal under a 355-nm laser, resulting in decreasing the laser-induced damage threshold of the KDP crystals.
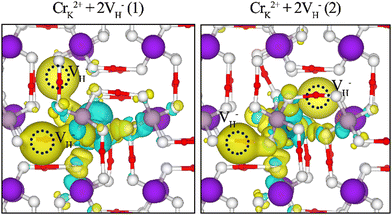 | ||
| Fig. 5 Electronic charge differences of CrK2+ + 2VH− cluster defects in the KDP crystals. Blue and yellow regions represent electron depletion and accumulation, respectively. | ||
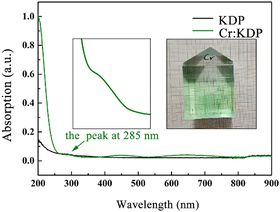
Cr3+ leads to the creation of multiple impurity states in the KDP crystals, which may result in multiple optical absorption peaks in the crystals through the jumping of free electrons in the crystals. To characterize the optical properties of the Cr3+-doped KDP crystals, we used an UV-visible spectrophotometer to measure in the 200–900 nm band in the absorption spectra of undoped KDP crystals and KDP crystals doped with 10 ppm Cr3+ ions samples used in this study were propagated by a rapid growth technique.48–50
Raw high-purity potassium dihydrogen phosphate and deionized water were mixed according to a solubility curve to form a KDP crystal growth solution with a saturation temperature of 55.5 °C, which was configured in a 5000-mL glass volumetric flask. A pre-prepared growth rack with seed crystals was placed into the filtered growth solution, and the solution was superheated at 70 °C for 48 h to maintain solution stability. After superheating, the solution was slowly cooled to 58.0 °C (2.5 °C above the saturation point), and then, the seed crystal protection device (a silica gel sleeve) in the growth rack was removed, and the solution was slowly cooled to 55.0 °C (0.5 °C below the saturation point) at a constant temperature for more than 48 h, at which time, the crystals entered into the spontaneous recovery phase of growth.
According to the solubility curve of the KDP crystals, the temperature reduction program was set to control the amount of precipitated crystals in the growth solution per unit temperature, and then, the rapid growth of the crystals was carried out. The temperature of the growth bath was controlled by FP23 with an accuracy of ±0.01 °C. To ensure the stability of the solution during the growth process, the crystal rotator frame was periodically rotated at 77 rpm, and the growth solution was withdrawn from the growth bath after the growth was completed. According to the solubility curve of the KDP crystals, the temperature reduction program was set to control the amount of precipitated crystals in the growth solution per unit temperature. The Cr3+-doped KDP crystals were produced by doping the overheated solution with 10 ppm CrCl3 with 99.99% metal basis purity. The doped crystals are shown in Fig. 6. The grown crystals were cut into 1 cm × 1 cm × 0.5 cm wafers along the z-direction to characterize their UV-visible absorption spectra.
The linear absorption of a crystal is one of the most important indicators for determining its optical performance, and a high linear absorption affects the output power of the laser. The higher the energy absorbed by the crystal, the more prone it is to laser-induced damage. There were three absorption peaks induced by the CrK2+ defect: at 285 nm, 451 nm and 650 nm. There were two spin-allowed transitions, 4A2g(F) → 4T1g(F) for 451 nm and 4A2g(F) → 4T2g(F) for 650 nm, which were researched in our previous study.12 From the calculation of the electronic structure (Fig. 4), the absorption peak at 285 nm was induced by electrons jumping toward the conduction band from the energy level of the donor impurity (which may be induced by Cr 3d spin-down electron states).
Ding et al. reported the laser-induced damage threshold of the crystals doped with 0–50 ppm Cr3+. Table 2 shows the damage thresholds of the KDP crystals doped with different concentrations of Cr3+. The damage thresholds of the crystals under triple-frequency pulsed laser irradiation showed a decreasing trend with increasing doping concentration of Cr3+ ions.11 Under 355-nm laser irradiation, the impurity states introduced by the Cr3+ cluster defects in the band gap of the crystals adversely affect the laser-induced damage threshold of the crystals through the physical mechanism of defect-assisted multiphoton absorption.29,30 However, Cr3+ ions cause additional optical absorption in the KDP crystals, which leads to an increase in the energy absorbed by crystal elements at high laser power, and this in turn adversely affects the laser-induced damage threshold of the crystal. According to EPR spectra and DFT calculations, such defect clusters can be stabilised in the KDP crystals. In practical applications, Cr3+ leads to a lower laser-induced damage threshold in the KDP crystals. The damage is severe during UV laser irradiation, and this reduces the energy of the output laser and lifetime of the upstream and downstream components and becomes a bottleneck for the further development of ICF engineering.
| Cr3+ concentration/10−6 | 0 | 10 | 20 | 30 | 40 | 50 |
| In prismatic sector/(J cm−2, 7.5 ns) | 3.97 | 3.81 | 3.39 | 3.35 | 3.44 | 3.21 |
Ionizing radiation such as X-rays or UV lasers may ‘‘passivate’’ damage-initiating defects by providing electrons that may alter the electronic structure of Cr3+ defects, thus causing them to absorb less or become non-absorbent at the operating laser frequency. Therefore, laser annealing could be applied to eliminate the effect of these cluster defects on the optical performance of the KDP crystals.
4. Conclusions
In conclusion, the stability, structure, electronic properties, and optical absorption of the Cr3+ cluster defects for the KDP crystal were investigated by DFT and UV-Vis spectroscopy. The two most stable cluster defect configurations were constructed. CrK2+ + 2VH− cluster defects cause larger distortions to the O–H bonds of the KDP crystals. Higher concentrations of the defects lead to a decrease in the structural stability of the crystals. There are three defect states caused by the CrK2+ + 2VH− (1) cluster defect at 2.8 eV, 3.6 eV and 4.7 eV and are mainly composed of the Cr 3d states and O 2p states. Two defect states were induced by the CrK2+ + 2VH− (2) cluster defect at 3.1 eV and 4.9 eV. There were three absorption peaks at 285 nm, 451 nm, and 680 nm induced by Cr3+ ions. The peak at 285 nm was induced by electrons jumping toward the conduction band from the energy level of the donor impurity. It can be concluded that CrK2+ + 2VH− cluster defects can have a large adverse effect on the electronic structure and optical properties of the crystals. During crystal growth and post-processing, the concentration of the CrK2+ + 2VH− cluster defect should be reduced.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Taishan Scholars Program of Shandong Province (No. tstp20231207).Notes and references
- L. N. Rashkovich and O. Shlakhova, KDP-Family Single Crystals, CRC Press, 2021 Search PubMed.
- D. N. Nikogosyan, Nonlinear Optical Crystals: A Complete Survey, Springer Science & Business Media, 2006 Search PubMed.
- R. Hawley-Fedder, P. Geraghty, S. Locke, M. McBurney, M. Runkel, T. Suratwala, S. Thompson, P. Wegner and P. Whitman, Proc. SPIE 5341-Optical Engineering at the Lawrence Livermore National Laboratory II, The National Ignition Facility, 2004, vol. 5341, pp. 84–101.
- W. Han, Y. Xiang, F. Li, F. Wang, L. Zhou, J. Zhao, B. Feng, K. Zheng, Q. Zhu and X. Wei, Appl. Opt., 2015, 54, 4167–4171 CrossRef CAS.
- L. A. Guzman, M. Suzuki, Y. Fujimoto and K. Fujioka, J. Phys.: Conf. Ser., 2016, 12024 CrossRef.
- B. C. Stuart, M. D. Feit, S. Herman, A. M. Rubenchik, B. W. Shore and M. D. Perry, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1749 CrossRef CAS PubMed.
- C. W. Carr, H. B. Radousky, A. M. Rubenchik, M. D. Feit and S. G. Demos, Phys. Rev. Lett., 2004, 92, 87401 CrossRef CAS PubMed.
- R. W. Hopper and Dr. R. Uhlmann, J. Appl. Phys., 1970, 41, 4023–4037 CrossRef CAS.
- M. D. Feit and A. M. Rubenchik, Laser-Induced Damage in Optical Materials: 2003, SPIE, 2004, pp. 74–82 Search PubMed.
- X. Sun, Y. Z. Zhang, M. X. Xu, S. T. Sun, L. L. Ji, Z. P. Wang, K. Y. Li, X. F. Cheng and X. G. Xu, J. Synth. Cryst., 2007, 36, 1240–1244 Search PubMed.
- J. X. Ding, B. Liu, S. L. Wang, X. M. Mu, Q. T. Gu, X. G. Xu, X. Sun, Y. Sun, W. J. Liu, G. X. Liu and S. J. Zhu, J. Inorg. Mater., 2011, 4, 354–358 CrossRef.
- L. Wei, L. Yang, X. Jiang, P. Wu, X. Zhao, L. Zhang, B. Liu, X. Chai, M. Xu, X. Sun and W. Hong, CrystEngComm, 2022, 24, 4948–4954 RSC.
- D. Bravo, R. Bottcher and F. J. Lopez, J. Phys.: Condens. Matter, 1992, 4, 2297–2308 CrossRef CAS.
- X. Jiang, Y. Li, L. Wei, M. Xu, L. Zhang, J. Chen and X. Sun, CrystEngComm, 2021, 23, 7412–7417 RSC.
- L. Zhang, Y. Wu, Y. Liu and H. Li, RSC Adv., 2017, 7, 2617–26178 Search PubMed.
- T. T. Sui, C. B. Wan, M. X. Xu, X. Sun, X. G. Xu and X. Ju, CrystEngComm, 2021, 23, 7839–7845 RSC.
- Y. Li, B. Liu, Y. Li, T. Sui, X. Zhao, M. Xu and X. Sun, CrystEngComm, 2022, 24, 8082–8088 RSC.
- J. Zhu, T. Liu, H. Hu and L. Zhao, Mater. Sci. Semicond. Process., 2024, 170, 107972 CrossRef CAS.
- H. Hu, W. Hong, T. Liu, L. Zhao and J. Zhu, CrystEngComm, 2023, 25, 5910 RSC.
- Y. Li, Z. Li, B. Liu, X. Sun, M. Xu, L. Zhang, X. Zhao and G. Lei, Crystals, 2024, 14, 410 CrossRef CAS.
- Y. Li, X. Jiang, P. Wu, L. Zhang, B. Liu, Y. Li, X. Zhao, X. Sun and M. Xu, Cryst. Res. Technol., 2023, 58, 202200107 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, Phys. Rev. Lett., 1985, 55, 1665–1668 CrossRef CAS PubMed.
- Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- K. Burke, M. Ernzerhof and J. P. Perdew, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- Y. Li, G. Hao, J. Bai, T. Sui, L. Wei, X. Sun, X. Zhao, M. Xu and B. Liu, CrystEngComm, 2023, 25, 2959–2965 RSC.
- C. S. Liu, N. Kioussis, S. G. Demos and H. B. Radousky, Phys. Rev. Lett., 2003, 91, 15505 CrossRef CAS PubMed.
- C. S. Liu, N. Kioussis, S. G. Demos and H. B. Radousky, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 91, 015505 CAS.
- K. Wang, C. Fang, J. Zhang, C. S. Liu and Z. Xian, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 4105 Search PubMed.
- C. S. Liu, C. J. Hou, N. Kioussis, S. G. Demos and H. B. Radousky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134110 CrossRef.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, A1133–A1357 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 8207–8215 CrossRef.
- T. M. Henderson, J. Paier and G. E. Scuseria, Phys. Status Solidi B, 2011, 248, 767–774 CrossRef CAS.
- S. O. Kucheyev, C. Bostedt, T. van Buuren, T. M. Willey, T. A. Land, L. J. Terminello, T. E. Felter, A. V. Hamza, S. G. Demos and A. J. Nelson, Electronic structure of KD2xH2(1−x)PO4 studied by soft x-ray absorption and emission spectroscopies, Phys. Rev. B, 2004, 70, 245106 CrossRef.
- X. Jiang, Y. Li, L. Wei, M. Xu, L. Zhang, J. Chen and X. Sun, CrystEngComm, 2021, 23, 7412–7417 RSC.
- Q. Zhang, F. Chen, N. Kioussis, S. G. Demos and H. B. Radousky, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 24108 CrossRef.
- S. B. Hendricks, Am. J. Sci., 1927, s5–14, 269–287 CrossRef.
- J. West, Ferroelectrics, 1987, 71, 1–9 CrossRef CAS.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- S. Lany, H. Raebiger and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 241201(R) CrossRef.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- L. E. Halliburton, Optical Science, Engineering and Instrumentation, Proceedings of SPIE, San Diego, CA, United States, 1997 Search PubMed.
- Y. Liwang, Z. Guozong and Z. Xinxin, J. Cryst. Growth, 2010, 318, 700–702 Search PubMed.
- V. P. Ereshiov, V. I. Bespalovl and V. I. Bredikhin, Sov. J. Quantum Electron., 1982, 12, 2343–2345 Search PubMed.
- J. J. De Yoreo and N. P. Zaitseva, J. Cryst. Growth, 1997, 180, 255–262 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |